Measurement of dynamic membrane mechanosensation using optical tweezers

Many cellular processes are orchestrated by dynamic changes in the plasma membrane to form membrane projections and endocytic compartments in response to extracellular cue changes. Our previous studies show that post-translational modifications of ACAP4 regulate membrane dynamics and curvature in response to epidermal growth factor and chemokine (C−C motif) ligand 18 stimulation (Zhao et al., 2013; Song et al., 2018). However, there is no quantitative measurement to annotate magnitude of dynamic membrane cytoskeletal remodeling in stimulus-elicited mechanosensation on the plasma membrane.

Stretching membrane tethers from cell surface projections are recognized as a standard method for cell surface mechanics study. Most of the studies on membrane tether focus on the minimum force required to maintain a tether (static force, f₀) and the coefficient of effective viscosity (η_eff). It is well accepted that f₀ is the measure of membrane tension and η_eff corresponds to the friction between lipid bilayer and membrane skeleton (Hochmuth et al., 1996). Currently used methods rely on stretching membrane tethers at different speeds, fit tensions and velocities into a straight line, and calculate f₀ and η_eff (Hochmuth et al., 1996; Waugh, 2009).

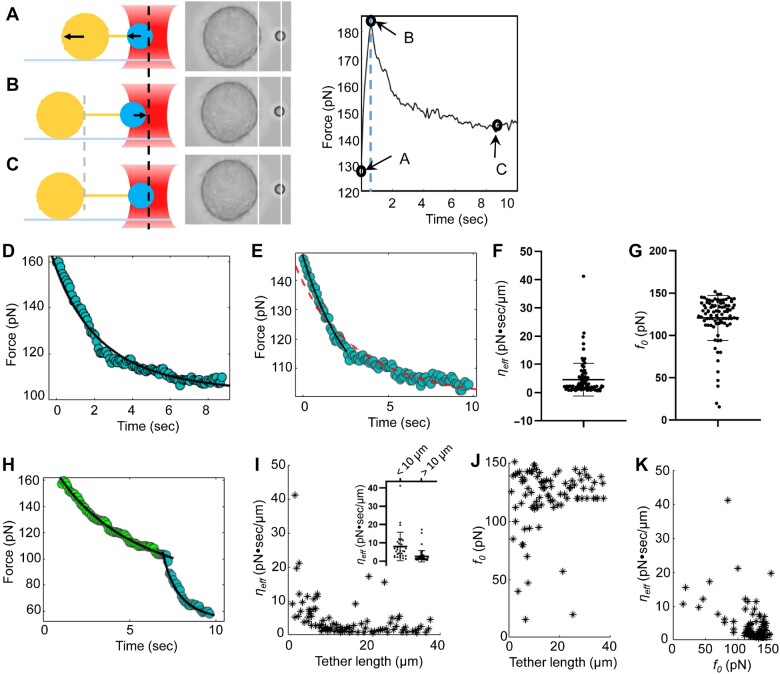
Optical tweezers is a powerful tool in the quantitative study of membrane tether obtained from biological samples (Sitarska and Diz-Munoz, 2020). Here, we determined η_eff and f₀ with membrane relaxation curves of HeLa cells. The cell first moved 0.5–1 µm away from an optical tweezers-trapped bead in 0.5 sec (Figure 1A). Once the cell ceased motion, the tension began to decrease and the bead was pulled back by optical tweezers (Figure 1B) until reaching an equilibrium (Figure 1C). We established a physical model including maximum tension f_s, effective viscosity coefficient η_eff, and static tension f₀ (Supplementary Materials and methods, equation (10)) to fit the tension vs. time curve. Most of the relaxation curves fitted well with our model directly (Figure 1D). For the rest of the data, only the initial phase of the first few seconds fitted well, while the overall relaxation curves deviated from our model (Figure 1E). This deviation is similar to relaxation curves obtained from artificial liposomes and plasma membrane spheres, which was reasoned by another slow linear but uncharacterized relaxation dynamics after elongation (Campillo et al., 2013). Since cells use membrane invaginations and surface projections to orchestrate the fast change of mechanical force during the stretching and membrane expansion processes (Raucher and Sheetz, 1999; Hamill and Martinac, 2001), it was speculated that an initial wave of lipid has been transported to establish the membrane tether site followed by second phase of lipid diffusion to the tether site for stable maintenance. Previous study on filopodia indicated that the actin shaft could induce coiling and axial shortening within cellular membrane tube (Leijnse et al., 2015). Thus, the actin dynamic could also be involved in the slow force decline. In this hypothetic model, relaxation curves are composed of dynamic processes derived from multiple cell membrane components from vectorial transport and lateral motion. The premise of effective research is to separate lipid flow from effects of other components through physical models as we discussed above.

Figure 1.

Quantitative measurement of dynamic membrane mechanosensation of HeLa cells using optical tweezers. (A–C) Membrane relaxation curves of HeLa cells. (A) The HeLa cell (big yellow circle) moves to the left and membrane tether elongates. The PS bead (small blue circle) captured by the optical tweezers (red object) is pulled left due to increased tension. The line between the two circles represents the membrane tether, and the arrows indicate motion directions. (B) Once the cell stops moving, the bead is pulled backward toward the center of the optical tweezers. (C) The bead stops moving until the tension decreases to f₀. Middle: the screenshot of each situation in the experiment. Right: graph shows the relaxation curve of the tether tension with time during the stretching process, in which the black circles correspond to the time from A to C. (D) A set of relaxation data and fitting curve. (E) An example of relaxation data deviated from the model fitting (red dash curve). The solid curve is the fitting result with the data from the first 2 sec only. (F and G) The distribution of effective viscosity η_eff and static force f₀. (H) A relaxation curve carrying a turning point in the middle. The left and right sections of the curve were fitted, respectively. (I) Correlation distribution between η_eff and tether length. The inset illustration shows the distribution of η_eff when the tether length is shorter or longer than 10 µm. (J) Correlation distribution between f₀ and tether length. (K) Correlation distribution between η_eff and static tension f₀.

We corresponded the fast decline phase to the flow of phospholipids from membrane to tethers and intercepted the data from the first two seconds of the curve and fitted out the η_eff and f₀ (Figure 1F and G; Supplementary Table S1). The fitted η_eff shows a clear plateau around 1.42 pN·sec/µm, which we attributed to cases that no membrane protein was stuck in the neck where membrane tethers attached. Since the curvature of phospholipid membrane changes dramatically in the neck where the tether attaches to the membrane, big η_eff might correspond to cases that membrane proteins of different sizes and quantities were stuck in the attachment point of the tether and blocked the free phospholipids flow.

There are two apparent turning points in some of the curves. We divided them into segments (Figure 1H). For curves containing one or more turning points, at least one of η_eff and f₀ changes significantly after the turning point, which indicates abundant dynamic changes in the process of membrane tether elongation (Supplementary Figure S3 and Table S2). We can reasonably suspect that protein molecules may be temporarily stuck in the border between membrane and tether until they got a chance to enter membrane tethers. Thus, relaxation curves divided into two parts with very different η_eff might represent the process of stuck protein leaving the neck region and going into the tether.

The relaxation curve method can obtain a large number of f₀ and η_eff for statistical analysis. We found the population of larger η_eff decreased as the tether length increased, big η_eff presenting more frequently on short tethers than on tethers >10 µm (Figure 1I, inset). In addition, when the tether length is longer, f₀ tends to concentrate between 110 and 115 pN, and the population of small f₀ becomes rare (Figure 1J). However, there is no significant correlation between f₀ and η_eff (Figure 1K), indicating that the two parameters are not significantly correlated.

In sum, we have characterized relaxation curves of HeLa cell membrane tether with established model. The relaxation curve method has collected a large number of f₀ and η_eff for statistical analysis, which enables us to determine the correlation of f₀, η_eff, and tether length. The delicate structure of relaxation curves provides the foundation for studying cytoskeletal remodeling due to vectorial and lateral membrane protein diffusion. In conclusion, our study established a quantitative measure to characterize the mechanosensation of epithelial cells in response to stimulus-elicited membrane dynamics.

[Supplementary material is available at Journal of Molecular Cell Biology online. We thank Dr Xuebiao Yao for input on the studies and manuscript editing. This work was financially supported by the grants from the National Natural Science Foundation of China (31870759, 61535011, and 21922706), the Fundamental Research Funds for the Central University (WK9110000025), the National Cancer Center Climbing Funds (NCC201812B036), Anhui Provincial Natural Science Foundation (2008085MH288 and 1908085MC64), and the New Coronavirus Infection Emergency Science and Technology Project, Clinical Research Hospital of Chinese Academy of Sciences (YD9110002010).]