Clinical trials in critical care: can a Bayesian approach enhance clinical and scientific decision making?

Abstract

Recent Bayesian reanalyses of prominent trials in critical illness have generated controversy by contradicting the initial frequentist conclusions. Many clinicians may be skeptical that Bayesian analysis, a philosophical and statistical approach that combines prior beliefs with data to generate probabilities, provides more useful information about clinical trials than the conventional frequentist approach. In this Personal View we introduce clinicians to the rationale, process, and interpretation of Bayesian analysis through a systematic review and reanalysis of interventional trials in critical illness. In the majority of cases, Bayesian and frequentist analyses agreed. In the remainder, Bayesian analysis identified interventions (1) where benefit was probable despite the absence of statistical significance, (2) where interpretation depended substantially on choice of prior distribution, and (3) where benefit was improbable despite statistical significance. Bayesian analysis in critical care medicine can help distinguish harm from uncertainty and establish the probability of clinically important benefit for clinicians, policymakers, and patients.

Introduction

Randomized trials evaluating interventions in critical illness are nearly universally analyzed using frequentist statistics. However, frequentist analysis addresses the probability of the data assuming there is no difference between treatment and control. This can lead to potentially misleading results that may cause critical care clinicians to abandon therapies where benefit is possible or adopt therapies where benefit is equivocal.^1-4 Challenges to interpreting frequentist analysis include multiple hypothesis testing, difficulty comprehending the proper meaning of the p-value and confidence intervals, inability to estimate the probability of clinical benefit, and no mechanism for incorporating prior information.^2,4,5 A Bayesian approach can address some aspects of these challenges^6-10 but the extent to which the systematic application of Bayesian analysis would revise interpretations of trial analyses in critical illness has not been evaluated.

Unlike frequentist analysis, Bayesian analysis can directly estimate the probability of clinically meaningful treatment benefit,^7-11 a quantity of direct interest and intuitive meaning for clinicians. Bayesian analysis combines observed trial data with prior information derived from expert opinion, clinical experience, basic science, and previous trials.^8,12,13 Critics of Bayesian analysis maintain that the incorporation of prior information introduces subjectivity into scientific analyses and is used to reframe “negative” trial results as “positive.”^3,14,15 However, clinicians unavoidably interpret trial results in light of prior information based on known mechanisms of effect and previously available data. Bayesian analysis aims to make the influence of this background information explicit by enabling investigators to quantify the influence of such prior information on the interpretation of the trial results.^7-10,16-21

Bayesian analyses are particularly relevant in critical care because many trials are too small to exclude minimally important differences in mortality. Prior information is most important when sample sizes are small to ensure a single underpowered but high-profile trial does not unduly spark widespread adoption or premature abandonment of an intervention for which confident conclusions about efficacy require additional data.^22-24 Recent Bayesian re-analyses have suggested alternative interpretations of important trials^6,25-27. The extent to which the systematic application of Bayesian analysis would reinterpret the available literature in clinical trials in critical care is uncertain.

The aim of this study was to determine the prevalence and nature of potential discordance between Bayesian and frequentist analyses of trials of critically ill patients and assess the extent to which Bayesian analyses may enhance scientific and clinical decision-making when interpreting trial results.

Methods

Systematic Review

The data are drawn from a systematic review focused on design bias and clinically important effects in trials of therapies for critical illness (Supplement p. 2).²⁸ Included studies were multicenter randomized superiority trials in critically ill patients with mortality as the primary outcome published between Jan 1, 2008 and Dec 31, 2018 in one of five journals: American Journal of Respiratory and Critical Care Medicine, Journal of the American Medical Association, The Lancet, The Lancet Respiratory Medicine, or New England Journal of Medicine. Journal selection was based on journals most likely to publish trials influential to trial design and clinical practice in critical illness, using both impact factor and content relevance. Critical illness was defined as illness or injury that “acutely impairs one or more vital organ systems such that there is a high probability of imminent or life-threatening deterioration in the patient’s condition” in accordance with the Centers for Medicare and Medicaid Services definition.²⁹ The timeframe was chosen to reflect trials designed after the uptake of lung-protective ventilation. Non-inferiority or cluster trials were excluded. Please refer to the supplement p.2 or reference 28 for details.

Minimum clinically important differences

The minimum clinically important difference (MCID) is the minimum benefit that patients or clinicians require from a therapy before they consider it beneficial; in the context of mortality, it can be defined as the minimum difference required to change clinical practice.^30,31 The MCID helps differentiate between statistical and clinical significance.^31-34 MCIDs are useful in Bayesian analysis because they provide clinically relevant thresholds for evaluating results or setting prior distributions. We estimated MCIDs by presenting 10 practicing critical care physicians with only the Background and Methods sections of the abstract for each included trial and then asking them to provide an estimate of “the smallest absolute risk reduction in mortality that would cause you to use this intervention.” The studies were presented to each clinician in a different random order and clinicians were blinded to the MCID estimates of other clinicians. The median value among the 10 estimates for each trial was used as its MCID in the subsequent Bayesian analysis. Please refer to the supplement p. 3 for further details.

Bayesian Analysis

Basic principles and terminology of Bayesian analysis are outlined in Box 1. Absolute risk reduction was used as the outcome in prior and posterior distributions. The work adheres to the ROBUST criteria for Bayesian analysis reporting.³⁵ All analyses were conducted using RStudio version 1.2.5033³⁶ and R version 3.6.3³⁷.

Box 1: Glossary of statistical terms.

The glossary below uses the example of a clinical trial designed to estimate the absolute risk reduction (ARR) for mortality between a new therapy and a standard therapy.

Bayesian inference: A form of inference that can use probability to quantify the evidence about an unknown quantity such as the absolute risk. A Bayesian analysis can find that there is, for example, a 60% probability that the absolute risk reduction is 3% or more. For a particular observed set of results from a clinical trial, these Bayesian probabilities can differ between analyses that use different prior distributions.

Bayes’ Rule: An equation expressing the relationship between prior probability, the likelihood of observed data, and posterior probability given the observed data.

Confidence interval (95%): An interval used in frequentist inference where 95% of intervals constructed in that manner with data generated in the same way will contain the true value.

For a given confidence interval, such as −1.5% to +2.0%, it is not correct to say that there is 95% confidence or 95% probability that the absolute risk lies between −1.5% and +2.0%. Any individual confidence interval either does or does not contain the true value.

Credible interval (95%): An interval used in Bayesian inference that is constructed such that there is a 95% chance that the true value lies in the interval, given the choice of model, prior distribution, and data.

Enthusiastic prior: This is one kind of archetypal prior. A prior distribution is described as enthusiastic if it expresses the view that the new therapy is beneficial and has a small chance of increasing mortality. For example, an enthusiastic prior for the absolute risk could be centered at an ARR of 5% and put only a 10% prior probability on values of ARR < 0% (harm).

Frequentist inference: A form of inference where probabilities are equal to proportions of frequencies calculated over hypothetical replications of a study. P-values and confidence intervals are common quantities calculated in frequentist inference.

Likelihood function: A mathematical function that calculates the probability of the observed data given a particular value of the absolute risk and the control group risk. Used in both frequentist and Bayesian inference.

Minimum clinically important difference (MCID): An example of a threshold chosen for clinical relevance to aid in interpretation of analyses. In this study the MCID is specific to an intervention and an outcome and represents the smallest treatment effect which would cause the clinician in question to change their practice.

Posterior distribution: The probability distribution that is the output of a Bayesian analysis. It can be interrogated to give the probability that the quantity of interest falls in certain ranges, for example, the probability that the absolute risk reduction is greater than the minimum clinically relevant effect.

Prior distribution: A probability distribution that summarizes information about the absolute risk reduction that does not come from the trial. It is one of the inputs to a Bayesian analysis. The prior distribution can be constructed based on any combination of data from other sources, knowledge of the local clinical context, understanding of the physiologic mechanism, personal experience, outcomes of related or similar trials, or opinion. The choice of any particular prior distribution must be justified.

Probability distribution: A probability distribution is a function that takes as input the value of a particular parameter (for example, absolute risk reduction) and outputs a probability (or probability density if the parameter is continuous) that the parameter takes that value.

P-value: One of the two most common outputs of a frequentist analysis. It is the probability of obtaining a result as or more extreme than the observed result in the actual trial, assuming the null hypothesis is true.

Skeptical prior: This is one kind of archetypal prior. A prior distribution is described as skeptical if it expresses the view that the new therapy likely has no effect and puts little prior probability on values of the absolute risk reduction that represent important increases or decreases in mortality. For example, a skeptical prior for the absolute risk reduction could be a normal distribution centered at a value of 0 – representing no difference between treatment and control arms – and with a total 20% probability on values of the absolute risk reduction greater than the minimum clinically relevant effect.

Uninformative prior: This is one kind of archetypal prior. A prior distribution is described as uninformative if it contains little-to-no information. For example, quantifying complete ignorance by allowing the prior distribution to be uniform across all possible values of absolute risk reduction (all possible values are equally likely) results in an uninformative prior, because it contains no information about what the particular value of absolute risk reduction will be.

Priors, Likelihoods, and Posteriors

Priors for the absolute risk reduction (ARR) were specified using normal distributions based on the approach of Spiegelhalter.^7,8 The uninformative prior was an improper prior set to a constant value.³⁸ The informative priors had mean set to be either skeptical (ARR = 0) or enthusiastic (ARR =2*MCID) with variance set to be equivalent to a 400-person randomized trial with mortality equivalent to the predicted control arm mortality used for sample size calculation. The rationale for setting the variance equal to a 400-person randomized trial is that in critical care medicine trials of this size can be influential but if the prior distributions contained more information then the implied certainty might violate accepted standards of equipoise. Further details of prior distributions are available in Table E4. The likelihood function was a normal distribution with mean and variance equal to their sample counterparts. If both prior and likelihood are normal distributions, the posterior is also a normal distribution.⁸

Outcomes

Outcomes were computed from the posterior distributions of absolute risk reduction for each intervention. Bayesian analyses were described as showing potential benefit if there was a greater than 50% probability that the absolute risk reduction equaled or exceeded the MCID and described as showing improbable benefit otherwise. The threshold of 50% was chosen because it represents the point where an outcome goes from unlikely (on average, does not happen) to likely (on average, does happen). Higher posterior probability of benefit may be preferred to support practice change for many therapies.

The primary outcome was the proportion of trials for which dichotomous interpretations of Bayesian and frequentist trials yielded potentially discordant conclusions, which occurred if:

1. the trial was positive by frequentist criteria (p < 0.05 and signal showing benefit) but the posterior probability of achieving the MCID was less than 50% or;

2. the trial was indeterminate or negative by frequentist criteria (p > 0.05 or signal showing harm) but the posterior probability of achieving the MCID was greater than 50%.

For frequentist analyses, if a trial reported a time-to-event mortality analysis in addition to binary mortality outcome at 28 or 60 days, the latter was used for p-value calculation.

Rates of potential discordance were computed using each of the three archetypal prior distributions (skeptical, uninformative, enthusiastic). Comparison using the skeptical prior was chosen for the primary outcome to reflect the belief, independent of intervention mechanism, that very large benefits or harms are unlikely in an evaluation of an intervention with clinical equipoise.

Sensitivity and reversal analyses

Sensitivity analyses assessed more conservative posterior probability thresholds, varying treatment effect thresholds, and a prior distribution where harm was likely. The frequency of potential discordance was computed using higher thresholds for probability of potential clinical benefit (75%, 90%). Additional clinical thresholds included any benefit (ARR > 0%) and the planned effect size obtained from each trial’s sample size calculation. The prior distribution representing probable harm from treatment had mean set to an increase in mortality equal in magnitude to the MCID and variance set to be equivalent to a 100-person randomized trial. A lower certainty was used for the prior positing probable harm because equipoise implies that the evidence in support of harm from an intervention is not strong in order for it to be tested in a randomized trial.

The extent to which the interpretation of a trial could be significantly influenced by prior beliefs was assessed by evaluating for prior-dependent reversal. Reversal was said to be present if a trial showed improbable benefit (posterior probability <50%) under the skeptical prior but potential benefit (posterior probability >50%) under the enthusiastic prior.

Results

Clinical trial characteristics

Eighty-two interventions published over 11 years were included (Table E1, Supplement). Median trial sample size was 1,030 (IQR 507-1,917) patients. Thirteen (16%) trials received industry funding, 24 (30%) were stopped early, and 47 (57%) involved non-pharmacologic interventions. Eight trials (10%) reported p < 0.05 in their primary analysis, of which four showed benefit and four showed harm.

Estimating the minimum clinically important difference

The minimum clinically important difference (MCID) for each trial ranged from 1% (3 trials) to 5% (6 trials) (Table E2 in Supplement). The MCIDs for pharmacologic interventions (median 2.5% [IQR 2-3%]) were similar to the MCIDs for non-pharmacologic interventions (median 3% [IQR 2-4%]) (Figure E2). Effect sizes used to plan trials were considerably larger than the MCIDs (median difference 5.5% [IQR 3%-7%]) (Table E3). Details about MCID estimators are available in the Supplement (p. 3-4).

Trial results from Bayesian analysis

The posterior probability of absolute risk reduction greater than or equal to the MCID exceeded 50% in 9 trials (11%) under the skeptical prior, 14 trials (17%) under the uninformative prior, and 22 trials (27%) under the enthusiastic prior.

Comparison of results from frequentist and Bayesian analyses

The relationship between the posterior probability of benefit (ARR ≥ MCID) and p-value is depicted in Figure 1 according to each prior.

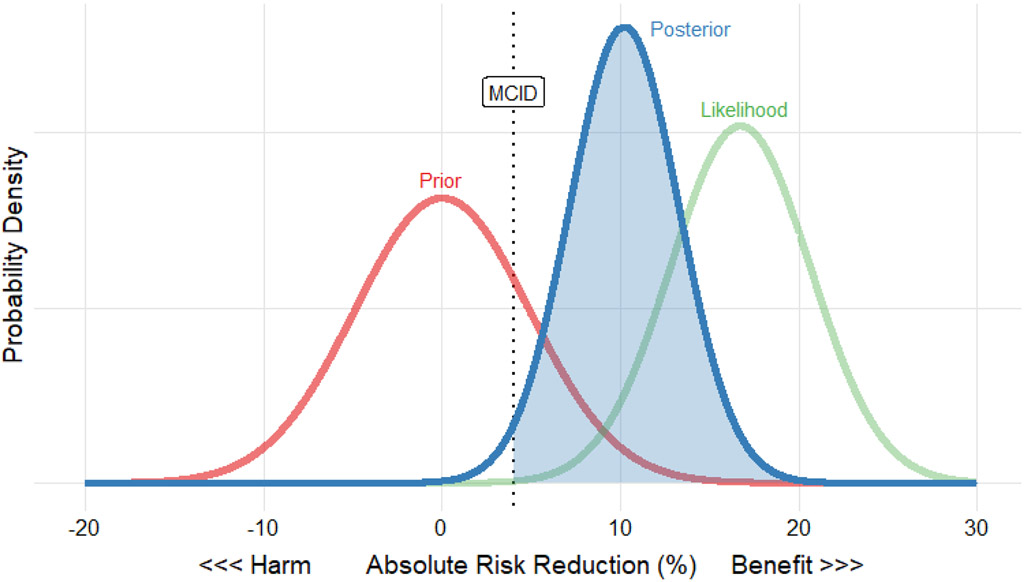
Figure 1 – Example Plot of Prior, Likelihood, and Posterior Distribution Using the Guérin (2013) “PROSEVA” Trial³⁹.

This figure shows the prior (red curve), likelihood of observed data (green curve), and posterior (blue curve) plotted together with absolute risk reduction on the x-axis and probability density on the y-axis. The prior distribution is skeptical, centered at an absolute risk reduction of 0, with variance equivalent to a 400-person trial. The likelihood is centered at the observed absolute risk reduction of the trial and has lower variance than the prior because the trial enrolled 466 patients. The posterior combines the prior and likelihood, resulting in a compromise between skepticism (perhaps based on previous proning trials, or the broader context of clinical trials in ventilation) and the observed mortality reduction. Although the posterior distribution is attenuated relative to the data, the resulting posterior probability of exceeding the 4% minimum clinically important difference (blue shaded area) is 98%, providing strong evidence that proning is beneficial even if one is skeptical before seeing the data from Guérin et al. Similar plots with user-specified MCID and prior distributions are available for every trial in the analysis through the accompanying interactive app.

Among 78 trials found to be indeterminate or negative by frequentist criteria, the posterior probability of ARR ≥ MCID exceeded 50% in 7 (9%) trials under the skeptical prior, 12 (15%) under the uninformative prior (listed in Table 2), and 20 (26%) trials under the enthusiastic prior (Table 1). Among 4 trials within this group reporting statistically significant harm (p<0.05), the probability of clinical benefit was 11% or less under all priors.

Table 2.

Studies in which Bayesian analysis showed potential benefit despite reporting a p value greater than 0·05 with frequentist analysis

Manuscript Name	Unadjusted Mortality Result (intervention versus control)	P value	Median Posterior ARR (95% credible interval)	Threshold value for treatment effect defining clinically important benefit estimated by authors		Posterior Probability (uninformative prior)
				Minimum clinically important difference	NNT implied by MCID*	ARR ≥ MCID	ARR ≤ 0
Effect of Noninvasive Ventilation vs. Oxygen Therapy on Mortality Among Immunocompromised Patients With Acute Respiratory Failure45	28-day mortality 24% (non-invasive ventilation) vs. 27% (oxygen therapy)	0.47	3.2% (−5.6 to 12%)	3%	33	52%	24%
Permissive Underfeeding or Standard Enteral Feeding in Critically Ill Adults52	90-day mortality 27% (underfeeding) vs. 29% (standard)	0.58	1.7% (−4.2 to 7.6%)	1.5%	67	52%	29%
Transfusion of plasma, platelets, and red blood cells in a 1:1:1 vs. a 1:1:2 ratio and mortality in patients with severe trauma53	30-day mortality 22% (1:1:1) vs. 26% (1:1:2:O	0.24	3.8% (−2.6 to 10%)	3%	33	60%	12%
Positive End-Expiratory Pressure Setting in Adults With Acute Lung Injury and Acute Respiratory Distress Syndrome54	28-day mortality 28% (high PEEP) vs. 31% (low PEEP)	0.31	3.4% (−3.1 to 9.8%)	2.5%	40	60%	15%
Vasopressin versus norepinephrine infusion in patients with septic shock55	28-day mortality 35% (vasopressin) vs. 39% (norepinephrine)	0.26	3.9% (−2.9 to 11%)	2.5%	40	66%	13%
Prednisolone (or Pentoxifylline) for Alcoholic Hepatitis56	28-day mortality 14% (prednisolone) vs. 18% (placebo)	0.07	4.2% (−0.3 to 8.6%)	2.5%	40	77%	3%
Extracorporeal Membrane Oxygenation for Severe Acute Respiratory Distress Syndrome25	60-day mortality 35% (ECMO) vs. 46% (usual care)	0.10	10.1% (−2.0 to 22%)	5.5%	18	77%	5%
Amiodarone, Lidocaine, or Placebo in Out-of-Hospital Cardiac Arrest57	Hospital mortality 76% (amiodarone) vs. 79% (placebo)	0.07	3.4% (−0.2 to 7.1%)	2%	50	77%	3%
Neuromuscular blockers in early acute respiratory distress syndrome58	90-day mortality 32% (neuromuscular blocker) vs. 41% (usual care)	0.08	9.1% (−1.1 to 19%)	4%	25	84%	4%
Comparison of dopamine and norepinephrine in the treatment of shock59	28-day mortality 49%(norepinephrine) vs. 53% (dopamine)	0.10	4.0% (−0.8 to 8.8%)	1.5%	67	84%	5%
Effect of Dexmedetomidine on Mortality and Ventilator-Free Days in Patients Requiring Mechanical Ventilation With Sepsis60	28-day mortality 23% vs. 31%	0.14	8.7% (−2.9 to 20%)	2.5%	40	85%	7%
Early lactate-guided therapy in intensive care unit patients61	Hospital mortality 34% (lactate-guided) vs. 44% (usual care)	0.07	9.6% (0 to 20%)	2%	50	93%	3%

^*Computed from estimated minimum clinically important difference (NNT = 100/MCID)

This table shows information about the studies where Bayesian analysis showed potential benefit despite frequentist analysis having a p-value > 0.05.

Table 1.

Bayesian analysis of critical care trials classified according to frequentist analysis across a range of posterior probability thresholds for clinical benefit

Treatment effect	Prior distribution	Posterior probability of treatment effect	Outcome of frequentist analysis
			Positive (4)	Negative or indeterminate (78)
MCID	Skeptical	> 90%	1 (25%)	0 (0%)
		> 75%	2 (50%)	2 (3%)
		> 50%	2 (50%)	7 (9%)
	Uninformative	> 90%	2 (50%)	1 (1%)
		> 75%	2 (50%)	7 (9%)
		> 50%	2 (50%)	12 (15%)
	Enthusiastic	> 90%	2 (50%)	2 (3%)
		> 75%	2 (50%)	7 (9%)
		> 50%	2 (50%)	19 (24%)
Any benefit (ARR>0)	Skeptical	> 50%	4 (100%)	36 (46%)
		> 90%	4 (100%)	3 (4%)
	Uninformative	> 50%	4 (100%)	36 (46%)
		> 90%	4 (100%)	7 (9%)
	Enthusiastic	> 50%	4 (100%)	61 (78%)
		> 90%	4 (100%)	18 (23%)
Planned effect	Skeptical	> 50%	0 (0%)	0 (0%)
	Uninformative	> 50%	1 (25%)	0 (0%)
	Enthusiastic	> 50%	0 (0%)	1 (1%)

MCID = Minimum clinically important difference

ARR = Absolute risk reduction

This table shows the number and percentage of studies according to frequentist classification (fourth and fifth columns) where the posterior probability of achieving clinical benefit (defined by first column) according to each prior (second column) is greater than the posterior probability threshold (third column). For example, among studies classified as negative by frequentist criteria there are zero studies where the posterior probability of clinical benefit exceeds 90% using the skeptical prior distribution and the MCID as the threshold for clinical benefit.

Among 4 trials with a statistically significant signal for benefit under frequentist criteria, the posterior probability of clinical benefit (ARR ≥ MCID) was less than 50% across all prior distributions in two trials.

The two trials showing potential benefit in both Bayesian and frequentist analyses across all priors were the Guérin 2013 trial of proning in ARDS³⁹ and the Annane 2018 trial of hydrocortisone with fludrocortisone in septic shock.⁴⁰

Sensitivity analyses using alternative clinical thresholds (“any benefit” i.e. ARR > 0% or “planned effect” i.e. ARR > effect size used for sample size calculation) and higher posterior probability thresholds are shown in Table 1, Figure 2, and Figure E2. Increasing the thresholds for clinical benefit and increasing the posterior probability thresholds to define benefit reduced the number of trials with potential discordance between frequentist and Bayesian analyses (Table 1).

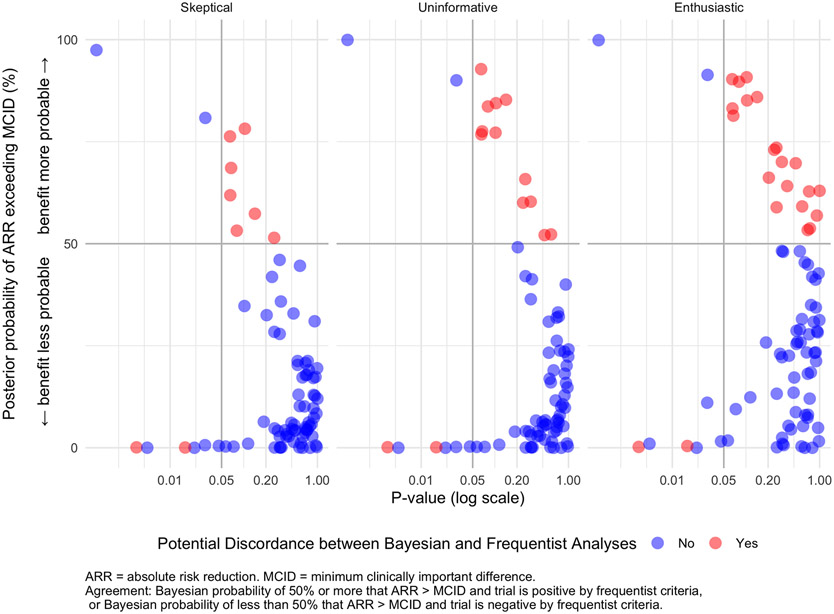
Figure 2 – Probability of Clinical Benefit Versus P-value.

This figure shows the relationship between the p-value and the posterior probability that the absolute risk reduction exceeds the minimum clinically relevant effect for each study. Each dot corresponds to a particular study. The color of the dot denotes agreement (blue) or potential disagreement (red) between frequentist and Bayesian analyses for that particular prior. Note that the blue dots in the quadrant with p-value < 0.05 and posterior probability of clinical benefit < 50% correspond to studies with p-value < 0.05 that showed harm. The posterior probability of exceeding the MCID increases as prior distributions shift from skeptical (left) to enthusiastic (right) but the p-values stay the same.

Susceptibility of trial interpretation to shifting priors

Shifting the prior from skeptical to enthusiastic reversed the Bayesian interpretation of the trial from improbable benefit (≤ 50% posterior probability of ARR ≥ MCID) to potential benefit (>50% posterior probability of ARR ≥ MCID) in 12 trials (15% of all trials). When using higher posterior probability thresholds of 75% or 90% to define potential benefit, shifting the priors from skeptical to enthusiastic reversed the Bayesian interpretation in 5 (6%) trials and 3 (4%) trials, respectively. Reversal was less likely at higher sample sizes (Figure E2). The trials with reversal according to the choice of prior are listed in Table E5.

The study is accompanied by an interactive application available at https://cyarnell.shinyapps.io/BRICCS-Interactive-App/ which allows investigation of the effects of different prior distributions according to user-selected outlook, certainty, and MCID.

Discussion

Across 82 clinical trials in critical care medicine published in high-impact journals, discordance between Bayesian and frequentist analyses was relatively uncommon. However, this investigation identified multiple trials where clinical benefit was more likely than not despite p-value > 0.05 and trials where clinical benefit was unlikely despite frequentist analysis suggesting benefit. We also identified trials where the probability of clinical benefit varied substantially according to choice of prior distribution, suggesting that these trials did not accrue sufficient information to resolve uncertainty about treatment effect. These examples demonstrate how incorporating Bayesian analyses into the reporting of trials may enhance and clarify their interpretation. Importantly, the post hoc Bayesian analyses presented in this paper should be interpreted as exploratory and hypothesis-generating, not definitive statements about treatment efficacy.

By estimating the probability of treatment benefit rather than the probability of obtaining the observed effect or greater under the null hypothesis, Bayesian analysis provides a more direct assessment of the strength of the evidence for or against an intervention. Bayesian analysis may disagree with frequentist analysis, depending on the posterior probability of benefit one requires to support use of a given therapy.^18-20,41,42 For example, this investigation identified several cases where the posterior probability of benefit was greater than 50% but the frequentist p-value exceeded 0.05. Most trials of interventions in critical illness are indeterminate by frequentist criteria⁴³ (p-value exceeds 0.05), so it is helpful to have a method that further clarifies the certainty with which potential benefit has been ruled out.

Two key points should be noted. First, our results show that Bayesian analysis cannot be regarded simply as a means of turning ‘negative’ results into ‘positive’ results. We found that Bayesian and frequentist analyses are discordant in only a minority of cases. The impression that Bayesian analysis converts indeterminate results into favourable ones may arise from a kind of publication bias whereby Bayesian reanalyses haveoften focused on trials with p-value > 0.05 and a large positive effect size, a scenario where Bayesian analysis is more likely to suggest potential benefit.^6,26 Second, it must be appreciated that there is no fixed value for posterior probability of benefit at which one can conclude that a treatment should be routinely employed in practice. Such judgments may depend on many considerations (e.g., adverse effects, costs, preferences, specific clinical scenario, patient goals and values). The strength of the evidence measured by posterior probability can be used to determine whether further investigation is required, to inform decision analyses, to formulate guideline recommendations, and to make clinical decisions.

Bayesian analysis enables investigators to incorporate judgments about minimum clinically important differences into quantitative analysis. Ideally these judgments are pre-specified in order to distinguish between statistical and clinical significance.^32,34,44 We found that the choice of MCID had an important influence on the interpretation of trials; indeed, there was low probability of benefit (as defined in terms of the MCID) in two trials deemed positive by frequentist criteria. Several considerations must be borne in mind. First, the choice of the MCID may vary by patient, clinician, or setting, and a lower MCID may reverse the conclusion. In our study, MCID estimates varied widely between authors for any given trial, suggesting substantial variability in judgments of clinically important treatment benefits and highlighting the need for more research into how judgments about MCID should be formulated. The MCIDs determined by the process used in this study were similar to published MCIDs in cardiac arrest literature³⁴ and generally much lower than the effect sizes used to plan the trials. Second, the MCID refers to a single outcome and does not include other potential benefits from a therapy. For example, a decrease in bleeding from tranexamic acid may improve both mortality and other outcomes related to severe bleeding not captured by a mortality endpoint. Third, although the absolute risk reduction is a more intuitively accessible measure of treatment effect and the measure on which MCIDs were defined, the relative risk may be the more generalizable measure—when a therapy is employed in a population with a higher baseline risk there may be an accompanying increased absolute benefit that exceeds the MCID. Last, our MCIDs were much smaller than the effect sizes used to plan the trial, meaning that the trials would be very unlikely to have sufficient statistical power to exclude a benefit equal to or smaller than the MCIDs we used. This may reflect the fact that trials are often planned based on the feasibility of patient recruitment to a given sample size, rather than based on the MCID s that are deemed to be feasible. To assist with clinical interpretation of trial results, future randomized trials should incorporate prospectively defined minimum clinically important differences for the primary outcome and use these for sample size calculations.

Several trials showed substantial variation in the posterior probability of clinical benefit according to choice of prior distribution. This is a quantitative expression of scientific controversy due to insufficient data, where the adoption of a skeptical stance as opposed to enthusiastic stance leads to different conclusions about its efficacy. One prominent example was the trial “Effect of Noninvasive Ventilation vs. Oxygen Therapy on Mortality Among Immunocompromised Patients With Acute Respiratory Failure”⁴⁵, which had a posterior probability of clinical benefit of 33% under skeptical priors that increased to 70% under enthusiastic priors. Shift in posterior probability of clinical benefit across different priors decreased with sample size. This analytical approach provides a means of quantifying the information available from a clinical trial and clarifies the basis for sample size calculation: a clinical trial should enroll a sufficient number of patients to obtain sufficient information to achieve consensus as to the presence or absence of meaningful treatment effect among both skeptics and enthusiasts.

This secondary analysis of randomized trials has several limitations. The most important limitation is that Bayesian analysis does not directly address inadequacy in fundamental aspects of trial design and conduct including enrolment, blinding, randomization, protocol adherence, outcome selection, measurement error, or missing data. Heterogeneity of treatment effect is an additional potential challenge in critical care trials which is not addressed by this analysis, although Bayesian hierarchical regression provides a powerful tool to analyze heterogeneity across predefined subgroups.⁴⁶ A further limitation is that the analysis focuses on concordance and discordance between Bayesian and frequentist analyses, potentially perpetuating a dichotomous approach to trial interpretation based on arbitrary thresholds for p-values or posterior probabilities. Individual trials should report the full posterior probability distribution in order to communicate the largest amount of information to readers. The goal of this investigation was different and intended to investigate the prevalence of discordance across multiple studies, which demands potentially arbitrary thresholds.

Further limitations relate to inherently subjective decisions in statistical modeling. Different implementations of a Bayesian approach for each trial may yield different results from those in this investigation.^{6,18,42,47-49} Our priors were defined as normal distributions based on pre-specified rules and only connected to their particular clinical scenario by the estimates of MCID. Alternative choices for the distributions such as beta-binomial or alternative methods for eliciting priors and MCIDs might obtain more appropriate distributions, although our spectrum of prior distributions encompassed a wide range of potential priors.⁵⁰ Determining the MCID and posterior probability of benefit necessary to use a given treatment could facilitate more personalized care by involving patients and families in decisions on these points. The use of online calculators such as that provided above could be implemented to quickly obtain posterior probability estimates that can help with shared decision-making.

Covariate adjustment was not used to improve precision as a consequence of using study-level data as opposed to individual-level data. Analytically, some criticisms of frequentist analysis could be addressed by a more thoughtful use of frequentist analytical tools and may not require adopting a Bayesian approach.⁵¹ From a clinical perspective, the analysis was limited to critical care trials, which increased the coherence of results across trials and enabled informed MCID estimation but sacrificed external validity. The MCID was assumed to be homogeneous across patients. This analysis did not consider secondary efficacy or safety endpoints, the totality of which are essential for interpretation of any clinical trial.

Conclusion

Bayesian and frequentist analyses of clinical trials generally yield concordant interpretations. However, Bayesian analysis may identify interventions where clinically important benefit is more probable than not despite the absence of frequentist statistical significance, where interpretation depends substantially on the choice of prior distribution, or where clinically important benefit is improbable despite frequentist statistical significance. Bayesian analysis can complement conventional frequentist statistics by distinguishing between indeterminate and negative results, quantifying the influence of prior beliefs, and providing direct estimates of the probability of clinical benefit.

Table 3.

Challenges for critical care trial design, analysis, and interpretation: frequentist versus Bayesian approaches

Problem	Description of problem in conventional analysis of critical care trials	Explanation of how a Bayesian approach could address this problem
Quantitative use of external information in trial analyses	Conventional trials do not quantify the influence of prior information in the analysis of a trial.	A Bayesian approach, including determination of a minimum clinically important difference and a set of defensible priors combining data and expert opinion, can provide the probability of benefit based on prior information and trial data.
Insufficient sample size	Sample sizes in critical illness trials are often too small to exclude clinically important differences in mortality and other outcomes.	Communicating results as the posterior probability of exceeding different clinically-relevant thresholds provides greater insight into the meaning of results from small trials as to whether treatment benefit has been adequately ruled in or out and whether there is persistent equipoise. The Bayesian paradigm can guide sample size estimation by clarifying the amount of information (sample size) required to achieve consensus across all defensible priors.
Applying results to clinical practice	Frequentist analyses provide no formal methods to guide how results might be adapted at the bedside depending on a clinician’s informed skepticism or enthusiasm for that therapy in that patient.	Knowing the probability of exceeding a clinically relevant threshold under different priors is more aligned with day-to-day clinical problem solving.
Adopting therapies with minimal clinical benefit	No benefit is too small to generate a significant p-value, if a trial enrolls enough patients. In clinical practice, patients and clinicians may require a certain amount of benefit before adopting or using a therapy.	The Bayesian approach allows flexible calculation of the probability of benefit at different thresholds which can be selected based on the characteristics of individuals or populations.
Abandoning therapies with potential clinical benefit	Interpretations of frequentist analyses may conflate indeterminate and truly negative results, leading to abandonment of therapies where clinical benefit has not been ruled out.	The posterior probability distribution quantifies the extent to which clinical benefit has or has not been ruled out.
Controversy about small trials with extreme results	Frequentist trials are analyzed in isolation, occasionally leading to strongly positive results that generate controversy or premature adoption of a therapy.	Quantifying the extent to which results change across differing prior distributions helps quantify the degree of scientific uncertainty around results from small trials.
Stopping trial enrolment for futility or benefit	Complicated rules around p-values and interim analyses can lead to early stopping of trials that could still have contributed helpful data to a clinical question.	Results from Bayesian analyses are not contingent on what you intended to do and allow decisions about stopping or continuing a trial to be based on the probability that a therapy will be beneficial.
Nonstandard trial designs require complex statistics	Nonstandard trial designs such as adaptive trials are potentially helpful yet awkward to design and analyze with frequentist principles.	Bayesian approaches make adaptive trial designs more analytically feasible.
Gleaning insights from subgroup analyses is difficult	Trials often include several clinically relevant subgroups but frequentist analysis requires either complex multiplicity corrections or the qualifier “exploratory”; trials often lack the sample size to demonstrate a definitive answer for the entire trial population, let alone a relevant subgroup.	Posterior probability distributions can be derived for the treatment effect in any subgroup of a trial, and prior distributions can also be specified for any subgroup. Bayesian hierarchical regression is a more sophisticated technique well-suited for this problem.46
Forming clinical guidelines from trial data requires accurate synthesis of data from multiple studies and trials	Frequentist analyses are quantitatively isolated and combining results through meta-analysis may not capture the full spectrum of information available in cohort or physiologic studies.	Investigating the range of posterior probabilities according to prior information could help make clinical guideline formulation from randomized trials more intuitive and informed.
Statistical support is required for safe conduct of randomized trials	Conventional frequentist trials often retain advanced statistical support for study design and analysis.	Trials designed with a Bayesian approach may require more specialized statistical support and expertise, which may be a barrier for some investigators and trials groups.
Trial outcomes may not be important to patients or clinicians	Frequentist analyses sometimes use surrogate outcomes in order to increase statistical power.	A Bayesian approach may be more flexible with regards to surrogate outcomes because it can capture the uncertain relationship between the surrogate and the true patient-important outcome, however, a Bayesian approach will not overcome a poorly-chosen surrogate outcome.
Missing outcome data may impede trial analysis	Conventional trials may become biased through missing outcome data.	Bayesian approaches do not necessarily offer any better options with regards to missing data.
Randomization is logistically difficult and may deter participation	Randomizing patients to treatments can sometimes be a barrier for patients and clinicians to participate in trials.	Randomization remains a central tool for quantitative causal inference, whether using frequentist or Bayesian methods.
Informed consent can be burdensome and deter participation	Processes of informed consent can be burdensome for clinicians and patients.	Different analytic paradigms do not obviate the need for ethical informed consent in trials.

Key Messages.

1. Bayesian analysis is an alternative approach to analyzing trial data which has potential advantages in comparison to conventional frequentist analysis including methods to incorporate prior information, the capacity to compare results to clinically relevant thresholds, and the ability to answer the clinical question “what is the probability that this therapy will benefit a patient?”

2. This study used Bayesian reanalysis across a systematic sample of randomized trials of patients with critical illness to investigate the extent to which the use of Bayesian reanalysis would revise the conclusions of trials originally analyzed with a frequentist approach.

3. Frequentist and Bayesian analyses generally agreed. However, Bayesian analysis identified some trials where clinically relevant benefit was probable despite the absence of statistical significance, where interpretation depended substantially on the prior information, and where clinically relevant benefit was improbable despite statistical significance.

4. Incorporating Bayesian analyses into clinical trial analysis plans will help inform clinical and scientific decisions.

Search Strategy.

For the overall manuscript (not for the trials included in the reanalyses) we searched MEDLINE and Google Scholar for articles published before September 28, 2020. We used the search terms “Bayesian analysis”, “Bayes”, “Bayes Theorem”, “Bayesian”, or “Bayesian reanalysis”, and “critical care” or “critical illness.” We also reviewed reference lists, bibliographies, and our personal files for additional relevant articles. The citations were chosen to provide a range of entries into Bayesian analysis for interested clinicians, including textbooks (Spiegelhalter, McElreath, and Kruschke) and antecedent review articles (Wijeysundera, Kalil); several citations relating to ongoing controversies in Frequentist statistics (Amrhein, Greenland); and examples of Bayesian reanalyses in critical illness (Goligher, Zampieri). Additional citations were included when helpful to support the research approach. Only articles published in English were included.