The influence of dietary patterns on outcomes in a Bayesian choice task

Abstract

Background and Aims

Previous research has investigated the impact of diet on cognition, but the focus has often been on general cognition. This paper reports on a preregistered cross‐sectional study aimed at testing for specific executive function differences across individuals who self‐reported one of four distinct dietary patterns: No Diet, No Sugar, Vegetarian, or Mediterranean Diet pattern. Our hypotheses were aimed at testing whether adherence to a specialty diet improved decision making relative to those who reported following No Diet.

Methods

We administered an incentivized Bayesian choice task to all participants. The task involved multiple components of information—existing information (base rate odds) as well as new information (sample draw evidence)—to allow a test of how these information components were used in making probability assessments, and how this may differ by self‐reported dietary pattern. Sample size, hypotheses, and analysis plans were all determined ex ante and registered on the Open Science Framework. Multi‐variate linear and non‐linear estimation methods were used to analyze the data.

Results

Our data failed to support our pre‐registered hypotheses. In fact, we found some evidence that self‐reported adherence to a specialty No Sugar Diet was associated with a reduced decision accuracy and was connected to an increased imbalance in how the participant weighted the two available sources of information when making choices.

Conclusion

Our results suggest that decision making is nuanced among dietary groups, but that short‐term incentivized decisions in an ecologically valid field setting are likely not improved solely by following promoted dietary patterns such as the Mediterranean or Vegetarian diets.

1. INTRODUCTION

The ability to engage in high level cognitive thinking is beneficial for decision making and adaptive reasoning, which can help one incorporate multiple sources of information into a decision. Recent studies between diet and cognition show that certain dietary patterns not only improve physical health but affect brain function in a way that results in higher‐level thinking. This paper examines the impact of self‐reported dietary patterns on decision making in a Bayesian choice task that targets high‐leveling reasoning skills useful in decision making environments. We followed a pre‐registered design, data collection, and analysis plan in our study, and we contribute additional exploratory analysis as well.

The objective of using a validated Bayesian choice task in our study was to test for specific executive function differences across individuals following different dietary patterns. The health and disease risk impact of certain dietary patterns have been consistently documented,^{1, 2, 3} but the evidence connecting diet and decision making is scarce, since available research examines the general cognitive effects of diet. There is a common perception that Western diets high in fat and sugar may harm cognition,⁴ while vegetarian‐based diets or Mediterranean dietary patterns may help improve cognitive functions.^{5, 6} If one looks more closely, however, the literature has been mixed regarding evidence on dietary patterns and more general cognition.^{7, 8, 9, 10} The best evidence compiled from systematic reviews of the research supports the beneficial role that diets rich with plants, nuts, and berries have on cognition. While a recent review of randomized controlled trials found that the Mediterranean dietary pattern largely produced insignificant cognitive effects,¹¹ it was also reported that most robustly designed studies reviewed suggested cognitive benefit associated with the Mediterranean diet. Another comprehensive review concluded that dietary patterns, specifically the Mediterranean diet, may improve cognition due to the cumulative effects of several beneficial dietary elements.¹² This paper aims to contribute to this literature by testing outcomes for a specific type of decision making across samples of individuals who self‐reported following no specific dietary pattern or self‐reported following a vegetarian, Mediterranean, or no‐sugar dietary pattern.

The Bayes task we study, which assesses how individuals incorporate two sources of information into a decision, has been shown sensitive to the use of heuristics as a simple decision strategy,¹³ and also shown sensitive to the effects of sleep deprivation or voluntary sleep restriction.^{14, 15} Sleep restriction has also been shown to harm decision making predominantly in more complex decision environments.^{16, 17} As such, the existing literature suggests we differentiate between more vs less complex Bayesian stimuli in our analysis as well. This study represents a merging of two previously separate literatures by examining decision outcomes in a vetted and unique executive function task across groups of participants who reported adherence to different dietary patterns of interest.

1.1. Hypotheses

Our hypotheses were pre‐registered based on the existing literature that has shown some possible cognitive benefits of more plant‐based or Mediterranean dietary patterns. While less evidence would suggest similar cognitive benefits of sugar‐free diets, we preregistered the hypothesis that such a “no‐sugar” diet would also improve performance on the Bayesian task. We also anticipated any benefits would be observed in a more difficult/complex Bayesian choice environment, compared to more simple ones. Also, though response times (RT) as a choice process measure must be examined with caution, we built upon the idea that deliberation (as opposed to more automatic quick‐thinking) is a longer response time decision process.¹⁸ Finally, our fourth hypothesis involves estimation of a model of decision making that assesses the decision weight one places on the prior odds vs the evidence. A Bayesian decision maker is hypothesized to place (equal) weight on both information sources, and our analysis will model results across dietary patterns and compared to previous results in the literature using this decision task.

Hypothesis 1. We hypothesize those who indicate adherence to a Mediterranean, Vegetarian, or No Sugar diet will make probability assessments (ie, Bayesian probability estimates) that are significantly more accurate than those indicating they do not follow any dietary pattern. We hypothesize that the greatest effect of dietary pattern on Bayesian accuracy will be among those following a Mediterranean dietary pattern.

Hypothesis 2. Improvements in Bayesian accuracy by those following the Mediterranean, No Sugar, or Vegetarian dietary patterns will be primarily observed in more difficult Bayesian choice environments (eg, such as those where the two sources of information regarding the likely state of the world in the decision task point to opposite states).

Hypothesis 3. More Bayesian accurate decisions will be associated with longer task response times. This will be most apparent in the more difficult Bayesian choice trials.

Hypothesis 4. Those following a Mediterranean, No Sugar, or Vegetarian dietary pattern will show more Bayesian decision tendencies (eg, weighting both sources of information in making choice), with the greatest Bayesian tendencies being for those following a Mediterranean diet.

2. METHODS

2.1. Survey and sample screening details

The methods used were preregistered on the Open Science Framework (https://osf.io/472bg)¹⁹ to establish hypotheses, sample sizes, variable specification, and analysis plans. When not describing pre‐registered hypotheses or analysis, we will refer to our analysis as exploratory. The basic methodology was to imbed a decision task within an online survey that would be administered to participants who self‐reported following one of three dietary patterns of interest or self‐reported no specific dietary pattern. All methods for data collection were carried out in accordance with the US Federal Policy for the Protection of Human Subjects, and our procedures were approved by the human subjects review board at Appalachian State University.

Our sample was recruited from the Prolific subject pool (prolific.ac), which is a service tailored for researchers as an alternative to Amazon's mTurk platform for online research studies.²⁰ One of the benefits of Prolific is the availability of a variety of sample screening options that allow the researcher to recruit custom samples based on one or more criteria captured by Prolific in each participant's profile with the service. Our inclusion criteria were: young adults between 20 and 45 years of age who were registered to take part in research studies on the Prolific platform; those self‐reporting one of the following dietary pattern: No Diet, No Sugar Diet, Mediterranean, or Vegetarian Diets were examined. The recruitment platform integrates seamlessly with popular survey software platforms to allow one to conduct online studies, such as our cross‐sectional behavioral study, with relative ease.

Self‐reported dietary patterns were given in response to the question “Do you currently follow any of the following diets?” for all but the No Sugar Diet, which was assessed in response to the question “Do you have any dietary restrictions?”—No Sugar Diet was not an option in the Prolific screening of diets, but was listed in the screening question for dietary restrictions (see Appendix S2 for survey details). Participants were not aware that dietary pattern was a necessary inclusion criterion for the study, which helped guard against misreporting of one's dietary pattern when re‐assessed in our survey to ensure we obtained the desired sample. By custom screening for each separate dietary pattern, we then targeted to recruit an approximately equal sample size of n = 100 for each group. Along with a self‐reported dietary pattern, we elicited each participant's self‐reported “strength of adherence” to their reported dietary preference. Therefore, our cross‐sectional data set is observational regarding dietary patterns, although there was no incentive to misrepresent one's self‐reported dietary pattern in our methodology. Rather, the protocol with Prolific's custom sample screening is that a research study is only offered to participants who meet all criteria set up by the researcher for sample eligibility, and participants had no way of knowing what participant characteristics may disqualify them from some studies but make them eligible for others. Subjects were compensated for participation using a flat fixed rate ($2.40 for a study with an estimated 18‐minute completion time) that met the Prolific platform's “fair‐pay” conditions, and an additional $1.00 bonus payment was offered as an incentive for accuracy on a randomly selected trial from the Bayes task described below. Appendix S2 contains the survey administered to participants.

Our preregistered sample size plans for n = 100 participants from each of the dietary groups was established based on an ex ante power analysis of a single regression coefficient in a linear multiple regression using G*Power 3.1.9.2. With an assumed α = .05, a total sample size of n = 400 participants has sufficient power (power of .80 as recommended for the social sciences) to identify small‐sized effects on a single variable of interest, and the sample size of n = 100 for each dietary pattern subgroup is sufficiently powered to identify medium‐sized single coefficient effects (our sample size also implies sufficient power for identifying interaction or moderating effects in the pooled sample). We additionally note that our decision task presents 20 trials of the Bayes task to each subject, which generates a panel data set of repeated measures per subject that add statistical power to the hypotheses testing.

2.2. The Bayesian decision task

The decision task is based on the design from Grether¹³ that has been modified and adopted by others in the literature.^{14, 15, 21} Assume two boxes are each populated with three balls. As shown in Figure 1, the LEFT box has two black and one white ball. Either the LEFT or RIGHT box will be selected in a trial. The participant is not told which box is selected for the current trail, but she is presented with two sources of information with which to form beliefs regarding which box was selected: the base rate or “prior odds” of either box being selected, and the results from drawing five balls with replacement from the chosen (but hidden) box. The prior odds were represented as the chances out of six that either box would be selected, ex ante, and this can be considered the initial information for that stimulus (trial). The results of the five‐ball sample draw can be considered the new evidence presented to the participant for that stimulus. As shown in Figure 1, the stimulus image offered a visually concise way to present the information to the participant, and the task varies the information on one or both dimensions across a series of 20 trials. In the original task, the response elicitation was dichotomous in the sense that, for a given set of prior odds and evidence, the participant was asked to indicate which box was thought to have been selected for that trial. Bayes rule can be used to calculate the actual posterior probability that the LEFT box was used, given the prior odds and the new sample evidence.

FIGURE 1.

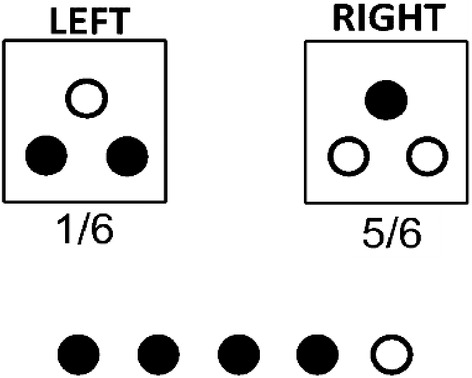
Bayes task stimulus. Example shows trial with Prior Odds of LEFT Box = 1/6 and sample evidence of four black balls drawn out of a sample draw (with replacement) of five total balls

The task we administered differed slightly from the original task¹³ in that we elicited the participant's subjective view of how likely it was that the LEFT box had been selected in that trial (ie, the “chances out of 100” that the LEFT box was used), which we call “Left Assess” ∈ [0, 100]. The incentive bonus was paid to a participant if Left Assess was within five above or below the true Bayesian probability on a randomly selected trial, and participants were fully aware of this. Table 1 shows the specific combinations of prior odds and evidence we used across the 20 total trials administered to each participant. The combinations of prior odds and evidence allowed us to identify 14 of these trials as “Hard” trials, which we defined as trials where the prior odds and evidence pointed towards different conclusions. For example, if the prior odds of the LEFT box were 4/6 (indicating the LEFT box is more likely to be used) but the number of black balls drawn in the sample evidence was 1 out of 5 (ie, a draw more likely if the RIGHT box rather than the LEFT box is used, given the LEFT box is populated with more black balls), then that stimulus is considered a “Hard” trial because the two sources of information each point towards a different box as more likely. The remaining six trials we considered “Easy” trials because the two information sources point toward the same box as being more likely (or, in the cases where the prior odds are 3/6, the prior odds are uninformative and the evidence should dictate which box is considered more likely to have been used). The 14 Hard trial stimuli are shaded, and the Easy trial stimuli are unshaded, in Table 1. Each subject saw the same set of stimuli, but the survey software presented the stimuli in randomized order to each participant.

TABLE 1.

Experimental design—Bayesian probability of box A (Bpr) given base rates and evidence (#stimuli per odds‐evidence combination shown in parenthesis)

Evidence in favor of LEFT Box (has 2 black balls 1 white ball)
Prior Odds of LEFT Box Selection	Black Balls = 0	Black Balls = 1	Black Balls = 2	Black Balls = 3	Black Balls = 4	Black Balls = 5	Total n
0/6						Bpr = 0.00	1
1/6				Bpr = .29	Bpr = .62	Bpr = .86	3
2/6			Bpr = .20	Bpr = .50	Bpr = .80	Bpr = .94	4
3/6		Bpr = .11	Bpr = .33	Bpr = .67	Bpr = .89		4
4/6	Bpr = .06	Bpr = .20	Bpr = .50	Bpr = .80			4
5/6	Bpr = .13	Bpr = .38	Bpr = .71				3
6/6	Bpr = 1.00						1
Total n	3	3	4	4	3	3	TOTAL STIMULI = 20

Note: Of the total possible combinations of prior odds and evidence, the indicates cells show the stimuli used and the Bayesian probability (Bpr) of that particular “Evidence” and “Prior Odds” combination for the stimulus. We classified 14 Hard (shaded) and six Easy (dashed border) trials among the set of 20 stimuli presented to each participant. Two degenerate choices (the extreme probabilities of 1 and 0) should constitute an “easy” choice for one fully understanding the task, but we employed the convention to label as “Hard Trials” those trials where the evidence and the prior odds point to opposing boxes (eg, Evidence indicated a more likely LEFT box used, but the Prior Odds indicated a more likely RIGHT box used). This is a more defensible categorization of Hard vs Easy trials given our modification of the task to elicit probabilities rather than a dichotomous response of Left or Right (in which case Bayesian probabilities closer to .50 indicate more difficult dichotomous choices, as categorized in Reference ¹⁵).

2.3. Variables

The key dependent variables generated from the Bayesian task include accuracy (Accuracy—at the participant and trial level) and two constructed variables, Bin Accuracy and Left Choice. Bin Accuracy measure accuracy dichotomously in a way that allows more direct comparison to previous research,^{14, 15} and Left Assess is transformed into a dichotomous measure, Left Assess, to allow our preregistered plan to estimate a decision model similar to previous research—early studies elicited a dichotomous choice of what one thought was the more likely box used, as opposed to our modification to elicit a continuous probability estimate in each trial. Specifically, we defined Left Choice = 1 if Left Assess > 50 (Left Choice = 0 if Left Assess < 50). This assumes that, had the participant been restricted to a dichotomous selection of the LEFT or RIGHT box, one's choice would be dictated by a subjective assessment of which box was more likely given the available information. Our plan to focus on this constructed variable, Left Choice, for the decision model analysis does not imply that we failed to exploit our continuous probability assessment measure in other analysis. For each trial for each participant, accuracy is defined continuously based on the absolute difference between Left Assess and the true probability for that trial (defined in the $\left[0,1\right]$ interval), given the base rate odds and the evidence:

$$\mathit{\text{Accuracy}}=1-\left|\left(\mathit{\text{Left Assess}}/100\right)-\mathit{\text{True Bayesian Probability}}\right|\in \left[0,1\right].$$

This continuous measure, Accuracy, is also used to construct Avg Accuracy measures that average across all trials, or across the subset of Hard or Easy trials. Accuracy will also be used in analysis by considering the data as a panel of 20 trials per participant. We also preregistered our plan to construct the binary measure of accuracy, Bin Accuracy, which equals 1 if the individual correctly identified the Bayesian more likely outcome. For example, if the true Bayesian probability of the LEFT box on a given trial was 0.64 and Left Assess for that participant on that trial was between 51 and 100, then we set Bin Accuracy = 1 (otherwise, Bin Accuracy = 0). While this constructed variable wastes some information, it allows a direct comparison to past research. The dichotomous dependent measures, Bin Accuracy and Left Choice, were preregistered as our way to conduct analysis replicating previous studies that have used this task, which helps relate our results to a broader literature.

Regarding covariates measures collected in the study, we obtained data on age, gender, cognitive measures, and dietary pattern descriptors. In addition to Age and Female (=1) as controls, we captured measures intended to described the cognitive reflection style of the individual (CRT score) and sleep measures that may help describe one's cognitive state, Last Week Avg Sleep and Sleepiness. CRT score is the individual's outcome ∈ [0, 6] on a six‐item version of the cognitive reflection test²² that measures one's style of thinking (high scores indicate more reflective and less impulsive thinking style). Sleepiness has been formally examined in the context of sleep deprivation for its impact on Bayesian decision making in this specific task,¹⁴ and so we included the commonly used nine‐item Karolinska sleepiness scale as a measure of current subjective sleepiness.²³ Additionally, we elicited a self‐report in the survey for one's average nightly sleep level over the prior week, Last Week Avg Sleep. Dietary pattern was further described with the variables Stick‐to‐Diet, which measured one's self‐reported strength of adherence to the dietary pattern indicated, and Supplements (=1) if the individual self‐reported taking dietary supplements. Finally, we preregistered plan to collect response times (RT) data on each decision trial, which allowed us to test our Hypothesis 3.

Participants were identified by the dietary pattern by use of indicator variables. Specifically, we constructed four dichotomous variables whose values would equal l (otherwise, 0) to identify the dietary pattern of the participant: No Diet, Mediterranean Diet, Vegetarian Diet, and No‐Sugar Diet. In the analysis that follows, we typically used the No Diet group as the reference category for our analysis. Importantly, the recruitment procedure was such that participants did know that dietary pattern was the reason they were invited into the study. The Prolific platform simply makes available studies for which the participant is eligible, and they choose to accept of decline participation. This helps minimize selection bias in the sense that participants did not report a particular dietary pattern just to gain eligibility to our study.

2.4. Statistical methods

Differences in covariate measures by dietary group were examined in pairwise group comparisons using nonparametric proportions tests or Mann‐Whitney median tests. We conducted analysis using both parametric and nonparametric methods to assess accuracy and response times from the task. Mann‐Whitney nonparametric tests were used to compare Avg Accuracy, Bin Accuracy, and RT on Bayes task stimuli by dietary group. Parametric analysis involved multivariate analysis with different levels of covariate controls. In this analysis, some models included a control for the participant's average response time, Avg RT, as an independent measure predicting Avg Accuracy. This parametric analysis was conducted at the participant level, pooling outcomes across all trials for each participant, to examine Avg Accuracy as a function of dietary group. Analysis was conducted on all trials, as well as on subsets of Hard or Easy trials. Analogous panel data estimations were conducted on the trial‐level data to model and test for determinants of Accuracy. In these instances, errors were clustered at the level of the participant to account for the panel nature of the data set (ie, 20 trials per participant: 14 Hard, six Easy trials).

Decision models were estimated using nonlinear probit analysis to predict the likelihood a participant chose the LEFT box as the more likely box, as a function of the base rate odds in favor of the LEFT box and the sample evidence likelihood of coming from the LEFT box. Here, we excluded trials for which Left Assess = 50 (this excludes 627 observations, or approximately 7.6% of the data, from the decision model analysis). Though we did not preregister our plan to do exclude these observations, it is clear that Left Choice is not uniquely defined when Left Assess = 50. All models were estimated with differing sets of covariates. Dietary group indicators entered in as independent variables in analysis of Accuracy and Left Choice. However, because Hypothesis 4 implies a test of decision weights by dietary group, we also estimated decision models predicting Left Choice on each separate dietary group. In general, our sensitivity analysis involved comparing accuracy both at the subject and trial level, across Hard vs Easy vs Pooled trials, and using models with and without additional covariates. Similarly, decision model sensitivity analysis involved the estimation of models with and without additional covariates, and on pooled (all trials) data as well as subsets of Hard and Easy trials data.

3. RESULTS

At the time of the study (April 1–3, 2020) the overall participant pool in Prolific was reported as n = 148 043 individuals. Within the desired age range, those eligible with the desired dietary patterns were: No Diet (n = 48 757); No Sugar Diet (n = 671); Mediterranean Diet (n = 3938); Vegetarian Diet (n = 3938). Our final sample size by dietary preference was: No Diet (n = 110), Mediterranean or “Medit” Diet (n = 104), Vegetarian or “Veggie” Diet (n = 108), and No‐Sugar Diet (n = 105). Table 2 shows the summary statistics on key individual‐specific control measures that will be used as independent variables in our analysis. Differences across mean or median values in paired comparisons of dietary pattern samples were tested using the two‐sample proportions test for dichotomous indicators Female and Supplements, or Mann‐Whitney tests for other variables. We report no significant differences in CRT score, Last Week Avg Sleep, or Sleepiness in any of the six paired comparisons across dietary group samples (P > .05 in each instance). Some differences across samples were found regarding Age, Female, Stick‐to‐diet, and Supplements. Regarding Age, participants were younger in No Diet compared to both Veggie Diet and No Sugar Diet participants (P < .01 in both tests), and both Medit Diet and Veggie Diet participants were younger than in No Sugar Diet (P < .01 in both tests). Proportions of Female participants were different in all pairwise sample comparisons (P < .05 or better) except in comparisons of No Diet vs Medit Diet and Medit Diet vs No Sugar Diet (P > .05). The most stark characteristic difference is perhaps the significantly higher proportion of Female participants in the Veggie Diet group compared to others.

TABLE 2.

Summary statistics

Variable	No diet	Mediterranean diet	Vegetarian diet	No sugar diet
Age	Mean: 26.827 sd: 5.744	Mean: 28.077 sd: 6.601	Mean: 29.130 sd: 6.440	Mean: 32.505 sd: 6.574
Female (=1)	Number (prop) 37 (33.636)	Number (prop) 43 (41.346)	Number (prop) 85 (78.704)	Number (prop) 53 (50.476)
CRT score	Mean: 3.700 sd: 2.057	Mean: 3.250 sd: 2.075	Mean: 3.426 sd: 1.987	Mean: 3.229 sd: 2.075
Stick‐to‐Diet	Mean: 5.891 sd: 1.941	Mean: 6.548 sd: 1.461	Mean: 8.065 sd: 1.536	Mean: 6.676 sd: 1.542
Supplements (=1)	Number (prop) 23 (20.909)	Number (prop) 23 (22.115)	Number (prop) 51 (47.222)	Number (prop) 38 (36.190)
Last week avg sleep	Mean: 7.355 sd: 1.163	Mean: 7.337 sd: 1.092	Mean: 7.456 sd: 1.200	Mean: 7.096 sd: 1.336
Sleepiness	Mean: 4.036 sd: 1.781	Mean: 3.904 sd: 1.862	Mean: 3.907 sd: 1.748	Mean: 4.019 sd: 1.819
Total participants (passed attention check)	110 (106)	104 (100)	108 (105)	105 (101)

Note: Of these total 427 participants, analysis was conducted on the n = 412 who passed the attention check within the survey (as was preregistered).

Abbreviations: number, number of participants; prop, proportion; sd, standard deviation.

Comparisons of differences in adherence to dietary preference and the use of dietary supplements was also present across our samples. Specifically, all participant in the specialized dietary categories (Medit, Veggie, and No Sugar) reported stronger adherence to their dietary choice than did the No Diet group (P < .01 in each test)—for the No Diet group, non‐adherence was presented to participants as a situation where one might try out different specific dietary patterns or follow what friends are doing. Also, those in the Veggie Diet sample reported a stronger adherence to the dietary pattern than did those either in the Medit Diet or No Sugar Diet groups (P < .01 in each test). Finally, regarding the use of dietary supplements, the proportion of participants in No Sugar and Veggie Diet who reported taking supplements was higher than with No Diet or Medit Diet participants (P < .01 for each test). However, there was no significant difference in Supplements between participants in Medit vs No Diet or Veggie vs No Sugar Diet (P > .05 in each instance).

3.1. Hypotheses 1 to 3 tests

The key hypothesis tests were conducted using multivariate regression analysis. Hypotheses 1 to 3 can each be evaluated using participant‐level data (pooling outcomes across trials) as well as using trial‐level data. We present evidence using both approaches, as well as sensitivity analysis using alternative specifications. For trial‐level analysis, the panel data set includes 20 trials per participant (14 Hard, six Easy). For this analysis 15 participants (3.5% of the sample) who failed the poison pill question in the survey were omitted, resulting in a sample of n = 412 participants included in the analysis. Our preregistration plan included nonparametric tests of Avg Accuracy and Bin Accuracy across dietary groups, for measures averaged across all trials as well as averaged just across the subsets Hard vs Easy trials. The results of these unconditional nonparametric tests, which are supported by multivariate estimation results we report in the main text, are given in Table S1.

Tables 3, 4, 5, 6 show estimation results used to evaluate Hypotheses 1 to 3 at the participant‐level as well as trial‐level. Participant‐level specifications are used in Tables 3 and 4 to examine whether dietary patterns significantly impact one's average level of Bayesian accuracy, which involves an evaluation of the coefficient estimates on the dietary pattern indicator variables (No Diet is the omitted reference group). Table 4 estimates similar models with the inclusion of a control variable for the Avg RT across trials (depending on the model, all trials, Hard trials, or Easy trials), which is used to test Hypothesis 3. Regressions both with and without additional control measures were also estimated. Positive and significant coefficient estimates on No Sugar Diet, Medit Diet, and Veggie Diet would support Hypothesis 1 in the models (1) and (2). Hypothesis 2 would involve a comparison of these coefficient estimates in the Hard vs Easy trial models of Tables 3 and 4. Our results are robust and fail to support either Hypothesis 1 or Hypothesis 2. There is no evidence in the pooled data (subject level) that individuals in any of the specialized dietary patterns had average Bayesian accuracy that was higher than for those in the No Diet group. If anything, Table 3 shows modest evidence that those following a No Sugar diet had average Bayesian Accuracy levels that were lower than those from the No Diet group, although this evidence fades in Table 4 when the additional control for Avg RT is included in models (2), (4), and (6) that include the full set of control measures. The positive and significant coefficient estimates on Avg RT in Table 4 support the initial premise of Hypothesis 3—longer Avg RT predicts increase Avg Accuracy in all types of trials. However, it does not appear that this effect differs across Easy vs Hard trials, which does not support the second component of Hypothesis 3. Thus, we report partial support for Hypothesis 3.

TABLE 3.

Subject‐level specifications (Hypotheses 1 and 2 tests)

Dep var: Avg accuracy ∈ [0,1]	All trials (20 trials per subject)		Hard trials (14 trials per subject)		Easy trials (six trials per subject)
Variable	(1) Coef (SE) [P‐value]	(2) Coef (SE) [P‐value]	(3) Coef (SE) [P‐value]	(4) Coef (SE) [P‐value]	(5) Coef (SE) [P‐value]	(6) Coef (SE) [P‐value]
Constant	0.768 (.008) [.000]	0.730 (.040) [.000]	0.756 (.008) [.000]	0.700 (.045) [.000]	0.796 (0.009) [.000]	0.800 (0.045) [.000]
No Sugar Diet (=1)	−0.033 (.011) [.003]	−0.023 (.012) [.050]	−0.035 (.013) [.006]	−0.022 (.013) [.089]	−0.029 (.012) [.016]	−0.024 (.013) [.071]
Medit Diet (=1)	0.0197 (.011) [.068]	−0.014 (.011) [.190]	−0.024 (.013) [.054]	−0.017 (.012) [.162]	−0.011 (.012) [.372]	−0.007 (.012) [.548]
Veggie Diet(=1)	−0.0125 (.011) [.255]	−0.008 (.012) [.531]	−0.017 (.012) [.180]	−0.009 (.014) [.510]	−0.003 (.012) [.819]	−0.004 (.014) [.754]
Age	‐	−0.001 (.001) [.145]	‐	−0.001 (.001) [.188]	‐	−0.001 (.001) [.223]
Female (=1)	‐	−0.008 (.008) [.316]	‐	−0.015 (.010) [.109]	‐	0.007 (.010) [.434]
CRT score	‐	0.010 (.002) [.000]	‐	0.011 (.002) [.000]	‐	0.008 (.002) [.000]
Stick to Diet	‐	0.001 (.002) [.571]	‐	0.001 (.003) [.593]	‐	0.001 (.003) [.672]
Supplements (=1)	‐	0.007 (.008) [.440]	‐	0.009 (.010) [.364]	‐	0.002 (.010) [.873]
Last Week Sleep level	‐	−0.0002 (0.003) [.935]	‐	0.001 (.004) [.772]	‐	−0.003 (.004) [.360]
Sleepiness	‐	0.003 (0.002) [.115]	‐	0.004 (.002) [.073]	‐	0.001 (.002) [.651]
N	412	412	412	412	412	412
R 2	.0224	.1112	.0194	.1119	.0170	.0548

Note: P‐values given are for two‐tailed tests (one‐tailed tests appropriate for preregistered hypotheses).

Abbreviation: SE = standard errors.

TABLE 4.

Subject‐level specification with response time control (Hypothesis 3)

Dep var: Avg accuracy∈ [0,1]	All trials (20 trials per subject)		Hard trials (14 trials per subject)		Easy trials (six trials per subject)
Independent variable	(1) Coef (SE) [P‐value]	(2) Coef (SE) [P‐value]	(3) Coef (SE) [P‐value]	(4) Coef (SE) [P‐value]	(5) Coef (SE) [p‐value]	(6) Coef (SE) [P‐value]
Constant	0.739 (.009) [.000]	0.724 (.039) [.000]	0.726 (.010) [.000]	0.705 (.043) [.000]	0.785 (.009) [.000]	0.796 (.045) [.000]
No Sugar Diet (=1)	−0.025 (.011) [.017]	−0.018 (.011) [.117]	−0.027 (.012) [.026]	−0.017 (.013) [.178]	−0.026 (.012) [.031]	−0.022 (.013) [.097]
Medit Diet (=1)	−0.021 (.011) [.052]	−0.015 (.010) [.142]	−0.025 (.012) [.037]	−0.019 (.012) [.115]	−0.011 (.012) [.381]	−0.008 (.012) [.540]
Veggie Diet (=1)	−0.011 (.010)	−0.007 (.012) [.580]	−0.017 (.012) [.151]	−0.010 (.013) [.466]	−0.000 (.012) [.995]	−0.002 (.014) [.864]
Average RT	0.001 (.000) [.000]	0.001 (.000) [.000]	0.001 (.000) [.000]	0.001 (.000) [.000]	0.001 (.000) [.006]	0.0004 (0.000) [.027]
Age	‐	−0.001 (.001) [.109]	‐	−0.001 (.007) [.138]	‐	−0.001 (.001) [.220]
Female (=1)	‐	−0.008 (.008) [.318]	‐	−0.015 (.009) [.109]	‐	0.008 (.010) [.431]
CRT score	‐	0.008 (.002) [.000]	‐	0.009 (.002) [.000]	‐	0.007 (.002) [.002]
Stick to Diet	‐	0.001 (.002) [.592]	‐	0.001 (.003) [.617]	‐	0.001 (.003) [.679]
Supplements (=1)	‐	0.007 (.008) [.401]	‐	0.009 (.009) [.337]	‐	0.002 (.010) [.853]
Last Week Sleep level	‐	−0.001 (.003) [.654]	‐	−0.000 (.004) [.933]	‐	−0.004 (.004) [.322]
Sleepiness	‐	0.003 (.002) [.094]	‐	0.004 (.002) [.064]	‐	.001 (.002) [.616]
N	412	412	412	412	412	412
R 2	.1170	.1755	.1072	.1708	.0353	.0663

Note: P‐values given are for two‐tailed tests (one‐tailed tests appropriate for preregistered hypotheses).

Abbreviation: SE = standard errors.

TABLE 5.

Trial‐level analysis of Bayesian accuracy—All trials

Dep var: Accuracy∈ [0,1]	All trials (20 trials per subject)
Independent variable	(1) Coef (SE) [P‐value]	(2) Coef (SE) [P‐value]	(3) Coef (SE) [P‐value]
Constant	0.758 (.010) [.000]	0.720 (.042) [.000]	0.718 (.043) [.000]
No Sugar Diet (=1)	−0.033 (.011) [.003]	−0.023 (.011) [.049]	−0.022 (.011) [.051]
Medit Diet (=1)	−0.020 (.012) [.088]	−0.014 (.012) [.226]	−0.014 (.012) [.222]
Veggie Diet (=1)	−0.013 (.011) [.261]	−0.008 (.012) [.527]	−0.008 (.012) [.529]
Trial	0.001 (.000) [.016]	0.001 (.000) [.016]	0.001 (.000) [.009]
Response time (sec)	‐	‐	0.00007 (.000) [.088]
Age	‐	−0.001 (.001) [.172]	−0.0009 (.001) [.170]
Female (=1)	‐	−0.007 (.008) [.294]	−0.008 (.008) [.294]
CRT score	‐	0.010 (.002) [.000]	0.010 (.002) [.000]
Stick to Diet	‐	0.001 (.002) [.571]	0.001 (.002) [.572]
Supplements (=1)	‐	0.007 (.008) [.401]	0.007 (.008) [.398]
Last Week Sleep level	‐	−0.0003 (.004) [.940]	−0.0003 (.000) [.925]
Sleepiness	‐	0.003 (.002) [.076]	0.003 (.002) [.074]
n	8240	8240	8240
Wald (Χ 2) test	14.50 [.006]	56.17 [.000]	58.68 [.000]
R2 (overall)	.0035	.0149	.0156

Note: Random effect generalized least squares estimates with error clustered at the subject level (412 clusters). P‐values given are for two‐tailed tests (one‐tailed tests appropriate for preregistered hypotheses).

Abbreviation: SE = standard errors.

TABLE 6.

Trial‐level analysis of Bayesian accuracy—hard vs easy trials

Dep var: Accuracy∈ [0,1]	Hard trials (14 trials per subject)			Easy trials (six trials per subject)
Independent variable	(1) Coef (SE) [P‐value]	(2) Coef (SE) [P‐value]	(3) Coef (SE) [P‐value]	(4) Coef (SE) [P‐value]	(5) Coef (SE) [P‐value]	(6) Coef (SE) [P‐value]
Constant	0.746 (.011) [000]	0.690 (.048) [.000]	0.688 (.048) [.000]	0.786 (.011) [.000]	0.789 (.046) [.000]	0.785 (.047) [.000]
No Sugar Diet (=1)	−0.034 (.013) [.007]	−0.022 (.013) [.086]	−0.022 (.013) [.091]	−0.030 (.013) [.020]	−0.024 (.014) [.093]	−0.023 (.014) [.100]
Medit Diet (=1)	−.024 (.0134) [.072]	−0.017 (.013) [.198]	−0.017 (.013) [.194]	−0.012 (.013) [.364]	−0.008 (.013) [.535]	−0.008 (.013) [.524]
Veggie Diet (=1)	−0.016 (.013) [.187]	−0.009 (.013) [.508]	−0.009 (.013) [.506]	−0.003 (.012) [.789]	−0.005 (.015) [.729]	−0.004 (.014) [.758]
Trial	0.001 (.001) [.059]	0.001 (.001) [.056]	0.0011 (.001) [.030]	0.001 (.001) [.102]	0.001 (.001) [.105]	0.001 (0001) [.048]
Response time (sec)	‐	‐	0.0001 (.000) [.036]	‐	‐	0.0002 (.000) [.074]
Age	‐	−0.001 (.001) [.201]	−0.001 (0.001) [.196]	‐	−0.001 (.001) [.255]	−0.001 (.001) [.259]
Female (=1)	‐	−0.015 (.009) [.093]	−0.015 (.009) [.093]	‐	0.008 (.009) [.408]	0.008 (.009) [.405]
CRT score	‐	0.011 (.002) [.000]	0.011 (.002) [.000]	‐	0.008 (.002) [.000]	0.007 (.002) [.000]
Stick to Diet	‐	0.001 (.003) [.582]	0.001 (.003) [.583]	‐	0.001 (.003) [.665]	0.001 (.003) [.667]
Supplements (=1)	‐	0.009 (.009) [.328]	0.009 (.009) [.325]	‐	0.002 (.009) [.864]	0.002 (.009) [.855]
Last Week Sleep level	‐	0.001 (.004) [.796]	0.001 (.004) [.816]	‐	−0.003 (.004) [.386]	−0.003 (.004) [.372]
Sleepiness	‐	0.004 (.002) [.045]	0.004 (.002) [.044]	‐	0.001 (.002) [.640]	0.001 (.002) [.629]
n	5768	5768	5768	2472	2472	2472
Wald (Χ 2) test	10.82 [.029]	53.04 [.000]	56.22 [.000]	9.24 [.055]	26.94 [.005]	33.48 [.001]
R2 (overall)	.0033	.0163	.0171	.0057	.0156	.0176

Note: Random effect generalized least squares estimates with error clustered at the subject level (412 clusters). P‐values given are for two‐tailed tests (one‐tailed tests appropriate for preregistered hypotheses).

Abbreviation: SE = standard errors.

We next turn to an evaluation of Hypotheses 1 to 3 using the panel data set of trial‐level observations. Here, the estimation results in Tables 5 and 6 are from specifications similar to the participant‐level analysis, with the addition of a Trial (=1‐10) control to account for learning across trials, and Response Time (in model 3 of Table 5 and models 3 and 6 of Table 6) of the trial used to evaluate Hypothesis 3. These estimations are random effects generalized least squares estimations with error terms clustered at the subject level to account for the non‐independence of the error term across trials for a given participant.

Results in Tables 5 and 6 largely mirror the results found in the pooled data analysis, which increases our level of confidence that we have identified the true effects in our data, some of which are null effects. Again, the evidence does not support Hypotheses 1 or 2 in Tables 5 and 6, and there is marginal evidence in the most complete specifications (P < .10) that No Sugar diet is associated with less accurate Bayesian assessments compared to a No Diet individual. The findings here are summarized in Figure 2, which shows the coefficient plots of the impact of dietary pattern on Accuracy at the trial level reported across the various specifications of Tables 5 and 6. Regarding Hypothesis 3, because it is difficult to identify differences in Tables 5 and 6 estimates of the RT coefficient given our rounding convention, Figure 3 presents these in the form of coefficient plots. Here, we display the RT estimates from model (3) of Table 5, and models (3) and (6) of Table 6, along with estimates from two other simple specifications, to further highlight our view of the Hypothesis 3 evidence. While it is clear that larger values of RT for a trial predicted an increased Accuracy in that trial, this beneficial effect of RT was not significantly different across types of trials (Easy vs Hard). Thus, we conclude partial support for Hypothesis 3, but we fail to find support for Hypotheses 1 and 2 in our data.

FIGURE 2.

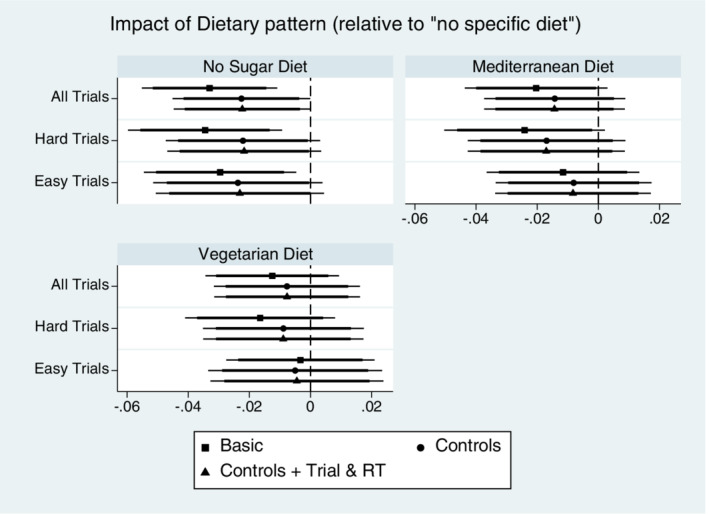
Accuracy Impact of dietary pattern on Bayesian accuracy. Coefficient estimates of Dietary pattern indicator variables describing Bayesian accuracy relative to the reference group of “no specific dietary pattern.” Point estimates shown with 95% (thin line) and 90% (thick line) confidence intervals for models with varied specifications of control variables and sample of trial difficulty. Coefficient estimates are from Tables 5 and 6 estimation results

FIGURE 3.

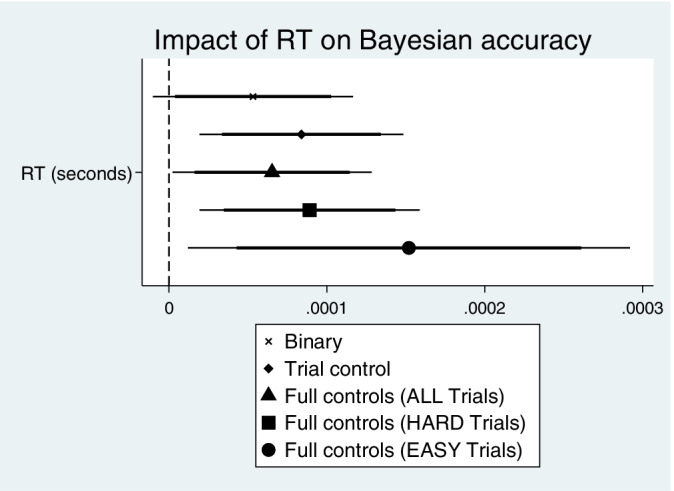
Response time impact on accuracy. Coefficient estimates shown are of the Response Time binary indicator variable in the trial‐level models of Accuracy. Point estimates shown with 95% (thin line) and 90% (thick line) confidence intervals for models with varied specifications of control variables and sample of trial difficulty. See model 5 in Table 5 and models 3 and 6 in Table 6 for the “Full controls” estimation results (full estimation results for the “Binary” and “Trial controls” models available on request)

Tables 3, 4, 5, 6 also highlight some exploratory findings that were not identified as hypotheses in our preregistration plans. For example, we found robust support across Tables 3, 4, 5, 6 that participants with higher CRT score have higher Bayesian accuracy. This supports the exploratory hypothesis that more reflective thinkers do better in Bayesian decision environments. Also, the coefficient estimates on the Trial variable in Tables 5 and 6 showed some support for the exploratory hypothesis that participants learn over time and improve accuracy across trials. While results regarding Sleepiness are less clear, the trial‐level estimation results in Table 6 models (2) and (3) indicated that sleepier participants had higher accuracy than less sleepy participants on Hard trials. This result is counter‐intuitive, but may give an indication of additional (and effective) compensatory effort expended in difficult Bayesian choice environments when aware of one's sleepiness.

3.2. Hypothesis 4 test

To estimate the Bayesian decision model for comparison with previous research, we first constructed the binary indicator, Left Choice, which equals one if the participant's probably assessment, Left Assess, was greater than 50 chances out of 100. This allows estimation of a model based on the dichotomous Left Choice measure where results can be directly compared to those in previous studies. The Bayesian decision model follows Grether,¹³

$$Y_{\mathit{it}}^{*}=\alpha +{\beta }_1\mathit{\text{lnLR}}{\left(L\right)}_t+{\beta }_2\mathit{ln}{\left(\frac{P_L}{1-P_L}\right)}_t+{\mu }_i+{\varepsilon }_{\mathit{it}}.$$ (1)

Here, $Y_{\mathit{it}}^{*}$ is the subjective log odds in favor of the LEFT box in trial t for subject i, which is a function of both evidence and base rate information in favor of the LEFT box for that trial. The key independent measures represent the base rate odds and evidence information of that trial, and the econometric specification is based on the foundation that one's subjective assessment of the event's likelihood, according to Bayes' rule, is a function of one's base rate assessment (the prior odds in our environment) and the new information (the sample evidence in our environment). In this choice setting, lnLR(L)_t is the “evidence” measure, which is defined as the log of the statistical likelihood ratio of the LEFT box—this likelihood ratio is likelihood of observing the sample evidence if the balls were drawn from the LEFT box divided by the likelihood of observing that sample if the balls were drawn from the RIGHT box. To capture the base rate odds of a given trial, $\mathit{ln}{\left(\frac{P_L}{1-P_L}\right)}_t$ is the log of the base rate odds ratio for the LEFT box (p _L is the prior odds that the LEFT box will be used for that trial. Together, we will refer to lnLR(L) and $\mathit{ln}{\left(\frac{P_L}{1-P_L}\right)}_t$ as the “Evidence” and “Base Rate” variables, respectively. As noted in Grether (198), $Y_{\mathit{it}}^{*}$ is typically not observed, and so the model can be estimated using probit techniques, where the observable dependent variable $Y_{\mathit{it}}$ equals one when $Y_{\mathit{it}}^{*}\ge 0$. We use our constructed variable, Left Choice, as the dependent variable in the model for a more direct comparison of our results with previous research. A Bayesian subject should place equal weight on both sources of information in forming one's belief, though a less strict interpretation of a Bayesian decision maker would simply assess whether or not significant weight is placed on both sources of information.

Table 7 reports marginal effects from the estimation of the basic decision model (1), along with the results from specifications that include main effect indicators for dietary categories and addition control variables from our previous regression specifications. The models are estimated for all trials as well as exclusively for the subset of Hard and Easy trials. Note that in the specifications given in Table 7, the coefficient estimates on the dietary indicators are not a test of Hypothesis 4, as there is no reason any particular diet should lead one to more likely indicate LEFT box in a given trial. Table 7 estimations serve to replicate previous findings that individuals weigh both the base rate odds and new evidence in making their assessment of a more likely LEFT or RIGHT box used for that trial. Results are consistent across the various specifications, with the key information variable coefficient weights summarized in the coefficient plots of Figure 4 (these are not marginal effects, but rather coefficient estimate plots that reflect the same qualitative differences as found in the marginal effects). While significant (positive) decision weight is placed on both sources of information, the overall tendency in the full sample is to weight evidence more than base rates odds.

TABLE 7.

Trial‐level analysis of Bayesian decision model

Dep Var = Left choice = 0,1	All trials (20 trials per subject)			Hard trials (14 trials per subject)			Easy trials (six trials per subject)
Independent Variable	(1) Coef (SE) [P‐value]	(2) Coef (SE) [P‐value]	(3) Coef (SE) [P‐value]	(4) Coef (SE) [P‐value]	(5) Coef (SE) [P‐value]	(6) Coef (SE) [P‐value]	(7) Coef (SE) [P‐value]	(8) Coef (SE) [P‐value]	(9) Coef (SE) [P‐value]
$\text{lnLR}\left(L\right)$ (Evidence)	0.069 (.005) [.000]	0.069 (.006) [.000]	0.069 (.006) [.000]	0.037 (.006) [.000]	0.037 (.006) [.000]	0.037 (.006) [.000]	0.163 (.010) [.000]	0.164 (.010) [.000]	0.165 (.010) [.000]
$\ln \left(\raisebox{1ex}{$P_L$}\!\left/ \!\raisebox{-1ex}{$1-P_L$}\right.\right)$ (Base rate)	0.040 (.002) [.000]	0.040 (.002) [.000]	0.040 (.002) [.000]	0.029 (.002) [.000]	0.029 (.002) [.000]	0.029 (.002) [.000]	0.135 (.036) [.000]	0.136 (.036) [.000]	0.135 (.036) [.000]
No Sugar (=1)	‐	0.024 (.020) [.241]	0.009 (.023) [.707]	‐	0.016 (.020) [.437]	0.002 (.023) [.940]	‐	0.051 (.038) [.182]	0.034 (.041) [.405]
Medit (=1)	‐	−0.001 (.019) [.967]	−0.002 (.020) [.905]	‐	−0.010 (.020) [.607]	−0.013 (.021) [.528]	‐	0.036 (.035) [.306]	0.042 (.036) [.239]
Veggie (=1)	‐	−0.001 (.017) [.969]	0.002 (.021) [.934]	‐	−0.010 (.018) [.566]	−0.006 (.023) [.800]	‐	0.040 (.034) [.235]	0.035 (.040) [.376]
Additional Controls	No	No	Yes	No	No	Yes	No	No	Yes
n	7613	7613	7613	5519	5519	5519	2094	2094	2094
Wald (Χ 2) model test	429.34 [.000]	434.86 [.000]	452.16 [.000]	225.22 [.000]	225.41 [.000]	241.39 [.000]	324.33 [.000]	332.02 [.000]	341.63 [.000]
Pseudo‐R 2	.0697	.0700	.0718	.0380	.0383	.0403	.2687	.2687	.2724

Note: P‐values given are for two‐tailed tests (one‐tailed tests appropriate for preregistered hypotheses). Probit regressions with errors clustered at the subject level. Marginal effects reported above. Additional control variable estimates in models (3), (6), and (9) are suppressed for space considerations. Trials where Left Assess = 50 were removed from analysis given they could not uniquely determine a value for the dichotomous dependent variable, Left Choice. See Table S2 for estimates of suppressed coefficients.

Abbreviation: SE = standard errors.

FIGURE 4.

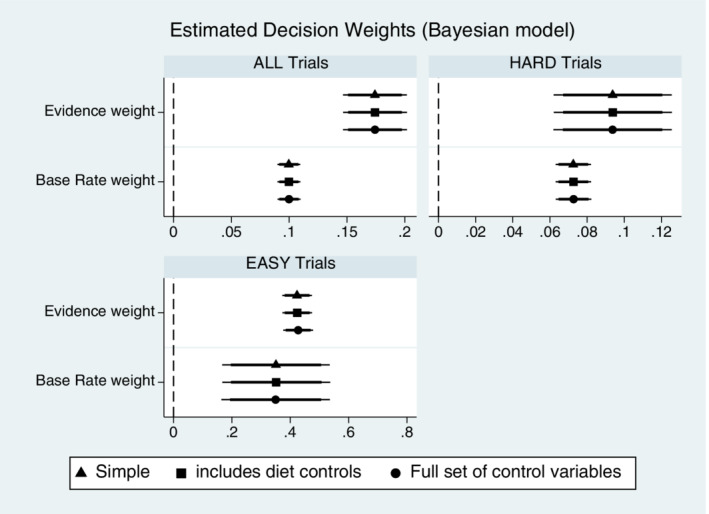
Estimated decision weights on base rates and evidence information in Bayesian decision model. Robustness analysis. X‐axis are scaled differently in each panel. See Table 7 for marginal effect of the coefficient estimates. Plots above show coefficient estimates (not marginal effects) on the information variables for the specifications in Table 7. Point estimates shown with 95% (thin line) and 90% (thick line) confidence

Table 8 shows the estimated marginal effects from the nonlinear probit decision models for the separate subsamples of each dietary group. The findings are unaffected when controlling for additional covariates (see Table S3 for these results). An alternative estimation approach would be to pool the data and evaluate Hypothesis 4 using interaction terms of each dietary group with both the base rate and evidence variables. The approach we take is one where we test the linear restriction that the weight on the base rate and evidence variables are equal for each model. Rejection of this null hypothesis indicates a significantly higher weight placed on one or the other source of information. We have already documented limited evidence to support the hypothesis that dietary patterns studied improve Bayesian accuracy relative to a No Diet group, but the decision weight model provides additional insights. The one finding from the earlier Hypotheses 1 and 2 tests was contrary to our expectation and indicated that the No Sugar group had marginally reduced Accuracy relative to the No Diet group, and so we continue to compare against the No Diet group as we interpret the Table 8 findings.

TABLE 8.

Trial‐level analysis of Bayesian decision model—By Dietary pattern (Marginal effects of Probit estimations shown)

Dep var: left choice = 0,1	All trials (20 trials per subject)				Hard trials (14 trials per subject)				Easy trials (six trials per subject)
Independent variable	No diet (1) Coef (SE) [P‐value]	No sug (2) Coef (SE) [P‐value]	Medit (3) Coef (SE) [P‐value]	Veggie (4) Coef (SE) [P‐value]	No diet (5) Coef (SE) [P‐value]	No sug (6) Coef (SE) [P‐value]	Medit (7) Coef (SE) [P‐value]	Veggie (8) Coef (SE) [P‐value]	No diet (9) Coef (SE) [P‐value]	No sug (10) Coef (SE) [P‐value]	Medit (11) Coef (SE) [P‐value]	Veggie (12) Coef (SE) [P‐value]
$\mathit{\text{lnLR}}\left(L\right)$ (Evidence)	0.082 (.012) [.000]	0.067 (.011) [.000}	0.067 (.011) [.000]	0.062 (.011) [.000]	0.053 (.013) [.000]	0.042 (.012) [.000]	0.033 (.013) [.010]	0.022 (.013) [.092]	0.129 (.018) [.000]	0.098 (.015) [.000]	0.114 (.016) [.000]	0.126 (.015) [.000]
$\ln \left(\raisebox{1ex}{$P_L$}\!\left/ \!\raisebox{-1ex}{$1-P_L$}\right.\right)$ (Base rate)	0.047 (.005) [.000]	0.030 (.003) [.000]	0.042 (.004) [.000]	0.042 (.004) [.000]	0.037 (.004) [.000]	0.022 (.003) [.000]	0.030 (.004) [.000]	0.028 (.004) [.000]	0.188 (.066) [.005]	0.148 (.065) [.026]	0.310 (.065) [.000]	0.328 (.071) [.000]
Wald (Χ 2) model test	112.50 [.000]	92.74 [.000]	97.07 [.000]	131.80 [.000]	69.27 [.000]	42.62 [.000]	53.13 [.000]	62.36 [.000]	76.64 [.000]	72.94 [.000]	82.98 [.000]	88.98 [.000]
Pseudo‐R 2	.0936	.0526	.0718	.0690	.0594	.0251	.0407	.0398	.2708	.1895	.2945	.3392
Χ2 test of Evidence = Odds weight	11.46 [.001]	13.60 [.000]	5.51 [.019]	3.10 [.078]	1.94 [.163]	3.30 [.069]	0.06 [.802]	0.24 [.626]	1.82 [.177]	1.57 [.210]	0.95 [.329]	0.27 [.606]
Observations	1973	1877	1837	1926	1412	1363	1336	1408	561	514	501	518

Note: P‐values given are for two‐tailed tests (one‐tailed tests appropriate for preregistered hypotheses). Probit regressions with errors clustered at the subject level. Marginal effects reported above. Trials where Left assess = 50 were removed from analysis given they could not uniquely determine a value for the dichotomous dependent variable, Left choice. See Table S3 for results from models that control for additional co‐variates.

Abbreviation: SE = standard errors.

To summarize the Hypothesis 4 tests, Table 8 highlights the general tendency for all dietary groups to place significantly more decision weight on the sample evidence relative to the base rate information—see results of the Χ ² coefficient tests in models (1) to (4) of Table 8 (also see Table S3). For Hard trials, we find no significant differences in the estimated decision weights on base rate vs evidence except for the No Sugar group, where a marginally significant greater decision weight is place on the evidence. For Easy trials, we estimate a statistically insignificant base rate on Easy trial from No Diet and No Sugar diet participants, but the linear test of the weights on both information sources fail to find evidence for statistically significant differences in decision weights for any of the dietary preference types (see Χ ² test results row shown in Table 8). This did not, however, translate to differences in accuracy (see Tables 5 and 6). The data thus failed to support Hypothesis 4 because all dietary groups over‐weighted the information in the pooled data estimates, and all placed statistically equal decision weight on both sources of information in Easy trials. Only in Hard trials is there some evidence that one dietary group stands apart from the others—No Sugar participants were estimated to continue overweighting evidence in Hard trials while other dietary group participants were more Bayesian. Figure 5 shows the coefficient plots for the simple specifications from Table 8. Figure 5 highlights the significant “All Trials” lesser weight placed on base rates compared to evidence across all dietary groups.

FIGURE 5.

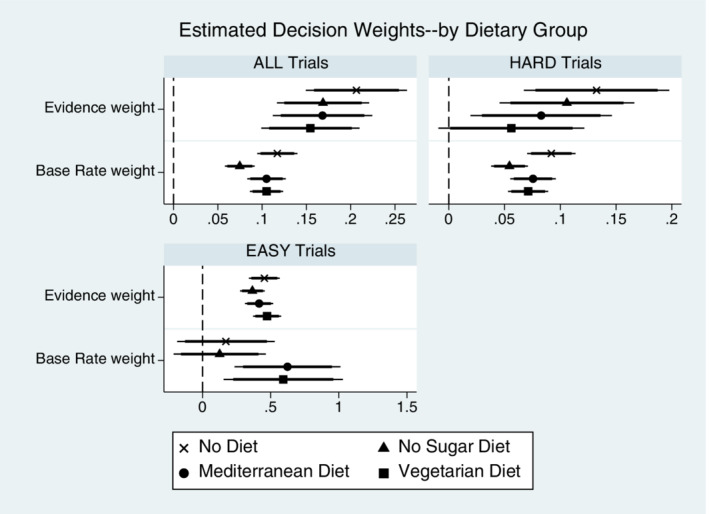
Evidence and Base Rate weights effects (by Dietary Group). X‐axis are scaled differently in each panel. See Table 8 for marginal effects of the coefficient estimates. Plots above show coefficient estimates (not marginal effects) on the information variables for simple specifications (no controls) in Table 8. Point estimates shown with 95% (thin line) and 90% (thick line) confidence. Results are qualitatively similar if estimating the models with the full set of control variables, as seen in Table 8

4. DISCUSSION

All groups achieved 70% to 80% accuracy across different trial types in the Bayesian task, but we found no evidence to support our preregistered hypotheses regarding accuracy improvements for those following several more common dietary patterns. If anything, our evidence suggests that following a No Sugar dietary pattern may harm accuracy in the task relative to not following any dietary pattern. Though research has attempted to document cognitive benefits of certain dietary patterns, our data would not support the claim that the dietary pattern itself makes any significant difference in one's ability to perform this particular cognitive task (ie, incorporating multiple sources of information into a decision).

In naturally occurring settings, individuals who pursue a particular dietary pattern likely pursue other lifestyle choices that may be important determinants of decision‐making capacity in cognitive tasks such as the Bayesian environment. It should also be noted that an individual in our data set who self‐reports a No Diet pattern may nevertheless consume healthy nutrients and/or be aligned in many ways with healthier dietary patterns that have shown some positive impact on cognitive outcome.¹² Much of the current research has defined cognitive outcomes in the context of more general metrics with a focus on limiting cognitive decline the often occurs in the elderly. Younger adults may be more resilient with respect to cognitive outcomes and dietary choice, with cumulative effects only being observed later in life.

To the extent that previous studies have shown beneficial cognitive effects of certain nutrients or dietary patterns, these studies differ from ours in important ways. We examined outcomes on a specific executive function task that involves a stricter focus on one particular component of decision making (ie, the ability to integrate multiple sources of information into a decision). Others have based conclusions of diet‐related cognitive benefits on more general assessments or more multi‐modal instruments (eg, the Mini‐Mental State Examination) to examine cognition, dementia, or age‐related cognitive decline.^{9, 12} We do not claim that information processing is the only component of executive function worth studying, but our selection of the Bayesian task was aimed at isolating the information‐integration component of decision making. Other commonly used executive function tasks, such as the Wisconsin Card Sorting Task (WCST) or the Iowa Gambling Task (IGT), involve multiple components of decision making or present confounds within the task. For example, the WCST assesses cognitive flexibility but also abstract reasoning and strategic planning. The IGT is considered a test of risk attitude by many, but unknown odds of a “good” or “bad” card in a deck implies that environment is one of uncertainty, not pure risk. Also, one may gain or lose money in the IGT, which confounds assessment of risk in the gains vs loss domains. Both the WCST and IGT tasks, as well as other executive function measures, have merit and contribute greatly to the literature. Our intent, however, was to focus on one specific component of decision making important for many consequential real‐world choices, and our task stimulus very simply presented all information in a way that would not also require working memory. Additionally, previous related research on diet and cognition typically has not incentivized one's performance on the cognitive instrument(s), and so our use of monetary incentives for quality decisions may have helped engage decision makers. Finally, recent research has documented the neural correlates of this specific Bayes task we used to be the bilateral executive function network, with both distinct and overlapping regions contributing to decision making in this particular task.²⁰ Future research may wish to examine the extent to which overlapping regions of neural activation may contribute to our null result regarding dietary patterns not having strong effects on decision making in this particular task domain.

4.1. Strengths and limitations

It is worth noting that our participants were first screened for self‐reported dietary pattern through the survey participant (Prolific) platform. They were then offered to participant in our study blind to the dietary pattern screening criteria, and this dietary pattern was then re‐assessed in our survey to verify that they matched the dietary pattern inclusion criterion. Because the initial screening was based on Prolific profile data gathered at an (unspecified) earlier point in time relative to our study, the fact that we required the participant to again pass the screening question in our survey indicates that we captured individuals who self‐reported the same dietary pattern at two different points in time. This should increase our confidence in the validity of the self‐reported dietary patterns in our data. Because participant enrolled in our study blind to the dietary pattern inclusion criteria, this means it was not possible to self‐report a particular dietary pattern just to become eligible for our study. This should limit concerns over the possibility of biased dietary pattern self‐reports in our data set.

While we felt it important in our study to restrict our focus to younger adults (eg, given our sample size per dietary group), a similar study focused on those at risk of age‐related cognitive decline would be useful. Also, a study with sufficient numbers of participants across a wider range of ages would allow for a more systematic examination of whether age moderates any link between dietary pattern and Bayesian choice (or whether any such moderating effect is linear or nonlinear). Future research should consider the importance of socioeconomic variables such as education and income level, while also considering innate cognitive abilities. Additionally, other lifestyle factors such as exercise and smoking status, or health indicators such as diabetes or BMI, were not assessed in our survey and such factors may be associated with executive functioning. Consideration of such covariates in future research would help eliminate confounds to more precisely identify the impact of dietary patterns on key decision‐making outcomes. We included a control for cognitive reflection style (CRT score), but future research could also evaluate whether innate cognitive ability moderates any potential connection between dietary pattern and decision making. One's cognitive ability or style may also contribute to one's choice of dietary pattern, although the evidence in our sample shows that no significant association between CRT score and one's dietary pattern (either in binary or with‐controls regressions of CRT score on dietary pattern indicators, P > .10 in all instances). Also, though we considered our focus on a specific and vetted high‐level cognitive task to be an asset, others may prefer examination of more general cognitive function measures. Nevertheless, we hope our study will be a useful contribution to the literature in ways that have not been previously presented.

As an observational study, this research is subject to the usual criticism that dietary intake was not experimentally varied and participants perhaps tracked over longer time periods. We also relied on self‐reported dietary pattern and did not collect data from food recall or diary reports. Participants self‐reported a relatively high adherence to their dietary pattern (mean value of 6.79 ± 1.81 on a 1 to 9 scale of adherence to dietary pattern), but we have no direct evidence on these reports. Additional research with alternative methodologies is needed to address these concerns. For this reason, we caution the reader to view our results in the context of our methodology. While these limitations exist, a strength of our data is that we generated a reasonably sized sample of data on a specific cognitive task that mimics a basic foundation of decision making (information updating), and we did so with parallel samples of individuals reporting specific dietary patterns of interest. Obviously, an experimental study is needed to generate data without confounding factors that may affect results. We captured subject‐specific information on certain characteristics that were used as co‐variates in our estimation equations, but such an econometric fix does not negate the fact that our data were generated in a largely uncontrolled environment. The generalizability of our key null findings can only be ascertained with additional research that addresses some of these methodological limitations.

5. CONCLUSION

This paper reported results from a pre‐registered study of self‐reported dietary patterns and decision making in an incentivized Bayesian decision task. The task is useful because it represents a building block environment for many more complicated decisions that involve the use of multiple information sources to make judgments. Consistent with previous research^{13, 14, 15} participants weighted both of the available information sources in making judgments. However, we found little support for our ex ante hypotheses regarding how self‐reported No Sugar, Medit, or Veggie dietary patterns would improve accuracy or lead to increased decision emphasis on both information sources over a singular source. If anything, relative to those who reported not following any specific dietary pattern, our data showed some evidence that those following a No Sugar diet may be somewhat less accurate in make Bayesian assessments in our task. While speculative, the decision model results indicated these No Sugar participants may be those who continued to overweight one source of information in the more complex decision trials. More research is needed to speak to this exploratory result. The one hypothesis for which we found partial support was not related to dietary preferences, but we did find support for our hypothesis that increased response times led to improved Bayesian accuracy (Hypothesis 3). This may be an indicator that a more deliberative thought process is in use when accuracy is higher.

Our results contribute to the literature on diet and cognitive performance. While more controlled studies are clearly needed, our findings are more aligned with the view that dietary patterns have negligible impact on decision making in precise tasks where incentives for good decisions are present. This is not to say that there are not clear and identifiable benefits of diet and certain nutrients on cognition, brain function, or overall well‐being, but in ecologically valid settings other factors may be equally important in short‐term decision quality. Related research on decision performance in settings with tight experimental controls, as well as random assignment and objective measurement of dietary intake, is worth pursuing. These and other questions are, for now, left to future research.

FUNDING

The Barnes program for faculty mentored research in the Walker College of Business at Appalachian State University funded the survey sample for this project. This funding program played no role in the design, data collection, analysis, or conclusions reached by the authors.

CONFLICT OF INTEREST

The authors report no conflicts of interest.

AUTHOR CONTRIBUTION

Conceptualization: David L Dickinson, Caleb Garbuio.

Data Curation: David L Dickinson, Caleb Garbuio.

Formal Analysis: David L Dickinson, Caleb Garbuio.

Funding Acquisition: David L Dickinson, Caleb Garbuio.

Investigation: David L Dickinson.

Methodology: David L Dickinson, Caleb Garbuio.

Project Administration: David L Dickinson, Caleb Garbuio.

Supervision: David L Dickinson.

Writing: David L Dickinson, Caleb Garbuio.

The authors declare that this research has been ethically and responsibly performed in accordance with Wiley's best practices guidelines on publishing ethics, which includes a declaration of no research misconduct. Research misconduct includes, but is not limited to, data fabrication and falsification, plagiarism, image manipulation, unethical research, biased reporting, authorship abuse, redundant or duplicate publication, or undeclared conflicts of interest.

TRANSPARENCY STATEMENT

The lead author (Dickinson) affirms that this manuscript is an honest, accurate, and transparent account of the study being reported; that no important aspects of the study have been omitted; and than any discrepancies from the study as planned (and, if relevant, registered) have been explained.

Supporting information

Appendix S1: Additional Results.

Appendix S2: Survey Administered.

Dickinson DL, Garbuio C. The influence of dietary patterns on outcomes in a Bayesian choice task. Health Sci Rep. 2021;4:e369. doi: 10.1002/hsr2.369

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are openly available on the Open Science Framework at DOI 10.17605/OSF.IO/ST94F.