Abstract
With the recent proliferation of mobile health technologies, health scientists are increasingly interested in developing just-in-time adaptive interventions (JITAIs), typically delivered via notifications on mobile devices and designed to help users prevent negative health outcomes and to promote the adoption and maintenance of healthy behaviors. A JITAI involves a sequence of decision rules (i.e., treatment policies) that take the user’s current context as input and specify whether and what type of intervention should be provided at the moment. In this work, we describe a reinforcement learning (RL) algorithm that continuously learns and improves the treatment policy embedded in the JITAI as data is being collected from the user. This work is motivated by our collaboration on designing an RL algorithm for HeartSteps V2 based on data collected HeartSteps V1. HeartSteps is a physical activity mobile health application. The RL algorithm developed in this work is being used in HeartSteps V2 to decide, five times per day, whether to deliver a context-tailored activity suggestion.
Keywords: Computing methodologies → Machine learning algorithms, Applied computing → Health care information systems, Mobile Health, Just-in-Time Adaptive Intervention, Reinforcement Learning
1. INTRODUCTION
With the recent proliferation of mobile health technologies, health scientists are increasingly interested in delivering interventions via notifications on mobile devices at the moments when they are most effective in helping the user prevent negative health outcomes and adopt and maintain healthy behaviors. The type and timing of the mobile health interventions should ideally adapt to the real-time information collected about the user’s context, e.g., the time of the day, location, current activity, and stress level. This type of intervention is called just-in-time adaptive intervention (JITAI) [28]. Operationally, a JITAI includes a sequence of decision rules (i.e., treatment policies) that take the user’s current context as input and specify whether and/or what type of intervention should be provided at the moment. Behavioral theory supplemented with expert opinion and analyses of existing data is often used to design these decision rules. However, these behavioral theories are often insufficiently mature to precisely specify which particular intervention should be delivered and when in order to ensure the interventions have the intended effects and optimize the long-term efficacy of the interventions. As a result, there is much interest in how to best use data to inform the design of JITAIs [3, 10, 12, 26, 33–35, 39, 41, 42].
In this work, we describe a reinforcement learning (RL) algorithm to continuously learn and optimize the treatment policy in the JITAI as the user experiences the interventions. This work is motivated by our collaboration on the design of the HeartSteps V2 clinical trial for individuals who have stage 1 hypertension. As the clinical trial progresses, the RL algorithm learns whether to deliver a context-tailored physical activity suggestion at each decision time.
The remainder of the article is organized as follows. We first describe HeartSteps, including HeartSteps V1 and HeartSteps V2, which is in progress at the time of writing. We then briefly introduce RL and identify key challenges in applying RL to optimize JITAI treatment policies in mobile health. Existing mobile health studies that have used RL are reviewed, as well as related RL algorithms. We then describe the HeartSteps V2 RL algorithm and the implementation and evaluation of this algorithm using a generative model built from HeartSteps V1 data. We discuss the performance of our algorithm based on the initial pilot data from HeartSteps V2. We close with a discussion of future work.
2. HEARTSTEPS V1 AND V2: PHYSICAL ACTIVITY MOBILE HEALTH STUDY
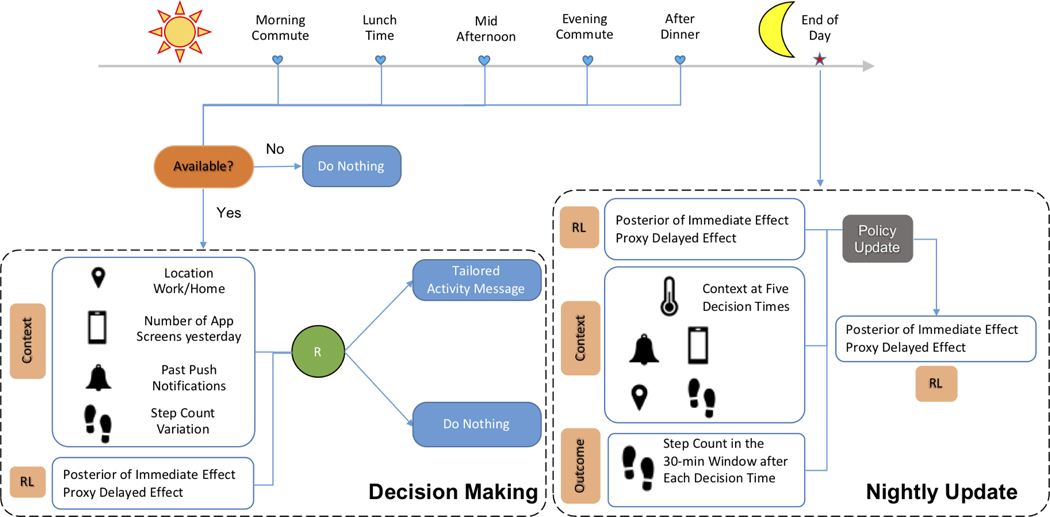
HeartSteps V2 is a 90-day physical activity clinical trial for improving the physical activity of individuals with blood pressure in the stage 1 hypertension range (120–130 systolic). In this trial, participants are provided a Fitbit tracker and a mobile phone application designed to help them improve their physical activity. The participant first wears the Fitbit tracker for one week and then installs the mobile app at the beginning of the second week. One of the intervention components is a contextually-tailored physical activity suggestion that may be delivered at any of the five user-specified times during each day. These five times are roughly separated by 2.5 hours, corresponding to the user’s morning commute, mid-day, mid-afternoon, evening commute, and post-dinner times. The content of the suggestion is designed to encourage activity in the current context and thus the suggestions are intended to impact near-time physical activity. The RL algorithm in this work is being used to decide at each time whether or not to send the activity suggestion as well as to optimize these decisions. An illustration of the study design and how the RL algorithm is used is described in Figure 1. Currently, HeartSteps V2 is being deployed in the field. We will provide an initial assessment of the proposed algorithm in Section 8.
Fig. 1.
An illustration of the study design and RL algorithm in HeartSteps V2 study. During each of the 90 days in the study, there are five user-specified decision times for potentially receiving a contextually-tailored walking suggestion message. At each decision time, the availability is first assessed. If the user is not currently available for treatment (e.g., the user is already walking or driving a vehicle), no message is sent. Otherwise, the RL algorithm uses the current context (e.g., location) and a summary of past history (e.g., yesterday’s app usage) to determine the randomization probability (i.e., πt) for sending the message; see Section 5.3 for details. After the five decision times in the day, the RL algorithm updates the treatment policy using the information collected during the day (e.g., the number of 30-minute step counts following each decision time); see Section 5.4 for details.
In order to design HeartSteps V2, our team conducted HeartSteps V1, which was a 42-day physical activity mobile health study[6, 18, 19, 25]. HeartSteps V1 has many similarities to HeartSteps V2 in terms of the intervention components but differs in the study population and the method of delivering interventions. The population in HeartSteps V1 is healthy sedentary adults. For the walking suggestion intervention component in HeartSteps V1, whether to provide a contextually-tailored walking suggestion message was randomized at each of the five user-specified times per day with a constant probability of 0.30 whenever the participant is available. The HeartSteps V1 walking suggestions have the same content as those of HeartSteps V2. While the HeartSteps V1 anti-sedentary message was randomized with probability 0.3 at the same five decision times, the anti-sedentary messages in HeartSteps V2 are delivered only when the participant has been sedentary during the past 40 minutes, with the randomization probability being adjusted on the fly to meet the average constraint on the number of anti-sedentary messages sent per day [24]. We used the data collected from HeartSteps V1 to inform the design of the RL algorithm for HeartSteps V2 (e.g., selecting the variables that are predictive of step counts and the efficacy of walking suggestion messages as well as forming a prior distribution) and to create a simulation environment (i.e., the generative model) in order to choose certain tuning parameters and evaluate the proposed RL algorithm (see Section 6 and 7 for details).
3. CHALLENGES TO APPLYING RL IN MHEALTH
Reinforcement learning (RL) is an area of machine learning in which an algorithm learns how to act optimally by continuously interacting with an unknown environment [38]. The algorithm inputs the current state, selects the next action, and receives the reward, with the goal of learning the best sequence of actions (i.e., the policy) to maximize the total reward. For example, in the case of HeartSteps, the state is a set of features of the user’s current and past context, the actions are whether to deliver an activity suggestion or not, and the reward is a function of near-time physical activity. A fundamental challenge in RL is the tradeoff between exploitation (e.g., selecting the action that seems the best given data observed so far) and exploration (to gather information to learn the best action, for example). RL has seen rapid development in recent years and shown remarkable success across many fields, such as video games, chess-playing, and robotic control. However, many challenges remain that need to be carefully addressed before RL can be usefully deployed to adapt and optimize mobile health interventions. Below we discuss some of these challenges.
-
(C1)
The RL algorithm must adjust for the longer-term effects of current action. In mobile health, interventions often tend to have a positive effect on the immediate reward, but can have a negative impact on future rewards due to a user’s habituation and/or burden [8, 17]. Thus, the optimal treatment can only be identified by taking into account the impact of current action on rewards farther into the future. This is akin to using a large discount rate (i.e., a long planning horizon) in RL.
-
(C2)
The RL algorithm should learn quickly and accommodate noisy data. Most online RL algorithms require the agent to interact many times with the environment prior to performing well. This is impractical in mobile health applications, as users can lose interest and disengage quickly. Furthermore, because mobile health interventions are provided in uncontrolled environments both context information and rewards can be very noisy. For example, step count data collected from a wrist band is noisy due to a variety of confounders, such as incidental hand movements. Additionally, the sensors do not detect the user’s entire context; non-sensed aspects of the current context act as sources of variance. Such a high noise setting typically requires even more interactions with the environment to select the optimal action. Additionally, while consideration of challenge (C1) motivates a long planning horizon, it has been shown that, in both practice and theory, a discount rate close to 1 often leads to high variance and slow learning rates [2, 11, 14, 21]. We need, then, to trade off carefully between bias and variance when designing the RL algorithm.
-
(C3)
The RL algorithm should accommodate some model mis-specification and non-stationarity. Since the context space is complex and some aspects of the contexts are not observed (e.g., engagement and burden), the mapping from context to reward is likely to exhibit non-stationarity over a longer period of time. Indeed, the analysis of HeartSteps V1 provides evidence of non-stationarity: there is strong evidence that the treatment effect of sending an activity suggestion on subsequent activity decreases over the time the user is in the study [19].
-
(C4)
The RL algorithm should select actions in a way such that after the study is over, secondary data analyses are feasible. This is particularly the case for experimental trials involving clinical populations. In these settings, an interdisciplinary team is required to design the intervention and to conduct the clinical trial. As a result, multiple stakeholders will want to analyze the resulting data in a large variety of ways. Thus, for example, off-policy learning [15, 40] and causal inference [4] as well as other more standard statistical analyses must be feasible after the study ends.
4. EXISTING RL-BASED MOBILE HEALTH STUDIES
There are few existing mobile health studies in which RL methods are applied to adapt the individual’s intervention in real time. Here we focus on the setting where the treatment policy is not pre-specified, but instead continuously learned and improved as more data is collected.
In [41], an RL system was deployed to choose the different types of daily suggestions to encourage physical activity in patients with diabetes in a 26-week study. The authors use a contextual bandit learning algorithm combined with a Softmax approach to select the actions (daily suggestions) to maximize increased minutes of activity. Paredes et al. [33] employed a contextual bandit learning algorithm combined with an Upper Confidence Bound approach to select the best among 10 types of stress management strategies when the participant requests an intervention in the mobile app. In [10], the authors reported a recent weight loss study in which one of three types of interventions is chosen twice a week over 12 weeks. Their RL system featured an explicit separation of exploration and exploitation: 10 decision times are predetermined for exploration (i.e., randomly selecting the intervention at each decision time) and the remaining 14 decision times are predetermined for exploitation (i.e., choosing the best intervention to maximize the expected reward based on the history). MyBehavior [34], a smartphone app that delivered personalized interventions to promote physical activity and dietary health, used EXP3, a multi-arm, context-free bandit algorithm to select the interventions. While the RL methods in the aforementioned studies aim to select actions so as to optimize the immediate reward, in a recent physical study reported in [42], the RL system at the end of every week used the participant’s historical daily step count data to estimate a dynamical model for the daily step count and used that model to infer the optimal daily step goals for the next 7 days, with the goal of maximizing the minimal step counts taken in the next week.
4.1. Existing RL Algorithms’ Insufficiency to Address Challenges
We argue that the above-mentioned RL algorithms are insufficient to address the challenges listed in Section 3 and thus we must generalize these algorithms in several directions. First, these studies use only a pure data collection phase to initialize the RL algorithms. But often there are additional data from other sources, such as a pilot study or prior expert knowledge. Challenge (C2) means that it is critical to incorporate such available information to speed up the learning in the early phase of the study. Second, the RL algorithms in these studies require knowledge of the correct model for the reward function, a requirement that is likely unrealistic due to the dimensionality and complexity of the context space and the potential non-stationarity noted in challenge (C3). It has been empirically shown that the performance of standard RL algorithms is quite sensitive to the model for the reward function [7, 12, 27]. Third, among the above-mentioned studies, only the algorithm used in [42] attempts to optimize rewards over a time period longer than the immediate time step. It turns out that there is a bias-variance trade-off when designing how long into the future the RL should attempt to optimize rewards. That is, only focusing on maximizing the immediate rewards speeds the learning rate (e.g., due to lower estimation variance) compared with a full RL algorithm that attempts to maximize over a longer time horizon. However, an RL algorithm focused on optimizing the immediate reward might end up sending too many treatments due to challenge (C1), i.e., the treatment tends to have a positive effect on immediate reward and negative effects on future rewards. Such an algorithm is likely to have a poorer overall performance than an algorithm that attempts to optimize over a longer time horizon to account for treatment burden and disengagement. Fourth, both [33] and [42] use algorithms that select the action deterministically based on the history, and [10] incorporates a pure exploitation phase. It is known that action selection probabilities close to 0 or 1 cause instability (i.e., high variance) in batch data analysis in challenge (C4) that uses importance weights, e.g., in off-policy evaluation [15, 40].
5. PERSONALIZED HEARTSTEPS: ONLINE RL ALGORITHM
In this section, we discuss the design of the RL algorithm in HeartSteps V2. Recall that this algorithm determines whether to send the activity suggestion at each decision time (see Figure 1). We first give an overview of how the proposed algorithm operates. We then describe each component in our setting, i.e., the decision times, action, states, and reward, and formally introduce our proposed RL algorithm.
5.1. Algorithm Overview
Below we provide an overview of how our proposed RL algorithm addresses the challenges listed in Section 3 that were not sufficiently addressed by existing RL algorithms.
5.1.1. Addressing Challenge (C1).
We introduce a “dosage” variable based on the history of past treatments. This is motivated by the analyses of HeartSteps V1 in which contexts with a larger recent dosage appears to result in the smaller immediate effect of treatment and lower future rewards. A similar “dosage” variable was explored in a recent unpublished manuscript [27] whose authors developed a bandit algorithm, called ROGUE (Reducing or Gaining Unknown Efficacy) Bandits. They use the “dosage” idea to accommodate settings in which an (unknown) dosage variable causes non-stationarity in the reward function. Our use of dosage, on the other hand, is to form a proxy of the future rewards, mimicking a full RL setting (as opposed to the bandit setting) while still managing variance in consideration of challenge (C2). We construct a proxy of the future rewards (proxy value) under a low dimensional proxy MDP model. Model-based RL is well studied in the RL literature [9, 29, 32]. In these papers, the algorithm uses a model for the transition function from current state and action to the next state. Instead, our algorithm only uses the MDP model to provide a low variance proxy to adjust for the longer-term impact of actions on future rewards.
5.1.2. Addressing Challenge (C2).
We propose using a low-dimensional linear model to model the differences in the reward function under alternate actions and using Thompson Sampling (TS), a general algorithmic idea that uses a Bayesian paradigm to trade off between exploration and exploitation [36, 37]. A relatively low-dimensional model is chosen to trade off the bias and variance to accelerate learning. The use of TS allows us to incorporate prior knowledge in the algorithm through the use of a prior distribution on the parameters in the reward model. We propose using an informative prior distribution to speed up the learning in the early phase of the study as well as to reduce the variance and diminish the impact of noisy observations. Note that TS-based algorithms have been shown to enjoy not only strong theoretical performance guarantees but also strong empirical performance in many problems in comparison to other state-of-the-art methods, such as Upper Confidence Bound [5, 16, 30, 31].
5.1.3. Addressing Challenge (C3).
To deal with challenge (C3), we use the concept of action centering in modeling the reward. The motivation is to protect the RL algorithm from a mis-specified model for the “baseline” reward function (e.g., in HeartSteps example with binary actions, the baseline reward function is the expected number of steps taken in the next 30 minutes given the current state and no activity suggestion). The idea of action centering in RL was first explored in [13] and recently improved in [20]. In both works, the RL algorithm is theoretically guaranteed to learn the optimal action without any assumption about the baseline reward generating process (e.g., the baseline reward function can be non-stationary). However, neither of these methods attempts to reduce the noise in the reward. We generalize action centering for use in higher variance, non-stationary reward settings.
5.1.4. Addressing Challenge (C4).
Lastly, in consideration of challenge (C4), the actions in our proposed RL algorithm are selected stochastically via TS (i.e., each action is randomized with known probability) and furthermore we restrict the randomization probabilities away from 0 and 1 to ensure that secondary analyses can be conducted when the study is over.
5.2. RL Framework
Let the participant’s longitudinal data recorded via mobile device be the sequence
Decision time.
We use t to index decision time. In HeartSteps V2, there are five decision times each day over the 90 days of the study (i.e., t = 1, . . ., 450). Where convenient we also use (l, d) to refer to the l-th decision time on study day d. For example, (l, d) = (5, 3) refers to the fifth time in day 3, which corresponds to the decision time t = 5(d − 1) + l = 15.
Action.
is the action or treatment at time t. In this work, we assume binary treatment, i.e., the action space = {0, 1}), where At = 1 if an activity suggestion is delivered and At = 0 otherwise.
Reward.
Rt is the (immediate) reward collected after the action At is selected. Typically, the reward is defined to capture the proximal impact of the actions. Recall that mobile health interventions are often designed to have a near-term impact on health outcomes. In HeartSteps, the reward is based on the step count collected 30 minutes after the decision time. Note that the raw step counts can be highly noisy and positively skewed [19]. The reward used in the RL algorithm is the log-transformed step count where the log transformation is to make the reward distribution more symmetric and less heavy-tailed; see how this log transformation is related to the modeling assumption in 5.4.
States.
St is the state vector at decision time t, which is decomposed into St = {It, Zt, Xt}. It is used to indicate times at which only At = 0 is feasible and/or ethical. For example, if sensors indicate that the participant may be driving a car, then the suggestion should not be sent; that is, the participant is unavailable for treatment (It = 0). Zt denotes features used to represent the current context at time t. In HeartSteps, these features include current location, the prior 30-minute step count, yesterday’s daily step count, the current temperature, and measures of how active the participant has been around the current decision time over the last week. Lastly, Xt ∈ is the “dosage” variable that captures our proxy for the treatment burden, which is a function of the participant’s treatment history. In contrast to HeartSteps V1, in HeartSteps V2, an additional intervention component, i.e., an anti-sedentary suggestion, will sometimes be delivered when the participant is sedentary. As the anti-sedentary suggestion can also cause burden, it is included in defining the dosage variable. Specifically, denote by Et the event that an walking suggestion is sent at decision time t − 1 (e.g., At−1 = 0) and any anti-sedentary suggestion is sent between time t − 1 and t. The dosage at the moment is constructed by first multiplying the previous dosage variable by a discount rate λ ∈ (0, 1) and incrementing it by 1 if any suggestions were sent to the user since the last decision time. Specifically, starting with the initial value X1 = 0, the dosage at time t + 1 is defined as Based on the data analysis result from HeartSteps V1, we choose λ = 0.95; see Section 6 for how this value is selected. As we will see in the next two sections, this simple form of dosage variable is used to capture the treatment burden and forecast the delayed impact of sending the walking suggestion. See Section 9 for a discussion of other choices.
5.3. Action Selection
At each decision time t = (l, d), the RL algorithm selects the action based on each participant’s current history (past states, actions and rewards), with the goal of optimizing the total rewards during the process. The proposed algorithm is stochastic, that is, the algorithm will output a probability for sending the walking suggestion message (Al, d is sampled from a Bernoulli distribution with probability ). Note that, at the beginning of study (d = 1), both the distribution (μ1, Σ1) and the proxy of delayed effect η1 are set based on HeartSteps V1; see details in Section 6. Without loss of generality, we implicitly assume throughout that the probability is part of the state Sl, d. The pseudo code of the proposed HeartSteps V2 RL algorithm is provided in Algorithm 1.
The reward function is denoted as The action selection is formed on the basis of a low dimensional linear model (to address challenge (C2)) for the treatment effect:
| (1) |
where the feature vector, f(s), is selected based on the domain science as well as on analyses of HeartSteps V1 data; see Section 6 for a discussion of how the features are selected. At the l-th decision time on day d, availability is ascertained with the dosage variable is selected based on
where the random variable β follows the Gaussian distribution which is the posterior distribution of the parameters obtained at the end of the previous day. The term proxies the negative long-term effect of delivering the activity suggestion at the moment given the current dosage level Xl, d = x (see the detailed formulation of ηd in Section 5.4.2). Note that when ηd(x) = 0, we recover the bandit formulation, i.e., the action is selected to maximize the immediate rewards ignoring any impact on future rewards. The probability πl, d of sending an activity suggestion given is clipped, i.e.,
| (2) |
The clipping function is This restricts the randomization probability of sending nothing and of sending an activity suggestion to be at least ϵ0 and ϵ1, respectively. The probability clipping enables off-policy data analyses after the study is over (challenge (C4)). This clipping also ensures that
ALGORITHM 1:
HeartSteps V2 RL Algorithm
 |
the RL algorithm will continue to explore and learn, instead of locking itself into a particular policy (challenge (C3)); see the discussion of ϵ0, ϵ1 in Section 6.
5.4. Nightly Updates
The posterior distribution of β for the immediate treatment effect and the proxy for the delayed effect are updated at the end of each day. Operationally, the nightly update is a mapping: that takes the current history up to day d as the input and outputs the posterior distribution and proxy of delayed effect, which are used in the action selection in the following day (d + 1). We discuss each of these in turn. A pseudo code of the proposed HeartSteps V2 RL algorithm is provided in Algorithm 1.
5.4.1. Posterior Update of Immediate Treatment Effect.
We use the following linear Bayesian regression “working model” for the reward to derive the posterior distribution of the treatment effect:
| (3) |
where we assume the error term {ϵt} is independent and identically distributed (i.i.d.) Gaussian noise with mean 0 and variance σ2. Recall that in HeartSteps V2, the reward is the log-transformed 30-minute step count following the decision time, in which the log-transformation brings the distribution close to a Gaussian distribution. We also note that the Gaussian assumption of the error term is merely used to derive the randomization probability (i.e., the posterior distribution of β). In fact, the theoretical result of the TS sampling algorithm does not rely on the Gaussian assumption [1]. The variance of the error term is estimated using HeartSteps V1 data and fixed throughout the study; see the discussion in Section 6.
From(3,) the working model for the mean reward function is Recall that f(s) is the feature vector that predicts the immediate treatment effect (1). Similarly, here the baseline feature vector g(s) is chosen to approximate the baseline reward function:
| (4) |
The baseline feature vector g(s) is selected based on the domain science and analyses of HeartSteps V1 data; see Section 6 for a discussion. The working models for both treatment effect and baseline reward are assumed to be linear in the feature vector and to have time-invariant parameters. Although these are rather strong assumptions, below we argue that action centering, (i.e. the use of πt in (3)) provides the robustness to the violation of these assumptions.
First, consider the action-centered term (At − πt) in the working model (3). As long as the treatment effect model (1) is correctly specified, the estimator of β based on the model (3) is guaranteed to be unbiased even when the baseline reward model (4) is incorrect [4], for example, due to the non-linearity in g(s) or non-stationarity (changes in α over time). That is, through the use of action centering, we achieve robustness against mis-specification of the approximate baseline model, (4), addressing the challenge (C3). The rationale of including the term πtf(St) in the Bayesian regression working model (3) is to capture the time-varying aspect of the main effect due to the action-centered term (since πt is continuously changing/updated during the study). Omitting this term would reduce the number of parameters in the model, but we have found in experiments that the inclusion of πtf(St) reduces the variance of the treatment effect estimates and thus speeds up learning. Second, in the case where the treatment effect model (1) is incorrect, for example, when the treatment effect is non-linear in f(St) or is non-stationary (e.g., with time-varying parameters), it can be shown [4] that the Bayesian regression provides a linear approximation to the treatment effect. When the action is not centered, the treatment effect estimates may not converge to any useful approximation at all, which could lead to poor performance in selecting the action.
The Bayesian model (3) requires the specification of prior distributions on α0, α1 and β. Here the priors are independent and given by
| (5) |
See Section 6 for a discussion of how the informative priors (challenge (C2)) are constructed using HeartSteps V1 data. Because the priors are Gaussian and the error in (3) is Gaussian, the posterior distribution of β given the current history is also Gaussian, denoted by Below we provide the details about the calculation of We first calculate the posterior distribution of all parameters, and the posterior distribution of β can then be identified. The posterior distribution of θ, denoted by given the current history can be found by
| (6) |
| (7) |
where denotes the joint feature vector and is the prior mean and variance of θ, e.g., Suppose the size of f(s) is p. Then the posterior mean of β, μd+1 is the last p elements of the above and the posterior variance of β, Σd+1 is the bottom-right corner matrix of size p by p in .
5.4.2. Proxy Delayed Effect on Future Rewards.
The proxy is formed based on a simple Markov Decision Process (MDP) for the states St = (Zt, It, Xt), in which we make the following working assumptions about the transition of states:
-
(S1)
the context {Zt} is i.i.d. with distribution F,
-
(S2)
the availability {It} is i.i.d. with probability pavail
-
(S3)
the dosage variable {Xt} makes transitions according to τ(x′|x,a)
We use this simple MDP to capture the delayed effect of delivering the intervention on the future rewards. The key assumption in this model is that the action impacts the future rewards only through the dosage since the context is assumed to be independent of the past actions. This assumption allows us to form a low-variance estimate of the delayed effect of treatment based only on the current dosage. Recall that the decision times in both HeartSteps V1 and V2 are roughly separated by 2–2.5 hours during the day. The impact of the current action on the next context is likely weak. We use HeartSteps V1 data to perform the Generalized Estimating Equations (GEE, [23]) analysis to confirm that the effect is in fact not significant for all of the selected context variables (see the list in Section 6).
To reduce the model complexity, we assume that the context and availability are both i.i.d. across times. This i.i.d. assumption is likely unrealistic (for example, the next temperature might depend on the current temperature), however it leads to a reduced variance of the estimator of the delayed effect as we do not need to learn a transition model for the context and availability. We believe that relaxing the i.i.d. assumption of context and availability in modeling the delayed effect could be an interesting future direction. Recall the definition of dosage variable at the beginning of Section 5.2: given the previous dosage x and whether the participant receives the previous walking suggestion message a, the next dosage x′ would be fully determined by knowing whether the participant has received any anti-sedentary messages since the last decision time. In (S3), the transition model τ(x′|x,a) essentially models the probability of receiving anti-sedentary messages between two decision times; see details below.
We now discuss how each component in the simple MDP is constructed. Given the history up to the end of day d, , we set (1) the average prior availability to be and (2) the empirical distribution on is the Dirac measure. For the transition model of the dosage variable, let psed be the probability of delivering any anti-sedentary suggestions between decision times given no activity suggestion was sent at the previous decision time. We set psed = 0.2 based on the planned scheduling of anti-sedentary suggestions (an average of 1 anti-sedentary suggestion uniformly distributed in a 12-hour time window during the day implies approximately 0.2 probability of sending an anti-sedentary message between two decision times). Then . Recall from Section 5.2 that λ = 0.95. Lastly, we specify the reward function at available decision times by are the posterior means based on the model (3). The mean reward at unavailable decision times has the same form but with posterior means from a similar linear Bayesian regression using the unavailable time points in .
We formulate the proxy of delayed effect based on the above constructed MDP as follows. Consider an arbitrary policy π that chooses the action π(S) at the state S = (Z,I,X) if the user is available (i.e., I = 1) and chooses action 0 otherwise (i.e., π(S) = 0 if I = 0). Recall the state-action value function for policy π under discount rate γ:
where the subscript π means the actions are selected according to the policy π. Also recall the state value function The value function Qπ is divided into two parts: where r(s, a) is the estimated reward function and
is the sum of future discounted rewards (future value, in short). excludes the first, immediate reward (Rt) and is only a function of (x,a) under the working assumptions (S1) and (S2). Note that the difference measures the impact of sending treatment at dosage x on the future rewards in the setting in which future actions are selected by policy π. We select the policy π to maximize the future value under the constraint that π depends only on the dosage and availability. Specifically, let It can be shown that H* is given by where the bivariate function solves the following equations:
for all x ∈ and i ∈ {0, 1}, where (i) is the constrained action space based on availability, i.e., (1) = {0, 1} and (0) = 0, r0 and r1(x,a) are the marginal reward function (marginal in the sense that it only depends on the dosage variable) given by r0(x) = ∫r((z, 0, x), 0)dF(z),r1(x, a) = ∫r((z, 1, x), a)dF(z). Finally, the proxy for the delayed effect is calculated by
| (8) |
where is the weighted average of the estimate H* and the initial function H1 calculated based only on data from HeartSteps V1. The selection of the discount rate γ and the weight w will be discussed in Section 6. This delayed effect is the mean difference of the discounted future rewards between sending nothing and sending an activity suggestion. From here we see that in (2) At, the action at decision time t is essentially selected to maximize the sum of discounted rewards, i.e., .
6. CHOOSING INPUTS TO THE RL ALGORITHM
We review the inputs required by the HeartSteps V2 RL algorithm and discuss how each is selected by the scientific team and on the basis of HeartSteps V1 data analysis. The list of required inputs is summarized in Table 2.
Table 2.
The list of parameters used in pilot HeartSteps V2.
| Symbol | Description | Value | Selection Criteria |
|---|---|---|---|
| λ | Discount rate in dosage variable | 0.95 | HeartSteps V1 data analysis (Sec. 6.2) |
| ϵ 0 | Minimal probability of sending nothing | 0.2 | Consideration of burden (Sec. 6.1) |
| ϵ 1 | Minimal probability of sending message | 0.1 | Sufficient exploration (Sec. 6.1) |
| γ | Discount rate in proxy delayed effect | 0.9 | Chosen by simulation (Sec. 6.4, 7) |
| w | Updating weight in the proxy delayed effect | 0.75 | Chosen by simulation (Sec. 6.4, 7) |
| p sed | Probability of receiving anti-sedentary message between two decision times | 0.2 | Set based on the planned schedule of anti-sedentary messages (Sec. 5.4.2) |
| σ 2 | Variance of error term | 2.652 | HeartSteps V1 data analysis (Sec. 6.3) |
| f(s), g(s) | Feature vector in modeling reward | Table 3 | HeartSteps V1 data analysis (Sec. 6.2) |
| (μα0, Σα0) | Prior distribution of α0 in baseline reward | Table 4 | HeartSteps V1 data analysis (Sec. 6.3) |
| (μβ0, Σβ0) | Prior distribution of β0 in treatment effect | Table 5 | HeartSteps V1 data analysis (Sec. 6.3) |
6.1. Probability Clipping
The scientific team decided ϵ0 = 0.2 and ϵ1 = 0.1 for the probability clipping to ensure enough exploration (in order to, for example, force the RL algorithm to continuously explore without converging to a deterministic policy). In addition, clipping at ϵ0 = 0.2 also introduces a soft constraint on the number of walking suggestion messages delivered per day. In particular, at most on average 5 × (1 − ϵ0) = 4 walking suggestion messages can be sent in a day assuming the participant is always available. Finally, the probability of selecting each action is greater than 0.1 and ensures the stability of causal inference after the study is over.
6.2. Feature Vector
Recall that the working model (3) requires the specification of the feature vectors f(s) and g(s) (transformed into [0, 1] in the algorithm) in (1) and (4). The feature vectors f(s), g(s) are chosen based on the GEE analysis using HeartSteps V1 data.
Specifically, each feature is included in a marginal GEE model with the prior 30-minute step count in the main effect model to reduce the variance. The candidate feature is included in both the main effect and treatment effect models. The procedure is done for each feature separately and a p-value is obtained. The feature is then selected into g(s) and f(s) at the significance level of 0.05. Although we found that the 30-minute step count before the decision time is highly predictive of the rewards (e.g., 30-minute step count after the decision), it is not significant in terms of predicting the treatment effect. Therefore, the prior 30-minute step count is included in the baseline features g(s), but not in the feature vector f(s) for treatment effect.
As mentioned in Section 5.2, we define the dosage in the form of We conducted GEE analysis for a variety of values of λ. When λ is relatively large, the dosage significantly impacts the effectiveness of the activity suggestions on the subsequent 30-minute step count and we selected λ = 0.95 (p-value 0.085).
A measure of how well the participant engages with the mobile app (e.g., the daily number of screens that the participant encounters) is planned to be included in both g(s) and f(s). This variable was not collected in HeartSteps V1. The scientific team believes this variable likely interacts with the treatment and thus decided to include it in the features. In both f(s) and g(s), the intercept term is also included. See Table 3 for the list of the selected features.
Table 3.
The list of selected features in HeartSteps V2 study. Step count variation is the standard deviation of the 60-min step count centered around the current decision time over the past seven days and then thresholded by the median of the past standard deviation. The app engagement is a binary indicator of whether the number of screens encountered in the app over the prior day is greater than the 40% quantile of the screens collected over the last seven days. All of the variables are in the baseline feature vector g(s). Location takes three possible values: home, work, and other. The third column indicates whether the variable is in the treatment effect feature vector f(s).
| Variable | Type | In treatment effect model? |
|---|---|---|
| Yesterday’s step count | Continous | No |
| Prior 30-minute step count | Continous | No |
| Location | Discrete | Yes |
| Current temperature | Continous | No |
| App engagement | Discrete | Yes |
| Dosage variable | Continous | Yes |
| Step variation level | Discrete | Yes |
6.3. Noise Variance and Prior Distribution in Reward Model
Recall the variance of the noise σ2 in the model (3). The variance σ2 can be learned on the fly, e.g., estimated by the residual variance in the model fitted by the current data. However to ensure the stability of the algorithm (since the step count can be highly noisy), we set the variance parameter using the data from HeartSteps V1, that is, σ2 is not updated during the study. We calculate the residual variance in the regression model using the above-selected feature and get σ2 = 2.652.
The prior distribution (5) is constructed on the basis of the analysis of HeartSteps V1 data. Specifically, we first conduct GEE regression analyses [23], using all participants’ data in HeartSteps V1 and assess the significance of each feature. To form the prior variance, on each participant we fit a separate GEE linear regression model and calculated the standard deviations of the point estimates across the 37 participant models.
We formed the prior mean and prior standard deviation as follows. (1) For the features that are significant in the GEE analysis using all participants’ data, we set the prior mean to be the point estimate from this analysis; we set the prior standard deviation to be the standard deviation across participant models from the participant-specific GEE analyses. (2) For the features that are not significant, we set the corresponding prior mean to be zero and shrink the standard deviation by half. (3) For the app engagement variable, we set the prior mean to be 0 and the standard deviation to be the average prior standard deviation of other features. Σα0, Σβ are diagonal matrices with the above prior variances on the diagonals; see Table 4 and 5 for the prior distributions. The same procedure is applied to form the prior mean and variance for the reward model at the unavailable times. This mean and variance will be used in the proxy value updates. The rationale of setting the mean to zero and shrinking the standard deviation for the non-significant features is to ensure the stability of the algorithm: unless there is strong evidence or signal detected from the participant during the HeartSteps V2 study, these features only have minimal impact on the selection of actions. In Section 7.1, we also apply the above procedure to construct the prior in the simulation.
Table 4.
Prior distribution of α0
| Variable | Mean | Std. |
|---|---|---|
| Intercept | 0 | 1.43 |
| Yesterday’s step count | 1.67 | 2.67 |
| Prior 30-minute step count | 3.79 | 1.55 |
| Other Location | 0 | 0.43 |
| Temperature | 0 | 1.63 |
| Work Location | 0 | 0.84 |
| Step variation level | 0 | 0.45 |
| Dosage | 0 | 1.67 |
| App Engagement | 0 | 1.33 |
Table 5.
Prior distribution of β0
| Variable | Mean | Std. |
|---|---|---|
| Intercept | 0.71 | 2.04 |
| Other Location | −0.33 | 1.38 |
| Work Location | 0 | 0.89 |
| Step variation level | 0 | 0.56 |
| Dosage | 0 | 1.85 |
| App Engagement | 0 | 1.34 |
6.4. Parameters in Proxy Delayed Effect
The initial proxy delayed effect, η1, and the estimation of proxy delayed effect, ηd, both require the initial proxy value estimates H1. To calculate H1 we use the same procedure as described in Section 5.4.2 to calculate H*, except that the empirical probability of being available, the empirical distribution of contexts, and the reward function are constructed using only HeartSteps V1 data.
Two remaining parameters need to be specified in estimating the proxy delayed effect: the discount rate γ and the updating weight parameter w (both part of the proxy MDP in Section 5.4.2) For simplicity, we refer to them as “tuning parameters” in the rest of the article. These tuning parameters are difficult to specify directly as the optimal choice likely depends on the noise level of rewards, how the context varies over time, and the length of the study. We propose to choose the tuning parameters, (w,γ), based on a simulation-based procedure. Specifically, we first build a simulation environment (i.e., a data generating model) using HeartSteps V1 data (see Section 7.1 for details). We then apply the algorithm as shown in Figure 1 with each candidate pair of tuning parameters. Finally, the tuning parameters are chosen to maximize the total simulated rewards. In Section 7, we demonstrate the validity of this simulation-based procedure to select the tuning parameters by three-fold cross-validation, showing that the selected tuning parameters in the training phase generalize well to the testing phase.
7. SIMULATION STUDY
In this section, we use HeartSteps V1 data to conduct a simulation study to demonstrate the validity of the procedure for choosing the inputs, including the tuning parameters, described in Section 6, the validity of using proxy values in the proposed algorithm addressing the challenge (C1) about the negative delayed effect of treatments, and the validity of using action centering to protect against model mis-specification (C3). Here the use of a previous dataset to build a simulation environment for evaluating an online algorithm is similar to [24]. In Section 8, we also provide the assessment of the proposed algorithm using pilot data from HeartSteps V2.
We carry out a three-fold cross validation (CV) procedure. Specifically, we first partition the HeartSteps V1 dataset into three folds. In each of the three iterations, two folds are marked as a training batch and the third fold is marked as a testing batch. The training batch is used to (1) construct the prior distribution, (2) form an estimate of noise variance, and (3) select the tuning parameters. We call this process the “training phase”. Note that the training batch serves the same purpose as HeartSteps V1. Next, the testing batch is used to construct a simulation environment to test the algorithm with the estimated noise variance, prior, and tuning parameters. The use of a testing batch is akin to applying the RL algorithm in HeartSteps V2. In Section 7.1 and 7.2 below, we will describe in greater detail how the training batch and the testing batch are used in each iteration of cross validation. Note that we will apply the same procedure three times.
We compare the performance to that of the Thompson Sampling Bandit algorithm, a version similar to [1]. The TS Bandit algorithm is a widely used RL algorithm showing good performance in many real-world settings [5]. At each decision time, it selects the action probabilistically according to the posterior distribution of reward with the goal of maximizing the immediate reward. We choose the TS Bandit as the comparator over other standard contextual bandit algorithms (e.g., LinUCB in [22]) because the TS Bandit is a stochastic algorithm that better suits our setting due to challenge (C4). In the TS Bandit, the expected reward is modeled by for some parameter θ. At each decision time t with context St = s and availability It = 1, the action At = a is selected with probability is the posterior distribution of the parameters θ given the current history under the Bayesian model of rewards with Gaussian prior and error. The main difference to our algorithm is that TS Bandit attempts to choose the action that maximizes the immediate reward, whereas our proposed algorithm takes into account the longer term impact of the current action per challenge (C1). In addition, the TS Bandit algorithm requires the correct modeling of each arm, while our method uses action centering (3) to protect against mis-specifying the baseline reward per challenge (C3) and only requires correctly modeling the difference between two arms, i.e., the treatment effect model in (1).
In the implementation of TS Bandit, we parametrize the reward model by where f(s) and g(s) are the same feature vectors used in our proposed algorithm. Furthermore, to allow for a fair comparison, the prior distribution of θ = (α, β) and the variance of error term σ2 are both constructed by the training batch using the same procedure that will be discussed in Section 7.1 and the probability of selecting each arm is clipped with the same constraints.
7.1. Training Phase
Prior distribution.
The algorithm requires three prior distributions: the prior of the parameters in the main effect when available, the prior of parameters in the treatment effect, and the prior of parameters in the mean reward when not available. The last one is used in calculating the proxy value. The prior distributions are calculated using the training batch as described in Section 6. We refer to the estimated GEE model using all participants’ data in the training batch as population GEE in what follows.
Noise variance.
We set the noise variance to be the variance of residuals obtained from the above population GEE.
Initial proxy value function.
Recall that the proxy value function requires the specification of the (1) context distribution, (2) availability probability, (3) the transition model of dosage, and (4) reward function (for available and unavailable times), as well as the discount factor γ; see Section 5.4.2. We form the initial proxy using the training batch by setting (1) the empirical distribution in the training batch, (2) the empirical availability probability in the training batch, (3) the average probability of receiving anti-sedentary message between decision time and (4) the reward estimates from population GEE.
Generative model to select tuning parameters.
Recall that the tuning parameters are (γ,w), corresponding to the discount rate in defining the proxy value and the updating weight in forming the estimated proxy value. The tuning parameters are chosen to optimize the total simulated rewards using the generative model of participants in the training batch. Below we describe how we form the generative model. For participant i, we first construct a 90-day sequence of context, availability, residuals by first creating the 42-day sequence of the context, availability, residual, where residual is obtained from the person-specific regression model fit. Then we extend this 42-day sequence to a 90-day sequence, by concatenating (90 − 42) days’ data, randomly selected from the 42-days’ data. Specifically, we randomly choose d from {1, . . ., 42} and append all data from day d onto the 42-day data and repeat until we have a 90-day data set. The sampling is done only once and the sequence is fixed throughout the simulation. The generative model for participants i in the training batch is given as follows. At time t = 1, 2, 3 . . ., 450,
-
(1)
Randomly generate a binary variable Bt with probability 0.2 (on average 1 per day). Here Bt is the indicator of whether there is any anti-sedentary suggestion sent between (t − 1) and t.
-
(2)
Obtain the current dosage
-
(3)
Set
-
(4)
Select the action At according to (2)
-
(5)
Receive the reward Rt defined as
| (9) |
where the coefficients (, , ) are set based on population GEE using the data of all participants in the training batch.
For a given candidate value of tuning parameters, together with the above-constructed noise variance and prior, the algorithm is run 96 times under each training participant’s generative model. The average total reward (over all training participants and re-runs) is calculated and we select the tuning parameters that maximize the average total reward. We use the grid search over γ ∈ {0, 0.25, 0.5, 0.75, 0.9, 0.95} and w ∈ {0, 0.1, 0.25, 0.5, 0.75, 1}. Recall that the training is done three times and each time uses two folds as the training batch. The selected tuning parameters for the three iterations in CV are given by (γ,w) = (0.9, 0.5), (0.9, 0.75), (0.9, 0.1).
7.2. Testing Phase
We build the generative model using the testing batch following the procedure described in Section 7.1 with the only difference being that in the testing phase the coefficients in generating the reward (9) are replaced by (, , ), which are the least squared estimates calculated using the testing dataset. We run the algorithm under each test participant’s generative model with the noise variance estimates, the prior distribution, and the tuning parameters selected from the training data. The algorithm is run 96 times per testing participant, and the average total reward over the runs is calculated.
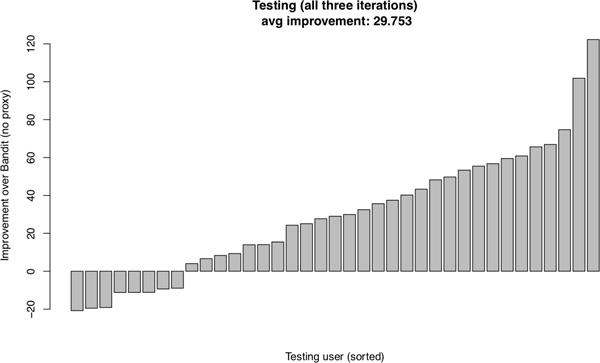
Recall that we conduct a three-fold cross validation. Every participant in HeartSteps V1 data is assigned to exactly one testing batch in the cross validation. The performance of our algorithm and that of the comparator, the TS Bandit algorithm, on each participant when assigned to the testing batch is provided in Figure 2. We see that for 29 out of 37 of the participants, the total rewards are higher for our approach than for the approach using the TS Bandit algorithm. The average improvement of the total rewards over TS Bandit is 29.753, which gives an improvement of 29.753/450 = 0.066 per decision time. Recall that the reward is the log-transformed 30-minute step count following each decision time. Translating back into the raw step count, we see the improvement is about (exp(0.066) − 1) × 100% = 6.8% increase in the 30-minute step count. Recall that the TS Bandit algorithm is sensitive to model mis-specification/non-stationarity and greedily maximizes the immediate reward. The simulation results demonstrate that the use of action centering and the proxy delayed effect effectively addresses the challenges (C1) and (C3).
Fig. 2.
Testing performance for all three iterations in the cross validation. Each bar corresponds to the improvement of the total reward of the proposed algorithm with the selected inputs and tuning parameters in the training phase over the total reward achieved by Thompson Sampling Bandit algorithm for a single participant.
8. PILOT DATA FROM HEARTSTEPS V2
HeartSteps V2 has been deployed in the field since June 2019. Our team has conducted a pilot study to test the software and multiple intervention components. The RL algorithm developed above was used to decide whether to trigger the context-tailored activity suggestion at each of the five decision times per day. The inputs to the algorithm (e.g., the choice of feature vectors, the prior distribution, and the tuning parameters) were determined according to Section 6. In other words, we used all the HeartSteps V1 data to choose the inputs following the procedure described in Section 7.1. Below we provide an initial assessment of the algorithm and discuss the lessons learned from the pilot participants’ data.
8.1. Initial Assessment
Recall that each participant in HeartSteps V2 wears the Fitbit tracker for one week before starting to use the mobile app; no activity suggestion is delivered during this initial week. Currently, there are eight participants in the field who have been in the study for over one week and are experiencing the RL algorithm. For each participant, we calculated the average 30-minute step count after each user-specified decision time during the first week and compared this to the average 30-minute step count in the subsequent weeks during which activity suggestions are delivered. This comparison is provided in Table 6. All except one participant (ID = 4) experienced positive increases in step count. We see that on average each participant takes 125 more steps in the 30-minute window following the decision time than in the first week.
Table 6.
The average step count 30 mins after each decision time in HeartSteps V2 pilot data
| Participant ID | Days in the study | Average 30-minute steps in the first week |
Average 30-minute steps after the first week |
Difference |
|---|---|---|---|---|
| 5 | 32 | 318.13 | 561.43 | 243.29 |
| 7 | 56 | 343.79 | 574.53 | 230.75 |
| 1 | 36 | 252.12 | 424.31 | 172.19 |
| 3 | 32 | 163.24 | 295.45 | 132.21 |
| 8 | 18 | 281.65 | 387.86 | 106.21 |
| 6 | 43 | 215.45 | 314.17 | 98.71 |
| 2 | 22 | 361.26 | 418.60 | 57.35 |
| 4 | 75 | 368.50 | 330.03 | −38.47 |
8.2. Lessons
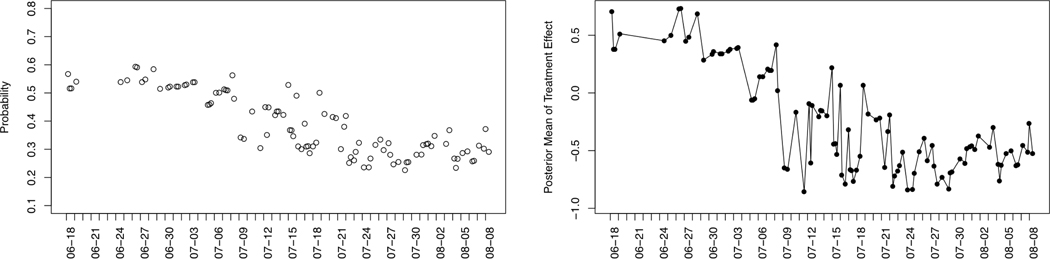
In this section, we discuss two lessons learned from the examination of the pilot participants’ data. We illustrate these lessons using data from participants ID=4 and ID=7. First, consider participant ID=4, who is not responsive to the activity suggestions (i.e., sending a suggestion does not significantly improve the step count). That is, as seen in Table 6 participant ID = 4 has step counts that decrease after the first week. Figure 3 shows the randomization probability and the posterior mean estimates for participant ID = 4. We see that for this participant the posterior mean estimates start with a positive value and drop below 0, i.e., no sign of the effectiveness of the suggestions is seen, however the randomization probability still ranges between 0.2 and 0.4. Given that HeartSteps is intended for long-term use (recall HeartSteps V2 is a 3-month study) and there are other intervention components (the weekly reflection and planning and the anti-sedentary suggestion message), randomizing with these probabilities is likely too much. In consideration of the user’s engagement and burden, it makes sense to reduce the chance of receiving intervention when the algorithm does not have enough evidence of the effectiveness of the intervention.
Fig. 3.
Participant ID = 4. Left: the randomization probability at the available decision times. The x-axis is the time stamp. The y-axis is the randomization probability. Right: the posterior mean estimates of treatment effect at the available times. The x-axis is the time stamp. The y-axis is the posterior mean
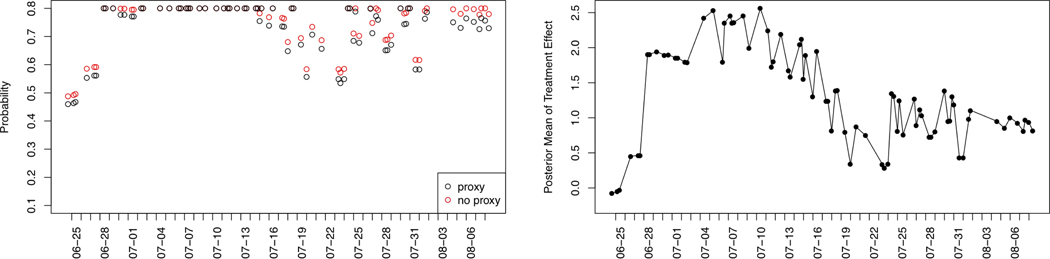
Next, consider participant ID =7, who appears highly responsive to the activity suggestions (see Table 6 and the right-hand graph in Figure 4 of the posterior mean of the treatment effect). First, we note that the probability clipping takes effect multiple times during this time period. That is, the randomization probability calculated in (2) exceeds the limit 1 − ϵ0 = 0.8 and thus reaching the average constraint on the number of suggestions per day (i.e., 0.8 × 5 = 4). The probability clipping or the induced average constraint is important to manage the user’s burden as we can see from the right-hand graph in Figure 4 that this participant’s responsiveness begins to decrease around time July 10. Next, the left-hand graph in this same figure shows that the randomization probabilities from our RL algorithm do not really start to decrease until 07–16. Ideally, the proxy value should be responding quickly to the excessive dose and signaling that the probability should decrease more. Note that the proxy is in fact reducing the probability of sending the walking suggestion when the delayed effect is present; see the left-hand graph in Figure 4 and compare the black points (which correspond to the actual randomization probability) to the red points (which correspond to the randomization probability without the proxy value adjustment). Ideally, we would like to see a bigger gap between the black and red points in the period from 07–16 to 07–15. We are currently revising the algorithm in response to these two lessons as discussed in Section 9.
Fig. 4.
Participant ID = 7. Left: the randomization probability at the available decision times. The x-axis is the time stamp. The y-axis is the randomization probability. The black points corresponds to the actual randomization probability and the red points corresponds to the randomization probability without the proxy adjustment (i.e., ηd = 0). Right: the posterior mean estimates of treatment effect at the available times. The x-axis is the time stamp. The y-axis is the posterior mean estimates (i.e., f(s)⊤μd).
9. DISCUSSIONS
Most of the parameters used in the algorithm for HeartSteps V2 are constructed based on a pilot study, HeartSteps V1. One natural concern is whether the parameters chosen from HeartSteps V1 can generalize well to HeartSteps V2. First, we note that while the populations in these two studies are different, we expect the sedentary behavior of participants to be similar. Also, recall that this work aims to develop an online RL algorithm, as opposed to simply applying a pre-specified treatment policy learned from a previous study in another new study. This is very different in that the former allows the underlying treatment policy to be continuously updated throughout the study. For example, we can see that the impact of the prior distribution would eventually get washed out as more data is collected from the participant. The parameters selected from HeartSteps V1 can be viewed as a “warm start” and do not prevent generalization too much in this online setting.
We recommend that scientists develop just-in-time adaptive interventions in an iterative, sequential manner. Specifically in the case of HeartSteps, our team first conducted HeartSteps V1 to gain some evidence of the effectiveness of interventions and to build the RL algorithm for use in HeartSteps V2. We then conducted another pilot study for HeartSteps V2 to evaluate the algorithm, and this pilot data will be used to further improve the design of the algorithm for the clinical trial.
This work is largely motivated by the design of the RL algorithm for use in a physical activity study. We believe the challenges mentioned in Section 3 arise in many mobile health applications and our solutions to address these challenges for HeartSteps can be applied in other settings. While this RL algorithm cannot be directly applied in other studies (since, for example, the inputs to the algorithm might be completely different depending on the application), the design considerations and the procedure used to select inputs described in Section 6 may be useful in other studies.
9.1. Limitations and Future Work
Our RL algorithm has several important limitations and we foresee several opportunities to improve it.
Building a more sophisticated model.
In designing the algorithm for HeartSteps V2, we used a relatively simple model and made several strong working assumptions; see Table 1. For example, in modeling the reward we assumed a low-dimensional linear model for both treatment effect and baseline reward. The modeling of the delayed effect was built on a simple MDP model in which the action does not impact the states except for the dosage variable. See the list of assumptions in Table 1. This is mainly because we have a limited amount of pilot data collected from HeartSteps V1 (37 participants) to train and validate a more complex model. With more pilot data, one could consider relaxing some of the assumptions. For example, modeling the dependence structure among the error terms (i.e., within-subject correlation) could potentially reduce the estimation error. Also, the current algorithm takes into account the delayed effect of treatment by using a pre-defined “dosage variable” capturing the burden. It would be interesting to develop a version in which more sophisticated measures of the burden and engagement (for example, a latent variable approach) are used to approximate the delayed effect and respond quickly to prevent disengagement.
Table 1.
Model assumptions in the proposed RL algorithm.
| Purpose | Model Assumption |
|---|---|
| Immediate treatment effect | Time-invariant linear baseline reward model |
| Immediate treatment effect | Time-invariant linear treatment effect model |
| Immediate treatment effect | i.i.d. Gaussian error |
| Proxy delayed effect | The states follows a Markov Decision Process with the i.i.d. context and availability and dosage transition |
Adjusting the tuning parameters online.
In the current algorithm, the tuning parameters (i.e., the discount factor γ and the updating weight w in the proxy value) are selected by a simulation-based procedure based on HeartSteps V1 data and fixed during the study. We did this mainly to ensure the stability of the algorithm. However, as we discussed in Section 6, the optimal choice of these tuning parameters is likely person-specific. It would be interesting to design a method that evaluates and/or adjusts these tuning parameters for each participant as more data is collected, especially for a long study.
Online monitoring.
The current algorithm has no mechanism to detect any sudden change of the participant’s environment or any unusual user behavior (e.g., the participant becomes sick). When these changes last for a long period of time, the algorithm needs a sufficient amount of data to adapt to the changes and may respond slowly. But the algorithm may not detect temporary changes at all and thus may provide too many treatments. It would be interesting to draw on techniques developed in the change-point detection literature so that the RL algorithm can pick up these changes more quickly.
Pooling across participants.
The algorithm described in this work learns the treatment policy separately for each participant (i.e., it is fully personalized). If the participants in the study are similar enough, pooling information from other participants (either those still in the study or those who have already finished) can speed up learning and achieve better performance, especially for those entering the study later.
10. CONCLUSION
In this paper, we developed a reinforcement learning algorithm for use in HeartSteps V2. Preliminary validation of the algorithm demonstrates that it performs better than the Thompson Sampling Bandit algorithm in synthetic experiments constructed based on a previous study, HeartSteps V1. We also assessed the performance of the algorithm using pilot data from HeartSteps V2. After HeartSteps V2 is completed, the data gathered will be used to further assess the algorithm’s performance and utility.
Acknowledgments
Permission to make digital or hard copies of all or part of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. Copyrights for components of this work owned by others than ACM must be honored. Abstracting with credit is permitted. To copy otherwise, or republish, to post on servers or to redistribute to lists, requires prior specific permission and/or a fee. Request permissions from permissions@acm.org.
Contributor Information
PENG LIAO, University of Michigan.
KRISTJAN GREENEWALD, IBM Research.
PREDRAG KLASNJA, University of Michigan.
SUSAN MURPHY, Harvard University.
REFERENCES
- [1].Agrawal Shipra and Goyal Navin. 2013. Thompson sampling for contextual bandits with linear payoffs. In International Conference on Machine Learning. 127–135. [Google Scholar]
- [2].Arumugam Dilip, Abel David, Asadi Kavosh, Gopalan Nakul, Grimm Christopher, Lee Jun Ki, Lehnert Lucas, and Littman Michael L. 2018. Mitigating Planner Overfitting in Model-Based Reinforcement Learning. arXiv preprint arXiv:1812.01129 (2018). [Google Scholar]
- [3].Bekiroglu Korkut, Lagoa Constantino, Murphy Suzan A, and Lanza Stephanie T. 2016. Control engineering methods for the design of robust behavioral treatments. IEEE Transactions on Control Systems Technology 25, 3 (2016), 979–990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Boruvka Audrey, Almirall Daniel, Witkiewitz Katie, and Murphy Susan A. 2018. Assessing time-varying causal effect moderation in mobile health. J. Amer. Statist. Assoc 113, 523 (2018), 1112–1121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Chapelle Olivier and Li Lihong. 2011. An empirical evaluation of thompson sampling. In Advances in Neural Information Processing Systems. 2249–2257. [Google Scholar]
- [6].Dempsey Walter, Liao Peng, Klasnja Pedja, Nahum-Shani Inbal, and Murphy Susan A. 2015. Randomised trials for the Fitbit generation. Significance 12, 6 (2015), 20–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Dimakopoulou Maria, Zhou Zhengyuan, Athey Susan, and Imbens Guido. 2017. Estimation considerations in contextual bandits. arXiv preprint arXiv:1711.07077 (2017). [Google Scholar]
- [8].Dimitrijević Milan Radovan, Faganel Janez, Gregorić Matej, Nathan PW, and Trontelj JK. 1972. Habituation: effects of regular and stochastic stimulation. Journal of Neurology, Neurosurgery & Psychiatry 35, 2 (1972), 234–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Fonteneau Raphaël, Korda Nathan, and Munos Rémi. 2013. An optimistic posterior sampling strategy for bayesian reinforcement learning. Neural Information Processing Systems 2013 Workshop on Bayesian Optimization (2013). [Google Scholar]
- [10].Forman Evan M, Kerrigan Stephanie G, Butryn Meghan L, Juarascio Adrienne S, Manasse Stephanie M, Ontañón Santiago, Dallal Diane H, Crochiere Rebecca J, and Moskow Danielle. 2018. Can the artificial intelligence technique of reinforcement learning use continuously-monitored digital data to optimize treatment for weight loss? Journal of behavioral medicine (2018), 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].François-Lavet Vincent, Fonteneau Raphael, and Ernst Damien. 2015. How to discount deep reinforcement learning: Towards new dynamic strategies. Neural Information Processing Systems 2015 Workshop on Deep Reinforcement Learning (2015). [Google Scholar]
- [12].Ghosh Avishek, Chowdhury Sayak Ray, and Gopalan Aditya. 2017. Misspecified linear bandits. In Thirty-First AAAI Conference on Artificial Intelligence. [Google Scholar]
- [13].Greenewald Kristjan, Tewari Ambuj, Murphy Susan, and Klasnja Predag. 2017. Action centered contextual bandits. In Advances in Neural Information Processing Systems. 5977–5985. [PMC free article] [PubMed] [Google Scholar]
- [14].Jiang Nan, Kulesza Alex, Singh Satinder, and Lewis Richard. 2015. The dependence of effective planning horizon on model accuracy. In Proceedings of the 2015 International Conference on Autonomous Agents and Multiagent Systems. International Foundation for Autonomous Agents and Multiagent Systems, 1181–1189. [Google Scholar]
- [15].Jiang Nan and Li Lihong. 2016. Doubly Robust Off-policy Value Evaluation for Reinforcement Learning. In International Conference on Machine Learning. 652–661. [Google Scholar]
- [16].Kaufmann Emilie, Korda Nathaniel, and Munos Rémi. 2012. Thompson sampling: An asymptotically optimal finite-time analysis. In International Conference on Algorithmic Learning Theory. Springer, 199–213. [Google Scholar]
- [17].Klasnja Predrag, Harrison Beverly L, LeGrand Louis, LaMarca Anthony, Froehlich Jon, and Hudson Scott E. 2008. Using wearable sensors and real time inference to understand human recall of routine activities. In Proceedings of the 10th International Conference on Ubiquitous Computing. ACM, 154–163. [Google Scholar]
- [18].Klasnja P, Hekler EB, Shiffman S, Boruvka A, Almirall D, Tewari A, and Murphy SA 2015. Micro-randomized trials: An experimental design for developing just-in-time adaptive interventions. Health Psychology 34, S (2015), 1220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Klasnja Predrag, Smith Shawna, Seewald Nicholas J, Lee Andy, Hall Kelly, Luers Brook, Hekler Eric B, and Murphy Susan A. 2018. Efficacy of contextually tailored suggestions for physical activity: A micro-randomized optimization trial of HeartSteps. Annals of Behavioral Medicine 53, 6 (2018), 573–582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Krishnamurthy Akshay, Wu Zhiwei Steven, and Syrgkanis Vasilis. 2018. Semiparametric contextual bandits. arXiv preprint arXiv:1803.04204 (2018). [Google Scholar]
- [21].Lehnert Lucas, Laroche Romain, and van Seijen Harm. 2018. On value function representation of long horizon problems. In Thirty-Second AAAI Conference on Artificial Intelligence. [Google Scholar]
- [22].Li Lihong, Chu Wei, Langford John, and Schapire Robert E. 2010. A contextual-bandit approach to personalized news article recommendation. In Proceedings of the 19th international conference on World wide web. ACM, 661–670. [Google Scholar]
- [23].Liang Kung-Yee and Zeger Scott L. 1986. Longitudinal data analysis using generalized linear models. Biometrika 73, 1 (1986), 13–22. [Google Scholar]
- [24].Liao Peng, Dempsey Walter, Sarker Hillol, Hossain Syed Monowar, Al’Absi Mustafa, Klasnja Predrag, and Murphy Susan. 2018. Just-in-time but not too much: Determining treatment timing in mobile health. Proceedings of the ACM on Interactive, Mobile, Wearable and Ubiquitous Technologies 2, 4 (2018), 179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Liao Peng, Klasnja Predrag, Tewari Ambuj, and Murphy Susan A. 2016. Sample size calculations for micro-randomized trials in mHealth. Statistics in Medicine 35, 12 (2016), 1944–1971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Martin Cesar A, Rivera Daniel E, Hekler Eric B, Riley William T, Buman Matthew P, Adams Marc A, and Magann Alicia B. 2018. Development of a control-oriented model of social cognitive theory for optimized mHealth behavioral interventions. IEEE Transactions on Control Systems Technology (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Mintz Yonatan, Aswani Anil, Kaminsky Philip, Flowers Elena, and Fukuoka Yoshimi. 2019. Non-stationary bandits with habituation and recovery dynamics. Operations Research (2019). to appear. [Google Scholar]
- [28].Nahum-Shani Inbal, Smith Shawna N, Spring Bonnie J, Collins Linda M, Witkiewitz Katie, Tewari Ambuj, and Murphy Susan A. 2017. Just-in-time adaptive interventions (JITAIs) in mobile health: key components and design principles for ongoing health behavior support. Annals of Behavioral Medicine 52, 6 (2017), 446–462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Osband Ian, Russo Daniel, and Van Roy Benjamin. 2013. (More) efficient reinforcement learning via posterior sampling. In Advances in Neural Information Processing Systems. 3003–3011. [Google Scholar]
- [30].Osband Ian and Van Roy Benjamin. 2017. On optimistic versus randomized exploration in reinforcement learning. arXiv preprint arXiv:1706.04241 (2017). [Google Scholar]
- [31].Osband Ian and Van Roy Benjamin. 2017. Why is Posterior Sampling Better than Optimism for Reinforcement Learning?. In International Conference on Machine Learning. 2701–2710. [Google Scholar]
- [32].Ouyang Yi, Gagrani Mukul, Nayyar Ashutosh, and Jain Rahul. 2017. Learning unknown markov decision processes: A thompson sampling approach. In Advances in Neural Information Processing Systems. 1333–1342. [Google Scholar]
- [33].Paredes Pablo, Gilad-Bachrach Ran, Czerwinski Mary, Roseway Asta, Rowan Kael, and Hernandez Javier. 2014. PopTherapy: coping with stress through pop-culture. In Proceedings of the 8th International Conference on Pervasive Computing Technologies for Healthcare. ICST (Institute for Computer Sciences, Social-Informatics and Telecommunications Engineering), 109–117. [Google Scholar]
- [34].Rabbi Mashfiqui, Aung Min Hane, Zhang Mi, and Choudhury Tanzeem. 2015. MyBehavior: automatic personalized health feedback from user behaviors and preferences using smartphones. In Proceedings of the 2015 ACM International Joint Conference on Pervasive and Ubiquitous Computing. ACM, 707–718. [Google Scholar]
- [35].Rivera Daniel E, Hekler Eric B, Savage Jennifer S, and Downs Danielle Symons. 2018. Intensively adaptive interventions using control systems engineering: Two illustrative examples. In Optimization of Behavioral, Biobehavioral, and Biomedical Interventions. Springer, 121–173. [Google Scholar]
- [36].Russo Daniel and Van Roy Benjamin. 2014. Learning to optimize via posterior sampling. Mathematics of Operations Research 39, 4 (2014), 1221–1243. [Google Scholar]
- [37].Russo Daniel J, Van Roy Benjamin, Kazerouni Abbas, Osband Ian, Wen Zheng, et al. 2018. A tutorial on thompson sampling. Foundations and Trends® in Machine Learning 11, 1 (2018), 1–96. [Google Scholar]
- [38].Sutton Richard S and Barto Andrew G. 2018. Reinforcement learning: An introduction. MIT press. [Google Scholar]
- [39].Tewari Ambuj and Murphy Susan A. 2017. From ads to interventions: Contextual bandits in mobile health. In Mobile Health. Springer, 495–517. [Google Scholar]
- [40].Thomas Philip and Brunskill Emma. 2016. Data-efficient off-policy policy evaluation for reinforcement learning. In International Conference on Machine Learning. 2139–2148. [Google Scholar]
- [41].Yom-Tov Elad, Feraru Guy, Kozdoba Mark, Mannor Shie, Tennenholtz Moshe, and Hochberg Irit. 2017. Encouraging physical activity in patients with diabetes: Intervention using a reinforcement learning system. Journal of medical Internet research 19, 10 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Zhou Mo, Mintz Yonatan, Fukuoka Yoshimi, Goldberg Ken, Flowers Elena, Kaminsky Philip, Castillejo Alejandro, and Aswani Anil. 2018. Personalizing Mobile Fitness Apps using Reinforcement Learning. In Companion Proceedings of the 23rd International on Intelligent User Interfaces: 2nd Workshop on Theory-Informed User Modeling for Tailoring and Personalizing Interfaces (HUMANIZE). [PMC free article] [PubMed] [Google Scholar]