Bayesian Variable Selection for Understanding Mixtures in Environmental Exposures

Summary

Social and environmental stressors are crucial factors in child development. However, there exists a multitude of measurable social and environmental factors—the effects of which may be cumulative, interactive, or null. Using a comprehensive cohort of children in North Carolina, we study the impact of social and environmental variables on 4th end-of-grade exam scores in reading and mathematics. To identify the essential factors that predict these educational outcomes, we design new tools for Bayesian linear variable selection using decision analysis. We extract a predictive optimal subset of explanatory variables by coupling a loss function with a novel model-based penalization scheme, which leads to coherent Bayesian decision analysis and empirically improves variable selection, estimation, and prediction on simulated data. The Bayesian linear model propagates uncertainty quantification to all predictive evaluations, which is important for interpretable and robust model comparisons. These predictive comparisons are conducted out-of-sample with a customized approximation algorithm that avoids computationally intensive model re-fitting. We apply our variable selection techniques to identify the joint collection of social and environmental stressors—and their interactions—that offer clear and quantifiable improvements in prediction of reading and mathematics exam scores.

1 |. INTRODUCTION

It is widely agreed that health and well-being are determined by multiple forces. Environmental exposures such as air pollution and lead adversely affect health and cognitive development, and are often elevated in disadvantaged communities. These same communities may also experience a multitude of social stressors: inadequate access to health care, poor housing, high unemployment, high crime, high poverty, and racial segregation, among others.^1,2 While social and environmental stressor co-exposures may or may not interact, they almost certainly cumulate. In addition, health and developmental impacts during childhood are strongly associated with poor outcomes in adults. Thus, understanding the effects of co-exposures to social and environmental stressors among children is critical to improving the nation’s health. Here, we develop methods to better understand the relationships among environmental mixtures and social context, as well as their impacts on developmental outcomes.

Although the evidence is not yet conclusive, a growing body of epidemiological research suggests that pre- and post-natal exposure to ambient air pollution, including PM_2.5, adversely impacts neurological development in children.³ Prenatal PM_2.5 exposure specifically has been linked with poorer function across memory and attention domains in children.⁴ Meanwhile, there is a plethora of evidence that lead exposure in young children, even at low levels, is associated with intellectual deficits,⁵ learning and behavioral disorders,⁶ and lower scores on intelligence and standardized tests.⁷ The adverse effects of childhood lead exposure persist into adulthood, affecting intelligence and socioeconomic status.⁸

Social stressors, often present in the same communities as these adverse environmental exposures, may also affect health and development. Neighborhood measures of poverty, disadvantage, and deprivation are associated with decrements in cognitive development in children,⁹ and a substantial body of evidence links segregation with adverse health outcomes.¹⁰ Despite evidence linking neighborhood conditions with health¹¹ and developmental outcomes in children,¹² the effects of environmental exposures such as air pollution and lead are not always evaluated in conjunction with neighborhood conditions.

Our overarching objective is to identify the environmental exposures (e.g., air pollution exposure, lead exposure) and social stressors (e.g., racial residential segregation, neighborhood deprivation, income status)—as well as their interactions—that predict child educational outcomes. For this task, we develop new decision tools for Bayesian variable selection. Although shrinkage and sparsity priors can encode prior beliefs or preferences for sparsity, the prior alone cannot select variables. In particular, the posterior distribution encapsulates information about variable importance, but a decision about the active or inactive variables is still required. A natural solution is a two-stage approach: after obtaining the posterior distribution of a Bayesian (linear) model, we extract sparse linear summaries that are optimized for prediction. From a decision analysis perspective, we pair a loss function with a novel model-based penalization scheme that enables simultaneous optimization for predictive accuracy and sparsity. Unlike marginal decision criteria that examine each regression coefficient individually—hard-thresholding,¹³ posterior inclusion probabilities,¹⁴ or posterior credible intervals that exclude zero¹⁵—our approach selects variables that are jointly predictive, which is particularly important in the presence of correlated variables. We quantify the predictive contributions of particular variables or sets of variables by comparing the out-of-sample predictive accuracy across distinct sparsity levels. Crucially, we leverage the predictive distribution of the Bayesian linear model to augment these predictive evaluations with posterior uncertainty quantification. The uncertainty quantification is valuable for informed comparisons and provides a mechanism for selecting the smallest subset among nearly-optimal linear models. For computational scalability, we design an approximation algorithm that avoids intensive model re-fitting for the out-of-sample evaluations and instead only requires a single model fit.

The statistical analysis is enabled by linking multiple administrative datasets to construct an analysis dataset that tracks children in North Carolina from birth through time of lead testing and finally time of 4th grade standardized testing in reading and mathematics. This work is also responsive to calls from leading researchers in support of research agendas that leverage longitudinal population-based data linkages.¹²

The paper is organized as follows: Section 2 introduces the comprehensive database constructed for our study; in Section 3, we develop in full the Bayesian variable selection methodology; results are presented in Section 4, which includes a simulation study; we conclude in Section 5.

2 |. DATA

The analysis dataset¹⁶ for this study was created by linking three administrative databases for the State of North Carolina (NC)—detailed birth records, blood lead surveillance data, and end-of-grade (EOG) standardized testing data—with extensive exposure data. The exposure data include ambient air quality and temperature, socioeconomic factors, and indices that measure racial isolation and neighborhood deprivation. In all, 25 variables and features are included. A short summary of the dataset is included here, with a comprehensive list of variables provided in the Appendix. More detailed discussion of the dataset is available in Bravo et al.¹⁷

Detailed birth records were obtained from the NC State Center for Health Statistics, Vital Statistics Department. The data include information on maternal demographics, maternal and infant health, and maternal obstetrics history for all documented live births in NC. The analysis dataset restricts to students born in 2000, which facilitates linking with the Census-based datasets below.

Blood lead surveillance records were obtained from the state registry maintained by the Childhood Lead Poisoning Prevention Program of the Children’s Environmental Health Unit, Department of Health and Human Services in Raleigh, NC. Blood lead levels are stored as integer values. The analysis dataset includes measurements from 2000-2011.

EOG standardized testing data were obtained from the NC Education Research Data Center of Duke University in Durham, NC. Children in NC in grades 3–8 are tested in reading and mathematics at the end of the school year.¹⁸ The database contains records for all EOG test results statewide for tests from the 1995–1996 school year to the present; the analysis dataset restricts to 4th grade EOG exams in reading and mathematics in 2010-2012. The dataset also includes identifying information such as name and birth date and data on demographics and socioeconomics, English proficiency, and school district.

Air pollution exposure metrics are based on daily 24-hour averages of ambient PM_2.5 concentrations obtained from two different sources: the US Environmental Protection Agency National Air Monitor Stations or State and Local Air Monitoring Stations (NAMS/SLAMS) monitoring network (1999-2000); and publicly available output from the Community Multiscale Air Quality (CMAQ) downscaler (2010-2012). These exposure metrics are converted into pre-natal exposure, which is the average exposure by trimester of pregnancy (1-13 weeks, 14-26 weeks, and 27 weeks to birth); chronic exposure, which is the average exposure for one year prior to EOG testing; and acute exposure, which is the average exposure for 30 days prior to EOG testing. The prenatal metrics use the closest monitor within 30km of the mother’s residence, while the chronic and acute metrics use the closest monitor within 30km of the child’s residence.

Ambient temperature data were obtained from the State Climate Office of NC. Temperature exposure was computed as the average exposure by trimester of pregnancy (1-13 weeks, 14-26 weeks, and 27 weeks to birth) using the nearest weather station within 50km of the mother’s residence.

Racial isolation (RI) and neighborhood deprivation (NDI) are critical indices that measure social stress. RI is based on 2000 and 2010 Census data using a previously derived local, spatial measure of RI,¹⁹ which is in turn derived from the global spatial isolation index developed by Reardon and O’Sullivan.²⁰ The RI index ranges from 0 to 1, with values close to 1 indicating the neighborhood environment is almost entirely non-Hispanic black (NHB). NDI values were calculated at the census tract level based on 2000 and 2010 Census data using a previously derived measure of NDI.²¹ The NDI empirically summarizes eight census variables representing five socio-demographic domains (income/poverty, education, employment, housing, and occupation), including: percent of males in management and professional occupations, percent of crowded housing, percent of households in poverty, percent of female headed households with dependents, percent of households on public assistance and households earning <$30,000 per year estimating poverty, percent earning less than a high school education, and the percent unemployed. Higher values of NDI indicate more severe neighborhood deprivation. To account for neighborhood dynamics, each child was assigned an RI and NDI value at time of birth and at time of EOG testing. RI and NDI at birth were assigned based on the child’s tract of residence at time of birth (obtained from the detailed birth records), using RI and NDI calculated from 2000 Census data. RI and NDI at time of EOG testing were assigned based on the child’s tract of residence at time of testing (obtained from the EOG testing data), using RI and NDI calculated from 2010 Census data.

Methods for receiving, storing, linking, analyzing, and presenting results related to this study were all governed by a research protocol approved by the Rice University Institutional Review Board.

3 |. METHODS

3.1 |. The Bayesian linear model

Bayesian linear regression provides a compelling platform from which to address the challenges in our analysis: the linear modeling structure inherits the interpretability of classical linear regression, while the prior distribution conveys advantages for regularization of unimportant variables, (posterior) uncertainty quantification, and improved predictions. Consider the paired observations ${\left\{y_i,x_i\right\}}_{i=1}^n$ where $y_i\in \mathbb{R}$ denotes the response variable and x_i is the p-dimensional predictor, which may include interaction terms. The Bayesian linear model is

$$y_i=x_i^{\prime }\beta +{ϵ}_i,{ϵ}_i\stackrel{\mathit{iid}}{\sim }N\left(0,{\sigma }^2\right)$$ (1)

$$\beta \sim p\left(\beta \right)$$ (2)

where p(β) denotes a prior distribution on the regression coefficients. The prior distribution (2) has long served as a mechanism for introducing regularization in the linear model: Bayesian ridge regression ${\beta }_j\sim N\left(0,{\sigma }_{\beta }^2\right)$ and the Bayesian lasso²² are adaptations of non-Bayesian regularization techniques which seek to combat multicollinearity and mitigate the effects of unimportant predictor variables. More commonly, Bayesian regression utilizes shrinkage priors such as the horseshoe prior²³ and the Dirichlet-Laplace prior,²⁴ which demonstrate improved point estimation and posterior contraction properties,^13,25 especially for sparse regressions in which many coefficients may be negligible. Shrinkage priors are continuous distributions, usually scale mixtures of Gaussian distributions, which are designed for both regularization and computational scalability. By comparison, sparsity-inducing priors, such as spike-and-slab priors,^26,27,28,29 place a positive probability on β_j = 0. Although conceptually appealing, sparsity-inducing priors face significant challenges for computation and inference. Nonetheless, sparsity-inducing priors are compatible with the methods introduced below.

Regardless of the choice of prior, Bayesian inference proceeds via the posterior distribution p(β|y) from model (1)–(2). The posterior distribution is rarely available analytically, especially for shrinkage priors, and therefore posterior inference most commonly uses Markov Chain Monte Carlo (MCMC) algorithms. For many choices of (2), an efficient elliptical slice sampler³⁰ is available for obtaining samples from the posterior distribution of the regression coefficients. Using these samples, posterior summaries such as expectations, standard deviations, and credible intervals are easily computable.

Although the posterior distribution p(β|y) encapsulates information about variable importance, additional tools are needed to select and evaluate joint subsets of variables. In practice, the vast majority of Bayesian variable selection proceeds marginally for each coefficient β_j, including hard-thresholding under shrinkage priors,¹³ marginal inclusion probabilities under sparsity-inducing priors,¹⁴ or selection based on credible intervals that omit zero.¹⁵ While useful summaries, these approaches fail to consider variables jointly, which is particularly important for correlated predictors and interactions. In addition, marginally-selected variables do not necessarily comprise an adequately predictive linear basis relative to the full model, and indeed are not constructed or evaluated for this purpose. The implication is that, for a set of marginally-selected variables, it is incorrect to interpret them jointly as a predictive model: for instance, we cannot claim that these variables are sufficient to explain the variability in the data. Marginal selection is not without benefits, for example as a tool to screen unimportant variables in ultrahigh-dimensional data,³¹ but must be interpreted carefully. Alternatively, some point estimation techniques produce sparse estimates of β within a Bayesian linear model,³² but these methods are not accompanied by uncertainty quantification for either the coefficients β or metrics for evaluating predictive accuracy associated with various sparsity levels. Consequently, techniques that provide both selection and uncertainty quantification for the selection process are at a premium.

3.2 |. Decision analysis for Bayesian variable selection

Bayesian variable selection is a decision problem: using the full model posterior, the task is to determine a minimal subset of variables that nearly preserve—or if possible, improve upon—the fitness of the full model. Fitness is evaluated using predictive performance and measured by a loss function, such as squared error loss. Importantly, the loss function may be augmented with a sparsity-inducing penalty, which admits a formal expression of the tradeoff between predictive accuracy and model simplicity. Decision analysis proceeds to minimize the posterior predictive expected loss; intuitively, this procedure averages the loss function over future or unobserved values of the response variable and then minimizes the resulting expression. Importantly, we obtain computationally convenient representations of this objective, with model selection uncertainty quantification (Section 3.4) and rapidly-computable out-of-sample comparisons (Section 3.5).

For any covariate value $\tilde{x}$, the linear model assigns a posterior predictive distribution to the associated response variable $\tilde{y}$:

$$p\left(\tilde{y}|y\right)=\int p\left(\tilde{y}|\theta \right)p\left(\theta |y\right)d\theta ,\theta =\left(\beta ,{\sigma }^2\right)$$ (3)

where $\stackrel{\sim }{y}|\theta ~N\left({\tilde{x}}^{\prime }\beta ,{\sigma }^2\right)$ is conditionally independent from the observed data y = (y₁, …, y_n)′. Notably, (3) defines a distribution over the possible realizations of the response variable at a particular covariate value and conditional on all observed data. The posterior predictive distribution is fundamental for point prediction, but also provides uncertainty quantification for predictive functionals, such as $\tilde{y}$ itself and measures of predictive loss (see Section 3.4).

More generally, consider the task of prediction at covariates ${\left\{{\tilde{x}}_i\right\}}_{i=1}^{\tilde{n}}$, which may be distinct from the observed covariates ${\left\{x_i\right\}}_{i=1}^n$. The choice of ${\left\{{\tilde{x}}_i\right\}}_{i=1}^{\tilde{n}}$ can target predictions for specific designs, subject characteristics, or subpopulations of interest. The corresponding predictive variables are denoted ${\left\{{\tilde{y}}_i\right\}}_{i=1}^{\tilde{n}}$, which are the unobserved or future values of the response variable at each predictor ${\tilde{x}}_i$. The posterior predictive distribution $p\left({\tilde{y}}_i|y\right)$ is given by (3) with ${\tilde{y}}_i|\theta \sim N\left({\tilde{x}}_i^{\prime }\beta ,{\sigma }^2\right)$, and is not required to be known analytically: samples ${\left\{{\tilde{y}}_i^s\right\}}_{s=1}^S\sim p\left({\tilde{y}}_i|y\right)$ are sufficient, which usually are obtained by sampling θ^s ∼ p(θ|y) from the posterior and ${\tilde{y}}_i^s\sim p\left({\tilde{y}}_i|{\theta }^s\right)$ from the aforementioned Gaussian distribution. Regardless of the choice of covariate values ${\left\{{\tilde{x}}_i\right\}}_{i=1}^{\tilde{n}}$, the posterior predictive distribution conditions on all available data.

For simultaneous evaluation of both predictive accuracy and model complexity, we consider the following loss function:

$${\mathcal{L}}_{\lambda }\left({\left\{\tilde{y}\right\}}_{i=1}^{\tilde{n}},\delta \right)=\frac{1}{\tilde{n}}\sum _{i=1}^{\tilde{n}}{\Vert {\tilde{y}}_i-{\tilde{x}}_i^{\prime }\delta \Vert }^2+\lambda \mathcal{P}\left(\delta \right)$$ (4)

where δ is a p-dimensional vector of linear coefficients and $\mathcal{P}$ is a complexity penalty. The complexity parameter $\lambda \ge 0$ controls the tradeoff between accuracy and complexity, with larger values of λ encouraging simpler models. The squared error loss measures fitness of the linear point prediction ${\tilde{x}}_i^{\prime }\delta$ for some value of δ, which is to be determined. Many choices of complexity penalization are available, but for the purpose of variable selection, we consider sparsity-inducing penalties such as ℓ₁-penalization and its variants (see Section 3.3). In this context, a simpler model is one which includes fewer variables, i.e., δ_j = 0 for some or many j ∈ {1, …, p}, and the goal is to maximize predictive performance in the presence of sparsity.

To obtain optimal coefficients δ for a given complexity level λ, we minimize the posterior predictive expectation of (4), which averages over the uncertainty implicit in each predictive variable ${\tilde{y}}_i$ conditional on the observed data y:

$${\widehat{\delta }}_{\lambda }=\arg \underset{\delta }{\min }{\mathbb{E}}_{\left[\tilde{y}|y\right]}{\mathcal{L}}_{\lambda }\left({\left\{{\tilde{y}}_i\right\}}_{i=1}^{\tilde{n}},\delta \right)$$ (5)

where the expectation is taken with respect to (3) for each $p\left({\tilde{y}}_i|y\right)$. By varying λ, the solution in (5) generates a path of optimal coefficients at varying complexity levels. From (3), it follows that ${\mathbb{E}}_{\left[\tilde{y}|y\right]}{\mathcal{L}}_{\lambda }\left({\left\{{\tilde{y}}_i\right\}}_{i=1}^{\tilde{n}},\delta \right)={\mathbb{E}}_{\left[\theta |y\right]}{\mathbb{E}}_{\left[\tilde{y}|\theta \right]}{\mathcal{L}}_{\lambda }\left({\left\{{\tilde{y}}_i\right\}}_{i=1}^{\tilde{n}},\delta \right)$. We evaluate these expectations sequentially. The penalty term is fixed and remains constant throughout, so for notational simplicity we consider the unpenalized case, λ = 0. Observing ${\mathbb{E}}_{\tilde{y}|\theta }{\tilde{y}}_i={\tilde{x}}_i^{\prime }\beta$, we simplify as follows:

$$\begin{gathered} {\mathbb{E}}_{\left[\tilde{y}|\theta \right]}{\mathcal{L}}_0\left({\left\{{\tilde{y}}_i\right\}}_{i=1}^{\tilde{n}},\delta \right)=\frac{1}{\tilde{n}}\sum _{i=1}^{\tilde{n}}{\mathbb{E}}_{\left[\tilde{y}|\theta \right]}{\Vert {\tilde{y}}_i-{\tilde{x}}_i^{\prime }\delta \Vert }^2=\frac{1}{\tilde{n}}\sum _{i=1}^{\tilde{n}}{\mathbb{E}}_{\left[\tilde{y}|\theta \right]}{\Vert \left({\tilde{y}}_i-{\tilde{x}}_i^{\prime }\beta \right)+\left({\tilde{x}}_i^{\prime }\beta -{\tilde{x}}_i^{\prime }\delta \right)\Vert }^2 \\ ={\sigma }^2+\frac{1}{\tilde{n}}\sum _{i=1}^{\tilde{n}}{\Vert {\tilde{x}}_i^{\prime }\beta -{\tilde{x}}_i^{\prime }\delta \Vert }^2 \end{gathered}$$

since ${\sigma }^2=\frac{1}{\tilde{n}}{\sum }_{i=1}^{\tilde{n}}{\mathbb{E}}_{\left[\tilde{y}|\theta \right]}{\Vert {\tilde{y}}_i-{\tilde{x}}_i^{\prime }\beta \Vert }^2$. Letting $\widehat{\beta }={\mathbb{E}}_{\theta |y}\left(\beta \right)$ and $\widehat{{\sigma }^2}={\mathbb{E}}_{\theta |y}\left({\sigma }^2\right)$ be the posterior expectations, the outer expectation of the loss function simplifies similarly:

$$\begin{gathered} {\mathbb{E}}_{\left[\theta |y\right]}\left\{{\sigma }^2+\frac{1}{\tilde{n}}\sum _{i=1}^{\tilde{n}}{\Vert {\tilde{x}}_i^{\prime }\beta -{\tilde{x}}_i^{\prime }\delta \Vert }^2\right\}=\widehat{{\sigma }^2}+\frac{1}{\tilde{n}}\sum _{i=1}^{\tilde{n}}{\mathbb{E}}_{\left[\theta |y\right]}{\Vert \left({\tilde{x}}_i^{\prime }\beta -{\tilde{x}}_i^{\prime }\widehat{\beta }\right)+\left({\tilde{x}}_i^{\prime }\widehat{\beta }-{\tilde{x}}_i^{\prime }\delta \right)\Vert }^2 \\ =\widehat{{\sigma }^2}+\frac{1}{\tilde{n}}\mathrm{trace}\left({\tilde{X}}^{\prime }\tilde{X}{\widehat{\Sigma }}_{\beta }\right)+\frac{1}{\tilde{n}}\sum _{i=1}^{\tilde{n}}{\Vert {\tilde{x}}_i^{\prime }\widehat{\beta }-{\tilde{x}}_i^{\prime }\delta \Vert }^2 \end{gathered}$$

where $\tilde{X}={\left({\tilde{x}}_1,\dots ,{\tilde{x}}_{\tilde{n}}\right)}^{\prime }$ is the specified design matrix and ${\widehat{\Sigma }}_{\beta }=Co{v}_{\left[\theta |y\right]}\left(\beta \right)$ is the posterior covariance of β. Conclusively, we omit additive constants that do not depend on δ to identify an equivalent expression for the optimal parameters from (5):

$${\widehat{\delta }}_{\lambda }=\arg \underset{\delta }{\min }\left\{\frac{1}{\tilde{n}}{\Vert \widehat{y}-\tilde{X}\delta \Vert }^2+\lambda \mathcal{P}\left(\delta \right)\right\}$$ (6)

where $\widehat{y}={\mathbb{E}}_{\left[\tilde{y}|y\right]}\tilde{y}=\tilde{X}\widehat{\beta }$ is the point prediction at $\tilde{X}$ under the linear model (1)–(2). This expectation is easily and quickly computable using posterior draws of β, e.g., $\widehat{y}\approx \tilde{X}\stackrel{\_}{\beta }$ for $\stackrel{\_}{\beta }=S^{-1}{\sum }_{s=1}^S{\beta }^s$ with β^s ∼ p(β|y).

The representation in (6) is valuable: the decision analysis posited in (5) is solved as a penalized least squares problem. For many choices of penalties $\mathcal{P}$, efficient algorithms exist for solving (6); all that is required is the pseudo-response variable $\widehat{y}=\tilde{X}\widehat{\beta }$ and the accompanying design matrix $\tilde{X}$. By varying λ, we obtain solutions to (5) that vary in complexity. When $\mathcal{P}$ is a sparsity-inducing penalty, we obtain subsets of variables that are optimized for the point predictions under the full model. For example, the ℓ₁-penalty, $\mathcal{P}\left(\delta \right)={\sum }_{j=1}^p|{\delta }_j|$, induces a lasso regression problem³³ with $\widehat{y}$ as data, so the parameters ${\widehat{\delta }}_{\lambda }$ are computable using standard software such as the glmnet³⁴ package in R.

There is a fundamental distinction between the linear coefficients β and δ. In particular, β is a parameter of the Bayesian model and therefore is endowed with a prior distribution. By comparison, δ is any p-dimensional vector, and in that sense is entirely disconnected from the Bayesian model. The operation in (5) optimizes δ based on the model and the loss function, and the solution (6) is an expected functional under the posterior distribution. Hence, it is not coherent to place a prior on δ or λ: these define the actions and loss functions, respectively, in the decision analysis but they are not parameters of the model. While the prior on β may record our preference for sparse linear coefficients, this does not guarantee sparsity of any particular posterior functional or summary. For illustration, consider the unpenalized case with λ = 0. Using any design matrix $\tilde{X}$, the (possibly nonunique) solution to (6) is simply ${\widehat{\delta }}_{\lambda =0}=\widehat{\beta }$, which is the posterior expectation of the regression coefficients in (1). However, this quantity is not sparse even in the case of sparsity-inducing priors and therefore cannot provide variable selection. By allowing λ > 0, we admit linear coefficients that jointly optimize for prediction and sparsity.

The decision analysis approach to variable selection has historical roots³⁵ with modern development.^36,37 Related approaches, often termed posterior summarization, have been developed for multiple linear regression and logistic regression,³⁶ nonlinear regressions,³⁸ time-varying parameter models,³⁹ functional regression,⁴⁰ graphical models,⁴¹ and seeming unrelated regressions.⁴² However, existing methods face several important limitations. First, they all rely on in-sample quantities for evaluation. Out-of-sample metrics are more suitable for predictive evaluation, which is essential for model comparison and selection. In-sample metrics have a greater risk of overfitting, and therefore may favor models that are unnecessarily complex. Second, these methods provide limited guidelines for model determination, and often use in-sample graphical summaries. It is important to identify both (i) the best model for predictive accuracy and (ii) the set of models that are close enough to the best model in predictive performance. Leaving precise definitions to the next section, we emphasize that these notions fundamentally rely on evaluations of predictive performance—which is most appropriately determined out-of-sample. Lastly, these approaches commonly adopt an adaptive penalty akin to the adaptive lasso⁴³ in place of the ℓ₁-penalty. However, these existing adaptive penalization schemes are not coherent within the decision analysis framework of (4) and (5). This issue is addressed and resolved in the next section.

3.3 |. Generalized penalties and the Bayesian adaptive lasso

The task of variable selection requires a sparsity-inducing penalty for $\mathcal{P}$. Equally important, the optimal coefficients are only available upon solving the penalized least squares problem (6). Mutual consideration of sparsity and computational scalability suggests ℓ₁-penalization, for which the penalized least square problem is equivalent to the lasso³³ using $\widehat{y}$ as data. However, the ℓ₁-penalty is known to introduce substantial bias for large coefficients, and cannot simultaneously provide correct variable selection and optimal estimation in a frequentist context.⁴³ Adaptive penalization methods^44,43 attempt to correct the suboptimality of the ℓ₁-penalty and have demonstrated wide success in practice. These approaches are distinct from the decision analysis framework of (4)–(5): the response variable in the penalized least squares problem (6) is $\widehat{y}$ and not the original data y. More generally, classical adaptive penalization methods do not operate in the same Bayesian framework of (1)–(2), and therefore require additional tools to provide uncertainty quantification.

In the context of decision analysis for Bayesian variable selection, several authors have considered adaptive penalties for $\mathcal{P}$.^{36,37,38,39,40} These approaches adopt a common form which mimics the adaptive lasso⁴³:

$${\mathcal{P}}^0\left(\delta \right)=\sum _{j=1}^p{\widehat{\omega }}_j^0|{\delta }_j|,{\widehat{\omega }}_j^0={|{\widehat{\beta }}_j|}^{-\gamma }$$ (7)

where $\widehat{\beta }={\mathbb{E}}_{\theta |y}\left(\beta \right)$ and $\gamma >0$, typically with γ = 1^36,38,40 or γ = 2.^37,39 The adaptive penalty in (7) does not introduce any additional complexity for computation relative to the ℓ₁-penalty. However, this approach is not coherent within the decision analysis framework of (4)–(5): the penalty function $\mathcal{P}$ is treated as known in (4), while (7) requires an estimate of a posterior quantity. Implicitly, this approach ignores the uncertainty in unknown model parameters.

We propose fully Bayesian model-based penalization, which allows the regularization behavior and notion of complexity in the predictive optimization problem to be informed by the model within a coherent decision analysis framework. Specifically, we generalize the loss function (4) as follows:

$${\mathcal{L}}_{\lambda }\left({\left\{\tilde{y}\right\}}_{i=1}^{\tilde{n}},\delta ,\theta \right)=\frac{1}{\tilde{n}}\sum _{i=1}^{\tilde{n}}{\Vert {\tilde{y}}_i-{\tilde{x}}_i^{\prime }\delta \Vert }^2+\lambda \mathcal{P}\left(\delta ,\theta \right)$$ (8)

where the penalty is now permitted to depend on model parameters θ. Within this framework, we introduce a Bayesian adaptive lasso penalty:

$$\mathcal{P}\left(\delta ,\theta \right)=\sum _{j=1}^p{\omega }_j|{\delta }_j|,{\omega }_j={|{\beta }_j|}^{-\gamma }$$ (9)

where γ > 0. Notably, (9) depends on the regression coefficients β, which are unknown and random quantities.

To extract optimal coefficients from the generalized loss function, we now integrate over two sources of uncertainty: (i) the predictive variables ${\tilde{y}}_i$ and (ii) the model parameters θ, in both cases conditional on the observed data y. The optimal coefficients are identified by minimizing the iterated expected loss:

$${\widehat{\delta }}_{\lambda }=\arg \underset{\delta }{\min }{\mathbb{E}}_{\left[\theta |y\right]}\left\{{\mathbb{E}}_{\left[\tilde{y}|y,\theta \right]}{\mathcal{L}}_{\lambda }\left({\left\{{\tilde{y}}_i\right\}}_{i=1}^{\tilde{n}},\delta ,\theta \right)\right\}.$$ (10)

Under the mild condition that ${\mathbb{E}}_{\left[\theta |y\right]}|\mathcal{P}\left(\delta ,\theta \right)|<\infty$ for some δ, the arguments in Section 3.2 imply that (10) is equivalent to

$${\widehat{\delta }}_{\lambda }=\arg \underset{\delta }{\min }\left\{\frac{1}{\tilde{n}}{\Vert \widehat{y}-\tilde{X}\delta \Vert }^2+\lambda \stackrel{\_}{\mathcal{P}\left(\delta \right)}\right\}$$ (11)

where $\stackrel{\_}{\mathcal{P}\left(\delta \right)}={\mathbb{E}}_{\left[\theta |y\right]}\mathcal{P}\left(\delta ,\theta \right)$ is the posterior expectation under (1)–(2). For the Bayesian adaptive lasso in (9), the penalty required to solve (11) is

$$\stackrel{\_}{\mathcal{P}\left(\delta \right)}=\sum _{j=1}^p{\widehat{\omega }}_j|{\delta }_j|{\widehat{\omega }}_j={\mathbb{E}}_{\left[\theta |y\right]}\left({|{\beta }_j|}^{-\gamma }\right).$$ (12)

The necessary weights are easily estimable using posterior simulations: ${\widehat{\omega }}_j\approx S^{-1}{\sum }_{s=1}^S{|{\beta }_j^s|}^{-\gamma }$ with β^s ∼ p(β|y). Therefore, the optimal coefficients in (10) are readily available—again using standard software such as the glmnet³⁴ package in R—with minimal additional costs relative to (non-adaptive) ℓ₁-penalization.

The adaptive weights in (12) are distinct from both the adaptive lasso⁴³ and previous approaches for sparse decision analysis.^{36,37,38,39,40} In the adaptive lasso, the estimator for the weights is ${|{\widehat{\beta }}_j^{ols}|}^{-\gamma }$ where ${\widehat{\beta }}_j^{ols}$ is the ordinary least squares estimate of β_j in (1). Notably, ${\widehat{\beta }}_j^{ols}$ is only well-defined for p < n; by comparison, (12) is valid for p > n for many choices of shrinkage priors in (2). More specifically, the adaptive lasso requires a consistent estimate of β_j in (1) in order to obtain both selection consistency and an optimal estimation rate. From the continuous mapping theorem, this is equivalent to consistent estimation of the weight ω_j = |β_j|^−γ, so in that context there is no need to distinguish between estimation of β_j and ω_j. However, from a Bayesian perspective, the order of estimation matters due to the presence of (posterior) expectations. Jensen’s inequality implies that the proposed weights are larger than those in ${\mathcal{P}}^0:{\widehat{\omega }}_j\ge {\widehat{\omega }}_j^0$. The discrepancy between the weights is greatest when $|{\widehat{\beta }}_j|$ is small; when $|{\widehat{\beta }}_j|$ is large, the weights are effectively indistinguishable. Therefore, the proposed penalty is more aggressive in weighting small coefficient estimates toward zero without introducing additional bias for the large coefficient estimates. Nonetheless, the effects of small sampled values of $|{\beta }_j^s|$ on ${\widehat{\omega }}_j$ can be mitigated by decreasing γ. More broadly, the proposed approach is coherent within a decision analysis framework: the loss function (8) depends on predictive and posterior variables ${\tilde{y}}_i$ and θ, respectively, which are integrated out using the posterior distribution under model (1)–(2).

3.4 |. Model determination from predictive performance

The decision analysis elicits optimal coefficients ${\widehat{\delta }}_{\lambda }$ in (10) for each value of the complexity parameter, λ. It is informative to evaluate and compare these coefficients at various levels of complexity. The goal is determine (i) which λ delivers the best predictive performance and (ii) which complexity levels λ are close enough in predictive accuracy relative to the best model. Criterion (ii) encapsulates the core tradeoff between accuracy and simplicity: although the best model might be complex, there may exist one or more simpler models that achieve nearly the same performance. In the context of variable selection, λ controls the tradeoff between accuracy and sparsity: for an ℓ₁-penalty or the Bayesian adaptive lasso (9), λ = 0 produces a solution with maximal complexity, so all variables are included, while λ → ∞ returns the null model. Alternative specifications of $\mathcal{P}$ are readily available, such as stepwise regression with forward selection or backward elimination, for which λ can be defined to index the model size. However, the resulting solutions ${\widehat{\delta }}_{\lambda }$ are not continuous in λ, which suggests a lack of stability and robustness.⁴⁵ Nonetheless, the subsequent methodology remains valid for any choice of penalty as long as (6) is numerically solvable.

Our approach for evaluating predictive performance follows two core principles, which are similarly emphasized by Kowal⁴⁶: (i) predictions should be evaluated out-of-sample and (ii) evaluations should be accompanied by full uncertainty quantification. Naturally, out-of-sample predictive evaluations are strongly preferred as more reliable assessments of the predictive capability of a model. In-sample metrics tend to favor more complex models, which simultaneously encourages overfitting and undermines the goal of producing simple or sparse solutions. Yet fundamentally, there is nonignorable uncertainty in the evaluation process: predictive performance is inherently random and will vary across different testing datasets, even for the same values of the predictors. This uncertainty is extremely valuable: it provides strength of evidence for a model and introduces a notion of equivalence among models with similar predictive performance. Importantly, the uncertainty quantification is provided automatically from model (1)–(2) and does not require additional assumptions.

Among frequentist methods, it is common to select the complexity parameter using cross-validation. It has been shown that accounting for the uncertainty in model evaluation can improve selection and reduce bias in prediction.^47,48 The one-standard-error rule⁴⁸ is a popular choice for model selection: instead of selecting the best model, this rule selects the simplest model within one standard error of the best model. Similarly, Lei⁴⁷ proposes a K-fold cross-validation procedure coupled with a multiplier bootstrap to construct a confidence set of acceptable models. These techniques are successful because they account for nonignorable uncertainty in the evaluation process, and then leverage that information for model selection. Our approach is conceptually adjacent to these methods, yet fundamentally different due to the presence of the Bayesian model (1)–(2). Bayesian analysis attributes uncertainty to a probability distribution. In the context of predictive evaluation, that distribution is the posterior predictive distribution. We use this distribution to construct interpretable metrics of predictive performance accompanied by full posterior uncertainty quantification.

Note that one approach for decision analytic Bayesian variable selection, called signal adaptive variable selection (SAVS),³⁷ claims to avoid the issue of selecting λ. However, SAVS uses the optimization criterion (6) with the penalty (7), but simply sets λ = 1. This does not obviate the need to select λ: it is just one possible choice for the sparsity level. Furthermore, this approach fails to provide any (out-of-sample) comparative evaluation for models of differing sparsity levels, and consequently cannot provide the necessary uncertainty quantification for predictive performance among models of varying complexity.

In conjunction with the concurrent work by Kowal,⁴⁶ we introduce two complementary notions of proximity in predictive performance, which are made precise below. First, let η ≥ 0 define a margin for acceptable performance: any model with predictive performance within η of the best model is considered acceptable. The margin η is selected by the scientific investigator and varies according to the need to achieve a certain level of accuracy, including η = 0, and may be expressed relative to the error variance σ² in (1). Second, note that predictive performance is inherently random: model accuracy will vary across different testing datasets, even for the same values of the predictors. In particular, a simplified (or sparse) model may not perform within η of the best model for a particular testing dataset, but nonetheless may achieve this margin with some (possibly small) probability. We define ε ∈ [0, 1] to be a probability level such that, according to the predictive distribution (3) under the linear model, there is at least ε probability that the simpler model matches or exceeds the predictive ability of the best model (within a margin of η). Acceptable models must satisfy these criteria, which depend on both the margin η and the probability level ε.

For concreteness, we proceed to measure accuracy using mean squared error (MSE), although the subsequent results are generalizable for other performance metrics. The in-sample MSE is defined by

$${\mathrm{MSE}}_{\lambda }^{in}=\frac{1}{n}\sum _{i=1}^n{\left(y_i-x_i^{\prime }{\widehat{\delta }}_{\lambda }\right)}^2$$ (13)

which evaluates the point prediction parameters ${\widehat{\delta }}_{\lambda }$ at the observed data ${\left\{y_i,x_i\right\}}_{i=1}^n$. For an analogous predictive quantity, consider the MSE evaluated at ${\tilde{y}}_i\sim p\left({\tilde{y}}_i|y\right)$ in (3):

$${\widetilde{\mathrm{MSE}}}_{\lambda }^{in}=\frac{1}{n}\sum _{i=1}^n{\left(y_i-x_i^{\prime }{\widehat{\delta }}_{\lambda }\right)}^2$$ (14)

which is the predictive (in-sample) MSE. Notably, (14) incorporates the distribution of future or unobserved values ${\tilde{y}}_i$ at covariate value x_i and conditional on all observed data. Since ${\widetilde{\mathrm{MSE}}}_{\lambda }^{in}$ is a predictive quantity, it is accompanied by posterior uncertainty quantification under model (1)–(2). However, ${\widetilde{\mathrm{MSE}}}_{\lambda }^{in}$ is an in-sample quantity: the distribution is conditional on all observed data ${\left\{y_i\right\}}_{i=1}^n$, and therefore incorporates the information in the observed value of y_i at each x_i. By comparison, out-of-sample prediction does not have the benefit of observing each y_i, so there is inherently greater uncertainty in the corresponding predictive distribution of ${\tilde{y}}_i$. It is the latter setting that is more representative of practical prediction problems.

To construct out-of-sample MSEs and predictive MSEs, we adjust the key components of (13) and (14)—namely, the optimal coefficients ${\widehat{\delta }}_{\lambda }$ and the predictive variables ${\widehat{y}}_i—\mathrm{to}$ condition only on a subset of the data, the training data, and evaluate on the remaining (now out-of-sample) testing data. Repeating this procedure for K distinct and randomly-selected training/testing splits reduces the sensitivity to any particular split, and produces a Bayesian K-fold cross-validation procedure. Let ${\mathcal{I}}_k$ denote the indices of the kth holdout (test) dataset, k = 1, …, K, with ${\cup }_{k=1}^K{\mathcal{I}}_k=\left\{1,\dots ,n\right\}$. The holdout sets ${\mathcal{I}}_k$ are typically equally-sized, mutually exclusive, and selected randomly from {1, …, n}. Let $y=\left\{y^{-{\mathcal{I}}_k},y^{{\mathcal{I}}_k}\right\}$, so $y^{-{\mathcal{I}}_k}$ and $y^{{\mathcal{I}}_k}$ refer to the training and testing datasets, respectively. For each fold k = 1, …, K, we define the out-of-sample MSE and predictive MSE as follows:

$${\mathrm{MSE}}_{\lambda }^{out}\left(k\right)=\frac{1}{|{\mathcal{I}}_k|}\sum _{i\in {\mathcal{I}}_k}{\left(y_i-x_i^{\prime }{\widehat{\delta }}_{\lambda }^{-{\mathcal{I}}_k}\right)}^2,{\widetilde{\mathrm{MSE}}}_{\lambda }^{out}\left(k\right)=\frac{1}{|{\mathcal{I}}_k|}\sum _{i\in {\mathcal{I}}_k}{\left({\tilde{y}}_i^{-{\mathcal{I}}_k}-x_i^{\prime }{\widehat{\delta }}_{\lambda }^{-{\mathcal{I}}_k}\right)}^2$$ (15)

where ${\widehat{\delta }}_{\lambda }^{-{\mathcal{I}}_k}$ minimizes the expected loss (10), but restricted to the training data $y^{-{\mathcal{I}}_k}$,

$${\widehat{\delta }}_{\lambda }^{-{\mathcal{I}}_k}=\arg \underset{\delta }{\min }{\mathbb{E}}_{\left[\theta |y^{-{\mathcal{I}}_k}\right]}\left\{{\mathbb{E}}_{\left[\tilde{y}|y^{-{\mathcal{I}}_{k,\theta }}\right]}{\mathcal{L}}_{\lambda }\left({\tilde{y}}^{-{\mathcal{I}}_k},\delta ,\theta \right)\right\}$$ (16)

and similarly ${\tilde{y}}_i^{-{\mathcal{I}}_k}\sim p\left({\tilde{y}}_i|y^{-{\mathcal{I}}_k}\right)$ is the predictive variable at $x_i$ but conditional only on the training data $y^{-{\mathcal{I}}_k}$. This out-of-sample predictive distribution is fundamentally distinct from the in-sample predictive distribution, $p\left({\tilde{y}}_i|y\right)=p\left({\tilde{y}}_i|y^{-{\mathcal{I}}_k},y^{{\mathcal{I}}_k}\right)$, which inappropriately conditions on the testing data $y^{{\mathcal{I}}_k}$. The out-of-sample MSEs in (15) better capture the essence of the prediction task, where the predictand is not available for model-fitting of (1)–(2) or solving (16). Since these quantities may be sensitive to the specific testing set ${\mathcal{I}}_k$, we average (15) over all K testing sets:

$${\mathrm{MSE}}_{\lambda }^{out}=\frac{1}{K}\sum _{k=1}^K{\mathrm{MSE}}_{\lambda }^{out}(k),{\widetilde{\mathrm{MSE}}}_{\lambda }^{out}=\frac{1}{K}\sum _{k=1}^K{\widetilde{\mathrm{MSE}}}_{\lambda }^{out}(k)$$ (17)

which is advocated in the literature.^47,46 When the holdout sets are mutually exclusive, each observation i = 1, …, n appears exactly once in (17). Computation of (17) requires solving (16) and obtaining the out-of-sample predictive distribution ${\tilde{y}}_i^{-{\mathcal{I}}_k}\sim p\left({\tilde{y}}_i|y^{-{\mathcal{I}}_k}\right)$. Although these quantities may be calculated using brute-force model re-fitting for each k = 1, …, K, we provide a substantially simpler and faster approximation in Section 3.5 which completely avoids the need for Bayesian model re-fitting.

Given the out-of-sample MSEs, we are now able to define formally the evaluation and selection procedure. First, we define the best model to be the minimizer of out-of-sample MSE:

$${\lambda }_{\mathit{min}}=\arg \underset{\lambda }{\min }{\text{MSE}}_{\lambda }^{\mathit{out}}$$ (18)

which equivalently identifies the complexity parameter λ_min corresponding to the smallest K-fold cross-validated MSE. This choice of λ serves as a reference point: we are interested in identifying models that perform nearly as well as λ_min, and among those, models with minimal complexity. Next, consider the out-of-sample predictive variable

$${\widetilde{\mathrm{gapMSE}}}_{\lambda }^{\mathit{out}}={\widetilde{\mathrm{MSE}}}_{\lambda }^{\mathit{out}}-{\widetilde{\mathrm{MSE}}}_{{\lambda }_{\mathit{min}}}^{\mathit{out}}$$ (19)

which is the gap between model λ and the best model λ_min. The set of acceptable models⁴⁶ is

$${\wedge }_{\eta ,\epsilon }=\left\{\lambda :\mathbb{P}({\widetilde{\mathrm{gapMSE}}}_{\lambda }^{\mathrm{out}}\le \eta {\sigma }^2)\ge \epsilon \right\}.$$ (20)

According to (20), any model with at least ε ∈ [0, 1] probability of matching the accuracy of the ${\text{MSE}}_{\lambda }^{\mathit{out}}\text{-optimal}$ model »_min within ησ² is considered acceptable. The probability $\mathbb{P}$ is computed with respect to the out-of-sample predictive distributions in (17) under model (1)–(2) and estimated using posterior predictive simulations. The set of acceptable models is nonempty, since λ_min ∈ Λ_η,ε for all η ≥ 0 and ε ∈ [0, 1]. More useful, (20) gathers the set of models which demonstrate near-optimal performance—some of which may be more simple or sparse than λ_min.

The acceptable set of models in (20) is equivalently derived using posterior predictive intervals⁴⁶: λ ∈ Λ_η,ε if and only if there exists a (1 – ε) lower posterior predictive credible interval for ${\widetilde{\mathrm{gapMSE}}}_{\lambda }^{\mathit{out}}/{\sigma }^2$ that includes η. Naturally, if the predictive interval for the increase in out-of-sample MSE excludes ε, such as ε = 0, then this choice of λ is deemed unacceptable and omitted from Λ_η,ε. From this interpretation, (20) is a Bayesian analog of “cross-validating with confidence” (CVC).⁴⁷ CVC computes a confidence set of acceptable models by testing the null hypothesis that each λ produces the best predictive risk; if the null is rejected, then λ is excluded from the confidence set. By comparison, the proposed Bayesian approach leverages the posterior predictive distribution—automatically available from the linear model (1)–(2) with no additional assumptions—which precludes the need for computationally-intensive bootstrapping procedures, and incorporates a margin η ≥ 0 to relax the accuracy requirements and permit simpler models.

From the set of acceptable models, we identify the simplest, or most penalized model:

$${\lambda }_{\eta ,\epsilon }=\max {\wedge }_{\eta \epsilon }.$$ (21)

Both λ_η,ε and Λ_η,ε depend on the complexity penalty $\mathcal{P}$ and the solution path. For a sparsity-inducing penalty $\mathcal{P}$, λ_η,ε is the smallest model along the λ path that belongs to the set of acceptable models Λ_η,ε. Selection via (21) is a Bayesian analog of the one-standard-error rule⁴⁸ which, instead of selecting the best model, selects the simplest model that is close enough to the best model. The intuition behind (21) is the same, but instead incorporates uncertainty quantification through the posterior predictive distribution.

3.5 |. Approximations for fast out-of-sample validation

The construction of the set of acceptable models Λ_η,ε hinges on the ability to estimate out-of-sample quantities, namely, (16) and (17). Re-fitting model (1)–(2) for each training set k = 1, …, K is impractical and may be computationally infeasible for moderate to large sample sizes n. We design an alternative approximation based on importance sampling that only requires a single model fit of (1)–(2) using the full dataset—which is necessary for standard posterior inference.

To proceed, we begin by simplifying the out-of-sample predictive expected loss in (16). Following the arguments in Section 3.2 – 3.3, it is straightforward to show

$${\widehat{\delta }}_{\lambda }^{-{\mathcal{I}}_k}=\arg \underset{\delta }{\min }\left\{n-|{\mathcal{I}}_k{|}^{-1}\right\}\sum _{j\notin {\mathcal{I}}_k}{({\widehat{y}}_{\lambda }^{-{\mathcal{I}}_k}-x_j^{\prime }\delta )}^2+\lambda \stackrel{\_}{\mathcal{P}{(\delta )}^{-{\mathcal{I}}_k}}$$ (22)

where ${\widehat{y}}_j^{-{\mathcal{I}}_k}={\mathbb{E}}_{\left[\tilde{y}|y^{-{\mathcal{I}}_k}\right]}{\tilde{y}}_j={\tilde{x}}_j^{\prime }{\widehat{\beta }}^{-{\mathcal{I}}_k}$ is the out-of-sample point prediction at ${\tilde{x}}_j$, ${\widehat{\beta }}^{-{\mathcal{I}}_k}={\mathbb{E}}_{\left[\theta |y^{-{\mathcal{I}}_k}\right]}\beta$ is the posterior expectation of β conditional only on the training data $y^{-{\mathcal{I}}_k}$, and similarly $\stackrel{\_}{\mathcal{P}{\left(\delta \right)}^{-{\mathcal{I}}_k}}={\mathbb{E}}_{\left[\theta |y^{-{\mathcal{I}}_k}\right]}\mathcal{P}\left(\delta ,\theta \right)$ is the posterior expectation of (9) conditional only on $y^{-{\mathcal{I}}_k}$. Given estimators of ${\widehat{\beta }}^{-{\mathcal{I}}_k}$ and $\stackrel{\_}{\mathcal{P}{\left(\delta \right)}^{-{\mathcal{I}}_k}}$, the out-of-sample predictive expected loss (16) is equivalent to a penalized least squares problem (22), which has the same form as the in-sample version (6) or (11). Importantly, (22) is efficiently solved for many choices of complexity penalty $\mathcal{P}$, including the Bayesian adaptive lasso penalty (9).

Building upon the representation in (22), we proceed to approximate the core quantities needed for out-of-sample evaluation: ${\widehat{\beta }}^{-{\mathcal{I}}_k}={\mathbb{E}}_{\left[\theta |y^{-{\mathcal{I}}_k}\right]}\beta$, $\stackrel{\_}{\mathcal{P}{\left(\delta \right)}^{-{\mathcal{I}}_k}}={\mathbb{E}}_{\left[\theta |y^{-{\mathcal{I}}_k}\right]}\mathcal{P}\left(\delta ,\theta \right)$, and ${\tilde{y}}_i^{-{\mathcal{I}}_k}\sim p\left({\tilde{y}}_i|y^{-{\mathcal{I}}_k}\right)$ for $i\in {\mathcal{I}}_k$. All approximations are constructed using the same importance sampling framework. For the regression coefficients, we approximate

$${\widehat{\beta }}^{-{\mathcal{I}}_k}=\int \beta p(\beta |y^{-\mathcal{I}k})d\beta =\int \beta p(\theta |y^{-\mathcal{I}k})d\theta \approx \sum _{s=1}^S{\beta }^s{w}_k^s$$ (23)

where θ = (β, σ²) are model parameters, ${\left\{{\beta }^s\right\}}_{s=1}^S$ are drawn from a proposal distribution, and ${\left\{{\omega }_k^s\right\}}_{s=1}^S$ are the importance weights. For the proposal distribution, we select the full posterior, $p\left(\theta |y\right)=p\left(\theta |y^{-{\mathcal{I}}_k},y^{{\mathcal{I}}_k}\right)$, which will produce an accurate approximation for $p\left(\theta |y^{-{\mathcal{I}}_k}\right)$ unless the testing points $y^{{\mathcal{I}}_k}$ are highly influential for the posterior of θ. For this proposal, the importance weights simplify to

$$w_k^s\propto 1/p(y_{{\mathcal{I}}_k}|{\theta }^s)=\prod _{i\in {\mathcal{I}}_k}1/p(y_i|{\theta }^s),{\theta }^s~p(\theta |y)$$ (24)

under the conditional independence assumption accompanying model (1). The importance weights in (24) constitute an out-of-sample adjustment: relative to (23), the in-sample posterior expectation is typically estimated by $\stackrel{\_}{\beta }=S^{-1}{\sum }_{s=1}^S{\beta }^s$.

The approximation for the penalty proceeds similarly: $\stackrel{\_}{\mathcal{P}{\left(\delta \right)}^{-{\mathcal{I}}_k}}\approx {\sum }_{s=1}^S\mathcal{P}\left(\delta ,{\theta }^s\right)w_k^s$, which further simplifies for the Bayesian adaptive lasso to $\stackrel{\_}{\mathcal{P}{\left(\delta \right)}^{-{\mathcal{I}}_k}}\approx {\sum }_{j=1}^p{\stackrel{\_}{\omega }}_j|{\delta }_j|$ with ${\stackrel{\_}{\omega }}_j={\sum }_{s=1}^S{w}_k^s{|{\beta }_j^s|}^{-\gamma }$. Importantly, the out-of-sample adjustment from (24) requires only (i) the posterior draws θ^s ∼ p(θ|y) and (ii) computation of the Gaussian likelihood (1), and therefore incurs minimal additional computational costs. The use of the full posterior distribution as the proposal for an out-of-sample predictive distribution has been employed successfully for Bayesian model selection⁴⁹ and evaluating predictive distributions.^50,46

To obtain draws from the out-of-sample predictive distribution ${\tilde{y}}_i^{-{\mathcal{I}}_k}\sim p\left({\tilde{y}}_i|y^{-{\mathcal{I}}_k}\right)$, we directly build upon the importance weights constructed in (24). The out-of-sample predictive distribution has the same form as the (in-sample) predictive distribution (3), $p\left({\tilde{y}}_i|y^{-{\mathcal{I}}_k}\right)=\int p({\tilde{y}}_i|\theta \left)p\right(\theta |y^{-{\mathcal{I}}_k})d\theta$, so draws from this distribution can be generated by iteratively sampling ${\theta }^s\sim p\left(\theta |y^{-{\mathcal{I}}_k}\right)$ and ${\tilde{y}}_i^s\sim p({\tilde{y}}_i|{\theta }^s)$. Again using the full posterior p(θ|y) as the proposal, we generate draws from the out-of-sample predictive distribution $p\left({\tilde{y}}_i|y^{-{\mathcal{I}}_k}\right)$ using sampling importance resampling (SIR) based on the importance weights in (24). Specifically, let $\tilde{S}⪡S$ denote the number of SIR simulations. Given samples ${\{{\theta }^s\}}_{s=1}^S$ from the full posterior, we iterate the following algorithm: (i) sample s* ∈ {1, …, S} with associated probabilities $\{w_k^1,\dots ,w_k^S\}$; (ii) sample ${\tilde{y}}_i^{s^{*}}\sim p({\tilde{y}}_i|{\theta }^{s^{*}})$ from the likelihood (1); (iii) discard s* and $w_k^{s^{*}}$ from the set of indices and weights; (iv) repeat for $\tilde{S}$ iterations. The final sample ${\{{\tilde{y}}_i^{s^{*}}\}}_{s^{*}=1}^{\tilde{S}}$ is distributed $p\left({\tilde{y}}_i|y^{-{\mathcal{I}}_k}\right)$. Sampling without replacement from step (iii) helps mitigate the effects of excessively large weights: when $w_k^{s^{*}}$ is large, the same value ${\tilde{y}}_i^{s^{*}}$ may be sampled many times and can produce a degenerate sample of ${\{{\tilde{y}}_i^{s^{*}}\}}_{s^{*}=1}^{\tilde{S}}$.

Using importance sampling and SIR, the out-of-sample predictive evaluations in (17)—including uncertainty quantification via the predictive MSE—are rapidly computable using only (i) posterior (predictive) simulations under the linear model (1)–(2), (ii) pointwise likelihood evaluations for the Gaussian distribution (1), and (iii) the solution to the penalized least square problem (22). For completeness, the algorithm is presented in Algorithm 1.

Note that steps 2(d) and 3 are the only components that depend on the complexity level λ. Therefore, the remaining steps represent a one-time cost for use with all approximating models or penalties. Similarly, only step 3 depends on the choice of metric: alternatives to MSE, such as mean absolute error, may be included at this stage without affecting the broader algorithm. For the Bayesian adaptive lasso penalty (9), the optimization in step 2(d) is done using the glmnet³⁴ package in R. In the event of large importance weights, the out-of-sample posterior expectations ${\widehat{\beta }}^{-{\mathcal{I}}_k}$ and ${\stackrel{\_}{\omega }}_j$ instead may be estimated using the sample means from the SIR draws, i.e., ${\widehat{\beta }}^{-{\mathcal{I}}_k}\approx {\tilde{S}}^{-1}{\sum }_{s^{*}=1}^{\tilde{S}}{\beta }^{s^{*}}$ and ${\stackrel{\_}{\omega }}_j\approx {\tilde{S}}^{-1}{\sum }_{s^{*}=1}^{\tilde{S}}{|{\beta }_j^{s^{*}}|}^{-\gamma }$. In particular, sampling without replacement eliminates the effect of excessively large importance weights. As a last resort, highly influential test data $y^{{\mathcal{I}}_k}$ can be evaluated out-of-sample without approximation, e.g., by re-fitting the linear model (1)–(2) on the training data $y^{-{\mathcal{I}}_k}$.

Algorithm 1.

Out-of-sample MSE and predictive MSE.

1.	Obtain posterior samples ${\left\{{\theta }^s\right\}}_{s=1}^S\sim p(\theta |y)$;
2.	For each holdout set k = 1, …, K:
	(a) Compute the (log) weights, $\log W_k^s\stackrel{c}{=}-\log p(y_{{\mathcal{I}}_k}|{\theta }^s)=-{\sum }_{i\in {\mathcal{I}}_k}\log p(y_i|{\theta }^s)$ using the (Gaussian) log-likelihood in (1), where $\stackrel{c}{=}$ denotes equality up to a constant;
	(b) Estimate ${\widehat{\beta }}^{-{\mathcal{I}}_k}\approx {\sum }_{s=1}^S{\beta }^s{W}_k^s$ and ${\stackrel{\_}{\omega }}_j={{\sum }_{s=1}^S{W}_k^s|{\beta }_j^s|}^{-\gamma }$;
	(c) Set ${\widehat{y}}_j^{-{\mathcal{I}}_k}={\tilde{x}}_j^{\prime }{\widehat{\beta }}^{-{\mathcal{I}}_k}\text{for}j\notin {\mathcal{I}}_{\text{k}};$
	(d) Compute ${\widehat{\delta }}_{\lambda }^{-{\mathcal{I}}_k}$ by solving (22) for each λ;
	(e) Sample ${\left\{{\tilde{y}}_i^{s*}\right\}}_{s*=1}^{\tilde{S}}$ from $p({\tilde{y}}_i|y^{-{\mathcal{I}}_k})$ using the SIR algorithm for $i\in {\mathcal{I}}_k$;
3.	Compute ${\mathrm{MSE}}_{\lambda }^{\mathit{out}}$ using ${\widehat{\delta }}_{\lambda }^{-{\mathcal{I}}_k}$ and ${\widetilde{\mathrm{MSE}}}_{\lambda }^{\mathit{out}}$ using ${\widehat{\delta }}_{\lambda }^{-I_k}$ and ${\left\{{\tilde{y}}_i^{s*}\right\}}_{s*=1}^{\tilde{S}}$ in (17).

Perhaps most interesting, the proposed analysis is conducted entirely with out-of-sample objectives using in-sample computing. In particular, the evaluation metrics (17) and the set of acceptable models Λ_η,ε—as well as the best model λ_min and the simplest acceptable model λ_η,ε—are all constructed from out-of-sample quantities. At the same time, all of the necessary computations are performed using in-sample quantities, namely, the posterior samples under the linear model (1)–(2) coupled with the importance sampling approximations described above. Consequently, the proposed approach reaps the benefits of out-of-sample predictive analysis with minimal additional computational burden relative to the original posterior sampler.

4 |. RESULTS

4.1 |. Simulation Study

The proposed techniques are evaluated using simulated data. We focus on three key properties: (i) variable and model selection capabilities, (ii) point prediction accuracy of the response variable, and (iii) point estimation accuracy of the regression coefficients. First, we investigate the ability of the acceptable model sets Λ_η,ε to identify the correct subset of active (nonzero) predictors. Naturally, this performance depends on the choice of margin η and the probability level ε, as well as other features of the simulation design such as the sample size and the strength of the signal. Next, we study the point prediction accuracy of the proposed decision analytic approach. The decision analysis optimizes for point prediction under a sparsity or complexity constraint. Thus, it is important to assess whether there are empirical gains in accuracy relative to the full Bayesian model, among other competitors. The estimation accuracy results are similar to the prediction results and are provided in the Appendix.

The simulated data are constructed to match the general features of the real dataset in Section 4.2, including the dimensionality of the data, the signal-to-noise ratio, and the correlations, discreteness, and interactions among the predictor variables. We construct p − 5 main effects and 5 interactions. First, we simulate continuous predictors x_i,j from marginal standard normal distributions with persistent correlation among predictors, Cor(x_i,j, x_i,j′ = (0.75)^|j−j′|, and randomly permute the columns. Next, discrete covariates are included by selecting 25% of these p − 5 covariates at random and binarizing at zero, i.e., among the selected predictors j we update x_i,j ← 1{x_i,j ≥ 0} for all i = 1, …, n. Matching the pre-processing steps in Section 4.2, the continuous predictors are centered and scaled to have sample mean zero and sample standard deviation 0.5, which helps align the continuous and binary variables on similar scales.⁵¹ The 5 interaction effects are then generated via multiplication. In particular, we include 7 signals among the p – 5 main effects and 2 signals among the 5 interactions. The main effect signals are ${\beta }_j^{*}=\pm 2$, while the interactions are smaller, ${\beta }_j^{*}=\pm 1.5$, with the signs distributed evenly. Each active interaction corresponds to at least one active main effect (weak hierarchy), while inactive interactions arise from both active and inactive main effects. The intercept ${\beta }_0^{*}=1$ is included and fixed throughout. Letting $y_i^{*}=x_i^{\prime }{\beta }^{*}$, we generate response variables $y_i=y_i^{*}+{ϵ}_i$ with independent errors ${ϵ}_i\sim N(0,{\sigma }_{\mathit{true}}^2)$, where ${\sigma }_{\mathit{true}}^2=\mathrm{var}(y_i^{*})/\mathrm{SNR}$ and SNR is the signal-to-noise ratio. We consider the designs (n, p) ∈ {(10,000, 100), (1,000, 100), (200, 500)} with weak (SNR = 0.5) and strong (SNR = 3) signals. The randomization steps are repeated for each of 500 simulations.

For each simulated dataset, we implement the Bayesian linear regression model (1)–(2) with a horseshoe prior.²³ Samples from the posterior and posterior predictive distributions are obtained using the elliptical slice sampler in the R package bayeslm.³⁰ We save S = 10,000 MCMC samples ${\left\{{\theta }^s\right\}}_{s=1}^S\sim p(\theta |y)$ after discarding 5,000 initial iterations as a burnin. Using these posterior samples, we solve (10) for ${\widehat{\delta }}_{\lambda }$ across a path of λ values using the glmnet³⁴ package in R. The out-of-sample evaluations from Section 3.4 are applied to this path of λ values, specifically using K = 10-fold cross-validation and $\tilde{S}=S/=\mathrm{5,000}$ SIR samples. For any choice of η and ε, we subsequently construct the set of acceptable models Λ_η,ε.

Among competing methods, we include both Bayesian and frequentist alternatives. To represent the full Bayesian linear model, we compute the posterior means of $\widehat{\beta }$, which are used in both estimation and prediction, and select variables based on whether the 95% highest posterior density interval for each β_j excludes zero. For frequentist methods, we include the adaptive lasso⁴³ with ordinary least squares weights; for p > n, we use the (non-adaptive) lasso.³³ The tuning parameter is selected using the one-standard-error rule⁴⁸ from 10-fold cross-validation and implemented using the glmnet³⁴ package in R. In addition, we include classical or exhaustive subset selection (after pre-screening to the first 30 predictors that enter the adaptive lasso model) using the leaps⁵² package in R with the final subset determined by Mallow’s C_p. Lastly, we include minimax convex penalization (MCP)⁵³ implemented using ncvreg⁵⁴ with the tuning parameter selected using 10-fold cross-validation.

Ideally, the set of acceptable models should include the true model, i.e., the subset of active variables $\{j:{\beta }_j^{*}\ne 0\}$. This task necessitates joint selection across all predictors, and is highly demanding: incorrect labeling of any one variable as active or inactive leads to an incorrect model. Since the set of acceptable models is nested by (ε, η)—increasing ε ∈ [0, 1] or decreasing η ≥ 0 shrinks the acceptable set—it is of interest to determine the largest values of ε and smallest values of η for which the true model is acceptable. For any model indexed by λ, consider the following constituent of (20):

$${\epsilon }_{\mathit{max}}(\lambda )=\mathbb{P}({\widetilde{\mathrm{gapMSE}}}_{\lambda }^{\mathit{out}}\le \eta {\sigma }^2).$$ (25)

Equivalently, ε_max(λ) is the maximum probability level ε for which λ belongs to the set of acceptable models with margin η. By design, for any smaller probability level ε′ ≤ ε_max(λ)—which provides more leniency for inaccuracy—λ remains acceptable, λ ∈ Λ_η,ε′. We are interested in ε_max(λ*), where λ* denotes the true model along the λ path. If the true model is not along the λ path, we set ε_max(λ*) = 0. This definition is important: it interrogates the ability of the entire procedure—including the elicitation of the λ path—to capture the true model, rather than merely checking whether the true model belongs to the acceptable set. Consequently, the true model must be both discovered and evaluated correctly to achieve ε_max(λ*) > 0.

For each simulated dataset, we compute ε_max(λ*) for a grid of η values. The results are presented in Figure 1 for SNR = 3. For the larger sample sizes (n, p) = (10,000, 100) and (n, p) = (1,000, 100), there is rapid convergence to ε_max(λ*) = 1, while ε = 0.05 is capable of capturing the true model often even without a margin η = 0. The high-dimensional case (n, p) = (200, 500) is more challenging: convergence to ε_max(λ*) = 1 does not occur for a majority of simulations. The reason is that the λ path in this p > n setting often does not include the true model, and for those simulations ε_max(λ*) = 0. As a result, increasing the margin η cannot admit the true model in the set of acceptable models. Importantly, these results suggest that the set of acceptable models produced by a small probability level ε, such as 0.05, and a small margin, including η = 0, can adequately capture the true model. However, the quality of the λ path of models is a limiting factor.

FIGURE 1.

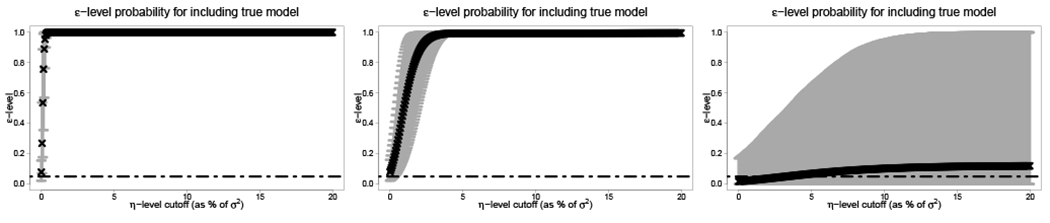
The maximum ε-level at which the true model is included for each η-margin (as percent of σ²). Left to right: (n, p) ∈ {(10,000, 100), (1,000, 100), (200, 500)} for SNR = 3. The horizontal line indicates ε = 0.05. The points (x-marks) are sample means and the gray bars are 90% intervals of ε_max(λ*) computed across 500 simulations.

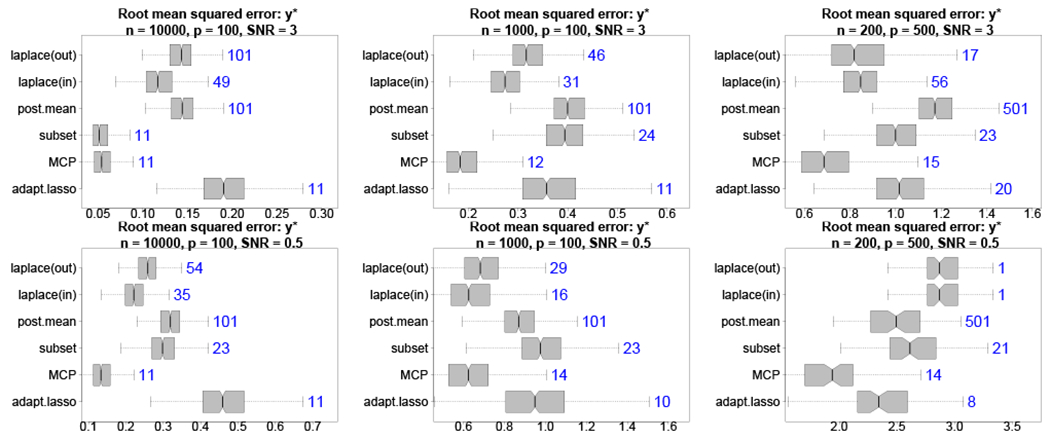
By design, the proposed decision analysis produces coefficient estimates that optimize for point prediction accuracy. Therefore, it is relevant and interesting to evaluate predictions of $y_i^{*}$. Informed by Figure 1, we consider the smallest acceptable model λ_η,ε with η = 0 and ε = 0.05, and compare the predictions and estimates to the aforementioned competitors. In addition to root mean squared errors (RMSEs) for y*_i, we compute the median size of the selected subsets across simulations for each method. The results are displayed in Figure 2 across various simulation designs. Most notably, the proposed out-of-sample approach is highly competitive and offers significant improvements relative to the full Bayesian model (i.e., the posterior mean), classical subset selection, and the adaptive lasso in nearly all cases. The distinction between the in-sample and out-of-sample version is most noticeable when the SNR is small, which favors the out-of-sample approach. The main competitor is MCP, which offers predictive accuracy yet tends to select too many variables. The most challenging setting is p > n with low SNR: since λ_η,ε selects as few variables as needed to satisfy (20), the weak signal results in overly sparse models. Decreasing λ includes additional variables and, when λ = 0, returns the posterior mean $\widehat{\beta }—\mathrm{which}$ is the best predictor in this setting. Our analysis in Section 4.2 considers the λ path from this broader perspective (see Figure 3).

FIGURE 2.

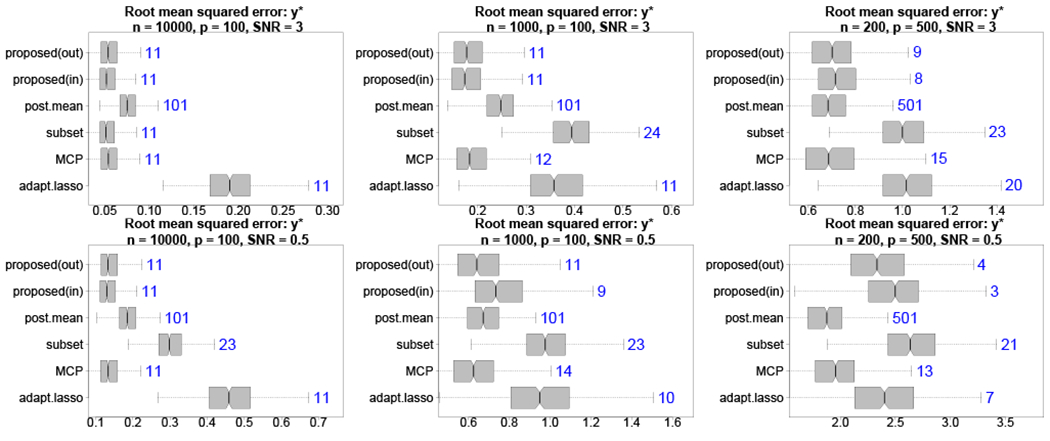
Root mean squared errors (boxplots) for $y_i^{*}=x_i^{\prime }{\beta }^{*}$ with median subset sizes (annotations) for high (top) and low (bottom) SNR with varying n, p. The proposed out-of-sample decision analytic approach provides highly competitive point predictions with fewer covariates than competing methods, including large improvements over the full Bayesian model and frequentist alternatives. Including the intercept, the true model size is 11.

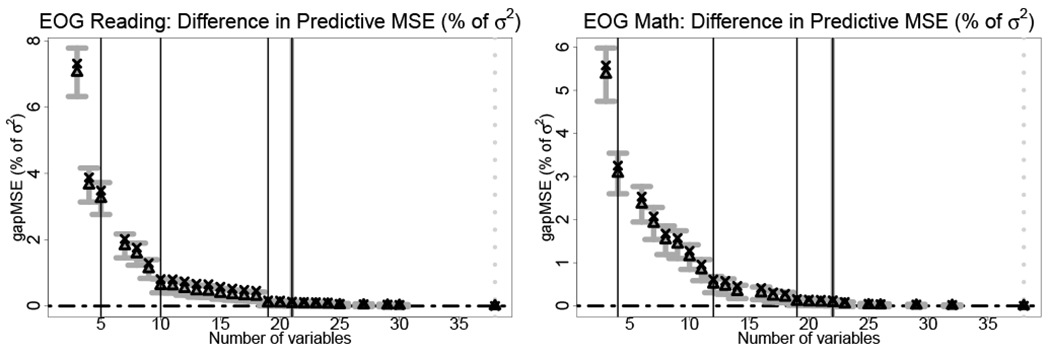
FIGURE 3.

The difference in out-of-sample predictive MSEs between each model along the λ path and the best λ_min model for EOG reading scores (left) and EOG math scores (right) as a percent of σ². Expectations (triangles) and 95% intervals (gray bars) from the predictive distribution are included along with the out-of-sample MSEs (x-marks). The vertical black lines denote the η_min(λ) values summarized in Table 2. The solid gray line denotes λ_0,0.05 and the dotted gray line denotes λ_min.

For completeness, we also assess marginal selection properties using true positive rates and true negative rates averaged across all predictors and simulations. The results are in Table 1. In general, the out-of-sample approach offers competitive performance that is similar to the adaptive lasso and MCP, but far superior to classical subset selection which tends to select too many variables. Most notably, the primary Bayesian competitor—selection based on HPD intervals—is excessively conservative and fails to identify many of the active variables. From a Bayesian perspective, joint variable selection using decision analysis offers clear improvements relative to this popular marginal selection technique.

TABLE 1.

True positive rates (TPR) and true negative rates (TNR) for synthetic data.

n = 10,000, p = 100, SNR = 0.5
	adaptive lasso	MCP	subset selection	HPD interval	proposed(in)	proposed(out)
TPR	1.00	1.00	1.00	1.00	1.00	1.00
TNR	1.00	0.99	0.86	1.00	1.00	0.99
n = 10,000, p = 100, SNR = 3
	adaptive lasso	MCP	subset selection	HPD interval	proposed(in)	proposed(out)
TPR	1.00	1.00	1.00	1.00	1.00	1.00
TNR	1.00	0.99	1.00	1.00	1.00	0.99
n = 1,000, p = 100, SNR = 0.5
	adaptive lasso	MCP	subset selection	HPD interval	proposed(in)	proposed(out)
TPR	0.90	0.92	0.95	0.77	0.81	0.89
TNR	0.99	0.96	0.86	1.00	1.00	0.99
n = 1,000, p = 100, SNR = 3
	adaptive lasso	MCP	subset selection	HPD interval	proposed(in)	proposed(out)
TPR	1.00	1.00	1.00	1.00	1.00	1.00
TNR	1.00	0.98	0.86	1.00	1.00	0.99
n = 200, p = 500, SNR = 0.5
	adaptive lasso	MCP	subset selection	HPD interval	proposed(in)	proposed(out)
TPR	0.42	0.50	0.54	0.06	0.24	0.30
TNR	0.99	0.98	0.97	1.00	1.00	1.00
n = 200, p = 500, SNR = 3
	adaptive lasso	MCP	subset selection	HPD interval	proposed(in)	proposed(out)
TPR	0.93	0.85	0.93	0.67	0.77	0.79
TNR	0.98	0.99	0.97	1.00	1.00	1.00

The Appendix includes RMSEs for β* (Figure B.1) and a sensitivity analysis on the choice of prior for β. Specifically, Figure B.2 replicates the results in Figure 2 under the Bayesian lasso prior²² instead of the horseshoe prior. The well-known deficiencies of the Bayesian lasso⁵⁵ propagate to the decision analysis, yet the proposed approach maintains large advantages relative to the full Bayesian model and some frequentist competitors.

4.2 |. Analysis of end-of-grade testing data

To identify joint collections of variables with predictive capabilities for educational outcomes, we apply the proposed methodology to end-of-grade (EOG) reading and mathematics scores. The EOG reading and mathematics scores were analyzed separately using the same sample of n = 16,839 students and the same set of p = 37 covariates including 12 interactions. The continuous predictors are centered and scaled to have sample mean zero and sample standard deviation 0.5—prior to computing interactions—which better aligns the continuous and binary variables on comparable scales.⁵¹ Posterior inference from the Bayesian linear model (1)–(2) with a horseshoe prior²³ was obtained using the bayeslm³⁰ package in R. We save S = 10,000 MCMC samples ${\{{\theta }^s\}}_{s=1}^S\sim p(\theta |y)$ after discarding 5,000 initial iterations as a burnin and thinning to every 10th iteration for more satisfactory effective sample sizes. Trace plots confirm convergence and good mixing of the MCMC samples. As in Section 4.1, we solve (10) for ${\widehat{\delta }}_{\lambda }$ across a path of λ values using the R package glmnet,³⁴ and apply the out-of-sample evaluations from Section 3.4 to this path of λ values using K = 10-fold cross-validation and $\tilde{S}=s/=\mathrm{5,000}$ SIR samples.

To quantify how particular variables or sets of variables contribute to the predictive ability of the model, we present the predictive MSEs for both EOG reading and EOG math scores in Figure 3 with accompanying variable selection details in Table 2. Specifically, we display posterior predictive means and 95% intervals for ${\widetilde{\mathrm{gapMSE}}}_{\lambda }^{\mathit{out}}$ from (19), which is the gap in predictive accuracy between each model along the λ path and the best model according to out-of-sample MSE. Figure 3 serves a different purpose from Figure 1: Figure 3 illustrates the predictive ability across sparsity levels λ, while Figure 1 explores the ability to select the “true” model as (η, ε) vary. Although λ and (η, ε) are linked, the selection capabilities (Figure 1) are distinct from relative predictive performance (Figure 3).

TABLE 2.

Variables selected (in order and incrementally) for EOG Reading (left) and Math (right) scores. The margin η_min(λ) expresses the difference in predictive MSE between the best model λ_min and the noted subset of variables (in addition to the preceding variables). As the margin decreases to zero, more variables are required to achieve optimal predictive performance. Variables selected by adaptive lasso (*) or credible intervals that exclude zero (+) are also denoted. The indicated groupings of η_min(λ) are marked in Figure 3.

EOG Reading Scores		EOG Math Scores
Margin ηmin(λ)	Variable Name	Margin ηmin(λ)	Variable Name
2.76% of σ2	(Intercept)*+ Temp_T2*+ mEdu:College*+ mRace:NH Black*+ EconDisadv*+	2.6% of σ2	(Intercept)*+ mEdu:College*+ mRace:NH Black*+ EconDisadv*+
0.4% of σ2	PM25_T1*+ mAge*+ mEdu:HS*+ Male*+ NDI_test*+	0.307% of σ2	Temp_T2*+ Temp_T3*+ PM25_T1*+ BWTpct*+ mEdu:HS*+ mRace:Hispanic*+ NotMarried+ PM25:chronic x RI_test*+
0.005% of σ2	Temp_T3*+ PM25_chronic BWTpct+ WeeksGest+ NotMarried+ PTB+ Smoker Blood_lead+ PM25:chronic x RI_test	0.013% of σ2	PM25_T3+ mAge+ PM25:chronic WeeksGest+ Smoker+ Blood_lead+ NDI_test
η = 0	mRace:Hispanic RI_test	η = 0	PTB RI_birth Blood_lead x NDI_birth

For both EOG reading and math scores, λ_min is the full model, which is unhelpful for selecting variables. However, the predictive uncertainty quantification provides an avenue for selection: by considering models with a nonnegligble probability of improving upon the best model λ_min, we obtain a set acceptable models with far fewer variables. The smallest acceptable model λ_η,ε for η = 0 and ε = 0.05 has 21 and 22 covariates for EOG reading and EOG math scores, respectively, and in each case ensures a probability of at least 5% that this sparse model is superior to the full model for out-of-sample prediction. Naturally, if we admit a margin η > 0, we obtain even smaller acceptable models: for η less than 0.4% of the error variance σ², the smallest acceptable models for both EOG reading and math scores have fewer than 15 variables. Figure 3 clearly illustrates that small models with fewer than 10 variables are noncompetitive, while the gains beyond around 25 variables are marginal.

To extract interpretable conclusions from Figure 3, we report the selected variables corresponding to these sparse models in Table 2. Variables are reported up to the smallest acceptable model for zero margin η = 0 and probability level ε = 0.05. We characterize the incremental gains offered by additional sets of predictors—expressed visually by the vertical jumps in Figure 3—by considering the effect of varying the margin η. For any fixed probability level, say ε = 0.05, each model along the λ path will be acceptable at some choice of margin η, which we denote by η_min(λ) = min{η : λ ∈ Λ_η,0.05}. For any larger η′ > η_min(λ), this model λ ∈ Λ_η′,0.05 remains acceptable. These values η_min(λ) are interpretable: they indicate a best case scenario in out-of-sample predictive performance (at the ε = 0.05 probability level) for each model λ relative to the best model λ_min. In particular, we are interested in large decreases in η_min(λ) that occur via addition of a small number of variables. These occurrences are indicated by vertical black lines in Figure 3 and demarcated in Table 2.

The results from Table 2 indicate substantial overlap in selected variables between EOG reading and EOG math scores. In addition, many of the basic demographic, social, and environmental variables are confirmed by adaptive lasso selection and (marginal) selection via the 95% posterior credible intervals that exclude zero. These variables include maternal characteristics (education level, ethnicity, age, and marital status), environmental exposures (temperature, PM_2.5, blood lead level), and social conditions (economically disadvantaged, neighborhood deprivation). The selected environmental exposures and social conditions cover a broad temporal spectrum, including the gestational period, at the time of birth, chronic exposures, and at the time of the exam.

The proposed approach selects additional variables that offer clear and quantifiable improvements in prediction accuracy. Perhaps most notably, we identify evidence for social and environmental interactions that predict EOG reading and math scores—even after adjusting for a multitude of other effects. For both EOG reading and math scores, we find that chronic PM_2.5 interacts with racial isolation at the time of the exam. EOG math scores are additionally predicted by interactions between blood lead level and neighborhood deprivation. Given the conservative nature of selection via credible intervals (see Table 1), it is unsurprising that these variables are undetected by that approach. Yet the evidence for interactions is nontrivial: these effects are present for η_min(λ) values as large as 0.307% of the error variance σ² for EOG math scores, and of course persist for η = 0. While η = 0 is a strict criterion, it is necessary to provide the assurance that the smallest acceptable model λ_0,0.05 is not definitively suboptimal relative to larger models. Cumulatively, these results suggest that a full predictive picture of EOG test scores requires simultaneous consideration of the exam topic; demographic, socioeconomic, and environmental variables; and interactions between environmental exposures and social conditions.

5 |. DISCUSSION

We have introduced a comprehensive and decision-analytic approach for Bayesian linear variable selection, which is designed to advance the state-of-the-art in exposure science. By representing variable selection as a decision problem, we are able to identify joint and optimal subsets of explanatory variables. The decision problem balances predictive accuracy with model complexity through a penalized loss function, and uniquely incorporates model parameters in the complexity penalty to improve selection and estimation capabilities. Out-of-sample predictive evaluations are conducted for each linear subset of variables, which inherit a posterior predictive distribution from the underlying Bayesian regression model. Using this out-of-sample predictive uncertainty quantification, we identify not only the best subset for prediction, but also those subsets that are nearly optimal with some nonnegligible probability. The collection of these acceptable models offers insights into the covariates needed—which and how many—for sufficiently accurate prediction. Comparisons on simulated datasets demonstrate the excellent variable selection, estimation, and prediction capabilities of the proposed approach.

Using population data from North Carolina, our analysis brings new understanding to the cumulative and interactive impact of social and environmental stressors on the educational growth of children as measured by their 4th grade end-of-grade exam scores in reading and mathematics. The selected variables span a broad temporal spectrum, including pre- and post-natal and throughout the life of the child. This more complete predictive picture of child educational outcomes highlights the critical roles of demographics and other information at birth, social stressors, environmental exposures, and key social-environmental interactions.

The next stage in our methodological development is to extend the decision analysis selection approach for (i) all pairwise interactions and (ii) nonlinear models. While our focus is restricted to interactions between social stressors and environmental exposures, other analyses may require consideration of the complete collection of pairwise interactions.^56,57 The proposed model-based penalization strategy (8) offers a path forward and welcomes hierarchical or interaction-sparsity penalties⁵⁸—as well as the accompanying estimation algorithms—into our decision analysis framework. For the nonlinear case, both the Bayesian linear model (1)–(2) and the formulation of the decision problem (4) will require modifications to incorporate nonlinearity. In particular, the abundance of nonlinear models demands careful consideration of the appropriate model specification, as well as the ability to evaluate the out-of-sample predictive capability of each nonlinear model efficiently. The decision analysis framework—in conjunction with the proposed fast out-of-sample approximation algorithms and accompanying mechanisms to elicit acceptable models—builds upon both Bayesian models and non-Bayesian penalized regression techniques, and consequently provides a promising path to achieve these goals.

APPENDIX

A. ADDITIONAL DETAILS ON THE DATA

The common restrictions are the following: singletons only (no plural births); no congenital anomalies; maternal age is 15-44; birth weight is at least 400g; gestational age is 24-42 weeks; mother’s race/ethnicity is non-Hispanic White, non-Hispanic Black, or Hispanic; birth order is 1-4. One acute PM_2.5 outlier (50% larger than all other values) was removed.

We estimated PM_2.5 exposures during pregnancy using ambient monitoring data from the nearest PM_2.5 monitor within 30km from a mother’s residence at time of the child’s birth. Air pollution exposure during pregnancy was calculated based on residence, birth date, and length of gestation. Specifically, the time period of exposure for each birth was calculated using the date of birth and the weeks of gestation at delivery, as recorded in the NCDBR. Using 24-hour average ambient PM_2.5 concentrations, we calculated average exposure for the first (1-13 weeks), second (14-26 weeks weeks), and third (27 weeks-birth) trimester.

We estimated chronic pre-test PM_2.5 exposure using downscaler-reported PM_2.5 concentrations at the census tract level for the census tract in which the child resided at time of EOG testing. Chronic pre-test PM_2.5 exposure was estimated based on the mean 24-hour average PM_2.5 concentration during the 12 months prior to the test date. The exact test date is not recorded in the EOG dataset, but the test month (May or June) is available. Thus, a mean of 24-hour average PM_2.5 concentration was generated for the 12 months prior to the first of May or June for each year of EOG data.

We estimated acute pre-test PM_2.5 exposure using downscaler-reported PM_2.5 concentrations at the census tract level for the census tract in which the child resided at time of testing. Acute pre-test PM_2.5 exposure was estimated based on the daily 24-hour average PM_2.5 concentration during the 30 days prior to the test date. Because only the test month is recorded in the EOG dataset, the acute exposure estimate is based on the mean 24-hour average PM_2.5 concentration in the 30 days prior to the first of May or first of June for each year of EOG data.

Since the EOG testing dataset spans multiple years (2010-2012), the reading and math scores were standardized within each year prior to analysis.

Economically disadvantaged students are indicated by participation in the free/reduced price lunch program (binary variable, 1 = participation in the program).

Air quality during gestation, life of the child, and at time of testing
PM25_T1	PM2.5 24 hour – Average of gestation weeks 1-13 (trimester 1) – ugm3
PM25_T2	PM2.5 24 hour – Average of gestation weeks 14-26 (trimester 2) – ugm3
PM25_T3	PM2.5 24 hour – Average of gestation weeks 27-delivery (trimester 3) – ugm3
Temp_T1	Temperature – Average of gestation weeks 1-13 (trimester 1) – Temperature
Temp_T2	Temperature – Average of gestation weeks 14-26 (trimester 2) – Temperature
Temp_T3	Temperature – Average of gestation weeks 27-delivery (trimester 3) – Temperature
PM25_chronic	PM2.5 Mean of 1 year prior to June 1 of the year of the EOG test
PM25_acute	PM2.5 Mean of 30 days prior to May 1 of the year of the EOG test
Birth information
BWTpct	Birthweight Percentile (based on clinical estimate of gestation)
WeeksGest	Weeks Gestation, Clinical estimate
mEdu	Mother’s Education Group at time of birth (NoHS = No high school diploma, HS = High school diploma, College = College diploma)
mRace	Mother’s Race/Ethnicity Group (White = White, NH Black = Non-Hispanic Black, Hispanic = Hispanic)
mAge	Mother’s Age at time of birth
Male	Male Infant? (1 = Yes)
NotMarried	Not Married at time of birth? (1 = Yes)
Smoker	Mother Smoked? (1 = Yes)
PTB	Pre-Term Birth (<37 wks, Clinical)? (1 = Yes)
Education / EOG test information
EOG_Reading	Reading scale score for chronologically first EOG test taken (4th grade); centered and scaled by year (2010, 2011, 2012)
EOG_Math	Math scale score for chronologically first EOG test taken (4th grade); centered and scaled by year (2010, 2011, 2012)
Blood lead level information
Blood_lead	Blood Lead Level (micrograms per deciliter); maximum value if there are multiple tests
Social / Economic factors
NDI_birth	Neighborhood Deprivation Index, at Birth
NDI_test	Neighborhood Deprivation Index, at time of EOG test
RI_birth	Residential Isolation for non-Hispanic Black, at Birth
RI_test	Residential Isolation for non-Hispanic Black, at time of EOG Test
EconDisadv	Participation in the free/reduced price lunch program (1 = Yes)

B. ADDITIONAL SIMULATION RESULTS

FIGURE B.1.

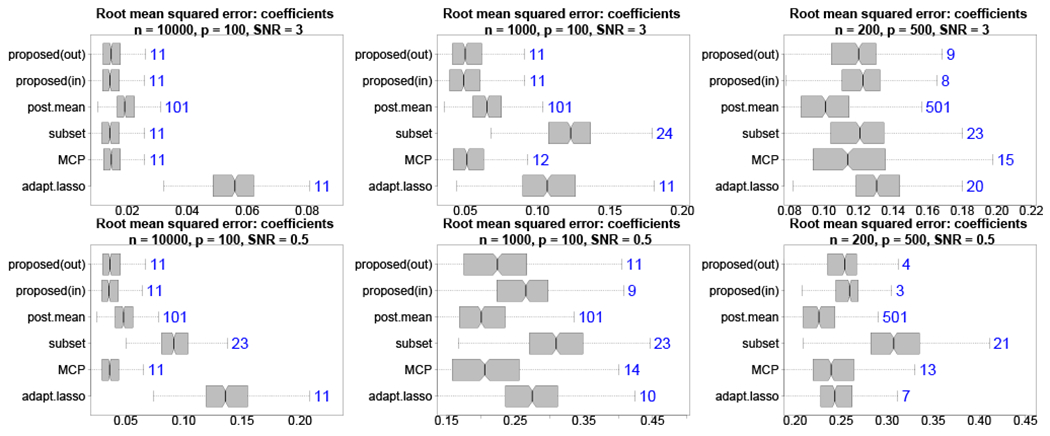
Root mean squared errors (boxplots) for β* with median subset sizes (annotations) for high (top) and low (bottom) SNR with varying n, p. The proposed out-of-sample decision analytic approach provides highly competitive point estimates with fewer covariates than competing methods, including large improvements over the full Bayesian model and frequentist alternatives. Including the intercept, the true model size is 11.

FIGURE B.2.

Using a Laplace prior for β: root mean squared errors (boxplots) for $y_i^{*}=x_i^{\prime }{\beta }^{*}$ with median subset sizes (annotations) for high (top) and low (bottom) SNR with varying n, p. The decision analytic approach cannot overcome the shortcomings of the Bayesian lasso prior, but nonetheless maintains large advantages relative to the posterior mean in most cases. Results (not shown) for estimation of β* are similar.