Accurate prediction of B-form/A-form DNA conformation propensity from primary sequence: A machine learning and free energy handshake

Summary

DNA carries the genetic code of life, with different conformations associated with different biological functions. Predicting the conformation of DNA from its primary sequence, although desirable, is a challenging problem owing to the polymorphic nature of DNA. We have deployed a host of machine learning algorithms, including the popular state-of-the-art LightGBM (a gradient boosting model), for building prediction models. We used the nested cross-validation strategy to address the issues of “overfitting” and selection bias. This simultaneously provides an unbiased estimate of the generalization performance of a machine learning algorithm and allows us to tune the hyperparameters optimally. Furthermore, we built a secondary model based on SHAP (SHapley Additive exPlanations) that offers crucial insight into model interpretability. Our detailed model-building strategy and robust statistical validation protocols tackle the formidable challenge of working on small datasets, which is often the case in biological and medical data.

Highlights

• •A robust machine learning model to predict A- or B-DNA conformation
• •Outcome of machine learning model is explained with free energy values
• •Our approach works well under class imbalance and limited data constraints

The bigger picture

The sequence in the genome of an organism encodes all the information of life. We combine a data-driven approach using machine learning (ML) and the results of free energy calculations to offer a fresh perspective on this long-standing problem of prediction of DNA conformation (A or B) from the sequence. We trained our ML model using sophisticated state-of-the art algorithms such as LightGBM along with a nested cross-validation strategy to overcome the common problems associated with data bias and overfitting when constrained by limited data size. Our study will serve the broader interest of researchers who are not only seeking accurate and reliable predictive models but also want to understand the physical and chemical origins behind the predictions.

We have developed a robust predictive machine learning-based predictive model to accurately predict DNA conformation (A or B) from just the DNA sequence. Unlike a black-box model, our approach offers key chemical and thermodynamic insights into predictions made by our models.

Introduction

The prediction of a DNA conformation from the mere knowledge of its sequence presents an opportunity to presume its role in specific biological processes. The biological processes, such as direct and indirect readout mechanisms in protein-DNA interactions, exploit the conformational flexibility exhibited by DNA. The A-DNA conformation is shorter and more compact than that of B-DNA. During B → A transition, the phosphate groups protrude outward and the minor groove becomes broad and shallow, forming more water bridges in accordance with the theory of economy of hydration proposed by Saenger et al.¹

The protein molecules such as transposase, endonuclease, and polymerase interact with B-DNA locally and convert a few dinucleotide steps to A form in a whole DNA.² A-philic DNA segments exhibit low energy cost for deformation, and thus proteins bind to such hotspots during indirect recognition mechanism to commence the transcription process.² The A form also participates in the protection of bacterial cells under extreme UV exposure.³ Whelan and coworkers have shown fully reversible B-DNA → A-DNA transition in living bacterial cells on desiccation and rehydration using Fourier transform infrared spectroscopy.⁴ Extremophiles such as SIRV2 virus (Sulfolobus islandicus rod-shaped virus 2) survives at extreme temperatures of 80°C and acidity of pH 3 by adopting complete DNA in the A form and aids protein to encapsidate DNA.⁵

Thus, it has become clear of late that A-DNA is merely not a non-functional conformation of DNA; it is an essential adaptation of DNA to survive harsh conditions. It is, therefore, intriguing to predict the sequence-structure relationship in DNA. Moreover, an understanding of sequence specificity of B-form → A-form transition and an a priori detection of the A-philic segment in the genome will unveil the possible hotspots of certain biological processes in specific genes of organisms.

Only a few studies have attempted prediction of DNA conformation from its sequence. Basham and coworkers derived A-DNA propensity energy (APE)⁶ based on the solvation free energy of trinucleotide steps to determine DNA structural preferences. However, APEs are unavailable for specific trinucleotide steps, thereby making this method inapplicable in general across a genomic DNA sequence. In a different approach, Tolstorukov and coworkers⁷ formulated free energy models for all ten unique dinucleotide steps (D-12 model) and 32 individual trinucleotide steps (T-32 model) from experimental data of midpoints in B-DNA → A-DNA transition studied earlier by others.^8,9 The T-32 model was found to be more accurate than the D-12 model. It inherently considers stereochemical effects present along the B → A transition as it is based on three consecutive DNA base steps. However, the absence of the TAA/TTA free energy values limits the application of this dataset for a DNA structure prediction. The comparison between these free energy methods and present machine learning (ML) model could be interesting. However, the lack of free energy values for all unique 32 trinucleotide steps in these models limits us from comparing these methods. For example, TAA/TTA step and CAG/CTG step (apart from many other steps) are absent in Tolstorukov's trimeric T-32 and Basham's APE model, respectively. This refrained us from using at least 2–4 sequences in each train and test fold and compare accuracies of these methods with our ML model.

Schneider and coworkers developed an automated workflow10, 11, 12 to analyze DNA local conformations. They classified DNA dinucleotide steps based on local backbone conformations. It was observed that DNA structure exhibits mixed A-form/B-form traits in the backbone torsional space, even though the overall structure appears as either A form or B form. Their work demonstrated a high-resolution atlas of local DNA conformations.

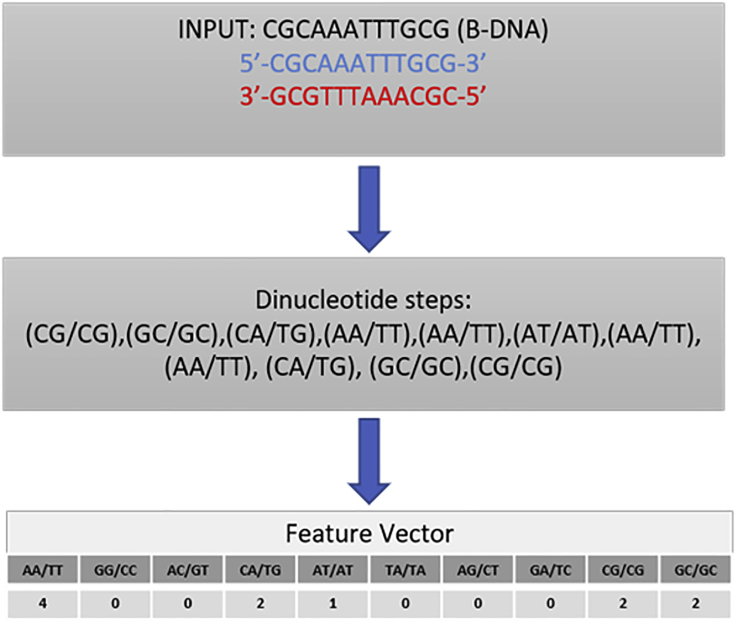
In our approach, we have focused on the development of a general and more accurate method based on an ML approach that considers occurrences of all ten unique dinucleotide steps to predict the conformational preference of a given DNA sequence (see Figure 1). In an ML-based approach, the inference is drawn based on observation alone. Therefore, although ML methods are suitable for prediction, the molecular or thermodynamic origin behind the prediction remains unknown. To address this issue, we have also built an explanatory model based on SHAP (SHapley Additive exPlanations) values¹³ for interpreting and explaining our model output. This method also incorporates the information obtained from free energy values that we obtained earlier to explain the molecular and thermodynamic basis of the prediction made by our ML model.

Figure 1.

Schematic illustration of feature extraction

Results

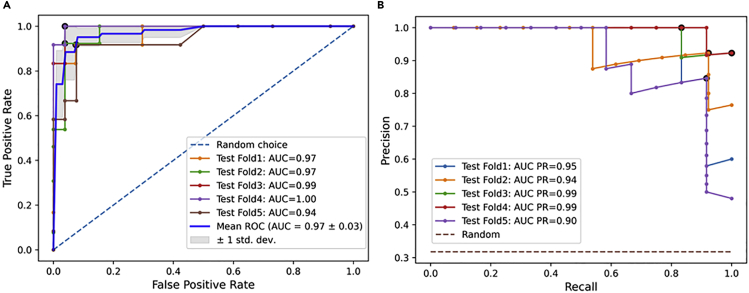
We describe here the results of the nested cross-validation (CV) performance of the LightGBM algorithm across different metrics used for model assessment (see Figure 2). We observed that the LightGBM algorithm gave the best overall classification results across all five test sets in the nested CV. Figure 3 shows receiver operator characteristic (ROC) curves and precision-recall (PR) curves plotted across all five different test sets (folds). Table 1 shows performance metrics across test sets. We obtained a mean ROC area under the curve (AUC) score of $0.97\pm 0.03$, a mean Matthews correlation coefficient (MCC) score of 0.83, a mean accuracy score of 92.7%, a mean F1 score of 0.881, a mean AUC PR of 0.956, and a mean average precision (average PR) of 0.957 on the test sets. The overall performance of our classifier summarized across different thresholds is given by the ROC AUC. Similar to the ROC curve, the PR curve can be used to test all the possible positive predictive values and sensitivities obtained through a binary classification. They are especially valuable for assessing how well an ML model performs on the positive class (A-DNA samples). A high area under the PR curve represents both high recall and high precision. Table 2 displays the per-class performance across all test sets. We observe both high precision and high recall values for each class label. Table 3 shows performance comparison between different ML algorithms. The weighted average returns the average score considering the proportion for each label in the dataset, whereas the macro average returns the average without considering the proportion for each label in the dataset. Furthermore, to ensure reproducibility, we also provide the values of tuned hyperparameters for each model and for all datasets in section C and Data S2 of supplemental information. Detailed results of other approaches are presented in section B of supplemental information (see random forest [Figure S4 and Table S2], support vector machine [SVM] classifier [Figure S5 and Table S3], logistic regression [Figure S6 and Table S4], and naive Bayes classifier [Figure S7 and Table S5]). Section G of supplemental information compares the results on repeated (k = 2) stratified nested CV (Figure S9), and Table S6 shows a comparison between using different methodologies for adjusting class imbalance.

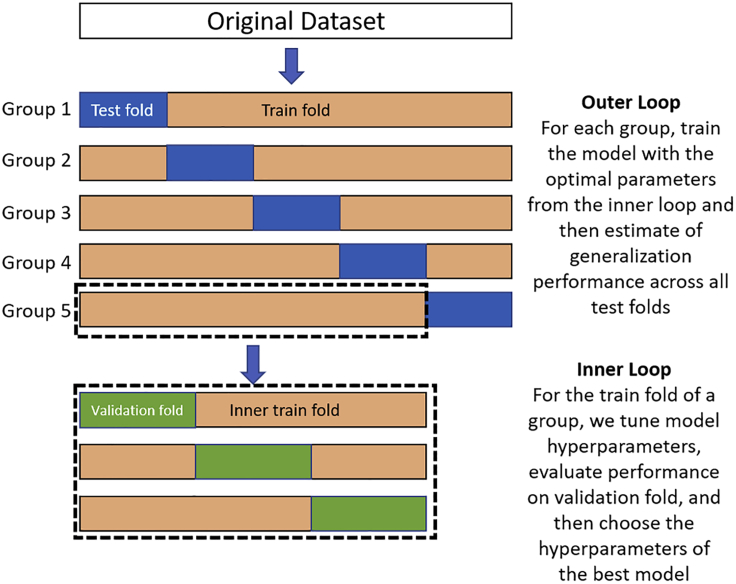
Figure 2.

Schematic display of nested 5-fold stratified cross-validation

A set of n observations is randomly split into five non-overlapping groups in the outer loop. Each group contains approximately the same percentage of samples of each target class as the complete set (stratification). In the inner loop, each training fold is divided again for another round of cross-validation (k = 3) to determine optimal hyperparameters for the classifier.

Figure 3.

Nested stratified 5-fold cross-validation performance of the LightGBM model

(A) Receiver operator characteristic (ROC) AUC curves.

(B) Precision-recall (PR) curves. AUC PR, area under curve of PR curves.

Table 1.

Classification performance of LightGBM algorithm with tuned hyperparameters (see section C in supplemental information) across different test folds

	Average PR	AUC PR	ROC AUC	Accuracy	F1	MCC
Test fold 1	0.954	0.952	0.969	0.923	0.857	0.822
Test fold 2	0.946	0.944	0.973	0.923	0.880	0.825
Test fold 3	0.987	0.986	0.994	0.947	0.917	0.878
Test fold 4	0.994	0.993	0.997	0.947	0.917	0.878
Test fold 5	0.906	0.904	0.939	0.895	0.833	0.756
Mean	0.957	0.956	0.974	0.927	0.881	0.832

Table 2.

Detailed model evaluation report across different test folds

		Precision	Recall	F1 score	Support
Test fold 1	B-DNA	0.90	1.00	0.90	27
	A-DNA	1.00	0.75	0.86	12
	macro average	0.95	0.88	0.90	39
	weighted average	0.93	0.92	0.92	39
Test fold 2	B-DNA	0.89	0.96	0.93	26
	A-DNA	0.91	0.77	0.83	13
	macro average	0.90	0.87	0.88	39
	weighted average	0.90	0.90	0.90	39
Test fold 3	B-DNA	0.96	0.96	0.96	26
	A-DNA	0.92	0.92	0.92	12
	macro average	0.94	0.94	0.94	38
	weighted average	0.95	0.95	0.95	38
Test fold 4	B-DNA	0.96	0.96	0.96	26
	A-DNA	0.92	0.92	0.92	12
	macro average	0.94	0.94	0.94	38
	weighted average	0.95	0.95	0.95	38
Test fold 5	B-DNA	0.96	0.92	0.94	26
	A-DNA	0.85	0.92	0.88	12
	macro average	0.90	0.92	0.91	38
	weighted average	0.92	0.92	0.92	38

Table 3.

Comparison between different ML algorithms

	Average PR	AUC PR	ROC AUC	Accuracy	F1	MCC
Random forest	0.888	0.885	0.945	0.881	0.829	0.747
SVM classifier	0.912	0.908	0.943	0.886	0.822	0.741
Logistic regression	0.910	0.906	0.945	0.896	0.821	0.758
Naive Bayes classifier	0.919	0.918	0.952	0.891	0.841	0.765
LightGBM	0.957	0.956	0.974	0.927	0.881	0.832

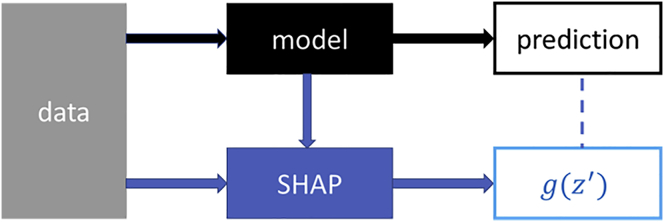
In LightGBM, boosting helps in reducing bias and variance in ensemble-based models, which is particularly useful for controlling overfitting. It builds trees in a stage-wise forward manner, where weak learners (trees) are added to address the shortcomings of existing weak learners. As the end result, the model is able to achieve high accuracy by increasing the importance of “difficult” observations (samples that have a complex non-linear decision boundary). As more trees are added, they rectify the misclassification error committed by existing learners. To control overfitting, we use the optimal value of regularization parameters: L1, L2 regularization, bagging fraction and frequency, number of leaves, and feature fraction (see section C in supplemental information). Another benefit of using gradient boosting is that after the boosted trees are constructed, it is relatively straightforward to retrieve importance scores for each attribute.¹⁴ To understand how individual dinucleotide steps affect the propensity of a sequence to assume a given conformation, we have used SHAP,¹³ a unified approach for explaining the output of any ML model. SHAP connects game theory with local explanations, uniting several previous methods, and representing the only possible consistent and locally accurate additive feature attribution method based on expectations.¹³ This explanation model uses simplified inputs, which toggle features on and off, rather than raw inputs to the original model. Figure 4 shows the schematic models of SHAP, where data are processed using the original model and using the SHAP criteria as mentioned above. $g\left(z^{\prime }\right)$is a linear function of binary variables (ON or OFF), which determines the role of individual inputs of features in the prediction. SHAP builds model explanations by asking the same question for every prediction and feature: “How does prediction i change when feature j is removed from the model?” as mentioned above.

Figure 4.

Schematics of SHAP (SHapley Additive exPlanations) model

To interpret and relate these SHAP values with the thermodynamics, we describe the concept of the absolute free energy values (see section E in supplemental information and Kulkarni and Mukherjee¹⁵ for further details). Thermodynamically, the conformation of a particular structure depends on the free energetic stability. Therefore, the propensity of a sequence to adopt a particular conformation should depend on the overall free energy of the sequence in that conformation. Keeping that in mind, we had earlier calculated the free energy cost (Table 3) for the formation of the A form of each of the ten dinucleotide steps, as discussed below.¹⁵

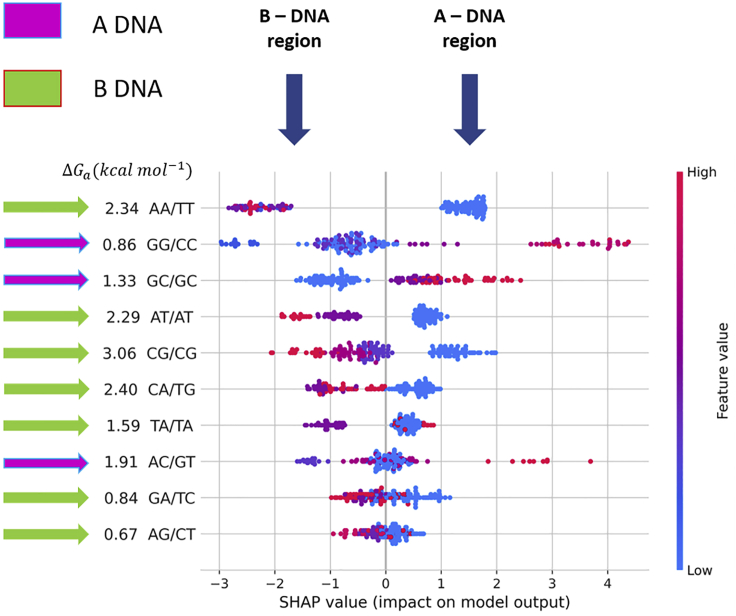
To obtain an idea about which features are most important for our model, we have plotted the SHAP values of each dinucleotide step (feature) for every sample. Figure 5 shows the SHAP summary plot, which sorts features by the sum of SHAP value magnitudes over all samples and uses these SHAP values to show the distribution of the impacts of each feature on the model output. The summary plot combines feature importance with feature effects. Each point on the summary plot is a Shapley value for a feature and an instance. The position on the y axis is determined by the feature and on the x axis by the Shapley value. The color represents the value of the feature from low to high (red means high impact, blue means low impact). Overlapping points are jittered in the y-axis direction, so we get a sense of the distribution of the Shapley values per feature. The features are ordered according to their importance. Traditionally AA/TT and GG/CC are considered to be the most B-philic and A-philic dinucleotide steps. We see that (AA/TT), a B-promoting dinucleotide step, and GG/CC, an A-promoting dinucleotide step, have the highest impact on our model prediction. The AA/TT step has the highest negative SHAP value, which corresponds to its highest contribution in predicting B-promoting DNA sequences. Similarly, the GG/CC and GC/GC have the highest positive SHAP value, which corresponds to their highest contribution in predicting A-promoting DNA sequences. GG/CC has lower junction free energy ($\left(\Delta G_{\text{J}}\right)$ compared with AA/TT and thus, lower mean cooperative length for B-to-A transition. High positive SHAP values for GG/CC support this free energy-based observation.

Figure 5.

SHAP summary

The plot sorts features by the sum of SHAP value magnitudes over all samples and uses SHAP values to show the distribution of the impacts of each feature on the model output. The color represents the feature value (red = high, blue = low). The horizontal scale represents the SHAP values, with the left side indicating B-DNA region (negative values) and the right side indicating A-DNA region (positive values). The absolute free energy value of each dinucleotide step is mentioned adjacent to its label.

CG/CG and AT/AT dinucleotide steps have highest negative SHAP values after AA/TT step, thus suggesting these steps as B-philic steps and supported by absolute free energy values. This tells us that they have a high negative impact (B-DNA prone) on the model prediction. Similarly, GC/GC and AC/GT are observed to be A-philic and B/A intermediate step, respectively, based on both positive SHAP values and low free energy values.

Absolute energy ($\text{Δ}{G}_{\text{a}}$) values indicate AG/CT and GA/TC as A-philic steps, whereas SHAP value distribution indicate these steps as B-philic steps. Dinucleotide steps AG and GA steps prefer B-form conformation over A form as observed in previous studies (Svozil et al.;¹⁰ Marathe et al.¹⁶; our review¹⁷). Earlier studies observed that structurally TA/TA and CA/TG steps exhibit high roll angle similar to A-form steps but still maintain flexible B form (Hassan and Calladine (1998) J. Mol. Biol. 282, 331–343). The flexible B form allows DNA bending or kinking during protein interactions. $\text{Δ}{G}_{\text{a}}$ values predicted TA and CA steps as neutral (neither A-philic or B-philic) and B-philic step, respectively.

For CA and TA steps, overall SHAP values are distributed close to the abscissa and neutral feature values (violet color) with negative SHAP values possibly indicate the intermediate nature of these steps. Thus, we can see that SHAP values have correctly predicted conformation preference in comparison with free energy values, demonstrating its classification efficiency over the free energy method.

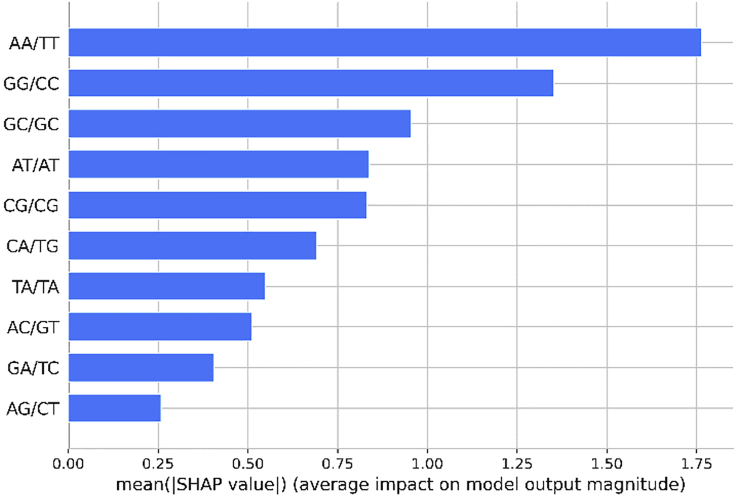
It is interesting to note that there is good agreement between these inferences drawn from our ML model with the absolute free energy values, except for TA and CA steps (Table 4). Figure 6 shows the standard bar plot obtained by taking the mean absolute value of the SHAP values for each feature. This plot shows how each dinucleotide step (feature) contributes to the prediction of the propensity of the A/B-promoting DNA sequence.

Table 4.

List of absolute energy values ($\text{Δ}{G}_{\text{a}}$) and mean of absolute SHAP values for all ten possible dinucleotide steps

Dinucleotide steps	$\text{Δ}{G}_{\text{a}}$(kcal/mol)
AA/TT	2.34
GG/CC	0.86
AC/GT	1.91
CA/TG	2.40
AT/AT	2.29
TA/TA	1.59
AG/CT	0.67
GA/TC	0.84
CG/CG	3.06
GC/GC	1.33

Note that $\Delta G_{\text{J}}$ values were calculated only for homonucleotide steps and not heteronucleotide steps. $\Delta G_{\text{J}}$ is 1.59 kcal/mol for AA/TT and 0.52 kcal/mol for GG/CC.

Figure 6.

Mean of absolute SHAP values show the average impact of each dinucleotide step in predicting whether a given sequence will attain A or B conformation

Discussion

In our approach, we have trained different ML algorithms using a set of known A-DNA/B-DNA sequences. The best ML approach (LightGBM) provides prediction with correctness of ∼93% and an MCC score of 0.832. As it turns out, our model is able to capture the complex relationship between the feature vectors (dinucleotide steps) that attribute to the final conformation assumed by a DNA sequence. Understanding why a model makes a specific prediction can be as important as the prediction's accuracy in many applications. This is crucial when we want to understand how each fundamental dinucleotide step contributes toward the conformation attained by a sequence. The highest accuracy for large modern datasets is often achieved by complex models that are difficult to interpret, such as an ensemble of several models or deep learning models. LightGBM¹⁸ is an implementation of a gradient boosting decision tree technique that offers a balanced tradeoff between accuracy and interpretability. For gaining further insight into the interpretability of our model, SHAP analysis was employed with which we could come up with a consistent and locally accurate additive feature attribution method based on expectations. Our study thus indicates that the conformational preference of a DNA lies in the fundamental free energetic driving force at a local dinucleotide level. Most of the DNA sequences used here, however, are short. Therefore, the cooperative effect may play a role in the case of longer DNA sequences, and an effort is under way to understand this. Our training set contains some hexamer or octamer A-DNA sequences. Such short oligonucleotides are affected by crystal packing forces.^19,20 At the same time, we also find nuclear magnetic resonance (NMR) structures with A form. We would also like to point out that crystal packing may have a role in producing A form for certain sequences. However, this influence is limited to only fa specific set of sequences. We believe that this has to do with the inherent propensities of these sequences to adopt the A form. For this reason, we do not find all short sequences adopting the A form. There are some short AT-rich sequences (PDB: 4U9M, 2G1Z) which are crystallized as B-DNA as opposed to crystal packing-derived A-DNA conformation. There are many 8- or 10-mer sequences that are in B form, just as not all A-DNA sequences are 8- or 10-mers. Therefore, it is not obvious that the length of the DNA sequence would dictate a particular conformation. The high predictive performance of our model indicates that there must be some inherent tendencies of these sequences to adopt the A form, and the objective of the present work is to capture that.

AA steps are highly B-philic due to the steric hindrance of their antisense counterpart TT step. A severe steric hindrance between protruding methyl groups of thymine base exists if it undergoes B → A transition and thus enhances the free energetic cost of the process. It is surprising to see that ML models can predict the AA step as the most B-philic step without the knowledge of the structure and interactions between the stacking base steps.

The GG step is well known to adopt or induce the A form in DNA sequences. Again, it is encouraging to note that the ML model can predict GG and GC as the most A-philic steps without any structural information. The eukaryotic and prokaryotic genomes contain DNA segments that can be easily converted to A form (A-DNA promoter sequences [APS]). These A-form segments can then be specifically recognized by DNA binding proteins during the indirect readout mechanism. Such APSs allow binding of certain transcription factor (TF) binding proteins²¹ and could play a role in protein-DNA binding mechanisms. Recently, Li et al. incorporated DNA sequence and shape as features along with information from X-ray and simulated structures to determine TF binding regions in DNA sequences.²²

Whitley and coworkers²¹ used Basham's trinucleotide solvation free energy method of A/B DNA structure prediction⁶ to find A-DNA promoters in the Xenopus tropicalis genome. Owing to the limited applicability of the aforementioned method, we believe that our proposed ML model can be implemented on other genomes to find unknown A-DNA promoter DNA steps a priori. Further study is under way to explore eukaryotic genome analysis as well as the genome of organisms that survive under stringent conditions using the A form of DNA.

Limitations of the study

We would now like to discuss the limitations of the present study. The DNA structures considered here are assigned as B-DNA or A-DNA because these structures do not contain mixed A-form/B-form dinucleotide steps. We assume that even with mixed A/B traits at the local level, based on the definition of recent studies the whole DNA structure appears as B or A due to prominent conformational preference of each dinucleotide step of the DNA. The cooperative effects of these dinucleotide steps contribute to the overall conformational preference in DNA oligonucleotides.

Finally, the classification of a sequence to A or B is based on the Nucleic Acid Database (NDB) data. Therefore, our goal was to apply the method to a given sequence and predict the A/B classification in conformity with the NDB (global) structural classification. As mentioned earlier, we tried to include in our curated dataset the sequences whose structures were obtained under similar experimental conditions so as to minimize the effect of varying experimental conditions.

At the moment, we are restricted by the paucity of a sufficient number of labeled DNA sequences. Out of 192 curated DNA sequences in the NDB dataset, 61 are A-DNA sequences and 131 are B-DNA sequences (supplemental information, section F [Data S1]). The lack of data is one of the significant challenges in any ML model. Furthermore, the severe class imbalance between A- and B-DNA is another limitation, although we have adopted several measures to overcome these limitations in the present study. Also, the present study focuses only on the canonical A-DNA or B-DNA conformation, with the objective of developing a method to understand the tendency of short DNA segments in long oligonucleotides to adopt these conformations. Thus, we have not considered non-canonical DNA structures. We also acknowledge that there are subclasses of this broad classification²³—different A-form conformers, conformers bridging A to B form and vice versa, a separate Z form, subdivision of B conformations into BI and BII form²⁴—which we could not categorize owing to the paucity of data in the NDB database.

Experimental procedures

Resource availability

Lead contact

The lead contact for this work is Arnab Mukherjee, arnab.mukherjee@iiserpune.ac.in.

Materials availability

The study did not generate new unique materials or reagents.

Methods

Data curation

The first step in an ML approach is data curation. Since we use a supervised learning approach, we collected A- and B-DNA structures from the Nucleic Acid Database (NDB repository).^25,26 The corresponding sequences were retrieved from the RCSB PDB²⁷ database by a parser written by us. We filtered out all redundant sequences along with all those sequences which had anything in addition to A, C, G, and T. Furthermore, we considered only the unbound double-stranded DNA structures. We removed all DNA sequences less than 5 base pairs long from our analysis as they are too short to be deciding a particular conformation. While selecting sequences for our study, we looked at the different experimental conditions under which different DNA structures were crystallized/labeled, namely "Crystallization Method," "Temperature (K)," "pH," "Crystal Growth Procedure," "R-free Values," and "Percent Solvent Content." In particular, for X-ray structures we selected those sequences that corresponded to structures with high R_free values and resolution. For NMR-based structures, we considered the “Sample Temperature,” “Sample pH Values,” “Solvent System,” “Ionic Strength,” and other relevant parameters. We have presented the distribution of different experimental conditions under which different structures were obtained in section A of supplemental information. To minimize the effect of the influence of varying experimental conditions, we tried to select the sequences obtained under similar conditions. We also checked for outlier samples using a skewness adjusted interquartile range method²⁸(see section A in supplemental information), which takes into consideration the skewness in the distribution for robust outlier detection. This helped us in obtaining those sequences for which the experimental conditions were similar, irrespective of the class label. Section A of supplemental information shows kernel density estimation plots of each experimental condition for both A- and B-DNA samples that we included in our dataset.

We also performed sequence similarity analysis across all sequences in a given class. We used the alignment-free sequence comparison approach that is based on the frequencies of k-mers (subsequences or words of length k).²⁹ This considers the “Euclidean distance” between k-mers frequency profiles of two sequences as a measure of the dissimilarity between them. The pairwise distance matrix hence obtained is normalized between 0 and 1. Unlike alignment-based methods, the alignment-free method does not assume the contiguity of homologous regions. They are also less dependent on substitution/evolutionary models and are comparatively computationally inexpensive. The choice of k depends on the nature and the length of the sequences. Smaller k-mers should be used when sequences are obviously different (e.g., they are not related), whereas longer k-mers can be used for very similar sequences.^30,31 For nucleotide sequences, $k$ is usually set to 4–10 for smaller sequences, and k = 8 or 10 is typically used for comparing longer sequences.^30,32 We considered $k=\left\{\mathrm{4,5,6}\right\}$ for comparing sequence similarity. The mean sequence similarity is $31.9\%$ for A-DNA samples and $28.7\%$ for B-DNA samples in our curated dataset. In our dataset, the smallest sequences are of length 6 and hence is the upper bound on the choice of k.

Our curated dataset contained 192 samples, of which 61 are A-DNA sequences and 131 are B-DNA sequences. The list of curated DNA sequences along with resolution (Å), R value, R_free (for crystallographic structures), and other relevant experimental conditions are mentioned in section F of supplemental information (Data S1).

Feature extraction

Feature extraction or “feature design” is an essential step in any ML approach. The characteristics of any object are called features. In a DNA sequence, relevant features could be the length of the DNA, the number and types of dinucleotide steps, or the number and types of tetranucleotide steps. In this study, we have considered the count of all ten unique dinucleotide steps in the given DNA sequence as our feature vectors (Figure 1). There are two main rationales behind our choice: (1) the dinucleotide step represents the smallest possible building block for DNA conformation;^33,34 (2) we have used the absolute free energy values for each dinucleotide step¹⁵ in model interpretation, explaining how a particular conformation can be attributed to structural and chemical aspects associated with each dinucleotide step.

We wish to mention that the lack of data precludes us from building a model that considers relative positions of the different dinucleotide steps in a sequence. Such a model, although desirable, would require a large number of training samples for training. Our approach, on the other hand, offers a viable compromise.

Pre-processing and adjusting the class imbalance

Data pre-processing involves the transformations that are applied to the data before feeding them to our ML models. For this classification problem, we have encoded the A-DNA samples as the positive class with the label “1” and the B-DNA samples as the negative class with the label “0.” Some ML models such as support vector machines with radial basis function as the kernel³⁵ and models that use L1 and L2 regularization assume that all features are centered around 0 and have variance in the same order.³⁶ We, therefore, standardized the features by removing the mean and scaling to unit variance. The standard score of a sample $x$ is calculated as

$$z=(x-u)/s\text{,}$$

where $u$ is the mean of the training samples and s is the standard deviation of the training samples. Centering and scaling happen independently on each feature by computing the relevant statistics on the samples in the training set.

We also observed a significant class imbalance (32% A-DNA versus 68% B-DNA curated, non-redundant sequences) that became apparent during the preliminary analysis. To address the class imbalance issue, in which training data belonging to one class outnumber the examples in the other, we tried two different strategies during the training stage. First, we adjusted the class weight. Due to the imbalanced number of positive (A-DNA) and negative (B-DNA) samples, the class weight option imposes a heavier penalty for errors in the minority class. Class weights are inversely proportional to class frequencies in the training data. The second strategy employed the SMOTE + TOMEK method,³⁷ which is a combination of oversampling and undersampling. SMOTE is an oversampling method that synthesizes new plausible examples in the majority class. Tomek-Links refers to a method for identifying pairs of nearest neighbors in a dataset that have different classes. Removing one or both examples in these pairs has the effect of making the decision boundary in the training dataset less noisy or ambiguous. Despite the differences between the two approaches, they deliver similar improvements.

Model building

In this stage, we considered different ML algorithms for our problem. Classification of a sequence into A-/B-DNA is a binary classification problem. We tried LightGBM¹⁸ (based on gradient boosting decision tree), SVM classifier with “RBF” and linear kernel,³⁵ random forest classifier, naive Bayes classifier, and logistic regression.³⁵ Each model outputs the probability $p\left(C_k\right|x)$ of a class, $C_k=\{0,1\}$, given a sequence $x$ (0 represents B-DNA and 1 represents A-DNA). We then used an optimal threshold for converting this probability into class labels. When selecting a classification algorithm for a particular problem, one has to simultaneously select the best algorithm for that dataset and the best set of hyperparameters for the chosen model. These hyperparameters are intrinsic to each algorithm and define the model architecture. The accuracy of a model on unseen data is critically dependent on the choice of suitable values for the hyperparameters. The search for optimal values for the hyperparameters is a process known as model selection. ML models such as LightGBM have several hyperparameters. These are the threshold parameter scale_pos_weight for adjusting the threshold for an imbalanced dataset, regularization parameters L1 and L2, number of leaves (for controlling the complexity of the model), number of iterations, learning rate, bagging fraction, and bagging frequency. Even fairly simple generalized additive models such as logistic regression have hyperparameters such as regularization, class_weight, or threshold. Most of these models would perform poorly on the unseen data if one were to use the default set of hyperparameters. Hyperparameter optimization can be accomplished in several ways: one can exhaustively consider all parameter combinations using grid search, use randomized search strategy to sample a given number of candidates from a parameter space with a specified distribution, or optimize the criterion of expected improvement (EI) using a Gaussian process/tree-structured Parzen estimator approach (TPE). We chose to use the optimization of EI criterion because it is intuitive and has been shown to work well in a wide variety of settings.³⁸ To tune the hyperparameters of our models, we used the TPE approach implemented in the Optuna framework.³⁹

We have used Intel Distribution for Python and Python API for Intel Data Analytics Acceleration Library (Intel DAAL)—named PyDAAL⁴⁰—to boost ML and data analytics performance. Using the advantage of optimized Scikit-learn (Scikit-learn with Intel DAAL) that comes with it, we were able to achieve faster training time and accurate results for the prediction problem.

Training and evaluation

In an ideal situation, we would have a large dataset to be able to train and validate our models (training samples) and have separate data for assessing the quality of our model (test samples). However, such data-rich situations are, more often than not, rare in the life sciences. In many practical applications, we seldom have the luxury of having a sufficiently large test set, which would provide an unbiased estimate of the generalization performance of our models. If we reserve too many data for training, this results in unreliable and biased estimates of the generalization performance; setting aside too many data for testing results in too few data for training, which in turn hurts model performance. For such situations where the dataset is small and reserving data for independent test sets is not feasible, the nested CV^41,42 procedure offers a viable alternative. Nested CV can be used for choosing an appropriate classifier (model) and optimizing its hyperparameters to obtain a reliable and unbiased estimate of generalization performance.^41,43 Model selection without nested CV uses the same data to tune model parameters and evaluate model performance. Information may thus “leak” into the model and overfit the data, leading to a phenomenon called “overfitting in model selection.”⁴³ We compared the performance of the machine learning algorithms, referred to as ML algorithms hereafter, by performing nested 5-fold stratified nested CV. This process consists of two nested CV loops which are often referred to as inner (internal) and outer (external) CV loops. We perform the model selection in the inner loop, and in the outer loop we estimate the generalization performance (see Figure 2 for a schematic overview of nested CV). In the outer loop, our dataset is randomly split into five non-overlapping groups. Stratification is used to preserve the percentage of samples for each class. In each group, these two disjoint subsets are referred to as the training and the test set. In each group, the test set is exclusively used for model assessment. In the inner loop, the training set is used for model building and model selection. In each iteration of the inner loop, the incoming training set is repeatedly split into inner training and validation datasets by a stratified 3-fold CV approach. The inner training folds are used to derive different models by varying the hyperparameters (tuning parameters) of the model family at hand, whereas the validation sets are used to estimate the models' performance. The hyperparameters corresponding to the model with the lowest CV error across the inner folds are chosen for training the outer loop model. Along with tuning of hyperparameters, we also choose the optimal threshold via a threshold-moving technique on the validation data. This involves choosing the threshold that corresponds to the maximum score on a chosen evaluation metric. For this purpose, we have chosen the F1 score metric. This tries to find the balance between precision and recall, which is extremely useful in scenarios when we are working with imbalanced datasets. Finally, in each iteration of the outer loop, we initialize the model with the tuned hyperparameters and threshold and use the test set to obtain an unbiased estimate of the selected model. We present below the pseudocode for the nested CV algorithm.

• For$i=1$ to $K_1$ $splits$ do://(outer loop)

  • Split $\mathcal{D}$ into ${\mathcal{D}}_i^{train},{\mathcal{D}}_i^{test}$ for the $i^{\prime }th$ split
  • For$j=1$ to $K_2$ $splits$ do://(inner loop)

    • Split ${\mathcal{D}}_i^{train}$ into ${\mathcal{D}}_j^{innertrain},{\mathcal{D}}_j^{validation}$ for the $j^{\prime }th$ split
    • sample parameter space (${\mathcal{P}}_{sets})$ using random search and TPE to get $P_j$

      • Initialize and train model $\mathcal{M}$ on ${\mathcal{D}}_j^{innertrain}$ with hyperparameter set ${\mathcal{P}}_j$
      • Tune hyperparameters to get $P_j^{\ast }$ and compute validation error $E_j^{validation}$ for $\mathcal{M}$ with ${\mathcal{D}}_j^{validation}$
  • Select optimal hyperparameter set $P^{\ast }$ from $P_{sets}$, where $E_j^{validation}$ is the least
  • Train $\mathcal{M}$ with ${\mathcal{D}}_i^{train}$, using $P^{\ast }$as hyperparameters
  • Compute test error metrics $E_i^{test}$ for $\mathcal{M}$ with ${\mathcal{D}}_i^{test}$

For assessment of the performance of our classification model, we have chosen accuracy, F1 score, MCC, ROC curve, and PR curves as our primary evaluation metrics. When there is a class imbalance, the accuracy alone cannot give an accurate assessment of the performance of a classification model. A classifier may proclaim all data points as belonging to the majority class and obtain a high-accuracy score while performing poorly on the prediction of minority class samples. Therefore, using accuracy as the sole criterion for model evaluation can lead to overoptimistic inflated results, especially on imbalanced datasets. ROC represents a probability curve, and the AUC of the ROC curve represents the measure of separability between the two classes. The higher the AUC-ROC score, the better the model is at distinguishing between A- and B-DNA samples. Precision is defined as the ratio of true positives and the sum of true positives and false positives. False positives are outcomes the model incorrectly labels as positive that are actually negative. In our example, false positives are B-DNA that the model classifies as A-DNA. In contrast, recall expresses the number of true positives divided by the sum of true positives and false negatives. In most problems pertaining to classification, one could give a higher priority to maximizing precision, or recall, depending on the problem one is trying to solve. However, in general, there exists a more straightforward metric that takes into consideration both precision and recall. This metric is known as the F1 score, the harmonic mean of precision and recall. Notably, the MCC coefficient considers true and false positives and negatives and is generally regarded as a balanced measure that can be used when there is a class imbalance.⁴⁴ It produces a more informative and truthful score in evaluating binary classifications than accuracy and F1 score. The formulas of these metrics are mentioned in section D of supplemental information. Section F of supplemental information contains the list of all samples used for training and testing for each iteration of the outer loop.

Published: August 12, 2021

Data and code availability

Data and code can be accessed at the following link: https://github.com/abhijitmjj/DNA-structure-prediction (code author and repo maintainer: Abhijit Gupta [github username: abhijitmjj]).

DNA structure prediction from its sequence code is available in the GitHub repository (https://github.com/abhijitmjj/DNA-structure-prediction). We intend to build a webserver for our program soon, where the user can provide raw sequences as the input and obtain the probabilities for them to attain A/B form conformation.