Abstract
As the world faced the devastation of the COVID‐19 pandemic in late 2019 and early 2020, numerous clinical trials were initiated in many locations in an effort to establish the efficacy (or lack thereof) of potential treatments. As the pandemic has been shifting locations rapidly, individual studies have been at risk of failing to meet recruitment targets because of declining numbers of eligible patients with COVID‐19 encountered at participating sites. It has become clear that it might take several more COVID‐19 surges at the same location to achieve full enrollment and to find answers about what treatments are effective for this disease. This paper proposes an innovative approach for pooling patient‐level data from multiple ongoing randomized clinical trials (RCTs) that have not been configured as a network of sites. We present the statistical analysis plan of a prospective individual patient data (IPD) meta‐analysis (MA) from ongoing RCTs of convalescent plasma (CP). We employ an adaptive Bayesian approach for continuously monitoring the accumulating pooled data via posterior probabilities for safety, efficacy, and harm. Although we focus on RCTs for CP and address specific challenges related to CP treatment for COVID‐19, the proposed framework is generally applicable to pooling data from RCTs for other therapies and disease settings in order to find answers in weeks or months, rather than years.
Keywords: Bayesian data and safety monitoring, International consortium for data sharing from ongoing RCTs, statistical analysis plan, stopping rules
1. INTRODUCTION
The coronavirus disease 2019 (COVID‐19) pandemic urgently requires rapid action to determine effective treatments. Over 1000 clinical trials to test treatment options for COVID‐19 have already been undertaken, but most have produced inconclusive results. 1 Although two vaccines have been authorized for emergency use, and other vaccine trials are underway, effective treatments for COVID are still needed. At the time of preparing this paper, the only treatment for COVID‐19 that has been approved by the Food and Drug Administration of the United States is remdesivir, 2 although the randomized clinical trial (RCT) did not show a significant benefit with respect to mortality.
The rapidly shifting locations of the pandemic constitute a major challenge for recruitment and completion of all COVID‐19 RCTs. Pooling existing and accumulating data from multiple studies holds promise for quickly finding answers to urgently needed questions as is the case with the COVID‐19 pandemic. In fact, several meta‐analyses (MA) of aggregate data from studies of treatments for COVID‐19 have already been conducted in an attempt to rapidly address questions about efficacy and safety; treatment with steroids 3 (by the World Health Organization, WHO) and treatment with hydroxychloroquine 4 are two examples. It is especially important during this crisis that pooling efforts are scientifically justified and that the analyses are prespecified and inferentially rigorous. 5 This will serve to ensure that the results are convincing to the medical community.
A promising treatment for COVID‐19 is the use of convalescent plasma (CP), a treatment that has shown potential benefit as far back as the 1918 influenza pandemic. More recently, CP was also used to treat other related infections such as Middle Eastern respiratory syndrome coronavirus (MERS‐CoV). Several observational studies, retrospectively comparing COVID‐19 patients treated with CP to nontreated COVID‐19 patients, have been undertaken. 6 , 7 , 8 However, rigorous evaluation of the efficacy of CP in treating COVID‐19 requires RCTs. The first such RCT was conducted at seven medical centers in Wuhan, China during the early stages of the pandemic. 9 Unfortunately, this trial terminated early because insufficient new cases were available for enrollment, and as a result, produced no conclusive evidence. Later, an RCT for CP from India that enrolled the targeted sample size of 464 patients reported no differences in clinical outcomes between patients treated with standard of care alone and those treated with standard of care plus CP. 10 Based on a retrospective evaluation of the transfused CP, however, the investigators found that about a quarter of the CP units used in the study lacked antibodies, while most of the study participants already had high levels of antibodies in their own plasma at randomization. A more recent RCT from Argentina also indicated lack of evidence for efficacy or harm for CP in a double‐blind comparison against placebo. 11 This well‐executed RCT, which used CP with high levels of antibodies, targeted COVID‐19 patients with severe pneumonia. Numerous additional RCTs using CP have been initiated, but as the COVID‐19 surge dissipated where these trials started, the pool of eligible participants for these trials has diminished. Wooding et al provide a summary of registered RCTs on the efficacy and safety of CP for COVID‐19 obtained from PubMed and summarized from the WHO International Clinical Trials Registry and clinicaltrials.gov (as of July 2020). 12 An impediment for recruitment into trials using CP in the United States is the emergency use authorization of the use of CP. 13 It is imperative to find a solution to the problem caused by the mismatch between enrolling sites for RCTs and COVID‐19 hotspots. 5
This paper describes a meta‐analytic approach to pooling individual patient data (IPD) from completed, early‐terminated, and ongoing RCTs for CP, as well as from new trials that might open up as the pandemic migrates to new regional hotspots of COVID‐19 infection. The goal is to continuously update and monitor the pooled IPD until sufficient evidence emerges to warrant a reliable conclusion. Regardless of whether it is based on aggregate data or IPD, a meta‐analysis is typically conducted following the completion of all the studies being considered. This means that there are very few unknowns regarding the number of studies and the sample sizes at the time of meta‐analysis. In contrast, we are conducting a meta‐analysis in real‐time to get answers as quickly as possible in light of the pandemic crisis. This means the analytic framework needs to be flexible enough to accommodate an unknown number of RCTs with an undetermined number of patients. Given the uncertain nature of the trajectory of the pandemic around the world, we also do not know the frequency and number of interim looks that will be required to closely monitor the incoming information to reach a conclusion as quickly as possible. The methods described here provide a statistical road map for how to conduct rigorous analysis in light of study uncertainty.
Pooling data from numerous trials and continuously monitoring the accumulating data presents logistical and statistical hurdles. 14 First, patient populations from different RCTs are heterogeneous with respect to demographic characteristics, medical history, severity of the COVID‐19 symptoms at time of randomization, and use of concomitant medications. Additional challenges for all investigations of treatments for COVID‐19 are the lack of sufficient experience with the disease at the start of the different RCTs, leading to rapidly changing patterns of treatment, and lack of consensus about the most relevant clinical outcome: time to hospital discharge, survival free of ventilation, mortality, and others have been used with various degrees of disagreement among the medical community regarding their importance. Complicating matters further for evaluation of CP is the fact that, unlike standard drug treatment, where the capsules or injections contain a fixed amount of the active component, CP used for transfusion does not contain a uniform or standardized amount of antibody. A further challenge is the fact that although all CP RCTs to date use the same experimental treatment (CP), they have compared CP to different control conditions: standard of care, saline, or non‐CP.
The statistical analysis plan (SAP) outlined in this paper is for the COMPILE (Continuous Monitoring of Pooled International Trials of CP for COVID‐19 Hospitalized Patients) study, 15 and it is fundamentally a description of how we have addressed the challenges presented by an IPD MA analysis. COMPILE hypothesizes that the compilation of the pooled datasets of IPD from RCTs will result in a data resource that can provide evidence with high degree of certainty regarding the efficacy (or harm) and safety of CP as a treatment for COVID‐19. COMPILE also aims to identify individual patient characteristics as well as characteristics of the CP that lead to better or worse outcome with the treatment. Ultimately, we feel that the heterogeneity of the patient populations and the variations in treatment enhance the likelihood of more widely generalizable conclusions.
The statistical approach for the data monitoring and analysis of the COMPILE study is based on a Bayesian clinical trial paradigm. 16 , 17 It utilizes continuous monitoring, using Bayesian stopping rules that allow for efficient, real‐time decisions without penalties for multiple data looks and ‐spending associated with the classic RCT group‐sequential monitoring approach. 18 , 19 Given the urgent need to identify effective therapeutic options for treating COVID‐19 in this world‐wide pandemic, frequent or continuous monitoring of the accumulating data collected in CP RCTs is critical. Bayesian monitoring enables straightforward, actionable rules for efficacy, harm, and safety, all of which incorporate information accrued across all studies; the process is based on estimation of the posterior probabilities, for example, of favorable or unfavorable odds ratios. The stopping rules will pertain to the execution of the COMPILE meta‐analysis itself, and will have no direct bearing on the conduct of the individual studies. During a pandemic, the rapid dissemination of high‐quality information is paramount, so once the criteria have been met for stopping the meta‐analysis, data collection will cease, the final analyses will be conducted, and results will be published; the individual studies can choose to continue to enroll patients.
The paper is structured as follows. In Section 2 we describe the necessary infrastructure to successfully engage unrelated RCTs from around the world in a joint effort to address this humanitarian crisis. Section 3 provides an overview of features characterizing the COMPILE study design. Highlights from the SAP of COMPILE, including a description of the stopping rules, are presented in Section 4. We conclude with a summary of the current state of the COMPILE study in Section 5.
2. LOGISTICS OF POOLING RCTS
The innovative approach to pooling IPD from completed and ongoing trials, including new trials that are in the process of starting up, presents unique logistical challenges not typically encountered when designing a conventional multisite RCT or MA of completed RCTs. Most critically important is the establishment of collaborations with investigators conducting RCTs around the globe. The pace of the pandemic, and the way it ebbs and flows in different parts of the world at different times, means that no single institution, or even single country, might be able to gather enough information and high‐quality data to understand in real time what therapies are effective.
A logistical first step is to develop data sharing agreements that the RCT teams and their institutions consent to sign. To be able to collect data from ongoing RCTs, the agreements must account for regulations regarding data sharing that vary across different countries. For example, research data from the United States must be compliant with the Health Insurance Portability and Accountability Act of 1996 (HIPAA), studies taking place within the European Union must satisfy the General Data Protection Regulations requirements, and sharing of research data from India must be approved by the Indian Council of Medical Research. A secure central repository needs to be established, along with a secure data transfer protocol for submitting newly accumulated, completely de‐identified, IPD to the repository on a regular basis. Because of the variability in regulations for data sharing, this step is most crucially important for investigators and institutions to agree to collaborate. For the COMPILE study, participating RCTs submit accumulated data every 2 weeks. Providing a safe and secure platform for conducting analyses by different research teams is essential to ensure equitable data access. This requires a virtual device infrastructure (VDI) where data are stored in a single location that is equipped with a range of data analytic tools; approved investigators with passwords can obtain snapshots of the database and conduct analyses within the VDI, without the need or ability of downloading the data and thus ensuring data integrity and security.
A collective data and safety monitoring board (cDSMB) needs to be established. Given the specific nature of the prospective meta‐analysis plan of ongoing studies, the cDSMB should involve members from the DSMBs of all collaborating RCTs. For ongoing RCTs, the Chair and the unblinded statistician from the individual RCT's DSMB should be members of cDSMB. A cDSMB Charter that specifies the responsibilities of the members of the Board must be drafted, discussed, and approved by the cDSMB members. Governance documents are needed to specify the processes for decision making and the responsibilities of various committees and working groups. In addition, a study protocol is needed that is accepted by all collaborating clinical trial teams. The SAP needs to be developed in a collaborative effort with participating study teams by team members who are blinded to the data from all studies, including their own study. An essential component of the SAP is a description of the process of continuous monitoring that includes establishing stopping rules for safety, efficacy and harm. This SAP, accepted by the cDSMB, is fundamental to the success of the study.
Finally, an essential requirement for such pooling initiatives is that they should be open to all qualified clinical trials. Ensuring the collaborations of all qualified RCTs would require a systematic and ongoing attempts to identify such trials and a dedicated efforts to describe the pooling initiative, to explain its objectives and to assist the RCTs' principal investigators (PIs) and institutions in finalizing the data sharing agreements.
3. THE COMPILE STUDY
3.1. Study design characteristics
Here we summarize the basic design characteristics of the COMPILE study.
Inclusion of RCTs
-
There is a dedicated public website that describes the COMPILE study and allows investigators to apply for participation. 15 In addition, the NYU COMPILE team regularly checks clinicaltrials.gov and clinicaltrialsregister.eu to identify qualifying trials and conducts systematic targeted outreach to the their investigators.
Target population
-
Eligible patients are hospitalized with COVID‐19 infection confirmed by polymerase chain reaction or antibody testing, age 18 or over, and not on mechanical ventilation at the time of randomization.
Parallel arms
-
All RCTs were designed as parallel‐arm trials comparing CP (and possibly other experimental treatments for COVID‐19) to a control. Only patients randomized to the CP or control arms are included in the COMPILE study.
Randomization
-
Only RCTs are included. The randomization schemes might differ across RCTs. When randomization is stratified, the RCT provides information about the strata. The RCTs might use different randomization ratios, most often 1:1 or 2:1 for CP:control.
Experimental treatment
-
CP administered to patients must have confirmed presence of SARS‐CoV‐2 antibodies documented by titer quantities or by a qualitative assay, assessed prospectively (prior to transfusion) or retrospectively (after the transfusion).
Control treatments
-
The control condition can be different in the collaborating RCTs. Possible controls are: (i) standard of care; (ii) saline; (iii) non‐CP.
Blinding
-
RCTs with standard of care as a control condition are not blinded; RCTs with saline or non‐CP are blinded.
Dosing
-
CP is provided in unit bags with 250 to 300 mL of plasma, varying across and within RCTs. Per protocol, the amount of CP administered varies from 1 to 4 units between RCTs. The RCTs with saline or non‐CP as control used unit bags similar to those used for CP.
Sample size
-
The number of studies included in the IPD MA will not be restricted. There is no predetermined maximum number of patients. The COMPILE study will continue to collect data from the collaborating RCTs until either stopping for safety, efficacy or harm is recommended, or until all RCTs have stopped recruitment, completed follow‐up, and resolved all outstanding data queries.
3.2. Evolving and unknown research environment
We recognize that the research environment is constantly changing as the pandemic ebbs and flows dramatically across time and space. We do not have the benefit of knowing when and where a surge will occur next. The prime motivation for the COMPILE study was the observation that many RCTs are unable to recruit sufficient patients following the rapid decline of COVID‐19 cases in a particular regions. Furthermore, we do not know which of those RCTs decided to end for lack of patients and which ones decided to stay dormant until the next surge. This study proposes an approach for designing, monitoring, and analyzing a study in the presence of unavoidable uncertainty during a pandemic.
3.3. Time points
Given the course of the COVID‐19 disease and the currently understood mechanism of action of CP in this disease, the results from CP treatment are expected to be manifested within one month. The primary time point for the COMPILE study is 2 weeks post‐randomization. Some studies were/are assessing patients at 2 weeks (day 14) and others at half month (day 15). Therefore the primary time point is defined as day day. A secondary time point is day days.
3.4. Outcomes
Early on in the COVID‐19 pandemic, the WHO proposed a measure of clinical status in COVID‐19 patients; this WHO clinical status scale has been used in COVID‐19 treatment studies almost uniformly across the world. Initial versions of the WHO scale had 7 or 8 points with the most severe status (death) denoted by 1. 20 , 21 The WHO published an 11‐point version of the COVID‐19 clinical status scale in June 2020, 22 with values ranging from 0 = uninfected to 10 = dead, see Table 1; larger values on this scale indicated more severe disease. A feature of the COMPILE trial was to establish a uniform outcome measure by converting the previous 7‐ and 8‐point scales to the more refined 11‐point scale. This involved first inverting the direction of the 7‐ and 8‐point scales and then applying the conversion algorithm provided in the Appendix (Section A.3).
TABLE 1.
WHO 11‐point COVID scale definition
| 0: | Uninfected, no viral RNA detected |
| 1: | Asymptomatic, viral RNA detected |
| 2: | Symptomatic, independent |
| 3: | Symptomatic, assistance needed |
| 4: | Hospitalized, no oxygen therapy |
| 5: | Hospitalized, oxygen by mask or nasal prongs |
| 6: | Hospitalized, oxygen by noninvasive ventilation or high flow |
| 7: | Intubation & mechanical ventilation, pO/FiO 150 (or SpO/FiO 200) |
| 8: | Mechanical ventilation, pO/FiO 150 (or SpO/FiO 200) or vasopressors |
| 9: | Mechanical ventilation, pO/FiO 150 and vasopressors, dialysis, or ECMO |
| 10: | Dead |
Abbreviations: pO, partial pressure of oxygen; ECMO, extracorporeal membrane oxygenation; FiO, fraction of inspired oxygen; SpO, oxygen saturation.
Because of the importance of the WHO 11‐point scale in COVID‐19 research and its wide use, this measure obtained at day following randomization is one of the bivariate outcomes in COMPILE. The second component of the bivariate outcome is a binary indicator of requirement for mechanical ventilation or worse (level 7, 8, 9, or 10 on WHO 11‐point scale) at day . This second primary outcome was selected based on its clinical importance, its ease of interpretation, and its relevance to nonresearchers and the general public. The investigators from the participating RCTs reached consensus on the bivariate outcomes, which may differ from individual RCT's predefined primary outcomes.
3.5. Data coordination and assessment process
A key element of the project is to assemble existing IPD from the collaborating RCTs into a single analytic data file. This requires continuous updating of the pooled data set with new de‐identified IPD from the ongoing RCTs and allowing for the inclusion of new CP RCTs, see Appendix (Section A.1 for details). A minimal dataset (MDS) of IPD for the COMPILE trial has been identified, see Appendix (Section A.2). Each collaborating RCT begins participation by programming the extraction of the MDS from their RCT's database and submitting their initial MDS deposit. Every other week thereafter, the RCTs update their MDS with newly acquired observations from existing and new patients (in addition to correcting errors in previous submissions).
The COMPILE data analysis team merges the new MDSs and conducts a set of prespecified analyses before each meeting of the cDSMB. COMPILE has established a rigorous predetermined process for continuous monitoring of the accumulating data that will continue until sufficient evidence emerges to enable reliable and convincing conclusions regarding the safety and efficacy (or harm) of CP in the target population. The schedule of cDSMB meetings is determined by the members of the cDSMBs and can be as often as every 2 weeks, depending on the rate of data accumulation. The cDSMB has a quorum when members from the individual DSMBs representing at least 80% of the collaborating RCTs are present. The cDSMB reviews the reports and makes recommendations regarding the conduct of the COMPILE study to the Steering Committee of the COMPILE Consortium, which consists of the PIs of the collaborating RCTs. Members communicate the discussions and recommendations of cDSMB meetings to the individual RCT DSMBs and each DSMB makes individual recommendations to the RCTs they are monitoring. The PIs of ongoing RCTs make individual decisions whether to stop recruitment, to finish follow‐up of the enrolled patients, or to continue their studies.
3.6. Interim monitoring
Given the urgency to identify effective therapeutic options for COVID‐19 patients in this world‐wide pandemic, frequent or continuous monitoring of the accumulating data collected in CP RCTs is absolutely necessary. COMPILE utilizes continuous monitoring, using Bayesian stopping rules that allow for real‐time decisions without the penalties for multiple data looks. Classic RCT monitoring based on ‐spending on the other hand is a less‐efficient approach to this problem. 17
The frequency of the cDSMB meetings will depend on the rate of data accumulation, but will not be less frequent than once a month. The final analysis will occur when the cDSMB has recommended stopping the study for safety, efficacy, or harm and the Consortium investigators have agreed to accept this recommendation. At each interim analysis, the posterior distribution of the parameter describing the pooled treatment effect will be reported (graphically and analytically) and the prespecified stopping criteria based on posterior probability calculations in terms of an odds ratio will guide the recommendations of the cDSMB. The guidelines for stopping are based on the posterior probability that the odds ratio exceeds a prespecified threshold.
4. STATISTICAL ANALYSIS
4.1. Primary efficacy analysis
The primary efficacy outcome is bivariate: (1) clinical status at 14 days 1 day post‐randomization, assessed using the WHO 11‐point ordinal outcome scale and (2) a binary indicator WHO score between 7 and 10 at 14 days 1 day post‐randomization (indicating ventilation requirement or death), see Sections 3.3 and 3.4. While the binary outcome is properly viewed as a subset of the ordinal outcome, we have chosen to accommodate two key functions: efficiency and interpretability. The ordinal scale provides the most efficient use of all available data and provides less variable estimates. The binary outcome is more easily interpreted by clinicians and patients who will ultimately make the treatment decisions. Taken together, the two outcomes provide a more complete picture for the research community with its myriad interests and needs.
4.1.1. WHO score at 14 days
The analysis of the first component of the primary outcome will be a cumulative proportional odds model for the ordinal WHO score at 14 days (1 day). Let Y be the WHO 11‐point scale, , with
and let
Assume that data from K RCTs are available, with subjects in the kth trial, . Denote the outcome for the ith patient from the kth trial on the 11‐point WHO ordinal COVID‐19 scale at 14 days (1 day) by , , and let denote a vector of covariates of length that includes age, sex, baseline WHO score, duration of symptoms before randomization, and quarter of the year when the patient was enrolled (1 = January‐March 2020, 2 = April‐June 2020, 3 = July‐September 2020, 4 = October‐December 2020, 5 = January‐March 2021). will indicate the treatment assignment for the ith subject in the kth RCT; if the patient was randomized to CP arm and if the patient was randomized to control. The following cumulative proportional odds () model for will be considered:
| (1) |
The parameters represent the respective probabilities for the ith subject in the kth RCT of being in state y at 14 days(1 day). The four parameters of the cumulative log‐odds model are , , , and . is a nuisance parameter, which should be very close to 0. However, model fitting improves when can be freely estimated. is a vector of coefficients for the five baseline covariates.
The 's represent the RCT‐specific intercepts or cut points for the cumulative odds model. Since CP treatment is the reference, the log‐odds defined from the cumulative probabilities of the CP arm are estimated by these 's. All , satisfy the monotonicity requirements for the intercepts of the proportional odds model (ie, for all , ).
is the kth RCT‐specific “control effect.” Because all RCTs will have the experimental treatment arm of CP, but may have different control treatment arms, the proposed statistical model has the following notation for control treatment effect modeling: c denotes control treatment type and can represent one of three levels: standard of care, ; non‐CP, ; saline, . Each of the K RCT's will be associated with one level of c. Each will be normally distributed around a pooled “control effect” , with a SD , also to be estimated. represents the variability in treatment effects across RCTs.
The proposed model conceptualizes the three control conditions as three “treatments” to be compared against the reference condition of CP. Each is in turn modeled as having a normal distribution around a pooled “control effect” . We use so that will correspond to the difference of log‐odds for CP and log‐odds for control, rather than control minus CP. , the key parameter of interest, represents the pooled cumulative odds ratio across all RCT's.
Further details regarding the prior distribution assumptions for the parameters described here are provided at the end of this section in Section 4.1.3.
4.1.2. Binary indicator of WHO score between 7 and 10 at 14 days
The analysis of the second component of the primary outcome will be a logistic (l) regression model where the event if the patient has a WHO score between 7 and 10 at 14 days ( 1 day) post‐randomization (and otherwise). The notation largely follows the model described for the first component of the primary outcome.
| (2) |
The parameters of the logistic model mirror the parameters in the cumulative odds model. The notable difference is that replaces , because there is only a single intercept for each RCT. The primary parameter of interest is , the pooled log‐odds ratio for the binary outcome across all RCT's.
4.1.3. Rationale for assumed prior distributions
The prior distributions we will use in Models (1) and (2) (above), and in Models (3), (4), and (5) (below) were selected based on extensive simulations that had three goals: (i) to understand the behavior of the estimating procedure in a variety of realistic situations for the number of the RCTs with different control conditions, sample sizes of the different RCTs, and reasonable‐to‐anticipate variations in the CP effects across RCTs and between control conditions; (ii) to compare the inferences from the Bayesian analysis with Bayesian monitoring to frequentist analysis with frequentist interim monitoring (with 3 to 5 interim looks) and to anchor the prior distributions to results consistent with inferences from frequentist analyses; this was an identified goal because the clinical community is still more familiar with and more comfortable with inferences from frequentist analyses; and (iii) to assess any convergence issues and sensitivity of the posterior distributions to variations in the postulated priors. Examples of simulation methodology that helped inform these decisions are available online. 23 , 24 , 25 , 26 , 27 The simulations were performed in R 28 and Stan. 29
Prior distributions for parameters can range from skeptical to less skeptical to diffuse. The most skeptical distributions have most of the mass close to zero, which will pull the posterior estimates towards zero. Diffuse priors (eg, uniform distributions) have mass spread out across the possible range of parameters, and allow the observed data to largely determine the shape of the posterior distribution. The overarching philosophy has been to be conservative (skeptical priors) with respect to efficacy effects, to be moderately conservative (less skeptical priors) with respect to parameters that will not influence decision making but are important to estimate, and to be least conservative or more flexible (diffuse priors) with respect to safety effects (to ensure we do not miss a safety issue) and nuisance parameters (to ensure stable model fitting).
Global intercept for the cumulative proportional odds models
-
In models (1) and (3), is a nuisance parameter, which should be very close to 0. However, model fitting improves when can be freely estimated. We propose a highly informative prior centered around 0, to reflect the belief that this parameter should be 0 while we allow its estimation, resulting in adequate estimation of the pooled treatment effect and regression coefficients.
RCT‐specific intercepts/cut points
-
are the RCT‐specific cut points of the cumulative proportional odds model. They are constrained to be monotonically increasing; the priors for these parameters are based on a modified distribution with 3 degrees of freedom. (The tails are a compromise between a Cauchy distribution and a normal distribution with equivalent scale parameters.) Stan implements this through the use of an inverse transformation function, where the MCMC draws are on an unconstrained parameter space and transformed back to the desired monotonic parameters. 30 In the binary outcome models for efficacy (2) and for safety (5) as well as in (4) for evaluating the effect of different antibody levels, the prior distribution for each is diffuse, which solves the problem by model fitting without the introduction of global intercept.
Covariate coefficients
-
The covariate coefficients each have a diffuse prior on the log‐odds scale, corresponding to little prior information about the effects, and allowing the data to quickly prevail in the estimation. Note that the (relatively) large variance of the Normal distribution () makes the prior diffuse without the need for heavy tails that the distributions allow. In this case, the Normal distribution and the t‐distribution result in similar posterior distributions for the parameters, but the Normal distribution achieves somewhat better model convergence.
RCT‐specific treatment effect
-
The RCT‐specific effects are denoted by . The prior distribution for the effect is centered on the control‐type effect associated with that RCT. The variation across RCTs (within each control type)— in the prior distribution—is a hyperparameter that will be estimated.
Between‐RCT variation
-
The variation across RCTs will be estimated using an informative prior distribution . The distribution with has wider tails than the slightly more informative distribution.
Control‐type effect
-
The prior distribution for the effects associated with different control conditions ( for efficacy and for safety) are centered on the pooled efficacy treatment effects and for the two components of the primary outcome, and on the overall safety treatment effect , respectively. The three types of control (standard of care, saline and non‐CP) are not expected to differ greatly from each other. Thus, we impose an informative prior with narrow tails.
Pooled treatment effects
-
In order to be conservative with respect to the efficacy analysis and to maintain desired operating characteristics of the model, we impose a skeptical prior on the pooled treatment effects and that are centered around 0. The of the Normal priors for the 's (on the log‐odds ratio scale) corresponds to a prior for the efficacy odds ratio with 95% of the density between 0.5 and 2. With this postulated skeptical prior we ensure that only large amount of information and strong evidence can alter the prior belief.
With respect to safety analysis, we want the flexibility to act as soon as even relatively weak evidence for safety concerns arises. Therefore, we use a diffuse prior for the pooled treatment effect on safety , namely .
4.2. Secondary efficacy analyses
Several secondary analyses are planned; see Section 4.4. Here we outline the analytic principles for investigating interactions between treatment and a prespecified covariate and the investigation of the effect of the quality and quantity of the CP on its efficacy, by reporting the planned analysis for addressing these specific questions.
4.2.1. Effect of duration of COVID‐19 symptoms prior to CP transfusion
The clinical understanding of the mechanisms of action of CP indicate that transfused antibodies should be most useful when administered soon after a patient is infected but before the patient's autoimmune system has had time to react while the virus is potentially taking hold. Thus, the effect of duration of symptoms prior to treatment with CP is of high importance, because knowledge of this feature could improve clinical practice. The COMPILE study collects information on duration of symptoms in the format of an ordinal variable, because patients are often uncertain about the precise onset of their symptoms: 0 to 3 days, 4 to 6 days, 7 to 10 days, 11 to 14 days, and 14 days. To explore the impact of symptom duration on the CP effect on the WHO 11‐point score, we will develop an extended version of the models described for the primary outcomes (Section 4.1). The extended version of the models will include RCT‐specific treatment by symptom duration interaction parameters , that are assumed to be normally distributed with a control‐type mean . In this model, there is an indicator variable that equals 1 if the duration of symptoms for the ith patient in the kth RCT falls in duration stratum s, and is 0 otherwise.
The extended version of the Bayesian model (1) is as follows:
| (3) |
The pooled effect of CP (on the log‐odds scale) across all RCTs for patients with symptom duration s will be . In this exploratory analysis, we will estimate the posterior probability for at each level of s to identify subgroups that might warrant further study.
Model (2) for the binary component of the primary outcome will be extended in a similar way to evaluate the interaction between treatment and duration of symptoms. Similar models will be employed to evaluate the interactions between treatment and sex, age, and baseline clinical status (measured by WHO 11‐point scale) on the primary and secondary outcomes.
4.2.2. Effect of donor CP antibodies on the efficacy of CP
The primary analysis of COMPILE will address the question whether treatment with CP (yes/no) is efficacious against any control treatment (standard of care, non‐CP or saline). The statistical models to address this primary question are discussed in Section 4.1. A second and equally important question that COMPILE aims to address is whether the quantity of CP that was transfused and/or the amount of antibodies in the CP matters and if so, how the quantity of CP and/or the amount of antibodies are related to the efficacy of treatment with CP. There are several ways to characterize the quality and quantity of CP. First, CP for transfusion comes in standardized units of sizes 250‐300ml and the CP treatment in the RCTs is indicated by the number of units. For example, RCTs collaborating in COMPILE used 1, 2, or 4 units of CP. Second, in order for a sample of plasma to be considered convalescent for SARS‐CoV‐2, it must contain a certain amount of anti‐SARS‐CoV‐2 antibodies. While guidelines regarding which measurement platforms should be used to assess the potency of the CP are beginning to emerge, RCTs across the globe have used different platforms that sometimes measure different types of antibodies. The COMPILE Antibodies Subcommittee conducted an investigation to enable conversion of measurements of antibodies obtained on different platforms in the different RCTs to a uniform scale. The Subcommittee recommended that the CP levels be classified into two groups – one reflecting low levels (ie, levels that are expected to be insufficient) or a second reflecting levels of antibodies that are not low. The third and most rigorous approach for assessing the effect of antibody levels on the efficacy of CP is based on measurements of antibody titer in samples from all transfused CP units performed on the same platform. Samples from almost all transfused CP units are preserved in all clinical trials. Obtaining those measurements requires coordination that will take time, but this will provide the most definitive answer to the question. In the meantime, we will use the measures described in the first two options as a surrogate for the actual antibody titers from the third option. Below is the proposed analytic model that assumes that treatment is scored on a 3‐point scale according to the second alternative:
zero antibodies – subjects randomized to the control condition in the RCTs will be considered to have received this level of treatment;
low‐level antibodies – subjects in the CP arm of the RCTs who received CP classified as low level according to the scale proposed by the Antibodies Subcommittee;
not low‐level antibodies – subjects in the CP arm of the RCTs, who received CP classified as not low level according to the scale proposed by the Antibodies Subcommittee.
Just as in the primary outcome model (1), the outcome is the WHO 11‐point score at Day 141. The observed data are , the individual WHO score for the ith patient in the kth study; is a vector of covariates as in the previous models, and takes a value of 0, 1, or 2, depending on the level of antibodies. For those randomized to the control condition, .
For the purposes of addressing the specific question about the effect of the amount of antibodies, all control conditions are considered the same, because the amount of antibodies received by the patients in the control arms is zero. In the model below, the cumulative odds for patients receiving zero antibodies will be reflected in , the study‐specific baseline log cumulative odds. The following model is proposed for the evaluation of the amount of antibodies in the CP:
| (4) |
If it is possible to measure the antibodies on a single platform so that the measures across RCTs (or a subset of RCTs) are directly comparable, we could extend the model further to include a continuous exposure :
4.3. Tertiary efficacy analyses
Mortality and time to hospital discharge
-
The tertiary outcomes will include overall mortality (time to death) and time to hospital discharge. The analysis of overall mortality will be based on a (frequentist) log‐rank stratified by RCT. Cox proportional hazards models will be employed to adjust for the covariates in the comprehensive covariates list (age, sex, etc.) and to evaluate interactions of baseline characteristics with treatment. The proportional hazards assumption will be evaluated using the method of cumulative martingale residuals. 31
Time to discharge (also to be analyzed using frequentist methods) is defined as the duration from randomization to hospital discharge to home, acute, or long‐term care facilities. Death before discharge is a competing risk event that precludes a successful discharge and thus will be properly accounted in the analysis of time to discharge. Gray's test 32 will be used to compare the subdistribution hazards (cumulative incidence function, CIF) of time to discharge between treatment groups. The Fine‐Gray regression model 33 will be employed to estimate treatment effect on the CIF adjusting for the comprehensive list of covariates.
Precision medicine analysis
-
A very important question for patients, clinicians, and researchers is to determine what are the patient characteristics associated with the greatest benefit from treatment with CP. These questions can be addressed using precision medicine methodology. We will employ existing and newly developed methodologies to identify biosignatures for response to CP treatment. Biosignatures are patient characteristics, or more likely combination of such characteristics, that are associated with heterogeneity of treatment effect. In its simplest form, a biosignature is a continuous variable (eg, a linear combination of baseline patient characteristics) that has a strong (large in magnitude, significant) interaction with the treatment indicator in the model for the outcome. 34 , 35 The methodologies developed for discovery of such biosignatures for treatment response fall under the rubric of developing optimal treatment decision rules; based on what is known about the patient at the time of treatment decision making, the goal is to give a particular treatment only to patients who are likely to benefit. Precision medicine is a highly active area of research, and new approaches are constantly being developed to address ever more complex clinical circumstances. 36 , 37 , 38 , 39
4.4. Summary of efficacy analyses
Table 2 provides a schematic representation of all the analyses that we plan to conduct for five outcomes: WHO score at day 14 1, WHO score at day 28 2, mortality at day 14 1, mortality at day 28 2, and time to discharge. Stopping rules for efficacy will be based on the noninteraction models of the bivariate primary outcome WHO score at day 14 1 and WHO score 7‐10 (yes/no); the treatment comparison is any CP vs Control = 1, 2, and 3. Stopping COMPILE for efficacy will be considered if both primary endpoints are met (see Section 4.6).
TABLE 2.
Planned analyses
| Interaction models | ||||||
|---|---|---|---|---|---|---|
| Description | Day | Adjustment | Age | Sex | Symptoms duration | WHO baseline |
| Primary analysis: comparison of CP vs Control (3 types) | ||||||
| 1. WHO score: cum. prop. OR | 14 | Parsimonious | x | x | x | x |
| 2. WHO 7‐10 (yes/no) | 14 | Parsimonious | x | x | x | x |
| Secondary analyses: comparison of CP vs Control (3 types) | ||||||
| 3. WHO score: cum. prop. OR | 14 | Expanded | x | x | x | x |
| 4. WHO 7‐10 (yes/no) | 14 | Expanded | x | x | x | x |
| 5. WHO score: cum. prop. OR | 28 | Expanded | x | x | x | x |
| 6. WHO 7‐10 (yes/no) | 28 | Expanded | x | x | x | x |
| Tertiary analyses: comparison of CP vs Control (3 types) | ||||||
| 7. All‐cause mortality (yes/no) | 14 | Expanded | x | x | x | x |
| 8. All‐cause mortality (yes/no) | 28 | Expanded | x | x | x | x |
| 9. Time to discharge | Expanded | x | x | x | x | |
| Tertiary analyses: dose‐response (comparison of no CP vs different number of CP units or levels of AB) | ||||||
| 10. WHO score: cum. prop. OR | 14 | Expanded | x | x | x | x |
| 11. WHO 7‐10 (yes/no) | 14 | Expanded | x | x | x | x |
| 12. WHO score: cum. prop. OR | 28 | Expanded | x | x | x | x |
| 13. WHO 7‐10 (yes/no) | 28 | Expanded | x | x | x | x |
| 14. All‐cause mortality (yes/no) | 14 | Expanded | x | x | x | x |
| 15. All‐cause mortality (yes/no) | 28 | Expanded | x | x | x | x |
| 16. Time to discharge | Expanded | x | x | x | x | |
Abbreviations: AB, antibodies; CP, convalescent plasma; RCT, randomized clinical trial; WHO, World Health Organization.
Parsimonious adjustment includes age, sex, WHO score at baseline, days since symptom onset and quarter when the patient was enrolled in the RCT.
Expanded adjustment also includes past medical history and concomitant medications at time of randomization.
4.5. Safety analyses
We propose monitoring for safety based on adverse events related to the transfusion of plasma. Specifically, we will compare the CP and control conditions with respect to the proportion of patients who experienced at least one of the following adverse events: (i) transfusion related acute lung injury (TRALI); (ii) transfusion associated circulatory overload (TACO); (iii) TRALI or TACO or COVID‐19‐related worsening symptoms—undifferentiated reaction (iv) arterial thrombotic event; or (v) venous thrombotic event.
We will use logistic regression models to evaluate the binary safety outcomes. Let be an indicator that the ith subject in the kth RCT experiences a transfusion‐related event. Similar to the consideration in Section 4.1, to accommodate the three different control conditions, we conceptualize the control conditions as three treatments to be compared against the reference condition (CP). The effects of the control conditions , on the transfusion‐related adverse events, will be denoted by , ; we will impose a hyper‐prior distribution for these three control effect parameters based on the assumption that they share the same prior distribution. The RCT‐specific log odds of having a severe transfusion‐related event in the CP arm, the reference group, will be estimated by , which corresponds to the kth trial's intercept. The following logistic regression model will be used to model Z:
| (5) |
The parameters of this logistic model mirror the parameters in the pimary outcome Model 2. The primary parameter of interest is , the pooled log‐odds ratio for an adverse event across all RCT's. Note that the prior for has a larger SD than the prior for the effect of the treatment () in Model (2). This prior for is considerably less skeptical and would allow for the posterior distribution to be largely determined by the data with smaller sample sizes. We take as the mean of the distribution to which belongs, so that will correspond to the difference of log‐odds for CP and log‐odds for control, rather than control minus CP.
4.6. Stopping guidelines
Stopping for efficacy
-
The primary analysis of the bivariate primary outcome—the WHO 11‐point ordinal scale at 14 days (1 day) and a binary indicator identifying if the WHO score at 14 days (1 day)—will be based on two models: the cumulative proportional odds model (1) for the first component and the logistic regression model (2) for the second component. In each model, the estimated log odds will be modeled as a function of a CP treatment indicator, the covariates, and the random effects for RCTs. Details about the analytic model and the initial priors were given in Section 4.1. The parameters of primary interest (the pooled treatment effects) in the cumulative proportional odds and logistic models (1) and (2) are and , respectively. We have proposed considerations for stopping the study based on the following posterior probabilities for the odds ratios (OR and OR):
and
When and , CP is more effective than control; we will require a very high level of certainty that this is the case. When and , it is considered that the beneficial effect of CP is more than trivial; we will require a moderate level of certainty that this is the case. The study will not be stopped unless all four criteria are met.
Stopping for harm
-
Stopping for harm will be based on the models used for the primary efficacy analyses (1) and (2). Evidence for harm due to CP will be based on the same odds ratios used in assessing evidence for efficacy. Observing odds ratios ( or ) that exceed 1 will indicate that CP is less effective than control (ie, CP is harmful). The stopping rule for harm is:
Note that the stopping rule for harm is much less stringent than the stopping rule for efficacy: the required level of certainty about possible harm is set at a lower threshold (0.80) than the level of certainty concerning efficacy (0.95); furthermore, it is sufficient if this lower level of certainty is satisfied with respect to only one of the bivariate outcomes, not both as in the case of assessing efficacy.
Stopping for safety
-
In the logistic regression model Section 5 for evaluating safety, described in Section 4.5, the parameter of interest (the overall CP effect on safety) is . We propose stopping for safety based on the posterior probability for the odds ratio (OR) of adverse events in the CP condition compared to the control condition (). The proposed stopping rule enforces considerations for stopping for safety reasons, even if only a relatively weak evidence for safety concerns is observed:
No stopping rules based on symptoms duration and donor CP antibodies
-
The COMPILE study does not have stopping rules based on the analysis of symptoms duraration and donor CP antibodies. At the end of COMPILE (due to either achieving one of the stopping criteria based on the primary analyses or if all studies have stopped recruitment and completed follow‐up) the posterior probabilities of from (3) and of from (4) will be used to make recommendations regarding the effect of symptom duration of the efficacy of CP and the therapeutic effects of CP with different levels of antibodies, respectively.
4.7. Practical measures to minimize bias
All interim analyses will be conducted by unblinded biostatisticians who are coordinating with the cDSMB. The cDSMB will review the results and make collective decisions. If there is a consensus among the cDSMB members that an action should be taken, a uniform recommendation will be passed to each of the individual RCT DSMBs. The recommendation will not be shared with the individual RCT teams or the IPD MA study team until there is a consensus among the cDSMB and the individual RCT DSMBs.
4.8. Documentation of interim analyses
Snapshots of the data available at each interim analysis will be preserved, as will all documentation of the analysis plans, programming code, and reports provided at each interim analysis. It will be possible to fully recreate the decision process from the trial archive at a time when any limitations of access to information by blinded statisticians becomes unnecessary.
5. DISCUSSION
This paper describes an innovative Bayesian design to pool data across multiple RCTs in order to rapidly test a treatment for COVID‐19 where the different trials share a common active treatment but where the control conditions can vary across trials. The development of this design was motivated by the critical need to find effective and safe treatments for COVID‐19 patients in the context of a global pandemic. This approach highlights the flexibility and power of adaptive Bayesian approaches, particularly with respect to the need to implement complex statistical models with varying degrees of hierarchy (eg, different RCTs and sites and control conditions). Additionally, the Bayesian approach lends itself naturally to multiple interim analyses that are critical in emergency situations such as the COVID‐19 pandemic.
This paper also discusses the numerous challenges of pooling IPD from unrelated RCTs in order to find answers faster during a global health crisis. An initiative such as the COMPILE consortium has not been undertaken previously and our experience in setting up, conducting, and reporting the results from the COMPILE study can be used to inform future such endeavors. While the this project was conceived during a humanitarian crisis, we hope that more general lessons can be learned; in particular, we hope that the good will among researchers around the globe exhibited in this initiative will persist, and that international collaborations such as COMPILE will continue to make medical research more generalizable and more efficient in non‐crisis situations.
As of the writing of this paper, there are eight RCTs from around the world collaborating in the COMPILE consortium, with data from over 1400 patients. The consortium is open for all RCTs of CP that include a target population of hospitalized patients with confirmed COVID‐19 who are not on mechanical ventilation at randomization. Discussions about collaboration are ongoing with several other RCTs that are at different stages of development—from just beginning recruitment to already fully completed.
CONFLICT OF INTEREST
The authors declare no potential conflict of interests.
ACKNOWLEDGEMENTS
The authors acknowledge E. Antman, MD and J. Hochman, MD, for their insightful ideas and guidance on developing the protocol for the COMPILE study. This work is supported by grant UL1TR001445 from NIH/NCATS (PI B. Cronstein).
A.1. Schema of COMPILE
Individual RCTs interested in participating in the COMPILE consortium sign a data sharing agreement. RCTs that have already ended agree to submit the MDS of variables for their patients who qualify for the COMPILE study, and to respond to questions from the data management and analysis teams until all queries are resolved. RCTs that are ongoing agree to submit the MDS for qualifying patients enrolled since the study start until the time of signing the Consortium agreement. They also agree to update the MDS every 2 weeks with new incoming patient data as well as to correct previously submitted data sets. The updating and submission of the evolving MDS continues until ether the RCT is stopped or the COMPILE study stops.
A secure FTP is provided for the submission of the MDSs, with individual passwords and folders for the individual RCTs. The data management and analysis teams update the COMPILE dataset and perform the analyses stated in the cDSMB Charter for review by cDSMB every 2 weeks.
The cDSMB, guided by the stopping rules spelled out in the Charter, makes recommendations to the RCTs' investigators. Upon recommendation by the cDSMB to terminate the COMPILE study, the investigators from the individual RCTs reserve the right to make their own decision regarding suspension their RCT. The PI of COMPILE in collaboration with the PIs of the participating RCTs prepares a manuscript for publication and submits to a venue mutually agreed upon by all PIs. After the main COMPILE manuscript is accepted for publication, the COMPILE database becomes available for use by investigators from the participating RCTs as well as external investigators after approval by the COMPILE Publications Committee and signing of a data use agreement. Approved investigators are given password‐protected access to a “toolbox” with a wide range of software for analysis and a “sandbox” where they can analyze the COMPILE data, without allowing the data to leave the secure platform.
FIGURE A1.
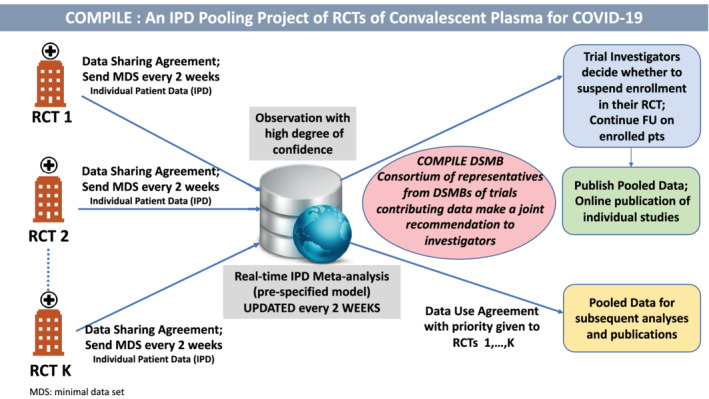
Schema of continuous monitoring of pooled international trials of experimental treatment for COVID‐19 hospitalized patients [Colour figure can be viewed at wileyonlinelibrary.com]
TABLE A1.
WHO 7‐points scale: inverted
| 1: | Not hospitalized without limitation in activity |
| 2: | Not hospitalized with limitation in activity |
| 3: | Hospitalized not on supplemental oxygen |
| 4: | Hospitalized on supplemental oxygen |
| 5: | Hospitalized on noninvasive ventilation or high flow nasal cannula |
| 6: | Hospitalized on invasive mechanical ventilation or ECMO |
| 7: | Death |
TABLE A2.
WHO 8‐points scale: inverted
| 1: | No clinical or virological evidence of infection |
| 2: | Not hospitalized without limitations on activities |
| 3: | Not hospitalized with limitation on activities |
| 4: | Hospitalized not on supplemental oxygen |
| 5: | Hospitalized on supplemental oxygen |
| 6: | Hospitalized on noninvasive ventilation or high flow nasal cannula |
| 7: | Hospitalized, on invasive mechanical ventilation or ECMO |
| 8: | Death |
TABLE A3.
WHO Conversion convention from the 7‐ and 8‐point scale to the 11‐point scale
| 7‐point | 8‐point | 11‐point |
|---|---|---|
| 1 (if no viral RNA detected) | 1 (if no viral RNA detected) | 0 |
| 1 (if asymptomatic) | 1 | 1 |
| 1 (if symptomatic, independent) | 2 | 2 |
| 2 | 3 | 3 |
| 3 | 4 | 4 |
| 4 | 5 | 5 |
| 5 | 6 | 6 |
| 6 (if pO2/FIO2 150 or SpO2/FIO2 200) | 7 (if pO2/FIO2 150 or SpO2/FIO2 200) | 7 |
| ‐ | ‐ | 8 |
| 6 (if pO2/FIO2 150 or SpO2/FIO2 200 or 6 (if pO2/FIO2 150 and vasopressors, dialysis, or ECMO) | 7 (if pO2/FIO2 150 and vasopressors, dialysis, or ECMO) | 9 |
| 7 | 8 | 10 |
TABLE A4.
Proportion of times (out of 2000) the stopping trigger was met under Bayesian and frequentist monitoring approach. The frequentist looks are happening less frequently that the Bayesian looks to limit spending. The stopping rules are Bayesian: and and and Frequentist: O'Brian‐Fleming approach with 5 data looks preserving overall , with the respective values at each look shown under the % information available
| Bayesian approach | O'Brian‐Fleming approach | ||||
|---|---|---|---|---|---|
| Information | % of simulation trigger met | Information | % of simulations | ||
| Effect |
|
||||
| 20% | 0.64 | 20%, | 0 | ||
| 33% | 0.2 | ||||
| 40% | 0.2 | 40%, | 0 | ||
| 50% | 0.39 | ||||
| 60% | 0.54 | 60%, | 0.2 | ||
| 67% | 0.39 | ||||
| 80% | 0.34 | 80%, | 0.25 | ||
| 90% | 0.25 | ||||
| 100% | 0.15 | 100%, | 1.23 | ||
| Type I error | Total | 3.1 | Total | 1.68 | |
| Effect |
|
||||
| 20% | 2.18 | 20%, | 0 | ||
| 33% | 3.77 | ||||
| 40% | 3.33 | 40%, | 0.2 | ||
| 50% | 2.73 | ||||
| 60% | 3.72 | 60%, | 2.28 | ||
| 67% | 2.58 | ||||
| 80% | 3.97 | 80%, | 5.36 | ||
| 90% | 2.98 | ||||
| 100% | 2.83 | 100%, | 8.24 | ||
| Power | Total | 28.09 | Total | 16.08 | |
| Effect |
|
||||
| 20% | 15.81 | 20%, | 0.1 | ||
| 33% | 22.13 | ||||
| 40% | 12.58 | 40%, | 7.88 | ||
| 50% | 12.68 | ||||
| 60% | 9.97 | 60%, | 29.91 | ||
| 67% | 4.91 | ||||
| 80% | 6.78 | 80%, | 28.13 | ||
| 90% | 4.28 | ||||
| 100% | 2.51 | 100%, | 17.85 | ||
| Power | Total | 91.65 | Total | 83.87 | |
A.2. Minimal dataset
Demographics and baseline clinical characteristics
-
Age
-
Sex
-
Blood group
-
Quarter of enrollment
-
Duration since symptoms onset at time of randomization
-
Days since COVID‐19 diagnosis at time of randomization
-
WHO clinical status score at randomization
-
Days from randomization to first transfusion (enter 0 for patients randomized to standard of care)
Medical history
-
History of diabetes
-
History of pulmonary disease
-
History of cardiovascular disease
Concomitant medications at randomization
-
Hydroxychloroquine
-
Antibacterial
-
Antiviral, not remdesivir
-
Remdesivir
-
Anti‐inflammatory, not steroids
-
Steroids
-
Antithrombotic
Potential transfusion‐related adverse events
-
Transfusion related acute lung injury (TRALI)
-
Transfusion associated circulatory overload (TACO)
-
Transfusion reaction other than TRALI and TACO
-
TRALI or TACO or COVID‐19 worsening symptoms – un‐differentiated reaction
-
Arterial thrombotic event
-
Venous thrombotic event
Outcomes
-
WHO score at day
-
WHO score at day
-
Days from randomization to discharge
-
Days from randomization to death
A.3. WHO clinical status scales
This appendix provides details on the 7‐ and 8‐points WHO ordinal outcome measures and the algorithm for converting those scales to the 11‐points scale version in Table 2.
A.4. Sample simulation studies
This section of the appendix addresses the issue of Type I error in the proposed statistical analysis and monitoring plan. We begin by stressing that the concept of P value is not relevant to the Bayesian framework, because P values assess the probability of the data given the null hypothesis, whereas the Bayesian approach evaluates the probability of a hypothesis given the data. One common feature of both Bayesian and frequentist monitoring guidelines is the probability that the study will be stopped early under each of the guidelines.
The total number of subjects in the COMPILE study could not be predicted and the exact number of interim looks could not be anticipated with any certainty. Using a range of assumptions, we compared the probability that a trigger for stopping would be reached under the proposed Bayesian analysis and under frequentist monitoring rules using the O'Brian‐Fleming approach.
The simulations performed to design the COMPILE study are important in their own right, and, because of their extensive volume, are a subject of another manuscript that we are preparing for publication. For illustration, we show here a brief comparison of the proposed stopping guidelines to one possible frequentist stopping rule, in one set of conditions for the number of RCTs, number of RCTs per control condition, sample sizes of the RCTs, and number of interim looks. In the example below, we use the cumulative odds model and the logistic model from the manuscript (Model 1 and Model 2), but without covariates.
Assumptions:
-
3 RCTs within each control type (standard of care, non‐CP, and saline solution)
-
–
1 large RCT with
-
–
2 small RCTs, each with
-
–
-
All RCTs are randomized in ratio 1:1 to CP vs control
-
O'Brian‐Fleming approach is with 4 interim and one final analysis at 20%, 40%, 60%, 80% and 100% of the data available
-
More frequent interim looks are assumed under the Bayesian paradigm at 20%, 33%, 40%, 50%, 60%, 67%, 80%, 90% and 100% information
-
Three sets of control‐specific treatment effects (as measured by for of the are considered
-
–(0,0,0), pooled effect on the scale is 0
-
–(0.1, 0.2, 0.3), pooled effect is 0.2
-
–(0.4, 0.5, 0.6), pooled effect is 0.5
-
–
Table A4 below shows the results.
When the simulated effect is , the sum of the probabilities of meeting the efficacy trigger at all interim looks under the Bayesian monitoring can be interpreted as a Type I error. When the efficacy of CP is simulated, the sum over all interim looks of the probabilities of meeting the Bayesian trigger for stopping for efficacy can be interpreted as power. The results show that the proposed analysis, including the priors and the stopping boundaries, conform with the conclusions that would be obtained under frequentist monitoring and analysis. This example shows the investigations that were done to study the operating characteristics of the proposed statistical plan for monitoring and analysis of the COMPILE study, and illustrates the materials that were discussed with our clinical co‐investigators concerned with Type I error.
Goldfeld KS, Wu D, Tarpey T, et al. Prospective individual patient data meta‐analysis: Evaluating convalescent plasma for COVID‐19. Statistics in Medicine. 2021;40:5131–5151. 10.1002/sim.9115
Funding information National Center for Advancing Translational Sciences, 3UL1TR001445‐05S3
DATA AVAILABILITY STATEMENT
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.
REFERENCES
- 1. Mullard A. COVID‐19 platform trial delivers. Nat Rev Drug Discov. 2020;19(8):501. [DOI] [PubMed] [Google Scholar]
- 2. Beigel JH, Tomashek KM, Dodd LE, et al. Remdesivir for the treatment of COVID‐19—final report. N Engl J Med. 2020;383(19):1813‐1826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Sterne JA, Murthy S, Diaz JV, et al. Association between administration of systemic corticosteroids and mortality among critically ill patients with COVID‐19: a meta‐analysis. JAMA. 2020;324(13):1330‐1341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Fiolet T, Guihur A, Rebeaud ME, Mulot M, Peiffer‐Smadja N, Mahamat‐Saleh Y. Effect of hydroxychloroquine with or without azithromycin on the mortality of coronavirus disease 2019 (COVID‐19) patients: a systematic review and meta‐analysis. Clin Microbiol Infect. 2021;27(1):19‐27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Petkova E, Antman EM, Troxel AB. Pooling data from individual clinical trials in the COVID‐19 era. JAMA. 2020;324(6):543‐545. [DOI] [PubMed] [Google Scholar]
- 6. Duan K, Liu B, Li C, et al. Effectiveness of convalescent plasma therapy in severe COVID‐19 patients. Proc Natl Acad Sci. 2020;117(17):9490‐9496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Shen C, Wang Z, Zhao F, et al. Treatment of 5 critically ill patients with COVID‐19 with convalescent plasma. JAMA. 2020;323(16):1582‐1589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Joyner MJ, Klassen SA, Senefeld J, et al. Evidence favouring the efficacy of convalescent plasma for COVID‐19 therapy. medRxiv; 2020. https://www.medrxiv.org/content/10.1101/2020.07.29.20162917v1. Accessed September 5, 2020.
- 9. Li L, Zhang W, Hu Y, et al. Effect of convalescent plasma therapy on time to clinical improvement in patients with severe and life‐threatening COVID‐19: a randomized clinical trial. JAMA. 2020;324(5):460‐470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Agarwal A, Mukherjee A, Kumar G, Chatterjee P, Bhatnagar T, Malhotra P. Convalescent plasma in the management of moderate COVID‐19 in adults in India: open label phase II multicentre randomised controlled trial (PLACID Trial). BMJ. 2020;371. https://www.bmj.com/content/371/bmj.m3939 Accessed September 15, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Simonovich VA, Burgos Pratx LD, Scibona P, et al. A randomized trial of convalescent plasma in COVID‐19 severe pneumonia. N Engl J Med. 2021;384(7):619‐629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Wooding DJ, Bach H. Treatment of COVID‐19 with convalescent plasma: lessons from past coronavirus outbreaks. Clin Microbiol Infect. 2020;26(10):1436‐1446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Caplan A. We don't know if convalescent plasma is effective against COVID‐19. with the emergency authorization, we might never know. STAT. 2020. https://www.statnews.com/2020/08/24/trump‐opened‐floodgates‐convalescent‐plasma‐too‐soon. Accessed September 23, 2020. [Google Scholar]
- 14. Bauchner H, Fontanarosa PB. Randomized clinical trials and COVID‐19: managing expectations. JAMA. 2020;323(22):2262‐2263. [DOI] [PubMed] [Google Scholar]
- 15.International convalescent plasma for COVID‐19 hospitalized patients pooling project: statistical modeling proposal; 2020. http://nyulmc.org/compile. Accessed September 5, 2020.
- 16. Jack Lee J, Chu CT. Bayesian clinical trials in action. Stat Med. 2012;31(25):2955‐2972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Pedroza C, Tyson JE, Das A, Laptook A, Bell EF, Shankaran S. Advantages of Bayesian monitoring methods in deciding whether and when to stop a clinical trial: an example of a neonatal cooling trial. Trials. 2016;17(1):1‐11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Berry SM, Carlin BP, Lee JJ, Muller P. Bayesian Adaptive Methods for Clinical Trials. Boca Raton, FL: CRC Press; 2010. [Google Scholar]
- 19. Saville BR, Connor JT, Ayers GD, Alvarez J. The utility of Bayesian predictive probabilities for interim monitoring of clinical trials. Clin Trials. 2014;11(4):485‐493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.WHO R&D blueprint novel coronavirus COVID‐19: therapeutic trial synopsis; February 2020. https://bit.ly/2RxJVq4. Accessed September 1, 2020.
- 21. Desai A, Gyawali B. Endpoints used in phase III randomized controlled trials of treatment options for COVID‐19. EClinicalMedicine. 2020;23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Marshall JC, Murthy S, Diaz J, et al. A minimal common outcome measure set for COVID‐19 clinical research. Lancet Infect Dis. 2020. https://www.sciencedirect.com/science/article/pii/S1473309920304837. Accessed July 5, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Goldfeld KS. Simulating multiple RCTs to simulate a meta‐analysis. ouR data generation; 2020. https://www.rdatagen.net/post/simulating‐mutliple‐studies‐to‐simulate‐a‐meta‐analysis. Accessed September 5, 2020.
- 24. Goldfeld KS. A Bayesian model for a simulated meta‐analysis. ouR data generation; 2020. https://www.rdatagen.net/post/a‐bayesian‐model‐for‐a‐simulated‐meta‐analysis. Accessed September 5, 2020.
- 25. Goldfeld KS. Diagnosing and dealing with degenerate estimation in a Bayesian meta‐analysis. ouR data generation; 2020. https://www.rdatagen.net/post/diagnosing‐and‐dealing‐with‐estimation‐issues‐in‐the‐bayesian‐meta‐analysis. Accessed September 5, 2020.
- 26. Goldfeld KS. Exploring the properties of a Bayesian model using high performance computing. ouR data generation; 2020. https://www.rdatagen.net/post/a‐frequentist‐bayesian‐exploring‐frequentist‐properties‐of‐bayesian‐models. Accessed September 5, 2020.
- 27. Goldfeld KS. Generating probabilities for ordinal categorical data. ouR data generation; 2020. https://www.rdatagen.net/post/generating‐probabilities‐for‐ordinal‐categorical‐data. Accessed September 5, 2020.
- 28. R Core Team R: a language and environment for statistical computing; 2013. https://www.R‐project.org/. Accessed July 8, 2020.
- 29. Stan Development Team Stan modeling language users guide; 2020. https://mc‐stan.org. Accessed July 8, 2020.
- 30. Stan Development Team Stan reference manual; 2020. https://mc‐stan.org/docs/2.25/reference‐manual/index.html. Accessed July 8, 2020.
- 31. Lin D, Wei L, Ying Z. Checking the Cox model with cumulative sums of martingale‐based residuals. Biometrika. 1993;80(3):557‐572. [Google Scholar]
- 32. Gray R. A class of K‐sample tests for comparing the cumulative incidence of a competing risk. Ann Stat. 1988;1141‐1154. [Google Scholar]
- 33. Fine JP, Gray RJ. A proportional hazards model for the subdistribution of a competing risk. J Am Stat Assoc. 1999;94(446):496‐509. [Google Scholar]
- 34. Petkova E, Ogden RT, Tarpey T, et al. Statistical analysis plan for stage 1 EMBARC (Establishing moderators and biosignatures of antidepressant response for clinical care) study. Contemp Clin Trials Commun. 2017;6:22‐30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Park H, Petkova E, Tarpey T, Ogden RT. A constrained single‐index regression for estimating interactions between a treatment and covariates. Biometrics. 2020. https://onlinelibrary.wiley.com/doi/full/10.1111/biom.13320. Accessed September 8, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Murphy SA. Optimal dynamic treatment regimes. J Royal Stat Soc Ser B (Stat Methodol). 2003;65(2):331‐355. [Google Scholar]
- 37. Qian M, Murphy SA. Performance guarantees for individualized treatment rules. Ann Stat. 2011;39(2):1180‐1210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Zhao Y, Zeng D, Rush AJ, Kosorok MR. Estimating individualized treatment rules using outcome weighted learning. J Am Stat Assoc. 2012;107(499):1106‐1118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Ciarleglio A, Petkova E, Ogden T, Tarpey T. Constructing treatment decision rules based on scalar and functional predictors when moderators of treatment effect are unknown. J Royal Stat Soc Ser C Appl Stat. 2018;67(5):1331. https://rss.onlinelibrary.wiley.com/doi/full/10.1111/rssc.12278. Accessed September 8, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.


