Abstract
In sequential analysis, hypothesis testing is performed repeatedly in a prospective manner as data accrue over time to quickly arrive at an accurate conclusion or decision. In this tutorial paper, detailed explanations are given for both designing and operating sequential testing. We describe the calculation of exact thresholds for stopping or signaling, statistical power, expected time to signal, and expected sample sizes for sequential analysis with Poisson and binary type data. The calculations are run using the package Sequential, constructed in R language. Real data examples are inspired on clinical trials practice, such as the current efforts to develop treatments to face the COVID‐19 pandemic, and the comparison of treatments of osteoporosis. In addition, we mimic the monitoring of adverse events following influenza vaccination and Pediarix vaccination.
Keywords: adaptive design, alpha spending, continuous monitoring, group sequential
1. INTRODUCTION
The regular practice for hypothesis testing is to conduct a single analysis based on a single data sample. Alternatively, with sequential hypothesis testing, one prospectively performs multiple hypothesis tests. Each test is performed when new data—that is, new observations—arrive, while guaranteeing the overall significance level by the end of the analysis.
The sequential approach is essential for many applications when it is urgent to reach a conclusion or decision, such as in post‐market medical product safety surveillance, or when it is unethical to continue a clinical trial when there is clear evidence of benefit or harm affecting one group.
Usually, the sequential analysis is based on monitoring a test statistic in comparison to a lower and an upper signaling threshold at each of the multiples sequential looks at the data. The sequential analysis is stopped as soon as the test statistic crosses one of the thresholds. Classical methods for sequential analysis are Wald's sequential probability ratio test (SPRT),1, 2 Pocock's test,3 O‘Brien‐Fleming's test,4 and Wang‐Tsiatis' method.5 For post‐market safety surveillance, recent methods are the maximized sequential probability ratio test (MaxSPRT),6 and the conditional MaxSPRT (CMaxSPRT).7
Instead of thresholds given in the scale of a test statistic, sequential testing can be based on alpha spending functions.8 The alpha spending function is a non‐decreasing function taking values in the interval, where is the significance level. Therefore, the alpha spending function dictates, in advance, the amount of Type I error probability to be spent at each of the multiple tests. This way, as an adaptive design, no matter the frequency at which the chunks of data arrive, or the cumulative sample size available at each test, the alpha spending function enables to find the thresholds accordingly.
Statistical performance evaluations and critical values calculations for sequential testing are usually obtained through asymptotic theory and/or normal distribution approximations.8 Recent developments have shown that exact calculations are possible for many applications.9, 10, 11 This is the approach of the present tutorial, which is devoted to offer practical examples on designing and conducting sequential hypothesis testing with binary and Poisson data. For this, we present step‐by‐step calculations accompanied with explanations on the underlying theory and proper interpretations of illustrative data analysis results.
The calculations for the illustrative examples are run with the R Sequential package.12 R Sequential is an easy‐to‐use tool for both the design and the practical implementation of sequential analysis. All calculations are exact, based on iterative numerical procedures, rather than using asymptotic theory, computer simulations, or normal distribution approximations.
For either Poisson or binary 0/1 data, this tutorial covers the following topics:
Data frequency: The number of new observations in each new data arrival does not have to be known a priori. We show how to perform sequential testing for continuous, group or mixed group‐continuous sequential analysis with unpredictable data frequency.
Probability model: For Poisson data, the expected counts may either be known or estimated from historical data with some uncertainty in the estimates. The binary model can be used for different studies where a dichotomous endpoint is monitored, including placebo‐controlled two‐arm clinical trials, self‐controlled designs, and matched cohort designs.
Alternative hypothesis: Unlike Wald's SPRT, here we use a composite alternative hypothesis. Both one and two‐tailed tests are supported.
Signaling thresholds: Signaling thresholds are calculated using Pocock's statistic, O‘Brien‐Fleming's statistic, Wang‐Tsiatis statistic, and Wald SPRT statistic, as well as any user specified alpha spending function. Conversely, we give examples on how to calculate the alpha spending implied by any of these test statistics.
Optimal alpha spending function: For a user‐specified alpha level, relative risk and statistical power, we exemplify the usage of alpha spending functions that minimizes expected time to signal or expected sample size. This is done for both with or without an added requirement on the maximum length of surveillance. The optimal solution is obtained using the method proposed by Reference 13.
Statistical performance metrics: Exact calculations are illustrated for statistical power, expected time of surveillance given that the null hypothesis is rejected, expected time of surveillance, and maximum maximum sample size. The latter three are calculated in the unit of sample size or number of events.
The content of this tutorial is organized in the following way: Next section presents definitions, notation and theoretical background that form the basis of this tutorial. Section 3 discusses planning and setting up sequential analysis testing according to pre‐experimental statistical performance measures such as maximum sample size, statistical power, expected time to signal and expected length of surveillance. Sequential analysis designing is discussed in light of well‐known test statistics (statistical measures of evidences) such as Wald's, Pocock's, O‘Brien‐Fleming's, and Wang‐Tsiatis' tests. In addition, Section 3 shows how to calculate and interpret flat and time‐variable signaling thresholds using the different test statistic scales. There, we also explain how to switch the calculations from these classical test statistic scales to the alpha spending scale, and vice‐versa. Section 4 presents four examples of sequential testing for the actual analysis in practice. The first example is based on simulated data with structure inspired by the recent placebo‐controlled two‐arm trials on treatments for COVID‐19 patients reported by References 14 and 15. The other three examples are based on real data for: (i) comparison of two treatments of osteoporosis by weighting five different adverse events in a propensity score matched cohort study, (ii) surveillance of neurological adverse events after Pediarix vaccination, and (iii) monitoring seizures after concomitant vaccination of inactivated influenza vaccine with 13‐valent pneumococcal conjugate vaccine. Section 5 contains the last comments and further software considerations.
2. EXACT SEQUENTIAL TESTING BACKGROUND
Let denote a discrete stochastic process indexed by continuous or discrete time. In essence, in this article is the cumulative number of events up to time . The distributions of interest in the present work involve: (i) the cases where is a positive integer, here also denoted by , and is the sum of Bernoulli outcomes with the success probability , , (ii) the cases where is a Poisson stochastic process with parameter , R, where is a known baseline rate under the null hypothesis, and (iii) is a Poisson stochastic process with parameter , unknown. Therefore, the parameter of interest is the relative risk (), and the underlying theory and results presented along this tutorial is applicable for any of the four pairs of hypotheses:
| (1) |
| (2) |
| (3) |
| (4) |
where , , and are specified by the user in advance. For the formats (1) to (3), a common choice is . Applications using for format (1) are relevant too. See, for example, the public master protocol for COVID‐19 vaccine active surveillance, by the U.S Food and Drug Administration (FDA).16 In that protocol, testing margin was settled through values of 1.25, 1.5, and 2.5, depending on the characteristics of each database.
The subset of the parameter space, implied by these hypotheses options under , shall be denoted simply by , where:
| (5) |
The relation of with the parametrization of the Bernoulli and Poisson probability models shall be further discussed in Sections 2.2, 2.4, and 2.5.
Conventionally, sequential testing methods consist of comparing a test statistic, say , against pre‐established signaling thresholds. The sequential testing concludes as soon as the test statistic reaches one of the thresholds. The thresholds are usually flat, such as with SPRT, MaxSPRT, Pocock's score test, and O'Brien & Fleming test, but time‐variable thresholds are used too, like those elicited with the alpha spending approach. In either case, group and continuous sequential testing designs can be defined in general as following.
Definition 1
(Group Sequential Analysis) For two sets of constants, , and , given in the scale of a test statistic, , and a sequence of times taken from the set , where is the maximum length of surveillance, also denoted by in the Bernoulli case, a group sequential analysis design is any procedure that ends the analysis for: (i) rejecting the null hypothesis if and for each , or (ii) failing to reject the null hypothesis if , or , and for each .
The rationale behind group sequential analysis is to perform tests only at pre‐defined times, where, if the maximum sample size is reached without a decision, then the maximum number of tests equals . Note that each test can have one or many events. In contrast, in continuous sequential design, outcomes arrive one‐by‐one, and a hypothesis test is performed after the arrival of each observation.
Definition 2
(Continuous Sequential Analysis) Let and denote real‐valued functions such that for each , where is also denoted by in the Bernoulli case, and let denote a test statistic. A continuous sequential analysis design is any procedure that ends the analysis for: (i) rejecting the null hypothesis if and for each , or (ii) failing to reject the null hypothesis if , or , and for each .
The classical Wald's SPRT is an example where both, upper and lower boundaries are used as in Definitions 1 and 2. In contrast, if the analysis is allowed to be concluded before time only under evidences against , such as with MaxSPRT and CMaxSPRT, then only and are used in the definitions above. Another possible situation, which has not received much attention in the literature, is that where only and are used. In such cases, the analysis is to stop before time only when evidences in favor of are found.
Definitions 1 and 2 are the so‐called ‘truncated’ designs, and this is so because they have a vertical threshold, . In practice, represents the maximum sample size (or maximum length of surveillance described in number of data observations that have accrued) for ending the analysis without rejecting the null hypothesis. Procedures without vertical thresholds are sometimes called "open‐ended designs."
For binary and Poisson counting data, as demonstrated by References 10, 11, and 13, the signaling thresholds can always be redefined in the scale of the original counting scale. For the pair of hypotheses in (1), the signaling threshold in the scale of is represented by an upper boundary, that is, is rejected for large values of . With the hypotheses in (2), is compared against a lower boundary, then is rejected for small values of . With the formats in (3) and (4), both large and small values of lead to rejection of .
It is important to emphasize that, for the formats (1) to (4), if the lower boundaries and are used to monitor , then the thresholds in the scale of are represented by inner boundaries, that is, one fails to reject for values consistently close to its average under .
2.1. Statistical performance measures
Three important statistical performance measures useful to compare and evaluate sequential analysis designs are: (a) statistical power, that is, the overall probability of rejecting the null hypothesis, (b) expected sample size, and (c) expected time to signal. While expected sample size is the average sample size when the analysis is stopped, irrespectively of the decision drawn about , the expected time to signal is a conditional expectation, defined as the average sample size when the null hypothesis is rejected. Although in practice group and continuous sequential methods are distinct in the matter of the number of looks at the data, theoretically we can establish a unified notation for these three statistical performance measures. As demonstrated by Reference 17, each group sequential design can be rewritten in terms of a continuous sequential design holding exactly the same statistical performance. Therefore, without lost of generality, these three metrics can be expressed using the notation for the continuous sequential design.
Let denote the number of events when the surveillance is interrupted. The statistical power is given by:
| (6) |
where is found by evaluating the very same expression (6) iteratively, for each , starting with , under the null hypothesis. That is:
| (7) |
The supreme in (7) is usually simple to evaluate for most of the probability distributions adopted in sequential analysis, and this is so because the probability argument in (7) is monotone with . Therefore, for hypotheses of the format in (1) to (3), the argument of the supreme is . For the format in (4), the argument that solves (7) is either or . This is valid for the probability models discussed in this article. Although the exact calculation can be performed by running a Markov Chain in , the specific analytical expression for the probability in (7), and so in (6), are somewhat intricate. For the detailed power functions in each case, we indicate expression (13) by Reference 11 for Poisson data, expressions (8) and (29) by Reference 13 for binary data, and expressions (16) and (22) by Reference 10 for conditional Poisson data.
The monotonicity of with respect to favors to find signaling thresholds and maximum length of surveillance in order to control the statistical power for target points of the parameter space. More precisely, for a target relative risk under , say , if a given sequential design leads to , then it holds that for each with the hypotheses in (1), or for each positive with the hypotheses in (2). Similarly, considering two target relative risks under , say and for (3), or and for (4), if and , then for each positive , and for each .
The expected time to signal, denoted by , is given by:
The expected sample size, denoted by , is given by:
Seeking a straightforward readability, the expected time to signal and the expected sample size will sometimes be referred through the acronyms ETS and ESS, respectively. Note that these two expectations are connected to each other, but the signaling thresholds that minimize and will usually differ. This topic shall be further discussed in Section 3.2.
2.2. Binary data
Binary data appears in many sequential analysis problems, such as for Simon's two‐stage group binomial sequential analysis,18 and placebo‐controlled two‐arm clinical trials, where patients exposed to a drug are compared with matched unexposed subjects. Let denote the number of exposed individuals in a total of subjects, and assume that
follows a Bernoulli distribution with success probability , for , and . In addition, are independent, that is,:
for arbitrary sequences . The Bernoulli probability is given by:
and denotes the matching ratio of the th observation. For instance, if there are controls matched to each case at the th test, then .
The Maximized Sequential Probability Ratio Test (MaxSPRT) statistic for the th observation, in the log‐scale, is given by:
where for the hypotheses in (1) to (3), and for the hypotheses in (4).
The subset of the parameter space under , , is defined according to (5), and is the maximum likelihood estimator of , which, in general, can be solved numerically for multiple different matching ratios over time. If the Bernoulli probability is fixed over time, that is, for each , then the MaxSPRT statistic simplifies to:
where the maximum likelihood estimator of is given by:
The MaxSPRT was specially developed for post‐market drug and vaccine safety surveillance, where the hypotheses are of the one‐tailed format in (1), and a flat upper signaling threshold, . That is, is rejected for the first such that , , otherwise, the analysis is finalized in favor of for . As demonstrated by Reference 6, for arbitrary significance level, , the exact can be calculated through an iterative numeric procedure by running a Markov Chain in the spirit of References 19, 20, 21.
The maximum likelihood estimator of can be solved numerically for multiple different matching ratios for both over time and within the same batch of data. This type of data frequently occur in post‐market drug safety surveillance, where matching or stratification variables are used for confounding control. The stratification variables create risk sets of comparable subjects. In these data sets, each record would include (1) a binary variable indicating whether the adverse event or outcome of interest was exposed to the treatment or comparator exposure and (2) the proportion of treatment group‐exposed patients in the risk set at the time the adverse event occurs. In this manner, the person‐time data that typically populate a stratified Cox proportional hazards regression model are the same data that populate what is known as a case‐centered logistic regression. The authors of Reference 22 showed that the models are mathematically identical and yield the same parameter estimates. In this manner, person‐time data can be treated as a sum of binary data and all of the functions described above can be used accordingly.
2.3. Multiple weighted binary endpoints
When there are multiple different outcomes, an important extension for binary sequential analysis is the possibility of considering weights reflecting practical interpretations, such as severity of different disease outcomes. For example, consider the case of two different outcomes, the first with weight , and the second with weight 1. That is, a single event of the first outcome would be equivalent to 2 independent outcomes of the second type. In general, if the first outcome type has weight and the second has weight 1, then the first would be considered times more severe than the second outcome type.
The authors of Reference 23 proposed a test statistic based on the weighted sum of the outcomes. For this, let , denote a sequence of ‐dimensional random vectors, where , with , and , for . Also, assume that is independent of for each or . To illustrate, suppose that a two armed sequential testing, where two groups, called exposure I and exposure II, are compared to each other. For the th test, counts the number of individuals from group I presenting the th endpoint. Therefore, is the total number of observations from endpoint accruing in the th test. The success probability is given by , where is the matching ratio between exposure I and exposure II with outcome , that is, is the probability of having an observation from exposure I presenting outcome . For example, if there are exposures I matched to each exposure II for endpoint , then .
For the th test, consider the test statistic defined as a composite endpoint, denoted by , constructed as a weighted sum of cumulative outcomes, that is:
| (8) |
where is the weight associated to the th outcome. Flat critical values in the scale of can be solved under arbitrary significance levels using numeric procedures.23 That is, is rejected for the first such that , where . Otherwise, the analysis is finalized in favor of for the first test such that .
2.4. Poisson data
Let denote the number of events up to the continuous time index, . Under , follows a Poisson distribution with mean , where is a known baseline function of . Under , is still Poisson, but now with mean . In this case, the MaxSPRT statistic, given in the log‐likelihood ratio scale, is given by:
where , for the hypotheses in (1) to (3), and for the hypotheses in (4).
The subset of the parameter space under , , is defined according to (5), and the maximum likelihood estimator of is given by:
The null hypothesis is rejected as soon as , with , where is the maximum sample size. For continuous sequential designs,6 shows that the exact critical value can be obtained by running a Markov Chain in the spirit of Reference 21. The solution by Reference 6 is also valid for group sequential analysis when observations are accrued following a fixed and common period of observation, which is the assumption behind the exact method by Reference 24 too. A generalized exact solution, valid for continuous, group or mixed continuous‐group sequential, including the applications where the periods of observations are unpredictable, was derived by Reference 11.
2.5. Conditional Poisson data for unknown baseline mean
The MaxSPRT statistic is a function of the data and of the Poisson rate under , . Therefore, MaxSPRT can be calculated only if is known. Otherwise, a conditional Poisson distribution can be used.7
Let denote the person‐time in the historical sample containing events, and let denote the cumulative person‐time observed until arrival of the th event during the surveillance period. As a consequence of the Poisson process, and for a known , follows a Gamma distribution with shape and scale .9 Likewise, for a known , follows a Gamma distribution with shape and scale . This way, the CMaxSPRT test statistic, in the scale of the log‐likelihood ratio, is given by:
where for the hypotheses in (1) to (3), and for the hypotheses in (4).
The subset of the parameter space under , , is defined according to (5). As derived by Reference 7, the maximum likelihood estimator of for each is given by:
The null hypothesis is rejected as soon as , with , where is the maximum sample size. Calculation of the exact , for arbitrary tuning parameters settings, is performed through numerical procedures.9
2.6. Minimum number of events before rejection of the null hypothesis
According to Reference 25, requiring a minimum number of events before allowing rejection of can reduce the expected time to signal. The idea is to establish a minimum number of events, say , in such a way that can only be rejected after having observed at least events after starting the analysis. Although all data observations affect the total sample size for the final decision, a decision against can only be taken after observing events or more. This approach provides gains in terms of expected time to signal. The authors of Reference 25 showed that, depending on the tuning parameters, values between 3 and 6 reduce the expected time to signal without affecting the overall statistical power of the sequential test. They also indicated that, in general, is a good choice.
2.7. Alpha spending
Usually, the approach for sequential testing is based on using signaling thresholds given in the scale of a test statistic. This is the case for both classical and new methods, such as the procedures of References 1, 3, 4, 6, 7, and 26. Alternatively, one can use an alpha spending function. Denoted by , it is a function that establishes the amount of Type I error probability to be spent at each time . For , four well‐known choices are:
Consider, for simplicity, that only the upper limit signaling threshold (), according to Definition 2, is used. Under a adaptive design, where data arrive with chunks of unpredictable sample sizes. Remind that denotes the number of events when the surveillance is interrupted, and is the maximum length of surveillance expressed in the scale of the number of events. For the th observed event, make . Note that with the Bernoulli data. The upper signaling threshold is elicited from the target alpha spending in the following way:
According to References 27, 28, 29, the power‐type function, , is useful to approximate Pocock's and O'Brien & Fleming's procedures. also approximates MaxSPRT designs. It produces a line for , a convex curve for , and a concave curve for . The authors of Reference 8 offers a detailed description on proper choices for in order to minimize expected time of surveillance for fixed power. values around 2, producing convex shapes, seems to provide small expected time of surveillance. If expected time to signal, instead of expected time of surveillance, is the target performance measure, then concave shapes () are more appropriate.11, 30 , is shown by Reference 31 to approximate O'Brien & Fleming's procedure.31 also explored in order to approximate Pocock's test. The results by Reference 31 were used by the authors of Reference 32 to derived exact calculations for discrete data. , introduced by Reference 33, is also a good option to mimic Pocock's test. As shown by References 11, 30, and , under concave curves, are more appropriate choices than and if minimizing expected time to signal is the meaningful design criterion for binomial and Poisson data. Instead, for conditional Poisson data10 show that a convex form for should be used, and that is a proper choice for most of the applications.
There are many proposed alpha spending functions in the literature. The authors of Reference 8 offer a rich overview and comparison of the most widely used functions.
As demonstrated by References 10, 11, and 13, methods based on signaling thresholds can always be rewritten in terms of an alpha spending function, but the reciprocal is not true. Therefore, the alpha spending approach is the most general for sequential analysis. The authors of Reference 13 derived the optimal alpha spending function for binomial data for a set of target performance measures, such as power, expected sample size, and expected time to signal. Their solution is obtained through linear programming.
3. SEQUENTIAL ANALYSIS PLANNING
For designing a sequential test procedure, it is often important to calculate statistical power, expected time to signal, expected sample size, and maximum sample size. As there are trade‐offs among these metrics, the sequential plan should be defined according to the design criterion of each application. For instance, for post‐market drug and vaccine safety surveillance, a large number of individuals are exposed to the drug/vaccine, then sample sizes are usually large even when the monitored event is rare. But, there is still the need for a fast identification of elevated threats from the drug, therefore minimizing the expected time to signal is a critical design criterion. Conversely, in Phase III clinical trials the number of individuals available for the study is usually of small or moderate magnitudes. Thus, minimizing the sample size by ending analysis early is of major importance since it applies that the number of affected individuals are minimized as well.
3.1. Sample size calculations with flat thresholds
Recall that the sequential analysis ends without rejecting when the sample size reaches a pre‐specified upper limit. Such upper limit must be defined in advance according to the desirable pre‐experimental performance measures. To show how this can be done in practice, we start with the conventional Wald's flat‐signaling threshold approach given in the scale of the log‐likelihood ratio. After defining the acceptable test size through the tuning parameter , the subset of the parameter space to form the null hypothesis (), and the size of the effect through the target power under meaningful points of , the next step is the calculation of the required sample size, .
3.1.1. Binomial data
For binomial data under a continuous sequential manner, Table 1 shows sample sizes calculated for testing under using , and power of 0.9 and 0.99 under and .
TABLE 1.
Sample sizes () with binomial data () for testing under for power = under and
|
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
Power | 0.25 | 0.5 | 0.75 | 1 | 2 | 3 | 4 | |
| 2 | 0.9 | 222 | 147 | 123 | 112 | 110 | 120 | 132 | |
| 2 | 0.99 | 373 | 245 | 212 | 194 | 192 | 216 | 238 | |
| 4 | 0.9 | 70 | 44 | 33 | 30 | 28 | 25 | 29 | |
| 4 | 0.99 | 113 | 73 | 57 | 53 | 46 | 47 | 50 | |
In practice, the number of events appearing during the sequential analysis is a portion of the total number of participants receiving the treatments, then one should plan the maximum length of surveillance according to a table, possibly with many other scenarios of , , and , in order to ensure a reasonable statistical power. For example, if a total of matched patients are randomized in two groups, say placebo and treatment groups, and if it is known that, under , around of the participants may present the monitored event, then the sequential procedure (with Wald's boundary) detects an increased relative risk of about 2 with power of 0.9 for values in between 1 and 2 (see the first line of Table 1). One may also evaluate the reverse, that is, based on the frequency at which the events occur under , one can obtain the minimum number of patients needed for detection of target relative risk, power, and alpha level. Evaluations like this are also important for determining the ratio for the number of placebo to treatment groups.
3.1.2. Poisson data
With Poisson data the predetermined upper limit on the sample size () is expressed in terms of the expected number of events under the null hypothesis. For instance, the sequential test may stop as soon as the cumulative sample size is such that there are at least expected events under . For a power of 0.9 and 0.99 with and for testing . Table 2 presents the related sample sizes (maximum length of surveillance) to comply with these performance requirements.
TABLE 2.
Sample sizes () with Poisson data for testing under for power = under and
|
|
Power |
|
||
|---|---|---|---|---|
| 2 | 0.9 | 18.32 | ||
| 2 | 0.99 | 32.83 | ||
| 4 | 0.9 | 2.77 | ||
| 4 | 0.99 | 5.29 |
If the baseline expected number of events () per test is unknown, one option is to use the CMaxSPRT test as described in Section 2.5. In this case, the sample size is expressed either in terms of the ratio of the cumulative person‐time in the surveillance population divided by the total cumulative person‐time in historical population (), or in terms of the number of events in the surveillance data (). For instance, the monitoring may end as soon as the sample size is such that the cumulative person‐time in the surveillance population is equal to the cumulative person‐time in historical population, or if there are 30 events in the surveillance data.
For testing , sample sizes in both scales are shown in Table 3 for selected numbers of events in the historical data.
TABLE 3.
Sample sizes in terms of the maximum length of surveillance by doses/person‐time (T) and by the cases in the surveillance data (), for powers of 0.9 and 0.99 under and
| Power | Power | |||||||
|---|---|---|---|---|---|---|---|---|
| c |
|
|
|
|
||||
| 50 | 66 | 0.79 | 290 | 3.89 | ||||
| 70 | 50 | 0.43 | 157 | 1.53 | ||||
| 100 | 43 | 0.25 | 96 | 0.65 | ||||
| 120 | 40 | 0.20 | 83 | 0.47 | ||||
| 150 | 38 | 0.15 | 73 | 0.33 | ||||
| 170 | 37 | 0.13 | 69 | 0.27 | ||||
| 200 | 36 | 0.11 | 64 | 0.21 | ||||
Naturally, in real data analysis the information may arrive in chunks of sizes greater than 1. But, the sample sizes in Tables 1, 2, and 3 still ensure the target power since group sequential testing is powerful than the continuous fashion under the same significance level.17 Section 4.3 presents a real data analysis to exemplify the usage of time specific alpha spending functions for preserving statistical power with unpredictable mixed group‐continuous data arrival structures.
3.2. Performance evaluations for arbitrary thresholds
For Poisson data with known baseline rates, suppose that one desires to test:
| (9) |
Consider the Wald's lower signaling thresholds 2.5, 2.6, 2.7, 2.8, and the upper signaling thresholds 3, 3.1, 3.2, 3.3, with expected number of events (group sizes) equal to 25, 20, 20, 25 (ie, ), respectively. Table 4 contains the performance measures of this very specific (non‐flat signaling threshold) sequential design.
TABLE 4.
Power, expected time to signal and expected sample size for Poisson data with known baseline rates using Wald's lower signaling thresholds 2.5, 2.6, 2.7, 2.8, and upper signaling thresholds 3, 3.1, 3.2, 3.3
|
|
Power | Expected time to signal | Expected sample size | |
|---|---|---|---|---|
| 0.3 | 0.978 | 25.000 | 26.402 | |
| 0.9 | 0.024 | 25.875 | 88.476 | |
| 1.0 | 0.022 | 41.019 | 88.932 | |
| 1.2 | 0.299 | 57.763 | 80.367 | |
| 1.5 | 0.965 | 42.791 | 44.451 |
Note: The expected number of events (group sizes) used are 25, 20, 20, 25 (ie, T = 90). The calculations were ran for .
Assume that one requires a statistical power of 0.9 for or . From Table 4, we see that this requirement is indeed satisfied since for and the powers are about 0.98 and 0.965, respectively. Note also that the type I error probabilities for values between 0.9 and 1 are smaller than 0.024. However, this is not a 0.024 level test because the type I error probability is close to 0.3 for . Therefore, the critical values should be conveniently modified in order to adjust the actual test size according to the nominal alpha level. A simplistic solution is to use the regular flat threshold approach again. For example, after checking a few scenarios, we found that the flat threshold promotes a 0.045 level test. But, the test no longer leads to power magnitudes greater than of 0.9 for around 0.3 and 1.5. Actually, the power is 0.662 for , and 0.782 for . This is an indication that a sample size greater than 90 is needed to satisfy the target power of 0.9.
The exercise above shows that guessing the signaling threshold is not an easy task as it demands to control desirable performance measures vis‐á‐vis the format of the hypotheses. A straightforward approach for planning non‐flat signaling thresholds is to use the alpha spending approach. In fact, the alpha spending function is a general method as virtually any sequential procedure can be rewritten in terms of an implicit alpha spending. For example, consider a twenty‐group sequential testing with test specific sample sizes all equal to 1 (ie, ). Using for testing , the critical values () in the scales of MaxSPRT, Pocock, OBrien‐Fleming, and Wang‐Tsiatis are 2.59, 2.83, 2.01, and 2.12, respectively. These critical values were obtained through a bisection procedure. The command lines are placed in the Appendix part.
Figure 1 shows the alpha spending curves for each test. We note that Wald's (MaxSPRT) and Pocock's alpha spendings are concave while O'Brien‐Fleming and Wang‐Tsiatis are convex. As illustrated with Table 5, such differences on the alpha spending shapes have critical implications in the pre‐experimental performance measures.
FIGURE 1.
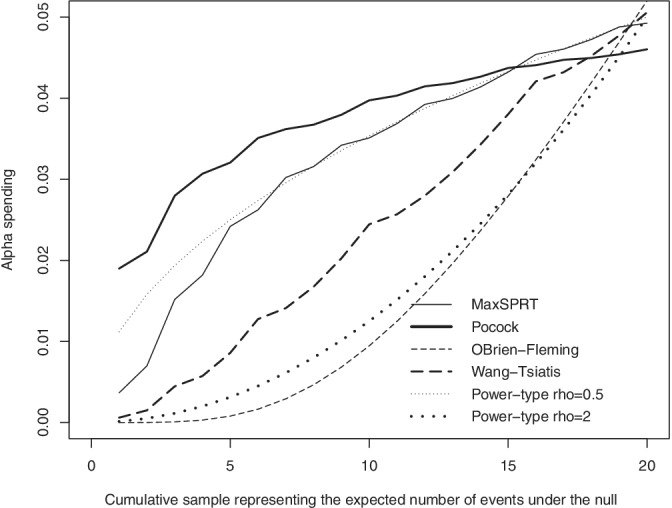
Alpha spending implied by flat signaling thresholds with Poisson data in the scale of MaxSPRT (), Pocock (), O'Brien‐Fleming (), and Wang‐Tsiatis () test statistics under and
TABLE 5.
Power, expected time to signal (ETS) and expected sample size (ESS) for MaxSPRT (), Pocock (), O'Brien‐Fleming (), and Wang‐Tsiatis () test statistics under and based on and samples of size 1
| MaxSPRT | Pocock | O'Brien‐Fleming | Wang‐Tsiatis | |
|---|---|---|---|---|
| Power | 0.95 | 0.93 | 0.98 | 0.97 |
| ETS | 7.06 | 7.10 | 9.41 | 7.91 |
| ESS | 7.68 | 8.06 | 9.66 | 8.28 |
According to Reference 11, for fixed power and level the expected time to signal is minimized with concave alpha spending shapes, while expected sample sizes are minimized with convex functions. The authors of Reference 11 showed that the power‐type family, function in (9), nearly‐minimizes expected time to signal with Poisson data for . But, for minimizing expected sample size,8 suggest that one should use around 1.5 or 2.
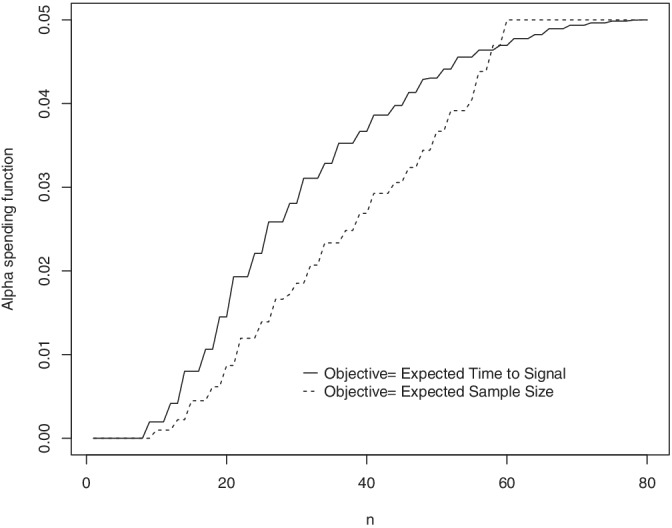
For a continuous sequential analysis, Figure 1 shows the power‐type alpha spending for and . Figure 2 shows the signaling thresholds, event‐by‐event, in the four test statistic scales elicited from these two choices of , and Table 6 shows the related statistical performance measures.
FIGURE 2.

Signaling thresholds for continuous sequential testing implied by the power‐type alpha spending with and for Poisson data in the scale of MaxSPRT, Pocock, O'Brien‐Fleming, and Wang‐Tsiatis test statistics under and .
TABLE 6.
Statistical performance measures by the power‐type alpha spending using under and based on in a continuous sequential fashion
| Performance measure |
|
|
||
|---|---|---|---|---|
| Statistical power | 0.95 | 0.97 | ||
| Expected time to signal | 6.90 | 8.48 | ||
| Expected sample size | 7.52 | 8.78 |
This way, no‐matter the frequency of the data arrival, the user can simply use the time‐specific alpha spending to calculate the critical value according to the actual amount of information (cumulative expected number of events under ) in hand. This type of unpredictable data frequency sequential testing shall be illustrated with real data in Section 4.4.
For the historical versus surveillance Poisson data (CMaxSPRT),10 suggest to use as it is near‐optimal in the sense of minimizing both expected time to signal and expected sample size in most of the real data applications.
3.3. Optimal sequential design for binomial data
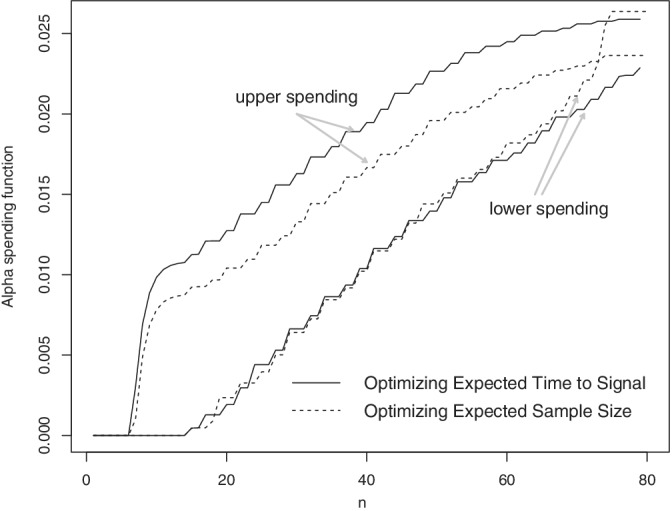
The alpha spending can be specified to optimize a performance measure of interest. For example, one can elicit the alpha spending shape that minimizes either the expected time to signal or the expected sample size. This is possible with the exact optimal solution introduced by Reference 13. For against , suppose that we want the alpha spending shape that minimizes the expected time to signal while guaranteeing statistical power of 0.8 for any relative risk greater than 2.
If we instead wish to minimize expected sample size. Figure 3 compares the optimal alpha spending solutions between these two different objective performance measures for , and . The optimal expected time to signal is 32.99, and the optimal expected sample size is 39.63. The optimal samples sizes are and , respectively. The curves in Figure 3 have different shapes. While the optimal expected time to signal is obtained under a concave alpha spending shape, the optimal expected sample size is reached with a convex alpha spending function.
FIGURE 3.
Optimal alpha spending shapes for expected time to signal and expected sample size under , , power equal to 0.8, and
For two‐tailed testing, that is, when the hypotheses are of the form against , one needs to specify two target powers, one to each of the two target relative risks under the alternative hypothesis. For example, suppose that we want to minimize expected time to signal, and both or should be detected with power of at least 0.8. Figure 4 shows the optimal alpha spending for two‐tailed testing under this parametrization.
FIGURE 4.
Two‐tailed optimal alpha spending shapes for expected time to signal and expected sample size under , , power equal to 0.8, and and
If there are restrictions on the sample size due to logistical, ethical and any other practical aspects, one can minimize expected time to signal and expected sample size while setting an upper bound on the maximum sample size. This is done through the input on the command line above. For example, for , if one wishes to minimize expected time to signal under a power of 0.8 for , , and , the optimal solution leads to a minimum expected time to signal equal to 40.00, which is greater than the minimum expected time to signal, 32.99.
The optimal solution proposed by Reference 13 also incorporates control on the precision of the relative risk estimate by the end of the sequential analysis through fixed‐width and fixed‐accuracy confidence intervals. This feature shall be exemplified with an illustrative clinical trial data in Section 4.1.
3.4. Schematics for sequential testing planning
This section presents a synthesis of the main decision directions, so far discussed in this article, for balancing the trade‐offs between statistical performance measures and the alpha spending plan. Such decisions are determinant to calculate the required sample size, that is, maximum length of surveillance.
The construction of a sampling design to collect the data takes in account ethical, logistical, and financial aspects. Concomitantly, the planning involves defining the hypotheses format, the overall alpha level, the target relative risk to detect under , and the target power. The data structure, and then the underlying probability model to be used in the inference phase, results from the sampling scheme as well.
Once the data probability model (eg, binary, Poisson, conditional Poisson) is identified/defined, which we refer to as step (A), the next step is to (B) establish the meaningful statistical metric to optimize between expected sample size and expected time to signal, then (C) select the alpha spending plan, and finally (D) elicit the maximum length of surveillance in compliance with the alpha level and target power.
The actual maximum length of surveillance to be calculated in step D depends on the format of the hypotheses, significance level, and target power. For instance, the diagram in Figure 5 illustrates this steps for testing:
with minimum number of events to start the surveillance equal to , , and target power of at least 0.9 for . Regarding the alpha spending shape, for this diagram we adopted the power‐type shape, that is, (see Section 2.7). By selecting the tuning parameter conveniently, the power‐type alpha spending works reasonably well to approximate the optimal alpha spending in each scenario.10, 11, 30 In order to emphasize the possible changes in the maximum length of surveillance, three values were used for , in the binary case, and for , in the conditional Poisson case. All the calculations for step D were based on the continuous sequential analysis scenario. This ensures that the actual performance in terms of significance level and statistical power satisfies the nominal requirements, no matter the real frequency at which the data arrives in each application.
FIGURE 5.
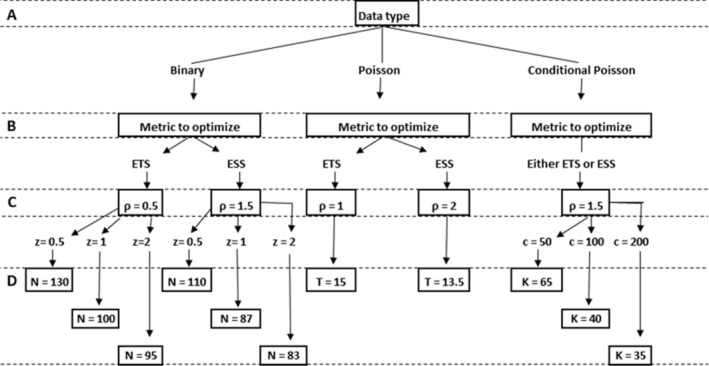
Diagram for setting a sequential analysis design for testing against under , , and target power of 0.9 for . For step C, values of the tuning parameter are selected to fix the power‐type alpha spending shape according to the performance metric to minimize between the expected time to signal (ETS) and the expected sample size (ESS)
Naturally, the sample sizes in step D will suffer considerable changes if any of the tuning parameters are different from those used in this example, such as the format of the hypotheses and the set of the parameter space under , and the target power.
It is important to note the key role of the alpha spending shape for the overall statistical performance of the sequential analysis. The values of , presented in step C of Figure 5, are offered as a rule of thumb, a summary of the results found in the literature on this topic. However, ideally, the alpha spending shape should be customized according to each application, where the trade‐offs appearing in the schematic presented here are confronted with the goals behind the design criterion/metrics to optimize, expected data frequency, or even intangible characteristics of each study.
4. DATA ANALYSIS EXAMPLES
4.1. Binomial data in placebo‐controlled two‐arm trial: monitoring adverse events in COVID‐19 studies
The efforts to develop treatments for COVID‐19 patients are urgent, therefore, important studies are currently in development in this direction. For example, the Adaptive COVID‐19 Treatment Trial (ACTT), detailed by Reference 14, is a randomized placebo‐controlled trial where intravenous remdesivir was administrated in 1062 adults hospitalized with COVID‐19. The individuals were randomly divided in two groups, where 541 were assigned to remdesivir, and 521 to the placebo group, then with a randomized ratio of . By the end of the analysis, the observed 131 severe adverse events from the remdesivir group and in 163 patients from the placebo group. We can also mention the study by Reference 15, where a randomized open‐label trial was conducted on hospitalized adult patients of SARS‐CoV‐2. A total of 199 individuals were randomly divided in two groups, 99 to the lopinavir‐ritonavir treatment, and the remaining 100 to the standard‐care group. In this case, . Severe adverse events were observed in 19 participants from the lopinavir‐ritonavir treatment, while 32 patients presented adverse events in the standard‐care group.
Using a data structure similar to that described by References 14 and 15, here we mimic a clinical trial for comparing two hypothetical treatments, say Treatment and Treatment . Then, suppose that a randomized double‐blind plan with randomized ratio is conducted to a total of patients. We want to test:
| (10) |
| (11) |
Aiming to minimize the number of patients affected by severe adverse events, the optimal alpha spending that minimizes expected sample size was used restricted to , and statistical power greater than or equal to 0.8 for either or . In addition, the optimal solution was constrained to a fixed‐width and a fixed‐accuracy confidence interval for with the following formats:
| (12) |
Figure 6 shows the optimal alpha spending solved according to the constraints above.
FIGURE 6.
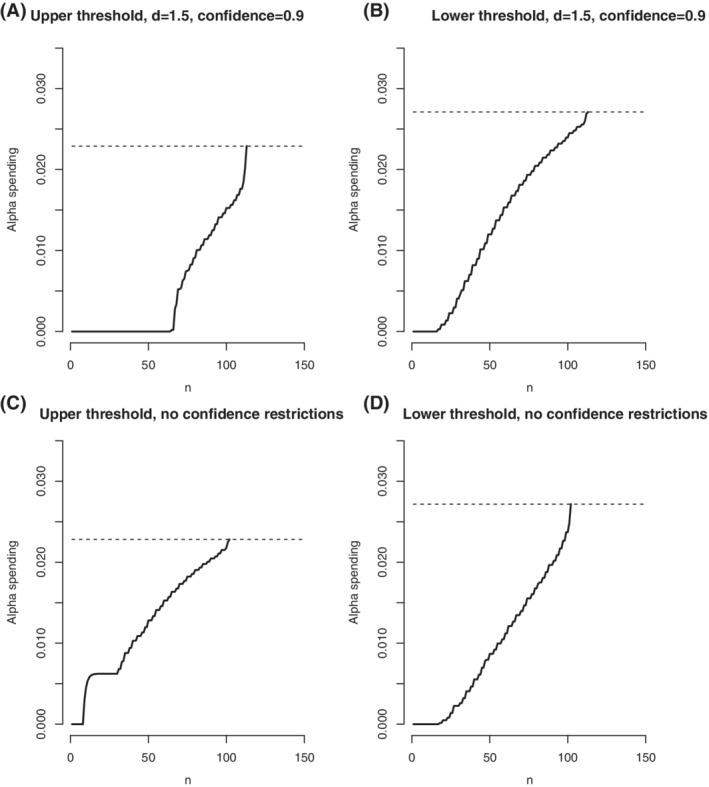
Optimal alpha spending minimizing expected sample size under , power for each and with hypothesis . Graphics A, and B, show the upper and lower cumulative alpha spending under fixed width and fixed accuracy confidence intervals, and graphics C, and D, shows the optimal alpha spending without confidence interval constraints for comparisons
In practice, patients may leave the study due to many different reason other the presenting adverse events. Therefore, the number of patients in each arm, here denoted by and at the th test, will decrease in time. For simulating this effect, a discrete uniform random variable in the support was subtracted in both arms for each test. The number of adverse events in each test () was generated using a , where . For the first test, we used . Finally, the adverse events from the Treatment group at the th test () were generated using a , where and , with under the alternative hypothesis.
The second and third columns of Table 7 present the number of patients in both Treatment and at each test. The lower and upper signaling thresholds, given in the scale of the number of events, are shown in columns 6 and 7 of Table 7. The number of adverse events from Treatment and the maximum likelihood estimates of are shown columns 8 and 9. We note that the null hypothesis is rejected in the 7th look since the number of events, 55, extrapolated the upper signaling threshold, 48. By construction, a confidence interval for is given by since and .
TABLE 7.
Analysis results on simulated randomized, double‐blind, placebo‐controlled trial for monitoring severe adverse events
| # Patients | cv |
|
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
Lower | Upper |
|
|
Rej. | |||||||
| 1 | 500 | 500 | 1 | 12 | na | 13 | 10 | 5 | No | |||||||
| 2 | 498 | 489 | 1.02 | 21 | 3 | 22 | 15 | 3.16 | No | |||||||
| 3 | 494 | 484 | 1.02 | 30 | 7 | 31 | 21 | 2.75 | No | |||||||
| 4 | 490 | 478 | 1.03 | 41 | 12 | 42 | 30 | 2.77 | No | |||||||
| 5 | 486 | 468 | 1.04 | 52 | 16 | 47 | 36 | 2.61 | No | |||||||
| 6 | 479 | 462 | 1.04 | 65 | 22 | 47 | 45 | 2.52 | No | |||||||
| 7 | 475 | 451 | 1.05 | 75 | 26 | 48 | 55 | 2.61 | Yes | |||||||
| 8 | 474 | 440 | 1.08 | 78 | 27 | 50 | 57 | 2.67 | Yes | |||||||
| 9 | 473 | 437 | 1.08 | 89 | 32 | 56 | 64 | 2.69 | Yes | |||||||
| 10 | 468 | 429 | 1.09 | 100 | 37 | 61 | 70 | 2.67 | Yes | |||||||
| 11 | 462 | 423 | 1.09 | 112 | 42 | 67 | 77 | 2.62 | Yes | |||||||
The critical values in this example were elicited from the optimal alpha spending shown in Figure 6, and the relative risk estimates were obtained with the command lines in the Appendix.
4.2. Multiple weighted binomial outcomes in propensity score matched patients: comparing two treatments of osteoporosis
The authors of Reference 23 applied the alpha spending approach to formulate a new methodology for monitoring multiple types of adverse events that are comparable through pre‐specified weights. They used real data to illustrate their method for five different outcomes with the following weights: hip and pelvis fracture (), forearm fracture (), humerus fracture (), serious infection (), and pneumonia (). They mimicked a sequential testing for comparing 9340 patients treated with denosumab to 9340 propensity score matched patients who initiated bisphosphonates for treatment of osteoporosis, therefore . The goal was testing:
where is the relative risk associated to the th type of adverse event.
Table 8 was extracted from Reference 23. It contains the cumulative sample size at each test in each of the five endpoints (columns 1 to 5), and the test statistic in column 6, denoted by , which is the ratio of exposure to exposure weighted sums, where exposure is for denosumab treatment and exposure is for bisphosphonates treatment. The lower and upper critical values, given in the scale of , are shown in columns 7 and 8. This table can be reproduced with the command lines shown in the Appendix:
TABLE 8.
Sequential analysis results for the data of treatment of osteoporosis
| Cumulative data per outcome | cv | |||||||
|---|---|---|---|---|---|---|---|---|
| H‐p frac. | F. frac. | H. frac. | Infec. | Pneum. |
|
Lower | Upper | |
| 0 | 0 | 0 | 1 | 0 | inf | na | na | |
| 1 | 2 | 0 | 5 | 3 | 1.68 | 0.05 | 19.75 | |
| 2 | 7 | 0 | 6 | 7 | 1.22 | 0.17 | 5.84 | |
| 3 | 9 | 1 | 10 | 10 | 0.94 | 0.25 | 3.96 | |
| 6 | 13 | 1 | 14 | 14 | 0.65 | 0.34 | 2.98 | |
| 10 | 17 | 1 | 20 | 16 | 0.69 | 0.39 | 2.54 | |
| 12 | 21 | 1 | 26 | 21 | 0.58 | 0.44 | 2.28 | |
| 15 | 29 | 1 | 28 | 27 | 0.55 | 0.48 | 2.09 | |
| 20 | 32 | 2 | 37 | 32 | 0.70 | 0.52 | 1.92 | |
| 23 | 44 | 4 | 48 | 43 | 0.76 | 0.58 | 1.73 | |
| 26 | 57 | 6 | 59 | 55 | 0.66 | 0.62 | 1.62 | |
| 32 | 72 | 8 | 79 | 60 | 0.74 | 0.66 | 1.52 | |
Note: The outcomes are Hip and pelvis fracture (), forearm fracture (), humerus fracture (), serious infection (), and pneumonia (). It was settled a maximum length of surveillance of . The overall significance level used was , with power‐type alpha spending . The critical values (cv) are shown in the scale of the test statistic given by the ratio between weighted sums from expose A to exposure B populations ().
As the test statistic stayed in between the lower and upper signaling thresholds during the sequential monitoring, the empirical information suggests that treatments and do not differ in terms of the risks of these five adverse events.
4.3. Poisson data in exposure‐outcome pairs: monitoring neurological adverse events after Pediarix vaccination
This example uses the data of neurological adverse events after Pediarix vaccination from the Kaiser Permanente Northern California. With a single injection, Pediarix protects children from diphtheria, tetanus, whooping cough, hepatitis B, and Polio. The authors of Reference 6 used continuous MaxSPRT to analyze severe neurological symptoms in the period 1‐28 days after the vaccination. Table 9 presents the data for the first 10 weeks out of 81 weeks of surveillance.
TABLE 9.
Sequential analysis results for the first 10 weeks of surveillance of neurological adverse events after Pediarix vaccination
| Test specific | Cumulative | Alpha spending | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Week |
|
#Events |
|
#Events | cv |
|
Target | Actual | |||
| 1 | 0.04 | 0 | 0.04 | 0 | na | 1 | 0 | 0 | |||
| 2 | 0.06 | 1 | 0.10 | 1 | 3 | 10 | 0.0035 | 0.0015 | |||
| 3 | 0.08 | 0 | 0.18 | 1 | 3 | 5.56 | 0.0047 | 0.0017 | |||
| 4 | 0.10 | 0 | 0.28 | 1 | 3 | 3.57 | 0.0059 | 0.0020 | |||
| 5 | 0.11 | 0 | 0.39 | 1 | 3 | 2.56 | 0.0070 | 0.0056 | |||
| 6 | 0.12 | 0 | 0.51 | 1 | 4 | 1.96 | 0.0080 | 0.0060 | |||
| 7 | 0.13 | 0 | 0.64 | 1 | 4 | 1.56 | 0.0089 | 0.0074 | |||
| 8 | 0.12 | 1 | 0.76 | 2 | 5 | 2.63 | 0.0097 | 0.0075 | |||
| 9 | 0.11 | 0 | 0.87 | 2 | 5 | 2.3 | 0.0104 | 0.0080 | |||
| 10 | 0.12 | 0 | 0.99 | 2 | 5 | 2.02 | 0.0111 | 0.0089 | |||
Note: The critical values (cv) are given in the scale of the cumulative events and were settled under a maximum length of surveillance of and based on the alpha spending implied by MaxSPRT, .
The second column of Table 9 contains the background rate () of adverse events under the null hypothesis (). From this table, we see that was not rejected until the 10th test. If more data are entered in the function for subsequent chunks of data, it will run and disclose the regular output table. Figure 7 shows realized and signaling thresholds in both the cases and the MaxSPRT scales. Note how irregular are the shapes of the thresholds as the testing time evolves. The observed empirical information reached the signaling threshold in the 32th test. This signal occurred when the total amount of information reported a relative risk estimate about 2.5.
FIGURE 7.
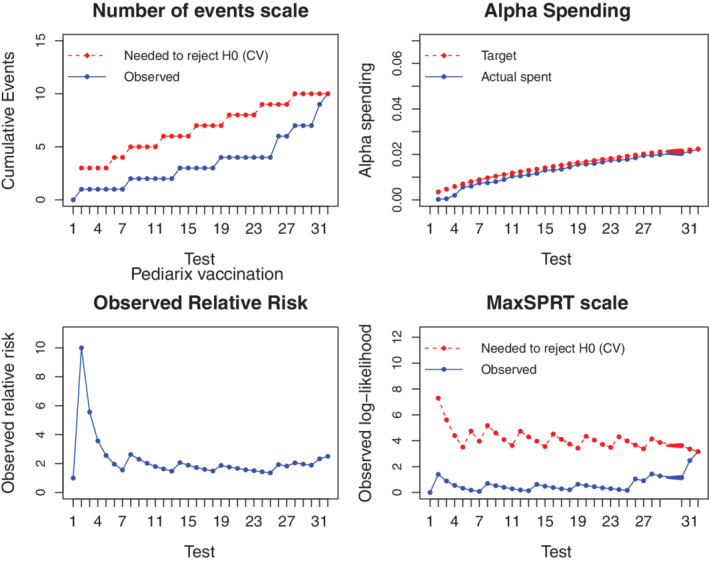
Critical values, observed data and alpha spending in the first 32 sequential tests for monitoring neurological adverse events after Pediarix vaccination. The critical values were settled under a maximum length of surveillance of and based on the alpha spending implied by MaxSPRT, . Evidences for rejecting the null () occurred in week 32 [Colour figure can be viewed at wileyonlinelibrary.com]
4.4. Conditional Poisson in historical versus surveillance data: monitoring seizures after influenza vaccination
This last example uses a time‐series of seizures during Days 0‐1 after application of concomitant vaccination with inactivated influenza vaccine (IIV) and 13‐valent pneumococcal conjugate vaccine (PCV‐13). The fifth column of Table 10 contains the cumulative number of doses applied to 6‐23‐month‐old children in the period of September 2013 to April 2014. The sixth column of this table contains the cumulative number of individuals presenting seizures in the surveillance period. This data has already been used by,10 and it come from three large U.S. health insurance or data companies (‘Data Partners’) participating in the U.S. Food and Drug Administration‐sponsored Sentinel system. See Reference 34 for more details about the Sentinel system.
TABLE 10.
Sequential analysis results for the surveillance of seizures after influenza vaccination
| Test specific | Cumulative | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Chunk |
|
#Events |
|
k |
|
LLR | cv |
|
||||
| 1 | 3877 | 0 | 3877 | 0 | na | na | na | na | ||||
| 2 | 3211 | 0 | 7088 | 0 | na | na | na | na | ||||
| 3 | 1 | 0 | 7089 | 0 | na | na | na | na | ||||
| 4 | 25975 | 1 | 33064 | 1 | 0.04 | 0 | 6.49 | 0.62 | ||||
| 5 | 8 | 0 | 33072 | 1 | 0.04 | 0 | 6.49 | 0.62 | ||||
| 6 | 34760 | 5 | 67832 | 6 | 0.09 | 0.77 | 3.31 | 1.80 | ||||
| 7 | 18497 | 3 | 86329 | 9 | 0.12 | 1.75 | 2.89 | 2.12 | ||||
| 8 | 173 | 0 | 86502 | 9 | 0.12 | 1.56 | 2.89 | 2.12 | ||||
| 9 | 17573 | 3 | 104075 | 12 | 0.14 | 2.81 | 2.45 | 2.35 | ||||
| 10 | 12058 | 0 | 116133 | 12 | 0.15 | 2.34 | na | 2.10 | ||||
Note: With a historical person‐time information of (doses) and adverse events in the historical period, the critical values (cv) are given in the scale of the log‐likelihood ratio (LLR) statistic. The maximum length of surveillance is under a power‐type alpha spending () with .
The authors of Reference 34 used Poisson MaxSPRT, with flat signaling threshold, based on the expected number of seizures estimated with the Data Partner‐specific rates related to IIV vaccination in historical influenza seasons. In a different direction, instead of using estimated rates as if it is the real rate under , here we use the conditional Poisson approach described in Section 2.5. For this application, the cumulative number of doses reflects the person‐time () for a given number of observed events (seizures). The time‐specific person‐time is denoted by , with . The historical information is composed by events in days 0‐1 after doses of IIV prior to licensure of PCV13.
We want to test if the relative risk is smaller than or equal to 1 (null hypothesis). Consider to setup the maximum length of surveillance as . It is important to check the pre‐experimental statistical performance resulting from this sample size choice. Using the power‐type alpha spending () for learning evidences of , we obtain a statistical power about 0.85, expected time to signal of 12.18, and expected length of surveillance equal to 13.35.
Note from the third column of Table 10 that new adverse events arrived in the surveillance period only in chunks 4, 5, 6, 7, and 9. Although one can revert the random variable taken the person‐time as the amount of information and the related number of events as the monitored random measure of evidence,9 hence the log‐likelihood ratio statistic can still be calculated even when no new adverse events arrives, that would never lead to the null hypothesis rejection since the likelihood decreases when the relative person‐time increases keeping the overall number of events fixed. Therefore, for futility, it is more convenient to keep the original framework by Reference 7, that is, the number of events are treated as the time index in the surveillance period, thus the monitored measure of evidence is the person‐time ratio for each fixed . But, unlike in Reference 7, here we use the flexible group‐sequential test instead of the continuous sequential manner. This ensures that alpha is spent only when new events arrive, increasing the overall statistical power of the sequential analysis.
After having twelve adverse events in only of the person‐time in the surveillance period relatively to the historical period, from Table 10 one can conclude in the 9th test that there are empirical evidences against , which occurred when the relative risk estimate was about 2.35.
5. CONCLUDING REMARKS AND SOFTWARE CONSIDERATIONS
This manuscript discuss sequential analysis hypothesis testing where the goal is to do inference of intrinsic characteristics of the analyzed phenomenon. Therefore, the ideas are not directly convertible for quality control problems, where the goal is to detect problems that suddenly appear during the surveillance, causing an abrupt increase in the relative risk.
Another point to emphasize is that we focused on exact calculations only. For those interested on easy‐to‐use tools based on the conventional practice of using approximations based on the asymptotic statistical theory or Monte Carlo simulations, we recommend the following R packages: ldbounds, Binseqtest, gsDesign, PwrGSD, seqDesign, seqmon, OptGSand, sglr.
Regarding the R Sequential package, a limitation is that it is only applicable for analyzing binomial, Poisson, or conditional Poisson data. For other probability distributions, such as Gaussian or exponential processes, we recommend GroupSeq and SPRT.
The reason we opted to use R Sequential in this tutorial is its flexibility to dealing with the data structure that usually appears in real applications. For instance, Sequential is used to conduct the sequential monitoring of adverse events according to the master protocol for COVID‐19 vaccine active surveillance in the United States.16
Unlike the R package Sequential, most R packages for sequential analysis are only designed for group sequential analysis. A review on available packages for group sequential designs is offered by Reference 35. Among the few alternative options for continuous sequential analysis, Binseqtest works only for binomial data, while SPRT only works for simple alternative hypotheses. Besides, although some of the packages cited above are able to provide statistical power and expected sample size calculations, such as OneArmPhaseTwoStudy, ph2rand, to the best of our knowledge, R Sequential is the only freely‐available package that also calculates expected time to signal. The calculation of sample size for a given target power and relative risk, the calculation of signaling thresholds for a given alpha spending, and the calculation of alpha spending for given pre‐experimental signaling thresholds, are also unique features of R Sequential.
It merits to remark that the package performs near‐automated data analysis. The functions automatically signal when the rejection thresholds are reached. After each analysis, the package delivers the results in the form of both tables and graphs. The package has a detailed user guide explaining how different features and parameter options are specified. For people unfamiliar with the R language, there is a web interface (http://www.sequentialanalysis.org) where users only have to specify the input data and the analysis parameters. With this online tool, users can perform many of the analyses shown in this article without having to install or write code in R.
This article only used the main features of R Sequential for planning and performing sequential analyzes with continuous, group, or mixed group‐continuous Poisson and binomial data. Further features, explanations, and examples are available in the PDF user guide, which accompanies the R Sequential package. All calculations in this article were run using version 3.3.1 from http://CRAN.R‐project.org/package=Sequential.
ACKNOWLEDGEMENTS
This research was funded by the National Institute of General Medical Sciences, USA, grant #RO1GM108999. Additional support was provided by Conselho Nacional de Desenvolvimento Científico e Tecnológico ‐ CNPq, Brazil, process #301391/2019‐0.
1.
Here we deliver the command lines for the calculations shown along the article using the Sequential package.
Command lines for Section 3
Table 1 was produced with command lines in similarity with the following:
SampleSize.Binomial(RR=c(2,4),alpha=0.05,
power=c(0.9,0.99),z=0.25,Tailed="upper")
Table 2 was produced with the following command line:
SampleSize.Poisson(alpha=0.05,power=c(0.9,0.99),M=1,D=0,
RR=c(2,4),Tailed="upper")
The following command line exemplifies how Table 3 was produced:
SampleSize.CondPoisson(cc=50,D=0,alpha=0.05,
power=c(0.9,0.99),RR=2)
Table 4 was produced with the following command line and outputs:
res<‐ Performance.Threshold.Poisson(SampleSize=90,
CV.lower=c(2.5,2.6,2.7,2.8),CV.upper=c(3,3.1,3.2,3.3)
GroupSizes=c(25,20,20,25),Tailed="two",
Statistic="MaxSPRT",Delta="n",RR=c(0.3,0.9,1,1.2,1.5))
res
$AlphaSpend_lower
[1] 0.006467484 0.006467484 0.006467484 0.006467484
$AlphaSpend_upper
[1] 0.00569632 0.01033923 0.01306292 0.01533008
$events_lower
[1] 14 30 47 68
$events_upper
[1] 39 63 87 116
$Performance
RR Power ESignalTime ESampleSize
[1,] 0.3 0.97843535 25.00000 26.40170
[2,] 0.9 0.02376536 25.87450 88.47603
[3,] 1.0 0.02179756 41.01881 88.93233
[4,] 1.2 0.29882956 57.76333 80.36673
[5,] 1.5 0.96483674 42.79107 44.45109
Critical values calculation in Section 3.2:
cv1<‐ 0; cv2<‐ 10; cvm<‐ (cv1+cv2)/2; alpha<‐ 0.05; alphain<‐ 0; count<‐ 0;
aux<‐ log(10/(10
(‐6)))/log(2)
while(abs(alpha‐alphain)>10
6)&count<aux){
count<‐ count+1
alphain<‐ Performance.Threshold.Poisson(SampleSize=20,
CV.upper=cvm,GroupSizes=rep(1,20),Tailed="upper",
Statistic="Pocock",RR=1)$Performance[[2]]
if(alphain>alpha)cv1<‐ cvmelse{cv2<‐ cvm}; cvm<‐ (cv1+cv2)/2}
resPocock<‐ Performance.Threshold.Poisson(SampleSize=20,
CV.upper=cvm,GroupSizes=rep(1,20), Tailed="upper",
Statistic="Pocock",RR=c(1,2))
The object resPocock$AlphaSpend contains the alpha spending implied by Pocock's test.
Figure 1 and Table 6 were obtained with the command lines similar to:
resM<‐ Performance.AlphaSpend.Poisson(SampleSize=20, alpha=0.05,RR=2,
alphaSpend=1, rho=0.5,gamma="n",Statistic="MaxSPRT",
Delta="n",Tailed="upper")
Performance.Threshold.Poisson(SampleSize=20,CV.lower="n",
CV.upper=resM$cvs,GroupSizes="n", Tailed="upper",Statistic="MaxSPRT",
Delta="n",RR=c(1,2))
The solutions for constructing Figure 3 can be obtained with the following command lines:
Optimal.Binomial(Objective="ETimeToSignal",N="n",z=1,
alpha=0.05,power=0.8,RR=2,GroupSizes="n",Tailed= "upper")
Optimal.Binomial(Objective="ESampleSize",N="n",z=1,
alpha=0.05,power=0.8,RR=2,GroupSizes="n",Tailed= "upper")
The content of Figure 4 was calculated with the following command lines:
Optimal.Binomial(Objective="ETimeToSignal",N="n",z=1,
p="n",alpha=0.05,power=c(0.8,0.8),RR=c(0.5,2),
GroupSizes="n",Tailed= "two")
For calculating the optimal solution of Section 3.3:
Optimal.Binomial(Objective="ETimeToSignal",N="80",z=1,
alpha=0.05,power=0.8,=2,GroupSizes="n",Tailed= "upper")
Command lines for Section 4
The lower and upper critical values presented in Table 8 of Section 4.2 can be reproduced with the following command lines:
AnalyzeSetUp.wBinomial(name="Treatments_AxB",N=1000,
alpha=0.05,M=1,rho=0.5,
title="Treatment A vs Treatment B comparison",
address="C:/Users/Example",Tailed="two")
Analyze.wBinomial(name="Treatments_AxB",test=1,
z=c(1,1,1,1,1),w=c(0.05,0.08,0.09,0.11,0.3),
ExposureA=c(0,0,0,0,1,0),ExposureB=c(0,0,0,0,0,0))
The critical values in the scale of the number of events and related alpha spending in Section 4.3 were obtained with command lines in similarity to:
AnalyzeSetUp.Poisson(name="PediarixVaccine",SampleSize=20,
alpha=0.05,M=1,AlphaSpendType="power‐type",rho=0.5,
title="Pediarix vaccination",address="C:/Users/Example")
Analyze.Poisson(name="PediarixVaccine",test=1,mu0=0.04,
events=0)
Analyze.Poisson(name="PediarixVaccine",test=2,mu0=0.06
,events=1)
⋮
Analyze.Poisson(name="PediarixVaccine",test=10,mu0=0.12
,events=0)
The calculations in Section 4.4 were obtained with the following command lines:
Performance.AlphaSpend.CondPoisson(K=20,cc=37,alpha=0.05,
AlphaSpend=1,GroupSizes="n",rho=1.5,gamma="n",
Tailed="upper",RR=2)
AnalyzeSetUp.CondPoisson(name="INFLUENZA",
SampleSizeType="Events",K=20, cc=37,alpha=0.05,
M=1,AlphaSpendType="power‐type",rho=1.5,
title="n",address="C:/Users/Example")
Analyze.CondPoisson(name="INFLUENZA",test=1,events=1,
PersonTimeRatio=0.044)
Analyze.CondPoisson(name="INFLUENZA",test=2,events=5,
PersonTimeRatio=0.046)
Analyze.CondPoisson(name="INFLUENZA",test=3,events=3,
PersonTimeRatio=0.025)
Analyze.CondPoisson(name="INFLUENZA",test=4,events=3,
PersonTimeRatio=0.024)
Command lines for the relative risk estimates in Table 7
MLE_R<‐ function(cases,SampleSizes,z)
{
# cases: number of new adverse events from Treatment in each test until the th test.
# SampleSizes: number (A+B) of new adverse events in each test until the th test.
# z: matching ratio in each test until the th test.
recand<‐ matrix(seq(0.01,10,0.01)”1)
lr<‐ function(rr){
return(prod( choose(SampleSizes,cases)*((1/(1+z/rr)) (cases))*((1‐1/(1+z/rr)) (SampleSizes‐cases)) ))
}
veccand<‐ apply(recand,1,lr)
Rhat<‐ seq(0.01,10,0.01)[veccand==max(veccand)]
return(Rhat)
}
Rparciais<‐ rep(0,length(cases))
for(i in 1:length(cases)){
casesh<‐ cases[1:i]
SampleSizesh<‐ ni[1:i]
zh<‐ z[1:i]
Rparciais[i]<‐ MLE_R(casesh,SampleSizesh,zh)
}
R. Silva I, Maro J, Kulldorff M. Exact sequential test for clinical trials and post‐market drug and vaccine safety surveillance with Poisson and binary data. Statistics in Medicine. 2021;40:4890–4913. 10.1002/sim.9094
Funding information Conselho Nacional de Desenvolvimento Científico e Tecnológico, 301391/2019‐0; National Institute of General Medical Sciences, RO1GM108999
DATA AVAILABILITY STATEMENT
Data sharing not applicable to this article as the illustrative data examples are either fictitiously generated through Monte Carlo simulation or taken from first author's previous publications.
REFERENCES
- 1.Wald A. Sequential tests of statistical hypotheses. Ann Math Stat. 1945;16:117‐186. [Google Scholar]
- 2.Wald A. Sequential Analysis. New York, NY: John Wiley and Sons; 1947. [Google Scholar]
- 3.Pocock SJ. Group sequential methods in the design and analysis of clinical trials. Biometrika. 1977;64:191‐199. [Google Scholar]
- 4.O'Brien PC, Fleming TR. A multiple testing procedure for clinical trials. Biometrics. 1979;35:549‐556. [PubMed] [Google Scholar]
- 5.Wang SK, Tsiatis AA. Approximately optimal one‐parameter boundaries for group sequential trails. Biometrics. 1987;43:193‐200. [PubMed] [Google Scholar]
- 6.Kulldorff M, Davis RL, Kolczak M, Lewis E, Lieu T, Platt R. A maximized sequential probability ratio test for drug and vaccine safety surveillance. Sequential Analysis: Design Methods and Applications. Vol 30; 2011;(1):58‐78. [Google Scholar]
- 7.Li L, Kulldorff M. A Conditional maximized sequential probability ratio test for pharmacovigilance. Stat Med. 2009;29:284‐295. [DOI] [PubMed] [Google Scholar]
- 8.Jennison C, Turnbull BW. Group Sequential Methods with Applications to Clinical Trials. London, UK: Chapman and Hall; 2000. [Google Scholar]
- 9.Silva IR, Li L, Kulldorff M. Exact conditional maximized sequential probability ratio test adjusted for covariates. Seq Anal. 2019;38(1):115‐133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Silva IR, Lopes WM, Dias P, Yih WK. Alpha spending for historical versus surveillance Poisson data with CMaxSPRT. Stat Med. 2019;28(12):2126‐2138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Silva IR. Type I error probability spending for post‐market drug and vaccine safety surveillance with Poisson data. Methodol Comput Appl Probab. 2018;20(2):739‐750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Silva I.R., Kulldorff M. Sequential: exact sequential analysis for Poisson and binomial data. R foundation for statistical computing‐ contributed packages. R Package Version 3.1. Vienna, Austria; 2019.
- 13.Silva IR, Kulldorff M, Yih WK. Optimal alpha spending for sequential analysis with binomial data. J R Stat Soc Ser B. 2020;82(4):1141‐1164. [Google Scholar]
- 14.Beigel JH, Tomashek KM, Dodd LE, et al. Remdesivir for the treatment of Covid‐19; final report. N Engl J Med. 2020;383:1813‐1826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cao B, Wang Y, Wen D, et al. A trial of Lopinavir–Ritonavir in adults hospitalized with severe Covid‐19. N Engl J Med. 2020;382(19):1787‐1799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.CBER Surveillance program. COVID‐19 vaccine safety surveillance: active monitoring master protocol; 2021. https://www.bestinitiative.org/wp‐content/uploads/2021/02/C19‐Vaccine‐S%afety‐Protocol‐2021.pdf. [Online Accessed April 08, 2021].
- 17.Silva IR, Kulldorff M. Continuous versus group sequential analysis for post‐market drug and vaccine safety surveillance. Biometrics. 2015;71(3):851‐858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Simon R. Optimal two‐stage designs for phase II clinical trials. Control Clin Trials. 1989;10:1‐10. [DOI] [PubMed] [Google Scholar]
- 19.Lin DY, Wei LJ, DeMets DL. Exact statistical inference for group sequential tests. Biometrics. 1991;47:1399‐1408. [PubMed] [Google Scholar]
- 20.Causey BD. Exact calculations for sequential tests based on Bernoulli trials. Commun Stat Simul Comput. 1985;14:491‐495. [Google Scholar]
- 21.Aroian LA. Sequential analysis, direct method. Technometrics. 1968;10:125‐132. [Google Scholar]
- 22.Fireman B, Lee J, Lewis N, Bembom O, Laan M, Baxter R. Influenza vaccination and mortality: differentiating vaccine effects from bias. Am J Epidemiol. 2009;170(5):650‐656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Silva IR, Kulldorff M, Gagne J, Najafzadeh M. Exact sequential analysis for multiple weighted binomial end points. Stat Med. 2020;39(3):340‐351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Grayling MJ, Wason JMS, Mander AP. Exact group sequential designs for two‐arm experiments with Poisson distributed outcome variables. Commun Stat Theory Methods. 2021;50(1):18‐34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kulldorff M, Silva IR. Continuous post‐market sequential safety surveillance with minimum events to signal. Revstat Stat J. 2017;15:1‐21. [PMC free article] [PubMed] [Google Scholar]
- 26.Gombay E, Li F. Sequential analysis: design methods and applications. Seq Anal. 2015;34:57‐76. [Google Scholar]
- 27.Kim K, Demets DL. Design and analysis of group sequential tests based on the type I error spending rate function. Biometrika. 1987;74(1):149‐154. [Google Scholar]
- 28.Jennison C, Turnbull BW. Interim analyses: the repeated confidence interval approach(with disussion). J Royal Stat Soc B. 1989;51:305‐361. [Google Scholar]
- 29.Jennison C, Turnbull BW. Statistical approaches to interim monitoring of medical trials: a review and commentary. Stat Sci. 1990;5:299‐317. [Google Scholar]
- 30.Silva IR. Type error 1 probability spending for post‐market drug and vaccine safety surveillance with binomial data. Stat Med. 2018;37(1):107‐118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lan KKG, DeMets DL. Discrete sequential boundaries for clinical trials. Biometrika. 1983;70(3):659‐663. [Google Scholar]
- 32.Stallard N, Todd S. Exact sequential tests for single samples of discrete responses using spending functions. Stat Med. 2000;19:3051‐3064. [DOI] [PubMed] [Google Scholar]
- 33.Hwang IK, Shih WJ, DeCani JS. Group sequential designs using a family of type I error probability spending functions. Stat Med. 1990;9:1439‐1445. [DOI] [PubMed] [Google Scholar]
- 34.Yih WK, Kulldorff M, Sandhu SK, et al. Prospective influenza vaccine safety surveillance using fresh data in the sentinel system. Pharmacoepidemiol Drug Saf. 2016;25:481‐492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Grayling MJ, Wheeler GM. A review of available software for adaptive clinical trial design. Clin Trials. 2020;17(3):323‐331. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data sharing not applicable to this article as the illustrative data examples are either fictitiously generated through Monte Carlo simulation or taken from first author's previous publications.


