Abstract
We measure labor demand and supply shocks at the sector level around the COVID-19 outbreak by estimating a Bayesian structural vector autoregression on monthly statistics of hours worked and real wages. Most sectors were subject to large negative labor supply and demand shocks in March and April 2020, with substantial heterogeneity in the size of shocks across sectors. Our estimates suggest that two-thirds of the drop in the aggregate growth rate of hours in March and April 2020 are attributable to labor supply. We validate our estimates of supply shocks by showing that they are correlated with sectoral measures of telework.
Keywords: Supply and demand shocks, COVID-19, Structural vector autoregressions, Sign restrictions
1. Introduction
The COVID-19 outbreak and subsequent public health policy response have caused widespread disruption in most economies. On one hand, authorities around the world have enforced containment and mitigation measures that entailed the supervised shutdown of entire sectors of their economies. On the other hand, in the face of uncertainty about health safety, agents voluntarily engaged in self-imposed social distancing. There are many aspects that make studying this shock interesting. First, there is its unprecedented nature, both in terms of magnitude and uncertainty regarding its persistence. Second, it combines features that are traditionally associated with both demand and supply shocks. Third, its effects across sectors in the economy have been extremely heterogeneous, with some industries shutting down almost completely (such as movie theaters), while others potentially benefiting from increased demand (such as general merchandise retailers). For many sectors, it is not clear whether this is mostly a demand or a supply shock.
This paper attempts to help answer that question by estimating labor demand and supply shocks at the sectoral level. Labor demand/supply shocks are defined here as unforeseen changes in employers/workers willingness to hire/work given the observed wage. We apply the general methodology proposed by Baumeister and Hamilton (2015) and use Bayesian structural vector autoregressions (SVARs) to model the joint dynamics of monthly real wages and hours worked for each 2-digit NAICS sector of the US economy, as well as for total private employment. Combined with priors on labor demand and supply elasticities that are informed by the literature, we use sign restrictions to identify and estimate sequences of labor demand and supply shocks. Our latest historical decomposition estimates are for the months of March–May 2020 that featured the controlled shutdown and subsequent reopening of parts of the US economy.
Total private employment fell by 16.24 percentage points (pp) in April 2020; we find that supply shocks accounted for 68.83% of this decrease. In other words, total private employment grew by 16.04 pp less in April 2020 (non-annualized) than its historical average and two-thirds of this negative growth is attributed to a negative labor supply shock. While most sectors that we consider were subject to negative supply shocks in this period, there is some heterogeneity in the size of both demand and supply shocks. The Leisure and Hospitality sector has experienced the largest disruption by far ( pp in March, 59% of which was supply, and pp in April, 63% of which was supply). The least-affected sectors were Utilities, Information, and Financial Activities. In fact, Information experienced positive demand shocks in March ( pp), and Utilities was the only sector with positive demand shocks in April ( pp). These patterns revert in May, with most sectors experiencing positive supply and demand shocks, particularly Leisure and Hospitality and Construction.
Since we only model hours and real hourly wages, the estimated labor supply and demand shocks are interpreted as shifts in the demand and supply curves. They are the net result of potentially many shocks – aggregate or sectoral – that affect household labor decisions (labor supply curve) or firms’ employment decisions (labor demand curve). Examples of major factors that may have resulted in shifts in the labor supply curve are the increase in the health risk of going to work, mandated lockdowns during the COVID-19 period, or certain features of the CARES Act (such as changes to unemployment insurance), as all of these may potentially affect the willingness to work at a given hourly real wage. On the other hand, demand shortages (Guerrieri et al., 2020, Baqaee and Farhi, 2020), supply disruptions, and fiscal and monetary policies during COVID-19, among others, may have potentially affected the willingness of firms to hire at a given hourly real wage—a labor demand curve shift. An important caveat of our methodology is that unexpected changes in wages could be the result of changes in the SVAR model parameters (labor demand/supply elasticities and parameters related to the lag structure) rather than shocks. In other words, movements in equilibrium wages and hours during March and April 2020 could be the result of structural breaks. Given the limited data and minimal structure in our empirical framework, it is impossible to disentangle shocks from structural breaks in model parameters.1
Even though our interpretation is broad, we believe that disentangling supply and demand shocks is important for the design of economic policy during this crisis (Baqaee and Farhi, 2020). Conceptually, our measure of labor supply shocks should be directly related to the state of the public health crisis: once the crisis is brought under control, negative supply shocks should disappear as workers are no longer reluctant to go to work and lockdowns are lifted. While demand shocks may also have a public health-related component (especially in sectors where consumption of goods and services involves a social component), they may be more related to the general state of the economy (reflecting low demand due to loss of income from workers or high uncertainty, for example). More specifically, the fall in employment and aggregate expenditure that are caused by this shock can lead to a reduction of activity in sectors that are not explicitly subject to the lockdown. This reduction in activity in non-lockdown sectors, which we identify as sectoral demand shocks, can be addressed via targeted stabilization policies, such as fiscal or credit policies. For these reasons, measuring demand and supply shocks at the sectoral level is important for the design of public policies that are aimed at minimizing long-term effects of the crisis.2
Our sectoral shock decomposition also provides natural moment conditions to help discipline quantitative work not only on the COVID-19 crisis, but also on other periods. There is a large set of shocks and models that are observationally equivalent in terms of being consistent with a number of standard moments while at the same being consistent with movements in hours worked and real earnings. One can formulate models in which the entirety of the drop in hours worked is attributed to shifts in the demand for labor, and other models where all of these movements arise from shifts in the labor supply. The results of our analysis restrict the set of models and shocks that are empirically plausible. Our estimated sectoral shock measures can also be potentially used as instruments for labor supply and demand shocks in empirical work in a variety of different settings, including, but not restricted to, the COVID-19 crisis. Our decomposition exercise is potentially vulnerable to some critiques, namely the role of composition effects in driving the joint dynamics of aggregate hours and hourly earnings. We do the best we can, given the available data, to provide upper bounds for the importance of supply shocks in the presence of extreme versions of these composition effects; we find that negative supply shocks would still be sizeable in the period under analysis.
Our paper relates to the emerging literature on the economic effects of the COVID-19 crisis, especially to studies related to the nature of the shocks affecting multi-sector economies.3 Baqaee and Farhi (2020) study the effects of the COVID-19 crisis in a disaggregated Keynesian model with multiple sectors, factors, and input–output linkages. They find that negative supply shocks are stagflationary and that negative demand shocks are deflationary, which serves as the basis for our identification. del Rio-Chanona et al. (2020) perform a sectoral analysis of demand and supply shocks in the US economy. Their measure of exposure to supply shocks aggregates a remote labor index across occupations at the sector level, while their exposure to demand shocks is based on Congressional Budget Office estimates. Instead, we jointly measure demand and supply shocks using a unified econometric framework and a single source of data. Guerrieri et al. (2020) show that under certain assumptions in a model with multiple sectors and incomplete markets, supply shocks can have effects that resemble those of demand shocks (“Keynesian supply shocks”). While the previously cited papers mostly focus on “aggregate” final output supply and demand, our paper focuses on labor market demand and supply shocks. Supply and demand shocks in both markets are not necessarily isomorphic: while an aggregate output demand shock also manifests itself as a demand shock in the labor market, a positive TFP shock, for example, is simultaneously an output supply shock and a labor demand shock. The shocks we estimate are not structural through the lens of an economic model as in Guerrieri et al. (2020), which means that we cannot disentangle these from other types of demand shocks. Their insights suggest that we may be underestimating the size of supply shocks in our exercise. There is also a new literature embedding epidemiology features in standard macroeconomic models and where epidemics generate reductions in economic activity that would be captured by our framework as both negative supply and demand shocks (Eichenbaum et al., 2020).
This paper is organized as follows: Section 2 describes the econometric framework; Section 3 describes the data; Section 4 presents the results from our historical decomposition exercise; Section 5 presents robustness checks as well as some validation exercises; and Section 6 concludes.
2. Methodology
We use the methodology proposed by Baumeister and Hamilton (2015) to identify labor supply and demand shocks in each sector .4 The methodology can be generally applied to any market, provided that data on prices and quantities are available; we specifically apply it to the US labor market. We use a SVAR to describe the joint dynamics of the growth rate of real wages and the growth rate of hours worked in a given sector. Let be the 2 × 1 vector of observables. Then the SVAR for sector takes the form
| (1) |
where is a 2 × 2 matrix describing the contemporaneous relations, is a 2 × 1 vector of constants, are the 2 × 2 matrices associated with each lag of , and is a 2 × 1 vector of structural shocks that are assumed to be i.i.d. and mutually uncorrelated ( is diagonal).
Let so that the first equation corresponds to labor demand and the second equation to labor supply. We assume that the contemporaneous relation matrix takes the form
| (2) |
where is interpreted as the elasticity of labor demand and as the elasticity of labor supply in sector .
The equations for labor market demand and supply in sector are then given by
| (3) |
| (4) |
It is important to emphasize that under this framework, the relative sizes of the impact of supply and demand shocks on equilibrium movements in the growth rate of hours depend crucially on the relative size of demand and supply elasticities. For example, assuming no intercepts and no lags, solving for the growth rates of hours and real wages yields
If we assume that the demand curve is downward sloping and the supply curve is upward sloping, we have the standard result that, ceteris paribus, a positive shift in the demand curve makes equilibrium hours increase and wages increase, while, ceteris paribus, a positive shift in the supply curve makes hours rise and wages fall. That is, if and , then and , while and . Moreover, note that the relative size effects of supply vs. demand shocks on employment and wages depend on the relative labor demand and supply elasticities . The flatter (steeper) the supply curve is relative to the demand curve, the weaker (stronger) the relative impact of a supply shock is on hours, and the stronger (weaker) its impact is on real wages.5 One can thus identify labor supply and demand shocks given data on hours and wages and values for the elasticities. Using those shocks, one can then decompose the movements in equilibrium wages and hours into demand and supply components. Fig. 1 presents a visual representation of the identification procedure.
Fig. 1.
Illustration of labor supply and demand identification.
Notes: Example where the decomposition of changes in equilibrium hours () between labor supply and demand shocks depends on the change in equilibrium wages () and on the labor elasticities ratio.
The reduced-form vector autoregression (VAR) associated with the SVAR model (1) is given by
| (5) |
where
| (6) |
| (7) |
We assume that prior beliefs about the values of the structural parameters are represented by a joint density . We then revise these beliefs when confronting them with sectoral data in our sample . Importantly, Baumeister and Hamilton (2015) show how these beliefs can be updated for any prior distribution that best summarizes prior available information. In principle this prior could incorporate any combination of exclusion restrictions, sign restrictions, and informative prior beliefs about elements of .
Priors.
Following Baumeister and Hamilton (2015), we use past studies to form informative priors about and . First, we impose sign restrictions on sectoral demand and supply elasticities: is negative and is positive. The sign restriction reflects our belief that the labor demand curve should be downward sloping and that the supply curve should be upward sloping. However, we do not place a uniform probability on all values that respect these sign restrictions. In particular, we assume prior distributions that reflect uncertainty about the true values for these parameters and that encompass both micro and macro estimates in the literature.
For the labor demand elasticity , we assume a truncated Student’s distribution (Baumeister and Hamilton, 2015, Baumeister and Hamilton, 2018) with location parameter , scale parameter 0.6 and degrees of freedom, so that we place a 90% probability on . This range reflects the labor demand elasticity estimates found in the micro and macro literatures.6 In terms of the labor supply elasticity, based on the findings of Chetty et al. (2011), we also use a Student’s distribution (Baumeister and Hamilton, 2015, Baumeister and Hamilton, 2018) with location parameter 0.6, scale parameter 0.6 and degrees of freedom, so that we place a 90% probability on . This interval thus includes the lower estimates reported by micro and macro estimates when movements in wages are persistent, and includes the high Frisch elasticities reported by macro studies of the business cycle, such as in Smets and Wouters (2007). Since we use the same prior for both elasticities, we have an implicit prior belief that unit supply and demand shocks have an equal impact on hours. Finally, our priors for labor demand and supply are assumed to be independent.7
In a meta-analysis that uses information from 151 different studies and encompasses a total of 1334 estimates, Lichter et al. (2015) find that, except for Construction and Manufacturing, the labor demand elasticity does not seem to vary substantially across the other sectors we consider. For Construction and Manufacturing, they find a point difference of demand elasticity relative to the aggregate economy of and , respectively. However, as for labor supply elasticity, there is reason to believe it varies across industries, as these have a different mix of workers in terms of, among many others, gender, wealth and education. Since we were not able to find evidence on how they vary across the industries we use, we imposed the same prior distribution for the labor elasticity in all sectors. In sum, because of the aforementioned reasons, we apply the same prior distribution for all sectors in our sample.
Next, we define the specification for our conditional prior distributions and . For the elements of the diagonal matrix , we assume that their reciprocals (the precision of the structural shocks) follow a gamma distribution with shape parameter and scale parameter . We set to , which puts a small weight on our prior of just four months of data, and set the scale parameter so that the prior mean of each element matches the precision of the structural shocks after orthogonalization of univariate autoregressions with four lags under . That is, , where is the variance–covariance of the univariate residuals series. is then the product of the two gamma distributions. Finally, is set in a way that conforms with the Bayesian VAR Minnesota priors on the reduced-form coefficients (Doan et al., 1984, Sims and Zha, 1998, Baumeister and Hamilton, 2019). Note that placing a prior on the reduced-form coefficients and conditioning on implicitly places a prior on since . Hence the normally distributed coefficients have mean for elements corresponding to their own lags and zero for all others. Moreover, our beliefs place a higher degree of certainty that higher lags should be zero. We follow Baumeister and Hamilton (2015) and set the hyperparameter , which controls the overall tightness of the prior; , which governs how quickly the prior for lagged coefficients tightens to zero for higher lags; and , which places essentially zero weight on the prior when estimating . The joint prior distribution is then given by:
| (8) |
Estimation.
Based on the Akaike information criterion, we set the number of lags to . We then use Bayesian methods to update our prior beliefs given the data . The posterior can be written as
| (9) |
The conditional posterior on the structural coefficients is a multivariate normal density because of natural conjugacy, and the updating follows the standard convex combination of prior means and OLS estimates, where the weights are based on the relative precision of the prior mean versus OLS estimates of the reduced-from representation (5), (7). Also because of natural conjugacy, the conditional posterior is also a gamma distribution. Finally, does not have a known distribution, and we use a random-walk Metropolis–Hastings algorithm to draw from it.
Identification.
It is important to note that given our priors and limited data, the model will be only set identified. This means that the historical decompositions will also be only set identified. This allows us to account not just for estimation uncertainty due to the limited amount of data but also for the fact that we do not have perfect knowledge about the underlying structure of the economy. The latter is particularly relevant in analyses of the COVID-19 pandemic period, as this shock triggered historically large changes in macroeconomic variables such as hours worked. The identified set is a function of both priors and data. However, given that we use symmetric priors for the labor supply and demand elasticities, the relative importance of supply and demand shocks in the historical decompositions will be a function of the data only.
3. Data
Our main source of data is the Current Employment Statistics (CES) database from the Bureau of Labor Statistics (BLS), from where we obtain monthly real wages and hours worked by sector from March 2006 to May 2020.8 The CES provides data for 14 main aggregate sectors: total private, mining and logging, construction, manufacturing, wholesale trade, retail trade, transportation and warehousing, utilities, information, financial activities, professional and business services, education and health services, leisure and hospitality, and other services. For each sector, we compute the monthly growth rate for real wages as the log difference of monthly average hourly earnings of all employees in 1982–1984 dollars. The growth rate of hours worked in a given sector is computed by taking the log difference of aggregate weekly hours of all employees in that sector. Given the unprecedented nature of the shocks, and as we discuss in more detail in the following section, we estimate the SVAR using data through February 2020. We then use the estimated model to perform a historical decomposition for the full sample, including March, April, and May 2020.
4. Results
Posteriors.
For most sectors the beliefs on elasticities are significantly revised towards macro literature estimates, namely for Leisure and Hospitality and Utilities. Demand elasticities are mostly revised upward (in absolute value), especially in the Construction and the Leisure and Hospitality sectors. Hence, we conclude that our identification of supply and demand shocks is strongly influenced by the data. A detailed description of the posterior estimates can be found the Online Appendix.9
Historical decompositions pre-COVID-19.
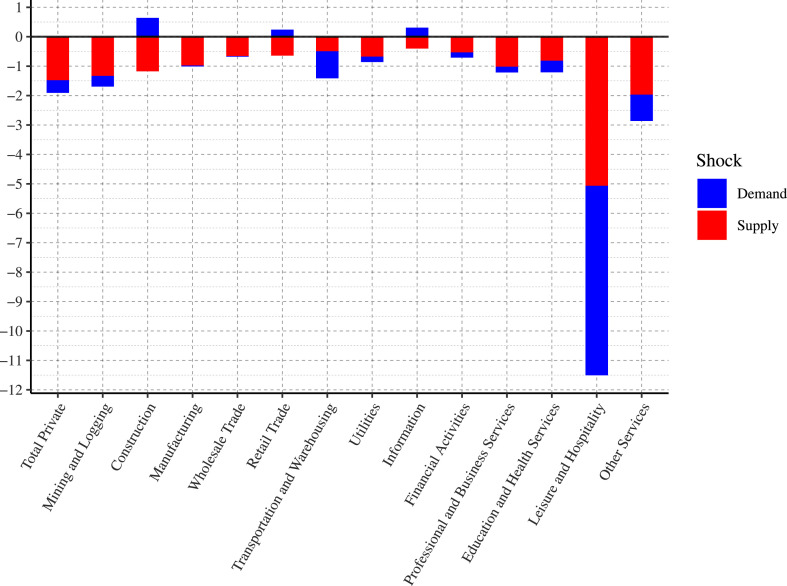
Fig. 2 plots the historical decomposition of the growth rate of hours for Total Private employment and the Leisure and Hospitality sector. These panels include only the estimation period, and exclude March–May 2020, which are analyzed separately in the following sections. They show that the growth rate of hours was subject to large negative shocks both to demand and to supply during the Great Recession. Consistent with standard narratives, the Great Recession begins with negative demand shocks in late 2007 and early 2008. Starting in late 2008 we also identify large negative labor supply shocks, which is consistent with a large literature on labor markets during this period (Elsby et al., 2010).10
Fig. 2.
Historical decomposition of the growth rate of hours: Total Private Employment, Leisure and Hospitality. Median and 95% credible sets.
4.1. The COVID-19 recession: March and April 2020
We now take a closer look at the results for the months of March and April 2020: the two months that featured a significant reduction in economic activity in the US and that coincide with the “the Great Lockdown.”11 Fig. 3, Fig. 4 contain our main set of results for NAICS 2-digit sectors and plot the medians of the historical decomposition of the growth rate of hours across sectors for March and April, respectively.12 The historical contribution of demand (supply) shocks to the sectoral growth rate of hours is the cumulative effect of all past and present demand (supply) shocks to the growth rate of hours. The combined negative effect of supply and demand on the growth rate of hours for total private employment was pp in March and in April. Negative supply shocks accounted for 71.5% and 68.8% of these effects, respectively.
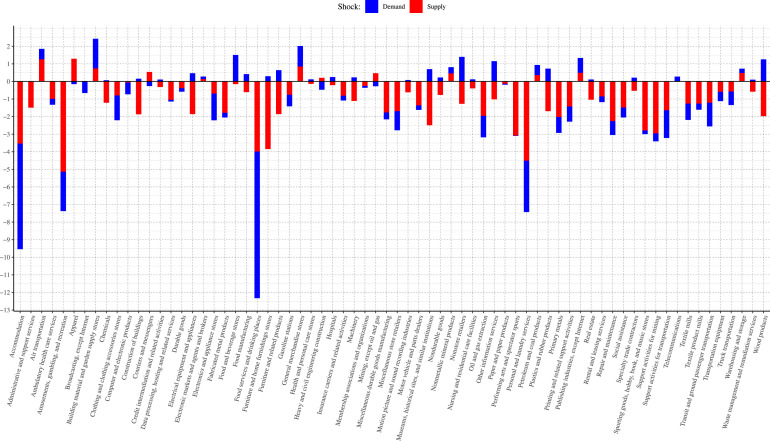
Fig. 3.
Historical decomposition of the growth rate of hours by NAICS 2-digit sectors in March 2020 .
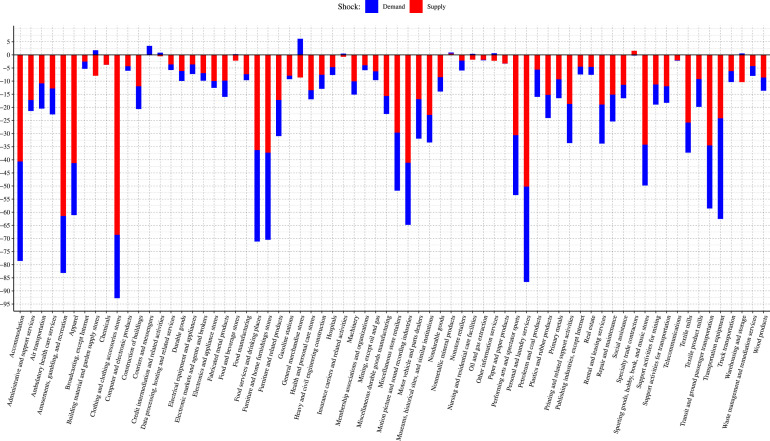
Fig. 4.
Historical decomposition of the growth rate of hours by NAICS 2-digit sectors in April 2020 .
Fig. 3 shows considerable heterogeneity in sectoral exposure to shocks. Leisure and Hospitality is the most negatively affected sector, with a combined effect of pp, of which 59% is supply. The least-affected sectors are Wholesale Trade ( pp), Financial Activities ( pp), and Information ( pp). Retail Trade, Wholesale Trade, and Construction experience small positive demand shocks, with the most significant demand shock being to Information ( pp). These results are consistent with the narrative regarding the beginning of the lockdown: high physical-contact services, concentrated in Leisure and Hospitality (and Other Services), experience large negative shocks to both demand and supply. As agents shift their consumption patterns, sectors such as Retail Trade and Wholesale Trade partly benefit. Finally, the Information sector benefits from a demand boost, as many firms increase their demand for technology services to implement telework arrangements.
Fig. 4 presents the shock decomposition for April, the first full month of the lockdown. Note the difference in scale that reflects the much larger magnitude of the shocks: the total decline in Total Private hours is of 16.24 pp, out of which 68.8% is attributable to supply. Leisure and Hospitality is the most-affected sector, as before, with a decline of 63.17 pp, of which 63% is supply. This is expected for a sector that relies on physical-contact-intensive activities. The negative labor supply shock results from lockdown measures that prevent workers from actually going to work, while the negative labor demand shock results from consumers not undertaking those activities. It should also be noted that other service sectors such as Education and Health Services also experienced negative supply and demand shocks comparable in magnitude to those experienced during the Great Recession.
Essentially all sectors in the economy are negatively affected in April, including sectors that experienced positive shocks in March (such as Information). The least-affected sectors are Utilities ( pp) and Financial Activities ( pp). As we show in the next section, these are sectors where a high percentage of jobs can be done at home. The supply/demand composition is overall similar across sectors. Sectors where demand was more relevant were Manufacturing (40%), Information (40%) and Education and Health Services (45%). This finding is consistent with the idea that even sectors that were not necessarily exposed to the lockdown measures could have been affected by a fall in aggregate demand.
Fig. 5 repeats the analysis at the 3-digit NAICS level and shows a much richer picture of the heterogeneous impact that COVID-19 had across sectors. It shows, for example, that Food Services and Drinking Places experienced large negative supply and demand shocks, while Food and Beverage Stores experienced a positive demand shock, reflecting substitution in consumption patterns during the lockdown. Second, we note that while supply shocks dominated the Leisure and Hospitality sector at the NAICS-2 aggregate level, demand shocks had a more prominent role than supply in its two most hit subsectors, Accommodation and Food Services and Drinking Places. Third, it shows that many sectors beyond those directly related to Information actually experienced positive labor demand shocks, in spite of also suffering negative supply shocks (Building Material and Garden Supply Stores, Food and Beverage Stores, among others). Fourth, many sectors were relatively unaffected by COVID-19. Fig. 6 repeats the analysis at the 3-digit NAICS level for April, showing a very different picture from March. Almost no sectors experienced positive demand shocks in April. Even those sectors whose activity is more insulated from the health risks posed by COVID-19 or that are not directly affected by lockdown measures experienced negative demand shocks. In contrast to March, labor supply was the dominant shock for the hardest hit sectors.
Fig. 5.
Historical decomposition of the growth rate of hours by NAICS 3-digit sectors in March 2020.
Notes: The data sample used for the historical decompositions in NAICS 3-digit sectors uses production and nonsupervisory employees only and starts in 1990.
Fig. 6.
Historical decomposition of the growth rate of hours by NAICS 3-digit sectors in April 2020.
Notes: The data sample used for the historical decompositions in NAICS 3-digit sectors uses production and nonsupervisory employees only and starts in 1990.
4.2. Reopening: May 2020
We now turn to the shock decomposition in May 2020, which corresponds to the reopening of the economy after a two-month lockdown. By this month, most states and local governments that had imposed stay-at-home or shelter-in-place orders started lifting these restrictions, triggering positive demand and supply shocks. Consistent with our previous results, we find that labor supply shocks were more positive in sectors that were most affected by the lockdown orders: Leisure and Hospitality (+19.35 pp, 74% supply) and Construction (+9.39 pp, 71% supply). Sectors such as Financial Activities and Information remained largely unaffected, consistent with the fact that these sectors are the ones with the largest shares of workers who can perform their tasks remotely (see Fig. 7).13
Fig. 7.
Historical decomposition of the growth rate of hours by sector in May 2020.
4.3. Interpreting the shocks
In this subsection we discuss how lockdowns, the expansion of unemployment benefits, and TFP shocks during COVID-19 can be understood through the lens of our empirical framework.
The role of lockdowns.
A large number of US state and local governments imposed lockdown measures during April. Conceptually, a temporary lockdown measure imposes a quantity restriction on hours worked on the labor market. Fig. 8 provides a visualization of how lockdown measures may affect labor shock identification under our empirical framework. Panel a) shows how lockdown measures affect labor markets in a setting without general equilibrium effects, where the demand for labor does not shift in response to the lockdown.14 In this case, the restriction on hours does not cause any movement in the demand for goods and services, therefore not impacting the demand for labor. Thus, this quantity restriction implies an increase in the equilibrium price, and the variation in hours is entirely explained by the supply shock. Panel b) illustrates the case where, due to general equilibrium effects, the demand for labor is also affected by the lockdown. In that case, there may still be an increase in wages, but it will be less than that predicted by a pure supply shock (i.e., a movement along the demand curve). In that case, the difference between the increase in wage that would be generated by a movement along the demand curve and the realized change in the wage reflects the size of the demand shock.
Fig. 8.
Lockdown impact on labor shocks.
Notes: Panel (a) shows how a sector lockdown affects shock identification in the absence of equilibrium effects. The lockdown works as a movement along the demand curve, and the new equilibrium wage-hour pair becomes . All of the movement in hours and wages is explained by a supply shock. Panel (b) shows how a sector lockdown affects shock identification with general equilibrium effects. In this case, the demand curve also contracts, which results in a larger decline in hours and a smaller increase (or a decrease) in the equilibrium wage.
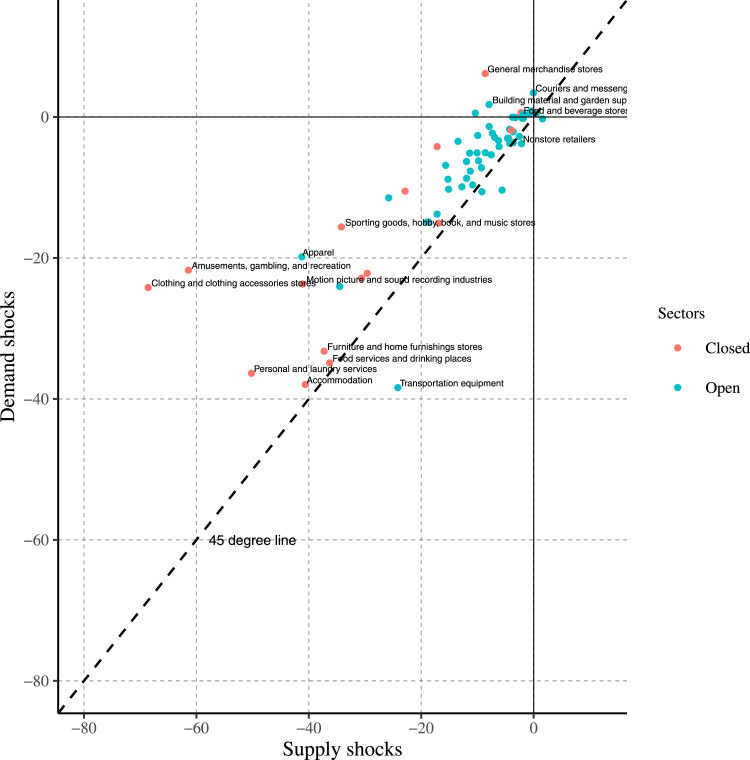
To understand how our shock estimates relate to lockdowns, we exploit the fact that there was substantial variation in terms of which sectors remained open and which ones were locked down at the NAICS 3-digit level. Fig. 9 plots our supply and demand shock estimates, in the x- and y-axes, respectively, along with the 45 degree line and an indication of whether each sector was “open” or “closed.” The figure shows that closed sectors tended to experience relatively larger (more negative) supply than demand shocks. Second, closed sectors experienced larger (negative) supply and demand shocks relative to open sectors. Third, there is substantial heterogeneity among closed sectors in terms of the relative size of supply and demand shocks, implying that lack of demand varied greatly across these sectors. For instance, Clothing and Clothing Accessories Stores suffered a much larger supply than demand shock, while Accommodation suffered supply and demand shocks of roughly equal sizes.
Fig. 9.
Supply and demand shocks across closed and open sectors during lockdown.
Labor vs. Output demand and supply shocks.
As we note in the introduction, our exercise measures labor market supply and demand shocks. This is different from other work on the analysis of aggregate output supply and demand shocks during the COVID-19 period (Baqaee and Farhi, 2020, Guerrieri et al., 2020). Aggregate (output) demand shocks should manifest themselves as demand shocks in the labor market as well: a contraction in the demand for goods and services, for example, should lead firms to reduce hiring for a given wage, everything else constant. Similarly, a negative labor supply shock through which workers are willing to work less hours for a given wage should also be interpreted as a negative aggregate (output) supply shock. One type of shock for which this mapping breaks is TFP: a negative TFP shock corresponds to a negative aggregate (output) supply shock, but it manifests itself as a negative demand shock in the labor market. For this reason, it is not straightforward to map our estimated shocks to aggregate output shocks, and hence our results are not directly comparable to those of other works.
We do, however, provide some suggestive evidence that the labor demand shocks we estimate do not reflect negative TFP shocks. The most plausible source of negative TFP shocks in March and April is supply chain disruptions: some industries and sectors found it hard to source necessary intermediate inputs due to border closures. If the labor demand shocks that we estimate reflect negative TFP shocks, we should then expect sectors that are more exposed to international trade disruptions to experience more negative labor demand shocks, both in March and April. Fig. 10 plots our labor demand shock estimates on the -axis against the total fraction of foreign intermediate inputs used in each sector.15 These figures show a very weak relationship between the two variables (and, if anything, a positive relationship in March), which suggests that our labor demand shock estimates are not capturing exposure to supply chain disruptions. While this evidence is only suggestive and does not allow us to completely exclude the possibility that there were other types of negative TFP shocks during this period, it does give us some confidence that the negative labor demand shocks that we estimate are likely to be associated with negative aggregate (output) demand shocks.
Fig. 10.
Demand shocks during COVID-19 vs. share of foreign intermediate inputs used in production.
ML: Mining and logging; C: Construction;M: Manufacturing; WT: Wholesale trade; RT: Retail trade; TW: Transportation and warehousing; U: Utilities; I: Information; FA: Financial activities; PBS: Professional and business services; EHS: Education and health services; LH: Leisure and hospitality; OS: Other services. Gray bands represent 95% confidence intervals. Data on share of foreign intermediate inputs taken from the OECD’s Trade in Value Added database.
UI expansion and the CARES Act.
One of the largest policy changes during the period of the analysis was the significant expansion of unemployment insurance (UI) generosity that resulted from the CARES Act of March 2020. Our shock estimates result from a reduced-form econometric model of the labor market, and we are therefore completely agnostic as to what extent the shocks reflect structural shocks hitting the economy or policy interventions. Standard models of labor search, however, would predict that an increase in UI generosity should increase the value of the worker’s outside option, which in turn would (weakly) increase the bargained/contracted wage rate for a given number of hours, everything else constant.16 In our reduced-form model, this should manifest itself as a negative labor supply shock.
Fig. 11 plots our measure of estimated supply and demand shocks for each sector on the -axis against the share of initial UI claims per industry for the months of March and April.17 . We find a significant negative correlation between the two variables: sectors corresponding to a larger share of UI claims in that month seem to have experienced both more negative labor supply and demand shocks. We do not intend to establish any causal relationship between the two variables, as this simple exercise does not control for many other sources of variation in the relative number of UI claims across sectors, but rather provide suggestive evidence of a relationship that would be predicted by simple models of the labor market.
Fig. 11.
Correlation between sectoral shocks and share of UI claims.
ML: Mining and logging; C: Construction; M: Manufacturing; WT: Wholesale trade; RT: Retail trade; TW: Transportation and warehousing; U: Utilities; I: Information; FA: Financial activities; PBS: Professional and business services; EHS: Education and health services; LH: Leisure and hospitality; OS: Other services. Gray bands represent 95% confidence intervals.
Another important feature of the CARES Act that further complicates the analysis of the potential role of UI expansion generosity: the fact that it also applied to furloughed workers. Furloughed workers remained part of employers’ workforces and do not need to look for work to be classified as unemployed in the CES data. A furloughed worker is registered in the CES with zero hours and zero earnings, and so our analysis treats them as having effectively left the labor market.
5. Robustness and validation
5.1. Methodological challenges posed by COVID-19
The different natures and sheer sizes of shocks during COVID-19 can pose challenges to our empirical exercise for a number of reasons; this section enumerates them and shows how we address them. First, they can make the residuals non-stationary, thus rendering the Wold decomposition invalid. Second, they can call into question the assumption of linearity either due to a structural break or because large shifts in supply and demand curves may push them into a region where their elasticities are no longer constant. Third, given that different occupations have different wages within each sector, if some occupations are affected differently during COVID-19, then changes in sectoral wages may be purely coming from changes in the composition of occupations.
The issues that arise when estimating a VAR with a sequence of extreme observations, such as those taken during COVID-19, and how to properly tackle them has been thoroughly discussed in Lenza and Primiceri (2020). In their work, they conclude that it is acceptable to drop these extreme observations for our purposes, which is that of parameter estimation. Hence, we follow their lead and address the first and second concerns by estimating the model excluding the COVID-19 months (March–May 2020). The second issue, regarding linearity/structural breaks, is hard to address with two data points without adding more structure to our empirical framework. Structural breaks would affect our historical decomposition results through changes in the SVAR labor elasticities and lag structure. For instance, the risk of being infected when going to work might affect not only workers willingness to work when offered the same wage, but also how agents supply labor at the margin when offered a full set of off-equilibrium wages — labor supply elasticity. If this is the case, what we define as a supply shock would be only a surprise from the point of view of the econometrician and not that of the agents. Hence, our historical decomposition estimates would be biased. Also, in terms of the lag structure, by extrapolating persistence from February to March, for example, one might get smaller residuals that are likely to overestimate the contribution of both labor demand and supply shocks during the COVID-19 crisis. While not being able to account for these issues, we attempt to assuage concerns regarding this second aspect by performing a validation exercise in Section 5.3, in which we argue that our identified shock series correlate with externally measured series such as a telework index.
5.2. Composition effects
One challenge to our identification assumptions is related to composition effects. A situation where a negative labor demand shock leads to the destruction of mostly low-wage jobs is consistent with a fall in the number of hours and an increase in the average real wage, which could be captured as a supply shock. Mongey et al. (2020), for example, document that workers employed in jobs with low ability to work from home tend to have lower incomes and were more likely to lose their jobs according to the March 2020 CPS. This concern is hard to address due to the lack of high-quality disaggregate data at a sufficiently high frequency. Nevertheless, we attempt to address this issue in three different ways.18
5.2.1. Production and nonsupervisory employees
Our first attempt at addressing this issue consists of repeating the baseline exercise for all NAICS-2 sectors, but using data on hours and earnings for employees in production and nonsupervisory roles only. By focusing on production employees, our exercise is repeated over a more homogeneous group of workers and is therefore less prone to be contaminated by composition effects. We find that this does not substantially alter our baseline results. Fig. 12, Fig. 13 present the shock decompositions for March and April 2020, respectively, using production employees.19 For total private employment, the fall in the growth rate of hours is slightly smaller in March (−1.91 pp vs. −2.59 pp) but larger in April (−18.6 pp vs. −16.24 pp). Supply shocks account for 77% of the drop in March and 68% in April. Overall, we find similar patterns across sectors. The importance of demand shocks increases in some sectors, namely in Leisure and Hospitality (56% in March, 43% in April) and Transportation (65% in March), but it falls in other sectors, suggesting that while there could be some composition bias, our baseline results seem to be relatively robust.
Fig. 12.
Historical decomposition of the growth rate of hours across sectors using production and nonsupervisory employees only, March 2020.
Notes: The sample for production and nonsupervisory employees we use to estimate our SVAR starts in 1984. Production and nonsupervisory employees CES series code for real wages is 32 and for aggregate weekly hours is 81.
Fig. 13.
Historical decomposition of the growth rate of hours across sectors using production and nonsupervisory employees only, April 2020.
Notes: The sample for production and nonsupervisory employees we use to estimate our SVAR starts in 1984. Production and nonsupervisory employees CES series code for real wages is 32 and for aggregate weekly hours is 81.
Additionally, Fig. 5, Fig. 6 show that our baseline results do not change much when our method is applied to hours and wages of production and nonsupervisory employees for industries at the NAICS-3 level. By focusing on a more disaggregated industry classification, we again attempt to apply our method to what is plausibly a more homogeneous set of workers.
5.2.2. CPS counterfactual
Our second method to address concerns regarding composition effects involves using micro data from the Current Population Survey (CPS, sourced from IPUMS) to compute the implied changes in average wages that would be observed if the joint dynamics of hours and wages were completely driven by composition effects in March and April. We find that this would have generated large increases in hourly earnings that are largely at odds with the observed micro data for March and April 2020 and could only be rationalized with implausibly large demand shocks over the same period.
We begin by computing counterfactual wage changes in specific sectors under the assumption that there are no labor supply shocks and that all changes in wages are attributed to composition effects. We focus on the three subsectors for which hours fell the most in April 2020: Travel accommodation (NAICS: 7211), Clothing and clothing accessories stores (448), and Food Services and Drinking Places (722).20 For each sector and occupation , we compute hours worked in the pre-pandemic period as well as average hourly earnings .21
We then take the observed (month-on-month) changes in hours worked in each of the sectors: −2.48% and −92.83% in Clothing Stores for March and April, respectively; −14.36% and −71.01% for Food & Drinking Places; −9.79% and −78.52% for Accommodation. For each sector, we rank all occupations in that sector by hourly earnings. Given that we observe hours worked for each occupation and in each sector, we drop the appropriate number of hours worked starting with the lowest-earning occupations until the fall in hours corresponds to the one observed in the data and we then recompute the average hourly earnings in that sector. We do this first for March, taking the 2019 CPS distribution of hours across occupations and sectors as the benchmark and applying the observed sectoral drop in hours for that month. We then apply the April drop in hours to the resulting distribution in March. This allows us to compute two counterfactual hourly earnings for each sector, one for each month. These results are shown in Table 1.
Table 1.
Counterfactual hourly earnings for selected sectors, assuming extreme composition effects. Note that these are not hourly wages, hence the differences in levels.
| Clothing stores | Accommodation | Food & drink places | |
|---|---|---|---|
| 2019 CPS hourly earnings | 21.16 | 17.61 | 14.82 |
| Counterfactual March 2020 | 21.47 | 18.55 | 15.35 |
| % March 2020 CF vs. 2019 CPS | +1.45% | +5.29% | +3.59% |
| % , data | −0.061% | −1.62% | −2.54% |
| Counterfactual April 2020 | 65.35 | 38.28 | 24.54 |
| % April 2020 CF vs. March 2020 CF | +204.43% | +106.39% | +59.80% |
| % , data | +11.33% | +3.05% | −1.11% |
By construction, and given that all these sectors experienced drops in hours in both March and April, the composition-effect counterfactual hourly earnings rise for these two months. Importantly, they rise by considerably more than in the data. In order to reconcile these composition effects with the observed changes in the data, these sectors would need to have suffered extreme labor demand shocks that would have resulted in considerable drops in the hourly earnings of the workers who remained employed, so as to offset the large increase driven by the composition effects.
We proceed to document that there is no evidence of large drops in wages for workers in occupations that would remain employed under the composition effects-only counterfactual. To do this, we use data from the 2020 Monthly CPS (also sourced from IPUMS) to track hourly earnings of workers who work in these sectors, in occupations that did not experience a fall in hours under our counterfactual scenario. We focus on the occupation with the largest percentages of hours worked in our counterfactual scenario for each sector: Customer service representatives for Clothing Stores (34.7% of hours worked in the April counterfactual, occupation code 5240) and Chefs and head cooks for both Accommodation (17.6% of hours worked in the April counterfactual, occupation code 4000) and Food & Drink (28.3% of hours worked in the April counterfactual). Fig. 14 shows that these hourly wages were relatively stable during March and April 2020.
Fig. 14.
Hourly wages for occupations with largest share of hours worked under composition effect counterfactual in each sector.
2020 Monthly CPS (IPUMS).
Our analysis of the micro data does not invalidate the possibility that composition effects played a role in explaining the joint dynamics of hours and hourly wages during the months of March and April 2020, but we hope to have convinced the reader that an extreme scenario in which there are no negative labor supply shocks and where all movements in wages are caused by demand shocks and composition effects would have resulted in dynamics for wages that are at odds with the micro data.
5.2.3. Constant wage counterfactual
Finally, we use the parameter estimates from our baseline estimation exercise to perform an alternative shock decomposition where we assume that wages did not increase at all for certain sectors. Composition effects should, in principle, generate opposite movements in wages and hours in March and April that would lead us to overestimate the importance of supply shocks. By imposing that wages remained flat and did not increase, and then using our baseline estimates to perform a historical decomposition, we are in a sense providing a lower bound for the importance of supply shocks for the period studied. We again focus on three of the hardest hit NAICS-3 sectors in April – Travel accommodation, Clothing and clothing accessories stores, and Food Services and Drinking Places – and show that even if we assume that wages did not increase in these sectors (and remained flat), supply shocks still played a very significant role.
The results of this counterfactual exercise, where wages are held constant, are shown in Table 2. These results show that the relative contribution of supply shocks to movements in hours falls by 10.6 pp for Clothing Stores, 3 pp for Accommodation, and actually rises by 0.9 pp for Food services & Drinking places. Thus supply shocks still play a dominant role in explaining movements in hours for these sectors even in the absence of observed increases in wages.
Table 2.
Counterfactual historical decomposition for selected sectors, assuming composition effects drive all the observed wage increase.
| Clothing stores | Accommodation | Food & drink places | |
|---|---|---|---|
| April Benchmark Historical Decomposition | 73.9% | 51.7% | 51.0% |
| April Counterfactual Historical Decomposition | 63.3% | 48.7% | 51.9% |
5.3. Validating the results: share of jobs that can be performed from home by sector
If confinement measures are empirically meaningful for labor supply, we should expect that our estimates of labor supply shocks will be positively correlated with the ability of workers to perform their tasks at home. Fig. 15 plots our estimated supply shocks (y-axis) for April 2020 against the share of jobs that can be done at home by sector (x-axis), taken from Dingel and Neiman (2020). Panel (a) confirms that such a correlation exists. Leisure and Hospitality, the sector with the smallest share of jobs that can be performed from home, was precisely the sector that was hit the hardest by a negative labor supply shock. Sectors with larger such shares endured smaller labor supply shocks, such as Financial Activities and Information. Despite the small number of observations, the relationship is statistically significant at the 5% level (p), and the share of workers that can perform their job at home per sector explains 34% of the variation of estimated supply shocks. Note also that this relationship is robust to excluding the Labor and Hospitality sector from the analysis; see panel (c). Panel (b) shows that there is also some correlation between the share of jobs that can be done at home and the estimated demand shock in April 2020, but panel (d) shows that this correlation is no longer statistically significant once we remove Labor and Hospitality.
Fig. 15.
Correlation between sectoral shocks in April 2020 and the sectoral share of jobs that can be done at home.
ML: Mining and logging; C: Construction; M: Manufacturing; WT: Wholesale trade; RT: Retail trade; TW: Transportation and warehousing; U: Utilities; I: Information; FA: Financial activities; PBS: Professional and business services; EHS: Education and health services; LH: Leisure and hospitality; OS: Other services. Gray bands represent 95% confidence intervals.
Furthermore, the relationship between this measure and the supply shocks is consistently stronger than that with demand shocks, even when we remove Leisure and Hospitality (which experienced both the largest demand and the largest supply shock during this period).
In the Online Appendix, we show that the validation exercise also holds for the month of March (Figure B.6). Additionally, it also shows that we obtain the opposite pattern in May 2020, with sectors where a smaller share of jobs can be done at home experiencing the most positive supply shocks. We also repeat the analysis for the months of March and April 2019: Figure B.7 shows that the statistically significant and positive correlation vanishes when this measure is compared with supply shocks estimated during a “normal” period.
6. Conclusion
In this paper, we employed Bayesian SVARs and informative priors to estimate sequences of labor supply and demand shocks for each major sector of the US economy. Focusing on the ongoing COVID-19 outbreak, we found that two-thirds of the fall in the growth rate of hours worked in March and April 2020 could be attributed to negative labor supply shocks. Most NAICS-2 sectors were subject to negative labor supply and demand shocks. One sector in particular – Leisure and Hospitality – was subject to historically large negative supply and demand shocks. Other sectors, such as Information and Retail Trade, experienced small supply shocks and, in some cases, positive demand shocks.
Although there are some valid concerns that our results could be partly driven by composition effects and that cannot be easily addressed, our results seem to be relatively robust to using narrower categories of workers and industries. We also showed that the size of our estimated supply shocks correlates with other measures, such as the fraction of jobs in each sector that can be performed from home. We believe that this serves as a validation of our shock identification strategy.
Properly measuring demand and supply shocks is essential for the design and implementation of economic policy during the COVID-19 outbreak. Negative labor supply shocks are more directly related to the ongoing public health crisis (and public health policy response), while labor demand shocks reflect economic forces that may persist beyond the public health crisis. Negative demand shocks may reflect a fall in aggregate demand that can be addressed via fiscal policy, particularly in sectors that are not directly affected by the lockdown (Guerrieri et al., 2020, Faria-e-Castro, 2021). Our shock decomposition could help policymakers to identify which sectors are most affected by lack of demand, and to appropriately design and target policies aimed at minimizing the effects of the current crisis on those sectors.22 We also think that our measurement exercise is useful for those conducting work on quantitative models of the COVID-19 crisis, as it provides moment conditions regarding movements in labor supply and demand that empirically plausible models should be able to match. Finally, the estimated series of shocks can also be used as instruments for labor supply and demand shocks in applied work.
Footnotes
We thank Christiane Baumeister, Jesús Fernández-Villaverde, Erik Hurst, and Peter Klenow for very helpful comments and discussions. We thank seminar participants at the Bank of England, Bank of Portugal, Federal University of Pernambuco, Federal Reserve Bank of St. Louis, and Bank of Mexico and conference participants at the NBER SI 2020 Micro Data and Macro Models session for comments and suggestions. We also thank Joao Barata and Serdar Birinci for enlightening conversations regarding the micro data. Joao Duarte and Pedro Brinca acknowledge funding from Fundação para a Ciência e a Tecnologia (UID/ECO/00124/2013, UID/ECO/00124/2019, PTDC/EGE-ECO/7620/2020, and Social Sciences DataLab, LISBOA-01-0145-FEDER-022209), POR Lisboa (LISBOA-01-0145-FEDER-007722, LISBOA-01-0145-FEDER-022209), POR Norte (LISBOA-01-0145-FEDER-022209) and CEECIND/02747/2018. The views expressed here are those of the authors and do not necessarily reflect the views of the Federal Reserve Bank of St. Louis or the Federal Reserve System. First version: May 12, 2020.
It should be noted that even from the point of the view of the economic agents themselves it is arguably hard to immediately know how to behave when offered a full set of different wages under this extreme environment. In any event, we acknowledge that the inability to identify structural breaks without more data or more structure is a limitation of our exercise.
The focus of this paper are labor demand and supply shocks, i.e. not “aggregate” (final output) demand and supply shocks. This means that while a negative TFP shock, for example, would be considered a negative supply shock in the market for final output, it materializes as a negative demand shock in our context (along with negative aggregate demand shocks). Thus not all negative demand shocks may necessarily entail an optimal response from fiscal and monetary policymakers. However, and as we show in the paper, there are reasons to believe that the negative demand shocks that we estimate are not caused by TFP.
Examples include Danieli and Olmstead-Rumsey (2020), Barrot et al. (2020), Bodenstein et al. (2020) and Faria-e-Castro (2021).
also includes a “Total Private Employment” sector.
Uhlig (2017) explicitly lays out all the basic assumptions required for identifying demand and supply shocks.
Hamermesh (1996) provides a survey of microeconometric estimates of labor demand elasticity and finds them to be between and , while Lichter et al. (2015) find that 80% of the estimates are between and . Some macro studies such as Akerlof and Dickens (2007) and Galí et al. (2012) find that the labor demand elasticity can be or even higher.
Our prior beliefs on distributions for labor demand and supply elasticities also reflect a variety of labor market frictions, such as wage stickiness.
Appendix A provides further details on the data and sector classifications.
Figure B.1 in the Online Appendix plots the prior distribution for the elasticities along a histogram of draws from the posterior. Table A.2 presents moments of the posterior distributions and Figure B.2 plots impulse response functions.
Figures B.3 and B.4 in the Online Appendix plot the estimated shocks for all other sectors.
Our procedure is agnostic regarding the extent to which the slowdown is driven directly by lockdown measures or by endogenous, voluntary behavior on the part of workers and consumers.
Tables A.3 and A.4 in the Online Appendix report the median values along with 95% credible intervals for these shocks and a test for difference of supply and demand.
Figure B.6 in the Online Appendix shows that this in fact is a systematic pattern: sectors with the smallest shares of jobs that can be done at home are precisely the ones that are most affected by the easing of restrictions and that experienced larger labor supply shocks in May.
These equilibrium effects could arise via complementarities in preference across goods as in Guerrieri et al. (2020) or via input–output networks as in Baqaee and Farhi (2020), among others.
This data is taken from the OECD’s Trade in Value Added database.
We want to highlight the “everything else constant” component of this prediction, and the fact that there were many other changes occurring at the same time during this period. A structural analysis is beyond the scope of this paper.
This share corresponds to the number of initial UI claims for workers in a given sector divided by the total number of UI claims across all sectors for that month. The data is taken from Economic Policy Institute (2020) and is only available for 19 states as these are the only states that report the NAICS code of the industry of UI claimants.
Alternatively, one could think of a situation where the most productive workers quit to stay at home due to increased risk of infection, for example. In order to maintain production, firms are then forced to employ less productive workers at lower wages. This could lead to a situation where what was initially a negative supply shock leads to a reduction in wages and an increase in hours (as the less productive workers need to work more hours to produce the same output). This situation is, however, inconsistent with the evidence presented in Mongey et al. (2020), that lower income workers were more likely to lose their jobs during this period.
Tables A.6 and A.7 in the Appendix describe the shocks along with 95% credible intervals.
We use the 2020 Annual CPS data referring to occupations and industries worked in 2019 due to better and more consistent data quality versus the 2020 Monthly CPS, and assume that data to be representative of the pre-pandemic period (February 2020).
We use the uhrsworkly variable for hours worked weekly. To compute average hourly earnings, we divide incwage by the product of uhrsworkly and wkswork1. We exclude observations for which incwage is either zero or missing, observations for which uhrsworkly is either missing or smaller or equal than 1, and observations for which wkswork1 is smaller than 20. All sector-occupation variables are computed by using the appropriate sample weights. We focus on production and non-supervisory employees. There is no CPS flag that is consistent with the CES definition; we exclude any occupations whose labels include the strings manage or supervis.
A natural caveat to this is that aggregate shocks may manifest themselves differently across sectors. That is, some aggregate shocks may be demand shocks in some sectors and supply shocks in others. Additionally, aggregate supply output shocks, such as TFP shocks, could also manifest themselves as demand shocks in the labor market. We provide some suggestive evidence that the demand and supply shocks do not seem to emanate from supply chain distortions, the most plausible source of TFP disturbances during the period of analysis.
Data for all employees is available from 2006 onwards, only. For all estimation exercises involving production and non-supervisory employees, the CES data series are longer and begin in 1990.
Supplementary material related to this article can be found online at https://doi.org/10.1016/j.euroecorev.2021.103901.
Appendix A. Data sources and sector classification
We use the Current Employment Statistics (CES) database from the Bureau of Labor Statistics (BLS) to obtain monthly average hourly earnings of all employees in 1982–1984 dollars (CES code: 13) and aggregate weekly hours of all employees (CES code: 56). The data starts in March 2006 and goes until April 2020, and all series are seasonally adjusted.23 Table 3 lists all used CES industry classifications as well as the associated NAICS codes. Production and nonsupervisory employees CES data used for NAICS 3-digit sectors starts in 1990 and the series code for real wages is 32 and for aggregate weekly hours is 81.
Table 3.
CES industry classification.
| Sector | BLS code | NAICS code |
|---|---|---|
| Total private | 05000000 | – |
| Mining and logging | 10000000 | 11–21 |
| Construction | 20000000 | 23 |
| Manufacturing | 30000000 | 31–33 |
| Wholesale trade | 41420000 | 42 |
| Retail trade | 42000000 | 44–45 |
| Transportation and warehousing | 43000000 | 48–49 |
| Utilities | 44220000 | 22 |
| Information | 50000000 | 51 |
| Financial activities | 55000000 | 52–53 |
| Professional and business services | 60000000 | 54–56 |
| Education and health services | 65000000 | 61–62 |
| Leisure and hospitality | 70000000 | 71–72 |
| Other services | 80000000 | 81 |
Regarding concerns on data quality during the months of the pandemic, a BLS press release published on May 8, 2020 reveals that the collection rate in the establishment survey remained unchanged. See https://www.bls.gov/news.release/archives/empsit_05082020.pdf.
Appendix B. Supplementary data
The following is the Supplementary material related to this article.
Supplemental material includes an online appendix with additional figures, as well as replication materials.
References
- Akerlof G.A., Dickens W.T. Unfinished business in the macroeconomics of low inflation: A tribute to George and Bill by Bill and George. Brook. Pap. Econ. Act. 2007;2007(2):31–46. [Google Scholar]
- Baqaee D., Farhi E. Harvard University; 2020. Supply and demand in disaggregated Keynesian economies with an application to the Covid-19 crisis. [Google Scholar]
- Barrot J.-N., Grassi B., Sauvagnat J. Sectoral effects of social distancing. Covid Economics. 2020;(3) [Google Scholar]
- Baumeister C., Hamilton J.D. Sign restrictions, structural vector autoregressions, and useful prior information. Econometrica. 2015;83(5):1963–1999. [Google Scholar]
- Baumeister C., Hamilton J.D. Inference in structural vector autoregressions when the identifying assumptions are not fully believed: Re-evaluating the role of monetary policy in economic fluctuations. J. Monetary Econ. 2018;100(C):48–65. [Google Scholar]
- Baumeister C., Hamilton J.D. Structural interpretation of vector autoregressions with incomplete identification: Revisiting the role of oil supply and demand shocks. Amer. Econ. Rev. 2019;109(5):1873–1910. [Google Scholar]
- Bodenstein M., Corsetti G., Guerrieri L. 2020. Social distancing and supply disruptions in a pandemic. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chetty R., Guren A., Manoli D., Weber A. Are micro and macro labor supply elasticities consistent? A review of evidence on the intensive and extensive margins. Amer. Econ. Rev. 2011;101(3):471–475. [Google Scholar]
- Danieli A., Olmstead-Rumsey J. Manuscript, Northwestern University; 2020. Sector-Specific Shocks and the Expenditure Elasticity Channel During the COVID-19 Crisis. [Google Scholar]
- del Rio-Chanona R.M., Mealy P., Pichler A., Lafond F., Farmer D. 2020. Supply and demand shocks in the COVID-19 pandemic: An industry and occupation perspective. [Google Scholar]
- Dingel, J.I., Neiman, B., 2020. How many jobs can be done at home? In: Working Paper 26948, National Bureau of Economic Research.
- Doan T., Litterman R., Sims C. Forecasting and conditional projection using realistic prior distributions. Econometric Rev. 1984;3(1):1–100. [Google Scholar]
- Economic Policy Institute . Data collected from various sources; 2020. Weekly UI initial claims by state and industry. [Google Scholar]
- Eichenbaum, M.S., Rebelo, S., Trabandt, M., 2020. The macroeconomics of epidemics. In: Working Paper 26882, National Bureau of Economic Research.
- Elsby M.W., Hobijn B., Sahin A. The labor market in the great recession. Brook. Pap. Econ. Act. 2010;41(1 (Spring):1–69. [Google Scholar]
- Faria-e-Castro M. Fiscal policy during a pandemic. J. Econom. Dynam. Control. 2021;125(C) doi: 10.1016/j.jedc.2021.104088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galí J., Smets F., Wouters R. Unemployment in an estimated New Keynesian model. NBER Macroecon. Annu. 2012;26(1):329–360. [Google Scholar]
- Guerrieri, V., Lorenzoni, G., Straub, L., Werning, I., 2020. Macroeconomic implications of COVID-19: Can negative supply shocks cause demand shortages? In: Working Paper 26918, National Bureau of Economic Research.
- Hamermesh D.S. Princeton University Press; 1996. Labor Demand. [Google Scholar]
- Lenza M., Primiceri G.E. National Bureau of Economic Research; 2020. How to estimate a VAR after March 2020. [Google Scholar]
- Lichter A., Peichl A., Siegloch S. The own-wage elasticity of labor demand: A meta-regression analysis. Eur. Econ. Rev. 2015;80:94–119. [Google Scholar]
- Mongey, S., Pilossoph, L., Weinberg, A., 2020. Which workers bear the burden of social distancing policies? In: Working Paper 27085, National Bureau of Economic Research. [DOI] [PMC free article] [PubMed]
- Sims C.A., Zha T. Bayesian methods for dynamic multivariate models. Internat. Econom. Rev. 1998:949–968. [Google Scholar]
- Smets F., Wouters R. Shocks and frictions in US business cycles: A Bayesian DSGE approach. Amer. Econ. Rev. 2007;97(3):586–606. [Google Scholar]
- Uhlig H. Advances in Economics and Econometrics: Volume 2: Eleventh World Congress, vol. 59. Cambridge University Press; 2017. Shocks, sign restrictions, and identification; p. 95. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental material includes an online appendix with additional figures, as well as replication materials.