Establishing Surface Correspondence for Post-surgical Cortical Thickness Changes in Temporal Lobe Epilepsy

Abstract

In pre- and post-surgical surface shape analysis, establishing shape correspondence is necessary to investigate the postoperative surface changes. However, structural absence after the operation accompanies focal non-rigid changes, which leads to challenges in existing surface registration methods. In this paper, we present a fully automatic particle-based method to establish surface correspondence that can handle partial structural abnormality in the temporal lobe resection. Our method optimizes the coordinates of points which are modeled as particles on surfaces in a hierarchical way to reduce a chance of being trapped in a local minimum during the optimization. In the experiments, we evaluate the effectiveness of our method in comparison with conventional spherical registration (FreeSurfer) on two scenarios: cortical thickness changes in healthy controls within a short scan-rescan time window and patients with temporal lobe resection. The post-surgical scan is acquired at least 1 year after the presurgical scan. In region of interest-wise (ROI-wise) analysis, no changes on cortical thickness are found in both methods on the healthy control group. In patients, since there is no ground truth available, we instead investigated the disagreement between our method and FreeSurfer. We see poorly matched ROIs and large cortical thickness changes using FreeSurfer. On the contrary, our method shows well-matched ROIs and subtle cortical thickness changes. This suggests that the proposed method can establish a stable shape correspondence, which is not fully captured in a conventional spherical registration.

1. INTRODUCTION

Temporal lobe epilepsy (TLE) is the most common and intractable seizure disorder^1,2. Patients often have a structural hippocampus abnormality with TLE. In some cases, their seizures may be reduced through surgical resection of the anterior hippocampus. Understanding of functional and structural changes caused by surgery could help to predict post-operative seizure control on the basis of post-operative imaging findings^3–7. Several existing studies explore the structural consequences of temporal lobe epilepsy surgery^3–7. According to the investigation in^4,5, the contralateral hippocampus exhibits significant volumetric reduction in patients. In addition to volume analysis, cortical surface analysis may be important in developing imaging prognostic markers of postoperative seizure control^3,8. Accordingly, it is necessary in cortical structural analysis to acquire a well-established shape correspondence between the paired surfaces.

Many existing surface registration methods are accurate in quantifying non-surgical cortical anatomy changes. Spherical parameterization shows great performance on surface registration^9–14. However, due to a large mapping distortion of the resected regions, spherical parameterization may not be accurate in the case of brain tissue resection. For instance, a shape correspondence established via conventional spherical registration¹⁵ often fails to transfer pre-surgical parcellation map to post-surgical surface due to large distortion introduced by removing tissues that generally yield significant uncertainty in the optimization of spherical registration as shown in Fig. 1. As such, this method may not be appropriate for use in spherical registration between pre- and post-surgical data.

Figure 1.

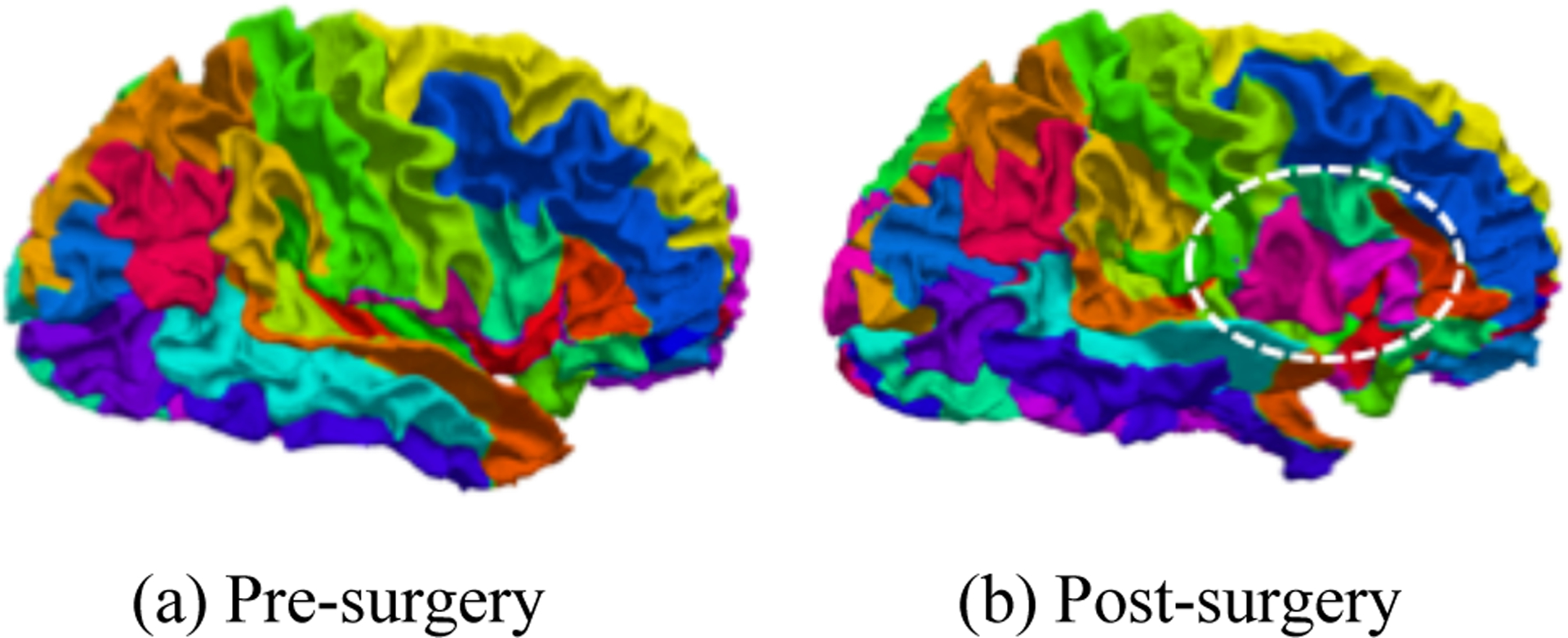
An example of failed shape correspondence using FreeSurfer. (a) parcellation map on the pre-surgical surface. (b) transferred parcellation map on the post-surgical surface. The parcellation map of pre-surgical surface is transferred to post-surgical surface using the correspondence established by FreeSurfer. The circle region shows that FreeSurfer failed to find the precise shape correspondence on post-surgical surface.

A particle-based approach is free from parametrization when establishing surface correspondence. This property gives particle methods a great potential to address intra-subject registration problem with surgical resection by avoiding explicit parametrization^16–20. Cates et al. originally proposed a particle framework, and Oguz et al.¹⁶ extended the original idea of particle ensemble over spatial locations in²⁰ to cortical surface matching by integration of local cortical geometry. In general, the particle approach requires significant inflation of the input surfaces, otherwise the Euclidean distances between particles becomes meaningless. To overcome implicit local matching, Datar et al.¹⁸ introduced geodesic distances to manually placed landmarks, which guarantees an isometry invariant correspondence. However, the accurate shape correspondence heavily depends on accurate landmark placement. In order to avoid manually placed landmarks, Agrawal et al.¹⁹ generated landmarks from deep neural networks, which results in huge workload to collect gold-standard landmarks.

In this paper, we explore ROI-wise post-surgical cortical thickness changes in temporal lobe epilepsy. For this purpose, we present a particle-based method for shape correspondence, in which spatial agreement of pre-labeled particles is optimized between pre- and post-surgical surfaces. In order to find the corresponding location of particles on the post-surgical surface, we minimize spatial discrepancy between paired particles. We propose a hierarchical way of optimization to give better initial guess of particles to avoid trapping in local minima. We evaluate the effectiveness of our method using cortical thickness changes for two cases: scan-rescan in control group acquired in a short time window as well as between pre- and post-surgical surfaces in patient group. We show comparable results to conventional spherical registration (FreeSurfer) in the healthy control group. In the patient group, FreeSurfer yields significant cortical thickness changes in several cortical regions with significant difference (p < 0.05), while our method shows subtle cortical changes compared with FreeSurfer.

2. METHOD

2.1. Data Acquisition and Pre-processing

The dataset we used in patient group contains 19 pairs of T1-weighted images (1× 1 × 1mm³) acquired from clinically diagnosed unilateral temporal lobe epilepsy patients. Each pair contains two scans from pre-surgery and post-surgery, respectively. In control group, we have 15 healthy subjects with two scans for each subject which are acquired within a few weeks of each other. In the patients, the post-surgical scan is acquired at least 1 year after the presurgical scan. In patient group, all resections occur in right hemisphere. In order to be consistent with patients, we used only the right hemisphere for healthy controls in our experiments.

The cortical surfaces were reconstructed via a standard FreeSurfer pipeline¹⁵ and inspected by experts. We first performed an initial affine alignment of surfaces for rotation correction. We then resample surfaces using 160k particles for dense shape correspondence. The resampled surfaces are used to establish shape correspondence.

2.2. Shape Correspondence

2.2.1. Particle Movement

The main goal of our method is to find intra-subject correspondence of each pair of surfaces. To this end, we fix particles on the pre-surgical surface and move those on post-surgical surface. We first fix particles on pre-surgical surface and put the initial guess of particles on post-surgical surface. Then we minimize the Euclidean distance between two particles with the same index on the paired surfaces, in order to make them have the same location on two surfaces. Formally, we define $F_B:{\Omega }_B\to {ℝ}^d$ and $F_A:{\Omega }_A\to {ℝ}^d$ as d-dimensional feature maps that quantify cortical geometry (e.g., spatial coordinate, local geometry, etc.). We consider the feature matching between two particles (u, v) as the following l₂-metric:

$$E_{sim}\left(u;v\right)={\Vert F_B\left(u\right)-F_A\left(v\right)\Vert }_2^2=\sum _{k=1}^d{\left[F_B^k\left(u\right)-F_A^k\left(v\right)\right]}^2.$$ (1)

Where ${\Omega }_B\subset {ℝ}^3$ and ${\Omega }_A\subset {ℝ}^3$ are pre- and post-surgical surfaces, respectively. After optimization, we can obtain the updated particles on post-surgical surfaces.

2.2.2. Hierarchical Optimization

A naïve optimization is involved with a large set of particles, which suffers from local minima without a strong initial guess. To address this issue, we place particles in a coarse-to-fine manner. We establish an initial set of particles as a connected graph on the cortical surface such as Delaunay triangulation, and subdivide the edges to increase the number of points at a finer level. Specifically, we first update spatial locations of particles at a coarse level and then place new particles at midpoints of edges for the spatial update at finer levels. In this way, we can provide a better initial guess of particle locations at each level than starting with a full set of particles.

2.3. Cortical Thickness Analysis

After intra-subject shape correspondence is established between surfaces in each pair, each particle is matched by location. We use cortical thickness to quantitatively evaluate the effectiveness of our method. We apply our method and observe thickness changes on both heathy group and patient group. We compute average cortical thickness in each ROI in this work. To this end, we transfer 49 labels in BrainCOLOR protocol²¹ from first scan to second scan via our established correspondence and mask out temporal lobe in patient group. Then we compute the average cortical thickness of all particles in a ROI-wise way on all paired surfaces. The full name of each ROI is listed in Table 1.

Table 1.

Acronym of 49 ROIs

ACgG	anterior cingulate gyrus	AIns	anterior insula	AOrG	anterior orbital gyrus
AnG	angular gyrus	Calc	calcarine cortex	CO	central operculum
Cun	cuneus	Ent	entorhinal area	FO	frontal operculum
FRP	frontal pole	FuG	fusiform gyrus	GRe	gyrus rectus
IOG	inferior occipital gyrus	ITG	inferior temporal gyrus	LiG	lingual gyrus
LOrG	lateral orbital gyrus	MCgG	middle cingulate gyrus	MFC	medial frontal cortex
MFG	middle frontal gyrus	MOG	middle occipital gyrus	MOrG	medial orbital gyrus
MPoG	postcentral gyrus medial segment	MPrG	precentral gyrus medial segment	MSFG	superior frontal gyrus medial segment
MTG	middle temporal gyrus	OCP	occipital pole	OFuG	occipital fusiform gyrus
OpIFG	opercular part of the inferior frontal gyrus	OrIFG	orbital part of the inferior frontal gyrus	PCgG	posterior cingulate gyrus
PCu	precuneus	PHG	parahippocampal gyrus	PIns	posterior insula
PO	parietal operculum	PoG	postcentral gyrus	POrG	posterior orbital gyrus
PP	planum polare	PrG	precentral gyrus	PT	planum temporale
SCA	subcallosal area	SFG	superior frontal gyrus	SMC	supplementary motor cortex
SMG	supramarginal gyrus	SOG	superior occipital gyrus	SPL	superior parietal lobule
STG	superior temporal gyrus	TMP	temporal pole	TrIFG	triangular part of the inferior frontal gyrus
TTG	transverse temporal gyrus

3. RESULTS

3.1. Parcellation Map

We used a parcellation map to evaluate the shape correspondence established by our method in a qualitative way as shown in Figure 3. We transferred pre-surgical parcellation map to post-surgical surface using the established correspondence by our method and FreeSurfer, respectively. After parcellation propagation, the patterns of the transferred parcellation map are similar with the pre-surgical one, while FreeSurfer shows huge distortion in a large portion of the non-resected regions. This suggests our method can establish more accurate correspondence than FreeSurfer.

Figure 3.

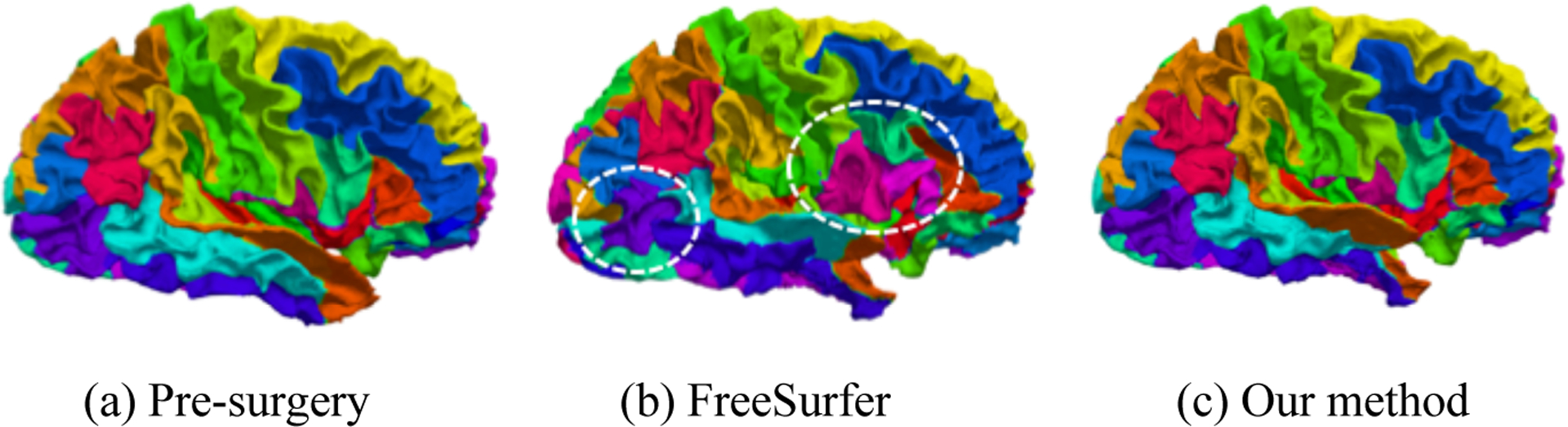
Parcellation map on a randomly chosen subject. (a) is pre-surgical parcellation. (b) is the propagated parcellation on post-surgical surface using correspondence established by FreeSurfer. (c) shows the propagated parcellation on post-surgical surface using our established correspondence. The circled areas are mismatched, which means FreeSurfer could not establish precise correspondence between pre- and post-surgical surfaces. By showing parcellation map, our method can establish more precise correspondence.

3.2. Cortical Thickness Analysis

We used cortical thickness to evaluate the effectiveness of our method in a quantitative way. We first applied our method on control group to establish shape correspondence between two scans of the same subject. The second scan in control group is acquired a few weeks after the first scan. Figure 4 shows the ROI-wise cortical thickness changes on control group. We performed and corrected paired t-tests on cortical thickness changes via false discovery rate (FDR)²² (q = 0.05). No significant cortical changes were found in our method and FreeSurfer. From the quantitative results, both methods can establish promising correspondence on healthy subjects as expected.

Figure 4.

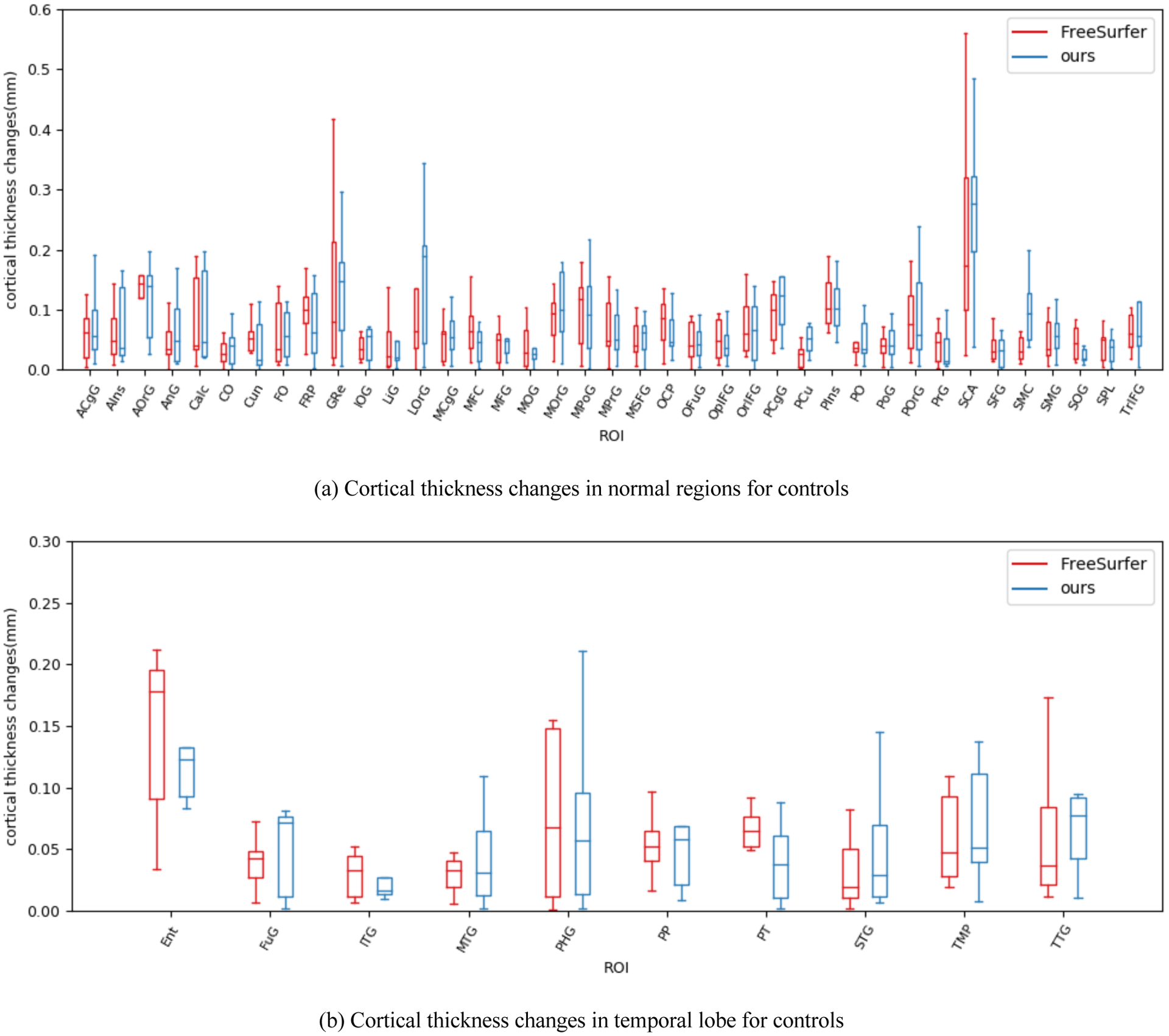
ROI-wise average cortical thickness changes on control group. (a) shows 39 ROIs from normal region. (b) shows 10 ROIs belonging to temporal lobe. The ROI-wise cortical thickness changes between first scan and second scan are small. There are no significant changes in cortical thickness for all ROIs.

We then tested our method on patient group which has 19 pairs of pre- and post-surgical surfaces. Figure 5 shows the ROI-wise cortical thickness changes. Since there is no ground truth available, we instead investigated the disagreement between our method and FreeSurfer. From Figure 5, several regions show large difference using FreeSurfer (e.g. MFC, ACgG and SCA). In order to explore the reason why this happened, we inspected the transferred parcellation map. As shown in Figure 6, their corresponding ROIs are not well matched. This suggested that pre-surgical ROIs are not transferred correctly to post-surgical surface using weakly established correspondence. In addition, we do not see obvious cortical thickness changes between pre- and post-surgery in Figure 6. Therefore, FreeSurfer are not able to fully address registration problem in temporal lobe resection. On the other hand, our method is independent of specific parameterization, which enables an improved correspondence between normal and resected surfaces (see Figure 5 and 6).

Figure 5.

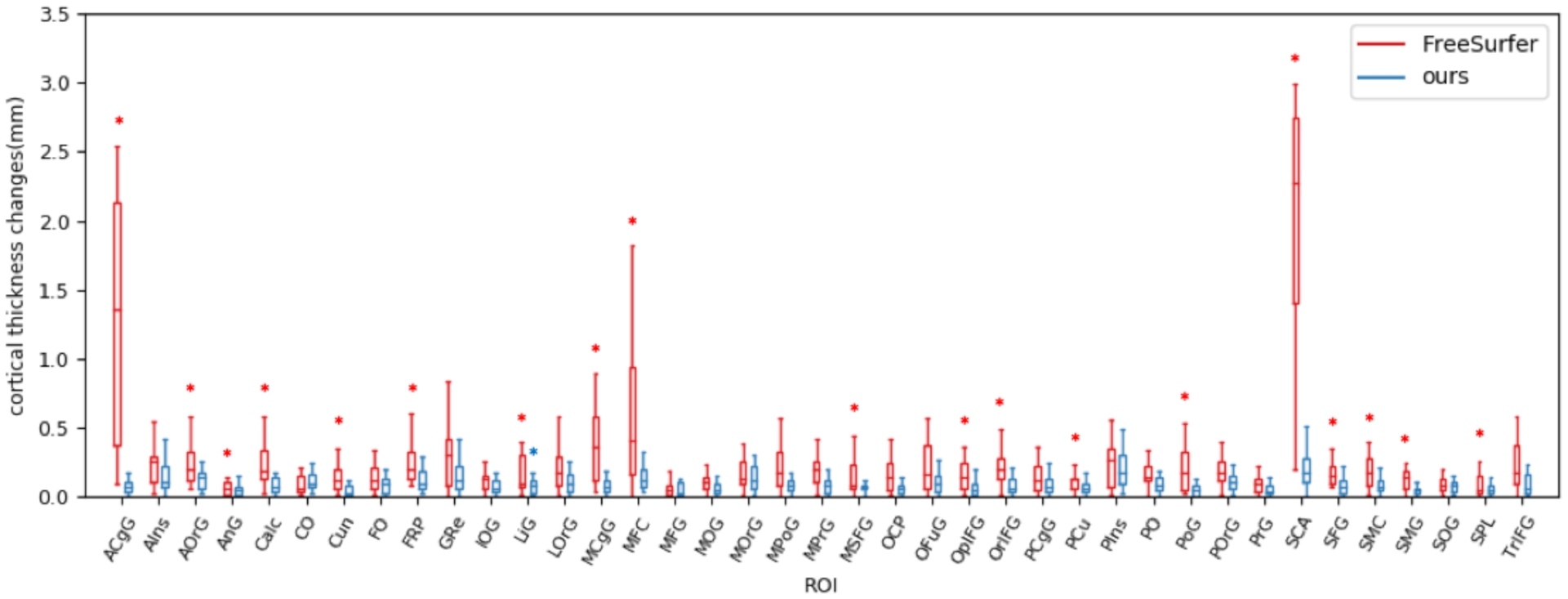
ROI-wise cortical thickness changes on patient group. There are 19 out of 39 ROIs that have significant thickness changes (red asterisk) using FreeSurfer. Lingual gyrus has significant cortical thickness changes (blue asterisk) using our method.

Figure 6.

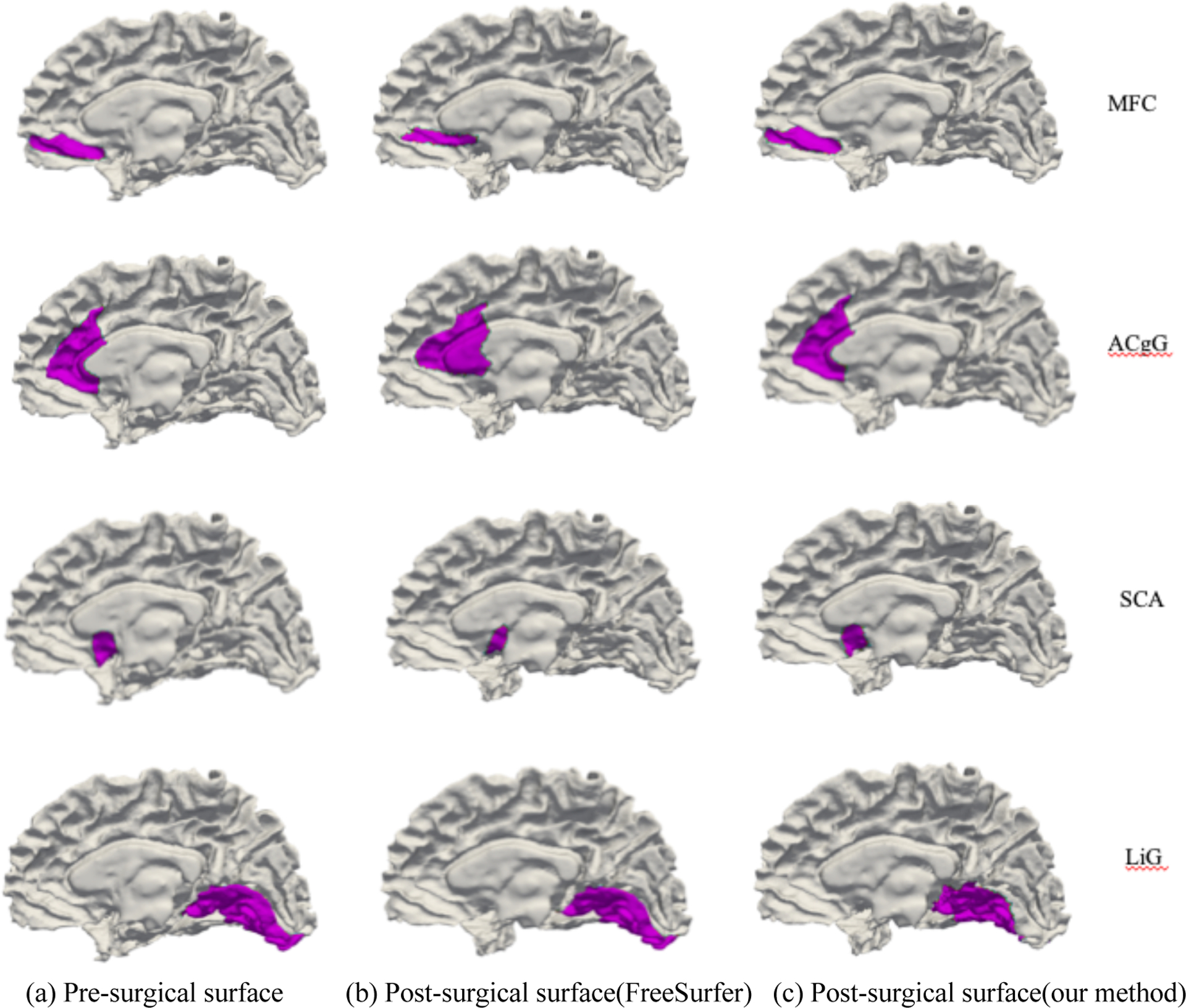
Four ROIs that have weak correspondence using FreeSurfer. (a) is the pre-surgical ROIs. (b) is the transferred ROIs using correspondence established by FreeSurfer. (c) is the transferred ROIs using correspondence established by our method. Pre-surgical ROIs are not able to be transferred to correct post-surgical locations using weak correspondence as shown in (b). Since we do not observe obvious changes between pre- and post-surgical surface, the significant ROI-wise cortical thickness changes in some regions are likely caused by mismatched ROIs.

4. CONCLUSION

In this work, we explored ROI-wise post-surgical cortical thickness changes after surgical resection in temporal lobe epilepsy. In order to obtain the corresponding cortical thickness on post-surgical surface, we first presented a particle-based method to establish shape correspondence between pre- and post-surgical surfaces. We minimized the Euclidean distance between corresponding particles on the paired surfaces to optimize the location of the particles on post-surgical surface. We optimized the particles in a hierarchical way to avoid local minima. In the experiment, we transferred pre-surgical parcellation map to post-surgical surface using our established correspondence and analyze the cortical thickness changes in a ROI-wise way. We evaluate the effectiveness of our method in comparison with conventional spherical registration (FreeSurfer) on two scenarios: cortical thickness changes in healthy control within a short scan-rescan time window and patients with temporal lobe resection. The result showed that no cortical thickness changes were captured in healthy controls using our established shape correspondence as well as FreeSurfer. In the patient group, Freesurfer found several regions with large differences that were not found using the proposed registration method, and this is likely to be due to errors in registration using the FreeSurfer method. After surgical resection, global and local distortion over cortical regions yielded the performance of spherical methods in registration. Compared with the unstable parcellation map and less realistic cortical thickness changes captured by FreeSurfer, our method can provide promising correspondence between normal and resected surfaces.

Figure 2.

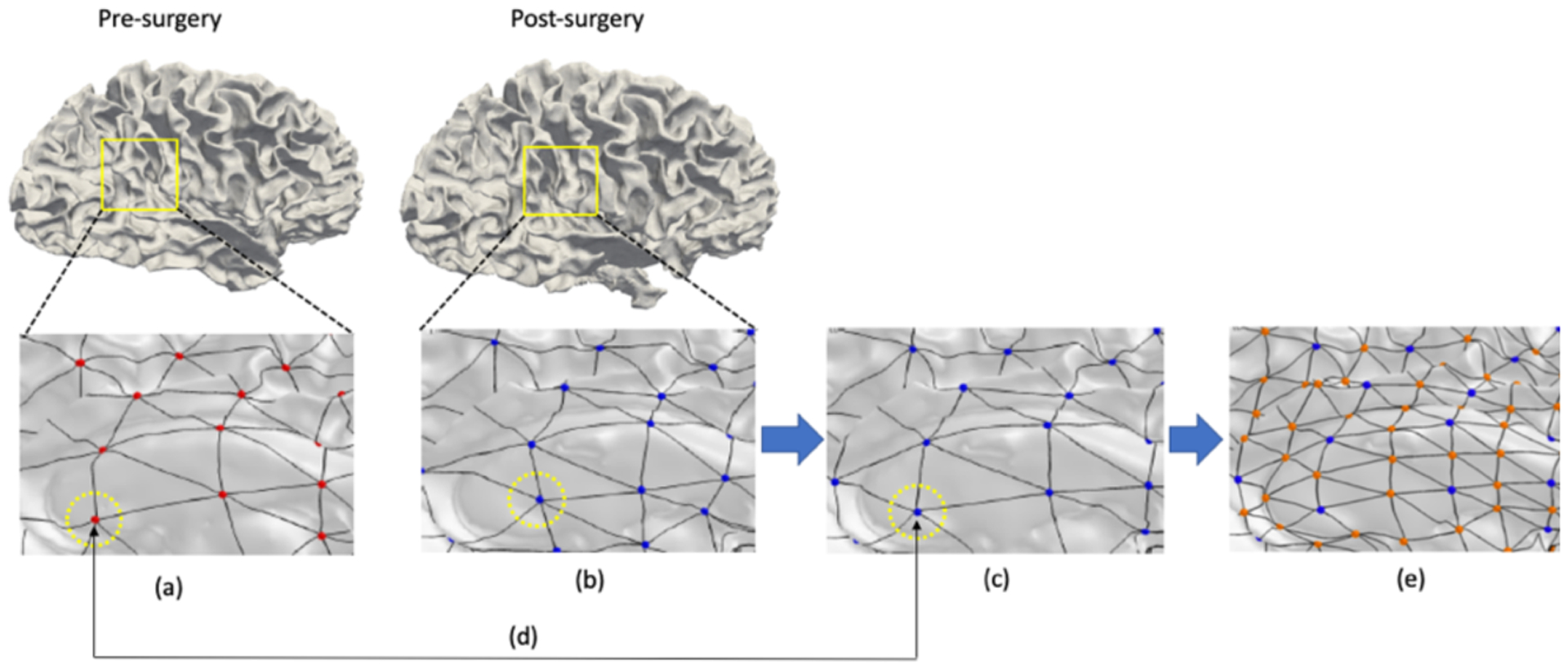
A schematic overview of the proposed method. (a) the fixed particles on pre-surgical surface. (b) the initial particles on post-surgical surfaces. (c) the updated particles on post-surgical surfaces after optimization. (d) the established correspondence between two particles. The particles with the same index have same locations on pre- and post-surgical surface. (e) the icosahedral subdivision to get a better initial guess of higher levels of optimization