Computational IR Spectroscopy of Insulin Dimer Structure and Conformational Heterogeneity

Abstract

We have investigated the structure and conformational dynamics of insulin dimer using a Markov state model (MSM) built from extensive unbiased atomistic MD simulations, and performed infrared spectral simulations of the insulin MSM to describe how structural variation within the dimer can be experimentally resolved. Our model reveals two significant conformations to the dimer: a dominant native state consistent with other experimental structures of the dimer, and a twisted state with a structure that appears to reflect a ~55° clockwise rotation of the native dimer interface. The twisted state primarily influences the contacts involving the C-terminus of insulin’s B chain, shifting the registry of its intermolecular hydrogen bonds and reorganizing its sidechain packing. The MSM kinetics predict that these configurations exchange on a 14 μs timescale, largely passing through two Markov states with a solvated dimer interface. Computational amide I spectroscopy of site-specifically ¹³C¹⁸O labeled amides indicates that the native and twisted conformation can be distinguished through a series of single and dual labels involving the B24F, B25F, and B26Y residues. Additional structural heterogeneity and disorder is observed within the native and twisted states, and amide I spectroscopy can also be used to gain insight into this variation. This study will provide important interpretive tools for IR spectroscopic investigations of insulin structure, and transient IR kinetics experiments studying the conformational dynamics of insulin dimer.

Graphical Abstract

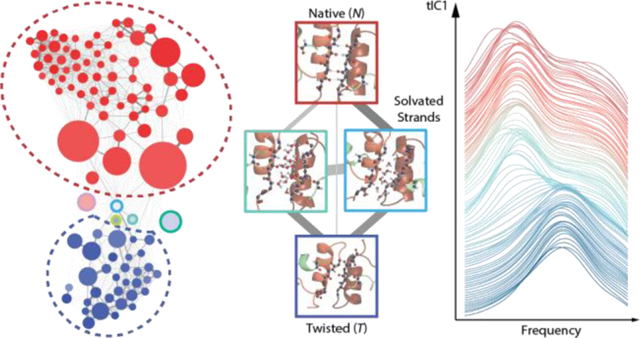
Introduction

Protein structure-function relationships have been rethought over the past two decades to account for the functional role of conformational disorder, which appears in intrinsically disordered proteins (IDPs) and proteins with intrinsically disordered regions (IDRs).¹ Proteins with structural heterogeneity and conformational disorder contain a variety of thermally accessible conformers undergoing rapid structural fluctuations or activated interconversion kinetics between free-energy basins on a complex free energy landscape.^2–4 Such IDPs and proteins with IDRs have been observed to be involved in many biological processes including regulation, signaling, and coupled-folding and binding to functional partners.^{1, 5}

Structural characterization of IDPs and proteins with IDRs requires an ensemble description, which creates numerous experimental challenges. Ensemble-structure determination is naturally an ill-posed problem in which degrees of freedom in relevant conformational states far exceed limited number of measurements and information content of experiments.⁶ Also, fast conformational fluctuations and activated conformational dynamics cannot be decoupled,⁷ meaning that conformational characterization inherently requires experimental probes with both high structural and temporal resolutions. Traditional structural tools are often limited by their intrinsic time resolution, which prohibits one from accessing conformational fluctuations and interconversion of conformers with time scales spanning many decades from picoseconds to microseconds.^8–11 NMR spectroscopy that measures chemical shifts and J couplings is limited by the coalescence time scale of ms such that faster conformational dynamics are averaged whereas relaxation experiments provide indirect structural information.¹² Optical spectroscopies do carry the advantage of femtosecond time-scales for their light-matter interaction, but in most cases have little structural information content. Advances are being made with IR and 2D IR spectroscopies which probe structure sensitive molecular vibrations with fs–ps time resolution, and thereby have the capability of structural characterization on a peptide or protein structure that is essentially static.^13–23

Despite intensive experimental advances to investigating protein structures, all experimental methods face challenges of structural interpretation, which inevitably require structure-based models. Molecular dynamics (MD) simulation offers atomistic descriptions of protein structures and motions. Also, recent efforts of force field (FF) developments have improved the ability to study disordered proteins.²⁴ Clustering methods and kinetic frameworks have been developed to analyze conformational dynamics such as time-structure independent component analysis (tICA)^25–28 and Markov State Models (MSMs),^29–30 which provides a natural structural basis for computing experimental properties and studying interconversion kinetics. Computational advances have laid foundations of rationalizing experimental evidence, predicting experimental outcomes, and even helping design suitable experiments.

Direct quantitative comparison of atomistic protein structures and IR experiments is now possible using computational amide I spectroscopy.³¹ Amide I IR spectroscopy, which probes the C=O stretching vibration of the polypeptide backbone in the 1600–1700 cm⁻¹ frequency range, can be used to interrogate local hydrogen bonding contacts to the carbonyl oxygen and structure-sensitive couplings between different amide carbonyls. This method can be used to predict traditional IR absorption and 2D IR spectra for simulated conformational distributions drawn from MD trajectories or MSMs, providing a unique route to investigate structure-spectrum correlations. Specifically, amide I vibrational frequencies can be predicted to high accuracy using spectroscopic “maps” that relate frequency to the local electrostatic potential or electric field from MD force fields at specific amide carbonyl sites.^32–39 Similarly, maps for vibrational coupling between different amide I vibrations are used to calculate the interaction of multiple backbone amide groups.^40–43 These maps have reached the point of predicting amide I spectroscopic observables to a high level of accuracy with 2 cm⁻¹ frequency uncertainty and provided a direct way to structurally interpret experimental IR spectra.³⁸ This approach has additional power when interpreting site-specific isotope-edited IR spectroscopy using computational spectroscopy with MD simulations and MSMs. This approach has been used for a number of peptides and proteins, such as spectroscopic investigation of various secondary structures,^44–46 conformational characterization of TrpZip2,¹⁶ disordered peptides and amyloid fibrils,^{22, 47} structural disorder of NTL9¹⁷ and CD3ζ transmembrane domain,⁴⁸ and investigating permeation mechanism of potassium ion in KcsA.^{20, 49–50}

In this study, we investigate the structural heterogeneity of insulin homodimer using a MSM built on MD simulations, and show how this structural variation can be interrogated using amide I IR spectroscopy of site-specifically isotope-labelled amide carbonyls. Insulin dimer dissociation is a necessary step prior to binding to insulin receptor, which is regarded as a coupled unfolding and unbinding process studied both computationally and experimentally.^51–56 Insulin monomer is a 51-residue peptide composed of two disulfide bonded chains with 21 residues on chain A and 30 residues on chain B. It has three α-helical segments, a β-turn located from B20Gly to B23Gly, and the B-chain C-terminus ranging from B24Phe–B30Thr is known to be disordered with the extent depending on mutations and solution environment.^57–64 This intrinsically disordered region folds and binds into a well-defined inter-monomer β-sheet in the native dimer structure stabilized by hydrogen bonding and sidechain packing of the aromatic triplet of B24Phe, B25Phe, and B26Tyr.^{51, 64–66} This B-chain C-terminus is also involved in the insulin receptor binding, exhibiting detachment of the B-chain C-terminus, a significant dihedral rotation on B24Phe, and hinging motion upon recognition with the insulin receptor,^67–70 which may share similar conformational transitions as in the dimerization.⁵⁴

Insulin dimer has also become a useful model system for investigating coupled folding and binding dynamics. Computational insulin dimerization studies have focused almost entirely on the conformational characterization in the monomeric state, with the current viewpoint that the dimer structure resembles published crystal structures. However, recent simulation study on mutant dimer, showed that mutation of B24Phe to Gly resulted in additional dimer conformations including strongly interacting dimer and weakly interacting dimer, which involves conformational change between B10His and B13Glu, and increased solvation of the dimer interface.⁷¹ A detailed description of the dimer conformational distribution still requires investigation, in particular accounting for changes of solvation environment such as pH, ionic strength, and temperature that can mediate dimer conformational changes and in turn dynamics of dimer dissociation and association.^72–73

Here, we present a computational study to characterize equilibrium conformational ensemble of insulin dimer is aqueous solution using MSMs built off extensive MD simulations, and computational amide I spectroscopy to predict how conformational substates can be observed in experiments. The MSM of insulin dimer provides an all-atom, high-resolution structural basis with associated interconversion rates to compare to IR structural and kinetics measurements. In addition to structures that are similar to previous experimental results, the MSM reveals a second major conformational state, the twisted dimer state with register-shifted β-strands, that has not been observed experimentally and computationally. Conformational exchange between twisted state and native state is predicted to occur on a 10–20 μs time scale. With the help of computational amide I spectroscopy, we proposed site-specific isotope labels that can effectively distinguish these two major conformational states, as well as intermediate configurations visited as they interconvert. This study forms a computational basis for experimental investigation of insulin dimer structures and kinetic experiments that can resolve conformational transition between these states.

Methods

Molecular Dynamics Simulations

MD sampling was initiated from the native crystal structure of wild-type human insulin dimer (PDB: 3W7Y) using the AMBER99sb-ildn force field (FF) and TIP3P water model.^74–75 To match the preferred low pH conditions for infrared spectroscopy that increase solubility, titratable side chains including HIS, GLU, and N-terminal NH₃⁺ were protonated. The COOH group was replaced by CONH₂ group because the AMBER FF does not have parameters for COOH. The protonated insulin dimer was solvated in a cubic water box, having 9000 water molecules and additional Na⁺ and Cl⁻ ions to represent the ionic strength of 0.15 M.

Potential energy minimization was performed to ensure a reasonable starting structure for further temperature equilibration. To equilibrate temperature, the system was then gradually heated to 310 K in the NVT ensemble for 20 ps. Subsequent density equilibration was performed in the NPT ensemble at 310 K and 1 atm for 100 ps. Production runs were performed in the NPT ensemble at 310 K and 1 atm using OpenMM on Folding@home.^76–77 Several rounds of MD simulations were performed, with starting structures reseeded from previous rounds to accumulate more statistics on rare conformational transitions and to explore new configurations faster than a direct single MD simulation. The aggregate sampling of insulin dimer consisted of 409 MD trajectories with the total sampling of 1.71 ms.

Construction of Dimer Markov State Model

The Markov State Model (MSM) of insulin dimer was constructed using MSMBuilder.⁷⁸ For clustering structures from MD sampling into conformational states, the collective variables (CVs) were inter-atomic distances between 102 C_α atoms in the dimer, resulting in 102×101/2 = 5151 C_α−C_α pairs. To ensure robustness of the results to outliers in the data, the quantile range was used instead of standard deviations. As the standardization routine to have normalized distance distributions, the distance values were scaled with RobustScaler module to remove the medians and to the quantile range between the 25th quartile and the 75^th quartile. Centering and scaling were performed independently on each pair. After scaling, time-structure independent components analysis (tICA) was applied on the time series data of all C_α−C_α pairs with the lag time of 125 ns.^27–28 The first 20 independent components (tICs) from tICA were selected as a subspace for subsequent k-medoids clustering, choosing k = 100 states.^79–80 These states were used as the basis for building the MSM with the lag time of 150 ns, with structures in each state drawn from the original MD sampling. Characterization of the MSM is described in the SI.

Visualization of the MSM Network

To visualize the MSM, network graphs were generated using Gephi 0.9.2,⁸¹ and the corresponding network layout was produced using the ForceAtlas algorithm.⁸¹ Markov states are treated as nodes with the radius proportional to its equilibrium population. Each node is connected with edges whose thicknesses reflect the sum of forward and backward transition probabilities between nodes. The ForceAtlas algorithm treats this network as a coupled spring-mass system, in which the spring constants correspond to the sum of the transition probabilities. Repulsive forces are added between each node to avoid spatial overlap of the nodes. The algorithm minimized the overall energy of the system by rearranging the layout of the network such that states stay in proximity to each other when they interconvert rapidly.

Simulations of Amide I Spectra

Amide I spectral simulations were performed using a mixed quantum-classical model that builds on atomistic structures drawn from classical MD simulations.³¹ Simulations of explicitly solvated structures for all 100 configurations within each of the 100 Markov states were performed using GROMACS 4.6.7,⁸² using the AMBER99sb-ildn force field and TIP3P water.^{74, 83} For each configuration, the solvent and ions were equilibrated around the position-restrained peptide for 100 ps at 300 K using the Berendsen thermostat.⁸⁴ Subsequent 1 ns production runs on the unrestrained protein were performed using the Nosé–Hoover thermostat under NVT conditions with a 1 fs integration step, and 20 fs/frame sampling rate for spectral simulations.^85–86 The final spectra for each Markov state was obtained by averaging the calculated spectra over all 100 initial configurations.

IR vibrational spectra were calculated from the Fourier transform of a transition dipole time-correlation function obtained from a mixed quantum-classical model implemented in the freely available g_amide and g_spec programs.^87–88 The model treats the amide I vibrations as a set of coupled oscillators assigned to each amide group of the backbone.^{31, 89} Collective electrostatic variables are used to translate, or “map”, a series of instantaneous structures along a trajectory onto a time-dependent Hamiltonian and transition dipole moment for the amide I vibrations. The amide oscillators, or “sites”, are identified by atomic positions of the CONH peptide backbone linkages. The vibrational frequency of each site is generated from a 4–site potential map (4P) which evaluates the electrostatic potential at the C, O, N and H positions and maps it to a vibrational frequency. The 4P map used in this study, 4PN-150, has a frequency prediction accuracy of σ=2.25 cm⁻¹.³⁸ In addition to the frequency of each site, vibrational coupling between amide I oscillators is obtained using coupling maps for mechanical through-bond coupling and electrostatic through-space coupling.⁴² Additional details are provided in the SI.

Amide I transition dipole correlation functions were calculated using a dynamic wavefunction propagation method,⁹⁰ using a Trotter expansion to reduce computation time.^91–92 The window time for calculations was set to 11 ps, equivalent to 3 cm⁻¹ frequency resolution. The model includes a 1.0 ps vibrational lifetime for amide I modes, to match experiments.^{89, 92} The isotope frequency shift of ¹³C¹⁸O isotope labels relative to ¹²C¹⁶O is set to −65 cm⁻¹.^93–94

Results

Insulin Dimer MSM

We performed 1.7 ms of aggregated unbiased equilibrium MD sampling of insulin dimer and constructed an all-atom, 100-state MSM using time-structure independent components analysis (tICA)^{25, 27–28} and k-medoids clustering. tICA variationally combines coordinates to maximize their auto-correlation time such that the resulting independent components (tICs) encode structural and kinetic information ordered by decreasing implied time scale.^27–28 K-medoids clustering is chosen to construct the MSM to identify statistically well-sampled states and to obtain a real-structure medoid instead of an average structure for the cluster.

The MSM contains dimer structures that are mostly compact, with a negligibly small number of configurations that are fully dissociated or loosely bound structures with non-specific contacts. Monomer conformations in the medoid structures are mostly within the range of folds observed in experimental structures, and individual Markov states vary in the degree of the structural disorder. Structural variation between dimers primarily reflects non-native contacts at the dimer interface between monomers, conformational variation, and unfolded segments. The time scales for exchange between states vary from a few μs to tens of μs. A summary of structural variables describing all 100 states is provided in the SI.

An overview of the MSM is presented as a network plot in Fig. 1a. Each Markov state is represented as a node (circle) whose radius is proportional to its equilibrium population in the MSM. Edges connecting these nodes correspond to pathways of state interconversions, with line thickness proportional to the sum of interconversion rates between pairs of states. The network layout is optimized such that states in proximity show fast state interconversion, giving a coordinate-free visualization of the equilibrium population and kinetics of the MSM.

Figure 1.

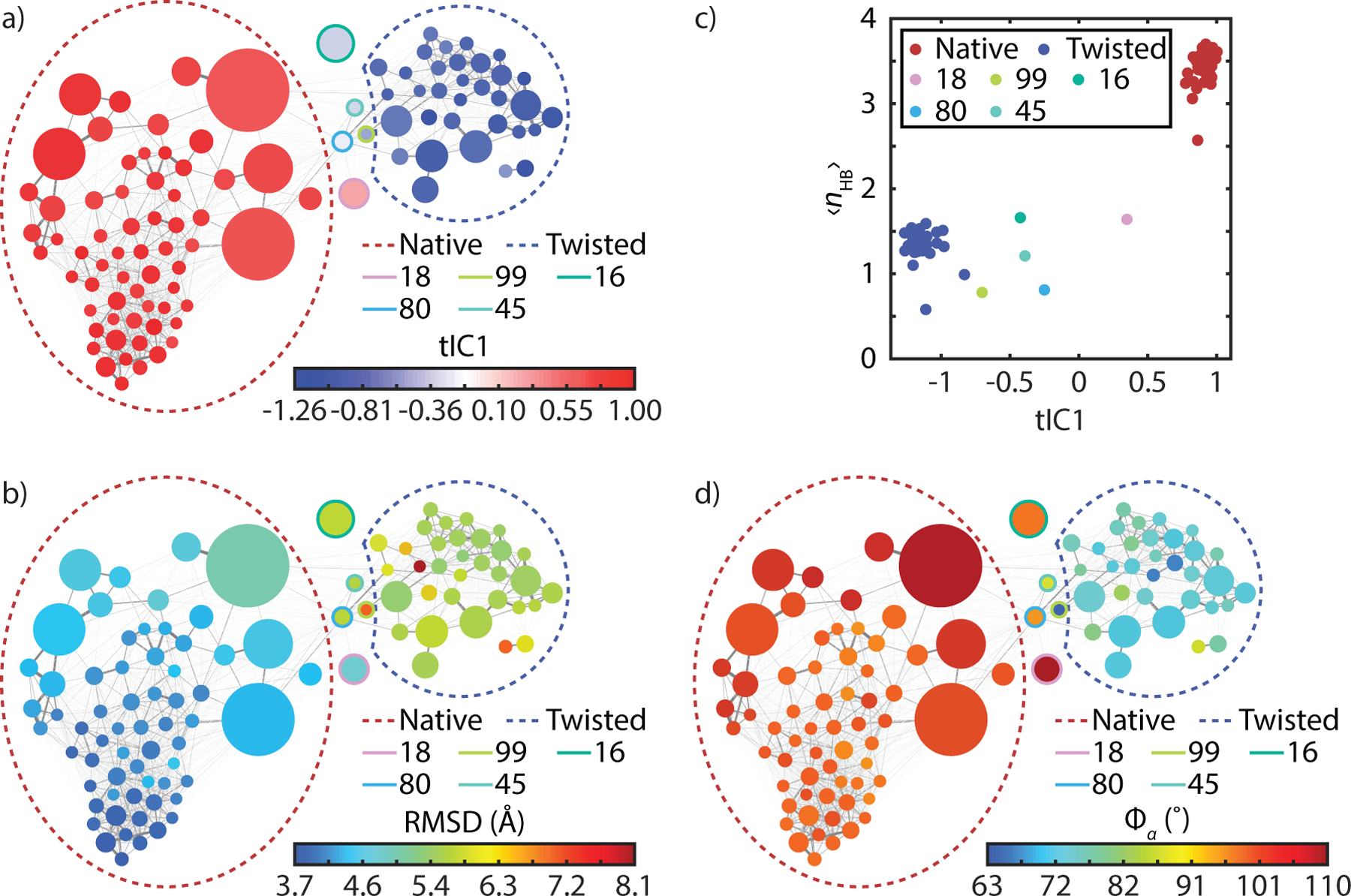
(a) Network representation of the dimer MSM with nodes color-coded by tIC1 values accounting for the slowest global process in the transition matrix. Thickness and color of the edges connecting nodes are proportional to the interconversion probabilities. Colored dashed circles identify the native and twisted states identified from a coarse-grained 3-state k-medoids clustering along tIC1. A full assignment of nodes to specific states is found in the SI. (b) Network plot color-coded by heavy atom RMSD with respect to crystal structure (PDB: 3W7Y). (c) Correlation of tIC1 with the average number of β-sheet HBs for the Markov state (ρ = 0.96). (d) Network plot color-coded by α pseudo-dihedral angles (ρ = 0.94).

The nodes of the network diagram in Fig. 1a are color-mapped to tIC1 values, illustrating that tIC1, the slowest kinetic process of the system, describes shifts in population between two large groupings of states. Color coding the network plot by the state’s average RMSD of heavy atoms relative to the dimer crystal structure (Fig. 1b), we observe that it is correlated with tIC1 (the correlation coefficient ρ = −0.64). The RMSD values vary from 3.7 Å to 8.1 Å across all 100 states, but the distribution is bimodally separated by states in the lower left with low RMSD configurations closest to x-ray dimer structures with values of 4–5 Å, and high RMSD values of >5.5 Å in the top right. This indicates that tIC1 is related to a significant conformational change in the dimer. We also calculated correlations of tIC1 to several collective variables (CVs), and found strong correlations (>0.8) to torsion angles, distances, and hydrogen bonds involving the B chains at the dimer interface (see Table 1 and SI).

Table 1.

Physical properties of the native (N) and twisted (T) dimer structures from the MSM, and their correlation coefficient to tIC1 (ρ): population percentage p, free energy change ΔG° using N as the reference state, RMSD of heavy atoms with respect to the crystal structure, average pseudo-dihedral angle between the B-chain helices 〈Φ_α〉, average number of amide HBs between inter-monomer β residues including B23G, B24F, B25F, B26Y$\langle n_{\text{HB}}^{\text{Amide}}\rangle$, average number of water-amide HBs of these β residues $\langle n_{\text{HB}}^{\text{water}}\rangle$, average number of inter-monomer contacts 〈n_MM〉, α contacts 〈n_α〉, and β contacts 〈n_β〉, backbone torsion angles ϕ/ψ for B22R and B23G, average distance of α contacts 〈d_α〉 and β contacts 〈d_β〉, and average number of HBs between A19 amide unit and B24 amide unit $\langle n_{\text{HB}}^{\text{A19}\cdots \text{B24}}\rangle$. Bracket average indicates the average over all structures within the same Markov state whereas the bar average refers to the weighted average over states based on their equilibrium population. Values in the parentheses indicate the standard deviation.

	Native (N)	Twisted (T)	ρ
p (%)	66	27
ΔG° (kJ/mol)	0	2.3
RMSD (Å)	4.4 (0.3)	5.6 (0.3)	−0.64
$\overline{\langle {\Phi }_{\alpha }\rangle }$ (°)	115.2 (15.3)	58.8 (14.7)	0.94
$\overline{\langle n_{\text{HB}}^{\text{Amide}}\rangle }$	3.4 (0.2)	1.4 (0.1)	0.96
$\overline{\langle n_{\text{HB}}^{\text{water}}\rangle }$	3.0 (0.3)	4.2 (0.5)	−0.71
$\overline{\langle n_{\text{MM}}\rangle }$	50.45 (0.65)	48.31 (1.84)	0.79
$\overline{\langle n_{\alpha }\rangle }$	3.28 (0.23)	2.47 (0.24)	0.69
$\overline{\langle n_{\beta }\rangle }$	5.79 (0.06)	2.93 (0.25)	0.97
B22R ϕ/ψ (°)	−99.2/4.6	−83.2/130.2	−0.82/0.95
B23G ϕ/ψ (°)	59.1/120.5	−65.0/−66.8	0.95/0.94
$\overline{\langle d_{\alpha }\rangle }$ (Å)	7.1 (0.33)	8.0 (0.42)	−0.80
$\overline{\langle d_{\beta }\rangle }$ (Å)	5.1 (0.09)	8.5 (0.69)	−0.83
$\overline{\langle n_{\text{HB}}^{\text{A19}\cdots \text{B24}}\rangle }$	0.60 (0.44)	0.80 (0.38)	−0.51

We used tIC1 values to group these two dominant clusters in order to understand the conformational changes that it describes. These coarse-grained states are shown as dashed circles in Fig. 1, and with the structural differences illustrated in Fig. 2. They appear related by twisted motion of the two monomers at the dimer interface, which leads to a disruption of native β-sheet contacts and a reconfiguration of sidechains at the dimer interface. Structural changes along tIC1 are described by several CVs used in previous simulation studies,^53–54 which are summarized in Table 1.

Figure 2.

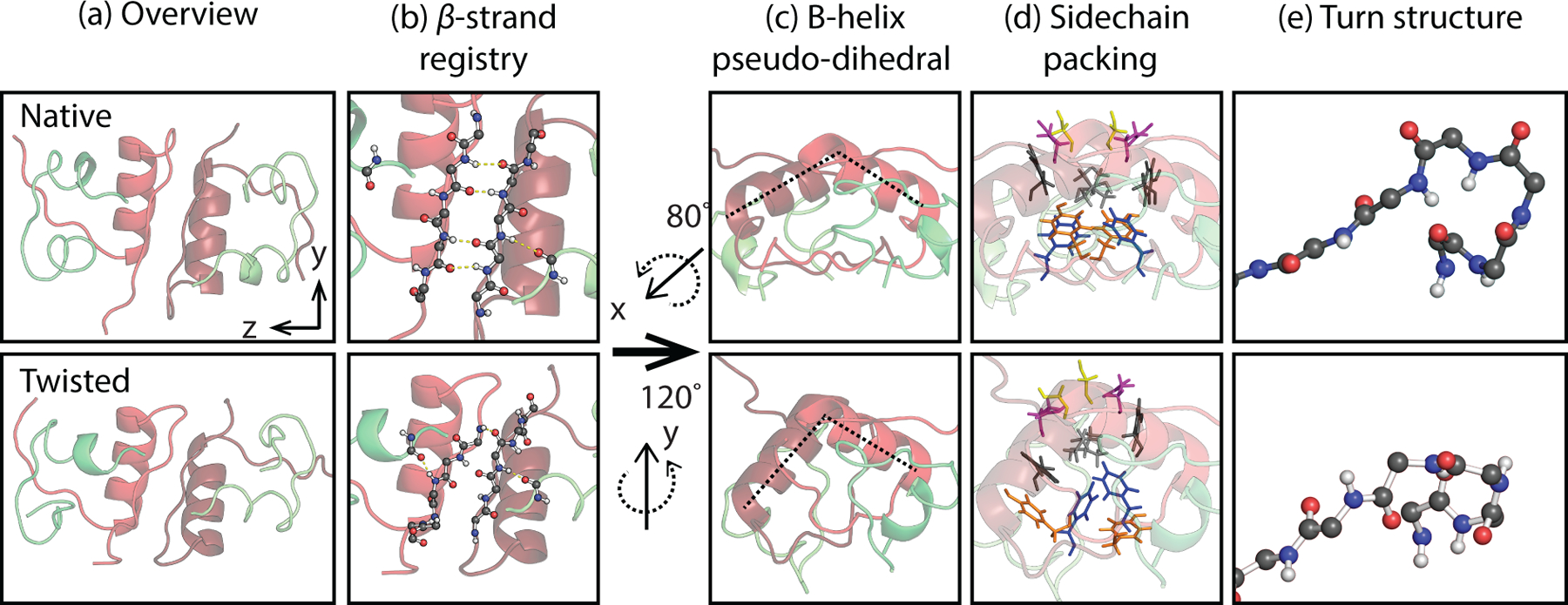
Structural differences between the native, $\overline{\langle \text{tIC}1\rangle }$~0.8, and twisted states, $\overline{\langle \text{tIC}1\rangle }$~−1.1, illustrated with MSM states 0 and 4 medoid structures. The columns illustrate (a) the overview of the structures, (b) the shift in β-sheet hydrogen-bond registry from B24 to B26, (c) the rotation of the B1 helix pseudo-dihedral angle from 103 to 74° (as indicated with dashed lines), (d) the changes in sidechain contacts at the dimer interface (Blue: B24F, Orange: B26Y; Gray: B16Y; Light gray: B12V; Magenta: B13E; Yellow: B9S), and (e) the change in turn structure for the B19C-B23G residues.

The dominant coarse-grained state, the native dimer (N), has the largest population of 66%, an average RMSD value of 4.4 Å, and tIC1 values from 1.0 to 0.77. Configurations within this state are similar to the crystal structure, exhibiting an intact inter-monomer β-sheet with an average of 3.4 inter-monomer hydrogen bonds (HBs) $\overline{\langle n_{\text{HB}}^{\text{Amide}}\rangle }$ of β residues including B23G, B24F, B25F and B26Y. The native state also has two pairs of intermolecular sidechain contacts between B24F and B26F (Fig. 2), as well as contacts between the two B25F sidechains and between the B16Y and B26Y sidechains, all of which contribute significantly to stabilizing the dimer.⁹⁵ Most of the conformational variation within the native state arises from disorder away from the dimer interface in the N-termini of the B chain and in the fold of the N-terminal helix of the A chain.

The other dominant coarse-grained state, the twisted dimer (T), has a population of 27%, a larger RMSD of 5.8 Å, 2.3 kJ/mol higher in free energy than in the native dimer (N), and tIC1 values from −0.83 to −1.26 (Table 1 and SI). Structures within this state appear as if one twisted the monomers of the native state clockwise (Fig. 2) around the inter-monomer axis, resulting in several conformational changes at the dimer interface. The β-sheet residues of the B-chain remain aligned but have a registry shift relative to the native structure by one amide unit and a decrease of 2 HBs between strands ($\overline{\langle n_{\text{HB}}^{\text{Amide}}\rangle }$ = 1.4). These strands appear wrapped around the dimer rather than the flat sheet observed in the native state. The unusual B20G–B23G turn of the native structure adopts a new configuration with canonical torsion angles. The native β-strand contacts between F and Y residues are replaced with non-native contacts between the two B24F sidechains. Most prominently the twisting motion is seen through the change in the relative orientation of the two B-chain helices, which can be quantified through an α-helix pseudo-dihedral angle $\overline{\langle {\Phi }_{\alpha }\rangle }$.⁵⁴ The helices rotate relative to each other by −55° on average from 115° to 59° between N and T states. Fig. 1d shows a network plot color-coded by the pseudo-dihedral angle, illustrating how this conformation change identifies the coarse-grained states.

We quantified changes to the average number of inter-monomer contacts involving the B-chain α-helix (n_α), the β-sheet residues (n_β), and all residues including non-native contacts (n_MM), which are the same observables for biasing the simulations of dimer dissociation in refs. 53–54 (See the SI). This showed that there was only a slight decrease of the number of α contacts from the native state to the twisted state, whereas the number of β contacts decreases by ~3 contacts, accounting for majority of loss of inter-monomer contacts n_MM (Table 1). This observation indicates that the conformational change along tIC1 perturbs mostly on the local structure along β-sheet residues and sidechain packing while minimally disrupting other contacts.

Kinetics

The remaining five states (16, 18, 45, 80, and 99) with intermediate tIC1 values are structurally diverse and account for 7% of the population (Fig. 4). Analysis of the top 20 tICs indicates that 11 tICs describe slow kinetics involving the transfer of population between one of these five intermediate Markov states and the rest, suggesting that these intermediate states are kinetic traps. From Fig. 1, we also infer that these intermediate states may play an important role in the transitions between the native and twisted states. To further investigate these intermediate states, we reduced the full MSM state space by lumping native and twisted states together and reduced the transition matrix for the resulting seven states using the method of Hummer and Szabo.⁹⁶ The network plot for this seven-state lumping is shown in Fig. 3a. One can see that states 80 and 45 act as on-pathway intermediates for the conversion of native and twisted forms, whereas 18, 99, and 16, which are identified in tICs 2–7, appear to be off-pathway, kinetic traps in this exchange process.

Figure 4.

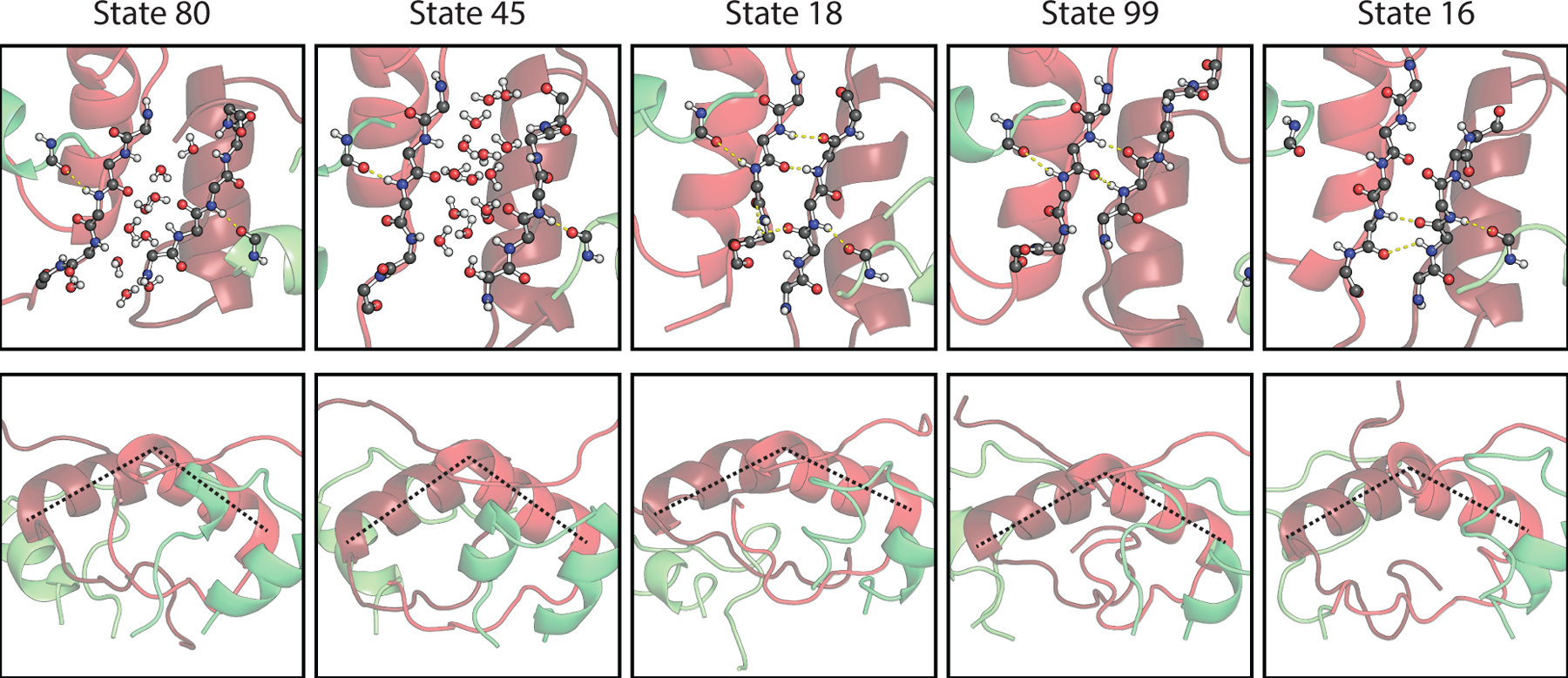
Structure of intermediate Markov states, showing a representative frame of each state with backbone atoms from A19Y and B23G–B27T, and a rotated side view illustrating the helix pseudo-dihedral angles.

Figure 3.

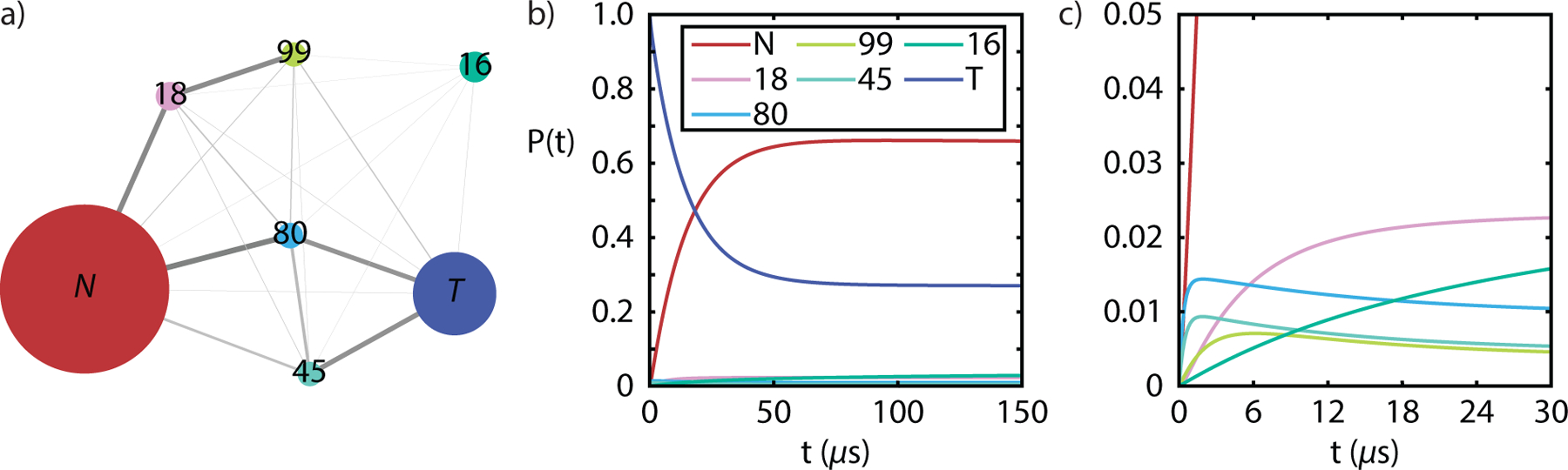
Seven-state lumping of native and twisted states with five intermediates. (a) Network plot for the new states and transition matrix. (b) Calculated equilibration kinetics tracking the exchange between native and twisted states when the population is initially in the twisted state.

With this seven-state lumping we also investigated the kinetics of dimer twisting with the reduced rate matrix. Fig. 3b shows the time dependent population changes in the 7 states when the system is initiated entirely in the twisted state. Native and twisted populations exchange with a time constant of 14 μs. Further reduction of the MSM to 3 states in which 80 and 45 are lumped as intermediates leads to a small increase in the observed kinetics to 21 μs for the exchange between N and T. In Fig. 3c we also see that population in states 80 and 45 rise with a time-scale of 460 ns and then re-equilibrate with a 21 μs decay as expected of on-path intermediates, whereas states 18 and 16 simply rise slowly to their equilibrium value. State 99’s behavior lies between the other indicating that it also plays a non-negligible role in the exchange of native and twisted forms.

Representative structure for the intermediate states are illustrated in Fig. 4. States 80 and 45 have water molecules that penetrate the two β-strands such that all of the native HBs present in the β-sheet are replaced by water molecules. This suggests that the primary mechanism of dimer twisting involves water disrupting the specific interactions of the β-sheet without significant disruption to the hydrophobic core. The remaining weak contacts between hydrophobic sidechains of the B-chain helix provide the orientational flexibility to reconfigure the β-strand sidechains and contacts in its new configuration.

A closer look at the makeup of the native and twisted states reveals that both contain conformational substates, which correspond to clustered groups in our network plot. Based on a reduction of the full MSM state space using a Robust Perron Cluster Cluster Analysis (PCCA+) of the first 20 eigenvectors of the transition matrix,⁹⁷ we identify four conformational substates which have native dimer contacts, but differ in their fold away from the dimer interface. For instance, two low RMSD native clusters mirror the crystal structure of insulin (N₀, N₁), whereas the another varies by the unfolding of the A1 helix of one insulin monomer (N₂). The third native substate (N₃) retains the intermolecular α and β contacts of the crystal structure, but have one or both A1 helices unfolded in both monomers, with considerable conformational disorder for the termini of all chains. The kinetics reveal that most conversion between native and twisted passes through the N₃ state. PCCA+ also reveals that the twisted state is primarily one block of well-folded configurations (T₁), with two minor substates (T₂ and T₃) that retain the twisted dimer interface, but vary in the structure and disorder of the A chains and chain termini. These states are discussed further below.

Computational spectroscopy

Spectral calculations for all 100 states and spectral trends.

The MSM predicts the presence of two dominant conformational states for insulin dimer, one of which corresponds to the well-known dimer structure, in addition to an observed rate constant of 14 μs for the interconversion between native and twisted forms. The prediction of these large-scale conformational changes that have not been previously observed, perhaps due to the μs interconversion timescale, raises the question of how such conformational changes could be observed experimentally. For this purpose, we investigated how local and global conformational changes of insulin dimer could be characterized with amide I infrared spectroscopy.

The amide I vibrational frequency shifts in proportion to the local electric field experienced by the carbonyl, and different carbonyl oscillators can couple to one another by through-bond (mechanical) and through-space (dipole-dipole) couplings.³¹ The patterns of characteristic CO frequency shifts and couplings for different secondary structures gives rise to characteristic frequencies and band shapes for α-helices and β-sheets. Most importantly, it is now possible to computationally model the protein amide I spectrum on the basis of atomistic structures drawn from MD simulation with quantitative accuracy. This tool has been used to characterize and refine conformational ensembles in peptides and small proteins.^{16–17, 19, 89, 92, 98}

Amide I spectroscopy can be performed in different manners when combined with site-specific isotope labeling strategies. In the absence of labels, the relatively small frequency variations among the different CO vibrations (σ~10 cm⁻¹) and similar coupling strength (V~0–10 cm⁻¹) means that vibrations spectrally overlap. This leads to broad absorption bands which are insensitive to local structural variation but can be used to quantify secondary structure content. We refer to these as unlabeled (UL) spectra. Alternatively, an isotope-labeled carbonyl—here ¹³C¹⁸O—can be used to shift the vibrational frequency well outside the band (≈ −60 cm⁻¹), which both spectrally isolates and vibrationally decouples it from other amides in order to identify site-specific contacts.^99–100 In addition to the single-label experiments, dual-label experiments which insert pair of specific isotope labeled carbonyls selected to interact strongly when in close proximity and alignment, are particularly effective for characterizing hydrogen bonding contacts between two residues of the main chain.

With computational IR spectroscopy, one can compute a spectrum from structures as an interpretive tool, and also predict which isotope labels will be most informative for revealing specific changes in conformation, solvation environment, and hydrogen-bond contacts. We used this strategy to computationally study the IR spectra associated with all 100 Markov states to identify isotope labeling strategies for investigations of structural heterogeneity in insulin dimer.

To begin we calculated the UL amide I absorption spectrum for all 100 Markov states. These spectra are shown in Fig. 5a, ordered by the state’s tIC1 value. We observe that all spectra are featureless asymmetric absorption bands, similar to experimental IR absorption spectra for the dimer,^51–52 but with little variation in the lineshape between states. Although the lineshape variations are nearly imperceptible within the N and T MSM states, the tIC1 value is found to correlate well with the frequency of the absorption maximum (ρ = −0.89). Population-weighted average spectra over the N and T states reveals a predicted 3 cm⁻¹ band shift between states, from $\overline{\langle {\omega }_N\rangle }$ ~ 1650 cm⁻¹ to $\overline{\langle {\omega }_T\rangle }$ ~ 1647 cm⁻¹ (b). The asymmetry of the native spectrum can be explained in terms of the two transitions expected from anti-parallel β-sheets,^{44, 51–52} including a weak ν_∥ vibrational transition at 1680 cm⁻¹ and a stronger ν_⊥ band at 1635 cm⁻¹. Second derivative spectra only marginally improve the spectral differences, so although there are predictable differences, it appears difficult to distinguish N and T configurations from UL spectra in practice.

Figure 5.

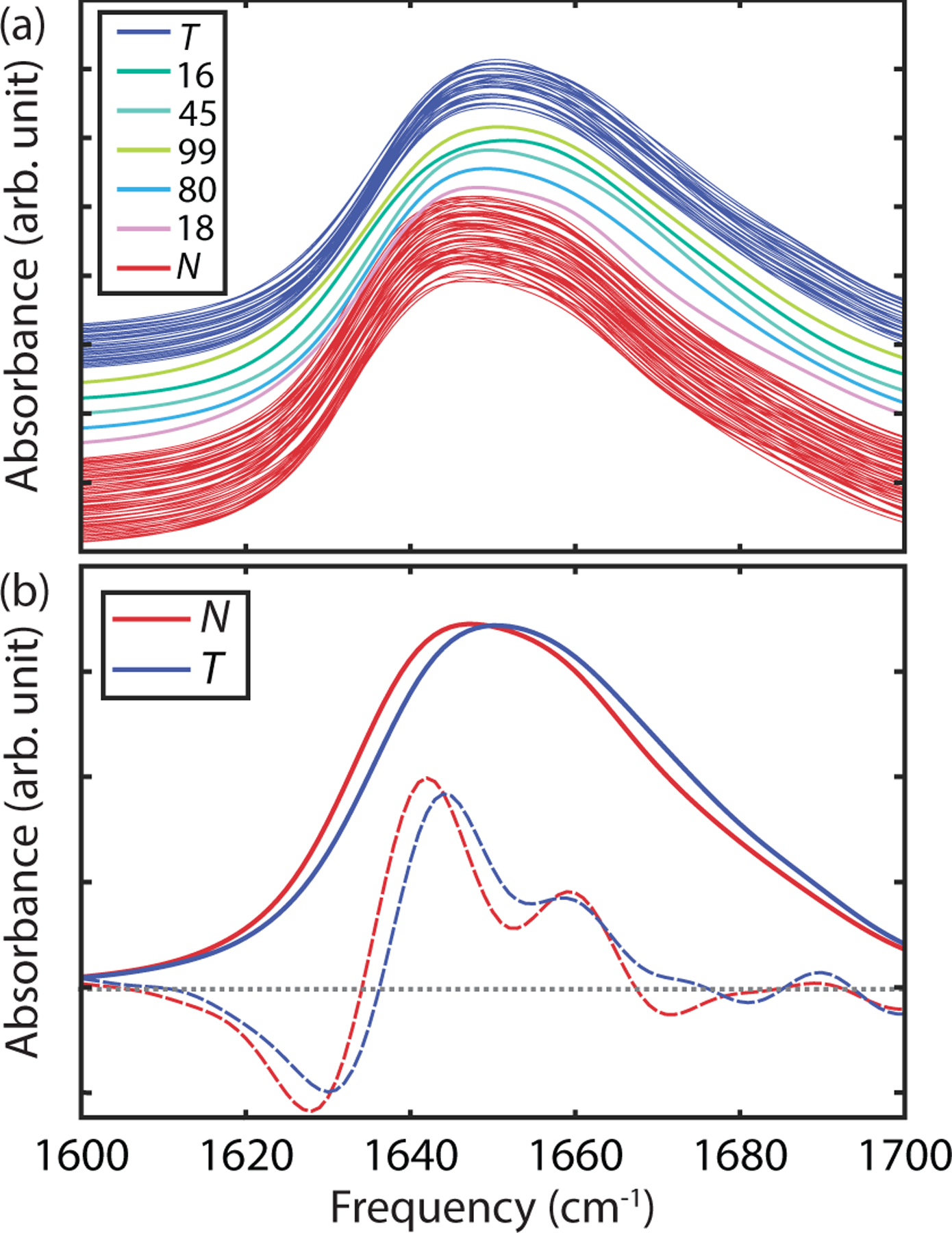
(a) Simulated UL FTIR spectra for all 100 Markov states ordered by increasing tIC 1 from top (twisted) to bottom (native). Spectra are vertically displaced for presentation purposes, and colored by their assignment to seven coarse-grained states (b) Comparison of population-weighted average IR spectra (solid line) and second-derivative spectra (dashed line) for the native and twisted states.

Since the N and T states vary most with the change of β-strand hydrogen bonds and other contacts at the dimer interface, changes in IR spectra between these states are more likely to be observed in spectra from isotope labels placed to interrogate these contacts.^99–100 To identify the most promising candidates, we performed calculations of isotope-edited IR spectra for all 100 states of the MSM starting with single site-specific labels for all 49 amide linkages of the monomer peptide backbone. These single labels shift in frequency depending on the local electric field experienced by the amide carbonyl, but is qualitatively best understood as being sensitive to the number and strength of hydrogen bonds to the carbonyl oxygen. Note that a single isotope label in this homodimer will result in two labels that can couple with one another depending on their proximity. The resulting spectra were analyzed individually or averaged by MSM population over all N and T coarse-grained states. Additionally, we performed calculations on 16 additional dual labels selected to isolate particular intra- and intermolecular contacts between the two amide groups.

To illustrate isotope labeling IR spectroscopy, Fig. 6 shows simulated IR spectra of UL insulin (black curve) and B24B25 double-labeled insulin for one MSM state with a native configuration (red curve). Upon ¹³C¹⁸O isotopic substitution on both B24 and B25 amide units on the β-sheet, there are additional isotope-edited features appearing between 1550–1620 cm⁻¹. To highlight vibrational features associated with labeling, we calculate the difference spectrum between B24B25-labeled insulin and UL insulin (dashed curve). From this isotope-labelled difference spectrum, one can see the positive absorption change with the peak frequency of 1576 cm⁻¹ corresponding to the labeled amide I vibrations, as well as negative features at 1635 and 1691 cm⁻¹ that arise from the loss of those unlabeled residues.

Figure 6.

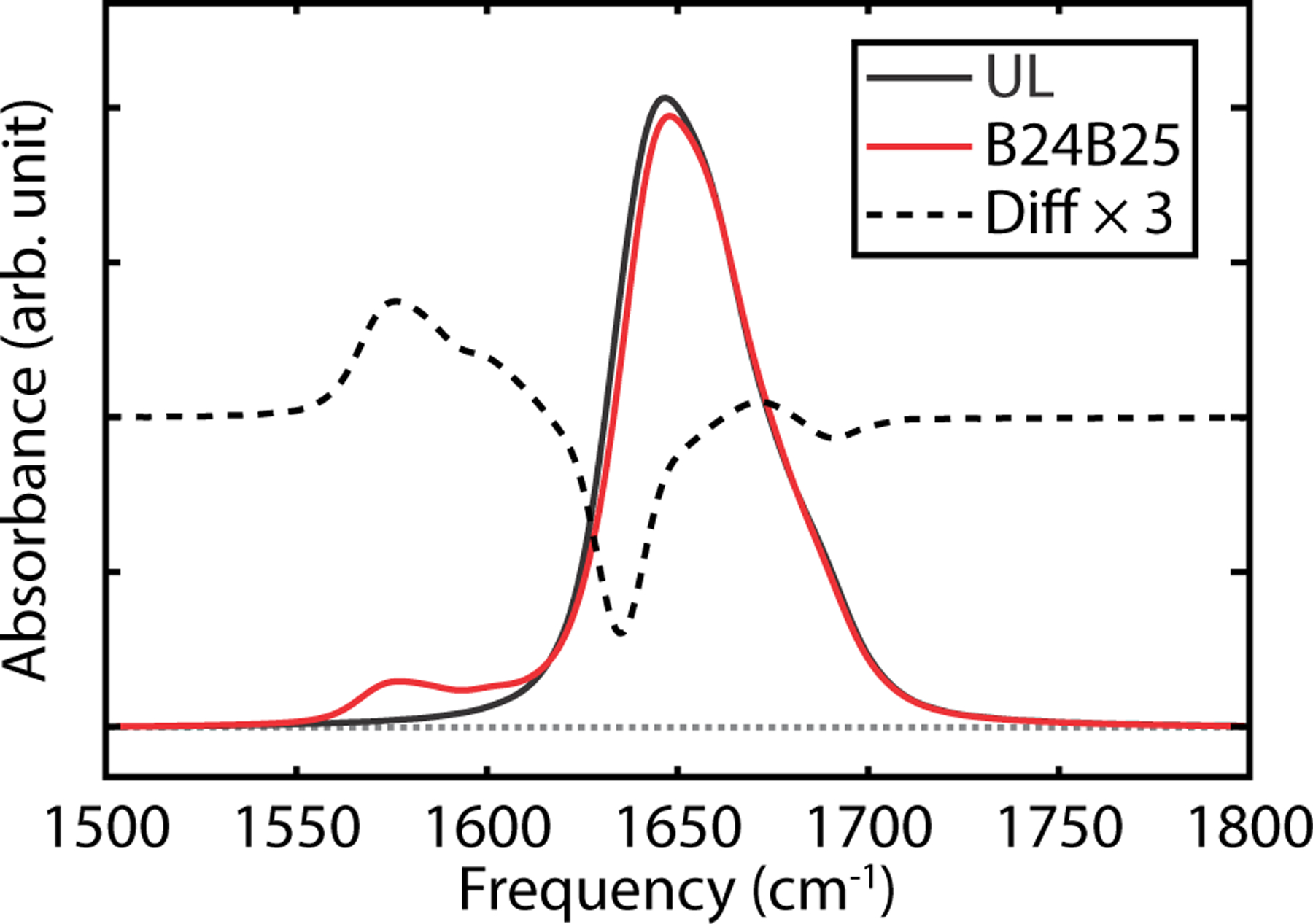
Simulated FTIR spectra of the native state 0 of the MSM. Simulated UL FTIR spectrum (black), B24B25 labeled FTIR spectrum (red) and difference spectrum, ΔA, between labeled spectrum and unlabeled spectrum (black dashed). Difference spectrum has been vertically displaced for presentation purpose.

Examples of the calculated isotope difference spectra for residues showing the largest frequency shifts between N and T states (>5 cm⁻¹) are shown in Fig. 7a. Overall 18% of the labels provided a spectrally resolvable distinction between N and T states. The largest spectral differences are observed for the B24, B25, and B26 single labels that form the β-sheet in the native state, as well as double-labels that include a label on one of these sites. Residues at the N-terminus of the A chain also report on a significant conformational change in the A2 helix relative to the B chain between N and T states, and the A4 and B11 labels report on a change in amide hydrogen bonding strength within the A1 and B helices, respectively. In all cases the frequency shifts observed are less than the linewidth, indicating that quantifying N and T populations in a mixture will be challenging with only one label; however, the pattern of spectral variation among multiple labels can be used for a more accurate determination.

Figure 7.

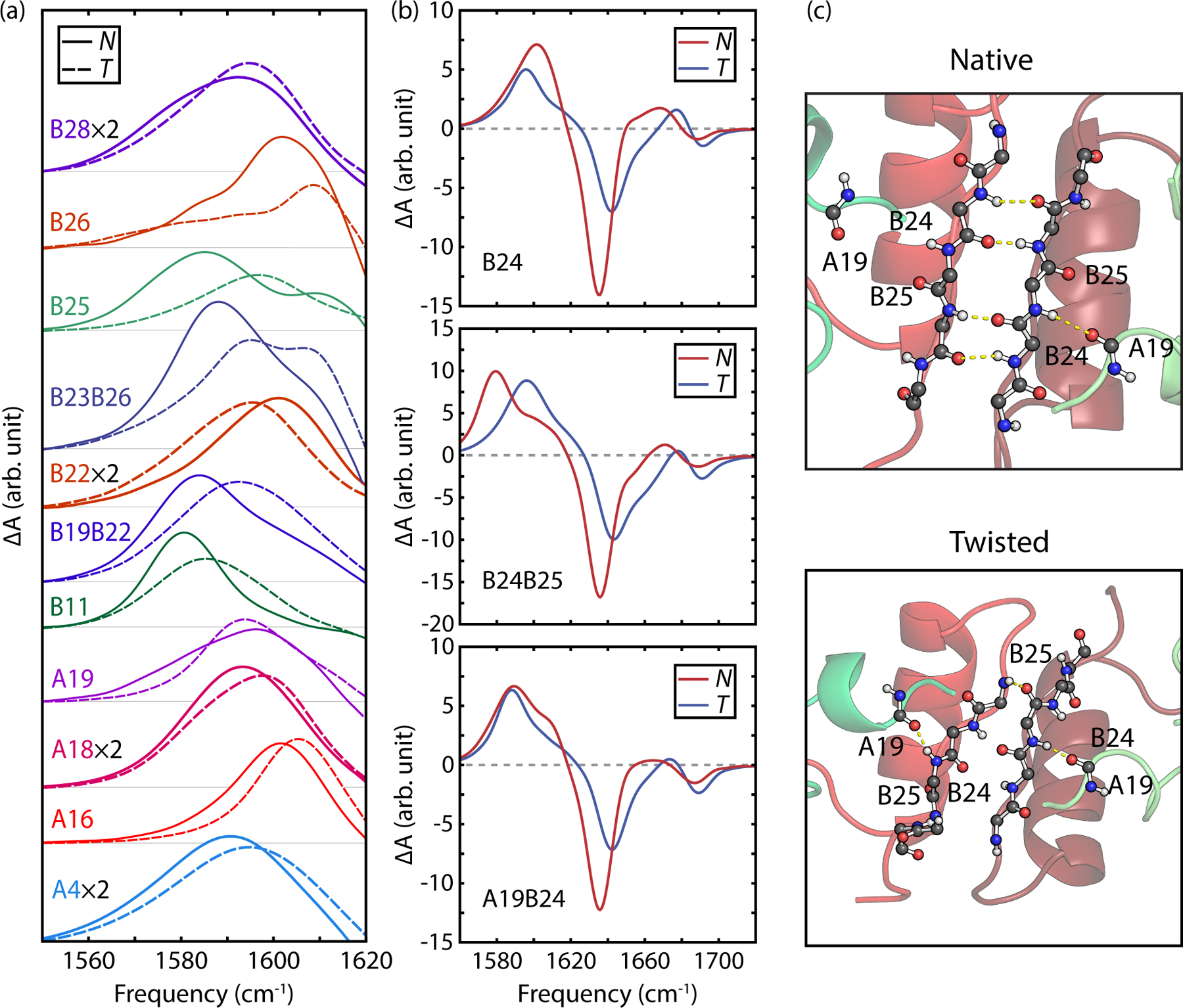
(a) Simulated isotope labeled IR difference spectra for several labels illustrating patterns of frequency shifts between the native and twisted states. (b) Simulated isotope difference spectra for B24, B24B25, and A19B24 labels including gain and loss features for N and T states. (c) Representative structures of both N and T states indicating structural differences in the A19, B24, and B25 carbonyls.

Looking closer at labels involving the dimer β-sheet residues, we now focus on the B24 single label, B24B25 dual label, and A19B24 dual label (Fig. 7b). The B24 and B24B25 labels are expected to probe intermolecular hydrogen-bond contacts within the β-sheet, whereas the A19B24 dual label should be sensitive to the intramolecular hydrogen bond between the A19 and B24 amide units in the native dimer, as illustrated in Fig. 7c. The resulting isotope-labeled difference spectra for N and T states are shown in Fig. 7b.

Overall, all three difference spectra exhibit common features, including an increase of absorption due to the isotope labelled residues between 1560–1620 cm⁻¹, and the loss of intensity from the unlabeled band in the frequency range above 1620 cm⁻¹. Labeled difference spectra of the native states (blue curves) share common loss features at 1635 cm⁻¹ and ~1690 cm⁻¹ corresponding to the ν_⊥ and ν_∥ modes of the β-sheet, respectively. For each label, the ν_⊥ loss peak for the T state is suppressed by about half from the N state and blue-shifted to 1642 cm⁻¹, and the ν_⊥ loss peak blue-shifts to 1693 cm⁻¹. We observe this pattern also in the A19, B25, and B23B26 label spectra.

Structurally, the B24-isotope label is sensitive to the register shift of the two β-strands between N and T configurations, partially due to a decrease in hydrogen bonding, but also because of the through-space coupling between B24 labels on each monomer changes significantly (−3 cm⁻¹ to 5 cm⁻¹). The calculated B24 difference spectra predicts that the N state has an asymmetric isotope-labeled amide I band peaked at 1602 cm⁻¹, whereas the T state exhibits a frequency down-shift to 1596 cm⁻¹, a decrease in intensity and change in spectral lineshape.

The B24B25 dual-label of each monomer introduces four labels total into the dimer, which effectively isolates the β-sheet of the native state. In Fig. 7b, the B24B25 difference spectrum of the N state has a peak frequency at 1580 cm⁻¹ and a shoulder at 1605 cm⁻¹, which we attribute to the isotope-edited ν_⊥ mode and ν_|| β-sheet modes.^{44, 101} The T state, in contrast, shows a symmetric labeled band with a peak frequency of 1596 cm⁻¹.

The A19B24 dual label probes the intramolecular H-bond contact between the A19 and B24 amide units away from dimer interface. The labeled difference spectrum of N shows a peak at 1589 cm⁻¹ and a pronounced shoulder at ~1610 cm⁻¹, whereas the T state is observed to have a more symmetric peak with about the same peak frequency. This reflects the changes in the number of H-bonds between the B24 N–H and A19 C=O, from an average of 0.86 for the T state to 0.59 for the N state.

These calculations establish that there are labeling strategies available to distinguish N and T configurations, however, with some of the labels investigated we also found patterns of spectral variation within with N and T states with slight variation in spectral lineshape corresponding to clusters within our network plot. In Fig. 8, we illustrate these shifts with the B24B25 dual label and compare how spectra for all native and twisted MSM states maps onto coarse-grained substates that were lumped with assistance of PCCA+. Although the N and T states share the general features described above, a closer look within 7 N and T coarse-grained substates reveals that the individual MSM states also have a different frequency, linewidth and lineshape to their label transition and loss features (Fig. 8a). For instance, we find the subset of states N₀, which correspond to the kinetically clustered lowest RMSD states of the MSM, have the lowest frequency labelled bands (<1575 cm⁻¹) compared to the N₁, N₂, and N₃ substates (>1575 cm⁻¹). This is illustrated by the averaged spectra in Fig. 8c. This comparison also reveals that there is very little spectral variation for the B24B25 label within the individual or coarse-grained twisted states. Only one T state (77) is clearly distinguishable by its low frequency resonance. Overall 16% of the labels calculated showed such spectral variation within substates.

Figure 8.

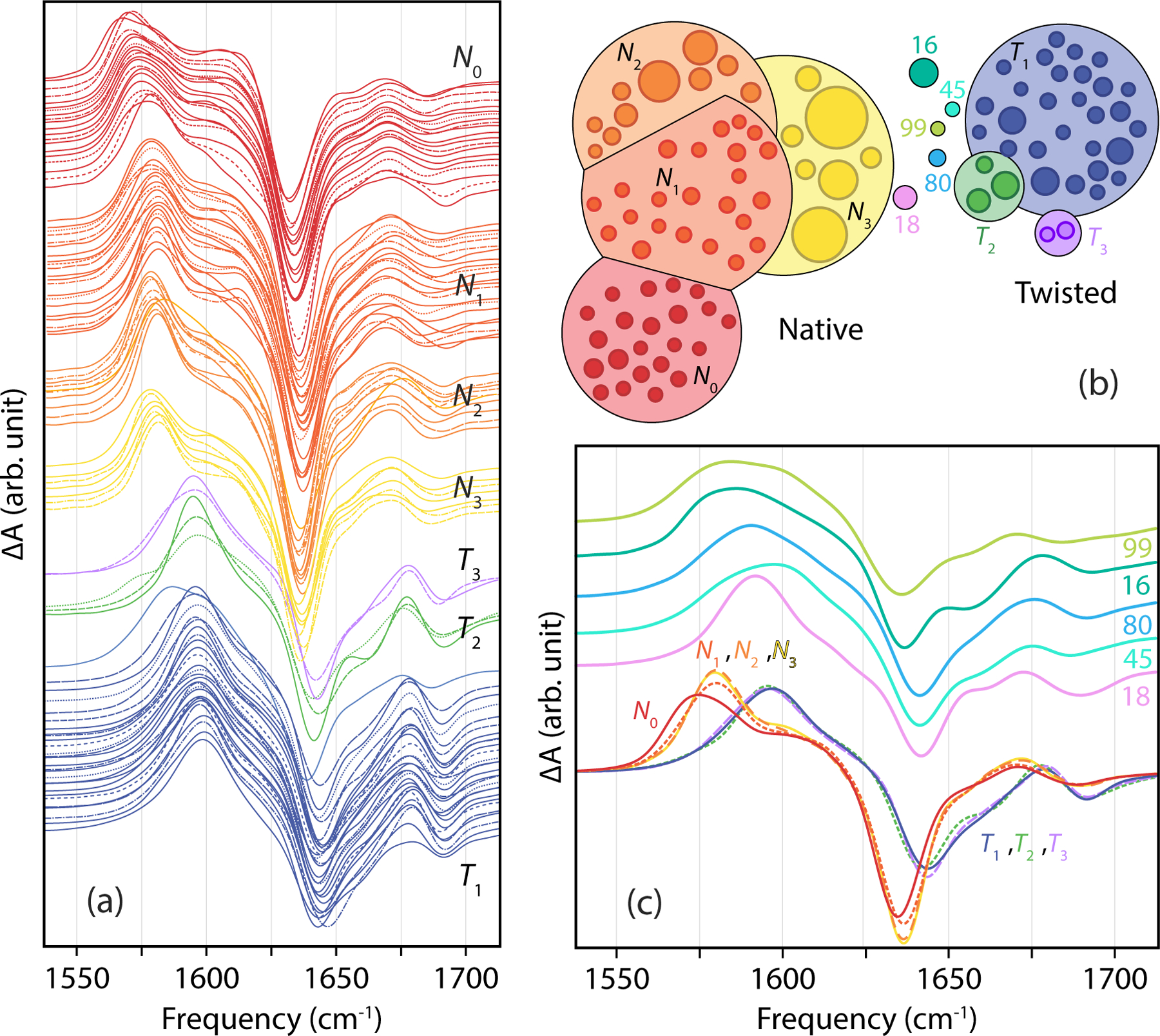
Spectral variation of the B24B25 label difference spectra among the 100 Markov states. (a) Individual spectra for native and twisted states ordered by peak transition frequency within the coarse-grained states obtained by PCCA+. (b) Corresponding color-coded native and twisted substates and intermediate states in 12-state coarse graining. (c) Comparison of population-weighted spectra for the four native and three twisted substates and the spectra of intermediate states.

Fig. 8c also compares the N and T spectra with those calculated for the five intermediate states. We observe that the intermediate states have significant spectral variation and are distinct from the native and twisted states. The spectra for these intermediate states do not share clear similarities with either N or T substates, and are much broader and featureless. Only state 18 has a clearly identifiable sharp resonance in its spectrum. These observations suggest that it may also be possible to distinguish the populations of intermediate states in IR kinetics measurements of structural interconversion of insulin dimer.

Discussion and Conclusions

Our investigation of the structural variation of insulin dimer using extensive all-atom simulations, Markov state modeling, and computational amide I spectroscopy predicts the presence of two dominant conformations to insulin dimer, and illustrate how they can be experimentally resolved through isotope-edited IR spectroscopy. The native and twisted dimer conformations primarily differ by the change of contacts at the interface between the two bound monomers, and in the backbone hydrogen bonding and sidechain packing of the B-chain β-strand residues that form the intermolecular β sheet in the native configuration. The MSM kinetics indicate that the exchange of native and twisted populations occurs on a 14 μs time-scale.

The twisted dimer conformation has, to our knowledge, not been experimentally observed. This is not surprising, given that it is a higher energy state than the native form and the predicted exchange kinetics are rapid; however, if present, confirming the presence of a twisted structure could have several consequences. On a fundamental level its presence should be considered in several factors varying from its influence on biological processes to interpretation of NMR experiments. It would influence our understanding of the role of many common B chain mutants found in insulin medications on the monomer-dimer equilibrium, and other principles for drug design. More generally, it provides evidence of the structural rearrangements and dynamical processes that can occur at protein-protein binding interfaces of complexes that are thought to bind in a unique site-specific manner.

From a dynamics perspective, it remains unknown what role a twisted dimer could play in the dimer dissociation and association processes, perhaps as an intermediate. Recent simulations of insulin dimer dissociation free energies described a broad distribution of possible energetically favorable dissociation pathways, bounded by two limiting cases: (1) a sequential process of disrupting B-chain α-helix contacts prior to B-chain β contacts (the α path), or (2) β contacts prior to α contacts (β path).⁵⁴ To investigate connections between MSM intermediate states and on-path structures during the course of dissociation in that study, we projected the dimer MSM onto collective variables (CVs) describing the dissociation (see Figure S3). As one might expect, the well-solvated β strands of states 45 and 80 lie along the β path when observing CVs involving β contacts, but the α pseudo-dihedral rotation lies closer to the α path in a high free energy region rarely visited in the sampling of dimer dissociation. The solvation of β-strands is also observed along the β path, highlighting the important role of water mediating protein conformational changes and binding.^{54, 102} It is possible that the dimer MSM contains structures not sampled for the biased sampling of dissociation free energy landscapes,^53–54 but it is also possible that variations in the side-chain protonation state or force field contribute to this discrepancy. On the other hand, projecting the dimer MSM onto the free energy landscape constructed by Bagchi and coworkers showed that the native state and the twisted state has the n_MM values of 50.45 and 48.31 respectively (Table 1), which in essence lies in the same free energy basin of the state A (n_MM in the Table 1 and Figs. 3–4 in ref. 53). As a result, the role of the twisted dimer in insulin dimer dissociation remains unclear at this time.

The simulation conditions we used were selected with IR spectroscopy in mind, since protonated sidechains (low pH) improves insulin solubility, destabilizes insulin hexamer, and reduces IR background absorptions from asymmetric COO⁻ vibrations in the same region as the labels. It is possible that these conditions favored the stabilization of the twisted configuration; however, a clear rationale is not apparent. The protonatable sidechains are away from the dimer binding interface, except for the case of B21E which may influence the conformation of the B19C–B23G turn.

To search for the presence of the twisted state, we find that IR spectroscopy targeting the B24, B25, and B26 residues in single and pairwise ¹³C¹⁸O isotope labelling provides the best strategy for spectroscopically distinguishing the N and T configurations. Temperature and pH dependent studies could be used to influence the equilibrium between N and T states. Such IR spectra could also be used to track the exchange kinetics between N and T states when used as the probe of a temperature-jump experiment. Separately, we did investigate the variation of computed UV circular dichroism spectra¹⁰³ between N and T states, and found no significant change in the spectral shape, but a decrease in the magnitude of the molar ellipticity in the T state.

While a few labels result in large spectral differences between N and T states, most of the expected spectral changes for any particular label are predicted to show a small up-shift or down-shift in vibrational frequency, often less than the linewidth of the transition. Therefore, a robust strategy for studying insulin dimer is best performed with multiple labels whose pattern of spectral peaks can act as a type of “bar code” to identify the presence of the twisted dimer state. Indeed, we believe that the calculated isotope-labeled difference spectra for all 100 Markov states form a unique basis set for structural ensemble refinement from experiments using maximum entropy or Bayesian refinement tools.^{19, 92} Finally, we note that the amide I spectral simulation tools presented here are equally applicable to 2D IR spectroscopy, which has improved capabilities for resolving isotope peak positions and distributions of spectra encoding structural variation. These observations set the stage for IR experimental studies to study insulin dimer structure and the dissociation/association equilibrium between the dimer(s) and monomer, and the kinetics of the coupled dimer conformational change and the dimer dissociation processes.