Accelerated forest fragmentation leads to critical increase in tropical forest edge area

Critical edge area of tropical forests is accelerating with negative consequences for the global carbon cycle and conservation.

Abstract

Large areas of tropical forests have been lost through deforestation, resulting in fragmented forest landscapes. However, the dynamics of forest fragmentation are still unknown, especially the critical forest edge areas, which are sources of carbon emissions due to increased tree mortality. We analyzed the changes in forest fragmentation for the entire tropics using high-resolution forest cover maps. We found that forest edge area increased from 27 to 31% of the total forest area in just 10 years, with the largest increase in Africa. The number of forest fragments increased by 20 million with consequences for connectivity of tropical landscapes. Simulations suggest that ongoing deforestation will further accelerate forest fragmentation. By 2100, 50% of tropical forest area will be at the forest edge, causing additional carbon emissions of up to 500 million MT carbon per year. Thus, efforts to limit fragmentation in the world’s tropical forests are important for climate change mitigation.

INTRODUCTION

Tropical forests are a crucial element of the earth system. They represent a relevant global carbon pool, harbor a large part of the terrestrial biodiversity, and provide important ecosystem services (1–3). However, large areas of tropical forests have already been lost through deforestation, and despite afforestation efforts, the extent of forest area continues to decline throughout the tropics (4–6).

Deforestation alters the remaining forest area, resulting in landscapes with isolated forest fragments (7–12) and declining biodiversity (13–15). Wind and drought stress can penetrate into a forest up to several hundred meters from the forest edge, thereby altering the forest microclimate and increasing tree mortality (7). These “edge effects” also affect species richness and forest dynamics in forest fragments and lead to a reduction of forest biomass near the edge of a fragment (16–19). In addition, fire frequency correlates with the distance to the forest edge, as most fires occur near the forest edge (20).

Given the alarming results of recent studies on the current state of forest fragmentation in the tropics (10, 21–23), a detailed assessment of changes of forest edge area and its consequences is required. However, spatially and temporally detailed information on the dynamics of forest fragmentation, such as transition rates among forest, forest edge, and nonforest areas, is not available for the entire tropics.

Here, we analyze the dynamics of forest fragmentation for the entire tropics using high-resolution forest cover maps for the years 2000 and 2010 (21 billion pixels for each year; each pixel, 30 m) (5). More specifically, we (i) apply an efficient clustering algorithm to determine the size and spatial configuration of all tropical forest fragments; (ii) identify the critical edge area (defined here as forest area within 100-m distance from the nearest forest edge); (iii) quantify transitions among forested, forest edge, and nonforested areas; and (iv) project the consequences of these transitions into the future using a dynamic fragmentation model.

RESULTS

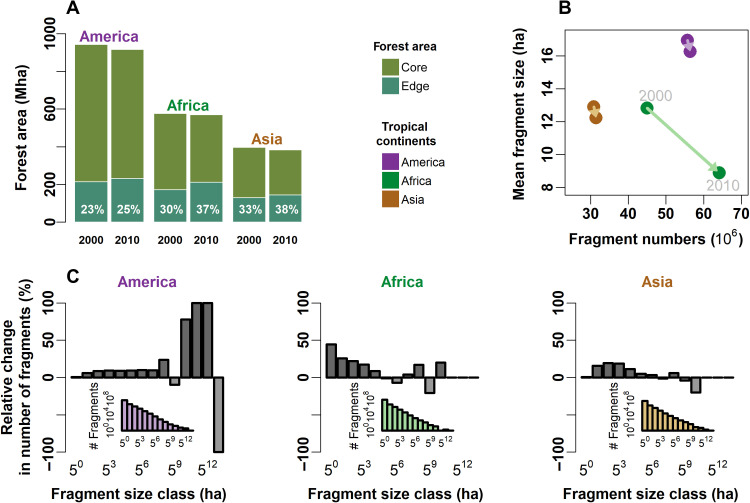
We detected more than 131 million forest fragments for the year 2000 and 152 million fragments for 2010 (Table 1). This increase is mainly due to changes in Africa, where the number of fragments increased during our 10-year study period from 45 million to 64 million (an increase of 42%; Fig. 1B). In the entire tropics, the average size of forest fragments decreased from 15 to 12 ha (Fig. 1B and Table 1).

Table 1. Statistical description of tropical forest fragmentation for each continent and the entire tropics.

Forest fragmentation was analyzed for the years 2000 and 2010. The edge area was determined by counting each forest pixel (30 m) with a distance of less than 100 m from the nearest forest edge. The fraction of edge area is the ratio between the total edge area and the forested area per continent (Mha = 10⁶ ha). The analysis assumed a threshold of 30% tree cover to separate forest from nonforest areas (see table S2 for the same analysis with a threshold of 50% tree cover). Please note that forests may also include plantations, as it is not possible to distinguish them with the forest cover maps.

		America		Africa		Asia		Total
	Unit	2000	2010	2000	2010	2000	2010	2000	2010
Total forested area	Mha	943	916	577	570	398	384	1918	1870
Net deforestation rate	1/year		0.29%		0.13%		0.34%		0.25%
Number of fragments	106	55.7	56.4	45.0	64.2	30.8	31.4	131.6	152.0
Number of fragments <10 ha	106	54.8	55.4	44.5	63.6	30.5	31.1	129.8	150.0
Average fragment size	ha	17	16	13	9	13	12	15	12
Core area	Mha	728	685	405	358	268	239	1401	1282
Edge area	Mha	215	232	172	212	130	145	517	589
Edge area fraction	% of forest area	23%	25%	30%	37%	33%	38%	27%	31%

Fig. 1. Continent-wide changes of tropical forest fragmentation from 2000 to 2010.

(A) Total forest edge area (<100-m edge distance) and forest core area (>100-m edge distance) for 2000 and 2010. An increase in edge area was detectable for all three tropical continents. The percentage values quantify the ratio of edge area to forested area. (B) Total number of forest fragments versus mean fragment size for each tropical continent for the year 2000 and 2010. The arrow indicates the transition during the 10-year period. (C) Relative change in the number of forest fragments in different size classes over a period of 10 years (2000 to 2010). The relative change is calculated by dividing the change in number of fragments in each size class by the total numbers in 2000 (size classes are 0 to 5⁰, 5⁰ to 5¹, ..., 5¹² to 5¹³ ha). Although fragment size distributions are more or less similar across continents (year 2010: small inlets; year 2000: fig. S1), the relative changes of fragments per size class differ.

In 2000, the fraction of forest edge area to total forest area was already high at 27% for the entire tropics but rose to 31% by 2010 (in Africa, the edge area fraction increased the most from 30 to 37%; Fig. 1A and Table 1). This change was mainly caused by a sharp increase in the number of small fragments (<10 ha), with an increase from 130 million in 2000 to 150 million in 2010 (Fig. 1C and Table 1). In America, the number of small fragments remained relatively stable, but some large fragments have split (Fig. 1C and fig. S9).

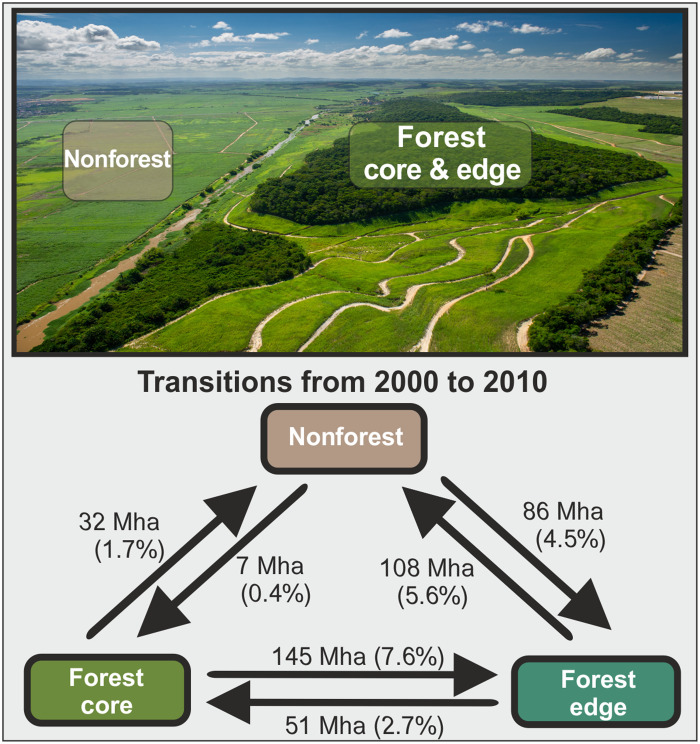
Our analysis revealed that forest fragmentation patterns are changing rapidly because of both deforestation and forest gain. Between 2000 and 2010, a total of 177 million ha (referred to as Mha hereafter) of forest core area was lost, either directly through deforestation (32 Mha) or through the creation of new edges as a result of deforestation (145 Mha; Fig. 2). In addition, 108 Mha of edge area has been lost through deforestation. However, forest gain of 93 Mha due to re- and afforestation was also observed, and 51 Mha of forest edge area recovered to intact forest core area (Fig. 2). The relative transitions between core and edge area are comparable for all three tropical continents (fig. S2).

Fig. 2. Transitions among forest core, forest edge, and nonforest areas through deforestation and forest gain (e.g., afforestation or reforestation) in the tropics between 2000 and 2010.

Deforestation accounted for 140 Mha in 10 years and forest gain for a total of 93 Mha, resulting in a net forest loss of 47 Mha. Here, forest area is divided into edge area (assuming <100-m distance from forest edge) and core area (>100 m). The numbers in parentheses show area changes relative to the total forested area in 2000 (1918 Mha). Picture: Remnants of Atlantic forest near Recife, Brazil (source: CacioM/Adobe Stock).

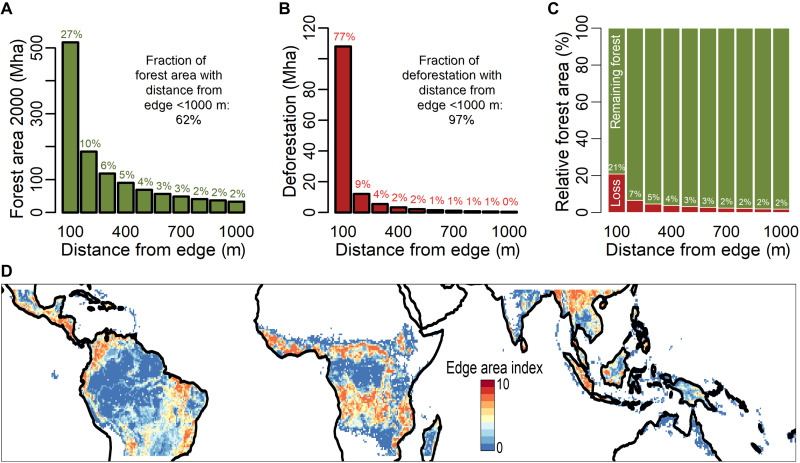
The spatial distribution of forest area within a forest fragment (either near the edge or deep in the core) plays a crucial role in ecological functions such as pollination and carbon cycling (16). We therefore analyzed the spatial pattern of all forest fragments in detail by calculating how much forest area was located within a certain distance from the edge of the forest fragments (Fig. 3A and fig. S3). In 2000, 27% of forest area was already in the edge area (<100 m). We found a power-law relationship between forest area and distance to forest edge with a coefficient close to −1 (Fig. 3A; for power-law fit, see fig. S4). Unexpectedly, this power-law relationship was similar for all tropical continents (fig. S4), although forest management and land use strategy may differ between continents. Detecting power laws in natural phenomena has been of long interest in various disciplines [e.g., earthquake magnitudes, word frequencies, and moon crater diameter; see (24)], as they can especially indicate phase transitions of the respective analyzed system (10, 24, 25).

Fig. 3. Forest edge area and deforestation in the tropics.

(A) Amount of forest area as a function of distance from forest edge (year 2000). Twenty-seven percent of the forest area is within 100 m to the forest edge (see Materials and Methods). (B) Amount of forest loss (due to deforestation) as a function of distance to forest edge (period 2000 to 2010). Seventy-seven percent of forest loss occurs at a distance of less than 100 m from the nearest forest edge. (C) Relative amount of deforestation (red) to forest area (green) within a given distance from the forest edge. (D) Map of tropical edge area (<100 m) for the year 2010. For this analysis, the high-resolution forest edge area map (30 m) was aggregated to a scale of 50-km pixel. The edge area index quantifies the amount of forest edge area (10⁴ ha) within each 50-km pixel (see Materials and Methods for more details; see fig. S5 for the frequency distribution of the edge area index).

The tropical-wide patterns of forest edge area are very heterogeneous (Fig. 3D), and regions with large amounts of forest edge areas occur, for example, in the areas of the Arc of Deforestation, in the southern part of the Congo Basin, and in Sumatra (Fig. 3D). Considering different forest biomes, most forest edge areas in the tropics were located in moist broadleaf forests and in fragmented savannah and shrubland landscapes (fig. S6).

We were also able to examine patterns of deforestation as a function of distance from the forest edge (Fig. 3B). Most forest loss occurred at the edge of forest fragments and only rarely within the core of a fragment. Up to 77% of forest loss occurred within 100 m of the forest edge (Fig. 3B; this pattern can also be described by a power law with an exponent close to −2; for power-law fit, see fig. S4). The loss of forest area, especially at the edge of forest fragments, led not only to increasingly smaller forest fragments but also to the isolation of forest fragments in the landscape. For example, the nearest 10-ha fragment was, on average, 1 km away, but the nearest 1000-ha fragment was 8 km (fig. S7).

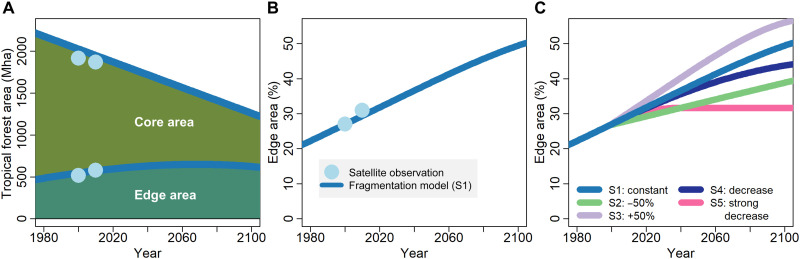
Given these tremendous changes in the past, how will forest fragmentation evolve in the future? To project the future development of tropical forest fragmentation, we used the fragmentation patterns revealed in our analysis to parameterize a spatial high-resolution fragmentation model that is inspired by percolation theory (see Materials and Methods). The model simulates deforestation for the entire tropics at a 30-m resolution, based on the observed deforestation rates in forest core and forest edge areas. Key characteristics of tropical forest fragmentation can be reproduced with this model (Fig. 4). The model projections show that forest area will shrink as deforestation progresses and forest edge area will increase by 2070 (assuming constant deforestation rates; Fig. 4A). By 2100, about half of the forest will be located in edge areas and thus subject to increased tree mortality (Fig. 4B). Even under optimistic deforestation assumptions (net deforestation rate only half as high as the current rate), the proportion of edge area to total forest area increases to 40% (Fig. 4C, scenario S2). Only if net deforestation rates decrease to zero by 2040 (i.e., deforestation equals afforestation and reforestation), the fraction of edge area will remain at about 30%, as currently observed (Fig. 4C, scenario S5).

Fig. 4. Tropical forest fragmentation simulated with a fragmentation model until 2100 (for details, see Materials and Methods; scenario S1 with constant deforestation rates).

(A) The projected forest area is classified into forest edge area (<100-m edge distance) and forest core area (>100 m). Observations of forest edge and core area derived from satellite maps are also shown [dots in (A) and (B); values from Table 1]. (B) Simulation results for the fraction of edge area (edge area divided by total forest area) assuming constant deforestation rates (scenario S1). Results from the analysis of the satellite maps are also included (dots; values from Table 1). (C) Simulation results for the fraction of edge area to the total forested area for five different deforestation scenarios. For scenario S1, the currently observed deforestation rate is assumed to continue through 2100. In scenarios S2 and S3, the deforestation rate is set 50% lower and higher, respectively, than currently observed. In scenarios S4 and S5, the deforestation rate decreases dynamically every year (in S5 more than in S4). Scenarios S1 to S5 are described in the “Scenarios of deforestation simulations” section in Materials and Methods.

DISCUSSION

The observed increase in the number of forest fragments and the strong decrease in mean fragment size will have serious consequences for forest ecosystems and the fauna inhabiting them (26–30), as the risk of extinction of local populations increases with decreasing fragment size and increasing fragment isolation (31, 32). While species-area relationships have been used in conservation ecology to roughly predict species extinction as habitat area shrinks (32), our spatially explicit fragmentation analysis provides data that can be used for more refined spatial analyses [e.g., (33)] to identify areas at high risk of species extinctions. Protecting forest areas and reforestation could mitigate the consequences of fragmentation such as species extinction.

Intact tropical forests are carbon sinks (34, 35), but land use can convert them into carbon sources (36). In addition, the altered microclimate in forest edges can cause higher tree mortality and therefore additional carbon emissions (22, 37). Applying the methodology of Brinck et al. (22) to our simulation results, we estimated additional carbon emissions of 450 to 550 million MT C/year (fig. S8; for details, see Materials and Methods) due to edge effects, which have to be added to the annual carbon emissions of 1500 million MT C due to deforestation (38).

More emphasis needs to be placed on reforestation and afforestation in future studies. Our study considers a time period of 10 years, for which the observed newly forested areas represent early successional forests. Forest in early succession can grow fast, absorbing more carbon compared to late successional forests (39, 40). Forests at different successional stages further differ in tree species composition and forest architecture, which further highlights the role of forest age for nature and biodiversity conservation. Differentiating, in addition, newly forested areas (e.g., afforested areas) brings up another important dimension to the carbon balance and biodiversity of tropical forests, with re- and afforestation also influenced by the surrounding landscape matrix (41, 42). Future studies detecting forest age, disturbance state (e.g., at fragment edges), and land use type (e.g., reforested area and plantations) from high-resolution remote sensing information can provide new insights in future fragmentation studies.

Although the patterns of forest fragmentation were similar in all three tropical continents [especially the fragment size distribution; see (10)], the amount of edge area showed differences and a particular strong increase in Africa. This could reflect high land use pressures (23) and extensive road development, for example, in the Congo Basin (43), which increased forest fragmentation and facilitated access to forested regions, promoting further deforestation. However, the road spread is also increasing rapidly on the other continents (44, 45). It can therefore be assumed that similar increases in forest edge area will soon be observable throughout the tropics.

While other studies investigated forest loss or forest carbon dynamics in intact forest systems, the detailed spatial resolution (30 m) of our analysis allowed us to quantify forest degradation that occurs on small spatial scales (<100 m). Our result that 31% of the forest area was, in 2010, already in edge areas is rather conservative, as we only assumed a small edge-depth penetration of 100 m. Other studies have shown that forest biomass can still be reduced up to 1.5 km from the edge of a forest fragment because of changes in microclimate and higher tree mortality (21). According to our analysis, 75% of forest area is already located within 1.5-km distance to the edge in the year 2010.

Our study suggests that the fragmentation of tropical forests will increase in the future with ongoing deforestation. In addition, deforestation can also alter the hydrological cycle with negative feedbacks on precipitation (46–48). Moist rainforests, for example, can dry up with severe consequences for the global climate (47). Degradation of forest edges further perturbs the hydrological cycle, which also accelerates desiccation and can intensify the risk to fall below a tipping point, at which recovery is no longer possible and ecosystem types can shift, e.g., from tropical forests to savannahs (48, 49). Fragmentation and degradation of tropical forests should therefore be given more attention and integrated in the discussion of tipping points in the future.

Our results provide detailed information on the dynamics of tropical forest fragmentation patterns and show a marked increase in forest edge area. Given the projection that 50% of forest area will be in the forest edge area by 2100, we conclude that conservation efforts to reduce forest edge areas in tropical forests are most important to avoid potentially severe consequences for carbon sequestration and biodiversity.

MATERIALS AND METHODS

Forest cover maps

We used high-resolution forest cover maps from 2000 and 2010 (5) with resolution of 1 arc sec per pixel (≈30 m at the equator), based on Landsat data. We used a bilevel forest/nonforest classification threshold value of 30% tree cover to generate forest/nonforest maps. This threshold seems appropriate to distinguish between forest and nonforest (10, 22, 23). The trends observed in this study remain the same when a 50% tree cover threshold is applied (see table S2). The original maps were processed as in the work of Brinck et al. (22) (ASCII format, WGS-84 projection). The area of each forested pixel is calculated depending on its geographical position. The analysis covers the whole tropics subdivided into three regions: America (23.5°N, −110.0°W to −23.5°S, −34.0°E), Africa (23.5°N, −18.0°W to −23.5°S, 50.0°E), and Asia (including tropical Australia; 23.5°N, 70.0°W to −23.5°S, 180.0°E).

Fragmentation detection algorithm

Each forest fragment in the tropics was detected by examining the forest/nonforest maps and by applying a cluster detection algorithm. A modified and extended Hoshen-Kopelman algorithm (50) served as a basis for this fragmentation analysis. The connection of a forest pixel to a forest fragment was determined by its four-pixel neighborhood. However, to deal with the large maps, we further developed an efficient cluster detection algorithm (10, 22). For each individual forest fragment, several attributes were calculated: forested area (hectares), perimeter length (meters), shape index, and position of the center of gravity. An additional feature in this study is that the algorithm determines the distance of each 30-m forest pixel to the nearest forest edge (a total of 21 billion forested pixels were analyzed in 2000 and in 2010, respectively). This allowed us to determine the exact forest edge area by marking all forest pixels with a distance to the forest edge of less than 100 m. A forest pixel is considered as an “edge” if two pixels along that side are nonforest pixels (two pixels represent a distance of around 60 m near the equator). If a nonforested area (e.g., river or road) is wider than 60 m, then this is considered as an edge, as solar radiation can change the microclimate in the forest. It is not possible to distinguish between natural and anthropogenic created edges. The cluster algorithm and its subsequent modules are implemented as a C++ program. An efficient implementation was achieved by parallelizing the calculations.

Statistics of tropical forest fragmentation

Fragmentation size distribution

The fragment size distribution is the number of fragments per size class. For logarithmic binning, we used the size classes [0,10⁰), [10⁰,10¹), [10¹, 10²), …, [10⁸, 10⁹) in hectares. For the analysis of the change in the number of fragments, we adopted for Fig. 1 the size classes to [0,5⁰), [5⁰,5¹), [5¹, 5²), …, [5¹², 5¹³) in hectares. The relative change (shown in Fig. 1) represents the increase or decrease in the number of forest fragments (over 10 years) divided by the total number of fragments in 2000.

Forest area

Total forested area was determined by summing up the area (hectares) of all forest fragments. Forest area is given in 10⁶ ha = Mha. Each forested pixel was marked either as edge area or as core area. A forest pixel was defined as an edge area if the distance to the nearest forest edge was less than 100 m. The total forest edge area was calculated by summing all forest pixels that are marked as edge area. Total forest core area is the sum of all forest pixels with a distance larger than 100 m from the forest edge. The fraction of edge area was calculated as the ratio between total edge area and total forested area. Please note that the area of each pixel was calculated on the basis of its geographical location and assuming a flat terrain. This implies that in mountains, the area of a pixel could possibly be larger. However, since no high-resolution digital elevation model is available (30 m is needed here), this could not be considered in this study.

Distance of forest pixel to forest edge

For the analysis of distance to forest edge, 100-m distance classes were introduced (0 to 100 m, 100 to 200 m, …; c.f. Fig. 3). For each forest pixel, the shortest distance to a pixel at the edge of a forest was calculated (forest pixel with a nonforest pixel in the neighborhood). Then, the forest area was summed up for each distance class (year 2000 in Fig. 3A and year 2010 in fig. S3). We also calculated the sum of the fragments’ forest area per distance class relative to the total forested area (Fig. 3A, percentage values). The same investigation was carried out for forest areas that were deforested between 2000 and 2010 by considering the distance of the former forest area to the edge of 2000 (Fig. 3B). Here, we also quantified the ratio of deforestation area per distance class to the total deforestation area (Fig. 3B, percentage values). In addition, for each distance class, the ratio of forest area within this distance class and deforestation area within this distance class was calculated (Fig. 3C).

We fitted a power-law function (y = a·x^b) to the relation between distance to forest edge (variable x) and (i) forest area in 2000, (ii) forest area in 2010, and (iii) gross deforestation area between 2000 and 2010 (each being variable y). As the observed relations appeared as straight lines when plotted on log-log axes and this pattern is a special feature of power-law functions (i.e., scale invariance), we decided to fit a power-law function to the data. For the statistical fit, we used a linear regression with both axes transformed to the natural logarithm: ln y = ln a + b·ln x, with specific focus on the exponent b (fig. S4).

Edge area index

For the global map of tropical edge area, an edge area index was used to quantify the amount of edge area in a certain region. For this analysis, the resulting high-resolution edge area map (30 m) was aggregated to a 50-km pixel scale. The edge area index was the amount of edge area (10⁴ ha) within each 50-km pixel. The maps of the edge area index are shown in Fig. 3D (year 2010) and in fig. S5A (year 2000). To calculate the change over 10 years, the index value of 2010 minus the value of 2000 was calculated for each 50-km pixel (fig. S5C).

Deforestation rate

Deforestation rate r (% per year) was calculated as the time-weighted rate of total forest area change over the 10-year period of 2000 to 2010

$$r=(1-{\left(\frac{{\text{forest}}_{2010}}{{\text{forest}}_{2000}}\right)}^{1/10})·100\%/\text{year}$$

Fragmentation model

A simple fragmentation model [fragmentation at the border (FRAG-B)] was used to simulate the spatial patterns of forest fragmentation. This model was inspired by percolation theory. In a previous study, it could be shown that typical patterns of tropical forest fragmentation (e.g., fragment size distribution) can be reproduced with this type of model (10).

The total land area of a continent was divided into 30-m pixels (America, 1.53 × 10¹⁰ pixels; Africa, 0.89 × 10¹⁰ pixels; Asia, 0.86 × 10¹⁰ pixels) with two states: forest or nonforest. The simulation starts with all pixels being forested. For each simulation time step, small forest patches with the size of a × a (pixel²) were selected at a random position according to a given deforestation rate r and deforested. In addition, we introduced a probability d of clearing forest at the border of forest fragments. For example, if d = 0.4, then 40% of deforestation happens in forest edge areas and 60% happens in forest core areas. Deforestation rates used for the simulation represent net deforestation rates [see also (10)].

The simulations were performed for each continent separately. Model parameters are shown in table S1. We derived deforestation rates and the fraction of border deforestation from forest cover maps (Table 1). We assumed constant deforestation rates for the whole simulation period (for further deforestation scenarios, see section below). The fraction of border deforestation d was taken from fig. S2 by calculating the ratio of net edge area loss (edge area loss minus edge area gain) to net total forest area loss per continent. The mean size a × a (pixel²) of deforestation patches was estimated from the study of Montibeller et al. (51).

Scenarios of deforestation simulations

In total, we simulated five deforestation scenarios by varying the net deforestation rates r (see Table 1 and table S1 for default value). In all scenarios, the deforestation rates per continent are taken from table S1 and are constant until the year 2000. The deforestation rate after the year 2000 was varied according to the scenario setting. Scenario S1, “constant”: The observed deforestation rates per continent were taken as a constant rate until the year 2100. Scenario S2, “−50%”: After the year 2000, all observed net deforestation rates were halved but are constant until 2100. Scenario S3, “+50%”: After the year 2000, all observed net deforestation rates were increased by 50% but are constant until 2100. Scenario S4, “decrease”: After the year 2000, the annual net deforestation rate decreased every year by 0.0012% [inspired by the scenario in (10)]. Scenario S5, “strong decrease”: After the year 2000, the annual net deforestation rates per continent decreased linearly to zero by 2040. After 2040, the net deforestation rates remain at zero. All scenarios are presented in fig. S10.

Connectivity (nearest neighbor analysis)

For each forest fragment, the closest neighboring forest fragment was determined. Starting from the forest edge area of a given forest fragment, the search was carried out in concentric circles to find the edge area of other forest fragments. The search radius was limited to a maximum of 4000 pixels in each direction. With this search radius, a nearest neighbor distance could be estimated for more than 98% of all forest fragments. For the remaining forest fragments, the distance was set to the maximum search radius.

Carbon emissions projection

The fragmentation model FRAG-B was also used to estimate, in a simple way, additional carbon emissions due to forest fragmentation caused by higher tree mortality in forest edge area. Simulations were conducted for the whole tropics (30-m pixels; see above). In each simulation year, forest fragmentation and forest edge area were analyzed by applying the same methods as to the observed forest cover maps (see the “Fragmentation detection algorithm” section). In addition, the age of edge area has been tracked. After the edge creation, the age of the edge area was set to zero. It was assumed that forest areas in the edge lose a total of 50% of their biomass due to higher tree mortality (22). This biomass loss was distributed equally over the 50 years after edge creation and thus leads to yearly carbon emissions. After 50 years, a new biomass equilibrium is reached for the forest in the edge area, and no further carbon emissions occurred (for this edge area). For intact forests, a mean aboveground biomass value of 90 MT C/ha was assumed (22).

Supplementary Materials

This PDF file includes:

Figs. S1 to S10

Tables S1 and S2

References