Variability and heritability of mouse brain structure: Microscopic MRI atlases and connectomes for diverse strains

Abstract

Genome-wide association studies have demonstrated significant links between human brain structure and common DNA variants. Similar studies with rodents have been challenging because of smaller brain volumes. Using high field MRI (9.4 T) and compressed sensing, we have achieved microscopic resolution and sufficiently high throughput for rodent population studies. We generated whole brain structural MRI and diffusion connectomes for four diverse isogenic lines of mice (C57BL/6J, DBA/2J, CAST/EiJ, and BTBR) at spatial resolution 20,000 times higher than human connectomes. We measured narrow sense heritability (h²) I.e. the fraction of variance explained by strains in a simple ANOVA model for volumes and scalar diffusion metrics, and estimates of residua technical error for 166 regions in each hemisphere and connectivity between the regions. Volumes of discrete brain regions had the highest mean heritability (0.71 ± 0.23 SD, n = 332), followed by fractional anisotropy (0.54 ± 0.26), radial diffusivity (0.34 ± 0.022), and axial diffusivity (0.28 ± 0.19). Connection profiles were statistically different in 280 of 322 nodes across all four strains. Nearly 150 of the connection profiles were statistically different between the C57BL/6J, DBA/2J, and CAST/EiJ lines. Microscopic whole brain MRI/DTI has allowed us to identify significant heritable phenotypes in brain volume, scalar DTI metrics, and quantitative connectomes.

1. Introduction

Structural and functional magnetic resonance imaging (MRI) have enabled new ways to systematically study the influence of DNA sequence differences on brain architecture and behavior. Investigators have used both conventional family linkage studies and genome-wide association studies (Thompson et al., 2001; Thompson et al., 2013; Thompson et al., 2014; Elliott et al., 2018; Hibar et al., 2015). New DTI methods provide enhanced structural detail, scalar measures of tissue cytoarchitecture, and structural connections across the entire brain (Hibar et al., 2015; Kochunov et al., 2015).

Experimental genetic studies that have used many of these MRI methods have been limited by the technical difficulties of scaling from the human brain (950–1800 cm³) down to the mouse brain (0.32–0.52 cm³) (Daianu et al., 2015, Keifer et al., 2015, Calabrese et al., 2015). Routine rodent brain connectomics is challenging because of the simultaneous demands of (1) reducing voxel volume by a factor of 3000, (2) providing sufficient diffusion weighting, (3) sampling an adequate number of gradient angles, (4) maintaining good signal-to-noise ratios, and (5) maintaining a reasonable scan time of less than 24 h per brain. All these requirements must be viewed in light of recent papers that highlight the problems of false negative tracts in structural diffusion connectomics (Thomas et al., 2014, Maier-Hein et al., 2017). A single 1.25 mm³ voxel, as used in the human connectome project, can encompass on the order of 100,000 neurons and their processes (Ugurbil et al., 2013). Errors in tractography that result from crossing and merging fibers can result in substantial false positive connections. We have addressed many of these technical challenges by developing improved MRI protocols and unique hardware and encoding methods (Wang et al., 2018, Johnson et al., 2018). We have validated and streamlined methods (Calabrese et al., 2015, Wang et al., 2018) that enable the required high throughput for quantitative genetic studies of large murine cohorts (Wang et al., 2018, Johnson et al., 2018).

The major goal of this study was to systematically estimate heritabilities for many brain structures and parameters of a small but diverse cohort of mice. We measured volumes, scalar DTI metrics, and connectomes for each of 166 regions of interest (ROI), bilaterally, including both grey matter and fiber tracts. Most of these ROI are subcortical structures and tracts, many of which are comparatively difficult to quantify in humans. In total, we estimated volumes and DTI parameters for cortical regions, subcortical forebrain nuclei, midbrain regions, hindbrain structures, cerebellar regions, and white matter tracts. Finally, we estimated the maximum residual coefficient of errors with the conservative assumption that the exclusive cause of right-left differences was technical instead of genuine structural asymmetry (Williams et al., 1996). Error terms were almost always under 5%, even for the smallest subcortical regions and tracts.

We addressed the following questions:

• What are the heritabilities of regional volumes and the different types of scalar metrics generated by DTI? Are connectome patterns heritable? Are there notable sex differences in heritability?

• To what extent are heritabilities compromised by errors of measurements, or by the size and shape of structures and tracts.

• How do differences in heritabilities and coefficient of variation map onto conventional neuroanatomical divisions and systems?

2. Methods

2.1. Experimental model and subject details

The Duke Institutional Animal Care and Use Committee (IACUCC) approved all the study protocols. We compared four mouse strains.

1. C57BL/6J (B6) —often referred to as “the mouse” —is the references strain for murine genomics and neuroscience. The B6 is the maternal parent of the large BXD family of strains (n of 150 progeny strains; (Ashbrook et al., 2019)). B6 is a member of the Mus musculus domesticus subspecies, and it has a mean brain weight of 479 ± 3.7 mg (n = 259, all brain data generated in our laboratory using relatively uniform methods, (Hager et al., 2012) and www.mbl.org/references/BrainWeightOfStrainofMice.xlsx, and GeneNetwork trait 49909).

2. DBA/2J (D2) —the oldest fully inbred strain —is the paternal parent of the BXD family, and, like B6, it has also been sequenced (Wang et al., 2016). D2 is also a Mus musculus domesticus, and it has a mean brain weight of 403 ± 4.5 mg (n = 154).

3. CAST/EiJ (Stein et al., 2012) is a fully inbred strain, derived from the Southeast Asian Mus musculus castaneus subspecies. This strain breeds well with other subspecies, and, although it is somewhat smaller, it has a mean brain weight of 395 ± 4.6 mg m (n = 23).

4. BTBR T + Itpr3^tf/J (BTBR) is a common inbred strain with well-known behavioral and neuroanatomical abnormalities including a highly penetrant callosal defect (Ellegood et al., 2013, Meyza and Blanchard, 2017, Faraji et al., 2018). BTBR is a Mus musculus domesticus with a brain weight of 487 ± 3.9 mg, close to that of B6 (n = 51).

The first three strains have comparatively normal CNS structure and connections, whereas BTBR is an acallosal strain (Ellegood et al., 2013, Meyza and Blanchard, 2017, Faraji et al., 2018). There is a 20% range of difference in mean brain volumes among these strains; B6 and BTBR have relatively large brains, whereas D2 and CAST have smaller brains (Ashbrook et al., 2019). Thus, we corrected all heritability estimates to eliminate effects of different overall brain volume by expressing the volume of each region of interest as a percentage of the whole brain volume for that specimen.

Four males and females for each strain were purchased from The Jackson Laboratory. Upon arrival at Duke, animals were housed in the CIVM vivarium for at least 10 days to minimize any stress from shipping. Animals were housed in individual HEPA-filtered cages with two to each cage. They were fed a standard laboratory chow ad libitum and maintained with a twelve-hour light/dark cycle. Animals were provided commercial lab bedding (https://andersonslabbedding.com/irradiated/bedrnest/)

Brains were left in the cranium and actively stained via perfusion fixation with Prohance, a gadolinium contrast agent that reduces the spin lattice relaxation time (T1) (Johnson et al., 2007). Animals were anesthetized to a surgical plane using Nembutal (@ dose of 75mg/kg). A catheter was inserted into the left ventricle of the heart. The animal was perfused with a peristaltic pump with a mixture of 0.9% saline and ProHance (10:1, v:v) followed by a mixture of 10% buffered formalin and ProHance (10:1, v:v). The skull was removed and placed in 10% buffered formalin @ 4 °C for 24 h. Mandibles were removed to enable use of a smaller radiofrequency coil. Tissue was then stored for at least three weeks in 1% Prohance/saline solution to rehydrate the tissue after fixation. This resulted in reduction of T1 to ~ 100 ms and T2* to ~ 25 ms. It also increased the apparent diffusion coefficient by ~ 4X so b values were increased commensurately to provide diffusion contrast comparable to in vivo studies. Recent studies (not included) have demonstrated that the tissue is remarkably stable over a period of up to 1 year: volume change < 2%; FA, AD, RD, MD change < 3%. Specimens were mounted in a 12-mm-diameter plastic cylinder. The cylinder was filled with fomblin, an inert fluorocarbon that reduces susceptibility artefacts. All animals were young adults at 90 (± 1) days of age.

2.2. Image acquisition

Magnetic resonance (MR) images were acquired on a 9.4T vertical bore Oxford magnet with Resonance Research gradients providing ~2000 mT/m maximum gradient. The system was controlled by an Agilent Direct Drive console. Specimens were mounted in a 12 mm diameter radiofrequency (rf) coil. The coil was constructed from a single sheet of silver foil which yields a low resistance. Necessary capacitance to tune the coil is added by placing a layer of dielectric material at the juncture of the two ends of the coil. The resulting unloaded Q is > 500. Three-dimensional (3D) diffusion weighted images were acquired with a Stejskal Tanner rf refocused spin echo sequence with TR/TE of 100/12.7 ms and b values of 4000 s /mm². Forty-six volumes were acquired, each with a different gradient angle along with five baseline (b0) images distributed throughout the four-dimensional (4D) acquisition. Sampling angles were uniformly distributed on the unit sphere. Compressed sensing was used with an acceleration of 4 X to reduce the acquisition time to 23.2 h/specimen (Wang et al., 2018). The result was a 4D image array with isotropic spatial resolution of 45 μm (voxel volume of 91 pl).

2.3. Image registration

The 4D array (256 × 256 × 420 × 51) was passed to a post-processing pipeline that first registered the five b0 images together. Then each of the diffusion-weighted 3D volumes was registered to this average to correct for eddy current distortion. The registered 4D array was passed to DSI Studio which generated scalar images: apparent diffusion coefficient (ADC), diffusion weighted image (DWI), axial diffusivity (AD), radial diffusivity (RD), mean diffusivity (MD), fractional anisotropy (FA), and color fractional anisotropy (ClrFA) using the DTI model (Yeh et al., 2020). Representative images (Supplement Fig. S1) demonstrated the complementary anatomic detail provided by these scalars to assist in the label registration.

2.4. Label registration

A 3D label set was registered onto each 4D volume in that volume’s native reference frame, that is, the reference frame in which the data were acquired. A symmetric Waxholm Space (WHS) (Johnson et al., 2010), i.e., an isotropic label set of 166 total ROIs in each half of the brain (Calabrese et al., 2015), was generated by reflecting the label set through the midline. The symmetrized label set minimizes bias in lateral comparisons (Bowden et al., 2011). The complete list of labels is available in the Supplemental Table S2. The labels were isotropic, i.e., they extended in all three planes at the same spatial resolution (45 mm) (Figure S3).

2.5. Coefficient of variation

Left and right labels were generated for each of the 32 specimens by creating a strain- and subject-specific spatial mapping to WHS. These maps are the source images (DWI, FA, AD, RD) referred to here as “WHS-Atlas”, including the label set of 166 regions per hemisphere. Figure S4 summarizes the path of the labels from the WHS Atlas to the individual specimen (Anderson et al., 2019). Because there were significant structural differences among the strains that might have pushed the registration pipeline beyond its capabilities, an intermediate hybrid average was generated for each strain. Averages were generated using a pipeline incorporating ANTS (Avants et al., 2011) with the following steps:

1. An automated skull stripping algorithm removed all the external tissue from the DWI and FA images;

2. A second stage of affine transform was applied, using the DWI;

3. Six iterations of non-linear registration were performed using the diffeomorphic Symmetrized-Normalization algorithm as implemented in the Advanced Normalization Tools software (Avants et al., 2011, Avants et al., 2010), and was driven by the FA contrast.

After each diffeomorphic warp, images were averaged to create a new template. An average of all the inverse warps was then applied incrementally to move the shape of this template towards the median shape of the group before being used as the target of the next iteration. The strain average for each strain was created from eight specimens in that strain. Merged strain averages were created for each strain/sex by using four B6/sex cases with the four data volumes of the strain/sex to which the labels were being mapped. Linear registrations used the Mattes similarity metric, whereas non-linear registration used cross-correlation (Anderson et al., 2019, Avants et al., 2011). For D2, the WHS-symmetric labels were warped using the appropriate transform chain and nearest neighbor interpolation such that each template had its own unedited label set. Before being propagated to the individual specimens, the template labels in the strain average were inspected and manually edited. It was necessary to refine the white matter of the cerebellum via thresholding of the template FA image. D2 and CAST required slight manual edits, primarily involving the boundary of the caudate-putamen, whereas significant edits were made to the BTBR template labels due to notable anatomical differences in the cortex and midline structures.

Soleimani et al have discussed the impact of nearest neighbor interpolation on the resampling which could lead to errors in estimating volumes which can be particularly troublesome when mapping the labels onto thin anatomic structures (Soleimani, 2020). We have tested for this possibility using a data set acquired at 25 um spatial resolution which was down sampled to 50 um. Passing the two data sets through our registration pipeline yielded volumes of all the structures that differed by < 2.6%.

2.6. Connectome generation

Tracts were generated using the generalized Q-sampling (GQI) fiber tracking algorithm in DSI studio with a maximum of three fibers per pixel (Yeh et al., 2013). The propagation direction was calculated by applying trilinear interpolation on the fiber orientations provided from neighborhood voxels. The next point was then determined by moving 0.02 mm in the propagation direction. The propagation process was repeated until the tracking trajectory exceeded either a turning angle of greater than 45° or the anisotropy value of the current position was below a predetermined threshold. Five million fibers were generated with whole brain seeding for a reference B6 specimen. The number of fibers for all other specimens was normalized to each specimen volume. For whole brain tractography (white matter and gray matter), the FA threshold was 0.1 with a minimum fiber length of 0.5 mm.

Whole brain connectomes were generated for each specimen in DSI studio using the registered label set with 166 regions of interest on each hemisphere. The seed and target regions were ordered based on their developmental origins. A complete key for region number and its anatomical definition is included in Supplemental Table S2.

2.7. Statistics

Heritability is the proportion of phenotypic variance that is explained by genetic differences. In fully homozygous strains, additive genetic variance (V_a) is the main source of differences between strains, and our estimates can be considered close to what is typically called narrow sense heritability (h²) (Wray NR, 2020). h² was estimated as the fraction of variance explained by strains in a simple ANOVA model.

To calculate empirical confidence intervals of heritabilities, we used two methods. First, h² values were recalculated, omitting one strain at a time. If heritability decreases when a particular strain is removed, the result indicates that the strain contributed a disproportionate fraction of V_a. The second method involved omitting four random individuals from the analysis and recalculating heritabilities. This process was performed 10,000 times to provide an empirical estimate of the distribution of possible heritabilities using all four strains. Note that heritability estimates depend on the choice of strains and many potential environmental and technical confounds. When environmental variance is minimized, heritability will be higher. When technical variance is high, heritabilities will be depressed.

Although subjective comparisons of connectomes can suggest regions in which there are differences, statistical comparisons are challenging. The high-dimensional nature of connectomics data necessitates multiple comparisons, a problem that Meskaldji et al have discussed in detail (Meskaldji DR et al., 2013). Since a comparison of two connectomes involves a large number of tests (between each of the 332 × 332 edges), we use the Bonferroni method to correct for this multiplicity. When this is done, few comparisons withstand the correction. In addition, the heritability calculations were essentially test statistics, whose sensitivity and specificity depended on the degree to which the data satisfied certain assumptions. Although those assumptions are often appropriate, for these data, exploratory analysis demonstrated that the assumptions were not valid. More specifically, we aggregated all the edge weights across each particular mouse strain. Pooling across strains would be expected to be a mixture of Gaussians, one per strain, if t-test theory were to hold. Kolmogorov–Smirnov test demonstrated that the edge distribution per strain was non-Gaussian, rendering any Gaussian-based parametric test invalid for these data, thereby motivating nonparametric tests. Results were similar for the volume and scalar metrics. However, due to nonparametric methods generally having lower power than their parametric counterparts, this approach for quantifying heritability failed to identify pronounced differences across strains (Martinez-Camblor and de Una-Alvarez, 2009). Therefore, we added a posthoc analysis based on a new method (omnibus embedding) for statistically determining heritability of connectomes (Levin et al., 2017). Instead of treating each edge as an independent object, we first assessed whether the connectome, as a whole, was heritable.

To answer this question, we leveraged recent developments in the statistical analysis of populations of graphs on a shared vertex set. This enabled us to find a joint low-dimensional representation of each node in each connectome, based on its connectivity profile, that is, its set of connections. In this way, we could use standard methods for subsequent inference. We posited a multivariate, non-parametric k-sample test hypothesis: For each node, was the low-dimensional representation for a given strain sampled from the same distribution as the other strains? This in turn allowed us to rank order the nodes based on the log of their adjusted p value providing insight into the specific nodes with the greatest phenotypic difference.

2.8. Data and code availability

Scalar data for each specimen were aggregated into a single Excel sheet which contains two separate lists—left and right sides—for all 166 labels followed by volume, mean values of FA, AD, and RD for each sub region. Volume data for each sub region of a given strain were normalized to the total brain volume of that strain. The data package for each specimen consists of 51 unregistered 3D MRI volumes; a registered 4D volume; scalar images; mean values from the 166 regions for the scalars; tractography files from DSI studio; and connectomes. The aggregated data set is > 500 GB. All data are freely available with a request to cite this publication at (https://civmvoxport.vm.duke.edu/voxbase/studyhome.php?studyid=402).

3. Results

3.1. Whole brain population atlases provide statistical measures of heritability

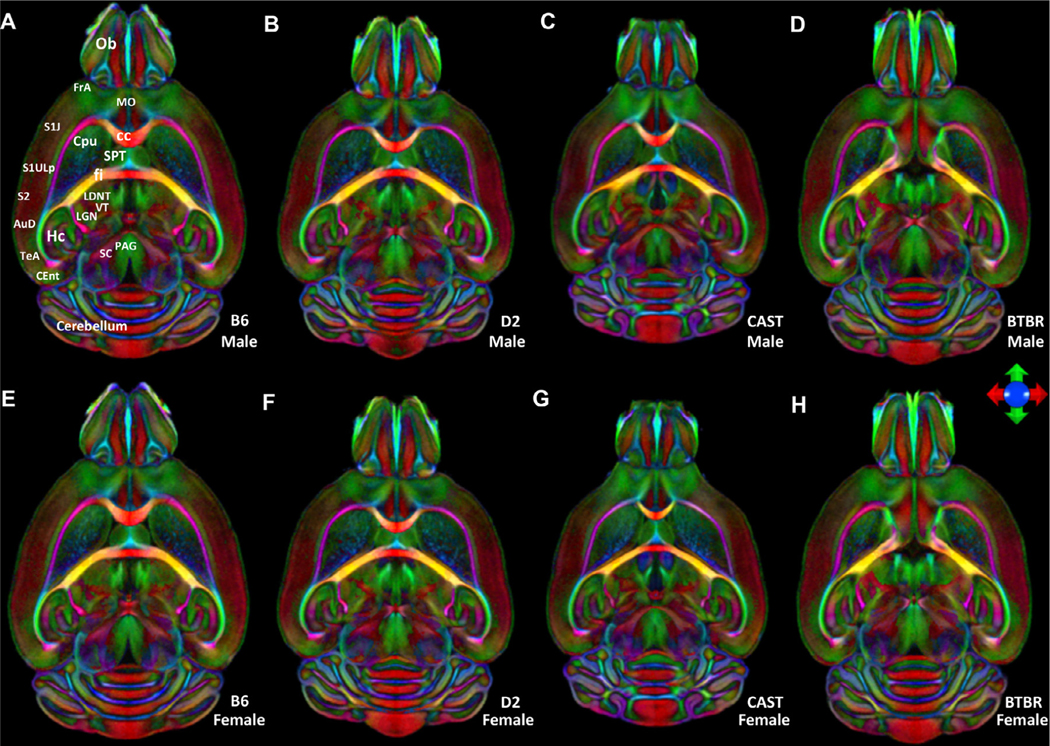
Differences in brain size and shape, regional volumes, and even fiber tracts were notable between strains but only rarely notable within strains or between sexes (Figs. 1, 2, and S5, S6). Our analysis highlights not only the more obvious morphological differences but also significant quantitative differences in the white matter anisotropy. For example, in the color fractional anisotropy image (ColorFA), the corpus callosum was much thicker and the saturation higher for the B6 line, which indicated higher anisotropy compared with D2 and CAST. At the extreme, the midline connection of the corpus was entirely absent in BTBR. In Fig. 1, even the finest details of shape parameters, for example the entry of olfactory nerve fibers into the olfactory bulb, were highly distinctive from one strain to another, but not between males and females (compare top and bottom male and female averaged brain images). Although we have not explored shape parameters in this work, they may provide additional differential phenotypes. We limited this study to an analysis of variability and heritability of (1) regional volumes; (2) scalar DTI metrics, e.g. fractional anisotropy (FA), radial diffusivity (RD), axial diffusivity (AD), and mean diffusivity (MD) and (3) connectomes.

Fig. 1.

Horizontal color FA images from the average male (top) and average female bottom). Images are color-coded averages of four cases per sex that highlight orientation of fiber tracts (the principal eigenvector). The icon shows the key for encoding the eigenvectors: green- anterior/posterior; blue- dorsal/ventral; red- left/right. (A) and (E) B6, (B) and (F) D2, (C) and (G) CAST, (D) and (H) BTBR. Ob: olfactory bulb; FrA: Frontal association Cortex; MO: Medial Orbital Cortex; S1J,S1ULP;: Primary Somatosensory Cortex;S2: secondary somatosensory cortex; AuD: secondary auditory cortex; TeA: Temporal association cortex; CEnt: caudomedial entorhinal cortex; HC: hippocampus; SC: superior colliculus; PAG: Periaquaductal grey; LGN: lateral geniculate nucleus; VT: ventral thalamic nuclei; LDNT: latero dorsal nucleus of thalamus; fi: Fimbria; cc: corpus callosum; SPT: Septum; Cpu: striatum

Fig. 2.

Horizontal color FA images from the average male (top) and average female bottom) at a second level. Images are color-coded averages of four cases per sex that highlight orientation of fiber tracts (the principal eigenvector). The icon shows the key for encoding the eigen vectors: green- anterior/posterior; blue- dorsal/ventral; red left/right. (A) and (E) B6, (B) and (F) D2, (C) and (G) CAST, (D) and (H) BTBR. Acb: accumbens nucleus; Cpu: striatum; ac: anterior commissure; GP: globus pallidus; ic: internal capsule; Pir: piriform cortex; ZI: zona incerta; Hc: Hippocampus; DLEnt: dorsal intermediate entorhinal; MEnt: medial entorhinal cortex; Cent: caudomedial entorhinal cortex; mcp: middle cerebellar peduncle; PnO: pontine reticular nu, oral part; Pr5VL: principal strigeminal, ventrol; icp: inferior cerebellar peduncle; CG: central gray.

The ColorFA is but one of ten different scalar images derived from the diffusion processing pipeline. Each image highlights different anatomy in a complementary fashion. Supplemental Fig. S1 shows a comparison of the alternative contrasts. For example, the DWI and FA were particularly useful in driving the label registration.

3.2. ROI volumes were heritable

For the most basic measurement, whole brain volume, our results are largely consistent with previous literature in volumes for male/female, respectively (in mm³) (Hager et al., 2012): B6 463 ± 11.3 vs 479 ± 3.7; D2 415 ± 8.8 vs 403 ± 4.5; CAST 363 ± 11.98 vs 395 ± 4.6; BTBR 414 ± 7.8 vs 487 ± 3.9 (Figure S7). However, the BTBR brain volume we measured was smaller than B6, not larger as has been reported [http://gn2.genenetwork.org/show_trait?trait_id=49909&dataset=MDPPublish]. There were highly significant strain differences (F = 146.262, df = 3, p = 1.49e −15).

3.3. Sex differences were minor

We next wanted to determine whether sex was an important driver of individual differences. For every scalar parameter (volume, FA, RD, AD, MD), ANOVA comparisons were carried out including strain, sex, and their interaction.

There was no significant sex difference in total brain volume for male vs female (445 ± 20 SE versus 442 ± 18 SE). For volume of individual ROIs, 34 regions had a significant (Benjamini-Hochberg (B-H) p ≤ 0.05) sex effect, 328 had a significant strain effect, and there was no significant strain by sex effect. The region with the most significant sex difference was the bed nucleus of the stria terminalis (BNST; right male = 0.0599 ± 0.0022, female = 0.0551 + 0.0032, p = 0.00002; left male 0.0599 + 0.0026, female 0.0556 + 0.00277, p = 0.0000780). This region is sexually dimorphic in humans (Allen and Gorski, 1990). Heritability estimates for volume were significantly correlated between sexes (r = 0.75).

In the scalar DTI metrics, there were fewer sex effects than for volume, and heritability estimates in each sex correlated well. For FA, two regions had a significant (B-H p ≤ 0.05) sex effect, 298 regions had a significant strain effect, and none had a strain by sex effect. There were no significant sex or sex by strain effects for RD, but 168 regions had a significant strain effect (B-H p ≤ 0.05). For MD, there were no significant sex or sex by strain effects, but 118 regions had a significant strain effect (B-H p ≤ 0.05). There were no significant sex or sex by strain effects for AD, but 109 regions had a significant strain effect (B-H p ≤ 0.05). These results showed that sex effects were relatively minor compared with strain effects, especially for DTI metrics.

3.4. Significant strain differences in most of the scalar measure

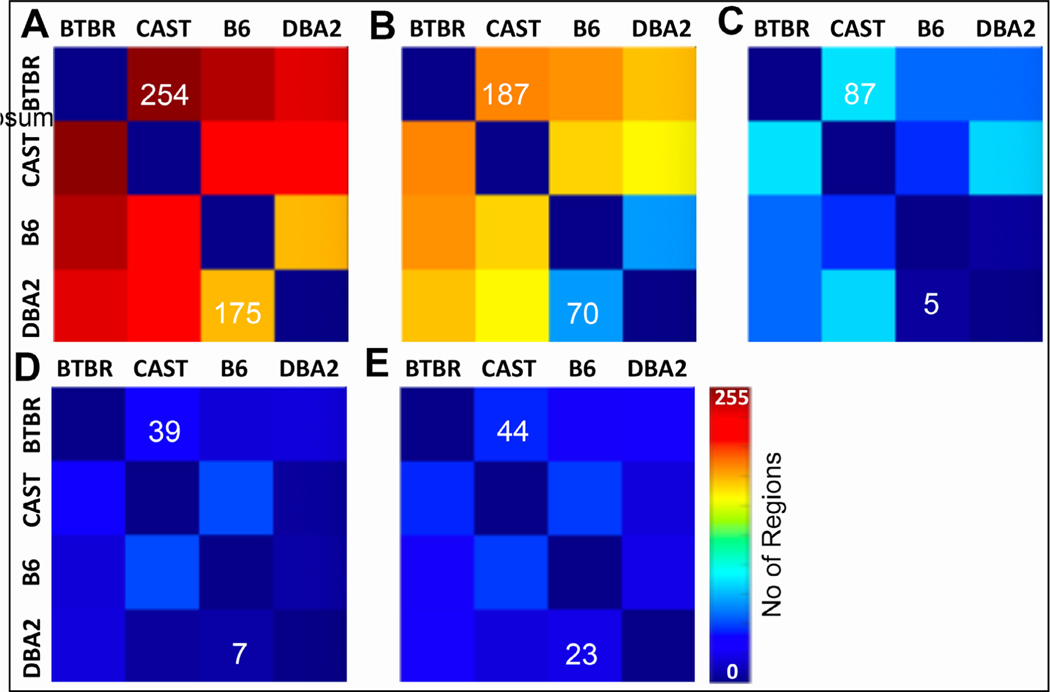
The data in Fig. 3 show that there were significant qualitative strain effects for all the scalar measures, but we wanted to quantify the extent to which strains and cases differed for any measurement. To fulfill this aim, we carried out ANOVA comparisons for each ROI and each measurement, using Tukey’s posthoc test to determine which strains were different. For volumetric data, 327 of 332 regions and tracts differed significantly (Benjamini-Hochberg corrected p < 0.05; Fig. 3 (A)). The five regions that did not differ were the left ventral tegmental area, right ventral orbital cortex, left dorsal acoustic stria, left lateral orbital cortex and right lateral orbital cortex. The differences in such a large number of regions confirmed our initial assertion, namely that BTBR and CAST would be most different from the ‘normal’ lab strains B6 and DBA2, but also that most brain regions would be significantly different between these two ‘normal’ strains. We observed similar results for the other measures: For FA, 298 regions had a significant ANOVA (Benjamini-Hochberg corrected p < 0.05), MD 128 regions, AD 117 regions, and RD 175 regions (Fig. 3 (b)–(e)).

Fig. 3.

ANOVA comparisons were performed to determine the number of regions of interest (from the total of 322 I.e. 2 × 166) that were statistically different between any two strains. Heatmaps help visualize which strain differences are the greatest. The heat scale goes from 0 to 255 where the color indicates the number of regions (out of 322) in which the metric (volume, FA, RD, MD, AD) is significantly different (Benjamini-Hochberg corrected p < 0.05). For example, volumes are significantly different in 254 regions when comparing BTBR and CAST; there are 176 regions that are different between DBA2 and B6. The color scale hopefully allows one to appreciate that volume is different between many regions while there are relatively few regions of interest (44–23) that are different in AD.

3.5. Volume and scalar metrics are heritable

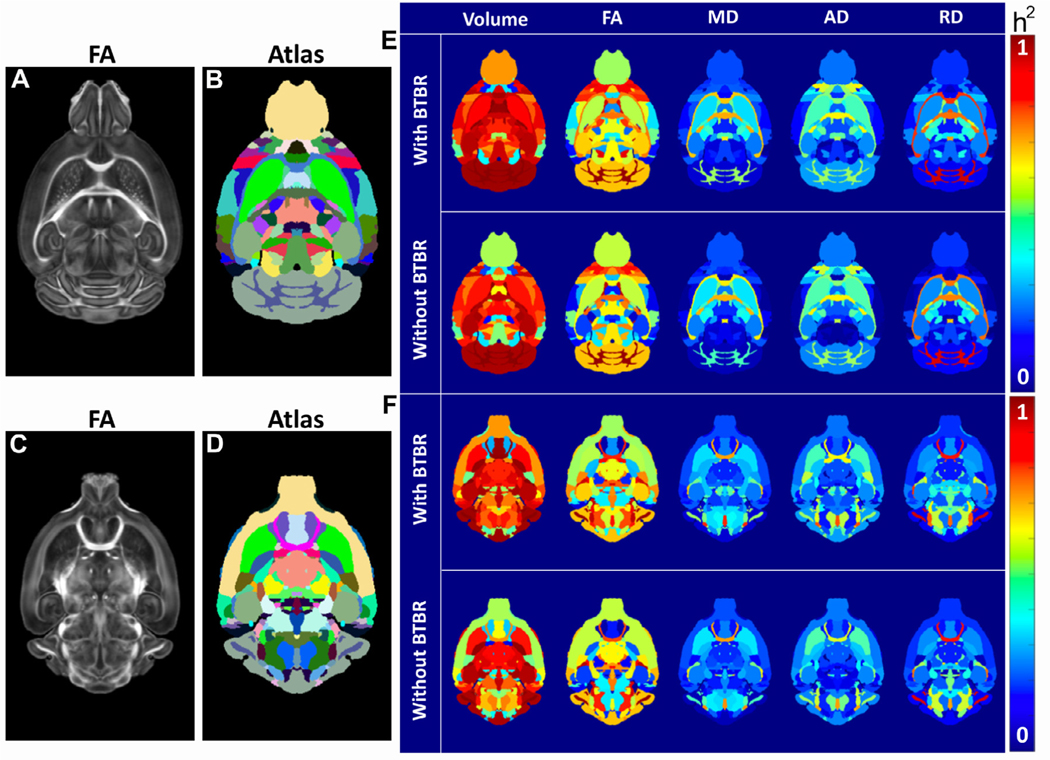
For most brain regions, there was a high heritability (h²) of volume. The FA had a high h² for a more limited number of regions. In general, MD, AD, and RD had low h² (Fig. 4). Often, a single outlier strain will drive these high heritabilities. To demonstrate this effect, we examined the heritability of the volumes of ten regions of interest, comparing estimates from the left and right hemisphere, recalculated when leaving one strain out (Fig. 4 (G)). The results demonstrate three important points. First, for many brain regions, one strain drove heritability because it was an outlier. Second, although BTBR and CAST were frequently outliers, there were also regions of DBA/2J or the ‘normal’ C57BL/6J that were outliers. Third, as expected, heritability was broadly the same across both hemispheres.

Fig. 4.

(A)–(F) Multiple Biomarkers are Heritable. (A) and (C) Representative dorsal slices from the FA images of the B6 and (B) and (D) the reference regions of interest. (E) and (F) Heritability (h2) is shown for volume, fractional anisotropy (FA), mean diffusivity (MD), radial diffusivity (RD), and axial diffusivity (RD) for these same two reference slices. (G) Heritability of the volume of 20 brain regions, across both hemispheres, dropping a strain (C57BL/6J = B6, DBA/2J = DB, BTBR = BT, CAST = CA, None dropped = No). ROIs are the hemisphere (left or right), our ROI number, and the region name.

The heritabilities for all measures in Fig. 4 (E) were not strongly dependent on their values, i.e. heritability was not necessarily higher for large values. This independence suggested that we could measure low values accurately; if low values had higher variability, they would have had lower heritability. Fig. S8 shows the h² ranking as ordered by ROI in a comparison of the four strains; Table S9 lists the top 20 regions from this rank-ordered list for each of the scalar metrics. Cerebellar white matter FA and FA from multiple regions of the cortex were highly heritable. Several regions were highlighted in both volume and diffusion changes, e.g., cingulate cortex- volume and FA; fimbria volume, RD, and AD; lateral lemniscus- volume, FA and AD. Multiple regions had correlated heritability in AD, RD, and FA.

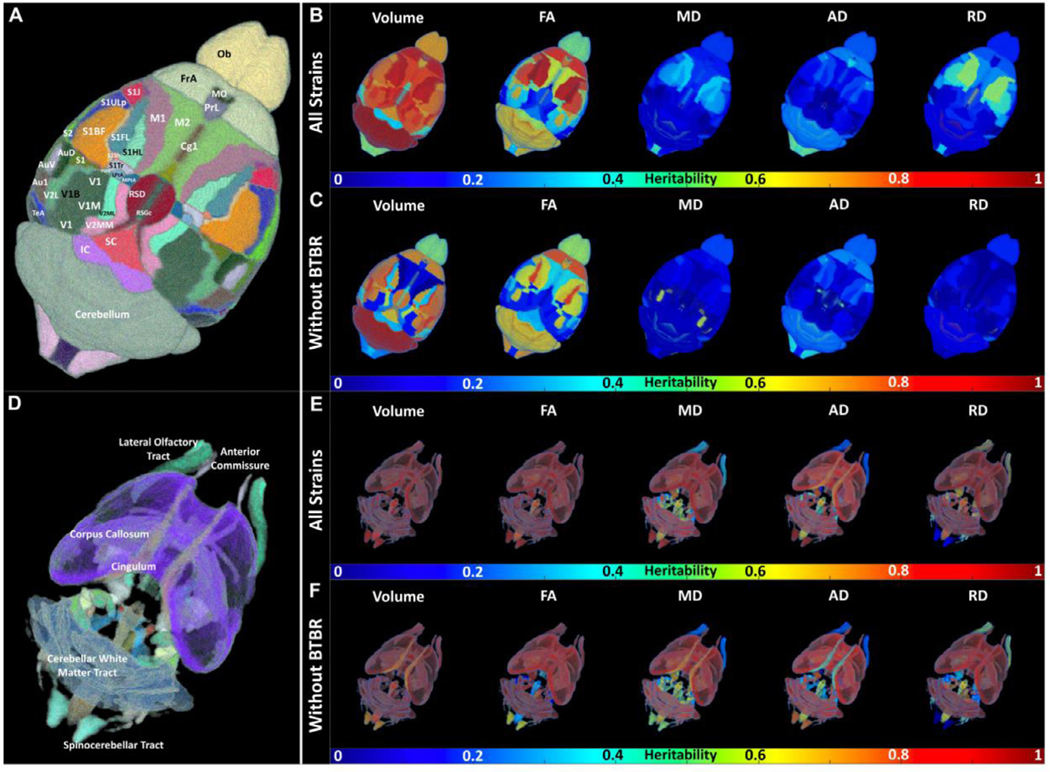
Fig. 5 illustrates the high heritability (h²) for the volume of many white matter and cortical regions. A number of regions had high heritabilities of FA, and MD, but the heritability of AD, and RD was generally low. To determine whether certain brain systems have higher heritability than others, we calculated the average heritability for the volume in five broad regions: forebrain, midbrain, hindbrain, white matter tracts, and ventricular.

Fig. 5.

Spatial distribution of heritability in cortex and white matter regions with and without BTBR strain. Heritability (h2) is shown for volume, fractional anisotropy (FA), mean diffusivity (MD), radial diffusivity (RD), and axial diffusivity (RD).

An ANOVA test showed highly significant differences between these brain parts (df = 4, F = 6.435, p = 5.39e-05). Tukey’s posthoc suggested that the forebrain (mean h² = 0.53, n = 180) drove these differences, with significant differences from hindbrain (mean h² = 0.64, n = 62, p = 0.005879) and white matter tracts (mean h² = 0.67, n = 64, p = 0.0002724).

We next wanted to determine whether one strain drove these differences, in a manner illustrated by Fig. 4 (G). Table 1 shows the significance of the difference between mean Tukeys post-hoc, with all strains, or dropping each strain. The difference between white matter tracts and forebrain was significant in all comparisons, suggesting it is not dependent upon one strain. However, the CAST strain appeared to drive the difference between forebrain and hindbrain, suggesting that CAST was an outlier for heritability of this system.

Table 1.

Tukey comparisons of mean heritability.

	All strains	D2	B6	CAST	BTBR
Midbrain –Forebrain	0.828	0.447	0.999	0.823	0.845
Hindbrain – Forebrain	0.006	0.004	0.072	0.999	0.0007
White matter tracts – Forebrain	0.0003	0.0003	0.003	0.015	0.006
Ventricular system – Forebrain	0.317	0.097	0.757	0.204	0.812
Hindbrain – Midbrain	0.855	0.989	0.505	0.912	0.653
White matter tracts – Midbrain	0.603	0.9187	0.195	0.927	0.851
Ventricular system – Midbrain	0.773	0.653	0.798	0.647	0.991
White matter tracts – Hindbrain	0.971	0.986	0.925	0.117	0.986
Ventricular system – Hindbrain	0.964	0.754	0.999	0.265	0.998
Ventricular system – White_matter_tracts	0.994	0.863	0.999	0.852	0.999

This table shows the significance of Tukey posthoc for comparisons of mean heritability across five brain systems, for all strains, and drops each strain individually. D2 = DBA/2J, B6 = C57BL/6J, CAST = CAST/EiJ, BTBR = BTBR T + Itpr3^tf/J.

3.6. Sex and hemisphere dependent coefficient of variation

The coefficient of variation (Peters et al., 2003) of individual ROI volume between left and right hemisphere for four strains were the following: D2: 0.0158 ± 0.0168; B6: 0.0157 ± 0.0199; CAST: 0.0156 ± 0.0163; BTBR: 0.0140 ± 0.0152. Figure S10 shows the CV of individual ROI as a function of the ROI volume. For most of the ROI in all strains, the CV was < 0.05. The CVs between male and female consistently showed low values: D2: 0.0373 ± 0.0301, B6: 0.0307 ± 0.0265, CAST: 0.0366 ± 0.0309, BTBR: 0.0282 ± 0.0276;

3.7. Connectomes for each strain

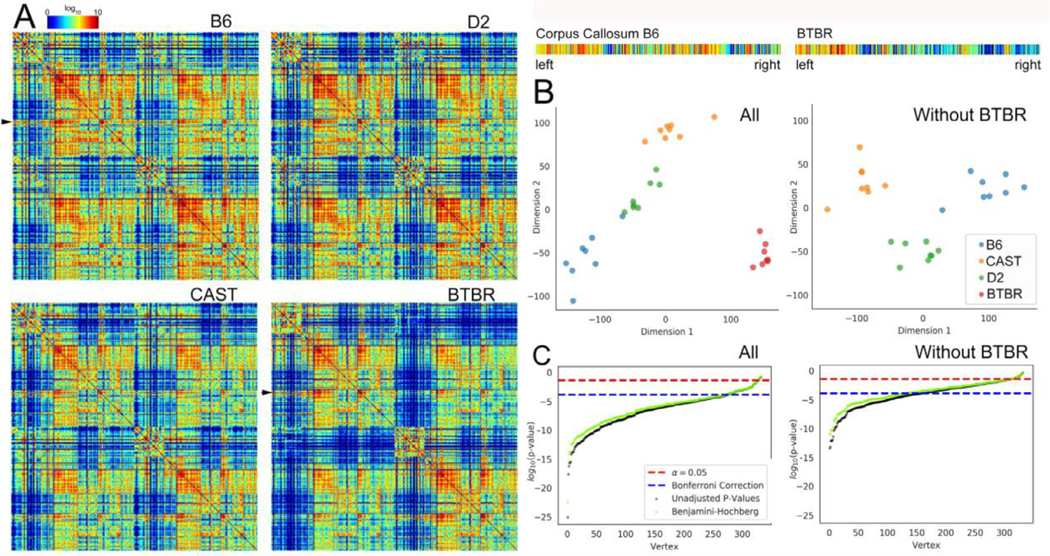
Fig. 6 (A) shows the whole brain connectome for all four strains: (a) B6; (b) D2; (c) CAST; (d) BTBR. The connection strength is shown with a log10 color scale that demonstrated an enormous range in connection within a single brain and across the strains. Each graph includes four sub sections: upper left- connections within left hemisphere, upper right- connections from left hemisphere to right, lower left- right hemisphere to left, and lower right- connections within right hemisphere. Visual comparisons reveal differences between the BTBR and the other strains. Reduction between the hemispheres is evident when one examines the upper right and lower left section of each quadrant. There are some intriguing differences between the more normal strains and the BTBR. The upper right-hand part of each quadrant shows connectivity between the isocortex and midbrain, hindbrain and white matter. The edge strengths in all these regions are considerably reduced in the BTBR. For example, the black arrows highlight the corpus callosum of the B6 and BTBR. Expanded plots of these nodes show the strength of connection between left and right hemisphere. The log color scale highlights the reduced connection between left and right hemisphere for the BTBR. While the suggestion is intriguing the statistical differences in the edge strength are not supported.

Fig. 6.

(A) Whole brain connectome for each strain. The connectomes (n = 8) of (a) B6; (b) D2, and (c) CAST strains were similar. The average connectome of the BTBR was significantly different with the reduced connectivity evident from the increased number of holes (dark blue entries). The seed nodes (Faraji et al., 2018) and targets (columns) are ordered according to the developmental origins. The arrows identify the corpus callosum (seed) which was extracted and magnified for comparison between B6 and BTBR. (B) Omnibus embedding improves the confidence in comparisons. The scatter plot shows clustering when the BTBR was included. When the BTBR was excluded, the clustering also shows statistical difference in the three similar strains. (C) Plot of log (p-value) from MANOVA comparisons in vertices across strain vs rank-ordered vertex shows roughly 280 vertices that were statistically different when all four strains were compared and 150 vertices that were different when the BTBR was excluded.

Figure S11 demonstrates that no edges on their own passed the typical level of significance (p < 0.05) after we used the Bonferroni method to correct for multiple comparisons. The omni manova comparison in Fig. 6 (B) demonstrates that the connectomes of a given strain tended to be more similar to one another than they were to the connectomes of other strains. Using classical multidimensional scaling to embed each connectome into just two dimensions, we found that the connectomes tended to form strain-specific groups (Levin et al., 2017, Borg, 2020). This connectome-wide group effect was preserved when we included and excluded the BTBR strain.

Fig. 6 (C) shows results of the multivariate, non-parametric k-sample testing which tests the differences in the profiles of each node of the connectome. The low-dimensional representation for a given node in a strain is tested to see how it differs from the low dimensional distribution in the other strains. The log of the p value is used to rank order the nodes. Thus, the nodes on the left are those with the highest difference. The figure shows that 280 of the 322 possible nodes were significantly different across all four strains, following the use of the Bonferroni method to correct the probability of false positives. The same analysis for the three control groups (excluding the BTBR) demonstrated fewer differences which is consistent with the original design of the study. We assumed there would be major differences when the BTBR was included because of the callosal defect. But there were at least 150 nodes that were significantly different when the BTBR was excluded. Moreover, there were multiple pairs of nodes for which both hemispheres were significantly different. Table S12 presents the top twenty nodes.

Fig. 7 shows the tractograms for four of the nodes in which the p values were the most significant. The corpus callosum was profoundly different in the BTBR, and it was the most highly ranked node when we compared all four strains. The termination at the mid line is obvious. The corpus callosum was also highly heritable when we excluded the BTBR. And this was consistent with the anatomical observations from Fig. 1 in both the morphology and intensity in the color FA. The substantia nigra, internal capsule, and fimbria were the next three most highly ranked nodes in the comparison of all four strains. The internal capsule and substantia nigra were also in the top four nodes when we compared the three similar strains, thus, these regions may be highly heritable across many strains. Examination of the tractograms affirmed the statistical findings. Tracts across the midline were substantially reduced for the BTBR in the substantia nigra and internal capsule and clearly less dense in the contralateral side for the fimbria compared with the other three strains.

Fig. 7.

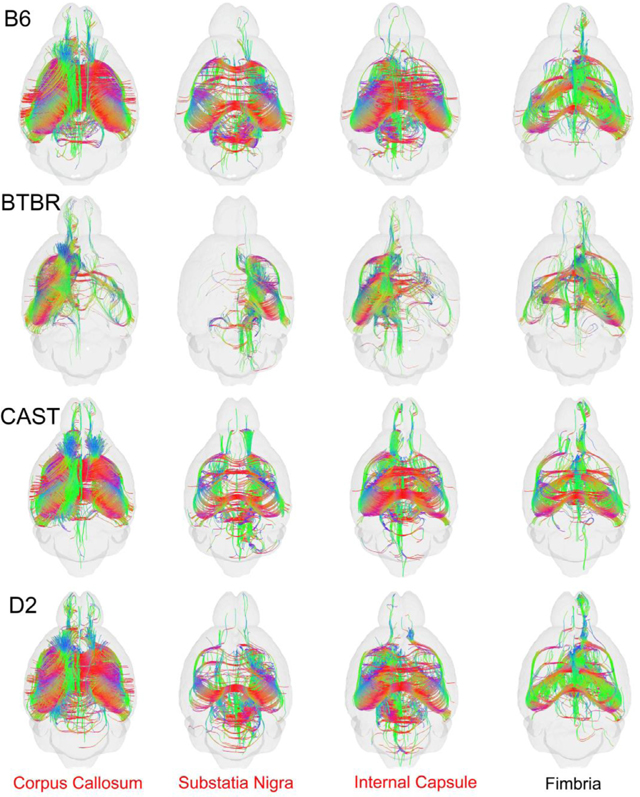
Tractograms for the top 4 nodes. derived from the omni MANOVA analysis including all four strains. The tractograms for the Fimbria for B6, CAST, and D2 were significantly different even when the BTBR was excluded.

4. Discussion

We have used state-of-the-art MRI workflows to study heritabilities in the mouse brain at three different levels: (1) volumetrically-defined brain structures, including more than 150 regions of interest—both nuclei, cortical regions, and fiber tracts, (2) scalar DTI parameters that were measures of tissue cytoarchitecture, and (3) variation in DTI-defined connectomes. For this initial work, we used four fully isogenic inbred strains of mice that differed greatly in genome sequence-—from 5 to 15 million variants distinguished any pair of strains (Ashbrook et al., 2019).

The most important findings are the following:

4.1. Microscopic MRI/DTI provides quantitative neuroanatomical phenotypes

Brain connectomes can vary over an enormous range of scale, over species, and between technologies. The electron microscopy connectome of Drosophila that was acquired at nanometer resolution was constructed at voxels on the order of 10⁻¹⁵ mm³ (Eichler et al., 2017). Clinical MRI acquires data with voxels on the order of 2 mm³ (Ugurbil et al., 2013). The mouse brain data in these studies were acquired with voxels < 10⁻⁵ mm³. Tract tracing in an EM image relies on different physical phenomena compared with a retroviral tracer which, in turn, is a considerably different tracing mechanism compared with diffusion. Thomas et al. (2014) and Maier-Hein et al. (2017) have explored the specificity and sensitivity of the diffusion based (human) connectome and concluded that frequently there can be more false positive connections than true positive connections. One explanation for a preponderance of false positives is that merging or crossing fibers can cause errors in tracking. This observation has driven us to push the spatial/angular resolution (in rodents) by nearly 5 orders of magnitude beyond that of clinical scans to limit the consequences of volume averaging (Calabrese et al., 2015). The data reported here are, to the best of our knowledge, the highest (spatial/angular) resolution available of genetically linked diffusion connectivity metrics in the mouse brain. And we have carefully catalogued the limits of sensitivity and specificity relative to retroviral tracers (Calabrese et al., 2015, Wang et al., 2018). Several investigators have used in vivo MRI to investigate structural connectivity in genetically engineered mice. Practical problems of life support limit the resolution in these studies to ~100 × 100 × 500 um with ~30 angular samples (Arefin et al., 2017, Hübner et al., 2017). Scans of post mortem specimens enable longer, higher resolution studies. In 2002, Zhang et al. reported some of the first DTI images of the post mortem mouse brain (Zhang et al., 2002), and, more recently, they have used the method to understand the function of Bcl-x in brain development (Zhang et al., 2005). Subsequent studies have extended spatial resolution and applied the method to unraveling morphologic changes in genetic models of neurologic disease (Jiang and Johnson, 2010, Bhagat et al., 2016). These studies relied on the scalar metrics (AD, RD, FA etc.), but they did not include any connectome. Generating the connectome adds a significant complication because one must acquire a “sufficient” number of angular samples to enable resolution of crossing and merging fibers. The term “sufficient” has been controversial. Calamante et al. have developed higher resolution tract density methods for connectomics in post mortem specimens at 100 um³ with 30 angular samples (Calamante et al., 2012). To enable comparison across the range of applications (human, mouse, in vivo, post mortem), we proposed the resolution index (RI), i.e., the product of the spatial and angular resolution (Johnson et al., 2018), i.e.

RI = Number of angular samples/voxel volume (mm³).

RI for the human connectome was 128 (Ugurbil et al., 2013). RI for Calamante’s study was 30,000 (Calamante et al., 2012). The RI for this work was (46/(0.045)³) i.e. 504,801.

4.2. Volume, FA, AD, RD, and connectomes are heritable

Virtually all the scalar metrics we measured were heritable at some level in some regions. Multiple investigators have demonstrated heritability of volumes in specific sub regions of the brain in both human and rodent studies (Stein et al., 2012, Peirce et al., 2003, Peper et al., 2007, Ashbrook et al., 2014). Other recent studies have detected significant global heritability of FA, AD and RD in human populations (Kochunov et al., 2015, Vuoksimaa et al., 2017). And studies have demonstrated heritability of specific regions of connectivity, in human (Zhang et al., 2018, Yeh et al., 2018). However, the work described here is the first to bring together a robust study of heritability of all these metrics (volume, FA, AD, RD, connection strength) in the mouse. We have demonstrated region specific heritability of volume, FA, AD, RD and connectivity.

We evaluated three strains (B6, D2, CAST) for which we expected neuroanatomical and connectome differences to be comparatively modest after correcting for global differences in brain volume. We expected a fourth strain (BTBR) to display major disruptions of interhemispheric connections. Working with isogenic animals (n = 8/strain) has enabled us to measure the within-strain variability of all traits with good precision, but with the caveat the we have sampled only a small number of genomes. Nonetheless, we could test the methods in detection of major differences (e.g. the BTBR) when the anatomy was so different that one needed to be concerned about artifacts from label registration and other experimental errors in the processing pipeline.

There was a remarkably robust collection of heritable phenotypes. Volume was highly heritable across the entire range of the structures included. Previously, we demonstrated that genotype accounted for ~ 60% of the variability of volume differences in 33 regions of the brains of a cohort of C57BL/6 mice and ten different strains from the BXD family (Badea et al., 2009). The average coefficient of variation of volume for the 33 structures across 11 strains was 15.2 ± 5.8%. The new studies described here provide the same data for 166 ROIs (in both hemispheres) with substantially improved precision. As shown in Fig. S10, the coefficient of variation within a strain for most of the regions was < 5%. The CV increased for smaller structures, i.e., structures with volumes < 0.1 mm ³ (Walsh and Lynch, 1998). We attribute the majority of the remaining variability to errors in label mapping. Correction of the volume heritability for this technical error is possible which would result in even higher estimates of heritability. We chose a more conservative approach i.e. not making such correction as the heritabilities are already quite high.

There were only nine ROIs (1.4%) with volumes > 0.1 mm³ with CV > 5%. The heritability was not strongly dependent on the absolute volume of the structure. More than 150 structures per hemisphere were highly heritable (> 0.8). Previous GWAS analysis of aggregated data from fifty other studies demonstrated heritability of volume in subcortical regions (Hibar et al., 2015, Hibar et al., 2017). The VETSA study compared 1237 twins by focusing on heritability of cortical thickness (Kremen and Prom_Wormley, 2010). The ENIGMA consortium expanded on the heritability of subcortical structures by comparing lateral symmetry using 15,847 MRI scans from 52 different data sets (Guadalupe et al., 2017). Elliott et al. used data from the UK Biobank to measure heritability across morphometric, diffusion and functional data in 8428 individuals (Elliott et al., 2018).

Kochunov et al. demonstrated that whole brain FA and RA had strong genetic dependence, whereas the genetic link to AD was not significant (Kochunov et al., 2015). A study of twins by Gustavson et al. revealed that all of the regions they measured were heritable and FA and MD accounted for roughly half the heritability in the tract subdivision (Predominantly, 2019). Recent studies from the UK Biobank have explored a number of image-derived phenotypes demonstrating regional heritability of FA, AD and RA (Elliott et al., 2018). Our work shows similar results with FA having the highest heritability of the scalar diffusion metrics. In the full group (including BTBR), the FA was strongly heritable (> 0.8) in ~130 of 166 regions of interest. Surprisingly, in the smaller group of more similar strains, heritability was still > 0.8 in more than 100 of the ROIs. AD and RD were not linked as strongly. But heritability was still > 0.8 in 50 ROIs for RA and in ~30 ROIs for AD.

Finally, the Human Connectome Project has generated multiple studies of heritability of specific structural circuits in the brain. Fig. 6 shows, again, a remarkably rich set of vertices (~280) with strong heritability across both hemispheres. As with the scalar metrics (Figs. 4 and 5), the evidence of genetic dependence in the connection strength was still present when we removed the BTBR strain from the analysis. A statistically robust comparison of connectomes is challenging because of false discovery. Trends that seem apparent in the color-coded adjacency matrices are influenced by the brain’s ability to integrate the patterns. Creation of a connectivity profile for each node exploits this effect of integration and yields a more statistically robust method to define the nodes that have the most difference across the strains.

5. Conclusion

The brain is the most complicated organ in the body. Understanding its genetic underpinnings starts with an understanding of brain structure. But the structure is fractal with collections of neurons linked through axons, collections of axons linked to local circuits, and circuits classified as short or long range. No single view or scale provides a complete picture, and no single method is sufficient to provide the full picture of the brain. Unwinding the genetic links to brain structure provides crucial knowledge to understanding a great many diseases and disorders (such as autism, dementia and Alzheimer’s disease). Sorting through the extraordinary complexity of data can quickly become over-whelming. Rank ordering the scalar metrics and the most critical nodes in the connectome brings specific circuits in focus. Sophisticated network analysis can then be used to construct hypotheses that connect structural changes to behavior. The methods shown here enable one to span the scale from meso to micro over the entire brain. When coupled to the power provided through isogenic colonies, our method promises a statistically robust approach to linking connectome to genome.