Dual-Use Transducer for Ultrasound Imaging and Pulsed Focused Ultrasound (pFUS) Therapy

Abstract

Pulsed focused ultrasound (pFUS) uses short acoustic pulses delivered at low duty cycle and moderate intensity to non-invasively apply mechanical stress or introduce disruption to tissue. Ultrasound-guided pFUS has primarily been used for inducing cavitation at the focus, with or without contrast agents, to promote drug delivery to tumors. When applied in tandem with contrast agents, pFUS is often administered using an ultrasound imaging probe, which has a small footprint and does not require a large acoustic window. The use of nonlinear pFUS without contrast agents was recently shown to be beneficial for localized tissue disruption, but required higher ultrasound pressure levels than a conventional ultrasound imaging probe could produce. In this work, we present the design of a compact dual-use 1 MHz transducer for ultrasound-guided pFUS without contrast agents. Nonlinear pressure fields that could be generated by the probe, under realistic power input, were simulated using the Westervelt equation. In water, fully developed shocks of 42 MPa amplitude and peak negative pressure of 8 MPa were predicted to form at the focus at 458 W acoustic power or 35% of the maximum reachable power of the transducer. In absorptive soft tissue, fully developed shocks formed at higher power (760 W or 58% of the maximum reachable power) with the shock amplitude of 33 MPa and peak negative pressure of 7.5 MPa. The electronic focus steering capabilities of the array were evaluated and found to be sufficient to cover a target with dimensions of 19 mm in axial direction and 44 mm in transversal direction.

I. Introduction

Cavitation induced by ultrasound combined with systemically administered ultrasound contrast agents (UCAs) has been extensively studied over the past decade, and successfully used for drug and gene delivery to solid tumors and diseased tissues [1]. Because UCA-aided drug delivery does not require very high ultrasound pressures, many studies have utilized conventional ultrasound imaging probes for both therapy and imaging guidance [2]. For therapy, this approach has the advantage of “built in” electronic focus steering and a small footprint of the probe, thus it does not require a very large acoustic window and can be acoustically coupled directly to the body. An intrinsic limitation of UCA-aided ultrasound therapy is that the UCAs are confined to blood vessels and the perivascular space, which limits their access to poorly vascularized tissue regions. This limitation is most relevant in tumors with increased interstitial pressure, high tumor cell density, and stromal barriers, e.g. pancreas tumors. Inducing de novo cavitation (i.e. without administration of UCAs) throughout tumor tissue using pulsed focused ultrasound (pFUS) has been shown to be very beneficial for overcoming these barriers to drug penetration in preclinical mouse model of pancreas cancer [3]. Until recently, it was assumed that the focal pressure levels required to nucleate and sustain inertial cavitation are substantially higher than for UCA-enhanced ultrasound and require a high-power HIFU transducer with large footprint and a need for water-based coupling stand-off. This limits the practicality of the approach, in addition to having to integrate separate ultrasound systems for therapy and imaging, essentially equivalent to using ultrasound-guided HIFU thermal ablation systems. Such systems have been used in a number of clinical trials for palliative pancreatic tumor ablation [4], and one of the biggest challenges has been a limited acoustic access to the tumor due to its location behind or adjacent to gas-containing bowel or stomach. Not only is the incident HIFU beam completely blocked by bowel gas in this condition, but it also carries high risk of severe collateral damage to the bowel. Bowel preparation through fasting pre-procedure and applying localized pressure to the abdominal wall (e.g. via small water-filled balloons) to either collapse the gas-containing structures or push them aside from the HIFU beam was found to be of paramount importance for treatment success and avoiding complications. In addition, because large parts of the conical HIFU beam are outside of the ultrasound imaging plane in ultrasound-guided HIFU ablation systems, avoiding bowel gas during treatment planning is further complicated. Thus, in order to improve both acoustic access, treatment planning, and ultrasound imaging guidance, the footprint of the HIFU beam on the skin surface should be minimized, and the imaging plane should be co-located with the HIFU beam as much as possible. Both requirements may be ideally achieved with a dual-use ultrasound imaging-therapy transducer array, such that some pushing on the abdomen can be applied by the transducer itself, and a target that can be imaged can also be treated.

We have recently demonstrated that the inertial cavitation activity that results in tissue permeabilization can be achieved at lower peak negative pressures if shock fronts develop in the focal waveform due to nonlinear propagation effects [5]. Further, the relationship between the shock amplitude and peak negative pressure was shown to be primarily determined by the F-number of a FUS transducer, with less focused transducers producing shocks at the lower peak negative pressure values [6]. Shocked waveforms are known to be achievable using diagnostic ultrasound probes at relatively low mechanical index (MI ~ 4–6), albeit at higher frequencies typically used for imaging (> 3 MHz) and recently for kidney stone pushing technology (2 MHz) than that optimal for pFUS (1–1.5 MHz) [3], [7], [8]. The goal of present work was to design an ultrasound transducer array with a small, imaging probelike, footprint, that would allow for both pFUS therapy with electronic focus steering, and ultrasound imaging for targeting and treatment guidance. The design process was based on the parameters of the acoustic field known to efficiently induce inertial cavitation at the focus, dimensions and depth of the primary target – pancreatic tumors, the achievable parameters of the driving electronics (Verasonics Ultrasound Engine, VUE) [9], and the properties of the piezoelectric material for building the array.

II. Materials and Methods

A. Design requirements and considerations

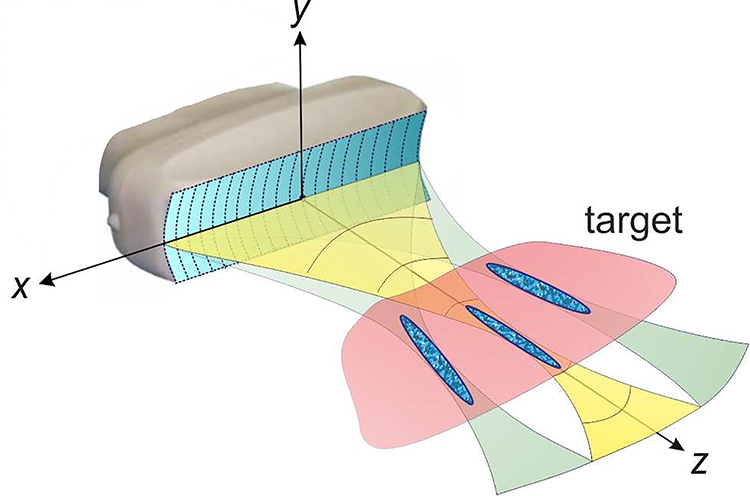
The overall design concept is illustrated in Fig. 1 and represents a linear multi-element array with a rectangular footprint typical for diagnostic ultrasound linear arrays [10]. Beam focusing and steering in the imaging plane (xz) for pFUS exposures is achieved by phasing the elements. In addition, cylindrical curvature or a lens could be applied to the radiating surface for additional focusing in the elevational plane (yz). Based on our prior experience, the operating frequency was set at 1 MHz [8], [11]. This frequency represents a reasonable compromise between pFUS efficiency (higher frequencies would result in formation of smaller and fewer bubbles [12]), and ultrasound imaging quality.

Fig. 1.

Conceptual diagram of a dual-use diagnostic-therapeutic ultrasound array for cavitation-based drug delivery applications. Pulsed focused ultrasound (pFUS) beam of sufficient intensity can be produced by the array and electronically steered in the transverse direction within the imaging plane of the array to cover the targeted tissue volume.

The choice of the overall aperture of the probe was dictated by a number of factors. First, the footprint of the probe was intended to be comparable to that of standard curvilinear ultrasound imaging probes, e.g. ATL C5–2, which is 54 mm × 12 mm [7]. The focal distance of interest corresponded to the typical depth of pancreas tumors when viewed by ultrasound imaging, which is 50 mm in average [13], [14]. Note that this depth is typically smaller than that reported from computed tomography (CT), positron emission tomography (PET) or magnetic resonance imaging (MRI) scans, because it is strongly dependent on the patient positioning and pressure applied on the abdomen [14]. Further, the formation of the shock front within the focal region at 6–8 MPa of peak negative pressure was required to effectively induce cavitation [5], [12]. For axially symmetric transducers, the peak pressures that correspond to shock formation are determined primarily by the transducer F-number, i.e. the ratio of the focal distance to transducer aperture diameter [6], [15]. For non-axially symmetric transducers, as the one considered here, the dependence of shock formation on transducer dimensions is harder to predict. However, based on our prior experience with the diagnostic curvilinear probe of 54 mm × 12 mm aperture size, the shock would form at 50 mm focal distance within the required range of peak negative pressures [7]. Finally, in order to obtain reasonable ultrasound imaging quality, the element pitch should not exceed 0.5λ, i.e. ~ 0.8 mm, and the number of elements being multiples of 128, for the ease of integration with VUE. Considering all of the above, the dimensions of the array were initially chosen to be 51.2 mm along the x-axis (i.e. 64 elements at 0.8 mm pitch) and 15 mm along y-axis. The width of the elements was taken as 0.72 mm and kerf as 0.08 mm, based on standard fabrication processes discussed with the manufacturer (Sonic Concepts, Inc., Bothell, USA). The primary goal of this study addressed by numerical modeling described below was whether these dimensions of the array would allow for reaching shock forming conditions at the focus while keeping the intensity at the array surface below the safety limit for the piezoelectric material.

The other important requirements were the pFUS focus steering range reaching 40 mm (or ±20 mm) in the transverse dimension, and the distance between the focus and the first prefocal null being less than half of the minimum axial dimension of the target of interest (~10 mm for pancreas tumors). In other words, the latter requirement ensures that the prefocal half of the focal lobe is located entirely inside the target. This empirical rule, introduced and discussed in detail by others [16], [17], is meant to avoid the excitation of prefocal cavitation in intervening tissues and consequent focus shielding. One other design consideration was whether or not to include focusing in the elevational plane (yz). On one hand, focusing in the elevational direction would increase the focal gain and therefore the amplitude of the generated shock. On the other hand, cylindrical focusing of the piezoelectric material or attachment of a lens would complicate the fabrication process and/or would be associated with losses. Therefore, the effect of cylindrical focusing in the elevational plane on the focusing gain was investigated here by considering two transducers: one with plane surface and one with cylindrically curved surface, with the radius of curvature F = 50 mm.

B. Breakdown limits of piezoelectric material

In selecting the realistic output levels for modeling, the breakdown limits for the piezoelectric material and the output limits of VUE driving electronics were considered. PZT-5H piezocomposite ceramic material was considered as the optimal candidate for transducer fabrication due to its relatively high dielectric constant. In comparison to PZT-4, simulation predicts that PZT-5H material yields 40% greater pressure per volt which is useful for high pulsed power and low duty cycle applications. The element impedance for this material in combination with a single quarter-wave matching layer is 2.5 kOhms and has a theoretical withstanding voltage of 564 V. Provided a conservative estimate of 50% electromechanical efficiency, the total acoustic power from 64 elements corresponding to the material breakdown would be 2 kWatts and the surface intensity – 265 W/cm². However, this estimate does not account for electrical safety such as channel-to-channel arching or electrode integrity. Therefore, in this study, operation at 80% of the withstanding voltage that corresponds to 1.3 kWatts acoustic power or 170 W/cm² surface intensity, will be considered as a maximum permissible one. This power level was determined from prior experience to be safe from the electric standpoint and it is well within the capabilities of the driving electronics of VUE with HIFU option that recently allowed for achieving 3.5 kWatts output electric power within pulses of up to 10 ms duration for boiling histotripsy [12].

C. Numerical models of linear and nonlinear array fields

Numerical simulations of linear acoustic fields generated in water by the probe were used for three purposes: to set a boundary condition in the plane z = 0 for the nonlinear propagation model; to evaluate the focus steering capabilities of the array; and to investigate the effect of focusing in the elevational plane on the focal gain. Nonlinear simulations were performed to evaluate shock-forming capabilities of the array in water and in tissue within its realistic power outputs.

A boundary condition for acoustic pressure was set at the initial plane, z = 0 mm, using the assumption of the uniform amplitude distribution of the normal oscillation velocity u_n at the surface of the array elements [18]. Characteristic pressure amplitude p₀ on the surface of the array was introduced using plane wave relation as p₀ = |u_n|ρ₀c₀. When modeling electronic focus steering along and transverse the array axis, a phase for each element was calculated from the path length difference between the element’s center and position of the steered focus. The calculated phase was included in the complex amplitude of the oscillation velocity for the area of a given element of the array. The focus location with coordinates (0, 0, 50) mm will be referred to as the default focusing location throughout the manuscript. Note that in the case of cylindrically focused array considered here, the axial coordinate of this point is the same as the center of the array’s curvature.

Transferring the distribution of the normal oscillation velocity given at the array’s surface to the acoustic pressure distribution at the initial plane included two steps. First, an auxiliary numerical hologram of the pressure field was calculated using the Rayleigh integral in the xy plane axially centered at half focal distance of the source, z = 25 mm [18]. Specific choice of z = 25 mm was not crucial; such plane could be located at any distance larger than several wavelengths from the transducer. For the Rayleigh integral calculation, the surface of the array was covered by a mesh of triangles with sides not exceeding 0.18 mm in length (0.12 of the wavelength at 1 MHz) and the normal component of the velocity u_n was specified at the surface of each triangle. The hologram was calculated within 250 mm × 250 mm spatial window. Then, the pressure field obtained in the plane z = 25 mm was propagated backward to the initial plane, z = 0 mm, using the angular spectrum method and was used as a boundary condition for both linear and nonlinear propagation models [19].

Numerical simulations of nonlinear acoustic fields generated in water by the proposed diagnostic probe at different output levels were performed using the one-directional version of the Westervelt equation. This equation has been shown to provide an accurate model to simulate nonlinear acoustic fields generated by HIFU transducers of different geometries, including strongly focused multi-element arrays [20], [21] and diagnostic probes operated at high powers [7]. The equation includes the effects of nonlinearity, diffraction, and thermoviscous absorption and can be generalized for frequency dependent absorption and dispersion in tissue [22]. The numerical model is described in detail elsewhere [20], [21], [23]. Here, a brief summary of the numerical algorithm is provided.

To model forward propagation of the ultrasound beam generated by the probe in water, the Westervelt equation was rewritten in a retarded coordinate system as:

$$\frac{{\partial }^{2}p}{\partial z\partial \tau }=\frac{c_0}{2}\Delta p+\frac{\beta }{2{\rho }_0{c}_0^3}\frac{{\partial }^2{p}^2}{\partial {\tau }^2}+\frac{\delta }{2c_0^3}\frac{{\partial }^{3}p}{\partial {\tau }^3}.$$ (1)

Here p is the acoustic pressure, z is the spatial coordinate along the beam axis (Fig. 1), t is the time, τ = t – z/c₀ is the retarded time, Δp denotes the full Laplace operator over three coordinates. Parameters of the propagation medium, c₀, ρ₀, β, and δ are the ambient sound speed, density, coefficient of nonlinearity, and thermoviscous absorption (sound diffusivity), correspondingly. The values of these parameters were chosen to represent water at the temperature 20°C: c₀ = 1482.4 m/s, ρ₀ = 997.6 kg/m³, β = 3.5, δ = 4.33 × 10⁻⁶ m²/s.

One example of nonlinear acoustic field simulation was also performed in soft tissue with the aim of comparing achievable amplitudes of the developed shock in water and in tissue. In these simulations, an additional operator L(p) was added to the right side of the equation (1). In the frequency domain, the operator governs frequency dependence of the absorption, α (f), and dispersion, c(f), in tissue:

$$\begin{array}{l}\alpha (f)={\alpha }_0{\left(f/f_0\right)}^{\eta },.\\ \frac{c(f)-c_0}{c_0}=-\frac{c_0{\alpha }_0}{2\pi f_0}\tan \left(\frac{\pi }{2}\eta \right)\left[{\left(f/f_0\right)}^{\eta -1}-1\right].\end{array}$$ (2)

Here α₀ is the absorption coefficient at the operational frequency of the array f₀, η is the exponent in the absorption law that is typically close to unity for soft tissues [22], dispersion of the phase velocity c(f) is introduced in accordance with the local dispersion relationship [22, 24].

Representative acoustic parameters for soft tissue were chosen as: c₀ = 1575 m/s, ρ₀ = 1054 kg/m³, β = 4.5, δ = 4.33 × 10⁻⁶ m²/s, α₀ = 0.6 dB/cm at 1 MHz, η = 1.2 [25].

The Westervelt equation was solved using the method of fractional steps with an operator splitting procedure of second-order accuracy [26]. According to the splitting procedure, the Eq. (1) was divided into several simpler equations to define operators separately describing diffraction, nonlinearity, and absorption effects. The pressure field was represented in either the time-domain or frequency-domain using a finite Fourier series expansion. Transitions between the time and frequency domains were accomplished using fast Fourier transform (FFT). The diffraction operator was calculated in the frequency domain for each harmonic component using the angular spectrum approach [19]. The nonlinear operator was calculated using two different methods. In smaller axial distances, where shock fronts are not yet formed, the frequency domain approach and the fourth-order Runge-Kutta method for solving the system of coupled nonlinear equations for harmonic amplitudes were employed [27]. As the steepness of the waveform increased and more harmonics were required, the nonlinear algorithm was automatically switched to a conservative time-domain Godunov-type scheme [28]. The switch to the Godunov-type scheme was made at the condition when the amplitude of the tenth harmonic exceeded 1% of the harmonic amplitude at the fundamental frequency. The absorption was calculated in the frequency domain using an exact solution in a form of decaying exponent for each harmonic. Parameters of the numerical scheme were: longitudinal step Δz = 0.2 mm, transversal steps Δx = Δy = 0.02 mm. The maximum number of Fourier harmonics was set equal to 1000.

III. Results

A. Comparison of linear fields of the arrays with and without elevational focusing

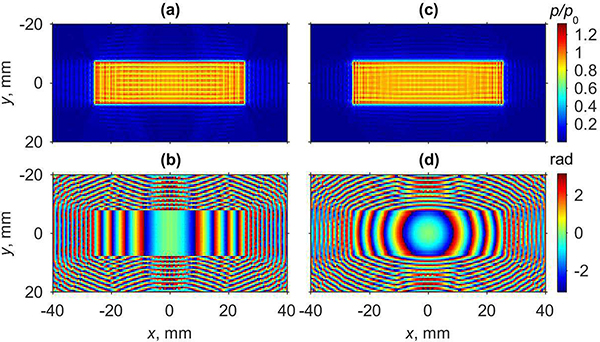
Amplitude and phase distributions of the pressure field holograms obtained at the plane z = 0 mm and used as a boundary conditions for calculating electronic steering to the default focusing location (0, 0, 50) mm are shown in Fig. 2. The left column, Fig. 2(a,b), corresponds to the transducer with plane radiating surface and the right column, Fig. 2(c,d), corresponds to the transducer with the surface cylindrically focused in the elevational direction. Pressure amplitude distributions for the plane and cylindrical transducers, Fig. 2(a,c), do not reveal a significant difference; in both cases the oscillation velocity across the transducer face was considered to be uniform, corresponding to a piston source. The phase distribution that corresponds to the plane transducer is uniform along the y-axis and shows almost parabolic phase variation along the coordinate x (Fig. 2(b)), which is related to electronic phasing applied to the array elements. For the cylindrical transducer, when electronic focusing is combined with geometrical focusing in the elevational direction, the phase distribution becomes radially symmetric (Fig. 2(d)).

Fig. 2.

Boundary conditions for plane (a,b) and cylindrically focused (c,d) arrays, with phase focusing to (0,0,50) mm location. Amplitude of the acoustic pressure in xy plane at z = 0 mm normalized to the characteristic pressure p₀ at the source surface (a,c) and its corresponding phase (b,d).

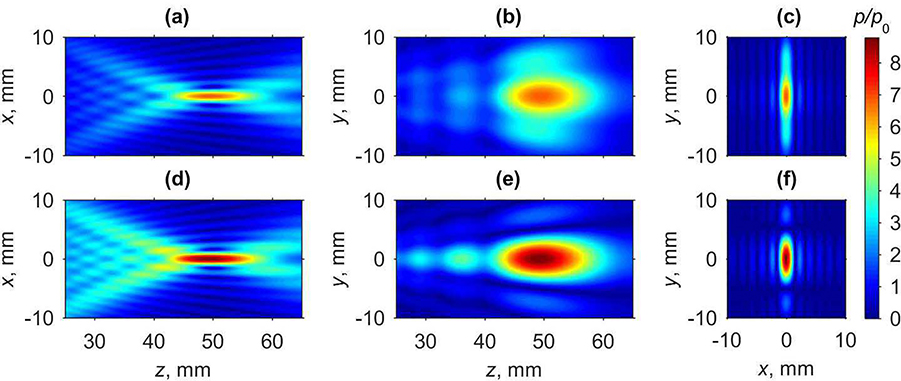
Fig. 3 depicts axial (xz and yz) and focal (xy plane at z = 50 mm) distributions of the pressure amplitude, normalized to the characteristic initial pressure p₀, for the plane (Fig. 3(a - c)) and cylindrical (Fig. 3(d - f)) transducers in water. For both arrays, tighter focusing of the pressure field is achieved in the xz plane compared to the yz plane since the transducers are more than 3 times longer in x direction than in y direction. Additional focusing of the cylindrical array has the most effect on the field structure in the elevational direction along the y-axis, whereas the field structure along other coordinates is similar for both arrays. For the plane array, the beam dimensions in the focal region defined at −6 dB level relative to the pressure magnitude at the focal point are: 1.9 mm beam width along the x-axis and 12.6 mm along the y-axis in the focal plane, and 16.0 mm length of the focal lobe along the z-axis. Corresponding dimensions for the cylindrical array are: 1.9 mm, 6.2 mm, and 16.0 mm. It is seen that for the cylindrical array only the beam width along the y-axis is smaller than for the plane one. Maximum pressure amplitude is achieved 0.5 mm prefocally for the plane array and 0.8 mm – for the cylindrical one. Linear pressure focusing gain of the plane transducer at the default focusing location is equal to 6.84. Adding element focusing along the y direction allowed for increasing the linear gain by 28% up to 8.72. In practice, elevational focusing can be achieved by curving the elements, as considered in this paper. Alternatively, the addition of a lens to the transducer face for focusing in the elevational direction can be used. Despite the fact that the lens may lead to amplitude losses of about 10–12%, the resulting focusing gain will still be improved compared to the case without the lens. Since focusing angle is a critical parameter that defines shock front amplitude at the focus [6], increasing a focusing gain without changing dimensions of the transducer is beneficial to achieve higher values of shock amplitude, however, at the expense of operating at higher powers. Consequently, in the rest of the manuscript only the cylindrically focused array is characterized with regard to its steering capabilities and generation of nonlinear acoustic fields with shocks.

Fig. 3.

Two-dimensional pressure amplitude distributions obtained using linear propagation modeling for transducers with active surface either plane (a - c) or cylindrically focused in the elevational direction (d - f): (a,d) distributions in the axial xz plane, (b,e) in the axial yz plane, and (c,f) in the focal xy plane. Pressure amplitudes are normalized to the characteristic initial pressure amplitude p₀ at the elements of the array.

B. Steering range of the array with elevational focusing.

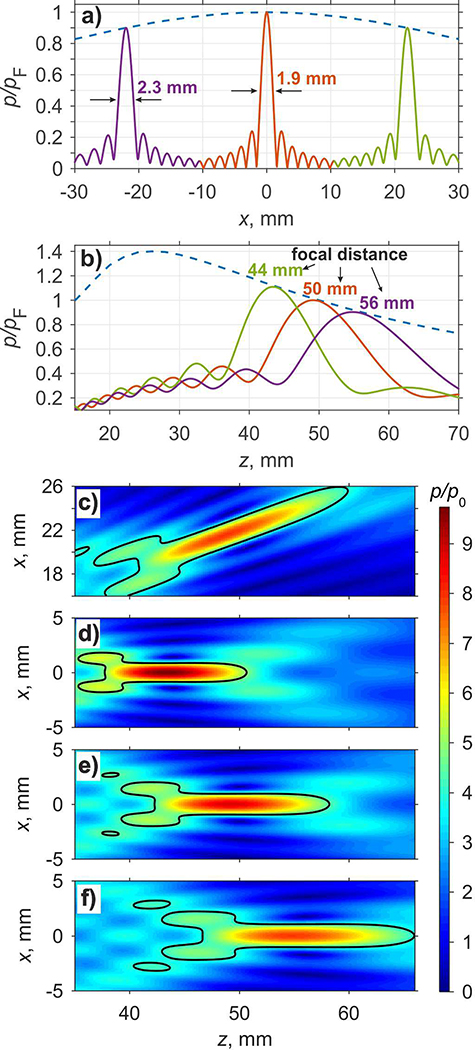
The results for evaluating focus steering capabilities of the cylindrically focused array in water are summarized in Fig. 4. The envelope for the focal pressure amplitude when steering in transverse direction along the x-axis in the plane z = 50 mm is shown in Fig. 4(a) by a dashed curve. Here, the focal pressure amplitude in the steered foci is normalized to the focal pressure in the case of steering to the default focusing location x = 0. Focal pressure drops to a 0.9 level relative to the focal pressure p_F in the default focusing location when the focus is steered to x = ±22 mm. These results demonstrate that transversal steering range of the proposed array is sufficiently large for the primary clinical target – pancreas tumors [16], [17].

Fig. 4.

Transverse (a) and axial (b) envelopes and beam patterns in the field of steered foci at 1.1, 1, and 0.9 focal pressure levels relative to the focal pressure pF in the default focusing location. Two dimensional pressure amplitude distributions (c – e) relative to the pressure amplitude p₀ at the source obtained in the axial xz plane of the array using linear propagation model: transverse focus steering at x = 22 mm and z = 50 mm (c), and for axial steering at z = 44 mm (d), z = 50 mm (e), and z = 56 mm (f).

The transverse beam pattern when focusing to the default location is shown in Fig. 4(a) as a solid curve in the center of the graph; corresponding transverse beam patterns when steering to x = ±22 mm are shown on the left and on the right. It is seen that with decrease of the focal pressure level by 10 % from the default level – a typical level defining practical limits of beam steering in other FUS systems [21] – the width of the focal maximum at −6dB level along the x-axis increases by 20 %, from 1.9 mm to 2.3 mm. When estimating the minimum beam width from two-dimensional distribution of the pressure amplitude calculated in xz plane for transversal focus steering to x = 22 mm (Fig. 4(c)), i.e. in perpendicular direction to the steered beam axis, its value is 2.2 mm. The length of the transversally steered focal lobe measured at −6 dB level increases by 26 % from 16.0 mm to 20.2 mm if calculated along the steered axis of the array.

Focal pressure amplitude in the foci steered in longitudinal direction along the z-axis is shown in Fig. 4(b) by dashed line. It is seen that the focusing gain, and therefore the focal pressure is the largest at z = 25 mm, i.e. when the focus is steered towards the transducer. Axial distributions of the normalized pressure amplitudes that correspond to the cases when focal pressure amplitude is equal to 0.9, 1.0, and 1.1 relative to the corresponding value at the default focusing point, are shown in Fig. 4(b), and the corresponding focusing locations are z = 56 mm, z = 50 mm, and z = 44 mm yielding the range of axial steering ±6 mm. The axial location of the maximum pressure amplitude is slightly prefocal relative to the intended focusing locations of z = 44 mm, 50 mm, and 56 mm by 0.6 mm, 0.8 mm, and 1.2 mm, correspondingly, and 1.4 mm prefocal for the transverse steering to x = 22 mm in the focal plane (Fig. 4(c)). Two dimensional distributions of the normalized pressure amplitude for the three axial steering cases (Fig. 4(d - f)) show that steering the focus away from the transducer in the axial direction resulted in the increase of the longitudinal dimensions of the focal lobe: 12.8 mm, 16.0 mm, and 19.2 mm, respectively, consistent with the decrease in the focal gain and increase in the effective F-number of the probe. The width of the focal lobe along x-axis also increases consistently with increase of the focal distance: 1.8 mm, 1.9 mm, and 2.1 mm.

C. Nonlinear pressure field of the array with no steering

Detail analysis of nonlinear simulations was performed in water for the cylindrically curved transducer in the case of steering to the default focusing location (0, 0, 50) mm with the boundary condition shown in Fig. 2(c,d) which was scaled by characteristic source pressure p₀. The ranges of p₀, corresponding characteristic surface intensity $I_0=p_0^2/2{\rho }_0{c}_0$, acoustic power used in nonlinear simulations, and the corresponding values of the peak positive and negative pressures achieved at the focus are listed in Table I. Acoustic power of the source was calculated as a product of the total active radiating surface of the transducer and the characteristic intensity I₀. The results for the focal pressure values that correspond to one representative example of nonlinear simulations in soft tissue are also reported for comparing with the calibration data obtained in the free-field in water.

TABLE I.

Characteristic source pressure p₀, corresponding intensity $I_0=p_0^2/2{\rho }_0{c}_0$, and acoustic power used in nonlinear simulations; corresponding peak positive and peak negative pressures at the default focusing point (z = 50 mm) in water.

Source pressure amplitude p0 (MPa)	Acoustic power of the source (W)	Peak intensity on the source I0 (W/cm2)	Peak positive pressure at the focus (MPa)	Peak negative pressure at the focus (MPa)
0.1	2.34	0.338	0.91	−0.83
0.2	9.35	1.35	1.9	−1.6
0.3	21.0	3	3.1	−2.3
0.5	58.4	8.5	5.8	−3.6
0.6	84.1	12.2	7.6	−4.2
0.8	149.6	21.6	12.6	−5.2
1.0	233.7	33.8	24.4	−6.2
1.1	282.8	40.9	32.0	−6.6
1.2	336.5	48.7	36.8	−7.1
1.3	395.0	57.1	40.3	−7.5
1.4	458.1	66.3	42.9	−7.9
1.5	525.8	76.1	45	−8.3
1.6	598.3	86.6	46.8	−8.6
1.7	675.4	97.7	48.3	−9
2.0	934.8	135.2	52	−10

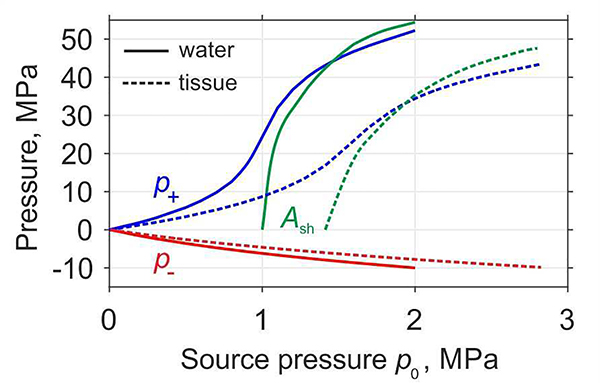
Resulting peak positive pressures (p+), peak negative pressures (p−), and shock amplitudes in the default focus location as functions of p₀ are plotted in Fig. 5 for propagation in water (solid curves) and in soft tissue (dashed curves). Dependences of the peak positive and negative pressures on pressure amplitude at the source are typical for focused transducers and are known as saturation curves [29]. Peak positive pressure exhibits initial smooth quasi-linear growth, followed by fast rise when shock begins to form, and then by saturation associated with rapid absorption of the wave energy at the shocks. Conversely, the magnitude of the peak negative pressure slowly and monotonically increases with increasing of acoustic output of the source. Source pressure at which the peak positive pressure is equal to the shock amplitude corresponds to the case of the fully developed shock [6]. For the current transducer design, the results show that fully developed shock forms in water at p₀ = 1.4 MPa, I₀ = 66.3 W/cm², and acoustic power of 458.1 W as marked in bold in the Table I. The amplitude of the fully developed shock front at the focus in water is 42.9 MPa, and the peak positive and negative pressures are 42.9 MPa and −7.9 MPa, respectively.

Fig. 5.

Dependences of the peak positive pressure (p₊), peak negative pressure (p₋), and shock amplitude (Ash) at the default focusing point (z = 50 mm) in water (solid curves) and in tissue (dashed curves) at increasing source output.

Soft tissue has higher absorption and nonlinearity than water, and this affects the acoustic field parameters. Higher absorption in tissue leads to lower peak pressure amplitudes compared to those obtained in water at the same source pressure level p₀, as observed in the saturation curves (Fig. 5). For strongly focused nonlinear beams, if the difference between water and tissue is only in absorption, peak pressure magnitudes in tissue would be the same as in water but at higher p_0t values scaled as p_0t = p₀·exp(α₀F) [30]. Due to the higher nonlinearity in tissue, the developed shock would have lower amplitude than in water, and the corresponding p_0t value is reduced. Both of these effects can be accounted for in a nonlinear derating procedure that is valid for strongly focused transducers, where the axial size of the focal lobe is much smaller than the focal distance [31]. However, neither procedure can be accurately applied here, because the focal lobe size is comparable to the focal distance (Fig. 4). Thus, an empirical approach to derating was used: derated p_0t levels for tissue were defined as ones that correspond to achieving the same nonlinear regime as in water.

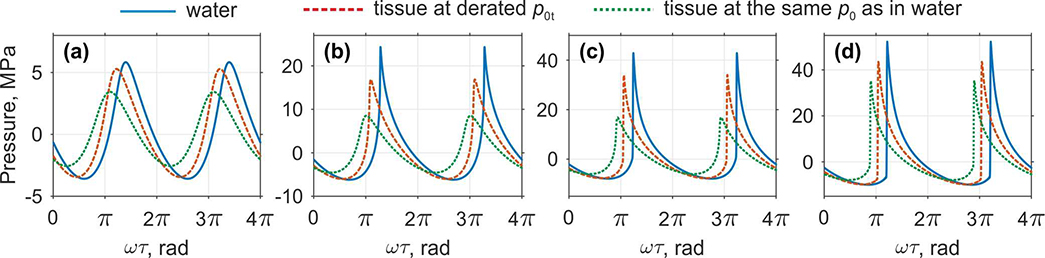
Focal pressure waveforms at z = F = 50 mm that correspond to different nonlinear regimes of focusing are shown in Fig. 6 for propagation both in water (solid curves), in tissue at the same source pressure level p₀ (dotted curves) and in tissue at the derated level p_0t (dashed curves). Focal waveform in water for the source pressure p₀ = 0.5 MPa corresponds to the upper threshold of quasi-linear regime with only few harmonics present in the spectrum, and the waveform is only slightly distorted. Quantitatively quasi-linear waveform distortion is defined by a criterion that less than 10% of the total intensity of the wave is concentrated at higher harmonics [6]. In tissue, the similar quasi-linear regime is observed at the derated p_0t = 0.7 MPa, that is 1.4 times higher than in water. Since nonlinear effects are insignificant in this case, peak pressures in tissue at the derated p_0t are only 5% lower than in water. At the same source pressure level p₀ = 0.5 MPa as in water, peak pressures in tissue are about 40% lower because of stronger attenuation.

Fig. 6.

Comparison of the pressure waveforms at the default focusing location of the probe (z = 50 mm) in water and in soft tissue for various characteristic source pressures p₀ that correspond to various nonlinear regimes: (a) quasi-linear (p₀ = 0.5 MPa in water, derated p_0t = 0.7 MPa in tissue), (b) nonlinear at the beginning of shock forming (p₀ = 1.0 MPa in water, derated p_0t = 1.4 MPa in tissue), (c) developed shock (p₀ = 1.4 MPa in water, derated p_0t = 1.9 MPa in tissue), and (d) saturated shocks (p₀ = 2.0 MPa in water, derated p_0t = 2.8 MPa in tissue). For better visibility the waveforms are slightly shifted along the time axis.

Shock front begins to form in water at the source pressure p₀ = 1.0 MPa and significant asymmetry between the peak positive and negative pressures appears (Fig. 6(b)). In tissue, formation of shock starts to occur at the derated p_0t = 1.4 MPa. In this case, the difference between peak positive pressures in water and tissue is more significant than in the quasi-linear one: p+ in tissue at derated p_0t is 30% lower than in water while p− differs only in 3%. Further, peak positive pressure in tissue at the same value of p₀ as in water is almost 3 times lower, 24.4 MPa in water versus 8.5 MPa in tissue.

At higher values of the source pressure, the shock amplitude increases and the waveform with fully developed shock forms in water at p₀ = 1.4 MPa as shown in the Fig. 6(c). In this case, the shock front begins from zero pressure and grows up to the peak positive pressure. Note that exactly the same coefficient 1.4 as in two previous cases (a,b) is obtained for the ratio of source pressures corresponding to the developed shock formation in water and in tissue. Therefore, this coefficient of 1.4 can be considered as derating coefficient for p₀ from water to tissue in this simulation case. Coincidentally, the ratio of shock front amplitudes in water (42.9 MPa) and tissue (33 MPa) is the same as the ratio of nonlinearity coefficients β = 4.5 in tissue and β = 3.5 in water. An example of the waveform that corresponds to strongly nonlinear saturation regime is shown in Fig. 6(d) for p₀ = 2.0 MPa both in water and in tissue and at derated p_0t = 2.8 MPa in tissue. The saturation occurs due to strong absorption of the wave energy at the shocks, which start to form prefocally, and strong asymmetry of the shocks leading to nonlinear refraction effects [32].

The comparison of the focal pressure waveforms and saturation curves in water and in tissue shows that derating of the acoustic field parameters to tissue for this simulation case can be done in two steps. First, take acoustic field parameters in water at the derated level p₀/1.4. Second, reduce the peak positive pressure by proportionally to the ratio of nonlinearity coefficients β in tissue and in water. Thus, further in the manuscript we will only consider the results obtained for propagation in water because in tissue at derated source pressures the results will be qualitatively similar.

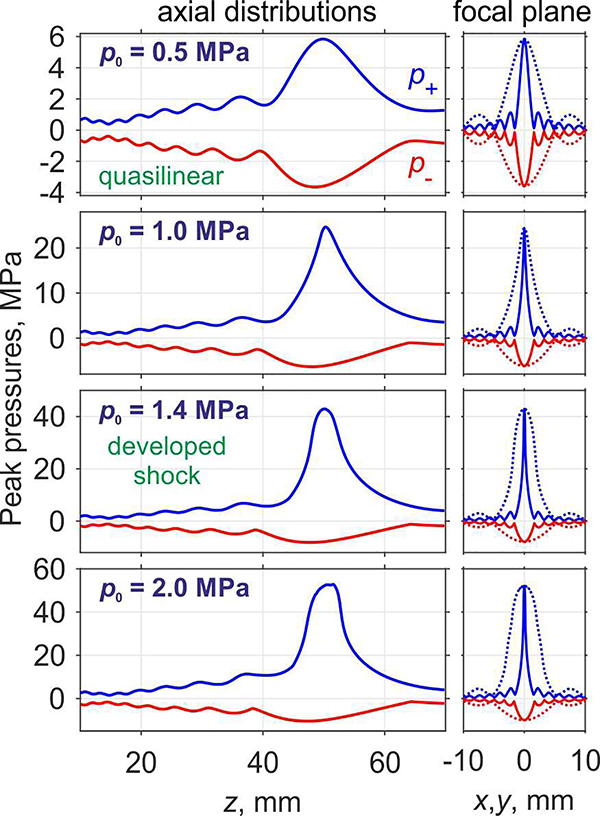
Changes in the shape of the main focal lobe due to nonlinear effects are detailed in Fig. 7, where axial and transverse distributions of the peak positive and peak negative pressures are presented for the default focus location in water and different source power levels. Transverse distributions in the focal plane at z = 50 mm are plotted by solid curves along the x-axis and by dashed curves along the y-axis. Corresponding two-dimensional distributions of the peak positive pressure and the peak negative pressure in the axial and focal planes are shown in Fig. 8 and Fig. 9, respectively.

Fig. 7.

Peak positive (p₊) and peak negative (p₋) pressure distributions along the z-axis of the probe (left column) and at the focal plane (right column) along the x-axis (solid line) and y-axis (dotted line) for various characteristic source pressures p₀ (indicated at the left upper corner of each row) in water.

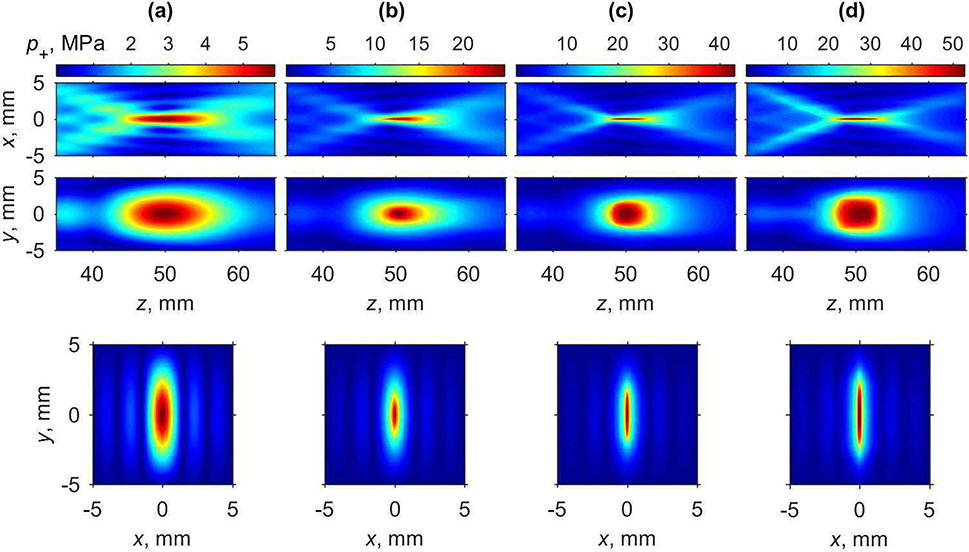
Fig. 8.

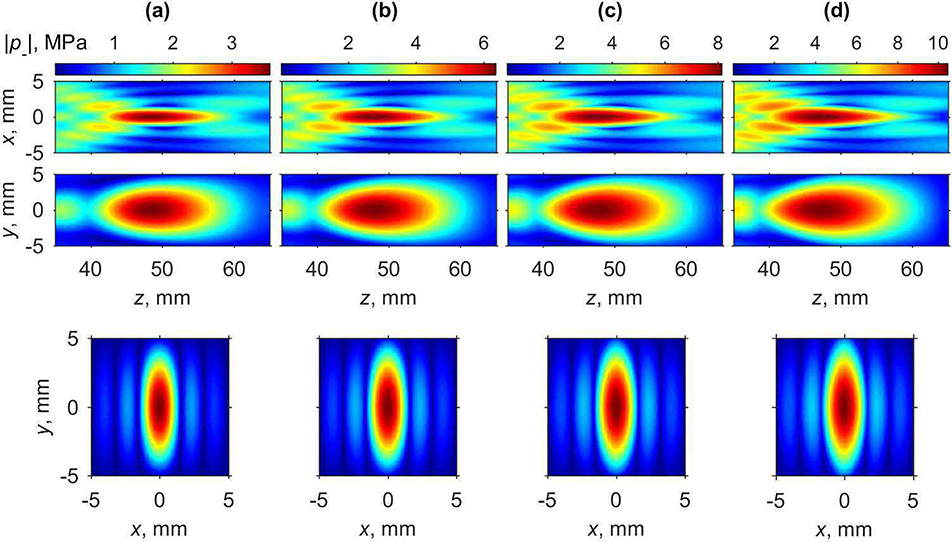
Two-dimensional peak positive pressure distributions in the axial plane xz (upper row), in the axial plane yz (middle row), and in the focal plane xy (lower row) for various characteristic source pressures p₀ corresponding to nonlinear regimes: (a) quasi-linear (0.5 MPa), (b) nonlinear at the beginning of shock forming (1.0 MPa), (c) developed (1.4 MPa), and (d) saturated shocks (2.0 MPa) in water.

Fig. 9.

Two-dimensional distributions of the absolute values of peak negative pressure in the axial plane xz (upper row), in the axial plane yz (middle row), and in the focal plane xy (lower row) for various characteristic source pressures p₀ corresponding to nonlinear regimes: (a) quasi-linear (0.5 MPa), (b) nonlinear at the beginning of shock forming (1.0 MPa), (c) developed (1.4 MPa), and (d) saturated shocks (2.0 MPa) in water.

The shape of the focal region for the peak positive pressure is changing in a non-monotonic way (Fig. 8). Initially, with increase of the source pressure, the axial and transversal dimensions of the peak positive pressure focal maximum become smaller. When the source pressure increases from the quasi-linear level (p₀ = 0.5 MPa) to the level at which shock front in the focus is forming (p₀ = 1.0 MPa), the axial and transversal dimensions of the beam along x-axis measured at −6 dB level decrease by about two-fold: from 14.1 mm to 8.9 mm and from 1.56 mm to 0.8 mm, respectively. At the same time, transversal size along the y-axis decreases by 1.6 times from 5.4 mm to 3.2 mm. At the source pressure corresponding to formation of fully developed shocks (Fig. 7, p₀ = 1.4 MPa), longitudinal size and transversal size along the x-axis decrease further down to its minimal values equal to 7.1 mm and 0.54 mm, respectively. Transversal size along the y-axis does not decrease further and is equal to 3.9 mm at this power level. Further increase of the source pressure toward nonlinear saturation regimes results in a slight increase of the dimensions of the focal maximum. Conversely, the shape of peak negative pressure focal maximum, as shown in Fig. 9, does not considerably change at higher array outputs; only slight increase in longitudinal and both transversal directions is observed. These changes are important in estimating the volume where therapeutic effect, i.e. tissue permeabilization, can be achieved for a single pFUS focus location. According to the current hypothesis, both sufficient peak negative pressure and the presence of shock are prerequisites for inducing most efficient cavitation activity [12] and therefore are expected to correlate to the bioeffect. Given that the area where the shocks are present correlates with peak positive pressure maximum, which is narrower than peak negative pressure maximum, its size will relate to that of the bioeffect. Thus, the dimensions of peak positive pressure focal maximum measured at −6 dB level, which in the case of fully developed shock are equal to 0.54 mm×3.9 mm×7.1 mm, may be useful metrics in planning of the treatment foci spacing.

Note here that the reported dimensions of the pancreatic tumors amenable to pHIFU treatment range within 2–7 cm (median 4–5 cm), and volumes within 10–177 cm³ (median about 60 cm³) [4]. These dimensions are within reach of electronic pHIFU focus steering within the imaging plane, and mechanical scanning of the probe can be implemented in the elevational direction. However, the estimated volume of bioeffect is 15 mm³, i.e. 4000 times smaller than the median target volume, therefore, treatment time is an important consideration. pHIFU pulsing protocol attributes, such as PRF and number of pulses delivered per point, and potentially possible sparser distribution of the foci, will need to be optimized to keep the treatment being efficient and treatment time clinically feasible.

D. Nonlinear pressure field of the array with steering

A limited set of simulations of focus steering in nonlinear array field were performed based on the results presented for the linear beam focusing in section B. The acoustic waveforms at escalating output power were simulated at the edges of the transverse and axial steering range, as defined for the linear beam steering: 10% drop in pressure amplitude when steering transversely and axially behind the focus, and 10% increase when steering axially toward the array. In the case of transverse steering, the same peak pressures and shock amplitude conditions were achieved at the steered focus location as in the default location, if the output power was increased by 20%, i.e. by the same factor as the ratio of focal intensities in the linear beam. This was expected as the same dependency was recently demonstrated for a multi-element HIFU array [33]. Conversely, the relationship between steering in the axial direction in linear and nonlinear regimes was found to be more complex. This is due to the changes in the effective F-number when steering axially, and the associated changes in peak focal pressure ratios and shock-forming conditions [6], [33]. Specifically, when the focus was steered distally (z = 56 mm) the developed shock formed at lower peak focal pressures (p₊ = 35 MPa, p₋ = 6.5 MPa) and at 16% lower power output (395 W, p₀ = 1.3 MPa), but it was also lower in amplitude (A_sh = 35 MPa). When steering proximally, conversely, the developed shock formed at higher peak focal pressures (p₊ = 53.4 MPa, p₋ = 9.7 MPa) and 22% higher power (561 W, p₀ = 1.55 MPa), and the shock amplitude was higher (A_sh = 53.4 MPa). Note that the desirable inertial cavitation behaviors were previously observed to be independent of exact shock amplitude and peak negative pressure, at least within the range of values stated above [12]. Therefore, the nonlinear steering capabilities of the array in the axial direction are expected to be equal to or greater than those determined for the linear beam focusing. This will be the subject of the future experimental studies when the array is fabricated.

IV. Discussion

This paper presents the design of a 1 MHz dual-use system for pFUS therapy and in-treatment ultrasound imaging. Simulations are performed to evaluate the system’s capabilities for creating nonlinear shock-wave fields in application for drug delivery to pancreas tumors. The cylindrically focused linear array design with selected dimensions (51.2 mm × 15 mm, radius of curvature 50 mm) was validated in simulations to satisfy all the criteria related to the target geometry, capabilities of the driving electronics (VUE system), and safety of the piezoceramic material. The array is currently being fabricated by Sonic Concepts, Inc. (Bothell, WA, USA). Specifically, pancreas tumors at stage III – locally advanced disease – that could benefit from pFUS-aided chemotherapeutic drug delivery are known to be located in average 5 cm deep, and can be 2–7 cm in size transversely and 2–4 cm in the depth dimension [16], [17]. Accordingly, the proposed array design is expected to provide effective electronic beam steering in both linear and strongly nonlinear, shock-forming regimes within ±22 mm of the focus in the transverse direction and ±6 mm in the axial direction. Further adjustment of the focus position could be achieved with mechanical translation of the probe. The dimensions of the focus under developed shock conditions were predicted to be 7.1 mm × 0.6 mm × 3.9 mm, which could be used for planning volumetric pFUS sonications. The peak negative pressure in the shock-forming conditions range was 6.0–7.9 MPa both in water and in soft tissue, i.e. within the 6–8 MPa range previously determined by us to be optimal for promoting consistent inertial cavitation in the form of sparse bubble clouds [5], [12]. The corresponding required acoustic output power for focusing in water ranged within 233–458 W, i.e. 3–5 fold lower than conservatively estimated safety threshold of 1.3 kW for the piezoelectric material PZT-5H. The power compensation for attenuation in intervening tissue was estimated based on simulations of nonlinear propagation in soft tissue with 0.6 dB/cm attenuation and the acoustic power corresponding to the developed shock formation (757 W) was found acceptable in terms of the available power range. Note also that substantially higher nonlinearity coefficient in tissue [25, 34] than in water proportionally reduced the developed shock amplitude at the focus [35].

The first prefocal null in the array field was located 10 mm from the focusing location, and can realistically be contained within the intended target. The dimensions of the focal region and the position of the prefocal null for axially symmetric, strongly spherically focused transducers are primarily determined by the transducer F-number and operating frequency [36]. The present array design could be characterized by two F-numbers in the imaging and elevational planes, which are equal to 1 and 3.3, respectively. Interestingly, the position of the prefocal null and the half-width sizes of the focal lobe in the imaging plane corresponded to what one would expect for a transducer with F-number of 1 [5]. This indicates that the influence of the elevational size of the array on the field structure in the imaging plane is relatively minor. However, this size and elevational focusing does affect the focusing gain (Fig. 3) and could be tailored for specific output power needs in other applications.

The ultrasound imaging capabilities and achievable image quality were not estimated in this work, and will be addressed when the array is fabricated. With the frequency of 1 MHz being quite low, it is hard to expect state of the art medical ultrasound image quality, but similar 1 MHz arrays have been successfully used by others in underwater sonar imaging, transcranial brain imaging and even small animal imaging [37]-[40]. It is important to note that ultrasound imaging here is only intended for treatment targeting and guidance in centimeter-sized region of interest that had been previously imaged with a higher resolution, higher image quality probe. A specific advantage that the current array has in guiding pFUS interventions in the pancreas is that the imaging and therapeutic fields are co-located. In a target with challenging acoustic access such as pancreas tumors, with gas-filled bowel representing both a barrier and a safety concern, this is very important.

V. Conclusions

A transducer array for ultrasound imaging-guided pFUS without contrast agents, with dual capabilities for both therapy and imaging, was designed and tested in nonlinear simulations. It was shown that the system provides acoustic field parameters at the focus necessary for inducing inertial cavitation throughout the target of interest, and is expected to provide sufficient imaging quality for targeting the tumor and monitoring cavitation. The applicability of the system is not limited to tumors or to drug delivery, but can be used for any therapeutic approach where mild to moderate microscopic disruption of tissue over a large volume is needed.

Biography

Maria M. Karzova received the M.S. degree in physics in 2012 and the Ph.D. degree in acoustics in 2016 from Moscow State University (MSU), Moscow, Russia, and École Centrale de Lyon (ECL), Ecully, France, according to the double Ph.D. program of the French Government. After graduation from the Ph.D. program, she was appointed by Moscow State University and currently she is a Senior Researcher at the Department of General Physics and Condensed Matter Physics of the Physics Faculty of MSU. She has been affiliated with the Department of Fluid Mechanics, Acoustics, and Energetics of ECL to work on irregular reflection of N-waves from smooth and rough surfaces. Her research interests are in nonlinear acoustics, therapeutic ultrasound, and optical methods for measuring acoustical pressure waveforms in air.

Petr V. Yuldashev received an M.S. degree in physics in 2008 and a Ph.D. degree in acoustics in 2011 from Moscow State University (MSU), Moscow, Russia, and École Centrale de Lyon (ECL), Ecully, France, according to the double Ph.D. program of the French Government. After graduation from the Ph.D. program, he was appointed by Moscow State University and currently is an Associate Professor at the Department of General Physics and Condensed Matter Physics of the Physics Faculty of MSU. He has been affiliated with the Department of Fluid Mechanics, Acoustics, and Energetics of ECL to work on the propagation of shock waves in a turbulent atmosphere and the utilization of nonlinear acoustics effects to calibrate high-frequency broadband microphones. His research interests pertain to simulation of nonlinear wave propagation in inhomogeneous media, shock wave focusing, sonic booms, and shadowgraphy measurement methods for acoustic phenomena.

Vera A. Khokhlova received the M.S. degree in physics in 1986 and Ph.D. and D.Sc. degrees in acoustics in 1991 and 2012, respectively, from Moscow State University (MSU), Moscow, Russia. After graduation from the Ph.D. program she was appointed by the Moscow State University and currently is an Associate Professor at the Department of Acoustics of the Physics Faculty of MSU. Starting from 1995 she is also affiliated with the Center for Industrial and Medical Ultrasound of the Applied Physics Laboratory (APL) at the University of Washington in Seattle. Her research interests are in the field of nonlinear acoustics, therapeutic ultrasound including metrology and bioeffects of high intensity focused ultrasound fields, shock wave focusing, nonlinear wave propagation in inhomogeneous media, and nonlinear modeling.

Fedor A. Nartov graduated from DSTU Technical lyceum, Rostov-on-Don, Russia. He is currently a B.S. student at the Department of Acoustics of the Physics Faculty of Moscow State University (MSU), Moscow, Russia. His research interests are high-intensity focused ultrasound (HIFU) in therapy and noninvasive surgery and numerical modeling in acoustics.

Kyle P. Morrison received the B.S. degree in manufacturing engineering from Western Washington University, in 2003, and his M.S. degree in medical engineering from the University of Washington, Seattle, WA, USA, in 2012. He is the President of Sonic Concepts, Inc. and leads its multi-disciplinary engineering teams that develop premium ultrasonic transducers and systems for preclinical and clinical applications.

Tatiana D. Khokhlova received her Ph.D. degree in physics in 2008 from Moscow State University (MSU), Moscow, Russia. After graduation from the Ph.D. program Dr. Khokhlova moved to the University of Washington (UW) in Seattle for postdoctoral training at Applied Physics Laboratory, and then completed a research fellowship at the Department of Medicine, UW. Dr. Khokhlova is currently an Associate Professor of Research at the Department of Medicine, UW. Her research interests are in physical acoustics, therapeutic ultrasound, and photoacoustic imaging.