Overcoming the quantum limit of optical amplification in monolithic waveguides

A compact, integrated, and ultralow-noise amplifier based on low-loss monolithic silicon nitride waveguides is demonstrated.

Abstract

Optical amplifiers are essential in numerous photonic applications. Parametric amplifiers, relying on a nonlinear material to create amplification, are uniquely promising as they can amplify without generating excess noise. Here, we demonstrate amplification based on the third-order nonlinearity in a single chip while, in addition, reporting a noise figure significantly below the conventional quantum limit when operated in phase-sensitive mode. Our results show the potential of nanophotonics for realizing continuous-wave parametric amplification that can enable applications in optical communications, signal processing, and quantum optics across a wide range of frequencies.

INTRODUCTION

Optical parametric amplifiers (OPAs) rely on a nonlinear material to create amplification, in contrast to stimulated emission as in conventional amplifiers. Because of their unique characteristic of providing a noise figure (NF) well below the 3-dB quantum limit (1) of conventional amplifiers when operated in a phase-sensitive mode (2), OPAs have attracted much interest in optical communication (3), ultrafast signal processing (4, 5), and quantum metrology (6). To date, continuous-wave (CW) operation has only been demonstrated in bulky systems, for example, using hundreds of meters of χ⁽³⁾-based highly nonlinear fiber (HNLF) (3) or using multiple χ⁽²⁾-based lithium-niobate planar waveguides that require periodic poling to generate phase matching and lossy free-space assemblies in between (7). In the past decades, extensive research has explored materials with high nonlinearity such as silicon (8), AlGaAs (9), nonlinear glasses (10, 11), graphene (12), and plasmonics (13). However, all demonstrations to date using a single compact waveguide for parametric amplification have operated with a pulsed pump but not in a CW operation prohibiting use in real applications. The reason for this is either waveguides with prohibitively high linear losses (8) or the use of materials that feature large nonlinear losses (10, 11) such as two-photon absorption (TPA) or free-carrier absorption (FCA) that will limit the pump power that can be used. Here, we address this challenge by using a very low-loss (1.4 dB/m) silicon nitride waveguide within a chip area of 23 mm² to demonstrate CW parametric amplification of 9.5 dB with an NF of 1.2 dB, well below the conventional 3-dB quantum limit.

Silicon nitride features a relatively large nonlinearity and does not suffer from nonlinear loss at telecommunications wavelengths (14). Its index contrast to the silica cladding simultaneously allows high-confinement, low-loss, and high-power handling ability by advanced nanofabrication techniques (15–17). Despite the success in high-Q microresonators (18), low-loss (<1 dB/m) meter-long Si₃N₄ waveguides have only been achieved with low confinement (19), which is not suitable for OPAs due to their weak nonlinearity. To achieve CW-pumped parametric amplification based on four-wave mixing (FWM) in Si₃N₄, dispersion-engineered long waveguides with both high nonlinearity and low propagation losses are needed. An estimation of this can be made by noting that the maximum parametric gain G ≈ exp{2γP[1 −1exp(−αL)]/α}·exp(−αL) (20), where γ is the Kerr nonlinearity parameter of the waveguide (~1 m⁻¹ W⁻¹ can be achieved in high-confinement Si₃N₄ waveguides), P is the pump power, and α is the linear attenuation coefficient (21). The waveguide loss is a key factor because it directly affects both the gain and NF (22). A schematic illustration of a waveguide OPA based on degenerate FWM is depicted in Fig. 1A. The input signal wave is amplified, and an idler wave is generated along the propagation while, simultaneously, the pump wave is attenuated.

Fig. 1. Schematic illustration of parametric amplification, Si₃N₄ chip, and performance characteristics.

(A) Schematic illustration of OPAs based on degenerate FWM. The green, orange, and light brown lines represent signal, pump, and idler waves, respectively. (B) Photograph of a representative Si₃N₄ chip containing nine waveguides, each with a length of 1.42 m. Photo credit: Z. Ye, Chalmers University of Technology. (C) Optical microscope image of one spiral waveguide unit. (D) OFDR trace of one Si₃N₄ waveguide. The measured propagation loss of TE polarization is 1.4 dB/m.

RESULTS

We fabricated high-confinement dispersion-engineered Si₃N₄ spiral waveguides using an advanced subtractive processing method (16). A photograph of a representative chip with nine Si₃N₄ waveguides is shown in Fig. 1B. We cascaded 23 spiral waveguide units (shown in Fig. 1C) to construct a 1.42-m-long waveguide within a device area of 23 mm². Stitching error compensation was implemented to overcome the drawback of limited writing fields (WFs) with electron beam lithography (EBL) (see the Supplementary Materials for detailed information). Optical frequency domain reflectometry (OFDR) was used to characterize the fabricated Si₃N₄ waveguide with a cross-sectional dimension of 690 nm by 2000 nm [supporting three transverse modes in transverse electric (TE) polarization], with the result shown in Fig. 1D. No notable defect along the 1.42-m Si₃N₄ waveguide was observed, which verifies the success of the stitching error compensation. The waveguide loss achieved for TE polarization was 1.4 dB/m, which is the lowest loss in high-confinement meter-scale Si₃N₄ waveguides to date. Twelve of 20 fabricated waveguides were defect free according to the OFDR measurements. The mean propagation loss of the defect-free waveguides was 1.7 dB/m. The dispersion of the fundamental TE (TE₀₀) mode was designed to be anomalous, thus being suitable for parametric amplification.

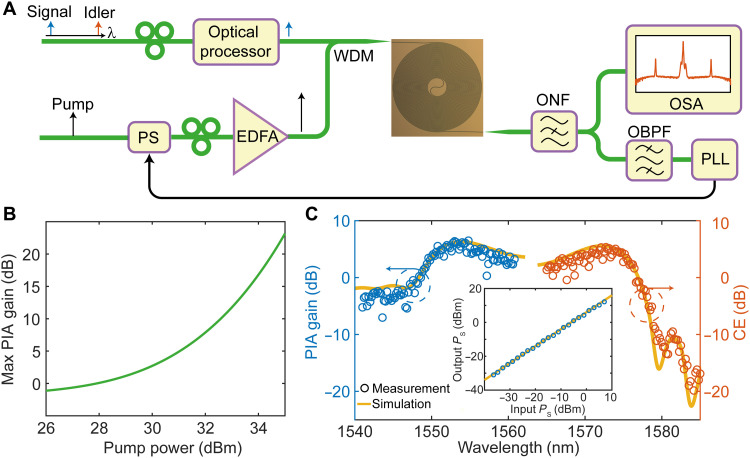
We performed CW-pumped parametric amplification experiments using the Si₃N₄ waveguide in both phase-insensitive and phase-sensitive mode. Figure 2A shows a schematic of the experimental setup (see Materials and Methods). For the phase-insensitive amplifier (PIA), only a signal and a CW 1563-nm pump were combined and injected into the waveguide. The PIA gain at the phase-matched signal wavelength was simulated using the nonlinear Schrödinger equation (NLSE) using a 1.42-m-long waveguide with a loss of 1.4 dB/m. Figure 2B shows the resulting PIA gain that increases exponentially with the pump power, reaching 20 dB with a pump power of 34.4 dBm. Typical measured on-chip PIA gain and conversion efficiency (CE) spectra are shown in Fig. 2C. The corresponding pump and signal powers at the waveguide input were estimated to be 34.4 and −22.5 dBm, respectively. Here, the on-chip PIA gain (CE) is defined as the ratio of the on-chip signal (idler) power at the output relative to the signal power at the input. The obtained maximum on-chip PIA gain and CE were 6.4 and 5.3 dB, respectively. To the best of our knowledge, this is the first experimental demonstration of both on-chip PIA gain and net CE in an integrated χ⁽³⁾ waveguide with a CW pump. Moreover, the experimental PIA gain and the CE spectral profiles agreed with simulated ones based on NLSE with a pump power of 31.5 dBm and a fitted dispersion β₂ = −45 ps²/km. More details on the simulations are presented in Materials and Methods. Here, the effective TE₀₀ pump power is 2.9 dB smaller than the estimated actual on-chip input pump power. We believe that the difference is mainly due to the coupling to higher-order modes and uncertainties in the nonlinear coefficient and coupling efficiency. The spectral variation of the gain and CE is likely due to the coupling between different transverse modes and pump launch instability. The bandwidth over which the PIA provides gain is 28 nm and can be broadened or moved to another wavelength band with modified dispersion engineering (23). The inset in Fig. 2C shows the on-chip signal output power at 1553 nm versus on-chip input signal power (P_s). Excellent linear parametric amplification of the signal is observed. To test the ability of the Si₃N₄ waveguide used in optical communication, we carried out a wavelength conversion experiment of 10 Gbps non–return-to-zero signal. Because of high CE, no additional EDFA was needed to preamplify the idler before optical detection. The penalties for outcoupled signal and converted idler were 0.3 and 1 dB at a bit error rate of 1 × 10⁻⁶, respectively (see the Supplementary Materials).

Fig. 2. Parametric amplification.

(A) The PIA and PSA experimental setup. WDM, wavelength-division multiplexer; PS, phase shifter; OSA, optical spectrum analyzer; ONF, optical notch filter; OBPF, optical band-pass filter; PLL, phase-locked loop. (B) Simulated maximum PIA gain versus pump power. (C) Spectra of on-chip PIA gain (blue circles) and CE (red circles) with an on-chip pump power 34.4 dBm. The simulated PIA gain and CE (solid yellow lines) spectra are with a pump power of 31.5 dBm on TE₀₀ mode. The inset figure shows the measured output signal power versus input signal power with the linear fitted slope indicating 6 dB gain.

As a next step, we investigated phase-sensitive amplification (PSA) using the Si₃N₄ waveguide. We coupled 34-dBm pump power at 1563 nm into the chip, and the powers of the input signal (1554 nm) and idler (1572 nm) were −26.5 dBm each. The output spectra of the PSA and PIA are shown in Fig. 3A. As can be seen, the PSA provides 5.2-dB additional gain at 1554 nm compared to the PIA due to the coherent superposition of amplified signal and idler (24). Figure 3B shows the measured PSA gain at five signal wavelengths. The maximum PSA gain was 9.5 dB at 1554 nm, which corresponds to nearly optimum phase matching. In addition, we measured the NF of both PIA and PSA with the same pump power as presented in Fig. 3C. Also shown with the lines are the NF from theory for both PIA and PSA in the ideal case (no waveguide loss) and in the present case (waveguide loss of 1.4 dB/m). The PSA NF in the ideal case is 3 dB for 0-dB PSA gain, which is due to the coinjection of signal and idler, while only the signal is recovered at the output (25). Note that a theory for the NF of a PSA with a lossy waveguide has not been described earlier, and the details of this can be found in the Supplementary Materials. The measured PIA NF at signal wavelength of 1556 nm is 3.3 ± 0.4 dB. Theoretically, the PIA NF reaches a maximum of 3.6 dB at a gain of 7 dB and drops to about 3.4 dB at 25-dB PIA gain, as the amplified excess optical noise then dominates over the waveguide loss in terms of contribution to the overall NF. For the PSA, the measured on-chip NF is about 1.2 ± 0.4 dB at 1556 nm. We note that the gain and NF reported above are the chip gain. When including the input and output coupling losses (2.5 dB per facet), the fiber-to-fiber gain and NF for the PSA were 4.5 and 3.7 dB, respectively. Figure 3D shows the normalized PSA gain with varying signal phase. The extinction ratio between maximum and minimum gain, which is an important factor for optical regeneration and squeezing (4), was 20 dB and, consequently, is promising in quantum optics (26).

Fig. 3. PSA characterization.

(A) Output spectra of PSA (blue line), PIA with only signal on (orange line), and PIA with only idler on (green line). The inset figure shows the additional 5.2-dB gain observed with the PSA. (B) On-chip PSA gain versus signal wavelength. (C) Measured and theoretical results of on-chip NF for the PIA and the PSA. The solid blue and orange curves are the theoretical results of PSA with 0 and 1.4 dB/m loss, respectively, in the 1.42-m-long waveguide. The dashed blue and orange curves are the theoretical result of PIA with 0 and 1.4 dB/m loss, respectively. (D) Normalized phase-sensitive gain with varying signal phase.

DISCUSSION

In summary, we have experimentally demonstrated a CW-pumped and ultralow-noise OPA in an integrated photonic waveguide in the telecommunication band. The achieved gain and NF represent a milestone toward chip-scale optical signal processing and excess-noise-free amplification. We expect that lower NF with higher OPA gain can be achieved by further reducing the waveguide losses, increasing the waveguide length (23), and reducing the cross-talk between the fundamental and higher-order optical modes. For practical applications, minimizing the coupling loss between the fiber and waveguide is also important as it leads to higher on-chip pump power and a corresponding exponential increase in OPA gain, as well as a reduced fiber-to-fiber NF. It should be noted that the OPA is scalable to other wavelengths because silicon nitride is transparent from the visible to the mid-infrared wavelength range. With the advantages of low noise and a small monolithic footprint, CW-pumped silicon nitride–based OPAs may open previously unattainable possibilities in optical communications (27), ultrafast spectroscopy (5), and quantum optics and metrology (6).

MATERIALS AND METHODS

Design, fabrication, and characterization of spiral waveguides

The design of the waveguide follows an Archimedean spiral so that the curvature of the waveguide varies slowly and continuously along the propagation length. The S-bend connecting clockwise and anticlockwise spirals and the connection between adjacent spiral waveguide units are designed using an algorithm to minimize the variation of the curvature (28). This adiabatic bend design helps to reduce the coupling from TE₀₀ mode to higher-order modes or radiation modes in the waveguide. The spiral waveguide unit was designed to fit within an 1 mm–by–1 mm EBL WF to reduce the number of stitching errors present at the border of WFs. The WFs were arranged so that there was only one stitching error at the waveguide connecting the two adjacent spiral units. The spiral waveguide unit, the arrangement of WFs, and the location of stitching error are depicted by Fig. 4. Typically, the stitching error of 1 mm–by–1 mm EBL WFs is tens of nanometers, which can result in substantial scattering loss. We noticed that our stitching error is systematic at every WF border, indicating that the stitching error is caused by the imperfect calibration of the WFs (29). Thus, we actively compensated the stitching error by precisely shifting the adjacent WFs according to the regular EBL without any stitching error compensation. The scanning electron microscopy images of the exposed resist with and without stitching error compensation are depicted in Fig. 4B. The regular EBL exposure leads to notable stitching errors in both vertical and horizontal direction, while no obvious offset is observed for EBL exposure with stitching error compensation. Si₃N₄ waveguides were fabricated using the process detailed in (16). Multipass EBL was implemented to further reduce the sidewall roughness and reduce the waveguide loss. The Si₃N₄ waveguide was annealed at 1200°C under argon ambient atmosphere to reduce the absorption loss caused by N─H bonds. The wafers were manually cleaved into chips.

Fig. 4. Images of spiral waveguides.

(A) Optical microscope image of two spiral waveguide units. The blue dashed boxes depict two adjacent WFs, and the red dashed box indicates the location of the stitching error. (B) Scanning electron microscopy images of the resist exposed by EBL with and without stitching error compensation.

The OFDR measurements were carried out as in (19). The reflected light was monitored, while the tunable laser was swept from 1520 to 1600 nm with a scanning rate of 8 nm/s, and the wavelength of the tunable laser was calibrated by a self-referenced fiber frequency comb (Menlo Systems FC-1500 with a repetition rate of 250 MHz). Inversely tapered waveguides with width of 340 nm were used at the input and output of the waveguides to maximize the excitation of fundamental mode when coupling from a lensed fiber to the waveguide. The average coupling loss between the lensed fiber and the Si₃N₄ waveguide was calculated by subtracting the measured propagation loss (2.0 ± 0.1 dB) based on OFDR from the total insertion loss (fiber to fiber, 7.0 ± 0.3 dB). Thus, the coupling loss was estimated to be 2.5 ± 0.2 dB per facet, considering equal coupling loss at both input and output facets.

Simulation of PIA with a Si₃N₄ waveguide

The propagation of the optical field along a Si₃N₄ waveguide is governed by the NLSE as

$$\frac{\mathrm{\partial }E}{\mathrm{\partial }z}+\frac{\mathrm{\alpha }}{2}E+\frac{{i\mathrm{\beta }}_2}{2}\frac{{\mathrm{\partial }}^{2}E}{\mathrm{\partial }{T}^2}=i\mathrm{\gamma }{\mid E\mid }^{2}E$$ (1)

where E is the slowly varying envelope of the overall optical field, β₂ is the group velocity dispersion coefficient at the pump wavelength, z is the optical propagation axis, and T is the relative time axis where a reference frame moves with the envelope at the group velocity (30). We considered third-order optical nonlinear effects, as represented by the nonlinear coefficient. Raman and Brillouin scattering, higher-order dispersion, and nonlinear optical losses due to TPA and FCA were neglected. The nonlinear coefficient of the TE₀₀ mode of the waveguide was set to be 1 W⁻¹ m⁻¹. Equation 1 was solved numerically with the split-step Fourier method (30).

OPA experiment details

The setup of the OPA was designed to operate in either phase-insensitive or phase-sensitive mode. For the PSA mode, phase-correlated signal, pump, and idler are needed at the input of the Si₃N₄ waveguide. Here, optical processing of the signal and pump was implemented before the OPA to realize this objective. The pump (27 dBm; amplified wave from a tunable C-band laser) was combined with a copolarized signal via a wavelength-division multiplexer (WDM) and launched into an HNLF. An idler was generated at the output via FWM with a CE of about −15 dB. This copier scheme was used due to its flexibility of signal wavelength tuning and high signal-to-noise ratio (SNR) of the generated idler. The relative phase of the three waves entering the Si₃N₄ waveguide dictates the magnitude of the gain in the PSA. The pump was then separated from the signal and idler using another WDM coupler and amplified by a high-power EDFA. A piezoelectric stretcher was used as an optical phase shifter to adjust the phase of the pump. The signal, pump, and idler waves were combined by another WDM coupler and coupled into the waveguide with a lensed fiber. We used an optical processor (WaveShaper, Finisar) to alternate between PIA and PSA mode, as well as equalizing the power of the signal and idler for PSA. For the PIA with signal (idler) on, the idler (signal) was blocked by the optical processor. The polarizations of the pump, signal, and idler were aligned to TE polarization of the waveguide. An optical notch filter was used to attenuate only the high-power pump at the waveguide output, and the output spectra were recorded by an optical spectrum analyzer. Because the pump and signal waves propagated through different optical paths, the relative phase between the pump and signal waves was not constant and slowly varying due to random temperature change and vibrations. A small portion of the amplified signal was filtered out and used as an error signal in a phase-locked loop with the stretcher compensating the random phase shift to maintain maximum PSA gain.

Because the OPA spectrum is symmetric around the pump wavelength, the signal wavelength was varied only on the short wavelength side of the pump wavelength in the PIA experiment. The optical SNR (OSNR) at the input to the waveguide was larger than 46 dB (0.1-nm bandwidth), while it was about 37 dB at the output. This ensured that the extracted NF is accurate and that the input signal can be nearly considered shot noise–limited. In the experiments, we recorded the fiber-to-fiber gain and NF, and we estimated the on-chip gain and NF by accounting for the average coupling loss (2.5 dB per facet) between the lensed fiber and Si₃N₄ waveguide. The NF of the parametric amplifier was calculated using the following formula (31)

$$\text{NF}=\frac{1}{G}+2\frac{P_{\text{ASE}}}{\mathit{\text{Gh}}\mathrm{\nu }B}$$ (2)

where G is the OPA gain, P_ASE is the power of amplified spontaneous emission at the OPA output spectrum with a resolution bandwidth (B) equivalent to 0.1 nm, h is the Plank constant, and v is the frequency of the signal laser. When taking the limited OSNR of input signal wave into account, the P_ASE cannot be exactly obtained directly from the OPA output spectrum because the measured noise power at the OPA output spectrum includes both amplified spontaneous emission of the OPA and the amplified noise originally coming from the noise of input signal wave. In our experiment, the noise of input signal wave is mainly from the residual of EDFA-amplified spontaneous emission, and the noise is similar at signal and idler wavelength. Therefore, we calculate the P_ASE using the following formula

$$P_{\text{ASE}}=P_{\text{noise}}^{\text{out}}-(G+\mathrm{\eta })\bullet P_{\text{noise}}^{\text{in}}$$ (3)

where η is the OPA CE, $P_{\text{noise}}^{\text{out}}$ is the noise power at the OPA output spectrum with a resolution bandwidth of 0.1 nm, and $P_{\text{noise}}^{\text{in}}$ is the noise power at input port at the signal and idler wavelength with a resolution bandwidth of 0.1 nm. Here, the measured NF at 1554 nm is 1.35 dB if the input signal wave is considered shot noise–limited and is 1.06 dB if the OSNR of input signal wave of 46 dB is taken into account. Considering both uncertainty of OSNR of input signal wave and fluctuation of noise power of OPA at output spectrum, we conclude that the on-chip NF is 1.2 ± 0.4 dB.

Supplementary Materials

This PDF file includes:

Sections S1 to S5

Figs. S1 to S6

References