Nanoscale molecular architecture controls calcium diffusion and ER replenishment in dendritic spines

Nanoscale organization and calcium influx in dendritic spines guarantee ER store refilling without depletion.

Abstract

Dendritic spines are critical components of neuronal synapses as they receive and transform synaptic inputs into a succession of calcium-regulated biochemical events. The spine apparatus (SA), an extension of smooth endoplasmic reticulum, regulates slow and fast calcium dynamics in spines. Calcium release events deplete SA calcium ion reservoir rapidly, yet the next cycle of signaling requires its replenishment. How spines achieve this replenishment without triggering calcium release remains unclear. Using computational modeling, calcium and STED superresolution imaging, we show that the SA replenishment involves the store-operated calcium entry pathway during spontaneous calcium transients. We identified two main conditions for SA replenishment without depletion: a small amplitude and a slow timescale for calcium influx, and a close proximity between SA and plasma membranes. Thereby, spine’s nanoscale organization separates SA replenishment from depletion. We further conclude that spine’s receptor organization also determines the calcium dynamics during the induction of long-term synaptic changes.

INTRODUCTION

Dendritic spines are cellular protrusions found on the surface of dendrites that function as a postsynaptic component of the neuronal synapse. Morphologically, spines commonly include two distinct features, a spine head and a spine neck, with the head engaging the presynaptic axon and the neck connecting the head with the postsynaptic dendrite. The size and shape of a spine (as well as the number of spines on a dendrite) are dynamic, plastic, and change in response to repeated synaptic activity, which directly affects synaptic plasticity and is therefore critical for processes such as learning and memory (1–4). Moreover, changes in shape, distribution, loss, and gain of dendritic spines have been associated with a range of human diseases, although the mechanisms remain incompletely understood (5, 6). Functionally, dendritic spines are sites of intense biochemical activity, whereby signals received from the synapse via glutamate receptors [such as N-methyl-d-aspartate receptors (NMDARs) and AMPA receptors (AMPARs)] lead to influx of the main second messenger, calcium ions (Ca²⁺). Although a single receptor activation event produces transient calcium influx, repeated activation of the receptor leads to rapid buildup of calcium concentration, resulting in calcium binding to buffers such as calmodulin (CaM), a calcium sensor protein, and subsequent biochemical activation of CaM-dependent protein kinase II (CaMKII) and subsequent downstream signaling (7). In general, high calcium concentrations in spines are associated with long-term potentiation (LTP), while low calcium is associated with long-term depression (LTD) (8). Thus, calcium dynamics in dendritic spines emerged as a key mechanism for the induction of synaptic plasticity in neurons. Calcium concentration in dendritic spines is tightly regulated (9–11) by the amplitude and timing of the influx through the receptors, binding and unbinding with proteins, buffers and pumps, and also by organelles that could sequester or release calcium, such as endoplasmic reticulum (ER) and an extension of smooth ER called spine apparatus (SA) that spans spine head and neck (3, 12–14).

The SA is involved in multiple signaling functions such as calcium regulation, protein synthesis, and cell apoptosis, and the absence of the SA results in a reduction of hippocampal LTP in the CA1 region and an impairment of spatial learning (15). In addition, SA facilitates calcium-induced calcium release (CICR) process through which calcium ions that entered dendritic spine due to synaptic activity cause release of additional calcium from intracellular calcium stores. The timing of CICR activation, on the order of a few tens of milliseconds, is governed by the fastest calcium ions arriving by diffusion at a ryanodine receptor (RyR) present mostly as clusters at the base of spines (16) and also involves sarco/ER Ca²⁺–adenosine triphosphatase (SERCA) (17). Therefore, calcium concentration increase in a spine head due to a synaptic stimulation is followed by a pronounced depletion of SA calcium reservoir within less than tens of milliseconds due to this avalanche phenomenon at the base of the spine. Whereas CICR calcium dynamics and flux in spines have been extensively studied, mechanisms that govern calcium store replenishment in SA are still imperfectly understood.

Recently, store-operated calcium entry (SOCE), mediated by STIM1 (stromal interaction molecule 1)-ORAI1 (Calcium Release-Activated Calcium Modulator 1) channel complex, has been implicated as important for the replenishment process in SA (18, 19). Calcium concentration inside the SA is sensed by ER membrane–anchored STIM1 regulatory protein that interacts with ORAI1 channel present at the plasma membrane (20). As the first step, the ORAI1 channels pump calcium into cytoplasm, followed by calcium entrance into the SA through SERCA pumps mostly located in the SA head (16). However, it remains unclear how SOCE could function to replenish calcium stores without triggering CICR activation. Here, we investigate the release and replenishment pathways that are both activated by calcium but could operate without interfering with each other. Resolving this enigma is crucial not only to determine the computational power of dendritic spines based on calcium signaling but also for characterizing calcium dynamics underlying the induction of LTP and LTD. To study these processes under different calcium influx conditions (large and small, fast and slow), we used a combination of calcium imaging, computational modeling and simulations, and STED (Stimulated Emission Depletion) microscopy. Our stochastic model predicted and our measurements confirmed that SA-amplified CICR occurs only under strong and fast calcium influx conditions, whereas slow and small amplitude calcium influx triggers SA replenishment via STIM1-ORAI1 pathway and SERCA pumps located proximal to the plasma membrane. Furthermore, we also examined using numerical simulations calcium dynamics at the base of spines during LTP and LTD and observed that the SA depletion time scale varies between LTP and LTD, resulting in a strong difference in the calcium levels at the base, which may determine the spine’s fate toward the direction of either enhancement or depression of synaptic efficacy. Together, our study reveals that nanoscale molecular architecture plays a critical role in controlling calcium diffusion and ER replenishment. Moreover, contrary to the view that calcium concentration inside the whole spine dictates potentiation or depression, the work presented here suggests that calcium concentration at the spine base is the main determinant of LTP versus LTD induction.

RESULTS

SOCE is associated with SA replenishment but not depletion

To investigate the mechanism of SA replenishment, following the methods developed in (21, 22), we blocked synaptic activity [calcium voltage channels and synaptic inputs using APV [(2R)-amino-5-phosphonovaleric acid]/DNQX (6,7-dinitroquinoxaline-2,3-dione)/tetrodotoxin (TTX)] in cultured hippocampal neurons that cotransfected with blue fluorescent protein and synaptopodin (SP), an actin-associated protein found in SA (12). The only known source of calcium under these conditions remains the SOCE mechanism associated with the STIM1-ORAI1 pathway (20). To monitor calcium fluctuations in spines containing SA, we used Fluo-4, a high-affinity calcium sensor (see also Materials and Methods). With this setup, we observed fluctuations that were restricted to spines and were not present in dendrites (Fig. 1, A and B, top). In addition, these calcium activity patterns associated with the STIM1-ORAI1 complex were much slower (on the order of seconds) and exhibited smaller amplitudes compared to the ones triggered by synaptic inputs (on the order of a few hundred milliseconds; figs. S1 and S2).

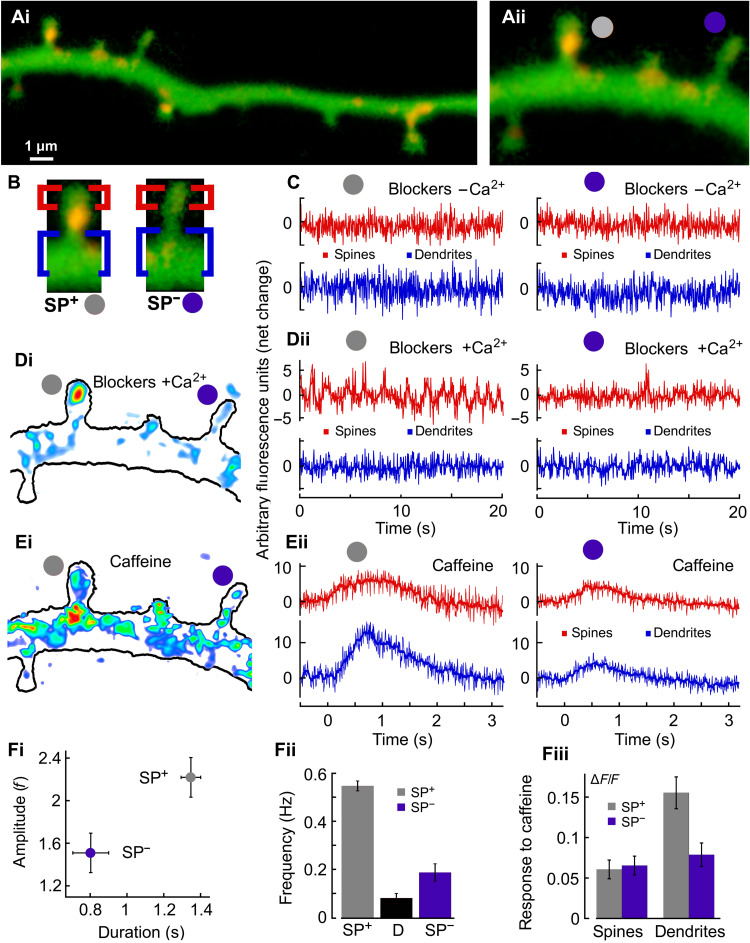
Fig. 1. Refilling or depleting the SA in dendritic spines with slow versus fast calcium transients.

(A) Top: Blue fluorescent protein (blue) and SP (red) cotransfected in hippocampal neurons, cultured for 3 weeks, and loaded with the Fluo-2 high-affinity calcium sensor. A large SP⁺ spine attached to an axon (blue arrowhead) and several SP⁻ spines can be seen. Bottom: Same region with a white contour and two regions of interest: behind (red) and in front of (blue) the SP-labeled SA are shown. Synaptic activity was blocked using tetrodotoxin (TTX; 1 μM), APV (50 μM), and DNQX (20 μM). Following a caffeine addition of 5 mM, release of calcium is observed toward the base of the spine but not in the spine head. (B) Top: Spontaneous calcium activity due to store-operated calcium entry (SOCE) only located in the spine head. Bottom: Time course of calcium activity in the head versus base following caffeine addition. Both are typical single realizations of the recordings. (C) Top: Segmented recording of spontaneous calcium activity in the spine head. Bottom: Overlapped average of the fluctuation segments larger than a predefined threshold of 1 SD (SD = 0.0457 in the example trial shown in the top). Bottom shows the average of 18 such sequences.

To confirm that the SOCE pathway leads to calcium accumulation in the SA, we depleted the SA calcium stores with caffeine (12) and found an asymmetric calcium release, mostly toward the base of the spine (Fig. 1B, bottom). This result is in agreement with the time scale of CICR activation and the underlying heterogeneous distribution of RyRs that are mostly located at the base of the spine (16). To further study calcium transients and develop numerical simulations, we needed to obtain a stereotype response. For that goal, we segmented the calcium time series, which was recorded in the spine head over a time scale of a few minutes. We defined a threshold (1 SD) to differentiate between calcium transient and background fluctuations (SD ≈ 0.0457 in Fig. 1C, top). We collected events and averaged them (Fig. 1C, bottom), resulting in a stereotype response that we fitted with a difference of two exponentials (fig. S3). The calcium concentration in the spine head has a correlation time of approximately 1 s, as revealed by the autocorrelation function (fig. S4), compatible with previous analysis on calcium transients in (23).

We then used this fit to determine the conditions that favor calcium accumulation in the SA by developing stochastic computational simulations for calcium diffusion inside a dendritic spine (Fig. 2A). For calcium inputs to the spine head, we simulated two distinct conditions: (i) a fast entry from synaptic inputs through NMDARs, which we modeled with an instantaneous calcium injection, and (ii) the SOCE activity (as observed in Fig. 1C, bottom), which we model with a slow calcium injection to the spine head.

Fig. 2. Modeling SA depletion and refilling with slow versus fast calcium inputs.

(A) Schematic of the spine domain (green) with its calcium inputs and regulators (see Materials and Methods for channel models). [B (i)] Simulated synaptic inputs with an instantaneous injection amplitude of N = 300 ions, repeated each time when the calcium in the spine reaches zero [B (ii) green curve at t = 0, 30.9, and 80.1 s. [B (ii)] Calcium dynamics in the spine head (green) versus base (magenta) following fast inputs. [B (iii)] SA reservoir of 500 ions depleted during fast inputs upon three CICR events. [C (i)] Slow calcium input to spine head with SOCE, fitted with a difference of two exponentials over 2 s (black curve, accounting for 94.5% of the distribution) and discretized into 25 bins (blue histogram: R² = 0:9986). The barcode represents the injection times of single ions. [C (ii)] Simulated calcium levels in the spine head and base during the slow input of [C (i)] (total injection N = 300; five trials averaged). [C (iii)] SA reservoir always increase without depletion under slow SOCE conditions with different numbers of SERCA pumps N_SERCA and SA plasma membrane distances d_SA.

Our results revealed that: (i) A fast synaptic input is associated with store depletion events through RyR-induced CICR. In the numerical simulations [Fig. 2B (i)], we verified this prediction by injecting 300 ions into the spine head to mimic fast synaptic inputs, then waited until the spine head was completely depleted of calcium, before injecting another batch of 300 ions. In all, we thus simulated three injections, at t = 0, 30.9, and 80.1 s and observed a sharp increase in calcium due to CICR occurring at the base a few milliseconds following each calcium injection into the spine head [Fig. 2B (ii)]. Calcium decay in the head is due to the uptake through SERCA pumps, the diffusion toward the base, and the absorption by pumps. A few milliseconds after each injection into spine head, we also observed a smaller second calcium peak due to the headward diffusion of calcium ions “generated” by CICR in the base region. When we started with 500 ions in the SA, after three stimulations, SA became totally depleted of calcium ions due to CICR [Fig. 2B (iii)] as predicted under these conditions (24). Note that the small increases in between the fast depletion events here are due to uptake of ions into SA through SERCA pumps.

(ii) In contrast, when we injected ions into the spine head at a slower rate, the SA was refilled by calcium without triggering CICR, despite the much smaller number of calcium ions present in the head [Fig. 2C (i) to (iii)]. By accounting for the spontaneous activity above the threshold SD (Fig. 1C), we model here the slow calcium inputs as a difference of two exponentials [black curve in Fig. 2C (i)] over a duration of 2 s, discretized into 25 bins and normalized to the total number N of calcium ions injected throughout the duration [histogram in Fig. 2C (i)]. Injection times of single ions are obtained from a uniform random distribution of input ion numbers corresponding to each bin [barcode representation in Fig. 2C (i)]. In contrast to synaptic inputs, the number of calcium ions in the spine base during slow inputs was extremely low, thus no calcium release events could be triggered through RyRs [Fig. 2C (ii), magenta].

For this mechanism of refilling to occur, we hypothesized that the distance d_SA between the SA and the plasma membrane is in the order of a few tens of nanometers. Therefore, for the simulations, we positioned SERCA and ORAI1 in close proximity inside the spine head. We then explored the impact of d_SA on the refilling of SA by changing this distance from 20 to 500 nm [Fig. 2C (iii)]. We found that the reduction of refilling due to the increased distance can be compensated with an increase in the number of SERCA pumps or by amplifying the calcium input. Therefore, these results suggest that the distance d_SA, the number of SERCA pumps N_SERCA, and the slow influx rate of calcium are key parameters favoring SA calcium refilling.

To further characterize the distribution of calcium fluxes in the SA, i.e., extrusion from the head or the arrival at the base of the spine, we followed the fate of each ion during numerical simulations. We simulated 300 injected ions each time over a slow input lasting 2 s [similar to Fig. 2C (i)], keeping the distance d_SA at a constant value of 20 nm. In an ensemble of 210 trials that we simulated, we analyzed the 161 in which a CICR did not occur. We observed that most ions (236 of 300) were bound to calcium extrusion pumps, while the number of ions that refilled the SA through SERCA pumps was 46 of 300. Around 14 of 300 remained in the spine domain or stayed as single occupants in SERCA or RyRs without triggering an opening within the simulated 2 s; only the remaining 4 of 300 ions reached the base and disappeared from the absorbing boundary.

Therefore, under these conditions, calcium concentration at the base of the spine remained too low to trigger a CICR, safely eliminating the possibility of triggering a depletion. To characterize the spatiotemporal conditions of calcium dynamics leading to SA replenishment, we also developed a mean-field computational model (section S4 and figs. S5 to S7), accounting for the mean number of calcium ions m_ca in the spine, the fraction n₁ of RyRs bound by one calcium ion, and the probability p₂ to trigger CICR by activating at least one RyR when two calcium ions are bound. The complete system of equations are

$$\begin{array}{c}{\stackrel{·}{\mathit{n}}}_1=-\mathrm{\mu }{\mathit{n}}_1+\mathrm{\lambda }{\mathit{m}}_{\text{ca}}({\mathit{n}}_{\mathrm{R}}-2{\mathit{n}}_1)\\ {\stackrel{·}{\mathit{m}}}_{\text{ca}}={\mathit{J}}_{\text{inj}}(\mathit{t})-\mathrm{\nu }{\mathit{m}}_{\text{ca}}-\mathrm{\lambda }{\mathit{m}}_{\text{ca}}({\mathit{n}}_{\mathrm{R}}-{\mathit{n}}_1)+\mathrm{\mu }{\mathit{n}}_1\\ {\stackrel{·}{\mathit{p}}}_2=\mathrm{\lambda }{\mathit{n}}_1{\mathit{m}}_{\text{ca}}(1-{\mathit{p}}_2)\end{array}$$ (1)

where μ is the unbinding rate of calcium to RyR, ν is the calcium extrusion rate from a spine, and λ is the forward rate of calcium binding to RyR. To study the fast synaptic inputs and SOCE, we used the two different initial conditions: (i) instantaneous injection of ions, modeled with a Dirac’s δ function at t = 0 (or equivalently with the initial condition m_ca(0) = N₀, n₁(0) = 0, p₂(0) = 0), and (ii) a slow injection, modeled by $J_{\mathit{inj}}(t)=A(e^{-{\mathrm{\lambda }}_{1}t}-e^{-a_{2}t})$ (fitted in fig. S3) with the initial conditions of m_ca(0) = 0, n₁(0) = 0, and p₂(0) = 0.

The probability to activate a RyR by two ions is

$${\mathit{P}}_2=\mathit{\text{Pr}}\{{\mathit{n}}_2(\infty )=1\}=1-{\mathit{e}}^{-\mathrm{\lambda }{\displaystyle {\int }_0^{\infty }}{\mathit{n}}_1(\mathit{u}){\mathit{m}}_{\text{ca}}(\mathit{u})\mathit{du}}$$ (2)

We also evaluated numerically the activation probability P₂ (fig. S8) and confirmed its agreement with the results of the stochastic simulations in Fig. 2: Even with a small (<500) number of ions, an instantaneous calcium influx J_inj(t) leads to a higher probability of SA calcium release, whereas a slower influx with such a number leads to CICR events at a much low probability. The solution of the system of Eq. 1 shows how the probability P₂ depends on the number N in fast synaptic inputs and on the amplitude A in the slow SOCE inputs (fig. S5 and sections S4.2 and S4.3). Therefore, both our mean-field model and the stochastic simulations strongly indicate that a slow calcium transient from the STIM1-ORAI1 pathway does not induce calcium release at the base of a dendritic spine but leads to SA refilling. Thus, we conclude that the biophysical conditions for SA replenishment and depletion are well separated (fig. S6). Collectively, our calcium imaging–based observations and our computational modeling suggest that SOCE plays role in replenishment exclusively and that spatial colocalization (proximity) of key molecular regulators in this process (SERCA and ORAI1) is critical for ensuring fidelity of replenishment while not triggering CICR.

Calcium redistribution in dendritic spines: Replenishment without release

To test the predictions generated using our computational modeling of SA replenishment, we explored the conditions for calcium replenishment in dendritic spines containing SA using calcium imaging of hippocampal cultured neurons. To identify spines containing SA, we used SP as a marker for SA (red puncta in Fig. 3, A and B). To demonstrate that the SA is refilled in the absence of any activity, we blocked both voltage-gated channels and glutamatergic receptors by adding TTX (1 μM), APV (50 μM), and DNQX (20 μM). In the absence of extracellular calcium, spines do not show any calcium transients regardless of whether they contain SA or not (Fig. 3C). By blocking the SOCE pathway (fig. S1), we confirmed that STIM1-ORAI1 is responsible for SA calcium replenishment. Moreover, we observed that the replenishment of calcium in SA through SOCE increases with duration of refilling (fig. S2).

Fig. 3. Local calcium storage in dendritic spines.

(A) Dendrite of a rat hippocampal cultured neuron, transfected with synaptopodin (SP) (red puncta) and loaded with Fluo-2. [A (ii)] Magnification of (A) with two spines with similar lengths ≈1.2 μm: left, SP⁺ (gray circle); right, SP⁻ (purple). (B) Labeling of SP^+/− spines with head (red) and base (blue) regions. (C) Recordings in calcium-free medium with activity blockers. Sustaining these conditions for 15 min partially depleted calcium stores and initiated SOCE (not shown). [D (i)] Colored representation of the background-subtracted calcium transient (low calcium, blue/cyan; and higher levels, red > yellow > green). [D (ii)] Recordings from the same regions with activity blockers and extracellular calcium (2 mM). [E (i)] Examples of caffeine-induced calcium transient {background levels subtracted; same colors as [D (i)]}. [E (ii)] Calcium release from internal stores due to caffeine bath application (5 mM) uniquely observed in the SP⁺ spine bases. [F (i)] Amplitudes and durations of calcium fluctuations in SP⁺ (gray dot) and SP⁻ spine heads (purple) (n = 16 for both, P < 0.001, t test). [F (ii)] Frequency of calcium fluctuations in SP⁺ heads (gray), dendrites (black), and in SP⁻ spines (purple). [F (iii)] Caffeine responses in SP⁺ spine heads, SP⁻ dendrites, and SP⁻ heads were approximately the same but significantly weaker than in the SP⁺ dendritic sites (all groups: n = 16, P < 0.001, ANOVA).

In contrast, when presented with extracellular calcium, notable transients occur only in the heads of SP⁺ spines [Fig. 3D (i) and (ii)]. Calcium entry did not lead to any calcium transient at the bases of both SP⁺ and SP⁻ spines, confirming our predictions (Fig. 2) that a slow calcium entry leading to SOCE does not activate RyRs. However, to confirm that RyRs were functional, we activated them using caffeine. This activation led to substantial transient increases in calcium at the base of SP⁺ spines only, where RyRs are mostly located [Fig. 3, E (i) and (ii) and F (iii)]. In these experiments, caffeine is present in the extracellular medium and trigger CICR with a slower time scale compared to our simulations where calcium ions are directly available in the spine head. To quantify the spontaneous calcium activity further [Fig. 3D (i) and (ii)], we also confirm that both the amplitudes [2.2 versus 1.54 arbitrary units (a.u.)] and the durations (1.4 versus 0.8 s) are significantly larger in SP⁺ spines compared to SP⁻ ones [Fig. 3F (i)]. In addition, the frequencies of activation [Fig. 3F (ii)] were higher in the spine head of SP⁺ (gray, 0.5 Hz) compared to SP⁻ spines (purple, 0.2 Hz) or dendrites (black, 0.1 Hz) [n = 16, P < 0.001, analysis of variance (ANOVA)]. Therefore, we conclude that SOCE occurs preferentially in the heads of SP⁺ spines and requires the presence of SA. In summary, these results confirm our initial theoretical predictions that in the absence of synaptic activity, calcium ions enter the spine through SOCE and are stored inside the SA stores.

STED microscopy reveals the colocalization of ORAI1 in plasma membrane and SERCA pumps in spines containing SA

Our stochastic simulations predicted that SOCE is the main source of calcium ions for the SA calcium replenishment process. We thus hypothesized that ORAI1 channels, which allow slow calcium entry from the plasma membrane, should be closely colocalized with SERCA pumps that refill the SA. In addition, we predicted that this colocalization should predominately occur in the heads of spines containing SA. To determine the association between SERCA and ORAI1 localization, we used superresolution STED imaging of immunostained hippocampal tissues (see Materials and Methods).

We confirmed that the colocalization frequency of ORAI1 and SERCA3 is significantly higher (Fig. 4, A and B) when SP is present (ORAI1 + SERCA3 + SP: 88.9 ± 0.73%, n = 19, P < 0.001) than when SP is absent (ORAI1 + SERCA3: 0.99 ± 0.24%, n = 19, P < 0.001). The colocalization of SP with ORAI1 or SERCA3 only is weak (ORAI1 + SP: 7.75 ± 0.61%, n = 19, P < 0.001; and SERCA3 + SP: 0.45 ± 0.16%, n = 16, P < 0.001) similar to spines with SP alone (1.88 ± 0.33%, n = 19, P < 0.001). Moreover, the average colocalization distance in SP⁺ spine heads is around 100 nm (106 ± 4 nm, n = 378), with a substantial population of SERCA and ORAI1 localized as closely as 30 nm, while their average distance is more than doubled to around 200 nm in the neck (221 ± 14 nm, n = 159, P = 0.0067) or at the base (210 ± 8 nm, n = 290, P = 0.0034) of a spine (Fig. 4, C and D). To conclude, these results reveal the short distance between SERCA and ORAI1 in spine heads containing SA, confirming the predictions of the stochastic simulations about SOCE-associated SA refilling.

Fig. 4. SERCA-ORAI1 distributions and consequences.

(A to D) Distances between SERCA3 and ORAI1 puncta in dendritic spines of hippocampal neurons from adult mouse brain slices. (A) Green fluorescent protein (GFP)–labeled neurons (green), immunostained for ORAI1 (magenta), SERCA3 (cyan), and SP (yellow). Representative images show the five conditions analyzed in (B). (B) Quantified colocalization between ORAI1, SERCA3, and SP proteins. Four slices, each with 279 to 364 spine heads were analyzed. (C). The three conditions analyzed in (D), with the same colors as in (A). (D) Quantified SERCA3-ORAI1 distances in spine head, neck, and base. Statistical analysis involved one-way ANOVA and Tukey’s multiple comparisons tests. (B) and (D). s: **P < 0.01, ***P < 0.001. (E) Schematic of calcium regulators in the simulated spine model also showing the distance d_SA between the plasma and SA membranes. (F) Normalized fractions of calcium entering SA under instantaneous inputs to spine heads for different amplitudes N with (black and red) and without (green) calcium pumps. Of the 100 trials, we chose here the ones without a RyR activation until there were no more ions to simulate. (G) Same fractions as in (F) during slow calcium influx with the previously shown 2-s protocol under different N values and when pumps were removed for N = 100. Error bars in (F) and (G) = SEM.

To examine the colocalization requirement further, we used our numerical strategy to evaluate how SERCA-ORAI1 distance d_SA (Fig. 4E) influences the number of ions entering the SA during fast synaptic inputs (Fig. 4F) and slow SOCE currents (Fig. 4G). Following a fast input with 100 or 300 injected calcium ions, we found that the fraction of calcium entering the SA is stable around 15 to 20% when d_SA varies from 0 to 250 nm (Fig. 4F, black and red curves). We found that a majority of remaining ions were extruded by calcium pumps. To evaluate the influence of the extrusion pumps on the calcium uptake, we repeated the same simulations after removing all extrusion pumps. In that case, the fraction of SA calcium uptake increases to ≈90% (Fig. 4F, green curve) as expected, because more ions remain in the cytoplasm.

For simulating SOCE conditions (Fig. 4G), we placed calcium ions at the top of the spine head with dynamics following the fit with a difference of exponentials lasting 2 s [Fig. 2C (i)] with different numbers of ions. By comparing the numbers of calcium ions entering SA divided by the total number N, we noted that slow inputs with N = 300 ions are much more successful in refilling the SA than the corresponding fast inputs (red curves in Fig. 4, F versus G). However, when there were no calcium pumps with N = 100 (green curves), this fraction was slightly lower under slow input conditions, compared to what we saw with the fast inputs. This is likely due to longer RyR activation times during slow calcium inputs (figs. S7 and S8), resulting in a larger ion loss by diffusion. In all cases, N = 100, 300, and 500 with calcium pumps during slow inputs (black, red, and blue curves in Fig. 4G), the ratio of calcium ions entering the SA to the total N decreases gradually when d_SA increases. This is in contrast to the stable behavior observed under the fast calcium input conditions and to the slow inputs when SA calcium pumps are absent (green curve in Fig. 4G). Moreover, we found that the probability P₂ of SA calcium depletion via CICR is extremely low during a slow calcium input, compared to a fast injection (fig. S8). The probability P₂ increased gradually with d_SA, and the conditional time to trigger such events was governed by the presence of calcium pumps in the head.

Therefore, calcium pumps play an unexpected role in preventing and delaying the RyR activation by controlling the arrival of calcium ions at the base of the spine. Together, the calcium injection rate and the distance between the SA and plasma membrane, along with the balance of SERCA and calcium pumps, shape the SA calcium uptake and the CICR activation probability.

Calcium dynamics in spines and SA during LTP versus LTD protocols

We next evaluated the consequences of calcium dynamics by the induction protocols of long-term synaptic potentiation and depression (Fig. 5, A to C). Although the role of calcium dynamics in LTP and LTD has been known for some time (8), the role of SA calcium stores in these processes remains unclear. It has been previously observed that only the SP⁺ spines increase their head sizes during LTP (17), suggesting that the presence of SA could be a critical factor in the plasticity of the synapse. To examine this possibility further, we used numerical simulations to investigate calcium dynamics during the LTP and LTD induction at a single spine level based on the molecular organization we delineated heretofore.

Fig. 5. Simulations of calcium transients in spines during LTP and LTD induction protocols.

(A) Schematic of a spine with SA and injected calcium. (B) Postsynaptic LTP protocol with 100-Hz stimulations followed by 30-s silences (SOCE only). The injection starts from N = 300 (or 500) and decays according to the model in Afterward, the injection was allowed to decay slowly with successive events, accounting for synaptic depression (26). (C) LTD protocol is induced by injecting a calcium spike every 1 s. [D (i)] Average number of calcium at the spine base during the first 250 ms of LTP induction. (Mean and SEM are from 20 trials). [D (ii)] Number of calcium ions in SA at the beginning of the LTP protocol (20 trials averaged). [D (iii)] Simulated SA refilling during the silent phase of LTP. Calcium input into spine head is a succession of the slow entry described in Fig. 2C (i). Time courses of SA calcium refilling (blue) that reach high, low, and medium values. Mean (red) and SEM are from 10 trials. [E (i)] Calcium response at the spine base after each 1-Hz spike of the LTD protocol over 300 time courses (30-s simulations ×10). [E (ii) and (iii)] Number of calcium ions in the SA during the first 250 ms and the total 30 s of the LTD protocol. (F and G) Interpretation of the LTP protocol as CICR at the base followed by SA replenishment, while during LTD, the calcium is maintained at low level.

We simulated spine calcium dynamics during LTP in two phases: (i) stimulation phase and (ii) silent phase. The first phase involves a 100-Hz calcium spike train that we started with N = 300 (or 500) calcium ions per spike. In this range of N, the increase in calcium concentration falls into the physiological range of ≈0.15 μM following a synaptic input (25). Afterward, the injection was allowed to decay slowly with successive events, accounting for synaptic depression (26). (See Materials and Methods for the numerical implementation). Both phases included a repetition of slow background input of calcium similar to the STIM1-ORAI1 pathway [N = 300 for 2 s; profile shown in Fig. 2C (i)]. We only simulated the first 250 ms (25 injections) of calcium dynamics of the stimulation phase and 30 s of the silent phase.

In the stimulation phase, we found that on average, the number of calcium ions in the spine head peaks around 50 ms (fig. S9, blue curve) and then decays with weakened inputs. During this time, less than 20 calcium ions reached the spine base [Fig. 5D (i)]; nonetheless, they led to several CICR events (green spikes in fig. S9). Increasing the number of initial calcium ions from 300 [Fig. 5D (i), red] to 500 (blue) reduces the onset time of these RyR responses. Because of these CICR events, the stored number of calcium ions in the SA decayed rapidly, leading to a nearly total SA depletion in about 250 ms [Fig. 5D (ii)].

During the second phase that only included slow inputs, we found that on average, a few hundreds of calcium ions replenish the SA through SERCA pumps [Fig. 5D (iii), red curve]. In some cases, SA calcium level could go up to more than 1500 ions and sometimes diminish to a very low level due to intermittent CICR events [blue curves in Fig. 5D (iii)]. We conclude that such variability in SA refilling is compensated by the repetitiveness of the LTP protocol, applying multiple high-frequency stimulations intermitted by silent periods. We also repeated the refilling phase of the LTP protocol by adding ectopic vesicular release events that introduce small amplitude calcium spikes (fig. S10). We found that the presence or absence of ectopic release did not considerably alter SA refilling.

We then investigated calcium dynamics during the LTD protocol (Fig. 5C): Calcium ions were injected at a slow rate of 1 Hz during 1 min. As we confirmed that the transient is much shorter, we decided to simulate calcium dynamics for the first 30 s. We first injected N = 300 ions to use ion concentrations identical to those used in the LTP protocol. We then increased the number of ions to N = 500 and confirmed that the results did not change. We observed that this input to spine head could trigger CICR events at the base of the spine and thereby increase the calcium at very low levels of 10 ions or less when averaged (orange curves in fig. S11, axis on the right).

To compare the LTD responses at the base with the ones generated by the LTP protocol, we averaged the number of calcium ions during the first 250 ms after each 1-Hz stimulation pulse [Fig. 5E (i)]. The number of calcium ions at the base during LTD simulations is only about one-tenth of the corresponding LTP simulation response [Fig. 5D (i)]. Moreover, the calcium release response at the base during the onset of each stimulation lasted shorter than the corresponding LTD response. In addition, the calcium depletion in the SA is slower during LTD stimulations and takes several seconds [Fig. 5E (ii) and (iii)], compared to the time scale of several hundred millisecond observed during the LTP stimulation [Fig. 5D (i)].

We conclude that the SA depletion time scale varies between LTP versus LTD induction protocols, resulting in a strong difference in the calcium levels at the base of the spine (Fig. 5, F and G). Overall, we propose that this difference could represent the underlying determinant of the spine’s fate toward either enhancement or depression of synaptic efficacy.

DISCUSSION

Despite being widely acknowledged as a critical factor of dendritic spine physiology, regulation of the calcium ion dynamics, especially the mechanisms that exert spatiotemporal control over the calcium release and replenishment, remains less clear. We focused on the role of SA in these processes and found that only strong and fast calcium influxes are amplified by the presence of SA in the spine, resulting in CICR at the spine base (Fig. 6A). In contrast, a slow and small amplitude calcium influx through the STIM1-ORAI1 pathway leads to SA replenishment through SERCA pumps located proximal to the plasma membrane (Fig. 6B). From our observations, we can conclude that calcium influx time scales, their amplitudes, and the spatial distance between ORAI1 and SERCA pumps guarantee that the two pathways (rapid depletion and slow replenishment) are not triggered at the same time (Fig. 6C).

Fig. 6. Physiological conditions for SA depletion versus replenishment.

(A) Synaptic currents entering the dendritic spines through NMDAR and AMPAR trigger CICR by activating RyRs at the base. (B) Small calcium inputs with slow time scales through ORAI1 channels located near the SA membrane are insufficient to trigger a CICR at the base. These ions are either absorbed into calcium pumps located in the spine head or replenish the SA calcium reservoir via the SOCE through SERCA pumps. (C) Phase space described by the main axes: calcium injection rate and the distance d_SA between the ORAI1 and SERCA channels. Refilling and depletion conditions of calcium in spines are well separated, so that both do not occur at the same time.

Perhaps the most prominent result of our analysis is the insight that nanoscale molecular architecture plays an essential role in regulating calcium ion release and replenishment. We observed evidence that the distance between the SA and the plasma membrane (d_SA) plays a major role, whereby calcium replenishment stops as d_SA increases past a certain point. More specifically, we propose that proximity of the two channels ORAI1 and SERCA is required for an optimal SA replenishment, an increase in this distance reduces the chance for the diffusing calcium ions to hit one of the SERCA located in the SA head, and thus they could escape to activate RyRs located at the base. We did observe that adding more SERCA pumps could partially compensate for a longer distance, suggesting that the effect also depends on SERCA density and distribution. Other key players in these processes are calcium pumps, as we show that they restrict small calcium inputs. Their presence increases the temporal separation of the calcium transient between the head and the base, generating an additional delay in CICR activation.

Although suggested to play in regulating calcium dynamics (27), we do not model here calcium buffers because: (i) for a fast CICR onset within a 5 ms, an ion bound to a slow buffer would not contribute; thus, a simple reduction in the available free ions is equivalent to calcium buffering (28). (ii) In the case of ORAI1 channel influxes through the plasma membrane, we do not expect buffers to affect SA replenishment due to the short distance d_SA in the range of 20 to 100 nm, which can contain only very few buffers. Nevertheless, similar to surface pumps, buffers could also help separating the depletion from the replenishment regime, as they introduce an asynchrony to the calcium arrival times to the spine base by absorbing calcium ions followed by delayed release. Overall, the present numerical simulations give an upper estimate of the calcium release probability, and therefore, SA replenishment that compensate such depletion events could be possible even with weaker (N < 300) SOCE inputs than what we simulated here.

At this stage, we conclude that a few molecular players such as SERCA, RyR, and surface pumps seem sufficient to guarantee the interplay between calcium SA refilling and depletion. In the broader context, we propose that these insights could be used to explain the proposed role of the dendritic spines as biochemical computation units (3). From this perspective, given that we observe that the SA depletion is achieved only during synaptic inputs and is unlikely during SOCE, the spine can function in an almost deterministic regime.

The main methodological development that enabled our analysis is the construction of the stochastic model that, unlike the models based on average reaction-diffusion equations, which usually ignore molecular details (25, 29–36), integrates local binding and organization of molecules, channels, and transporters (37, 38). Therefore, the stochastic modeling allows monitoring of diffusion trajectory of each ion separately, thus providing insights into the level of single molecules usually at the expense of high computational cost.

The ability to analyze a system at the single molecule (stochastic) manner is especially important for a system like dendritic spines, given that many of spine processes occur at low copy numbers. For example, AMPARs are of the order of few tens; NMDARs could be less than 10 (8, 39). SERCA pumps and RyR are less than hundreds (40, 41), and the residual level of calcium in spines also ranges below 100 ions. Here, stochastic modeling allows us to estimate relevant statistics to quantify the fluctuations due to low copy numbers.

Thus, in the present modeling and simulations of the spine with a SA, we accounted for the spatial organizations of RyR, ORAI1, and SERCA, which allowed us to obtain accurate nanophysiological predictions about the geometrical organization required for calcium store replenishment versus depletion. We were also able to model and examine how calcium ion release and replenishment affects two fundamental processes essential for synaptic plasticity, learning, and memory: LTP and LTD.

Synaptic plasticity is classically thought to result from calcium elevation in spines, activating a variety of molecular pathways. During this process, both spine head volume and the number of AMPARs increase rapidly within a few minutes (42). Spines with SA predominantly undergo LTP (15, 17, 43). Chemical LTP preferentially enlarges and enhances volume of the head and the surface of the postsynaptic density of dendritic spines containing SA (44). The need of local calcium increase at the base could lead to protein synthesis, as several machineries such as ribosomes and mitochondria (45) are located near the base of the spine neck (46). Thus, if local protein synthesis near SA is regulated by calcium ions due to CICR, then the products could directly be delivered to the stimulated spines to achieve the postsynaptic changes underlying LTP (47) or LTD (48).

Our analysis of calcium dynamics during the LTP-LTD protocols revealed the store depletion level, the total duration, the overall strength, and the initial height of the calcium response at the spine base. At this stage, it remains unclear whether there is a molecular mechanism that compares calcium transients between spine head and base during synaptic plasticity. However, we showed that the number of calcium ions at the base during LTD is only about 10% of the calcium concentration during LTP. This increased calcium concentration at the base during potentiation has been previously shown to regulate trafficking of AMPAR and or NMDAR (8, 49–51). It would therefore be interesting to investigate how these receptors could be selected by local calcium elevation. In addition, this elevation at the spine base could also restrict receptor diffusion and interactions, result in potential well nanodomain trapping (52, 53) or phase separation (54), and create an asymmetric receptor influx in spines. Last, calcium elevation at the base of spines could trigger ER mitochondria calcium communication (45, 55) to produce the adenosine 5′-triphosphate required for the spine homeostasis and for the remodeling of spine shape and volume (56).

We also identified a key difference in SA depletion time scales between LTP and LTD, suggesting that this is also a key determinant of whether a given dendritic spine enhances or depresses synaptic signal. Moreover, in our simulations of the LTD protocol, failure to induce CICR prevents SA depletion and leads to a larger calcium accumulation. Thereby, subsequent inputs could trigger a large calcium increase at the base of the spine. This scenario could explain the instability of LTD induction that could accidentally result in LTP, especially in the presence of secondary calcium sources such as voltage-gated channels.

Although these additional aspects of calcium dynamics in dendritic spines remain to be examined in future studies, our current work found the critical role that molecular architecture plays in regulating calcium ion release and replenishment in dendritic spines. The architecture imposes constraints on the two opposing processes, thus ensuring fidelity and spatiotemporal control, which ensures that calcium stores within SA are replenished without triggering calcium release.

MATERIALS AND METHODS

Ethics statement

Animal handling was done in accordance with the guidelines of the Institutional Animal Care and Use Committee of the Weizmann Institute of Science (approval number: 00650120-3 from 20 January 2020 for 3 years), Collège de France, and the appropriate Israeli and French laws and national guidelines. Experiments were carried out according to the guidelines of the European Community Council Directives of 1 January 2013 (2010/63/EU) and of the local Animal Welfare Committee. All efforts were made to minimize the number of used animals and their suffering.

Calcium imaging experiments

Culture preparation

Cultures were prepared as detailed elsewhere (57). Briefly, rat pups were decapitated on the day of birth (P₀), and their brains were removed and placed in a chilled oxygenated Leibovitz L-15 medium (Gibco) enriched with 0.6% glucose and gentamicin (20 μg/ml; Sigma-Aldrich). Hippocampal tissue was dissociated after incubation with trypsin and deoxyribonuclease and passed to the plating medium consisting of 5% horse serum and 5% fetal calf serum prepared in minimum essential medium (MEM; Gibco) and enriched with 0.6% glucose, gentamicin, and 2 mM GlutaMAX (Gibco). Approximately 10,000 cells in 1 ml of medium were plated in each well of a 24-well plate, onto a glial layer, which has been grown for a week before the plating of the neurons. Cells were left to grow in the incubator at 37°C, 5% CO₂ for 3 days, following which the medium was switched to 10% horse serum in enriched MEM, and in addition of 5-fluoro-2-deoxyuridine + uridine (20 and 50 μg/ml, respectively; Sigma-Aldrich) to block glial proliferation. The medium was replaced 4 days later by 10% horse serum in MEM. The same medium was used after the transfection, and no further changes were made until cultures were used for experimentation.

Transfection

Transfection was conducted at 7 to 8 days in vitro. A Lipofectamine 2000 (Invitrogen) mix was prepared at 1 μl per well with 50 μl per well Opti-MEM (Invitrogen) and incubated for 5 min at room temperature in the hood. Separately, a mix of 2 μg per well total DNA in 50 μl per well Opti-MEM was prepared and also incubated for 5 min. Then, two preparations were coincubated for 15 min at room temperature in the hood. This mix was then added to the each culture well at the amount of 100 μl per well and allowed to induce the transfection during 3 hours before a final change of medium. In most cases, at least 20 neurons per well were transfected. In these experiments, SP-short subcloned into pEGFP-C1 (BD Biosciences, Clontech) (58) or into mCherry was used. For morphological analysis, a blue fluorescent protein (BFP) plasmid was cotransfected with the SP construct. Cotransfected cells displayed no apparent differences in spontaneous calcium activity, morphology, spine density, and survival compared with BFP-only transfected cells or nontransfected cells. The distribution and pattern of the expression of the SP plasmid were similar to those of the endogenous SP (12). Cotransfection efficiency for the plasmids using this method is nearly 90%. Experiments were conducted routinely at 7 to 10 days after transfection. Cultures were used at the same age for comparisons.

Imaging and drug application

Cultures were incubated for 1 hour in high-affinity Fluo-2 acetoxymethyl (AM) (2 μM; Invitrogen, Carlsbad, CA, USA) containing recording medium containing 129 mM NaCl, 4 mM KCl, 1 mM MgCl₂, 2 mM CaCl₂, 4.2 mM glucose, and 10 mM Hepes; pH was adjusted to 7.4 with NaOH, and osmolality to 320 mosm with sucrose. Alternatively, K⁺ Fluo-4 salt solution was injected into transfected neurons with sharp micropipettes and allowed to diffuse for 0.5 hours before imaging. In the latter case, no BFP transfection was required, and cell morphology could be detected based on Fluo-4 basal fluorescence. After loading of calcium, sensor cells were imaged using an LSM 880 Zeiss (Germany) upright confocal microscope equipped with 40× 1–numerical aperture (NA) water immersion objective. Spontaneous calcium transients were detected in both SP and BFP cotransfected and nontransfected neurons using fast scan mode (10 to 20 Hz per frame). Bath application of the blockers TTX (1 μM), APV (50 μM), and DNQX (20 μM) (all from Sigma-Aldrich) was used to eliminate action potentials, postsynaptic potentials, neurotransmitter release, and activity-induced calcium transients. Caffeine (5 mM) was added using quick bath perfusion and then washed out rapidly, while fast calcium transients from dendritic segments with SP⁺ and SP⁻ spines of cotransfected cells were recorded. In some cases, a caffeine-containing patch pipette (diameter 1 to 2 μm, 15 mM) was positioned close to individually identified dendritic segments of a SP-transfected neuron, and responses to local pressure application of caffeine in neighboring SP⁺ and SP⁻ spines of the same dendritic segment were imaged. Images were obtained at high speed for detecting rapid changes in [Ca²⁺]i (10 to 20 Hz, restricted, horizontally oriented scan region). In latter case, distance between the caffeine containing pipette and individual dendritic spines was chosen carefully to be similar for all cases.

Data analysis

Fluorescence intensity was calculated using ZEN (Zeiss, Germany), ImageJ (National Institutes of Health, Bethesda, MD, USA), and MATLAB software (MathWorks Inc., Natick, MA, USA). Dendritic protrusions were categorized into spine types based on their morphological measurements. SP⁺ and SP⁻ dendritic spines that were used for calcium imaging were identified in BFP transfected of Fluo-4–microinjected neurons and analyzed independently. Statistical comparisons were made with t tests or ANOVA, as appropriate, using MATLAB and KaleidaGraph (Synergy Software, Reading, PA, USA).

Experiments using STED

AAV production and injection

This was performed as previously described in (16). Briefly, a green fluorescent protein (GFP) cassette was placed under the control of a hSynapsin promoter in a serotype 9 adeno-associated virus (AAV). Two-month-old C57Bl6 mice were anesthetized under ketamine/xylazine in 0.9% NaCl. AAVs were diluted in phosphate-buffered saline (PBS) to 1.02 × 1013 vg/ml, and 1 μl of virus was injected into the hippocampal region. After 2 weeks, the mice were euthanized and the brains extracted after 2% paraformaldehyde/PBS intracardiac perfusion.

Immunohistochemistry and STED microscopy

This was also performed as previously described in (16). Briefly, 40-μm-thick brain slices were permeabilized and blocked for 2 hours in 0.25% Triton X-100/0.2% gelatin in PBS at room temperature. Primary and secondary antibodies were diluted in the same solution and incubated for 2 hours at room temperature followed by overnight at 4°C. In addition to the primary and secondary antibodies used in (16), anti-ORAI1 (mouse, 1:100; Abcam ab244352), anti-SP (guinea pig, 1:100; Synaptic Systems, 163004), anti-chicken Star Green (goat, 1:200; Abberior, STGREEN-1005), and anti-guinea pig Alexa Fluor 405 (goat, 1:500; Abcam, ab175678) were used in this study.

For the distance measurements between SERCA3 and ORAI1, Z stacks of 100-nm steps images were taken using a three-color superresolution three-dimensional (3D) STED microscope [Abberior Instruments GmbH; as also described in (16)]. Note that the distances that are measured below 100 nm are located in the same Z plane, as the Z step of our stack acquisition is 100 nm. Thus, the errors in the distance measurements are minimized compared to 2D microscopy systems.

Superresolution was used for SERCA3 and ORAI1 channels. All channels were then deconvolved using Huygens software and analyzed using an in-house–developed plugin on ImageJ to measure the distance between two maximas in 3D (maximum distance of 400 nm as a cutoff threshold). Between 83 and 120 interactions (distance from ORAI1 to SERCA3 less than 400 nm) per slice were analyzed in the spine head, between 27 and 52 in the neck, and between 45 and 88 at the base. Four slices were analyzed. The violin plots represent all the dots analyzed (378 in the head, 159 in the neck, and 290 at the base).

For the presence of SP, images were taken with another set of immunostained slices with an additional 405-nm laser for the excitation of the SP Alexa Fluor 405, using a Zeiss Axio Observer Z1 with a CSUW11 Spinning-disk scan head (Yokogawa 63×/1.4-NA objective lens). Z stacks of 150-nm steps were taken and analyzed with ImageJ software. Colocalization frequencies were calculated over the total number of spine head analyzed. Nineteen field of views from four animals were analyzed. Sixty to 80 spine heads were analyzed per field of view. Each interaction type was assigned to one of the five categories of colocalization type.

Statistical analysis

All data are expressed as means ± SEM. Statistical significance for within-group comparisons was determined by one-way ANOVAs (followed by Tukey’s post-test) on GraphPad Prism.

Stochastic model of calcium dynamics and numerical simulations

Modeling and simulation of calcium diffusion in a dendritic spine

To simulate calcium transients in a spine, we use the following model: The dendritic spine geometry is made of a large spherical head connecting the dendrite by a cylindrical neck (21, 59). We added an SA as a “spine inside a spine” with a similar geometry (Fig. 2A). The parameter for radii of the spine head, spine neck, SA head, and SA neck is summarized in table S2.

The motion of calcium ions are modeled with Brownian diffusion described by the stochastic equation $\stackrel{·}{\mathit{X}}=\sqrt{2\mathit{D}}\stackrel{·}{\mathit{w}}$, where w represents Wiener white noise, δ-correlated in both space and time: For distinct time and space coordinates X, X′ and t, t′, therefore, 〈w(X, t)w(X′, t′)〉 = δ(X − X′)δ(t − t′), where δ(. ) is Dirac’s δ function. We simulate a discretized form of this motion using the Euler’s scheme: ${\mathit{X}}_{\mathit{n}}={\mathit{X}}_{\mathit{n}-1}+\sqrt{2\mathit{D}\mathrm{\Delta }\mathit{t}}·\mathrm{\eta }$. Here, X_t = {X, Y, Z} is the position of a particle at time t, and η is a normal random variable with three independent components generated by the NumPy library of Python. The diffusion coefficient of calcium in the medium is D, while Δt is the width of a single time step (values in table S2). We chose the largest Δt such that reducing it further neither alters the calcium fluxes through SERCA pumps nor the RyR activation times.

We consider the small baseline concentration of free initial calcium in the medium to be zero; thus, we introduce calcium in two ways: either we position instantaneously a total of N calcium ions at single point at the top of the spine head (fast synaptic inputs) or we introduce calcium ions one after the other according to a distribution, which follows a difference of two exponentials (the STIM1-ORAI1 pathway is described below).

After entering the spine, ions can diffuse within the spine domain until it reaches the bottom of the neck. Spine base is modeled as an absorbing boundary; thus, ions arriving at the base of the spine do not appear again in the simulation. In our model, we neglected any electrostatic interactions between the ions and the membranes of the spine or the SA, from which ions are reflected with the classical Snell-Descartes law.

Moreover, calcium ions have two valence charges that can create an electric interaction with the surface charge density located on the dendrite membrane. However, in the presence of a small calcium influx, the possible interaction of the ion with the rest of the medium is described by the Debye length in an order of a few nanometers (60, 61). Therefore, as there is a minimum distance of 20 nm between the two membranes in our model, we neglected the electrodiffusion of calcium ions.

Modeling calcium channels and pumps

Calcium extrusion pumps

Calcium extrusion pumps are located on the inner surface of the spine head and are modeled as absorbing circular disks having a catchment radius of 10 nm as previously calibrated in (59). To match a decay time scale of 6 ms recorded for calcium fluorescents in the spine head, we calibrated the number of pumps to be 50 (16). If we increase this catchment area, we would need to reduce the number of pumps to keep this calcium decay time fixed.

Ryanodine receptors

We model RyRs as circular disks located on the surface of SA with a catchment radius of 10 nm where calcium ions are bound. There are n_R=36 RyRs located at the base (Fig. 2A). Of these, 12 are located on the segment of the SA parallel to the dendrite. The remaining 24 form four rings (six receptors in each ring) in the SA neck. Opening of a RyR is triggered by the arrival of two calcium ions into the receptor site. When a first calcium ion arrives at a receptor, it stays bound for 10 ms and then unbinds to diffuse to a distance of one Brownian step. The RyR is opened only if the second one arrives within this 10-ms window. We confirmed that results in RyR opening times and probabilities are largely independent of this window size, when varied from 10 ms to ∞. After the arrival of a second ion to the RyR calcium, ions are released with a delay of 0.25 ms. The number of calcium ions released per RyR starts from 8 and decays to 6 and 7, followed by another cycle of 8-7-6 as reported in (16). After each release, RyRs are inactivated for 3 ms, during which they do not bind to calcium ions.

SERCA pumps

Classical models of SERCA pumps are based on a four-state Markov chain model, where most of the parameters are unknown [p.43, after equation 2.47 in (36)]. We model here SERCA pumps using the same formulation as we previously implemented in (16) with a stochastic model of four states: 0, ions bound; 1, ion bound; 2 ions bound; and refractory state. A pump is opened by the arrival of two successive ions within a 10-ms window. If a second ion does not arrive within this time, then the first ion is released at a distance given by one Brownian step. In case of an opening event, the two ions get translocated into the SA, and the pump remains inactive for its refractory period. Hence, our model uses only two parameters: the first ion’s waiting time of 10 ms and the refractory time of 100 ms. The catchment radius of SERCA pumps R = 10 nm is justified by the atomic-level description given in (62). The positioning of SERCA pumps are on the top hemisphere of the SA head, according to a uniform random distribution (Fig. 2A).

Influx through the STIM1-ORAI1 pathway

We do not model here explicitly the transfer of ions from the extracellular to the intracellular medium upon the activation of ORAI1 channels that form complexes with STIM1 molecules. Instead, to simulate the SOCE inputs through ORAI1 channels, we use the time course extracted from the calcium fluorescence signal of the spine head (Fig. 1C and fig. S3). In addition, we vary the distance d_SA between the plasma membrane and the SA membrane that governs the proximity between ORAI1 channels and SERCA pumps.

Simulation of LTP and LTD protocols for calcium injection

1) LTP protocol: The 1-s high-frequency stimulation during the LTP protocol is simulated as a series of calcium spikes into the top of the spine head. The amplitude of this spike is a decreasing number of ions proportional to the fraction E of synaptic resources in the effective state that we compute using the facilitation-depression model (26) described by

$$\frac{\mathit{dR}}{\mathit{dt}}=\frac{\mathit{I}}{{\mathrm{\tau }}_{\text{rec}}}-{\mathit{U}}_{\text{se}}\mathit{Rf}(\mathit{t})$$ (3)

$$\frac{\mathit{dE}}{\mathit{dt}}=-\frac{\mathit{E}}{{\mathrm{\tau }}_{\text{inac}}}+{\mathit{U}}_{\text{se}}\mathit{Rf}(\mathit{t})$$ (4)

$$\mathit{I}=1-\mathit{R}-\mathit{E}$$ (5)

Here, I and R are the inactive and recovered fractions of synaptic resources that add up to the normalized amount of total resources with value 1. The two time constants τ_rec = 0.3 s and τ_inac = 0.2 s govern the recovery and the inactivation of the resources, respectively (63). The stimulation protocol is modeled by the function f(t) made of 100-Hz train of δ−Dirac impulses during 1 s: $\mathit{f}(\mathit{t})={\Sigma }_{\mathrm{\lambda }=1}^{100}\mathrm{\delta }(\mathit{t}-0.01\mathrm{\lambda })$. Last, U_se is the fraction of synaptic resources in the recovered state getting activated by each instantaneous input. During the first 250 ms that we simulated, the value of E decayed from 1 to 0.47, which depends weakly on U_se. This decay simulates the gradual reduction of the synaptic input amplitude into spines.

In addition to these injections of fast calcium spikes, we also maintain the model of slow input of calcium [through ORAI1 channels as in Fig. 2C (i), with N = 300 ions during 2 s]. During the simulation of the refilling phase of the LTP protocol [Fig. 5D (ii)], the high-frequency stimulation is absent; hence, only this slow calcium influx was available.

2) LTD protocol: For each stimulation pulse of LTD, we injected calcium ions instantaneously every 1 s over a duration of 1 min (we only simulate the first 30 s of the protocol to investigate the SA calcium dynamics). We predetermined the number of ions contained in injected pulse to be constant at N = 300 or 500. In addition to these fast injections, throughout all LTP simulations, we also inject a repetition of the slow calcium influx as mentioned before.

Supplementary Materials

This PDF file includes:

Sections S1 to S8

Figs. S1 to S11

Tables S1 and S2

References

Other Supplementary Material for this manuscript includes the following:

Data S1 to S5

View/request a protocol for this paper from Bio-protocol.