Uncovering biomarkers during therapeutic neuromodulation with PARRM: Period-based Artifact Reconstruction and Removal Method

Summary

Advances in therapeutic neuromodulation devices have enabled concurrent stimulation and electrophysiology in the central nervous system. However, stimulation artifacts often obscure the sensed underlying neural activity. Here, we develop a method, termed Period-based Artifact Reconstruction and Removal Method (PARRM), to remove stimulation artifacts from neural recordings by leveraging the exact period of stimulation to construct and subtract a high-fidelity template of the artifact. Benchtop saline experiments, computational simulations, five unique in vivo paradigms across animal and human studies, and an obscured movement biomarker are used for validation. Performance is found to exceed that of state-of-the-art filters in recovering complex signals without introducing contamination. PARRM has several advantages: (1) it is superior in signal recovery; (2) it is easily adaptable to several neurostimulation paradigms; and (3) it has low complexity for future on-device implementation. Real-time artifact removal via PARRM will enable unbiased exploration and detection of neural biomarkers to enhance efficacy of closed-loop therapies.

Graphical abstract

Highlights

• •PARRM removes artifacts that obscure neural activity in neuromodulation recordings
• •PARRM is effective with both low- and high-sampling-rate recordings
• •PARRM is adaptable to several neurostimulation paradigms
• •The low complexity of PARRM makes it suitable for future on-device implementation

Motivation

Electrophysiological recordings concurrent with electrical stimulation of the brain and spinal cord are often corrupted by stimulation artifact. The removal of stimulation artifact is a necessary step toward identifying neural biomarkers that can be consistently used to titrate neuromodulation therapies or discover the underlying disease neuropathology. Thus, we developed a Period-based Artifact Reconstruction and Removal Method (PARRM) to provide a solution to removing such artifacts from low- and high-sample-rate recordings. PARRM is adaptive to changes in artifact shape, is robust to aliasing, and has low computational overhead readily implementable for use in real time. Our method aims to enable the investigation, and eventual development, of closed-loop neuromodulation therapies.

Dastin-van Rijn and Provenza et al. developed the Period-based Artifact Reconstruction and Removal Method (PARRM) to remove stimulation artifacts from electrophysiological recordings. PARRM is superior to comparable methods, adaptable to several neurostimulation paradigms, and of low complexity for future on-device implementation. These features make PARRM effective for identifying neural biomarkers for closed-loop therapies.

Introduction

The development of closed-loop electrical neuromodulation therapies, for example adaptive deep brain stimulation (aDBS) and adaptive spinal cord stimulation (aSCS), would revolutionize the efficacy of neurostimulation therapies for the treatment of many disorders, including Parkinson's disease (PD) (Little et al., 2016; Rosin et al., 2011; Swann et al., 2018), epilepsy (Bergey et al., 2015; Sun and Morrell, 2014), essential tremor (Herron et al., 2017), obsessive-compulsive disorder (OCD) (Provenza et al., 2019), treatment-resistant depression (TRD) (Provenza et al., 2019; Widge et al., 2017), and chronic pain (Mekhail et al., 2020). Although significant advances have been made in biomarker identification in PD and epilepsy (Bergey et al., 2015; Bronte-Stewart et al., 2009), there is no definitive biomarker for a single mental disorder, including OCD and TRD, or chronic pain (Mekhail et al., 2020; Provenza et al., 2019; Widge et al., 2017). Biomarker identification and development of an adaptive neurostimulation system requires a hardware platform that is capable of simultaneous sensing and stimulation. This is particularly challenging when the neural signal of interest originates in or nearby the stimulation target, as the amplitude of stimulation therapy is typically several orders of magnitude greater than the amplitude of signals of interest in the brain and spinal cord. Therefore, recordings for adaptive control are heavily contaminated by high-amplitude, high-frequency stimulation artifact (Zhou et al., 2018). To extract the underlying neural signatures of disease state, it is necessary to remove the stimulation artifact.

Typically, high-frequency artifacts are removed by using a low-pass filter; however, limited sampling rates of existing implantable DBS and SCS devices and aliasing of stimulation pulses into low frequencies render low-pass filters ineffective. Existing stimulation artifact removal methods robust to aliasing typically fall into one of three categories: signal reconstruction via deletion and interpolation, decomposing and subtracting components of the signal related to the artifact, and subtracting a template of the artifact at each stimulation pulse. Methods based on deletion interpolation rely on accurate detection of stimulation artifacts that are removed and replaced by some prediction of the underlying neural signal (Sellers et al., 2019; Waddell et al., 2009). However, higher-order stimulation harmonics are attenuated by brain tissue and anti-aliasing filters, resulting in a lengthened artifact waveform (Sun et al., 2014). The impact of the anti-aliasing filter is especially significant at lower sampling rates. Under these conditions, deletion and interpolation are ineffective due to considerable signal loss over the duration of each artifact (Zhou et al., 2018). An exception to this issue is the Hampel filter, as it operates in the frequency domain (Allen et al., 2010). Signal decomposition methods utilize the similar structure of artifacts across a large number of electrodes in order to remove the signal as a common feature (Khorasani et al., 2019; Mena et al., 2017; O'Shea and Shenoy, 2018). These methods have shown significant success but require a large number of recording channels to be effective (Lau et al., 2012). Traditional template subtraction methods have proved successful, although they rely on accurate detection of each stimulation pulse (Erez et al., 2010; Hashimoto et al., 2002; Qian et al., 2017; Sun and Hinrichs, 2016; Sun et al., 2014). Existing methods for identifying individual stimulation pulses in recorded data (e.g., thresholding) are not robust to low sampling rates, the presence of other spurious high-amplitude artifacts, or stimulation artifacts with broad peaks (Caldwell et al., 2020). To our knowledge, there are currently no effective methods for removal of stimulation artifacts from low-channel-count local field potential (LFP) recordings sampled at less than twice the frequency of stimulation without contaminating the underlying neural signal, thus greatly hindering the identification of biomarkers using recordings from implanted devices.

Low sampling rates are often desirable to improve power and bandwidth efficiency for recordings controlled by implantable neurostimulation devices. Currently there are two commercial DBS systems and two research DBS systems available in the United States that are capable of simultaneous therapy and sensing. The Percept (Medtronic, Minneapolis, MN) and the NeuroPace RNS (NeuroPace, Mountain View, CA) are available commercially, and the Activa PC + S and Summit RC + S (Medtronic) are available for research. The commercial devices are both limited to a sampling rate of 250 Hz (Koeglsperger et al., 2020; Skarpaas et al., 2019), whereas the research devices have configurable sampling rate capabilities ranging from 200 to 1,000 Hz (Stanslaski et al., 2012, 2018). Lower sampling rates are necessary to maximize recording time or minimize data offloading time for devices that store data onboard and to minimize data loss during streaming for devices that are capable of streaming data out (Stanslaski et al., 2012, 2018). Even in cases when implantable DBS devices are capable of sampling at 500 Hz or greater, choosing a low sampling rate (250 Hz or less) can be advantageous for maximizing battery life and number of recording channels. Compared with externalized systems, such as those used in epilepsy monitoring units (sampling rates of 2 kHz and higher), sampling rates of existing implantable DBS devices are limited (Chan et al., 2008; Jouny et al., 2011; Stanslaski et al., 2012). To enable classification of neural biomarkers for aDBS or closed-loop SCS, it is necessary for artifact removal to be effective for low-resolution LFPs sensed by using a fully implantable device.

To overcome the challenges in removing periodic stimulation from neural recordings, we have developed an artifact removal method, Period-based Artifact Reconstruction and Removal Method (PARRM), to remove high-frequency stimulation artifact in low- and high-resolution LFP recordings. We demonstrate that PARRM has superior performance to existing state-of-the-art filters in saline experiments and computer simulations at typical sampling rates for implanted devices. Additionally, we have successfully applied PARRM to five unique in vivo recording paradigms across a range of sampling and stimulation conditions and demonstrate that PARMM enabled the recovery of a previously obscured biomarker in a PD participant. Lastly, we provide evidence that PARRM could be implemented online to enable real-time biomarker detection.

Results

Design of PARRM

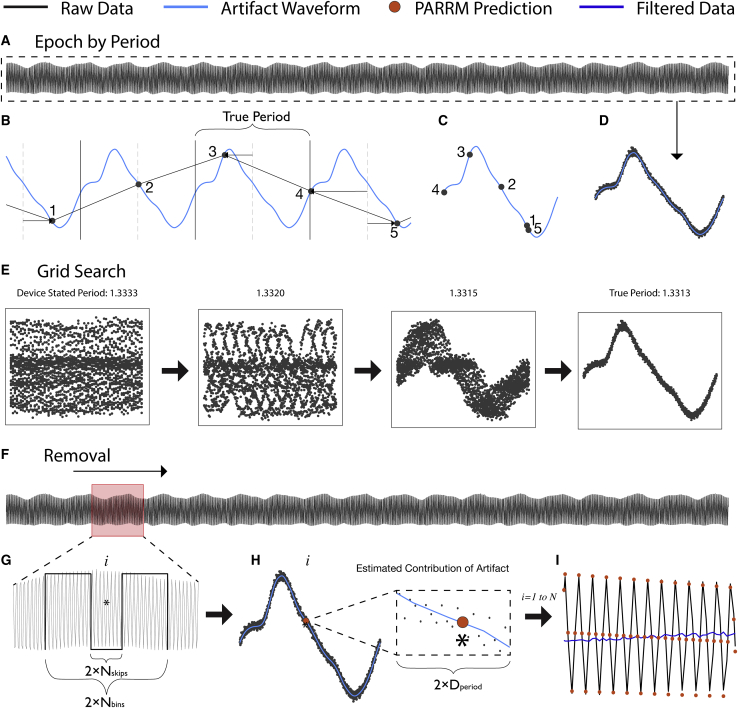
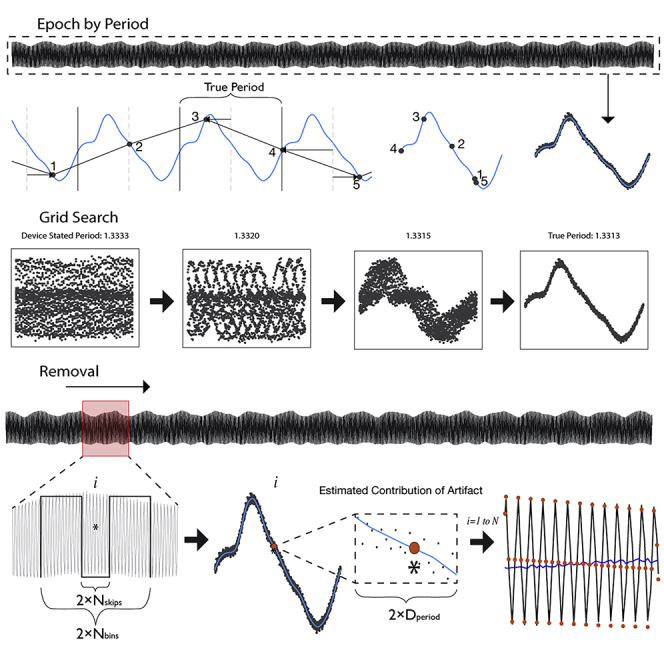
PARRM subtracts an estimate of the stimulation artifact at each time bin from the recorded signal at that time bin. The artifact estimate is formed by averaging the recorded signal at other time bins that are close to the current time bin in both time and stimulation phases. The artifact is presumed to be roughly identical for all of these time bins. Averaging reduces the influence of brain signals and additional sources of noise so that the estimate is primarily artifact. This process can be implemented as a linear filter (i.e., a weighted average using a sliding window). PARRM needs a precise estimate of the stimulation period in relation to the sampling rate. Slight inaccuracies in device system clocks can necessitate using a data-driven method to determine this period, which is done by finding the period that, when the data are divided into epochs the length of one period and overlapped, the samples will consolidate around the shape of the high-resolution artifact waveform. The complete process of data-driven period finding, artifact estimation, and signal reconstruction is illustrated in Figure 1 and Video S1.

Figure 1.

Illustration of stimulation period determination, template reconstruction, and template subtraction via PARRM

(A) Entire LFP recording sampled at 200 Hz (black) is used to identify the true period.

(B) An illustration of a five-sample snippet of the LFP recording divided into epochs by using the true period and overlaid with the high-resolution waveform (light blue). Black points indicate individual raw LFP samples.

(C) The epochs for all five samples are overlaid on the timescale of the true period.

(D) When all epochs in the recording are overlaid by using this procedure, all samples consolidate around the shape of the high-resolution artifact waveform on the timescale of the true period.

(E) The period suggested by the device sampling and stimulation rates is inexact and does not result in a consolidated waveform. Using a grid search centered around the stated period, a series of periods are evaluated to find the true period that produces the most consolidated samples.

(F) A sliding window is applied to the entire recording to estimate the contribution of the stimulation artifact at each sample.

(G) For each window, a rectangular kernel (length $N_{\text{bins}}$), ignoring the center (length $N_{\text{skips}}$) is used to estimate the value of the artifact at each sample of interest $i$ (asterisk).

(H) Samples within a distance, $D_{\text{period}}$, on the timescale of the artifact period are averaged together to produce the estimate of the amplitude of the artifact (orange point) at sample $i$.

(I) The estimated value of the artifact is then subtracted at each sample over the entire recording to recover the signal of interest (dark blue).

PARRM recovers simple sinusoidal signals in saline

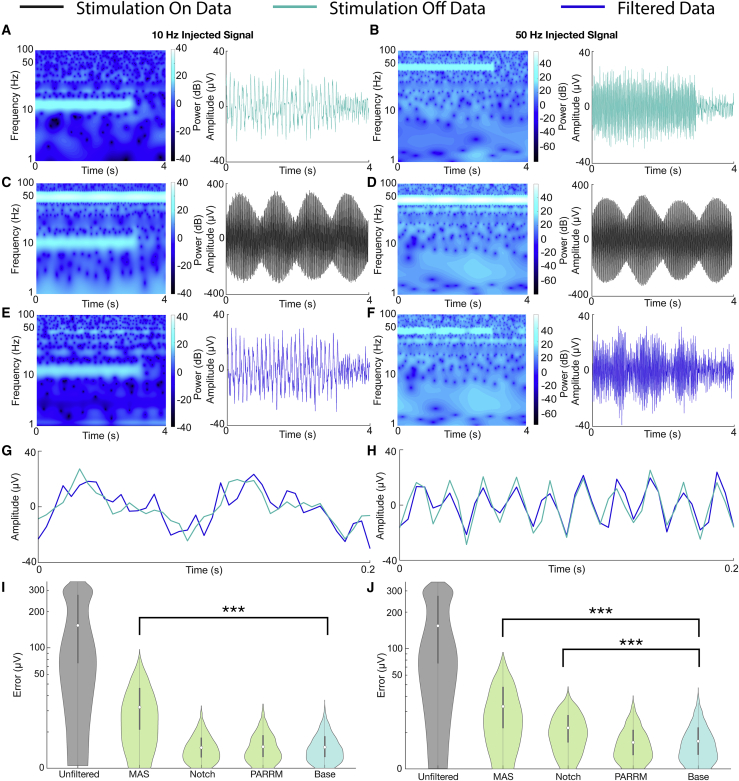
PARRM was used to remove the DBS artifact and recover the underlying injected signal and noise in saline. In artifact-free (DBS off) recordings, both the 10 Hz and 50 Hz injected signals are clearly visible in both the frequency and time domains prior to signal offset (Figures 2A and 2B). When stimulation is turned on, high-amplitude artifacts are visible in the frequency domain at 0 Hz and 50 Hz, obscuring the 50 Hz injected signal but not the 10 Hz signal. In the time domain, both the 10 Hz and 50 Hz signals are obscured (Figures 2C and 2D). After filtering using PARRM, the effects of stimulation are removed in both the frequency and time domains (Figures 2E and 2F). In the case of the 50 Hz signal, this is achieved despite the artifact being aliased to the same frequency as the injected signal.

Figure 2.

PARRM effectively recovers sinusoidal signals at frequencies separate from and coincident with the aliased artifact

(A and B) Spectrogram and time-voltage series of (A) 10 Hz and (B) 50 Hz sinusoidal signals injected into saline sampled at 200 Hz with stimulation off.

(C and D) Spectrogram and time-voltage series of (C) 10 Hz and (D) 50 Hz sinusoidal signals injected into saline sampled at 200 Hz during concurrent 150 Hz stimulation.

(E and F) PARRM-filtered spectrogram and time-voltage series of (E) 10 Hz and (F) 50 Hz sinusoidal signals injected into saline sampled at 200 Hz during concurrent 150 Hz stimulation.

(G and H) A 0.2 s snippet of PARRM-filtered and artifact-free time-voltage series of (G)10 Hz and (H) 50 Hz sinusoidal signals injected into saline sampled at 200 Hz during concurrent 150 Hz stimulation.

(I and J) Evaluation of filter performance based on time domain absolute error between artifact-free and filtered (I) 10 Hz and (J) 50 Hz injected signals sampled at 200 Hz during concurrent 150 Hz stimulation. Asterisks indicate significant differences from absolute errors on the order of baseline noise (Wilcoxon rank sum, ∗∗∗p < 0.0005).

The similarity between the artifact-free and filtered signals is visually apparent in 0.2 s of data for both the 10 Hz and 50 Hz injected signals (Figures 2G and 2H). We then quantified filter performance by comparing the distribution of absolute errors between artifact-free signals and unfiltered, moving average subtraction (MAS)-filtered, notch-filtered, and PARRM-filtered signals to a baseline noise recording (no stimulation, no injected signal) (Figures 2I and 2J). Filtering using MAS did not reduce the error to the level of baseline for either injected signal (p < 0.0005). Although effective at 10 Hz (p > 0.05), notch filtering removed the injected signal along with the artifact, leading to a large reduction in error yet still significantly different from baseline (p < 0.0005). For both the 10 Hz and 50 Hz injected signals, PARRM outperformed the other methods with no significant difference (p > 0.05) from baseline, indicating that the remaining errors were expected to be due to noise in saline.

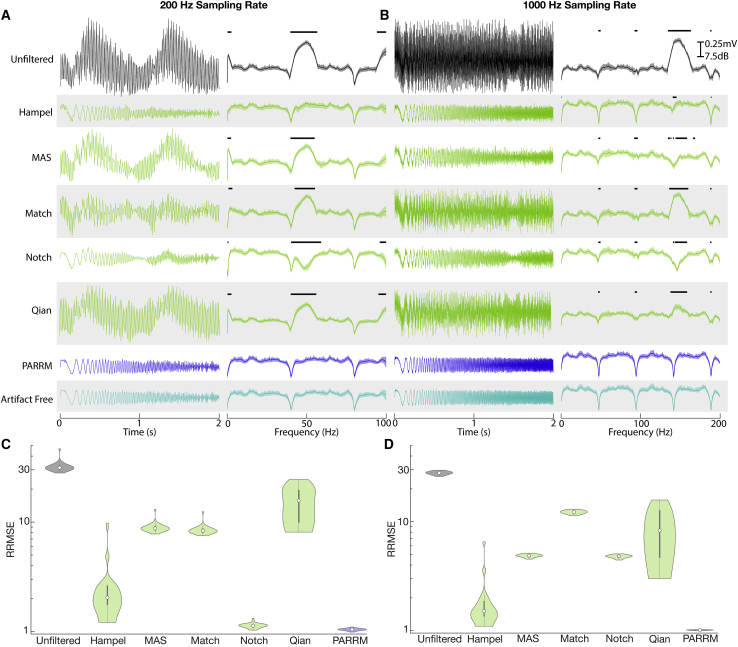
PARRM recovers complex, multi-frequency signals in computer simulations

Having shown that PARRM is effective for recovering simple sinusoidal signals recorded in saline, we next sought to compare the method's performance with a series of state-of-the art filters in recovering more complex, injected, chirp signals for simulated data (Figure S2). When all chirps were averaged, PARRM recovered a signal with minimal distortion and noise in the time domain at both low and high sampling rates, unlike MAS, matched, and Qian filters (Figures 3A [left] and 3B [left]). Additionally, PARRM showed no significant differences in the frequency domain at either sampling rate (Figures 3A [right] and 3B [right]). This was true even at frequencies affected by artifact where other filters either overfiltered (notch) or underfiltered (MAS, matched, and Qian). Lastly, PARRM had a relative root-mean-squared error (RRMSE) close to 1 for both sampling rates, indicating effective signal recovery on a single-trial basis, exceeding performance of the Hampel filter (Figures 3C and 3D). For all three metrics, PARRM exceeded or matched performance of all other filters for both low and high sampling rates.

Figure 3.

PARRM performance exceeds state-of-the-art filters for non-stationary signals at low and high sampling rates in simulated data

(A) Averaged time-voltage series and windowed power spectral density of 30 simulated linear chirps (0–100 Hz, 2 s duration, variable separation) during concurrent 150 Hz stimulation for unfiltered, Hampel-filtered, MAS-filtered, match-filtered, notch-filtered, Qian-filtered, PARRM-filtered, and artifact-free recordings sampled at 200 Hz. Black solid bars indicate significant difference from artifact-free signal (two-sample t test, p < 0.05).

(B) Average time-voltage series and average windowed power spectral density of 30 simulated linear chirps (0–200 Hz, 2 s duration, variable separation) during concurrent 150 Hz stimulation for unfiltered, Hampel-filtered, MAS-filtered, match-filtered, notch-filtered, Qian-filtered, PARRM-filtered, and artifact-free recordings sampled at 1,000 Hz. Black solid bars indicate significant difference from artifact-free signal (two-sample t test, p < 0.05).

(C and D) Evaluation of filter performance based on time domain relative root-mean-squared error (RRMSE: ratio between MSE of artifact-free versus theoretical chirp to MSE of filtered versus theoretical chirp) of simulated chirps during concurrent 150 Hz stimulation sampled at (C) 200 Hz and (D) 1,000 Hz.

Next, a parameter sweep was performed to test the effect of varying chirp length (1–10 s), amplitude (0.5–5 V), pulse width (30–180 μV), and frequency (80–180 Hz) on PARRM performance, measured by RRMSE and relative R ratio (Figure S3). Effects for chirp length and pulse width were all within the margin of error. RRMSE and relative R ratio increased for increasing stimulation amplitude. RRMSE and relative R ratio decreased for stimulation frequencies above 100 Hz. All changes were at most 8% different from baseline, indicating that PARRM performed well for a wide range of stimulation parameters and recorded signals.

PARRM significantly attenuates stimulation artifacts from Activa PC + S

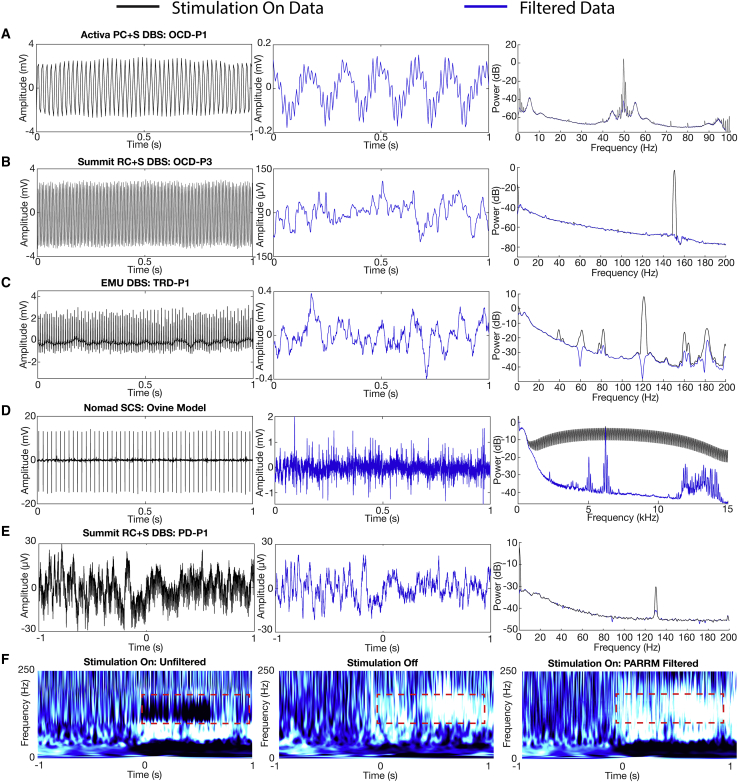
We then applied PARRM to an extensive dataset of 1,012 recordings from two human neuropsychiatric DBS participants (NCT03457675). Prior to application of PARRM, the unfiltered electrophysiological signal recorded during stimulation for both participants displayed a large artifact, obscuring the LFP signal of interest (Figures 4A [left] andS4A [left]). After the application of PARRM, the amplitude of the resulting signal was reduced by a factor of 20. However, unexpected oscillations with non-stationary frequency content, centered at approximately 6 Hz and 3 Hz for OCD-P1 and OCD-P2, respectively, remained after filtering (Figures 4A [center] andS4A [center]). Non-stationary artifacts were not explained by variability on the scale of the period or jitter in the location of the stimulation pulses (Figure S5). Average power spectral densities were computed for all recordings and confirmed that the expected stimulation harmonics were well attenuated for both participants (Figures 4A [right] and S4A [right]).

Figure 4.

Demonstration of PARRM in human participants with DBS, intracranial EEG recordings during concurrent DBS, and spinal cord stimulation in ovine model

(A–E) Raw time-voltage LFP trace, PARRM-filtered time-voltage LFP trace, and average power spectral density (PSD) before (black) and after (blue) PARRM filtering, collected during (A) 150 Hz stimulation sampled at 200 Hz by using Activa PC + S in OCD-P1 left VC/VS, (B) 150.6 Hz stimulation sampled at 1,000 Hz by using Summit RC + S in OCD-P3 right BNST, (C) 120 Hz stimulation sampled at 2,000 Hz in TRD-P1 left ventral prefrontal cortex during a cognitive control task, (D) 50 Hz spinal stimulation sampled at 30 kHz in ovine model by using Ripple Nomad, and (E) 130.2 Hz stimulation in STN sampled at 1,000 Hz by using Summit RC + S in PD-P1 recorded in right M1 during movement task. Left: one unfiltered trial in time domain. Center: PARRM-filtered trial in time domain. Right: PSD of whole task.

(F) Averaged continuous wavelet transforms for a movement task zeroed to motion cue for stimulation on unfiltered data, stimulation off, and stimulation on PARRM-filtered data recorded using the Summit RC + S in PD-P1 recorded in right M1. Location of high-gamma biomarker is indicated by the dashed red line.

PARRM removes artifacts in a wide range of therapeutic stimulation paradigms

After establishing the suitability of PARRM to deep brain recordings during DBS therapy, we evaluated the applicability of PARRM to different neuromodulation modalities to recover neural signals during (1) 150.6 Hz DBS by using the Summit RC + S for OCD in the right bed nucleus of stria terminalis (BNST) and left ventral capsule/ventral striatum (VC/VS) (Figures 4B and S4B), (2) 120 Hz DBS in an epilepsy monitoring unit (EMU) setting recording from left prefrontal cortex and amygdala (Figures 4C and S4C), (3) 50 Hz and 10 kHz SCS during rest in sheep recording approximately from spinal segments L5 to S1 (Figures 4D and S6D), and (4) 130.2 Hz DBS by using the Summit RC + S for PD in the subthalamic nucleus (STN) recording from right M1 (Figure 4E). The effectiveness of PARRM for each setting was evaluated by comparing filtered recordings with unfiltered recordings using raw time domain traces and power spectral densities. In all four modalities, PARRM was able to attenuate the stimulation artifacts at every amplitude and frequency, leading to large reductions in artifact amplitude in both the time and frequency domains. PARRM was able to accurately remove artifacts and their harmonics at both low and high frequencies and, in the case of the EMU recording, identified and attenuated aliased artifacts. Lastly, PARRM was applied to data from M1 recorded by using the Summit RC + S during a movement task whereby the subject was receiving concurrent 130.2 Hz DBS in the STN for PD. PARRM removed artifacts in the time domain on a single-trial basis and reduced artifact amplitude in the frequency domain (Figure 4E). When all trials were averaged, PARRM was able to recover a known high-gamma biomarker for movement onset that was previously obscured by stimulation artifact (Figure 4F). Together, these analyses demonstrate that PARRM is readily adaptable to a wide range of neural recording paradigms and can enable the recovery of neural biomarkers otherwise obscured by stimulation artifacts.

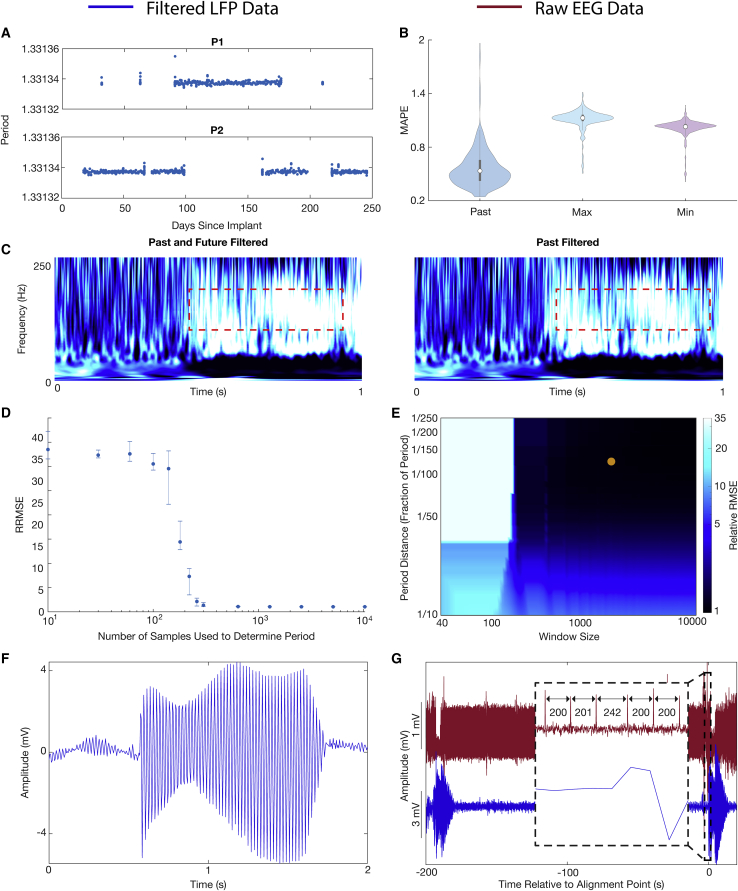
Potential for online application of PARRM in implantable technologies

The feasibility of implementing PARRM as an online method for low-sampling-rate recordings was investigated by using LFPs sampled at 250 Hz by the Activa PC + S over 250 days. Using 1,012 recordings from two Activa PC + S participants both in the clinic and at home, we estimated potential variability in the period over the 250-day span. Variation in the period was minimal (standard deviation of ${10}^{-5}$ samples) with the maximum and minimum differing from the median by only $2\times {10}^{-5}$samples. The estimated period was consistent across both devices with only a $2\times {10}^{-7}$sample difference between the medians (Figure 5A). Data filtered by using past samples only and extreme periods were compared with data filtered by using the standard PARRM approach in which both past and future samples are used and an accurate period is estimated. The similarity between these approaches was quantified by using median absolute percentage error (MAPE). Using only past samples resulted in an MAPE of 0.6% when compared with a two-sided filter. Filtering using extreme periods and past samples resulted in an MAPE of approximately 1% when compared with a two-sided filter (Figure 5B). Lastly, a PARRM filter using only past samples was applied to the movement task data from M1, resulting in a similar biomarker compared with using past and future samples (Figure 5C).

Figure 5.

Practical considerations for implementing signal recovery via PARRM in real time

(A) Exact period estimations in samples over 1,012 recordings for P1 and P2 over 250 days since DBS implant.

(B) Median absolute percent error (MAPE) between the standard PARRM filtering approach (using past and future samples, and exact period estimation) and by using past samples only with an exact period estimation, past samples only with the maximum period across the 1,012 recordings, and past samples only with the minimum period across the 1,012 recordings.

(C) Comparison of averaged continuous wavelet transforms when filtered by using PARRM with past and future samples versus past samples alone.

(D) PARRM performance measured by relative root-mean-squared error (RRMSE) is dependent on the number of samples used to determine the period. Error bars show the spread.

(E) Heatmap of RRMSE as a function of period distance ($D_{\text{period}}$) and half window size ($N_{\text{bins}}$). Darker blue indicates superior PARRM performance. Orange point indicates the $D_{\text{period}}$ and $N_{\text{bins}}$ that were used for all analysis.

(F) Voltage-time LFP trace after PARRM filtering containing a jump in the period.

(G) LFP (blue) and concurrent EEG (red), aligned by using location of period jump identified in both recordings.

We then sought to estimate the minimum number of samples that were necessary to guarantee an accurate estimate for the period based on RRMSE with the simulated chirp data. RRMSE followed a roughly sigmoidal relationship with the number of samples used. RRMSE and its variability decreased with the increasing number of samples. Improvement (decrease) beyond 1,000 samples was minimal (1% difference) (Figure 5D). We then computed the RRMSE as a function of two filter parameters: the period distance ($D_{\text{period}}$) and the half window size ($N_{\text{bins}}$). We found that increasing the window size and decreasing the period distance generally improved RRMSE. Improvement beyond a period distance of 1/150th of a period and 2,000 samples was minimal (Figure 5E). Improvements in RRMSE were not fully explained by the total number of samples averaged for each parameter combination (Figure S6A). These results demonstrate that PARRM can be implemented with minimal onboard memory, enabling real-time artifact removal.

PARRM is robust to spurious changes in stimulation artifact

Lastly, we verified that PARRM is robust to spurious jumps in the stimulation period. After a jump in the period, PARRM temporarily filters using the incorrect phase of the artifact. However, because of the moving filter window, PARRM performance recovers a few seconds after a period jump (Figure 5F). These period jump events can be used to our benefit to align LFP recordings with external sensors, such as electroencephalography (EEG) (Figure 5G). These jumps can be located on the high-sampling-rate (30 kHz) EEG as increases in the difference between subsequent peaks. In the LFP, these events can be located by filtering using PARRM twice: once with a past window, and again with a future window. The peak in the product of the five-sample moving standard deviations of these two filtered recordings corresponds to the location of the alignment point (Figure S6B). These results demonstrate that PARRM can be robust to potential recording errors in an online environment and can assist in temporal alignment of concurrent recordings.

Discussion

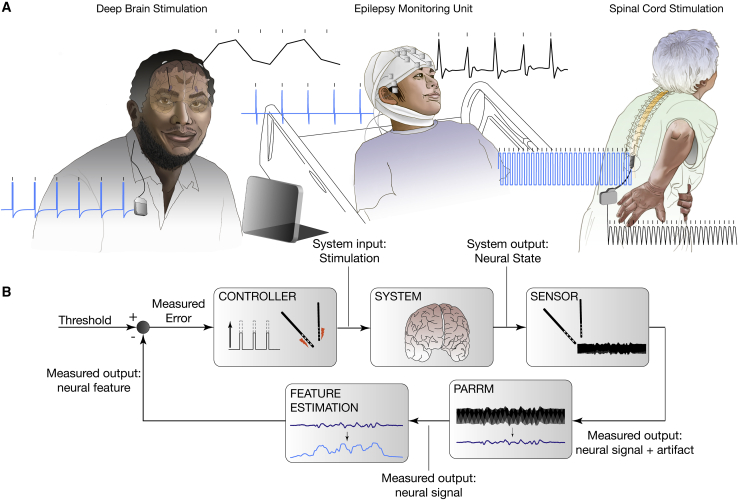
In summary, we have developed a method, PARRM, which removes electrical stimulation artifacts in low- and high-sampling-rate LFP recordings even in cases where the frequency of the underlying neural signal overlaps with the frequency of aliased artifacts (Figure 2). Before the development of PARRM, it was impossible to completely remove aliased artifacts resulting from stimulation frequencies or harmonics greater than the Nyquist frequency (125 Hz for recordings sampled at 250 Hz) without contaminating the underlying neural signal. Stimulation frequencies over 125 Hz are clinically relevant for PD, OCD, TRD, and pain (Dayal et al., 2017; Miller et al., 2016; Ramasubbu et al., 2018). This capability opens the door for use of power-efficient implantable neurostimulation devices without sacrificing data quality and is particularly useful for the two existing commercial DBS systems capable of concurrent stimulation and sensing at 250 Hz: the Percept and the NeuroPace RNS (Koeglsperger et al., 2020; Skarpaas et al., 2019). PARRM is a low-complexity algorithm that can develop templates for subtraction based on past data samples, requiring minimal computational resources and onboard storage, and could be implemented on existing and future neurostimulation devices (Figure 6).

Figure 6.

Real-time artifact removal via PARRM could enable biomarker detection during ongoing neurostimulation to enhance efficacy of closed-loop neuromodulation

(A) Three example applications of closed-loop neuromodulation: DBS applied at 150 Hz via the Activa PC + S for treatment of refractory OCD (top), DBS applied at 120 Hz in an epilepsy monitoring unit-like (EMU-like) scenario for treatment of TRD, and SCS applied at 50 Hz for treatment of chronic pain. Blue trace shows theoretical injected DBS waveform and black trace shows DBS waveform sampled in vivo at 200 Hz, 2 kHz, and 30 kHz, via Activa PC + S, Blackrock Cerebus, and Ripple Nomad, respectively.

(B) Control policy for closed-loop DBS. Electrodes in the brain sense neural signals and artifacts. PARRM attenuates stimulation without contaminating the underlying neural signal, enabling feature estimation for the closed-loop control of stimulation amplitude to relieve symptoms.

To set up PARRM for application in a closed-loop setting, it would first be necessary to record a calibration dataset to compute the exact period for the intended stimulation frequency if an exact value is not already known. Figure 5D shows the length of this recording that would be necessary to produce an effective filter using typical Activa PC + S parameters. The optimal length of this recording would depend on the stimulation frequency and the duration of the artifact on the scale of the period leading to potentially more or less data being required than the example. Once the period is known, a PARRM filter can be designed and implemented on the device. So long as the stimulation pulses do not saturate the amplifier, this configuration could be used to remove stimulation artifacts in real time.

Because of the conditions of our benchtop saline experiments including impedance mismatch of electrodes in saline versus the human brain, most validation steps were completed via computational simulations. We chose to simulate our most limited recording scenario: the Activa PC + S at a sampling rate of 200 Hz. Although the simulated waveform was not based on exact parameters of every component of the Activa PC + S device circuit, we believe that the simulations do not detract from the validation of the method. The simulated artifact waveform closely matches the reconstructed waveform observed during benchtop saline testing (Figure S1C). The simulation was an efficient way to evaluate PARRM performance over a vast array of DBS parameters and conditions. In the future, we hope that DBS device companies will consider publishing Simulink models of the DBS waveforms produced by their devices to aid in artifact characterization and removal.

We found that when applying PARRM to Activa PC + S recordings, distinct, low-frequency, non-stationary oscillations remained. Non-stationary oscillatory artifacts, varying on a timescale shorter than the filter window, cannot be successfully mitigated by using PARRM. We investigated whether these non-stationary oscillations might have been the product of variable noise dependent on the phase of the waveform where a point was sampled, or might have resulted from jitter in the true pulse location within a period compared with the pulse location predicted by PARRM. However, when this noise and jitter were incorporated into simulations, neither addition replicated the non-stationary oscillations (Figure S7). Given that these oscillations did not appear in saline recordings and could not be replicated via the addition of noise or jitter, we hypothesize that they arise from interactions between the electrical stimulation and the unique chemical medium and structural environment of the brain and should be investigated further in future studies. Recording configurations that minimize such artifacts, as well as aperiodic artifacts from other sources, are valuable for maximizing PARRM performance.

Artifact removal via PARRM will enable unbiased exploration of neural biomarkers that might have previously been obscured by stimulation artifacts. More broadly, PARRM might be applicable in any domain in which a periodic artifact should be removed to recover an underlying signal of interest. Although more development is needed before PARRM can be applied to perform onboard artifact rejection during concurrent neurostimulation therapy and sensing, PARRM could ultimately contribute to the accurate detection of neural biomarkers and the development of closed-loop neuromodulation therapies.

Limitations of the study

PARRM is adaptable to a wide range of stimulation paradigms and is effective for both low- and high-sample-rate recordings, including cases with aliased artifacts due to low sampling rates. Optimal PARRM performance depends on the ability to identify a highly periodic signal in the data in order to design a filter that is well adapted to the artifact's shape. However, if the artifact is not highly periodic in nature, this procedure is ineffective. The assumption of high periodicity demonstrably holds for artifacts seen in most electrical stimulation therapies (e.g., DBS and SCS) but is not valid for electrocardiogram artifacts often affecting EEG recordings. Additionally, many of the choices of parameters were specific to the examples we explored in this study, including DBS, SCS, and stimulation during an EMU recording session, and we have not exhaustively explored the parameter space. As a result, the PARRM as demonstrated in this article might be less effective in environments we did not actively explore. Although PARRM is flexible to changes in artifact shape on timescales longer than the filter window, it is not robust to short timescale changes. An example of this behavior can be seen in the PC + S data where the harmonic component of the artifact was well removed but residual oscillations remained. These effects are non-stationary in nature and can take the form of unpredictable pulse-to-pulse changes in shape or gradual fluctuations that still operate on a timescale less than the optimal filter window. For PARRM to sufficiently attenuate stimulation artifacts, such features would have to be negligible compared with the neural signal of interest. These issues significantly affected only one of our recording paradigms, so we were unable to determine how commonplace they are or how best to simulate their severity.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and algorithms
MATLAB	Mathworks	https://www.mathworks.com/products/matlab.html
EEGLAB	(Brunner et al., 2013)	https://sccn.ucsd.edu/eeglab/index.php
jsPsych	(de Leeuw, 2015)	https://www.jspsych.org/
PARRM	This paper	https://github.com/neuromotion/PARRM
SIMULINK	Mathworks	https://www.mathworks.com/products/simulink.html
Other
Activa PC+S	Medtronic	Discontinued – commercial product Percept PC
Summit RC+S	Medtronic	https://www.braininitiative.nih.gov/sites/default/files/pdfs/rcs_device_information_508c.pdf
tCRE	CRE-Medical (v2.0)	https://cremedical.com/product-2/
Nomad	Ripple Neuro	(now Trek) https://rippleneuro.com/ripple-products/grapevine-processors/

Resource availability

Lead contact

Further information and requests for resources may be directed to and will be fulfilled by the Lead Contact, Prof. David Borton (david_borton@brown.edu).

Materials availability

This study did not generate new unique reagents.

Data and code availability

Code for PARRM and an example data set is available on GitHub (https://github.com/neuromotion/PARRM). Data used to produce the manuscript are available from the corresponding author on request.

Experimental model and subject details

Human LFP recordings from implanted DBS devices for OCD

Research subjects were four participants, each with a history of long-standing OCD, that underwent clinically indicated DBS surgery for treatment of OCD. Two participants (OCD-P1, 31y/o male and OCD-P2, 39y/o female) were implanted with the Activa PC+S (Medtronic, Minneapolis, MN, USA) device, and two participants (OCD-P3, 37y/o female and OCD-P4, 40y/o male) were implanted with the Summit RC+S (Medtronic, Minneapolis, MN, USA) device. Each participant gave fully informed consent according to study sponsor guidelines, and all procedures were approved by the local institutional review board at Baylor College of Medicine (H-40255, H-44941).

DBS leads (Model 3778) were intracranially placed bilaterally in the VC/VS or BNST based on clinical indications and connected to the Activa PC+S or Summit RC+S to enable control of DBS and LFP recordings. OCD-P1, OCD-P3, and OCD-P4 received bilateral stimulation while OCD-P2 received unilateral stimulation. LFP was sensed with bipolar contacts around the stimulation contact at a sampling rate of 200 Hz (Activa PC+S) or 1000 Hz (Summit RC+S). Scalp EEG sampled at 30 kHz was concurrently recorded using tripolar concentric ring electrodes (tCRE, CRE-Medical, University of Rhode Island, RI, USA).

Human intracranial electroencephalography recordings

A research subject with a history of treatment-resistant depression (TRD-P1, 37y/o male) was implanted with clinical depth electrodes (PMT, Chanhassen, MN, USA) spanning the amygdala, prefrontal cortex, orbitofrontal cortex and cingulate cortex, as well as bilateral DBS electrodes (Vercise Gevia; Boston Scientific, Marlborough, MA, USA) in the VC/VS and subcallosal cingulate. Research protocols were approved by the institutional review board at Baylor College of Medicine (H-43036, H-40255), and the research subject provided written and verbal voluntary consent to participate in the study.

Intracranial electroencephalographic (iEEG) signals from depth electrodes were recorded at 2 kHz with a bandpass of 0.3-250 (4th order Butterworth filter) using a 256 channel Blackrock Cerebus system (Blackrock Microsystems, Salt Lake City, UT, USA). Stimulation was concurrently delivered through DBS electrodes using Cerestim (Blackrock Microsystems, Salt Lake City, UT, USA) to deliver continuous stimulation at 130 Hz, 100 μS pulse width and 4-6 mA. In order to remove line noise, notch filters were applied at 60, 120, and 180 Hz.

Sheep spinal electrophysiological recordings

One sheep (13m/o male) underwent surgery to implant a custom-built 24 contact SCS device on the epidural surface of the spinal cord from approximately the L5-S1 spinal segments. All study procedures were conducted with the approval of the Brown University Institutional Animal Care and Use Committee (19-04-0002) and in accordance with the National Institutes of Health Guidelines for Animal Research (Guide for the Care and Use of Laboratory Animals). Device wires were externalized and connected to a Nomad (Ripple Neuro, Salt Lake City, UT, USA) neural interface system to allow for simultaneous stimulation and recording of the spinal cord at 30 kHz. Stimulation was controlled by a custom-written MATLAB (Mathworks, Natick, MA, USA) script to deliver current at levels typically used for chronic pain management using SCS (0-2000 μA, 50 Hz and 10 kHz).

Human LFP recordings from implanted DBS devices for PD

One PD patient (PD-P1, 40y/o male) was implanted with bilateral cylindrical quadripolar deep brain stimulator leads into the subthalamic nucleus (STN, Medtronic model 3389) and bilateral placement of paddle-type quadripolar cortical paddles into the subdural space over motor cortex (MC, Medtronic model 0913025). Each pair of STN and MC leads was connected bilaterally to a Summit RC+S device in a pocket over the pectoralis muscle (Medtronic Summit RC+S model B35300R).

The paddle lead was placed in the subdural space through the same frontal burr hole used for the subthalamic lead. At least one contact covered the posterior precentral gyrus (presumed primary motor cortex), approximately 3 cm from the midline on the medial aspect of the hand knob. The STN leads were implanted in the motor territory of the STN. Placement was confirmed with movement-related single-cell discharge patterns. The study was approved by the hospital institutional review board (IRB) at University of California San Francisco Medical Center under a physician sponsored investigational device exemption (G180097) and was registered at ClinicalTrials.gov (NCT03582891). The patient provided written consent in accordance with the IRB and Declaration of Helsinki.

Method details

Period-based artifact reconstruction and removal method (PARRM)

At each time bin $t$, PARRM subtracts an estimate of the stimulation artifact at time bin $t$ from the recorded signal at time bin $t$ (Figure 1). The estimate of the stimulation artifact is formed by averaging the recorded signal at other time bins that are in a temporal region near time bin $t$ and also approximately at the same phase of stimulation as time bin $t$ (Tzou et al. 2013). The artifact is presumed to be roughly identical for all of these time bins, including time bin $t$. Averaging reduces the influence of brain signals and additional sources of noise, so that the subtracted signal is primarily artifact.

Let $T$ denote the stimulation period relative to the sampling rate (in units of sampling time bins). The time bins included in the average are those times bins $s$ such that

$$N_{skip}<\left|s-t\right|\le N_{bins}$$

and such that

$$\left|s-t\right|\left(modT\right)\le D_{period}or\left|s-t\right|\left(modT\right)\ge T-D_{period},$$

where $a\left(modT\right)$ denotes $a$ modulo $T$, and where $0\le N_{skip}<N_{bins}$ and $0\le D_{period}\le T$ are user-chosen design parameters. (The additional criterion $s-t<0$ can be included so that only past observations are used to estimate the stimulation artifact) Let $B_t$ denote the collection of those times bins $s$ that are used for averaging and let $\left|B_t\right|$ denote the number of such time bins. Using $r_t$ to denote the recorded signal at time bin $t$, the corrected signal is $c_t$ defined by

$$c_t=r_t-\frac{1}{\left|B_t\right|}\sum _{s\in B_t}{r}_s=\sum _{i=-N_{bins}}^{N_{bins}}{w}_i{r}_{t-i}$$

where $w_i$ is a list of weights defined by $w_0=1$, and $w_i=-1/\left|B_0\right|$ if $-i\in B_0$, and $w_i=0$ otherwise. The final expression shows that the PARRM correction can be implemented by a fixed linear filter (with the filter weights denoted by $w_i$), making it fast and simple to implement. (If the additional criterion $s-t<0$ is used, then the final summation would begin at $i=0$). The final formula also needs to be scaled near the start and end of stimulation to account for edge effects. These modifications are described in more detail in the “PARRM linear filter derivation and modifications” section of the methods.

The design parameters for the PARRM filter are $N_{bins}$, $N_{skip}$, and $D_{period}$. Larger choices of $N_{bins}$ allow more data to be averaged in order to estimate the artifact, reducing estimation variability. But larger choices of $N_{bins}$ also lengthen the temporal window used to estimate the artifact, perhaps introducing estimation bias if the artifact shape is changing in time. Because neural signals have temporal autocorrelation, it is important to avoid averaging data too close to time bin $t$ or the neural signal itself could be subtracted during artifact removal. Larger choices of $N_{skip}$ help to mitigate this danger, but also reduce the amount of data used to estimate the artifact. Similar to $N_{bins}$, larger choices of $D_{period}$ allow more data to be averaged, but also introduce more estimation bias by temporally smoothing the estimated artifacts.

Filter parameter selection

The first parameter chosen when optimizing PARRM for a new recording was the period distance D_period. We decided on the value of D_period depending on the shape of the reconstructed stimulation waveform. We identified the size of the smallest feature in the waveform in samples and chose D_period to be small enough such that samples within that feature would be relatively stationary. For the PC+S, RC+S, SCS, and EMU recordings this parameter was set to 0.01, 0.01, 0.005, 0.005 samples respectively. We then increased the half window size N_bins until the artifact appeared to be significantly attenuated in both the time and frequency domains. For the PC+S, RC+S, SCS, and EMU recordings the final value of this parameter was set to 2000, 6000, 6000, 1000 samples respectively. Choice of the value for N_skips would become more relevant once a signal of interest was known so as to avoid including samples within that signal. This parameter was set to 20 samples for all recording paradigms. In the future, we intend to automate the choice of these parameters.

Period estimation

PARRM needs a precise estimate $T$of the stimulation period relative to the sampling rate. $T$ can be determined via several methods. This paper uses an automated, data-driven method that works by searching for a period that creates a strongly resolved template (Figures 1E and S1A). For each candidate period $\delta >0$, the method estimates a waveform template with this period and then quantifies deviation from the estimated template. The candidate period with the smallest deviation is selected as the final estimate $T$of the period that is used by PARRM. A similar period finding method was described by Tzou et al. (Tzou et al., 2013).

Let $m\ge 0$ be an integer. For each potential period $\delta >0$ and each parameter vector $\beta =({\beta }_1,\dots ,{\beta }_{2m+1})$ define the functions

$$f_{\beta ,\delta }\left(t\right)={\beta }_1+\underset{j=1}{\overset{m}{\sum {\beta }_{2j}}}\sin \left(\frac{2\pi jt}{\delta }\right)+\sum _{j=1}^m{\beta }_{2j+1}\cos \left(\frac{2\pi jt}{\delta }\right)$$

The function $f_{\beta ,\delta }$ is a periodic function with period $\delta$. Each $f_{\beta ,\delta }$ is a candidate artifact waveform. The parameter vector $\beta$ controls the strength of the different frequencies that define $f_{\beta ,\delta }$, and $m$ controls the number of allowed frequencies. Let $\left(\left(t_k,y_k\right):k=1,\dots ,n\right)$ be a collection of (time, value) pairs. The $y_k$ value used here is the change in recorded LFP amplitude at time $t_k$ with some preprocessing to obtain standardized units, reduce the influence of outliers, and reduce the size of the dataset; see a more detailed discussion later in the methods. Mean squared error is used to measure how well the function $f_{\beta ,\delta }$ fits these pairs:

$$mse\left(\beta ,\delta \right)=\frac{1}{n}\sum _{k=1}^n{\left(y_k-f_{\beta ,\delta }\left(t_k\right)\right)}^2$$

For fixed $\delta$, the optimal $\beta$, say, $\hat{\beta }\left(\delta \right)=mse(\beta ,\delta )$, can be computed exactly using linear regression techniques; see more detailed discussion later in the methods. The final estimate of the period is

$$T=argmi{n}_{\delta }mi{n}_{\beta }mse\left(\beta ,\delta \right)=argmi{n}_{\delta }mse\left(\hat{\beta }\left(\delta \right),\delta \right).$$

The minimization over $\delta$ is complicated by many local minima, spurious ‘distractor’ solutions that mimic the harmonics of the true waveform (Figure S1A), and high sensitivity to small changes in $\delta$. The examples in this paper use a penalized, stagewise search that begins with smaller intervals of data (to reduce the sensitivity to $\delta$), smaller $m$ (to reduce the number of local minima), and a penalty for higher frequency solutions (to help avoid distractor solutions); see more detailed discussion later in the methods. This seems to be the most delicate part of the period-finding procedure. Once $T$ is found, it is fixed for PARRM. Simpler methods for period finding are under active development and will be described in a future publication.

Implementation of state-of-the-art filters

Hampel filter, moving average subtraction, matched filter, Qian filter, and notch filter performance were used as a comparison point to PARRM performance. Hampel filters interpolate artifactual components in the frequency domain and have been shown to be an effective approach for removing DBS artifacts in EEG recordings. We implemented a standard Hampel filter in MATLAB based on the method described by Allen et al. (Allen et al., 2010). Moving Average Subtraction (MAS) employs peak finding to identify each stimulation pulse in an up-sampled recording before averaging neighboring pulses to construct a local template, and has been shown to be effective in signal recovery for low and high sampling rate EEG recordings during DBS. Following the method described by Sun and Hinrichs et al., we implemented a similar filter in MATLAB (Sun and Hinrichs, 2016). Matched filters estimate the amplitude and phase of a series of sinusoidal harmonics of the artifact by maximizing cross correlation and have been shown to be effective in signal recovery for simulated DBS artifacts added to EEG data. We implemented a matched filter in MATLAB using six matched components based on the method described by Sun et al. (Sun et al., 2014). The filter described by Qian et al. (Qian filter) overlaps a large number of upsampled stimulation artifacts to produce a single high-resolution template and was successfully applied to remove DBS artifacts from low and high resolution LFP data (Qian et al., 2017). We implemented a Qian filter in Matlab following the procedure described in their paper. Notch filters at the stimulation frequency and its harmonics are an effective method for removing DBS artifacts by completely attenuating power at affected frequencies. Second order Infinite Impulse Response (IIR) notch filters with a half-power distance of 5 Hz were applied at the stimulation harmonics and their aliases using the MATLAB designfilt and filtfilt functions. For recordings sampled at 200 Hz, a high-pass finite impulse response (FIR) filter with 2 dB stopband attenuation, transition band between 2 and 3 Hz, and a passband ripple of 0.1 dB and a 20th order low-pass IIR filter at 97 Hz with 0.1 dB of passband ripple were used to attenuate the aliased components at 0 and 100 Hz (for 150 Hz stimulation).

Experimental validation of PARRM in saline

The artifact removal method was validated by simulating the recording conditions in the brain using a setup in a saline solution (Figure S1B). The DBS lead (Model 3778) and case were immersed on opposite sides of a plastic container containing 1x phosphate buffered saline solution at room temperature. A platinum electrode connected to a waveform generator was placed adjacent to the stimulating electrode to simulate LFP (Figure S2). Single frequency (10 Hz and 50 Hz) oscillations were injected by the waveform generator alongside 2 V, 150 Hz, 90 μs pulse width stimulation. The efficacy of the removal method was characterized by comparing the distributions of absolute errors of the artifact free injected signal with unfiltered, moving average subtraction (MAS) filtered, notch filtered, and PARRM filtered signals. Baseline noise was estimated during recordings where stimulation was off and there was no injected signal from the waveform generator.

Experimental validation of PARRM using Simulink

The recording circuit for the Activa PC+S device was simulated using Simulink (Mathworks, Natick, MA, USA) (Stanslaski et al., 2012). The simulation input was a train of modeled DBS pulses sampled at 120 kHz, and the output was the simulated stimulation waveform as if it were being recorded by the Activa PC+S (Figure S1C). The Simulink model is available by request (see Availability statement). By default, a stimulation frequency of 150 Hz, amplitude of 2 V, and pulse width of 90 μs were used. The simulation reached a steady state after two seconds. The final stimulation waveform was then used to create pulse trains that match the simulated injected signal in length. Each simulated pulse train was downsampled by a factor of 601 or 121 (199.67 Hz or 992 Hz) to replicate the true sampling rate, which deviates slightly from the sampling rate stated by the device (200 Hz or 1000 Hz). For each simulation, the stimulation pulse train was added to a series of 30 linear chirps. Each chirp was two seconds in length and separated from the following chirp by one second with 0.1 seconds of jitter. Chirp amplitude was twice the root mean squared amplitude of the baseline noise. Gaussian noise equal in magnitude to what was observed in saline was added to each simulation. For the signals sampled at roughly 200 Hz, chirps ranged from 0 to 100 Hz. For the signals sampled at roughly 1000 Hz, chirps ranged from 0 to 200 Hz. PARRM performance using simulated data was compared to that of a Hampel filter, MAS filter, matched filter, Qian filter, and notch filter. A parameter sweep was run to test PARRM performance across varying stimulation frequencies (80-180 Hz), amplitudes (0.5-5 V), pulse widths (30-180 μs), and chirp lengths (1-10 s).

Spectral analysis

Time frequency decomposition was performed using a continuous complex Morlet wavelet transform. For data sampled at 200 Hz, 500 steps from 0 to 100 Hz were used. Wavelets were constructed using one cycle at the minimum frequency up to 20 at the maximum frequency. Steps were linearly spaced for analysis of chirp signals and logarithmically spaced for analysis of stationary sinusoidal signals. For data sampled at 1000 Hz, 500 linearly spaced steps from 0 to 200 Hz were used. Wavelets were constructed using one cycle at the minimum frequency up to 30 at the maximum frequency also with linearly spaced steps. For analyzing the frequency content of each chirp, we computed a windowed power spectral density using the decomposition. The power for each frequency was computed by averaging the power in a window centered at the time the frequency of interest occurred during the linear chirp. The window size was four samples for the 200 Hz recordings and 20 samples for the 1000 Hz recordings. Stationary power spectral densities were computed using the MATLAB pspectrum function.

Estimation of filter performance

Visual comparison: averaged chirp

In order to visually compare the different filtering approaches, all 30 chirps were averaged together to produce a single average chirp. This method was used to visually show how well each filter was able to recover the signal over many trials.

Frequency domain chirp comparison metric: Windowed PSD

In order to compare how well each filtering approach was able to recover the chirp signal in the frequency domain, the distribution of power was compared for each frequency. Power was computed by calculating the decibel ratio of the signal of interest and the concurrent noise.

Time domain chirp comparison metric: Relative root mean squared error

In order to compare how well each filtering approach was able to recover the chirp signal in the time domain, the distributions of relative root mean squared error were compared. Relative root mean square error (RRMSE) was calculated for each chirp by dividing the root mean squared error between the filtered and theoretical chirp signals by the root mean squared error of the artifact free and theoretical chirp signals.

Parameter sweep metric: Relative R Ratio

In order to compare how well each filtering approach was able to recover the chirp signal in the frequency domain as a whole, the distribution of relative R ratios was computed (Qian et al., 2017). Relative R ratio was computed as

$$R=mean\frac{lo{g}_{10}\left(\frac{P_{filtered}\left(f\right)}{P_{theor}\left(f\right)}\right)}{lo{g}_{10}\left(\frac{P_{free}\left(f\right)}{P_{theor}\left(f\right)}\right)}$$

where $P_{filtered}$ is the power for the filtered signal, $P_{theor}$ is the power for the theoretical chirp signal (without noise), and $P_{free}$ is the power for the chirp signal without stimulation artifact.

Movement task

A movement task written using jsPsych was presented to PD-P1 on a laptop touch screen computer (de Leeuw, 2015). The patient was presented with a target appearing in one of four locations on the screen followed by a cue to move and a baseline period (each lasting up to three seconds). The patient performed 60 reaches (15 to each target, randomized) with therapeutic deep brain stimulation off or on in the STN. Synchronization of neural data and task data were done using the clock of the patients’ study computer. Two channels were recorded from motor cortex with a 1000 Hz sampling rate.

For movement-related changes in spectral power, data were filtered using a two-way 3rd order FIR filter (eegfilt from EEGLAB toolbox with fir1 parameters) and bandpassed in frequencies between 1-200 Hz (Brunner et al., 2013). Data from all trials were aligned relative to the onset of movement and averaged. The averaged amplitude was normalized by a 1000 ms window prior to cue presentation (time 0). Data were z-scored by subtracting the average baseline amplitude and dividing by the baseline standard deviation. This z-score procedure was performed for each frequency separately.

Feasibility for use of PARRM as an online method

Using 1012 recordings from two human participants implanted with the Activa PC+S, we investigated whether it would be feasible to implement PARRM using an existing device. For PARRM to be effective as an online method, filter performance should depend on past samples only (rather than past and future samples) and should be robust to any foreseeable variation in the stimulation period over time. Additionally, the recording duration required to make an initial period estimate should be minimal, and filtering should require minimal resources onboard the device. To this end, a 40-second-long segment from each of the 1012 recordings was filtered using PARRM. The period was estimated for each recording. Extreme periods were identified by finding the maximum and minimum period over all the 1012 recordings. Data filtered using past samples only and extreme periods were compared to data filtered using the previously described approach where both past and future samples are used, and an accurate period is estimated. In total, the data were filtered using (1) past and future samples and accurate periods, (2) past samples only using accurate periods, (3) past samples only using minimum extreme periods, and (4) past samples only using maximum extreme periods. In order to quantify the magnitude of difference between the four filtering approaches, the median absolute percentage error (MAPE) between the original approach and the alternative approach was computed for each recording. Additionally, the RRMSE was found as a function of the number of samples used to determine the period, the period distance, and the window size for simulated chirps sampled at 200 Hz.

LFP synchronization with external sensors

For one of the human participants (OCD-P1) implanted with the Activa PC+S, we synchronized the LFP recording with concurrent EEG. Synchronization was achieved by identifying ‘jumps’ in the stimulation period which occurred simultaneously in both recordings. Jumps in the difference between EEG peak times found using the MATLAB findpeaks function were used to locate these events in the EEG. In LFP recordings, these events were located by comparing data filtered using only past versus only future samples. A moving standard deviation with a window of five samples was computed for both recordings and the ‘jump’ corresponded to the peak in their product.

Exploration of non-stationary oscillations leftover in human Activa PC+S data

Given the presence of residual nonstationary oscillations following filtering using PARRM, we investigated whether they were sourced from features we initially considered to be negligible; namely noise dependent on the artifact phase and jitter in the artifact peak location (Figure S5). In order to find the phase dependent noise, we overlaid all samples on the time scale of one period. A 1000 sample moving standard deviation was then computed to calculate the expected noise as a function of artifact phase. Gaussian noise with standard deviation corresponding to the phase of each sample was then added to LFP artifacts reconstructed using PARRM in order to evaluate whether the noise recreated the nonstationary oscillations that PARRM was unable to remove. Since we concurrently recorded high resolution (30 kHz) EEG, we were able to estimate the true locations of the artifact pulses using this recording. In order to quantify any jitter in the location of the EEG artifact peaks, we reconstructed a typical EEG artifact using PARRM. We then convolved this reconstruction with EEG upsampled by a factor of 10 using linear interpolation in order to estimate the jitter in peak location for each artifact. This jitter was then added to LFP artifacts reconstructed using PARRM in order to evaluate whether the addition recreated the nonstationary oscillations that PARRM was unable to remove.

PARRM linear filter derivation and modifications

Here we give details of the derivation that PARRM can be implemented as a linear filter. The corrected signal is defined earlier in the methods as

$$c_t=r_t-\frac{1}{\left|B_t\right|}\sum _{s\in B_t}{r}_s.$$

Ignoring edge effects and inspecting the definition of $B_t$, we see that $s\in B_t$ if and only if $s-t\in B_0$. Or, equivalently, $u\in B_0$ if and only if $u+t\in B_t$. Hence, we can express

$$c_t=r_t-\frac{1}{\left|B_0\right|}\sum _{u\in B_0}{r}_{u+t}=r_t-\frac{1}{\left|B_0\right|}\sum _{i=-N_{bins}}^{N_{bins}}{\chi }_{B_0}\left(i\right)r_{t+i}=r_t-\frac{1}{\left|B_0\right|}\sum _{i=-N_{bins}}^{N_{bins}}{\chi }_{B_0}\left(-i\right)r_{t-i},$$

where ${\chi }_B\left(a\right)=1$ if $a\in B$ and ${\chi }_B\left(a\right)=0$ if $a\notin B$. Defining the weight vector $w$ as in the early discussion and observing that ${\chi }_{B_0}\left(0\right)=0$, we see that the final expression can be expressed as the convolution

$$c_t=\sum _{i=-N_{bins}}^{N_{bins}}{w}_i{r}_{t-i},$$

which is the familiar formula for a discrete linear filter. Note that the derivation is unchanged if we modify $B_t$ to have the additional restriction that $s-t<0$, meaning that only past observations are used to estimate the stimulation artifact.

This derivation ignores edge effects that occur for those $t$ such that $t-N_{bins}$ or $t+N_{bins}$ extends beyond the recording period or is outside of the period of stimulation. We use the original definition of $c_t$ in these cases, where $B_t$ includes only those time bins that are recorded during the stimulation period.

Period finding details

The earlier methods section describes the optimization criterion for selecting the stimulation period $T$ used by PARRM. Here we describe the exact preprocessing used to create the $y_k$ values, the details of linear regression optimization step, the details of the stagewise search over candidate periods $\delta$, and the values of the design parameters.

Preprocessing

We begin with an electrophysiological signal recorded during stimulation. Each channel of the recording is processed as follows: (1) The signal is differenced, i.e., the signal at time step $t-1$ is subtracted from the signal at time step $t$. Differencing helps remove low frequency modulations unrelated to the artifact. (2) The (differenced) signal is divided by the mean absolute value of the (differenced) signal to give a unitless, standardized measurement. (3) Any values of this standardized signal greater than 3 are set to 3 and any values less than -3 are set to -3. This clipping of large magnitude observations helps remove the influence of outliers. The preprocessing results in a collection of $(t_k,y_k)$ pairs, where $t_k$ is the time bin and $y_k$ is the final (differenced, standardized, clipped) signal. Finally, we subsample these pairs in some way to obtain a smaller dataset, e.g., by taking all pairs from a shorter interval or by choosing pairs uniformly at random (without replacement). This subsample is the collection of $\left(\left(t_k,y_k\right):k=1,\dots ,n\right)$ pairs referenced earlier in the methods and below.

Linear regression

For each $(t_k,y_k)$ pair, define the row vector $x_k=\left(x_{k1},x_{k2},\dots ,x_{kM}\right)$ for $M=2m+1$ by $x_1=1$, $x_{2j}=sinsin(2\pi j{t}_k/\delta )$, and $x_{2j+1}=coscos(2\pi j{t}_k/\delta )$, for $j=1,\dots ,m$. Then

$$mse\left(\beta ,\delta \right)=\frac{1}{n}\sum _{k=1}^n{\left(y_k-f_{\beta ,\delta }\left(t_k\right)\right)}^2=\frac{1}{n}\sum _{k=1}^n{\left(y_k-\beta \cdot x_k\right)}^2,$$

where $a\cdot b$ is the usual Euclidean dot product. This is the usual mean squared error formulation of simple linear regression. The minimizing $\beta$ is well known to be

$$\hat{\beta }\left(\delta \right)=mse\left(\beta ,\delta \right)={\left(x^{T}x\right)}^{-1}{x}^{T}y,$$

where $x$ is the $n\times M$ matrix with $k$th row $x_k$, where $y=(y_1,\dots ,y_n)$ is a column vector, and where the final expression uses standard notation for matrix transpose, inverse, and multiplication.

Period search

As described earlier in the methods we want to compute

$$T=argmi{n}_{\delta }mse\left(\hat{\beta }\left(\delta \right),\delta \right)$$

or, if we have $L$ simultaneously recorded channels, then we want to compute

$$T=argmi{n}_{\delta }\sum _{l=1}^{L}mse\left(\widehat{{\beta }_l}\left(\delta \right),\delta \right),$$

where $\widehat{{\beta }_l}\left(\delta \right)$ is the linear regression solution for the $l$th channel. We use Matlab’s fminsearch function (with the default parameters) which is an implementation of the Nelder-Mead simplex algorithm (Lagarias et al., 1998). The search requires an initial guess ${\delta }_0$. We use a complicated method to arrive at a good initial ${\delta }_0$.

Define the function

$$h\left(\beta \right)=\sum _{j=1}^{2m+1}{p}_j{\beta }_j^2$$

for $p_j=j/(2m^2+3m+1)$, which makes $p$ sum to one. The function $h$ serves as a penalty to express a preference for $\beta$’s that emphasize low frequencies, helping to avoid higher frequency ‘distractor’ solutions that mimic the harmonics of the true waveform (Figure S1A). Now define the function

$$F\left(\delta ,\lambda \right)=mse\left(\hat{\beta }\left(\delta \right),\delta \right)+\lambda h(\hat{\beta }\left(\delta \right))$$

or, for multiple channels,

$$F\left(\delta ,\lambda \right)=\sum _{l=1}^{L}mse\left(\widehat{{\beta }_l}\left(\delta \right),\delta \right)+\lambda h\left(\widehat{{\beta }_l}\left(\delta \right)\right).$$

An initial estimate for the stimulation period is made by dividing the sampling rate by the DBS stimulation frequency (e.g., 1.33 = 200 Hz sampling rate / 150 Hz stimulation rate). A grid of 201 points with a spacing of ${10}^{-4}$ and a grid of 201 points with a spacing of ${10}^{-5}$ are centered at this initial estimate. For each of these grid points $\delta$, we evaluate $F(\delta ,1)$ using $m=5$ and the $n=5000$ data points at the center of the recording. We select the five $\delta$ that give the lowest values of $F(\delta ,1)$ and use these as five separate initialization points for Matlab’s fminsearch function to minimize $F(\delta ,1)$. Of the five optimized $\delta$, we choose the one with smallest $F(\delta ,1)$. This $\delta$ becomes the new seed for a second stage of the search. The second stage is like the first, except that we build the grids around the new seed $\delta$. Also, the grids have spacings of ${10}^{-4}/2$ and ${10}^{-5}/2$, respectively, and we use $m=10$ and $n=10000$. The optimal $\delta$ found in the second stage is used to seed the third and final stage. Now the grids have spacings ${10}^{-4}/3$ and ${10}^{-5}/3$, respectively, and we use $m=20$ and $n=25000$. Also, the $n=25000$ data points are chosen uniformly at random (without replacement) from the recording. The final $\delta$ selected from this third stage is used as the initial starting point ${\delta }_0$ of the search described in the main text to obtain

$$T=argmi{n}_{\delta }F(\delta ,0)$$

with $m=20$ and with the same $n=25000$ datapoints from stage 3 of the search. Note that there is no penalty for spurious solutions in the final optimization.

We developed this search procedure in an ad hoc manner experimenting with several recordings of human LFP using the PC+S device and then found that it worked well across a variety of datasets and stimulation devices. Many of the choices and parameters are arbitrary and we have not carefully explored the effects of changing them. Visual inspection of the windowed data and how tightly it adheres to the resulting waveform makes it easy to verify if the procedure has worked properly. We are actively developing simpler and more robust period finding approaches that integrate more tightly with the PARRM filtering, but they will be described in future work.

Quantification and statistical analysis

Statistical details and software used for various types of data analyses in this work are cited in the appropriate sections in the STAR Methods. Briefly, all statistical tests were two-sided with α = 0.05. For the saline experiment, significant differences from baseline noise were estimated using a Wilcoxon-Rank Sum test. For the computational simulations, significant differences between each filtered signal and the artifact free signal (chirp without simulated DBS) at each frequency were computed using a 2-sample t-test.

Published: June 1, 2021