Behavioral and Neural Bases of Tactile Shape Discrimination Learning in Head-Fixed Mice

Jinho Kim; Andrew Erskine; Jonathan Andrew Cheung; Samuel Andrew Hires

doi:10.1016/j.neuron.2020.09.012

. Author manuscript; available in PMC: 2021 Dec 9.

Published in final edited form as: Neuron. 2020 Sep 30;108(5):953–967.e8. doi: 10.1016/j.neuron.2020.09.012

Behavioral and Neural Bases of Tactile Shape Discrimination Learning in Head-Fixed Mice

Jinho Kim ¹, Andrew Erskine ¹, Jonathan Andrew Cheung ¹, Samuel Andrew Hires ^1,^2,^*

PMCID: PMC8443268 NIHMSID: NIHMS1730970 PMID: 33002411

SUMMARY

Tactile shape recognition requires the perception of object surface angles. We investigate how neural representations of object angles are constructed from sensory input and how they reorganize across learning. Head-fixed mice learned to discriminate object angles by active exploration with one whisker. Calcium imaging of layers 2–4 of the barrel cortex revealed maps of object-angle tuning before and after learning. Three-dimensional whisker tracking demonstrated that the sensory input components that best discriminate angles (vertical bending and slide distance) also have the greatest influence on object-angle tuning. Despite the high turnover in active ensemble membership across learning, the population distribution of object-angle tuning preferences remained stable. Angle tuning sharpened, but only in neurons that preferred trained angles. This was correlated with a selective increase in the influence of the most task-relevant sensory component on object-angle tuning. These results show how discrimination training enhances stimulus selectivity in the primary somatosensory cortex while maintaining perceptual stability.

In Brief

Tactile shape recognition requires the perception of object surface angles. Kim et al. show how excitatory neurons in the primary somatosensory cortex construct object-angle representations from sensory input components. Task-relevant sensory components gain influence on object-angle tuning across angle discrimination training, coincident with selective sharpening of trained angle representations.

INTRODUCTION

Tactile recognition of the shape of objects is essential for skilled interactions with the world. Whether with hands (Gibson, 1962) or with whiskers (Carvell and Simons, 1990), active tactile shape perception involves purposeful interaction with objects in search of shape-relevant tactile features (Katz, 1925; Lederman and Klatzky, 1987). Interactions with these features cause deformation and stresses within the sensing tissue (Sripati et al., 2006; Whiteley et al., 2015), driving primary sensory afferent activity (Adrian and Zotterman, 1926; Coste et al., 2012; Furuta et al., 2020; Hensel and Boman, 1960; Severson et al., 2017; Zucker and Welker, 1969). From these patterns of actively gathered sensory input, the brain produces tactile perception, yielding rich internal representations of the external world (Bensmaia et al., 2008; Bodegård et al., 2001; Fitzgerald et al., 2004; Fortier-Poisson and Smith, 2016; Isett et al., 2018; Pruszynski and Johansson, 2014; Pubols and Leroy, 1977). How these representations are assembled from sensory input, organized within the cortex, and altered to meet behavioral demands is poorly understood.

A primary component of tactile shape recognition is perception of the local orientation angle of object surfaces. In humans, active exploration with individual fingertips provides sufficient information to perceive surface angles (Pont et al., 1999; Wijntjes et al., 2009). In mice, the means by which surface angles are determined with whiskers is unknown. It could require the integration of touch across multiple whiskers (Brown et al., 2020) via labeled line (Knutsen and Ahissar, 2009) or latency cues (Szwed et al., 2003). Alternatively, each whisker could function like a fingertip, providing sufficient information to perceive surface angles during active touch. The speed and accuracy with which mammals can identify complex shapes with whiskers (Anjum et al., 2006; Catania et al., 2008) suggest that each whisker conveys rich information about local object features, including horizontal (Cheung et al., 2019; Mehta et al., 2007) and radial location (Bagdasarian et al., 2013; Pammer et al., 2013; Solomon and Hartmann, 2011), texture (Jadhav et al., 2009), and surface angles. Here, we investigate how sensory components of single-whisker touch allow the discrimination of object angles.

For object features or sensory components to influence behavior, they must have neural correlates. Neurons in the primary somatosensory cortex (S1) of anesthetized rodents encode direction-specific responses to passive whisker deflections (Andermann and Moore, 2006; Bruno et al., 2003; Kremer et al., 2011; Kwon et al., 2018; Lavzin et al., 2012; Simons and Carvell, 1989). S1 activity is required for active object orientation discrimination with multiple whiskers (Brown et al., 2020). Thus, S1 is a likely location of the neural representations of object angles and underlying sensory input. We map representations of deflection direction and object angles in S1 of anesthetized and behaving mice. From this, we demonstrate how whisker features of passive and active touch construct object-angle tuning during active tactile sensing.

Representations of stimulus features in primary sensory cortices can change across association learning, although the nature of these changes varies across studies. Reports from chronic imaging across stimulus discrimination training show that the proportion of stimulus-selective neurons increases (Chen et al., 2015; Poort et al., 2015), the selectivity of individual neurons increases (Khan et al., 2018; Poort et al., 2015), or the representations remain stable (Peron et al., 2015). These differences may be due to variations in stimulus control or task design. Here, we identify which aspects of the cortical representations of stimulus features and sensory input are plastic and which are stable across discrimination training. This reveals how training reshapes both stimulus feature and sensory input encoding in a task-relevant manner.

RESULTS

Single Whiskers Provide Sufficient Tactile Information to Discriminate Surface Angles of Touched Objects

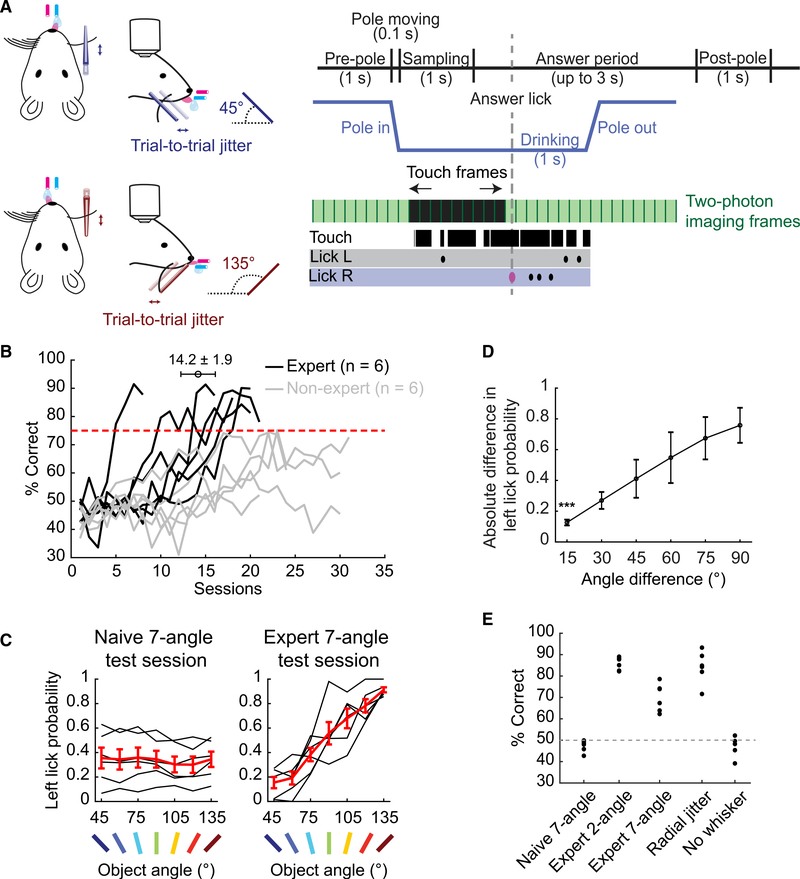
We hypothesized that active touch with a single whisker provides mice with sufficient information to discriminate the surface angles of touched objects. To test this hypothesis, we developed a novel lick left/right whisker-guided object-angle discrimination task. We trimmed mice to a single whisker (C2) and investigated whether they could learn to discriminate the angle of a smooth pole, randomly presented at 45° and 135° from the horizontal plane on an anteroposterior axis beside the face while head-fixed (Figure 1A). Mice were water-restricted for motivation. Following an object sampling period (1 s), correctly licking first to the right (45° object angle) or left (135°) port during an answer period (up to 3 s) released a small (2–4 μL) water reward (Figure S1A). The anteroposterior location of the pole was jittered (2 mm range) during every trial to ensure that mice were discriminating object angles, rather than detecting the presence of objects at a particular elevation or location.

Figure 1. — (A) Two-choice object-angle discrimination task design (left). Single trial example of touch, imaging, and licking (right).

(B) Learning curves. The error bar represents mean ± SEM number of sessions until mice become experts.

(C) Left lick probability in 7-angle test sessions, before (left) and after (right) learning. Black: individual mice. Red: means ± SEMs (n = 6 expert mice).

(D) Choice dependence on angle difference, in expert 7-angle test sessions. (n = 6; means ± SDs).

(E) Performance of expert mice at different experimental stages (n = 6).

See also Figure S1.

The behavior proceeded through acclimation, 2-angle training, 7-angle testing, and control stages based on the rate of progress of each mouse (Figure S1B). Operant aspects of the task were stable across training sessions (Figures S1C–S1F). Six of 12 mice reached expert performer criteria of >75% correct in 3 consecutive 2-angle training sessions (Figure 1B). Before and after training to expert level on 2-angle discrimination, mice were tested on a complementary 7-angle discrimination task to gauge their discrimination acuity (45°–135° at 15° increments, randomly presented). Water rewards matched the angle orientation of the 2-angle training (45°–75° right, 90° random, and 105°–135° left port). In the naive 7-angle test, mice performed at chance (Figure 1C). Two-angle expert mice performed at 70.0% ± 2.7% on the follow-up 7-angle test. Moreover, there was a significant difference in choice even for 15° angle differences (Figure 1D). This shows that head-fixed mice can discriminate object angles with a single whisker to at least 15° of precision without dedicated training in fine-angle discrimination. To exclude the possibility that mice used other unknown whisker-dependent cues on angle discrimination, we jittered the radial distance of the object within a 5-mm range for expert mice. This had no significant effect on 2-angle discrimination performance (Figure 1E). Finally, trimming the whisker caused performance to fall to chance in all of the mice across 3 days of whisker-free training, indicating that mice relied on whisker tactile stimuli to solve the task (Figure 1E).

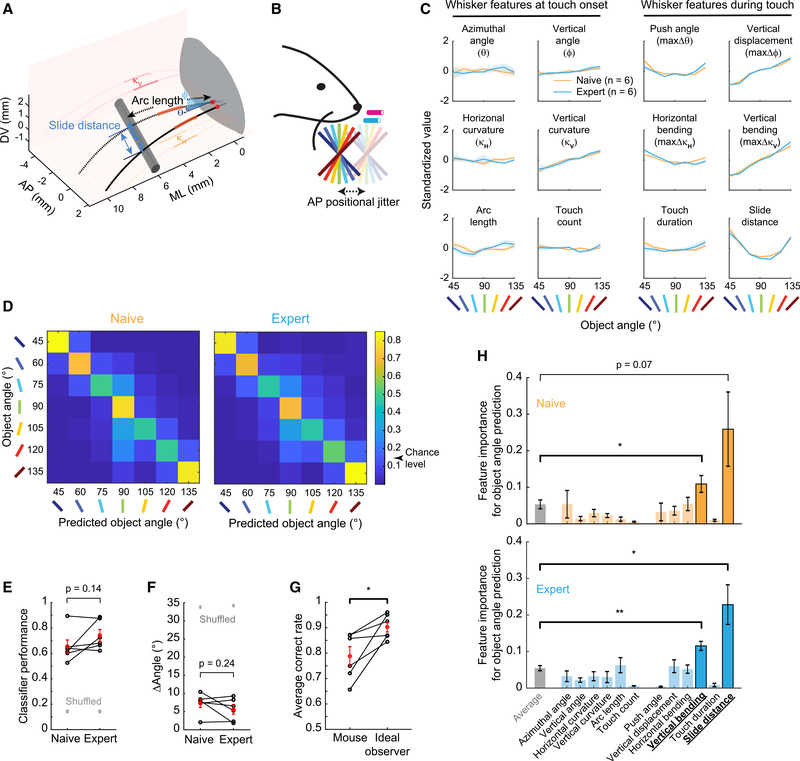
Which features of whisker-object interactions allow single whiskers to discriminate object angles? We recorded whisker motion and object interaction from 2 perspectives at 311 fps, traced both views, and generated 3-dimensional (3D) reconstructions of whisker trajectories (average error rate 1.0 ± 0.0 frames per trial; <0.08%) with semi-automated contact detection (Figures S2A–S2D; STAR Methods, Touch Frame Detection). From these reconstructions, we quantified 12 sensory features of whisker-object interactions during the 7-angle test sessions (Figures 2A, 2B, S2E, S2F; STAR Methods, Whisker Feature Analysis). These included 6 features of whisker motion at touch onset: azimuthal angle at base (θ), elevation angle at base (ϕ), horizontal curvature (κ_H), vertical curvature (κ_V), base-to-contact path distance (arc length), and touch count in a trial. These also included 6 force-generating features of whisker dynamics during touch: maximum change in azimuthal (push angle; maxΔθ) and elevation angle (vertical displacement; maxΔϕ), maximum change in horizontal (horizontal bending; maxΔκ_H) and vertical curvature (vertical bending; maxΔκ_V), slide distance along object, and touch duration during a protracting whisk (Figures 2A and 2C). Whisker features were selected from those encoded in S1 or the trigeminal ganglion (Hires et al., 2015; Peron et al., 2015; Ranganathan et al., 2018; Szwed et al., 2003, 2006) and their vertical or spatial counterparts. Whisker features at touch onset are used by mice to determine the horizontal location of objects (Cheung et al., 2019), but here they showed little relationship to the touched object angle (Figure 2C, left 2 columns). In contrast, most whisker features during touch co-varied with the object angle in both naive and expert sessions, suggesting a stable utility for discrimination (Figure 2C, right 2 columns).

Figure 2. — (A) Whisker features. Dotted: touch start. Solid: touch end. Red: whisker base points. Blue: contact points. AP, anteroposterior; DV, dorsoventral; ML, medio-lateral.

(B) Seven-angle test task.

(C) Standardized values of 12 whisker features across 7 angles before (orange) and after (cyan) training.

(D) Average performance of multinomial GLMs in predicting object angles from all whisker features, in naive (left) and expert (right) 7-angle test sessions.

(E) GLM object-angle prediction accuracy in naive and expert sessions. Black: each mouse. Red: means ± SEMs. Gray: shuffled angles.

(F) Angle prediction error as in (E).

(G) GLM-based ideal observers versus mice performance in expert 7-angle test sessions.

(H) Whisker feature importance in predicting object angles in 7-angle test sessions. Significant features highlighted.

Data are shown in means ± SEMs (n = 6). p values are from paired t tests.

See also Figure S2.

Do these 12 whisker features provide sufficient information to discriminate the object angle to 15° resolution? We built multinomial generalized linear models (GLMs) with lasso regularization to predict 7 object angles using all 12 trial-averaged whisker features as input parameters (STAR Methods, Whisker Feature Analysis – GLM). These GLMs correctly identified the presented object angles before (65.5% ± 5.2%) and after (74.2% ± 4.5%) task mastery (Figures 2D and 2E), compared to 14.3% correct in shuffled data. The average errors in angle prediction were 7.29° ± 1.15° and 5.57° ± 1.23°, respectively, compared to 33°–34° in shuffled data (Figure 2F). There was no significant difference in prediction capability between naive and expert test sessions (Figures 2E and 2F), confirming that the sensory input provided similar angle-discriminative information before and after training. Ideal observers using these model predictions to choose between lick right (predicted 45°–75°) and left (predicted 105°–135°) achieved 90.3% correct rate, which is significantly higher than the performance of mice on those angles in the expert test sessions (78.8% correct; Figures 2G and S2G). We conclude that these 12 features provide sufficient information to accurately discriminate object angles to at least 15°.

To identify the features that are the most important for discriminating object angles, we removed each feature and assessed the degradation in model fitting (fraction deviance explained; STAR Methods, Whisker Feature Analysis – Feature Importance) using the remaining 11 features (i.e., “leave-one-out”). This approach identified slide distance and vertical bending as the 2 most important features for object-angle prediction (Figure 2H). The relative importance of these 2 features remained in expert sessions (Figure 2H), further supporting the stability in sensory information content before and after 2-angle training.

Touch Evokes Object-Angle Representations in S1

The ability of mice to discriminate object angles with a single whisker (Figure 1) implies the existence of neural representations of touched object angles in the brain. Where are these found, and is specialized training required for them to emerge? To investigate this, we performed 2-photon volumetric calcium imaging with GCaMP6s in excitatory neurons of layers 2–4 (L2–4) of the barrel cortex (alternating blocks of 4 planes at 6–8 volumes/second) during naive 7-angle test sessions (n = 12 mice, average of 444 ± 49 active neurons in L2/3 C2, 821 ± 75 in L2/3 non-C2, 136 ± 32 in L4 C2, and 182 ± 38 in L4 non-C2 per mouse; TetO-GCaMP6s × CaMKIIα-tTA; STAR Methods, Two-Photon Microscopy). Imaging was targeted to the C2 whisker barrel column and surround via intrinsic signal imaging and calcium responses during passive deflection. We used suite2p (Pachitariu et al., 2017) for cell segmentation and neuropil correction and MLspike (Deneux et al., 2016) for spike inference. Active neurons were identified by region of interest (ROI) morphology and calcium trace kinetics (STAR Methods, Imaging Data Processing).

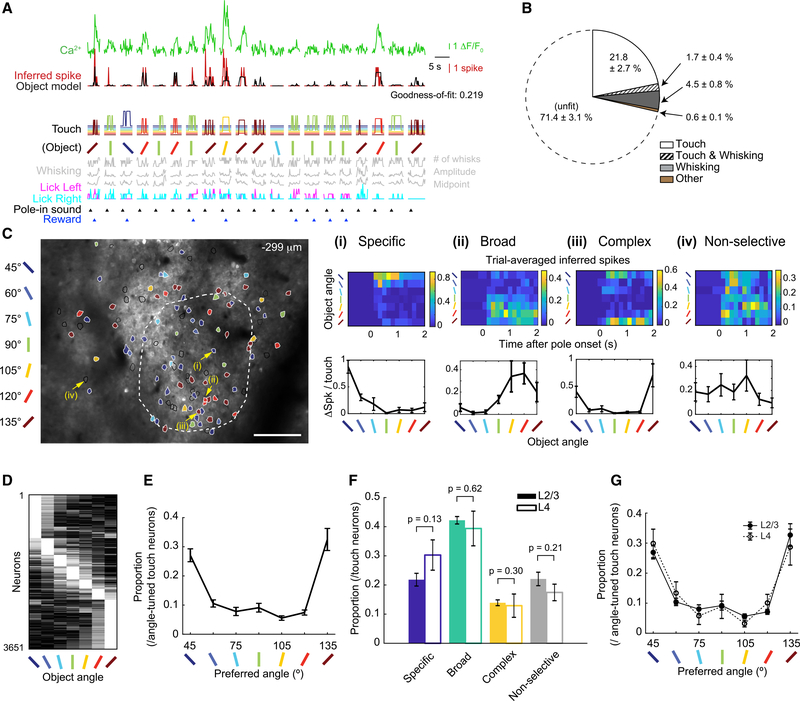
To identify touch-responsive neurons, we built an “object model”—a Poisson GLM with lasso regularization for each neuron that fit the inferred spike counts for each imaging frame in the session using 5 behavioral classes (i.e., touch, whisking [Figure S3A], licking, sound, and reward [Figure 3A]; STAR Methods, GLM for Neuronal Activity – ‘Object Model’). This model separated the effects of touch from non-touch classes on inferred spikes. Among the active neurons, 36.8% ± 3.3% were fit by the GLM (i.e., goodness-of-fit >0.1 for the whole session; Figure S3B). Each fit neuron was assigned 0, 1, or more classes based on a leave-one-out approach. Exclusively touch was the most common class among the fit neurons. Of all of the active neurons, 23.5% ± 2.8% were responsive to touch. Whisking and mixed touch and whisking made up most of the rest of the fit neurons, with <1% of active neurons well fit to licking, sound, or reward (Figure 3B).

We next tested the extent to which touch-responsive neurons encoded the angle of touched objects. Angle tuning was determined by one-way analysis of variance (ANOVA) of responses across angles, and confirmed by a shuffling test to minimize false positives (STAR Methods, Object-Angle Tuning Calculation). To prevent potential signal contamination from behavioral outcome (e.g., water rewards), calculations were restricted to touch frames before the first lick in the answer period (i.e., the answer lick). Among touch-responsive neurons, 78.0% ± 2.3% showed significantly greater touch-evoked activity in response to ≥1 object angles. These angle-tuned neurons were heterogeneously distributed across L2–4 within and around the primary barrel column (Figures 3C and S3C).

Angle-tuned responses fell into 4 types based on a post hoc test (Figure 3C): (1) specific (the preferred angle was significantly different from all others), (2) broad (≥2 adjacent angles were similar between themselves but significantly different from the rest), (3) complex (≥2 non-adjacent angles were similar between themselves but significantly different from the rest), and (4) non-selective (no response was significantly different from another). A substantial number of neurons were selective to each of the 7 angles, tiling the tested angle space (Figure 3D).

To confirm that angle tuning did not result from behavior classes other than touch, we compared the angle tuning preferences from inferred spikes to preferences calculated from the object model. The population distributions were nearly identical (Figures S3D and S3E). Angle tuning preferences from touch-only object models (removing behavioral classes other than touch from the model after fitting; STAR Methods, Object-Angle Tuning Calculation) were again nearly identical (Figures S3D and S3E) to those from inferred spikes, indicating that angle tuning preference was independent of neuronal responses to behaviors other than touch, such as whisking and licking.

Because L2/3 receives strong input from L4 (Hooks et al., 2011; Lefort et al., 2009), we hypothesized that there would be a greater proportion of complex angle-tuned neurons in L2/3 than in L4. To our surprise, there was no significant difference either in the relative proportion of specific, broad, complex, and non-selective angle tuning (Figure 3F; STAR Methods, Cortical Depth Estimation) or in the distribution of preferred angles across layers (Figure 3G). We confirmed these results in a pair of Scnn1a-Tg3-Cre mice that exclusively expressed GCaMP6s in L4 after injecting Cre-dependent GCaMP6s virus (LeMessurier et al., 2019; Madisen et al., 2015) (Figures S3F and S3G). We speculate that this homogeneity in tuning across layers may be particular to single-whisker tactile exploration as the lateral integration of touch information across multiple whiskers is not present.

Whisker Features That Best Discriminate Object Angles Also Best Drive Angle Tuning in S1

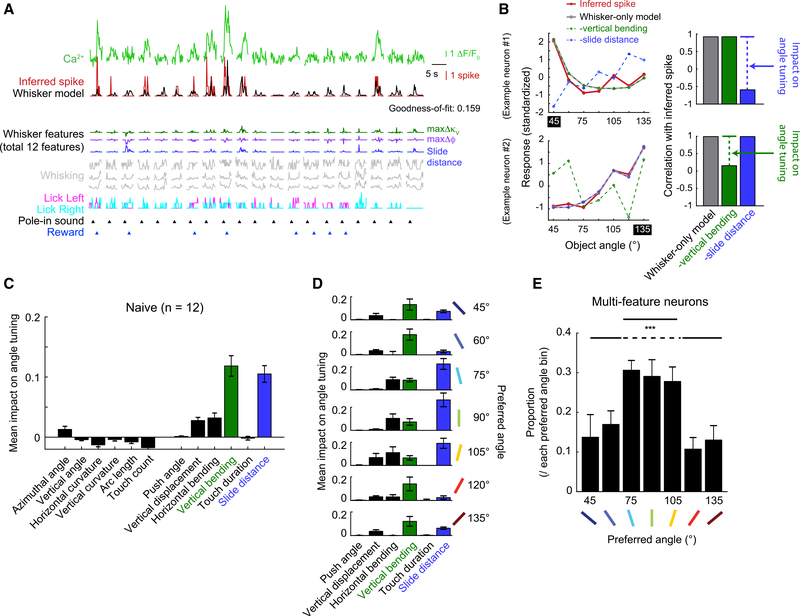
Our prior analysis showed that object-angle discriminability is most influenced by 2 tactile features, slide distance and vertical bending during touch (Figure 2H). We hypothesized that these 2 features would have the greatest influence on the object-angle-tuned responses found in S1. To test this hypothesis, we first built a “whisker model” for each touch-responsive neuron (Figure 4A) by swapping the touch input parameters of the object model (Figure 3A) with the 12 whisker features we previously used to predict the object angle (Figures 2C and 2D). These 2 models had performed similarly in fitting session-wide inferred spikes of touch-responsive neurons (Figure S4A), justifying using this whisker model for further analysis.

To quantify the impact of each whisker feature on angle tuning, we built angle tuning curves based on the output of the whisker model. On average, there was a high correlation (R = 0.78 ± 0.02) between angle tuning from inferred spikes and the whisker model (Figure S4B). Removing behavior classes other than whisker features from the model (i.e., whisker-only model) had a negligible impact on this correlation (R = 0.78 ± 0.02; Figure S4B), demonstrating that angle tuning is primarily constructed from these 12 whisker features. To determine the impact of each feature in establishing angle tuning, we calculated the reduction in correlation between observed angle tuning curves and these whisker-only model reconstructions when single whisker features were removed from the model. We highlight this process in 2 example neurons whose tuning was highly dependent on slide distance or vertical bending (Figure 4B). Across the population, whisker features during touch had much more influence than features at touch onset (Figure 4C). Reflecting their relative importance in the 7-angle classification (Figure 2H), vertical bending and slide distance had a greater average impact on angle tuning than any other feature (Figures 4C and S4C). We conclude that object-angle tuning in S1 primarily reflects the angle-discriminative features of whisker dynamics during object contact.

We examined whether a whisker feature’s impact on tuning was dependent on a neuron’s preferred object angle (Figure 4D). Vertical bending had a higher impact on angle tuning in neurons that preferred extreme angles. Slide distance had a higher impact on neurons preferring intermediate angles (75°–105°). Horizontal bending also emerged as an influential feature for these intermediate angles. Thus, the diversity of angle tuning preferences reflect an angle-specific relationship with whisker features.

Is each neuron sensitive to only 1 whisker feature, or do multiple features combine to create a higher-order representation of the external world? To answer this, we examined the number of whisker features that had a strong impact on angle tuning in each neuron. We defined strongly affecting features as those whose removal reduced the correlation between model and observed angle tuning curve by at least 0.1 (Figure S4D). Across the population, 67.5% of angle-tuned neurons had at least 1 whisker feature with a strong impact on angle tuning, 19.3% ± 0.9% of neurons had ≥2 features, and 5.1% had ≥3 features (Figure S4D). These multi-feature neurons were unevenly distributed across angle preferences. Neurons preferring intermediate angles (75°–105°) were more likely to be strongly affected by >1 whisker feature (Figure 4E). The proportion of multi-feature neurons was similar across layers (Figure S4E). We conclude that the diverse selectivity of S1 neurons for features of the external world (e.g., object angle) is established by the heterogeneous sampling of ≥1 features of sensory input (e.g., whisker features).

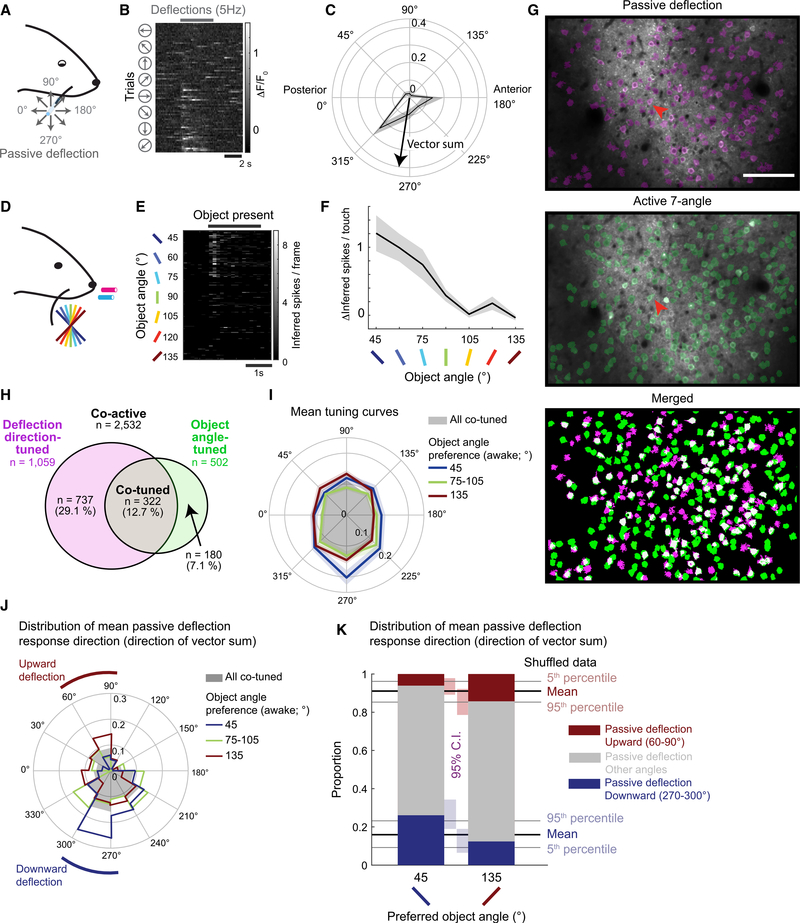
To what extent do active touch processes influence object-angle tuning? To address this question, we mapped calcium responses to passive whisker deflections in 8 directions under light isoflurane anesthesia (Figures 5A–5C) in 9 mice before their naive 7-angle active test sessions (Figures 5D–5F; 5.8 ± 4.3 days before; 72 planes from L2–4). Across all of the passive deflection-responsive neurons, the 8-angle vector sum of deflection responses was broadly distributed (Figure S5A). However, the average response to vertical deflections was 28.8% higher than horizontal deflections (Figure S5B), which is consistent with a recent report in L2/3 of S1 in mice (Kwon et al., 2018). In a subset of planes (37 planes over 9 mice), we were able to identify the same neurons in matched fields of view between the passive deflection sessions and naive 7-angle test sessions (Figure 5G). Of 2,532 neurons active in both sessions, 1,059 neurons (41.8%) were significantly tuned to the passive deflection direction, while 502 neurons (19.8%) were significantly tuned to the object angle (Figure 5H). Only 64.1% (322/502) of these object-angle-tuned neurons exhibited tuning to the deflection direction, while only 30.4% (322/1,059) of the deflection-direction-tuned neurons were also tuned to the object angle. The partial overlap between these 2 classes shows that tuning to the passive deflection direction is neither necessary nor sufficient to produce object-angle-tuned responses during active touch.

Figure 5. — (A) C2 whisker piezo deflection with glass capillary under light isoflurane anesthesia.

(B) Example neuron response to passive whisker deflection (red arrow in G), sorted by deflection direction.

(C) Passive deflection-direction tuning curve from (B). Means ± SEMs of ΔF/F₀.

(D) Active touch naive 7-angle test sessions.

(E) Neuronal response during active object touch, sorted by object angle. Same neuron as in (B).

(F) Object-angle tuning curve (means ± SEMs) from (E).

(G) Example FOV and overlaid ROI maps from matched anesthetized (top) and awake (center) experiments. The white neurons (bottom) are active in both sessions.

(H) Assortment of passive deflection-direction-tuned (magenta), active object-angle-tuned (green), and tuned in both sessions (co-tuned; gray), among all matched co-active neurons (white in G).

(I) Mean deflection-direction tuning curves of all co-tuned neurons (gray), overlaid with those preferring 45° (red), 75°–105° (green), or 135° (blue) object angle during naive 7-angle test sessions. Lighter colors are SEMs.

(J) Distribution of mean passive deflection response direction of all co-tuned neurons (gray), or preferring 45° (red), 75°–105° (green), or 135° (blue) object angle during naive 7-angle test sessions.

(K) Proportion of mean passive deflection response direction within neurons that preferred 45° or 135° object during naive 7-angle test sessions. Passive directions grouped by upward (60°–90°; red), downward (270°–300°; blue), and other directions (gray).

See also Figure S5.

Within co-tuned units, there was a weak relationship between the passive deflection direction and the object angle preference. The average response to downward deflections was slightly higher for neurons preferring the 45° object angle (Figure 5I). Similarly, 45°-preferring neurons had a tendency to prefer down and back passive deflections, while 135°-preferring neurons had a slight bias to up and back (Figures 5J, 5K, and S5C). This is consistent with the expected direction of forces applied during the active touch of those object angles. However, the relatively small magnitude of the bias and the diversity of passive deflection-direction preferences across object-angle tuning leads us to conclude that active processes during object angle discrimination profoundly reshape deflection-direction tuning preferences across the S1 population.

S1 Maintains Angle Tuning Preferences Despite Changes in Active Ensemble Membership across Training

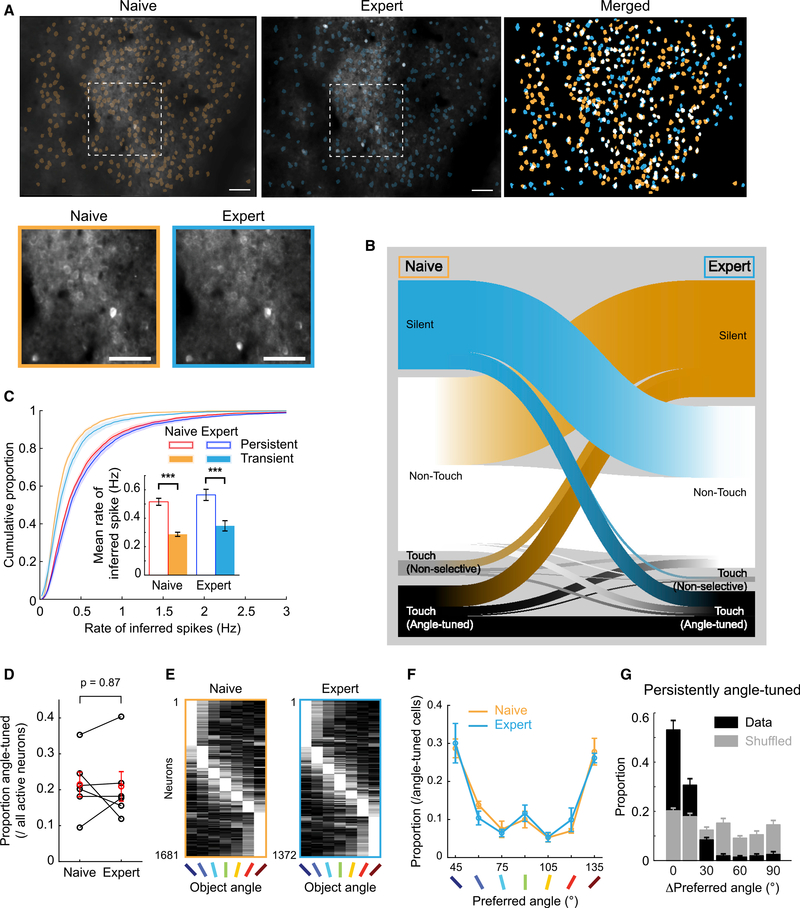
Mice improve discrimination task performance with training (Figure 1), and mice have a robust representation of object angles in S1 neurons (Figure 3). Discrimination performance could be enhanced by changes in the object angle representations in S1. However, primary sensory cortical representations may need to remain steady to support perceptual stability. We investigated the relationship between discrimination training and object angle representations in S1 by comparing the activity patterns of the same neurons in 7-angle test sessions before and after 2-angle discrimination training to expert performance (11,351 neurons from 6 mice with paired sessions separated by an average of 16 ± 2 sessions; Figures 6A and S6; STAR Methods, Matching Planes across Sessions).

The most prominent change was in the composition of the ensemble of active neurons during a session. Only 39.1% ± 3.8% of tracked neurons were active in both naive and expert sessions (i.e., persistent neurons; Figure 6B), with more superficial imaging planes showing slightly higher turnover than deeper planes (Figure S7A). The proportion of turnover was largely independent of touch-responsive category (i.e., non-touch, non-selective touch, angle-tuned touch; Figures S7B and S7C). Persistent neurons had significantly higher activity than transient neurons before and after training (Figure 6C).

Despite the high turnover rate, the proportion of active neurons that were angle tuned was stable (Figure 6D). There was also no significant change in the proportion of preferred object angles before and after training (Figures 6E and 6F). This was true in both L2/3 and L4 (Figure S7E) and for both for the transient and persistent populations (Figure S7F). Moreover, the persistently angle-tuned neurons had stable angle preferences, with 83.8% ± 1.7% changing their preferred angle ≤15° (Figure 6G). Thus, despite the high turnover of active ensemble membership, L2–4 of S1 provide a similar pool of object angle preferences to draw from, which could support perceptual stability with appropriate population sampling.

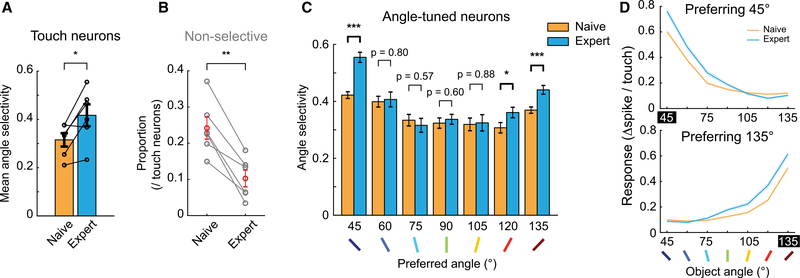
Angle Selectivity Increases in Neurons Tuned to Trained Object Angles

Were there any changes in the neural representations of object angles in S1 that could support improved discrimination performance? Across mice, the angle selectivity of touch neurons significantly increased following 2-angle training (Figure 7A). This was due, in part, to a significant reduction in the proportion of non-selective touch neurons in S1 (Figure 7B). A greater proportion of non-selective touch neurons became angle tuned with training than vice versa (Figure 6B). The selectivity increase was also seen in angle-tuned neurons, but only in neurons that preferred 45° or 135° (Figures 7C, 7D, and S7G). Thus, changes in object feature encoding were specific to trained angles, rather than a general sharpening of object-angle tuning.

Figure 7. — (A) Mean angle selectivity across training, from all touch-responsive neurons. Black circles: each mouse. Paired t test.

(B) Proportion of non-selective touch-responsive neurons across training. Black: each mouse; red: mean. Paired t test.

(C) Mean angle selectivity of neurons from naive versus expert sessions, respectively, binned by preferred object angle. Two-sample t tests (n = 492 and 409 in 45°, 239 and 150 in 60°, 111 and 91 in 75°, 139 and 143 in 90°, 107 and 74 in 105°, 122 and 156 in 120°, and 471 and 349 in 135°).

(D) Average object-angle tuning curves for naive and expert sessions, for neurons preferring 45° and 135°.

Data are shown in means ± SEMs.

See also Figure S7.

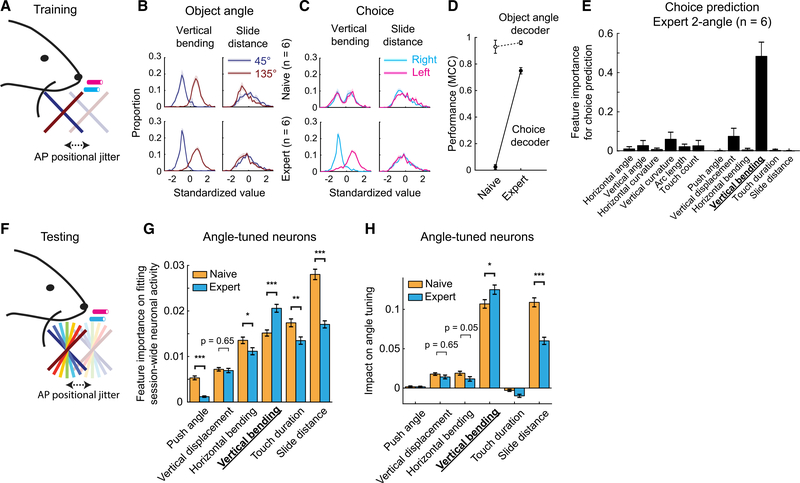
How was this sharpening in angle tuning achieved? Since object angles can be discriminated by whisker features (Figure 2), and they are used to create object-angle tuning in S1 neurons (Figure 4), we suspected that 2-angle discrimination training (Figure 8A) may change the encoding of whisker features in S1. During 2-angle training, vertical bending had distinct distributions for 45° and 135° trials, while slide distance did not (Figure 8B). After training, vertical bending discriminated choice on 2-angle sessions, while slide distance did not (Figure 8C). We built binomial GLMs to predict either object angles or choice from all 12 whisker features. As expected from the 7-angle prediction (Figures 2D-E), object angles could be well predicted from these 12 whisker features before and after training (Figure 8D). However, choice could be predicted only in expert sessions (Figure 8D), reflecting the learned association between object angles and choices after training. Using leave-one-out methods, we found that vertical bending was the dominant choice-predictive feature in expert 2-angle training sessions (Figure 8E). This remained true in choice prediction in expert 7-angle test sessions (Figure S8A), suggesting that mice applied the same discrimination rule learned in training to those test sessions. Thus, while both slide distance and vertical bending were useful for 7-angle decoding (Figures 2C, H) and neuronal tuning (Figure 4C), only 1 of those features, vertical bending, was relevant to the trained task.

The relevance of whisker features for 2-angle discrimination (Figure 8B) was correlated to training-related changes in their encoding during 7-angle test sessions (Figure 8F). Training significantly increased the importance of vertical bending in predicting inferred spike trains of 7-angle test sessions, and significantly decreased the importance of slide distance (Figures 8G and S8B). It also significantly increased the impact of vertical bending on angle tuning, while significantly reducing the impact of slide distance (Figures 8H and S8C). Finally, training also increased the proportion of neurons where vertical bending had a major impact on angle tuning, while decreasing the proportion of slide distance (Figures S8D and S8E). We conclude that discrimination training selectively enhanced the cortical representation of task-relevant features of sensory input while degrading the representation of task-irrelevant features, resulting in improved neural selectivity for trained stimuli that persisted in related discrimination tasks.

DISCUSSION

Calcium imaging allowed us to observe the reorganization of neural representations of object angles and sensory features across weeks of training. However, this approach has limitations. Whisker dynamics and single touch responses in S1, particularly L4, are much faster than the indicator decay rate and imaging volume rate (Chen et al., 2013; Hires et al., 2015). This limits our mapping to a “rate code” for object angle and sensory features averaged across touches, while spike timing and synchrony could also play significant roles in driving perception and behavior (Zuo et al., 2015). We used a GCaMP6s mouse line (Wekselblatt et al., 2016) that has high single-spike SNR, low ΔF/F₀ variability, and a linear relationship in calcium response to 1–4 action potentials within a 200-ms window in vivo (Huang et al., 2020), which is well suited for the observed firing rates of excitatory neurons in L2–4 of S1 during active touch (Hires et al., 2015; O’Connor et al., 2010). However, GCaMP6s is dim in the absence of activity, so determining whether a neuron fell silent or simply went out of focus required corroborating evidence. Our matched depth and optical sectioning calibration (Figure S6), inferred spikes per session distribution (Figure S7D), and consistency with prior reports of turnover (Chen et al., 2015; Gonzalez et al., 2019; Ziv et al., 2013) support that our observed turnover in active ensemble membership across training reflects true changes in population activity.

One of our goals was to investigate how object feature and sensory input encoding changes during stimulus-reward association learning. Possible confounders include activity changes due to operant learning or motor strategy refinement and shifts in reward anticipation or attention across training. We controlled for operant learning by stepwise training (Figure S1B), mapping neural responses only after operant task components were solidified (Figures S1D–S1F). In contrast to prior tactile tasks (Chen et al., 2015; Peron et al., 2015), object-angle discrimination resulted in stable motor engagement and gathering of sensory information before and after training (Figure 2). Compared to go/no-go tasks (Chen et al., 2015; Khan et al., 2018; Poort et al., 2015), our 2-choice task balanced reward anticipation across the presented stimuli and disambiguated choice from attentional lapses. In this context, the proportion of active neurons that discriminated task-relevant object features was stable across training (Figure 6D), consistent with Peron et al. (2015), but in contrast to Chen et al. (2015), Khan et al. (2018), and Poort et al. (2015). Training on 2-angle discrimination while testing on 7-angles revealed that increased neural selectivity to the trained stimulus feature (Khan et al., 2018; Poort et al., 2015) was specific to the stimuli presented during training (45° and 135°), and did not generalize across stimulus feature class (object angle; Figure 7C). Tracking how these changes are distributed across S1 neurons that target different brain regions (Chen et al., 2015; Yamashita and Petersen, 2016) across phases of learning could reveal distinct circuit mechanisms for refining shape perception and tactile-guided behaviors.

How is representational stability maintained in the face of active ensemble turnover (Figure 6)? The simplest explanation is that the neurons in S1 maintain object feature preferences across learning, independent of active ensemble participation. This would be consistent with primary visual cortex neurons maintaining stimulus selectivity before and after monocular deprivation (Rose et al., 2016) and CA1 neurons maintaining place preference across weeks despite variation in active ensemble participation (Ziv et al., 2013; Gonzalez et al., 2019). This possibility is supported by the remarkable stability of angle preference in persistently angle-tuned neurons (Figure 6G). The combination of active ensemble variability with stable object preference could reflect the changing intrinsic excitability of excitatory neurons (Barth et al., 2004; Desai et al., 1999; Yiu et al., 2014) or local inhibitory networks that enforce firing rate homeostasis (Dehorter et al., 2015; Gainey et al., 2018; Goldberg et al., 2008). As long as population tuning preferences remain stable (Figures 6E–6G), changes in activity may average out and allow downstream neurons to maintain consistent selectivity.

Why were 45° and 135° overrepresented in the S1 population tuning? Preferred angle distributions were unaffected by 2-angle training, so the overrepresentation does not reflect a preference shift toward reward-predictive stimuli. It is possible that all angles 0°–180° are equally represented, with <45° and >135° pooled into the 2 most extreme bins, or deflections out of the plane of whisking and body movement could be more likely to represent behaviorally relevant objects. The significantly larger average responses and bias in preferred directions to vertical compared to horizontal passive deflections (Figures 5I, S5A, and S5B) provide some support for this possibility. Combining this weak directional bias in passive tuning with active touch processes, such as sticking and slipping along the pole (Huet and Hartmann, 2016; Isett et al., 2018), could further increase the prevalence of tuning to extreme angles, since they are associated with the longest slide distances (Figure 2C).

Tactile shape perception is normally accomplished by the simultaneous touch of multiple digits or whiskers along a contour during free exploration. To understand tactile 3D shape perception requires knowing the capability and limitations of single touch sensors in local surface perception and how they are encoded in the brain. Humans can perceive surface angles with single fingertips (Pont et al., 1999; Wijntjes et al., 2009). However, the central representations of surface angles remain unknown. We show that mice are also able to discriminate surface angles with single whiskers and map the S1 representations involved in this perceptual process. However, important questions remain. Whether the spatial pattern of follicle strain and mechanosensor activation evoked by whisker motion and bending is sufficient to explain the S1 representation, or if efference copy also shapes it remains to be explored. A comprehensive understanding of tactile 3D shape representation and perception will require investigating how signals from multiple whiskers are integrated in S1 and beyond, as well as the identification of where and how body orientation invariant shape representations emerge.

STAR★METHODS

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Samuel Andrew Hires (shires@usc.edu).

Materials Availability

This study did not generate new unique reagents.

Data and Code Availability

The datasets generated during this study and code used to analyze data and generate figures are available at https://github.com/hireslab/Pub_S1AngleCode.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Animals

We used 2–4 months old male (n = 4) and female (n = 8) CaMKII-tTA × tetO-GCaMP6s mice (#007004 and #024742, respectively; The Jackson Laboratory), and 2 male Scnn1a-Cre mice (#009613; The Jackson Laboratory). Mice were maintained on a 12:12 reversed light:dark cycle. Six mice were singly housed after surgery due to the incompatibility with cage mates. After water restriction, health status was assessed every day following a previously reported guideline (Guo et al., 2014). All procedures were performed in accordance with the University of Southern California Institutional Animal Care and Use Committee Protocol 20731.

METHOD DETAILS

Cranial window surgeries

Before each surgery, buprenorphine-SR and ketoprofen were injected subcutaneously at 0.5 and 5 mg/kg, respectively. Animals were anesthetized using isoflurane (3% induction, 1%–1.5% maintenance). On the first surgery, a straight head bar was attached on the skull. We performed intrinsic optical signal imaging (ISI) of the C2 whisker representation using a piezo stimulator and 635 nm LED light under light isoflurane anesthesia (0.8 – 1.0%) at least 3 days after the surgery. All whiskers except C2 were trimmed before ISI and remained trimmed throughout the experiments. On the second surgery, a 2 × 2 mm square of skull centered at C2 location was removed and replaced by a glass window which was made by fusing a 2 × 2 mm glass and a 3 × 3 mm glass (both 0.13–0.17 mm thickness) with ultraviolet curing glue (Norland optical adhesive 61, Norland Inc.). We confirmed C2 location about 3 days after the cranial window surgery with a second ISI session. Water restriction started 3–10 days after the second ISI.

Virus injections

In 3 male and 1 female CaMKII-tTA × tetO-GCaMP6s mice, AAV1-CaMKIIα0.4-NLS-tdTomato-WPRE (custom made by Vigene Biosciences, MD, USA) was injected during the cranial window procedure. For Scnn1a-Cre mice, AAV1-Syn-Flex-GCaMP6s-WPRE-SV40 (a gift from Douglas Kim & GENIE Project (Addgene viral prep # 100845-AAV1; http://addgene.org/100845; RRID: Addgene_100845)) was injected. We pulled a glass capillary (Wiretrol® II, Drummond) into 10–20 μm in tip diameter using a micropipette puller (Model P-97, Sutter Instrument), and beveled the tip to about 30°. After filling the capillary with mineral oil (M5904, Sigma-Aldrich), we withdrew virus solution (titrated to 10¹² GC/mL using 0.001% Pluronic F-68 in saline) from the tip using a plunger. Care was taken not to introduce an air gap between mineral oil and virus solution. We injected virus solution at the 4 corners of a 200 μm square whose center matched to that of identified C2 region, 50 nL per site over 5 min. We waited for 2 min after each virus injection before withdrawing. Depth of the pipette tip was 400 μm for Scnn1a-Cre mice, and 200 and 400 μm for others.

Behavioral task

We developed a 2-choice task for object surface angle discrimination with a single whisker (Figures 1 and S1). In the 2-angle training sessions, a smooth black pole with 0.6 mm diameter (a plunger for glass capillary, Wiretrol® II, painted with black lubricant, industrial graphite dry lubricant, the B’laster Corp.) was presented in each trial on the right side of a head-fixed mouse, coming from the front, with an angle of either 45° or 135°. The pole was positioned 5–8 mm laterally from the face. The lateral distance from the face was kept consistent within a mouse across sessions, except for “Radial jitter” sessions, where it varied 0–5 mm more lateral from the trained position. The rotation axis of the pole was orthogonal to the body axis in the horizontal plane, and the angle was rotated in the sagittal plane such that 45° (pointing caudal) made the whisker move down upon protracting sliding touch, while 135° (pointing rostral) made it go up (Figure 1A). Mice were given 3–4 μl of water reward for correct trials (i.e., when they licked the right lick port for 45° and left for 135°). The amount of water reward was adjusted to target 600 trials performed per session (553 ± 147 trials, mean ± SD). Wrong answers were not punished, except for a few sessions of impulsive licking (5.3 ± 3.1 sessions in 4 mice, mean ± SD). In these sessions we punished mice with 2 s time-outs for wrong answers. The time-out could be re-triggered by additional licks during this time-out period. Pole presentation was followed by a 1 s sampling period, where licking was ignored, and then a 3 s answer period, where licking triggered trial outcome. The pole retracted 1 s after an answer lick, defined as the first lick during the answer period time. The behavioral task was controlled and time-synced by MATLAB-based BControl software (C. Brody, Princeton University). Pole rotation was controlled using an Arduino and a micro servo (SG92R, TowerPro), and planar pole position was controlled by a set of 2 motorized actuators (Zaber), each moving in anterior-posterior axis and medio-lateral axis, respectively. The pole was presented using a pneumatic slide (Festo).

We trained mice in a stepwise manner to control for operant learning (Figures S1B–S1F). After 7–10 days of water restriction, we confirmed C2 location and defined imaging field-of-view (FOV) and planes (below, Two-Photon Microscopy section). We then acclimated mice to head fixation and water reward from a lick port. After 1–3 days, each mouse underwent 1–2 days of sound cue-pole-water reward association training (“Pole timing” sessions). A piezo sound cue was given at the beginning of each trial, and water reward was given upon mouse’s licking 1 s after the pole presentation. At this training point, a single lick port was present at the center, and the angle of the pole was 90°. Chronic two-photon imaging started from this session (reference FOV from this session; see Matching Planes across Sessions (Figure S6)). Once they learned the structure of task and reward timing (<5% of miss trials in more than 100 consecutive trials; up to 2 sessions), we introduced 2 lick ports (separated by 3 mm). Learning rates (Figure 1B) were measured from this session.

To reduce biased licking to one side of the lick ports, we varied the probability of each pole presentation based on correct rate history. Consecutive same-angle presentation was limited to 5 times. We introduced 0–2 mm of jitter in anterior-posterior pole position to prevent solving the task by the presence of the pole at specific spatial coordinates. The pole was presented near the coronal plane of the C2 whisker base. We adjusted pole height in each mouse depending on their whisking geometry to approximately center the distribution of touch points to 0° whisker azimuth.

Mice were deemed experts when their performance surpassed 75% correct rate for 3 consecutive sessions. Miss trials (11.7 ± 10.8%, mean ± SD) were ignored for performance calculations, but included in other analyses (for object-angle tuning and whisker feature encoding). Before and after learning, we tested discrimination and angle tuning representations with varying object angles, 45° to 135° at 15° intervals (7-angle sessions, Figures 1C and S1B). The 90° pole was randomly rewarded. In these test sessions, we used pseudo-random pole presentations, to evenly distribute the number of trials in each object angle.

Whisker video recording and tracking

We used a CMOS camera (Basler acA800–500um), a telecentric lens (0.09X½” GoldTL™ #58–259, Edmund optics), a mirror and an LED backlight to simultaneously image both front- and top-views of the whisker (Figures S2A and S2B). The mirror was tilted in two axes: 45° relative to the horizontal plane to capture top-down view (Figure S2B), and 13.3° relative to the coronal plane to capture the whole whisker in front view (Figure S2A). The latter is corresponding to the angle between mouse’s face and body axis. We removed hair from right side face and upper front trunk to prevent hair from blocking front view whisker, using a hair removal lotion (Magic razorless cream shave, Softsheen-Carson). We recorded whisker motion using StreamPix software (NorPix Inc.), and used BControl and Ardunio to trigger the camera in 311 Hz (about 10× of two-photon resonance imaging frequency of a single plane).

We used the MATLAB version of Janelia whisker tracker (Clack et al., 2012) to track the whisker. We masked whiskers 1 mm from the face to minimize tracking errors near the face (Pammer et al., 2013), both in front and top-down views. Based on the property of telecentric lens and the geometric relationship of two views, we could reconstruct 3D whisker shape. The reference points to match the two views were whisker base points, which are the intersections between the whisker and the face mask in each view. In each frame, we visited each point of top-down view whisker trace, and matched the corresponding point in the front view based on the tilt angle of the mirror, resulting in 3D Cartesian coordinates (Figure S2C). Touch point, arc length along the whisker from the mask to the touch point, and whisker curvature at 3 mm along the whisker from the mask were calculated after 3D reconstruction.

Touch frame detection

Touch detection on a vertical pole (90°) can be accomplished from pole-to-whisker distance and whisker curvature with semi-automated (Pammer et al., 2013) or automated (Severson et al., 2017) curation. This method cannot be applied for angled poles, however, because the shadow of the angled pole precludes pole-to-whisker distance calculation. Therefore, we devised a new analytic method for detecting touch frames from simultaneous 2-view whisker videography.

Non-touch frames can be detected based on the two view frame-by-frame changes in whisker position relative to the pole angle, using constraints imposed by pole geometry. For example, when the pole is tilted at 45° angle (Figure 1A; blue pole), if the whisker-pole intersection point moves back at the top-view and does not go up at the front view, one can be sure the whisker is not in contact with the pole at the latter frame. If the whisker-pole intersection point moves up at the front view, it is not determined from the video.

To visualize this concept, we defined 2 artificial axes from the whisker video: one (x) along the top-view pole edge and the other (y) along the front-view pole edge (Figure S2D). Origins of each axis could be defined at any arbitrary points along each pole edge, and we defined them at the edges of the image. For each frame we calculated the intersection point between the whisker and the pole edge as an (x,y,z) triple, where x equals the intersection between whisker trace and pole edge along the pole axis in the top-view, y is the equivalent for the front-view, and z is the position of pole base. Plotting the (x,y,z) intersection point for each frame of the same presented object angle in the session revealed an empty space corresponding to the pole (Figure S2D, red arrow) flanked by two dense parallel hyperplanes (‘touch planes’) produced by protraction (touching the rear side of the pole) or retraction touch (touching the front side of the pole). Frames where the intersection point (x,y,z) fell upon either ‘touch planes’ were candidate touch frames. The touch plane orientation was calculated by finding the two angles which maximized the variance in the location of the projection of all intersection points onto a rotating hyperplane, using Radon transform twice sequentially. The plane was then translated in its orthogonal direction to maximize the number of intersection points that fell within the plane.

We verified this approach by comparing the touch frame detection between our method and two-dimensional whisker tracking from the top-view of the 90° pole. The overall match was 98.21 ± 0.92% of touch frames, 0.50 ± 0.21% false positive, 1.28 ± 0.85% false negative, with 1.43 ± 0.57 frames of touch onset error and 1.45 ± 0.56 frames of touch offset error (mean ± SD, n = 5).

Whisker feature analysis

We investigated which whisker variables (i.e., sensory input components), among 12 whisker features listed in the Results section, might have influenced mice to discriminate the pole angle and to decide which side to lick.

The definition and calculation of each whisker feature (Figures 2A–2C) is as follows:

Azimuthal angle at base (θ; in °): The angle of whisker at base compared to the mediolateral axis, when looked down at from the top. Whisker at base is where the whisker intersects with the face mask. Positive value means more protracted.
Vertical angle at base (φ; in °): The angle of whisker at base compared to the mediolateral axis, when looked back at from the front. Positive value means higher, more dorsal position.
Horizontal curvature (κ_H; in mm⁻¹): Curvature of top-down projected whisker shape, at 3 mm away from the whisker base along the 3D shape of the whisker. Negative value means that the apex of the curve is pointing anterior.
Vertical curvature (κ_V; in mm⁻¹): Curvature of the whisker at × mm away from the whisker base along the 3D shape of the whisker, when looked back from the front at the angle of θ, i.e., the plane of the whisker projection is parallel to the azimuthal angle at follicle (θ). We used this projected shape of whisker to calculate κ_V. Positive value means the apex of the curve is pointing upward.
Arc length (in mm): Length of the whisker segment between the whisker base and the whisker-pole intersection point.
Touch count (number of protraction touches in a trial, for behavior analyses in Figures 2 and 8; number of protraction touches in a frame, for fitting neural activity): In the rare case of multiple protraction whisks while in continuous contact with the pole, each whisk was as a protraction touch. A protraction whisk is defined by a whisk of amplitude >2.5° (See ‘active whisking’ in section GLM for Neuronal Activity - ‘Object Model’).
Push angle (maximum change in azimuthal angle; maxΔθ; in °): max(θ(t) - θ(0)), where θ(0) means θ at touch onset, and θ(t) means θ during each ‘protraction touch’ frame at time t. The value is always positive because of the definition of ‘protraction touch’.
Vertical displacement (maximum change in elevation angle; maxΔφ; in °): sign(φ(t_max) - φ(0)) X max(|φ(t) − 4(0)|), where sign(φ(t) - φ(0)) means the sign of φ at each frame during ‘protraction touch’ at time t minus φ at touch onset, and t_max means the time point t where |φ(t) - φ(0)| was at the maximum. The value can be either positive (when whisker went up) or negative (when whisker went down). We first calculated the absolute value of difference between φ at each frame and touch onset. Then we took the maximum absolute value multiplied by its corresponding sign.
Horizontal bending (maximum change in horizontal curvature; maxΔκ_H; in mm⁻¹): max(κ_H(t) - κ_H (0)). Values are negative during ‘protraction touch’, with rare exceptions.
Vertical bending (maximum change in vertical curvature; maxΔκ_V; in mm⁻¹): sign(κ_V(t_max) - κ_V(0)) X max(| κ_V(t) - κ_V(0)|). Values can be both positive and negative.
Slide distance (distance slid along the object during a protracting whisk; in mm): Travel distance along the object from the onset of touch to the peak of the protraction whisking during each ‘protraction touch’. The onset of touch is defined at each protraction touch.
Touch duration (time spent touching object during a protracting whisk; in s): Duration of each ‘protraction touch’.

Whisker feature analysis – GLM

We built either binomial (for choice and 2-angle prediction) or multinomial (7-angle prediction) generalized linear model (GLM) with lasso regularization (0.95 alpha of elastic-net, to make the model behave similarly to lasso while preventing wild behavior with if input variables are highly correlated; Friedman et al., 2010; Runyan et al., 2017), using standardized 12 whisker features as input parameters and either choice or object angle as the target. We used the MATLAB version of glmnet (Friedman et al., 2010). For each session, the model was trained on 70% of randomly selected trials. Training data was stratified based on target feature (choice or object angle). The regularization parameter of the elastic-net was calculated in 5-fold cross-validation, and the model performance was tested in the remaining 30% of trials.

We iterated this procedure 10 times to reduce errors from random assignment in the training set (reasoning and validation of this iteration are noted in the calcium imaging analysis section below). We averaged coefficients from 10 iterations for the final model.

For binomial models, we used Matthew’s correlation coefficient (MCC) as a performance measure to prevent effects from unequal samples (Figure 8D). For multinomial models (Figures 2D and 3E), the performance was measured by the averaged correct rate of prediction across object angles after bootstrapping (sampling with replacement) 100 samples per presented object angle. We averaged performance from 10,000 bootstrapping per mouse, and calculated shuffled data performance from bootstrapping after randomly permuting presented object angles (average from 10,000 processes). Differences between presented and predicted object angles were calculated from the same bootstrapping and shuffled data (Figure 2F).

Whisker feature analysis - Feature importance

We calculated variable importance by comparing ‘leave-one-out’ models to the ‘full model’. A ‘full model’ is a GLM using all 12 features. From this trained ‘full model’, removing one feature without retraining (equivalently, setting the corresponding coefficient to 0) results in a ‘leave-one-out’ model. When comparing ‘leave-out-out’ models to the ‘full model’, we used fraction deviance explained (%DE; Agresti, 2013), a generalized version of fraction variance explained for exponential family regression models. The reduction in %DE in each ‘leave-one-out’ model from the ‘full model’ is defined as feature importance. A feature that leads to larger reduction in % DE has higher impact on the ‘full model’ compared to the ones that lead to smaller reduction. This method is similar to methods of shuffling each feature in the trained model (Breiman, 2001a, 2001b; Fisher et al., 2019), but prevents random effects of shuffling which can lead to enhanced false negative results. The overall results were not affected by changing the model approach from feature removal to feature shuffling.

Two-photon microscopy

We used a two-photon microscope (Neurolabware) which consists of a Pockels cell (350–105-02 KD*P EO modulator, Conoptics), a galvanometer scanner (6215H, Cambridge Technology), a resonant scanner (CRS8, Cambridge Technology), an objective (W Plan-Apochromat 20×/1.0, Zeiss), a 510 nm emission filter (FF01–510/84–50, Semrock), and a GaAsP photomultiplier tube (H10770B-40, Hamamatsu). We used 80 MHz 940 nm laser (Insight DS+, Spectra-Physics) for GCaMP6s excitation. The scope was controlled by a MATLAB-based software Scanbox with custom modifications. In each session, we took interleaved volumetric calcium imaging to cover L2/3 to L4 (100–450 μm from pia), using an electrically tunable lens (ETL; EL-10–30-TC-NIR-12D, Optotune). Each volumetric imaging consisted of 4 planes, either 44 or 53 μm apart, spanning 131 (4 mice) or 165 μm (8 mice), respectively. Resulting imaging frequency was 6.07 (4 mice) or 7.72 (8 mice) volumes per second depending on the size of the FOV (650 × 796 or 512 × 796). Pixel resolution was either 0.7 (4 mice) or 0.82 μm (8 mice) per pixel. Laser power was controlled at each plane respectively. Every 5 trials, we alternated the objective position to cover another volume. Average power after the objective was about 70 mW for upper volume and 150 mW for lower volume. To further reduce heating (Podgorski and Ranganathan, 2016), we blanked the laser between trials with inter-trial interval of 3 s, which resulted in average duty cycle of about 60%.

To confirm C2 location, we imaged at around 400 μm depth while stimulating the C2 whisker using a piezo actuator in mice anesthetized with 0.7%–1.0% isoflurane. Stimulation consisted of 4 s of 5 Hz, with inter-trial interval of 10 s. Subtracting averaged GCaMP6s signal during baseline (3 s before stimulation) from that during stimulation gave a clear C2 region.

Imaging data processing

We used Suite2p (Pachitariu et al., 2017) for cell region-of-interest (ROI) selection and calcium trace extraction, and MLspike (Deneux et al., 2016) for spike deconvolution. Neuropil signal was subtracted by a lower value between the coefficients of 0.7 or minimum value of soma signal divided by neuropil signal, to prevent negative signal (Pluta et al., 2017). Baseline fluorescence (F₀) was calculated by the 5^th percentile of 100 s of rolling window (600–780 frames over about 8000 frames in total; Sofroniew et al., 2015). Active cells were further classified as those having 95^th percentile of ΔF/F₀ larger than 0.3. One action potential value for MLspike was set to 0.3 as well (Chen et al., 2013; Sofroniew et al., 2015). No ROI which had neuron-like morphology and at least 1 observed inferred spike failed to pass this activity criteria. The noise parameter for MLspike was calculated as a standard deviation of a ‘no signal’ period. ‘No signal’ periods were reconstructed from concatenating 5-frames sliding windows having standard deviation less than 5^th percentile from the session, allowing overlap.

For analyzing imaging data from passive whisker deflection experiments under light anesthesia (Figure 5), we used ΔF/F₀ for analysis because there were no confounding effects from behavior. In this case, F₀ was calculated as a median of 10 s rolling window. ROIs were manually selected based on morphology and fluorescence traces calculated by Suite2p.

GLM for neuronal activity - ‘Object model’

We used Poisson GLM with lasso regularization (elastic net with 0.95 alpha) to fit inferred spikes of each neuron using 5 classes of behavior (Figure 3A). The definitions, calculation methods, and reasoning of parameter setting of these classes are as follows:

Touch: We used a binary vector of touch frames as touch parameter. Touch is further divided into 8 groups – 7 for each angle and 1 for all angles. This input (predictor) had 0–2 frame delays. Including more than 2 delays did not improve the fitting. Positive delay means spike events followed touch events. A model using binary touch performed better at fitting than using touch duration or touch count in each frame. Total number of touch predictors was 8 × 3 = 24.
Whisking: We used 3 parameters for whisking – number of whisks, whisking amplitude, and midpoint (Figure S3A, right bottom). Amplitude is defined by q span within a whisking cycle, and midpoint is defined by the center value within a whisking cycle. These were quantified by Hilbert decomposition of whisker azimuthal angle at base (θ) with a 6–30 Hz band-pass filter (Hill et al., 2011). Each whisking period was divided by time points where the phase changed from >3 (end of the previous cycle) to <−3 (start of the next cycle; phase can range from −π to π). We considered active whisking only when max(θ) – min(θ) within each whisking period was larger than 2.5° (Severson et al., 2017). Amplitude and midpoint were averaged in each frame. This input had −2 to 4 delays. Negative delay means spike events precede whisking events. This could conceivably happen from efference copy of motor signal from M1 (Hill et al., 2011; Petreanu et al., 2012). Total number of whisking predictors was 3 × 7 = 21.
Licking: We used number of licks on each side as licking parameters. Dividing into lick onset and offset (Allen et al., 2017; Chen et al., 2016) or binarizing lick bouts (Pho et al., 2018) did not perform better than number of licks alone. Delays were −2 to 1 frames, resulting in 2 × 4 = 8 predictors.
Sound: There were three sources of salient sound in our behavior task set up – a piezo beep at the beginning of each trial, and the pneumatic valve controlling pole presenting slider during both presenting and retracting. We observed that only the pole presenting sound cue resulted in significant impact on model fitting. Delays were 0 to 3 frames, resulting in 4 predictors.
Reward: We used binary vector of whether a reward was given on left or right lick port. Delays were 0 to 4 frames, resulting in 2 × 5 = 10 predictors.

At each session, 70% of trials were randomly selected for training, the regularization parameter was calculated from 5-fold cross-validation, and fitting was tested in the remaining 30% of trials. Training data was stratified based on touch, choice, angle of the object, and the total number of spikes in each trial. Data was standardized before dividing into training and test sets.

We repeated this procedure 10 times, and used averaged coefficients as the final model. This was because the response is sparse in the barrel cortex, even more when using calcium signal as the proxy of neuronal activity (Huang et al., 2020), and randomization can result in false negatives. Averaging coefficients from multiple iterations is equivalent to cross-validation, and it may result in overfitting. However, we found this method was more conservative (when used with threshold of %DE 0.1) than using the statistical test from chi-2 distribution of deviance (Agresti, 2013) or the Akaike information criterion.

We used %DE as the measure of fitting (Agresti, 2013). Distribution of %DE was similar to that of auditory cortex or posterior parietal cortex of mice during an auditory spatial localization task (Figure S3B; Runyan et al., 2017). Threshold of being fit was set to 0.1 (Figure S3B; Runyan et al., 2017), which roughly corresponded to a correlation coefficient of 0.2. This threshold resulted in relatively consistent results from multiple iterations and in similar proportion of touch neurons compared to a previous report (Peron et al., 2015).

First, we decided if a neuronal activity was fit using 5 classes of event during the task – touch, whisking, licking, sound cue, and reward. If %DE was larger than 0.1, then it was defined fit. This suggested that this set of 5 event classes could explain inferred spikes well. Then, the predictive classes were defined within fit neurons by the ‘leave-one-out’ method. We removed each group of predictors (e.g., all 24 predictors of ‘touch’) from the ‘object model’ without retraining (equivalent of setting all coefficients corresponding to this group of predictors to 0), and calculated %DE. If %DE was reduced more than the threshold (0.1) from that of the ‘object model’, then that removed behavioral class was assigned to the neuron. We note that this method depends on the distribution of input parameters, and may be specific to the current task structure. Each fit neuron could be assigned to one or more classes, or no class at all (Figure 3B).

Object-angle tuning calculation

We used analysis of variance (ANOVA) with shuffling methods to calculate object-angle tuning at touch. We analyzed touch-responsive neurons only. Touch frames were defined as the frames when touch occurred, with delays of 0 and 1 frames to capture delayed calcium response to touch. We considered frames before the answer lick only, to prevent contamination from behavioral outcome (i.e., water reward.). We defined the response as the number of inferred spikes per touch in each trial. We quantified the response by subtracting the mean number of inferred spikes during baseline (before pole up) from the total number of inferred spikes in all touch frames, and then dividing by the number of touches within the trial. We grouped responses into each object angle, and ran ANOVA. If the resulting p value was lower than 0.05, at least one bin was significantly different from 0, and at least one pair of bins had significantly different responses after post hoc analysis (Tukey’s honestly significant difference), it passed the first round. Among these neurons, we compared F-statistics (between-group variance / within-group variance) of 10,000 shuffled object angles to that of original data. If more than 5% of them (i.e., 500) had F-statistics larger than the original, then we defined those neurons to be not tuned. This second process was to prevent false positive errors, where randomly assigning touch responses into 7 bins could result in statistically uneven distribution.

We further considered possible confounding effects from responses to other categories of behavior by calculating angle tuning on neuronal activities reconstructed from the ‘object model’ (Figures S3D and S3E). We first confirmed that full object models recapitulate object-angle tuning, by applying ANOVA and shuffling methods described above. Thus, we could use object models to evaluate the role of each parameter in constructing object-angle tuning. Specifically, we applied the same methods on the neuronal activities reconstructed from touch parameters only, and confirmed that object-angle tuning did not result from responses to other categories of behavior, such as whisking and licking.

We defined angle selectivity as max(response) – mean(other 6 responses). We did not normalize this subtraction for two reasons: 1) we do not know true baseline firing rate, and 2) because mean responses across neurons were highly variable, leading to bias toward low response neurons with higher angle selectivity if normalized.

Cortical depth estimation

To compare object-angle tuning (Figures 3F and 3G) and whisker feature combination (Figure S4E) between L2/3 and L4, we first estimated the boundary depth between L2/3 and L4 using L4-specific expression of GCaMP6s (AAV-Flex-GCaMP6s injection to Scnn1a-Cre mice). We used septa (gap between barrels) contrast as the indication of L4. First we identified septa at around 400 μm depth, drew lines across multiple septa, and calculated the contrast (standard deviation of intensity across the lines) across depth. We estimated L2/3-L4 boundary as the starting point of this contrast, which was at around 350 μm.

Before each imaging session, dura was identified from autofluorescence and set to 0 μm. Depth of each imaging plane was recorded by the movement of the objective along the rotation angle of 35°. Imaging plane tilt angle of the cranial window relative to the object lens was approximated in each mouse using dura imaging. The boundary of dura was detected from the planes of 2 μm interval z stack imaging, from where no significant fluorescence could be detected to where the whole FOV was under the dura. Using this dura estimation across depth, we calculated imaging plane tilt angle by averaging the slope of dura depth in x and y directions. Each neuron’s depth was calculated based on its x-y position by applying this imaging plane tilt angle to the depth of corresponding imaging planes. Neurons residing deeper than 350 μm were defined as L4 neurons, and shallower than 350 μm as L2/3 neurons.

GLM for neuronal activity - ‘Whisker model’

To investigate the impact of each of the 12 whisker features in angle tuning, we built Poisson GLMs with lasso regression to fit each neuron’s inferred spikes using whisker features. In this model, we used 5 behavioral categories as in the ‘object model’, except that we swapped touch components with whisker feature components. Of 12 whisker features listed above, we averaged at touch features (except for touch counts), and summed during touch features, in each frame. The difference was because during touch features were calculated as changes. Averaging all whisker features except touch counts resulted in no significant differences in the result. Each feature had 0 to 2 delays as in touch in the object model, resulting in 36 input parameters in total. We used ‘leave-one-out’ models to calculate the importance of each whisker feature on fitting the session-wide neuronal activity (Figures 8G and S8B).

We calculated angle tuning from ‘whisker model’ (Figure 4B) in the same manner as angle tuning using inferred spikes. We first confirmed that ‘whisker-only model’ (removing input parameters of other categories of behaviors from the full ‘whisker model’) had negligible effect on angle tuning curve (Figure S4B). Further analyses were performed on this ‘whisker-only model’ (Figures 4, 8, S4, and S8). To calculate the impact of each whisker feature on angle tuning curve, we removed each feature (3 input parameters) from the ‘whisker-only model’, calculated angle tuning curve, and then measured the correlation with the angle tuning curve from inferred spikes (Figure 4B). Reduction in this correlation value compared to that from the whisker-only model was defined as impact on angle tuning (Figure 4B).

Passive whisker deflection under anesthesia

To identify the C2 barrel column and to compare passive whisker deflection response to active tactile responses (Figure 5), we deflected C2 whisker for 4 s at 5 Hz (20 deflections per trial) using a glass capillary attached to a stripe piezo actuator (APC International Ltd., PA, USA) controlled by a piezo driver (A-301, A.A. Lab Systems Ltd., Israel). The driver was controlled and synched with a whisker monitoring camera using BControl, Ephus software (Suter et al., 2010), and Arduino. The tip of the glass capillary was positioned at ~2 mm away from the whisker base. Whisker tracking during passive deflection showed that deflection cycles resembled square waves of 85 ms trough duration, 15 ms of deflection (amplitude of 15°, 1150°/s), 85 ms peak duration, and 15 ms of return. We deflected the whisker at the angular direction of 0° (backward) to 315° in 45° steps (Figure 5), 10 trials per angle per volume (total 160 trials per session). Each trial lasted for 10 s, typically consisting of 1–3 s baseline, 4 s stimulation, and 3–5 s post-stimulation. Intertrial-interval was at least 3 s, during which the imaging laser was blocked to reduce heating.

All passive deflection experiments were performed under light anesthesia (0.5%–0.8% isoflurane). Body temperature was monitored and controlled using a thermal blanket (Harvard apparatus). Depth of anesthesia was monitored by whisker movement (forward stretched whiskers indicating too low anesthesia depth) and breathing rate (lower than ~60 bpm with gagging indicating too high anesthesia depth).

Passive whisker deflection response analysis

We used CircStat, a MATLAB toolbox for circular statistics (Berens, 2009), for calculating the vector sum of mean neuronal responses to 8 angular deflections. Confidence intervals were calculated using the distribution from 10,000 sets of bootstrapped data (sampling with replacement). Random probability was calculated by 10,000 sets of shuffled data, where mean tuned angle (direction of vector sum) was shuffled while keeping object-angle tuning the same.

Matching planes across sessions (Figure S6)

To match two-photon imaging volume-of-views across training, we compared spatial correlation between multiple depths to a reference image before each experiment session. We matched the top FOV of each imaging volume (2 per mouse). Reference images were from the first awake experimental session (Figure S6A). Before each experimental session, we first roughly matched the area following surface vasculature, and the cortical depth from the dura. Then, we applied a two-step automatic search (Figures S6B–S6D). First, we took 10 s images from 10 planes separated by 10 μm around the roughly matched depth (Figure S6B). Images were registered using 2-dimensional Fourier transform (Scanbox, Neurolabware), and then the mean images were again registered with the reference image based on intensity (MATLAB imregister function). We calculated spatial correlation from each of these 10 registered mean images with the reference image, and plotted them against depth (Figure S6D; open circles). We then started the second step from the depth where the correlation value was the highest (arrow on the top of Figure S6D), and after adjusting x-y position according to the intensity-based registration. We iterated the above methods using a 2-μm interval (Figures S6C and S6D; filled circles). Finally, matching depth was estimated from the peak of a smoothed curve of these spatial correlation values (Figure S6D, arrow at the bottom).

Matching the depth of imaging plane is critical in quantifying number of neurons being silent (Figures 6A and S7A–S7C), because a neuron could have simply been missed from the imaged plane on the other session. To calculate the probability of missing a neuron out of imaging plane, we quantified depth range in detecting single cells and relative difference of imaging plane depths across sessions (before and after learning; naive and expert 7-angle test sessions). Probability of missing a neuron can then be calculated as depth difference divided by depth range.

To quantify the range of depth that single cells could be detected over, we used rare cases of chronically fluorescent neurons while taking z stack images (3 neurons out of 12 mice; Figure S6E). By visual inspection from 2-μm interval z stack images, we estimated this depth range as ± 20 μm around the midpoint of the cell. This relatively wide range may be due to under-filling the objective’s back aperture, which we implemented to reduce scattering and increase signal-to-noise ratio when imaging deeper cortical depths (Kondo et al., 2017).

The relative difference of imaging plane depths was calculated similar to processes described above (Figure S6D), using a template z stack imaging of each mouse. Across imaging planes, the depth difference was 3.2 ± 3.8 μm (mean ± SD; Figure S6F). Thus, the probability of missing a neuron was about 3.2/40 = 0.08, assuming equal cell detectability across the range (Figure S6E). This is much lower than the proportion of neurons which became silent or active in expert sessions (Figures 6B, S6F, and S7A–S7C).

We validated this GCaMP based approach with tdTomato. One of 4 mice expressing tdTomato in the nucleus of excitatory neurons reached expert performance. The depth difference estimation was similar between the tdTomato-expressing mouse and GCaMP6s-only mice (Figure S6F). Furthermore, the tdTomato-expressing mouse had similar neuron disappearing and appearing rates when compared to other GCaMP6s-only mice (Figure S6F). This result, along with the low probability of missing a neuron in our microscope system across sessions (Figure S6E) and the similarity with previous reports (Chen et al., 2015; Gonzalez et al., 2019; Ziv et al., 2013), supports that variability in plane matching across paired sessions had an acceptably small impact on quantifying ensemble turnover rate.

QUANTIFICATION AND STATISTICAL ANALYSIS

All statistical analyses were performed using MATLAB. When comparing mouse-averaged mean values between naive and expert sessions (n = 6), we used either paired 2-tailed t test or Wilcoxon rank test, depending on Lilliefors normality test with a threshold at 0.05. When comparing values between pooled neurons from naive and expert sessions (Figures 8G and 8H), we used paired 2-tailed t test. We did not correct for family-wise error rate. All data were presented in mean ± SEM except for those noted otherwise. P values were shown up to 2 decimal places when larger than or equal to 0.05. In other cases, p values were presented as * for < 0.05, ** for < 0.01, and *** for < 0.001.

Supplementary Material

NIHMS1730970-supplement-1.pdf^{(8.7MB, pdf)}

Highlights.

Mice can discriminate object surface angle using a single whisker
Excitatory neurons in primary somatosensory cortex represent touched object angles
Object-angle tuning is most affected by vertical bending and slide distance
Training increases the influence of task-relevant sensory inputs on angle tuning

ACKNOWLEDGMENTS

We thank Jonathan Sy, Vincent Huang, and Sadaf Hashemian for their help in curating whisker-object touch frames and 2-photon calcium imaging ROIs. We thank Stefanie Walker for the art. This project was funded by the NIH/NINDS New Innovator Award 1DP2NS105554.

Footnotes

DECLARATION OF INTERESTS

The authors declare no competing interests.

SUPPLEMENTAL INFORMATION

Supplemental Information can be found online at https://doi.org/10.1016/j.neuron.2020.09.012.

REFERENCES

Adrian ED, and Zotterman Y (1926). The impulses produced by sensory nerve endings: Part 3. Impulses set up by Touch and Pressure. J. Physiol. 61, 465–483. [DOI] [PMC free article] [PubMed] [Google Scholar]
Agresti A (2013). Categorical Data Analysis, Third Edition (Wiley; ). [Google Scholar]
Allen WE, Kauvar IV, Chen MZ, Richman EB, Yang SJ, Chan K, Gradinaru V, Deverman BE, Luo L, and Deisseroth K (2017). Global Representations of Goal-Directed Behavior in Distinct Cell Types of Mouse Neocortex. Neuron 94, 891–907.e6. [DOI] [PMC free article] [PubMed] [Google Scholar]
Andermann ML, and Moore CI (2006). A somatotopic map of vibrissa motion direction within a barrel column. Nat. Neurosci. 9, 543–551. [DOI] [PubMed] [Google Scholar]
Anjum F, Turni H, Mulder PGH, van der Burg J, and Brecht M (2006). Tactile guidance of prey capture in Etruscan shrews. Proc. Natl. Acad. Sci. USA 103, 16544–16549. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bagdasarian K, Szwed M, Knutsen PM, Deutsch D, Derdikman D, Pietr M, Simony E, and Ahissar E (2013). Pre-neuronal morphological processing of object location by individual whiskers. Nat. Neurosci. 16, 622–631. [DOI] [PubMed] [Google Scholar]
Barth AL, Gerkin RC, and Dean KL (2004). Alteration of neuronal firing properties after in vivo experience in a FosGFP transgenic mouse. J. Neurosci. 24, 6466–6475. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bensmaia SJ, Denchev PV, Dammann JF 3rd, Craig JC, and Hsiao SS (2008). The representation of stimulus orientation in the early stages of somatosensory processing. J. Neurosci. 28, 776–786. [DOI] [PMC free article] [PubMed] [Google Scholar]
Berens P (2009). CircStat: A MATLAB Toolbox for Circular Statistics. J. Stat. Softw. 31, 1–21. [Google Scholar]
Bodegård A, Geyer S, Grefkes C, Zilles K, and Roland PE (2001). Hierarchical processing of tactile shape in the human brain. Neuron 31, 317–328. [DOI] [PubMed] [Google Scholar]
Breiman L (2001a). Random Forests. Mach. Learn. 45, 5–32. [Google Scholar]
Breiman L (2001b). Statistical Modeling: The Two Cultures (with comments and a rejoinder by the author). Stat. Sci. 16, 199–231. [Google Scholar]
Brown J, Oldenburg IA, Telian GI, Griffin S, Voges M, Jain V, and Adesnik H (2020). Spatial integration during active tactile sensation drives elementary shape perception. BioRxiv 10.1101/2020.03.16.994145v1. [DOI] [PMC free article] [PubMed]
Bruno RM, Khatri V, Land PW, and Simons DJ (2003). Thalamocortical angular tuning domains within individual barrels of rat somatosensory cortex. J. Neurosci. 23, 9565–9574. [DOI] [PMC free article] [PubMed] [Google Scholar]
Carvell GE, and Simons DJ (1990). Biometric analyses of vibrissal tactile discrimination in the rat. J. Neurosci. 10, 2638–2648. [DOI] [PMC free article] [PubMed] [Google Scholar]
Catania KC, Hare JF, and Campbell KL (2008). Water shrews detect movement, shape, and smell to find prey underwater. Proc. Natl. Acad. Sci. USA 105, 571–576. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chen T-W, Wardill TJ, Sun Y, Pulver SR, Renninger SL, Baohan A, Schreiter ER, Kerr RA, Orger MB, Jayaraman V, et al. (2013). Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature 499, 295–300. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chen JL, Margolis DJ, Stankov A, Sumanovski LT, Schneider BL, and Helmchen F (2015). Pathway-specific reorganization of projection neurons in somatosensory cortex during learning. Nat. Neurosci. 18, 1101–1108. [DOI] [PubMed] [Google Scholar]
Chen JL, Voigt FF, Javadzadeh M, Krueppel R, and Helmchen F (2016). Long-range population dynamics of anatomically defined neocortical networks. eLife 5, e14679. [DOI] [PMC free article] [PubMed] [Google Scholar]
Cheung J, Maire P, Kim J, Sy J, and Hires SA (2019). The Sensorimotor Basis of Whisker-Guided Anteroposterior Object Localization in Head-Fixed Mice. Curr. Biol. 29, 3029–3040.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
Clack NG, O’Connor DH, Huber D, Petreanu L, Hires A, Peron S, Svoboda K, and Myers EW (2012). Automated tracking of whiskers in videos of head fixed rodents. PLOS Comput. Biol. 8, e1002591. [DOI] [PMC free article] [PubMed] [Google Scholar]
Coste B, Xiao B, Santos JS, Syeda R, Grandl J, Spencer KS, Kim SE, Schmidt M, Mathur J, Dubin AE, et al. (2012). Piezo proteins are pore-forming subunits of mechanically activated channels. Nature 483, 176–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
Dehorter N, Ciceri G, Bartolini G, Lim L, del Pino I, and Marín O (2015). Tuning of fast-spiking interneuron properties by an activity-dependent transcriptional switch. Science 349, 1216–1220. [DOI] [PMC free article] [PubMed] [Google Scholar]
Deneux T, Kaszas A, Szalay G, Katona G, Lakner T, Grinvald A, Rózsa B, and Vanzetta I (2016). Accurate spike estimation from noisy calcium signals for ultrafast three-dimensional imaging of large neuronal populations in vivo. Nat. Commun. 7, 12190. [DOI] [PMC free article] [PubMed] [Google Scholar]
Desai NS, Rutherford LC, and Turrigiano GG (1999). Plasticity in the intrinsic excitability of cortical pyramidal neurons. Nat. Neurosci. 2, 515–520. [DOI] [PubMed] [Google Scholar]
Fisher A, Rudin C, and Dominici F (2019). All Models are Wrong, but Many are Useful: Learning a Variable’s Importance by Studying an Entire Class of Prediction Models Simultaneously. J. Mach. Learn. Res. 20, 1–81. [PMC free article] [PubMed] [Google Scholar]
Fitzgerald PJ, Lane JW, Thakur PH, and Hsiao SS (2004). Receptive field properties of the macaque second somatosensory cortex: evidence for multiple functional representations. J. Neurosci. 24, 11193–11204. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fortier-Poisson P, and Smith AM (2016). Neuronal activity in somatosensory cortex related to tactile exploration. J. Neurophysiol. 115, 112–126. [DOI] [PMC free article] [PubMed] [Google Scholar]
Friedman J, Hastie T, and Tibshirani R (2010). Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 33, 1–22. [PMC free article] [PubMed] [Google Scholar]
Furuta T, Bush NE, Yang AE-T, Ebara S, Miyazaki N, Murata K, Hirai D, Shibata KI, and Hartmann MJZ (2020). The Cellular and Mechanical Basis for Response Characteristics of Identified Primary Afferents in the Rat Vibrissal System. Curr. Biol. 30, 815–826.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gainey MA, Aman JW, and Feldman DE (2018). Rapid Disinhibition by Adjustment of PV Intrinsic Excitability during Whisker Map Plasticity in Mouse S1. J. Neurosci. 38, 4749–4761. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gibson JJ (1962). Observations on active touch. Psychol. Rev. 69, 477–491. [DOI] [PubMed] [Google Scholar]
Goldberg EM, Clark BD, Zagha E, Nahmani M, Erisir A, and Rudy B (2008). K+ channels at the axon initial segment dampen near-threshold excitability of neocortical fast-spiking GABAergic interneurons. Neuron 58, 387–400. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gonzalez WG, Zhang H, Harutyunyan A, and Lois C (2019). Persistence of neuronal representations through time and damage in the hippocampus. Science 365, 821–825. [DOI] [PubMed] [Google Scholar]
Guo ZV, Hires SA, Li N, O’Connor DH, Komiyama T, Ophir E, Huber D, Bonardi C, Morandell K, Gutnisky D, et al. (2014). Procedures for behavioral experiments in head-fixed mice. PLOS ONE 9, e88678. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hensel H, and Boman KKA (1960). Afferent impulses in cutaneous sensory nerves in human subjects. J. Neurophysiol. 23, 564–578. [DOI] [PubMed] [Google Scholar]
Hill DN, Curtis JC, Moore JD, and Kleinfeld D (2011). Primary motor cortex reports efferent control of vibrissa motion on multiple timescales. Neuron 72, 344–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hires SA, Gutnisky DA, Yu J, O’Connor DH, and Svoboda K (2015). Low-noise encoding of active touch by layer 4 in the somatosensory cortex. eLife 4, e06619. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hooks BM, Hires SA, Zhang Y-X, Huber D, Petreanu L, Svoboda K, and Shepherd GMG (2011). Laminar analysis of excitatory local circuits in vibrissal motor and sensory cortical areas. PLOS Biol. 9, e1000572. [DOI] [PMC free article] [PubMed] [Google Scholar]
Huang L, Knoblich U, Ledochowitsch P, Lecoq J, Reid RC, de Vries SEJ, Buice MA, Murphy GJ, Waters J, Koch C, et al. (2020). Relationship between simultaneously recorded spiking activity and fluorescence signal in GCaMP6 transgenic mice. BioRxiv 10.1101/788802v2. [DOI] [PMC free article] [PubMed]
Huet LA, and Hartmann MJZ (2016). Simulations of a Vibrissa Slipping along a Straight Edge and an Analysis of Frictional Effects during Whisking. IEEE Trans. Haptics 9, 158–169. [DOI] [PMC free article] [PubMed] [Google Scholar]
Isett BR, Feasel SH, Lane MA, and Feldman DE (2018). Slip-Based Coding of Local Shape and Texture in Mouse S1. Neuron 97, 418–433.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]
Jadhav SP, Wolfe J, and Feldman DE (2009). Sparse temporal coding of elementary tactile features during active whisker sensation. Nat. Neurosci. 12, 792–800. [DOI] [PubMed] [Google Scholar]
Katz D (1925). Der Autbau der Tastwelt. Zeitschr. Psychol. (Suppl. 7), 1–131. [Google Scholar]
Khan AG, Poort J, Chadwick A, Blot A, Sahani M, Mrsic-Flogel TD, and Hofer SB (2018). Distinct learning-induced changes in stimulus selectivity and interactions of GABAergic interneuron classes in visual cortex. Nat. Neurosci. 21, 851–859. [DOI] [PMC free article] [PubMed] [Google Scholar]
Knutsen PM, and Ahissar E (2009). Orthogonal coding of object location. Trends Neurosci. 32, 101–109. [DOI] [PubMed] [Google Scholar]
Kondo M, Kobayashi K, Ohkura M, Nakai J, and Matsuzaki M (2017). Two-photon calcium imaging of the medial prefrontal cortex and hippocampus without cortical invasion. eLife 6, e26839. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kremer Y, Léger J-F, Goodman D, Brette R, and Bourdieu L (2011). Late emergence of the vibrissa direction selectivity map in the rat barrel cortex. J. Neurosci. 31, 10689–10700. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kwon SE, Tsytsarev V, Erzurumlu RS, and O’Connor DH (2018). Organization of orientation-specific whisker deflection responses in layer 2/3 of mouse somatosensory cortex. Neuroscience 368, 46–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lavzin M, Rapoport S, Polsky A, Garion L, and Schiller J (2012). Nonlinear dendritic processing determines angular tuning of barrel cortex neurons in vivo. Nature 490, 397–401. [DOI] [PubMed] [Google Scholar]
Lederman SJ, and Klatzky RL (1987). Hand movements: a window into haptic object recognition. Cognit. Psychol. 19, 342–368. [DOI] [PubMed] [Google Scholar]
Lefort S, Tomm C, Floyd Sarria J-C, and Petersen CCH (2009). The excitatory neuronal network of the C2 barrel column in mouse primary somatosensory cortex. Neuron 61, 301–316. [DOI] [PubMed] [Google Scholar]
LeMessurier AM, Laboy-Juárez KJ, McClain K, Chen S, Nguyen T, and Feldman DE (2019). Enrichment drives emergence of functional columns and improves sensory coding in the whisker map in L2/3 of mouse S1. eLife 8, e46321. [DOI] [PMC free article] [PubMed] [Google Scholar]
Madisen L, Garner AR, Shimaoka D, Chuong AS, Klapoetke NC, Li L, van der Bourg A, Niino Y, Egolf L, Monetti C, et al. (2015). Transgenic mice for intersectional targeting of neural sensors and effectors with high specificity and performance. Neuron 85, 942–958. [DOI] [PMC free article] [PubMed] [Google Scholar]
Mehta SB, Whitmer D, Figueroa R, Williams BA, and Kleinfeld D (2007). Active spatial perception in the vibrissa scanning sensorimotor system. PLOS Biol. 5, e15. [DOI] [PMC free article] [PubMed] [Google Scholar]
O’Connor DH, Peron SP, Huber D, and Svoboda K (2010). Neural activity in barrel cortex underlying vibrissa-based object localization in mice. Neuron 67, 1048–1061. [DOI] [PubMed] [Google Scholar]
Pachitariu M, Stringer C, Dipoppa M, Schröder S, Rossi LF, Dalgleish H, Carandini M, and Harris KD (2017). Suite2p: beyond 10,000 neurons with standard two-photon microscopy. BioRxiv 10.1101/061507v2. [DOI]
Pammer L, O’Connor DH, Hires SA, Clack NG, Huber D, Myers EW, and Svoboda K (2013). The mechanical variables underlying object localization along the axis of the whisker. J. Neurosci. 33, 6726–6741. [DOI] [PMC free article] [PubMed] [Google Scholar]
Peron SP, Freeman J, Iyer V, Guo C, and Svoboda K (2015). A Cellular Resolution Map of Barrel Cortex Activity during Tactile Behavior. Neuron 86, 783–799. [DOI] [PubMed] [Google Scholar]
Petreanu L, Gutnisky DA, Huber D, Xu NL, O’Connor DH, Tian L, Looger L, and Svoboda K (2012). Activity in motor-sensory projections reveals distributed coding in somatosensation. Nature 489, 299–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
Pho GN, Goard MJ, Woodson J, Crawford B, and Sur M (2018). Task-dependent representations of stimulus and choice in mouse parietal cortex. Nat. Commun. 9, 2596. [DOI] [PMC free article] [PubMed] [Google Scholar]
Pluta SR, Lyall EH, Telian GI, Ryapolova-Webb E, and Adesnik H (2017). Surround Integration Organizes a Spatial Map during Active Sensation. Neuron 94, 1220–1233.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]
Podgorski K, and Ranganathan G (2016). Brain heating induced by near-infrared lasers during multiphoton microscopy. J. Neurophysiol. 116, 1012–1023. [DOI] [PMC free article] [PubMed] [Google Scholar]
Pont SC, Kappers AML, and Koenderink JJ (1999). Similar mechanisms underlie curvature comparison by static and dynamic touch. Percept. Psychophys. 61, 874–894. [DOI] [PubMed] [Google Scholar]
Poort J, Khan AG, Pachitariu M, Nemri A, Orsolic I, Krupic J, Bauza M, Sahani M, Keller GB, Mrsic-Flogel TD, and Hofer SB (2015). Learning Enhances Sensory and Multiple Non-sensory Representations in Primary Visual Cortex. Neuron 86, 1478–1490. [DOI] [PMC free article] [PubMed] [Google Scholar]
Pruszynski JA, and Johansson RS (2014). Edge-orientation processing in first-order tactile neurons. Nat. Neurosci. 17, 1404–1409. [DOI] [PubMed] [Google Scholar]
Pubols LM, and Leroy RF (1977). Orientation detectors in the primary somatosensory neocortex of the raccoon. Brain Res. 129, 61–74. [DOI] [PubMed] [Google Scholar]
Ranganathan GN, Apostolides PF, Harnett MT, Xu N-L, Druckmann S, and Magee JC (2018). Active dendritic integration and mixed neocortical network representations during an adaptive sensing behavior. Nat. Neurosci. 21, 1583–1590. [DOI] [PMC free article] [PubMed] [Google Scholar]
Rose T, Jaepel J, Hübener M, and Bonhoeffer T (2016). Cell-specific restoration of stimulus preference after monocular deprivation in the visual cortex. Science 352, 1319–1322. [DOI] [PubMed] [Google Scholar]
Runyan CA, Piasini E, Panzeri S, and Harvey CD (2017). Distinct timescales of population coding across cortex. Nature 548, 92–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
Severson KS, Xu D, Van de Loo M, Bai L, Ginty DD, and O’Connor DH (2017). Active Touch and Self-Motion Encoding by Merkel Cell-Associated Afferents. Neuron 94, 666–676.e9. [DOI] [PMC free article] [PubMed] [Google Scholar]
Simons DJ, and Carvell GE (1989). Thalamocortical response transformation in the rat vibrissa/barrel system. J. Neurophysiol. 61, 311–330. [DOI] [PubMed] [Google Scholar]
Sofroniew NJ, Vlasov YA, Hires SA, Freeman J, and Svoboda K (2015). Neural coding in barrel cortex during whisker-guided locomotion. eLife 4, e12559. [DOI] [PMC free article] [PubMed] [Google Scholar]
Solomon JH, and Hartmann MJZ (2011). Radial distance determination in the rat vibrissal system and the effects of Weber’s law. Philos. Trans. R. Soc. Lond. B Biol. Sci. 366, 3049–3057. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sripati AP, Bensmaia SJ, and Johnson KO (2006). A continuum mechanical model of mechanoreceptive afferent responses to indented spatial patterns. J. Neurophysiol. 95, 3852–3864. [DOI] [PMC free article] [PubMed] [Google Scholar]
Suter BA, O’Connor T, Iyer V, Petreanu LT, Hooks BM, Kiritani T, Svoboda K, and Shepherd GMG (2010). Ephus: multipurpose data acquisition software for neuroscience experiments. Front. Neural Circuits 4, 100. [DOI] [PMC free article] [PubMed] [Google Scholar]
Szwed M, Bagdasarian K, and Ahissar E (2003). Encoding of vibrissal active touch. Neuron 40, 621–630. [DOI] [PubMed] [Google Scholar]
Szwed M, Bagdasarian K, Blumenfeld B, Barak O, Derdikman D, and Ahissar E (2006). Responses of trigeminal ganglion neurons to the radial distance of contact during active vibrissal touch. J. Neurophysiol. 95, 791–802. [DOI] [PubMed] [Google Scholar]
Wekselblatt JB, Flister ED, Piscopo DM, and Niell CM (2016). Large-scale imaging of cortical dynamics during sensory perception and behavior. J. Neurophysiol. 115, 2852–2866. [DOI] [PMC free article] [PubMed] [Google Scholar]
Whiteley SJ, Knutsen PM, Matthews DW, and Kleinfeld D (2015). Deflection of a vibrissa leads to a gradient of strain across mechanoreceptors in a mystacial follicle. J. Neurophysiol. 114, 138–145. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wijntjes MWA, Sato A, Hayward V, and Kappers AML (2009). Local Surface Orientation Dominates Haptic Curvature Discrimination. IEEE Trans. Haptics 2, 94–102. [DOI] [PubMed] [Google Scholar]
Yamashita T, and Petersen C.C.h. (2016). Target-specific membrane potential dynamics of neocortical projection neurons during goal-directed behavior. eLife 5, e15798. [DOI] [PMC free article] [PubMed] [Google Scholar]
Yiu AP, Mercaldo V, Yan C, Richards B, Rashid AJ, Hsiang H-LL, Pressey J, Mahadevan V, Tran MM, Kushner SA, et al. (2014). Neurons are recruited to a memory trace based on relative neuronal excitability immediately before training. Neuron 83, 722–735. [DOI] [PubMed] [Google Scholar]
Ziv Y, Burns LD, Cocker ED, Hamel EO, Ghosh KK, Kitch LJ, El Gamal A, and Schnitzer MJ (2013). Long-term dynamics of CA1 hippocampal place codes. Nat. Neurosci. 16, 264–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
Zucker E, and Welker WI (1969). Coding of somatic sensory input by vibrissae neurons in the rat’s trigeminal ganglion. Brain Res. 12, 138–156. [DOI] [PubMed] [Google Scholar]
Zuo Y, Safaai H, Notaro G, Mazzoni A, Panzeri S, and Diamond ME (2015). Complementary contributions of spike timing and spike rate to perceptual decisions in rat S1 and S2 cortex. Curr. Biol. 25, 357–363. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

NIHMS1730970-supplement-1.pdf^{(8.7MB, pdf)}

Data Availability Statement

The datasets generated during this study and code used to analyze data and generate figures are available at https://github.com/hireslab/Pub_S1AngleCode.

[R1] Adrian ED, and Zotterman Y (1926). The impulses produced by sensory nerve endings: Part 3. Impulses set up by Touch and Pressure. J. Physiol. 61, 465–483. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R2] Agresti A (2013). Categorical Data Analysis, Third Edition (Wiley; ). [Google Scholar]

[R3] Allen WE, Kauvar IV, Chen MZ, Richman EB, Yang SJ, Chan K, Gradinaru V, Deverman BE, Luo L, and Deisseroth K (2017). Global Representations of Goal-Directed Behavior in Distinct Cell Types of Mouse Neocortex. Neuron 94, 891–907.e6. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R4] Andermann ML, and Moore CI (2006). A somatotopic map of vibrissa motion direction within a barrel column. Nat. Neurosci. 9, 543–551. [DOI] [PubMed] [Google Scholar]

[R5] Anjum F, Turni H, Mulder PGH, van der Burg J, and Brecht M (2006). Tactile guidance of prey capture in Etruscan shrews. Proc. Natl. Acad. Sci. USA 103, 16544–16549. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R6] Bagdasarian K, Szwed M, Knutsen PM, Deutsch D, Derdikman D, Pietr M, Simony E, and Ahissar E (2013). Pre-neuronal morphological processing of object location by individual whiskers. Nat. Neurosci. 16, 622–631. [DOI] [PubMed] [Google Scholar]

[R7] Barth AL, Gerkin RC, and Dean KL (2004). Alteration of neuronal firing properties after in vivo experience in a FosGFP transgenic mouse. J. Neurosci. 24, 6466–6475. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R8] Bensmaia SJ, Denchev PV, Dammann JF 3rd, Craig JC, and Hsiao SS (2008). The representation of stimulus orientation in the early stages of somatosensory processing. J. Neurosci. 28, 776–786. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R9] Berens P (2009). CircStat: A MATLAB Toolbox for Circular Statistics. J. Stat. Softw. 31, 1–21. [Google Scholar]

[R10] Bodegård A, Geyer S, Grefkes C, Zilles K, and Roland PE (2001). Hierarchical processing of tactile shape in the human brain. Neuron 31, 317–328. [DOI] [PubMed] [Google Scholar]

[R11] Breiman L (2001a). Random Forests. Mach. Learn. 45, 5–32. [Google Scholar]

[R12] Breiman L (2001b). Statistical Modeling: The Two Cultures (with comments and a rejoinder by the author). Stat. Sci. 16, 199–231. [Google Scholar]

[R13] Brown J, Oldenburg IA, Telian GI, Griffin S, Voges M, Jain V, and Adesnik H (2020). Spatial integration during active tactile sensation drives elementary shape perception. BioRxiv 10.1101/2020.03.16.994145v1. [DOI] [PMC free article] [PubMed]

[R14] Bruno RM, Khatri V, Land PW, and Simons DJ (2003). Thalamocortical angular tuning domains within individual barrels of rat somatosensory cortex. J. Neurosci. 23, 9565–9574. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R15] Carvell GE, and Simons DJ (1990). Biometric analyses of vibrissal tactile discrimination in the rat. J. Neurosci. 10, 2638–2648. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R16] Catania KC, Hare JF, and Campbell KL (2008). Water shrews detect movement, shape, and smell to find prey underwater. Proc. Natl. Acad. Sci. USA 105, 571–576. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R17] Chen T-W, Wardill TJ, Sun Y, Pulver SR, Renninger SL, Baohan A, Schreiter ER, Kerr RA, Orger MB, Jayaraman V, et al. (2013). Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature 499, 295–300. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R18] Chen JL, Margolis DJ, Stankov A, Sumanovski LT, Schneider BL, and Helmchen F (2015). Pathway-specific reorganization of projection neurons in somatosensory cortex during learning. Nat. Neurosci. 18, 1101–1108. [DOI] [PubMed] [Google Scholar]

[R19] Chen JL, Voigt FF, Javadzadeh M, Krueppel R, and Helmchen F (2016). Long-range population dynamics of anatomically defined neocortical networks. eLife 5, e14679. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R20] Cheung J, Maire P, Kim J, Sy J, and Hires SA (2019). The Sensorimotor Basis of Whisker-Guided Anteroposterior Object Localization in Head-Fixed Mice. Curr. Biol. 29, 3029–3040.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R21] Clack NG, O’Connor DH, Huber D, Petreanu L, Hires A, Peron S, Svoboda K, and Myers EW (2012). Automated tracking of whiskers in videos of head fixed rodents. PLOS Comput. Biol. 8, e1002591. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R22] Coste B, Xiao B, Santos JS, Syeda R, Grandl J, Spencer KS, Kim SE, Schmidt M, Mathur J, Dubin AE, et al. (2012). Piezo proteins are pore-forming subunits of mechanically activated channels. Nature 483, 176–181. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R23] Dehorter N, Ciceri G, Bartolini G, Lim L, del Pino I, and Marín O (2015). Tuning of fast-spiking interneuron properties by an activity-dependent transcriptional switch. Science 349, 1216–1220. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R24] Deneux T, Kaszas A, Szalay G, Katona G, Lakner T, Grinvald A, Rózsa B, and Vanzetta I (2016). Accurate spike estimation from noisy calcium signals for ultrafast three-dimensional imaging of large neuronal populations in vivo. Nat. Commun. 7, 12190. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R25] Desai NS, Rutherford LC, and Turrigiano GG (1999). Plasticity in the intrinsic excitability of cortical pyramidal neurons. Nat. Neurosci. 2, 515–520. [DOI] [PubMed] [Google Scholar]

[R26] Fisher A, Rudin C, and Dominici F (2019). All Models are Wrong, but Many are Useful: Learning a Variable’s Importance by Studying an Entire Class of Prediction Models Simultaneously. J. Mach. Learn. Res. 20, 1–81. [PMC free article] [PubMed] [Google Scholar]

[R27] Fitzgerald PJ, Lane JW, Thakur PH, and Hsiao SS (2004). Receptive field properties of the macaque second somatosensory cortex: evidence for multiple functional representations. J. Neurosci. 24, 11193–11204. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R28] Fortier-Poisson P, and Smith AM (2016). Neuronal activity in somatosensory cortex related to tactile exploration. J. Neurophysiol. 115, 112–126. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R29] Friedman J, Hastie T, and Tibshirani R (2010). Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 33, 1–22. [PMC free article] [PubMed] [Google Scholar]

[R30] Furuta T, Bush NE, Yang AE-T, Ebara S, Miyazaki N, Murata K, Hirai D, Shibata KI, and Hartmann MJZ (2020). The Cellular and Mechanical Basis for Response Characteristics of Identified Primary Afferents in the Rat Vibrissal System. Curr. Biol. 30, 815–826.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R31] Gainey MA, Aman JW, and Feldman DE (2018). Rapid Disinhibition by Adjustment of PV Intrinsic Excitability during Whisker Map Plasticity in Mouse S1. J. Neurosci. 38, 4749–4761. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R32] Gibson JJ (1962). Observations on active touch. Psychol. Rev. 69, 477–491. [DOI] [PubMed] [Google Scholar]

[R33] Goldberg EM, Clark BD, Zagha E, Nahmani M, Erisir A, and Rudy B (2008). K+ channels at the axon initial segment dampen near-threshold excitability of neocortical fast-spiking GABAergic interneurons. Neuron 58, 387–400. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R34] Gonzalez WG, Zhang H, Harutyunyan A, and Lois C (2019). Persistence of neuronal representations through time and damage in the hippocampus. Science 365, 821–825. [DOI] [PubMed] [Google Scholar]

[R35] Guo ZV, Hires SA, Li N, O’Connor DH, Komiyama T, Ophir E, Huber D, Bonardi C, Morandell K, Gutnisky D, et al. (2014). Procedures for behavioral experiments in head-fixed mice. PLOS ONE 9, e88678. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R36] Hensel H, and Boman KKA (1960). Afferent impulses in cutaneous sensory nerves in human subjects. J. Neurophysiol. 23, 564–578. [DOI] [PubMed] [Google Scholar]

[R37] Hill DN, Curtis JC, Moore JD, and Kleinfeld D (2011). Primary motor cortex reports efferent control of vibrissa motion on multiple timescales. Neuron 72, 344–356. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R38] Hires SA, Gutnisky DA, Yu J, O’Connor DH, and Svoboda K (2015). Low-noise encoding of active touch by layer 4 in the somatosensory cortex. eLife 4, e06619. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R39] Hooks BM, Hires SA, Zhang Y-X, Huber D, Petreanu L, Svoboda K, and Shepherd GMG (2011). Laminar analysis of excitatory local circuits in vibrissal motor and sensory cortical areas. PLOS Biol. 9, e1000572. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R40] Huang L, Knoblich U, Ledochowitsch P, Lecoq J, Reid RC, de Vries SEJ, Buice MA, Murphy GJ, Waters J, Koch C, et al. (2020). Relationship between simultaneously recorded spiking activity and fluorescence signal in GCaMP6 transgenic mice. BioRxiv 10.1101/788802v2. [DOI] [PMC free article] [PubMed]

[R41] Huet LA, and Hartmann MJZ (2016). Simulations of a Vibrissa Slipping along a Straight Edge and an Analysis of Frictional Effects during Whisking. IEEE Trans. Haptics 9, 158–169. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R42] Isett BR, Feasel SH, Lane MA, and Feldman DE (2018). Slip-Based Coding of Local Shape and Texture in Mouse S1. Neuron 97, 418–433.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R43] Jadhav SP, Wolfe J, and Feldman DE (2009). Sparse temporal coding of elementary tactile features during active whisker sensation. Nat. Neurosci. 12, 792–800. [DOI] [PubMed] [Google Scholar]

[R44] Katz D (1925). Der Autbau der Tastwelt. Zeitschr. Psychol. (Suppl. 7), 1–131. [Google Scholar]

[R45] Khan AG, Poort J, Chadwick A, Blot A, Sahani M, Mrsic-Flogel TD, and Hofer SB (2018). Distinct learning-induced changes in stimulus selectivity and interactions of GABAergic interneuron classes in visual cortex. Nat. Neurosci. 21, 851–859. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R46] Knutsen PM, and Ahissar E (2009). Orthogonal coding of object location. Trends Neurosci. 32, 101–109. [DOI] [PubMed] [Google Scholar]

[R47] Kondo M, Kobayashi K, Ohkura M, Nakai J, and Matsuzaki M (2017). Two-photon calcium imaging of the medial prefrontal cortex and hippocampus without cortical invasion. eLife 6, e26839. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R48] Kremer Y, Léger J-F, Goodman D, Brette R, and Bourdieu L (2011). Late emergence of the vibrissa direction selectivity map in the rat barrel cortex. J. Neurosci. 31, 10689–10700. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R49] Kwon SE, Tsytsarev V, Erzurumlu RS, and O’Connor DH (2018). Organization of orientation-specific whisker deflection responses in layer 2/3 of mouse somatosensory cortex. Neuroscience 368, 46–56. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R50] Lavzin M, Rapoport S, Polsky A, Garion L, and Schiller J (2012). Nonlinear dendritic processing determines angular tuning of barrel cortex neurons in vivo. Nature 490, 397–401. [DOI] [PubMed] [Google Scholar]

[R51] Lederman SJ, and Klatzky RL (1987). Hand movements: a window into haptic object recognition. Cognit. Psychol. 19, 342–368. [DOI] [PubMed] [Google Scholar]

[R52] Lefort S, Tomm C, Floyd Sarria J-C, and Petersen CCH (2009). The excitatory neuronal network of the C2 barrel column in mouse primary somatosensory cortex. Neuron 61, 301–316. [DOI] [PubMed] [Google Scholar]

[R53] LeMessurier AM, Laboy-Juárez KJ, McClain K, Chen S, Nguyen T, and Feldman DE (2019). Enrichment drives emergence of functional columns and improves sensory coding in the whisker map in L2/3 of mouse S1. eLife 8, e46321. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R54] Madisen L, Garner AR, Shimaoka D, Chuong AS, Klapoetke NC, Li L, van der Bourg A, Niino Y, Egolf L, Monetti C, et al. (2015). Transgenic mice for intersectional targeting of neural sensors and effectors with high specificity and performance. Neuron 85, 942–958. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R55] Mehta SB, Whitmer D, Figueroa R, Williams BA, and Kleinfeld D (2007). Active spatial perception in the vibrissa scanning sensorimotor system. PLOS Biol. 5, e15. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R56] O’Connor DH, Peron SP, Huber D, and Svoboda K (2010). Neural activity in barrel cortex underlying vibrissa-based object localization in mice. Neuron 67, 1048–1061. [DOI] [PubMed] [Google Scholar]

[R57] Pachitariu M, Stringer C, Dipoppa M, Schröder S, Rossi LF, Dalgleish H, Carandini M, and Harris KD (2017). Suite2p: beyond 10,000 neurons with standard two-photon microscopy. BioRxiv 10.1101/061507v2. [DOI]

[R58] Pammer L, O’Connor DH, Hires SA, Clack NG, Huber D, Myers EW, and Svoboda K (2013). The mechanical variables underlying object localization along the axis of the whisker. J. Neurosci. 33, 6726–6741. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R59] Peron SP, Freeman J, Iyer V, Guo C, and Svoboda K (2015). A Cellular Resolution Map of Barrel Cortex Activity during Tactile Behavior. Neuron 86, 783–799. [DOI] [PubMed] [Google Scholar]

[R60] Petreanu L, Gutnisky DA, Huber D, Xu NL, O’Connor DH, Tian L, Looger L, and Svoboda K (2012). Activity in motor-sensory projections reveals distributed coding in somatosensation. Nature 489, 299–303. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R61] Pho GN, Goard MJ, Woodson J, Crawford B, and Sur M (2018). Task-dependent representations of stimulus and choice in mouse parietal cortex. Nat. Commun. 9, 2596. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R62] Pluta SR, Lyall EH, Telian GI, Ryapolova-Webb E, and Adesnik H (2017). Surround Integration Organizes a Spatial Map during Active Sensation. Neuron 94, 1220–1233.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R63] Podgorski K, and Ranganathan G (2016). Brain heating induced by near-infrared lasers during multiphoton microscopy. J. Neurophysiol. 116, 1012–1023. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R64] Pont SC, Kappers AML, and Koenderink JJ (1999). Similar mechanisms underlie curvature comparison by static and dynamic touch. Percept. Psychophys. 61, 874–894. [DOI] [PubMed] [Google Scholar]

[R65] Poort J, Khan AG, Pachitariu M, Nemri A, Orsolic I, Krupic J, Bauza M, Sahani M, Keller GB, Mrsic-Flogel TD, and Hofer SB (2015). Learning Enhances Sensory and Multiple Non-sensory Representations in Primary Visual Cortex. Neuron 86, 1478–1490. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R66] Pruszynski JA, and Johansson RS (2014). Edge-orientation processing in first-order tactile neurons. Nat. Neurosci. 17, 1404–1409. [DOI] [PubMed] [Google Scholar]

[R67] Pubols LM, and Leroy RF (1977). Orientation detectors in the primary somatosensory neocortex of the raccoon. Brain Res. 129, 61–74. [DOI] [PubMed] [Google Scholar]

[R68] Ranganathan GN, Apostolides PF, Harnett MT, Xu N-L, Druckmann S, and Magee JC (2018). Active dendritic integration and mixed neocortical network representations during an adaptive sensing behavior. Nat. Neurosci. 21, 1583–1590. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R69] Rose T, Jaepel J, Hübener M, and Bonhoeffer T (2016). Cell-specific restoration of stimulus preference after monocular deprivation in the visual cortex. Science 352, 1319–1322. [DOI] [PubMed] [Google Scholar]

[R70] Runyan CA, Piasini E, Panzeri S, and Harvey CD (2017). Distinct timescales of population coding across cortex. Nature 548, 92–96. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R71] Severson KS, Xu D, Van de Loo M, Bai L, Ginty DD, and O’Connor DH (2017). Active Touch and Self-Motion Encoding by Merkel Cell-Associated Afferents. Neuron 94, 666–676.e9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R72] Simons DJ, and Carvell GE (1989). Thalamocortical response transformation in the rat vibrissa/barrel system. J. Neurophysiol. 61, 311–330. [DOI] [PubMed] [Google Scholar]

[R73] Sofroniew NJ, Vlasov YA, Hires SA, Freeman J, and Svoboda K (2015). Neural coding in barrel cortex during whisker-guided locomotion. eLife 4, e12559. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R74] Solomon JH, and Hartmann MJZ (2011). Radial distance determination in the rat vibrissal system and the effects of Weber’s law. Philos. Trans. R. Soc. Lond. B Biol. Sci. 366, 3049–3057. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R75] Sripati AP, Bensmaia SJ, and Johnson KO (2006). A continuum mechanical model of mechanoreceptive afferent responses to indented spatial patterns. J. Neurophysiol. 95, 3852–3864. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R76] Suter BA, O’Connor T, Iyer V, Petreanu LT, Hooks BM, Kiritani T, Svoboda K, and Shepherd GMG (2010). Ephus: multipurpose data acquisition software for neuroscience experiments. Front. Neural Circuits 4, 100. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R77] Szwed M, Bagdasarian K, and Ahissar E (2003). Encoding of vibrissal active touch. Neuron 40, 621–630. [DOI] [PubMed] [Google Scholar]

[R78] Szwed M, Bagdasarian K, Blumenfeld B, Barak O, Derdikman D, and Ahissar E (2006). Responses of trigeminal ganglion neurons to the radial distance of contact during active vibrissal touch. J. Neurophysiol. 95, 791–802. [DOI] [PubMed] [Google Scholar]

[R79] Wekselblatt JB, Flister ED, Piscopo DM, and Niell CM (2016). Large-scale imaging of cortical dynamics during sensory perception and behavior. J. Neurophysiol. 115, 2852–2866. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R80] Whiteley SJ, Knutsen PM, Matthews DW, and Kleinfeld D (2015). Deflection of a vibrissa leads to a gradient of strain across mechanoreceptors in a mystacial follicle. J. Neurophysiol. 114, 138–145. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R81] Wijntjes MWA, Sato A, Hayward V, and Kappers AML (2009). Local Surface Orientation Dominates Haptic Curvature Discrimination. IEEE Trans. Haptics 2, 94–102. [DOI] [PubMed] [Google Scholar]

[R82] Yamashita T, and Petersen C.C.h. (2016). Target-specific membrane potential dynamics of neocortical projection neurons during goal-directed behavior. eLife 5, e15798. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R83] Yiu AP, Mercaldo V, Yan C, Richards B, Rashid AJ, Hsiang H-LL, Pressey J, Mahadevan V, Tran MM, Kushner SA, et al. (2014). Neurons are recruited to a memory trace based on relative neuronal excitability immediately before training. Neuron 83, 722–735. [DOI] [PubMed] [Google Scholar]

[R84] Ziv Y, Burns LD, Cocker ED, Hamel EO, Ghosh KK, Kitch LJ, El Gamal A, and Schnitzer MJ (2013). Long-term dynamics of CA1 hippocampal place codes. Nat. Neurosci. 16, 264–266. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R85] Zucker E, and Welker WI (1969). Coding of somatic sensory input by vibrissae neurons in the rat’s trigeminal ganglion. Brain Res. 12, 138–156. [DOI] [PubMed] [Google Scholar]

[R86] Zuo Y, Safaai H, Notaro G, Mazzoni A, Panzeri S, and Diamond ME (2015). Complementary contributions of spike timing and spike rate to perceptual decisions in rat S1 and S2 cortex. Curr. Biol. 25, 357–363. [DOI] [PubMed] [Google Scholar]

PERMALINK

Behavioral and Neural Bases of Tactile Shape Discrimination Learning in Head-Fixed Mice

Jinho Kim

Andrew Erskine

Jonathan Andrew Cheung

Samuel Andrew Hires

SUMMARY

In Brief

INTRODUCTION

RESULTS

Single Whiskers Provide Sufficient Tactile Information to Discriminate Surface Angles of Touched Objects

Figure 1. Mice Can Learn to Discriminate Object Surface Angles with a Single Whisker.

Figure 2. Vertical Bending and Slide Distance Are the Most Important Whisker Features for Object-Angle Discrimination.

Touch Evokes Object-Angle Representations in S1

Figure 3. Angle-Tuned Touch-Responsive Excitatory Neurons Are Distributed across L2–4 Barrel Cortex of Naive Mice.

Whisker Features That Best Discriminate Object Angles Also Best Drive Angle Tuning in S1

Figure 4. Vertical Bending and Slide Distance Best Explain Object-Angle Tuning Curves of S1 Excitatory Neurons.

Figure 5. Weak Relationship between Passive Whisker Deflection-Direction and Object-Angle Tuning.

S1 Maintains Angle Tuning Preferences Despite Changes in Active Ensemble Membership across Training

Figure 6. Stable Object Angle Preference Despite Active Ensemble Turnover after 2-Angle Discrimination Training.

Angle Selectivity Increases in Neurons Tuned to Trained Object Angles

Figure 7. Object Angle Discrimination Training Enhanced Angle Selectivity of S1 Neurons Only for Trained Angles.

Figure 8. Two-Angle Discrimination Training Enhanced the Influence of the Reward-Relevant Whisker Feature on Neural Activity and Angle Tuning.

DISCUSSION

STAR★METHODS

RESOURCE AVAILABILITY

Lead Contact

Materials Availability

Data and Code Availability

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Animals

METHOD DETAILS

Cranial window surgeries

Virus injections

Behavioral task

Whisker video recording and tracking

Touch frame detection

Whisker feature analysis

Whisker feature analysis – GLM

Whisker feature analysis - Feature importance

Two-photon microscopy

Imaging data processing

GLM for neuronal activity - ‘Object model’

Object-angle tuning calculation

Cortical depth estimation

GLM for neuronal activity - ‘Whisker model’

Passive whisker deflection under anesthesia

Passive whisker deflection response analysis

Matching planes across sessions (Figure S6)

QUANTIFICATION AND STATISTICAL ANALYSIS

Supplementary Material

Highlights.

ACKNOWLEDGMENTS

Footnotes

REFERENCES

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases