School openings and the COVID-19 outbreak in Italy. A provincial-level analysis using the synthetic control method

Abstract

Schools have been central in the debate about COVID-19. On the one hand, many have argued that they should be kept open, given their importance to youngsters and the future of the country, and the effort many countries have made in establishing protocols to keep them safe. On the other hand, it has been argued that open schools further the spread of the virus, given that these are places with large-scale interaction between teenagers and adults accompanying their children, as well as a major source of congestion on public transportation. We aim to identify the effect of school openings on the spread of COVID-19 contagion. Italy offers an interesting quasi-experimental setting in this regard due to the scattered openings that schools have experienced. By means of a quantitative analysis, employing a synthetic control method approach, we find that Bolzano, the first province in Italy to open schools after the summer break, had far more cases than its synthetic counterfactual, built from a donor pool formed from the other Italian provinces. Results confirm the hypothesis that despite the precautions, opening schools causes an increase in the infection rate, and this must be taken into account by policymakers.

1. Introduction

A growing debate about the efficacy of non-pharmaceutical measures in containing the COVID-19 outbreak has emerged over the last year [3,18,26,28]. Differently from classical policies aimed at strengthening the health system, non-pharmaceutical measures, with their long history of use in the fight against pandemics [6], try to reduce the probability of people contracting the virus [3,23]. Following Hale et al. [16], different national governments adopted heterogeneous measures to contrast the spread of the virus. In building a composite indicator, Hale et al. [16] build a taxonomy of eight different policy actions: i) school closure; ii) workplace closure; iii) cancelation of public events; iv) restrictions on gathering size; v) closure of public transportation; vi) “stay at home” requirements; vii) restrictions on national movement; and viii) restrictions on international travel. The present study focuses on the first family of measures, namely school closures, assessing their effectiveness in combatting the spread of COVID-19, by means of a quantitative analysis that exploits a quasi-experimental setting which occurred in Italy in September 2020.

The second wave of the pandemic, which began in European countries at the end of the 2020 summer, turned the public debate toward the possible effects of opening schools on containment of the COVID pandemic (Lai et al., 2020; Tian et al., 2020; [3,27]). It is worth noting that during the first wave, most of the countries facing the pandemic adopted school closures as a first non-pharmaceutical measure, which was subsequently the most widely adopted measure in the whole world. By 18 March 2020, no fewer than 107 countries had implemented national school closures [27]. Indeed, despite the pedagogical importance of face-to-face teaching activities, keeping schools open may increase the diffusion of the virus via two mechanisms that act as catalysts for the spread of infection, namely: the presence of numerous people in relatively small classrooms, and the increase in the numbers of people using local public transport to reach schools [4].

The present paper aims to contribute to the scientific literature evaluating the efficacy and impact of school closures in fighting the spread of COVID-19, by means of a synthetic control method (henceforth SCM) based on Italian provincial-level data.

As pointed out by Alfano and Ercolano [3], Italy is an interesting case study with regard to COVID-19, for several reasons. Among these, other than the heterogeneity of Italian regions (Ercolano, 2012) and the importance of different stocks of social capital with regard to NPI compliance [5], there is the fact that at the beginning of September the spread of the virus started to increase in different provinces, due in part to the final authority on school re-openings being left by the national government to the different regions. Indeed, while the central government is responsible for deciding the total number of days in the school year, local governments are responsible for planning the calendar. This means that any of Italy's 19 regions, along with the 2 autonomous provinces of Trento and Bolzano, may decide when to open schools in the territory they govern.

For this reason, it is possible to observe different starting days for school openings across Italy. In 2020, the autonomous province of Bolzano was the first Italian province to open schools, and did so on 7 September, while the majority of the regions, following governmental advice, opened schools on 14 September. Other regions delayed the opening to 16 September (Friuli), 22 September (Sardinia), or as late as 24 September (Abruzzo, Basilicata, Calabria, Campania and Puglia).

It is notable that even in early 2021 the autonomous province of Bolzano remains among the Italian provinces paying the highest price for the epidemic. Looking at the political debate, Arno Kompatscher, president of the province, announced the need to enforce extraordinary local measures, stricter than the national ones, at a press conference held on 5 February 2021. Accordingly, since 8 February Bolzano has been the only Italian province in a strict lockdown, with many shops (considered non-essential) forced to stay closed, and a ban on all citizens leaving their municipality of residence, as well as the closure of junior-high and high schools. At the time of writing, the last available update of the European map from the European centre for Disease Prevention and Control (i.e. the version published on 25 February) colours Bolzano in dark red, signifying a 14-day notification rate per 100.000 inhabitants of over 500, among the worst in Europe. When adjusting the cases for the population size of each Italian region, on 25 February the autonomous province of Bolzano was the area where COVID-19 had the highest relative incidence. Is Bolzano paying the cost of a longer second wave in part due to an early opening of its schools?

Our empirical framework relies on the specificity of the Italian case; SCM allows us to evaluate the evolution of the pandemic in reality, against a synthetic counterfactual scenario [1]. More specifically, with this design we aim to assess the effect of opening schools in the province of Bolzano, which as mentioned above was the province that opened its schools more than a week before neighbouring provinces (and two weeks before late openers). From this process, we may derive the effect of opening schools on the spread of COVID-19. In order to do so, we build a synthetic control unit that mimics the trend observed in Bolzano before schools opened. Therefore, any difference observed after schools opened in Bolzano can be imputed to the early opening of schools in this province.

To the best of our knowledge, this paper is the first attempt to use this methodology to measure the impact of school openings on containment of the pandemic using local level data, thus relying on a common legal, institutional and cultural framework that increases the internal consistency of the analysis. It is worth noting that a recent contribution to this literature uses SCM design to evaluate school closure in a cross-countries perspective [22]. Our paper could add further clarity regarding the effectiveness of such measures and the methodological approach providing first evidence based on local data.

SCM has also been used to evaluate the effects of other policies designed to prevent the spread of COVID-19, namely lockdown measures [10] and the use of face masks [25]. This approach should mitigate some of the typical limitations of other methodological approaches based on cross-regional comparisons. Indeed, previous results (such as [4]) may simply describe, on average, the correlation between school openings and the spread of the pandemic. But in the absence of a counterfactual, these results could also be derived from unobservable characteristics within regions. Instead, SCM allows us to assess a causal effect of the opening of schools on the evolution of the contagion, and therefore provides very valuable information to policymakers.

The rest of the paper is structured as follows: Section 2 shows the background related to the topic; Section 3 describes the data and methodology; Section 4 presents the results, while Section 5 discusses it. As usual the final paragraph presents the conclusions.

2. Background

There is growing debate about the efficacy of school closures in containing the spread of pandemic. This measure can be effective by means of a twofold mechanism: on the one hand, implementing physical distancing among children, and on the other hand, encouraging children's parents to stay home (i.e. not taking them to school), thereby reducing social contact and occasions for infection.

A part of the literature, whose evidence for the efficacy of such measure comes principally from results extracted by previous studies on other diseases, such as SARS [9], suggests that at the moment school closures may have undefined benefits but more defined costs [20].

Nevertheless, the evidence from this literature, which has focused especially on influenza [8], is nuanced. Some studies suggest that closing schools is neither necessary nor useful in reducing the spread of infection, if certain alternative policies are adopted [21].

A study focused on the closure of kindergartens and primary schools in Hong Kong in 2008, analysing prospective influenza surveillance data before, during, and after the closure, did not detect a substantial effect on community transmission [12]. Kawano and Kakehashi (2015), using a regression model based on the Oita case in Japan during the H1N1 pandemic of 2009, argued that school closure is effective in reducing the spread of the virus, and recommended a closure period longer than 4 days. Rashid et al. [24] take a different approach, suggesting that school closures might be effective not because they prevent children from meeting each other, but because by forcing parents to work at home, this policy manages to reduce the spread of the virus in workplaces. According to Jackson et al. [17], school closures appear to be correlated with a reduction in influenza transmission, especially among school-aged children, but some authors suggest that the heterogeneity in the available data does not allow us to identify an optimal strategy. Luca et al. [19], using a data-driven spatial metapopulation model calibrated on the 2008/2009 influenza season in Belgium, suggest that holidays reduce the peak of influenza epidemics.

As regards the studies focused on the COVID-19 pandemic, although recent contributions recognize the effectiveness of such measures in containing the spread of virus, the efficacy of school closure is still ambiguous [13], unlike other physical distancing measures and proper hand washing. According to Viner et al. [27], school closure may be capable of preventing 2–4% of deaths, but this reduction rate seems much lower than other physical distancing measures. Alfano and Ercolano [4], by means of a panel model based on Italian provincial level data, show that school openings have a positive and exponential effect on the number of new cases, and suggest that we pay due attention to the important trade-off between on-site school activities and the safeguard of public health. Marziano et al. (2020), investigating the Italian case by means of a mathematical model, detect that the reopening of some schools in spring may be correlated with a marginal effect on the spread of COVID. Moreover, the authors suggest that great attention should be paid to collective measures in periods where individual-level measures may be less effective, due to a larger incidence in the community.

Moving on to a cross-countries perspective, Neidhöfer and Neidhöfer [22], analysing the effectiveness of the mitigation strategies adopted in three different countries (namely Italy, Argentina and South Korea), find a positive effect of school closures, especially when these measures have been adopted early. By means of SCM, the authors construct different counterfactual scenarios based on the observed development of the epidemic in countries where school closures were enacted later or not at all. Indeed, SCM represents a methodological solution for constructing control units based on the available information on countries characteristics, providing a more appropriate comparison to the affected unit than any other unaffected unit taken individually [7]. Nevertheless, the international comparison from which the donor pool is extracted may also represent a methodological caveat, due to the issues associated with combining the different measures adopted by each country.

Our work contributes to this literature by providing an SCM design, based on Italian provincial data, in order to assess the efficacy of school closures through a unique measure at a sub-statal level, thus giving a further and more robust proof of the policy's efficacy (making it clear both at a national and sub-national level). This is far more relevant for countries (such as Italy) where local governments are responsible for deciding school closure policies during the pandemic.

3. Materials and methods

SCM is designed to evaluate the effects of treatments performed on a small number of units [1,2]. Our empirical setting is coherent with this scenario, as we exploit the decision by the province of Bolzano to open its schools earlier than any other province in Italy. Therefore, the treated unit in our analysis is the province of Bolzano, and the treatment is the opening of schools, which occurred on 7 September 2020. The rationale behind using SCM is that all the units (the provinces in our empirical setting) behave similarly before the treatment, and only one of them differs from the others. However, since all the provinces are different from one another, the idea is to build a counterfactual (synthetic) unit by estimating a weighted average of the non-treated units (known as the donor pool). The weights are computed in order to have a synthetic control unit that matches the treated unit on the relevant variables before the treatment. Therefore, differences between treated and synthetic control units after the treatment depend on the treatment itself [1].

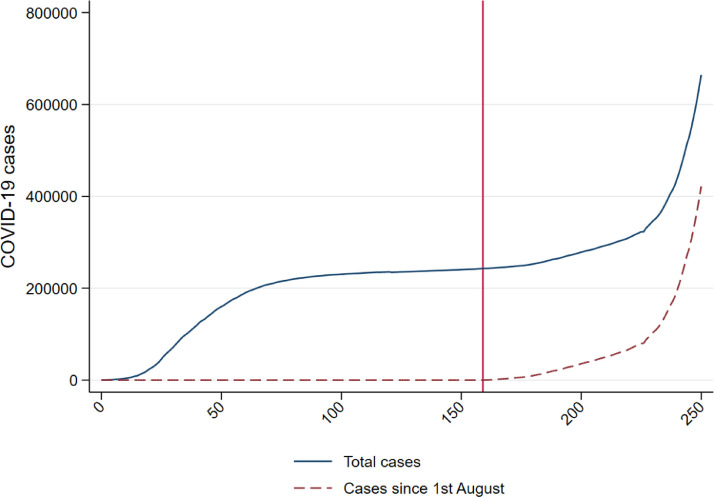
Counterfactual analyses require a careful identification of the outcome variable, which in our case, however, is bound by data availability at sub-national level. Unfortunately, we cannot follow Neidhöfer and Neidhöfer [22] because the number of deaths is not available at the sub-national level. Also, positive case-to-test ratios are impossible to compute because the number of tests is not provided at the level of our analysis. For this reason, we perform the analysis on the log of cases after the first wave and on a seven-day moving average of daily new cases. The log of cases takes into account the exponential nature of the evolution of the COVID-19 pandemic. However, since the pandemic had a rather heterogeneous impact during the first wave in Italy (which lasted from around the end of February to the beginning of June), we focus on the total number of cases observed since 1 August (i.e., the cumulative sum of daily new cases reported after that date). Indeed, by using the total number of cases observed from the beginning of the pandemic we would underestimate the variation of positive cases in regions where the pandemic struck more severely during the first wave, and overestimate the variation of cases where the first wave was less acute. For this reason, we track the evolution of the pandemic from 1 August, when the curve of contagion became flat (as presented in Fig. 1 ), and take as outcome variable the log of the total number of cases observed after that day (for the sake of clarity we will call this variable “total new cases”).

Fig. 1.

Total COVID-19 cases in Italy, from the beginning of the pandemic (22 February) and from 1 August (second wave). Vertical line represents 1 August.

In order to provide a more detailed picture of the evolution of the spread of the virus, we also replicate the analysis using a seven-day moving average of daily new cases, computed as the average of the cases for each day and the six days before, in order to smooth the data from the variation observed on different weekdays.

To build a counterfactual, we require the synthetic control unit to track the outcome variables as closely as possible each day up to seven days before the treatment. We also require the synthetic control unit to be as close as possible to a number of variables that potentially predict the spread of the virus within a province. We include the total number of cases the day before the treatment, because a greater number of cases during the first wave could impact on herd immunity and on citizens’ behaviour, a proxy for income per capita in the province, total population, the share of population at schooling age, population density, the share of population in the province living in municipalities with less than thirty thousand inhabitants, and finally the demand for local public transportation (expressed as passengers per year per inhabitant), as public transportation is a potential driver for contagion [15]. Data about COVID-19 infections are gathered from the Italian Ministry of Health's dataset, which reports official data for each province and day; income per capita in the province is computed by dividing the total taxable income of the province by the population of the same province (data about taxable income are taken from the Italian Ministry of Economic and Finance, MEF, and data about population are taken from ISTAT); all the other data are extracted from the Italian National Statistics Institute (ISTAT) database.

At a first step of the analysis, we include all the provinces other than Bolzano in the donor pool. This choice allows us to perform the computation of weights on a large number of provinces, therefore exploiting the potential of SCM. We next run a set of placebo tests, performing the same analysis on all the provinces in the donor pool. According to Galiani and Quistorff [[14], p. 836], “if the distribution of placebo effects yields many effects as large as the main estimate, then it is likely that the estimated effect was observed by chance”. This allows us to calculate the p-values of the estimated effect. However, the placebo effect may be imprecisely matched in the pre-treatment period, which would result in p-values being too conservative. For this reason, we weight placebo effects using their pre-treatment match quality (measured as the root mean squared prediction error, or RMSPE) to obtain standardized p-values [14]. Finally, we perform a further robustness check for both our outcome variables by computing a different SCM method [11], which allows us to verify the size of the pre-treatment error via a non-parametric estimation of the synthetic control.

The main limitation of SCM is its external consistency (or lack thereof). Indeed, the generalization of the results of this study to different contexts should be made with extreme caution, given the intrinsic limitations on the external validity of the procedure. However, the evidence presented in this article could nonetheless help in solving a part of the puzzle about the spread of the pandemic, and suggests the impact that school openings have had on the unfolding of the pandemic, at least in Italy.

Nevertheless, in our opinion, local data may overcome the issues related to cross-national heterogeneity in the implementation of measures of contrast to the pandemic. As pointed out by Hale et al. [16], a univocal measure of government responses to COVID-19 is hard to build: looking at the case of schools, the authors state (p. 8) that in each country “in some places, all schools have been shut; in other places, universities closed on a different timescale than primary schools; in other places still, schools remain open only for the children of essential workers.” Instead, a local-based approach can rely on more homogeneous measures, which could be one of the possibilities for overcoming such limitations.

Table 1 summarizes the seven predictors for Bolzano and of synthetic Bolzano in the estimation, with the log of total cases as outcome variable, where the latter is constructed with positive weights assigned to Reggio nell'Emilia, Aosta, Trento and Crotone, in descending order. Table 2 provides a summary for the estimation performed using the seven-day moving average of new cases, where the synthetic control is built from Aosta, Reggio nell'Emilia, Torino and Roma.

Table 1.

Profile of synthetic Bolzano using total cases.

Variables	Bolzano	Synthetic Control
Log new total COVID-19 cases	5.537668	5.534209
Total COVID-19 cases	3003	4968.366
Income	22,067.89	21,400.83
Total population	532,080	494,984.8
Population between 6 and 18 (percent)	0.138203	0.130311
Population density	71.9027	209.2393
Population in municipalities under 30,000 inhabitants (percent)	0.720762	0.67813
Local public transport demand	112.2986	82.60034
RMSPE	–	0.0419693

Table 2.

Profile of synthetic Bolzano using 7-day moving average.

Variables	Bolzano	Synthetic Control
Seven-day moving average of new cases	8.75	8.781946
Total COVID-19 cases	3003	3648.46
Income	22,067.89	20,918.85
Total population	532,080	482,806.6
Population between 6 and 18 (percent)	0.138203	0.12335
Population density	71.9027	127.4076
Population in municipalities under 30,000 inhabitants (percent)	0.720762	0.680643
Local public transport demand	112.2986	61.42207
RMSPE	–	2.044566

4. Results

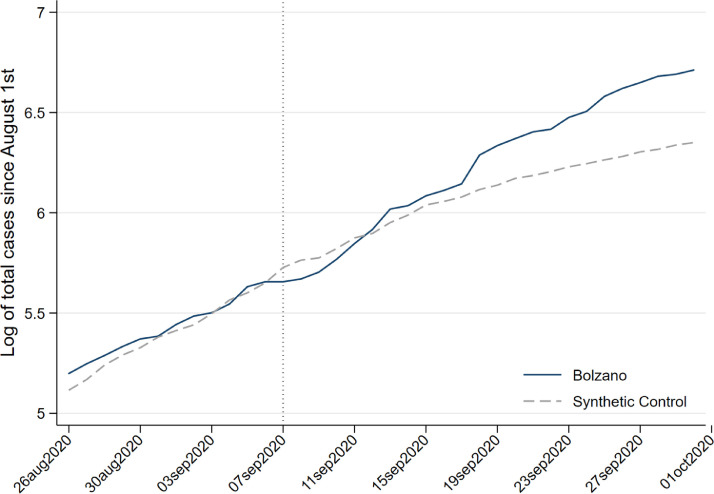
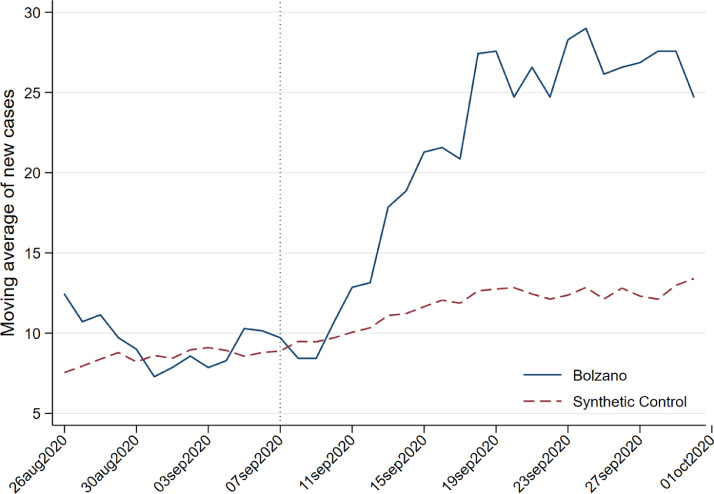
Fig. 2 shows a graphic representation of the infection dynamic in Bolzano province (solid line) compared with a counterfactual outcome for Bolzano (dashed line) built from all the other Italian provinces (which, as explained previously, at the time had closed schools, given that Bolzano was the first province to open them). The vertical axis measures cumulative infections in logs, while the horizontal axis represents calendar days, starting from 26 August. As can be seen, the period before the vertical line (placed at 7 September, the day on which Bolzano opened its schools) suggests that our choice of variables created a counterfactual that follows a dynamic that is quite similar to that of Bolzano, given how closely the two lines overlap.

Fig. 2.

SCM with synthetic Bolzano built from a donor pool composed of all Italian provinces.

After the schools opened, the dynamic of COVID incidence in the real Bolzano grows more than that in its counterfactual. The incidence of COVID in the former gets bigger than in the latter on 13 September, 6 days after the opening of schools, and continues to grow more than the counterfactual. In supplementary material we provide Table A3, which analytically summarizes the data from which the graph for Bolzano and synthetic Bolzano is built. It shows that 15 days after the opening of schools, the gap between the two widens considerably, jumping to an incidence of 0.19. This time lag is coherent with the time needed to suspect someone of being infected and test them, suggesting that schools have an impact on this. Hence, these findings suggest that the opening of schools has indeed had a significant impact on the rate of COVID-19 infections.

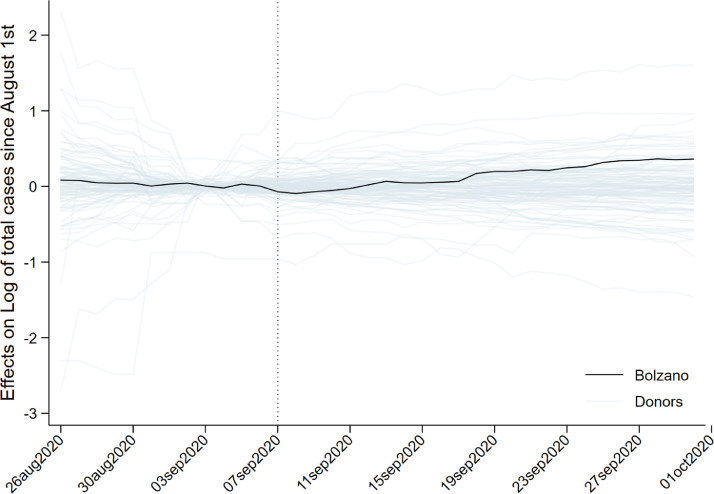
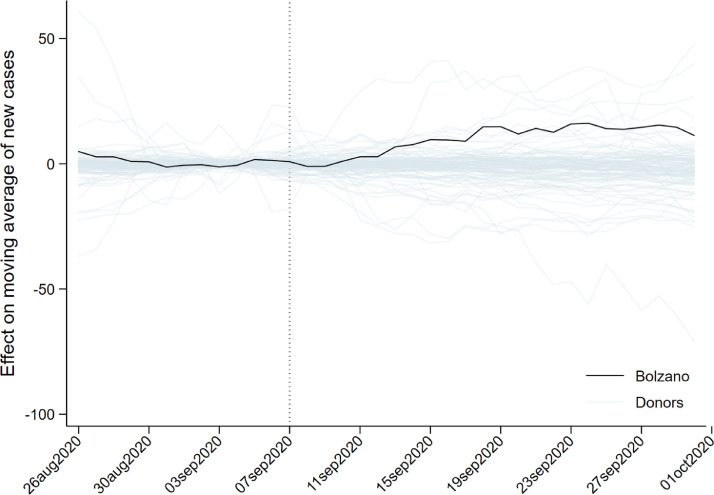
Fig. 3 reports the difference between each province in the donor pool and its estimated synthetic counterfactual, showing the placebo effects estimated for all the provinces in the donor pool contrasted with the effect estimated for Bolzano, which is represented by the solid black line. The trend of Bolzano starts to increase around 10 days after the opening of schools, becoming higher than the majority of the placebo effects. This corresponds to lower standardized p-values (as shown in Table A1 in supplementary material): on 22 September the effect estimated for Bolzano is larger than 92% of the placebo effects (i.e. 1 – the standardized p-value). All this suggests that the incidence measured in Bolzano is due to what differentiated this province from others at the time: namely, the opening of schools.

Fig. 3.

Effects estimated for all the provinces in the donor pool for the same treatment period.

It should be noted that this finding is in line with the average amount of time the literature suggests is needed to present symptoms after a COVID-19; 97.5% of those who develop symptoms do so within 11.5 days of infection, with a 95% confidence interval of between 8.2 and 15.6 days [19]. The number of cases in Bolzano continues to grow more than in the synthetic Bolzano throughout the period analysed, going from a delta of 0.065835 in the incidence rate in the population, observed on 18 September, ten days after the opening of schools, to a delta of 0. 3,530,488 at the end of the month. All this suggests the highly significant role of school openings in the spread of the infection.

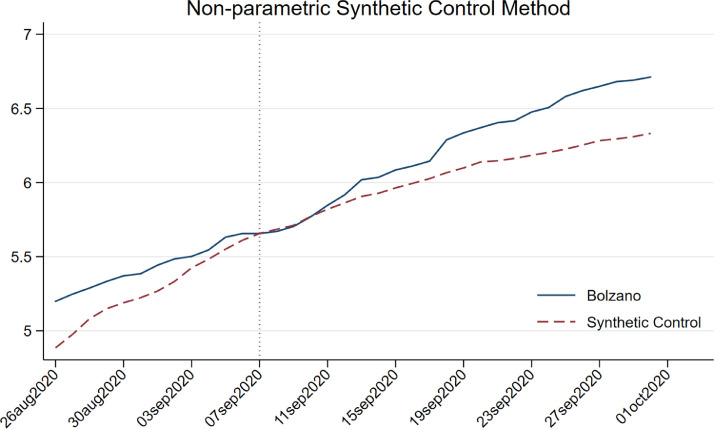
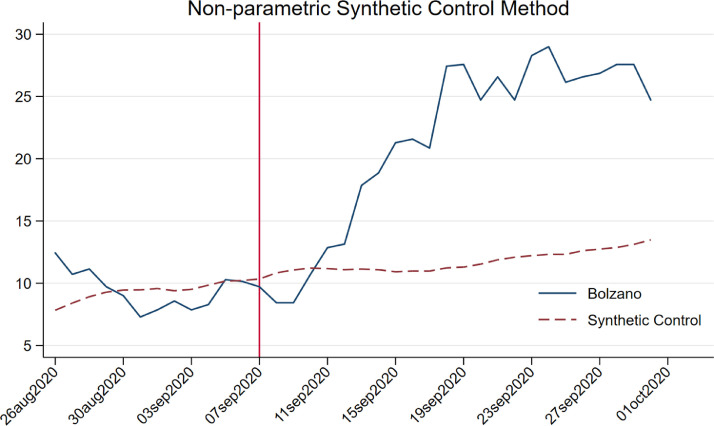
Fig. 4 reports the results of an SCM performed by means of a non-parametric estimation. We follow Cerulli [11] in computing the optimal bandwidth (the outcome is available in the supplementary material, Figures A1 and A2) for a tricube kernel, which best fits our data. As a result, the RMSPE rises to 0.17, and the pre-treatment fit does not appear superior to the parametric method. Nevertheless, the post-treatment period shows a similar pattern to the parametric estimation, as the log of total cases after 1 August increases more in Bolzano than in its synthetic counterpart.

Fig. 4.

Non-parametric SCM with synthetic Bolzano built from a donor pool composed of all Italian provinces. Kernel: Tricube, Bandwidth 0.1.

In Fig. 5 we replicate the analysis using a seven-day moving average of new cases as outcome variable. Before school openings Bolzano shows a less stable pattern than its synthetic counterfactual, however the two trends are comparable. After the treatment, Bolzano shows a rise in the seven-day moving average of new cases; this is not observed in the counterfactual, which increases, but only very slightly. Again, we test the robustness of this result by estimating placebo effects for all the provinces in the donor pool, and show the effects in Fig. 5. The darker line, which represents Bolzano, shows a sizable rise after school openings. In fact, ten days after schools opened in Bolzano, the seven-day moving average reports about 9 new cases more in Bolzano than in its synthetic counterfactual, which is an effect larger than those estimated for 93% of the placebo tests. On 25 September the difference doubles, with Bolzano reporting about 16 more new cases, an effect larger than those estimated for 94% of the placebo tests. Finally, we perform a non-parametric estimation, which is shown in Fig. 6 . After the computation of the optimal bandwidth the RMSPE drops to 1.876, and the results are definitively comparable with those of the previous estimation (Fig. 7 ).

Fig. 5.

SCM with synthetic Bolzano built from a donor pool composed of all Italian provinces.

Fig. 6.

Effects estimated for all the provinces in the donor pool for the same treatment period.

Fig. 7.

Non-parametric SCM with synthetic Bolzano built from a donor pool composed of all Italian provinces. Kernel: Tricube, Bandwidth 1.4.

5. Discussion

Schools are a very important part of human formation. Children and teenagers obtain much more from the hours spent in school than what they simply learn in classes (which, nonetheless, is a very important thing in creating socialized women and men and forging the citizens of tomorrow). Nonetheless, schools play a major role in creating opportunities for students and their relatives to meet. During a pandemic, this means increasing opportunities for the virus to circulate.

Even if schools are tightly controlled and various protocols are put in place to prevent undetected infections occurring within their walls, students have to reach school buildings somehow, and it is hard to control their behaviour once classes are over. Furthermore, accompanying children to school means increasing circulation within the city and filling the public transportation system, in the event that parents, whether from choice or necessity, cannot reach their children's schools with private transportation.

All this suggests that school openings do indeed have an effect on the spread of infection. This is what our analysis suggests: the first province in Italy to open the schools, two weeks after opening, had an incidence of COVID-19 cases that was much higher than what a counterfactual, built synthetically from data in other Italian provinces, suggests it ought to have been.

6. Conclusion

While the external validity of our results is questionable, and should of course be taken with caution, our findings suggest that opening schools causes an increase in COVID-19 cases. While this does not necessarily mean that the cost in terms of the spread of infection is lower than the cost of imposing distance learning on a generation of students, it is an important result that policymakers should take into account when deciding how to face the pandemic.

Accordingly, we may suggest to policymakers that any decision to open or re-open the schools should be considered very carefully. Indeed, a rushed re-opening of schools may condemn hard-won results from social-distancing policies and other sacrifices to waste.