Volumetric prediction of breathing and slow drifting motion in the abdomen using radial MRI and multi-temporal resolution modeling

Abstract

Abdominal organ motions introduce geometric uncertainties to radiotherapy. This study investigates a multi-temporal resolution 3D motion prediction scheme that accounts for both breathing and slow drifting motion in the abdomen in support of MRI-guided radiotherapy. Ten-minute MRI scans were acquired for 8 patients using a volumetric golden-angle stack-of-stars sequence. The first five-minutes was used for patient-specific motion modeling. Fast breathing motion was modeled from high temporal resolution radial k-space samples, which served as a navigator signal to sort k-space data into different bins for high spatial resolution reconstruction of breathing motion states. Slow drifting motion was modeled from a lower temporal resolution image time series which was reconstructed by sequentially combining a large number of breathing-corrected k-space samples. Principal components analysis (PCA) was performed on deformation fields between different motion states. Gaussian kernel regression and linear extrapolation were used to predict PCA coefficients of future motion states for breathing motion (340 ms ahead of acquisition) and slow drifting motion (8.5 s ahead of acquisition) respectively. k-space data from the remaining five-minutes was used to compare ground truth motions states obtained from retrospective reconstruction/deformation with predictions. Median distances between predicted and ground truth centroid positions of gross tumor volume (GTV) and organs at risk (OARs) were less than 1 mm on average. 95- percentile Hausdorff distances between predicted and ground truth GTV contours of various breathing motions states were 2 mm on average, which was smaller than the imaging resolution and 95-percentile Hausdorff distances between predicted and ground truth OAR contours of different slow drifting motion states were less than 0.2 mm. These results suggest that multi-temporal resolution motion models are capable of volumetric predictions of breathing and slow drifting motion with sufficient accuracy and temporal resolution for MRI-based tracking, and thus have potential for supporting MRI-guided abdominal radiotherapy.

1. Introduction

Precision abdominal radiotherapy is challenged by complex motions (Wysocka et al 2010, Abbas et al 2014). Displacements and deformations of abdominal organs during treatment delivery may result in under dosage to the target volume and/or over dosage to organs at risk (OARs) (Balter et al 1996, Aruga et al 2000, Jayachandran et al 2010). The recent advent of MRI-guided radiation therapy shows promise for improved treatment precision by gating treatment delivery based on tumor and/or nearby tissue position changes (Wojcieszynski et al 2016). However, linear accelerator gating involves multiple steps including imaging, localization and evaluation of structure positions relative to the gating window. The time required to complete these steps results in system latency and will negatively impact gating efficiency/accuracy (Borman et al 2018). To mitigate such latency, it is desirable to predict the future state of patient anatomic configurations as opposed to the last measured state.

While various methods have been proposed for MRI-based motion prediction, most existing studies have focused on predicting low-dimensional motion information such as a motion traces of individual tracking points (Yun et al 2012, Yun et al 2013, Bourque et al 2018), which may be oversimplified for the complex motion patterns of abdominal organs. Recent work by Ginn et al (Ginn et al 2020) proposed a regression-based method to predict motion information across the entire imaging field of view of Cine-MRI, yet 2D imaging was not sufficient to predict out-of-plane motions. The long acquisition time for volumetric imaging makes high temporal resolution 3D motion prediction a challenging task. Several studies have investigated estimation of 3D motion information from 2D Cine MRI (Bjerre et al 2013, Stemkens et al 2016, Paganelli et al 2018, Mickevicius and Paulson 2019) and a fast 3D imaging technique (Feng et al 2020) has also been proposed with the aim of reducing imaging latency resulting from synthesis of 3D images from 2D samples. However, system latency in MRI-guided radiotherapy includes additional time-consuming elements such as image analysis and action implementation on the linear accelerator, which necessitates prediction of motion states ahead of acquisition despite utilization of fast imaging. Furthermore, high temporal resolution 3D imaging or motion estimation usually requires combining pre-learned motion models with acquired image samples. Although abdominal motion can be triggered by many factors, including breathing, change of organ filling status and change of internal anatomic organ arrangements (Wysocka et al 2010, Abbas et al 2014), only breathing motion states have been modeled in most studies (Zhang et al 2007, Li et al 2011, Fayad et al 2012). Non- respiratory motion in the abdomen has been shown to be significant for radiotherapy (Mostafaei et al 2018, Liu et al 2021). Therefore, breathing-only motion modeling may be insufficient in guiding accurate radiation treatment delivery.

In this study, we proposed a volumetric motion prediction algorithm that combines volumetric radial MRI acquisition with patient-specific motion modeling. Abdominal organ motions induced by both breathing and internal anatomical rearrangements were investigated. The radial sampling pattern allowed for reconstruction of multi-temporal resolution volumetric image time series, from which motions occurring over different time scales could be extracted and modeled separately. Principal component analysis (PCA)- based motion models were used to reduce the problem of predicting high-dimensional deformation vector fields between a reference state and different motion states to that of predicting low dimensional motion model parameters. We evaluated the motion prediction accuracy by comparing predicted centroid positions and contours of both tumor targets and OARs to the ground truth obtained from retrospective image reconstruction.

2. Methods and materials

2.1. Image acquisition

Under an institution review board approved protocol (The University of Michigan Institutional Review Board, HUM00068061), MRI examinations of 8 patients with intrahepatic tumors were investigated. Each examination consisted of a 10 min free-breathing scan acquired using a golden-angle stack-of-stars spoiled gradient echo sequence (Chandarana et al 2014, Feng et al 2016) with fat suppression, as part of a scan protocol designed to assess liver function using dynamic contrast-enhanced (DCE)-MRI (Cao et al 2013, Wang et al 2016, Simeth et al 2018). Radial readout lines were acquired in the axial plane whereas Cartesian phase encoding was performed in the caudal-cranial direction. A stack of radial k-space samples (termed ‘spoke’ for convenience) was collected every 170 ms. The total number of k-space spokes from each examination was 3500. All MR images were acquired using an in-house 3 Tesla scanner (Skyra, Siemens Medical Systems, Erlangen, Germany) with an 18-channel flexible surface coil (BodyMatrix) placed anteriorly and 1 or more posterior 4-channel coils embedded in the patient couch (Spine Matrix). The field of view covered the liver, stomach and a large portion of the intestines. The imaging parameters ranged from 1.14 to 1.21 ms for echo time, 2.71–4.51 ms for repetition time, 10°–14° for flip angle, 2–2.45 mm for in-plane voxel size and 3–4 mm for slice thickness. The size of the imaging matrix was 192 × 192, the number of slices was 64 and the bandwidth was 900 Hz per pixel.

2.2. Multi-temporal resolution image time series reconstruction

A multi-temporal resolution image time series was reconstructed for each patient using data from the first 5 min of each examination (1750 spokes). A previously published technique (Johansson et al 2018a) was first used to reconstruct high temporal resolution image volumes to assess and label the breathing motion state of each spoke and subsequently extract high spatial resolution breathing motion states through k-space sorting and binning. Here we give a brief overview of the method. High temporal resolution image series was reconstructed using a Gaussian temporal view sharing filter (Barger et al 2002) that centered around each k-space spoke with σ = 1 spoke at the center and σ = 3 spokes at the periphery. Rigid body registration was performed across the image time series, from which displacements of liver at different time points were estimated and used as a respiratory signal (Johansson et al 2018b). k-space spokes were then sorted from inhale to exhale based on their respiratory signal. High spatial resolution breathing motion states were reconstructed by combining the sorted k-space spokes using a Gaussian view sharing filter with σ = 175 spokes at center and σ = 350 spokes at periphery with a sampling rate of 175 spokes, which resulted in 11 breathing motion states. Finally, deformable registration was performed across reconstructed breathing motion states and the resulted deformation fields were applied to back projections of k-space spokes to correct all spokes to the exhale state.

After removal of breathing motion, an image time series with lower temporal resolution was reconstructed to illustrate changes induced by slow drifting motion, as previously done for slow anatomical configuration change analysis (Liu et al 2021). The time series was reconstructed by applying a Gaussian temporal view sharing filter (Barger et al 2002) that combined breathing motion-corrected spokes sequentially with σ = 200 spokes at the center and σ = 500 spokes at the periphery of the k-space with a sampling rate of 100 spokes, yielding 18 slow drifting motion states. The width of the Gaussian filter was chosen such that cyclic gastrointestinal (GI) motions that occur at a higher temporal rate (2–3 cycles min⁻¹) (Mutic and Dempsey 2014) were blurred out, with remaining visible changes primarily attributable to slow drifting motions of GI structures.

2.3. Breathing motion modeling and prediction

2.3.1. Breathing motion modeling

Figure 1 shows the workflow of breathing motion states reconstruction and modeling. The first image volume of the slow drifting motion time series, which was reconstructed by combining k-space spokes acquired at the beginning of the examination and corrected to the exhale state, was chosen as the reference image. Cubic B-spline deformable registration, implemented in NiftyReg (Modat et al 2010) with normalized mutual information as the cost function, which has been shown effective in aligning breathing motion states in previous studies (Johansson et al 2018a), was used to match the reference image to reconstructed breathing motion states. The B-spline grid spacing was 3 × 3 × 2 voxels and penalties on the log of Jacobian determinant and the bending energy were 0.8 and 0.005 respectively, which are the same as previous studies (Johansson et al 2018a). The deformable registration process produced a series of deformation fields B = [B₁, B₂, …, B₁₁] ∈ R^{192 × 192 × 64 × 3 × 11}, where B_i described changes of abdominal configurations from reference to breathing motion state i.

Figure 1.

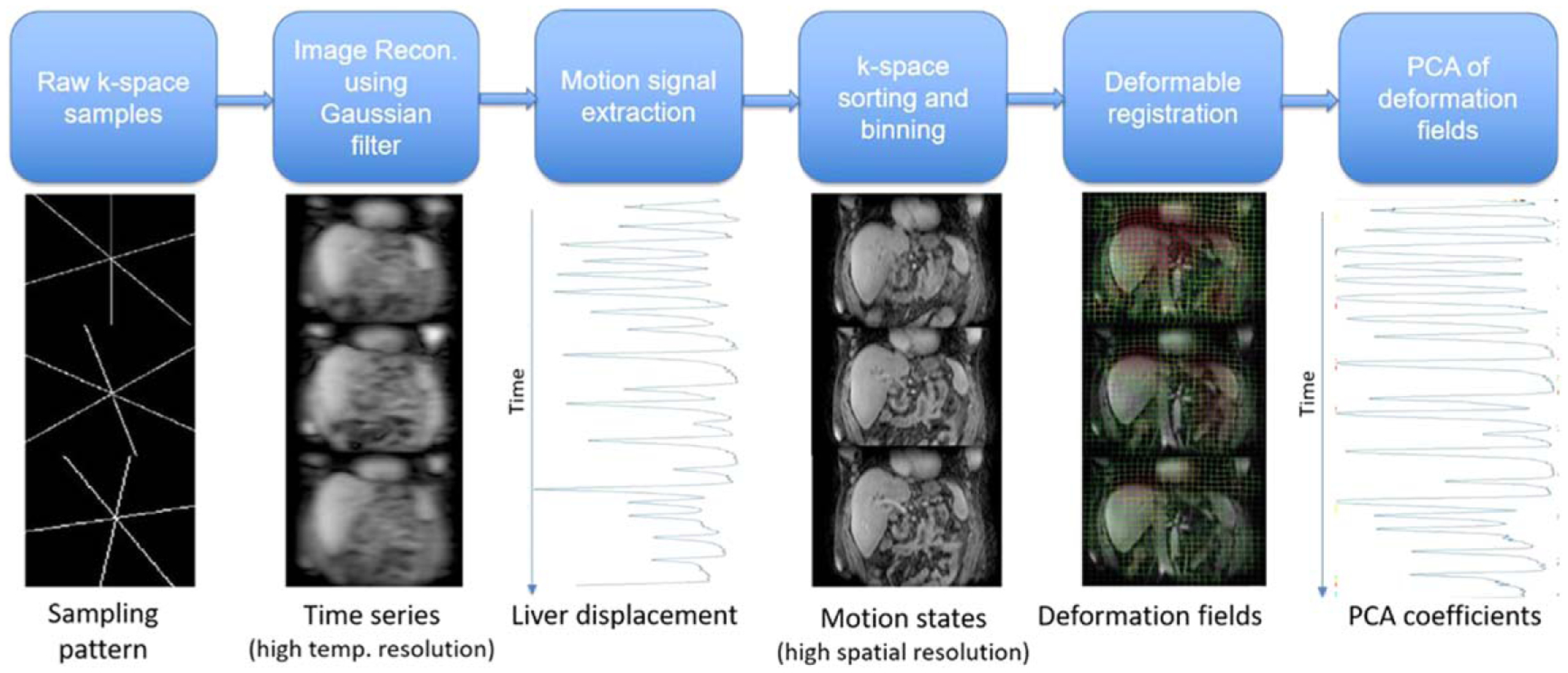
Workflow of breathing motion model construction.

For a compact description of breathing motion state, a breathing motion model was constructed by performing PCA on the deformation fields. Each deformation field Bi ∈ R^{192×192×64×3} was organized into a vector b_i. PCA was performed on the matrix M = [b₁, b₂, ⋯, b₁₁] to reduce the high dimensional breathing motion state b_i to a single parameter α_i, by projecting b_i onto the orthogonal space spanned by the leading PCA mode m₁

$${\alpha }_i=m_1{m_1}^T\left(b_i-m_0\right),$$ (1)

where m₀ is the mean vector of M. Linear interpolation of the PCA coefficient array α = [α₁, α₂, ⋯, α₁₁] to a vector $\tilde{\mathit{\alpha }}$ of length 1750 and re-sorting $\tilde{\mathit{\alpha }}$ based on the respiratory motion signal associated each k-space spoke with a motion state parameter $\tilde{\alpha }$.

2.3.2. Breathing motion prediction via kernel regression

Figure 2 describes the workflow for breathing motion prediction. Sparse radial spokes acquired with high temporal resolution were reconstructed into low spatial resolution image samples. Future motion states were estimated by nonlinear kernel regression between acquired image samples and motion model parameters (PC coefficients), where high spatial resolution deformation fields were reconstructed by combining estimated PC coefficients with PC modes and used to deform the reference image volume to match future motion states. Specifically, for a k-space spoke k_i acquired at time point t_i, an image volume I_i was reconstructed using a view sharing filter with σ = 1 that centered around k_i and combined spokes k_i−1 and k_i+1 at the k-space periphery to reduce aliasing. The associated motion model parameter β_i was calculated as a weighted sum of motion model parameters ${\tilde{\alpha }}_j$, j = 1, 2, ⋯, 1750 from the training dataset, where the weights were determined by a Gaussian kernel function $K(x)=\frac{1}{h\sqrt{2\pi }}{e}^{-{\left(\frac{x}{h\sqrt{2}}\right)}^2}$ that calculates the nonlinear distance between I_i and training image samples I_j. Specifically, we calculated x as the averaged intensity differences between I_i and I_j across voxels that are within the boundaries of the liver volume defined on the reference image and determined β_i as

$${\beta }_i=\frac{\sum _{j=1}^{1750}K(x){\tilde{\alpha }}_j}{\sum _{j=1}^{1750}K(x)}.$$ (2)

Figure 2.

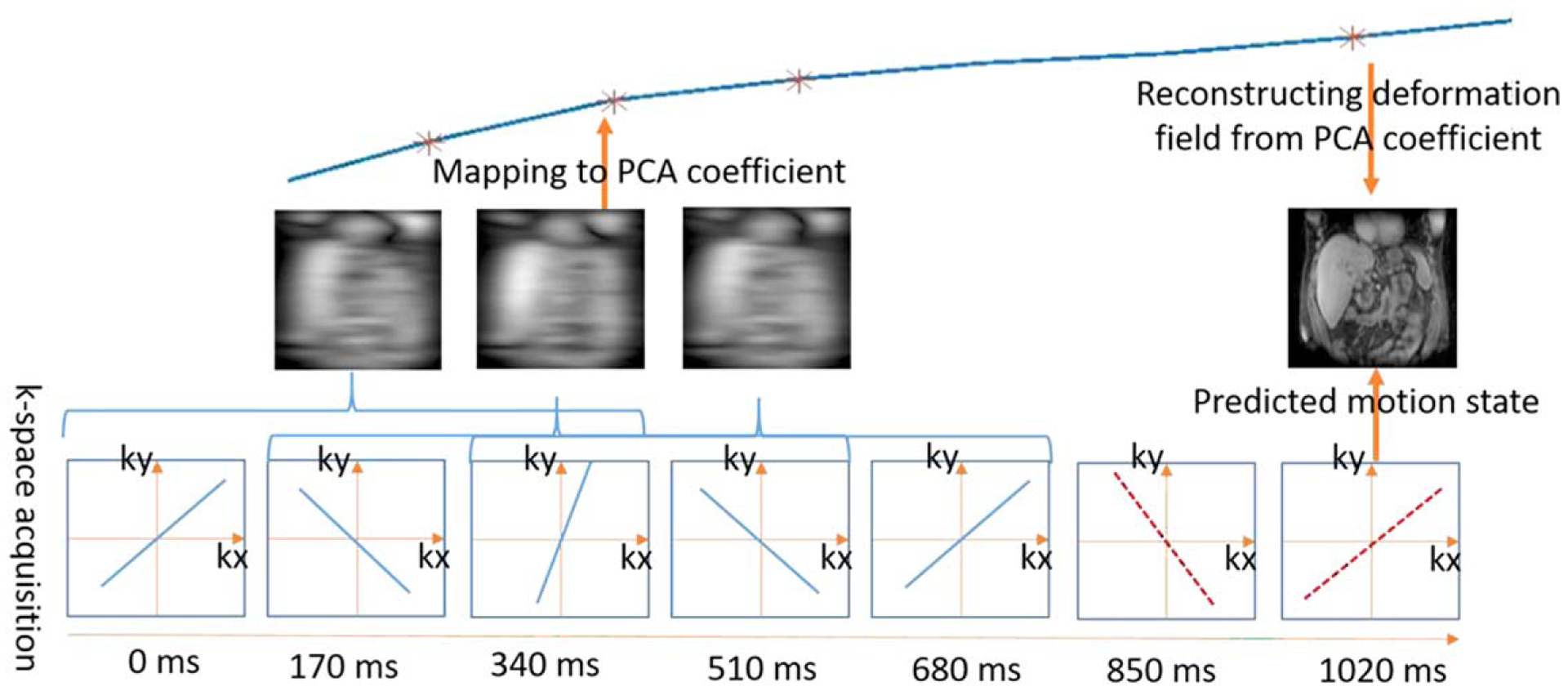
Workflow of breathing motion prediction. Acquired k-space spokes (blue lines) were reconstructed into image volumes using a view sharing filter. The corresponding motion model parameters were calculated through Gaussian kernel regression and used to predict the motion model parameter of future k-space spokes (red dashed lines). The motion state of the future k-space spokes was reconstructed from the predicted motion model parameters.

To account for contrast difference between different image volumes, each image volume was normalized to unity. The width of the Gaussian kernel, h, was selected by 2-fold cross validation on the training dataset. In our experiment, we set h = 0.1 for all patients.

For real time motion estimation, system latency needs to be accounted for, including the time required to calculate motion model parameters and the time required for the treatment delivery system to respond to the change of motion state. In this study, a latency time of 340 ms was considered, which is within the range of reported MRI-guided radiation therapy system latencies (Modat et al 2010, Crijns et al 2012, Green et al 2018). As the motion model parameter β_i was calculated from an image volume reconstructed using both spoke k_i and its neighboring spokes k_i−1, k_i+1, predicting a motion state 340 ms ahead of acquisition would require predicting motion model parameters associated with the k-space spoke at time point t_i+3. Gaussian kernel regression was used to predict motion model parameter ${\widehat{\beta }}_{i+3}$ by comparing observed motion model parameter vector β_i = [β_i−2, β_i−1, β_i] to motion model parameter vectors ${\tilde{\mathit{\alpha }}}_j=\left[{\tilde{\alpha }}_{j-2},{\tilde{\alpha }}_{j-1},{\tilde{\alpha }}_j\right]$ from the training dataset

$${\widehat{\beta }}_{i+3}=\frac{\sum _{j=2}^{1747}K\left({\mathit{\beta }}_i-{\tilde{\mathit{\alpha }}}_j\right){\tilde{\alpha }}_{j+3}}{\sum _{j=2}^{1747}K\left({\mathit{\beta }}_i-{\tilde{\mathit{\alpha }}}_j\right)}.$$ (3)

After obtaining the motion model parameter ${\widehat{\beta }}_{i+3}$, the motion state 340 ms ahead of the current acquisition time point was reconstructed as

$${\widehat{\mathit{d}}}_{i+3}={\mathit{m}}_0+{\widehat{\beta }}_{i+3}{\mathit{m}}_1.$$ (4)

2.4. Slow drifting motion model construction and prediction

The same reference image used for breathing motion modeling was used for slow drifting motion modeling. Similar with previous studies (Liu et al 2021), a mask that covers the GI region but excludes liver, heart and lungs was manually contoured on the reference volume. B-spline deformable registration using NiftyReg (Modat et al 2010) was then performed within the GI mask to match reference GI structures to image volumes of the slow motion time series. The B-spline grid spacing was 2 × 2 × 1 voxels and penalties on the log of Jacobian determinant and the bending energy were 0.8 and 0.001 respectively. Accuracy of the deformable registration method has been validated in previous studies by comparing contours of GI structures manually defined on deformed and target motion states (Liu et al 2021). The resulting deformation fields described changes of reference GI structures due to slow drifting motion. Figure 3 shows example slow drifting motion states before and after deformable registration. Visible GI structure changes can be observed between different motion states, while the consistent position of the liver suggests the efficacy of breathing motion correction and indicates that the changes of GI configuration were due to non-breathing motions.

Figure 3.

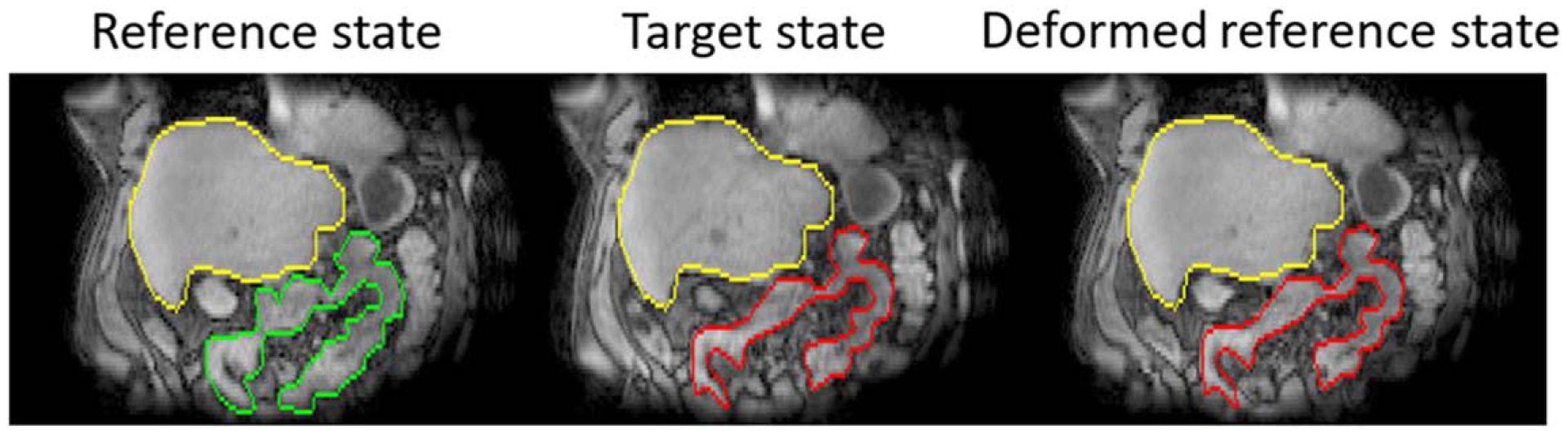
Example slow drifting motion states. Volumes of interest (VOIs) within the abdomen were drawn on reference (green) and target motion states (red) independently. Overlaying target VOIs with the deformed reference state shows agreement between deformed reference volumes and target volumes. Liver VOIs (yellow) were contoured on reference states and overlaid with both target states and deformed reference states.

As slow drifting motion was non-periodic over the 10 min scan time window, motion patterns of time points far away from each other were not correlated. Therefore, a temporal sliding window approach that incorporated only recent motion patterns was used for slow drifting motion prediction. Specifically, motion information obtained between time points t_i and t_i−3 were used to predict the motion state at time t_i+3. First, deformation fields S_i, S_i−1, S_i−2 and S_i−3 that aligned the reference scan to image volumes at t_i, t_i−1, t_i−2 and t_i−3 respectively were vectorized and organized into a matrix [s_i−3, s_i−2, s_i−1, s_i]. PCA was then performed on the matrix to obtain the mean deformation vector k₀, the leading PCA mode k₁ and the mode coefficients [γ_i−3, γ_i−2, γ_i−1, γ_i]. Linearly extrapolating the coefficient array [γ_i−3, γ_i−2, γ_i−1, γ_i] to ${\widehat{\gamma }}_{i+3}$ predicted motion state at time point t_i+3 as ${\widehat{\mathit{s}}}_{i+3}={\mathit{k}}_0+{\widehat{\gamma }}_{i+3}{\mathit{k}}_1\text{.}$

The predicted motion states were updated every 17 s, which corresponds to the time interval between neighboring image samples of the acquired time series. As the view sharing filter combined 500 spokes around the spoke acquired at time point t_i for image reconstruction, 250 more spokes needed to be collected after t_i to obtain the corresponding motion state s_i, which would require 42.5 more seconds of sampling. The temporal interval between the predicted time point t_i+3 and the observed motion state s_i was therefore 17 × 3 − 42.5 = 8.5 s.

2.5. Evaluation of prediction accuracy

We evaluated the proposed prediction scheme using the last 5 min of scan data from each imaging session, which contains 1750 spokes that are associated with 1750 breathing motion states and 18 slow drifting motion states. Predicted breathing motions of gross tumor volumes (GTV) in the liver and slow drifting motions of OARs in the gastrointestinal tract, including small bowel, colon, duodenum and stomach were compared to ground truth motion states, which were obtained by retrospective image reconstruction and deformable registration the same as the training stage. Specifically, GTV and OAR volumes defined on clinical planning CT images were first transferred to the reference MRI. Both predicted and ground truth deformation fields were then applied to GTV and OAR volumes. The accuracy of motion prediction was evaluated by differences between predicted and ground truth volume centroid positions and 95-percentile Hausdorff distances between volume contours. Dice coefficients between OAR volumes with and without motion prediction was also calculated.

3. Results

Figure 4 shows example predicted and ground truth GTV contours overlaid with different breathing motion states. Figure 5 plots motion traces of GTV centroids in left-right (LR), anterior-posterior (AP) and superior-inferior (SI) direction for an example patient. Despite breathing irregularities, predicted GTV motions showed good consistency with the ground truth. Across the 8 patients evaluated, the median distances between predicted and ground truth GTV centroid positions were 0.4 ± 0.3 mm, 0.3 ± 0.1 mm and 0.5 ± 0.2 mm in lateral, AP and SI directions respectively, and the averaged 95-percentile Hausdorff distance between ground truth and predicted GTV contours during the 5 min examination was 2.0 ± 0.3 mm.

Figure 4.

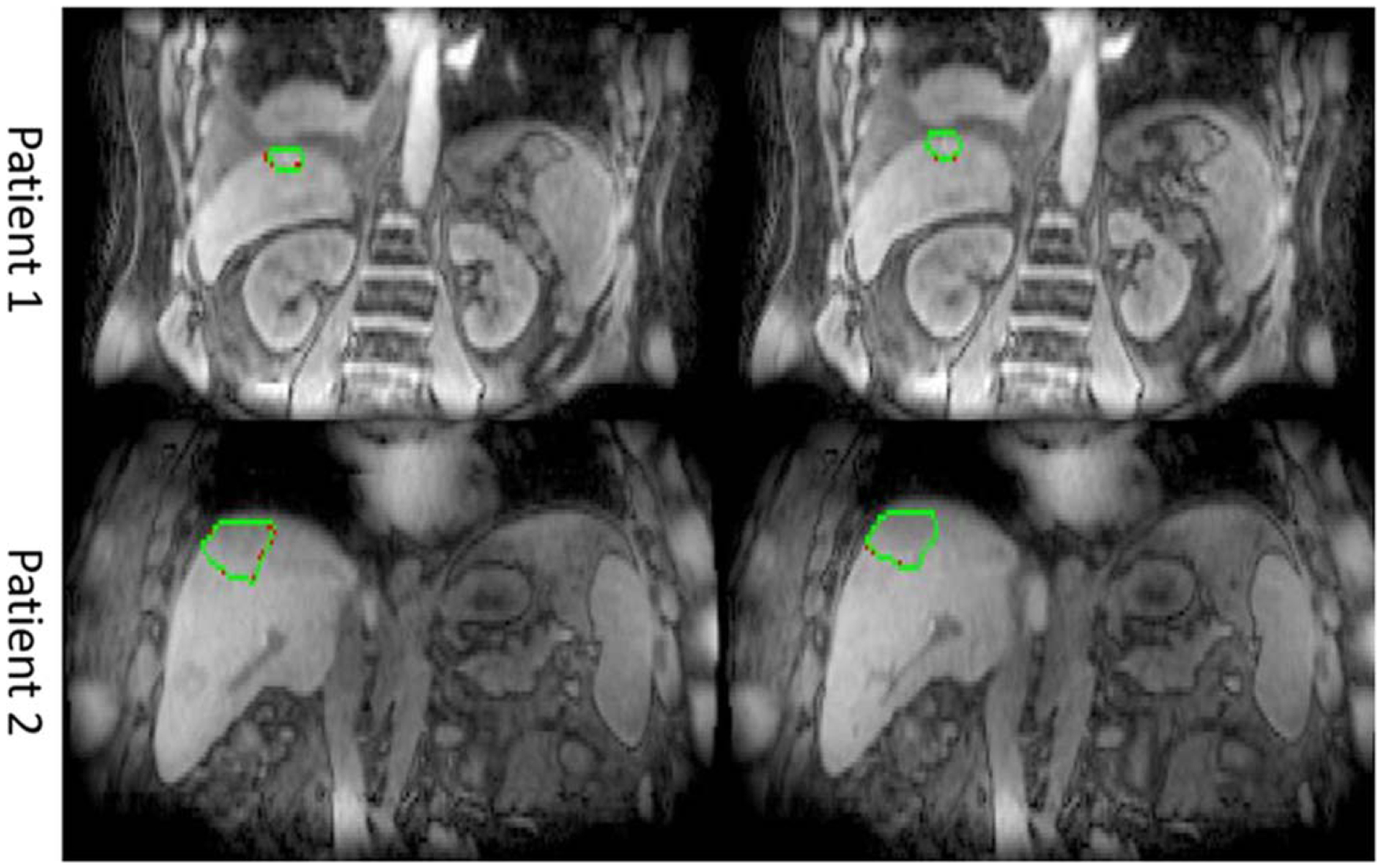
Predicted (green) and ground truth (red) GTV contours of different breathing motions states.

Figure 5.

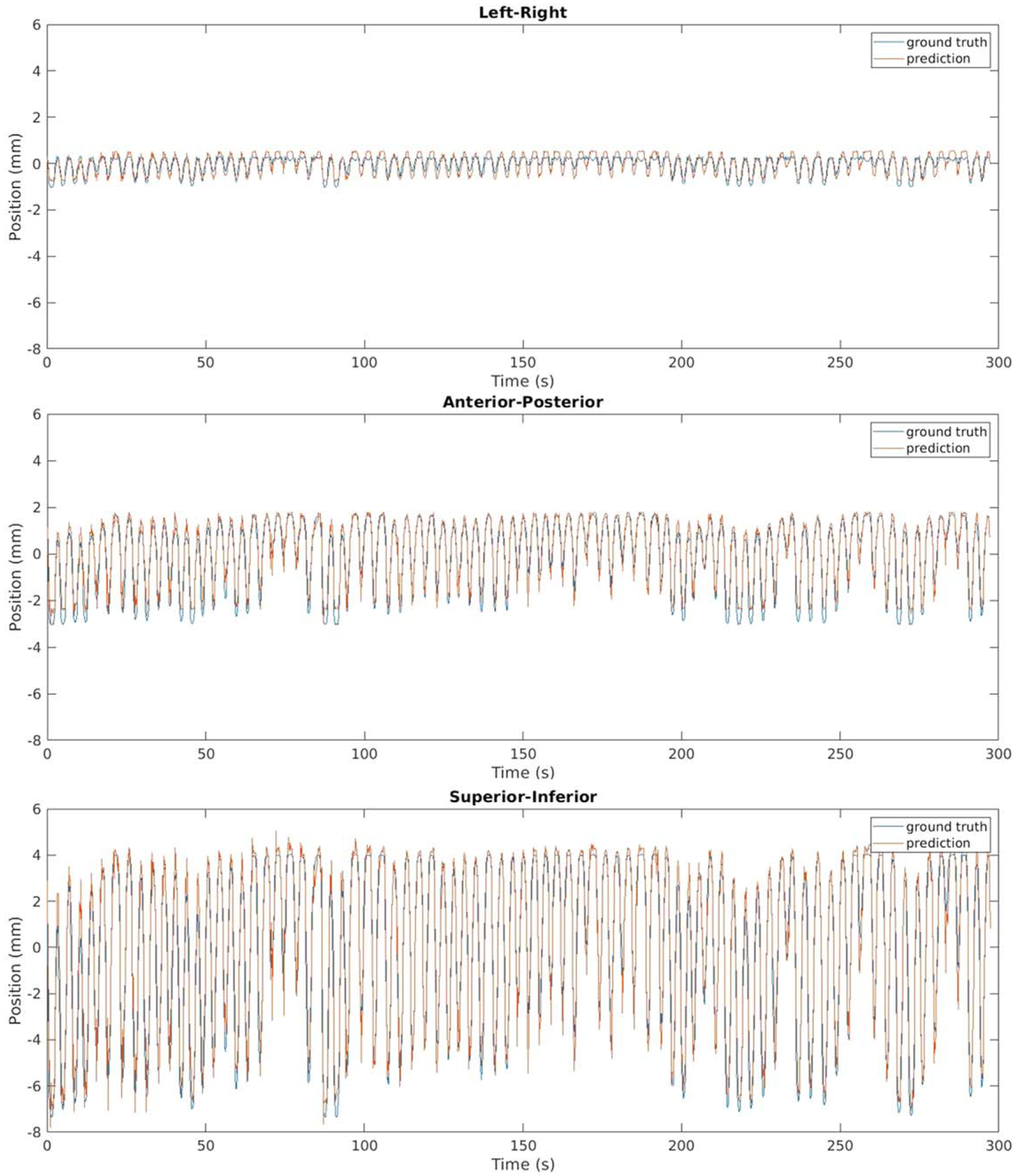
Positions of GTV centroid in 3 orthogonal directions for an example patient.

Similar results were observed for slow drifting motion prediction. Reference GI structures deformed by predicted and ground truth deformation fields showed good agreement while visible changes were observed before and after deformation, as shown in figure 6. Figure 7 compares predicted and ground truth centroid positions of multiple OARs including small bowel, colon, duodenum and stomach. The averaged median distances between predicted and ground truth centroid positions for all OARs were less than 0.2 mm in all three directions. The averaged 95-percentile Hausdorff distances between predicted and ground truth OAR contours during the 5 min examination were less than 0.2 mm for all organs/patients evaluated while the average 95-percentile Hausdorff distances between reference OAR contours without motion prediction and the ground truth were 3.9 ± 0.6 mm, 3.8 ± 0.6 mm, 3.9 ± 0.7 mm and 3.6 ± 0.8 mm for small bowel, colon, duodenum and stomach respectively. The averaged Dice coefficients between predicted and ground truth OAR volumes during the 5 min examination were greater than 0.97 for all OARs evaluated while the averaged Dice coefficients between reference OAR without motion prediction and ground truth OAR volumes were 0.86, 0.87, 0.77 and 0.88 for small bowel, colon, duodenum and stomach respectively. The improvement of contour agreement and volume overlap with slow drifting motion prediction suggests the need to monitor such motion during radiation treatment delivery.

Figure 6.

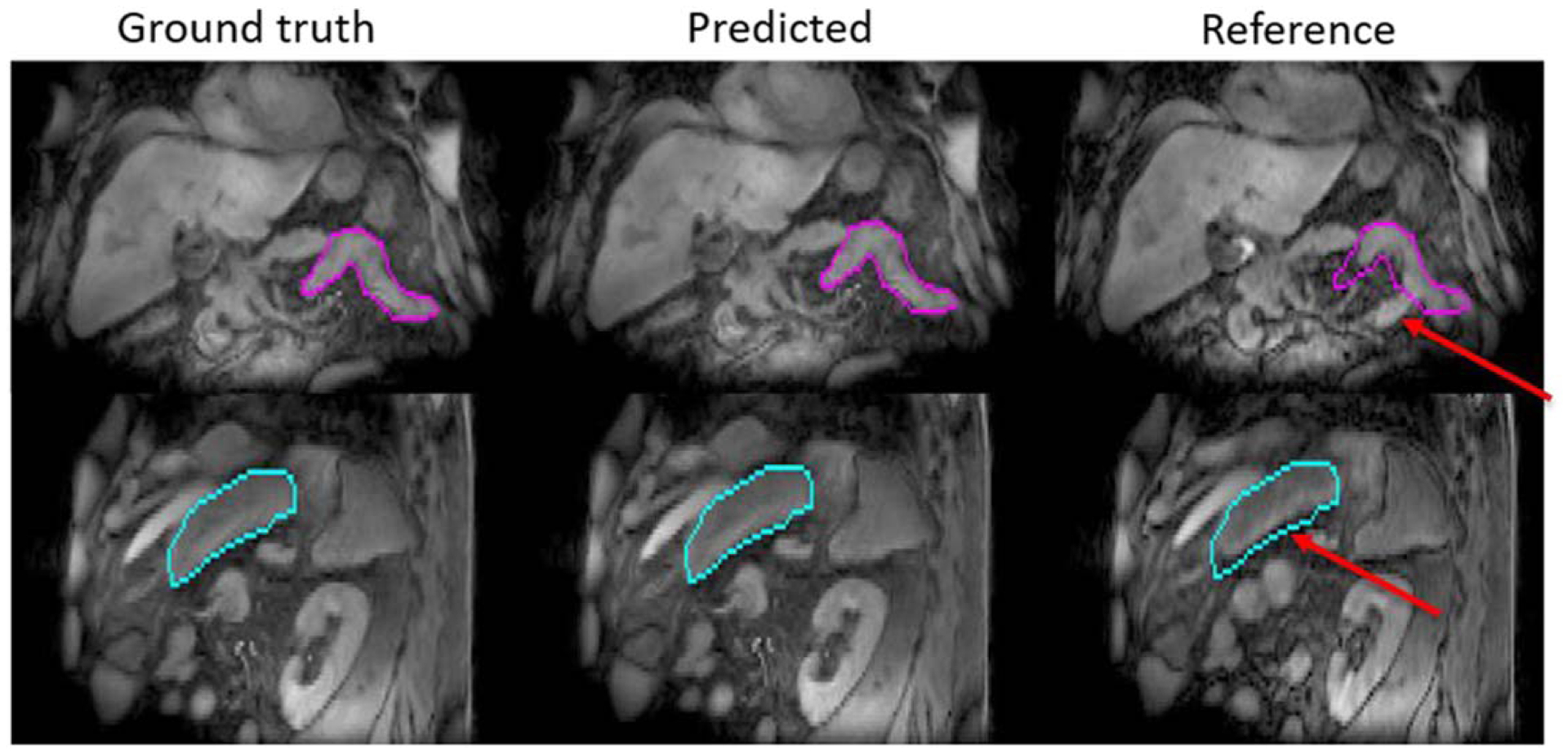
Example slow drifting motion prediction results. Contours of GI structures (magenta and cyan) were drawn on ground truth motion states and overlaid with predicted as well as reference motion states. Red arrows point to changes between ground truth and reference motion states.

Figure 7.

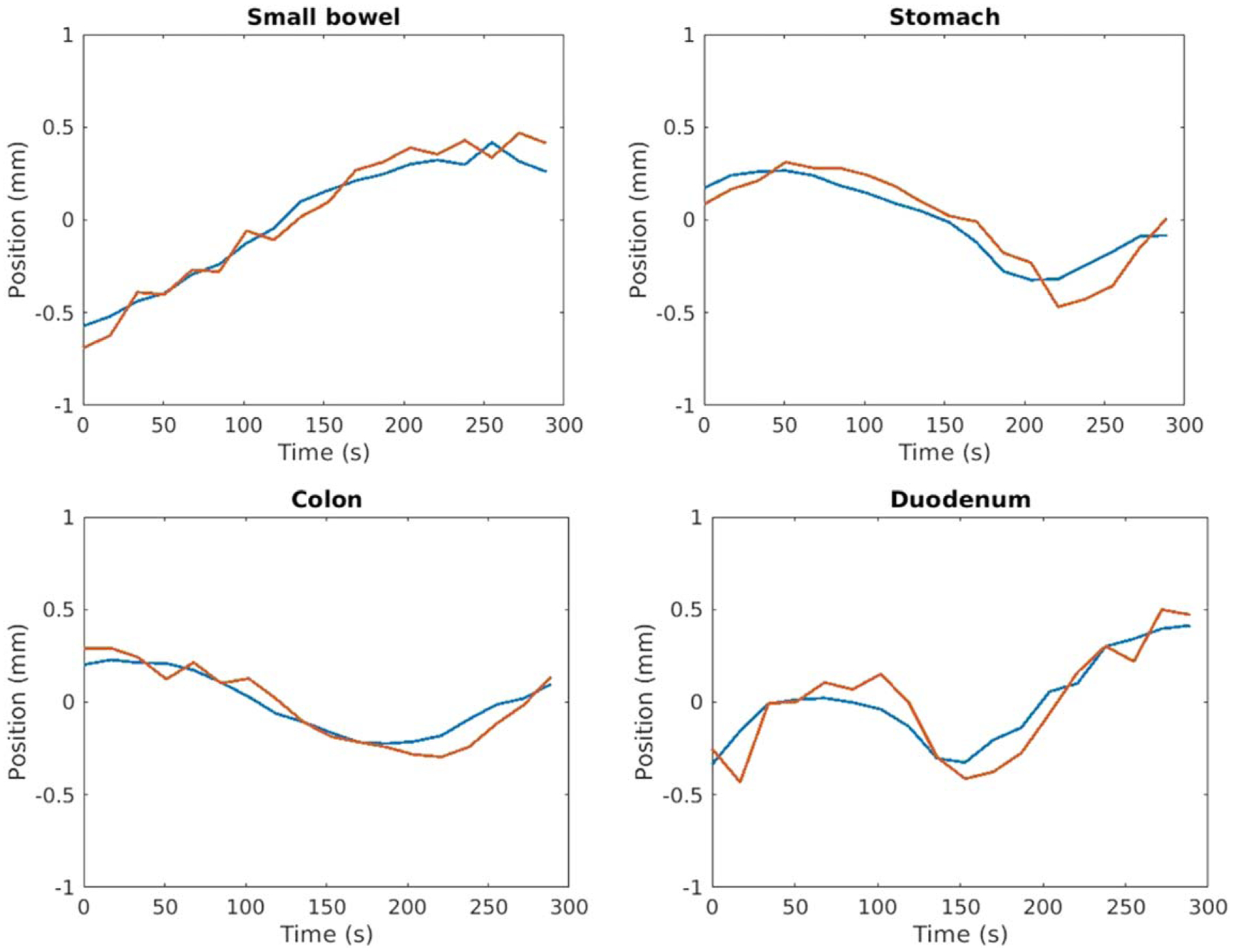
Example positions of OAR centroids in the superior-inferior direction. The predicted positions (red) maintain sub-mm accuracy relative to ground truth positions (blue).

4. Discussion

This study investigated volumetric prediction of abdominal motion in support of MRI-guided radiotherapy. The proposed method contains a training stage where patient-specific motion models were constructed and a prediction stage where future motion states were estimated by combing observed image samples with the motion model. Fast and semi-cyclic breathing motion was modeled from high temporal resolution image samples obtained through radial sampling, which served as a navigator signal to sort k-space samples into different bins for high spatial resolution motion states reconstruction; while slow and non-cyclic drifting motion was modeled from a lower temporal resolution image time series, which was reconstructed by sequentially combining a large number of k-space samples for high spatial resolution. A simple PCA model with the leading principal component only was determined experimentally to be sufficient for motion prediction. Gaussian kernel regression and linear extrapolation of PC coefficients were used respectively to predict future breathing (340 ms ahead of acquisition) and slow drifting (8.5 s ahead of acquisition) motion states. Comparing to recent methods of 2D breathing motion prediction using Cine MRI (e.g. Ginn et al 2020), our method achieves similar accuracy in target centroid estimation in the superior-inferior direction (median distance of 0.5 mm versus 0.63 mm) with comparable prediction interval (340 ms versus 330 ms), while providing additional motion information in other directions and of other types of motion, for both tumor targets and the surrounding OARs. Future work will evaluate the proposed method more thoroughly for clinical use, including evaluating the accuracy of gating decisions based on predicted motion states. By predicting motion information across a volumetric space, motions of both tumor and surrounding organs can be monitored during treatment delivery, which is desirable for abdominal radiotherapy given the proximity of OARs to targets. Median distances between predicted and ground truth centroid positions of GTV and OARs were less than 1 mm on average for both breathing and slow drifting motions in all 3 orthogonal directions (anterior-posterior, left-right and superior-inferior). 95-percentile Hausdorff distances between predicted and ground truth GTV contours of various breathing motions states were 2 mm on average, which was smaller than the imaging resolution (2–2.45 mm in-plane and 3–4 mm cross-plane) and averaged 95-percentile Hausdorff distances between predicted and ground truth OAR contours of different slow drifting motion states were less than 0.2 mm. These results suggest the potential of the proposed method in supporting MRI-guided precision abdominal radiotherapy.

The training stage of the proposed method involves acquisition of a 5 min 4D MRI, which can be done during the time interval of daily MRI review and plan adaptation without adding significant burden to the clinical workflow. The length of the 4D MRI may be further reduced without comprising the prediction accuracy. The scalability of the algorithm with respect to training data size will be investigated in future studies. The prediction stage of breathing motion involves simple image intensity comparison and linear combination of 1D parameters, which is similar in computational resources as existing work (Feng et al 2020, Ginn et al 2020). The prediction of slow drifting motion involves more complicated operations such as breathing motion correction, which will result in a longer system latency. However, since such motion happens at a slower rate than breathing motion, lower temporal resolution and longer prediction interval can be used to mitigate the latency. Furthermore, the proposed method calculates deformation fields associated with future motion states directly, thus contours of target and OARs can be updated without deformable registration, which will also reduce system latency.

By combining different numbers of radial samples through view sharing, we were ableto reconstruct image time series of different temporal resolutions to focus on different types of abdominal motion, such as fast breathing and slow anatomical configuration changes. The framework of motion prediction based on multi-temporal motion modeling can be extended to predict other types of GI motion, such as cyclic movements of bowel structures and antral contraction (Johansson et al 2021), which will be investigated in future studies to better support precision abdominal radiotherapy. Several limitations of current work will also be addressed in future studies. First, the breathing motion model was trained from a fixed length of an examination and used to predict motion states afterwards. Changes of patient motion patterns between training and prediction stages may not be captured by the motion model and will negatively impact the prediction accuracy. An adaptive model that is updated with newly acquired image samples may improve the algorithm robustness. A method to detect outlier motion patterns will also be of interest for future investigation. Second, the stack-of-stars radial sequence performs radial sampling in the axial plane, which leads to low spatial resolution inthe SI direction where motion magnitude is the largest. 3D radial sampling may have the potential of further improving motion prediction accuracy. Third, the current MATLAB implementation of the algorithm is not very efficient. Code optimization in other programming languages will allow a better understanding of the latency of the proposed method, as well as resources required for computationally intensive operations such as breathing motion correction. The proposed method has the potential of improving precisions in both tumor targeting and normal tissue avoidance, which may allow higher dose to be safely delivered to abdominal targets that are in proximity to OARs and thus improve treatment outcomes.

5. Conclusion

This study proposed a MRI-based motion prediction algorithm that provides 3D motion information across the entire volumetric imaging space. Deformation vectors between different motion states and a reference state were predicted by combining acquired radial MRI samples with patient-specific motion models. Multi- temporal resolution motion models were constructed using temporal view sharing filters with different width, which permit motion prediction of both breathing and slow drifting motion with sub-voxel accuracy. The proposed method has the potential of supporting MRI-guided abdominal radiotherapy for improved treatment delivery precision.