Abstract
A manifestation of hydrogen bonding between the dication and anions attributed to their relative position of the anions around the cation can influence both the conformational equilibrium and the physical properties of ionic liquids. With this view, we studied the electronic structure and normal frequencies using density functional theory calculations to analyze the hydrogen-bonding interactions in dicationic ionic liquids. The conformers are distinguished based on the hydrogen-bonding sites of the cation and anion. The weak hydrogen bonding between the dication and anions in dication ionic liquids can lead to greater conformational equilibrium compared to the monocation system. Consequences of these interactions for the vibrational spectrum are analyzed to provide an insight into the conformational equilibrium in dicationic ionic liquids at the molecular level.
Introduction
Ionic liquids (ILs) are composed of an organic cation and an organic or an inorganic anion through hydrogen bond interactions. ILs are one of the popular research areas because of their unique and interesting properties such as low melting points below 100 °C, and they possess superior physical properties such as low vapor pressure, high thermal and chemical stabilities, nonflammability, low melting point, and wide temperature range for synthesis and catalysis.1 The advantage of ILs is the possibility of changing their properties by varying the nature of the couple cation/anion.2,3 Similar to monocationic ILs, dicationic ILs (DILs) are popular because of their application in various fields such as replacement of traditional organic solvents, catalysts in organic reactions, and lubricants at high temperature.4 DILs are a subclass of ILs, characterized by two cationic head groups linked to flexible aliphatic chains. The structures of the DILs can be composed of homoanionic, two identical anions, or hetroanionic, two nonidentical anions, ILs. The physical properties and their potential applications depend on the type and length of the linker between the two cations and/or on the nature of the cation. DILs can be a good candidate for an electrolyte in electrochemical devices such as lithium-ion batteries, fuel cells, dye-sensitized solar cells, and supercapacitors.2,5,6
In analogy with the characterization of the ILs, the factors affecting the physicochemical properties of DILs are mainly the relatively higher number of interactions between the anions and cations and the length of alkyl chains. In addition to physical properties, the intermolecular interactions, and consequently, the position of these anions around the dication play an important role in the expansion of the network structures, such as larger clusters of ion pairs in the liquid phase.7
Vibrational spectroscopy is an invaluable option for a deeper understanding of the interactions and structures of ILs.8 IR and Raman spectroscopy are popular and provide information about the nature of the interactions and their consequences in the vibrational spectra. The assignment of frequencies in the experimental spectrum is relatively challenging for a reliable interpretation of vibrational spectra. A common approach is performing quantum chemical calculations to calculate vibrational frequencies to be compared to experimental data.9−12 The comparison of the vibrational frequencies calculated from quantum calculations can provide microscopic information hidden in the vibrational spectra. Thus, the presence of molecular interactions and the consequent changes in terms of frequency shifts can be revealed using vibrational spectroscopy.
In this paper, we investigate the effect of the position of the bulky Tf2N anion around the dication on the hydrogen bonding, conformational equilibrium, and the vibrational frequencies of 1,3-bis(3-methylimidazolium-1-yl)propane bis(trifluoromethanesulfonyl)imide ion pairs. The ILs containing inorganic bis(trifluoromethanesulfonyl)imide (Tf2N) anion are of great interest because of their use in making hydrolytically stable, “hydrophobic” ionic liquids with low viscosity and high electrical conductivity. The Tf2N is one of the most widely studied anions due to its unique properties such as charge diffusion and weak cation coordination. The delocalization of the negative charge around the S–N–S core of the Tf2N anion reduces the strength of cation–anion interactions.13 This enables the formation of low melting fluid ionic liquids with a wide range of cations such as ammonium, pyridinium, imidazolium, and pyrrolidinium cations.14,15 The Tf2N anion can form hydrogen bonding via SN and SO bonds with the cation. In addition to cation–anion distance, the orientation of the bulky Tf2N anion can also affect the interaction strength. In this respect, it is important to understand the conformation analysis based on the hydrogen-bonding strength and its relevant changes in the vibrational spectrum.
We are interested in gaining insights into how the position of the bulky Tf2N anion around the dication influences the structure and how it manifests in the vibrational spectrum. Different conformers based on different binding sites between the cation and anion will be studied, and the interaction strength will be rationalized by assignment of the stretching frequency like SO and SN of the anion. Our approach can provide insights into molecular interactions and conformational equilibrium, which can be helpful to experimental scientists.
Results and Discussions
Conformation and Energetics
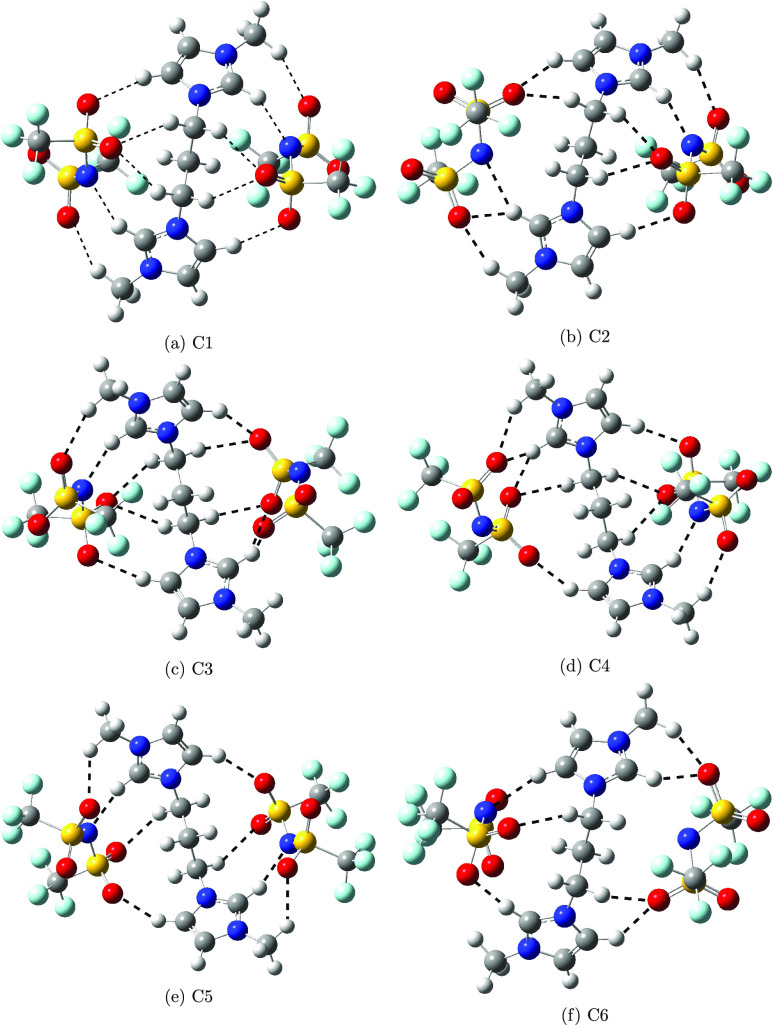
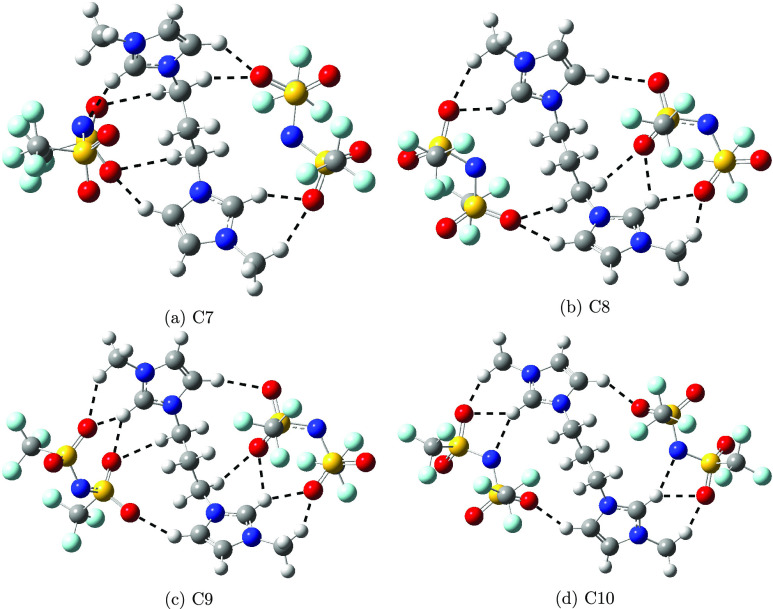
Optimized geometries of cations and anions are displayed in Figure 1. The electronic energy and relative stabilization energy with respect to the lowest energy conformer for all conformers, including the conformation of cation and both anions, are reported in Table 1. Optimized geometries of the first 10 conformers are shown in Figures 2 and 3. Optimized geometries of the C11–C25 conformers are shown in Figures S1–S3. The lowest energy conformer adopted trans conformation of the cation and also trans conformation for both anions. The relatively different orientation of anions is predicted toward the cation in cis and trans conformers. Two anions are oriented in such a way as to minimize the repulsion of CF3 groups toward the cis conformer of the cation. This orientation of anions significantly affected the conformer stabilization of energy. The first 10 lowest energy conformers preferred the trans conformation of cation compared to the cis conformation. The trans conformation of the anion is relatively preferred over cis conformation in the first 10 lowest energy conformations. Conformers 1, 2, and 9 have trans conformations in the cation as well as in both anions. Thus, the orientation of the cation and anion in DILs plays an important role in the stabilization of conformation.
Figure 1.
Optimized geometries of cation and anion conformers.
Table 1. Cation, Anion A, Anion B, SCF Electronic (AU) and Relative Stabilization Energies (kJ/mol) of Different Conformers.
| conformer | cation | anion A | anion B | SCF energy | relative energy |
|---|---|---|---|---|---|
| C1 | trans | trans | trans | –4303.3023421 | 0.00 |
| C2 | trans | trans | trans | –4303.3016555 | 1.80 |
| C3 | trans | cis | trans | –4303.3015218 | 2.15 |
| C4 | trans | cis | trans | –4303.3013409 | 2.63 |
| C5 | trans | cis | cis | –4303.300968 | 3.61 |
| C6 | trans | cis | trans | –4303.3008833 | 3.83 |
| C7 | trans | cis | trans | –4303.3008656 | 3.88 |
| C8 | trans | trans | trans | –4303.2987148 | 9.52 |
| C9 | trans | cis | trans | –4303.2982696 | 10.96 |
| C10 | trans | cis | cis | –4303.2981795 | 10.93 |
| C11 | trans | trans | trans | –4303.2955766 | 17.76 |
| C12 | cis | trans | trans | –4303.295037 | 19.18 |
| C13 | trans | cis | trans | –4303.2949906 | 19.30 |
| C14 | trans | cis | cis | –4303.2947856 | 19.84 |
| C15 | trans | cis | cis | –4303.2947029 | 20.06 |
| C16 | trans | cis | cis | –4303.294646 | 20.21 |
| C17 | cis | trans | trans | –4303.294627 | 20.26 |
| C18 | trans | cis | trans | –4303.2944598 | 20.70 |
| C19 | cis | cis | cis | –4303.294308 | 21.09 |
| C20 | trans | trans | trans | –4303.2938367 | 22.33 |
| C21 | trans | trans | trans | –4303.2937873 | 22.46 |
| C22 | trans | cis | cis | –4303.29343 | 23.40 |
| C23 | cis | cis | cis | –4303.2903218 | 31.56 |
| C24 | cis | cis | cis | –4303.2899926 | 32.42 |
| C25 | trans | cis | trans | –4303.2890723 | 34.84 |
Figure 2.
Optimized geometries of C1–C6 conformers.
Figure 3.
Optimized geometries of C7–C10 conformers.
Hydrogen Bonding
We studied different conformers based on hydrogen-bonding sites and the orientation of ions, cation, and anion of DILs. Here, we characterized the hydrogen bonding by the distance between the hydrogen of the CH bonds and the electronegative atoms, nitrogen, and oxygen of the anion, if it is less than or equal to 2.5 Å. Hereafter, we will refer to the hydrogen atom attached to the ring carbon atom between two nitrogen atoms as C2H. The C2H bond is relatively polar compared to the other CH bonds of the cation and can form a relatively stronger hydrogen bond with the anion compared to the rest of the CH bonds.16 Here, we discussed the hydrogen-bonding analysis of the first 10 lowest energy conformers. The selected hydrogen-bonding distances of the C1–C10 conformers are compared in Tables 2 and 3. The C2H can form a stronger hydrogen bond through nitrogen and oxygen atoms compared to the fluorine of the anion. The conformers exhibiting the C2H···N interactions are lower in energy compared to the C2H···O interactions. For example, the C1 and C2 conformers have two C2H···N interactions, one from each anion, and the C2 conformer has an additional one C2H···O interaction compared to the C1 conformer. The distance for C2H···N interactions in the C1 conformer is relatively similar, whereas one C2H···N interaction in the C2 conformer is relatively strong and another is relatively weak compared to those in the C1 conformer. The difference in the strength of interactions in terms of distance is due to the orientation of anions toward cations. The angle in both C-C2H···N interactions in the C1 conformer is 147.5°, whereas the angles for C-C2H···N are 143.1 and 153.2° in the C2 conformer. Out of the two interactions in the C2 conformer, one of the interactions is close to linearity, and the other interaction is far from linearity compared to the interactions in the C1 conformer. Thus, the conformer stabilization depends on both hydrogen-bonded interactions and the orientation of anions toward the cation. In addition to the C2H···N interaction, the C2H···O interaction is also predicted in the C2 conformer.
Table 2. Selected Hydrogen-Bonded Distance between Ring Hydrogen of the Cation and Anion (Å) in C1–C10 Conformers.
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| H2A | NB | 2.132 | 2.079 | 2.331 | |||||||
| H2A | NA | 2.179 | 2.483 | ||||||||
| H2A | O1A | ||||||||||
| H2A | O2A | 2.159 | 2.223 | 2.026 | 2.266 | ||||||
| H2A | O4A | 2.379 | 2.169 | 2.143 | |||||||
| H2A | O3A | 2.175 | |||||||||
| H2A | O1B | 2.076 | |||||||||
| H2A | O3B | 2.052 | |||||||||
| H2B | NB | 2.182 | 2.112 | ||||||||
| H2B | NA | 2.129 | 2.144 | 2.132 | 2.330 | ||||||
| H2B | O1A | ||||||||||
| H2B | O2A | 2.082 | |||||||||
| H2B | O4A | 2.312 | |||||||||
| H2B | O2B | 2.320 | |||||||||
| H2B | O4B | 2.082 | |||||||||
| H2B | O3B | 2.048 | 2.058 | 2.177 |
Table 3. Selected Hydrogen-Bonded Distance between Alkyl Hydrogen of the Cation and Anion (Å) in C1–C10 Conformers.
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| HMA | O2A | 2.441 | 2.383 | 2.444 | |||||||
| HMA | O4A | ||||||||||
| HMA | O3A | 2.355 | 2.492 | ||||||||
| HMA | O3B | 2.382 | |||||||||
| HMB | O3A | 2.384 | 2.376 | ||||||||
| HMB | O1B | 2.453 | |||||||||
| HMB | O3B | 2.375 | 2.372 | ||||||||
| HMC | O1A | 2.477 | 2.327 | ||||||||
| HMC | O4A | 2.429 | |||||||||
| HMC | O1B | 2.491 | |||||||||
| HMC | O3B | 2.386 | 2.459 | ||||||||
| HMD | O4A | 2.465 | |||||||||
| HMD | O3A | 2.383 | 2.359 | ||||||||
| HMD | O2B | 2.462 | |||||||||
| HMD | O3B | 2.385 | 2.363 | 2.356 | |||||||
| HRB | NB | 2.340 | |||||||||
| HRB | O1A | 2.227 | 2.206 | 2.250 | 2.143 | ||||||
| HRB | O4A | 2.168 | 2.279 | ||||||||
| HRB | O1B | 2.170 | |||||||||
| HRB | O4B | 2.257 | |||||||||
| HRB | O3B | 2.157 | |||||||||
| HRA | O4A | 2.257 | 2.200 | ||||||||
| HRA | O3A | 2.243 | |||||||||
| HRA | O1B | 2.171 | 2.181 | 2.336 | 2.143 | ||||||
| HRA | O4B | 2.246 | 2.246 | 2.168 | |||||||
| HMG | O1A | 2.264 | 2.252 | ||||||||
| HMG | O2A | 2.304 | |||||||||
| HMG | O1B | 2.255 | 2.391 | ||||||||
| HMG | O4B | 2.317 | |||||||||
| HMG | O3B | 2.352 | 2.308 | 2.218 | |||||||
| HMH | O1B | 2.258 | |||||||||
| HME | O1A | 2.390 | |||||||||
| HME | O4A | 2.272 | 2.251 | ||||||||
| HME | O1B | 2.273 | |||||||||
| HME | O3B | 2.274 | |||||||||
| HMF | O3A | 2.219 | |||||||||
| HMF | O1B | 2.264 |
Among the first 10 conformers, stronger C2H···O interactions are predicted in the C6 conformer compared to those interactions in the first two lowest energies. The hydrogen bond through C2H is stronger compared to the hydrogen of CH2 groups. These weak interactions become important for conformer stabilization when the relative energy difference is very small. Here, the stabilization of the conformer is also governed by the hydrogen-bonding interactions through CH2 groups. In addition to stabilization, the hydrogen-bonding interactions through the CH2 group help the bulky anion-like Tf2N in stabilizing around the cation. As expected, the increase in the C2H bond distance of the cation and SN and SO bonds of the anion participating in the interactions is observed in all of the conformers. The change in distance compared to free cation and anion can be correlated with the strength of the interactions (Tables 4 and 5).
Table 4. Bond Distances between Sulfur and Nitrogen of the Anion (Å) in C1–C25 Conformers.
| S35NB | S36NB | S50NA | S51NA | |
|---|---|---|---|---|
| C1 | 1.626 | 1.631 | 1.626 | 1.631 |
| C2 | 1.625 | 1.632 | 1.627 | 1.632 |
| C3 | 1.608 | 1.615 | 1.625 | 1.633 |
| C4 | 1.603 | 1.620 | 1.626 | 1.632 |
| C5 | 1.634 | 1.617 | 1.634 | 1.617 |
| C6 | 1.619 | 1.627 | 1.631 | 1.627 |
| C7 | 1.628 | 1.620 | 1.631 | 1.627 |
| C8 | 1.597 | 1.627 | 1.631 | 1.628 |
| C9 | 1.603 | 1.619 | 1.627 | 1.598 |
| C10 | 1.623 | 1.629 | 1.623 | 1.629 |
| C11 | 1.604 | 1.617 | 1.625 | 1.600 |
| C12 | 1.604 | 1.631 | 1.614 | 1.610 |
| C13 | 1.621 | 1.629 | 1.632 | 1.628 |
| C14 | 1.623 | 1.606 | 1.628 | 1.593 |
| C15 | 1.634 | 1.620 | 1.622 | 1.628 |
| C16 | 1.616 | 1.614 | 1.618 | 1.613 |
| C17 | 1.634 | 1.601 | 1.620 | 1.637 |
| C18 | 1.635 | 1.613 | 1.630 | 1.593 |
| C19 | 1.628 | 1.625 | 1.623 | 1.616 |
| C20 | 1.597 | 1.627 | 1.615 | 1.605 |
| C21 | 1.621 | 1.637 | 1.617 | 1.640 |
| C22 | 1.626 | 1.613 | 1.629 | 1.592 |
| C23 | 1.611 | 1.606 | 1.595 | 1.621 |
| C24 | 1.614 | 1.603 | 1.596 | 1.623 |
| C25 | 1.599 | 1.621 | 1.595 | 1.632 |
Table 5. Bond Distance between Sulfur and Oxygen of the Anion (Å) in C1–C25 Conformers.
| S35O4A | S35O3A | S36O1A | S36O2A | S50O4B | S50O3B | S51O1B | S51O2B | |
|---|---|---|---|---|---|---|---|---|
| C1 | 1.473 | 1.474 | 1.471 | 1.460 | 1.473 | 1.474 | 1.471 | 1.460 |
| C2 | 1.472 | 1.474 | 1.470 | 1.460 | 1.461 | 1.477 | 1.479 | 1.460 |
| C3 | 1.477 | 1.481 | 1.478 | 1.458 | 1.473 | 1.474 | 1.471 | 1.460 |
| C4 | 1.477 | 1.480 | 1.480 | 1.458 | 1.472 | 1.474 | 1.471 | 1.460 |
| C5 | 1.474 | 1.461 | 1.473 | 1.472 | 1.474 | 1.461 | 1.473 | 1.472 |
| C6 | 1.473 | 1.478 | 1.475 | 1.463 | 1.460 | 1.480 | 1.477 | 1.461 |
| C7 | 1.473 | 1.467 | 1.474 | 1.468 | 1.460 | 1.479 | 1.477 | 1.461 |
| C8 | 1.482 | 1.469 | 1.458 | 1.482 | 1.460 | 1.480 | 1.476 | 1.460 |
| C9 | 1.476 | 1.481 | 1.480 | 1.458 | 1.482 | 1.458 | 1.469 | 1.482 |
| C10 | 1.479 | 1.461 | 1.460 | 1.478 | 1.479 | 1.461 | 1.460 | 1.478 |
| C11 | 1.483 | 1.468 | 1.458 | 1.482 | 1.479 | 1.459 | 1.473 | 1.482 |
| C12 | 1.476 | 1.476 | 1.477 | 1.462 | 1.484 | 1.460 | 1.460 | 1.482 |
| C13 | 1.479 | 1.463 | 1.461 | 1.475 | 1.459 | 1.477 | 1.479 | 1.461 |
| C14 | 1.480 | 1.476 | 1.484 | 1.458 | 1.459 | 1.483 | 1.482 | 1.468 |
| C15 | 1.475 | 1.459 | 1.459 | 1.478 | 1.479 | 1.461 | 1.459 | 1.479 |
| C16 | 1.473 | 1.478 | 1.474 | 1.469 | 1.479 | 1.481 | 1.477 | 1.464 |
| C17 | 1.473 | 1.461 | 1.478 | 1.477 | 1.460 | 1.479 | 1.476 | 1.461 |
| C18 | 1.476 | 1.463 | 1.473 | 1.475 | 1.459 | 1.482 | 1.480 | 1.469 |
| C19 | 1.476 | 1.460 | 1.460 | 1.476 | 1.474 | 1.467 | 1.468 | 1.476 |
| C20 | 1.483 | 1.468 | 1.457 | 1.483 | 1.482 | 1.458 | 1.459 | 1.482 |
| C21 | 1.461 | 1.480 | 1.474 | 1.462 | 1.460 | 1.481 | 1.474 | 1.461 |
| C22 | 1.478 | 1.463 | 1.480 | 1.470 | 1.459 | 1.482 | 1.481 | 1.469 |
| C23 | 1.461 | 1.485 | 1.481 | 1.459 | 1.479 | 1.482 | 1.479 | 1.456 |
| C24 | 1.460 | 1.484 | 1.482 | 1.460 | 1.480 | 1.480 | 1.479 | 1.457 |
| C25 | 1.477 | 1.481 | 1.480 | 1.457 | 1.485 | 1.468 | 1.459 | 1.475 |
Vibrational Frequency Analysis
Vibrational frequency analysis can provide microscopic information about the structure and the ionic interactions of the system. The consequences of the molecular interactions manifest in the vibrational spectrum and result in the frequency shifts of the normal vibrations. The interpretation of these interactions may be a difficult task in the experimental spectrum. A good approach is to perform quantum chemical calculations to calculate the normal vibrations and compare those with the experimental spectrum. This combined approach of comparison of simulated vibration spectra with the experiment helps in assigning the vibrations of experimental spectra.9−12,17−19
The population of the conformers can influence the physical properties of ILs and is mainly distinguished based on the interanionic distance and orientation of the ions of the ionic liquids. These two factors influence the frequency shifts of the characteristic stretching vibrations such as C2H of the cation or SO and SN of the anion. With this view, we discussed the selected stretching vibrations such as CH of the cation and SO and SN of the anion of the first four conformers to understand the consequences of the molecular interactions to the vibrational spectrum. We compared these vibrations in Table 6. The intense vibrations like CF stretch, CH bending such as CH2 or CH3 rocking or wagging, etc., are not discussed in this paper. The CF bond does not play an important role in stabilization energy in the present study and can form relatively weak interaction with the CH bonds on the cation. The analysis of these vibrations does not provide insight into the conformational equilibrium in terms of the molecular interactions between the anion and cation.
Table 6. Normal Vibration (in cm–1) and Intensity of Selected Bonds in the Cation and Anion of C1–C4 Conformers.
| vibrations | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| CRB-HRB + CRA-HRA stretch | 3246 (223) | |||
| CRB-HRB stretch | 3289 (120) | 3272 (101) | 3283 (107) | |
| CRA-HRA stretch | 3181 (202) | 3247 (149) | 3194 (281) | |
| C2B-H2B + C2A-H2A Stretch | 3212 (468) | 3233 (422) | 3239 (343) | |
| C2B-H2B Stretch | 3183 (293) | |||
| C2A-H2A Stretch | 3282 (172) | |||
| CH ring rocking | 1335 (442) | 1334 (275) | 1333 (356) | 1333 (335) |
| CH ring rocking | 1331 (48) | 1332 (51) | 1329 (48) | 1330 (62) |
| CH ring rocking | 1329 (294) | 1328 (615) | ||
| 1319 (89) | ||||
| SO2 asymm stretch | 1284 (191) | 1282 (181) | 1283 (199) | 1283 (182) |
| SO2 asymm stretch | 1282 (182) | |||
| C2H ring rocking | 1223 (71) | |||
| 1213 (75) | 1215 (73) | 1213 (26) | ||
| 1195 (110) | 1195 (66) | 1196 (148) | 1194 (158) | |
| 1193 (72) | 1190 (108) | 1193 (85) | 1193 (104) | |
| 1189 (227) | 1189 (152) | |||
| SO2 symm stretch | 1105 (81) | 1107 (212) | 1107 (101) | 1107 (164) |
| 1104 (289) | 1100 (237) | 1105 (445) | 1105 (511) | |
| 1092 (47) | 1093 (321) | 1092 (203) | 1092 (176) | |
| 1091 (427) | 1090 (95) | 1092 (203) | 1090 (481) | |
| SN asymm stretch | 988 (790) | 987 (589) | 1011 (287) | 1011 (251) |
| 984 (244) | 979 (454) | 987 (504) | 987 (512) | |
| C2H wag | 920 (94) | 927 (56) | 927 (43) | 921 (50) |
| 901 (29) | 914 (24) | |||
| SN symm strech | 713 (151) | 716 (115) | 716 (53) | 716 (53) |
The CH ring vibrations, C2B-H13 and C2A-H3, are coupled in the C1 conformer, whereas these vibrations are split in the C2–C4 conformers. As mentioned earlier, the C2H bond makes a stronger hydrogen bonding with the anion compared to the other CH bonds, which results in a frequency shift to a lower wavenumber, red shift, compared to the corresponding vibrations in the free state. These stretching vibrations can be correlated with the strength of the interactions. A larger red shift and blue shift are predicted in the C3 conformer for C2B-H13 and C2A-H3 stretching vibrations, respectively, compared to those vibrations in the C1, C2, and C4 conformers. The overall relative strength of hydrogen bonding between the C2B-H13 and C2A-H3 bonds is relatively small in the C1, C2, and C4 conformers compared to the C3 conformer, resulting in coupled stretching vibrations of these bonds in the C1, C2, and C4 conformers. The interaction strength based on the intermolecular distance between the anion and cation is relatively similar in the C2B-H13 and C2A-H3 bonds in C1, C2, and C4 conformers compared to the C3 conformer. One of the interesting properties of vibrational spectroscopy is that the manifestation of molecular interactions can be predicted by analyzing a frequency shift of the stretching vibration. The number of molecular interactions in the dication system is relatively higher than that in the monocation system. One can expect more conformation equilibrium in the dication system compared to the monocation system.
It should be mentioned here that the CH bending vibrations are intense and do not show a significant frequency shift in terms of wavenumber within a conformer. For example, the CH ring rocking vibration is predicted in the range of 1335–1328 cm–1. These vibrations are intense in all of the conformers and cannot be used to distinguish the presence of conformers, in contrast to the C2H vibrations. No significant change is predicted for the SO stretching vibrations in the present study because the C2H···N interactions are predicted to be more dominating compared to the C2H···O interactions. On the other hand, the doublet for the SN stretching vibration in C1 (988 and 984 cm–1) and C2 (987 and 979 cm–1) conformers is separated by 4 and 8 cm–1, respectively, whereas this separation increases to 24 cm–1 in C3 and C4 conformers (1011 and 987 cm–1). Thus, the assignment of molecular vibration can provide useful insight into conformational equilibrium and the hydrogen bonding in dication ionic liquids.
Conclusions
The effect of the bulky anion around the dication on the structure and normal vibrations is studied by employing density functional and B3LYP calculations. Different conformers are simulated based on the conformers, cis and trans, of the cation and anion and the hydrogen-bonding sites of the cation and anion. The trans conformation of the anion, as well as the cation, are predicted in the lowest energy conformer. Our simulation results predicted a conformational equilibrium between different dication ionic liquid conformers due to weak hydrogen-bonding interactions between the cations and anions. Our theoretical studies predicted that vibrational frequencies can be used to probe the conformational equilibrium in the experiment and can also be used as a tool for the frequency assignment of the vibrational spectrum. The C2H and SN stretching vibrations are important to distinguish between conformers, whereas other intense vibrations are relatively less sensitive to molecular interactions. It would be interesting to study the dynamics of hydrogen bonding in a dication system using classical molecular dynamics simulations in the future.
Computational Method
Two cation conformers based on the orientation of the C2H proton, namely cis and trans, are investigated in the present work. The cis conformation has the C2H proton of both rings on the same side, whereas the C2H protons of these rings are on the opposite side in the trans conformation. Hybrid density functional theory incorporating Becke’s three-parameter exchange with the Lee, Yang, and Parr (B3LYP)20,21 correlation functional was employed for conformer optimization using the Gaussian 16 program,22 with the internally stored 6-31G(d,p) basis set. Stationary point geometries were characterized as the saddle points or local minima on the potential energy surface by examining the number of imaginary frequencies and the eigenvalues of the Hessian matrix. The cis cation conformer is relatively more stable by 0.27 kJ/mol than the trans conformation of the cation. Similar to the cation conformer, we also investigated the cis and trans conformations of the anion based on CF3 group orientations.14
We simulated different conformers based on the hydrogen-bonding sites of the cation and anion. The CH bond of C2H is relatively more polar compared to the other CH bonds of the cation, which plays an important role in stronger cation–anion interactions. Like the cation, the SO and SN bonds can form relatively stronger hydrogen bonding compared to CF3 groups of the anion. With this view, we considered these binding sites of the cation and anion in building the initial structure of the conformer. As stated earlier, the cation and the anion both exhibit two conformers. We considered several conformer possibilities based on the cation and anion conformation, for example, two trans anions around cis cation or two cis anions around trans cations or one cis and one trans around the cis or trans conformer of the cation. One of the motives to study different conformers is to understand a conformational equilibrium in terms of the hydrogen bonding between the cation and anion at the molecular level.
Acknowledgments
This research was supported by the Office of Scholarly Innovations & Student Research.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c03017.
Optimized geometries of the C11–C25 conformers are shown in Figures S1–S3; optimized coordinates of C1–C25 conformers in Å (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Welton T. Solvents for synthesis and catalysis. Chem. Rev. 1999, 99, 2071–2083. 10.1021/cr980032t. [DOI] [PubMed] [Google Scholar]
- Endres F.; Abedin S. Z. E. Properties of ionic liquid solvents for catalysis. Phys. Chem. Chem. Phys. 2006, 8, 2101–2116. 10.1039/b600519p. [DOI] [PubMed] [Google Scholar]
- Wilkes J. S. Properties of ionic liquid solvents for catalysis. J. Mol. Catal. A: Chem. 2004, 214, 11–17. 10.1016/j.molcata.2003.11.029. [DOI] [Google Scholar]
- Patil R. A.; Talebi M.; Xu C.; Bhawal S. S.; Armstrong D. W. Synthesis of thermally stable geminal dicationic ionic liquids and related ionic compounds: an examination of physicochemical properties by structural modification. Chem. Mater. 2016, 28, 4315–4323. 10.1021/acs.chemmater.6b01247. [DOI] [Google Scholar]
- McEwen A. B.; Ngo H. L.; LeCompte K.; Goldman J. Electrochemical Properties of Imidazolium Salt Electrolytes for Electrochemical Capacitor Applications. J. Electrochem. Soc. 1999, 146, 1687–1695. 10.1149/1.1391827. [DOI] [Google Scholar]
- Seki S.; Kobayashi Y.; Miyashiro H.; Ohno Y.; Usami A.; Mita Y.; Kihira N.; Watanabe M.; Terada N. Lithium Secondary Batteries Using Modified-Imidazolium Room-Temperature Ionic Liquid. J. Phys. Chem. B 2006, 110, 10228–10230. 10.1021/jp0620872. [DOI] [PubMed] [Google Scholar]
- Guglielmero L.; Guazzelli L.; Toncelli A.; Chiappe C.; Tredicucci A.; Pomelli C. S. An insight into the intermolecular vibrational modes of dicationic ionic liquids through far-infrared spectroscopy and DFT calculations. RSC Adv. 2019, 9, 30269–30276. 10.1039/C9RA05735H. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paschoal V. H.; Faria L. F. O.; Ribeiro M. C. C. Vibrational Spectroscopy of Ionic Liquids. Chem. Rev. 2017, 117, 7053–7112. 10.1021/acs.chemrev.6b00461. [DOI] [PubMed] [Google Scholar]
- Dhumal N. R. Molecular interactions in 1,3-dimethylimidazolium-bis(trifluromethanesulfonyl)imide ionic liquid. Chem. Phys. 2007, 342, 245–252. 10.1016/j.chemphys.2007.10.004. [DOI] [Google Scholar]
- Dhumal N. R.; Kim H. J.; Kiefer J. Molecular Interactions in 1-Ethyl-3-methylimidazolium Acetate Ion Pair: A Density Functional Study. J. Phys. Chem. A 2009, 113, 10397–10404. 10.1021/jp907394v. [DOI] [PubMed] [Google Scholar]
- Dhumal N. R.; Kim H. J.; Kiefer J. Electronic structure and normal vibrations of the 1-ethyl-3-methylimidazolium ethyl sulfate ion pair. J. Phys. Chem. A 2011, 115, 3551–3558. 10.1021/jp1122322. [DOI] [PubMed] [Google Scholar]
- Dhumal N. R.; Noack K.; Kiefer J.; Kim H. J. Molecular Structure and interactions in the ionic liquid 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide. J. Phys. Chem. A 2014, 118, 2547–2557. 10.1021/jp502124y. [DOI] [PubMed] [Google Scholar]
- Gejji S. P.; Agrawal P. R.; Dhumal N. R. Ab initio structure and vibrational frequencies of lithium aromatic sulfonyl imide salt. Theor. Chem. Acc. 2002, 107, 351–356. 10.1007/s00214-002-0339-9. [DOI] [Google Scholar]
- Gejji S.; Suresh C.; Babu K.; Gadre S. Ab Initio Structure and Vibrational Frequencies of (CF3SO2)2N-Li+ Ion Pairs. J. Phys. Chem. A 1999, 103, 7474–7480. 10.1021/jp984474k. [DOI] [Google Scholar]
- Holbrey J. D.; Reicherta W. M.; Rogers R. D. Crystal structures of imidazolium bis(trifluoromethanesulfonyl)imide ’ionic liquid’ salts: the first organic salt with a cis-TFSI anion conformation. Dalton Trans. 2004, 2267–2271. 10.1039/B405901H. [DOI] [PubMed] [Google Scholar]
- Liu J.; Kim H.; Dhumal N. R.; Kim H. J. Vibrational spectroscopy of imidazolium-based ionic liquids: A combined MD/DFT study. J. Mol. Liq. 2019, 292, 111282 10.1016/j.molliq.2019.111282. [DOI] [Google Scholar]
- Talaty E.; Raja S.; Storhaug V.; Dölle A.; W R C. Raman and infrared spectra and ab initio calculations of C2-4MIM imidazolium hexafluorophosphate ionic liquids. J. Phys. Chem. B 2004, 108, 13177–13184. 10.1021/jp040199s. [DOI] [Google Scholar]
- Madden P.; Wilson M.; Hutchinson F. Raman spectra of ionic liquids: interpretation via computer simulation. J. Chem. Phys. 2004, 120, 6609–6620. 10.1063/1.1650831. [DOI] [PubMed] [Google Scholar]
- Berg R.; Deetlefs M.; Seddon K.; Shim I.; Thompson J. Raman and ab initio studies of simple and binary 1-alkyl-3-methylimidazolium ionic liquids. J. Phys. Chem. B 2005, 109, 19018–19025. 10.1021/jp050691r. [DOI] [PubMed] [Google Scholar]
- Becke A. D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
- Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; Li X.; Caricato M.; Marenich A. V.; Bloino J.; Janesko B. G.; Gomperts R.; Mennucci B.; Hratchian H. P.; Ortiz J. V.; Izmaylov A. F.; Sonnenberg J. L.; Williams-Young D.; Ding F.; Lipparini F.; Egidi F.; Goings J.; Peng B.; Petrone A.; Henderson T.; Ranasinghe D.; Zakrzewski V. G.; Gao J.; Rega N.; Zheng G.; Liang W.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Throssell K.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M. J.; Heyd J. J.; Brothers E. N.; Kudin K. N.; Staroverov V. N.; Keith T. A.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A. P.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Millam J. M.; Klene M.; Adamo C.; Cammi R.; Ochterski J. W.; Martin R. L.; Morokuma K.; Farkas O.; Foresman J. B.; Fox D. J.. Gaussian 16; Gaussian, Inc.: Wallingford, CT, 2016. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.