Abstract
Molecular docking excels at creating a plethora of potential models of protein–protein complexes. To correctly distinguish the favorable, native-like models from the remaining ones remains, however, a challenge. We assessed here if a protocol based on molecular dynamics (MD) simulations would allow distinguishing native from non-native models to complement scoring functions used in docking. To this end, the first models for 25 protein–protein complexes were generated using HADDOCK. Next, MD simulations complemented with machine learning were used to discriminate between native and non-native complexes based on a combination of metrics reporting on the stability of the initial models. Native models showed higher stability in almost all measured properties, including the key ones used for scoring in the Critical Assessment of PRedicted Interaction (CAPRI) competition, namely the positional root mean square deviations and fraction of native contacts from the initial docked model. A random forest classifier was trained, reaching a 0.85 accuracy in correctly distinguishing native from non-native complexes. Reasonably modest simulation lengths of the order of 50–100 ns are sufficient to reach this accuracy, which makes this approach applicable in practice.
Introduction
Modeling molecular processes in living organisms is a challenging endeavor in every aspect. Ideally, one would have to capture every component of the molecular machinery throughout all states of their biological journey. It is however already computationally highly demanding to process only a fraction of those interacting pathways in full detail; thus, one has to compromise on the level of details and/or the size of the simulated system. Docking is a molecular modeling approach commonly used to target large-scale interactions of two or more binding partners of any nature. It proficiently explores the possible binding modes throughout the conformational/interaction space, what is referred to as sampling. A number of software packages like HADDOCK,1,2 LightDock,3,4 ATTRACT,5,6 IMP,7,8 or ROSETTA9,10 allow to efficiently utilize the available experimental and/or bioinformatics information to eliminate sampling of irrelevant binding modes and guide protein–protein docking to meaningful outcomes. The next step is to detect the most favorable poses among the plethora of possible solutions, for which a scoring function is used.
Another persisting challenge, which is to different extents addressed by protein–protein docking programs, is protein flexibility.11−14 Molecular dynamics (MD) can account for conformational changes needed for binding at different levels. On a smaller scale, i.e., at the level of atoms, sidechains, loops, small molecules, or interfaces, MD is commonly applied to refine docked complexes with the aim of improving their quality.15−21 MD can be used at a more extensive level, where the docking process is simulated; however, modeling spontaneous association and dissociation of proteins is very rare unless coarse-grained models or enhanced sampling methods are used.22−25 With regard to all-atom MD simulations, enhanced sampling techniques like Markov states models,26−29 umbrella sampling combined with replica exchange MD,30−35 elastic-network approaches,35 string method,36 metadynamics,37,38 and other methods have been used to sample conformational change prior to or during binding and to facilitate such binding events under the condition that the binding interface is known.39 Such simulations also present a great opportunity to evaluate binding affinities of known protein–protein complexes. Perthold and Oostenbrink developed GroScore40 using nonequilibrium free-energy calculations in an explicit solvent to score 22 000 protein complexes from several Critical Assessment of PRedicted Interaction (CAPRI)41 sets.42,43 Kingsley et al.44 used steered MD and potentials of mean force (PMF) to distinguish between native and non-native poses in 10 docked complexes from ZDOCK.45 Thirty-nine docked complexes generated by HADDOCK2.2 webserver2 were ranked by Simões et al.46 with molecular mechanics-Poisson Boltzmann surface area (MM-PBSA)47 calculations. Takemura et al.48 developed evERdock, which uses the energy representation (ER) method49 to approximate free-energies of binding and distinguish native from non-native docking models after only 2 ns of MD in an explicit solvent.
Recently, alternative and computationally cheap approaches using machine learning (ML) algorithms have been developed to score protein–ligand50−54 and protein–protein55−58 complexes, as well as to detect binding interfaces.59−63 Geng et al.64,65 developed a scoring function (iScore) that combines random walk graph kernel (GraphRank) score with HADDOCK energetic terms. The DOcking decoy selection with Voxel-based deep neural nEtwork (DOVE) approach was created by Wang et al., which uses a convolutional deep neural network for evaluating protein docking models and is also available as a webserver.66 Ballester et al. used a random forest algorithm with 36 features to predict the binding affinities of protein–ligand complexes.67,68 Yet, another popular method that assesses the quality of protein models is Voronoi tessellation-based method.69−71 Olechnovič and Venclovas developed VoroMQA,72 also available as a webserver, which uses contact areas derived from Voronoi tessellation of the protein structure and tested their approach on critical assessment of structure prediction (CASP)73 data set. In supervised machine learning, algorithms first learn from labeled data so that they can apply the learned correlation to new data and predict their labels. There are various classifiers, for example, K-nearest neighbors, support vector machine and its variations, naive Bayes, or decision trees, which can be merged into the random forest. However, despite all these efforts, correct and consistent identification of near-native docked models of biomolecular complexes remains a challenge.74,75
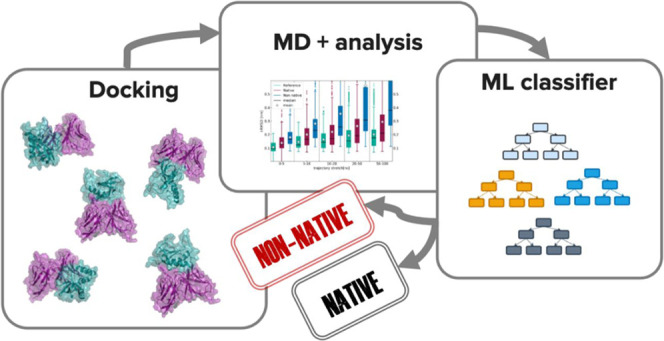
In this work, we address the scoring problem by combining standard MD simulations and machine learning to differentiate native from non-native models of protein–protein complexes. We selected 25 complexes from the Docking Benchmark Version 576 docked using a local version of HADDOCK2.4 for which the default HADDOCK score was not consistently able to correctly identify on top of the models closest to the reference structure. For each complex, we selected four models from two top-scoring clusters corresponding to near-native and wrong solutions. These, together with the reference crystal structure of the complex, were simulated in explicit solvent for 100 ns each (combined total of 48 μs for all models, references, and their replicate simulations). The resulting trajectories were analyzed, and eight features, including CAPRI criteria calculated with respect to the starting model, were extracted to build the machine learning model afterward.
These properties are studied by comparison to both the known reference crystal structure and the starting conformation using MD. Properties from multiple trajectory stretches of 10 and 20 ns were extracted, normalized, and fed into a random forest (RF) classifier created with the scikit-learn library.77 The RF classifier was trained on sets of 20 protein–protein complexes and subsequently tested and validated on independent sets of five complexes.
Materials and Methods
Dataset
Two hundred and thirty complexes were chosen from the Docking Benchmark Version 5 (BM5)76 and docked with HADDOCK version 2.4,1 applying restraints derived from the true interface (ambiguous restraints based on residues making contacts within a 3.9 Å cutoff). These ambiguous restraints have the property to bring the interfaces together without predefining their exact orientation. From these complexes, 25 (13 of which have the top-ranked cluster as a non-native model) were selected for our MD approach. Two training and validation sets were defined. Both have as common complexes in the training set the following 15 systems: 1BJ1, 1BUH, 1E4K, 1E6J, 1EAW, 1JPS, 1KAC, 1NSN, 1OC0, 1PXV, 1RV6, 1VFB, 2A5T, 2NZ8, and 3EO1. Training set 1 has, in addition, five proteins: 1GPW, 1KTZ, 2OOB, 3S9D, and 4G6M. Complexes 1YVB, 2HRK, 2O8V, 2Z0E, and 3F1P form the independent test set. To assess the impact of the exact composition of the training set on the performance of the RF classifier, in the second set, the training set 2, those two sets of five complexes were swapped (from training to test and vice versa). Complexes with two best scoring clusters were selected where one yielded models of high quality (native), while the other contained mostly incorrect models (non-native). From these clusters, the four best models per cluster were selected for MD simulations. In addition, four replicas of the reference (experimental) structure were run for all systems, but 1YVB, 2HRK, 2O8V, 2Z0E, and 3F1P were added at a later stage. Complexes were selected based on criteria such as complete loops at the protein–protein interface and no ions or cofactors present to avoid any issue with those during MD simulations. Missing side-chains and loops outside the interface were built using MODELLER version 9.12.78,79 Various quality measures and scores are shown for the native and non-native complexes in Table 1 (see also Figure S1).
Table 1. Average Properties of Top Four Models of the Native and Non-Native Clusters Selected for Further Characterization by MDa.
| system | DockQ | Fnat | iRMSD (Å) | LRMSD (Å) | BSA (Å2) | HADDOCK score | |
|---|---|---|---|---|---|---|---|
| 1E6J | nat | 0.70 ± 0.07 | 0.76 ± 0.04 | 1.52 ± 0.30 | 3.83 ± 0.30 | 1395 ± 36 | –73.9 ± 1.4 |
| non-nat | 0.11 ± 0.01 | 0.44 ± 0.33 | 5.63 ± 4.13 | 10.95 ± 4.13 | 1374 ± 34 | –59.0 ± 1.0 | |
| 1GPW | nat | 0.72 ± 0.02 | 0.68 ± 0.04 | 1.43 ± 0.08 | 2.08 ± 0.08 | 2322 ± 84 | –128.0 ± 3.8 |
| non-nat | 0.06 ± 0.01 | 0.38 ± 0.30 | 8.73 ± 7.31 | 15.29 ± 7.31 | 2253 ± 96 | –96.5 ± 0.7 | |
| 1HCF | nat | 0.63 ± 0.03 | 0.75 ± 0.02 | 1.62 ± 0.10 | 5.79 ± 0.10 | 1899 ± 45 | –95.8 ± 2.1 |
| non-nat | 0.21 ± 0.23 | 0.52 ± 0.30 | 5.17 ± 4.55 | 14.07 ± 4.55 | 1885 ± 46 | –73.2 ± 2.9 | |
| 1JPS | nat | 0.72 ± 0.03 | 0.77 ± 0.03 | 1.16 ± 0.13 | 4.72 ± 0.13 | 2076 ± 62 | –99.8 ± 1.7 |
| non-nat | 0.02 ± 0.00 | 0.40 ± 0.38 | 8.14 ± 6.99 | 26.95 ± 6.99 | 2117 ± 84 | –110.0 ± 4.7 | |
| 1KAC | nat | 0.48 ± 0.03 | 0.43 ± 0.04 | 2.36 ± 0.13 | 5.30 ± 0.13 | 1598 ± 41 | –69.6 ± 3.7 |
| non-nat | 0.05 ± 0.00 | 0.24 ± 0.19 | 8.28 ± 5.93 | 17.91 ± 5.93 | 1639 ± 56 | –55.8 ± 3.7 | |
| 1OC0 | nat | 0.50 ± 0.03 | 0.54 ± 0.05 | 2.52 ± 0.10 | 5.48 ± 0.10 | 1336 ± 59 | –81.3 ± 1.1 |
| non-nat | 0.15 ± 0.00 | 0.31 ± 0.23 | 4.63 ± 2.12 | 8.82 ± 2.12 | 1334 ± 54 | –87.9 ± 5.2 | |
| 1PXV | nat | 0.46 ± 0.02 | 0.45 ± 0.03 | 3.08 ± 0.03 | 5.26 ± 0.03 | 1913 ± 116 | –56.1 ± 5.5 |
| non-nat | 0.07 ± 0.00 | 0.28 ± 0.17 | 8.54 ± 5.45 | 16.33 ± 5.45 | 2024 ± 144 | –59.2 ± 3.7 | |
| 2NZ8 | nat | 0.28 ± 0.01 | 0.33 ± 0.01 | 3.62 ± 0.09 | 10.91 ± 0.09 | 2083 ± 40 | –72.3 ± 5.0 |
| non-nat | 0.10 ± 0.00 | 0.19 ± 0.13 | 5.92 ± 2.30 | 14.12 ± 2.30 | 2626 ± 559 | –102.4 ± 14.9 | |
| 2O8V | nat | 0.45 ± 0.04 | 0.49 ± 0.15 | 3.20 ± 0.23 | 5.78 ± 0.23 | 906 ± 59 | –60.8 ± 1.3 |
| non-nat | 0.14 ± 0.03 | 0.36 ± 0.17 | 6.90 ± 3.76 | 12.49 ± 3.76 | 807 ± 110 | –55.1 ± 1.9 | |
| 3EO1 | nat | 0.46 ± 0.01 | 0.61 ± 0.01 | 2.47 ± 0.07 | 8.76 ± 0.07 | 1865 ± 78 | –82.7 ± 7.7 |
| non-nat | 0.05 ± 0.00 | 0.36 ± 0.26 | 6.62 ± 4.14 | 28.90 ± 4.14 | 2014 ± 164 | –86.7 ± 1.3 | |
| 1BJ1 | nat | 0.84 ± 0.05 | 0.91 ± 0.01 | 0.75 ± 0.14 | 3.89 ± 0.14 | 1880 ± 37 | –156.2 ± 1.3 |
| non-nat | 0.06 ± 0.00 | 0.51 ± 0.40 | 6.48 ± 5.73 | 21.61 ± 5.73 | 1967 ± 99 | –109.9 ± 5.4 | |
| 1EAW | nat | 0.64 ± 0.12 | 0.70 ± 0.10 | 1.76 ± 0.55 | 4.54 ± 0.55 | 1735 ± 71 | –97.4 ± 13.9 |
| non-nat | 0.19 ± 0.03 | 0.49 ± 0.22 | 3.65 ± 1.99 | 10.82 ± 1.99 | 1788 ± 118 | –104.9 ± 14.0 | |
| 1KTZ | nat | 0.81 ± 0.02 | 0.86 ± 0.03 | 0.90 ± 0.04 | 3.83 ± 0.04 | 1057 ± 19 | –65.4 ± 1.0 |
| non-nat | 0.07 ± 0.01 | 0.50 ± 0.36 | 5.26 ± 4.36 | 25.06 ± 4.36 | 1084 ± 31 | –75.2 ± 1.5 | |
| 1NSN | nat | 0.62 ± 0.01 | 0.66 ± 0.01 | 2.02 ± 0.12 | 3.60 ± 0.12 | 2222 ± 92 | –110.8 ± 2.4 |
| non-nat | 0.04 ± 0.00 | 0.33 ± 0.33 | 9.48 ± 7.46 | 13.97 ± 7.46 | 2299 ± 114 | –116.4 ± 4.1 | |
| 1RV6 | nat | 0.67 ± 0.05 | 0.72 ± 0.02 | 1.68 ± 0.25 | 3.75 ± 0.25 | 1747 ± 66 | –89.3 ± 1.6 |
| non-nat | 0.07 ± 0.00 | 0.39 ± 0.33 | 6.60 ± 4.92 | 13.28 ± 4.92 | 1860 ± 125 | –110.2 ± 1.8 | |
| 1VFB | nat | 0.74 ± 0.04 | 0.74 ± 0.02 | 1.26 ± 0.12 | 3.23 ± 0.12 | 1439 ± 36 | –77.2 ± 1.1 |
| non-nat | 0.06 ± 0.00 | 0.40 ± 0.34 | 6.94 ± 5.68 | 13.74 ± 5.68 | 1511 ± 76 | –82.6 ± 2.1 | |
| 2A5T | nat | 0.46 ± 0.02 | 0.56 ± 0.03 | 2.88 ± 0.13 | 7.10 ± 0.13 | 2272 ± 73 | –129.3 ± 2.6 |
| non-nat | 0.19 ± 0.01 | 0.44 ± 0.13 | 4.63 ± 1.76 | 11.50 ± 1.76 | 2640 ± 381 | –107.9 ± 1.9 | |
| 2OOB | nat | 0.70 ± 0.08 | 0.91 ± 0.05 | 1.60 ± 0.30 | 5.35 ± 0.30 | 995 ± 28 | –56.0 ± 0.6 |
| non-nat | 0.11 ± 0.00 | 0.52 ± 0.39 | 4.90 ± 3.31 | 12.04 ± 3.31 | 1043 ± 56 | –75.1 ± 2.1 | |
| 3S9D | nat | 0.50 ± 0.03 | 0.49 ± 0.04 | 2.06 ± 0.05 | 5.95 ± 0.05 | 2205 ± 153 | –81.5 ± 10.5 |
| non-nat | 0.05 ± 0.00 | 0.27 ± 0.22 | 8.07 ± 6.01 | 17.28 ± 6.01 | 2408 ± 232 | –120.5 ± 1.5 | |
| 4G6M | nat | 0.86 ± 0.01 | 0.92 ± 0.01 | 0.96 ± 0.04 | 1.86 ± 0.04 | 1912 ± 68 | –123.8 ± 0.9 |
| non-nat | 0.06 ± 0.00 | 0.50 ± 0.43 | 7.99 ± 7.03 | 12.94 ± 7.03 | 1951 ± 73 | –91.8 ± 12.6 | |
| 1YVB | nat | 0.68 ± 0.05 | 0.74 ± 0.04 | 1.29 ± 0.14 | 5.13 ± 0.14 | 1619 ± 32 | –108.8 ± 1.8 |
| non-nat | 0.12 ± 0.00 | 0.46 ± 0.29 | 5.63 ± 4.34 | 12.45 ± 4.34 | 1636 ± 72 | –99.6 ± 3.1 | |
| 2HRK | nat | 0.57 ± 0.02 | 0.77 ± 0.03 | 2.73 ± 0.11 | 5.33 ± 0.11 | 1747 ± 34 | –90.1 ± 2.1 |
| non-nat | 0.06 ± 0.00 | 0.42 ± 0.35 | 8.38 ± 5.66 | 14.99 ± 5.66 | 1701 ± 56 | –93.1 ± 1.5 | |
| 2O8V | nat | 0.42 ± 0.03 | 0.48 ± 0.08 | 3.37 ± 0.19 | 6.84 ± 0.19 | 845 ± 44 | –73.5 ± 6.8 |
| non-nat | 0.14 ± 0.01 | 0.36 ± 0.13 | 8.03 ± 4.66 | 13.44 ± 4.66 | 833 ± 35 | –62.8 ± 1.6 | |
| 2Z0E | nat | 0.47 ± 0.03 | 0.45 ± 0.03 | 2.60 ± 0.16 | 5.33 ± 0.16 | 2365 ± 31 | –95.5 ± 2.0 |
| non-nat | 0.07 ± 0.00 | 0.28 ± 0.18 | 6.53 ± 3.93 | 15.82 ± 3.93 | 2237 ± 136 | –67.7 ± 12.6 | |
| 3F1P | nat | 0.53 ± 0.01 | 0.60 ± 0.02 | 3.23 ± 0.17 | 4.22 ± 0.17 | 2265 ± 50 | –129.3 ± 2.6 |
| non-nat | 0.05 ± 0.00 | 0.31 ± 0.29 | 9.30 ± 6.07 | 13.86 ± 6.07 | 2184 ± 90 | –107.9 ± 1.9 | |
The DockQ score (101) was calculated as in ref (101). Fnat is the fraction of native contacts that takes into account any atom pair-forming contacts between proteins within a 5 Å distance cutoff (Fnat = 1 = 100% for the reference). The interface root mean square deviations (i-RMSD) were calculated on the backbone of residues within 10 Å of the other protein. The ligand RMSD (l-RMSD) was calculated by fitting on the backbone of the first molecule and calculating the RMSD of the backbone atoms of the second molecule. The buried surface area (BSA) represents the difference between the solvent-accessible area of the separated components and the complex. The HADDOCK score is the score used in ranking of HADDOCK models in the final refinement stage (1.0 Evdw (van der Waals intermolecular energy) + 0.2 Eelec (electrostatic intermolecular energy) + 1.0 Edesol (desolvation energy) + 0.1 Eair (distance restraints energy)).
Molecular Dynamics Simulations
The selected complexes were simulated and subsequently analyzed using the GROMACS simulation package80 version 2019 and the CHARMM36m81 forcefield. Protein structures were first optimized in a vacuum using the steepest-descent algorithm (up to 5000 steps), and subsequently, solvated in a rhombic dodecahedral box of TIP3P82 water. The minimal solute to box distances was set to 1.4 nm, and sodium and chloride ions were added to neutralize the box and reach a concentration of 150 mM. A second optimization stage was performed (up to 25 000 steps if convergence, standard settings, was not reached before). A first MD run of 50 ps was then performed at 50 K in the NVT ensemble using a velocity-rescaling thermostat83,84 with a 0.1 ps time constant. Initial velocities were randomly assigned according to a Maxwell–Boltzmann distribution at 50 K and the system was subsequently heated up to 150 and 300 K. During this equilibration phase, all heavy atoms of the proteins were positionally restrained using a decreasing force constants of 1000 (50 K), 100 (150 K), and 10 (300 K) kJ mol–1 nm–2 in x-, y-, and z-coordinates. Production runs of 100 ns in length were performed in an NPT ensemble using the Berendsen barostat84 with isotropic pressure scaling, a time constant of 1 ps, and an isothermal compressibility of 4.5 × 10–5 bar–1. For all of MD simulations, the leapfrog integration scheme85 with a timestep of 2 fs was used and covalent bonds were restrained using the LINCS algorithm.86 Neighbor searching was performed using a Verlet-based cut-off scheme updated every 10 steps with a cut-off of 1 nm. For the van der Waals interactions, a twin range cut-off with a smooth switch to zero between 1 and 1.2 nm was used. The Particle Mesh Ewald method87 was used to calculate the long-range electrostatics. The total simulation time for all complexes sums up to 48 μs. Trajectory frames were written to disk every 500 ps for further analysis.
Analysis
The definition of the fraction of common contacts, interface residues, and ligands followed the CAPRI classification.88 Intermolecular contacts were considered as any atom pair between proteins within 5 Å, and the contact evolution as a function of simulation time was calculated using the gmx hbond-contact analysis tool. Interface residues are defined as residues, with at least one atom within 10 Å of the other molecule, and interface RMSD (i-RMSD) was calculated on the backbone of these residues. Ligand RMSD was calculated by fitting on the backbone of the first molecule and calculating the RMSD of the backbone atoms of the second molecule. The DockQ values reported in Table 1 are based on a combination of all of these properties (Fnat, i-RMSD, l-RMSD) as described in ref (89). The distances between centers of mass of proteins, hydrogen bonds, and buried surface area were calculated using the standard GROMACS analysis tools (gmx distance, gmx hbond, and gmx sasa). The interaction energy terms were calculated as the sum of short-range Coulombic and Lennard-Jones interactions between the two proteins or between the proteins and water. To compensate for the varying size of the systems and interfaces for further machine learning analysis, all properties were evaluated relative to their values at the beginning of the trajectory. Hence, only changes of the properties over time are observed and not their absolute numbers. These time series were extracted for all trajectories and were used to feed the random forest classifier.
Random Forest Model for Native vs Non-Native Classification
To select the most accurate classifier for our task, we evaluated the performance of the following set of binary classifiers available in the Scikit-learn library:77 gnb = Gaussian naive Bayes, KNN = K neighbors classifier (n_neighbors = 1), MNB = multinomial naive Bayes, BNB = Bernoulli naive Bayes, LR = logistic regression, SDG = stochastic gradient descent classifier, SVC = support vector classification, LSVC = linear SVC, NSVC = Nu SVC, RF = random forest classifier (see Figure S7). These classifiers were tested on the training set every 10 ns, using repeated K-fold cross-validation with 10 splits and 10 repeats with a test size of 25% (i.e., five complexes). Since random forest showed the highest accuracy throughout the entire trajectory, it was selected for our approach. Random forest combines multiple components of randomness. First, the training set is divided into multiple bootstrapped copies and predictions from these are aggregated, which reduces the variance, or overfitting compared to individual decision trees. Moreover, to further decrease the correlation among trees, a random subset of features is selected at each tree split. In this work, the Scikit-learn library77 0.23.1 was used again to create the random forest classifier. The Grid Search algorithm was used to search for the optimal parameters based on the last 20 ns of trajectories of training set 1, as described in the dataset part of the Materials and Methods section. The following parameters were used to create the random forest classifier: the number of trees in the forest was set to 1000, bootstrap samples were used when building trees, square root of features were selected at each split, the maximum depth of the tree was set to 50, the minimum number of samples required to split an internal node was set to 2, and the minimum number of samples required to be at a leaf node was set to 1. The model was subsequently trained on different 20 ns patches of the trajectory. The average receiver operating characteristic (ROC) curve, accuracy, and f1-score were calculated from 10 times 10-fold cross-validation optimization. Accuracy is calculated as the fraction of correct predictions (true-positive (TP) + true-negative (TN)) out of the total number of predictions (TP + TN + false-positive (FP) + false-negative (FN)). F1-score is calculated as TP/(TP + 1/2 (FP + FN)). The true-positive rate (TPR), also known as sensitivity, is the fraction of TP out of the positives and true-negative rate (TNR) and the fraction of TN out of the negatives. The relationship between these two metrics is reflected in the ROC curve.
Results
Twenty-five protein–protein complexes from BM576 modeled with HADDOCK using true interface information (but no specific contacts) were selected on the basis that their two best-scoring clusters showed models of utterly different quality (near-native and non-native). For about half of those complexes (13 out of 25), HADDOCK ranks on top of a non-native model. Our aim was to use MD simulations complemented by machine learning to distinguish native from non-native models. The quality of all models, together with the buried surface area and HADDOCK score, are listed in Table 1 (see also Figure S1).
Standard MD
For each complex, the four best-scoring models per native and non-native clusters were selected and simulated, each with two replicas per model, for 100 ns using GROMACS. Additionally, for the 20 complexes of training set 1, simulations of the reference structure (crystal structure; four MD replicas per reference structure) were performed and analyzed. Properties of all complexes and models were measured with respect to both the reference crystal structure of the complex and the docking model used as starting conformation for MD simulations. For training the machine learning model, relative values with respect to the start of the production run (ref-orig) were used as input, which partly normalizes the differences due to the varying size of the complexes.
Can MD Improve the Quality of the Models?
The quality of protein–protein complexes is commonly assessed by comparing a number of properties to their reference (usually, experimental) structure. In CAPRI, those properties are ligand-RMSD, interface-RMSD, and fraction of native contacts.
In the first part of our work, we looked at these properties during the course of the MD trajectories of both the HADDOCK models and the reference crystal structures and compared them with the experimental crystal structure of the complex. Figure 1 shows the distributions of l-RMSD, i-RMSD, and Fnat with respect to the respective reference crystal structures for all of the 20 complexes of the training set 1 and their evolution over different stretches along the simulation. This analysis is based on a total of 160 simulations of both native and non-native clusters, and 80 simulations of the reference crystal structures, each of 100 ns in length.
Figure 1.
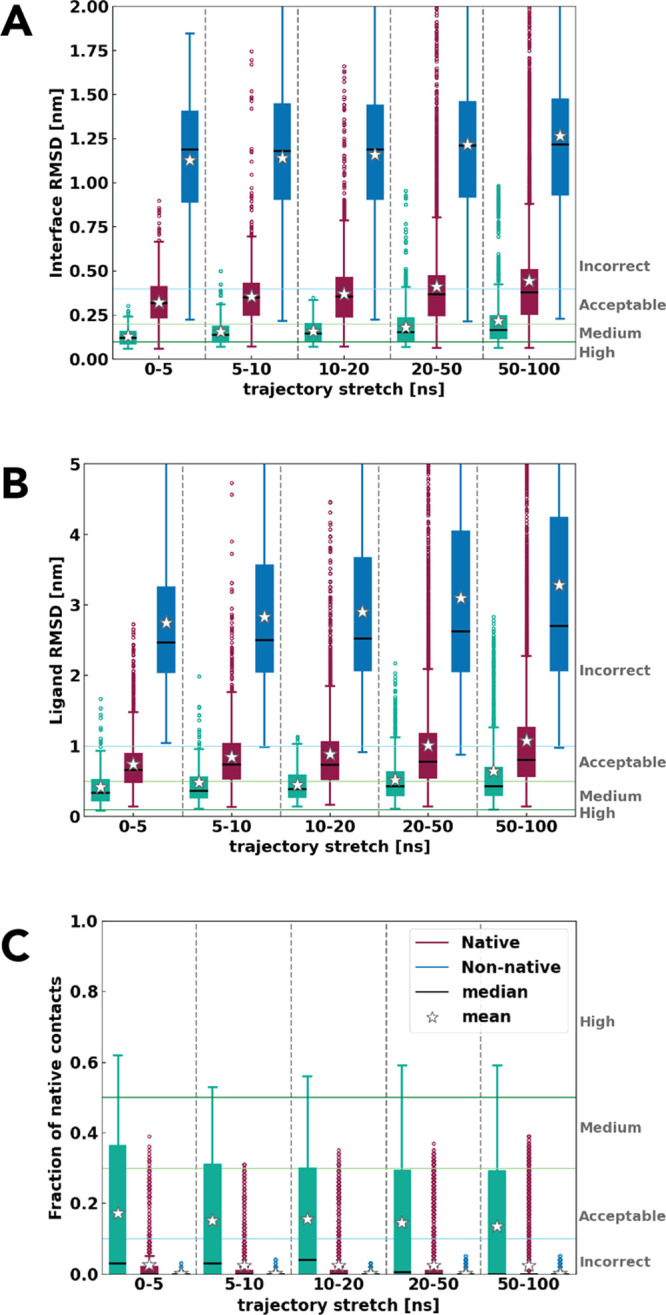
(A) Interface-RMSD, (B) ligand-RMSD, and (C) fraction of native contacts for native, non-native, and reference structures from the complex crystal structure for all 20 complexes. The boxplot shows the interquartile range with its median as black lines, mean as stars, whiskers in error bars, and outliers in circles. Reference in green, native clusters in burgundy, and non-native in blue.
As expected, all systems including those started from the reference crystal structures undergo changes along the course of the simulation. The magnitude of these changes is, however, somewhat surprising: in the first 5 ns of the production runs, even the reference structures lose on average up to 80% of their original contacts (Figure 1C). This might be due to the initial rearrangement of the residues during the heating up phases of the simulation and the relatively tight definition of intermolecular contacts (5 Å). Indeed, with regard to the simulation of the reference structures, we noticed in all cases only small changes in the conformation of the backbone at the partner’s interface (Figure S2). All three groups of complexes deviate further from the crystal structure over time, which results in poorer model quality toward the end of the simulation. In particular, while the reference simulations remain within the acceptable quality CAPRI category during the entire trajectory, near-native docked models reach the incorrect area by the end of the simulation, while non-native models never reach the correct category. Despite this, a clear and consistent separation of native and non-native models is evident throughout the entire course of the simulation for all three properties reported in Figure 1. While 100 ns of MD simulation is not able to improve the quality of the initial models, it clearly allows differentiating between near-native and non-native models based on a comparison to the known crystal structure.
Can MD Distinguish between Native and Non-Native Complexes Based on CAPRI Measures?
The second question we wanted to address in our work is if standard MD is able to capture any different behavior of native and non-native models. This is particularly important because in a realistic scenario there will be no reference structure available. To assess this, we selected for each simulation the model at the starting point of the production run as a reference (hereafter ref-orig). Figure 2 depicts the same properties as Figure 1, which we denote by an additional “-orig” label to distinguish from the same values with respect to the reference crystal structure (l-RMSDorig, i-RMSDorig, and Fnatorig), so as to highlight their behavior relative to the initial binding mode (ref-orig). For both ligand and interface RMSDorig, the reference crystal structures show the lowest values, pointing to the (expected) higher stability of the experimental complexes compared to their docked models. More interestingly, the near-native complexes show overall higher stability (less deviations from the initial values) than the non-native ones. Even though the distributions of both RMSDorigs are largely overlapping, their means are clearly distinguishable at the end of the simulation (the difference from ref-orig amounts to ∼0.5 nm for i-RMSDorig and ∼1 nm for l-RMSDorig, respectively; Figure 2A,B). Importantly, these differences increase over the simulation time most often due to the increasing instability of non-native complex configurations in the second half of the simulations (Figures S2 and S3). A similar trend is seen in the decrease of Fnatorig over time (Figures 2C and S4). While the reference and native structures lose up to 70 and 80% of initial contacts, respectively, the non-native models lose almost all of them toward the end of the simulation.
Figure 2.
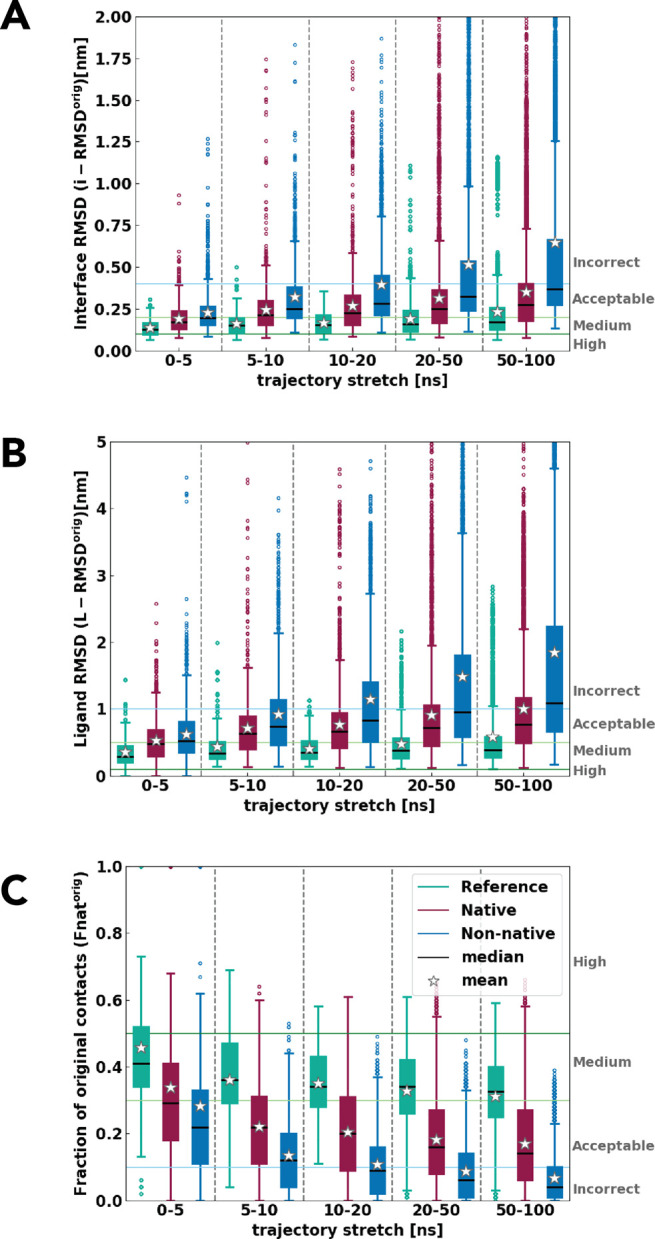
(A) Interface-RMSDorig, (B) ligand-RMSDorig, and (C) fraction of native contacts (Fnatorig) for native, non-native, and reference crystal structures with respect to the beginning of the trajectory for all 20 complexes. The boxplot shows the interquartile range with its median as black lines, mean as stars, and whiskers and outliers in circles. Reference in teal, native clusters in burgundy, and non-native in blue.
Interestingly, the trends are evident within the first 5 ns of the simulation, where even the reference simulations lose up to 50% of original contacts. This implies that even such a short stretch of plain MD causes significant changes in the protein interfaces, as already highlighted by Figure 1. We speculate that such a sudden loss of contacts, occurring during the first part of the simulation, is a consequence of the optimization of the interactions among the packed sidechains (deriving from both modeling or experiments). Consistent with this hypothesis, previous work exploiting extremely long MD simulations to study protein–protein association events showed that successful events (measured by l-RMSD values lower than 3 Å) led to complexes featuring a fraction of native contacts largely variable but generally lower than 0.5.22 Moreover, such a relatively low fraction was associated to a retained hydration of the interacting surfaces, which remained more than 50% solvated compared to their unbound state. Further, it has been shown experimentally that typical crystallization conditions as low (cryogenic) temperature and low hydration tend to contort protein interfaces compared to physiological conditions.91 By comparing crystal structures obtained at cryogenic and room temperatures, Fraser et al.90 observed that more than 35% of sidechains are remodeled during cryocooling, which can impair their functional motion. Low temperatures and hydration lead to more compact protein packing, smaller protein volume, and thus, increased buried surface area, i.e., increased number of contacts between molecules.91 This tighter packing could therefore be quickly resolved during the MD simulation, where, besides the loss of native contacts, we also observed a slight decrease in the buried surface.
For a comparison, CAPRI criteria are also indicated in Figure 2. These should help to illustrate the order of structural changes occurring at the interface and the rearrangement of the complex during MD. In all three properties non-native models enter the incorrect category in the second half of the simulation (e.g., after 50 ns), while reference and native models remain in the acceptable to the medium quality area (Figures S2–S4).
A number of additional properties were measured for selected complexes. Figure S5A,B shows the evolution of the buried surface area and of the distance between the COMs of the two binding partners. While for reference structures both properties are relatively stable throughout the simulation, for non-native models, the BSA is consistently decreasing while the distance between the center of masses increases. By the end of the trajectory, the variations amount, on average, to 5 nm2 and 0.3 nm, respectively. The number of hydrogen bonds is as well slightly decreasing (Figure S5C) for the non-native complexes. An identical behavior can be seen in the nonbonded interaction energies between proteins and proteins and water, as depicted in Figure S5D,E. As expected, due to the initial (generally unfavorable) conformation of non-native complexes, the interaction between protein partners becomes weaker with increasing simulation time for these models. This is compensated by more favorable interactions with water, which can be seen in the decrease of the nonbonded interaction energy. The native complexes do not deviate considerably from their reference complexes, which is consistent with the previous findings and CAPRI properties. Such a clear distinction in the behavior of native and non-native complexes during standard MD of 100 ns or less is rather remarkable. We, therefore, decided to exploit the measured properties to develop a machine learning model that could help us in classifying models as native or non-native based on their simulation properties.
Can Machine Learning Help in Identifying Native Poses?
Properties calculated from simulations of 20 HADDOCK models of the training set 1 were mixed and labeled as native and non-native, based on the quality of the initial model they were extracted from. They were divided into trajectory stretches of 20 ns. An example of such distribution of all properties and their scatter plots in the last 20 ns of the trajectory is shown in Figure S6. To choose the most fitting classifier for our purposes, the trajectory was divided into stretches of 10 ns and, for each of these time frames, a number of classifiers from the Scikit library were trained. Ten nanoseconds was used to obtain a more detailed overview of ML classifying accuracy along the trajectory. The accuracy scores for all of them are summarized in Figure S7. The random forest classifier reached clearly higher accuracy than the other ones and was chosen for further classification of the complexes. Random forest combines bootstrapping of the training set with random feature selection at each tree split. First, the search for optimal parameters was performed using the grid search algorithm based on the last 20 ns of trajectories from the training set. The best parameters were selected, which are listed in the Materials and Methods section. Subsequently, the model was trained considering different trajectory stretches. Its accuracy was calculated within its own cross-validated training set 1. On top of the inherent randomness that random forest involves, stratified K-fold cross-validation with 100 splits was used. Accuracy, precision, recall, f1-score, and area under curve (AUC) of the receiver operating characteristic (ROC), calculated for 5 trajectory stretches of 20 ns are summarized in Table 2. The accuracy of the RF classifier starts at 0.77 and reaches 0.86 in the last 20 ns of the simulation. Similar trends can be seen in all performance metrics. Interestingly, after 40–60 ns, all metrics start converging.
Table 2. Scoring Performance of the RF Classifier Based on the Cross-Validated Training Set 1 and Both Validation Sets.
| trajectory stretch | 0–20 ns | 20–40 ns | 40–60 ns | 60–80 ns | 80–100 ns | validation set 1 | validation set 2 |
|---|---|---|---|---|---|---|---|
| accuracy | 0.77 | 0.83 | 0.85 | 0.85 | 0.86 | 0.60 | 0.75 |
| precision | 0.79 | 0.86 | 0.87 | 0.86 | 0.88 | 0.61 | 0.71 |
| recall | 0.76 | 0.81 | 0.84 | 0.84 | 0.85 | 0.61 | 0.84 |
| f1 | 0.76 | 0.82 | 0.85 | 0.84 | 0.85 | 0.59 | 0.77 |
| roc_auc | 0.86 | 0.92 | 0.93 | 0.93 | 0.94 | 0.60 | 0.83 |
RF classifiers allow the evaluation of the importance of the various features used in training. Figure S9 summarizes feature importance assessed on the last 20 ns of the trajectory of the training set 1. Changes in i-RMSDorig, BSAorig, and Fnatorig are the most important in distinguishing native from non-native models, while the number of hydrogen bonds shows the smallest importance. However, overall, the relative differences between property importance were not very substantial.
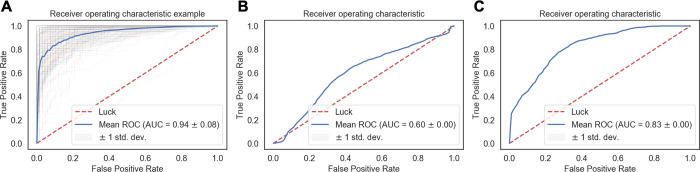
While the RF classifier performed well on the cross-validated training test alone, a fair comparison would be to test its accuracy on an external validation test. To this end, five additional complexes were selected (validation set 1), and their native and non-native models were simulated for 100 ns as for the training set 1 (see the Materials and Methods section). CAPRI properties of the validation set throughout the trajectory are shown in Figure S8. Surprisingly, here the differences between native and non-native complexes were not as high as in the training set. When the model was tested on the independent validation set, its accuracy and f1-score reached 0.60 and 0.59, respectively (Table 2). This is significantly lower than for the original training set. The same is observed for the AUC with 0.60 against 0.93 for the training set (Figure 3B). Prompted by this finding, we performed another round of training and validation of the model using a different distribution of complexes between training and test sets (training set 2 and validation set 2) (see the Materials and Methods section). For this, five randomly selected complexes from the original training set were swapped with the validation set. After training on this second data set, the RF classifier shows a better performance in distinguishing native from non-native models for the validation set with accuracy and AUC of 0.75 and 0.83, respectively (Table 2 and Figure 3C). This implies that the model accuracy depends on the nature of the initial complexes and their stability during MD. But even in the unfavorable scenario where the behavior of both classes of complexes was rather similar (validation set 1), our model was able to correctly identify native complexes with an accuracy of 60%.
Figure 3.
Receiver operating characteristic (ROC) curves showing (A) training set 1 using stratified K-fold cross-validation split 100 times. Individual splits are shown in thin lines and their mean and shown in blue bold line. (B) Validation set 1 and (C) validation set 2.
Discussion
The flexible nature of proteins and their interfaces naturally evolve into dynamic interactions among binding partners.92−94 Our work makes use of such dynamics to tackle the intricate task of correctly scoring models of protein–protein complexes obtained by docking. There are not many MD approaches known to focus on this task without using enhanced sampling or free-energy calculations. In this work, native and non-native models of 25 complexes from the docking benchmark 5 docked with HADDOCK2.4, and their reference crystal structures were simulated in multiple copies, each for 100 ns in length (cumulative time: 48 μs). The trajectories were analyzed and their properties were used to feed a random forest classifier.
Running MD simulation on docked models could lead to a spontaneous complex rearrangement to a more favorable position (aka induced fit) provided sufficient sampling. Here, by comparing simulated HADDOCK models and their structures at the beginning of the production run (ref-orig) to the original reference crystal structure, we first assessed if MD simulations would allow improving the quality of the models. Significant changes were observed at the interface of all simulated structures, even the crystal structure. However, little to no improvement was observed for the near-native models. Perhaps, much longer time scales would be necessary to capture spontaneous rearrangements of protein complexes, similar to long plain MD simulations that have been used to observe domain rearrangement in single proteins.95−97 Pan et al.22 observed reversible binding and unbinding of multiple protein complexes in the time scale of hundreds of microseconds using the tempered binding approach and dedicated hardware built in-house. In that work, the native binding was not reached by the sampling of the entire protein surface while proteins stayed in close contact, but rather after a repeated dissociation and reassociation of the complex (mimicked by docking here). This observation was analogous to ours since we also did not observe any rearrangement from non-native to native binding pose while the proteins stayed in contact. One can assume that protein–protein reassociation would be needed in our case too; however, this can hardly be achieved in the 100 ns time scale of our simulations. Nonetheless, the simulations revealed a clear difference in the behavior of non-native and native models or the reference during that time scale.
In the second part of our work, we examined in a realistic scenario, i.e., in the absence of a reference structure, if MD simulations could be used as a scoring tool to distinguish native from non-native models. For this, properties of the simulations were compared to their values at the beginning of the trajectory, measuring thus changes with respect to the original starting model. Here, clearly, the crystal structures followed by the native models exhibited the highest stability in contrast to the non-native models. This is a promising observation, where, without any prior knowledge of model quality, one can see differences in their stability during simulation which allows pointing out the less stable/non-native models.
Previous studies have also addressed the problem of identifying native solutions using postdocking simulations. Radom et al.98 could similarly distinguish decoys from native structures based on their stability during MD and noticed a few exceptions, where the wrong binding pose would find the correct conformation throughout the simulation. Akin cases were seen in our study as well; nonetheless, they were statistically not significant enough to influence the overall trend.
Kozakov et al.,99 on the other hand, used a combination of docking and Monte Carlo (MC) minimization to assess the stability of near-native and non-native enzyme–inhibitor and antibody–antigen complexes. They observed that all near-native clusters were stable, i.e., multiple trajectories converged into a particular region within the cluster. Moreover, they could identify half of false-positive (non-native) clusters, which showed lower stability. MC minimization offers another relatively fast alternative to MD in terms of identifying native poses.
Prévost et al.39 used a similar MD ranking approach for docked complexes. They suggested altering the CAPRI scoring criteria and take the dynamic properties (l-RMSD, i-RMSD, and Fnat) into account by comparing simulations of the reference crystal structures of the complexes. To correlate system properties to the simulated reference, instead of its crystal structure, could be advantageous, yet in our case, somewhat redundant since they were already able to observe stability differences even without the reference present.
Based on these findings, a machine learning model was developed to classify complexes as native or non-native in an automated manner rather than by visual inspection of the properties as a function of simulation time. The performance of the model was assessed on cross-validated training sets as well as two independent validation sets. The accuracy on the training set reached 0.85 and ranged between 0.60 and 0.75 for validation sets. While the accuracy on the training set was increasing as a function of the simulation time window considered, it seems to converge after 50 ns. This would indicate that shorter simulations of 50 ns might already be sufficient for this kind of classification in the future. However, despite the promising indications arising from our study, a larger and more diverse dataset is certainly desirable to reduce possible overfitting and generalize the methodology.
Such a combination of docking, molecular dynamics simulation, and machine learning, as used in this work, are becoming more common.100,101 Still their application to protein–protein interactions remains limited. Several studies have focused on scoring docked protein–protein models neglecting their dynamic nature. Pfeiffenberger et al.56 applied an extremely randomized tree classifier to rank poses generated by SwarmDock102,103 for 11 CAPRI targets classified by their ligand RMSD. Using 109 molecular descriptors, they obtained accuracy between 0.6 and 0.7 in distinguishing native from non-native complexes with residue–residue contact descriptors, which is comparable to our results. Das and Chakrabarti104 employed a support vector machine to differentiate between native and non-native interfaces using features like accessible, buried surface area, and frequency of salt bridges or hydrogen bonds. An F1-score of 0.8 was achieved on an external dataset in distinguishing between native and non-native models. Both studies found that the key features for protein–protein interactions are intermolecular contacts and accessible/buried surface area. Comparable accuracies (0.7–0.9) were obtained by the DOVE approach66 on validation and training sets. iScore64 as a graph-kernel-based scoring method ranked among the top-scoring approaches on the CAPRI scoring set. Our MD-based scoring method not only reaches a state-of-the-art technique level of accuracy but also introduces a novel way to incorporate information about the dynamics of protein complexes into scoring. The encouraging results obtained show that, even if the behavior of the complexes remains similar for both native and non-native models, the RF classifier is able to distinguish them in up to 75% of the cases. From the feature importance analysis, the most important properties for classifying the quality of a model are suggested to be the fraction of native contacts, interface RMSD, and buried surface area with respect to the starting model.
Acknowledgments
The authors thank the entire computational structural biology group at the Utrecht University for fruitful discussions, and, in particular, Dr. Francesco Ambrosetti for his input on machine learning. This research used the Savio computational cluster resource provided by the Berkeley Research Computing program at the University of California, Berkeley (supported by the UC Berkeley Chancellor, Vice Chancellor for Research, and Chief Information Officer).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.1c00336.
Initial ligand RMSDs and HADDOCK scores of the native and non-native clusters for all 25 complexes (Figure S1); evolution and distributions of interface RMSDs, ligand RMSDs, and a fraction of native contacts, respectively, for the 20 complexes in the training set 1 (Figures S2–S4); changes in BSA, the distance between center of masses, number of hydrogen bonds, and nonbonded intermolecular energies for the 20 complexes in the training set 1 (Figure S5); pair plots of measured properties for the last 20 ns of simulations of native and non-native complexes (Figure S6); accuracy scores of different classifiers from the Scikit library compared per timepoint of the trajectory (Figure S7); box plots for the interface and ligand RMSDs and for the fraction of original contacts for the 5 complexes of the validation set 1 (Figure S8); feature importance of various terms in the classifier (Figure S9) (PDF)
This work was financially supported by the European Union Horizon 2020 projects BioExcel (675728, 823830).
The authors declare no competing financial interest.
Notes
All MD trajectories without water and their topologies are deposited in zenodo (http://doi.org/10.5281/zenodo.4629895). GROMACS scripts, extracted features, and jupyter notebooks with Random Forest classifiers are available in the Github repository (https://github.com/haddocking/MD-scoring).
Supplementary Material
References
- Dominguez C.; Boelens R.; Bonvin A. HADDOCK: A protein-protein docking approach based on biochemical or biophysical information. J. Am. Chem. Soc. 2003, 125, 1731–1737. 10.1021/ja026939x. [DOI] [PubMed] [Google Scholar]
- van Zundert G. C. P.; Rodrigues J.; Trellet M.; Schmitz C.; Kastritis P. L.; Karaca E.; Melquiond A. S. J.; van Dijk M.; de Vries S. J.; Bonvin A. The HADDOCK2.2 Web Server: User-Friendly Integrative Modeling of Biomolecular Complexes. J. Mol. Biol. 2016, 428, 720–725. 10.1016/j.jmb.2015.09.014. [DOI] [PubMed] [Google Scholar]
- Jiménez-García B.; Roel-Touris J.; Romero-Durana M.; Vidal M.; Jimenez-Gonzalez D.; Fernandez-Recio J. LightDock: a new multi-scale approach to protein-protein docking. Bioinformatics 2018, 34, 49–55. 10.1093/bioinformatics/btx555. [DOI] [PubMed] [Google Scholar]
- Roel-Touris J.; Bonvin A.; Jimenez-Garcia B. LightDock goes information-driven. Bioinformatics 2020, 36, 950–952. 10.1093/bioinformatics/btz642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zacharias M. Protein-protein docking with a reduced protein model accounting for side-chain flexibility. Protein Sci. 2003, 12, 1271–1282. 10.1110/ps.0239303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Vries S. J.; Zacharias M. ATTRACT-EM: A New Method for the Computational Assembly of Large Molecular Machines Using Cryo-EM Maps. PLoS One 2012, 7, 49733 10.1371/journal.pone.0049733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russel D.; Lasker K.; Webb B.; Velazquez-Muriel J.; Tjioe E.; Schneidman-Duhovny D.; Peterson B.; Sali A. Putting the Pieces Together: Integrative Modeling Platform Software for Structure Determination of Macromolecular Assemblies. PLos Biol. 2012, 10, e1001244 10.1371/journal.pbio.1001244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alber F.; Forster F.; Korkin D.; Topf M.; Sali A. Integrating diverse data for structure determination of macromolecular assemblies. Annu. Rev. Biochem. 2008, 77, 443–477. 10.1146/annurev.biochem.77.060407.135530. [DOI] [PubMed] [Google Scholar]
- Wang C.; Bradley P.; Baker D. Protein-protein docking with backbone flexibility. J. Mol. Biol. 2007, 373, 503–519. 10.1016/j.jmb.2007.07.050. [DOI] [PubMed] [Google Scholar]
- Chaudhury S.; Berrondo M.; Weitzner B. D.; Muthu P.; Bergman H.; Gray J. J. Benchmarking and Analysis of Protein Docking Performance in Rosetta v3.2. PLoS One 2011, 6, e22477 10.1371/journal.pone.0022477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonvin A. M. Flexible protein-protein docking. Curr. Opin. Struct. Biol. 2006, 16, 194–200. 10.1016/j.sbi.2006.02.002. [DOI] [PubMed] [Google Scholar]
- Rodrigues J.; Bonvin A. Integrative computational modeling of protein interactions. FEBS J. 2014, 281, 1988–2003. 10.1111/febs.12771. [DOI] [PubMed] [Google Scholar]
- Karaca E.; Bonvin A. A Multidomain Flexible Docking Approach to Deal with Large Conformational Changes in the Modeling of Biomolecular Complexes. Structure 2011, 19, 555–565. 10.1016/j.str.2011.01.014. [DOI] [PubMed] [Google Scholar]
- Zacharias M. Accounting for conformational changes during protein-protein docking. Curr. Opin. Struct. Biol. 2010, 20, 180–186. 10.1016/j.sbi.2010.02.001. [DOI] [PubMed] [Google Scholar]
- Guterres H.; Lee H. S.; Im W. Ligand-Binding-Site Structure Refinement Using Molecular Dynamics with Restraints Derived from Predicted Binding Site Templates. J. Chem. Theory Comput. 2019, 15, 6524–6535. 10.1021/acs.jctc.9b00751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Król M.; Tournier A. L.; Bates P. A. Flexible relaxation of rigid-body docking solutions. Proteins: Struct., Funct., Bioinf. 2007, 68, 159–169. 10.1002/prot.21391. [DOI] [PubMed] [Google Scholar]
- Wang J. N.; Alekseenko A.; Kozakov D.; Miao Y. L. Improved Modeling of Peptide-Protein Binding Through Global Docking and Accelerated Molecular Dynamics Simulations. Front. Mol. Biosci. 2019, 6, 163 10.3389/fmolb.2019.00112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu K.; Kokubo H. Exploring the Stability of Ligand Binding Modes to Proteins by Molecular Dynamics Simulations: A Cross-docking Study. J. Chem. Inf. Model. 2017, 57, 2514–2522. 10.1021/acs.jcim.7b00412. [DOI] [PubMed] [Google Scholar]
- Guterres H.; Im W. Improving Protein-Ligand Docking Results with High-Throughput Molecular Dynamics Simulations. J. Chem. Inf. Model. 2020, 60, 2189–2198. 10.1021/acs.jcim.0c00057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernández-Rodríguez M.; Rosales-Hernandez M. C.; Mendieta-Wejebe J. E.; Martinez-Archundia M.; Basurto J. C. Current Tools and Methods in Molecular Dynamics (MD) Simulations for Drug Design. Curr. Med. Chem. 2016, 23, 3909–3924. 10.2174/0929867323666160530144742. [DOI] [PubMed] [Google Scholar]
- Pfeiffenberger E.; Bates P. A. Refinement of protein-protein complexes in contact map space with metadynamics simulations. Proteins: Struct., Funct., Bioinf. 2019, 87, 12–22. 10.1002/prot.25612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan A. C.; Jacobson D.; Yatsenko K.; Sritharan D.; Weinreich T. M.; Shaw D. E. Atomic-level characterization of protein-protein association. Proc. Natl. Acad. Sci. U.S.A. 2019, 116, 4244–4249. 10.1073/pnas.1815431116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahmad M.; Gu W.; Geyer T.; Helms V. Adhesive water networks facilitate binding of protein interfaces. Nat. Commun. 2011, 2, 261 10.1038/ncomms1258. [DOI] [PubMed] [Google Scholar]
- Piana S.; Lindorff-Larsen K.; Shawa D. E. Atomistic Description of the Folding of a Dimeric Protein. J. Phys. Chem. B 2013, 117, 12935–12942. 10.1021/jp4020993. [DOI] [PubMed] [Google Scholar]
- Souza P. C. T.; Thallmair S.; Conflitti P.; Ramirez-Palacios C.; Alessandri R.; Raniolo S.; Limongelli V.; Marrink S. J. Protein-ligand binding with the coarse-grained Martini model. Nat. Commun. 2020, 11, aac4750 10.1038/s41467-020-17437-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plattner N.; Doerr S.; De Fabritiis G.; Noe F. Complete protein-protein association kinetics in atomic detail revealed by molecular dynamics simulations and Markov modelling. Nat. Chem. 2017, 9, 1005–1011. 10.1038/nchem.2785. [DOI] [PubMed] [Google Scholar]
- Siebenmorgen T.; Zacharias M. Computational prediction of protein-protein binding affinities. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2020, 10, 1744 10.1002/wcms.1448. [DOI] [Google Scholar]
- Paul F.; Wehmeyer C.; Abualrous E. T.; Wu H.; Crabtree M. D.; Schoneberg J.; Clarke J.; Freund C.; Weikl T. R.; Noe F. Protein-peptide association kinetics beyond the seconds timescale from atomistic simulations (vol 8, 2017). Nat. Commun. 2018, 9, 1095 10.1038/s41467-018-03452-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfenden R.; Andersson L.; Cullis P. M.; Southgate C. C. B. Affinities of amino-acid side-chains for solvent water. Biochemistry 1981, 20, 849–855. 10.1021/bi00507a030. [DOI] [PubMed] [Google Scholar]
- Periole X.; Zeppelin T.; Schiott B. Dimer Interface of the Human Serotonin Transporter and Effect of the Membrane Composition. Sci. Rep. 2018, 8, 5080 10.1038/s41598-018-22912-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagy G.; Oostenbrink C.; Hritz J. Exploring the binding pathways of the 14-3-3zeta protein: Structural and free-energy profiles revealed by Hamiltonian replica exchange molecular dynamics with distancefield distance restraints. PLoS One 2017, 12, e0180633 10.1371/journal.pone.0180633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siebenmorgen T.; Zacharias M. Evaluation of Predicted Protein Protein Complexes by Binding Free Energy Simulations. J. Chem. Theory Comput. 2019, 15, 2071–2086. 10.1021/acs.jctc.8b01022. [DOI] [PubMed] [Google Scholar]
- Patel J. S.; Ytreberg F. M. Fast Calculation of Protein-Protein Binding Free Energies using Umbrella Sampling with a Coarse-Grained Model. Biophys. J. 2017, 112, 196A. 10.1016/j.bpj.2016.11.1087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazim R.; Suh D.; Choi S. Advances in Molecular Dynamics Simulations and Enhanced Sampling Methods for the Study of Protein Systems. Int. J. Mol. Sci. 2020, 21, 6339 10.3390/ijms21176339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perthold J. W.; Oostenbrink C. Simulation of Reversible Protein-Protein Binding and Calculation of Binding Free Energies Using Perturbed Distance Restraints. J. Chem. Theory Comput. 2017, 13, 5697–5708. 10.1021/acs.jctc.7b00706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suh D.; Jo S.; Jiang W.; Chipot C.; Roux B. String Method for Protein-Protein Binding Free-Energy Calculations. J. Chem. Theory Comput. 2019, 15, 5829–5844. 10.1021/acs.jctc.9b00499. [DOI] [PubMed] [Google Scholar]
- Basciu A.; Malloci G.; Pietrucci F.; Bonvin A.; Vargiu A. V. Holo-like and Druggable Protein Conformations from Enhanced Sampling of Binding Pocket Volume and Shape. J. Chem. Inf. Model. 2019, 59, 1515–1528. 10.1021/acs.jcim.8b00730. [DOI] [PubMed] [Google Scholar]
- Basciu A.; Koukos P. I.; Malloci G.; Bonvin A.; Vargiu A. V. Coupling enhanced sampling of the apo-receptor with template-based ligand conformers selection: performance in pose prediction in the D3R Grand Challenge 4. J. Comput.-Aided Mol. Des. 2020, 34, 149–162. 10.1007/s10822-019-00244-6. [DOI] [PubMed] [Google Scholar]
- Prévost C.; Sacquin-Mora S. Moving pictures: Reassessing docking experiments with a dynamic view of protein interfaces. bioRxiv 2020, 2020, 415885 10.1101/2020.12.08.415885. [DOI] [PubMed] [Google Scholar]
- Perthold J. W.; Oostenbrink C. GroScore: Accurate Scoring of Protein-Protein Binding Poses Using Explicit-Solvent Free-Energy Calculations. J. Chem. Inf. Model. 2019, 59, 5074–5085. 10.1021/acs.jcim.9b00687. [DOI] [PubMed] [Google Scholar]
- Janin J.; Henrick K.; Moult J.; Ten Eyck L.; Sternberg M. J. E.; Vajda S.; Vakser I.; Wodak S. J. CAPRI: A Critical Assessment of PRedicted Interactions. Proteins: Struct., Funct., Bioinf. 2003, 52, 2–9. 10.1002/prot.10381. [DOI] [PubMed] [Google Scholar]
- Lensink M. F.; Wodak S. J. Score_set: A CAPRI benchmark for scoring protein complexes. Proteins: Struct., Funct., Bioinf. 2014, 82, 3163–3169. 10.1002/prot.24678. [DOI] [PubMed] [Google Scholar]
- Lensink M. F.; Wodak S. J. Docking, scoring, and affinity prediction in CAPRI. Proteins: Struct., Funct., Bioinf. 2013, 81, 2082–2095. 10.1002/prot.24428. [DOI] [PubMed] [Google Scholar]
- Kingsley L. J.; Esquivel-Rodriguez J.; Yang Y.; Kihara D.; Lill M. A. Ranking protein-protein docking results using steered molecular dynamics and potential of mean force calculations. J. Comput. Chem. 2016, 37, 1861–1865. 10.1002/jcc.24412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen R.; Li L.; Weng Z. P. ZDOCK: An initial-stage protein-docking algorithm. Proteins: Struct., Funct., Bioinf. 2003, 52, 80–87. 10.1002/prot.10389. [DOI] [PubMed] [Google Scholar]
- Simões I. C. M.; Coimbra J. T. S.; Neves R. P. P.; Costa I. P. D.; Ramos M. J.; Fernandes P. A. Properties that rank protein: protein docking poses with high accuracy. Phys. Chem. Chem. Phys. 2018, 20, 20927–20942. 10.1039/C8CP03888K. [DOI] [PubMed] [Google Scholar]
- Kollman P. A.; Massova I.; Reyes C.; Kuhn B.; Huo S. H.; Chong L.; Lee M.; Lee T.; Duan Y.; Wang W.; Donini O.; Cieplak P.; Srinivasan J.; Case D. A.; Cheatham T. E. Calculating structures and free energies of complex molecules: Combining molecular mechanics and continuum models. Acc. Chem. Res. 2000, 33, 889–897. 10.1021/ar000033j. [DOI] [PubMed] [Google Scholar]
- Takemura K.; Matubayasi N.; Kitao A. Binding free energy analysis of protein-protein docking model structures by evERdock. J. Chem. Phys. 2018, 148, 105101 10.1063/1.5019864. [DOI] [PubMed] [Google Scholar]
- Takemura K.; Guo H.; Sakuraba S.; Matubayasi N.; Kitao A. Evaluation of protein-protein docking model structures using all-atom molecular dynamics simulations combined with the solution theory in the energy representation. J. Chem. Phys. 2012, 137, 215105 10.1063/1.4768901. [DOI] [PubMed] [Google Scholar]
- Khamis M. A.; Gomaa W.; Ahmed W. F. Machine learning in computational docking. Artif. Intell. Med. 2015, 63, 135–152. 10.1016/j.artmed.2015.02.002. [DOI] [PubMed] [Google Scholar]
- Shen C.; Ding J. J.; Wang Z.; Cao D. S.; Ding X. Q.; Hou T. J. From machine learning to deep learning: Advances in scoring functions for protein-ligand docking. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2020, 10, 7068349 10.1002/wcms.1429. [DOI] [Google Scholar]
- Lima A. N.; Philot E. A.; Trossini G. H. G.; Scott L. P. B.; Maltarollo V. G.; Honorio K. M. Use of machine learning approaches for novel drug discovery. Expert Opin. Drug Discovery 2016, 11, 225–239. 10.1517/17460441.2016.1146250. [DOI] [PubMed] [Google Scholar]
- Li J.; Fu A. L.; Zhang L. An Overview of Scoring Functions Used for Protein-Ligand Interactions in Molecular Docking. Interdiscip. Sci.: Comput. Life Sci. 2019, 11, 320–328. 10.1007/s12539-019-00327-w. [DOI] [PubMed] [Google Scholar]
- Nguyen D. D.; Wei G. W. AGL-Score: Algebraic Graph Learning Score for Protein-Ligand Binding Scoring, Ranking, Docking, and Screening. J. Chem. Inf. Model. 2019, 59, 3291–3304. 10.1021/acs.jcim.9b00334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moal I. H.; Barradas-Bautista D.; Jimenez-Garcia B.; Torchala M.; van der Velde A.; Vreven T.; Weng Z. P.; Bates P. A.; Fernandez-Recio J. IRaPPA: information retrieval based integration of biophysical models for protein assembly selection. Bioinformatics 2017, 33, 1806–1813. 10.1093/bioinformatics/btx068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfeiffenberger E.; Chaleil R. A. G.; Moal I. H.; Bates P. A. A machine learning approach for ranking clusters of docked protein-protein complexes by pairwise cluster comparison. Proteins: Struct., Funct., Bioinf. 2017, 85, 528–543. 10.1002/prot.25218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moal I. H.; Moretti R.; Baker D.; Fernandez-Recio J. Scoring functions for protein-protein interactions. Curr. Opin. Struct. Biol. 2013, 23, 862–867. 10.1016/j.sbi.2013.06.017. [DOI] [PubMed] [Google Scholar]
- Martin O.; Schomburg D. Efficient comprehensive scoring of docked protein complexes using probabilistic support vector machines. Proteins: Struct., Funct., Bioinf. 2008, 70, 1367–1378. 10.1002/prot.21603. [DOI] [PubMed] [Google Scholar]
- Melo R.; Fieldhouse R.; Melo A.; Correia J. D. G.; Cordeiro M.; Gumus Z. H.; Costa J.; Bonvin A.; Moreira I. S. A Machine Learning Approach for Hot-Spot Detection at Protein-Protein Interfaces. Int. J. Mol. Sci. 2016, 17, 1215 10.3390/ijms17081215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tahir M.; Hayat M. Machine learning based identification of protein-protein interactions using derived features of physiochemical properties and evolutionary profiles. Artif. Intell. Med. 2017, 78, 61–71. 10.1016/j.artmed.2017.06.006. [DOI] [PubMed] [Google Scholar]
- Moreira I. S.; Koukos P. I.; Melo R.; Almeida J. G.; Preto A. J.; Schaarschmidt J.; Trellet M.; Gumus Z. H.; Costa J.; Bonvin A. SpotOn: High Accuracy Identification of Protein-Protein Interface Hot-Spots. Sci. Rep. 2017, 7, 8007 10.1038/s41598-017-08321-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cunningham J. M.; Koytiger G.; Sorger P. K.; AlQuraishi M. Biophysical prediction of protein-peptide interactions and signaling networks using machine learning. Nat. Methods 2020, 17, 175–183. 10.1038/s41592-019-0687-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Northey T. C.; Baresic A.; Martin A. C. R. IntPred: a structure-based predictor of protein-protein interaction sites. Bioinformatics 2018, 34, 223–229. 10.1093/bioinformatics/btx585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geng C. L.; Jung Y.; Renaud N.; Honavar V.; Bonvin A.; Xue L. C. iScore: a novel graph kernel-based function for scoring protein-protein docking models. Bioinformatics 2020, 36, 112–121. 10.1093/bioinformatics/btz496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renaud N.; Jung Y.; Honavar V.; Geng C. L.; Bonvin A.; Xue L. C. iScore: An MPI supported software for ranking protein-protein docking models based on a random walk graph kernel and support vector machines. Softwarex 2020, 11, 100462 10.1016/j.softx.2020.100462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X.; Terashi G.; Christoffer C. W.; Zhu M. M.; Kihara D. Protein docking model evaluation by 3D deep convolutional neural networks. Bioinformatics 2020, 36, 2113–2118. 10.1093/bioinformatics/btz870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ballester P. J.; Mitchell J. B. O. A machine learning approach to predicting protein-ligand binding affinity with applications to molecular docking. Bioinformatics 2010, 26, 1169–1175. 10.1093/bioinformatics/btq112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ballester P. J.; Schreyer A.; Blundell T. L. Does a More Precise Chemical Description of Protein-Ligand Complexes Lead to More Accurate Prediction of Binding Affinity?. J. Chem. Inf. Model. 2014, 54, 944–955. 10.1021/ci500091r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernauer J.; Bahadur R. P.; Rodier F.; Janin J.; Poupon A. DiMoVo: a Voronoi tessellation-based method for discriminating crystallographic and biological proteinprotein interactions. Bioinformatics 2008, 24, 652–658. 10.1093/bioinformatics/btn022. [DOI] [PubMed] [Google Scholar]
- Esque J.; Leonard S.; de Brevern A. G.; Oguey C. VLDP web server: a powerful geometric tool for analysing protein structures in their environment. Nucleic Acids Res. 2013, 41, W373–W378. 10.1093/nar/gkt509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poupon A. Voronoi and Voronoi-related tessellations in studies of protein structure and interaction. Curr. Opin. Struct. Biol. 2004, 14, 233–241. 10.1016/j.sbi.2004.03.010. [DOI] [PubMed] [Google Scholar]
- Olechnovič K.; Venclovas C. VoroMQA: Assessment of protein structure quality using interatomic contact areas. Proteins: Struct., Funct., Bioinf. 2017, 85, 1131–1145. 10.1002/prot.25278. [DOI] [PubMed] [Google Scholar]
- Moult J.; Fidelis K.; Kryshtafovych A.; Schwede T.; Tramontano A. Critical assessment of methods of protein structure prediction (CASP) - round x. Proteins: Struct., Funct., Bioinf. 2014, 82, 1–6. 10.1002/prot.24452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moal I. H.; Torchala M.; Bates P. A.; Fernandez-Recio J. The scoring of poses in protein-protein docking: current capabilities and future directions. BMC Bioinf. 2013, 14, 286 10.1186/1471-2105-14-286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vangone A.; Oliva R.; Cavallo L.; Bonvin A. M. J. J.. Prediction of Biomolecular Complexes. In From Protein Structure to Function with Bioinformatics; Rigden D. J., Ed.; Springer: Dordrecht, Netherlands, 2017; pp 265–292. [Google Scholar]
- Vreven T.; Moal I. H.; Vangone A.; Pierce B. G.; Kastritis P. L.; Torchala M.; Chaleil R.; Jimenez-Garcia B.; Bates P. A.; Fernandez-Recio J.; Bonvin A.; Weng Z. P. Updates to the Integrated Protein-Protein Interaction Benchmarks: Docking Benchmark Version 5 and Affinity Benchmark Version 2. J. Mol. Biol. 2015, 427, 3031–3041. 10.1016/j.jmb.2015.07.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedregosa F.; Varoquaux G.; Gramfort A.; Michel V.; Thirion B.; Grisel O.; Blondel M.; Prettenhofer P.; Weiss R.; Dubourg V.; Vanderplas J.; Passos A.; Cournapeau D.; Brucher M.; Perrot M.; Duchesnay E. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Sali A.; Webb B.; Madhusudhan M. S.; Shen M.-Y.; Marti-Renom M. A.. MODELLER, 9.12; University of California: San Francisco, 2013. [Google Scholar]
- Šali A.; Blundell T. L. Comparative protein modeling by satisfaction of spatial restraints. J. Mol. Biol. 1993, 234, 779–815. 10.1006/jmbi.1993.1626. [DOI] [PubMed] [Google Scholar]
- Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindahl E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
- Huang J.; Rauscher S.; Nawrocki G.; Ran T.; Feig M.; de Groot B. L.; Grubmuller H.; MacKerell A. D. CHARMM36m: an improved force field for folded and intrinsically disordered proteins. Nat. Methods 2017, 14, 71–73. 10.1038/nmeth.4067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
- Bussi G.; Donadio D.; Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; Dinola A.; Haak J. R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
- Wang F. G.; Landau D. P. Efficient, multiple-range random walk algorithm to calculate the density of states. Phys. Rev. Lett. 2001, 86, 2050–2053. 10.1103/PhysRevLett.86.2050. [DOI] [PubMed] [Google Scholar]
- Hess B.; Bekker H.; Berendsen H. J. C.; Fraaije J. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. . [DOI] [Google Scholar]
- Darden T.; York D.; Pedersen L. Particle Mesh Ewald - An N.log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
- Méndez R.; Leplae R.; De Maria L.; Wodak S. J. Assessment of blind predictions of protein-protein interactions: Current status of docking methods. Proteins: Struct., Funct., Bioinf. 2003, 52, 51–67. 10.1002/prot.10393. [DOI] [PubMed] [Google Scholar]
- Basu S.; Wallner B. DockQ: A Quality Measure for Protein-Protein Docking Models. PLoS One 2016, 11, e0161879 10.1371/journal.pone.0161879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraser J. S.; van den Bedem H.; Samelson A. J.; Lang P. T.; Holton J. M.; Echols N.; Alber T. Accessing protein conformational ensembles using room-temperature X-ray crystallography. Proc. Natl. Acad. Sci. U.S.A. 2011, 108, 16247–16252. 10.1073/pnas.1111325108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atakisi H.; Moreau D. W.; Thorne R. E. Effects of protein-crystal hydration and temperature on side-chain conformational heterogeneity in monoclinic lysozyme crystals. Acta Crystallogr., Sect. D: Struct. Biol. 2018, 74, 264–278. 10.1107/S2059798318000207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerstein M.; Echols N. Exploring the range of protein flexibility, from a structural proteomics perspective. Curr. Opin. Chem. Biol. 2004, 8, 14–19. 10.1016/j.cbpa.2003.12.006. [DOI] [PubMed] [Google Scholar]
- Boehr D. D.; Nussinov R.; Wright P. E. The role of dynamic conformational ensembles in biomolecular recognition. Nat. Chem. Biol. 2009, 5, 789–796. 10.1038/nchembio.232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halakou F.; Gursoy A.; Keskin O. Embedding Alternative Conformations of Proteins in Protein-Protein Interaction Networks. Methods Mol. Biol. 2020, 2074, 113–124. 10.1007/978-1-4939-9873-9_9. [DOI] [PubMed] [Google Scholar]
- Yi M.; Tjong H.; Zhou H.-X. Spontaneous conformational change and toxin binding in alpha 7 acetylcholine receptor: Insight into channel activation and inhibition. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 8280–8285. 10.1073/pnas.0710530105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nury H.; Poitevin F.; Van Renterghem C.; Changeux J. P.; Corringer P. J.; Delarue M.; Baaden M. One-microsecond molecular dynamics simulation of channel gating in a nicotinic receptor homologue. Proc. Natl. Acad. Sci. U.S.A. 2010, 107, 6275–6280. 10.1073/pnas.1001832107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindorff-Larsen K.; Maragakis P.; Piana S.; Shaw D. E. Picosecond to Millisecond Structural Dynamics in Human Ubiquitin. J. Phys. Chem. B 2016, 120, 8313–8320. 10.1021/acs.jpcb.6b02024. [DOI] [PubMed] [Google Scholar]
- Radom F.; Pluckthun A.; Paci E. Assessment of ab initio models of protein complexes by molecular dynamics (vol 14, e1006182, 2018). PLoS Comput. Biol. 2018, 14, e1006182 10.1371/journal.pcbi.1006182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozakov D.; Schueler-Furman O.; Vajda S. Discrimination of near-native structures in protein-protein docking by testing the stability of local minima. Proteins: Struct., Funct., Bioinf. 2008, 72, 993–1004. 10.1002/prot.21997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z.; Sun H. Y.; Shen C.; Hu X. P.; Gao J. B.; Li D.; Cao D. S.; Hou T. J. Combined strategies in structure-based virtual screening. Phys. Chem. Chem. Phys. 2020, 22, 3149–3159. 10.1039/C9CP06303J. [DOI] [PubMed] [Google Scholar]
- Jamal S.; Grover A.; Grover S. Machine Learning From Molecular Dynamics Trajectories to Predict Caspase-8 Inhibitors Against Alzheimer’s Disease. Front. Pharmacol. 2019, 10, 19 10.3389/fphar.2019.00780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torchala M.; Moal I. H.; Chaleil R. A. G.; Fernandez-Recio J.; Bates P. A. SwarmDock: a server for flexible protein-protein docking. Bioinformatics 2013, 29, 807–809. 10.1093/bioinformatics/btt038. [DOI] [PubMed] [Google Scholar]
- Moal I. H.; Bates P. A. SwarmDock and the Use of Normal Modes in Protein-Protein Docking. Int. J. Mol. Sci. 2010, 11, 3623–3648. 10.3390/ijms11103623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das S.; Chakrabarti S. Classification and prediction of protein-protein interaction interface using machine learning algorithm. Sci. Rep. 2021, 11, 1761 10.1038/s41598-020-80900-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.