Abstract

Understanding the lateral organization in plasma membranes remains an open problem and is of great interest to many researchers. Model membranes consisting of coexisting domains are commonly used as simplified models of plasma membranes. The coarse-grained (CG) Martini force field has successfully captured spontaneous separation of ternary membranes into a liquid-disordered and a liquid-ordered domain. With all-atom (AA) models, however, phase separation is much harder to achieve due to the slow underlying dynamics. To remedy this problem, here, we apply the virtual site (VS) hybrid method on a ternary membrane composed of saturated lipids, unsaturated lipids, and cholesterol to investigate the phase separation. The VS scheme couples the two membrane leaflets at CG and AA resolution. We found that the rapid phase separation reached by the CG leaflet can accelerate and guide this process in the AA leaflet.
Introduction
Lipids are an important structural component of the cell membrane and are involved in many important biological processes.1,2 The relative mobility (or fluidity) of the individual lipid molecules is temperature dependent and correlated with the phase state of the membrane. Every lipid has a characteristic transition (or melt) temperature; above the melting temperature, pure phospholipid bilayers are in a fluid state and below this temperature, they are in the solid (gel) phase. The liquid crystalline phase is the most physiologically relevant state of membranes, resembling a two-dimensional (2D) fluid with the lipids freely diffusing in the plane of the membrane. Lateral diffusion of lipids in the gel phase is about 100 times slower than the one in the fluid phases.3 In the gel phase, lipids are fully extended and hexagonally ordered, and with few gauche defects remaining.4,5 The gel and liquid phases can coexist in two component membranes containing high and low melting temperature lipids.6
A high cholesterol concentration strongly changes the fluid structure of bilayers and drives the system into a new phase, the liquid ordered phase (Lo).7,8 Ternary mixtures of lipid membranes containing cholesterol, high and low melting temperature lipid species, exhibit the coexistence of two macroscopic liquid phases, that is, Lo, the cholesterol-rich phase and liquid disordered, cholesterol-poor phase (Ld) over a wide range of temperatures and compositions.9,10 The lipids in the Lo region show slower diffusion rates and a higher molecular order in the hydrocarbon chains.11,12 The coexistence of these two liquid phases in membranes has been investigated using a diverse range of experimental techniques.13 Using fluorescence microscopy, Veatch and Keller observed spontaneous lateral domain separation in unilamellar vesicles composed of a mixture of DOPC (dioleoyl-phosphatidylcholine)/DPPC(dipalmitoyl-phosphatidylcholine) and cholesterol.14 Baumgart et al. observed long-range domain ordering in the form of locally parallel stripes in giant unilamellar vesicles through high-resolution fluorescence imaging.15 In ternary mixtures of DOPC/sphingomyelin/cholesterol, Lo domain dynamic properties were observed in a certain range of cholesterol concentration through confocal fluorescence microscopy and fluorescence correlation spectroscopy.16 Structures similar to Lo and Ld domains are also observed in giant plasma membrane vesicles.17,18
The idea of the Lo/Ld coexistence in a ternary membrane mixture was adopted as a fundamental mechanism driving plasma membrane heterogeneities in the context of the raft model.19 Although giant plasma membrane vesicles and plasma membranes after cell death show miscibility phase transitions, macroscopic phase separation is not generally observed in the plasma membrane of living cells.13,20 Therefore, the raft idea as a mechanism that drives the lateral organization of the live cell plasma membrane remains controversial.
Molecular dynamics (MDs) simulation is a robust and indispensable tool to complement experimental techniques. It is able to describe the target system at molecular resolution and acts like a “computational microscope”.21 MD is a powerful technique for investigating a variety of biological systems. For instance, the phase coexistence of membranes containing DPPC, dilinoleoyl-phosphatidylcholine (DLiPC), and cholesterol has been investigated at the coarse-grained (CG) level more than a decade ago, showing good agreement with experimental data.45,22 The onset of phase separation or raft formation can nowadays also be realized in simulations with all atomic (AA) resolution.23 However, due to the slow underlying kinetics of phase separation, it remains difficult to reach equilibrium in AA simulations. To remedy this problem, in this paper, we apply the virtual site (VS) hybrid method24 combining the accuracy of AA models with the speed of CG models. We study a ternary membrane composed of DPPC, DLiPC, and cholesterol and investigate the phase separation. The VS scheme couples the two membrane leaflets, one at CG and the other at AA resolution. We found that the rapid phase separation reached by the CG leaflet can accelerate and guide this process in the AA leaflet.
Method
Simulation Setup
We have applied the VS hybrid scheme as described in ref (24). to a membrane system as illustrated in Figure 1. The system is partitioned into two subsystems, that is, AA and CG. The crux of the method is that each subsystem interacts with itself at its corresponding level of description and that the interaction between the subsystems is at the CG level using the VS multiscale approach.25−27 It was previously shown that the VS multiscale method can properly reproduce the potentials of mean force (PMFs) between pairs of apolar amino acid side-chain analogs, yet failed to reproduce correct PMFs for the polar and charged AA solutes in the CG solvent.28 Therefore, to avoid polar resolution interfaces, we propose a dual resolution membrane structure with the AA–CG interface at the interleaflet region, constituting an apolar environment, illustrated in Figure 1.
Figure 1.

Virtual site hybrid scheme of a ternary membrane. DPPC, DLiPC, and cholesterol are represented by green, red, and magenta, respectively. The water is rendered by the transparent surface and the virtual sites on AA resolution are not shown for clarity.
This VS approach requires a mapping of the particles in the AA model to the CG beads, defining interaction sites through which the AA system interacts with the CG system. This hybrid technique is achieved through virtual sites located at the center of mass of the corresponding AA atoms
| 1 |
| 2 |
Mk and 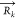 are the total mass of the particles
assigned
to VS bead k and the position of the VS bead, respectively.
The k-th VS bead is constructed from Nk AA atoms with mass mki and position
are the total mass of the particles
assigned
to VS bead k and the position of the VS bead, respectively.
The k-th VS bead is constructed from Nk AA atoms with mass mki and position 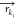 for the i-th atom of the k-th VS bead. Depending on the mass of the AA particles,
the force acting on the VS is distributed over its corresponding AA
atoms as
for the i-th atom of the k-th VS bead. Depending on the mass of the AA particles,
the force acting on the VS is distributed over its corresponding AA
atoms as
| 3 |
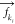 and
and  are the forces acting on AA atom ki belonging to bead k, and on VS bead k. The VS hybrid scheme
naturally combines the CG and AA models, where the AA model is a more
detailed description of the molecule of interest. CG particles feel
forces only at the CG level, originating either at particles in the
CG subsystem or at the VS. Direct interactions between AA atoms and
CG beads are not included, because these would constitute a double
counting of interactions.
are the forces acting on AA atom ki belonging to bead k, and on VS bead k. The VS hybrid scheme
naturally combines the CG and AA models, where the AA model is a more
detailed description of the molecule of interest. CG particles feel
forces only at the CG level, originating either at particles in the
CG subsystem or at the VS. Direct interactions between AA atoms and
CG beads are not included, because these would constitute a double
counting of interactions.
Here, we combine the atomistic in-house GROMOS force field (described and tested in24) and the CG Martini force field29 in a double membrane setup (Figure 1). We kept the resolution interfaces at the apolar region in the centers of the bilayers, and restrained water penetration through the membranes to prevent mixing of AA and the CG solvent. The details and validation of this setup can be found in ref (24).
The membrane consists of a DPPC/DLiPC/cholesterol ternary mixture (molar ratio, 42:28:30 and 718) lipids in each bilayer, which forms coexisting Lo and Ld domains as shown previously.46 The ternary membrane is simulated in a box of 15 nm × 15 nm × 18 nm. The simulations were carried out using the GROMACS (2016) software,30 with an integration time step of 4 fs. The Verlet cut-off scheme was used for the nonbonded interactions and the allowed energy error due to the Verlet buffer is 0.005 kJ/mol/ps per atom. The potential modifiers were used to shift the complete LJ and Coulomb potential value to zero at a cutoff of 1.4 nm. Electrostatic interactions were treated using PME with a 0.12 nm Fourier grid spacing. The temperature was maintained at 295 K by integrating the equations of motion with the leapfrog stochastic dynamics integrator31,32 with inverse friction constants of 1 ps to CG (or VS) particles and 0.1 ps to AA particles. AA lipids, AA water, CG lipids, CG water, and VS beads were coupled separately to the thermostat. The pressure was kept constant at 1 bar independently in the lateral and normal directions using the Berendsen barostat33 in a semi-isotropic pressure bath (τp = 0.5 ps). The compressibility was set to 4.6 × 10–6 bar–1. The AA bonds were constrained with the LINCS algorithm, and simple point charge water34 was constrained using SETTLE.35 A flat bottom potential was applied on the polar headgroup of cholesterol (CG or VS ROH beads) to restrain flip-flop, as used in ref (36). Restraining of cholesterol has only minor effects on the membrane properties, including the degree of phase separation, interleaflet registration, lipid order parameter, etc.36 However, additional modifications were found to be necessary to prevent AA cholesterol entering the CG leaflet and causing artefacts. In particular, the attractive VS-mediated interactions of AA cholesterol with CG beads were reduced (for more information, see Supporting Information, Figures S1–S4 and Tables S1 and S2).
In the VS hybrid model, the AA leaflets are either in the phase-separated or the phase-mixed state. To build this membrane, we ran full CG simulations to get membranes in the phase-separated or the phase-mixed state. One of the CG leaflets is mapped into AA resolution with the backmapping software tool backward37 and is coupled to another CG leaflet. More details are described in the Results section and in ref (24). For reference, bilayers were also simulated at full AA resolution using the CHARMM force field and built with the CHARMM-GUI web server.38 These bilayer systems were simulated using the equilibration and production protocol provided by CHARMM-GUI. The trajectory files and input files have been shared in the Zedono server: https://sandbox.zenodo.org/record/779354#.YHL_ougzY2w.
Analysis
The analysis shown in this paper is mainly focused on one of the two hybrid membranes, but similar results were obtained for both membranes. The extent of phase separation in the membrane was quantified using the contact fraction fi–j between two lipid species i and j. The contact fraction was computed using the same procedure described in ref (39)., and defined as
| 4 |
| 5 |
where ci–j represents the number of contacts between the two lipid species. A distance threshold of 1.1 nm between the phosphate bead (PO4) of DPPC and DLiPC was applied. In this formulation, complete phase separation corresponds to fDPPC–DLiPC = 0, and ideal mixing corresponds to fDPPC–DLiPC = 0.6 (equaling the mole fraction of DPPC lipids with respect to total PC lipids). A value exceeding 0.6 indicates an enhanced mixing of DLiPC with DPPC, while values smaller than 0.6 indicate more self-contacts, and therefore more nonrandom mixing. The exact value of fDPPC–DLiPC for which phase separation occurs is hard to define, given finite size effects due to the limited size of the simulated systems. A value of fDPPC–DLiPC = 0.2, as reported previously for the current DPPC/DLiPC/cholesterol system,46 signals clear phase separation. The contact fraction fCHOL–DLiPC between cholesterol and DLiPC was evaluated similarly. A value of 0.4 represents ideal mixing, above which cholesterol prefers to interact with DLiPC lipids, below which cholesterol prefers DPPC lipids. To compare the extent of phase separation between our simulations and atomistic simulations reported in the literature, we also computed the DPPC enrichment parameter as described in Gu et al.23
The level of phase separation is also quantified by the lipid mixing entropy.40 The mixing entropy is defined as
| 6 |
where p1 and p2 represent the probability of neighboring contacts formed by the same and different lipid type, respectively. The neighboring lipids are determined through Voronoi tessellations of the lipid head groups, using the PO4 CG (or VS) beads of DPPC and DLiPC lipids. More details can be found in ref (41).
A number of other membrane organizational or structural parameters were analyzed to quantify effects of the VS scheme on the membrane.
The lipid order parameter P was defined as
| 7 |
When the order parameter is computed at the CG level, θ represents the angle between the CG bond of the lipid and the bilayer normal (approximated as the z unit vector of the simulation box). When the deuterium order parameter is computed at the AA level, θ represents the angle between the orientation of the C–H bond vector with respect to the bilayer normal. The angle brackets represent the ensemble average over equivalent bonds for a given lipid type in a simulation frame.
The 2D bond-orientational order parameter42 Ψ6k was used to describe lipid packing of membranes in our simulations. The bond-orientational order parameter is defined as
| 8 |
where θkl represents the angle between the vector  connecting the position
of a center lipid
(l) to its six nearest neighbors (k), and the reference vector r⃗. To deal with
the height mismatches of lipid and its neighbors, the position of
the center and neighboring lipids are fitted to a plane through their
singular value decomposition. The reference vector r⃗ starts from l and points to the x-axis direction, and is also fitted to the plane. More
details can be found in ref (41). Locations of DPPC, DLiPC, and cholesterol were defined
by the positions of C2A/C2B and D2A/D2B and the center of mass of
R1/R2/R3/R4/R5 CG (or VS) beads, respectively.
connecting the position
of a center lipid
(l) to its six nearest neighbors (k), and the reference vector r⃗. To deal with
the height mismatches of lipid and its neighbors, the position of
the center and neighboring lipids are fitted to a plane through their
singular value decomposition. The reference vector r⃗ starts from l and points to the x-axis direction, and is also fitted to the plane. More
details can be found in ref (41). Locations of DPPC, DLiPC, and cholesterol were defined
by the positions of C2A/C2B and D2A/D2B and the center of mass of
R1/R2/R3/R4/R5 CG (or VS) beads, respectively.
The partial density and membrane thickness landscape were also computed to measure and visualize the lipid distribution in the membrane. These 2D landscapes were computed through a grid placed on the XY plane of the membrane (10 × 10 cells) and the last 0.5 μs of the simulations were used to average the landscape. Membrane thickness landscape was computed based on the average distance of PO4 beads in both leaflets. All landscapes were calculated using g_thickness and g_mydensity software43 freely available from http://perso.ibcp.fr/luca.monticelli.
The DPPC density landscape grid at the CG or VS level is used to compute the domain registration landscape. The two leaflets are considered separately. If the density of DPPC in a certain cell is larger than the mean value of the DPPC cell density, this cell is marked as the Lo region. The match between the local grids of two leaflets is used to form the registration landscape.
We used the APL@Voro tool to calculate the local neighbor number and area per lipid based on Voronoi tessellation. The VS of C2 and D2 in PC lipids and R5 in cholesterol attached on top of the AA leaflets are used as references. APL@Voro provides the graphical user interface and is compatible with GROMACS file formats. More details can be found in ref (44).
Results
Phase Separation in the VS Hybrid Membrane
We carried out simulations of a DPPC/DLiPC:cholesterol ternary mixture (molar ratio, 42:28:30) at 295 K using the Martini CG force field. As described previously,45 at this state point, the lipids phase segregate to form a DPPC- and cholesterol-rich Lo phase, and a DLiPC-rich Ld phase. The last frame of the CG simulation is shown in Figure 2a. Using the last frame of this simulation, we built two different starting configurations for the GROMOS/Martini VS hybrid systems. In one of the starting configurations, the AA leaflet is also phase separated (obtained via backmapping of the CG structure, shown in Figure 2a left), and in the other configuration the AA leaflet is homogeneously mixed (Figure 2b left). In both setups, the CG leaflet is phase separated, as shown in Figure 2a right and Figure 2b right. From these starting points, two simulations of 10 μs each were performed. As a control, a purely AA membrane, starting from the randomly distributed lipids was performed.
Figure 2.
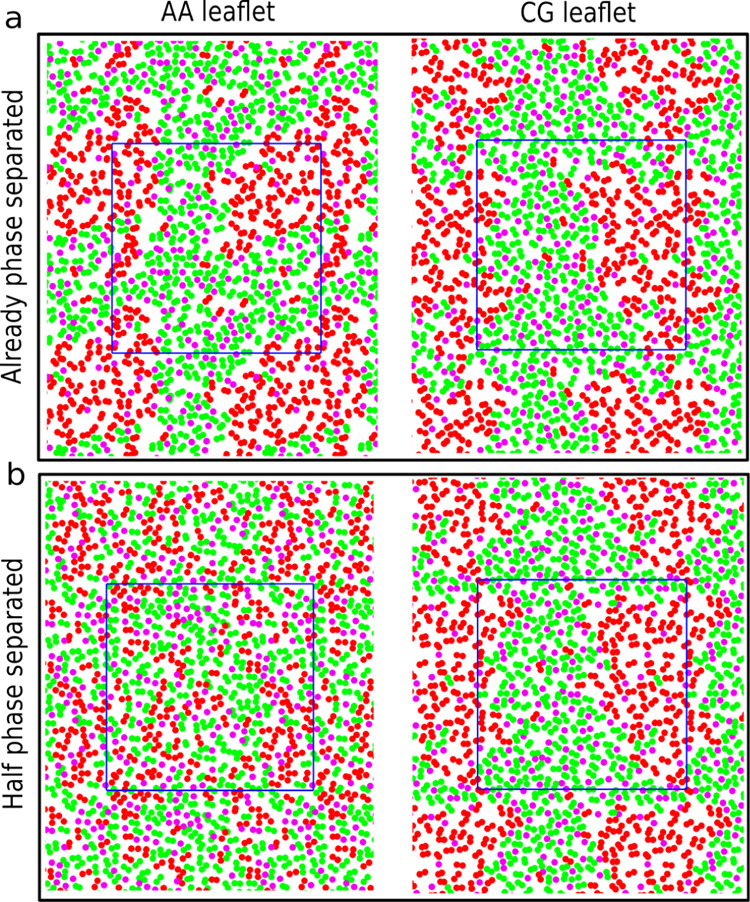
Ternary membrane setup. (a) and (b) Starting structures of the two VS hybrid systems: already phase-separated and half phase-separated systems, respectively. The snapshots in the left and right represent the two leaflets in one membrane with different resolutions. DPPC, DLiPC, and cholesterol are represented by green, red, and magenta, respectively. Only the linker beads (DPPC and DLiPC) or the head group bead (cholesterol) are depicted in the top view. The membranes are shown with the periodic images and the simulation boxes are represented in blue lines.
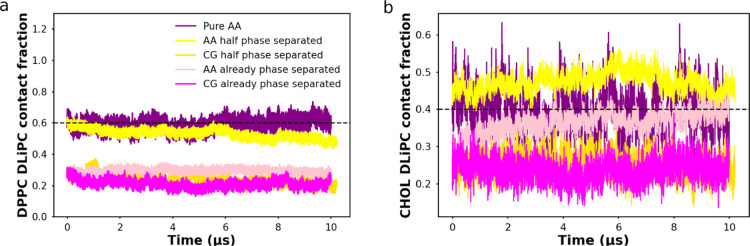
To monitor the extent of phase separation, we computed the DPPC–DLiPC contact fraction for each of the two leaflets (both resolutions), as shown in Figure 3a. A relatively high contact fraction denotes mixing, whereas low contact fraction hallmarks the phase-separated state. As seen from Figure 3a, in the purely AA system, the DPPC–DLiPC contact fraction fluctuates around 0.6, meaning the fully mixed initial state barely changes after 10 μs. Shown in Figure 3b, the cholesterol and DPPC contact fraction was also computed to quantify the location of cholesterols. A relatively high DLiPC–cholesterol contact fraction (above 0.4) suggests the cholesterol prefers to interact with DLiPC lipids, while a lower contact fraction means the preference to the DPPC lipids. In the pure AA simulation, contact fraction fluctuates around 0.4, suggesting that the cholesterol has no preference between DPPC and DLiPC lipids. These findings could be visually verified through the last snapshot of the simulation, shown in Figure 4c.
Figure 3.
Lipid contact fraction. (a) DPPC–DLiPC contact fraction. The horizontal dashed line represents ideal mixing, above which DLiPC lipids prefer to contact DPPC lipids (more mixed), below which DLiPC lipids prefer to contact with themselves (more separated). (b) Contact fraction between cholesterol and DLiPC. The horizontal dashed line represents ideal mixing, above which cholesterol prefers to interact with DLiPC lipids, below which cholesterol prefers DPPC lipids.
Figure 4.

Top view of AA leaflets and the side view of bilayer membranes. The last frames of the simulations of the membranes starting from the already phase separated (a), half phase separated (b), fully AA (c), and AA backmapped from the half phase-separated system (d) are illustrated. Only lipid tails are shown and the color scheme is the same as shown in Figure 2.
In the half phase-separated membrane, as we can see from Figure 3a, the DPPC–DLiPC contact fraction of the CG leaflet fluctuates around 0.2, while the DPPC–DLiPC contact fraction of the AA leaflet steadily decreases during the10 μs simulation. Thus, the CG leaflet keeps the phase-separated state and the AA leaflet, initially in the mixed state, starts to phase separate. In Figure 3b, the contact fraction between DLiPC and cholesterol shows that the cholesterol stays in the ordered region in the CG leaflet. Counterintuitively, the cholesterol–DLiPC contact fraction stays above 0.4 in the AA leaflet, suggesting that the cholesterols prefer to contact the DLiPC lipids rather than DPPC lipids. Similar conclusions can also be drawn using the mixing entropy, as discussed in the Supporting Information (Figure S9). Interestingly, from the snapshot of the AA membrane in Figure 4b, we observe that the saturated chains of the DPPC lipid form a local hexagonally ordered arrangement reminiscent of a gel phase. To test whether this behavior is caused by the VS hybrid scheme, the last frame of the half phase-separated membrane in VS hybrid model (Figure 4b) was backmapped to fully AA resolution. A similar state (phase separation level and local ordered arrangement) to the hybrid AA leaflet was preserved in the backmapped AA simulation for at least 1 μs, shown in Figure 4d. This indicates that the membrane structure predicted by the VS hybrid model is reasonable in pure AA simulation. In the subsequent backmapped simulation, the DPPC/DLiPC contact fraction did not change significantly for 1 μs (Figure S10a) and the local ordered structure persists in the membrane (Figure S10b). This suggests that the phase separation state and local ordered arrangement are not artifacts caused by the VS hybrid model.
DPPC lipids apparently form highly ordered domains inside the Lo region, at least when simulated at AA resolution. To distinguish lipids in the highly ordered phase from lipids in the Lo phase, we use a Voronoi tessellation diagram44 to represent the 2D organization of the bilayer. Voronoi cells appear in a honeycomb-like form (or a perfect hexagon) similar to lipids in the gel phase with stretched and straight lipid chains.46 In Figure 5a,c, the Voronoi tessellation diagrams are colored either by the area per lipid or the number of neighbor lipids for the AA leaflets of hybrid membranes. We found that the lipids in the hexagonal order (hexagonal Voronoi cell) are formed in the middle and lower parts of the bilayer. As expected, these cells have six lipid neighbors (cyan color) and a lower area per lipid (blue color). The bond-orientational order parameters of the AA leaflets increase with simulation time (Figure S9), suggesting stabilization of the more ordered arrangement. The phase separations and the hexagonal arrangement can also be observed in the DPPC density and thickness landscapes, shown in Figures S5 and S6. From Figure S5, we also found that the cholesterols are mainly located in the fluid DPPC region and DPPC–DLiPC interface region. This agrees with the observation from Sodt et al.47 that, in the Lo phase, local regions of hexagonally packed lipids are separated by interstitial regions enriched in cholesterol. Therefore, in the phase separation process, the DPPC lipids form hexagonal substructures in the Lo region, and thus the cholesterols are squeezed out of the Lo phase and increase contact with the DLiPC lipids.
Figure 5.
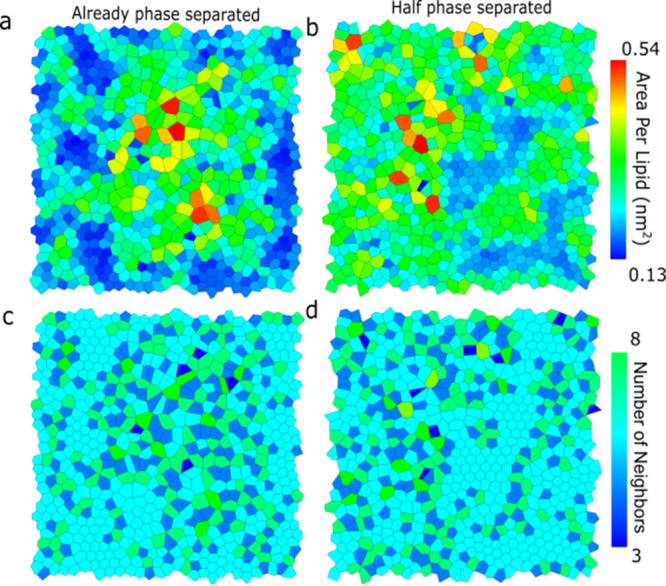
Voronoi tessellation diagrams for already phase-separated (a,c) and half phase-separated (b,d) systems. Voronoi tessellation diagrams are colored either by the area per lipid [nm2] (a,b) or the number of neighbor lipids for the AA leaflets of hybrid membranes (c,d). In Voronoi diagrams colored by the number of lipids neighbors, the cyan represents six neighbors.
In the case of the already phase-separated membrane, as can be seen from the temporal evolution of the DPPC–DLiPC contact fraction in Figure 3a, both leaflets keep the phase-separated state. Shown in Figure 3b, in the CG leaflet, the cholesterol stays in the DPPC-rich region. On the contrary, and in line with the results obtained with the half phase-separated system, the cholesterol–DLiPC contact fraction increases to 0.4 in the AA leaflet, denoting more contact between cholesterol and DLiPC lipids. The appearance of a local hexagonal order is also observed from the last snapshot in Figure 4a, the Voronoi tessellation diagram in Figure 5b,d, and DPPC density in Figure S5a. However, note that the AA leaflets in the hybrid simulation starting from already phase-separated and half phase-separated membranes have not fully converged after 10 μs, as indicated by the DPPC–DLiPC and cholesterol–DLiPC contact fraction in Figure 3. It is highly possible that the converged contact fraction is between the values predicted in the systems with the two different starting structures. Note that the analysis shown so far only focused on one of the two hybrid membranes of our double-membrane setup. The analysis of the other membrane shows a very similar behavior (Figures S7 and S8).
Discussion
Our results show that phase separation cannot be reached during 10 μs in the fully AA simulation, while it is realized in the VS hybrid model regardless of the starting configurations. This suggests that, in the dual resolution models, the coupling between the two leaflets is strong and the phase separation in the CG leaflet can guide and accelerate the phase separation kinetics of the AA leaflet. This mechanism is further demonstrated by a strong domain registry between the two leaflets, especially in the hexagonally ordered lipid regions and disordered regions, as found in both systems starting with different configurations (Figures S6c,d). There is a possibility that the AA system does not have the intrinsic driving force to phase separate, and is actually forced into this state due to the strong coupling. As such, our hybrid method would lead to an artificial result. We do not expect this to be the case, for a number of reasons. First, the experimental phase diagram clearly predicts a stable Ld/Lo coexistence at the state point considered. Second, both Martini and GROMOS force fields are calibrated using free energies obtained from the experimental data, making them compatible and well suited for dual resolution simulations. Finally, we showed via backmapping that the phase-segregated state is stable in a subsequent AA simulation (Figure 4d).
An important consideration is how effective the proposed VS method is. To provide a quantitative estimate of how much speedup is obtained, is difficult. The phase separation between Lo and Ld phases in ternary membranes has been thoroughly investigated using Martini CG simulations,22,46 but far less so using atomically detailed models. In a 9 μs united atom simulation, Hakobyan et al.48 found the onset of phase separation in a ternary membrane composed of DPPC, DLiPC, and cholesterol at 300 K. Gu et al.23 observed a coexistence of Lo and Ld phases in a ternary membrane composed of DPPC, DOPC, and cholesterol at 270 K in about 10 μs using the Slipid forcefield. Similar to our simulations, the two AA simulations23,48 are not fully converged after about 10 μs. To compare the extent of phase separation, we computed the enrichment value of DPPC lipids in the DPPC environment based on the AA leaflet of the half phase-separated system. We obtained a value of 1.16 ± 0.02 at the end of the simulation, which is close to the value of 1.12 ± 0.02 at 270 K reported in the work of Gu et al.23 Taken together, these data suggest that the kinetics of phase separation—not unexpectedly—are very much state point dependent, and may also depend on the details of the forcefield used. At least for the composition and forcefield (GROMOS-based) used in the current work, coupling to a CG leaflet appears to significantly speed up the phase separation process.
Apart from phase separation, an interesting observation is the appearance of local hexagonal order in the Lo domain, at least in the leaflet modeled with AA resolution. Such a local hexagonal ordering of saturated chains in the Lo region was also found in the ternary membrane composed of DPPC, DOPC, and cholesterol, simulated with the CHARMM force field at 298 K by Sodt et al.47 They reported 0.321 ± 0.003 for the mean order parameter of lipids in the Lo domain, which is close to the value of 0.351 ± 0.005 computed from the AA leaflets of the half phase-separated system. This high level of order also agrees well with the value of 0.36 extracted by Sodt et al.,47 based on the 2H NMR experiment.49 In a small-angle neutron scattering experiment,50 nanodomains with a hexagonal order were also observed in a membrane composed of DPPC and cholesterol. Therefore, our simulations provide further evidence supporting the existence of a local hexagonal order of saturated chains in the Lo region. Note that the hexagonal ordering is only observed in the AA leaflet, while the CG monolayer is unable to capture the hexagonal ordering in the Lo domain. Thus, there is a discrepancy between the two leaflets with different resolutions. The hexagonal ordering in the Lo region is not observed in standard Martini simulations either.46 A plausible reason for this discrepancy is that, at AA resolution, DPPC lipids form local gel-like structures because the simulation temperature is about 20 K lower than the transition temperature of DPPC (314 K). At such low temperature, lipids tend to adopt the highly packed hexagonal arrangement characteristic of the gel phase. However, the transition temperature of Martini DPPC lipids is 295 ± 5 K.46 Hence, the temperature is not low enough for Martini DPPC lipids to locally form a gel-like structure. With the forthcoming release of the new version of the model Martini 3,51 the phase transition temperature of Martini DPPC lipids could possibly be improved.
There are several different approaches to combine CG and AA simulations, including interface approaches,25,52,53 keeping both AA and CG molecules in one system; the serial multiscale methods,54,55 switching resolution if interesting events occur; adaptive resolution methods,56−58 changing resolution on the fly when molecules cross the resolution boundary; and resolution exchange approaches,59−61 connecting simulations at different resolutions through the Hamiltonian replica exchange method. The VS hybrid scheme, belonging to the interface approach, is easy to use and compatible with most standard MD packages (e.g., Gromacs30). Apart from studying phase separation, the dual-resolution membrane setup can also be applied to investigate a number of other processes, which would benefit from having AA detail in the leaflet of interest, such as the preliminary phase (stalk formation) of membrane fusion,62 the effect of asymmetric ionic concentrations across the membrane,63 peripheral membrane protein binding,64 and shape transformations of fluid vesicles.65 However, atoms or molecules should not cross the resolution interface because the VS hybrid scheme can only produce correct PMF between apolar molecules.24 A future direction would be to improve the PMF between hybrid polar and charged groups, which allows the resolution interface to be located in the polar or charged region.
The VS hybrid model can be improved in many other ways. For instance, MDs with Alchemical Steps (MDAS),66 proposed by Elber and co-workers, can be used to investigate heterogeneous biological membranes. The traditional simulation is combined with an alchemical trajectory, which switches the positions of randomly chosen pairs of lipids. Higher sampling efficiency has already been observed in the DOPC–POPC membrane.67 This algorithm can be combined with our hybrid VS model to further increase the sampling efficiency. In addition, the efficiency of our hybrid VS model can be improved by applying mean field force approximation boundary potentials, which replace the excess bulk solvent around a membrane,68 by using the Dry Martini force field69 to model the CG leaflets, or applying a multiple time step approach for different resolution levels, such as reversible RESPA.70
Conclusions
We showed that for a particular state point and force fields chosen in this study, Lo/Ld phase separation cannot be achieved in a full AA simulation within a 10 μs simulation time, while it is realized in the VS hybrid setup regardless of the starting configurations. This suggests that the phase separation in the CG leaflet can guide and accelerate the phase behavior of the AA leaflet. In addition, in the AA leaflet of the hybrid membrane, we observed the appearance of local hexagonal ordering of the lipid tails in the Lo domains, in agreement with experimental data and in support of previous simulation results. Taken together, we believe that our multiscale simulation setup is a useful method to speed up the process of phase separation in multicomponent bilayers, and may provide more insights to understand the molecular scale structural organization of cell membranes.
Acknowledgments
Y.L. was supported by the China Scholarship Council, 973 Program (201606070099).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.1c00151.
Parameter details of the recalibration of the VS hybrid scheme and cholesterol interactions with molecules in different resolutions (PDF).
Author Contributions
S.J.M. designed the research, Y.L. performed the research and analyzed the data, and Y.L., W.P., A.H.V., and S.J.M wrote the article.
The authors declare no competing financial interest.
Supplementary Material
References
- Subramaniam S.; Fahy E.; Gupta S.; Sud M.; Byrnes R. W.; Cotter D.; Dinasarapu A. R.; Maurya M. R. Bioinformatics and Systems Biology of the Lipidome. Chem. Rev. 2011, 111, 6452–6490. 10.1021/cr200295k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fahy E.; Subramaniam S.; Murphy R. C.; Nishijima M.; Raetz C. R. H.; Shimizu T.; Spener F.; van Meer G.; Wakelam M. J. O.; Dennis E. A. Update of the Lipid Maps Comprehensive Classification System for Lipids. J. Lipid Res. 2009, 50, S9–S14. 10.1194/jlr.r800095-jlr200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schram V.; Lin H. N.; Thompson T. E. Topology of Gel-Phase Domains and Lipid Mixing Properties in Phase-Separated Two-Component Phosphatidylcholine Bilayers. Biophys. J. 1996, 71, 1811. 10.1016/s0006-3495(96)79382-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koynova R.; Caffrey M. Phases and Phase Transitions of the Phosphatidylcholines. Biochim. Biophys. Acta, Rev. Biomembr. 1998, 1376, 91–145. 10.1016/s0304-4157(98)00006-9. [DOI] [PubMed] [Google Scholar]
- Nagle J. F.; Tristram-Nagle S. Structure of Lipid Bilayers. Biochim. Biophys. Acta, Rev. Biomembr. 2000, 1469, 159–195. 10.1016/s0304-4157(00)00016-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dreier J.; Brewer J.; Simonsen A. C. Systematic Variation of Gel-Phase Texture in Phospholipid Membranes. Langmuir 2014, 30, 10678–10685. 10.1021/la5023054. [DOI] [PubMed] [Google Scholar]
- Mouritsen O. G. The Liquid-Ordered State Comes of Age. Biochim. Biophys. Acta, Biomembr. 2010, 1798, 1286–1288. 10.1016/j.bbamem.2010.02.017. [DOI] [PubMed] [Google Scholar]
- Marsh D. Liquid-Ordered Phases Induced by Cholesterol: A Compendium of Binary Phase Diagrams. Biochim. Biophys. Acta, Biomembr. 2010, 1798, 688–699. 10.1016/j.bbamem.2009.12.027. [DOI] [PubMed] [Google Scholar]
- Davis J. H.; Clair J. J.; Juhasz J. Phase Equilibria in Dopc/Dppc-D62/Cholesterol Mixtures. Biophys. J. 2009, 96, 521–539. 10.1016/j.bpj.2008.09.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uppamoochikkal P.; Tristram-Nagle S.; Nagle J. F. Orientation of Tie-Lines in the Phase Diagram of Dopc/Dppc/Cholesterol Model Biomembranes. Langmuir 2010, 26, 17363–17368. 10.1021/la103024f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vist M. R.; Davis J. H. Phase Equilibria of Cholesterol/Dipalmitoylphosphatidylcholine Mixtures: Deuterium Nuclear Magnetic Resonance and Differential Scanning Calorimetry. Biochem 1990, 29, 451–464. 10.1021/bi00454a021. [DOI] [PubMed] [Google Scholar]
- Oldfield E.; Chapman D. Effects of Cholesterol and Cholesterol Derivatives on Hydrocarbon Chain Mobility in Lipids. Biochem. Biophys. Res. Commun. 1971, 43, 610–616. 10.1016/0006-291x(71)90658-9. [DOI] [PubMed] [Google Scholar]
- George K. S.; Wu S. Lipid Raft: A Floating Island of Death or Survival. Toxicol. Appl. Pharmacol. 2012, 259, 311–319. 10.1016/j.taap.2012.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veatch S. L.; Keller S. L. Organization in Lipid Membranes Containing Cholesterol. Phys. Rev. Lett. 2002, 89, 268101. 10.1103/physrevlett.89.268101. [DOI] [PubMed] [Google Scholar]
- Baumgart T.; Hess S. T.; Webb W. W. Imaging Coexisting Fluid Domains in Biomembrane Models Coupling Curvature and Line Tension. Nature 2003, 425, 821–824. 10.1038/nature02013. [DOI] [PubMed] [Google Scholar]
- Kahya N.; Scherfeld D.; Bacia K.; Poolman B.; Schwille P. Probing Lipid Mobility of Raft-Exhibiting Model Membranes by Fluorescence Correlation Spectroscopy. J. Biol. Chem. 2003, 278, 28109–28115. 10.1074/jbc.m302969200. [DOI] [PubMed] [Google Scholar]
- Baumgart T.; Hammond A. T.; Sengupta P.; Hess S. T.; Holowka D. A.; Baird B. A.; Webb W. W. Large-Scale Fluid/Fluid Phase Separation of Proteins and Lipids in Giant Plasma Membrane Vesicles. Proc. Natl. Acad. Sci. U.S.A. 2007, 104, 3165–3170. 10.1073/pnas.0611357104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lingwood D.; Ries J.; Schwille P.; Simons K. Plasma Membranes Are Poised for Activation of Raft Phase Coalescence at Physiological Temperature. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 10005–10010. 10.1073/pnas.0804374105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levental I.; Levental K. R.; Heberle F. A. Lipid Rafts: Controversies Resolved, Mysteries Remain. Trends Cell Biol. 2020, 30, 341–353. 10.1016/j.tcb.2020.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorgoglione V.; Palmitessa V.; Lofrumento D. D.; La Piana G.; Abbrescia D. I.; Marzulli D.; Lofrumento N. E. Ceramide-Induced Activation of Cytosolic Nadh/Cytochrome C Electron Transport Pathway: An Additional Source of Energy for Apoptosis. Arch. Biochem. Biophys. 2010, 504, 210–220. 10.1016/j.abb.2010.09.011. [DOI] [PubMed] [Google Scholar]
- Ingólfsson H. I.; Arnarez C.; Periole X.; Marrink S. J. Computational ’microscopy’ of cellular membranes. J. Cell Sci. 2016, 129, 257–268. 10.1242/jcs.176040. [DOI] [PubMed] [Google Scholar]
- Risselada H. J.; Marrink S. J. The Molecular Face of Lipid Rafts in Model Membranes. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 17367–17372. 10.1073/pnas.0807527105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baoukina S.; Mendez-Villuendas E.; Bennett W. F. D.; Tieleman D. P. Computer Simulations of the Phase Separation in Model Membranes. Faraday Discuss. 2013, 161, 63–75. 10.1039/c2fd20117h. [DOI] [PubMed] [Google Scholar]
- Gu R.-X.; Baoukina S.; Tieleman D. P. Phase Separation in Atomistic Simulations of Model Membranes. J. Am. Chem. Soc. 2020, 142, 2844–2856. 10.1021/jacs.9b11057. [DOI] [PubMed] [Google Scholar]
- Liu Y.; De Vries A. H.; Barnoud J.; Pezeshkian W.; Melcr J.; Marrink S. J. Dual Resolution Membrane Simulations Using Virtual Sites. J. Phys. Chem. B 2020, 124, 3944–3953. 10.1021/acs.jpcb.0c01842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rzepiela A. J.; Louhivuori M.; Peter C.; Marrink S. J. Hybrid Simulations: Combining Atomistic and Coarse-Grained Force Fields Using Virtual Sites. Phys. Chem. Chem. Phys. 2011, 13, 10437–10448. 10.1039/c0cp02981e. [DOI] [PubMed] [Google Scholar]
- Wassenaar T. A.; Ingólfsson H. I.; Priess M.; Marrink S. J.; Schäfer L. V. Mixing Martini: Electrostatic Coupling in Hybrid Atomistic-Coarse-Grained Biomolecular Simulations. J. Phys. Chem. B 2013, 117, 3516–3530. 10.1021/jp311533p. [DOI] [PubMed] [Google Scholar]
- Liu Y.; Pezeshkian W.; Barnoud J.; de Vries A. H.; Marrink S. J. Coupling Coarse-Grained to Fine-Grained Models Via Hamiltonian Replica Exchange. J. Chem. Theory Comput. 2020, 16, 5313–5322. 10.1021/acs.jctc.0c00429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wassenaar T. A.; Ingólfsson H. I.; Prieß M.; Marrink S. J.; Schäfer L. V. Mixing MARTINI: Electrostatic Coupling in Hybrid Atomistic-Coarse-Grained Biomolecular Simulations. J. Phys. Chem. B 2013, 117, 3516–3530. 10.1021/jp311533p. [DOI] [PubMed] [Google Scholar]
- Marrink S. J.; Risselada H. J.; Yefimov S.; Tieleman D. P.; de Vries A. H. The Martini Force Field: Coarse Grained Model for Biomolecular Simulations. J. Phys. Chem. B 2007, 111, 7812–7824. 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- Van Der Spoel D.; Lindahl E.; Hess B.; Groenhof G.; Mark A. E.; Berendsen H. J. C. Gromacs: Fast, Flexible, and Free. J. Comput. Chem. 2005, 26, 1701–1718. 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
- Van Gunsteren W. F.; Berendsen H. J. C. A Leap-Frog Algorithm for Stochastic Dynamics. Mol. Simul. 1988, 1, 173–185. 10.1080/08927028808080941. [DOI] [Google Scholar]
- Goga N.; Rzepiela A. J.; de Vries A. H.; Marrink S. J.; Berendsen H. J. C. Efficient Algorithms for Langevin and Dpd Dynamics. J. Chem. Theory Comput. 2012, 8, 3637–3649. 10.1021/ct3000876. [DOI] [PubMed] [Google Scholar]
- Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; DiNola A.; Haak J. R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
- Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; Hermans J.. Interaction Models for Water in Relation to Protein Hydration. In Intermolecular Forces: Proceedings of the Fourteenth Jerusalem Symposium on Quantum Chemistry and Biochemistry, Jerusalem, Israel, April 13–16, 1981; Pullman B., Ed.; The Jerusalem Symposia on Quantum Chemistry and Biochemistry, Vol. 14; Springer: Dordrecht, Netherlands, 1981; pp 331−342. 10.1007/978-94-015-7658-1_21 [DOI]
- Miyamoto S.; Kollman P. A. Settle: An Analytical Version of the Shake and Rattle Algorithm for Rigid Water Models. J. Comput. Chem. 1992, 13, 952–962. 10.1002/jcc.540130805. [DOI] [Google Scholar]
- Thallmair S.; Ingólfsson H. I.; Marrink S. J. Cholesterol Flip-Flop Impacts Domain Registration in Plasma Membrane Models. J. Phys. Chem. Lett. 2018, 9, 5527–5533. 10.1021/acs.jpclett.8b01877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wassenaar T. A.; Pluhackova K.; Böckmann R. A.; Marrink S. J.; Tieleman D. P. Going Backward: A Flexible Geometric Approach to Reverse Transformation from Coarse Grained to Atomistic Models. J. Chem. Theory Comput. 2014, 10, 676–690. 10.1021/ct400617g. [DOI] [PubMed] [Google Scholar]
- Hsu P. C.; Bruininks B. M. H.; Jefferies D.; Cesar Telles de Souza P.; Lee J.; Patel D. S.; Marrink S. J.; Qi Y.; Khalid S.; Im W. CHARMM-GUI Martini Maker for modeling and simulation of complex bacterial membranes with lipopolysaccharides. J. Comput. Chem. 2017, 38, 2354–2363. 10.1002/jcc.24895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Domański J.; Marrink S. J.; Schäfer L. V. Transmembrane Helices Can Induce Domain Formation in Crowded Model Membranes. Biochim. Biophys. Acta 2012, 1818, 984–994. 10.1016/j.bbamem.2011.08.021. [DOI] [PubMed] [Google Scholar]
- Camesasca M.; Kaufman M.; Manas-Zloczower I. Quantifying Fluid Mixing with the Shannon Entropy. Macromol. Theory Simul. 2006, 15, 595–607. 10.1002/mats.200600037. [DOI] [Google Scholar]
- Pantelopulos G. A.; Nagai T.; Bandara A.; Panahi A.; Straub J. E. Critical Size Dependence of Domain Formation Observed in Coarse-Grained Simulations of Bilayers Composed of Ternary Lipid Mixtures. J. Chem. Phys. 2017, 147, 095101. 10.1063/1.4999709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halperin B. I.; Nelson D. R. Theory of Two-Dimensional Melting. Phys. Rev. Lett. 1978, 41, 121. 10.1103/physrevlett.41.121. [DOI] [Google Scholar]
- Barnoud J.; Rossi G.; Monticelli L. Lipid Membranes as Solvents for Carbon Nanoparticles. Phys. Rev. Lett. 2014, 112, 068102. 10.1103/PhysRevLett.112.068102. [DOI] [PubMed] [Google Scholar]
- Lukat G.; Krüger J.; Sommer B. Apl@Voro: A Voronoi-Based Membrane Analysis Tool for Gromacs Trajectories. J. Chem. Inf. Model. 2013, 53, 2908–2925. 10.1021/ci400172g. [DOI] [PubMed] [Google Scholar]
- Marrink S. J.; Risselada J.; Mark A. E. Simulation of Gel Phase Formation and Melting in Lipid Bilayers Using a Coarse Grained Model. Chem. Phys. Lipids 2005, 135, 223–244. 10.1016/j.chemphyslip.2005.03.001. [DOI] [PubMed] [Google Scholar]
- Sodt A. J.; Sandar M. L.; Gawrisch K.; Pastor R. W.; Lyman E. The Molecular Structure of the Liquid-Ordered Phase of Lipid Bilayers. J. Am. Chem. Soc. 2014, 136, 725–732. 10.1021/ja4105667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hakobyan D.; Heuer A. Phase Separation in a Lipid/Cholesterol System: Comparison of Coarse-Grained and United-Atom Simulations. J. Phys. Chem. B 2013, 117, 3841–3851. 10.1021/jp312245y. [DOI] [PubMed] [Google Scholar]
- Lafleur M.; Cullis P. R.; Bloom M. Modulation of the Orientational Order Profile of the Lipid Acyl Chain in the L? Phase. Eur. Biophys. J. 1990, 19, 55–62. 10.1007/bf00185086. [DOI] [PubMed] [Google Scholar]
- Armstrong C. L.; Marquardt D.; Dies H.; Kučerka N.; Yamani Z.; Harroun T. A.; Katsaras J.; Shi A.-C.; Rheinstädter M. C. The Observation of Highly Ordered Domains in Membranes with Cholesterol. PLoS One 2013, 8, e66162 10.1371/journal.pone.0066162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Souza P. C. T.; et al. Martini 3: A General Purpose Force Field for Coarse-Grained Molecular Dynamics. Nat. Methods 2021, 18, 382–388. 10.1038/s41592-021-01098-3. [DOI] [PubMed] [Google Scholar]
- Machado M. R.; Dans P. D.; Pantano S. A Hybrid All-Atom/Coarse Grain Model for Multiscale Simulations of DNA. Phys. Chem. Chem. Phys. 2011, 13, 18134–18144. 10.1039/c1cp21248f. [DOI] [PubMed] [Google Scholar]
- Gowers R. J.; Carbone P.; Di Pasquale N. A Different Approach to Dual-Scale Models. J. Comput. Phys. 2020, 413, 109465. 10.1016/j.jcp.2020.109465. [DOI] [Google Scholar]
- Tschöp W.; Kremer K.; Hahn O.; Batoulis J.; Bürger T. Simulation of Polymer Melts. Ii. From Coarse-Grained Models Back to Atomistic Description. Acta Polym. 1998, 49, 75–79. . [DOI] [Google Scholar]
- Rzepiela A. J.; Schäfer L. V.; Goga N.; Risselada H. J.; De Vries A. H.; Marrink S. J. Reconstruction of Atomistic Details from Coarse-Grained Structures. J. Comput. Chem. 2010, 31, 1333–1343. 10.1002/jcc.21415. [DOI] [PubMed] [Google Scholar]
- Praprotnik M.; Delle Site L.; Kremer K. Adaptive Resolution Molecular-Dynamics Simulation: Changing the Degrees of Freedom on the Fly. J. Chem. Phys. 2005, 123, 224106. 10.1063/1.2132286. [DOI] [PubMed] [Google Scholar]
- Heyden A.; Truhlar D. G. Conservative Algorithm for an Adaptive Change of Resolution in Mixed Atomistic/Coarse-Grained Multiscale Simulations. J. Chem. Theory Comput. 2008, 4, 217–221. 10.1021/ct700269m. [DOI] [PubMed] [Google Scholar]
- Zavadlav J.; Podgornik R.; Melo M. N.; Marrink S. J.; Praprotnik M. Adaptive Resolution Simulation of an Atomistic DNA Molecule in Martini Salt Solution. Eur. Phys. J. Spec. Top. 2016, 225, 1595–1607. 10.1140/epjst/e2016-60117-8. [DOI] [Google Scholar]
- Fukunishi H.; Watanabe O.; Takada S. On the Hamiltonian Replica Exchange Method for Efficient Sampling of Biomolecular Systems: Application to Protein Structure Prediction. J. Chem. Phys. 2002, 116, 9058–9067. 10.1063/1.1472510. [DOI] [Google Scholar]
- Liu P.; Voth G. A. Smart Resolution Replica Exchange: An Efficient Algorithm for Exploring Complex Energy Landscapes. J. Chem. Phys. 2007, 126, 045106. 10.1063/1.2408415. [DOI] [PubMed] [Google Scholar]
- Lyman E.; Ytreberg F. M.; Zuckerman D. M. Resolution Exchange Simulation. Phys. Rev. Lett. 2006, 96, 028105. 10.1103/PhysRevLett.96.028105. [DOI] [PubMed] [Google Scholar]
- Markvoort A. J.; Marrink S. J. Lipid Acrobatics in the Membrane Fusion Arena. Curr. Top. Membr. 2011, 68, 259–294. 10.1016/b978-0-12-385891-7.00011-8. [DOI] [PubMed] [Google Scholar]
- Khalili-Araghi F.; Ziervogel B.; Gumbart J. C.; Roux B. Molecular Dynamics Simulations of Membrane Proteins under Asymmetric Ionic Concentrations. J. Gen. Physiol. 2013, 142, 465–475. 10.1085/jgp.201311014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naughton F. B.; Kalli A. C.; Sansom M. S. P. Association of Peripheral Membrane Proteins with Membranes: Free Energy of Binding of Grp1 Ph Domain with Phosphatidylinositol Phosphate-Containing Model Bilayers. J. Phys. Chem. Lett. 2016, 7, 1219–1224. 10.1021/acs.jpclett.6b00153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan H.; Huang C.; Zhang S. Dynamic Shape Transformations of Fluid Vesicles. Soft Matter 2010, 6, 4571–4579. 10.1039/c0sm00244e. [DOI] [Google Scholar]
- Fathizadeh A.; Elber R. A Mixed Alchemical and Equilibrium Dynamics to Simulate Heterogeneous Dense Fluids: Illustrations for Lennard-Jones Mixtures and Phospholipid Membranes. J. Chem. Phys. 2018, 149, 072325. 10.1063/1.5027078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cherniavskyi Y. K.; Fathizadeh A.; Elber R.; Tieleman D. P. Computer Simulations of a Heterogeneous Membrane with Enhanced Sampling Techniques. J. Chem. Phys. 2020, 153, 144110. 10.1063/5.0014176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Risselada H. J.; Mark A. E.; Marrink S. J. Application of Mean Field Boundary Potentials in Simulations of Lipid Vesicles. J. Phys. Chem. B 2008, 112, 7438–7447. 10.1021/jp0758519. [DOI] [PubMed] [Google Scholar]
- Arnarez C.; Uusitalo J. J.; Masman M. F.; Ingólfsson H. I.; de Jong D. H.; Melo M. N.; Periole X.; de Vries A. H.; Marrink S. J. Dry Martini, a Coarse-Grained Force Field for Lipid Membrane Simulations with Implicit Solvent. J. Chem. Theory Comput. 2015, 11, 260–275. 10.1021/ct500477k. [DOI] [PubMed] [Google Scholar]
- Tuckerman M.; Berne B. J.; Martyna G. J. Reversible Multiple Time Scale Molecular Dynamics. J. Chem. Phys. 1992, 97, 1990–2001. 10.1063/1.463137. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.