Medical waste management during coronavirus disease 2019 (COVID-19) outbreak: A mathematical programming model

Abstract

Municipal solid waste (MSW) directly impacts community health and environmental degradation; therefore, the management of MSW is crucial. Medical waste is a specific type of MSW which is generally divided into two categories: infectious and non-infectious. Wastes generated by coronavirus disease 2019 (COVID-19) are classified among infectious medical wastes; moreover, these wastes are hazardous because they threaten the environment and living organisms if they are not appropriately managed. This paper develops a bi-objective mixed-integer linear programming model for medical waste management during the COVID-19 outbreak. The proposed model minimizes the total costs and risks, simultaneously, of the population’s exposure to pollution. This paper considers some realistic assumptions for the first time, including location-routing problem, time window-based green vehicle routing problem, vehicles scheduling, vehicles failure, split delivery, population risk, and load-dependent fuel consumption to manage both infectious and non-infectious medical waste. We apply a fuzzy goal programming approach for solving the proposed bi-objective model, and the efficiency of the proposed model and solution approach is assessed using data related to 13 nodes of medical waste production in a location west of Tehran.

1. Introduction

Municipal solid waste (MSW) has increased along with growth in the urban population (Cheng et al., 2020). The waste management organization of Tehran municipality published a report that demonstrates more than three million tons of MSW were produced in Tehran during 2017 (http://statistics.tehran.ir). Plenty of definitions and categories are introduced in the literature for MSW, and the large number of definitions leads to confusion (Buenrostro et al., 2001). The most appropriate MSW definition depends on the location of the municipality and the time period (Zhou et al., 2015). As an example, Heinen (1995) once declared that MSWs must contain domestic residues and cannot have commercial or hazardous components. On the other hand, United States Environmental Protection Agency (EPA) categorizes municipal solid waste as that generated by commercial, institutional, and residential sources. In another example, Brunner and Ernst (1986) define MSW as the waste collected by authorized organizations and municipalities. An efficient summary of MSW was introduced by Buenrostro et al. (2001), in which the term MSW refers to the following seven categories: residential, institutional, commercial, construction (demolition), industrial, agricultural-animal husbandry, and special.

MSW management is a public service that incorporates an efficient economic and environmental waste disposal system for the citizens. Traditional MSW disposal systems such as landfills are no longer effective due to the lack of adequate land and/or the consequences of soil and water pollution (Abdel-Shafy and Mansour, 2018). Thus, alternative solutions such as incineration, composting, or recycling, gasification are proposed (Fatimah et al., 2020, Mohammadi et al., 2019, Zhou et al., 2015), but their implementation requires scarce and complicated technologies. The selection of a proper MSW disposal system should be based on the geographical location and climate as well as on the population’s lifestyle (Buenrostro et al., 2001). Choosing a MSW disposal system without having a complete understanding of its attributes is likely to result in unnecessary costs and environmental damages. Iran is no exception; Tehran’s officials report that up to 20% of the city’s municipality budget for collecting and disposing MSWs has been wasted because a proper MSW disposal system was not selected in a scientific way (http://pasmand.tehran.ir).

Recently, a lot of studies are devoted to MSW management using mathematical programming approaches with various assumptions and specifications, including capacitated location-allocation (Yu and Solvang, 2017, Rathore et al., 2020, Tirkolaee et al., 2020), vehicle routing problem (VRP) (Hannan et al., 2018, Louati et al., 2019, Höke and Yalcinkaya, 2021), location-routing problem (Rabbani et al., 2018, Asefi et al., 2019); uncertainty (Yadav et al., 2017, Tirkolaee et al., 2018, Singh, 2019, Wang et al., 2021), and so on.

This study is conducted to introduce a new mixed-integer linear programming (MILP) model with the purpose of MSW management considering risks related to the population exposed to pollution, location-allocation, and green VRP. Multiple vehicles of different types are supposed to start their tour from separation centers and return in time after collecting MSWs from waste-generating nodes. In separation centers, collected MSWs will be separated and sorted before moving into recycling, compost, incineration, or landfill centers. In addition, the vehicles’ fuel consumption with respect to the extra weight of MSWs are considered as a part of the total cost of the supply chain. This has an indirect impact on reducing the pollution generated by vehicles while collecting MSWs. The main contributions of this paper are listed as follows:

• •Formulating a novel multi-product, multi-period and bi-objective MILP model for MSW management with location-allocation, time window-based green VRP, population risks, vehicles scheduling and failure, split delivery, and load-dependent fuel consumption minimization considerations
• •Developing a novel fuzzy goal programming for converting the proposed bi-objective model into a single objective one under uncertainty
• •Using Tehran municipality actual data as a case study to measure efficiency and practicality of the proposed model and solution approach.

The remainder of this paper is structured as follows. In Section 2, we investigate the related literatures. Section 3 presents the proposed model. In Section 4, we implement a case study in Iran to represent the applicability of the proposed model. Discussions are presented in Section 5. 6, 7 are allocated to sensitivity analysis and managerial implications, respectively. Finally, the conclusion is presented in Section 8.

2. Literature review

2.1. Municipal solid waste

Health and economic considerations for the disposal of environment polluting materials, such as solid wastes, has attracted growing research attention, especially during recent years (Chowdhury et al., 2019, Rani et al., 2020). Considering the undeniably destructive consequences of applying improper waste collection and disposal systems in both rural and urban area, this is definitely an inevitable part of public healthcare and prevention that must be acknowledged before treatment strategies are pursued (Darmian et al., 2020, Sharma et al., 2021). Due to basic environmental principles, the time to collect and dispose waste should be minimized (Rathore and Sarmah, 2020). All residents have to make sure they do not violate green waste disposal codes that have been in place since the 19th century. These basic notions and obligations have led to the introduction of MSW management. This field has been studied extensively in the literature of waste management, for which mathematical programming is observed to be very popular among the contributing researchers. Huang et al. (2001) developed a MILP model for MSW management purposes. They applied a chance constrained and fuzzy theory based integrated approach to solve their proposed model under uncertain circumstances. Li and Huang (2006) presented an interval-parameter two-stage MILP model to support the long-term of MSWs management in Regina. In order to accommodate uncertainty in their proposed model, they applied both two-stage stochastic programming and interval linear programming in parallel. Another optimization approach has been introduced by Badran and El-Haggar (2006) for MSW management in Said port. They applied a MILP model to do waste management while minimizing total costs. Eiselt and Marianov (2014) developed a bi-objective MILP model to locate optimum landfill places for MSWs. The objective of their model was to simultaneously minimize both total costs and pollution. Xu et al. (2014) developed a fuzzy chance constrained mixed-integer programming (MIP) model to manage MSW under circumstances with multiple uncertainty. Their proposed model involves strategic to tactical decisions that lead to minimizing cost of supply chain. Yu et al. (2015) devoted their work to optimizing long-term performance of MSW management systems via formulating a bi-objective mathematical model. They proposed a dynamic programming approach for solving the bi-objective linear model which leads in optimizing long-term performance of MSW systems. Their model simultaneously evaluates both economic efficiency and environmental pollution emissions of a MSW management system in multiple consecutive time periods. An optimal collection and transportation scheme for MSW management is studied by Das and Bhattacharyya (2015) that aims to optimize the transportation route. They formulated an MIP model to represent the highlighted MSW collection and transportation problem. Then, they applied a heuristic method to solve this problem. Obtained results demonstrated that application of the proposed approach leads into decreasing more than 30% of the distance that shall be undertaken for MSW collection. Lee et al. (2016) formulated a MILP model to manage MSWs. This model defines the optimum number of facilities required to process MSWs in addition to estimating the incinerated and landfilled MSW amounts. The results obtained after implementing this approach in Hong Kong showed high efficiency and accurate performance of the proposed model. Louati (2016) developed a multi-objective mathematical model to do MSW management through formulating a supply chain with VRP considerations. Multiple transfer stations, collection sites, different types of vehicles, and time windows for waste collection are considered in their proposed model. They formulated a multi-objective MIP model, whose practicality was investigated through a case study in the city of Danang. Shirazi et al. (2016) proposed a linear mathematical model to reduce the number of transfer stations as well as processing times through integration of MSW system. The data collected for MSW system of Tehran city is used to validate this model. According to the obtained results, number of transfer stations reduced from 11 to 10 while number of required processing units reduced from 10 to 6 due to application of the proposed model. A multi-objective MILP model with simultaneous environmental and socio-economic considerations was suggested by Harijani et al. (2017a). Their model incorporates facility optimization, waste to facility allocation, waste and products transportation between facilities in order to maximize the profit and social impacts where minimizing environmental destructive consequences at the same time. Harijani et al. (2017b) also presented a systematic approach to establish a recycling system that incorporates uniform utilization of MSWs which brings sustainability to the system while maximizing the profit. They developed a multi-period MILP model to search for optimum system design. Optimum facility selection, including capacity and location, allocation of MSW to facilities, MSW transportation between facilities, and distribution of recycled material form the scope of this model. Mohammadi et al. (2019) structured a multi-product and multi-period MILP model that makes optimum tactical to operational decisions while designing a waste supply chain. Waste supply chains are considered in their study to have collection, separation, and distribution centers as well as plant and landfill. The objective of this model is to maximize supply chain’s total profit. The results obtained due to implementing this model, in an area located in Mexico, validates the flexibility and practicality of the model. An MILP model for managing MSWs was formulated by Yousefloo and Babazadeh (2020) that considers economic and environmental aspects. Their model simultaneously minimizes total costs and risk and uses the ε-constraint method to solve the bi-objective model. Mohsenizadeh et al. (2020) presented a bi-objective MILP model for managing MSWs with the aim of minimizing total costs and emissions. They investigated the effect of speed variations of vehicles on changes in objective functions. Finally, they evaluated their proposed model's performance using data from the MSW management system of Ankara.

2.2. Medical waste management during COVID-19 outbreak

Zambrano-Monserrate et al. (2020) describe multiple indirect effects of COVID-19 on the environment. Increasing the medical waste was one of the significant side effects of the COVID-19 outbreak, and multiple researchers thought about how to better manage the waste flow using different models. We review the main vital works as follows. Yu et al. (2020) formulated a reverse logistic network design in multi-period multi-objective tradition for managing COVID-19 in the epidemic outbreak, and they validated the model in Wuhan, China. The results depicted installing temporary incinerators could help in managing medical wastes. Kargar et al. (2020) developed a MILP model to minimize costs, transportation risk, and the quantity of medical waste in generation centers. The model was validated by using a case study from Iran and demonstrated a trade-off between objectives for better managing waste flows. Nikzamir and Baradaran (2020) presented a bi-objective model considering costs and emissions of contamination that could be intensified during the COVID-19 outbreak. They modeled the transferring time between nodes as random variables and used a meta-heuristic algorithm for solving that complex model. Valizadeh and Mozafari (2021) showed how cooperation between municipal waste collectors could reduce cost as well as residual waste during COVID-19 pandemic. In another paper, Valizadeh et al. (2021) showed the role of the government in the outbreak using a robust mathematical model. They used a stochastic programming approach for modeling the condition and solving the model by the Benders decomposition with Karush-Kuhn-Tucker conditions. Tirkolaee et al. (2021) analyzed the case study using an MIP model with time windows in the COVID-19 pandemic era. They minimized traveling time, environmental risk, violation from time windows, and priorities in provided services. They used a fuzzy chance-constrained approach for solving these conditions.

As shown in Table 1 , the location-routing problem in medical waste management has been considered by researchers, and most of the papers presented are multi-objective and examine population risk. With the outbreak of the COVID-19 pandemic, some medical waste management papers have moved in this direction. In this paper, for the first time, a bi-objective MILP model takes into account the assumptions of location-routing problem, time window-based green vehicle routing problem, vehicles scheduling, vehicles failure, split delivery, population risk, and load-dependent fuel consumption for medical waste management during COVID-19 outbreak under uncertainty.

Table 1.

The papers published in medical waste management using mathematical programming approach.

Author(s)	Solution approach	Multi-objective	Multi-product	Multi-period	Time window	Location problem	VRP	Vehicles failure	Emissions	Load-dependent fuel consumption	Heterogeneous vehicles	Vehicles scheduling	Population risk	Uncertainty	COVID-19
Hajar et al. (2018)	CS	√	–	√	√	√	√	–	–	–	–	–	√	–	–
Wichapa and Khokhajaikiat (2018)	MH	√	–	–	–	√	√	–	–	–	–	–	–	–	–
Homayouni and Pishvaee (2020)	CS	√	√	–	–	√	–	–	–	–	–	–	√	√	–
Kargar et al. (2020)	CS	√	–	√	–	√	–	–	–	–	–	–	√	√	√
Nikzamir and Baradaran (2020)	MH	√	√	–	√	√	√	–	√	–	√	–	√	–	√
Nikzamir et al. (2020)	E	√	√	–	√	√	√	–	√	–	√	–	√	–	–
Tirkolaee et al. (2021)	CS	√	–	√	√	√	√	–	–	–	√	–	√	√	√
Valizadeh and Mozafari (2021)	MH	–	√	√	–	–	–	–	–	–	√	–	–	√	√
Valizadeh et al. (2021)	E	√	√	–	–	√	–	–	–	–	–	–	–	√	√
This paper	CS	√	√	√	√	√	√	√	√	√	√	√	√	√	√

CS: Commercial solvers, MH: Meta-heuristics, E: Exact methods.

3. Proposed model

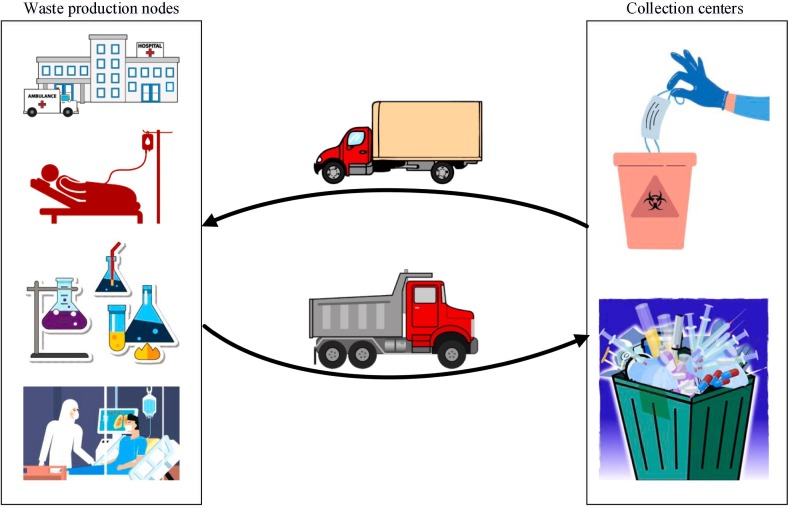
In this section, a bi-objective MILP model is developed for the management of medical wastes in the event of a pandemic COVID-19 outbreak. The proposed model is a multi-product, multi-period and bi-echelon one including waste production nodes and potential collection centers; total cost and pollution risk are simultaneously minimized in this model. Waste production nodes include laboratories, hospitals, temporary hospitals, clinics, and health centers, which fall into two categories, namely nodes that produce COVID-19 wastes and are considered hazardous wastes and nodes that produce both infectious (hazardous) and non-infectious wastes. Vehicles move from collection centers to waste generation nodes and return to collection centers before the allowed time window following the collection of wastes. In Fig. 1 , the overall structure of the network under study has been illustrated.

Fig. 1.

Structure of under study network.

The following points constitute the assumptions of the proposed model for an accurate statement of the problem:

• •The network under study is a bi-echelon supply chain including waste production nodes and potential collection centers.
• •The supply chain of multiple products in multiple time periods is modeled through this study.
• •Whereas the location of the medical waste production nodes is assumed to be fixed, the solver is free to propose the optimum location(s) for the collection centers.
• •There is a finite number of vehicles with limited capacity, among which the solver is tasked to find the optimum set of vehicles to be supplied.
• •Vehicles are heterogeneous.
• •Split delivery is possible.
• •The time required to move between each pair of nodes in deterministic and an input to the model.
• •This study aims to find the optimum route to visit all medical waste production and collection centers through solving a multi-depot VRP with capacitated distribution centers.
• •Vehicles’ fuel consumption depends on the weight of the waste with which the vehicle is loaded.
• •Hard time window constraints are considered for vehicles returning to distribution centers.
• •The vehicles’ failure is considered.

Indices

$w$	Waste	$w\in \left\{1,2,...,W\right\}$
$m,n$	Waste production node	$m,n\in \left\{1,2,...,M\right\}$
$c$	Potential collection center	$c\in \left\{1,2,...,C\right\}$
$v$	Vehicle	$v\in \left\{1,2,...,V\right\}$
$t$	Time period	$t\in \left\{1,2,...,T\right\}$

Parameters

${\xi }_v^{\mathit{CP}-VH}$	Capacity of vehicle v
${\xi }_{\mathit{wc}}^{\mathit{CP}-CL}$	Capacity of collection center c for type w waste
${\xi }_{\mathit{wmt}}$	Amount of type w waste being produced in node m in time period t
${\eta }_v^{\mathit{CST}-VH}$	Cost of hiring vehicle v
${\eta }_c^{\mathit{CST}-CL}$	Set-up cost for collection center c
${\alpha }_{\mathit{mn}}$	The distance between nodes m and n
${\beta }_{\mathit{mc}}$	The distance between node m and collection point c
${\alpha }_{\mathit{vmn}}^{\mathit{TM}}$	The time required to go from node m to node n using vehicle v
${\beta }_{\mathit{vmc}}^{\mathit{TM}}$	The time required to go from node m to collection point c using vehicle v
${\delta }_m$	The time required to collect wastes from node m
${\lambda }_{\mathit{wm}}\left\{\begin{array}{c}1\\ 0\end{array}\right)$	If either type w waste is hazardous or node m is exposed
	Otherwise
${\varpi }_{\mathit{wct}}$	Processing cost per unit of type w waste in collection center c in time period t
$P{R}_{\mathit{vt}}$	The failure probability of vehicle v in time period t
$\mathit{WG}{H}_w$	Weight per unit of type w waste
$\phi$	Time window for returning to the collection center
${\psi }_{\mathit{mn}}$	Population exposed along the route that connects nodes m and n
$F{C}_v$	Fuel consumption rate per km for vehicle v
$\mathit{EF}{C}_v$	Extra fuel consumption rate per kg for vehicle v
$\mathit{FCG}$	Fuel supply cost per gallon
$\mathit{bigm}$	A very large number

Variables

${\mu }_c^{\mathit{CL}}\left\{\begin{array}{c}1\\ 0\end{array}\right)$	Binary	In case of setting up collection center c
		Otherwise
${\mu }_v^{\mathit{VH}}\left\{\begin{array}{c}1\\ 0\end{array}\right)$	Binary	In case of supplying vehicle v
		Otherwise
${\gamma }_{\mathit{vmnt}}\left\{\begin{array}{c}1\\ 0\end{array}\right)$	Binary	In case of moving vehicle v from node m to n in time period t
		Otherwise
${\vartheta }_{\mathit{vc}}\left\{\begin{array}{c}1\\ 0\end{array}\right)$	Binary	In case of allocating vehicle v to collection center k
		Otherwise
${\tau }_{\mathit{uvmt}}\left\{\begin{array}{c}1\\ 0\end{array}\right)$	Binary	In case of arriving vehicle u before vehicle v to node m in time period t
		Otherwise
$A_{\mathit{wvmt}}\left\{\begin{array}{c}1\\ 0\end{array}\right)$	Binary	In case of vehicle v carrying type w waste into node m in time period t
		Otherwise
$h{f}_{\mathit{mvt}}\left\{\begin{array}{c}1\\ 0\end{array}\right)$	Binary	In case of vehicle v contains hazardous waste while visiting node m at time t
		Otherwise
${\chi }_{\mathit{vmt}}$	Positive	The time that vehicle v arrives at node m in time period t
$Y_{\mathit{wvcmt}}$	Positive	The amount of type w waste collected by vehicle v from node m and delivered to collection center c in time period t
$E_{\mathit{wvmt}}$	Positive	Cumulative amount of type w waste in vehicle v at the time of arriving at node m in time period t

Mathematical Model

Objective functions

$$\begin{array}{c}\mathit{Min}{Z}_1=\sum _v{\eta }_v^{\mathit{CST}-VH}\times {\mu }_v^{\mathit{VH}}+\sum _c{\eta }_c^{\mathit{CST}-CL}\times {\mu }_c^{\mathit{CL}}+\sum _{w,v,c,m,t}{\varpi }_{\mathit{wct}}\times Y_{\mathit{wvcmt}}+\\ FCG\times \sum _{v,m>1,n>1,t}(F{C}_v+EF{C}_v\times E_{\mathit{vmt}}\times WG{H}_w)\times {\alpha }_{\mathit{mn}}\times {\gamma }_{\mathit{vmnt}}+\\ FCG\times \sum _{v,m>1,c,t}F{C}_v\times {\beta }_{\mathit{mc}}\times {\vartheta }_{\mathit{vc}}\times {\gamma }_{v1mt}+\\ FCG\times \sum _{w,v,m>1,c,t}(F{C}_v+EF{C}_v\times E_{\mathit{wvmt}}\times WG{H}_w)\times {\beta }_{\mathit{mc}}\times {\vartheta }_{\mathit{vc}}\times {\gamma }_{vm1t}\end{array}$$ (1)

$$\mathit{Min}{Z}_2=\sum _{v,m,n,t}P{R}_{\mathit{vt}}\times {\psi }_{\mathit{mn}}\times h{f}_{\mathit{vmt}}$$ (2)

$$\mathit{Subjected}to:$$

$$\sum _m{\gamma }_{\mathit{vmnt}}⩽1\forall v,n,t$$ (3)

$$\sum _m{\gamma }_{\mathit{vmnt}}=\sum _m{\gamma }_{\mathit{vnmt}}\forall v,n,t$$ (4)

$$\sum _{w,m}{Y}_{\mathit{wvcmt}}⩽{\xi }_v^{\mathit{CP}-VH}\forall v,c,t$$ (5)

$$\sum _{v,m}{Y}_{\mathit{wvcmt}}⩽{\xi }_{\mathit{wc}}^{\mathit{CP}-CL}\forall w,c,t$$ (6)

$$\sum _{v,c}{Y}_{\mathit{wvcmt}}⩾{\xi }_{\mathit{wmt}}\forall w,m,t$$ (7)

$$\sum _{w,m}{Y}_{\mathit{wvcmt}}⩽bigm\times {\vartheta }_{\mathit{vc}}\forall v,c,t$$ (8)

$$\sum _c{\vartheta }_{\mathit{vc}}⩽bigm\times {\mu }_v^{\mathit{VH}}\forall v$$ (9)

$$\sum _{w,c}{Y}_{\mathit{wvcnt}}⩽bigm\times \sum _m{\gamma }_{\mathit{vmnt}}\forall v,n,t$$ (10)

$${\chi }_{\mathit{vnt}}+(1-{\gamma }_{\mathit{vmnt}})\times bigm⩾{\chi }_{\mathit{vmt}}+{\alpha }_{\mathit{vmn}}^{\mathit{TM}}\forall v,m,n>1,t$$ (11)

$$\phi +bigm\times (1-{\gamma }_{vm1t})⩾{\chi }_{\mathit{vmt}}+{\beta }_{\mathit{vmc}}^{\mathit{TM}}\times {\vartheta }_{\mathit{vc}}\forall v,m>1,c,t$$ (12)

$$\sum _c{\vartheta }_{\mathit{vc}}⩽1\forall v$$ (13)

$$Y_{\mathit{wvcmt}}⩽bigm\times {\mu }_c^{\mathit{CL}}\forall w,v,c,m,t$$ (14)

$$E_{\mathit{wvnt}}+bigm\times (1-{\gamma }_{\mathit{vmnt}})⩾E_{\mathit{wvmt}}+\sum _w{Y}_{\mathit{wvcmt}}\forall w,v,c,m,n>1,t$$ (15)

$$E_{wv1t}⩾\sum _{w,m}{Y}_{\mathit{wvcmt}}\forall w,v,c,t$$ (16)

$$E_{\mathit{wvmt}}⩽bigm\times A_{\mathit{wvmt}}\forall w,v,m,t$$ (17)

$${\chi }_{\mathit{umt}}-{\chi }_{\mathit{vmt}}+bigm\times {\tau }_{\mathit{uvmt}}⩾{\delta }_m\forall u\ne v,m>1,t$$ (18)

$${\tau }_{\mathit{uvmt}}+{\tau }_{\mathit{vumt}}⩽3-\sum _n({\gamma }_{\mathit{vmnt}}+{\gamma }_{\mathit{umnt}})\forall u\ne v,m>1,t$$ (19)

$$\mathit{bigm}\times h{f}_{\mathit{mvt}}⩾\sum _w(A_{\mathit{wvmt}}\times {\lambda }_{\mathit{wm}})\forall v,m>1,t$$ (20)

The objective of this model is to minimize both the supply chain’s cost and population exposure risk at the same time. Considered cost items are as follows: vehicle hiring cost, collection centers’ set-up cost, waste processing cost, and vehicle’s fuel cost with respect to the extra load being carried via vehicles. On the other hand, minimizing the risk of population exposure to pollution implies the necessity of selecting low-populated routes that are about to be covered by the vehicles carrying hazardous wastes. The point here is that, once a vehicle picks up hazardous waste (either its type is hazardous or it is being picked up from an exposed location), then the vehicle is exposed and the risk of population exposure increases accordingly. This is formulated through equations (2), (20).

According to VRP conditions, each vehicle is allowed to visit each waste production node at most once in each time period; no vehicle may visit a waste production node more than once in a single time period. Also, if a vehicle enters a node, it should leave it after service. These conditions are considered in constraints (3), (4), respectively. Capacity limitations for vehicles are considered in constraint (5). In other words, each purchased vehicle is allowed to collect a maximum amount of waste as much as its capacity. Capacity limitations for collection centers to prevent overloading are guaranteed by constraint (6). It means that the total amount of waste collected by vehicles and transferred to a collection center should not exceed the capacity of the collection center. The total waste produced in each waste production node in each time period should be collected. Constraint (7) provides these conditions. If a vehicle is not given to a collection center, it is not possible to carry waste from waste production nodes to collection centers. It is ensured in constraint (8). Vehicles can be assigned to collection centers if they are purchased. Constraint (9) indicate this prerequisite. Constraint (10) states that the condition for collecting waste from waste production nodes is to visit nodes by vehicles. The sub-tour elimination constraint is presented in constraints (11), (12). In addition, constraint (12) ensures that all vehicles leaving the collection center should return to the collection center before the specified time window. Each vehicle should not be allocated to more than one collection center. This requirement is considered in constraint (13). Vividly, a collection center that is not set-up and prepared can neither accept nor process any waste, which is demonstrated through constraint (14). Weights of the loads of waste being collected by vehicles and processed in collection centers are calculated through constraints (15), (16). The cumulative amount of wastes being carried by a vehicle into each node is calculated via constraint (17). Application of constraints (18), (19) results in no vehicles being allowed to collect waste from the same location at the same time.

3.1. Linearization step

The only non-linear term is the product of two binary variables of $z_{\mathit{vijt}}$ and ${\theta }_{\mathit{vk}}$ in the first objective function. Therefore, a new binary variable, i.e., $\theta z_{\mathit{vkijt}}$, is introduced to replace the non-linear product of $z_{\mathit{vijt}}$ and ${\theta }_{\mathit{vk}}$in the first objective function. Thus, the linear first objective function is as follows.

$$\begin{array}{c}\mathit{Min}{Z}_1=\sum _v\mathit{ve}{h}_v^{\mathit{cost}}\times y_v+\sum _k\mathit{co}{l}_k^{\mathit{cost}}\times x_k+\sum _{w,v,k,i,t}\mathit{pro}{c}_{\mathit{wkt}}^{\mathit{col}}\times {\lambda }_{\mathit{wvkit}}+\\ fue{l}^{\mathit{cost}}\times \sum _{v,i>1,j>1,t}(fue{l}_v+fue{l}_v^{+}\times k{g}_{\mathit{vit}})\times di{s}_{\mathit{ij}}^{\mathit{dep}}\times z_{\mathit{vijt}}+\\ fue{l}^{\mathit{cost}}\times \sum _{v,i>1,k,t}\mathit{fue}{l}_v\times di{s}_{\mathit{ik}}^{\mathit{dep}-col}\times \theta z_{vk1it}+\\ fue{l}^{\mathit{cost}}\times \sum _{v,i>1,k,t}(fue{l}_v+fue{l}_v^{+}\times k{g}_{\mathit{vit}})\times di{s}_{\mathit{ik}}^{\mathit{dep}-col}\times \theta z_{vki1t}\end{array}$$ (21)

Constraint (21) enforces $\theta z_{\mathit{vkijt}}$ to one where both $z_{\mathit{vijt}}$ and ${\theta }_{\mathit{vk}}$are true.

$$\theta z_{\mathit{vkijt}}⩾z_{\mathit{vijt}}+{\theta }_{\mathit{vk}}-1$$ (22)

3.2. Multi-objective solution approach

Previous researchers have eagerly attempted to find the appropriate methods to solve multi-objective problems (Mardan et al., 2019, Pinto and Li, 2020, Sosa and Dhodiya, 2021; Atmayudha, Syauqi, & Purwanto, 2021). The goal programming method is one of the most popular methods in this regard (Zandkarimkhani et al., 2020). Every method consists of its advantages and merits. Regarding the goal programming method, it has been found that this method would be more efficient when there are several objective functions in this model; the behind it is for each one of the objective functions, one aspiration will be targeted. Considering this method, there will be an attempt to change the undesirable deviations regarding each objective function into the minimum level (Nasr et al., 2021). One important point that should be clearly considered in this method emphasizes that the aspiration levels must be exactly determined regarding the deterministic goal programming model; however, this parameter cannot be accurately determined for real world problems, mostly due to the uncertainty variable. One solution to this problem is employing the fuzzy theory, which incorporates uncertainty (Kim et al., 2000). Thus, we can consider the goal programming method be incorporated with the fuzzy theory to provide an efficient and practical approach in order to solve the problem goals in the presence of uncertainty (Nasr et al., 2021). The multi-objective solution approach, which is utilized in the current study for solving the multi-objective problem, is inspired by the method proposed by Nasr et al. (2021). The considered multi-objective solution approach is presented in the following sections.

Step 1: Defining the goals of the objective functions

At first, all decision-makers are asked to determine accurately the amounts and domains of each goal. In this regard, the optimal values of each objective function, obtained as the result of the optimization of the model regarding each individual objective function, are provided to decision-makers and then they are asked to assign each goal to its correspondent objective function in accordance with its obtained optimal value. Here, it is assumed that $Z_j^{\mathit{Max}}$ and $Z_i^{\mathit{Min}}$ indicate the optimal values of the maximization and minimization objective functions, respectively. Moreover,${\mathrm{\Phi }}_i$ and ${\mathrm{\Psi }}_j$ refer to their corresponding goals as the following:

$$Z_i^{\mathit{Min}}⩽{\mathrm{\Phi }}_i\forall i$$ (23)

$$Z_j^{\mathit{Max}}⩾{\mathrm{\Psi }}_j\forall j$$ (24)

There are two objective functions in the proposed model; both are of the minimization type, so there will be:

$$Z_i^{\mathit{Min}}⩽{\mathrm{\Phi }}_i\to \left\{\begin{array}{c}{Z}_1^{\mathit{Min}}⩽{\mathrm{\Phi }}_1\\ Z_2^{\mathit{Min}}⩽{\mathrm{\Phi }}_2\end{array}\right)$$ (25)

Step 2: Implementation of the goals of the programming model

In this step, the proposed model is indicated in the form of the model of the goal programming in the following way:

$$\underset{i}{\mathit{Min}}{\xi }_i^{+}$$ (26)

s.t.

$$Z_i-{\xi }_i^{+}+{\xi }_i^{-}={\mathrm{\Phi }}_i\forall i$$ (27)

$$\mathit{System}constraints$$

in which, ${\xi }_i^{+}$ shows the goals' positive deviations, and ${\xi }_i^{-}$ indicates the corresponding negative deviations.

Step 3: Converting the bi-objective model into a single objective one

Here, for converting the bi-objective model into a single-objective one, the method proposed by Tavana et al. (2020) was utilized in the current study.

Notations

${\xi }_i^{\mathit{up}+}$	Upper bound of${\xi }_i^{+}$
${\xi }_i^{\mathit{low}+}$	Lower bound of${\xi }_i^{+}$
${\mu }_i$	Membership function of${\xi }_i^{+}$
$w_i$	Weight of${\mu }_i$

Mathematical model

$$\mathit{Max}\sum _i{w}_i\times {\mu }_i$$ (28)

$$s.t.$$

$${\mu }_i⩽\frac{{\xi }_i^{\mathit{up}+}-{\xi }_i^{+}}{{\xi }_i^{\mathit{up}+}-{\xi }_i^{\mathit{low}+}}\forall i$$ (29)

$$Z_i-{\xi }_i^{+}+{\xi }_i^{-}={\mathrm{\Phi }}_i\forall i$$ (30)

$$\mathit{System}constraints$$

Therefore, using a newly developed fuzzy goal programming approach, the multi-objective model, which has been proposed in the current study, was converted into a single-objective model.

4. Case study

It has been almost 18 months since the first patient was diagnosed with COVID-19 in Wuhan. During this time, many efforts have been made to prevent the outbreak of this virus (Govindan et al., 2020, Hellewell et al., 2020, Chowdhury et al., 2021). Unfortunately, up to now (June 30, 2021), more than 184 million people have been infected with the virus, out of whom about 3.94 million cases have died. The discovery of various vaccines, including Pfizer-BioNTech, Oxford-AstraZeneca, and others, promises the eradication of the virus in the near future. However, it is noteworthy that the virus has changed over time and, recently, two specific types of this mutated virus (i.e., one in the United Kingdom and the other in South Africa) have been approved by the World Health Organization (WHO), known as the N501Y mutation. This mutation in the virus has reduced the efficiency of some vaccines and brought about the inefficiency of many vaccines. In addition, the mutated type of the virus has a higher outbreak and infection rate. The spread of the mutated form of the virus, on the one hand, and the limited access to vaccines, on the other hand, has led to an increase in the number of infected people, especially in developing countries. In Iran, this issue has resulted in an increase in the number of patients, as well. In this regard, in cities where the number of patients has increased sharply, the government has set up temporary hospitals to provide COVID-19 patients with necessary services to supplement the work of existing hospitals. A lack of management of wastes produced in these temporary hospitals can occasion more acute conditions because these hospitals have been set up in residential areas. Accordingly, the pollution caused by their wastes is a serious danger to the residents of these areas.

4.1. Data gathering

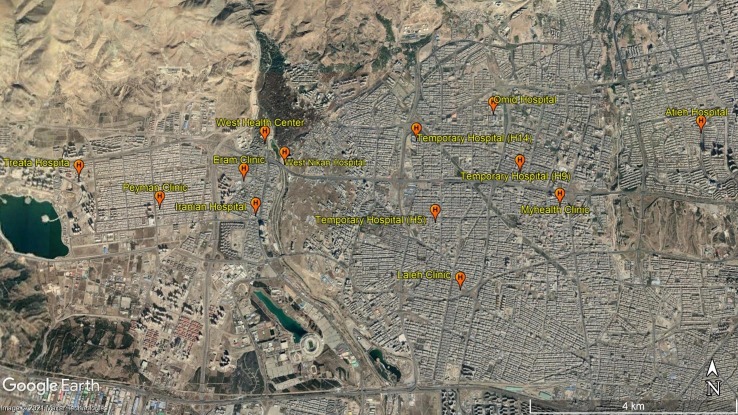
The performance of the proposed model is evaluated in this section using the data related to 13 hospitals, temporary hospitals, and healthcare centers in the west of Tehran. Among the 13 waste generating nodes, 8 provide healthcare services to patients with COVID-19. Hospital wastes are also divided into 5 categories, including paper waste, non-infectious plastic waste, infectious plastic waste, metal waste, and glass waste, out of which infectious plastic and metal waste are included in the category of hazardous wastes. It should be noted that the amount of generated waste has been collected over a period of one month in this study. Each week is considered as a time period and waste collection from production centers was done on a daily basis. To collect data every day during each week, a uniform distribution was used wherein the lower limit represents the lowest amount and the upper limit represents the highest amount of waste generated per week. Also, the loading time of the waste in the waste generation nodes has been considered as a function of the amount of generated waste. Since the proposed model is a strategic-operational model, it has been implemented at the beginning of each time period (beginning of each week). The results are then applied to all days of the week, and the model must be run again with new data every week. Fig. 2 shows the geographical location of 12 waste generating nodes and 3 potential collection centers.

Fig. 2.

Geographical location of waste production nodes.

The set-up costs of collection centers are presented in Table 2 . For example, the number 265,000 in the first row and first column of this table indicates that the cost of setting up collection center 1 (Shamsabad) is $265,000.

Table 2.

Set-up costs of collection centers.

Collection centers	$c=1$(Shamsabad)	$c=2$(Chitgar)	$c=3$(Makhsoos)	Unit
${\eta }_c^{\mathit{CST}-CL}$	265,000	244,000	238,000	Dollar ($)

The processing costs of waste in the collection centers for each time period are presented in Table 3 . The capacity of all three potential collection centers has been considered large enough that each center alone has the capacity to collect all the waste. However, the distance of these centers from the waste-generating factories, the processing cost, and the cost of setting up the centers can distinguish them from each other. For example, as it can be seen, Chitgar collection center has a higher operating cost than Makhsoos collection center, but it has lower transportation and processing costs due to its proximity to waste generating plants and proximity to the city.

Table 3.

Processing cost of waste in each collection center.

${\varpi }_{\mathit{wct}}$($)	$t=1,2,3and4$
	$c=1$	$c=2$	$c=3$
$w=1$	1360	1385	1480
$w=2$	1435	1450	1575
$w=3$	1285	1305	1410
$w=4$	1210	1240	1315

Table 4 states that the features provided by maps.google.com are used to calculate the geographical and time distances and resident population between nodes. For example, the distance between Omid and Atieh hospitals is 8.5 km, which maps.google.com calculates.

Table 4.

Geographical and time distance and population between nodes.

Parameters	Value	Unit
${\alpha }_{\mathit{mn}}$	maps.google.com	Kilometer
${\beta }_{\mathit{mc}}$	maps.google.com	Kilometer
${\alpha }_{\mathit{vmn}}^{\mathit{TM}}$	maps.google.com	Minute
${\beta }_{\mathit{vmc}}^{\mathit{TM}}$	maps.google.com	Minute
${\psi }_{\mathit{mn}}$	maps.google.com	Person

Vehicle characteristics, including capacity, fuel consumption, and purchase cost, are shown in Table 5 . For example, the number 4.5 in the first row and first column of this table indicates that the capacity of vehicle 1 is equal to 4.5 tons.

Table 5.

Data related to vehicles.

Vehicle	v = 1	v = 2	v = 3	v = 4	v = 5	v = 6	Unit
${\xi }_v^{\mathit{CP}-VH}$	4.5	4.5	3.5	3.5	3	3	Ton
${\eta }_v^{\mathit{CST}-VH}$	12,200	12,200	12,000	12,000	11,500	11,500	$
$F{C}_v$	0.167	0.167	0.151	0.151	0.149	0.149	Litre/Km
$\mathit{EF}{C}_v$	0.19 × 10-3	0.19 × 10-3	0.17 × 10-3	0.17 × 10-3	0.16 × 10-3	0.16 × 10-3	Litre/Km

Table 6, Table 7, Table 8, Table 9, Table 10 show the uniform distribution function to simulate the amount of waste produced by each node. For example, U(28,35) in the second row and the first column of Table 6 represents the amount of paper waste produced by node 2 (Atieh hospital). Because node 1 is considered the collection center, the amount of waste produced by this node is considered zero.

Table 6.

The amount of paper waste produced by each node.

Node	t = 1	t = 2	t = 3	t = 4
Collection center (m = 1)	0	0	0	0
Atieh hospital (m = 2)	U(28,35)	U(34,39)	U(18,21)	U(22,28)
Eram clinic (m = 3)	U(35,42)	U(44,48)	U(19,25)	U(33,39)
Iranian hospital (m = 4)	U(14,18)	U(23,38)	U(10,13)	U(44,46)
Laleh clinic (m = 5)	U(40,50)	U(45,50)	U(25,27)	U(55,58)
Myhealth clinic (m = 6)	U(69,75)	U(73,88)	U(36,40)	U(49,54)
Omid hospital (m = 7)	U(21,27)	U(34,39)	U(16,19)	U(26,31)
Peyman clinic (m = 8)	U(33,35)	U(40,43)	U(23,27)	U(21,27)
H5 (m = 9)	U(18,26)	U(33,36)	U(9,12)	U(22,25)
H9 (m = 10)	U(44,52)	U(50,53)	U(30,32)	U(33,38)
H14 (m = 11)	U(22,26)	U(29,35)	U(18,21)	U(26,32)
Treata hospital (m = 12)	U(44,53)	U(61,66)	U(25,29)	U(41,46)
West health center (m = 13)	U(26,33)	U(32,37)	U(18,22)	U(30,35)
West Nikan hospital (m = 14)	U(10,17)	U(23,37)	U(8,9)	U(27,29)

U denotes uniform distribution; m = 1 is considered as collection center.

Table 7.

The amount of non-infectious plastic waste produced by each node.

	t = 1	t = 2	t = 3	t = 4
m = 1	0	0	0	0
m = 2	U(90,110)	U(108,116)	U(88,94)	U(74,79)
m = 3	U(105,118)	U(123,134)	U(98,106)	U(83,88)
m = 4	U(73,91)	U(88,94)	U(100,107)	U(64,70)
m = 5	U(116,124)	U(109,118)	U(78,84)	U(80,85)
m = 6	U(125,133)	U(145,148)	U(90,95)	U(73,79)
m = 7	U(82,90)	U(96,105)	U(101,110)	U(65,69)
m = 8	U(75,82)	U(87,93)	U(113,119)	U(59,66)
m = 9	U(43,50)	U(67,75)	U(84,93)	U(47,50)
m = 10	U(94,102)	U(99,108)	U(38,44)	U(62,68)
m = 11	U(55,60)	U(64,78)	U(77,80)	U(60,65)
m = 12	U(64,71)	U(50,56)	U(94,100)	U(83,85)
m = 13	U(49,56)	U(87,95)	U(66,73)	U(58,64)
m = 14	U(44,49)	U(39,46)	U(50,55)	U(72,79)

Table 8.

The amount of infectious plastic waste produced by each node.

	t = 1	t = 2	t = 3	t = 4
m = 1	0	0	0	0
m = 2	U(145,170)	U(111,118)	U(93,98)	U(123,126)
m = 3	U(122,138)	U(104,110)	U(87,91)	U(93,99)
m = 4	U(114,123)	U(89,96)	U(76,85)	U(102,106)
m = 5	U(151,165)	U(130,136)	U(92,99)	U(105,111)
m = 6	U(182,193)	U(141,144)	U(100,104)	U(83,88)
m = 7	U(162,179)	U(129,135)	U(87,91)	U(116,122)
m = 8	U(131,141)	U(100,108)	U(104,108)	U(98,103)
m = 9	U(125,135)	U(100,104)	U(107,115)	U(118,123)
m = 10	U(139,150)	U(84,90)	U(114,119)	U(74,80)
m = 11	U(94,99)	U(65,69)	U(77,79)	U(91,95)
m = 12	U(75,102)	U(111,116)	U(92,97)	U(84,88)
m = 13	U(108,120)	U(105,110)	U(83,87)	U(95,100)
m = 14	U(100,113)	U(82,87)	U(90,95)	U(72,79)

Table 9.

The amount of metal waste produced by each node.

	t = 1	t = 2	t = 3	t = 4
m = 1	0	0	0	0
m = 2	U(15,20)	U(22,26)	U(30,33)	U(18,22)
m = 3	U(23,26)	U(31,35)	U(13,17)	U(18,21)
m = 4	U(27,34)	U(37,40)	U(21,25)	U(19,22)
m = 5	U(18,25)	U(22,25)	U(33,36)	U(40,43)
m = 6	U(32,36)	U(28,31)	U(19,25)	U(13,17)
m = 7	U(15,19)	U(29,33)	U(20,22)	U(24,28)
m = 8	U(40,49)	U(37,42)	U(14,19)	U(25,29)
m = 9	U(38,45)	U(30,33)	U(23,27)	U(19,22)
m = 10	U(13,16)	U(24,28)	U(17,24)	U(21,28)
m = 11	U(22,26)	U(25,27)	U(19,23)	U(33,36)
m = 12	U(30,35)	U(39,43)	U(11,16)	U(21,28)
m = 13	U(27,34)	U(33,36)	U(20,22)	U(24,29)
m = 14	U(9,12)	U(15,18)	U(31,34)	U(32,37)

Table 10.

The amount of glass waste produced by each node.

	t = 1	t = 2	t = 3	t = 4
m = 1	0	0	0	0
m = 2	U(25,30)	U(27,31)	U(26,33)	U(18,22)
m = 3	U(72,78)	U(80,04)	U(54,62)	U(52,56)
m = 4	U(31,36)	U(44,48)	U(20,24)	U(39,43)
m = 5	U(40,45)	U(51,55)	U(17,20)	U(25,29)
m = 6	U(38,46)	U(43,49)	U(21,25)	U(19,22)
m = 7	U(24,29)	U(35,38)	U(19,24)	U(42,46)
m = 8	U(18,23)	U(25,30)	U(11,15)	U(31,37)
m = 9	U(21,24)	U(29,34)	U(23,28)	U(25,30)
m = 10	U(18,23)	U(22,28)	U(14,17)	U(27,30)
m = 11	U(39,43)	U(31,35)	U(16,20)	U(24,26)
m = 12	U(19,25)	U(28,30)	U(24,28)	U(11,14)
m = 13	U(16,19)	U(20,26)	U(29,31)	U(30,35)
m = 14	U(25,28)	U(23,29)	U(18,22)	U(34,37)

4.2. Results

In this section, using case study data, the performance of the proposed model is evaluated. For this purpose, we convert the bi-objective model to a single objective one by the proposed fuzzy goal programming approach. To this end, goal 1 is considered $500,000 and goal 2 is 800,000 people, respectively. The single objective model is as follows:

$$\mathit{Max}{w}_1\times {\mu }_1+w_2\times {\mu }_2$$ (31)

$$s.t.$$

$${\mu }_1⩽\frac{718,675-{\xi }_1^{+}}{718,675}$$ (32)

$${\mu }_2⩽\frac{153,637-{\xi }_2^{+}}{153,637}$$ (33)

$$\begin{array}{c}{Z}_1=\sum _v\mathit{ve}{h}_v^{\mathit{cost}}\times y_v+\sum _k\mathit{co}{l}_k^{\mathit{cost}}\times x_k+\sum _{w,v,k,i,t}\mathit{pro}{c}_{\mathit{wkt}}^{\mathit{col}}\times {\lambda }_{\mathit{wvkit}}+\\ fue{l}^{\mathit{cost}}\times \sum _{v,i>1,j>1,t}(fue{l}_v+fue{l}_v^{+}\times k{g}_{\mathit{vit}})\times di{s}_{\mathit{ij}}^{\mathit{dep}}\times z_{\mathit{vijt}}+\\ fue{l}^{\mathit{cost}}\times \sum _{v,i>1,k,t}\mathit{fue}{l}_v\times di{s}_{\mathit{ik}}^{\mathit{dep}-col}\times \theta z_{vk1it}+\\ fue{l}^{\mathit{cost}}\times \sum _{v,i>1,k,t}(fue{l}_v+fue{l}_v^{+}\times k{g}_{\mathit{vit}})\times di{s}_{\mathit{ik}}^{\mathit{dep}-col}\times \theta z_{vki1t}\end{array}$$ (34)

$$Z_2=\sum _{v,m,n,t}P{R}_{\mathit{vt}}\times {\psi }_{\mathit{mn}}\times h{f}_{\mathit{vmt}}$$ (35)

$$Z_1-{\xi }_1^{+}+{\xi }_1^{-}=500,000$$ (36)

$$Z_2-{\xi }_2^{+}+{\xi }_2^{-}=800,000$$ (37)

$$\mathit{Constraints}(3)to(20)andConstraint(22)$$

The optimal values of decision variables and objective functions are obtained by running the single objective model in GAMS software using CPLEX solver, which are given below ($w_1$ and $w_2$ are considered 0.7 and 0.3, respectively):

• •The first and second objective functions' optimal values are $672,528 and 842,293 people, respectively.
• •The Chitgar's collection center is set up.
• •Vehicles 1, 3, 4, 5, and 6 are purchased.
• •The routes traveled by vehicles in each scenario are presented in Table 11 .

Table 11.

The routes traveled by vehicles in each time period.

Vehicle	Time period	Routes
$v=1$	$t=1$	$\mathit{Chitgar}\to m=13\to m=14\to m=3\to m=8\to m=12\to Chitgar$
	$t=2$	$\mathit{Chitgar}\to m=2\to m=6\to m=10\to m=11\to m=7\to Chitgar$
	$t=3$	$\mathit{Chitgar}\to m=13\to m=14\to m=3\to m=8\to m=12\to Chitgar$
	$t=4$	$\mathit{Chitgar}\to m=2\to m=6\to m=10\to m=11\to m=7\to Chitgar$
$v=3$	$t=1$	$\mathit{Chitgar}\to m=12\to m=8\to m=5\to m=3\to Chitgar$
	$t=2$	$\mathit{Chitgar}\to m=6\to m=8\to Chitgar$
	$t=3$	$\mathit{Chitgar}\to m=12\to m=8\to m=5\to m=3\to Chitgar$
	$t=4$	$\mathit{Chitgar}\to m=5\to m=3\to m=8\to m=12\to Chitgar$
$v=4$	$t=1$	$\mathit{Chitgar}\to m=5\to m=6\to Chitgar$
	$t=2$	$\mathit{Chitgar}\to m=5\to m=3\to m=8\to m=12\to Chitgar$
	$t=3$	$\mathit{Chitgar}\to m=5\to m=6\to Chitgar$
	$t=4$	$\mathit{Chitgar}\to m=6\to m=8\to Chitgar$
$v=5$	$t=1$	$\mathit{Chitgar}\to m=10\to m=11\to m=7\to Chitgar$
	$t=2$	$\mathit{Chitgar}\to m=6\to m=5\to m=9\to m=4\to Chitgar$
	$t=3$	$\mathit{Chitgar}\to m=10\to m=11\to m=7\to Chitgar$
	$t=4$	$\mathit{Chitgar}\to m=13\to m=3\to m=8\to m=12\to Chitgar$
$v=6$	$t=1$	$\mathit{Chitgar}\to m=6\to m=5\to m=9\to m=4\to Chitgar$
	$t=2$	$\mathit{Chitgar}\to m=5\to m=9\to m=14\to m=4\to Chitgar$
	$t=3$	$\mathit{Chitgar}\to m=13\to m=3\to m=8\to m=12\to Chitgar$
	$t=4$	$\mathit{Chitgar}\to m=5\to m=9\to m=14\to m=4\to Chitgar$

The routes traveled by each vehicle in each time period are presented in Table 11. For example, the first row of this table states that vehicle 1, in time period 1, starts from the Chitgar collection center and first goes to the West health center. After collecting waste from this node, it visits West Nikan hospital, Eram clinic, Peyman clinic, and Treata hospital, respectively, and finally returns to Chitgar collection center. It should be noted that this vehicle only collects hazardous wastes of these nodes (as mentioned earlier, nodes with COVID-19 patients are all hazardous). It is noteworthy that vehicles 1, 5, and 6 are allocated to collect either hazardous wastes or wastes from nodes containing COVID-19 wastes, and non-hazardous wastes are collected by vehicles 3 and 4. The second objective function prevents hazardous and non-hazardous wastes from being placed in a vehicle simultaneously. In other words, if the importance (weight) of the second objective function is reduced or the second objective function is eliminated, it is possible for hazardous and non-hazardous waste to be placed next to each other in vehicles. Although this reduces the number of vehicles purchased and chain costs, it potentially generates the infection of non-hazardous wastes and increases the volume of hazardous wastes, posing severe risks to the environment and the community. Another noteworthy point is that by not considering the scheduling constraints (i.e., constraints 17 and 18), the routes traveled by the vehicles will be shortened, and this will lead to reduced emissions and chain costs. However, it increases the waiting time of vehicles in the nodes, and increasing the waiting time of vehicles carrying hazardous waste increases the risk of hazardous waste emissions, so considering scheduling constraints, while it may lead to increased costs, the health of the community people and the protection of the environment is more assured.

5. Discussion

This paper presented a novel bi-objective mathematical programming model for medical waste management during the COVID-19 outbreak. The investigation of the literature shows that although this problem has been studied previously in papers such as Kargar et al., 2020, Tirkolaee et al., 2021, this paper pursues a different vision of the issue. Hence, according to the best of our knowledge, for the first time, this paper has considered factors such as separation of infectious wastes from non-infectious wastes in the process of collection by vehicles, reduction of waiting time for vehicles to enter waste production nodes, and failure of vehicles carrying hazardous (infectious) wastes for managing medical waste during COVID-19 outbreak. Considering these assumptions leads to results that can be useful for decision-makers. For example, the results showed that vehicles with a lower probability of failure (higher reliability) were assigned to collect infectious wastes, and vehicles with lower reliability were allocated to collect non-infectious wastes. The second objective function also caused infectious and non-infectious wastes to be separated from each other and not loaded into a vehicle simultaneously. Another noteworthy point is that vehicles' waiting time to enter the wastes production nodes for vehicles carrying infectious wastes was zero, which also indicates the effectiveness and efficiency of the proposed model. In order to increase robustness of the optimum solution, the following points should be considered:

• •In the proposed model, a parameter called the failure probability of vehicles is defined and included in the second objective function to increase the robustness of the understudy supply chain network. This leads to allocate vehicles that have higher reliability to collect infectious waste.
• •One factor that increases the probability of disruption in the network is assigning loads in excess of the capacity of the centers and vehicles. For this purpose, the capacity of centers and vehicles is defined deterministically to increase the robustness of the supply chain network under consideration.
• •One of the practical strategies in collecting hazardous waste is collecting waste during low traffic hours. Observations made in the understudy supply chain show that the transfer time between the two desired hospitals, during low traffic hours, is almost the same in different periods and has a maximum variance of 4%. Accordingly, in the proposed model, to provide service at certain times (low traffic hours), a parameter called time window is defined, which leads to increased robustness of the supply chain network.

6. Sensitivity analysis

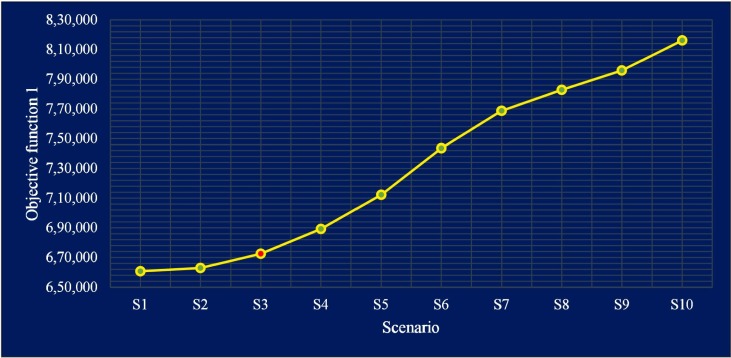
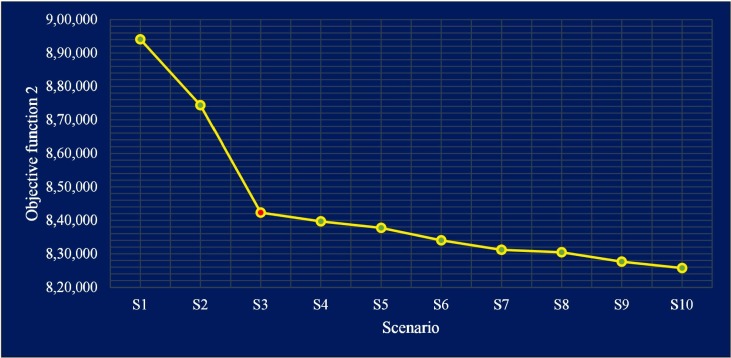
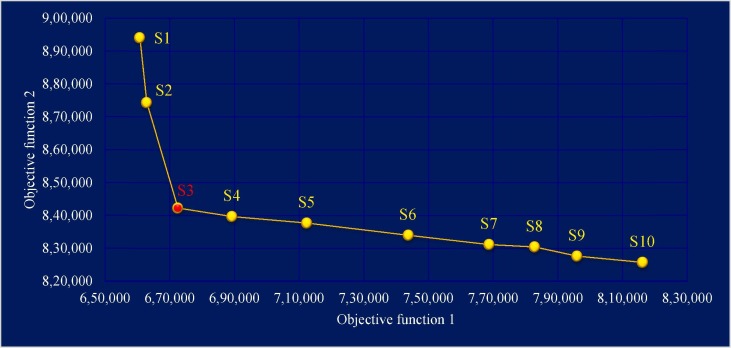
This section aims to investigate the accuracy of the behavior and performance of the proposed model and create a Pareto frontier using different scenarios. A sensitivity analysis of objective function coefficients allows decision-makers to access compromise solutions without relying on extreme points. It is expected that by increasing and decreasing the coefficient of an objective function, this objective function's value does not get worse or better, respectively. Table 12 represents the scenarios and objective functions values for each scenario. Also, in Fig. 3, Fig. 4 , the first and second objective functions values for each scenario are illustrated, respectively. The Pareto frontier obtained from different scenarios is also shown in Fig. 5 .

Table 12.

The objective functions value obtained from each scenario.

Scenario	$w_1$	$w_2$	Objective function 1	Objective function 2
S1	0.8	0.2	660,738	894,092
S2	0.75	0.25	662,882	874,333
S3 (Case study)	0.7	0.3	672,528	842,293
S4	0.65	0.35	689,245	839,691
S5	0.6	0.4	712,314	837,725
S6	0.55	0.45	743,636	834,006
S7	0.5	0.5	768,701	831,169
S8	0.45	0.55	782,824	830,444
S9	0.4	0.6	795,905	827,637
S10	0.35	0.65	816,176	825,734

Fig. 3.

The first objective function value for each scenario.

Fig. 4.

The second objective function value for each scenario.

Fig. 5.

Pareto frontier obtained from sensitivity analysis of objective function's coefficients.

As shown in Table 12, by increasing the first objective function's coefficient and simultaneously decreasing the coefficient of the second objective function, the values of the first and second objective functions decreased and increased, respectively, and vice versa. These results indicate the correct performance and logical behavior of the proposed model and solution approach. The Pareto frontier presented in Fig. 5 also allows decision-makers to make optimal decisions according to the real world's requirements. Decision-makers who care about the health of people in the community do not pay attention to costs and choose scenarios that have the lowest risk to the population at risk of infection, but uncommitted decision-makers, regardless of the population at risk, choose the scenarios that impose the least costs to the chain.

7. Managerial implications

This paper presents a flexible and practical model for medical waste management during the COVID-19 pandemic. The results of the proposed model help managers and decision-makers to adopt a scenario that imposes the least risk to the network given the budget. One of the unique features of this model is the consideration of reliability for vehicles. This issue leads to transfer infectious waste by highly reliable vehicles; in this case, the risk of population exposure to pollution is reduced. Also, to make appropriate decisions, decision-makers can identify low traffic hours and set a specific time window for collecting waste to increase the chain's efficiency and to reduce the fuel consumption of vehicles because traffic leads to increased fuel consumption. In addition, vehicle scheduling reduces vehicle waiting time on waste generation nodes, reducing population risk and vehicle fuel consumption. Due to its comprehensiveness, the proposed model is highly flexible and can be implemented in other supply chain networks by applying minor changes. For example, the proposed model can be used to collect hazardous industrial materials. Also, by eliminating the second objective function and constraint (20), the proposed model becomes a more general and flexible model that can be used to manage MSW and even purchase products from suppliers or collect returned products from customers to be used.

8. Conclusions and future research directions

Medical waste management during COVID-19 outbreak is of great importance; its inefficient management, in addition to harming the environment, also endangers human lives. Therefore, this paper presents a bi-objective MILP model for managing both infectious and non-infectious waste under uncertainty. The proposed model aims to minimize total costs and risk of population exposure to pollution simultaneously, and a fuzzy goal programming approach was used to solve this model. The location-routing problem, vehicles scheduling, load-dependent fuel consumption, split delivery, population risk, and time window are some of the practical assumptions of the proposed model. For better management of medical wastes, factors such as separation of infectious wastes from non-infectious wastes in the process of collection by vehicles, reduction of waiting time for vehicles to enter wastes production nodes, and failure of vehicles carrying infectious wastes for the first time in this paper was considered. Finally, the validation of the proposed model and solution approach was evaluated using Tehran municipality actual data.

In addition to its advantages, each paper suffers from some limitations that may pave the way for future research. Accordingly, some of the following researches are suggested:

• •Adding treatment, recycling, and disposal centers to the proposed network;
• •Considering social issues such as job creation in order to design a sustainable network for medical waste management;
• •Developing a meta-heuristic or heuristic algorithm for solving proposed problem in large scales and using big data (Govindan and Gholizadeh, 2021).

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.