Evolutionary and functional lessons from human-specific amino acid substitution matrices

Abstract

Human genetic variation in coding regions is fundamental to the study of protein structure and function. Most methods for interpreting missense variants consider substitution measures derived from homologous proteins across different species. In this study, we introduce human-specific amino acid (AA) substitution matrices that are based on genetic variations in the modern human population. We analyzed the frequencies of >4.8M single nucleotide variants (SNVs) at codon and AA resolution and compiled human-centric substitution matrices that are fundamentally different from classic cross-species matrices (e.g. BLOSUM, PAM). Our matrices are asymmetric, with some AA replacements showing significant directional preference. Moreover, these AA matrices are only partly predicted by nucleotide substitution rates. We further test the utility of our matrices in exposing functional signals of experimentally-validated protein annotations. A significant reduction in AA transition frequencies was observed across nine post-translational modification (PTM) types and four ion-binding sites. Our results propose a purifying selection signal in the human proteome across a diverse set of functional protein annotations and provide an empirical baseline for interpreting human genetic variation in coding regions.

INTRODUCTION

The study of population genetic variation has led to countless scientific and medical applications. Illustrative examples include tracing of ancient migration patterns, estimating the pathogenicity of genetic variants, identifying functional elements in the genome, and assessing the adaptivity and conservation of genes and other genomic regions (1–3). Such inquiries are predicated on robust background models for the dynamics of genetic variation, which are expected to accurately capture the propensities of different genetic variants in various contexts (4,5). For example, a common way to identify functional elements in the genome is to quantify evolutionary conservation, namely a deviation from the expected dynamics of genetic variation. Deciding whether the variants observed in a genomic region deviate from the expected dynamics is dependent on the propensities assigned to these types of variants under the background model. A background model for single-nucleotide variants (SNVs) in coding regions should be able to describe the probabilities of synonymous and nonsense alterations (6,7), as well as all the different types of missense variants (8). Models of genetic variation in coding regions are also useful for estimating the functional damage caused by variants in these regions (9). Indeed, most prediction algorithms that estimate the damage or pathogenicity of variants (e.g. SIFT, Polyphen2 and CADD) rely on such background propensities (10–12). Although variant evaluation tools are heavily used in clinical settings to assess the impact of mutations on human diseases (13–15), the background propensities on which they rely are usually based on long-term cross-species evolution and are not optimized for variants within humans (16–19).

Many models of genetic variation dynamics are based on molecular clocks, which attempt to capture the time spans per mutation events (20,21). However, unlike in other model organisms, time-based mutation rates are challenging to estimate in humans, due to the lack of controlled environments and complex population and reproduction patterns (e.g. migration, admixture, ancestral population-structure, parental age and generation time) (22,23, Rahbari, 2016 #641,24,25). To overcome these challenges, an attempt to estimate human mutation rates was made by counting de novo mutations within parent-child samples. However, the short timescale of such analyses (up to a few generations) mostly ignores the effects of natural selection (26,27). An alternative approach, which circumvents most of these challenges, is to ignore the timescales of mutation events and focus instead on their relative probabilities.

Traditionally, studies of genetic variation dynamics in coding regions make use of amino acid (AA) substitution matrices such as PAM and BLOSUM (28–30). These matrices score AA substitutions by their likelihood (or likelihood ratio), as derived from empirical observations. Specifically, these classic matrices rely on multiple sequence alignment (MSA) of evolutionarily related homologous sequences across species (31) for the deduction of substitution propensities. Notably, a minor error was observed in the compilation of the original BLOSUM matrices (32), and attempts to correct the matrices showed slightly improved performance with respect to homology search (33). Nevertheless, the original BLOSUM62 is still the de facto standard and the default substitution matrix used across protein database searches (e.g. in BLAST), sequence alignment and other bioinformatics tools (31,34–36). In the past 40 years, numerous other substitution matrices have been developed to overcome many of the limitations of PAM and BLOSUM, or to address specific tasks such as the identification of remote homologies (37,38), various genomic or protein regions (e.g. protein domains) (39,40) or different types of proteins (e.g. membrane proteins, enzymes, etc.) (41).

AA substitution matrices also indirectly capture the chemical and biophysical properties of AA and are thus heavily used in the study of protein evolution (42,43). However, since existing matrices are all based on cross-species homology, they are not optimized for human-centric studies. Additionally, current cross-species AA substitution matrices lack directionality (i.e. they do not distinguish between substitution of a first AA to a second AA from a substitution of the second to the first).

The exponential growth in the number of whole-genome and whole-exome sequences, including that of healthy humans (3,44, Fu, 2013 #637), provides an opportunity to form a robust human-specific background model of genetic variation. To this end, we exploited a rich collection of >7M polymorphic sites in the exomes of over 60 000 unrelated, healthy individuals extracted from the Exome Aggregation Consortium (ExAC) (44). From this comprehensive dataset, we constructed a set of human-specific substitution matrices. These matrices provide a solid baseline for genetic and proteomic variation, which may be used for deriving evolutionary and functional insights. We analyze the information contained in our matrices and compare them to the classic matrices. We further used the developed methodology to expose protein-functional constraints, as reflected by post-translational modification (PTM) and ion-binding sites. We provide the community with a generic framework for utilizing aggregated genetic variation data to produce substitution matrices for a broad range of genetic, functional and evolutionary tasks.

MATERIALS AND METHODS

Data

To construct human-specific codon and AA substitution matrices, we combined genetic variation data with annotations of coding genes. Human genetic variants were extracted from ExAC (44), which provides a good combination of quantity and quality of genetic data in the human population. While ExAC is biased towards individuals of European ancestry, it also includes other ethnicities. Specifically, the distribution of ethnic groups in ExAC is: 36% Finnish, 36% Non-Finnish European, 10% South Asian, 7% African or African American, 6% Native American, 5% East Asian and 1% Others. Importantly, the cohort of ExAC was chosen to minimize bias of pathogenic variants, by excluding individuals with rare genetic diseases. We treat each variant as a substitution from the major allele, defined as the most frequent allele in the population, to the minor allele, which is any other allele observed in the specific exomic location.

Functional gene annotations were based on the UniProt database and the GENCODE project. The exact procedure of combining genetic and proteomic annotations is described in (45). Briefly, we used version 19 of GENCODE (compatible with version GRCh37 of the human reference genome, which was used by ExAC). We recovered the DNA sequences of the genes annotated in GENCODE using UCSC’s reference genome. We considered only the protein-coding regions of genes (annotated as ‘CDS’ in GENCODE). Protein sequences and protein annotations (e.g. PTMs) were taken from UniProt for all 20 168 reviewed human proteins (from the SwissProt section). We only considered the GENCODE gene isoforms identical to the primary UniProt protein sequences. We discarded genes that failed this exact one-to-one mapping, ending up with 18 115 successfully mapped genes. These combined genetic-proteomic gene entities allowed us to determine the protein-level consequences of genetic variants (e.g. synonymous, missense or nonsense). This pipeline is available as an independent open-source Python library (https://github.com/nadavbra/geneffect).

ExAC recorded 8 307 864 high-quality genetic variants (with ethnic distribution as detailed above). From this dataset, 427 491 indels were removed. Of the remaining variants, 326 369 genomic positions contained multiallelic variants, which were counted as 631 985 nucleotide substitutions, contributing 305 616 additional variants. From this dataset, 82 991 nonsense variants were discarded. Of the 8 102 999 nucleotide substitutions, 4 693 538 were within the coding regions of the 18 115 mapped protein-coding genes and were interpreted as observed codon substitutions. Each substitution of codons differing by exactly one nucleotide was observed ∼9000 times on average (and at least 573 times across all codon pairs; the total counts per each codon pair is reported in Supplementary Dataset S1). The high number of observations, even for the rarest codon substitutions, ensures the robustness of the estimated codon-substitution probabilities to random noise.

PTMs and ion-binding site annotations

PTMs and ion-binding site annotations were extracted from UniProt, except for ubiquitination annotations, which were obtained from PhosphoSitePlus (46). For a small number of cases, PTM proteomic locations of variants mapped to locations on the reference genome coding for inappropriate AA. We discarded these instances. Importantly, both UniProt and Phosphosite annotations are supported by experimental evidence and literature support.

Constructing probabilistic substitution matrices from genetic variation in the human population

HC¹ (Human Codon substitution matrix to the power of 1) represents the estimated substitution probability of each pair of the 61 coding codons (i.e. excluding the three stop codons). Each non-diagonal entry of HC¹ was calculated by:

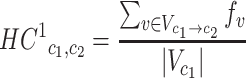(1)

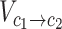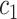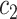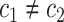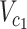Where denotes the set of all variants substituting codon to (), the set of all variants substituting 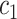to any codon (including a self-substitution), and 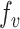the frequency of the 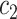allele in a variant 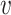substituting 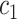to 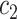(as derived from ExAC).

The diagonal values were calculated by:

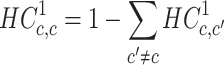(2)

We assumed the directionality of each variant to be from the major to the minor allele. In particular, we always have that 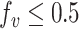. Note that the major allele is not always the reference allele (i.e. the allele matching the human reference genome). Specifically, this is not the case in ∼8% of the ∼5M processed variants. Since ExAC’s only offers aggregated data about each exomic position independently, this construction ignores possible dependences between variants.

The non-substitution (diagonal) values of the matrix complement the sum of each row to 1. This, along with the normalization in Equation (1), yields a row-stochastic matrix, meaning that each row 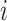of the matrix can be interpreted as the distribution of conditional substitution probabilities (from the 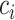codon to every other codon). Each entry, in turn, may be interpreted as the conditional probability of observing 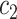in a genomic position where 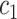is the major allele.

The amino acid substitution matrix HA¹ (Human Amino acid substitution matrix to the power of 1) is derived from HC¹ by considering codon frequencies:

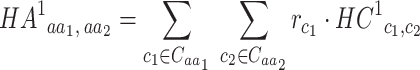(3)

Where 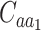and 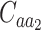denote the sets of codons that code for the AA 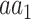and 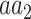, respectively, and 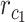is the frequency in which 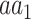is coded by the 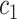codon, relative to all the codons of 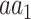(i.e. ).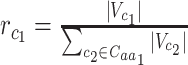

As with HC¹, an entry of HA¹ may be conceived as the conditional probability of observing AA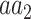 in a proteomic position in which 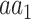is the major allele.

As HC¹ and HA¹ were generated through statistical analysis of single-nucleotide variations, substitutions between codons that differ in more than one nucleotide cannot be directly inferred. Since most codon pairs differ by more than one nucleotide, both HC¹ and HA¹ are sparse matrices. To estimate substitution frequencies between pairs of codons requiring multiple consecutive substitution events to transition between them, we treat HC¹ and HA¹ as the transition matrices of Markov chains. For every number of consecutive substitutions k, the k-th power matrices HC^k (Human Codon substitution matrix to the power of k) and HA^k (Human Amino acid substitution matrix to the power of k) represent the Markov chains that are the result of repeating the original Markov chains k times. To obtain a complete substitution matrix (i.e. with non-zero substitution probabilities for all possible substitutions), we chose to take HA¹ to the power of 3, since 3 is the lowest number of nucleotide substitutions required between each pair of coding-codons. The resulting matrix is denoted HA³.

Comparing the AA substitution model to a nucleotide substitution model

To examine to what extent our substitution matrix reflects evolutionary signals at the AA level, we compared it to a matrix derived from nucleotide substitution frequencies, HAN¹ (Human Amino Acid substitution matrix based on Nucleotide substitution probabilities to the power of 1), which we used as a simple background model. We first constructed a 4×4 nucleotide substitution matrix, HN¹ (Human Nucleotide substitution matrix to the power of 1), derived from the same set of variants used to construct HC¹. We then used this nucleotide-level matrix to derive an expected 61×61 codon substitution matrix, by considering the probability of a codon substitution to be the product of the probabilities of the single-nucleotide substitutions involved in that codon (e.g. the substitution of CTG to TTA was assigned the probability of C to T multiplied by the probability of T to T and the probability of G to A). This codon-level substitution matrix was then projected into a 20×20 AA substitution matrix, through the same process used to convert HC¹ to HA¹ (see previous section). The resulting AA-level matrix reflects the expected probabilities of AA substitutions given only the substitution preferences of single nucleotides while assuming a lack of evolutionary pressure at the level of codons or AA. By dividing the empirical HA¹ with this background model (entry-wise), we obtained the observed-to-expected probability ratios of all AA substitutions and could determine which AA substitutions show a substantial deviation from the background model. Additionally, we tested for statistical significance of each of the deviations by using the entries of HAN¹ as a background model for the observed probabilities in HA¹. Specifically, for each AA substitution, we considered the probability of that substitution (given the source AA) based on the corresponding entry in HAN¹. Based on this binomial distribution, we calculated the probability of obtaining the observed number of substitutions underlying HA¹ (i.e. 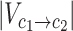) or more extreme deviations from the expected probability, resulting the reported p-values.

Deviation from symmetry

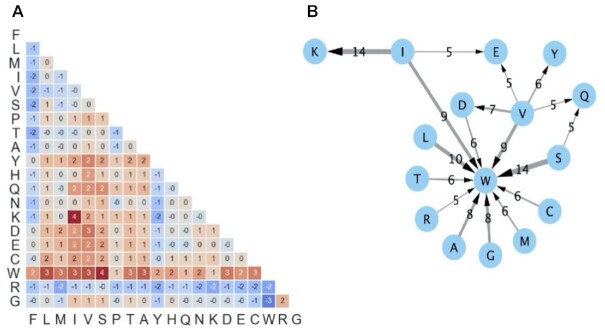
To quantify the strength of directionality observed in the substitution matrix, we measured the deviation of AA substitutions from symmetry by calculating the ratios between the conditional probabilities of substitutions to the conditional probabilities of the opposite substitutions. For example, the directionality of the substitution of lysine (K) to arginine (R) under HA³is measured by 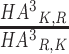. In other words, we divided HA³, entry-wise, by (HA³)^T. To enhance readability, the matrix shown in Figure 3A is lower triangular, and its entries are transformed by log₂. This means that positive entries signify substitutions that are preferred over their opposite substitution.

Figure 3.

Deviation from symmetry. (A) The asymmetry of an AA substitution is measured by the probability-ratio between each substitution and its opposite (shown in log2 scale). Probabilities are derived from a version of HA3 which does not include synonymous probabilities (so that each row represents the conditional probabilities of non-synonymous substitutions). (B) Network representation of AA substitutions that substantially deviate from symmetry (defined by a ratio of at least 5). For example, serine (S) is 14 times more likely to substitute into tryptophan (W) than the other way around. Wider arrows signify stronger asymmetry (i.e. higher ratios).

Comparison to BLOSUM and PAM

To compare our substitution models to the score matrices of BLOSUM, Spearman’s correlation coefficient (ρ) was measured for each row of HA³ with each corresponding row of the examined BLOSUM matrix (Figure 4). For each BLOSUM matrix, its average correlation with HA³ was used to summarize these measurements. Furthermore, to examine the effect of the power of the HA¹ matrix on these correlations, the average correlation coefficient was calculated for each BLOSUM version and different powers of HA¹. We compared our models to the original (uncorrected) BLOSUM matrices, since they are the standard matrices used in the field. Similar analyses were repeated for the PAM matrices.

Figure 4.

Comparison to the BLOSUM and PAM substitution matrices. (A) Spearman’s correlation coefficients (ρ) between the rows of HA³ and the corresponding rows of different versions of the BLOSUM matrices. For example, the rightmost bar refers to the consistency between the substitution probabilities of glycine (G) according to HA³ and the corresponding substitution scores according to BLOSUM₁₀₀. Dotted lines signify the average correlation coefficients across all AA. (B) Spearman’s correlation coefficients (ρ) between the rows of HA³ and the corresponding rows of different versions of the PAM matrices. (C) The average correlation coefficients between BLOSUM matrices and different powers of HA¹. Increasing powers of HA represent an increasing number of consecutive substitutions (which signify longer evolutionary timescales). (D) Average correlation coefficients between PAM matrices and different powers of HA¹.

Functional annotation analysis

To demonstrate the capacity of our human-specific substitution model to reflect protein functional annotations (Tables 1 and 2, Figure 5), we examined nine major PTMs (acetylation, hydroxylation, disulfide bond formation, methylation, N-linked glycosylation, O-linked glycosylation, phosphorylation, succinylation and ubiquitination; Table 1) and three types of ion-binding sites (zinc, magnesium and iron; Table 2). For each PTM or ion-binding site, we considered the set of variants at the annotated proteomic locations, and generated new codon and AA substitution matrices corresponding to that subset of variants (e.g. HA¹_iron-binding, HC³_{ubiquitination} etc.). These matrices were generated through the same method by which the global matrices (e.g. HA¹ and HC³) were constructed, and they differ only by the subset of used variants (within the ExAC dataset). To highlight the unique aspects of the substitution profiles for these functionally annotated sites, compared to unannotated sites (Figure 5), each annotation-specific matrix was divided by its corresponding non-annotation matrix, element-wise (i.e. the matrix derived from all the other variants).

Table 1.

Statistically significant AA substitutions in PTM sites

PTM annotation	From AA	To AA	# sub. w/ annotation	# sub. w/o annotation	# variants FDR q-value	AF FDR q-value	Trenda
Acetylation	A	A	212	1 54 569	1.94E-02		E
	A	T	51	91 640	4.15E-10	1.27E-02	D/D
	A	V	122	84 602	3.16E-02		D
	K	K	398	48 774	6.89E-03		E
	K	N	128	22 414	2.35E-02		D
	K	Q	63	10 543		4.75E-02	D
Disulfide bond	C	C	2014	25 117	9.70E-32		E
	C	F	311	5700	6.68E-03		D
	C	G	238	4429	8.13E-03	2.62E-02	D/D
	C	R	648	11 634	3.93E-04	6.99E-05	D/D
	C	S	412	8104	2.56E-06	1.01E-02	D/D
	C	W	175	3205	4.18E-02		D
	C	Y	870	16 183	6.68E-08	5.26E-05	D/D
Hydroxylation	K	K	105	49 091	7.65E-05		E
Methylation	K	K	54	49 140	2.36E-03		E
	R	R	154	86 468	3.05E-02		E
N-linked Glycosylation	N	D	657	16 080	1.79E-02		D
	N	H	274	7345	6.70E-03		D
	N	N	2441	51 886		2.25E-02	E
O-linked Glycosylation	S	S	82	1 48 408		1.74E-02	E
	T	T	105	1 42 197		1.44E-02	E
Phosphorylation	S	A	285	9066	4.08E-02	2.68E-03	D/D
	S	F	1054	25 354	4.47E-04		E
	S	L	1176	30 503		3.41E-02	D
	S	G	706	21 817	6.68E-03		D
	S	S	5403	1 43 087	1.96E-02		E
	S	T	669	19 274		3.39E-04	D
	T	T	1471	1 40 831		3.41E-02	D
	Y	H	85	15 654	1.38E-02		D
	Y	Y	454	50 960	3.06E-06		E
Succinylation	K	E	66	28 051		2.08E-02	D
	K	K	106	49 066		2.08E-02	D
	K	R	86	35 506		2.08E-02	E
Ubiquitination	K	E	4091	24 020		3.40E-10	D
	K	I	324	2060		1.47E-03	D
	K	K	7536	41 630	1.67E-06	3.47E-07	E/D
	K	M	422	2752	4.78E-02	5.41E-03	D/D
	K	N	2980	19 562	3.29E-10	7.44E-09	D/D
	K	Q	1477	9129	4.78E-02		D
	K	R	5420	30 168	1.30E-03	2.47E-09	E/D
	K	T	1589	9119		1.40E-07	D

^aTrends of significant differences between annotated and unannotated residues. Symbols indicate enrichment (E) or depletion (D). When both statistical tests, based on the number of variants (left) and allele frequency (right), are significant (q-value < 0.05), then two distinct symbols are shown. Synonymous substitutions that maintain the same AA are shown in bold.

Table 2.

Statistically significant AA substitutions in ion-binding sites

Ion-binding annotation	From AA	To AA	# sub. w/ annotation	# sub. w/o annotation	# variants FDR q-value	Trend
Iron	H	H	70	45 629	8.67E-04	E
Magnesium	D	D	73	69 334	1.72E-04	E
Zinc	H	H	182	45 517	2.25E-06	E
	H	R	56	27 688	1.29E-03	D
	C	C	132	27 001	2.25E-06	E

Figure 5.

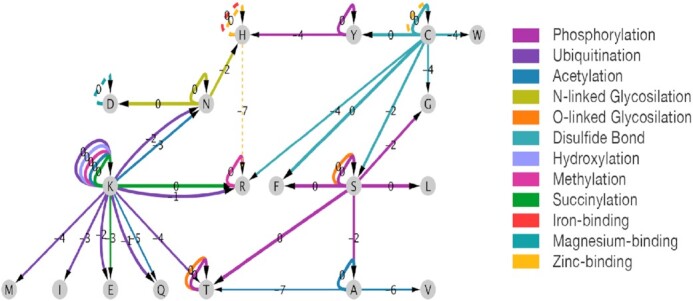
Enrichment of AA substitutions in PTM and ion-binding sites. Each edge represents a substitution between a source and a target AA in the context of a specific annotation (indicated by edge color). Dashed arrows indicate ion-binding annotations. Edges are annotated with the log2 ratio of the substitution probabilities between annotated and unannotated sites. Arrow widths signify the magnitude of these ratios.

To test the significance of each annotation-specific substitution (e.g. lysine [K] to proline [P] in ubiquitination sites), we examined two complementary aspects of significance, based on either (i) the number of annotated variants or (ii) their allele frequencies (AF). In terms of the number of variants, a substitution may exhibit a significantly higher or lower number of variants in sites annotated by that PTM or ion binding. To test whether a substitution 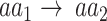is significantly associated with an annotation in terms of the number of variants, we considered the set of all variants whose major allele is 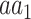, and used Fisher’s exact test to determine if the subset of these variants that substitute into 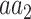is enriched with the subset of variants with the tested annotation. Likewise, to test differences in AF, we used Mann–Whitney U test (two-tailed) to compare the AF of the variants inducing the tested substitution which are in annotated versus unannotated sites (e.g. lysine [K] to proline [P] variants in ubiquitinated versus non-ubiquitinated sites). In both tests, we required a sample size of at least 50 annotated variants. To control the false discovery rate, Benjamini–Hochberg FDR was applied for each of the two types of tests, across all annotation-specific substitutions, with a significance threshold of 0.05. In this work we show the annotation-specific substitutions that are FDR-significant according to at least one of the two tests (Tables 1 and 2 and Figure 5). Significant annotation-specific substitutions are labeled as either enriched (E) or depleted (D) for each of the two tests. With respect to the number of variants, we consider it to be enriched if the odds-ratio is >1. With respect to the AF test, we consider it to be enriched when the average AF of annotated variants is greater than that of unannotated variants.

RESULTS

Constructing human-specific coding substitution matrices

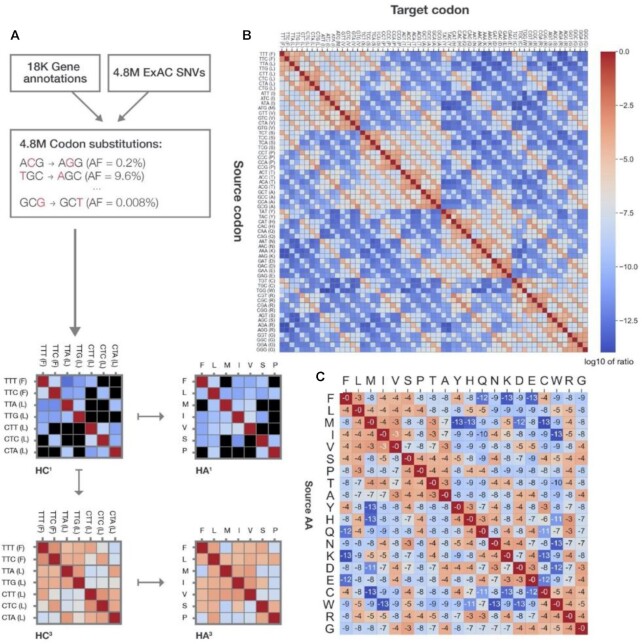
To construct an AA substitution matrix that is specific to the human population (Figure 1A), we merged data from two complementary sources: (i) the ExAC population database, which reports on >7M high-quality single nucleotide variants (SNVs) from the exome sequences of 60 706 non-related individuals (44) and (ii) genomic annotations for all human coding genes. By projecting the >7M SNVs on the gene annotations, we inferred >4.8M observed codon substitutions, found in 37% of all codons in the human coding genome. Overall, 65% of the substitutions are missense, 33% are synonymous and 2% are stop-gain (nonsense) variants.

Figure 1.

Producing human-specific substitution matrices from population genetic variation. (A) We combined 4.8M SNVs with 18K gene annotations to construct a human-specific codon substitution matrix, denoted HC¹, in which each entry represents a codon substitution probability. To capture codon substitutions that differ by more than a single nucleotide, we extended the sparse HC¹ into a complete HC³matrix through a Markovian process. We further derive corresponding matrices at amino acid resolution, HA¹and HA³, in which each entry represents the probability of an amino acid substitution. (B) HC³ (log₁₀ scale). (C) HA³ (log₁₀ scale).

From these codon substitutions and their corresponding allele frequencies (AFs), we constructed a 61×61 codon substitution matrix, denoted HC¹ (standing for Human Codon substitutions). The rows and columns of HC¹represent all codons (excluding the three stop codons), with rows representing source codons and columns representing the target codons of substitutions. Rows are normalized so that each entry represents the conditional probability of a codon substitution.

To provide substitution probabilities at AA resolution, we transformed HC¹into a 20×20 AA substitution matrix, denoted HA¹. As our construction relies on SNVs, HC¹can capture only pairs of codons that differ by up to a single letter. As a result, 84% of all codon substitutions in HC¹ are assigned zero probability. Likewise, 57.5% of HA¹values are zero. To model the propensities of all replacements, we considered three consecutive transitions of HC¹, thereby deriving a complete codon substitution matrix denoted HC³ (Figure 1B) and a corresponding AA substitution matrix HA³ (Figure 1C). The numeric values of HC¹, HA¹, HC³, and HA³, are provided in Supplementary Dataset S2.

Patterns of amino acid substitutions in the human population

We examined whether the observed 20×20 AA substitution frequencies are exclusively determined by the transition propensities of nucleotide substitutions. To this end, we constructed a 4×4 single-nucleotide substitution matrix derived from all the reported SNVs, denoted HN¹ (Figure 2A; Supplementary Dataset S3, Supplementary Figure S1). This matrix accounts for all 16 single-nucleotide replacement frequencies observed across coding regions in the human population. From HN¹, we derived a 20×20 AA substitution matrix, denoted HAN¹, which represents the expected AA substitution probabilities under the background model of single-nucleotide substitution propensities described by HN¹. We then compared the expected values of HAN¹to the empirically observed values of HA¹through an element-wise division of the two matrices (Figure 2B). We observe that substitutions of tryptophan (W) to cysteine (C) or serine (S) are roughly 8-fold lower than expected by this naive nucleotide-based background model. Similarly, a substitution from isoleucine (I) to lysine (K) is 16-fold lower than expected. Overall, we reveal that the expected-to-observed ratios are >2 (or <0.5) for 11% of AA pairs, and >1.5 (or <0.66) for 20% of AA pairs. By considering HAN¹ as a background model and testing the likelihood of the observed probabilities in HA¹, we validated that the differences between the matrices across all AA substitutions (as reported above) are indeed robust and could not have been produced by chance (P-value < 1E-300; see Materials and Methods). These results expose evolutionary signals, even at the low resolution of AA.

Figure 2.

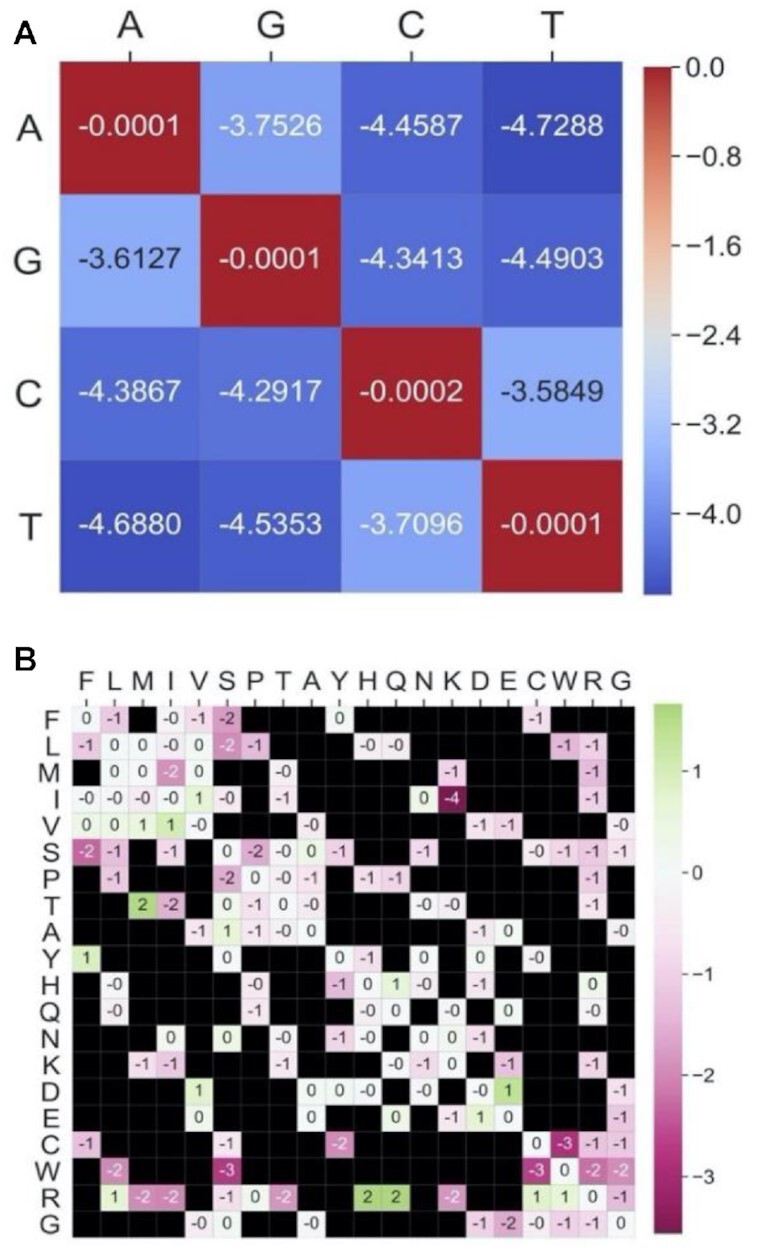
Deviation from single-nucleotide propensities. (A) Values of HN1, the human-specific single-nucleotide substitution matrix capturing the propensities of nucleotide transitions (log10 scale). (B) Observed-to-expected ratios of the entries in HA1 (log2 scale), based on a background model derived from the 4×4 frequencies of nucleotide substitutions described in (A). A log-ratio close to 0 signifies a substitution whose observed frequency is as expected by the substitution tendencies of the nucleotides in the involved codons. Negative log-ratios (colored pink) represent substitutions that are less common than would be expected by their nucleotide composition, while positive log-ratios (green) represent frequencies that are higher than expected.

A probabilistic substitution model is substantially enriched by considering the directionality replacements. We utilized information on the allele frequencies (AF) of genetic variants to deduce the most likely direction of each observed substitution. We measured the asymmetries of substitutions by the ratio between each AA replacement to its opposite (Figure 3A) and highlighted extreme signals of asymmetry (Figure 3B). Some AA substitutions show an order-of-magnitude stronger tendency in one direction compared to the other direction. The AA with the most extreme directionality is tryptophan (W). Specifically, most AA are more likely to substitute into this AA than the other way around. Notably, serine (S) exhibits a 14-times higher tendency to substitute into tryptophan (W) than the opposite substitution. Tryptophan is a biochemically distinct AA, signified by maximal hydrophobicity, bulkiness and the lowest solvation potential (47). From a structural perspective, tryptophan has been implicated in lipid anchoring of membranous proteins (48), binding hotspots and substrate-binding sites (49). Whereas tryptophan (W) emerges as a target hub, valine (V) and isoleucine (I) tend to be source hubs (Figure 3B).

Examining the directionality of AA substitutions (Figure 3) at codon resolution reveals that the directional signal is often dominated by a specific codon substitution (Supplementary Figure S2). For example, In the case of isoleucine (I) to lysine (K), it is the AAA (K) to ATA (I) codon substitution which dominantly defines the asymmetry of the AA substitution, by occurring 8 times more frequently in that direction than the opposite (Supplementary Dataset S3). Similarly, we observe that valine (V) is more likely to substitute into tyrosine (Y) in the context of the target codon TAT (Y), while an opposite tendency is in fact observed for the second codon of tyrosine (TAC). Note that the substitution of valine (V) to tyrosine (Y) requires more than one step of nucleotide replacements.

Human-specific and cross-taxa substitution matrices capture different signals

To highlight the unique features of the human-specific AA substitution matrices, we compared HA³ with the (original) BLOSUM and PAM matrices (Figure 4). We observe that the correlation in substitution propensities between HA³ and the BLOSUM matrices is similar for BLOSUM₆₂ and BLOSUM₁₀₀ (average across all 20 AA: ρ = 0.52; Figure 4A) but lower for BLOSUM₃₀ (ρ = 0.45). As BLOSUM₃₀ captures longer evolutionary distances, it is expected to be more different from the human-specific matrix. BLOSUM₃₀ also shows greater variability across different AA. Interestingly, isoleucine (I) and tryptophan (W) exhibit higher correlations for the scores of BLOSUM₃₀ than those of BLOSUM₆₂ and BLOSUM₁₀₀. It should be noted, however, that AA-specific correlations are prone to noise, as they are based on only 20 values (while the overall trend, based on 400 values, are much more robust).

A similar conformity analysis was performed for a set of PAM matrices (Figure 4B). The observed correlations in the case of the PAM matrices (average ρ of 0.61–0.68) are higher than those observed for the BLOSUM matrices. The most substantial conformity of HA³ is noted for PAM₁₀, which represents substitution probabilities between highly similar protein sequences. A correlation analysis was also performed for PAM₁, yielding the highest conformity (ρ = 0.69; Supplementary Figure S3). Notably, tyrosine (Y) and cysteine (C) register consistently low conformity between the human-specific and cross-taxa matrices (BLOSUM and PAM). Similar analyses were also conducted based on Pearson’s (rather than Spearman’s) correlation, showing the same trends. However, the correlations in the case of the BLOSUM matrices (average ρ of 0.75–0.80) are higher than those observed for the PAM matrices (Supplementary Figure S4).

HA³ represents the expected pairwise substitution probabilities following three consecutive single-nucleotide substitutions. We inquired whether the correlations reported for HA³ are sensitive to the selection of exactly three transitions in the Markovian process. We repeated the comparison between HA^k and BLOSUM (Figure 4C) or PAM (Figure 4D) for different values of k, namely following different numbers of single-nucleotide transitions. We observe that the degree of conformity is steady along many consecutive substitutions. We conclude that these results are robust to the choice of k = 3, which is the minimal number of single-nucleotide substitutions required to obtain all possible AA replacements. HC³ and HA³ have the distinct advantage of avoiding ad-hoc numerical manipulations to pull codon substitution probabilities away from zero, such as adding a small epsilon term (for codons that differ by more than one nucleotide). Instead, the Markov chain framework rigorously imputes probabilities for all codon substitutions.

The human-specific substitution model exposes protein function preservation

We investigated how AA substitution tendencies change in the context of protein functional sites. To this end, we examined nine prominent PTMs (acetylation, disulfide bond, hydroxylation, methylation, N- and O- glycosylation, phosphorylation, succinylation and ubiquitination) and three types of ion-binding sites (zinc, magnesium and iron). Altogether, we examined 92 625 experimentally validated functional sites covering 12 746 unique proteins. We tested for differences in AA substitution propensities between annotated and unannotated sites according to two complementary aspects of significance: (i) the number of variants and (ii) their allele frequencies (AFs). We found 41 substitutions with significantly different propensities in the context of specific PTM sites (Table 1). For example, alanine (A) to threonine (T) substitutions are significantly depleted in acetylated sites with respect to both the number of observed variants (FDR q-value = 4.2E-10) and their allele frequencies (FDR q-value = 1.3E-02). The most significant association is the conservation of cysteine (C) residues involved in disulfide bonds (FDR q-value = 9.7E-32). We attribute this result to the fundamental importance of disulfide bonds in stabilizing the structural fold of a protein. Generally, we find residues to be preserved in the majority of PTMs, while variants causing AA replacement (i.e. missense variants) are generally depleted. For ion-binding residues, 5 AA substitutions were found to be significantly different in annotated sites (Table 2). A complete summary of all AA substitutions with respect to all PTM and ion-binding sites is available in Supplementary Dataset S4.

Having determined which AA substitutions exhibit significant changes in functional sites, we applied our model to examine these differences in the context of substitution propensities (Figure 5 and Supplementary Figure S5). Specifically, we considered the entry-wise ratios of HA³ between annotated and unannotated sites by reconstructing the matrix for each of the two states (e.g. the substitution propensity ratio between phosphorylated serine [S] to alanine [A] and non-phosphorylated serine [S] to alanine [A]). AA substitutions that appear particularly unfavored in specific functional contexts are acetylated lysine (K) to glutamine (Q), zinc-binding histidine (H) to arginine (R), and hydroxylated alanine (A) to valine (V) or threonine (T). Lysine (K) can undergo many types of PTMs, several of which display a strong selection signal under our model. Specifically, lysine (K) residues modified by ubiquitin, acetyl, and succinyl show a high preservation tendency compared to unmodified lysine residues. Even though we considered each lysine (K) independently, it should be noted that the same lysine residues can be used for different PTM types, depending on cell state. For example, the majority of succinyl-modified lysine residues overlap with acetylation sites (50). We did not analyze less prevalent types of lysine modifications (e.g. sumoylation) due to limited experimental evidence.

Collectively, these results are best explained by a signal of negative selection associated with major functional sites in the human proteome. We conclude that a human-centric model of AA substitution propensities based on genetic variation in the human population is a powerful and intuitive tool to study AA across functional contexts such as PTMs and ion binding.

DISCUSSION

In this study, we have presented a set of data-driven novel substitution matrices at codon and AA resolutions based on the natural occurrence of genetic variation in the healthy human population. This human-centric approach reflects the short evolutionary timescale of modern humans (51), while the classic BLOSUM and PAM (as well as many others) substitution matrices are based on MSA sequences from organisms whose common ancestor is dated back many millions of years. The purpose of this work is to highlight patterns in human genetic variation that are not captured by the traditional substitution matrices, which were designed for remote homology searches. Despite this fundamental difference, HA³ still shows a moderate correlation with the classic matrices (Figure 4). In particular, matrices that reflect shorter evolutionary distances (e.g. BLOSUM₁₀₀ and PAM₁₀) exhibit higher similarity to the human-centric matrix.

In this work, we used a Markov chain model to derive the non-sparse matrices HC³ and HA³ from the empirical HC¹ and HA¹ matrices. The construction of these matrices through a Markov chain process assumes that multiple-nucleotide codon changes are derived from independent single-nucleotide substitutions. In reality, complex codon changes can sometimes occur as a single indel event, for example through a series of alterations by the DNA repair systems (52). Indeed, codon substitution frequencies show substantial variability between species due to differences in DNA repair pathways (53). This is one reason why generalization of human-centric substitution models to other taxa would be inappropriate. As future work, richer models could be utilized to create more accurate matrices.

Notable differences in substitution propensities between the cross-species and human-centric evolutionary contexts are observed for cysteine (C), tyrosine (Y) and tryptophan (W) (Figure 4). These AA are specified by unique biochemical, functional and structural features (43). Specifically, these three AA have a strong interface propensity and a negative solvation potential (54), and contribute uniquely to folding and protein-protein interaction interfaces in the human proteome (55). Furthermore, these AA are the most likely to occur in rare mutations causal of human disease (56).

We argue that a human-centric model is more appropriate for assessing the impact of human mutations in coding genes, a practice central to genetic consulting and the identification of causal mutations in human diseases. For the task of non-synonymous mutation inference, dozens of prediction tools and algorithms have been developed. With few exceptions (e.g. FIRM, (45)), the vast majority of these tools (e.g. Panther, PhD‐SNP, PolyPhen2, SIFT, SNAP, and SNPs&GO MutPred, nsSNPAnalyzer) incorporate long-range evolutionary information from cross-species conservation into the underlying model (15–17,57–59). We anticipate that the incorporation of short-term, human-centric models such as HA3 could be beneficial to mutation impact evaluation.

Key processes in multicellular organisms are mediated by a network of PTMs (e.g. differentiation, cell division, inflammation and metabolism). In humans, most proteins are subject to multiple PTMs, which greatly increase the proteome's functional repertoire (60,61). Even though ∼200 types of PTMs have been detected by mass spectrometry, only a handful have been systematically studied (62,63). In this study we focused on 9 common types of PTMs and 3 types of ion binding (which may only occur in 10 specific AA), limiting our analysis to experimentally-validated sites. Notably, PTM detection is condition-specific and quite sensitive to experimental protocols. Despite this inherent noise, we were able to establish the enrichment or depletion of certain AA replacements in the context of functional annotations with high confidence (Tables 1 and 2). A particularly strong signal was detected for phosphorylation sites (phosphotyrosine, phosphoserine and phosphothreonine), ion-binding sites, and cysteine residues that form disulfide bonds. Indeed, many human diseases result from missense mutations in codons of cysteine which destroy essential disulfide bridges (64,65). Thanks to our human-specific substitution models, we were also able to quantify the enrichment of AA substitutions across PTM and ion-binding sites (Figure 5).

Interestingly, even the short-term view explored in this study exposes a robust signal of negative natural selection at codon and AA resolution (Figure 2 and Supplementary Figure S2). While most homologues showing high conservation across species are under negative selection, this conservation is typically restricted to folded domains, while loops, intrinsically disordered regions, interdomain linkers and protein tails exhibit relatively low sequence similarity across homologues. Nonetheless, such regions of low conservation are actually the preferred targets for PTMs (e.g. N'-acetylation in protein tails, or phosphorylation and ubiquitination in loops and disordered regions). Due to the lack of cross-species conservation in those sites and differences in cellular contexts (e.g. species-specific kinome), the question of whether human PTM sites are under neutral, negative, or positive selection could not be resolved with cross-species data and remained to be tested (66,67). Our analyses provide evidence for purifying selection in unstructured protein regions (Tables 1 and 2). Another advantage of studying the selection of PTMs from a human-centric perspective is that exact PTM sites are often not conserved between species. Indeed, the conservation signal for most PTMs is negligible across species, and sometimes even shows positive selection (68,69). It was proposed that the amounts of modifiable sites, rather than their exact positions, is the conserved property in many proteins (70,71).

An essential property of the constructed matrices we present is their asymmetry (Figure 3), while AA substitutions matrices from cross-species MSA are usually symmetric by design. Indeed, we have detected substantial asymmetry for some AA (Figure 3B). Specifically, tryptophan (W) and valine (V) appear to be central hubs of such directional tendencies. We found that tryptophan (W), and, to a lesser extent, glutamic acid (E) and glutamine (Q), are common substitution targets. Valine (V), and, to a lesser extent, serine (S) and isoleucine (I), act as substitution sources. Overall, we categorized all 20 AA as substitution sources, targets or a mixture of the two (Supplementary Figure S5). Interestingly, the AA marked as sources include all 6-codon AA (R, S, L) and most 4-codon ones. Inspecting the substitution matrices at codon resolution confirms that some codons may dominate the signal at the AA level (e.g. the ATA to AAA substitution dominates the asymmetric replacement of isoleucine to lysine). Under this view, the 6 serine (S) codons exhibit distinct substitution patterns, leading to broad functional implications (72). Specifically, regions that are subjected to accelerated evolution tend to substitute within a specific set of serine (S) codons, while conserved regions in the same proteins tend to substitute within the complementary set of serine codons. The specific DNA (i.e. codon) alterations dominating some of the AA substitutions, as observed in this work, might be attributed to evolutionary processes at the DNA (rather than protein) level, which could be shaped by cellular mechanisms such as DNA repair (53,73).

In summary, we have constructed human-specific substitution matrices and characterized their unique properties. Given the robustness and interpretability of these matrices, we encourage their use as a baseline model for codon and AA replacement in the human population. An example of such analysis was demonstrated in the context of PTMs and ion-binding sites (Figures 4 and 5), where our model provided a robust baseline allowing the exposure of selection signal. This was allowed by partitioning of the protein residue space within the human proteome into two groups (e.g. those subject to a specific PTM and those that lack evidence for it), and comparing the set of genetic variants occurring in the human populations between these two groups with respect to our AA substitution model (HA³). Similarly, our model could be used to study differences with respect to other protein or residue partitions (e.g. extracellular proteins, protein–protein interfaces, proteins expressed in the brain or those related to the immune system). To allow the extension of this methodology to other datasets, including specific human subpopulations, we provide the source code of our methods (see Materials and Methods). Likewise, we anticipate that our methodology could be easily applied to other organisms with rich genetic variation data [e.g. mouse (74) and primates (21,75)].

DATA AVAILABILITY

The ExAC dataset can be downloaded from https://console.cloud.google.com/storage/browser/_details/gnomad-public/legacy/exacv1_downloads/release0.3/ExAC.r0.3.sites.vep.vcf.gz. The substitution matrices, codon counts, and further results are available in the supplementary data. The entire source code of this study is available at http://www.github.com/tairsha/taxa-specific-substitution-matrix.

SUPPLEMENTARY DATA

Supplementary Data are available at NARGAB Online.

FUNDING

Israel Science Foundation [2753/20].

Conflict of interest statement. None declared.