Vaccine uptake and constrained decision making: The case of Covid-19

Abstract

Policy makers require support in conceptualizing and assessing the impact that vaccination policies can have on the proportion of the population being vaccinated against COVID-19. To this purpose, we propose a behavioural economics-based framework to model vaccination choices. We calibrate our model using up-to-date surveys on people attitudes toward vaccination as well as estimates of COVID-19 infection and mortality rates and vaccine efficacy for the UK population. Our findings show that vaccine campaigns hardly reach herd immunity if the sceptics have real-time information on the proportion of the population being vaccinated and the negationists do not change their attitudes toward vaccination. Based on our results, we discuss the main implications of the model's application in the context of nudging and voluntariness versus mandatory rule-based policies.

Credit author statement

The authors have nothing to declare.

1. Introduction

The coronavirus disease 2019 (COVID-19) pandemic has been producing devastating effects in terms of life losses, fall of economic activities, loss of social life, education, and debt accumulation (for a review: Buheji et al., 2020, and Maria et al., 2020). The recent development of COVID-19 vaccines has given hope for a recovery. Return to some form of normalcy crucially depends on the ability of a country to reach the herd immunity threshold (HIT). However, this is not automatic and cannot be taken for granted.

Policy makers will have to make important decisions regarding what strategies to adopt to reach HIT in their populations in which many individuals may have mixed beliefs about vaccine efficacy and safety and consequently different attitudes toward a vaccination against COVID-19 (Ward et al., 2020). Several infectious disease models have been recently developed that are able to predict the likely trajectory of infections and impact of policies aimed to tackle the spread of the virus in the population, such as lockdown measures (for instance, Bhadauria et al., 2021 and Galanis and Hanieh, 2021). However, adapting these epidemiological models to the true population typically requires modelling expertise and data capacity that are not always available to decision makers. Furthermore, only a minority of these models formally address the behavioural aspect of the individual's choice of vaccinating against COVID-19 which is key to the success of any vaccination campaign. With the aim to support decision makers in conceptualizing and assessing the impact that vaccination policies can have on the proportion of the population being vaccinated, in this paper we propose a behavioural economics-based framework to model choice to vaccinate against COVID-19 and discuss the main implications of its application in the context of nudging and voluntariness versus obligation policies.

The literature on choice to vaccinate extends widely to include behavioural economics methods. Worthy of note, Bauch and Earn (2004) game theoretic model on child vaccination showed that in a population of self-interested individuals even a minimal perceived risk of vaccine precludes the eradication of vaccine-preventable disease. Betsch et al. (2013) emphasised that failure to reach herd immunity crucially depends on communication strategies. Implementing campaigns focussed on social more than private benefits may foster framing away from self-interest and stimulate other-regarding preferences. Bhattacharyya and Bauch (2010) departed from descriptive evidence on the Measles-Mumps-Rubella scare in the United Kingdom (UK) and developed a dynamic model where infection prevalence and disease risk affect the proportion of timely vaccinators, delayed vaccinators, and non-vaccinators. Oraby et al. (2014) argued that social norms can explain the gap between theoretical predictions on the impossibility to achieve herd immunity based on the assumption of purely self-interested behaviour and the historical observation that outcomes close to herd immunity are indeed achieved.

Building on this literature, we adopt a novel modelling approach by applying a theoretical paradigm to vaccination against COVID-19 which differs in its manifestation from other infectious diseases in several ways. The timing of vaccine development and test has been accelerated by combining different phases of the development cycle. Moreover, vaccination campaigns take place in an informational environment that is strongly affected, and possibly biased, by social media and the web in general (Lancet Infect Dis, 2020; Puri et al., 2020). Finally, vaccine production and distribution are taking an unparalleled scale and vaccination decisions can impact on future lockdowns with high social and economic costs.

Section 2 presents our choice to vaccinate model and describes the base case assumptions. The following section 3 focuses on the calibration of the model in the UK context, predicting the proportion of the vaccinate population. The following sections, from 4 to 6, relax some assumptions of the model proposed in section 2, and qualitatively discuss the consequences of changes in variations to the base case scenario and the underpinning theoretical paradigm. Section 7 concludes by summarising key messages.

2. The model

We model the decision to take the vaccine over two fixed time periods, t1 and t2 (we use this time interval to apply historical probabilities of infection reported since the onset of the COVID-19 disease available at end 2020; 18-month period may be a reasonable horizon in which individuals expect that COVID-19 pandemic can still last after they get vaccinated. Robustness on the period shows that our findings are invariant if we consider a different time interval). The overall population P is composed by a proportion of non-vaccinable, NV, and three groups of vaccinable individuals, i.e., the rationals, VR, the sceptics, VS, and the negationists, VN. Note that the word rational in this context refers to the model where people maximise their utilities based on rational preferences, as standard in economics and social science optimisation model. The subset of non-vaccinable individuals include those who may not be eligible for a vaccine such as young children, pregnant women, or immunocompromised patients. The group of rationals take the most credited historical probabilities as reference point to inform their choice to take the vaccine. The sceptics are wary of the adverse effects associated with the vaccine, overestimating the probability of harm and underestimating vaccine effectiveness, but open to change attitudes. We assume that in t2 the sceptics can update their biased probabilities according to the vaccination results they observe in the first period in a Bayesian fashion. The negationists share with the sceptics the biased probabilities but they will not update them in t2.

2.1. The rationals’ choice

VR decide to take the vaccine in period t1 if the perceived benefits are higher than the perceived costs. For each rational individual belonging to the j-th age class, the benefit of vaccination is given by the avoided expected loss from infection

$$g_{VR}:=g_{VR}\left(p_{Ct\left(j\right)},p_{CH\left(j\right)},p_{EF},CI\right)=\left[p_{Ct}{p}_{CH\left(j\right)}\left(1-p_{IGIt1}\right)p_{EF}CI\right]$$

where p_Ct(j) is the probability, conditional on the j-th age class, of being infected when no one is vaccinated during the whole period, t1+t2, p_CH(j) is the probability, conditional on the j-th age class, of incurring in health problems after being infected, p_IGIt1 is a factor reducing the probability of infection proportional to the share of the vaccinated population in t1, p_EF the probability that the vaccine is effective (i.e., the vaccine efficacy), and CI is the cost of COVID-19 infection (e.g. dying after getting infected).

The cost of taking the vaccine in each period can be described as:

$$c:=c\left(p_H\right)=p_{H}CD$$

where p_H is the probability of incurring in any severe side effect from vaccination and CD is the cost of vaccination harm.

Thus, VR choose to be vaccinated if and only if

$$g_{VR}>c,$$

that is

$$\left[p_{Ct1\left(j\right)}{p}_{CH\left(j\right)}\left(1-p_{IGIt1}\right)\left(1-p_{EF}\right)CI\right]-p_{H}CD>0$$

In order to reduce the dependence of our findings from empirical and likely arbitrary parameters, we assume that CI and CD both correspond to the extreme harm, that is death (In section 4 we relax this assumption and consider differential non-death costs for both options). Thus, our equation reduces to

$$\left[p_{Ct1\left(j\right)}{p}_{CH\left(j\right)}\left(1-p_{IGIt1}\right)p_{EF}\right]-p_H>0$$ (1)

We define (1) as the Self-Interest Rationality Inequality (SRI).

The sceptics’ choice.

In the same vein as VR, VS make their choice to take the vaccine if the perceived benefits are greater than the perceived costs. For each skeptic belonging to the j-th age class, the benefits of vaccination in each period ti, i = 1,2, is given by the perceived avoided expected loss from infection

$$g_{VS}:=g_{VS}\left({\hat{p}}_{Ct\left(j\right)},{\hat{p}}_{CH\left(j\right)},{\hat{p}}_{EFti},CI\right)=\left[{\hat{p}}_{Ct}{\hat{p}}_{CH\left(j\right)}\left(1-{\hat{p}}_{IGIti}\right){\hat{p}}_{EFti})CI\right]$$

where p^_Ct(j) is the perceived probability of being infected, conditional on the j-th age class, when no one is vaccinated during the whole period, t1+t2, p^_CH(j) is the perceived probability, conditional on the j-th age class, of incurring in health problems after being infected, p^_IGIti is a factor reducing the perceived probability of infection proportional to the share of the vaccinated population in ti, p^_EFti the perceived probability that the vaccine is effective in period ti, and CI is the cost of infection (e.g., dying after getting infected).

In each period ti, i = 1,2, the perceived cost of taking the vaccine can be described as:

$$c_{VS}\left({\hat{p}}_{Hti}\right)={\hat{p}}_{Hti}CD$$

where p^_H is the probability of incurring in any severe side effect from vaccination and CD the cost of vaccination harm.

Thus, VS choose to get vaccinated if and only if

$$g_{VS}>c_{VS},$$

that is

$$\left[{\hat{p}}_{Ct\left(j\right)}{\hat{p}}_{CH\left(j\right)}\left(1-{\hat{p}}_{IGIti}\right){\hat{p}}_{EFti}CI\right]-{\hat{p}}_{Hti}CD>0$$

For sake of comparability between groups, we assume that CI and CD are equal and corresponding to the death (in section 4 we relax this assumption and consider differential non-death costs for both options). Thus, our equation reduces to

$$\left[{\hat{p}}_{Ct\left(j\right)}{\hat{p}}_{CH\left(j\right)}\left(1-{\hat{p}}_{IGIti}\right){\hat{p}}_{EFti}\right]-{\hat{p}}_{Hti}>0$$ (2a)

We define (2) as the Self-Interest Scepticism Inequality (SSI).

The negationists’ choice.

As mentioned above, VN do not change their attitudes toward vaccination, irrespective of any potential benefits which they may perceive throughout the entire period of time as they observe other individuals in the population getting vaccinated. Thus, for VN, the perceived cost of vaccination is assumed to be always greater than the perceived benefits.

2.2. Model assumptions

To model a realistic scenario, we make the following assumptions the relaxation of which shall not invalidate our analysis.

Assumption 1. Sceptics have biased beliefs. In t1, the VS have upward biased beliefs about the probability of vaccination harm and downward biased beliefs about the vaccine effectiveness. This corresponds to assuming p^_Ht1 > p_H and p^_Eft1 < p_EF.

Assumption 2. Sceptics update their beliefs using Bayesian updating. In t2, VS update their biased probabilities in a Bayesian fashion according to vaccination data they observe in t1. This corresponds to assuming p^_Ht2 = α p^_Ht1 + (1 – α) p_H for some α in (0,1), and p^_EFt2 = β p^_EFt1 + (1 – β) p_EF for some β in (0,1).

Assumption 3. Only rationals can get vaccinated in the first period. Since sceptics are defined as those who would like to first observe what happens to the vaccinated people and then choose whether to be vaccinate, we assume that only VR can get vaccinated in t1. This is equivalent to assume that [p^_Ct(j) p^_CH(j) (1 – p^_IGIt1) p^_EFt1] – p^_Ht1 < 0.

3. Calibration of the model: results for the United Kingdom

The purpose of this section is to calibrate our model using data from the UK. In particular, based on available data on Covid-19 cases and deaths by age groups from January 29, 2020 to July 21, 2020, we analyse how our model would predict the share of people preferring to get the vaccine. This analysis consists of three steps. First, we split the population into three groups, namely the negationists, the sceptics, and the rationals, based on the most recent surveys on vaccine hesitancy. Second, we see how many rationals would find convenient to get the vaccine once they know historical probability of infection and deaths, and safety and efficacy of the vaccine. Third, we analyse how many sceptics will take the vaccine as a function of their updating beliefs.

Table 1 shows the UK parameters used to calibrate our model. The risks of infection and death due to COVID-19 are non-negligible (4.2% and 2.4%–30%, respectively), and a large majority of the people (71.7%) declared they are willing to be vaccinated (i.e., rationals).

Table 1.

Variable description and sources.

Variable	Description			Value	Source
UK Population	2018 Projections of population in the UK in mid-2019, by age group		Total	67,195,769	Office for National Statistics (https://www.ons.gov.uk/peoplepopulationandcommunity/populationandmigration/populationprojections/datasets/tablea21principalprojectionukpopulationinagegroups)
			0–16	13,472,807
			17	614,669
			18–19	1,529,111
			20–39	17,586,797
			40–59	17,496,512
			60–79	12,776,246
			80+	3,356,670
			Total	66,832,812
COVID-19 infections	No. of confirmed cases in the period January 30, 2020–July 21, 2021a	0–19		976,419	Public Health England (https://coronavirus.data.gov.uk/details/download), Public Health Wakes (https://gov.wales/coronavirus) Public Health Scotland (https://www.gov.scot/publications/coronavirus-covid-19-data-definitions-and-sources/), Northern Ireland Department of Health (https://covid19.who.int/region/euro/country/gb)
		20–39		2,051,621
		40–59		1,554,594
		60–79		605,395
		80+		261,475
		Total		5,449,504
Probability of being infected during period ti (pCti)	COVID-19 infections out of the UK population, for one third of the period (i.e., 6 months)		0–19	0.02129161	Authors' elaboration, assuming pCt1 = (no. of Covid-19 infectious)/(UK population size) and (1 - pCt1)3 = 1 – pC(t1+t2)
			20–39	0.04050406
			40–59	0.03054043
			60–79	0.01605106
			80+	0.02667072
			Total	0.02795392
COVID-19 deaths	No. of confirmed deaths due to COVID-19 in the period January 3, 2020–July 20, 2021a, by age group		0–19	48	Office for National Statistics (https://www.ons.gov.uk/peoplepopulationandcommunity/birthsdeathsandmarriages/deaths/bulletins/deathsregisteredweeklyinenglandandwalesprovisional/weekending9july2021), Public Health Scotland (https://www.opendata.nhs.scot/dataset/covid-19-in-scotland/resource/9393bd66-5012-4f01-9bc5-e7a10accacf4), Northern Ireland Statistics and Research Agency (https://www.nisra.gov.uk/publications/weekly-deaths-week-ending-2-july-2021)
			20–39	954
			40–59	9574
			60–79	50,861
			80+	89,682
			Total	151,119
Probability of death due to the infection (pCH(j) over the period January 2020–July 2021a)	Total COVID-19 deaths out of UK Population		0–19	4.9159E-05	Authors' elaboration based on ONS data on COVID deaths and population size https://www.ons.gov.uk/peoplepopulationandcommunity/birthsdeathsandmarriages/deaths/datasets/weeklyprovisionalfiguresondeathsregisteredinenglandandwales)
			20–39	0.000465
			40–59	0.00615852
			60–79	0.08401292
			80+	0.34298308
			Total	0.02773069
Probability that the vaccine is harmful (pH)	Number of confirmed deaths due to the vaccine			10–6	Hypothesised.
Vaccine efficacy (pEF)	COVID-19 cases without onset at least 7 days after the second dose.			84%	Average of AZD1222 (AstraZeneca, https://www.astrazeneca.com/media-centre/press-releases/2021/azd1222-us-phase-iii-primary-analysis-confirms-safety-and-efficacy.html, 76%) and BNT162b2 (Pfizer Biontech, https://www.pfizer.com/news/press-release/press-release-detail/pfizer-and-biontech-confirm-high-efficacy-and-no-serious, 91.3%) vaccine efficacy.
Rationals	Share of people willing to take the vaccine if SRI holds in t1.			71.7%	The Oxford coronavirus explanations, attitudes, and narratives survey (https://doi.org/10.1017/S0033291720005188)
Sceptics	Share of people willing to take the vaccine if SSI holds in t2.			16.6%	The Oxford coronavirus explanations, attitudes, and narratives survey (https://doi.org/10.1017/S0033291720005188)
Negationists	Share of people not willing to take the vaccine.			11.7%	The Oxford coronavirus explanations, attitudes, and narratives survey (https://doi.org/10.1017/S0033291720005188)

^aThe periods refer to the oldest and newest data available; some countries have data starting in March 2020 and ending on 9 July.

3.1. Model predictions

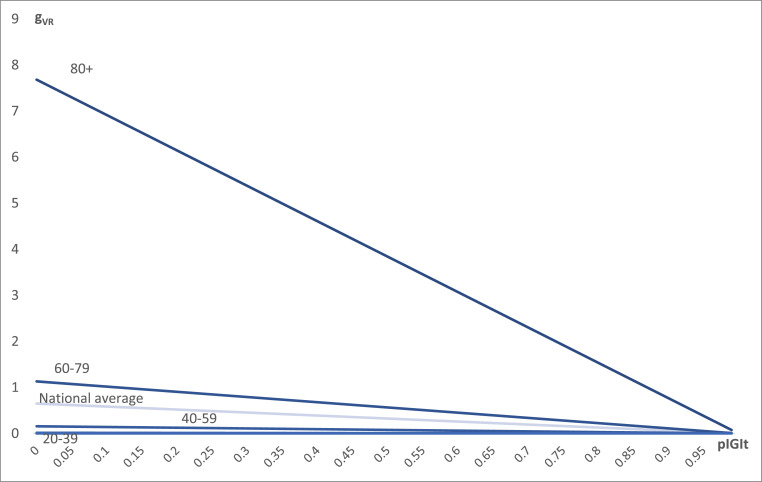
Table 2 shows our model calibrated with the UK data in t1, and Fig. 1 plots the trend of SRI as the share of vaccinated people increases. This corresponds to the vaccination choice of the rationals in t1. We observe that all age groups find it convenient to be vaccinated, except for all people aged below 20. For those aged 20–39, it would not be convenient if the share of vaccinated people were 93%, which is not possible as rationals in t1 are 71.7%.

Table 2.

Share of vaccinated rationals in t1.

Variable \ Age class	0–19	20–39	40–59	60–79	80+	Total
Probability of being infected (pCt)	0.0213	0.041	0.031	0.016	0.027	0.028
Probability to die due to infection (pCH(j))	0.07%	0.70%	3.01%	12.68%	30.32%	24.29%
Probability that the vaccine is harmful (pH)	10−6	10–6	10–6	10–6	10–6	10–6
Vaccine efficacy (pIN)	0.84	0.84	0.84	0.84	0.84	0.84
Share of vaccinated population above which vaccination costs higher than benefits	0.00	0.93	0.99	0.99	0.99	0.99

Notes: The share of vaccinated population is computed based on utility function of the rationals (equation SRI) and data as in Table 1.

Fig. 1.

The net benefit of the vaccination as a function of the share of immune people in UK. Notes: The horizontal axis shows the number of vaccinated people in the first period; the vertical axis shows the utility function of rational people. Lines are shown for positive values of the utility function of people aged 80+, 60–79, 40–59, 20–39, based on parameters as in Table 2; people aged 0–19 are not shown as they never have positive utility.

Thus, at the end of the first period the number of vaccinated people is approximately 36.7 million, corresponding to 54.9% of the total population in UK.

3.2. Sceptics updating mechanism analyses

In t2, we analyse the sceptics updating mechanism and consider two cases: one with overestimated vaccine side effects and another with underestimated vaccine efficacy.

Overestimated vaccine side effects (p^_Ht1= 10⁻³). We assume that in t1 sceptics have prior biased probability of the vaccine side effects equal to 10⁻³, meaning that they believe there is 1 death every 1000 vaccinated individuals. In t2, sceptics update their biased beliefs about the vaccine side effects based on what observed in t1, according to p^_Ht2 = α p^_Ht1 + (1 – α) p_H for some α in (0,1). The lower α, the less biased the updated probabilities are. Thus, the vaccine will be convenient for the sceptics if and only if SSI holds.

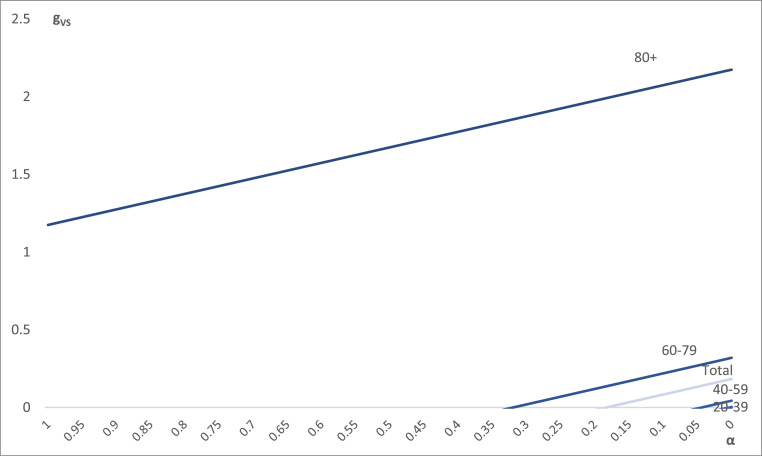
Table 3 shows the parameters we used for our calibration, and Fig. 2 shows how sceptics’ utility evolves depending on how close to the true parameters they update their beliefs. We show that sceptics aged above 80 always choose to get vaccinated. For those aged 60–79, the updating coefficient for the vaccine being convenient is 0.31, meaning that they require a relatively big update if starting from the assumed probability that the vaccine is harmful, i.e., 10⁻³). The coefficient is even smaller for people aged 40–59, while people aged below 40 will never find the vaccine convenient unless they completely remove their bias.

Table 3.

Minimum updating coefficients by age group.

Variable \ Age class	0–19	20–39	40–59	60–79	80+	Total
Probability of being infected (pCt)	0.0213	0.041	0.031	0.016	0.027	0.028
Probability to die due to infection (pCH(j))	0.07%	0.70%	3.01%	12.68%	30.32%	24.29%
Probability that the vaccine is harmful (pH)	10−3	10–3	10–3	10–3	10–3	10–3
Vaccine efficacy (pIN)	0.84	0.84	0.84	0.84	0.84	0.84
Share of vaccinated people in t2	37.8%	37.8%	37.8%	37.8%	37.8%	37.8%
Updating coefficient α for the vaccine to be convenient	Never convenient	Never convenient	0.04	0.31	Always convenient	0.18

Notes: The share of vaccinated population is computed based on utility function of the rationals (equation SSI) and data as in Table 1.

Fig. 2.

The net benefit of the vaccination as a function of the updating coefficient. Notes: The horizontal axis shows the updating coefficient referring to the vaccine safety (α = 1 means p_H = 10^−3; α = 0 means p_H = 10⁻⁶); the vertical axis shows the utility function of skeptic people. Lines are shown for positive values of the utility function of people aged 80+, 60–79, 40–59, 20–39, based on parameters as in Table 3; people aged 0–19 are not shown as they never have positive utility.

Underestimated vaccine efficacy (p^_EFt1= 0). Under this scenario we assume that in t2 the sceptics will update their biased beliefs about the vaccine efficacy based on what observed in the first 6 months 1 according to p^_EFF = β p^_EFF + (1 – β) p_H for some β in (0,1). The lower β, the less biased the updated probabilities are. Thus, the vaccine will be convenient for the sceptics if and only if SSI holds.

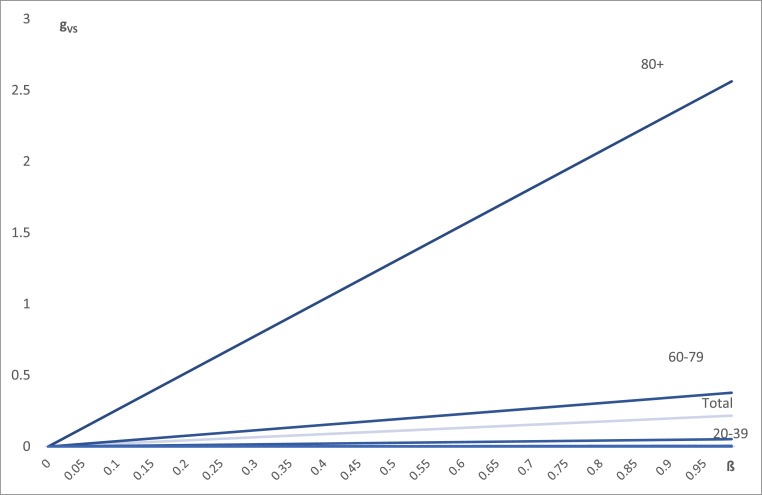
In this case, we observe that for sceptics aged below 20 it is never convenient to get the vaccine; on the contrary, for those aged above 40 it is always convenient, as long as the vaccine efficacy is 1–2%; People aged below 20–39 require an efficacy of at least 19% (Table 4 and Fig. 3 ).

Table 4.

Minimum updating coefficients by age group.

Variable \ Age class	0–19	20–39	40–59	60–79	80+	Total
Probability of being infected (pCt)	0.0213	0.041	0.031	0.016	0.027	0.028
Probability to die due to infection (pCH(j))	0.07%	0.70%	3.01%	12.68%	30.32%	24.29%
Probability that the vaccine is harmful (pH)	10−3	10–3	10–3	10–3	10–3	10–3
Vaccine efficacy (pIN)	0.84	0.84	0.84	0.84	0.84	0.84
Share of vaccinated people in t2	71.7%	71.7%	71.7%	71.7%	71.7%	71.7%
Updating coefficient β for the vaccine to be convenient	Never convenient	0.19	0.02	0.01	0.01	0.01

Fig. 3.

The net benefit of the vaccination as a function of the updating coefficient. Notes: The horizontal axis shows the updating coefficient referring to the vaccine safety (β = 1 means fully efficacy, i.e., p_EF = 100%;^; β = 0 means no efficacy, i.e., p_EF = 0%); the vertical axis shows the utility function of skeptic people. Lines are shown for positive values of the utility function of people aged 80+, 60–79, 40–59, 20–39, based on parameters as in Table 4; people aged 0–19 are not shown as they never have positive utility for efficacies below 100%.

Thus, at the end of the second period the number of vaccinated people among the sceptics is between 4% and 8.4%, depending on their updated beliefs. This makes the total number of vaccinated people between 58.9% and 63.3% of the total population in UK.

3.3. Reachable levels of vaccine uptake at the end of t2

British children aged below 16 have been initially excluded from the UK vaccination campaign (see https://www.gov.uk/government/publications/priority-groups-for-coronavirus-covid-19-vaccination-advice-from-the-jcvi-2-december-2020/priority-groups-for-coronavirus-covid-19-vaccination-advice-from-the-jcvi-2-december-2020), and they correspond to 13,472,807 children, that is 20.05% of the total population. Negationists count for 11.7%, and people who are immune because they have already been infected account for 8.15%. Assuming that 11.7% of contagions belong to negationists and that 5.3% of contagions belong to children (i.e., contagions are equally distributed among the corresponding group), this makes the potential total share of vaccinable individuals no higher than 65.6% of the UK population.

Under base case assumptions, we estimated that 63.3% of the overall population takes the vaccine after the second period. If we add up people already immune because of the infection (8.2%) and we substract vaccinated people for whom the vaccine is not efficace (16%), our predictions suggest that in the UK the proportion of immune population is equal to 61.3%.

3.4. Our model predictions and observed data as of July 2021

Our model calibration predicts the number of vaccinated people based on ex ante attitudes toward Covid-19 vaccination. In this subsection, we compare our results with observed data on the vaccination campaign in the UK, to see how our model is reliable and how we may explain some differences, if any.

Table 5 shows the cumulative number of vaccinated people by age group in the UK on July 22, 2021, and the share of them in their corresponding age group.

Table 5.

Number of people who get the first dose of a Covid-19 vaccine in the UK before July 23, 2021.].

Age group	People vaccinated	Share of vaccinated with respect to the corresponding age group
18–39	12,880,976	0.674
40–59	16,010,857	0.915
60–79	12,604,044	0.987
80+	3,170,090	0.944
Total	44,665,967	0.668

The total number of vaccinated (66.8) is very close to our prediction (63.3), and so is the distribution among the age group, as non-vaccinated people are almost only aged below 40.

This difference may be explained by different factors. First, surveys on attitudes may not correspond true behaviour of people, who may change their views when actually need to choose whether to take the vaccine. Second, the vaccination campaign in the UK may have been able to increase the number of rationals or to make sceptics’ beliefs closer to the true parameters. Third, the presence of new variants and severe symtphoms, which have not been considered in our model, may have also played a role in the updating mechanism of the sceptics. In the next section we disucss all these changes to the best case scenario of our model, and in the following sections we also discuss how the vaccination campaign may be effective by nudging people on different parameters or regulating access to a number of services for vaccinated people only.

4. Changes to base case scenario

In this section we discuss what would happen if we modified some base case assumptions of our model, namely, the cost of infection, the share of negationists, the vaccine side effects, the time horizon, and the regional heterogeneity of infection and deaths.

Including COVID-19 severe symptoms. Unlike what was assumed for the presented analyses, COVID-19 may not only cause death, but also severe symptoms that require, for instance, admission to Intensive Care Unit. While we acknowledge that we may also take into account severe symptoms induced by the vaccine, we may reasonably assume that severe symptoms due to COVID-19 outweigh those due to the vaccine, hence the model would underestimate the share of vaccinated individuals. The difficulty here lies in comparing the (limited) negative value of health consequences with the (potentially infinite) negative value of death. A specific approach could estimate the probability of serious health consequences (i.e., hospitalisation) as a multiple of the probability of death and attribute a proportion of the death damage to health consequences of hospitalisation.

Proportion of negationists. The share of negationists we considered was based on the last available ex ante surveys where respondents were asked whether they were willing to take vaccine or not. We need to use ex ante surveys (dated on December 2020) as current surveys may be influenced by the start of the vaccination campaign and the share of negationists may be over or under represented. In fact, this share may not be time-invariant. For instance, ad hoc communication campaigns (like the ones we propose in section 5) can frame negationists' beliefs and make them as those of sceptics or rationals. This would contribute to increase the number of vaccinated individuals. More specifically, framing negationists’ beliefs would be more effective at increasing this number if they changed their attitude sooner than later, (as their incentive to change it with the purpose of reaching herd immunity decreases as the number of vaccinated people increases) or if they are disproportionally distributed among the elderly (as they will have always a marginally higher incentive to take the vaccine compared to the younger cohorts).

The vaccine side effects and the new variants. So far, we have considered a scenario where one vaccine can be more or less effective and assumed its safety. However, we might consider the hypothesis that the vaccine may cause severe side effects other than death. This, of course, would reduce the incentive to take the vaccine across all age groups. In a more realistic scenario, we shall assume that the vaccine would become less effective at preventing the infection due to a virus mutation. This might lead to opposing scenarios. On one hand, a new variant may reduce the vaccine efficacy, similarly reproducing a scenario where vaccine side effects are perceived to be greater for all individuals, including the rationals. On the other hand, if a new variant emerges, then people may be more willing to collectively accelerate the vaccination process to prevent the virus from spreading faster and threatening public health with new variants. Among these two competing scenarios, the latter requires collective choices, which are harder to achieve if not properly supported by campaign leaders and public institutions.

A different time-horizon. A change in the time horizon can also have important consequences. In our model rational individuals take the decision within a 6-month period. If however they would instead evaluate the problem each single day, the daily cost of being infected would likely be very limited and they would find it optimal to procrastinate their decision. In this case, we fall in a “carpe diem paradox”: people would be more willing to take the vaccine if they have to do so within one month rather than the soonest available day.

Heterogeneous probability of infection and death. The probability of death due to the infection was not conditional on local living conditions, which has shown to be a primary determinant. As shown by several researches and consistently with the syndemic concept, COVID-19 deaths depend on several local factors such as, for instance, commuting flows and particulate matter (Becchetti et al., 2020). People living in large and more polluted cities will thus be more likely to choose to accept the vaccine.

The role of social media A main feature that makes the current vaccination campaign different from those analysed in the past is the role played by information, especially that one gathered via social media and internet in general. On one hand, the web increases the flow of information per unit of time available to individuals; on the other hand, it reduces the factors that allow readers to discriminate about news reliability. Moreover, web media sources compete for attracting users' attention as the higher the number of clicks their contents receive, the higher the advertising revenues they earn. To maximise clicks, there is a high incentive to publish extreme (and in general more negative) news that can attract attention (Branton and Dunaway, 2008; Benson, 2002; Benson and Saguy, 2005). All these concurring factors might frame individuals’ capacity to discriminate their reliability as well as their probabilities beliefs.

To analyse the effect of web-sourced news on the equilibrium outcome, first, we allow the probability of vaccination harm to vary randomly according to a distribution based on individual's beliefs and expectations The SRI condition becomes

$$\left[p_{Ct}{p}_{CH\left(j\right)}\left(1-p_{IGIt}\right)\left(1-p_{IN}\right)CI\right]-{\pi }_{H}CD>0$$

where π_H = p_H + ε, and ε ∼ N (0,σ_πH).

Then, we assume that individuals are risk averse and test the impact of a shock increasing the variance of such distribution on individual choice to vaccinate.

Expected utility of vaccination choice for a risk averse individual can be simplified to

$$V=SRI-g\left(Var\left(SRI\right)\right)$$ (2b)

where g is the risk aversion coefficient. An increase in variance is such that dV/dVar(SRI) < 0 for risk averse individuals reducing in equilibrium the propensity to vaccinate and therefore the share of the first group. In addition, we may argue that only the negative side of the distribution changes occurs (i.e., higher probability of negative news), and obviously the result becomes even stronger quantitatively: web and social media increase the perceived risk and contributes to reduce the vaccinated share in equilibrium.

Taking other-regarding preferences into account. In addition to a self-regarding assessment, we may argue that other-regarding preferences could play as an additional factor motivating people to take the vaccine to preserve the health of other people. IAs is well known in the behavioural economics literature, at least some individuals can switch from purely self-regarding to other-regarding preferences when proper frames are used. More specifically, individuals have been shown to cooperate more in a “social exchange study” than in a “business transaction study” (Batson and Moran, 1999), and substantially more in a “community game” than in a “Wall Street game” (Kay and Ross, 2003; Liberman et al., 2004) where what changes is just the title and not the structure of the game. If this is the case, communication policies based on solidarity frames (giving more robust signals than just changing titles) can help. Of course, this depends on how the campaign is perceived by the population.

Thus, we rewrite the utility function of the individuals who must decide whether to vaccinate or not as

$$U_i=f_1{a}_1\left(SR{I}_i\right)+f_2{a}_2\left(R{G}_i\right)+f_3{a}_3(\Sigma U_{jidfi}|C{H}_i)+f_4{a}_4(\Delta \Sigma U_{jidfi}|C{H}_i)$$ (3)

The first argument in (3) is the self-interest rationality inequality where SRI is defined as in (1) (see section 2), a₁ is the self-interest preference parameter and f₁ is the activation factor of that preference.

The second is a relational good argument that is, the enjoyment that individuals have in cultivating relationships. According to the literature social relationships and relational goods are a special kind of local public goods characterised by local non-excludability and anti-rivalry (Gui and Stanca, 2010; Becchetti et al., 2011; Corneo, 2005). A relational good (e.g., a party or a social meeting) can be enjoyed only by those who are invited to participate (local non-excludability) while their fruition not only does not reduce the value of the good, but it is a necessary condition for enjoying the good (anti-rivalry). The empirical literature provides ample evidence that relational goods have strong positive effects on life satisfaction (Becchetti et al., 2008).

The third is the sum of the utility of other individuals with a₃ being the other-regarding preference parameter and f₃ the activation factor of that preference. The fourth “generativity” argument is the change in utility that the vaccination choice of individual i generates on other individuals, with a₄ being the generativity preference parameter and f₄ the activation factor of that preference.

The assumption behind the generalized theoretical model is that, according to frames (activated by proper communication campaigns) that make salient our self-regarding, other-regarding or generativity preferences increasing the related activation factors, individuals give higher weight to one of the three arguments.

The model can accommodate risk aversion if we replace (2) with

$$H_i=f_1{a}_1\left(V_i\right)+f_2{a}_2\left(\Sigma V_{jidfi}\right)+f_3{a}_3\left(\Delta \Sigma V_{jidfi}|C{H}_i\right)$$ (4)

where V_i=(SRI_i) - g (Var(SRI))

Sub-herd immunity equilibria. We have shown that the final number of immune people may lie at the lower bound of the conventional HIT of 60–75%. However, even a small proportion of vaccinated people may help, in the first period, to alleviate hospital pressure. Pressure on hospitals is primarily driven by patients with more severe symptoms, namely people aged above 65 and already suffering from existing diseases (Knights et al., 2020). Therefore, although herd immunity is hardly reachable in the best case scenario, especially in the first period, hospital pressure may be alleviated using vaccination policy targeted on the most vulnerable groups and analysing attitudes towards vaccination of these groups. To achieve this intermediate goal the age-class sequence of vaccination is also important. On one hand, it would be better to start from the youth since they may be more responsible for spreading the virus. On the other hand, starting from the elderly may rapidly impact deaths and hospital pressure. The impossibility to vaccinate children below 16 has oriented policy-makers toward the second option.

5. Nudging policy implications

There are relevant policy implications related to our model and findings. How should the optimal policy look like when individuals fall in the procrastination paradox by applying a 1-day horizon rather than a 1-month horizon? In this respect, nudging policies inducing individuals to frame on longer run cost-benefit analyses of vaccine uptake should be advisable (Korn et al., 2018; Ratzan et al., 2021). In this section we explain why some nudges may be particularly effective and we link our model parameters to different communication campaigns.

To reduce procrastination, policies may emphasise the cost of not taking the vaccine immediately or may design a limited number of slots for the vaccine. While both policies target the sceptics, the former acts on their beliefs and the latter on physical constaints. If people know that in the first month there is only one reserved slot for them to take the vaccine, the time frame becomes a 1-month horizon. However, the trade-off of this limited-slot policy is that people might not be always available and rescheduling might have additional costs and delay herd immunity.

In addition to procrastination, number of doses and effective communication of vaccine's safety and efficacy are essential for the sceptics' choice. However, HIT may still not be reached if i) we do not relax the assumption of perfect information on the total vaccinated share and the true HIT, and ii) we do not assume that communications campaigns reduce the share of negationists. As for the perfect information assumption, we argued that may not hold in practice as there is a huge uncertainty about the true HIT and authorities are not required to reveal timely information on the aggregate number of vaccinated people. As for communication campaigns, providing information on health condition of the vaccinated people, and activating solidarity frames remain essential to reduce the negationist share and achieve herd immunity.

Based on our theoretical framework, we can propose the following different types of nudging campaigns that act on relational good, other-regarding preferences, and generativity as modelled in (3).

• i)Messages that stimulate preferences for relational goods (acting on f₂)

“With your vaccination choice you can hug your beloved and live without constraints your relational life with the already vaccinated population”.

• ii)Messages that stimulate other-regarding preferences of the youths (acting on f₃)

“With your vaccination choice you can save your parents, your grandparents and any other person of your community”.

• iii)Messages that stimulate preferences for generativity (acting on f₄)

“With your vaccination choice you can bring us closer to herd immunity and improve lives of the current and future generations“

• iv)Messages that highlight the risk to reduce risk aversion

• “We have vaccinated so far X million people in the world, of whom a few unit (or none) had severe side effects.”

The above communication campaigns examples fall into the definition of nudging, which is according to Hansen “[…] a function of (I) any attempt at influencing people's judgment, choice or behaviour in a predictable way (1) that is called for because of cognitive boundaries, biases, routines, and habits in individual and social decision-making, and which (2) works by making use of those boundaries, biases, routines, and habits as integral parts of such attempts” (Hansen, 2016).

More specifically, both communication strategies (i.e., on health conditions of the vaccinated group and on framing solidarity) do not rely on cognitive biases but they simply make salient some factors that are expected to affect individual vaccination choices. It is obviously important that these campaigns reveal true and verifiable information, have an appropriate tone, and avoid negative reactions of the public opinion. Differently, the other two suggestions (i.e., limiting time slots for vaccination and keeping imperfect information about the total share of vaccinated) are instead directed to alter individuals choice set, though the latter may not be necessary in presence of uncertainty about the HIT.

6. Voluntariness versus obligation to vaccinate

Our model assumes that the vaccination decision is a voluntary decision. This would be unarguably preferable in case it would be sufficient to achieve herd immunity. Differently, if the government aims at achieving herd ummunity but voluntary vaccination programmes would not be effective, there are two alternative policies. One would be a mandatory vaccination (in some countries like Italy, this would be possible by Constitutions, where restrictions to freedom of choice can be imposed for superior public health reasons). Alternatively, it is possible to use strong incentives to vaccination such as licences required to get access to means of transport or other social activities. Obligation to vaccine uptake can be effective if it is possible to monitor and verify compliance (as it is the case when licences must be shown to public officials when using public means of transport).

Politicians may be reluctant to use the mandatory option since this might create resentment and undermine consensus, especially among the non-rational groups. In fact, opinions on if and how the vaccine should be signalled are not homogeneous, either among scientists (Aranzales et al., 2021). In order to maximise both political consensus and success of the vaccination campaign, the optimal choice could be to start with a voluntary vaccination plan coupled with the above-described nudging strategies to see whether this is enough to achieve herd immunity. If herd immunity is not achieved, the government could then condition access to means of transport and some other public services (e.g., shops, parks, cinemas and recreation facilities) to the exhibition of a vaccination passport. This limitation could be also partially left part to the private sector. For example, airline and hotel companies might require vaccination documents to take flights or stay at hotels guests, respectively. This requirement, whether compulsory or not, could also represent for firms a positive signal to compete on.

What would make mandatory vaccination more accepted is the threat of lockdown measures. The economic costs are likely to be higher for individuals working in sectors where sales require spatial agglomeration of consumers (passengers mobility, performing arts, restaurants, etc.). The wider social costs are likely to be perceived stronger by young people who have lost an irrecoverable year of social life.

However, lockdown is a public measure and therefore the usual free rider problem applies. The purely self-interested individual knows that choice not to vaccinate is not pivotal and can free ride by not taking vaccine while enjoying the ease of lockdown, unless everyone thinks the same and free-rides. If we take this feature into account, other-regarding and generativity preferences should be embedded in the model and therefore our suggested communication policies are still valid. With or without other-regarding preferences, the choice to make the vaccine mandatory can solve the coordination failure and technically prevent free riding limiting social and economic activities to vaccinated people only.

7. Concluding remarks

Managing the impacts of the pandemic on population health, the healthcare sector, and the whole economy is a global priority. While the development of effective COVID-19 vaccines can represent a way to significantly minimise these impacts, attitudes toward vaccination are mixed and likely to affect the desired outcomes. In this paper, we outline a simple model with the goal of predicting the share of vaccinated population based on the current evidence, with the primary aim to provide relevant insights for policymakers. While the model is relatively simple in its basic structure and cannot be compared to epidemiological models in terms of prediction accuracy, it is likely to be appealing to a non-specialist audience.

Some policy measures will be crucial to solve the “behavioural free market failure” and achieve the highest level possible of vaccinations. First, communication on outcomes of the first stage and information about the lives of the first group after vaccination are essential for updating of prior probabilities of the second group of sceptics and therefore the final success of the vaccination campaign. Second, communication campaigns trying to create solidarity frames can be critical to switch members of the population from purely self-regarding to other regarding preferences. Third, time slots for vaccination should be limited to avoid the “carpe diem paradox” and the risk of infinite procrastination.

Even if we assume that the negationist share could fall with communication campaigns, the goal of herd immunity and the eradication of COVID-19 in the UK is hardly reachable if the sceptics are perfectly informed about the total vaccinated share as, in proximity of the HIT, vaccination costs outweigh its benefits. In such case, only imperfect information about the total vaccinated share of the population or a share of individuals of the skeptic group with other-regarding preferences can solve the problem. We finally discuss, given the criticality of the situation and the infeasibility of achieving herd immunity, even in the best-case scenario, a range of alternatives between the two extremes of fully voluntary and compulsory vaccination choice. More specifically, we show that a pattern of soft constraints imposed by the private sector can eventually emerge as a mere result of market competition thereby increasing individuals’ incentive to vaccinate.

Our model provides a framework that could be extended to other countries with the application of country specific parameters. New information about crucial model assumptions can lead to the revision of the best-case scenario and its insights can be a starting point for future research on the optimality of vaccination policies in other contexts.

Declaration of competing interest

None.