Abstract
The outbreak of the COVID-19 pandemic has drastically disrupted the air cargo industry. This disruption has taken many directions, one of which is the demand imbalance which occurs due to the sudden change in the cargo capacity, as well as demand. Therefore, the random change leads to excessive demand in some routes (hot-selling routes), while some other routes suffer from a big shortage of demand (underutilized routes). Routes are substitutable when there are several adjacent airports in the Origin & Destination (O&D) market. In this market, demand imbalance between substitutable routes occurs because of the above reasons. To tackle the demand imbalance problem, a novel model is introduced to estimate the quantity combinations which maintains the balance between underutilized and hot-selling routes. This model is a variant of the classic Cournot model which captures different quantity scenarios in the form of the best response for each route compared to the other. We then cultivate the model by integrating the Puppet Cournot game with the quantity discount policy. The quantity discount policy is an incentive which motivates the freight forwarders to increase their orders in the underutilized routes. After conducting numerical experiments, the results reveal that the profit can increase up to 25% by using the quantity discount. However, the quantity discount model is only applicable when the profit increase in the hot-selling route is greater than the profit decrease in the underutilized route.
Keywords: Cournot duopoly model, Quantity discount, Air cargo, Demand imbalance, Capacity allocation
1. Introduction
Air cargo transportation significantly affects the world economic development by connecting a wide range of cities around the world and facilitating the world trade movement (Pearce, 2019). IATA (2017) attributes the importance of air cargo transportation to many reasons, including the safe and fast movement of perishable goods, a more humane means for carrying live animals and suitable treatment of high value and weather sensitive products.
However, the outbreak of COVID-19 has led to many disruptions in the air cargo industry. For example, in April 2020, IATA (2020) reported that the global demand for air cargo fell by 27.7% compared with the demand in 2019. Similarly, the global lockdown of borders upon the outbreak of the COVID-19 pandemic has led to either flight restrictions or even cancelation, and consequently the cargo capacity has also shrunk by 42% compared to the capacity in 2019 (Maneenop and Kotcharin, 2020). The irregularity in the cargo demand and capacity has caused a complex demand imbalance between the existing capacity and demand. This imbalance intensifies in the O&D market. In the O&D market, the nearby airports are considered substitutable. For example, the competition authorities in UK classified substitutable airports into two classes; first the primary airports such as London, Heathrow and Gatwick. Second, the secondary airports, (e.g. Luton and Stansted)(European Competition Authorities, 2002). The substitutability between these airports depends on the passengers and freight forwarders' preferences. Therefore, the existence of multiple adjacent airports on the point of origin and on the point of destination forms many substitutable cargo routes. The capacity utilization in these substitutable routes represents a big dilemma to airlines, especially for combination airlines which operate both cargo and passengers' services. This dilemma appears when the demand on certain routes are much higher than other routes or even higher than the routes’ capacity. The demand imbalance is described as the next:
In regular conditions, airlines offer bookings and selling cargo capacity twelve month before a flight departure. Several freight forwarders book or buy cargo space by means of long-term contracts or in spot market sales (Gupta, 2008). In the planning stage, and based on the forecasted demand, the airline determines the network capacity and assigns aircraft for each route. After the planning period, carriers usually experience contradictory demand-capacity gaps on different routes. In some routes, the cargo ordered by freight forwarders exceeds the capacity (hot-selling), while in some other routes, the ordered cargo quantities are not sufficient to fill even half of its capacity (underutilized). The Civil Administration of China states that the hot-selling routes represent 24.5 percent of all operating routes, and the underutilized routes represent 33.6 percent of all operating routes (Feng et al., 2015). The reasons for this imbalance problem are summarized as follows; first, the difference in the trade movement between cities, shown clearly between Asia-North America and Middle East-Europe lanes (IATA, 2018). Second, Boeing (2018) reported that the increased use of passengers wide-body aircraft leaves more empty space in the belly-hold. This occurs because of the difference between the passengers and cargo traffic which affects the carrier's plan and the route's capacity. Furthermore, combination airlines might also use dedicated freighters (e.g. Emirates, and Singapore airlines). However, this leads to complicated planning operations, especially on the assignment of aircraft (i.e. loading cargo to dedicated freighters or to passengers' belly-hold), and complex terminal operations, and therefore, more expected disruption (Merkert and Ploix, 2014).
As aforementioned, the outbreak of COVID-19 has caused a great disruption in cargo demand and capacity which also led to demand imbalance between substitutable routes. To deal with the demand imbalance problem, carriers need to estimate the cargo quantities to give better utilization between the hot-selling and the underutilized routes. Then, they need to find incentives to motivate the freight forwarders to follow these pre-planned quantities. However, in the existing literature, the balance between hot-selling and underutilized routes were considered in two aspects; an aspect that segments the freight forwarders according to the ordering size, then the large freight forwarders have a greater chance of getting more cargo space in the hot-selling routes, and the small forwarders are allocated to underutilized routes (Feng et al., 2015a). The other aspect does not consider the hot-selling routes and proposes a solution to fill the unused space in the underutilized routes (e.g. (Shaban et al., 2019; Shaban et al., 2018). In this regard, we introduce a novel model, that we name the Puppet Cournot game, to estimate the optimum cargo quantities giving a balance between the hot-selling and the underutilized routes.
This game is a variant of the classic Cournot model. The airline is the only player running the game through the classic Cournot model, treating two types of routes; the hot-selling route and the underutilized route. The airline plays the game with complete information to share the pie of the overall profit between the hot-selling and the underutilized routes. Therefore, the airline plays the game twice; once for the hot-selling route to maximize its profit, and the other to maximize the profit of the underutilized route. The aim of this game is to solve the demand imbalance between the two routes and increase the overall profit of the airline. The Puppet Cournot captures different quantity scenarios in the form of the best response for each route with respect to the other. These scenarios are most likely dependent on the market demand of the two routes. In comparison with the traditional Cournot model, the Nash equilibrium of the Puppet Cournot game does not give a symmetrical solution because the demand in the hot-selling route is higher than the demand in the underutilized route. Also, the determined Nash equilibrium point in the Puppet Cournot represents a reverse point in which the routes exchange their roles. In more detail, for Route 1 and 2, hot-selling and underutilized respectively, our approach gives the best response for this condition until reaching the reverse point. After the reverse point, the best response is given for the condition that Route 1 and 2 become underutilized and hot selling respectively.
Although the Puppet Cournot game gives the quantity balance scenarios to the carrier, it does not consider the thirst of freight forwarders for booking cargo space on the hot-selling routes. Consequently, it is necessary to cope with this issue. The quantity discount policy provides the incentive to freight forwarders to follow the quantity plans of the airline. The quantity discount is mainly used to change the buyers ordering quantities and maximize both the profit of seller and buyer. The seller offers a reduction of the unit price when the buyer orders quantity above a certain break point (Dolan, 1987).It is found significant to use quantity discount policy as an incentive to motivate freight forwarders to increase their orders in the underutilized route. Therefore, we integrate the Puppet Cournot with the quantity discount in order to estimate the optimal preplanned quantities which satisfies both airline and freight forwarders. The integration of the quantity discount to the Puppet Cournot model follows these assumptions. (1) Each freight forwarder orders a fixed amount from the hot-selling and the underutilized routes. (2) In the imbalance condition, the freight forwarders order from the hot-selling route is greater than the underutilized route. (3) A quantity discount is offered to the freight forwarder who orders more in the underutilized route and reduces the same amount in the hot-selling route.
The contribution of this work can be described as follows: (i) except for (Feng et al., 2015) who addressed the demand imbalance problem during the booking horizon by using the strategic foreclosure approach, to the best of our knowledge, most of the related research studies in air cargo capacity allocation and management have only dealt with air cargo allocation by doling out each individual route capacity to multiple freight forwarders. The capacity allocation between the hot-selling and underutilized routes has not been fully considered. In our research, we propose a different capacity allocation solution between two routes. Our approach treats the airline as the puppeteer who controls the Cournot game in order to adjust the quantities in the hot-selling and the underutilized routes. Consequently, the Puppet Cournot model is firstly introduced in this paper. The value of the Puppet Cournot model stems from the quantity scenarios which fix the imbalance between the underutilized and the hot-selling routes. (ii) although quantity discount is used in several applications, it has not received much attention in transportation practice. Also, as far as we know, it has not been used in air cargo research. Therefore, the integration between the Puppet Cournot model and the quantity discount policy provides an important scientific contribution. To summarize, this work contributes in designing a proactive capacity allocation plan to avoid demand imbalance. Finally, it is worthwhile to note that our model resembles McAfee et al. (1989) the multiproduct monopolist model, but the monopoly power of an airline during a disruption may not be able to fit McAfee's model, plus it is not feasible to obligate freight forwarders to get a bundle of hot-selling and underutilized routes. This claim is supported by the report of European Competition Authorities (2002) which refers to the elevated competition among airlines in the substitutable routes.
To summarize, air cargo industry represented in the top management of combination carriers can undertake the Puppet Cournot duopoly game. The application of this game necessitates the airline to collect the historical records of the demand in the hot-selling and the underutilized routes. Also, the cost function of each route is necessary to estimate the best quantity responses. Moreover, the game results imply that the market is split between the two routes. In other words, the Puppet Cournot game model divides the overall demand of the airline between the hot-selling route and the underutilized route. The results give the best quantity scenarios in each route, and hence solve the imbalance problem at any circumstance even after the COVID-19.
The rest of the paper is organized as follows. In section 2, we discuss the literature of the three major topics of this work, air cargo capacity management, Cournot model applications and quantity discount. In section 3, we present the Puppet Cournot model formulation for our problem. Then, we upgrade the model to an integrated Puppet Cournot and quantity discount model, in section 4. In section 5, the experimental analysis and results discussion are presented. In section 6, we state the conclusions, recommendations, and future work.
2. Literature review
This research provides a capacity preplanning model through the integration of the Puppet Cournot and quantity discount models. In the literature, air cargo capacity allocation has received great interest, however, very few studies have been conducted to solve the cargo demand imbalance problem between hot-selling and underutilized routes.
2.1. Air cargo capacity allocation before COVID-19
Before the disruption caused by the COVID-19, the high cargo demand lead carriers to study the cargo overbooking (Kasilingam, 1997; Lin et al., 2017; Popescu et al., 2006), then decide whether to accept or reject cargo orders. Consequently, they can maximize their profit by selling the capacity at the best prices for some forwarders and reject others – an accept-reject policy (Chao and Li, 2017; Levin et al., 2012; Levina et al., 2011). Furthermore, several studies have been used to support cargo capacity management and allocation, such as the contracting between the airline and single freight forwarders (Amaruchkul et al., 2011). As the airline receives the cargo from multiple freight forwarders and the sum of the cargo demand exceeds the route capacity, capacity allocation models are used to maximize the airline's profit by doling out the capacity to multiple freight forwarders (Amaruchkul and Lorchirachoonkul, 2011). Although these studies are necessary to maximize the airline's profit in a one route scale, it is necessary only when the demand is considerably high. Moreover, it is not valid to solve the allocation problem when the airline operates two or more routes, and the demand is high on some routes and low in others.
In the focus of the demand variation between the different routes, few studies have dealt with the demand imbalance among the different routes. Feng et al. (2015) addressed demand balancing between the hot-selling and the underutilized routes by employing strategic foreclosure to develop a tying mechanism. Which classified the freight forwarders into partners and excluded1 the forwarders. A freight forwarder who orders more quantity in the hot-selling route gets more quantity in the underutilized route. Whereas, the excluded forwarders’ orders are allocated into the underutilized routes, however, the model represents complete discrimination between the big and small freight forwarders. Shaban et al. (2019) claimed that the imbalance problem can be solved by filling the capacity of the underutilized route, so they proposed an extra-baggage model. However, they did not consider the relationship between the hot-selling and the underutilized routes. In this regard, we address the imbalance demand between a hot-selling and an underutilized route and define the relationship between the two routes.
2.2. Cournot model and quantity discount
Augustin Cournot was the first to estimate optimal production quantities between two independent firms who compete for perfectly substitutable products the “Cournot duopoly” (Cournot, 1838). The Cournot duopoly model has undergone many changes and development. For example, Edgeworth (1925) claimed that a duopolist can increase revenue by simply reducing the product price, provided that the other duopolist's price is fixed, and gives the same results in the Cournot duopoly and oligopoly. This claim has been tackled by Sonnenschein (1968) who stated that the Cournot model has two different interpretations which was not clear to Edgeworth. Dowrick (1986) integrated the Cournot and leader-follower Stackelberg models to discuss asymmetric duopolies. However, for a duopolist, the comparison between the Cournot model and hierarchical Stackelberg model showed that the Stackelberg profit is greater than the Cournot profit (Anderson and Engers, 1992). Vives (1984) studied the effect of information in the Cournot model, and claimed that the Cournot based information model never gives an optimal market outcome. Ewerhart (2014) studied the Cournot duopoly game for a biconcave demand. Most of the research which adopted or developed the Cournot model followed the original Cournot setup which entails two players performing the game, whereas our model aims at playing the Cournot game with one player as a puppeteer (Carrier). This puppeteer controls two rivals (hot-selling and underutilized routes).
The Cournot adoption is used to estimate the best pre-allocation plan between the two cargo routes, by ignoring the freight forwarder who is thirsty to order cargo quantities in the hot-selling route rather than the underutilized route. Consequently, it is crucial to find a method to attract freight forwarders to increase their purchase in the underutilized route. A quantity discount strategy is an effective method to sell more quantity by decreasing the total of buyers' costs (Crowther, 1964). Yin and Kim (2012) developed an analytical model to apply an all-unit quantity discount in shipping transportation lines. They employed quantity discount to characterize the tariff in a container line. Qiu and Lee (2019) used the Stackelberg (Leader-follower) game to set a single quantity discount break point in the dry port system. They adopted Monahan (1984) settings to estimate the optimal single break-point under an all-quantity discount policy. Our approach aims at avoiding the cargo demand imbalance problem by providing the airline with particular quantities which balance the hot-selling and underutilized routes. Also, it can be used as a reference during the booking horizon. This can be achieved by integrating the Puppet Cournot model with a quantity discount policy to maximize the overall airline's profit by using the common properties of the Cournot model and the quantity discount policy.
3. The Puppet Cournot model
Suppose that an airline sells cargo capacity in two substitutable routes, Route 1 and Route 2. In Route 1, the market demand of the cargo exceeds the airline capacity and it becomes a hot-selling route, while the market demand is drastically insufficient to fill up the capacity of Route 2 which makes it underutilized. It is assumed that the airline sells the unit cargo at price and in the hot selling route and the underutilized route, respectively. The price of each route is sensitive to the actual ordered cargo quantities, such that , and , where is the actual ordered cargo quantity of the hot-selling route, is the actual ordered cargo quantity of the underutilized route, and and are the equations coefficients.2 Also, the forecasted demand in the hot-selling route is and the forecasted demand in the underutilized route is . Furthermore, it is assumed that the sum of the ordered cargo quantities equals the overall demand.
In connection with the demand imbalance between the hot-selling and the underutilized routes, it is supposed that the airline considers them as two profit resources. The profit of the two routes are gained individually. In this regard, the overall profit of the airline is the sum of the individual profit in the hot-selling and underutilized routes. Since the basic objective is to solve the imbalance between these two routes, the airline plays the game to maximize its overall profit by reducing the overbooking costs in the hot-selling routes and by decreasing the shortage costs in the underutilized routes. To do that, the airline plays the game for the two routes as the puppeteer, so we call this game the “Puppet Cournot game”. The advantage of using the Puppet Cournot game in the demand imbalance problem is that the airline is able to determine the best quantity allocation scenarios , and between a hot-selling and an underutilized route, respectively. This can be achieved by estimating the best response of each route to the other. In addition, the model uses the price as a function of the quantity, which is also reversely used to set the prices in both routes. As a proactive plan, it is theoretically supposed that an airline should estimate the profit in the forecasted demand in both the hot-selling and the underutilized routes. i.e. the revenue is obtainable from the routes demand, because the actual demand during the profit expectation is not available during the proactive planning phase. However, airline incurs operational cost for actual sold quantity. This intuition stems from the fact that the fixed cost of exceeds the 57% of the total flight cost, regardless of the amount of cargo, whereas any other costs are incurred based on the actual quantity allocated to aircraft (Shaban et al., 2019). Therefore, the airline profit from Route 1 (CPR1) is,
| (1) |
where is the unit cargo operational cost in Route 1, and similarly, the carrier's profit from Route 2 (CPR2) is,
| (2) |
where is the unit cargo operational cost in Route 2. Then, the airline runs the Puppet Cournot game to estimate the best quantity allocation of Route 1 and Route 2 based on the historical demand data.
The application of our “Puppet Cournot” model introduces the following proposition.
Proposition 1
Let ) are the optimal quantity allocation scenarios, the Puppet Cournot game solves the demand imbalance between Route 1 and Route 2 in the form of the quantity best response of each route to the other as follows ,
- i.
; and
- ii
The unique Nash equilibrium is the point in which the airline receives quantities
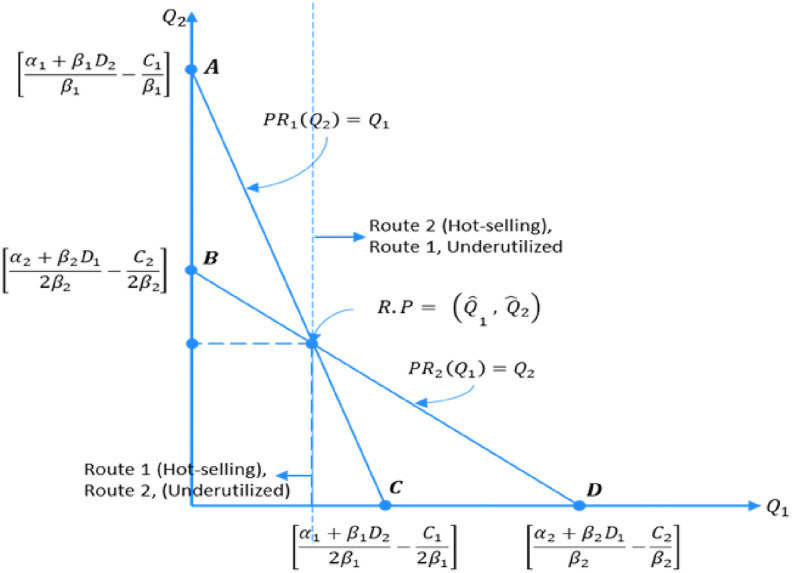
The unique Nash equilibrium represents the point at which the imbalance between Route 1 and Route 2 is exchanged in which the demand of Route 1 is drastically less than its capacity, and the demand in Route 2 exceeds its capacity. This means that Route 1 becomes underutilized, and Route 2 becomes hot-selling. Fig. 1 shows that the Route 1 and Route 2 are substitutable routes, and this leads to a role exchange between the two routes in different seasons. In other words, the route may be a hot-selling route in a particular season, while it changes to underutilized in another season. Moreover, two more reasons can change the route from hot-selling to underutilized and vice versa; first the cargo dimensions (volume and weight), and the second is the change in route capacity which depends on the aircraft assignment. Therefore, the Nash equilibrium in this model represents the reverse point ( The point divides the graph into two areas, the left side provides the best response when Route 1 is the hot-selling and Route 2 is underutilized. On the right side, the best response of each route to the other is obtainable when Route 1 is underutilized, and Route 2 is hot-selling.
Fig. 1.
Schematic diagram of the exchange between the hot-selling and the underutilized routes.
The values of and points in Fig. 1 reveal that the reverse process is asymmetric, i.e., it is similar to the asymmetric Cournot duopoly model, and thus, the reverse calculation in the Puppet Cournot model does not depend only on the quantity, but it also depends on the route capacity and the gap between the demand and the capacity. However, it can be symmetric, if and only if the capacity and demand of the route are identical, and the values of these points will be , and . Consequently, the Nash equilibrium represents the condition that the airline sells equal quantities in both routes, and in this case, the problem is changed from the imbalance problem to either shortage, if the overall demand is not sufficient to fulfill the two routes capacities, or an overbooking problem, when the cargo demand is excessively booming, and the sum routes capacities cannot cover that demand.
Although the Puppet Cournot game provides calculations of the quantities which maintain the balance between the hot-selling and the underutilized routes, the implementation of this method is very difficult, because it is not applicable to force the freight forwarders to follow the quantity allocation plan of the carriers. Consequently, it is necessary to find an incentive policy to encourage the freight forwarders to change the ordering policy and fit the optimum quantity allocation of airline in the hot-selling and underutilized routes. In the next section, we propose a quantity discount strategy to encourage freight forwarders to buy the cargo quantities from the two competing routes, according to the Puppet Cournot results.
4. The Puppet Cournot-Quantity discount (PCQD)Model
In this section, a quantity discount policy is adopted to encourage the freight forwarders to change their ordering between the hot-selling route and the underutilized route. The difference between the Puppet Cournot-Quantity Discount model (PCQD) and the traditional quantity discount model is that the airline aims to balance the hot-selling route and the underutilized route, while the traditional quantity discount is used to reduce the number of orders by increasing the quantity in each order, when the overall demand is fixed along the booking horizon. Moreover, the PCQD model has some features and some assumptions. They can be summarized as follows:
-
•
The sum of the hot-selling and the underutilized routes demand is fixed,
-
•
Since the cargo service is perishable, it is not available in the hot-selling and the underutilized routes after the flight departure.
-
•
Even though the quantity discount is only offered for Route 2 or the underutilized route, the hot-selling route or Route 1 is also affected and the carrier's overall capacity allocation as well.
-
•
As commonly used in the literature, the quantity discount has no effect on the market demand, but it changes the freight forwarders purchases between the hot-selling routes and the underutilized routes.
-
•
The demands of the hot-selling route and the underutilized route are deterministic.
Referring to the first assumption, the sum of Route 1 and Route 2 demands equals the sum of the order quantities in these routes, which is also used in the above model. Based on the other assumptions, the model uses a quantity discount as an incentive to freight forwarders in the underutilized routes to solve the imbalance problem between the hot-selling and underutilized routes. In this manner, the cargo unit price in the underutilized route decreases by increasing the ordered quantity. Also, it is supposed that the increase in cargo quantity in the underutilized route decreases the cargo quantity in the hot-selling route. The new quantities when applying the quantity discount policy can be described by the following equation,
| (3) |
where is the discount factor, and . Moreover, and when , i.e. the airline does not offer quantity discount to freight forwarders.
As a consequence of the quantity change, the price in Route 2 (underutilized route) changes as well. This change yields the discount factor . The price decreasing ratio of Route 2 is a function of the decreasing quantity in the Route 1 (hot-selling route).
| (4) |
The advantage of setting the quantity discount in this form is that the extra-quantity in the hot-selling routes is passed to the underutilized routes. From equation (3), the quantity in the hot-selling route is decreased by ratio . This is reflected on the price decrease in the underutilized route. In addition, the airline is supposed to tie the quantity discount in the underutilized route with the reduced quantity in the hot-selling route . Consequently, when a freight forwarder reduces the ordered quantity in the hot-selling route, the airline offers a price discount in the underutilized route. The resultant of the quantity discount model should also be able to maximize the carrier's profit. The profit of airline from Route 1 with the quantity discount is
| (5) |
and the carrier's profit from the discounted quantity in Route 2 is
| (6) |
The combination of the properties of equations (3), (4), (5), (6) leads to the following fundamental proposition.
Proposition 2
For the integrated Puppet Cournot-quantity discount (PCQD) model, the optimum quantity combinations of Route 1 and Route 2, which solves the imbalance problem, is obtainable from the best response of Route 1 to the quantity in Route 2;
- i.
,
the best response of Route 2 to each ordered quantity in Route 1
- ii.
and the Discount Reverse Point is
- iii
,
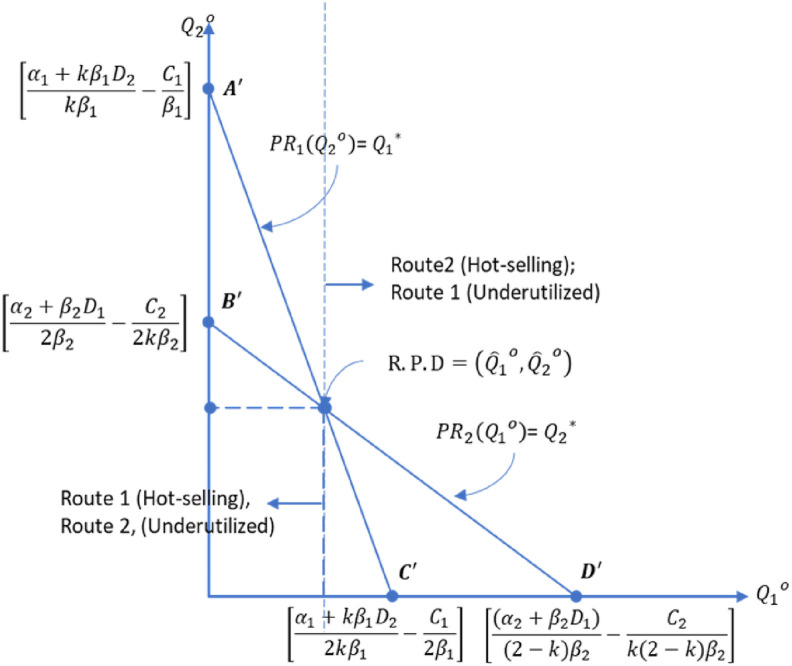
Fig. 2 shows the major changes in the Puppet Cournot game when it is combined with the quantity discount policy to that obtained from the pure Puppet Cournot. The points and change to and The change is a consequence of using the discount factor . Also, in Fig. 2, the values of and are changed to and . The coefficient is decreased to . The value of increases by the decrease of the discount ratio . Furthermore, the discount factor changes the value of to by increasing the cost value, which makes the value . The discount factor affects the point and changes it to where the value of is reduced because of two factors; first, it decreased upon the increase of the cost factor by where . Second, the overall value of is decrease by the value .
Fig. 2.
A schematic diagram of the quantity discount under Cournot setup
For the same parameters, the change in the best responses in Route 1 and Route 2 should also affect the sum of the Route 1 and Route 2 profits. In this regard, a numerical analysis is inevitably needed.
5. Numerical analysis and results
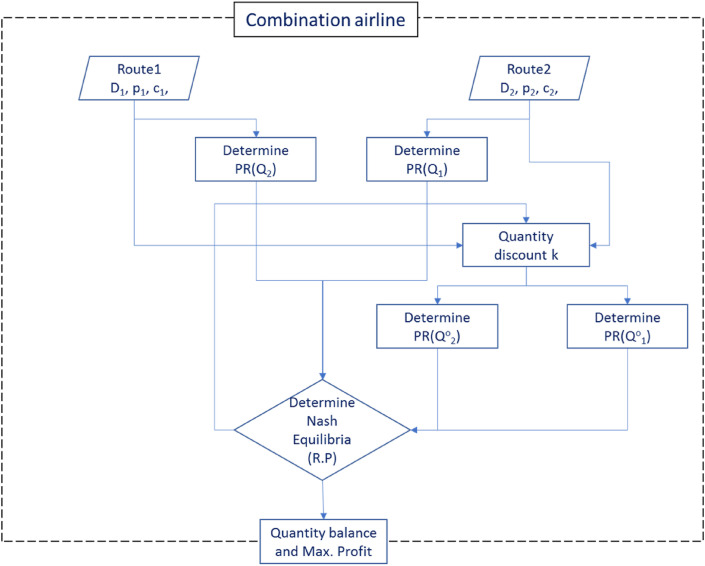
It is worth to note that the PCQD model takes advantage of the Cournot model to estimate the optimum quantity reactions for Route 2 when the freight forwarder orders a certain quantity in Route 1 and vice versa. Also, it revokes the operation cost reduction from the quantity discount policy. In this section, we investigate the effect of the PCQD model in solving the demand imbalance problem. The flowchart in Fig. 3 summarizes the calculation process of the Puppet Cournot discount model. The game starts from the pure Puppet Cournot to the Puppet Cournot-quantity discount model. Also, the flowchart reveals that an airline can exploit the Puppet Cournot solution as an initial negotiation step. If the freight forwarder agrees, so the game ends. The quantity discount policy is an alternative plan in the case that the freight forwarder rejects the offer of the first step.
Fig. 3.
Flowchart of the Puppet Cournot-quantity discount model.
In the beginning, we conduct numerical analysis to examine the quantity allocation between the hot-selling and the underutilized routes, when the pure Puppet Cournot game is adopted. The allocated quantities are achieved by using the best response of each route to the other. In this manner, we use the extracted demand data from (Feng et al., 2015). The price-based quantity equation has been determined by using the International Air Transport Association (IATA) Tact rates (IATA, 2009). A linear regression model was used to estimate the coefficients of the price equation in the hot-selling route and the inverse demand function coefficients in Route1 are , . Similarly, the price function coefficients in Route 2 are , . The operating costs in Route 1 and Route 2 are , and respectively. Moreover, the deterministic demand has been extracted from (Feng et al., 2015). We use the average demand from these data, where the demand in Route 1 is , and the average demand in Route 2 is .
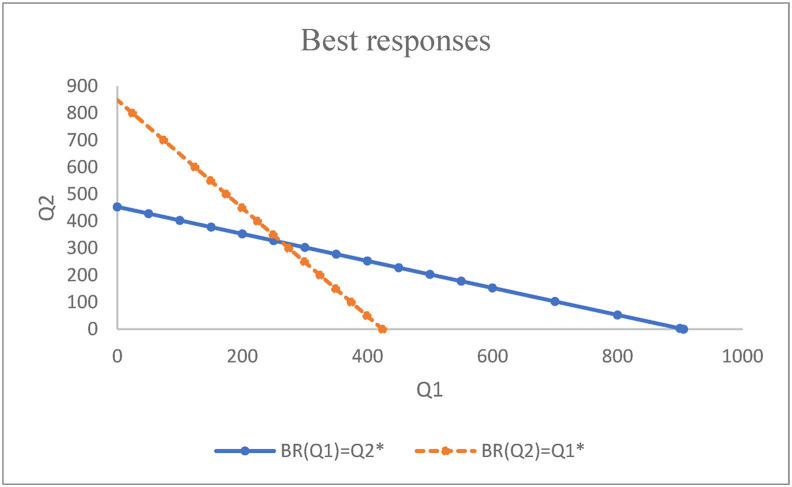
By applying the Cournot model, the results in Proposition 1 are shown in Fig. 4 . Also, the actual response lines are represented. From the actual best responses, the points and values are and . The change in these four points affect the best response which is practical proof to the applicability of our model, because the change in these points depends directly on the route prices and costs.
Fig. 4.
The best responses of the Puppet Cournot model.
Also, the cost differs in the distinct routes, and so our model gives suitable quantity balancing between any two competing routes, as long as the airline has the price-quantity equations and the flight cost functions.
As discussed, the quantity discount advantage is taken to attract freight forwarders to purchase in the underutilized routes. However, it is not always an acceptable choice to carriers. The subsequent proposition describes the effect of integrating quantity discount with the Cournot setup.
Proposition 3
The quantity balance between the hot-selling and the underutilized routes with the PCQD model leads to an increase in the total airline profit if and only if,
This proposition states that the quantity discount is not always applicable to be used with the Puppet Cournot game, and it is only applicable in the condition . For further details, the situations in Route 1 and Route 2 are different because of the Cournot duopoly property, i.e. the fixed cost and the unit cargo price are affected by the quantity change. In the PCQD model, the quantities in Route 1 and Route 2 change inevitably because the discount is proposed when the quantity is reduced in Route 1 by the discount factor , and the discounted quantity from Route 1 is added to the quantity in Route 2. Proposition 3 shows that the profit in Route 1 is always increasing when applying the quantity discount, because the quantity decrease reduces the total operation cost by . Also, in the Puppet Cournot model, the cargo price is a negative function of quantity, which means that the price increases when the quantity decreases. On the other hand, the quantity increase because of the quantity discount leads to profit decrease in Route 2. The profit decrease in Route 2 can be reduced if This most likely happens when the quantity in Route 1, after applying the discount factor , becomes less than the ordered quantity .This explains the reasons for the profit upsurge. To summarize, Proposition 3 provides the constraint that limits the application of the PCQD model, i.e. the quantity discount is only applicable if the airline profit increases. Also, the quantity discount value affects the best response of Route 1 to Route 2 and vice versa.
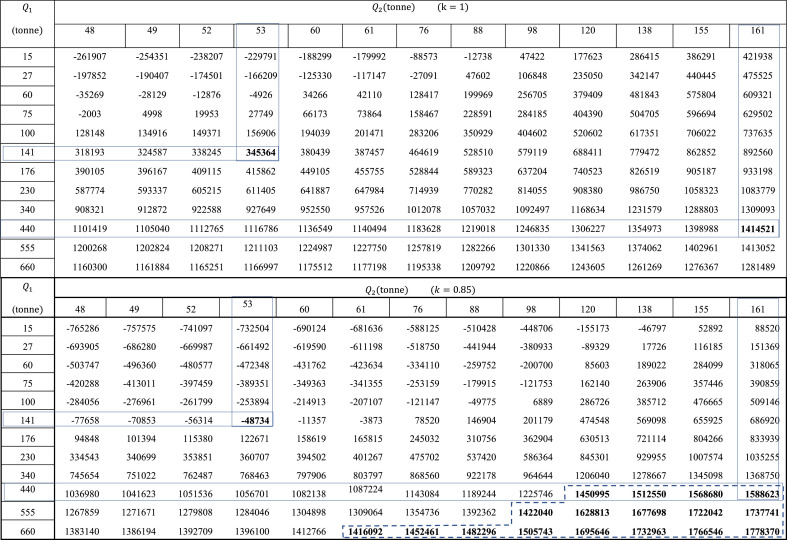
Table 1 shows the difference between the pure Puppet Cournot and the Puppet Cournot-quantity discount models. The results strongly correspond with the context of Proposition 3. For example, for the quantity combination , and tonnes, the airline gains an amount of 345364 USD when not applying the quantity discount policy, whereas the airline loses an amount of 48734 USD. On the other hand, the quantity combination , and tonnes, the profit of the airline increases almost by 12% when the quantity discount is applied. Furthermore, the profit maximization when offering the quantity discount reaches more than 25%, as it is shown in the dashed contour in Table 1.
Table 1.
The sum of airline profits when no quantity discount , and with quantity factor .
6. Managerial implications
With complete information, the top management of combination carriers can undertake the Puppet Cournot duopoly game. The application of this game necessitates the airline to collect the historical records of the demand in the hot-selling and the underutilized routes. Also, the cost function of each route is necessary to estimate the best quantity responses. The game results imply that the market is split between the two routes. In other words, the Puppet Cournot game model divides the overall demand of the airline between the hot-selling route and the underutilized route. The results give the best quantity scenarios in each route, and hence solve the imbalance problem at any circumstance even after the COVID-19. The game in this form is applicable if the airline is monopolistic. This means that the airline can use the power of the monopoly to control the market by applying the Puppet Cournot model.
When the airline has rivals, it is recommended to use the quantity discount as a marketing strategy. The aim of using the quantity discount is to convince freight forwarders to change their demand between the hot-selling and the underutilized routes. Since the overall demand is fixed, the airline uses the quantity discount to pump an amount of cargo from the hot-selling route to the underutilized route. Furthermore, Proposition 3 implies that the unit cargo price in a hot-selling route increases when adopting a quantity discount policy. Consequently, the airline is recommended to control the discount factor to avoid the exaggerated increase in the hot-selling route price. Similarly, the quantity increase in the underutilized route is reflected on its unit cargo price and this also should be considered.
Controlling the value of the discount factor is one of the main difficulties which face the carriers' top management. In more detail, the demand gap between hot-selling and the underutilized routes may affect the determination of the discount factor. This gap brings a trade-off between the carrier's profit and the discount factor. When the demand gap is large, the airline may need to increase the discount amount, and hence, the best response for the quantity in the underutilized route increases. The increase in the underutilized route leads to a decrease in its unit cargo price which may decrease the airline's profit.
Finally, Based on Merkert and Ploix (2014) study, our allocation plan gives airlines' managers preliminary information which can be used to decide whether to assign dedicated freighter to allocate cargo on the belly-hold space of passengers’ wide-bodied aircraft. This is mainly dependent on the estimated balancing quantities from our model.
7. Conclusions
The outbreak of the COVID-19 has caused demand imbalance disruption between substitutable routes. The demand imbalance in cargo routes takes place when the demand in a route exceeds its capacity (hot-selling route), and the route is underutilized when the demand is not sufficient to fulfill its capacity. This paper helps the airline to set the best quantity combination between the hot-selling and the underutilized routes, solving the demand imbalance problem. It is assumed that (i) the two routes, hot-selling and underutilized routes, shares the full demand, (ii) the airline operation costs are fixed on both routes, and (iii) the price of cargo units is dependent on the sold quantity. We propose the novel Puppet Cournot model to cope with this problem. The Puppet Cournot model is a duopoly game between the hot-selling and the underutilized routes but the whole game is controlled by the airline. The model gives the best responses for each route so that airline negotiations with the freight forwarder can be based on these quantity limits.
Although the Puppet Cournot model gives the best quantity scenarios which provide a balance between hot-selling and the underutilized routes, the airline needs an incentive to persuade the freight forwarders to follow the proposed allocation quantities from the Puppet Cournot setup. In this regard, we integrate a quantity discount strategy with the Cournot model. The integration of the Cournot setup and quantity discount policy leads to an increase in the profit in a certain route and profit decrease in the other route. This brings the conclusion: the quantity discount cannot always be used to attract freight forwarders. It can only be used when the increase in a route profit surpasses the profit drop in the other route.
Further, this research is a proactive step which can be used as a preliminary stage in the capacity selling strategies between the airline and the freight forwarders. For example, there are different strategies to sell the capacities in the hot-selling and the underutilized routes, such as the pricing mechanism. Our approach is expected to contribute in solving the price-demand change by the pre-estimation of the optimum cargo quantities because the Cournot model uses the price-based quantity, hence, price-demand sensitivity is already considered in our model. Furthermore, a combinatorial auction is another option to solve the imbalance problem, and our model helps the airline to set quantities in the hot-selling and the underutilized routes which can be used as a reference for the accepted auctions. In addition, the combination of the hot-selling and the underutilized quantities from this model can be used as a reference for the airline when they negotiate the quantity booking in the two routes.
7.1. Research limitations and suggested future directions
In this section, we discuss the limitations of this research and possible suggestions to overcome these limitations and help in the development of this research stream in the future.
For example, regarding the discount factor, its values have a direct effect on changing the quantity combination between the two routes. Because the profit function is neither convex nor concave in the discount factor, the optimum values of the quantity discount need further investigation in the future by using advanced optimization methods. Moreover, The Puppet-Cournot-Quantity Discount model is formulated in the deterministic routes’ demand, although the demand of the air cargo is very random, and it changes rapidly. Formulating the demand in stochastic environment would give more realistic results. Moreover, although the quantity discount policy is very popular incentive, it is not always applicable when solving the demand imbalance problem. Therefore, it would be better to find another incentive to overcome the quantity discount limitations.
In addition, the models in this research are built with fixed prices to set the allocation balance quantities between the hot-selling routes and the underutilized routes. It is suggested that joint prices and quantities are also modelled. Also, the models are formulated in a single period domain, although airlines offer the capacity for selling twelve months before the departure of the flight. Researchers divided booking horizon into guaranteed or long-term contracts, medium-term contracts and dynamic prices, and spot market with free sales. In this regard, the Puppet Cournot model focuses on the guaranteed contracts, but because freight forwarders arrive sequentially, airlines could increase their profit by implementing dynamic domain during the negotiation process. This means that our model ignores freight forwarder's negotiation power which leads to another limitation of this research.
Declaration of interest statement
We wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.
Acknowledgments
The work described in this paper was supported by a grant from the Research Grants Council of the Hong Kong Special Administrative Region, China (Project No. PolyU 15201414); a grant from The Natural Science Foundation of China (Grant No. 71471158); and a grant from the Research Committee of The Hong Kong Polytechnic University under student account code RUMZ.
Footnotes
Excluded freight forwarders here means that airline exclude them from allocation on the hot-selling routes, then they are allocated on the underutilized routes.
These coefficients can be estimated based on the International Air Transport Association (IATA) Tact rules (IATA, 2009).
Appendix A.
Proposition 1
Proof: In this problem, by recalling the assumption that the best response is the quantity which achieves the balance between Route 1 and Route 2, i.e. the best responses are the optimum scenarios of the cargo quantities which should be sold in each route to maximize the airline's profit. The partial differentiation of profit in Route 1 with respect to the Route 1 cargo quantity is . From the problem description, , and the airline is expected to sell quantities in Route 1 more than the market demand in Route 2, i.e. . Therefore, , and . In addition, . Hence, the carrier's profit in Route 1 is concave in , and gives the best response of Route 1 to the quantity in Route 2.
Similarly, the first derivative of the carrier's profit in Route 2 with respect to the cargo quantity is , and the best response of Route 2 to the quantity in Route 1 is estimated by .
The best response of Route 1, and the best response of Route 2, are two linear equations. The intersection of these two equations stands for the unique Nash equilibrium of this game.
Proposition 2
Proof: When applying the quantity discount to sell the cargo quantity in the underutilized route (Route 2), the airline profit in Route 1 is influenced by the price discount factor , i.e. the airline offers a price discount in Route 2 by the discount factor , when the freight forwarder reduces the quantity ordered in Route 1 by the ratio. Similar to Proposition 1, the airline profit in Route 1 can be represented by a quadratic function of the sold cargo quantity in Route 1. The partial derivative of this profit under quantity discount with respect to the quantity ordered from Route 1 is , and . Consequently , and the second derivative is . Therefore, the airline profit is concave in the sold quantity from Route 1. The carrier's best response of Route 1 to the ordered quantity in Route 2 can be estimated when Likely, under quantity discount policy, the airline profit from Route 2 with respect to the ordered quantity is , and the best response of the quantities in Route 2 to the ordered quantities in Route 1 can be achieved when . Moreover, the partial derivatives of the airline profit in both the underutilized route and hot-selling route with respect to the new quantities and , respectively, gives two linear equations. The intersection of these two lines is the Nash equilibrium of the Puppet Cournot quantity discount game .
Proposition 3
Proof This proposition states the impacts of using the quantity discount factor on the airline profit. The total airline profit from the Puppet Cournot game is , and the total airline profit from the PCQD model is Intuitively, the airline profit will be increased if . Under the Puppet Cournot model, this condition can be achieved when , because it considers the two routes compete on the quantities. From this standpoint, the profit difference from upgrading the Puppet Cournot game to the Puppet Cournot- Quantity Discount (PCQD) model in Route 1 can be determined by
and
Therefore, and the profit increases when . and the profit increases when .
References
- Amaruchkul K. A note on air-cargo capacity contracts. Prod. Oper. Manag. 2011;20(1):152–162. doi: 10.1111/j.1937-5956.2010.01158.x. [DOI] [Google Scholar]
- Amaruchkul K., Lorchirachoonkul V. Air-cargo capacity allocation for multiple freight forwarders. Transport. Res. E Logist. Transport. Rev. 2011;47(1):30–40. doi: 10.1016/j.tre.2010.07.008. [DOI] [Google Scholar]
- Anderson S.P., Engers M. Stackelberg versus Cournot oligopoly equilibrium. Int. J. Ind. Organ. 1992;10(1):127–135. doi: 10.1016/0167-7187(92)90052-Z. [DOI] [Google Scholar]
- Boeing World air cargo forecast 2018-2037. 2018. http://www.boeing.com/resources/boeingdotcom/commercial/about-our-market/cargo-market-detail-wacf/download-report/assets/pdfs/2018_WACF.pdf Retrieved from.
- Chao C.-C., Li R.-G. Effects of cargo types and load efficiency on airline cargo revenues. J. Air Transport. Manag. 2017;61:26–33. doi: 10.1016/j.jairtraman.2015.11.006. [DOI] [Google Scholar]
- Cournot A.A. Machmillan & Co., LTD; 1838. Researches into the Mathematical Principles of the Theory of Wealth. [Google Scholar]
- Crowther J.F. Rationale for quantity discounts. 1964;42(2):121–127. [Google Scholar]
- Dolan R.J. Quantity discounts: managerial issues and research opportunities. Market. Sci. 1987;6(1):1–22. doi: 10.1287/mksc.6.1.1. [DOI] [Google Scholar]
- Dowrick S. von Stackelberg and Cournot duopoly: choosing roles. Rand J. Econ. 1986;17(2):251–260. doi: 10.2307/2555388. [DOI] [Google Scholar]
- Edgeworth F.Y. vol. 1. Macmillan; 1925. The pure theory of monopoly; pp. 111–142. (Papers Relating to Political Economy). [Google Scholar]
- European Competition Authorities . 2002. Mergers and Alliances in Civil Aviation.https://ec.europa.eu/competition/publications/eca/report.pdf Retrieved from. [Google Scholar]
- Ewerhart C. Cournot games with biconcave demand. Game. Econ. Behav. 2014;85:37–47. doi: 10.1016/j.geb.2014.01.001. [DOI] [Google Scholar]
- Feng B., Li Y., Shen H. Tying mechanism for airlines' air cargo capacity allocation. Eur. J. Oper. Res. 2015;244(1):322–330. doi: 10.1016/j.ejor.2015.01.014. [DOI] [Google Scholar]
- Gupta D. Flexible carrier–forwarder contracts for air cargo business. J. Revenue Pricing Manag. 2008;7(4):341–356. doi: 10.1057/rpm.2008.29. [DOI] [Google Scholar]
- IATA . 2009. The air cargo tariff manual. Retrieved 2009. [Google Scholar]
- IATA IATA cargo strategy. 2017. http://www.iata.org/whatwedo/cargo/Documents/cargo-strategy.pdf Retrieved from.
- IATA Forecasting air freight demand. 2018. https://www.iata.org/publications/economics/Reports/freigh-forecast/Forecasting-air-freight-demand.pdf Retrieved from.
- IATA Air cargo capacity crunch: demand plummets but capacity disappears even faster. 2020. https://www.iata.org/en/pressroom/pr/2020-06-02-01/ Retrieved from.
- Kasilingam R.G. An economic model for air cargo overbooking under stochastic capacity. Comput. Ind. Eng. 1997;32(1):221–226. doi: 10.1016/S0360-8352(96)00211-2. [DOI] [Google Scholar]
- Levin Y., Nediak M., Topaloglu H. Cargo capacity management with allotments and spot market demand. Oper. Res. 2012;60(2):351–365. doi: 10.1287/opre.1110.1023. [DOI] [Google Scholar]
- Levina T., Levin Y., McGill J., Nediak M. Network cargo capacity management. Oper. Res. 2011;59(4):1008–1023. doi: 10.1287/opre.1110.0929. [DOI] [Google Scholar]
- Lin D., Lee C.K.M., Yang J. Air cargo revenue management under buy-back policy. J. Air Transport. Manag. 2017;61:53–63. doi: 10.1016/j.jairtraman.2016.08.012. [DOI] [Google Scholar]
- Maneenop S., Kotcharin S. The impacts of COVID-19 on the global airline industry: an event study approach. J. Air Transport. Manag. 2020;89:101920. doi: 10.1016/j.jairtraman.2020.101920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McAfee R.P., McMillan J., Whinston M.D. Multiproduct monopoly, commodity bundling, and correlation of values. Q. J. Econ. 1989;104(2):371–383. doi: 10.2307/2937852. [DOI] [Google Scholar]
- Merkert R., Ploix B. The impact of terminal re-organisation on belly-hold freight operation chains at airports. J. Air Transport. Manag. 2014;36:78–84. doi: 10.1016/j.jairtraman.2014.01.003. [DOI] [Google Scholar]
- Monahan J.P. A quantity discount pricing model to increase vendor profits. Manag. Sci. 1984;30(6):720–726. doi: 10.1287/mnsc.30.6.720. [DOI] [Google Scholar]
- Pearce B. Cargo outlook. 2019. https://www.iata.org/pressroom/media-kit/Documents/economics-cargo-day-2018.pdf Retrieved from.
- Popescu A., Keskinocak P., Johnson E., LaDue M., Kasilingam R. Estimating air-cargo overbooking based on a discrete show-up-rate distribution. Interfaces. 2006;36(3):248–257. doi: 10.1287/inte.1060.0211. [DOI] [Google Scholar]
- Qiu X., Lee C.-Y. Quantity discount pricing for rail transport in a dry port system. Transport. Res. E Logist. Transport. Rev. 2019;122:563–580. doi: 10.1016/j.tre.2019.01.004. [DOI] [Google Scholar]
- Shaban I.A., Wang Z.X., Chan F.T.S., Chung S.H., Eltoukhy A.E.E., Qu T. Price setting for extra-baggage service for a combination carrier using the newsvendor setup. J. Air Transport. Manag. 2019;78:1–14. doi: 10.1016/j.jairtraman.2019.04.003. [DOI] [Google Scholar]
- Shaban I.A., Wang Z.X., Chan F.T.S., Chung S.H., Qu T. An extra-baggage service price setting with reference to cargo prices using multi-item newsvendor model. Comput. Ind. Eng. 2018 doi: 10.1016/j.cie.2018.10.041. [DOI] [Google Scholar]
- Sonnenschein H. The dual of duopoly is complementary monopoly: or, two of cournot's theories are one. J. Polit. Econ. 1968;76(2):316–318. [Google Scholar]
- Vives X. Duopoly information equilibrium: Cournot and bertrand. J. Econ. Theor. 1984;34(1):71–94. doi: 10.1016/0022-0531(84)90162-5. [DOI] [Google Scholar]
- Yin M., Kim K.H. Quantity discount pricing for container transportation services by shipping lines. Comput. Ind. Eng. 2012;63(1):313–322. doi: 10.1016/j.cie.2012.03.008. [DOI] [Google Scholar]