Hematoma Segmentation Using Dilated Convolutional Neural Network

Abstract

Traumatic brain injury (TBI) is a global health challenge. Accurate and fast automatic detection of hematoma in the brain is essential for TBI diagnosis and treatment. In this study, we developed a fully automated system to detect and segment hematoma regions in head Computed Tomography (CT) images of patients with acute TBI. We adapted the structure of a fully convolutional network by introducing dilated convolution and removing down-sampling and up-sampling layers. Skip layers are also used to combine low-level features and high-level features. By integrating the information from different scales without losing spatial resolution, the network can perform more accurate segmentation. Our final hematoma segmentations achieved the Dice, sensitivity, and specificity of 0.62, 0.81, and 0.96, respectively, which outperformed the results from previous methods.

I. INTRODUCTION

Traumatic brain injury (TBI) is associated with a high mortality and morbidity rate. To facilitate the diagnosis and evaluation of TBI, Computed Tomography (CT) is the preferred imaging modality during the first 24 hours after the injury [1] because of its low cost, rapid scanning capability, and availability. The volume, location, and shape characteristics of hematoma detected in CT are significant factors for the physician to evaluate the severity of the TBI and perform appropriate treatment [2]. Also, many studies show that the volume of brain hematoma is vital for outcome prediction and agent efficacy estimation [3], [4].

Since the manual examination of CT scans is tedious and prone to errors in the estimation of hematoma volume, automatic hematoma detection and segmentation can efficiently decrease medical costs by reducing the time for image analysis, while providing more accurate clinical parameters for the physician to make appropriate and timely medical decision. It is a challenging task because CT has poorer tissue contrast than MRI.

Despite this challenge, many CT-based hematoma segmentation algorithms have been proposed. A semi-automated brain hematoma segmentation method was introduced in [5], where the user can provide a fixed intensity threshold to initialize seed point and then the region growing was performed for the segmentation. Liao et al. [6] found candidate hematoma regions using ‘standard’ thresholds and connectivity and the multi-resolution binary level set segmentation was applied to divide the soft tissue regions into normal brain tissues and hematomas. In [7], a Gaussian Mixture Model (GMM) was built by taking four components (i.e., hematomas, gray matter regions, white-matter regions, and catheter, respectively) of Gaussian density and calculating the density using Expectation Maximization (EM) until convergence was reached. Most of the methods rely on intensity values to generate seeds or region-of-interest mask as the first step. Although there are textbook CT numbers for different tissues, the variation of CT numbers due to various scanning parameters and physical complications such as scattering has been pointed out by many studies [8], and it is common that the intensity range of hematoma tissue overlaps that of normal brain tissue.

Recently, convolutional neural networks (CNNs) have achieved extensive success in image recognition and segmentation. They are supervised models that can learn discriminative features automatically, often outperforming models using hand-crafted and knowledge-based features. Grewal et al. [9] proposed Recurrent Attention DenseNet that uses DenseNet architecture as a baseline CNN to learn slice-based features. These features are then integrated into a Long Short-Term Memory network that utilizes the 3D context to make a final, pixel-wise classification. In [10], a 3D CNN with patch-wise training followed by a fully connected conditional random field was proposed for brain lesion segmentation.

In this work, we proposed a fully convolutional network (FCN) combined with dilated convolutions to segment hematoma in patients with acute TBI. It takes inputs of arbitrary size and produces correspondingly-sized output with pixel-wise prediction. The modern CNNs integrate multi-scale contextual information via successive down-pooling layers, and this down-pooling will reduce the resolution of the dense prediction. To overcome this conflict, we integrated dilated convolutions, proposed by Yu et al. [11], that aggregate multi-scale contextual information without losing resolution. In our experiments, we found that the model we designed outperformed the previous methods and achieved a satisfying segmentation for brain hematomas.

II. Methods

A. Preprocessing

All the CT scans are stored in Digital Imaging and Communication in Medicine (DICOM) format. We first performed the CT numbers conversion:

$$I_{HU}=I_{\mathit{\text{raw }}}\times \mathit{\text{ slope }}+\mathit{\text{ intercept }}$$ (1)

where I_raw is the image with gray values stored in DICOM format, I_HU is the transformed image with CT numbers, and slope and intercept are parameters retrieved from the DICOM header file. CT number is defined in Hounsfield units (HU).

A linear mapping shown in (2) was performed to scale the dynamic range of HU in 16-bit DICOM format into 8-bit grayscale:

$$I(i,j)=\{\begin{array}{ll}0\hfill & I_{HU}(i,j)<a\hfill \\ \frac{I_{HU}(i,j)-a}{b-a}\times 255\hfill & a\le I_{HU}(i,j)\le b\hfill \\ 255\hfill & I_{HU}(i,j)>b\hfill \end{array}$$ (2)

where I is the image after intensity scaling, $a=wc-\frac{ww}{2}$, $b=wc+\frac{ww}{2}$, and ww and wc are the window width and the window center, respectively, obtained from the DICOM header file. Although CT numbers have a wide range, neural soft tissue only lies in a small interval. Commonly, a window width of 80 HU and window center of 40 HU, i.e., a = 0 HU and b = 80 HU, are used to visualize brain CT images. In this study, as acute hematomas are usually brighter than brain tissues, we used a = 0 HU and b = 140 HU to cover more pathologic tissue.

B. Architecture

U-net is an extension of FCN proposed in [12] that can be trained using relatively few images. It is named by its U-shape where the input is down-sampled by successive max-pooling layers and then up-sampled to generate dense predictions. We modified U-net by incorporating dilation convolution as described in [11].

Let us define the discrete convolution operator * as

$$(F*k)(p)=\sum _{s+t=p}F(s)k(t)$$ (3)

where $F:{\mathbb{Z}}^2\to ℝ$ is a discrete function and $k:{\Omega }_r\to ℝ$, Ω_r = [−r, r]², $r\in \mathbb{Z}$ is a discrete filter of size (2r + 1)², t are from [−r, r]², s, p are from ${\mathbb{Z}}^2$. With a dilation factor l, the dilated convolution is defined as

$$(F*k)(p)=\sum _{s+lt=p}F(s)k(t)$$ (4)

Since we removed most of the down-pooling and up-pooling layers, we named the left side of our architecture as the localization path and the right side as the segmentation path to elucidate their roles. As shown in Figure 1, our architecture is comprised of 4 blocks, with each block having two 3×3 convolutional layers in the localization path and two convolutional layers in the segmentation path. For the first block, the convolutional layers are followed by a 2 × 2 max pooling layer with a stride of 2 in the localization path and a 2 × 2 up-sampling layer using repetition in the segmentation path to reduce the GPU memory load and computational cost. As described in [11], without down-sampling layers, the dilated convolutions can aggregate multi-scale context information and avoid losing resolution, which will increase the accuracy of dense prediction. Thus, in remaining blocks, all down sampling and up sampling layers are removed and convolutional layers are dilated with a dilation factor k. A batch normalization layer [13] is added after every convolutional layer, and then the rectified linear unit (ReLU) is used as the activation function. In CNNs, as the inputs pass increasing numbers of convolutional layers, the feature maps become coarser and tend to represent features in a higher level. To compensate the loss of fine structure information and combine coarse, high level information with fine, low level information, the feature maps F_i1 from the block i in localization path are concatenated with the input I_i2 in segmentation path of the same block, i.e. the feature maps F_(i+1)2. As a result, the channel dimension of inputs for the first convolutional layers in each blocks segmentation path are doubled as: {F_i1, F_(i+1)2}. Finally, the feature maps from the first blocks segmentation path go through a 1 × 1 convolutional layer and an element-wise soft-max function to generate the final segmentation map.

Fig. 1.

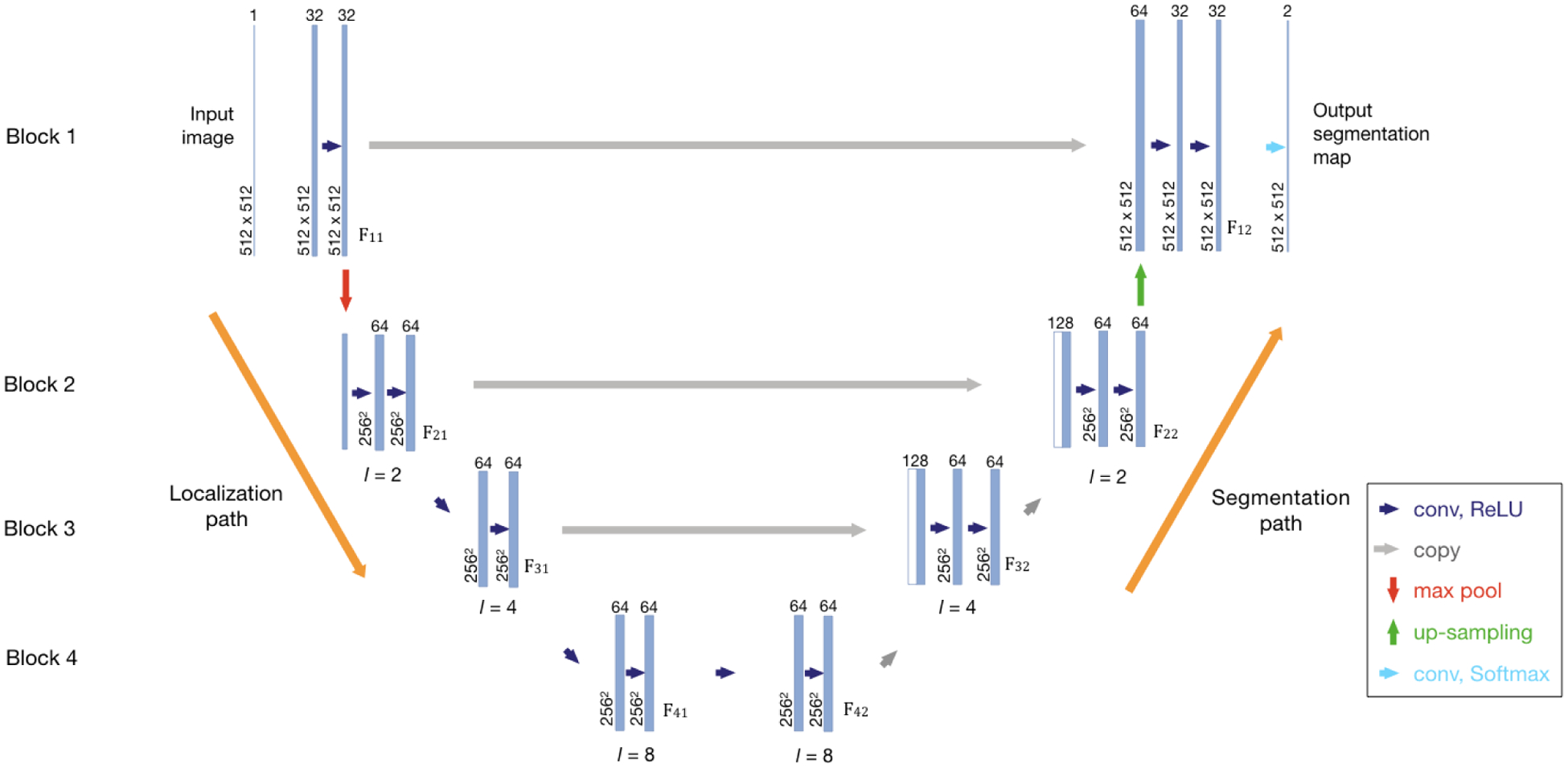
The Network Architecture. The left side of the network is the localization path, and the right side is the segmentation path. The spatial size and the number of feature maps are given. The network contains four blocks, and each block consists of convolution layers in both paths. In the same block, the feature maps from the localization path are concatenated with the input of the segmentation path. F_ij denotes the feature maps from blocks, where i is the index of block. If j = 1, the feature maps are in the localization path. Otherwise, they are in the segmentation path. The dimensions of feature maps and the dilation factor l used in each block are given.

In our design, the left side of the architecture aims to utilize contextual information and extract textural features to distinguish different components in brain and predict a rough localization mask and the right side integrates both low-level and high-level features to make final segmentation. But it should be noted that the localization and segmentation process cannot be separated explicitly.

C. Training

The preprocessed CT images and manually labeled segmentation masks were used to train the network. Considering the limited number of training images with hematomas, we used rotation and elastic transforms to augment our training data; enabling the learning algorithm to infer rotation and transformation invariance. A general image transformation can be defined as

$$T(x+\Delta x,y+\Delta y)=I(x,y)$$ (5)

where I is the input image and T is the distorted image. In the elastic transform [14], a displacement field is first generated where Δx and Δy are random values sampled from the uniform distribution U(−1, 1). After that, a Gaussian distribution with standard deviation σ and multiplied by a scale factor α was used to convolve Δx and Δy. When σ is large, the resulting values are close to 0, which is the average of random values and when σ is small, the displacement field is a completely random filed. In this study, we used σ = 5, α = 3 to generate distorted images as in (5). No change in the image size was induced by implementing these data transformations.

In the last layer, the number of feature channels is the same as the number of classes K. In this study, K = 2. The loss is defined by a sum of a pixel-wise weighted cross entropy over the final feature map:

$$\mathit{\text{loss}}=\sum _{x\in \Omega }w(g(x))\text{ log}\left(a_{g(x)}(\text{x})\right)$$ (6)

where a_k(x) is the activation in the k^th feature channel at the position x ∈ Ω , g : Ω → {1, …, K}, $\Omega ={\mathbb{Z}}^2$ is the ground truth at the pixel level, and $w(g(\text{x})):\left\{1,\dots ,\text{K}\right\}\to ℝ$ is a weight function to put pixels in different classes with predefined importance. In this study, considering that the hematoma regions were much smaller than normal regions, we gave pixels belonging to hematomas two times the importance to avoid bias.

The L2 weight decay regularization of 0.0005 was used to improve the generalization ability of the model. The Adam optimizer was used to minimize the cross-entropy loss with an initial learning rate of 10⁻⁴. The learning rate was reduced to 1/10th of the current value when the validation loss stopped decreasing after 20 epochs. The network weights were initialized according to the Xavier scheme as described in [15]. The model was trained for 200 epochs with a batch size of 10.

D. Post-processing

The output of the CNN usually contains some small false positive regions which is result from the heterogeneities in the intensity of soft tissues. A simple post-processing method was designed based on the prior knowledge that a hematoma should be large enough to be of clinical importance. In this study, we assumed hematomas regions are always more than 1 cm in thickness. In other words, if there is a hematoma region in one image, then there must be other connected regions of hematoma similarly located on the slices either above or below that image. Otherwise, we can either say that the hematoma detected in this image is very likely to be a false positive or it is a very small hematoma that is not clinically important. We used the breadth-first search algorithm to find out and remove such false positives.

E. Evaluation

We computed accuracy, sensitivity, and specificity of the pixel level predictions for each patient. The Dice coefficient was calculated for each patient to evaluate the overall segmentation performance and it takes the format:

$$\mathit{\text{ Dice }}=\frac{\left|X\cap Y\right|}{\left|X\right|+\left|Y\right|}$$ (7)

where X is the predicted hematomas and Y is the hematomas in the ground truth, and |X| denoting the number of pixels in X. The volume of the hematoma can calculated as:

$$\mathit{\text{Volume }}=\left|X\right|\times \mathit{\text{ slice spacing }}\times {\mathit{\text{ pixel spacing }}}^2\times {10}^{-3}$$ (8)

where slice spacing and pixle spacing can be determined by parameters in DICOM metadata. The volume is in cm³.

III. Experimental Results

The dataset we used consists of 27 cases from a dataset of patients with Acute TBI admitted at University of Michigan Health System and 35 cases from Progesterone for Traumatic brain injury: Experimental Clinical Treatment (ProTECT) [7]. The ProTECT study involved adults who experienced a moderate to severe head injury and patient were enrolled in an emergency department within 4 hours of their injury. In total, 2433 axial CT images of 4.5 to 5mm slice thickness from 62 patients who suffered from acute TBI were used in this study. We randomly split the data into the training set (n=48) and test set (n=14). An experienced medical expert sifted and examined through 2D cross-sectional slices, manually drew the boundary around hematoma regions on every slice to generate the ground truth.

Figure 2 gives two examples of our segmentation result compared with the ground truth. The first row in Figure 2 shows our model is resistant to the effect of the bones and other anatomical structures. The second row presents a challenging case, where the hematoma regions are dispersed around the skull and with different shapes. Our model can accurately localize the hematoma regions and perform a delicate segmentation.

Fig. 2.

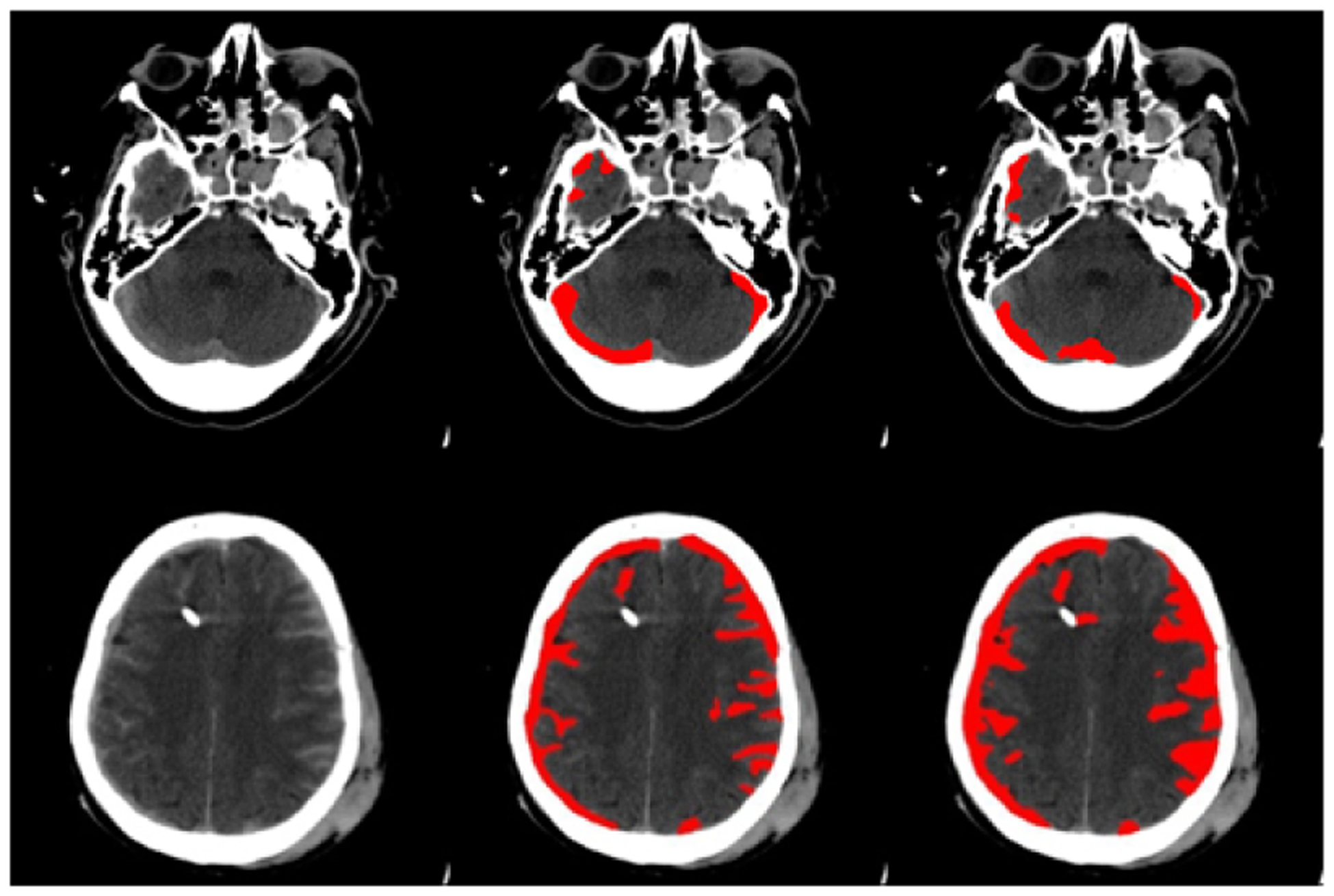
Segmentation results. Each row gives an example of the segmentation compared with the ground truth. The left column: images after intensity stretch; the middle column: ground truth; the right column: segmentations from our method

We evaluated the performance of our model on different volumes of brain hematomas. Clinically, the volume of a hematoma can reflect the severity of TBI. The larger the hematoma, the more important it is that our model detect and segment it successfully. From Table I, our method can segment larger hematomas with a very high Dice score.

TABLE I.

Evaluation of the model on different volumes of hematomas

Size	Tiny	Small	Medium	Large	Very Large
Volume	<1	1–10	10–25	25–50	>50
Dice (stddev)	0.49 (0.25)	0.59 (0.18)	0.66 (0.18)	0.70 (0.19)	0.80 (0.081)

Finally, the segmentations achieved by our trained model were compared with the ground truth, and Table II is a summary of that evaluation. A previous method using GMM combined with EM and the original U-net were used for the comparison. The results show that our trained model has better segmentation performance.

TABLE II.

Overall segmentation performance

Method	Dice	Sensitivity	Specificity	Accuracy
Our proposed method	0.62	0.81	0.96	0.95
U-net [12]	0.58	0.76	0.94	0.92
GMM [7]	0.39	0.51	0.91	0.88

IV. Conclusion

In this paper, we presented a modified U-net integrated with dilated convolution. Our results show that removing down/up-sampling layers and integrating dilated convolution can improve the resolution of dense prediction and improve the final segmentation performance. The Dice score for hematoma segmentation is 0.62, and it achieved a significant increase compared with GMM. Future work could continue to improve the segmentation performance by integrating 3D contextual information.