Reactivity of a Gold-Aluminyl Complex with Carbon Dioxide: A Nucleophilic Gold?

Abstract

A gold-aluminyl complex has been recently reported to feature an unconventional gold nucleophilic center, which was revealed through reactivity with carbon dioxide leading to the Au-CO₂ coordination mode. In this work, we computationally investigate the reaction mechanism, which is found to be cooperative, with the gold–aluminum bond being the actual nucleophile and Al also behaving as electrophile. The Au–Al bond is shown to be mainly of an electron-sharing nature, with the two metal fragments displaying a diradical-like reactivity with CO₂.

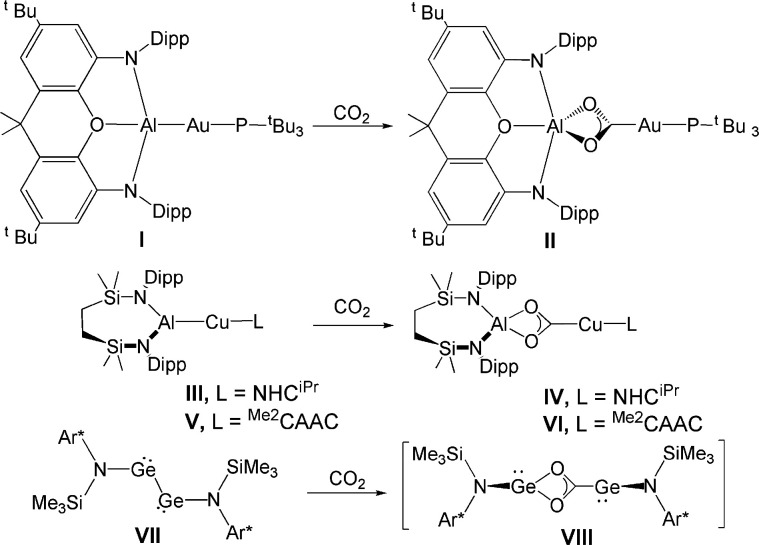
Recently, a striking reactivity of CO₂ with a complex bearing a Au–Al bond has been reported.¹ A combination of the new generation aluminyl anion² [K{Al(NON)}]₂ with a phosphine gold ^tBu₃PAuI affords the [^tBu₃PAuAl(NON)] complex (I) which, in reaction with CO₂ (1 atm at room temperature in toluene), leads to the stable [^tBu₃PAuCO₂Al(NON)] complex (II), where Au binds to the CO₂ carbon atom (Scheme 1). This CO₂ coordination mode has been considered as the revealing of an unconventional nucleophilic behavior of gold, which, in contrast, is well-known to be an extremely powerful electrophile in organic reactions involving unsaturated CC bonds.³ The authors suggested that the aluminyl anion [Al(NON)]⁻ is able to induce an extremely polarized Au(δ-)-Al(δ+) bond, with a significant negative charge at the gold site, which is able to reverse its reactivity. DFT calculations combined with quantum theory of atoms in molecules (QTAIM) charge analysis have shown a substantial electron transfer from [Al(NON)]⁻ to [^tBu₃PAu]⁺ (1.56 electrons) and a negative charge at Au (−0.82).¹ This picture seems to be consistent with the difference in electronegativity values of the two metals (Au = 2.54, Al = 1.61 on the Pauling scale) and with the relativistic effects on gold which stabilize and contract the 6s orbital,⁴ resulting in the gold highest electron affinity (2.30 eV) among transition metals (other coinage metals have considerably smaller values, Cu 1.23 eV; Ag 1.30 eV).⁵ Complex I is not the only complex in which Au would act as a nucleophile toward polar multiple bond.⁶ Two copper-aluminyl complexes (III and V in Scheme 1) have been reported to insert CO₂ into the Cu–Al bond, resulting in complexes IV and VI (Scheme 1), which are very much similar to complex II in terms of structure and kinetic stability.⁷ A significant covalency of the Al–Cu bond and only slightly negative charges on Cu (e.g., −0.09 in III) have been calculated, revealing here only a small polarization of the M(δ-)-Al(δ+) bond.

Scheme 1. Examples of Nucleophilic Gold (I),¹ Copper (III, V),⁷ and Amido-Digermyne (VII)¹² Compounds and Their CO₂ Insertion Reaction Products (II, IV, VI, and VIII).

In addition to strongly polarized M(δ-)-Al(δ+) bonds in heterodinuclear complexes,⁸ CO₂ activation by homodinuclear main-group element species,^9,10 including diradicals,¹¹ is not uncommon. Frenking and Jones¹² demonstrated that the facile reduction of CO₂ to CO by a symmetric amido-digermyne compound (VII) proceeds through an asymmetrical intermediate (VIII) that bears a structural analogy with complex II.

The similar coordination modes of CO₂ in the Au–Al, Cu–Al, and Ge–Ge bonds is eye-catching, in view of the different degrees of polarization of the insertion metal–metal site, which is expected to determine the effectiveness of the metal nucleophilic behavior. This prompted us to computationally investigate the mechanism of the CO₂ insertion into the pioneering nucleophilic [^tBu₃PAuAl(NON)] complex which has not been explored yet and the actual nucleophilic ability of Au in this “unorthodox reaction “.¹³ We demonstrate that the nucleophilic attack is actually performed by the Au–Al σ bond, revealing a bimetallic (Au/Al) cooperation in the CO₂ binding. The attack is also assisted by a secondary interaction, involving the partially empty 3p_x atomic orbital of Al, which exploits its Lewis acidity. Transition state and intermediate structures found here suggest a radical-like insertion of CO₂ in the Au–Al bond, which has been consistently shown to have an electron-sharing character.

The free energy profile for the CO₂ insertion into the Au–Al bond of I was calculated using density functional theory (DFT) with the inclusion of relativistic effects, solvation, and dispersion interactions (see SI for computational details), and it is shown in Figure 1. Complex I was slightly simplified at the NON site (denoted as NON’). The modeling effect is evaluated in Table S1. The optimized geometries of [^tBu₃PAuAl(NON’)], RC, TSI, INT, TSII, and [^tBu₃PAuCO₂Al(NON’)] (PC) complexes are reported in the SI (Figure S1) and show good agreement with available experimental data (Figure S2 and Table S2).

Figure 1.

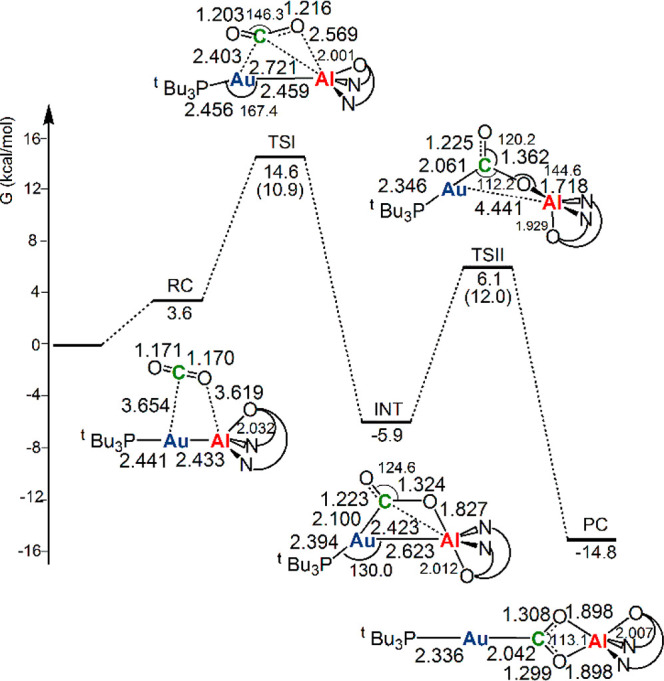
Free energy reaction profile for the CO₂ insertion into the Au–Al bond in the [^tBu₃PAuAl(NON’)] complex. ΔG values refer to the energy of the separated reactants taken as zero. Activation free energy barriers are reported in parentheses. Selected interatomic distances (Å) and bond angles (degrees) are given with the molecular structures.

The nucleophilic attack to the CO₂ carbon atom has a relatively low activation free energy barrier (ΔG^# = 10.9 kcal/mol). At the TSI, the carbon atom of CO₂ is both very close to Au (2.403 Å) and at a relatively short distance from Al (2.721 Å), and a substantial bending of CO₂ and asymmetry between the two C–O bonds are also observed (see Table S3 for the evolution of the most relevant Mayer’s bond orders along the reaction path). Subsequent complete bonding of CO₂ carbon atom to Au and oxygen atom to Al leads to the formation of intermediate INT, which is stabilized by 20.5 kcal/mol. As a result, the Au–Al bond distance slightly increases and the ^tBu₃PAu moiety coordinates almost linearly with the carbon atom of CO₂. A second transition state (TSII) is located with an activation free energy barrier ΔG^# of 12.0 kcal/mol, showing a substantial breaking of the Au–Al bond. Finally, the oxygen atom of CO₂ attack to the electrophilic Al center leads to the thermodynamically stable product complex PC. The overall CO₂ insertion into the Au–Al bond is exergonic by −14.8 kcal/mol.

To get insights into the nature of the CO₂ insertion process, we analyze the first activation barrier using the Activation Strain Model (ASM)¹⁴⁻¹⁶ (main results in Figure 2, left panel). The ASM formalism is briefly summarized in the SI, and all the results are reported in Table S4.

Figure 2.

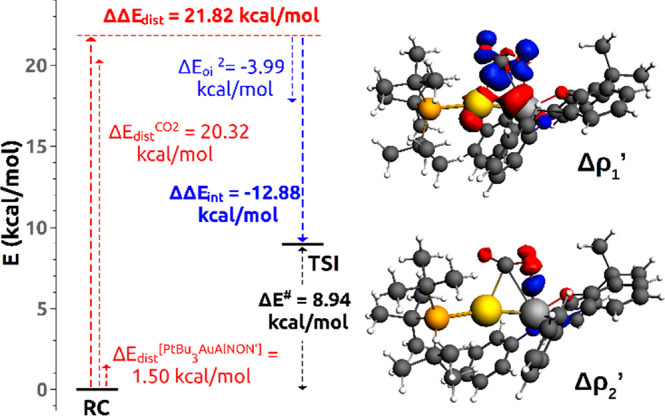
Activation Strain Model (ASM) decomposition of the electronic energy activation barrier ΔE^# (left) (see text). Isodensity surfaces (2 me/a₀³) for the NOCV deformation density maps (charge flux is red → blue) corresponding to the Δρ₁’ (top right) and Δρ₂’ (bottom right) contributions to the CO₂-[^tBu₃PAuAl(NON’)] fragments interaction in the transition state TSI.

The distortion energy contribution (ΔΔE_dist = 21.82 kcal/mol) to the electronic energy activation barrier (ΔE^#=8.94 kcal/mol) is almost completely associated with the CO₂ bending (20.32 kcal/mol, see Table S5), whereas the stabilizing interaction contribution (ΔΔE_int= −12.88 kcal/mol) mainly arises from the orbital interaction energy at TSI (−53.30 kcal/mol) (see Table S6). The results of the ETS-NOCV¹⁷ method coupled with the Charge Displacement (CD) Analysis¹⁸ (see SI for methodological details) are summarized below. In Figure 2 (right panel), the two most important components (Δρ₁’ and Δρ₂’) of the total deformation density are shown.

The main interaction component (Δρ₁’) is clearly characterized by an electron density depletion localized on both Au and Al atoms and by an electron density accumulation at the CO₂ site. This component is associated with a significant energy stabilization (−41.20 kcal/mol) and a charge transfer from the Au–Al bond region to carbon dioxide of 0.326 e. The decomposition into the donor and acceptor NOCV orbitals¹⁹ (Figure S3) shows that the electron density accumulation has the main contribution from the LUMO of CO₂, while the electron density depletion shows contributions from the HOMO–2 and HOMO of the [^tBu₃PAuAl(NON’)] fragment, both representing the Au–Al σ bond, where Al 3s3p_z–Au 6s6p_z type orbitals are involved. Component Δρ₂’ reveals an electron density accumulation at the Al center (note that its shape recalls that of an atomic p_x orbital), coming from one of the oxygen atoms of CO₂. Decomposition into donor and acceptor NOCV orbitals (Figure S4) shows that the main contribution to the donor orbital is the HOMO of CO₂, whereas a clear characterization of the acceptor orbital is less straightforward, since several delocalized unoccupied MOs, all with small Al 3p_x orbital mixing, contribute to it. The Δρ₂’ contribution is not negligible: 0.047 e are transferred toward Al from CO₂, with an associated orbital interaction energy of −3.99 kcal/mol (which notably accounts for one-third of the interaction stabilization to the activation barrier ΔΔE_int).

The reaction mechanism in Figure 1 bears surprising analogies with the first steps of the reaction profile for the reduction of CO₂ to CO by [LGe-GeL] (see Figure 3 of ref (12)), although complex II does not evolve to CO elimination (the resulting oxide complex [^tBu₃PAuOAl(NON’)][CO] has been calculated to be highly unstable with ΔG = 29.8 kcal/mol). The high reactivity of digermynes has been often attributed to the nonnegligible biradical character in these systems.^11,19,20 A possible diradicaloid character of the Au–Al bond in the [^tBu₃PAuAl(NON)] complex is certainly very intriguing. Remarkably, the coordination modes of CO₂ in the separated neutral open shell doublet [^tBu₃PAu(CO₂)]· and [CO₂Al(NON’)]· fragments closely match those found at the TSI and INT (Figures S5, S6 and discussion therein). This prompted us to review the Au–Al bond nature in complex I. We carry out the CD-NOCV analysis on the [^tBu₃PAuAl(NON’)] complex by choosing the open-shell radical fragments [^tBu₃PAu]· and [(NON’)Al]· on the basis of EDA analysis²¹ using different fragmentations (Table S7 and ref (22)). The main results of the CD-NOCV analysis are reported in Figure 3.

Figure 3.

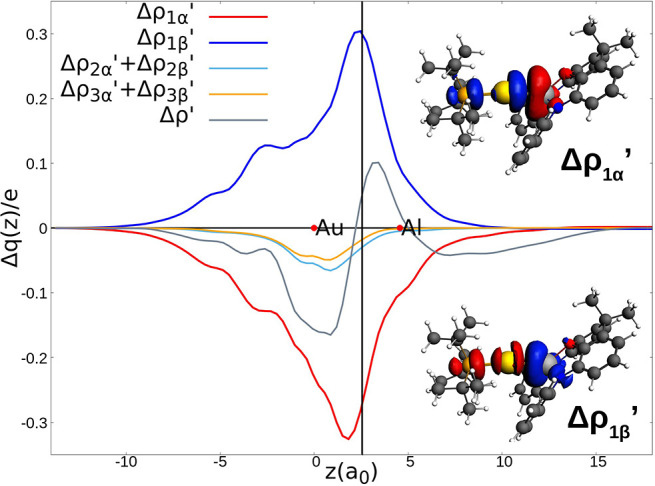
Charge Displacement (CD-NOCV) curves for the interaction between doublet [^tBu₃PAu]· and [(NON’)Al]· fragments in the [^tBu₃PAuAl(NON’)] complex. Red dots indicate the position of the nuclei along the z axis. The vertical solid line marks the isodensity boundary between the fragments. Positive (negative) values of the curve indicate right-to-left (left-to-right) charge transfer (see Supporting Information for details). Insets: isodensity surfaces (1 me/a₀³) of the two NOCV deformation densities Δρ_1α’ (top, right) and Δρ_1β’ (bottom, right) (charge flux is red → blue).

The CD-NOCV curves clearly exhibit two similar main charge fluxes in opposite directions, which consist of an electron transfer from Au toward Al (Δρ_1α’, red curve and inset in Figure 3) and from Al toward Au (Δρ_1β’, blue curve and inset in Figure 3). These two charge fluxes have also similar CT absolute values (0.272 and 0.299 e for Δρ_1α’ and Δρ_1β’, respectively), associated orbital interaction energies (−32.66 and −24.49 kcal/mol for Δρ_1α’ and Δρ_1β’, respectively), and NOCV eigenvalues (0.45 and 0.42 for Δρ_1α’ and Δρ_1β’, respectively) as shown in Table S8. Other contributions to the Au–Al bond (CD-NOCV curves labeled as Δρ_2α’ + Δρ_2β’ and Δρ_3α’ + Δρ_3β’) describe the π back-donations (see Figure S7) and are definitely smaller in magnitude. The CD curve associated with the total deformation density (Δρ’) shows an almost symmetric charge accumulation at the bonding region with a slightly positive CT (0.05 e) going from the radical [(NON’)Al]· to [^tBu₃PAu]·, which can be associated with the net polarization of the Au–Al bond. To definitely assess the electron-sharing bond nature, the CD-NOCV analysis for a nonpolar covalent bond system, such as the homonuclear Au₂ molecule, is presented in Figures S8, S9 for comparison. The CD-NOCV curves in Figure 3 and Figure S8 are indeed very similar.

We also find that this bonding scheme is not peculiar of the Au–Al bond in [^tBu₃PAuAl(NON’)]. A qualitatively analogous picture has been also obtained for two complexes with a Cu–Al bond, i.e., a model [^tBu₃PCuAl(NON’)] (where we substituted gold with copper and reoptimized the structure) and the experimental complex III.⁷ (see Tables S9, S10 and Figures S10, S11; for a comparative EDA, see Table S11). Before concluding, we comment on the two main theoretical points which suggested in ref (1) the formation of a strongly polarized Au–Al bond with a large negative charge on Au, i.e., (i) the Au/Al difference in the atomic electronegativity values and (ii) the atomic charge on Au. Concerning point (i), although the large Au/Al atomic electronegativity difference (0.93 on the Pauling scale, 2.12 (calculated) and 2.19 (experimental) on the Mulliken scale (see Table S12) seems to be inconsistent with an electron-sharing bond, the calculated Mulliken “molecular electronegativity” is practically identical (2.56 vs 2.53 eV for [^tBu₃PAu]· and [Al(NON’)]·, respectively) (Table S13). For point (ii), the atomic charges show a huge variability range with the chosen method (consistently with the highly directional and diffuse HOMO of the aluminyl anion, Figure S12): q^Au, from −0.83 to +0.22; q^Al, from 2.18 to 0.18 (Table S14) which makes an assessment of the bond polarization based on these numbers impossible.

In summary, the reactivity shown here points out that both Au and Al centers act as nucleophiles (radical-like mechanism), with the electrophilic behavior of Al also assisting the interaction with CO₂. The Au–Al bonding picture in [^tBu₃PAuAl(NON)] is consistent with an Au(0) involved in an electron-sharing bond-type. An important general conclusion is that the reactivity of metal-aluminyl complexes with CO₂ resulting in M-CO₂ coordination mode cannot be considered in itself as a probe for a strongly polarized M(δ-)-Al(δ+) bond and for the metal behaving as a standard nucleophilic center. We believe that the interpretative framework given here may be useful for future experimental investigations on CO₂ capture and reduction by these unconventional bimetallic complexes.

Glossary

Abbreviations

NON

4,5-bis(2,6-diisopropylanilido)-2,7-ditert-butyl-9,9-dimethylxanthene

NHC^IPr

N,N′-di-isopropyl-4,5-dimethyl-2-ylidene

^Me2CAAC

1-((2,6-di-isopropylphenyl)-3,3,5,5-tetramethyl-pyrrolidin-2-ylidene)

SiN^Dipp

(CH₂SiMe₂NDipp)₂

Ar*

C₆H₂{C(H)Ph₂}₂Me-2,6,4.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.1c06728.

• Methodology and computational details; optimized geometries; Mayer’s bond order along the path; Activation Strain Model and EDA results; donor and acceptor NOCV orbital decomposition; analysis of the [(NON’)Al] and [^tBu₃PAu] fragments; selection of fragmentations for bonding analysis; CD-NOCV analysis complete results; CD-NOCV and EDA analysis of [^tBu₃PCuAl(NON’)] and [NHC^iPrCuAlSiN^Dipp] complexes; Au, Al, and “molecular” ionization energy and electron affinity; AIM, Mulliken, Hirshfeld, VDD, Multipole Derived, CM5 calculated atomic charges on Au and Al; [(NON’)Al] HOMO electron density map (PDF)

Author Contributions

^$ D.S., L.B., and P.B. contributed equally to this paper

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript. All authors contributed equally.

The authors declare no competing financial interest.