Advances in Micro-CT Imaging of Small Animals

Abstract

Purpose:

Micron-scale computed tomography (micro-CT) imaging is a ubiquitous, cost-effective, and non-invasive three-dimensional imaging modality. We review recent developments and applications of micro-CT for preclinical research.

Methods:

Based on a comprehensive review of recent micro-CT literature, we summarize features of state-of-the-art hardware and ongoing challenges and promising research directions in the field.

Results:

Representative features of commercially available micro-CT scanners and some new applications for both in vivo and ex vivo imaging are described. New advancements include spectral scanning using dual-energy micro-CT based on energy-integrating detectors or a new generation of photon-counting x-ray detectors (PCDs). Beyond two-material discrimination, PCDs enable quantitative differentiation of intrinsic tissues from one or more extrinsic contrast agents. When these extrinsic contrast agents are incorporated into a nanoparticle platform (e.g. liposomes), novel micro-CT imaging applications are possible such as combined therapy and diagnostic imaging in the field of cancer theranostics. Another major area of research in micro-CT is in x-ray phase contrast (XPC) imaging. XPC imaging opens CT to many new imaging applications because phase changes are more sensitive to density variations in soft tissues than standard absorption imaging. We further review the impact of deep learning on micro-CT. We feature several recent works which have successfully applied deep learning to micro-CT data, and we outline several challenges specific to micro-CT.

Conclusions:

All of these advancements establish micro-CT imaging at the forefront of preclinical research, able to provide anatomical, functional, and even molecular information while serving as a testbench for translational research.

Introduction

Micro-computed tomography, also known as micro-CT, is the preclinical analogue of clinical CT, providing higher spatial resolution (voxel size <= 100 microns) for imaging small animal models of disease. Several review papers have presented the physical principles and applications of micro-CT imaging [1, 2]. The growing interest in small animal models and the development of new x-ray detectors stimulated considerable development of dedicated small animal scanners in the 1990s. Now, micro-CT systems have become highly sophisticated and are an essential part of preclinical imaging centers in both academia and industry.

There are several major differences between micro-CT and clinical CT scanners. To accommodate higher spatial resolution requirements, micro-CT scanners use micro-focus x-ray sources. Most commonly, these sources utilize a fixed tungsten anode and operate at lower voltages (20–100 kVp) and much lower anode currents (50–1000 μA) than clinical scanners. Furthermore, unlike clinical CT scanners with curved detector arrays, micro-CT systems generally utilize flat-panel detectors with small pixel sizes (≤150 μm²) and a cone-beam scanning geometry. This configuration is shared with some C-arm CT systems used in interventional radiology. Depending on the application, tolerances on radiation dose and acquisition time may be more relaxed for micro-CT scanners to manage noise in high-resolution scans.

In this review paper, we start with state-of-the-art, commercially available micro-CT scanners and present a few new applications for both in vivo and ex vivo imaging. Next, we summarize new developments associated with dual energy and photon counting micro-CT which enable quantitative differentiation of tissues and nanoparticle contrast agents. These nanoparticles have numerous applications in the burgeoning field of cancer theranostics. We also describe micro-CT research in phase contrast imaging, which promises to make the modality more sensitive to density changes in soft tissues. Finally, we review the impact deep learning has had on CT imaging and predict its future applications. Deep learning is of significant interest within the CT community, and has the potential to solve several challenging problems in preclinical micro-CT; therefore, we dedicate roughly one-third of this review paper to deep learning topics.

State-of-the-art, commercial micro-CT scanners

In Table 1 we summarize system specifications for commercial micro-CT scanners from different manufacturers. All of these micro-CT systems use high precision movements during acquisitions and have sensitive electronics. They are self-shielded cabinet systems and have multiple layers of safety interlocks and emergency stops to prevent accidental radiation exposure. The user interface of such scanners can be controlled from the computer screen and from an embedded touchscreen. Commercial micro-CT scanners generally include software needed to collect, reconstruct, and analyze data and utilize GPU-based reconstruction code for fast performance. They can also include software for good laboratory practice which, when activated, provides necessary data protection [3]. Furthermore, the imaging data can be saved in various formats (BMP, JPG, TIFF) or exported as DICOM files.

Table 1.

Specifications of current commercial micro-CT scanners. Notes: Only representative ex vivo scanners for biological samples are included in this cable. Additional ex vivo, industrial, and nano-CT scanners are available from manufacturers like Nikon, Zeiss, Werth, Yxlon, Rigaku, and Bruker. Discontinued product lines from GE and Siemens are excluded from this table.

Type	Scanner Manufacturer/Model	Diameter FOV (mm)	Length (mm)	Spatial Res.	kVp	Scanning Time	Gating	Other Characteristics
Ex Vivo Systems	Bruker SkyScan 1272	75 mm	70 mm	Max. 0.4 μm	20 – 100 kVp	Mins to hrs depending on resolution	Not needed for ex vivo imaging	- 16-position sample changer to increase throughput - Automatic selection of scan parameters
	Scanco μCT 40	36.9 mm	80 mm	3–72 μm (pixel size)	30–70 kVp	Mins to hrs depending on resolution	Not needed for ex vivo imaging	- Optional sample changer that accommodates up to 10 sample holders
In Vivo Systems	Bruker SkyScan 1278	80 mm	200 mm	50 μm nominal res.	20–65 kVp	-Continuous rotation or step-and-shoot mode -Scanning time down to 7.2 sec	- Prospective and retrospective gating, image-based intrinsic gating - Complete software solution for cardiac function analysis in 4D	- GPU-accelerated reconstruction - 2D/3D morphological analysis and visualization - Exchangeable animal cassettes that can be used in all Bruker in-vivo imaging instruments. - Low-dose acquisitions down to 6 mGy - 4-position automatic filter changer
	Bruker SkyScan 1276	80 mm	300 mm	Max. 2.8 μm	20–100 kVp	Scanning time down to 3.9 sec	Prospective and retrospective, time and image based intrinsic gating	- In vivo micro-CT scanner with ex vivo imaging capabilities - Circular and helical (spiral) scanning trajectory - s/w for cardiac image analysis
	PerkinElmer Quantum GX2	FOVs: 18, 36, 72, and 86 mm	240 mm	Preset high res. mode: 2.3 μm voxel size	Max: 90 kVp	Preset high speed mode: 3.9 sec	- Intrinsic retrospective gating - Dual phase respiratory and cardiac gating	- Multi-modal co-registration (from IVIS Spectrum or FMT) with micro-CT imaging data. - Multispecies imaging capabilities (zebrafish, mouse, rat, guinea pig, rabbit)
	MiLabs U-CT	Up to 130 mm	Up to 712 mm	Max 2.4 μm voxel size	65 kVp (80 kVp optional)	Down to 5 sec for total body mouse	- Sensor free respiratory and cardiac gating for up to four mice simultaneously - Optional: sensor based respiratory and cardiac gating	- Radiation dose: < 2 mGy - Circular and helical scanning - Dual energy CT - X-ray fluoroscopy - Imaging from small samples up to 5 kg rabbits - Capability to image in an over- or under-pressure cell for immunocompromised or infected animals from mice up to rabbits - Upgradable with PET, SPECT, and 3D CT-guided optical imaging in any combination
	Inviscan IRIS and IRIS-XL	> 90 mm	120 mm	< 30 μm		Scan time: < 7.3 s (ultra-fast mode), 20 s (speed mode), 1 min (high resolution scan)	- Dynamic 4D acquisition - Software based respiratory and cardiac gating	- Low dose: < 6.5 mGy - Either standalone of combined with micro- PET
	Molecubes, X-Cube	35 mm	63 mm	50 μm		< 1 min fastest scan	Gating is available	- Iterative reconstruction techniques - Multimodal small animal bed allows for easy and modular multimodal imaging with SPECT and PET
In Vivo Hybrid Systems (multi-modality)	Medico nanoScan	100 mm	120 mm	30 μm	Up to 80 W		Not available	- Multiple animal imaging: up to 4×60 g mice 2×500 g rats - Mainly combined with PET or SPECT - Low dose down to 1 mSv for whole body scan
	Sofie Gnext PET-CT	104 mm	120 mm	50 μm	25–80 kVp	1 min, fastest scan	Not available	- Combined with PET - Single and multi-mouse imaging, rat and small non-human primate imaging
	PerkinElmer G8 PET / CT	100 mm	50 mm	200 μm	59 kVp	sub-minute CT scan	Not available	- Combined with PET - Fully-integrated animal management system and 3-clicks-to-data workflow - Average dose: 50.1 mGy
	Bruker Albira Si	70 mm	70 mm	90 μm with minimum 5 μm voxel	10 – 50 kVp	minutes	Not available	- Combined with PET and/or SPECT - Dynamic 2D X-ray mode for fluoroscopic imaging
	Bruker Si78 PET/CT	70 mm	200 mm	Max 50 μm	20–65 kVp maintenance-free X-ray source	fastest total body scan: 7.2 sec	Gated PET and CT imaging for cardiac imaging or respiration triggering	- Low dose scanning < 6 mGy - Radiation shielding: < 1 μSv/h at 10 cm from surface
	Sedecal SuperArgus Compact PET/CT	100 mm	50 mm	50–100 μm		−15 sec	Available for PET	- Combined with PET - 3 models available r – 100 mm bore for mouse, rats or marmosets up to 3 kg; R – 160 mm bore for multi-animal imaging, as well as rabbits up to 6 kg; or P – 260 mm bore for non-human primates, canine or porcine up to 10 kg. Each model can be configured with 2, 4, or 6 PET rings
	MRSolutions MRS*PET/CT 80	112 mm	80 mm	Up to 18 μm	40–90 kVp	minutes	Not available	- Uses MRS*PET CLIP-ON technology - Variable zoom - Dual Energy - Suitable for both in-vivo and ex-vivo applications
Photon Counting Systems	Mars Bioimaging Preclinical Spectral CT System	100 mm	280 mm	30–100 μm (user selects)	30–120 kVp	8 mins for 30 × 15 mm volume	Not available	- Uses photon counting detector with 8 energy bins - Detector constructed from CZT-Medipix3RX detector modules with 110-μm2 pixels - Charge summing mode improves spectral measurement accuracy - Radiation dose: 20–80 mGy

We group commercial micro-CT scanners into four categories (Table 1): 1) ex vivo systems, 2) in vivo systems, 3) in vivo hybrid systems (multi-modality), and 4) photon counting systems. While ex vivo micro-CT is not a primary focus of this review paper, the Bruker SkyScan 1272 and the Scanco μCT 40 are examples of high-resolution, 3D, ex vivo scanners which operate in a rotating specimen geometry. Exemplary features of the SkyScan 1272 include its “Genius-Mode” which automates the process of selecting scan parameters such as the magnification, energy, filters, exposure time, and background corrections. The spatial resolution delivered in scanning biological specimens can be as high as 0.4 μm; however, high-resolution scans may take several hours. Radiation dose is generally not a concern for ex vivo scanning. The scanner can optionally be equipped with an external 16-position sample changer to queue multiple scans for increased throughput.

By contrast, commercial in vivo micro-CT systems have a movable animal bed surrounded by a rotating gantry. For acquisition, the anesthetized animal is placed on the bed and is inserted into the bore of the gantry. Some of the in vivo micro-CT scanners are sold as standalone systems (e.g. PerkinElmer Quantum GX2) and can be quite versatile, having several available physical magnifications and allowing high-resolution (<10 μm) ex vivo scanning. Such scanners can image mice with a single scan or larger animals such as rats and guinea pigs by extending the scan field of view. Scanning times vary depending on imaging requirements and can be on the order of seconds for lower-resolution acquisitions or longer when high spatial resolution is required. Some in vivo scanners use integrated cradles or exchangeable animal cassettes that allow co-registration with data acquired with other modalities (e.g. fluorescence molecular tomography, FMT; micro-PET; micro-SPECT). These systems from Bruker, PerkinElmer, MiLabs, or Inviscan come equipped with physiological monitoring and also provide prospective or retrospective gating for cardiac and respiratory imaging. Gating enables cardiopulmonary studies to analyze functional metrics such as cardiac output and ejection fraction through 4D post-processing software. These scanners are also designed and optimized for lower-resolution longitudinal imaging at low radiation dose (as low as 5–6 mGy), allowing researchers to follow and characterize disease progression at multiple imaging time points. This is extremely important in cancer studies where the radiation associated with imaging may otherwise apply a therapeutic dose to tumors.

The third category of micro-CT systems combine CT scanning with PET (or SPECT), where CT provides anatomical context and enables attenuation correction during reconstruction. In comparison to standalone micro-CT systems, hybrid scanners may provide lower resolution (e.g. PerkinElmer G8 PET / CT has 200 μm resolution) or lack gating capabilities. However, there are also exceptions. For example, the Bruker Si78 PET/CT has a 50 μm resolution and also includes gated micro-CT capabilities.

Notably, most micro-CT systems employ flat-surface, 2D x-ray detectors (i.e. flat-panel detectors) leading to a cone-beam scanning geometry. Advances in complementary metal oxide semiconductor (CMOS) technology led to the production of these large area detectors. CMOS detectors also feature high frame rates and relatively low cost, making them ideal for in vivo, small animal micro-CT imaging. As an alternative, some commercial systems use cooled, charge-coupled device (CCD) detectors, for example, the Bruker SkyScan 2214 nano-CT scanner. Cooled CCD detectors are preferred in applications involving low x-ray fluences because they have lower levels of dark noise than CMOS detectors.

With the exception of the last scanner, all systems in Table 1 use energy integrating detectors which are affected by limited contrast capabilities. Our last selected commercial scanner is based on an energy resolving detector. The MARS preclinical CT scanner (MARS Bioimaging, Ltd.; Christchurch, New Zealand) uses a photon counting detector (PCD) based on the Medipix3 chip developed at CERN (Geneva, Switzerland) [4]. This PCD has 8 energy thresholds and a charge summing mode which can improve spectral performance. The scanner has physiological support and monitoring capabilities for in vivo studies but does not provide gating. Nevertheless, as detailed in the Spectral micro-CT section of this review, PCD-based scanners provide improved material discrimination [5] [6] and allow the use of nanoparticle contrast agents that can be functionalized for molecular x-ray imaging [7].

Commercially available contrast agents for micro-CT

Due to a lack of inherent contrast for soft-tissue imaging, the majority of micro-CT scans make use of high atomic weight contrast agents. In Table 2 we present examples of commercially available contrast agents for micro-CT. These include low molecular weight iodinated contrast agents in clinical use, such as Isovue-370, and nanoparticle-based contrast agents. For in vivo small-animal imaging, the use of clinical contrast agents is particularly difficult. Small animals have much higher renal clearance rates than humans, so injected contrast agents are rapidly excreted. To overcome the rapid clearance of traditional contrast agents, blood pool contrast agents have been developed, which exhibit prolonged blood residence time and stable enhancement for minutes to hours. Typically, these contrast agents are based on iodine, gold, or barium because of their high x-ray attenuation, biocompatibility, relevant biochemistry, cost, and/or clinical relevance. Nanoparticle contrast agents for micro-CT have also been developed using other metals, including silver, gadolinium, bismuth, ytterbium, tantalum, and thorium [8].

Table 2.

Examples of commercially available contrast agents for micro-CT.

Contrast Agent	Contrast Element	Characteristics
Bracco Imaging, Iopamidol (Isovue-370)	Iodine	- Small molecular weight contrast agent used in humans - Rapidly excreted by the kidneys - Can be used for perfusion micro-CT or to study kidneys
MediLumine, Fenestra LC/VC	Iodine	- Lipid emulsion containing an iodine-based compound - VC is for vascular contrast, LC is for liver contrast - Used for in vivo preclinical imaging
Binitio Biomedical, eXIA 160, eXIA 160XL	Iodine	- Aqueous, colloidal, poly-disperse contrast agents behaving initially as blood pool contrast agents - Subsequently taken up by the myocardium and other metabolically active tissues over time [9] - Metabolized by catabolic pathways in the body thus enabling metabolic imaging of the myocardium and brown adipose tissue - Used for in vivo preclinical imaging
Miltenyibiotec, ExiTron nano 6000,12000	Barium	- Nanoparticle-based blood pool contrast agents - Accumulates over time, particularly in the liver and spleen - Used for in vivo preclinical imaging
Nanoprobes, Aurovist 15	Gold	- Nanoparticle-based blood pool contrast agent - Accumulates over time, particularly in the liver and spleen - Used for in vivo preclinical imaging
Scarletimaging, BriteVu	Barium	It is used only for ex vivo studies as an intravascular agent to cast the cardiovascular system down to the capillary level.

Applications of modern micro-CT imaging

Next, we present some recent applications of micro-CT for in vivo and ex vivo imaging in small animals. Supplemental data acquisition and reconstruction parameters for the figures presented in this and future sections are included in Table 3.

Table 3.

Summary of data acquisition and reconstruction parameters for the figures in this work. PCD: Photon Counting Detector. EID: Energy Integrating Detector.

Figure	Scanner Model	Acquisition and Reconstruction	Contrast Agent(s)	Voxel Size (Resolution)	Reported Dose
1	CosmoScan FX Rigaku Corporation	- 2 min. at 90 kVp, 88 μA, FOV 45 mm - CosmoScan Database software	N/A	90 μm	Not reported
2	- Custom-built system within a refurbished clinical CT gantry - Dexela 2923 MAM EID, Perkin Elmer Inc. - L10951 source, Hamamatsu Photonics K. K.	- 5 min. at 60 kVp, 50 W - 11.7 ms exposure per projection - 10 cardiac, 4 respiratory phases - Intrinsic gating - Motion compensated reconstruction [10] - Post-reconstruction denoising [11]	ExiTron nano 12,000 (Ba based), nanoPET Pharma GmbH	<75 μm (10% MTF: 7.5 lp/mm)	5 Gy (0.5–2 Gy results also demonstrated)
3	- Custom-built ex vivo scanner - Rotating specimen geometry - XCounter Thor PCD, Direct Conversion AB - L9181-02 source, Hamamatsu Photonics K. K.	- 2 h at 80 kVp, 0.2 mA - Helical acquisition with 2.5 cm vertical translation (1070 projections, 1070°) - Split Bregman algebraic reconstruction regularized with rank-sparse kernel regression [12]	BriteVu (Ba based), Scarlet Imaging	38 μm (10% MTF: 6.5–7.1 lp/mm)	N/A (ex vivo)
4	- Custom dual-source, dual-energy in vivo scanner - Vertical subject geometry - Dexela 1512CL EID (CsI), Perkin Elmer Inc. - G-297 sources, Varex Imaging	- Chain 1: 40 kVp, 50 mA, 25 ms - Chain 2: 80 kVp, 40 mA, 10 ms - Circular scan (360 projections, 360°) - Analytical reconstruction - Post-reconstruction denoising with joint bilateral filtration [13]	- Iodine liposomes [14] – 15 nm AuroVist gold nanoparticles	63 μm (10% MTF: 3.4 lp/mm)	57 mGy
5A	Same as Fig. 4	- Chain 1: 40 kVp, 50 mA, 25 ms - Chain 2: 50 kVp, 80 mA, 12.5 ms - Circular scan (720 projections, 360°) - Split Bregman algebraic reconstruction regularized with rank-sparse kernel regression [12]	- Iodine liposomes [14] - Gadolinium liposomes [15]	123 μm (10% MTF: 3.4 lp/mm)	162 mGy
5B	- Custom-built in vivo scanner - Vertical subject geometry - SANTIS 0804 ME prototype PCD, Dectris AG - G-297 source, Varex Imaging	- 3 min. at 80 KVp, 2 mA, 200 ms - Helical acquisition, 1.25 cm vertical translation (900 projections, 1070°) - Energy thresholds: 25, 34, 50, 60 keV - Split Bregman algebraic reconstruction regularized with rank-sparse kernel regression [12]	- Iodine liposomes [14] - Gadolinium liposomes [15]	123 μm (10% MTF: 3.5 lp/mm)	43 mGy
6	Same as Fig. 5B	- 90 sec. at 80 KVp, 5 mA, 10 ms - Helical acquisition, 1.25 cm vertical translation (9000 projections, 1070°) - 10 cardiac phases, retrospective gating - Energy thresholds: 25, 34, 40, 55 keV - Split Bregman algebraic reconstruction regularized with rank-sparse kernel regression [12]	- Iodine liposomes [14] – 15 nm AuroVist gold nanoparticles	123 μm (10% MTF: 2.8–3.0 lp/mm depending on energy threshold)	190 mGy
7	Similar to Fig. 4		- Iodine liposomes [14]
8	- Edge-illumination XPC imaging - Pixirad-2 PCD [16] - MicroMax-007 HF, Rigaku source (Mo anode) - 30 μm Mo source filter	- 18 h at 40 kVp, 30 mA, 1 s - 1441 projection angles over 360° - 5 phase steps, 4 dithering steps per angle - Reconstruction with filtered backprojection (Hilbert filter for phase) - Sample translation during scanning to reduce ring artifacts	N/A	(19 μm FWHM)	Not measured (lower dose 300 mGy scan also presented)
9	Same CT data as in Fig. 6	- Only 25 keV threshold data used for 4D CNN training - 10 cardiac phases, retrospective gating - Split Bregman algebraic reconstruction regularized with rank-sparse kernel regression [12] (Fig. 9B; CNN training labels; 9000 projections over 1070°) - Unregularized algebraic reconstruction (Fig. 9C; CNN training inputs; subsampled to 2250 projections over 1070°)		123 μm (10% MTF: 2.7 lp/mm, 4D CNN output, Fig. 9D)
10	- Non-contrast scans: TomoScope Duo commercial scanner, formerly CT Imaging GmbH - Contrast-enhanced scans: InSyTe μCT commercial scanner, Trifoil Imaging	- Non-contrast scans: 90 sec. per scan, 65 kVp, 1 mA; 720 projections over 360° - Contrast-enhanced scans: 75 kVp, 230 ms; 207 projections over 360°	- No contrast or ExiTron nano 6000 (Ba based), nanoPET Pharma GmbH	- Non-contrast scans: 80 μm spatial resolution reported - Contrast scans: 280 μm voxels - Segmentations processed with 240 μm voxels	Not reported

CT is one of the principal modalities used for diagnosing lung pathology and has become increasingly important for diagnosing virus-induced lung infections during the COVID-19 pandemic. In translational efforts, micro-CT has been used for preclinical research toward finding an efficient vaccine and antiviral drugs against COVID-19. In particular, we give the example of a study in Syrian hamsters as a small animal model for SARS-CoV-2 infection and treatment development [17]. The authors examined the progression of lung inflammation caused by SARS-CoV-2 infection and the recovery processes. The micro-CT images showed severe lung abnormalities in all infected animals (Fig. 1). The lung abnormalities were first detected at day 2 post infection and then progressed to more severe lung consolidation at 8 days post-infection. High-dose infected animals had more severe lung abnormalities compared to low dose infections.

Fig. 1.

Micro-CT imaging of the lungs of infected Syrian hamsters. (A) Axial CT images of the thorax in moek-infected control, low dose-infected, and high dose- infected animals showing lung abnormalities over a 14-day period (white arrowheads). Lnng abnormalities were first detected 2 days postinfection, and the most severe changes were observed 8 days postinfection in virus-infected animals. The high dose-infected animals had, overall, more severe lnng abnormalities compared to the low dose-infected animals. Lnng abnormalities began to improve 10 days postinfection for both low dose- and high dose-infected animals. On day 14 postinfection, the high dose-infected animals had a higher degree of residual lung abnormalities compared to the low dose-infected animals, highlighted by the black arrowhead. Pneumomediastinum is labeled by the white asterisk (*). Note that the day 0 control image was only obtained for the high dose-infected animal and is not available for the low dose-infected or mock-infected animals. (B-H) Dorsal/coronal plane reconstruction CT images of the thorax in low dose-infected and high dose- infected animals showing (B) a control image, (C and D) initial lung changes, (E and F) most severe lung changes, and (G and H) the beginning of the recoveiy phase over time. The high dose-infected animals had more severe lung abnormalities than the low dose-infected animals. Figure reproduced from [17] with cropping under the Creative Connnons CC BY license.

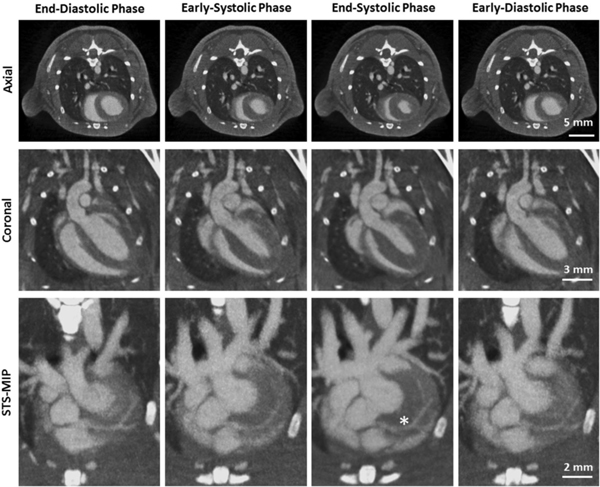
Micro-CT can deliver valuable anatomical and functional information in cardiac studies in small animals. High temporal and spatial resolution and relatively short scanning times allow for high-throughput studies. An increasing number of research groups have demonstrated the use of micro-CT for cardiac morphology and global ventricular systolic indices, such as stroke volume, ejection fraction, and cardiac output [18–22]. Cardiac micro-CT has also been used to assess functional parameters of systolic emptying or diastolic filling in an experimental model of pulmonary arterial hypertension in rats [23]. Recently, using a custom-built system integrated into a clinical CT gantry, even murine coronary arteries have been imaged using phase correlated reconstructions (Fig. 2) [24]. The authors show that with a radiation dose of 1 Gy the left coronary artery can be visualized and all major branches can be identified. This is an important achievement given the small size of the coronaries (<100 microns) and their continuous motion due to both the heart beating (up to 600 beats/min) and respiration (up to 230 breaths/min). However, the high radiation dose level is an issue which prevents longitudinal studies. We expect that future improvements in low-dose reconstruction will allow longitudinal imaging of the coronary arteries in mouse models.

Fig. 2.

Phase-correlated reconstructions of a mouse showing different cardiac motion States (eolumns). The first row illustrates axial slices, the seeond row coronal slices, and the third row a sliding thin slab-maximum intensity projections (STS-M1P). The asterisk marks the first bifurcation of the left coronaiy artery. (C = 300HU, W = 1500HU). Figure reproduced from [24] without modification under the Creative Commous CC BY license.

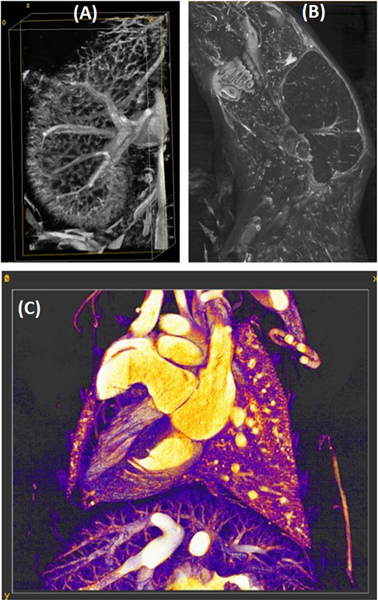
High resolution images provided by ex vivo micro-CT using staining or vascular casting promise to bridge the gap between in vivo small animal imaging and conventional histology or pathology. Staining methods for ex vivo micro-CT mostly use iodine or phosphotungstic acid [25], but other high atomic number compounds based on barium or lead can be used. In Fig. 3, we show examples of ex vivo micro-CT imaging using a commercial compound based on barium (BriteVu®; Scarlet Imaging, Murray, UT) to visualize mouse vasculature in the kidneys, the head, and the thorax.

Fig. 3.

Examples of high-resolution, ex vivo vascular imaging using micro-CT and BriteVu as a vascular contrast agent. We illustrate mouse vasculature in the kidney (A), the head (B), and the thorax (C).

Spectral micro-CT

While clearly remarkable, the applications of micro-CT previously described do not require novel x-ray technologies. We believe that the future of CT imaging is related to spectral imaging. Spectral CT takes advantage of the energy dependence of x-ray attenuation to quantitatively separate materials within the subject—e.g. separating extrinsic iodine or gold based contrast agents from bone and soft tissues. The most common form of spectral CT imaging, dual-energy (DE) CT, performs two separate scans of the same subject, each with a different accelerating voltage of the x-ray tube (a different source “kVp”). Most current CT systems perform DE CT with energy-integrating x-ray detectors (EIDs) which record an output signal that is proportional to the detected x-ray photon flux, weighted by the x-ray energy and integrated across the entire x-ray energy spectrum.

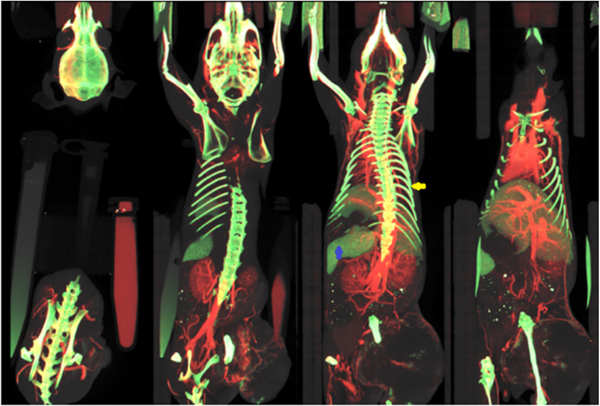
Using spectral CT data, material decomposition into basis material maps is possible both in the projection domain or post-reconstruction, in the image domain. For example, post-reconstruction decomposition [26] can be performed to create volumetric maps of photoelectric effect (PE) and Compton scattering (CS) basis functions [27] and other contrast materials (e.g. based on iodine, gadolinium, gold, barium). Under certain assumptions, such decompositions can be performed with DE micro-CT data acquired with EIDs [28–30]. However, DE-EID CT faces significant limitations: with only two EID measurements, gold-based nanoparticles in the spleen are not differentiable from calcium in bones (Fig. 4).

Fig. 4.

DE CT imaging enables quantitative, 3D mapping of extrinsic contrast agents (iodine, red; gold, green) and soft tissues (gray) present in the subject (coronal maximum intensity projections shown through a live mouse). However, because DE CT with EIDs provide only two independent measurements with limited sensitivity, it is difficult to separate certain intrinsic materials, such as bones (see ribs, yellow arrow), from gold nanoparticles accumulated in the spleen (blue arrow). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

A newly emerging CT detector technology, energy-discriminating or photon-counting x-ray detector (PCD) technology, can address this limitation. PCDs have several advantages over current EID technology. Unlike EIDs, PCDs count incoming x-ray photons and bin them based on their recorded energy, providing dual- and even multi-energy information with a single CT scan. Further benefits associated with PCD technology include reduced electronic noise, higher contrast-to-noise ratios, improved spatial resolution, and improved dose efficiencies [31]. Current PCDs have two to eight hardware energy thresholds (bins) per detector pixel, facilitating the separation of multiple extrinsic contrast agents based on different elements [32]. These elements have unique x-ray attenuation signatures (K-edges) which allow their separation from intrinsic tissues with an optimal degree of specificity and sensitivity.

The large-scale use of PCDs in both clinical and preclinical CT systems is limited by spectral distortions inherent in the photon detection process (charge sharing, pulse pile-up, and related physical effects) [33]. Even with proper spectral calibration of the detector, these sources of distortion degrade the fidelity of spectral measurements. Particularly, there are significant trade-offs between the size of PCD pixels and the energy resolution of PCD scans due to charge sharing between neighboring detector pixels. Charge sharing occurs when incoming photons are recorded as two or more lower energy photon due to the division of signal between neighboring pixels. Since high spatial resolution is required for micro-CT imaging, using PCDs for preclinical imaging presents challenges. There are, however, hardware solutions to compensate for charge sharing which include anti-coincidence charge-summing circuitry [4]. Alternative software solutions for spectral correction are described in the Deep learning for micro-CT section of this review.

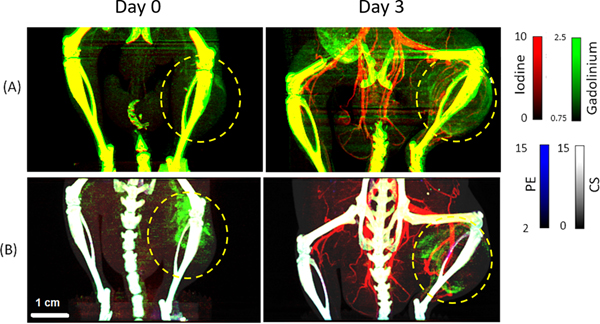
There are also hybrid micro-CT systems that include a PCD and EID within the same system [12, 34]. The Duke hybrid micro-CT configuration enabled a direct comparison between PC and DE EID micro-CT in experiments using both phantoms and mice for anatomical and functional imaging of tumors [35]. Fig. 5 illustrates this comparison. Mice with p53/MCA sarcoma tumors [36] were intravenously administered a liposomal gadolinium (Lip-Gd) contrast agent (0.4 mg Gd kg⁻¹ body weight) and imaged 3 hours later with both DE-EID and PC micro-CT (Day 0). 3 days later, the same animals were injected with liposomal iodine (Lip-I) (1.32 mg I kg⁻¹ body weight) and re-imaged. The PCD binned x-ray photons using 4 energy thresholds set to 25, 34, 50 and 60 keV. PC micro-CT decreased the overlap between spectral measurements allowing distinct separation of the two contrast materials from soft tissue (gray) and bone (white). According to the Rose criterion applied to the experimental results, the detectability limits for I and Gd were approximately 2.5 mg/mL for both DE-EID and PC micro-CT, even though for PC micro-CT the radiation dose was 3.8 times lower and two additional basis materials were decomposed (PE, CS). Additionally, PC micro-CT provided lower background signal and better simultaneous visualization of tumor vasculature and intratumoral Gd compared to DE EID micro-CT decompositions.

Fig. 5.

Application of in vivo DE EID CT (A) and PC CT (B) in delayed-phase imaging of a sarcoma tumor (yellow circles; maximum intensity projection images shown). At Day 0, 3 h after injection, liposomal gadolinium (green, mg/mL) has already begun to accumulate within the sarcoma tumor (yellow circles), allowing visualization and quantification of tumor vascular permeability. On Day 3, immediately after liposomal iodine injection (red, mg/mL), material decomposition can be used to correlate tumor vascular permeability (gadolinium signal) and tumor vascular density (iodine signal). These signais are indicative of tumor response to potential therapies. Additional spectral information provided by PC CT reduces background signal and improves separation of contrast materials from bone and soft tissues (photoelectric effect, PE map, blue; Compton scattering, CS map, gray) compared with DE EID CT. (For interpretation of the referenees to colour in this figure legend, the reader is referred to the web version of this article.)

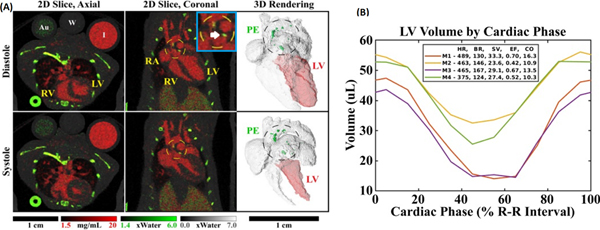
Successful PCD-based in vivo cardiac micro-CT imaging has been demonstrated in a study of APOE knockout mice [37]. Technically, this study is significant because it demonstrates successful navigation of the trade-offs between spatial, temporal, and spectral resolution required for micro-CT imaging of the mouse heart within reasonable radiation dose constraints (~190 mGy dose to image 10 cardiac phases with four PCD energy bins). Scientifically, this study is significant because APOE knockout mice represent a model of atherosclerosis, showing a marked increase in total plasma cholesterol and reliably developing atherosclerotic lesions when fed on a high-fat diet [38]. Fig. 6A illustrates the results of image-domain material decomposition of one of these cardiac data sets. Effective separation is seen between calcium in the bones and calcified plaques (green, PE map) and iodine in the vasculature of the lungs and heart (red). The 10-phase cardiac sequence also allows for cardiac function analysis (Fig. 6B).

Fig. 6.

Photon-counting cardiac CT in the mouse. (A) Matching 2D slices are shown at diastole and systole in axial and coronal orientations. Complementary 3D renderings show the four chambers of the heart and the aortic arch, including a segmentation of the left ventricle (LV) used to derive cardiac functional metrics. Decomposition was performed into three basis materials: iodine (red), photoelectric effect (PE, green), and Compton scattering (gray). Calibration vials containing gold (Au, 5 mg/mL), water (W), and iodine (I, 12 mg/mL) can be seen in the axial slices. Calcified atherosclerotic plaques (white arrow) appear prominently within the PE map, near the aortic val ve and within the aortic arch, and are denoted by dashed circles. (B) Left ventricular volume curves are plotted along with a ta ble of the heart rate (HR, beats/min), breathing rate (BR, breaths/min), stroke volume (SV, μL), ejection fraction (EF), and cardiac output (CO, mL/min) for 4 mice (M#). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Developments in CT theranostics

Many applications of preclinical micro-CT use nanoparticle (NP) contrast agents which are based on materials like iodine, barium, gadolinium, or gold. Low molecular weight contrast agents used for clinical imaging rapidly clear from the blood pool in mice, while NPs may remain in circulation for hours or days depending on their size and biochemistry. Liposomes (Lip), one of the most extensively studied NP platforms, encapsulating I or Gd have been used as contrast agents for blood-pool, cancer, and cardiovascular imaging applications [39–42]. Such NPs are also ideal for CT-based theranostics: they can serve both diagnostic imaging and therapy. Notably, Lip-I and Lip-Gd have similar size and biodistribution patterns to liposomal drugs such as Doxil (Janssen), and thus can serve well as imaging surrogates in drug delivery studies [43].

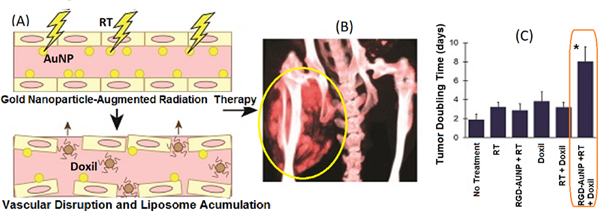
Alternatively, gold nanoparticles (AuNPs) are also used for both spectral micro-CT imaging and therapies. In addition to providing high contrast for x-ray imaging, AuNps can amplify the local effectiveness of radiation therapy (RT): they absorb therapeutic x-rays efficiently and then release that energy to immediately surrounding tissues, increasing the locally delivered dose in regions of high NP concentration. This radiation augmentation has been studied by several groups to effectively treat cancer in multiple animal models [44–51]. Local enhancement of RT was also described with tumor vascular-targeted RGD-AuNPs [43]. In addition to targeting RGD receptors for micro-CT based molecular imaging, RGD-AuNPs induced tumor vascular disruption during RT, prompting extensive tumor cell death and facilitating increased delivery of liposomal chemotherapeutics. The study showed the value of DE EID micro-CT in providing non-invasive visualization of the NP probe distribution within treated sarcoma tumors. The authors studied the combination of RGD-AuNP based RT augmentation (Fig. 7) with the delivery of a liposomal drugs (Doxil) [43]. The combination of RGD-AuNP augmented RT and Doxil proved to be the most effective combination in delaying the tumor doubling time.

Fig. 7.

(A) AuNPs + RT causes vascular disruption and boosts deliveiy of liposomes. (B) DE EID CT shows Lip-I in a sarcoma (ellipse). Lip-I served as surrogate for Doxil. (C) The combined therapy with RGD-AuNPs + RT and Doxil showed a significant growth delay (increase in tumor doubling times) compared to all other treatment groups.

CT theranostics extends to more than RT or chemotherapy. AuNPs also exhibit high absorbance of light at their surface plasmon resonance wavelength. For many AuNP shapes (e.g. nanorods, nanoshells, nanostars), this plasmon resonance occurs in the near infrared region, which is optimal for use with photothermal heating. In photothermal heating, nanoparticles convert laser light into heat, which leads to local hyperthermia. This effect can be used for tumor ablation. The use of NPs for combined micro-CT imaging and photothermal therapy has been reviewed [52]. Au nanorods [53] and hollow Au nanoshells [50] have both been used for combined micro-CT imaging, radiation therapy, and photothermal therapy. Au nanostar theranostic probes were used for micro-CT imaging and photothermal therapy in a mouse model of primary soft tissue sarcoma [54].

Reconstruction of CT data

Reconstruction of CT data involves mathematically inverting the data acquisition process to digitally reproduce the distribution of x-ray attenuation within component tissues or materials. Scanning dynamic objects, such as a beating heart, requires projection gating strategies to ensure data consistency; otherwise, reconstructions will represent the average attenuation over the data acquisition interval. Interested readers will find more information on common CT scanning geometries and on data requirements and gating techniques for accurate reconstruction in prior works [55].

Most commonly, CT data acquisition and reconstruction workflows are engineered for compatibility with analytical reconstruction (AR) algorithms. AR algorithms reconstruct an image by inverting an integral transform of the distribution of the linear attenuation coefficients, i.e., the Radon transform or the x-ray transform [56]. Such integral transforms are ideal representations of the (forward) x-ray projection process underlying the data acquisition step. When acquiring data in a circular, cone-beam geometry, the solution to this inverse problem is not exact [57] and hence approximated solutions are employed. Approximate AR algorithms are attractive for their computational speed, and they are commonly used to initialize more advanced algorithms. The most used analytical algorithms are variations on filtered backprojection (FBP), where a frequency-domain filter is applied to rows of CT projection data prior to inversion of the data acquisition process. Common examples of FBP include the FDK algorithm [58], for reconstruction of circular, cone-beam data, and the WFBP algorithm [59], for data acquired with a helical geometry. Notably, more computationally expensive, theoretically exact reconstruction algorithms are also available for helical, cone-beam CT [60].

To maintain constant image noise, imaging dose must be increased inversely to image voxel size with a fourth-power relationship [61]. In other words, at constant object size moving from 500-μm voxels in a clinical scan to 100-μm voxels in a preclinical scan would require a ~625-fold increase in imaging dose to maintain image noise. For in vivo micro-CT in mice, these dose constraints compound with additional challenges of imaging mice with high heart rates (up to 600 beats/min) and respiratory rates (up to 230 breaths/min). Therefore, dose and noise reduction strategies are equally important for reducing exposure to human patients and for fundamentally enabling advanced preclinical imaging applications. In line with the computational efficiency of FBP algorithms, computationally efficient approaches to image noise reduction include windowed frequency filters used for FBP (e.g. Cosine, Hamming window), which trade spatial resolution for reduced image noise, and post-reconstruction image denoising with neighborhood-based filters (e.g. bilateral filtration [62]).

Iterative reconstruction (IR) techniques model both the forward (projection) and inverse (backprojection) of the data acquisition process, incrementally updating the reconstructed data such that its synthetic reprojections better agree with the physically acquired projection data [63]. IR is more computationally expensive than AR, but offers numerous potential benefits in handling non-ideal imaging geometries, missing data, redundant data, and image noise and artifacts [64, 65]. Continuing advancements in parallel computing hardware (e.g. GPUs) and software now enable simultaneous IR of temporal and spectral x-ray CT data sets spanning multiple volumes (multiple phases and/or energies). For instance, multi-channel regularization such as patch-based singular value thresholding [66], rank-sparse kernel regression [12], oriented filtering [11], and deformable image registration [10] exploit prior knowledge of data structure to dramatically improve the fidelity of reconstructed images. These data regularizers are often incorporated as “plug-and-play” regularizers within robust algebraic reconstruction frameworks such as the Alternating Direction Method of Multipliers (ADMM) and the split Bregman method [67, 68].

Advanced model-based IR techniques further incorporate accurate models of the x-ray source spectral properties, the detection process, and x-ray physics into the reconstruction problem to improve reconstruction quality. For instance, modeling the polychromatic nature of x-ray sources and more realistic photon statistics can improve the accuracy of spectral CT reconstruction [69, 70]. Modeling blur and noise correlations introduced by the finite size of the x-ray source focal spot can yield reconstructions with higher spatial resolution [71]. Finally, modeling complex physical phenomena and signal correlations inherent in PCD CT [33, 72] during reconstruction may be required to fully realize the potential of the technology.

Most recently, deep learning has emerged as a means to approximate or supplement IR techniques, improving data regularization and significantly reducing computation time. New deep learning approaches to CT image denoising and reconstruction are discussed in the Deep learning for micro-CT section of this review paper.

Phase contrast micro-CT

Addressing poor contrast resolution in soft tissues is an on-going challenge for CT imaging. For in vivo imaging, this challenge can be addressed through the use of exogenous contrast agents and spectral CT (Figs. 4–7), while for ex vivo imaging vascular casting in whole animals (Fig. 3) and direct staining of small biological samples [73] are possible. X-ray phase contrast (XPC) imaging provides a compelling alternative to these x-ray absorption imaging methods and does not require contrast agents. Rather than treating x-rays as particles, XPC signal is derived from the treatment of x-rays as electromagnetic waves. Specifically, the complex index of refraction for x-rays is expressed as n=1−δ+iβ, where β describes the absorption of x-rays and δ describes x-ray phase shifts. Both quantities depend on the x-ray wavelength (energy). For diagnostic x-rays (10–100 keV) and biological soft tissues, δ is up to three orders of magnitude larger than β and falls off more slowly with increasing x-ray energy, providing a strong signal for imaging [74, 75].

In our previous micro-CT review paper from 2014 [2], we outlined and described several classes of XPC imaging systems with the potential for CT imaging. Broadly these systems can be classified into propagation-based systems, which rely on the propagation distance of x-rays after they have been refracted within the sample to resolve phase changes, analyzer-crystal based systems, which exploit Bragg diffraction within single crystals to measure phase changes, and grating interferometers, which use micron-scale gratings to create interference fringes in x-ray waves that are sensitive to phase changes caused by the sample. Requirements on x-ray beam coherence limited the use of these systems to large synchrotron facilities until Pfeiffer et al. demonstrated an effective adaptation of the Talbot-Lau grating interferometer for use with polychromatic laboratory sources. Their adaptation used an additional source grating which collimated the source beam into an array of individually coherent x-ray line sources suitable for differential phase recovery [76]. Despite their advancement, this and several other early laboratory XPC systems required significant scanning times (hours to tens of hours) to acquire tomographic data suitable for reconstruction. These systems were limited by the x-ray flux of collimated or filtered laboratory sources and the need to acquire projections in several steps to recover phase information. In addition to reconstructing phase information, these systems allowed the reconstruction of absorption images and small-angle scatter images (dark-field images, [77]).

In this review paper, we summarize two recent applications of XPC enhanced imaging to preclinical micro-CT and highlight the advancements they represent in the field. First, the work of Reichardt et al. [78] applies tomographic, propagation-based XPC imaging to study the orientation of muscle fibers in the mouse heart. Phase information provides contrast between muscle fibers in x-ray CT scans at spatial resolutions which are not generally attainable with MRI or ultrasound (<10 μm). Fiber tracking algorithms are applied to the reconstructed data to study heart microstructure. Rather than performing a stepping procedure to recover phase information at each projection angle, they reconstruct a mixed absorption and XPC image after post-processing their projection data to reduce artifacts. Key to the success of their imaging system is a newer technology known as a liquid metal jet (LMJ) x-ray source (Excillum, AB; Kista, Sweden). LMJ sources fill a gap between the high flux provided by a synchrotron and the availability of laboratory sources, providing higher flux at the small focal spot sizes required for XPC imaging [79]. Reported scan times ranged from ~1–2 hours to obtain low-noise data at high spatial resolution (5–10 μm).

Second, the work of Hagen et al. [80] demonstrates an alternative to the Talbot-Lau grating interferometer for XPC imaging with a standard laboratory x-ray source. Specifically, their edge illumination (EI) approach employs two gratings which are selectively opaque to x-rays: a source grating, which creates an array of narrow x-ray beamlets, and a complementary detector mask. The source grating satisfies the beam coherence requirements for phase retrieval. Stepwise translation of the source grating at each projection angle variably blocks the primary x-ray beamlets at the detector mask while recording signal from refracted x-rays. Stepwise translation data allows post-scan computation of phase information in addition to absorption data. Alternatively, as in the work of Reichardt et al. [78], a mixed absorption-phase image can be reconstructed by imaging with the source grating at a single position and post-processing the projection data prior to reconstruction. Notably, imaging with small x-ray beamlets and a detector mask further allowed enhancement of spatial resolution via sub-pixel translation of their sample between scans (dithering).

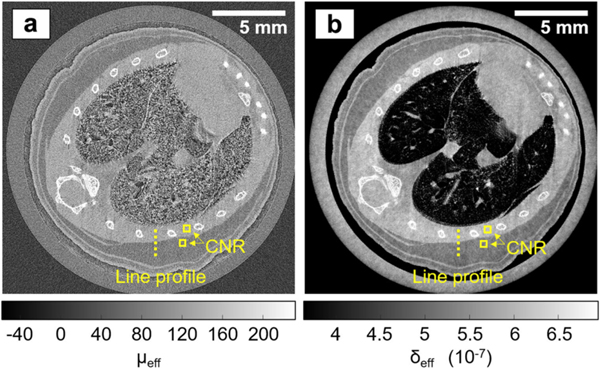
Fig. 8 reproduces results from the work of Hagen et al. using dithering to improve spatial resolution (19 μm in the phase image) and stepwise translation of the source grating to allow separate reconstruction of the attenuation (Fig. 8a) and phase (Fig. 8b) data (ex vivo mouse data). The authors report that the contrast-to-noise ratio (CNR) measured between fat and muscle increased 3-fold from the attenuation image to the phase image, demonstrating the advantages of XPC imaging. The results in Fig. 8 represent an 18-hour scan, but the authors also performed a 13-minute scan at a single source grating position and without the use of dithering (50 μm spatial resolution). This second scan represents an important step toward high-throughput XPC enhanced imaging; however, the reported 300 mGy dose may be high for longitudinal in vivo imaging, and the authors note a loss of spatial resolution around bones caused by assumptions made when processing mixed absorption-phase data.

Fig. 8.

Sub-pixel resolution EI XPC micro-CT images of a mouse chest, acquired with the dithered, multi-franie scheme. (a) Reconstructed attenuation image. (b) Reconstructed phase image. Figure reprodueed from [79] without modifieation under the Creative Commous CC BY license. Note that the line profiles and CNR boxes shown in this figure were used to measure contrast-to-noise ratios and spatial resolution in the cited work.

In addition to polychromatic laboratory sources, LMJ sources, and synchrotron facilities, we note a fourth class of x-ray sources with potential for XPC imaging in small animals: compact light sources (CLS). Broadly, these CLS exploit physical interactions between lasers and free electrons (inverse Compton scattering; Thomson scattering) to produce x-rays in the keV range. Because the laser light is focused on the point of interaction, x-rays can be generated with a photon flux, beam divergence, and focal spot size suitable for XPC imaging. Furthermore, because of the electron beam energies involved, CLS can be constructed at a scale suitable for installation at research facilities or hospitals. Additional benefits of CLS include quasi-monochromatic x-rays at tunable energies, which can reduce spectral artifacts and improve image contrast, and extremely short x-ray pulses, which can benefit dynamic experiments. In 2015, XPC imaging was demonstrated using a prototype CLS from Lyncean Technologies, Inc. (Fremont, CA) [81]. The commercial product was later installed at the Munich Compact Light Source and has since been used for micro-CT imaging, propagation and grating-based XPC imaging, and K-edge subtraction imaging [82]. Alternative CLS designs have been presented by other groups [83], and it has been shown in simulations that CLSs may provide an ideal solution for in vivo dynamic imaging in small animals [84].

Deep learning for micro-CT

In the past decade, deep learning (DL) has touched nearly every aspect of medical imaging, transitioning the field from hand-crafted feature classifiers employed by a select few experts to data-driven learning of complex relationships employed ubiquitously in the field. In this review paper, we focus on the impact of recent developments on the broader field of x-ray CT because many of these developments apply equally to clinical and preclinical CT. We then feature several recent works which have successfully applied these techniques to micro-CT data, and we outline several challenges specific to micro-CT which may be addressed with DL. In the interest of brevity, we assume familiarity with fundamental DL concepts such as convolution neural network (CNN) structures (e.g. ResNet [85], U-Net [86], GAN [87]) and supervised learning with batched, stochastic gradient descent. For those unfamiliar with DL, we recommend as background reading one of several high-quality review papers which provide an overview of fundamental concepts [88, 89].

Data

Regardless of the target application, successful DL projects share several common traits: the utilization of high-performance computing hardware and software, training on large, high-quality data sets, and open-source distribution of sample code and pre-trained models. Since computing hardware and software are largely application agnostic and numerous examples of open-source code distribution can be found on popular code-sharing sites, it stands to reason that the bottleneck in many DL projects is the availability of application-specific training data. For CT imaging specifically, open-access datasets and databases such as the Mayo Clinic Low Dose CT Grand Challenge dataset [90], the NIH-funded Cancer Imaging Archive, and preclinical micro-CT scans with organ segmentations [91] represent cornerstones for reproducible research and the assessment of newer models. In the future, these data sources and their processing pipelines will be harmonized through shared cloud computing platforms like the FLI-IAM architecture [92] and by community standards like those proposed by the Global BioImaging network [93]. For now, however, these data sources are notable exceptions to the “siloed” nature of medical imaging data: data must be pooled between health organizations to provide sufficient data for model training, but privacy, legal, and financial concerns and inconsistent data processing restrict such pooling. The interested reader can find more information on federated learning, a partial solution to these problems, in relevant literature [94].

Preclinical micro-CT data provides a compelling alternative to clinical CT data for DL research. Preclinical systems can reproduce the system geometries, x-ray physics, and most imaging protocols associated with clinical CT while placing fewer constraints on the acquisition and distribution of CT data sets. In the subsequent sections of this review, we highlight several preclinical DL projects with strong potential for clinical translation. Furthermore, we highlight several challenges unique to DL micro-CT projects and outline several promising directions for ongoing research.

Denoising and iterative reconstruction

Image denoising with DL has advanced real-world performance in one of the most thoroughly studied areas of digital signal processing by augmenting traditional signal models and inversion techniques with data-driven learning. The denoising problem is inherent in most DL tasks as networks must learn to generalize their performance over training data in the presence of noise. For CT denoising, there is an inverse relationship between radiation dose, which can be harmful to patients, and the noise level in reconstructed images. To reduce imaging dose, the x-ray exposure per projection or the number of projections is reduced, resulting in photon starvation or view undersampling artifacts. Using traditional signal models, it is often difficult and computationally expensive to robustly reconstruct this low-dose data. This difficulty has made computationally efficient DL methods attractive for processing low-dose CT data.

In literature, supervised learning methods for CT denoising and reconstruction are the most popular [95–101]: networks are trained to reproduce full-dose CT data from low-dose inputs. Ideally, the trained network can then be applied to newly acquired low-dose data, recovering the full-dose data at minimal risk to the patient. Because this approach often approximates traditional reconstruction methods and involves signal recovery from corrupted measurements, it is sometimes referred to as “reconstruction” even when the network performs image-domain denoising only [97, 102]. Supervised learning is particularly attractive when projection data sets are available because realistic photon noise can be added to the projections, simulating a large number of lower-dose acquisitions, or the number of projections can be artificially reduced. There are, however, several issues with this paradigm. The limited availability of clinical projection data and memory constraints associated with 3D processing have led many authors to reproject reconstructed data in a simpler 2D geometry, possibly separating the problem from reality. Furthermore, trained networks often perform poorly when applied to data under- or un-represented in the training set (e.g. data with higher levels of noise [103], different spatial resolution [104], different contrast [105]). This can lead to unpredictable or misleading behavior when the DL model is applied to new data.

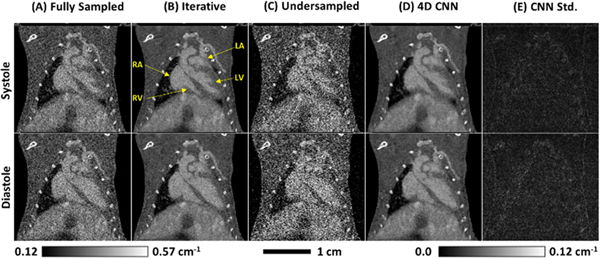
Figure 9 illustrates an example of image-domain denoising applied to preclinical micro-CT data [102]. Extending the above supervised learning paradigm to time-resolved, volumetric image data, a CNN was trained to reproduce iterative reconstructions of full-dose, cardiac micro-CT data sets from quarter-dose reconstructions. Dose was reduced by using a subset of projections for reconstruction, allowing four independent results from the same data set to be compared. This study demonstrates that supervised learning, commonly applied to 2D image data, readily extends to time-resolved, volumetric image data and can closely reproduce the spatial resolution and noise properties of computationally expensive, iterative reconstructions.

Fig. 9.

Application of a trained, 4D CNN to in vivo testing data. (A) Fully sanipled reconstruction results shown for comparison. (B) Iterative reconstruction results (equivalent to training labels). (C) Undersampled reconstruction results (equivalent to training data). (D) Undersampled reconstruction results passed through the 4D CNN. (E) Voxel-wise Standard deviation measured in (D), over four independent subsets of 2250 projections. Note that the calibration bar at the bottom, right applies to (E) only.

Supervised training requires labeled or paired datasets. Assembling sufficient data for training may be difficult (clinical projection data), impractical (manual labeling), or impossible (noise-free data) in certain applications. This has led to a number of alternative training strategies which relax or eliminate supervision requirements. For denoising, the “Noise2Noise” model uses pairs of noisy images which share the same underlying, noise-free image [106]. Because the network cannot learn to reproduce random noise in the training target, it instead converges to a denoised image close to the true, noise-free image (under mild statistical assumption). This model inspired a self-supervised learning model called “Noise2Void” which uses unpaired, noisy images [107]. Pixels removed from the noisy input image are used as labels, and the network is trained to infer the intensity value of the missing pixels by learning feature correlations. The Noise2Void model may be attractive for dynamic imaging applications (cardiac CT, perfusion imaging) where it is difficult to assemble redundant, noisy image pairs, but the Noise2Void authors demonstrate that the Noise2Noise model performs slightly better when image pairs are available.

For both supervised and unsupervised training, variational models represent an important class of DL models for medical imaging. Decades of literature exist on analytical and iterative optimization (reconstruction) techniques and regularization penalty functions for medical image processing. Variational models borrow the structure of these proven techniques, guiding stochastic training with domain-specific priors, while maintaining the myriad benefits of data-driven generalization. Successful application of variational models has been demonstrated in both MRI [108] and CT [97, 98, 100, 101, 109] denoising and reconstruction tasks. As we will illustrate in the following sub-sections on other DL applications, the incorporation of domain-specific knowledge into DL projects is a clear trend and will be critical to the adoption of DL technology in routine practice.

Spectral processing

In this review paper, we talk extensively about the future of quantitative imaging using dual-energy and multi-energy CT. DL methods have been proposed to overcome a number of challenges associated with spectral CT data, including high levels of noise, missing data, and physical degradation of the recorded signal. Noise amplification during material decomposition and spectral post-processing limits sensitivity to contrast materials and low-contrast features, particularly for low-dose acquisition protocols. Supervised training of CNNs represents an ideal solution to this problem because networks can learn to identify valid combinations of spatial features and spectral contrast, enforcing data-driven priors in a way that is difficult to reproduce with analytical approaches [105, 110, 111]. Similarly, supervised training has been applied to correct or compensate for sources of spectral distortion inherent in photon-counting CT [112, 113]. Complex and expensive modeling is required to accurately simulate the detection process in PCDs [33, 72]. We anticipate that DL will play a key role in efficiently incorporating these physical models into routine corrections applied to PC data. Finally, we note a trend in recent literature: estimating missing spectral information with DL priors. This has been demonstrated in the context of spectral extrapolation for dual-energy field-of-view extension [114], estimation of virtual monoenergetic images from single-energy data [115], and estimation of material maps form single-energy data [116]. Success in these applications speaks to the power of DL to model and enforce underlying relationships between image features and spectral contrast; however, significant work remains to understand the limitations and uncertainty inherent in these methods, with particular regard to unique or pathological data which may poorly represented.

Segmentation and registration

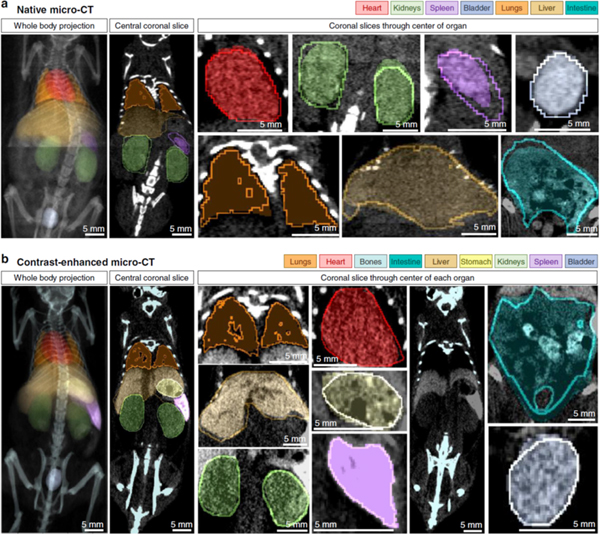
In addition to robust processing methods, image registration and segmentation are fundamental for extracting quantitative data from medical images. For instance, when performing a longitudinal cancer study, automatic segmentation of tumor volumes combined with registration between time points can be used to track tumor growth and to classify features indicative of treatment outcomes [117, 118]. DL has advanced the state-of-the-art for image segmentation both in terms of accuracy and speed [119–121]. Here, we feature the work of Schoppe et al. [119] who use a dataset of pre- and post-contrast micro-CT scans of the mouse, including multi-organ segmentations, [91] to train a DL model (Figure 10). Their work demonstrates whole-body, multi-organ segmentation within one second. Furthermore, they tackle several important issues related to segmentation, including the modeling of uncertainty between human segmenters and transfer learning between imaging modalities.

Fig. 10.

Qualitative results of segmentation performance. Filled, semi-transparent areas show AIMOS (segmentation model) prediction for (a) native micro-CT and (b) contrast enhanced micro-CT (contrast agent: ExiTron nano 6000, nanoPET Pharma GmbH). Opaque lines indicate human expert annotations. Left column shows mean-intensity projections for the whole-bodv sean. Second column shows representative coronal slices. Remaining columns of figure show individual organs (coronal slice through center of oigan). Figure reproduced frorn [118] without modification under the Creative Commous CC BY lieense.

Image registration is a similarly active area of DL and medical imaging research because of its role in quantitative image analysis. Following recent review papers on the subject [122, 123], DL approaches to registration began with supervised learning of image similarity metrics. Replacing common metrics like mean-squared-error or mutual information, these learned metrics can then be minimized iteratively and at progressively higher resolution levels to map a moving image to a fixed image. Several works have demonstrated superior registration performance with learned similarity metrics, particularly when registering data from different imaging modalities [124, 125]; however, the performance of these methods is limited by the computational cost of iterative optimization. This has led to a number of more recent works where networks are trained to estimate the final image transformation directly [126, 127]. Differentiable transformer modules [128] can be incorporated into these direct registration models to apply the transformation within the model and to return the registered moving image. Both supervised and unsupervised learning approaches to image registration have been used. Specifically, there is increasing focus on unsupervised, direct estimation of registration parameters, to make efficient use of unpaired training data [127], and adversarial penalty functions, to learn more realistic transformations [129]. GPU memory limitations continue to be a bottleneck in training models for 3D, deformable image registration.

Super-resolution

Physical and practical constraints associated with imaging often limit spatial resolution below what is optimal for a specific application. Conceptually, post-process enhancement of spatial resolution is an attractive solution; however, this “super-resolution” inverse problem is inherently ill-conditioned, even when an accurate forward model of the imaging system is available. Recent works have demonstrated that domain-specific DL can excel in this and related “image-to-image translation” problems under the assumption of a shared latent space [130]. Practically, this means that if low- and high-resolution image patches can be mapped to the same compressed representation, they can be interchanged to enhance resolution. With regard to x-ray CT, You et al. proposed GAN-CIRCLE to enhance the spatial resolution of both micro-CT scans of bone and clinical CT scans of human paitents [131]. To overcome instabilities often associated with adversarial training and inverse problems, they used cycle-consistency constraints: estimated high-resolution images must map back to their low-resolution inputs and vice versa. Zheng et al. similarly used the GAN-CIRCLE model to enhance clinical CT scans with high resolution textures learned from ex vivo micro-CT data of the same anatomic region (lungs) [132]. They added additional mean-squared-error constraints between the model inputs and outputs to ensure that intensity information remained consistent following resolution upsampling and downsampling. Finally, Holbrook et al. [133] demonstrated that PCD CT data acquired at low resolution could be fused with high-resolution EID CT data in a DL-based implementation of “pan-sharpening,” allowing high-resolution material decomposition. This hybrid approach to spectral CT has numerous potential advantages, including dose reduction and improved spectral fidelity associated with larger PCD pixels [33].

Artifact and scatter corrections

CT data sets often suffer from ring artifacts (variations in detector gain), metal artifacts (view-dependent photon starvation), and scatter (low-frequency background signal). Given the pervasive nature of these problems, numerous calibration procedures and analytical and iterative methods have been proposed to deal with them [134]. DL provides an attractive solution to these problems because their physical origins are well understood and can be reproduced when generating synthetic training data for supervised learning. Furthermore, DL provides a computationally efficient means to address low spatial frequencies and to optimize corrections for specific imaging systems and protocols. Example ring artifact correction papers include the work of Nauwynck et al. [135], who trained a multi-resolution U-Net to remove synthetic rings from clinical data, and the work of Holbrook et al. [136] who trained a similar residual U-Net to remove synthetic rings from preclinical data. In both cases, application of the trained network to testing data with real ring artifacts showed significant high-frequency artifact reduction, but additional room for improvement addressing low-frequency artifacts. For metal artifact correction, Liao et al. [137] combined an adversarial penalty function with a multi-resolution metal mask to inpaint metal traces in sinogram data and achieved superior artifact suppression to several non-DL methods. Finally, Maier et al. [138] demonstrated effective application of DL to estimate scattered signal from x-ray projections. Their network reproduced gold-standard Monte Carlo scatter estimates at varying dose levels, source kVps, and anatomic regions and effectively removed CT number inaccuracies and streaking artifacts from reconstructed images.

Challenges and future directions

In this section, we have provided a broad overview of DL applications in x-ray CT, while highlighting several successful DL projects targeting preclinical micro-CT. Because the hardware, software, and computing resources utilized for DL projects are application agnostic, preclinical micro-CT will continue to serve as a crucial testing ground for future clinical applications. Notably, there are several general and unique challenges associated with preclinical micro-CT and DL. First, limited availability of training data at both the clinical and preclinical levels will continue to the slow the progress of application-specific DL projects. This limitation is compounded by the lack of standards in preclinical CT which would otherwise facilitate pooling data from different sources. Second, CT data is inherently three dimensional, yet most DL projects process data in two dimensions due to computational constraints. Overcoming these limitations through hardware and algorithm improvements will undoubtedly lead to many new and improved applications. Finally, while preclinical micro-CT allows greater flexibility in imaging protocol design and data sharing, it also faces strict trade-offs between image resolution, noise, and temporal and spectral resolution. These trade-offs complicate label generation for supervised learning. Clever solutions to these problems or alternative unsupervised learning methods will be crucial for advanced DL applications like PCD CT, XPC CT, and in vivo cardiac imaging.

Discussion and conclusions

This review paper provides a broad overview of current applications and research topics related to preclinical micro-CT technology. We began by highlighting several commercial micro-CT scanners, which provide prepackaged imaging solutions for in vivo and ex vivo studies, and then transitioned to state-of-the-art applications like in vivo, PCD-based spectral imaging, hybrid diagnostic-therapeutic agents for molecular imaging and theranostics, and laboratory-based XPC imaging. The promise of these newly developing applications has established micro-CT as a translational testbench for future clinical applications. Finally, we surveyed numerous facets of DL applied to classic medical imaging problems (denoising, segmentation, registration) and to CT-specific imaging problems (spectral and artifact corrections, low-dose reconstruction). It is clear that data-driven DL in tandem with domain-specific knowledge and hardware and software developments will continue to push the bounds of what is possible in the field.

Looking forward, we are excited by future applications of preclinical and clinical CT technology. We believe that the future lies in multi-dimensional imaging applications which enhance the anatomical imaging CT is known for with functional and molecular information. For instance, future applications of coronary CT angiography using PCDs will inherently sample spectral information. This spectral information can then be used to reduce image artifacts and to improve the quantification of calcium deposits in atherosclerosis studies. Targeting nanoparticle contrast agents to the site of plaques may even allow non-invasive characterization of atherosclerotic plaque composition. Newer computational methods like DL will be required to handle the large volumes of data associated with these applications and to improve the robustness of such methods while controlling radiation dose to the patient. In sum, many of the advancements we have discussed in this review will be applied in coordination to enable fundamentally new CT imaging applications.

• Commercially available micro-CT scanners and recent applications are described.

• Spectral micro-CT and phase contrast micro-CT promise improved contrast.

• Micro-CT and nanoparticle contrast agents can serve in theranostics studies.

• Deep learning will have a great impact on future micro-CT developments.