Integrating Risk Assessment and Decision‐Making Methods in Analyzing the Dynamics of COVID‐19 Epidemics in Davao City, Mindanao Island, Philippines

Abstract

The COVID‐19 pandemic has become a public health crisis in the Philippines and the attention of national and local health authorities is focused on managing the fluctuating COVID‐19 cases. This study presents a method that integrates risk management tools into health care decision‐making processes to enhance the understanding and utilization of risk‐based thinking in public health decision making. The risk assessment consists of the identification of the key risk factors of the COVID‐19 contagion via bow‐tie diagrams. Second, the safety controls for each risk factor relevant to the Davao City context are taken into account and are identified as barriers in the bow‐tie. After which, the prioritization of the identified COVID‐19 risks, as well as the effectiveness of the proposed interventions, is performed using the analytic hierarchy process. Consequently, the dynamics of COVID‐19 management initiatives were explored using these priorities and a system of ordinary differential equations. Our results show that reducing the number of COVID‐19 fatalities should be the top priority of the health authorities. In turn, we predict that the COVID‐19 contagion can be controlled and eliminated in Davao city in three‐month time after prioritizing the fatalities. In order to reduce the COVID‐19 fatalities, health authorities should ensure an adequate number of COVID‐ready ICU facilities. The general public, on the other hand, should follow medical and science‐based advice and suspected and confirmed COVID‐19 patients should strictly follow isolation protocols. Overall, an informed decision‐making is necessary to avoid the unwanted consequences of an uncontrolled contagion.

1. INTRODUCTION

The COVID‐19 pandemic (World Health Organization [WHO], 2020a), caused by the coronavirus SARS‐CoV‐2 (Gorbalenya et al., 2020) calls the attention of public health authorities around the world (Wee, McNeil Jr., & Hernández, 2020) to seek and recommend effective control measures to mitigate its risk and spread while softening the economic impact of the virus. The first reports on the clusters of pneumonia‐like cases of the contagion were recorded during the last week of December 2019 by the Municipal Health Commission in Wuhan, a city in Hubei Province of China with a population of over 11 million (WHO, 2020b). The virus spread into other parts of the country quickly that resulted in a surge of COVID‐19 confirmed cases with new cases that peaked in February 2020 reaching more than 5,000 confirmed positive cases in a single day. After a few months of the first reported cases in China, the contagion outbreak was on the rise beyond China and had spread to the other parts of the rest of the world. Since the 11th of March 2020, the date when the disease escalated into a global pandemic (Zhang, Hu, & Ji, 2020), COVID‐19 has spread to over 200 countries. As of the 25th of June 2020, a total of approximately 9.4 million confirmed cases, 4.7 million recoveries, and over 481,000 deaths have been reported around the world (European Centre for Disease Prevention and Control [ECDC], 2020).

One of the reasons for the fast spread of COVID‐19 is its high transmissibility and there is currently no available vaccine or drug treatment that can be administered for protect individuals against the virus (Adhikari et al., 2020). Although COVID‐19 is less lethal as compared to SARS (severe acute respiratory syndrome) or MERS‐COV (Middle East respiratory syndrome coronavirus) (Petrosillo, Vicenconte, Ergonul, Ippolito, & Petersen, 2020), this infectious disease has caused major health global crisis, due to the overburdening of hospitals and healthcare services. The number of active cases can surpass the hospital's capacity to treat the impaired. There has been overwhelming numbers of patients that require hospital admission and prolonged stays of greater than a week and up to 2 months (Rees et al., 2020). Such high levels of admissions can paralyze hospital facilities and health workers. Thus, in areas or territories that lack hospital preparedness, critical care crises and deaths due to the limited hospital capacity are inevitable (Carenzo et al., 2020; Oshitani, Kamigaki, & Suzuki, 2008). To avoid these adverse outcomes, it is indeed necessary for the spread of the virus to be controlled by keeping the disease incidence as low as possible to minimizing medical treatment cases so that the pandemic is manageable within the current health care system. To control the virus, different government units and policy‐recommending bodies impose prevention and control strategies, such as observing social distancing, practicing frequent hand washing, undergoing mandatory quarantine and participating in voluntary self‐quarantine, wearing of face masks, and implementing community lockdown/containment, to reduce and manage the risks of spreading the disease (Adhikari et al., 2020; Güner, Hasanoğlu, & Aktaş, 2020; Wilder‐Simth & Freedman, 2020).

One of the countries that is prone to experiencing COVID‐19 hospital burden is the Philippines, a developing country with a population that is rapidly growing. According to German, Miña, Alfonso, and Yang (2018), rapid population growth can affect hospital capacity. As of May 2020, the nationwide COVID‐19 count has risen to over 12,000 total confirmed cases, with over 800 deaths, and 2,400 recovered cases (Department of Health [DOH], 2020a). Specifically, in Davao City of southern Philippines, the largest city in the country, a total of 222 confirmed cases, 117 recoveries, and 25 deaths were recorded on the 20th of May, 2020. Since March 2020, the local government unit has placed the city in different levels of community quarantine while the testing rate is being increased to slow the spread of the disease and flatten the epidemic curve (Anderson, Heesterbeek, Klinkenberg, & Hollingsworth, 2020).

There have also been several quantitative studies that were conducted to aid decisionmakers in controlling the epidemic in the city. One of these is through mathematical modeling of the infectious disease where the impacts of the control interventions to the disease are described (Adhikari et al., 2020; Liu et al., 2018; Zhang, Jin, Sun, Zhou, & Ruan, 2011). However, the complex nature of COVID‐19 spread within the country brought by its archipelagic structure has posed a challenge to the national government in terms of predicting disease spread and prescribing interventions for the country as a whole. As a result of this, local government units impose their intervention schemes at the regional scale leading to varying degrees of success due to the risks involved in implementing “pro‐poor solutions” (Mercado, 2020). The success of mathematical models in controlling infectious diseases depends on the assumptions made about the system. Erroneous assumptions lead to spurious results and projections. Thus, to better understand the COVID‐19 dynamics in developing countries like the Philippines with various control interventions being set in place, one has to determine how the country manages the risks associated with the disease given the limited resources. This can be achieved by considering the results of risk assessment methods and incorporating it in the model formulation.

An example of a risk assessment tool is the bow‐tie (BT) analysis, which visually presents the risk factors leading to an unwanted event and the impacts that might result from the unwanted event as well as the controls or safety barriers that could be deployed to prevent and mitigate the unwanted event (Culwick, Merry, Clarke, Taraporewalla, & Gibbs, 2016; Van Nunen et al., 2018). The BT analysis can be accompanied by an AcciMap (Forbes, Heitman, & McCulloch, 2020) to highlight the individuals or parties who are responsible for ensuring the reliability of the controls (Tabibzadeh, Stavros, Ashtekar, & Meshkati, 2017). The BT analysis allows us to map out the complete scenario of relationships among threats and consequences with their appropriate controls. This feature offers decision‐support techniques (Badreddine & Amor, 2010), such as the analytic hierarchical process (AHP), the feasible steps to further assess the risks quantitatively. In particular, AHP can be used to prioritize the risks factors according to the quantified judgment of a decisionmaker (Aminbakhsh, Gunduz, & Sonmez, 2013). The method of AHP emphasizes the role of judgment in setting priorities.

This article presents a novel methodology for analyzing disease dynamics by considering the findings from risk assessment methods and decision‐making techniques. We will demonstrate this idea by showing how the spread of COVID‐19 in Davao City, Philippines can be better understood by applying the international standard for risk ISO 31000 (AS/NZS ISO 31000:2018). We began by establishing the context using a mathematical model and data to describe the effect of existing interventions imposed by the local government unit to control the spread of COVID‐19 among people living in Davao City. Failure to manage the risks effectively, the unwanted event, which in this case is an uncontrolled contagion becomes inevitable. Then, we used risk assessment tools to answer the question: Which risk factors identified to be associated with the contagion should be given priority by management to control the contagion with the limited resources? Finally, we linked the results of the risk assessment to the epidemic model and showed the resulting disease dynamics from the prioritized controls and interventions for the treatment of the risks.

Being able to include expert and informed judgments into the collected epidemiological data is another crucial step to ensure that the interventions are effective and implementable for a significant period of time. Hence, this article demonstrates how judgment is included in the integrated risk assessment methods. It is also important to note that only one set of judgments was utilized in the article to simplify the demonstration purposes. The detailed discussion for the incorporation of judgments is found in Sub‐section 3 of the Methodology section.

2. METHODOLOGY

2.1. Data sets

Two types of data sets were collected in this study and used as inputs for the integrated analysis. One data set is a time‐series data set containing: (i) daily reported confirmed COVID‐19 cases, (ii) daily reported COVID‐19 deaths, and (iii) the daily reported recoveries from COVID‐19 in the city from March 15 to September 30, 2020. This data set was obtained from the official social media reports of the local health agency, Department of Health Region XI, in Davao City, Philippines. The data set was used for analyzing an epidemic model for COVID‐19 dynamics in the city. The other data set was a collection of the responses or judgments from a knowledgeable citizen of the city. It was utilized to demonstrate the decision‐theory aspect of the integrated analysis. The scope of this article is to highlight how an expert opinion is analyzed in the BT and AHP integration. The main contribution of this article, therefore, is to provide a proof of concept and demonstrate the novelty of this methodology.

2.2. Risk Assessment Methods

2.2.1. Bow‐tie Analysis

A BT completely represent an accident scenario qualitatively and quantitatively (Khakzad, Khan, & Amyotte, 2012). Quantitatively, the logical relationship between the components of an accident or an unwanted event scenario is elucidated graphically by the BT. This aids the decisionmaker in understanding which possible combination of threats would lead to the uncontrolled COVID‐19 contagion and which controls’ or safety barriers’ failure would escalate the uncontrolled COVID‐19 contagion to a particular consequence. Once the BT has been constructed, quantitative analysis can be performed by assigning probabilities to the threats of the left‐hand side of the BT and the safety barriers of the right‐hand side of the BT. Specifically, the threats are the primary events (PE) while the unwanted event is the top event (TE).

BT is effective in providing the structure consisting of relationships between the risk factors. However, the structure can be static in terms of catching up with variations. Integrating quantitative techniques into the BT can take advantage of case‐specific data and BT updating mechanisms to revise the failure probabilities obtained from the initial generic data in the design phase of the system (Khakzad et al., 2012). BT's compatibility with quantitative and dynamic risk assessment methodologies allowed it to incorporate the characteristics of prevention, simultaneity, and immediacy by providing additional steps in the analysis of the risk probability (Folch‐Calvo, Brocal, & Sebastián, 2019).

2.2.2. AcciMap

The Accimap technique produces a multilayered visualization of the various causes of an unwanted event which is usually an accident (Branford et al., 2011). The causes are arranged according to their causal remoteness from the outcome. This technique was developed by Rasmussen (1997) as part of the process for generating proactive risk management strategies for complex sociotechnical systems. Accimap analysis can also be adapted to show the support actions, artifacts, and activities that are required to ensure controls are implemented and monitored and maintained over time.

2.3. Analytic Hierarchy Process

Analytic hierarchy process (AHP) is a robust and flexible mathematical tool for decision‐making processes that utilize expert's opinion as important inputs (Mustafa & Al‐Bahar, 1991; Erdogan, Šparauskas, & Turskis, 2017). This method has been widely used in literature for risk management related studies that focus on construction projects (Aminbakhsh et al., 2013; Erdogan, Šaparauskas, & Turskis, 2017), supply‐chains (Sharma & Pratap, 2013; Salomon, Tramarico, & Marins, 2016; Tramarico, Mizuno, Salomon, & Marins 2015), and healthcare projects (Hillerman, Souza, Reis, & Carvalho, 2017; Ho & Chen 2017). In this study, the steps used in performing the AHP analysis were based on the process described by Thibadeau (2007): (1) setting‐up the hierarchical layers; (2) setting‐up the degrees of preference of the variables identified in each layer; (3) making pairwise comparisons regarding consistency ratio; and (4) generating hierarchical decisions.

2.3.1. Setting‐up the Hierarchical Layers

The clustering of the activities in each of the layers must be closely related to each other (Saaty, 1990) to ensure the clear association of the clustered activities when comparisons between them are made (Mustafa & Al‐Bahar, 1991). Specifically, the cluster results of the BT analysis were used to ensure that the clustering of activities for each of the AHP layers is homogenous, as described in Fig. 1. Fig. 2 on the other hand displays the clusters and the associated model for the BT where T1–T4 represent the threats events, C1–C3 represent consequences events, T1‐PC1–T4‐PC4 represent the preventive controls, and C1‐PB1–C3‐PB3 represent the mitigative controls. Overall, two layers were considered for AHP: the (1) threats and consequences layer and the (2) alternatives layer.

Fig 1.

Schematic of generating priorities for BT‐AHP.

Fig 2.

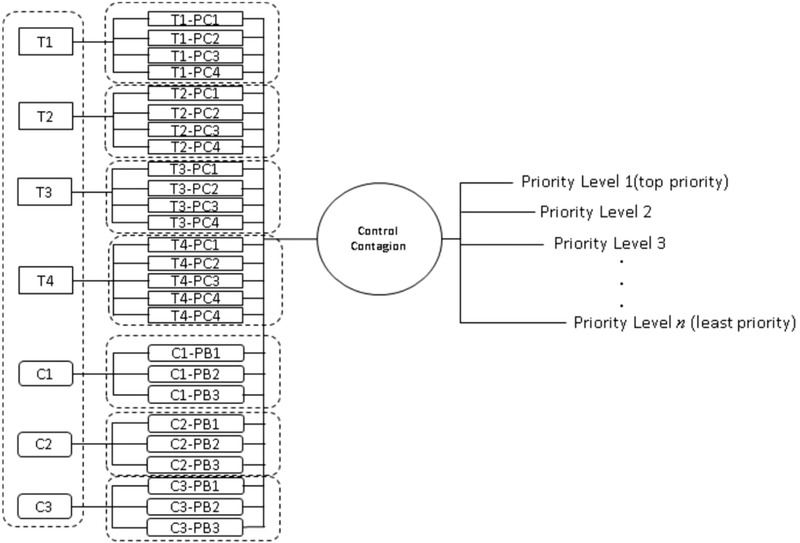
BT‐AHP model for COVID‐19 response in Davao City.

2.3.2. Setting‐up the Degrees of Preference of the Variables

In this study, pairwise comparison of each of the events found in the Threats and Consequences layer {T1, T2, T3, T4, C1, C2, C3, C4} were done by asking an expert on how more valuable (i.e., degree of preference) an event to the other event (i.e., T1 versus T2) (Sharma & Pratap, 2013; Vidal, Marle, & Bocquet, 2011). It should be noted that the term “expert” is referred to an individual who has attained sufficient engineering experience to evaluate the identified risks (e.g. professional engineers, plant or site managers, superintendents, and academic staff) (Li, Al‐Hussein, Lei, & Ajweh, 2013). The same procedure was also done for each set of controls in the alternatives layer that were grouped accordingly with respect to their relationships in the Threats and Consequences layer, that is the set of alternatives {T1–PC1, T1–PC2, T1–PC3, T1–PC4} with respect to T1. The categorization for the degree of preference or how valuable one event or alternative to another as shown in Table I follows the suggestions of Kil, Lee, Kim, Li, and Newman (2016).

Table I.

Degree of Preference for the Pairwise Comparison for AHP

Intensity of Importance	Definition	Explanation
1	Equal importance	Two events contribute equally to the objective
3	Moderate importance	Experience and judgment slightly favor one event over another
5	Strong importance	Experience and judgment strongly favor one event over another
7	Very strong or demonstrated importance	An event is favored very strongly over another; its dominance demonstrated in practice
9	Extreme importance	The evidence favoring one event over another is of the highest possible order of affirmation
2, 4, 6, 8	Intermediate values between the two adjacent judgments

2.3.3. Making Pairwise Comparisons with Reference to Consistency Ratio

The pairwise comparisons and checking of the consistency ratio were performed using SuperDecisions software, an opensource (Kabak, Erbaş, Çetinkaya, & Özceylan, 2018) developed by the team of Thomas Saaty (Creative Decisions Foundation, 2020). The consistency ratio must be at most 0.10 so that the estimated relative importance of the variables is deemed acceptable (Saaty, 1990), implying that the expert's judgment is dependable (Erdogan et al., 2017).

2.3.4. Generating Hierarchical Decisions

The local weights generated for each pairwise comparisons per layer were multiplied to generate the global weights. For example, the local weight of T1 was multiplied by each of the local weights of T1–PC1, T1–PC2, T1–PC3, and T1–PC4. The global weights were then ranked accordingly in ascending order with 1 as the highest order of priority.

2.3.5. Quantifying BT Analysis

The proposed AHP interventions, which are in parallel with the BT controls, are quantified in terms of both their local weights and global weights. The local weight is with respect to the threat or consequence line they belong to while the global weight is with respect to the overall prescribed interventions to control the COVID‐19 contagion.

2.4. A COVID‐19 Epidemic Model

2.4.1. Model Description

The model developed in this study was based on a Susceptible‐Exposed‐Infected‐Removed (SEIR) model proposed by Anderson et al. (2020) with some modifications. The host population in the system is divided into five subpopulations: susceptible, exposed, confirmed infectious, unconfirmed infectious, and recovered (see Fig. 3). Mathematically, we denote these subpopulations as S(t), E(t), I_r (t), I_u (t), and R(t), respectively, that is, as functions of time t (in days).

Fig 3.

A general framework for the compartmental representation of transmission dynamics of COVID‐19 used for model fitting and projections with the collected data sets.

As seen in Fig. 3, the subpopulations are represented as hexagonal compartments. The population size of each compartment varies mechanistically according to the inflow (arrows going in) and outflow rates (arrows going out). Let us consider the dynamics of the exposed population in the diagram to illustrate the idea. Based on Fig. 3, the exposed population grows as a result of the susceptible population acquiring the virus directly (i.e., contact with infectious individuals) or indirectly (i.e., contact with contaminated surfaces). On the other hand, an exposed population decays as exposed individuals leave the compartment. This can happen in various ways: (1) when an exposed individual is vaccinated, (2) when the individual progresses to the next phase of infection as viral load increases but remains untested or unconfirmed, or (3) when the individual is confirmed to have the virus via testing. Notice that the diagram does not show an arrow that points from the unconfirmed infectious compartment to the confirmed infectious compartment. This is done to highlight the limited testing capacity in Davao City, Philippines which is our case study. A detailed discussion on model equations and assumptions is found in Appendix A.

2.4.2. Methods of Analysis

The epidemic model is formulated as a system of differential equations with fixed values for the initial conditions and rate parameters. Estimation procedures for unknown model parameters were done by fitting the model to the COVID‐19 data set using a least‐squares method via lsqcurvefit command (refer to https://www.mathworks.com/help/optim/ug/lsqcurvefit.html for the documentation). The set of parameter estimates with the minimum residual error was considered as the best estimate. In this study, model simulations were also performed to make projections about the disease. All the numerical methods for model fitting and simulations were implemented in MATLAB version R2020a.

3. RESULTS AND DISCUSSIONS

3.1. Fitted Model of COVID‐19 Cases in Davao City, Philippines

The mathematical model, given by Eqn (1) below, was fitted to the COVID‐19 data sets in Davao

City:

$$\begin{array}{c}{\displaystyle \frac{dS}{dt}=-\frac{\beta }{N}S\left({\sigma }_0{I}_u+{\sigma }_1{I}_r\right)-vS+rR-\epsilon S,}\hfill \\ {\displaystyle \frac{dE}{dt}=\frac{\beta }{N}S\left({\sigma }_0{I}_u+{\sigma }_1{I}_r\right)-\alpha E-vE+\epsilon S,}\hfill \\ {\displaystyle \frac{d{I}_r}{dt}=\alpha \rho E-\mu I_r-\gamma I_r-v{I}_r,}\hfill \\ {\displaystyle \frac{d{I}_u}{dt}=\alpha \left(1-\rho \right)E-\mu I_u-\gamma I_u-v{I}_u,}\hfill \\ {\displaystyle \frac{dR}{dt}=\gamma \left(I_u+I_r\right)-rR-vR.}\hfill \end{array}.$$ (1)

The model parameter descriptions and the corresponding values are presented in Table II.

Table II.

Model Parameter Descriptions

Symbol	Description	Values
$\beta$	Transmission rate (per day)	1.6895
${\sigma }_0$	Multiplicative factors for the infected compartments	0.5333
${\sigma }_1$		0.8300
$\nu$	Vaccination rate (per capita per day)	0, 0.05
$r$	Transition rate from recovered to susceptible compartment	10−7
$\epsilon$	Indirect transmission rate	10−5
$\alpha$	Transition rate from being exposed to becoming infectious	0.2710
$\rho$	The proportion of exposed individuals being reported	0.1328
$\mu$	Disease‐induced mortality rate	0.0365
$\gamma$	Reporting rate	0.8795
N	Population	1.65 million
$S_0$	Initial susceptible population	1.4689×105
$E_0$	Initial exposed population	569
${I_r}_0$	The initial infected population that were confirmed or reported	22
${I_u}_0$	The initial unreported infected population	146
$R_0$	The initial recovered population	1,838

Note: Bold‐faced values are estimated values from the model fitting procedure.

Using the parameter values in Table II, we plot the fitted model along with the data on the daily cumulative COVID‐19 cases in Fig. 4. We can see from the plot that the model slightly overestimates the cumulative cases toward the latter part of the data. On the other hand, the model captures the average trends of the new cases, deaths, and recoveries, as seen in the Fig. A1 found in Appendix section. The computed basic reproduction number is 1.0432, which falls within the 95% Confidence Interval estimate for the statistical estimate of the basic reproduction number (see Appendix B and Fig. A2). This finding implies that the model precisely describes the underlying mechanism of COVID‐19 dynamics in Davao City under different tiers of quarantine.

Fig 4.

The plots of the daily cumulative COVID‐19 cases (top), deaths (bottom left), and recoveries (bottom right) in Davao City under different quarantine levels (colored bars), that is, community quarantine (CQ), enhanced CQ (ECQ), general CQ (GCQ), and modified GCQ, and the fitted model for cumulative cases, deaths, and recoveries (black curve). The computed basic reproduction number is 1.0432.

3.2. Risk Assessment of COVID‐19 Contagion

3.2.1. BT Analysis for COVID‐19 Contagion

The BT analysis aims to provide a layered perspective of the COVID‐19 contagion. It visibly defines the threats we want to prevent and the consequences we want to mitigate as shown in Fig. 5 with the uncontrolled contagion as the unwanted event along with the proactive perspective from its left‐hand side and the reactive approaches to its right‐hand side.

Fig 5.

Bow‐Tie Analysis for COVID‐19 Contagion for Davao City, Philippines.

These controls are known, however not all interventions are necessarily implemented in actual in the city. For example, vaccination is widely perceived to be an effective control of the increasing number of confirmed positive COVID‐19 patients but has not been implemented at the time when this manuscript was submitted for peer‐review process (November 2020). Hence, the BT enables us to quickly visualize the safety barriers to stop the progression of the risk factor toward the uncontrolled contagion using more explicit demonstration of risk control both existing and perceived.

Applying a risk‐based approach, the left‐hand side begins by identifying each of the threats (in purple) followed by its series of appropriate controls (in gray) to constitute one threat line. In this case, four threat lines for each of the four threats that could lead to or cause the uncontrolled COVID‐19 contagion outbreak was identified. These threats are the spreading of infection from unreported and/or asymptomatic infectious individuals, the increasing number of confirmed positive COVID‐19 patients, airborne viable virus, and surface contaminated with the viable virus.

The BT presents the threats that may be quite common and not limited to the Philippines. However, it can be noted that the prescribed controls for each threat carefully and specifically considers the case of Davao City. The controls on the left‐hand side of the BT are preventive in their function as barriers that impede the progression of the threats to not reach the unwanted event of uncontrolled contagion. Most risk‐based approaches provide multiple layers of defenses to prevent the initiation of the outbreak or from it getting worse. For example, the South Korean government has adopted sequential barriers strategy in hospitals to control unexpected outbreaks consisting of gate screening, specialized clinics, and preemptive isolation of pneumonia patients (Noh et al., 2020). This barrier‐based strategy is based on the risk management model referred to as the Swiss cheese model.

The first line of control is to barricade city borders and suspend all incoming flights to all but essential personnel. This is supported by the study findings of Klepac, Kissler, and Gog (2018) showing the increase in the spread of viral diseases due to human mobility and contact patterns. By putting city barricades, the chain of transmission can be disconnected and the disease hampered. Restrictions can apply although asymptomatic at the start of the disease since anyone can be a carrier even without the usual symptoms of flu‐like symptoms of fever and dry cough.

Another control is the mass targeted testing in high‐density population areas since this will remove the infectious people from the susceptible population. The 14‐day quarantine for all incoming people, which also addresses the typical asymptomatic period at the start of the disease, is also another COVID‐19 control. Furthermore, self‐isolation and the use of personal protective equipment (PPE) to prevent in‐home infection transfer can reduce the rate of spread of the disease.

Coşkun, Yıldırım, and Gündüz (2020) found that the fast transmission rate of the outbreak has been expedited in high‐density population areas which in turn increases the number of confirmed positive COVID‐19 patients. Consequently, it is necessary to avoid crowding in certain places. Thus, the implementation of the Enhanced Community Quarantine (ECQ) is appropriate which includes limiting human mobility using coded Food & Medicine Passes.

Tracing each patient's mobility and contact patterns in the last three weeks and identifying persons under investigation (PUIs) is an important control to the increasing number of confirmed positive COVID‐19 patients. Data sets that provide joint social and movement patterns in a network of contacts are immensely rare (Klepac et al., 2018). However, Read et al. (2014) were able to capture both contact patterns and human mobility in Guangdong, China, which contained self‐reported information about the distance at which particular contacts took place. Approaches like the aforementioned study offer useful data especially in determining the local dynamics of the disease transmission. Klepac et al. (2018) found that once the transmission chain has been successfully established in the local area or cluster, the transmission dynamics from then onwards becomes autonomous. Similarly, Cremin et al. (2018) found a strong time effect observed within each outbreak, with the majority of transmission observed within short windows of time each day when frequent contacts occurred. Despite this, there remains a need for a better understanding of how contact patterns and human mobility data translate into disease transmission dynamics (Klepac et al., 2018). The use of vaccination is one of the most effective and known strategy in making sure that infectious disease is controlled (Lachica et al., 2020; Vairo et al., 2017). Vaccination reduces the risk of disease transmission which essentially reduces the size of the susceptible population (Ibuka et al., 2016; Stier, Berman, & Bettencourt, 2020). Combining these two controls, vaccination can be targeted toward units with the highest human mobility and highest number of contact patterns (Ibuka et al., 2016; Muellner, Fournié, Muellner, Ahlstrom, & Pfeiffer, 2018).

It is recognized that there are threats that appear more critical than others. Adequately enough, the BT structure takes into account time‐sequence and reliability of controls clearly for each threat line scenario. Upstream controls are the first line of defense to provide the soonest and most urgent response especially for such case where human lives are at stake. If the upstream controls fail then downstream impedes the progression toward the unwanted event.

3.2.2. AcciMap for COVID‐19 Contagion

However, if despite the preventive controls the uncontrolled contagion still did occur, the controls on the right‐hand side of the BT are putting mitigative actions to avoid worst‐case consequences from further occurring. Several factors lead to the failure of preventive controls which are mainly referred to as erosion factors. Erosion factors are determined to be critically important to ensure the effectiveness of each of the controls. Such factors are illustrated and described in Fig. 6. This should take into account the population demographics where residents in the older age groups would not be reached by the announcements about food and medicine (FM) pass instructions and updates if the communication is largely done through social media. However, the effective and fast communication of the city government will not be adequate in enforcing the rules to the residents for them to comply accordingly. Police forces must be deployed to monitor throughout the city and to set‐up checkpoints in strategic locations to only allow residents with the scheduled code of the FM pass. Nevertheless, if a number of residents still fail to comply with the ECQ rules, the reliability and effectiveness of ECQ as a control for COVID‐19 contagion is reduced.

Fig 6.

Accimap for COVID‐19 Contagion

Several Philippine media sources reported that self‐isolation has been one of the most evident and widely implemented control measures (Sabillo, 2020; DOH, 2020b). However, a number of suspected COVID‐19 positive individuals and the quarantined individual were noncompliant to it (Pazzibugan, 2020; Talabong, 2020). In addition to failure to comply with proper self‐isolation, news media reported city residents who failed to comply with physical distancing (Malasig, 2020) and FM pass rules (Saron, 2020). Apparently, individual city resident compliance directly affects all preventative controls that are at the left‐hand side of the uncontrolled contagion. This clearly shows that the noncompliance of individual city residents significantly reduces the reliability and effectiveness of preventative controls. In effect, the reduced reliability of city‐wide controls pushes to progress toward the uncontrolled contagion. In terms of the BT, the chronological sequence of the event is pushed from the threats of the left‐hand side into the right direction toward the BT knot of unwanted event.

3.3. Analytic Hierarchy Process Results

Since the uncontrolled contagion has already occurred in Davao City, all these three consequences are taking place simultaneously with the ongoing existence of the threats after the preventive controls has been implemented for a period of time. For example, the first fatality case for COVID‐19 in the city was recorded about two to three weeks after a number of confirmed positive patients have been reported and after the ECQ started its implementation, that is April 4, 2020. At this point, both the threats and consequences need to be managed simultaneously. This means that with the limited resources of the city, decisionmakers need to allocate manpower, funds, and other means of support to additionally manage the increasing number of fatalities from COVID‐19, the economic hardship issues experienced by the low‐income households (Martin, Markhvida, Hallegatte, & Walsh, 2020), and other matters such as the mental well‐being issues experienced by the community due to ECQ (Poudel & Subedi, 2020).

In the real‐world scenarios, decisionmakers need to deal with COVID‐19 threats and consequences altogether. To do this complex task, AHP is utilized in order to consider preventive and mitigative controls altogether. In utilizing AHP, each of the BT threats and consequences are translated into their respective AHP variable. An AHP variable becomes the positive and desired objective that is generated from its counterpart negative threat or consequence to be avoided. For example, in order to manage an infection, spread from person to person, effective control of the infection spread is the desired objective. As shown in Fig. 7, all seven identified objectives aim to achieve the overall AHP's goal of “a controlled contagion,” which is in parallel with the BT's unwanted event of “uncontrolled contagion.” AHP quantifies how to achieve the goal of controlling the contagion by generating the weights for the preventive and mitigative controls based on the BT threat line or consequence line they belong to as shown in Table III.

Fig 7.

AHP diagram of Bow‐Tie Analysis for COVID‐19 Contagion.

Table III.

AHP‐Generated Priorities for Bow‐tie Analysis for COVID‐19 Contagion

AHP Variables (or Scenarios a )	Local Weight a	Alternatives (or Interventions)	Local Weight c	Global Weight	Priority
1 Control infection spread from unreported/ asymptomatic infectious person	0.1383	1.1 Barricade city borders	0.4169	0.0577	2
		1.2 Mass testing in high density areas	0.4169	0.0577	2
		1.3 14‐day quarantine for incoming people	0.1216	0.0168	8
		1.4 Self‐isolation and use of PPEs	0.0447	0.0062	14
2 Decrease confirmed positive	0.1308	2.1 Implement ECQ	0.2515	0.0329	5
		2.2 Strictly enforced isolation of PUIs and PUM	0.3916	0.0512	3
		2.3 Trace patients' mobility for the last 3 weeks and identify PUIs	0.2736	0.0358	4
		2.4 Vaccination	0.0833	0.0109	10
3 Reduce risks of contact with airborne viable disease	0.0301	3.1 Social distancing for prolonged occupation	0.4874	0.0147	9
		3.2 Physical distancing for temporal exposures	0.1182	0.0036	16
		3.3 Usage of barriers/PPEs for close proximity interactions like shops	0.1182	0.0036	16
		3.4 Mandatory wearing of face masks	0.2762	0.0083	12
4 Reduce risks of contact with virus contaminated surfaces	0.0357	4.1 Disinfect high density areas	0.4831	0.0173	7
		4.2 Clean household and commercial shops surfaces before and after use	0.1393	0.0050	15
		4.3 Disinfect hands before touching face	0.0569	0.0020	16
		4.4 Use disposable gloves and do not touch face when contacting surfaces	0.0891	0.0032	17
		4.5 Shut down nonessential shops	0.2316	0.0083	13
5 Reduce number of fatalities	0.5709	5.1 Ensure adequate number of COVID‐ready ICU facilities	0.3333	0.1903	1
		5.2 Follow medical and science‐based advice	0.3333	0.1903	1
		5.3 Patients should avoid contact with others unless cleared by medical professionals	0.3333	0.1903	1
6 Maintain good mental health amidst ECQ	0.0293	6.1 Encourage quality time with family	0.3333	0.0098	11
		6.2 Maintain good wellness practices	0.3333	0.0098	11
		6.3 Protect frontliners from social discrimination	0.3333	0.0098	11
7 Consider food security of low‐income households	0.0648	7.1 Employers should provide alternative work options to contractual workers	0.3333	0.0216	6
		7.2 Government should provide financial assistance and feeding program	0.3333	0.0216	6
		7.3 Encourage private sectors to consider food distribution	0.3333	0.0216	6

^a The risk factors in Fig. 7 were interpreted as the scenarios which the decisionmaker has to prioritize.

^b CR for the AHP categories: 0.0945.

^c CR for the AHP variables: 1.1–1.4: 0.0783; 2.1–2.4: 0.0989; 3.1–3.4: 0.0579; 4.1–4.5: 0.0873; 6.1–6.3 and 7.1–7.3: 0.0000

The AHP results show that the highest local weight is assigned to reducing the number of COVID‐19 fatalities. A weight of 0.5709 implies that 57% of the city's overall manpower, funds and resources must be allocated in reducing the number of COVID‐19 fatalities. Meanwhile, the remaining half of the overall resources should mostly be allocated in controlling the ongoing threat of infection spread from unreported/asymptomatic infectious persons and decreasing the number of confirmed positive COVID‐19 patients in the city population. On the other hand, the 2.9% allocation of resources for maintaining good mental health amidst ECQ, although relatively least among the variables, implies that this consequence is recognized as important and needs to be addressed through appropriate interventions. In fact, mental health interventions as reflected in the AHP alternatives still rank 11 out of the 17 prescribed interventions.

Based on the results, the top priority interventions in the context of Davao City COVID‐19 crisis are to (1) ensuring an adequate number of COVID‐19‐ready ICU facilities and ventilator units in hospitals, (2) following medical health and science‐based advice, and (3) COVID‐19 patients should avoid contact with others unless cleared by medical professionals. All the aforementioned priorities alongside maintaining to barricade city borders, suspending all incoming flights to all but essential personnel, and mass targeted testing in high‐density population areas, as preventive actions, will result in a controlled COVID‐19 contagion.

3.4. COVID‐19 Dynamics according to Bow‐tie and Accimap‐based AHP Results

From the preceding discussion, we explore possible COVID‐19 dynamics if the decisionmaker chooses to implement the interventions to reduce the number of fatalities. We also explored other potential COVID‐19 dynamics when other risks are considered as a top priority. Table IV summarizes the interventions to be prioritized according to the AHP result and its implications to the parameters of the COVID‐19 model.

Table IV.

The Considered Risk Scenarios (i.e., AHP Variable and the Associated COVID‐19 Model Parameter and Parameterization Direction

AHP Variable (or Scenarios)	Associated COVID‐19 model Parameter	Parameterization Direction
Reduce number of fatalities	1.1. Disease‐induced mortality rate, $\mu$	$\downarrow$
	1.2. Transition rate a from being exposed to becoming infectious, $\alpha$	$\uparrow$
Control infection spread from unreported/asymptomatic infectious person	2.1. Transmission rate, $\beta$	$\downarrow$
	2.2. Proportion of exposed individuals being reported, $\rho$	$\uparrow$
Decrease confirmed positive	3.1. Multiplicative factor associated to the COVID‐19 confirmed or reported cases, ${\sigma }_1$	$\downarrow$
	3.2. Initial susceptible population, $S_0$	$\downarrow$
	3.3. Vaccination rate, v	$\uparrow$
Reduce risks of contact with virus contaminated surfaces	4.1. External viral source, $\epsilon$	$\epsilon =0$
Reduce risks of contact with airborne viable disease	5.1. Transmission rate, $\beta$	$\downarrow$

^a Transition rate was included in the associated COVID‐19 model parameter in reducing the number of fatalities to mathematically illustrate that the infectious compartments indeed are nonzero.

In terms of the COVID‐19 model, the reduction of the number of fatalities happens when the disease‐induced mortality rate $\mu$ is low (Lahrouz, El Mahjour, Settati, & Bernoussi, 2018). With low $\mu$, COVID‐19 infected individuals have high chances to recover from the disease or gain immunity through vaccination. Next, controlling the infection spread from unreported/asymptomatic infectious individuals is associated with low transmission $\beta$ and high reporting proportion $\rho$. With low $\beta$, disease spread is also slowed down. Meanwhile, even if the disease spread out, high $\rho$can help in controlling the spread of the disease (Do Do Prado et al., 2020) since reported individuals have laboratory‐confirmed results and appropriate medications/actions are thereby provided.

On the other hand, it should be emphasized that to essentially decrease the number of COVID‐19 positive patients, vaccination regimens should be made available so people will have immunity against COVID‐19. However, this scenario may not be practical and readily available as vaccine development can be time‐consuming (e.g. first case of Polio was in 1894 while Sabin's polio vaccine was licensed in 1960 (The College of Physicians of Philadelphia, 2020). Furthermore, it is imperative to schedule regular disinfection to reduce the risks of contact with virus‐contaminated surfaces (Shen et al., 2020) to eliminate COVID‐19 viruses on surfaces. This translates to making the model parameter$\epsilon =0$. Lastly, reducing the risks of contact with the airborne viable disease is associated with the transmission rate, that is, low transmission rate implies a low risk of it. From Table IV, we now investigate through our model simulations the relative comparison on how these priorities affect the projected COVID‐19 dynamics as shown in Fig. 8.

Fig 8.

Projected cumulative number of confirmed cases without vaccination (upper left) and with vaccination (upper right) and cumulative number of deaths without vaccination (lower left) and with vaccination (lower right). Initialization for this simulation was based on Section 3.1. The status quo parameters are displayed in Table II. Default parameters for the scenario analysis are the status quo parameters. Scenario 1: $\beta$is reduced by 20%, $\mu$is reduced by 50%, and $\alpha$is increased by 50%. Scenario 2: $\beta$is reduced by 7% and $\rho$is increased by 10%. Scenario 3: ${\sigma }_1$is reduced by 5%, $S_0$is reduced by 30%, and $\nu =0.05.$ Scenario 4: $\epsilon =0$. Scenario 5: $\beta$is reduced by 2%.

As observed in the upper and lower left simulations (in the absence of COVID‐19 vaccines), scenario 1 or the reduction of the number of fatalities (e.g. ensuring an adequate number of COVID‐19‐ready ICU facilities and ventilator units in hospitals) apparently supressed the potential rise in the new COVID‐19 positive cases. Consequently, scenario 1 positively impacted the number of new deaths as reflected blue plateauing curve, that is, few new deaths. Scenarios 2 and 3 share similar dynamics in terms of the cumulative cases and deaths, as well as scenarios 4 and 5. Furthermore, observe that in all of simulations, the status quo scenario (i.e., the current efforts of the city government) yielded the highest number of confirmed cases and deaths relative to all the scenarios. The status quo projection is based on the existing protocols in the context of COVID‐19 in Davao City, Philippines. It is then apparent that prioritization of the alternatives to be implemented can improve the COVID‐19 dynamics in the city.

On the other hands, the simulations on the right also share similar COVID‐19 dynamics with the simulations on the left. However it is notable that scenario 3 (decreasing the number confirmed COVID‐19 cases), which was modelled mainly using the vaccination rate v, had the lowest number of cumulative COVID‐19 cases. In this simulation, vaccination per capita was set to 5%, that is, 1 in 20 people is vaccinated per day. Although scenario 1 and 3 are relatively comparable to each other. Such observations were noticed also in terms of the cumulative number of deaths. Nevertheless, scenario 1 had the lowest number of cumulative deaths but with a slight difference from scenario 3. Furthermore, regardless if the COVID‐19 vaccine is available or not, we have shown that COVID‐19 can be eliminated in three‐month time after the decisionmaker implements interventions that reduces the number of fatalities.

3.5. Insights on the Integrated Risk Assessment and Decision‐Making Methods in Analyzing COVID‐19 Dynamics

The integrated frameworks of risk assessment and decision making methods in analyzing COVID‐19 dynamics shows that reducing the number of COVID‐19 fatalities should be the top‐most priority (e.g. ensuring adequate number of COVID‐ready ICU facilities). For instance, the case‐fatality rate of Germany (0.6%) is lower compared to Italy (10.1%). According to Lee et al. (2020) such difference can be attributed to their health care resource availability. Germany had 23,890 critical care unit beds while Italy only had 7,550. Reducing the number of COVID‐19 fatalities, in turn, can suppress the emergence of new COVID‐19 infections. However, decreasing the number of confirmed COVID‐19 cases apparently receives the highest priority in the context of COVID‐19 in Davao City, Philippines. Our results are parallel with the health‐care crises management of Germany and even Singapore with a 0.3% case‐fatality rate, which had a successful management of the contagion. Prioritization of risks to be managed and interventions to be applied are deemed necessary to manage the contagion.

This article also highlights the direct linkage of the implementation of control interventions, according to the integrated frameworks, to the potential disease dynamics of COVID‐19. To evaluate the effect of the government interventions (e.g., mandatory self‐isolation) through the expected number of new COVID‐19 cases and deaths can be used as a better way to communicate the government's executive orders on public health protocols visually. Communication of technical results from scientific information plays an increasingly important role for scientists and scientific institutions to the general public and policymakers. Flemming, Cress, Kimmig, Brandt, and Kimmerle (2018) found that visual emotionalization affects people's perception of risk: positive visuals tend to decrease the risk perception. The linking of the government intervention to COVID‐19 dynamics can potentially make people compliant to health protocols to avoid the effects of an uncontrolled contagion.

This pandemic has posed an enormous challenge not only to clinicians, health‐care workers, and epidemiologists but also to decision‐makers (Wolkewitz & Puljak 2020). Months into the outbreak, the demand of frameworks for a rapid assessment of the outbreak using the available data has escalated. Such assessments can be used to craft the most effective approaches in the standard of care, which is imperative and remains to be at present (WHO, 2018). The implementation of these health protocols has been faced with various challenges such as timeliness of data, lack of multidisciplinarity in the decision‐making bodies, to name a few. All of which are required to effectively implement evidence‐based public health and care in a less complicated but evidence‐based manner.

3.5.1. Quickened Effective Decisions

Decisionmakers including the Philippine local government units need a quickened understanding of complex information of the disease as a whole for immediate actions. When the actual and projected disease information (e.g., cases, fatalities) can be presented as a result of the implementation of an intervention, the more likely that scientific and risk‐based recommendations be used in decision making. Dynamic and up‐to‐date visualization platforms can accelerate comprehension of decisionmakers on complex mathematical modeling data and various quantitative results since the pattern recognition of the platform users is enhanced (Folorunso & Ogunseye, 2008).

Quantitative results by themselves may not directly increase the chance of successful implementation of the decisions, hence its dynamic relevance must be included. Khakzad et al. (2012) added that the static structure of some quantitative methods often fails to catch up with variations and they often use generic data rather than being case‐specific. Consequently, it does not help in producing the most effective approaches in the standard of care in a timely manner.

3.5.2. Interdisciplinarity as a Collaborative Environment

A number of methods is needed to handle these public health problems because of the complex social, economic, political, biological, hereditary, and environmental causes. Baum (1995) argues that there are underlying issues that are crucial to contemporary public health debates. It is further argued that “public health researchers are most effective when they are eclectic in their choice of methods” (Baum, 1995, p.1). Although the risk assessment framework is more commonly used in complex sociotechnical systems in the industrial workplace, a similar methodology approach can be applied in a public health crisis. The risks that are considered in the lenses of technical and organizational viewpoints are also vital in managing pandemic crises, emergency preparedness, action response, human resilience, health systems, to name a few. Traditional discipline‐specific methods may fail to capture unexpected factors and variations which sociotechnical systems treat as a usual uncertainty.

A gap has been recognized between the clinical level changes (i.e., spikes in COVID‐19 cases) and the corresponding management implications. This study has demonstrated the integration of risk‐based methodology into health care decision making and potentially enhance the understanding and utilization of risk management tools in public health. The insights produced from the integrated risk assessment support the practical collaboration between the academia, government, and health care sector to pursue effective and proactive risk management strategies.

The integrated approach is beneficial in many ways such as gaining the advantage of multiple perspectives to a common problem. Another benefit is the use of more robust tools in health care management which have already been widely accepted in other disciplines. Such benefits are supported and validated in the growing discipline of resilient health care (RHC) (Hollnagel & Braithwaite, 2019). Resilience, according to Fairbanks et al. (2014), is the ability to adjust before, during, or following events (changes, disturbances, or opportunities). Even though that this concept of resilience is industrial in nature, such a concept can also be seen in the operating rooms (ORs), ICUs, clinics, and home care settings, to name a few. It was further argued that although different in many aspects, the industrial workplace and public health management both involve substantial risks in the use of facilities and equipment done by humans for direction and control. With the aforementioned discussion, a multidimensional approach in the aspect of contagion management that minimizes the fatalities is necessary and, thus, continues to evolve.

4. CONCLUSION AND RECOMMENDATIONS

This article has demonstrated the importance of integrating risk assessment and decision‐making methods to give a clear overview of the risk factors that lead to the uncontrolled COVID‐19 contagion. The risk factors have been identified and visualized using the BT to show precisely the respective controls and how they lead to decrease the probability of the uncontrolled contagion from occurring. If the unwanted event of the contagion outbreak does occur, mitigative strategies further reduces worsening the scenarios. The article has provided an explicit illustration of using BT and AHP to incorporate information from a set of judgments to prioritize identified controls. A mathematical model that describes the dynamical system of COVID‐19 was then used to project COVID‐19 dynamics upon prioritizing the risks to be dealt with. To our knowledge, this is the first kind of such approach in integrating risk management tools, decision making tools, and epidemiological modeling in understanding COVID‐19.

Based on the integrated BT and AHP analysis, reducing the number of COVID‐19 fatalities should be the number one priority of the local government unit. From the local government's end, this can be done by ensuring adequate number of COVID‐ready ICU facilities. By doing so, we conclude that, even in the absence of a vaccine, COVID‐19 can be controlled and eliminated in the city within three‐month time after prioritizing the said risk.

However, one potential limitation of this analysis is that generalization of control interventions and risks to manage across the epidemic timeline. We recommend exploring a time‐specific prioritization of control interventions and explore the potential changes in the dynamics of COVID‐19. Key epidemiological measures such as the basic reproduction number can also be used to evaluate the impact of the aforementioned prioritization in terms of COVID‐19 epidemicity. Furthermore, potential COVID‐19 dynamics based on an uninformed decision‐making process can be explored and compared to the COVID‐19 dynamics based on informed decision making.

APPENDIX 1.

The SEIR Model

The model, like many COVID‐19 models, consider four main compartments: susceptible (S), exposed (E), infectious (I), and recovered (R) individuals. Exposed individuals are those individuals that resulted from a contact between a susceptible and infectious individual. These individuals are considered infected but not yet infectious (i.e., latent phase). The infectious population is split into two: confirmed or reported (I_r ) and unconfirmed or unreported (I_u ). The model parameters are the transmission rate $\beta$, the multiplicative factors ${\sigma }_0$ and ${\sigma }_1$, the transition rate, $\alpha$, from being exposed to becoming infectious, the proportion of exposed individuals being reported $\rho$, the reporting rate $\gamma$, and the disease‐induced mortality rate $\mu$. We denote the initial population sizes as S ₀, E ₀, I_{r 0}, I_{u 0}, and R ₀, which are also considered as model parameters. The total population size N = S + E + I_r + I_u + R is assumed to be constant to simulate the spread of the disease in Davao City in a closed population. In this study, the parameters $\beta$, ${\sigma }_0$, ${\sigma }_1$, $\rho$, $\gamma$, $E_0$, and $I_{u0}$ were estimated using three data sets, namely daily cases, deaths, and recoveries. The rest of the parameters were held fixed to be estimated based on rough estimates and benchmarked from existing literature.

Fig A1.

The plots of the daily active COVID‐19 cases (left), deaths (right‐top), and recoveries (right‐bottom) in Davao City and the fitted model (blue curves).

Further assumptions have been set for the population compartments as follows:

1. The populations are well‐mixed. All the members of the human population interact with each other.

2. Susceptible individuals become exposed to the virus when they interact with infected individuals. The rate of direct transmission is expressed as $\beta$. Furthermore, Susceptible individuals also become indirectly exposed to the virus when contact on contaminated surfaces happen. This contact rate is represented as $\epsilon$.

3. Exposed individuals become infectious with a rate $\alpha$. A proportion $\rho$ of the exposed population is reported and becomes confirmed infectious individuals while the rest ($1-\rho$) becomes unconfirmed infectious.

4. Infectious individuals become recovered sometime after they were tested positive for the virus. Furthermore, these recovered individuals become susceptible to the disease again.

5. Infectious individuals die via disease‐induced mortality rate $\mu$.

6. Susceptible, exposed, and infected individuals gain immunity against the disease when vaccination regimen is available at rate v.

7. The rate of change of each compartment is obtained by getting the difference of the inflow and outflow rates.

APPENDIX 2.

Reproduction Number

The time‐varying daily reproduction number in this article was computed following the methods of Cori, Ferguson, Fraser, and Cauchemez (2013), with prior mean ${\mu }_{SI}=2.6$ and standard deviation ${\sigma }_{SI}=2$ (Abbott et al., 2020; Imai et al., 2020) and mean ${\mu }_{SI}=4.8$ and standard deviation ${\sigma }_{SI}=2.3$ (Nishiura, Linton, & Akhmetzhanov, 2020). Furthermore, a window of 7 was used in estimating the time‐varying daily reproduction number.

Fig A2.

The plot of the statistical basic reproductive number (R_t ). The statistical basic reproduction number varies from 0.3536 to 3.6866 from March 15, 2020 to September 30, 2020. The following are the key statistics of the statistical basic reproductive number: R_t (Mean) = 1.1514 and 95% CI [1.0923, 1.2104], R_t lower bound = 0.8875 and 95% CI [0.8410, 0.9347], and R_t upper bound = 1.4488 and 95% CI [1.3715, 1.5206].