Maximally selective single cell target for circuit control in epilepsy models

Darian Hadjiabadi; Matthew Lovett-Barron; Ivan Georgiev Raikov; Fraser T Sparks; Zhenrui Liao; Scott C Baraban; Jure Leskovec; Attila Losonczy; Karl Deisseroth; Ivan Soltesz

doi:10.1016/j.neuron.2021.06.007

. Author manuscript; available in PMC: 2022 Aug 18.

Published in final edited form as: Neuron. 2021 Jun 30;109(16):2556–2572.e6. doi: 10.1016/j.neuron.2021.06.007

Maximally selective single cell target for circuit control in epilepsy models

Darian Hadjiabadi ^1,^2,^11,^*, Matthew Lovett-Barron ^1,³, Ivan Georgiev Raikov ², Fraser T Sparks ^4,^5,⁶, Zhenrui Liao ^4,^5,⁶, Scott C Baraban ⁷, Jure Leskovec ^8,⁹, Attila Losonczy ^4,^5,⁶, Karl Deisseroth ^1,¹⁰, Ivan Soltesz ²

PMCID: PMC8448204 NIHMSID: NIHMS1714843 PMID: 34197732

Summary

Neurological and psychiatric disorders are associated with pathological neural dynamics. The fundamental connectivity patterns of cell-cell communication networks that enable pathological dynamics to emerge remain unknown. Here, we studied epileptic circuits using a newly developed computational pipeline that leveraged single-cell calcium imaging of larval zebrafish and chronically epileptic mice, biologically constrained effective connectivity modeling, and higher-order motif-focused network analysis. We uncovered a novel functional cell type that preferentially emerged in the preseizure state – the superhub – that was unusually richly connected to the rest of the network through feedforward motifs, critically enhancing downstream excitation. Perturbation simulations indicated that disconnecting superhubs was significantly more effective in stabilizing epileptic circuits than disconnecting hub cells that were defined traditionally by connection count. In the dentate gyrus of chronically epileptic mice, superhubs were predominately modeled adult-born granule cells. Collectively, these results predict a new, maximally selective and minimally invasive cellular target for seizure control.

eTOC blurb

Hadjiabadi et al reveal a novel functional cell type – the superhub – that preferentially emerges in the preseizure brain to powerfully propagate excitation. Disconnecting superhubs in simulations stabilizes epileptic circuits more effectively than disconnecting traditional hubs, predicting a new single-cell target for seizure control.

Introduction

Methods in network science have been instrumental in deciphering neural communication associated with neurological disorders (Bullmore and Sporns, 2009; Fornito et al., 2015). One such disorder, epilepsy, is characterized by spontaneous and recurrent seizures that arise from abnormal neural activity and synchronization across brain regions (Jiruska et al., 2013; Kramer and Cash, 2012). Epilepsy impacts over 60 million individuals worldwide and many of these children and adults have medically uncontrolled seizures and suffer from debilitating cognitive and emotional comorbidities. One primary reason for this is that current anti-epileptic treatments lack spatial, temporal and cell type-specificity and instead attempt to broadly restrict excitability that can at best mask symptoms while resulting in various side-effects (Löscher and Schmidt, 2011). Recently, a number of experimental studies demonstrated that it is possible to control spontaneous chronic seizures and comorbidities through closed-loop interventions. Importantly, these studies targeted specific cell ensembles in given brain regions and delivered intervention stimuli selectively only at particular times, all with minimal side-effects (Bui et al., 2018; Krook-Magnuson and Soltesz, 2015; Krook-Magnuson et al., 2013, 2015). Although these experiments targeted groups of cells, the most desirable target for intervention would be single cells that exert maximal control over epileptic networks. In this study, we searched for a novel class of potential neuronal targets that could serve as maximally selective controllers for interventions to stabilize epileptic dynamics. To achieve this ambitious goal, we sought to uncover new features of cell-cell communication networks extracted from experimental data that are essential for pathological seizure dynamics to emerge.

One common feature of complex networks is the presence of richly connected yet sparse hub neurons (Barabási and Albert, 1999). It has been shown that these neurons are critical for influencing network dynamics in biological neural circuits (Bocchio et al., 2020; Bonifazi et al., 2009; Morgan and Soltesz, 2008). Specifically, experimental studies have shown that hub neurons orchestrate network synchrony in the developing brain (Bonifazi et al., 2009) and maintain their effectiveness in adulthood (Bocchio et al., 2020). Simulations in a large-scale data-driven hippocampal dentate gyrus computational model of temporal lobe epilepsy (TLE) predicted that perturbation of a population of neurons that included hubs was sufficient to initiate a seizure (Morgan and Soltesz, 2008). These efforts have sparked significant interest in targeting hub neurons for effective seizure control (Bui et al., 2018; Krook-Magnuson et al., 2015). While hub neurons are traditionally identified by considering lower-order connectivity patterns at the level of nodes and edges, there is current interest in elucidating the higher-order organization of complex networks. Specifically, the higher-order organization of a complex network can be understood by identifying how small patterns of interconnections called motifs, which are widely believed to inform network function (Benson et al., 2016; Sporns and Kötter, 2004), are distributed throughout the network and causally drive functional dynamics. Therefore, it remains an open question whether a specialized subset of hub neurons can be leveraged for improved selective seizure control based on their surrounding higher-order network structure.

To address the latter question, we deployed whole-brain cellular resolution calcium imaging to capture neural dynamics in larval zebrafish, whose neuronal circuitry shares many conserved features with mammals (Lovett-Barron et al., 2017) and thus have been instrumental in basic (Burrows et al., 2020; Liu and Baraban, 2019) and translational (Baraban et al., 2013; Burrows et al., 2020) epilepsy research. Imaging was performed in a well-characterized zebrafish model of acute seizures (Baraban et al., 2005). The underlying cell-cell effective connectivity (i.e. communication) networks for baseline and preseizure neural dynamics were extracted (Sompolinsky et al., 1988; Sussillo and Abbott, 2009) and biologically constrained to the zebrafish neuroanatomical connectome for the first time (Kunst et al., 2019). Simulated perturbation of a single traditional hub neuron significantly destabilized preseizure networks compared to baseline networks. Higher-order motif-focused analysis (Yin et al., 2017) on traditional hubs revealed that network instability in epileptic circuits is causally linked to a specific subset of hubs – which we call superhubs - whose surrounding neighborhood is rich in feedforward motifs, enhancing downstream excitation. Disconnecting these specialized superhub neurons robustly stabilized networks to perturbation, even though superhubs did not have the highest connection count among the broader hub cell class.

Importantly, similar results were also found in the hippocampal dentate gyrus of chronically epileptic mice compared to control, indicating that our key findings hold in the mammalian brain and in a model of chronic temporal lobe epilepsy (TLE). Furthermore, superhubs in mice with chronic TLE were identified as being predominantly adult born granule cells (abGCs), which are thought to play key roles in driving epileptiform activity in the DG network (Sparks et al., 2020) following seizure-induced reorganization (Danzer, 2018, 2019) and integration into the circuit (Toni et al., 2007, 2008). Collectively, these results identify superhubs as representing a new class of maximally selective potential targets for the control of epileptic networks.

Results

Whole brain calcium imaging of larval zebrafish acute seizure model at single cell resolution

Whole brain larval zebrafish (Tg[elavl3:H2B-GCaMP6s; N = 3) imaging was performed with volumetric two-photon microscopy for 25 minutes at 2Hz capture rate (Figure 1A, see Methods). This imaging approach enabled us to study intracellular calcium activity, where increases in the measured calcium signal correspond to an increase in neuronal firing rate. Five minutes of baseline calcium data were recorded for each fish followed by 15 mM pentylenetetrazole (PTZ) (Baraban et al., 2005; Liu and Baraban, 2019) bath application, which blocks inhibitory GABA_A conductance (Huang et al., 2001). Each fish exhibited at least one seizure prior to cessation of imaging. LFP recording was not included as previous studies have shown robust correlation between calcium signal and field potentials in PTZ model (Liu and Baraban, 2019). Anatomical volume stacks were registered and neural somata (Figure 1B) were extracted with methods used by Lovett-Barron et al. (2017). We extracted fluorescence time series from 5000–7000 active neurons per fish across all major brain regions (Figure 1C).

Figure 1: — A: Representative z-plane images acquired from whole-brain cellular resolution two-photon microscopy of larval zebrafish before PTZ application (Baseline; top) and during PTZ-induced seizure (Seizure; bottom).

B: Extracted neural somata point cloud. Colors indicate major brain regions. Orange: telencephalon; Green: diencephalon; Blue: mesencephalon; purple: rhombencephalon

C: (Top) Population mean calcium signal and (bottom) heatmap of single-cell functional calcium dynamics from neurons extracted in B. PTZ application, seizure initiation, and seizure termination are demarcated by black arrows at bottom. Imaging was performed for 25 min and PTZ was added 5 min into the imaging session.

D: Correlation coefficient matrices of single-cell calcium dynamics during baseline, preseizure, and seizure epochs.

E: Quantification of network synchrony from correlation coefficient matrices in (D) show that single-cell calcium dynamics during seizure epoch are significantly more synchronized compared with single-cell calcium dynamics in baseline (one-sided paired t test, adjusted p = 0.034) and in preseizure (one-sided paired t test, adjusted p = 0.006) epochs. Bar graphs represent the mean of the population (N = 3 zebrafish).

F: Single-cell calcium traces over major anatomical regions plotted during baseline and preseizure epochs. Note the differences in vertical scale bars.

The start of the preseizure state was defined as 1 minute after PTZ was introduced to account for transient activity. Seizure initiation was defined as three standard deviations above the population mean calcium signal during baseline (pre-PTZ) and termination was defined as when the population mean signal dropped below this threshold. In agreement with prior literature (Liu and Baraban, 2019), calcium dynamics within the detected seizure periods lasted 35–40 seconds and displayed significantly higher synchronicity (i.e. hypersynchronous state) compared to baseline (one-sided paired t test, adjusted p = 0.034) and preseizure (one-sided paired t test, adjusted p = 0.006) epochs (Figures 1D,E; synchronization, in baseline network: 0.28 ± 0.024; preseizure network: 0.375 ± 0.04; seizure network: 0.55 ± 0.038). For this work, we will be modeling baseline and preseizure calcium dynamics (Figure 1F), and we will not be focusing on seizure or post-seizure periods.

Cellular resolution effective connectivity modeling to extract cell-cell communication networks

Effective connectivity modeling was performed with chaotic recurrent neural networks (RNN) (Sompolinsky et al., 1988) (Figure 2A, see Methods) to extract cell-cell communication networks. These methods have been previously successful in fitting cellular-resolution calcium dynamics in the zebrafish (Andalman et al., 2019). Each neuron imaged experimentally is represented by a node in the model. The parameters of the model are the effective connections between nodes, interpreted as how much causal influence a source has on its target over a sub-second temporal window and can vary in sign and magnitude. The self-perpetuating chaotic dynamics were controlled through FORCE learning (Sussillo and Abbott, 2009; Methods), which uses a recursive least square optimization on the connectivity parameters to reproduce a specified target output.

Target outputs were the experimentally acquired calcium dynamics. We furthermore employed a 10% sparsity constraint ( $\frac{N * (N - 1)}{10}$ total parameters) to match reported connectivity patterns (Song et al., 2005) and to prevent overfitting. One major issue is whether local minima visited during optimization lead to parameter sets that are realistic given the underlying neuroanatomy. To mitigate this, we constrained the optimization procedure using the known zebrafish structural connectome (Kunst et al., 2019) (Figure 2B, Methods). Specifically, weights are adjusted proportional to how strongly connected the regions in which the source soma and target soma inhabit (Figure 2C, “Learning rule”). Preseizure networks were optimized from best-fit baseline networks in order to untangle cell-cell effective rewiring caused by PTZ (Figure 2C, “Training pipeline”). For consistency, this was repeated three times with different initial conditions for each fish. Models converged for both baseline and preseizure state (Figure 2C, “Training pipeline”) and FORCE learning captured individual and global calcium dynamics (Figure 2D, note scale bars).

Community detection using the Leiden algorithm (Traag et al., 2019) on the constrained optimized parameter matrix identified relevant macroscale anatomical structures which were not observed in the unconstrained models (Figure S1; see Methods). Furthermore, model dynamics were primarily driven by synaptic transmission and not noise (Figures S2A,B). For each modeled zebrafish, the outgoing inhibition per neuron, calculated as the absolute value of the sum of outgoing negative effective weights, decreased on average across the population after PTZ application (Figure S2C). This suggests that the modeled communication networks capture the primary effect of PTZ, which is known to be a reduction of inhibitory conductances (Huang et al., 2001).

Identification of outgoing and incoming traditional hubs

Traditional hub neurons were segregated into two classes based on connection count: incoming and outgoing (Figure 3A). Outgoing hubs project while incoming hubs receive numerous strong connections. The optimized parameter matrix was binarized by keeping only the strongest excitatory connections (top 10%; Figure 3B). The outgoing and incoming degree distributions across brain states were quantified and displayed heavy-tailed properties as reported experimentally (Bonifazi et al., 2009) (Figure 3C). Outgoing hubs were defined as the top 10% (i.e., 90^th percentile and above) of cells with the most outgoing connections and incoming hubs were defined as the top 10% of cells with the most incoming connections (note that changing the cutoff to a different percentile did not alter the key findings, see below). The cutoff values were independently calculated for incoming and outgoing hubs and between baseline and preseizure distributions (Figure 3C).

Importantly, the normalized outgoing (baseline: 0.0129 ± 0.0006; preseizure: 0.0135 ± 0.0005) and incoming (baseline: 0.0131 ± 0.00022; preseizure: 0.0124 ± 0.0007) hub cutoff thresholds, reported as the outgoing and incoming cutoff threshold divided by the number of possible connections a single node can make in a graph with N nodes (i.e., N-1) was not significant between modeled baseline and modeled preseizure networks (two-sided unpaired t test p > 0.05) (Figure 3D). Additionally, the percent change of the average outgoing (incoming) degree of outgoing (incoming) hubs in modeled preseizure networks relative to modeled baseline networks was not statistically different than 0 (two-sided unpaired t test, p > 0.05; outgoing hubs percent change in outgoing degree: 5.4% ± 6%; incoming hubs percent change in incoming degree: −5.8% ± 7.8%) (Figure 3D). The spatial locations of outgoing and incoming hub neurons were visualized in the zebrafish anatomy for both baseline and preseizure networks (Figure 3E). Outgoing hubs were primarily located in the diencephalon and incoming hubs were primarily located in the mesencephalon and the telencephalon (Figure 3F). PTZ did not cause significant changes in the macroscale anatomical locations of outgoing and incoming hubs (Figure 3F) (two-sided unpaired t test, p > 0.05).

Perturbation of individual outgoing hubs destabilize preseizure networks

Chaotic recurrent neural networks are a generative model and can therefore create synthetic calcium traces for each cell. Single-cell perturbation simulation studies are of growing importance for studying functional properties of large neural populations and have to date elucidated how activity is coordinated in recurrent cortical networks (Sadeh and Clopath, 2020). With this in mind, we tested the hypothesis that the modeled preseizure networks are more sensitive to perturbation of a single hub neuron compared to baseline networks. Simulated perturbations involved 500ms depolarizing current injection into a single hub neuron after 20% of epoch duration had elapsed. We quantified the effect of perturbation on global network dynamics by measuring the ‘trajectory deviation’, which is the time-normalized Euclidean distance between the mean population calcium signal of the unperturbed network and the mean population calcium signal of the perturbed network. Intuitively, the trajectory deviation metric captures how far network dynamics deviate after a user-defined perturbation, relative to the unperturbed network. The larger the trajectory deviation, the more effect a perturbation has on the system. Note that only one neuron was depolarized at a time during a given perturbation simulation.

Depolarizing a single outgoing hub in the preseizure network caused significantly higher deviation (one-sided Mann-Whitney U test. p < 0.001) in global dynamics (Figures 4B,C) compared to equivalent simulations in baseline networks (Figures 4A,C). Depolarizing a single incoming hub and a single non-hub had significantly less influence in both networks compared to depolarizing individual outgoing hubs (Figure 4C, Figures S3A,B). Additionally, the effect of perturbation of single neurons was larger in modeled preseizure networks than in modeled baseline networks. Importantly, perturbation of a single incoming hub affected dynamics to a greater degree (one-sided Mann-Whitney U test, p < 0.001) in preseizure networks compared to baseline networks (Figure 4C). We normalized the trajectory deviation distribution acquired from perturbing individual outgoing hubs by the median trajectory deviation from the incoming hub population. The data show that perturbation of a single outgoing hub in the preseizure state altered global dynamics more significantly compared to baseline networks both within individual fish (one-sided Mann-Whitney U test, p < 0.001) (Figure 4D) and across the population (one-sided paired t-test, p = 0.041) (Figure 4E; % deviation, baseline: 170% ± 24%; preseizure: 327% ± 66%). Taken together, these results suggest that preseizure networks are more sensitive to perturbations and that perturbing even a single outgoing hub neuron can significantly influence global dynamics.

Figure 4: — A: Modeled control network response to perturbation (black arrows) of a single outgoing hub. (Top) Population mean calcium signal of experimental data (cyan), unperturbed model (blue), and perturbed model simulation (red). (Bottom) PCA analysis reveals little change in network dynamics in response to perturbation.

B: Perturbation of a single outgoing hub in modeled preseizure network showing significant changes to network dynamics compared to A.

C: Violin plots show that perturbing individual outgoing hubs (one-sided Mann-Whitney U test, p < 0.001; N = 310 modeled cells) and incoming hubs (one-sided Mann-Whitney U test, p < 0.001; N = 300 modeled cells) in modeled preseizure networks (purple) had significantly higher influence on network dynamics compared to similar simulations in baseline networks (gray). See also Figure S3. Center marker of the violin plot represents the median.

D: Outgoing hub trajectory deviation distributions in modeled baseline (gray) and preseizure networks (purple) normalized by incoming hub median trajectory deviation score for the respective populations. Perturbation of outgoing hubs in preseizure state has significantly more influence over network dynamics (one-sided Mann-Whitney U test, p < 0.001; N = 310 modeled cells). Center marker of the violin plot represents the median.

E: Median values from (D) were extracted for each fish and plotted, revealing that preseizure networks have significantly reduced resiliency to perturbation of a single outgoing hub (one-sided paired t test, p = 0.041). Bar graphs represent the mean of the population (N = 3 zebrafish).

**F,G:** Visual representation of connections between outgoing and incoming hubs for baseline (F) and preseizure (G) network after constrained FORCE learning. Graphs were generated using the Barnes-Hut algorithm (Barnes and Hut, 1986). Gray edges: outgoing hubs (O.H.) to incoming hubs (I.H.); Purple edges: incoming hubs (I.H.) to incoming hubs (I.H.); Golden edges: outgoing hubs (O.H.) to outgoing hubs (O.H.). See also Figure S3.

H: Toy model of connections between outgoing (green) and incoming (blue) hubs for baseline (top) and preseizure (bottom) networks.

Visualizing connections between outgoing and incoming hubs

PTZ application did not significantly change several parameters associated with the outgoing and incoming degree distributions (Figures 3C,D) and did not significantly reorganize which macroscale anatomical regions the hub cells occupied (Figures 3E,F). Therefore, we hypothesized that nuanced rewiring of microcircuit effective connectivity patterns may be critical for understanding the increased sensitivity of the network to perturbation in the preseizure state (Figure 4). We visualized the connectivity patterns between outgoing and incoming hubs for baseline (Figure 4F) and preseizure (Figure 4G) networks using force-directed graphs (Barnes and Hut, 1986) (Methods). Importantly, nodes clustered in the force-directed graphs are highly connected. We observed an increased number of outgoing – outgoing hub connections (Figure 4G, note golden edges forming a ‘core’; see also Figure S3C) in the preseizure networks compared to the baseline networks. We next performed rich-club analysis (Smilkov and Kocarev, 2010; Towlson et al., 2013) to determine if the increase in connections between outgoing hubs in the preseizure networks led to the emergence of a ‘rich-club’ phenomenon. Intuitively, a rich-club describes a highly privileged group of strongly connected nodes that are very tightly connected with one another. This idea is captured by measuring the rich-club coefficient, which varies as a function of degree k and is normalized to random graphs. If the coefficient is greater than 1 as k approaches k-max, the highest observed degree in the graph, then this implies the existence of a rich-club. We observed that both the baseline and preseizure networks exhibited a rich-club phenomenon only when considering the fully directed graph, and that the outgoing rich-club coefficient was higher for the preseizure network (Figure S3D). Therefore, this further validates the observed increase in effective connections between outgoing hubs (Figure S3C) in the preseizure brain and the existence of the golden ‘core’ in Figure 4G.

To better interrogate how effective connections in the preseizure networks are distributed across the outgoing hub population, we turned to understanding the distribution of higher-order motifs, which are, as previously mentioned, small patterns of interconnections that are thought to provide insight on the functional properties of complex systems (Benson et al., 2016; Sporns and Kötter, 2004). In a baseline toy model (Fig 4H, top), there is a single connection between outgoing hubs and two feedforward motifs present. Based on observations in Fig 4G, there are more connections between outgoing hubs. Thus, the preseizure toy model (Fig 4H, bottom) includes an additional connection between outgoing hubs 2 and 3. As a result of adding a single connection, there are now four feedforward motifs present in the network. Therefore, we hypothesized that the multiplicative emergence of feedforward motifs may be a core feature of cell-cell communication networks that destabilize the preseizure brain.

Preferential emergence of superhubs in the preseizure brain

Graph clustering is an intuitive method to isolate groups of nodes in a network that form numerous intra-group connections. Specifically, we predict the emergence of superhubs – hubs surrounded by higher-order motifs - using a higher-order motif-focused local clustering concept. To this effect, we deployed the Motif-based Approximate Personalized PageRank (MAPPR) algorithm (Yin et al., 2017) which finds higher-order motif-focused clusters. The inputs to the algorithm were the directed binarized graph (Figure 3B), a motif M, and an individual outgoing hub identified in Figure 3C (i.e., the seed). The algorithm finds an optimal local cluster surrounding the seed that is rich in M with run-time that is invariant of the graph size (Figure 5A, left). Traditional edge clustering was also performed as a control using the APPR algorithm (Andersen et al., 2006) (Figure 5A, right). Note that the MAPPR algorithm is a more generalized form of the APPR algorithm, as the latter only considers simple edges. To find optimal clusters, both algorithms minimize a conductance metric (edge conductance for APPR; motif conductance for MAPPR; see Methods), The edge (motif) conductance metric was furthermore used to capture how much information or activity propagates from the traditional (motif-focused) cluster to the rest of the network (Figure 5B) and can be thought of as an analog to conductance in an electrical circuit.

Edge conductance and feedforward motif conductance were elevated in the modeled preseizure networks both across individual fish (Figure 5C; edge conductance: one-sided Mann-Whitney U test, p < 0.001; feedforward motif conductance: one-sided Mann-Whitney U test, p < 0.001) and across the population (Figures 5D; edge conductance: baseline, 0.39 ± 0.0068; preseizure, 0.41 ± 0.005; one-sided paired t test, p = 0.011; feedforward conductance: baseline, 0.145 ± 0.01; preseizure, 0.218 ± 0.017; one-sided paired t test, p = 0.033). However, the increase in feedforward motif conductance relative to baseline was significantly higher (one-sided paired t test, p = 0.047) than edge conductance (51.8% ± 22.7% versus 2.4% ± 0.55%; Figure 5E). We also performed local higher order motif-focused clustering on additional motifs, such as cycles, but found no examples of cycle motifs surrounding outgoing hubs. More specifically, motif enumeration using an efficient detection algorithm (Wernicke, 2006) showed that <10 cycles existed in the full zebrafish network for both baseline and preseizure states, whereas feedforward motifs were extremely dominant (>25,000) (Figure S4). Therefore, these data suggest that a subset of outgoing hubs in preseizure networks allows excitation to propagate more readily to the rest of the network via feedforward motifs, predicting the preferential emergence of “superhubs.” Importantly, both individually (baseline Spearman’s rho = −0.005, p > 0.05; preseizure Spearman’s rho = 0.054, p > 0.05) and as a group (unpaired two-sided t test, p > 0.05), feedforward motif conductance was not correlated to outgoing degree of the outgoing hub (Figure 5F). These findings were not dependent on the sparsity constraint used (Figure S5). Additionally, feedforward motif conductance was not correlated to other widely used network measures that leverage traditional edge information, such as local clustering coefficient (Watts and Strogatz, 1998; Figure S6A) and betweenness centrality (Freeman, 1977; Figure S6B).

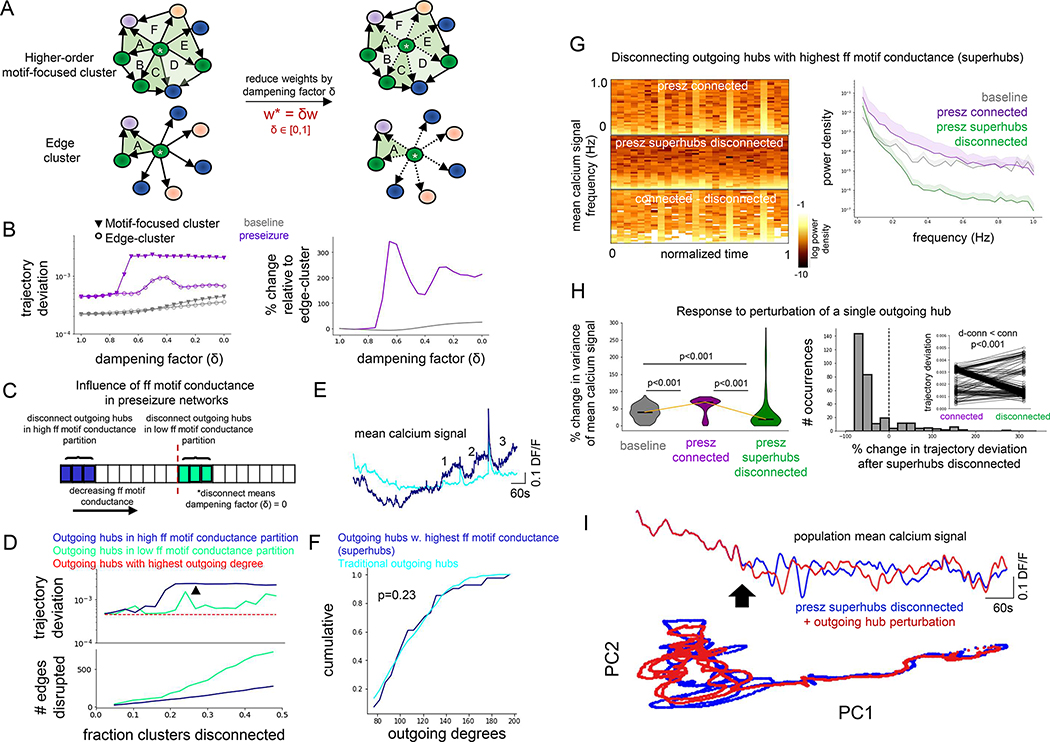
Disconnecting superhubs stabilizes preseizure networks

Our evidence so far suggests a correlation between two findings: 1) Perturbation of a single outgoing hub in preseizure networks has significant influence on global network dynamics; 2) Emergence of superhubs in the preseizure state, defined as outgoing hub neurons with elevated feedforward motif conductance, which may play a critical role in propagating excitatory activity to the rest of the network. To establish a causal link, we performed several computational experiments. These simulations involved targeted attacks on hub neurons. The motivation for this is that complex networks in nature are vulnerable to attacks on hub neurons (Albert et al., 2000), and which has been validated in neural circuits through closed-loop optogenetic studies (Bui et al., 2018; Krook-Magnuson et al., 2013).

We first compared the role of feedforward motifs versus simple edges on network function. Edges that projected from outgoing hubs and targeted neurons in its local motif-focused cluster or its local edge cluster were damped by a factor ranging from 0 (disconnect) to 1 (no change) (Figure 6A). Dampening the outputs of outgoing hubs to their respective motif-focused cluster had greater effect on network activity in both baseline and preseizure networks than dampening the output of outgoing hubs to their respective traditional edge cluster (Figure 6B, left). However, this effect was more pronounced for the preseizure state (Figure 6B, right).

Figure 6: — A: Edge weights of all outgoing hubs targeting its edge cluster constituents and higher-order motif-focused cluster constituents were dampened to explore relative importance of simple edges versus edges belonging to feedforward motifs on network dynamics.

B: (Left) Connections from outgoing hubs projecting to their traditional edge-cluster (open circle) and to their higher-order motif-focused cluster (closed triangle) were progressively dampened for modeled baseline (gray) and preseizure (purple) networks. Dampening higher-order motif-focused clusters had greater effect on network dynamics than dampening traditional edge clusters, as measured by trajectory deviation. (Right) Trajectory deviation from dampening higher-order motif-focused clusters relative to dampening traditional edge clusters shows a greater effect in the preseizure network than the baseline network.

C: Schematic for testing the effect of disconnecting outgoing hubs with the highest feedforward motif-conductance versus lowest feedforward motif-conductance on modeled preseizure network dynamics.

D: (Top) Trajectory deviation versus fraction of higher-order motif-focused clusters disconnected in the high feedforward motif-conductance (blue) and low feedforward motif-conductance (green) partitions show that disconnecting higher conductance clusters has greater effect on network dynamics. The black arrowhead is located at the 27.5% cutoff for superhubs (N = 41 modeled cells), which is where blue trace exhibits a stable plateau in the trajectory deviation. (Bottom) Number of edges disconnected for each group shows that the high conductance partition (blue) contains fewer edges than the low conductance partition (green).

E: Mean calcium signal of outgoing hubs with the highest feedforward motif-conductance values (i.e. superhubs) and the traditional outgoing hub population. Note the numbers identifying an increase in the mean calcium signal of superhubs preceding and between high-calcium events.

F: Outgoing degree cumulative distribution for superhubs (N = 41 modeled cells) versus traditional outgoing hubs (N = 269 modeled cells). Importantly, superhubs are not biased towards the highest outgoing degrees (one-sided KS-test, p = 0.23).

G: (Left) mean population calcium signal spectrograms generated from unchanged/connected preseizure network (top), preseizure network with superhubs disconnected (middle), and difference. Right: power spectral density (PSD) of mean population calcium signal for baseline (gray), connected preseizure (violet), and preseizure network with superhubs disconnected (green). Disconnecting superhubs reduces power over the measured frequency ranges.

H: (Left) The variance (i.e., total power) of the mean population calcium signal is measured before and after perturbation of a single outgoing hub and the percent change is quantified. The percent change in total power is elevated when perturbing individual outgoing hubs in the fully connected preseizure network (purple) compared to baseline network (gray) (one-sided Mann-Whitney U test, adjusted p < 0.001), indicating that the preseizure network is more unstable. The percent change in total power is significantly lower in the preseizure network with superhubs disconnected (green) compared to the fully connected preseizure network (purple) (one-sided Wilcoxon signed-rank test, adjusted p < 0.001). Furthermore, the percent change in total power after perturbing individual hubs is significantly lower between the preseizure network with superhubs disconnected (green) and the baseline network (gray) (one-sided Mann-Whitney U test, adjusted p < 0.001), altogether providing evidence that disconnecting superhubs very robustly stabilizes preseizure networks. N = 310 modeled cells for all groups. Center marker of violin plots represents the median. (Right) Percent change of the network trajectory deviation is significantly reduced after disconnecting superhubs (one-sided Wilcoxon signed-rank test, p < 0.001; N = 310 modeled cells). This was quantified by measuring trajectory deviation before and after perturbation of a single outgoing hub in the fully connected preseizure network and the preseizure network with superhubs disconnected. See also Figure S6.

I: (Top) mean population calcium signal of a disconnected preseizure network before (blue) and after (red) perturbation of a single outgoing hub. (Bottom) principal-component analysis (PCA) before (blue) and after (red) perturbation.

Second, we validated that outgoing hubs with the highest feedforward motif-conductance (i.e., could propagate activity downrange more easily) have greater influence over network dynamics than outgoing hubs with low feedforward motif-conductance. Outgoing hubs in preseizure networks were ranked based on their feedforward motif conductance score and split into either top half or bottom half. Within each half, an equivalent fraction of motif-focused clusters was disconnected from the network (Figure 6C; dampening factor = 0.0) in decreasing order. Simulations confirmed that disconnecting outgoing hubs in the high feedforward motif-conductance partition was more effective in changing global network activity (Figure 6D, top). Interestingly, this effect was observed despite more edges being removed in the bottom half group (Figure 6D, bottom), and in total represented less than 0.1% of all edges in the network. We additionally verified that disconnecting hubs with the highest outgoing degree did not significantly alter network dynamics (Figure 6D, top, red trace), further suggesting that the higher-order organization of preseizure networks gives critical insight into network function. Based on Figure 6D (top, blue trace), the trajectory deviation reached a plateau when approximately a quarter of the outgoing hubs, ordered by decreasing feedforward motif-conductance values, was disconnected from the network. Therefore, we considered the outgoing hubs with the top 27.5% feedforward motif-conductance value (i.e., just after a stable plateau was reached with the trajectory deviation following the progressive disconnection of the outgoing hubs with the highest feedforward conductance values, indicated by the black arrowhead in Fig 6D) as superhubs, and outgoing hubs that scored below this were deemed traditional outgoing hubs (note that increasing this percentile cutoff further to 30% or 35% did not change the key results). Superhubs displayed increased activity preceding and in between high calcium events compared to the traditional outgoing hub population (Figure 6E, note periods indicated by numbers 1–3) and were not biased towards having the highest outgoing degree values (one-sided Kolmogorov-Smirnov [KS] test, p > 0.05) (Figure 6F). Therefore, feedforward motif conductance gives important insight into network function and that this insight could not have been revealed through mining the network for simple edges. As an additional validation, disconnecting individual superhubs had greater effect on network dynamics than disconnecting individual traditional outgoing hubs (Figure S6C).

Third, we tested the hypothesis that disconnecting superhubs rendered the network more stable to perturbation. Disconnecting all superhubs in the preseizure network at the same time dampened oscillatory power over all frequency bands for most measured time periods (Figure 6G). Next, we perturbed a single outgoing hub and recorded the percent change in signal variance (i.e., total power) of the mean population calcium signal before and after perturbation. This perturbation experiment was repeated for all outgoing hubs. As expected, the percent change in signal variance in response to single outgoing hub perturbation in the fully connected preseizure network was significantly higher than in the baseline network (39.8% to 69.1%; one-sided Mann-Whitney U test, adjusted p < 0.001) (Figure 6H, left, baseline vs presz connected), indicating that the preseizure network is more unstable. Importantly, disconnecting all superhubs from the preseizure network simultaneously significantly reduced the percent change in signal variance in response to single outgoing hub perturbation from 69.1% to 19.2% (one-sided Wilcoxon signed-rank test, adjusted p < 0.001) (Figure 6H, left, presz connected vs presz superhubs disconnected) and this percent change was furthermore lower than baseline networks (one-sided Mann-Whitney U test, adjusted p < 0.001). Collectively, these data provide evidence that disconnecting superhubs robustly stabilized preseizure networks. Disconnecting superhubs significantly decreased the trajectory deviation of global network activity in response to single outgoing hub perturbation compared to the fully connected preseizure network (one-sided Wilcoxon signed-rank test, p < 0.001) (Figures 6H,I). In addition, control simulations showed that disconnecting superhubs resulted in a significantly lower percent change in signal variance (i.e., more effectively stabilized the network) in response to perturbation than either disconnecting the same number of traditional outgoing hubs randomly (19.2% versus 57.1%, one-sided Wilcoxon signed-rank test, p < 0.001) or the same number of traditional outgoing hubs with the lowest feedforward motif-conductance values (19.2% versus 77.4%; one-sided Wilcoxon signed-rank test, p < 0.001) (Figures S6D,E).

Therefore, the network is more resilient to perturbation when superhubs are disconnected. Taken together, these three computational experiments reveal that the higher-order microcircuit connectivity architecture surrounding hub neurons is a critical novel feature of stability in epileptic networks.

Superhubs in a mouse model of chronic temporal lobe epilepsy

Next, we tested the hypothesis that superhubs may also play a role in the pathological activity dynamics of a chronically epileptic mammalian brain circuit. Specifically, we sought to determine whether our key findings from the zebrafish acute seizure model also held in chronically epileptic mice. Therefore, we applied the same computational pipeline as above on 2-photon single cell resolution calcium imaging data obtained from the dentate gyrus (DG) of healthy control (N = 3) and epileptic mice (N = 3) using the intrahippocampal kainic acid (KA) model of chronic TLE, the most prevalent form of epilepsy in adults. Mice expressed GCaMP6f in dorsal DG and the epileptic group had KA injected unilaterally into the ipsilateral ventral hippocampus. 2p calcium imaging of DG granule cells was performed in healthy and in chronically epileptic mice (Figures 7A,B, note differences in vertical axis of the scale bars). Granule cell (GC) calcium dynamics were modeled for both groups of mice using FORCE optimization (600–800 neurons/mouse; 3–5 minute window; Figure 7C) and incoming and outgoing hubs were identified (Figure 7D) with similar methods as used in zebrafish.

Figure 7: — A: Experimental setup. Control and chronically epileptic mice were virally injected with GCaMP in dentate gyrus (DG) and imaged with 2p microscope.

B: DG granule cell DF/F for control and chronically epileptic mouse.

C: Model fits of experimentally recorded granule cells from chronically epileptic granule mouse using FORCE learning.

D: Outgoing and incoming degree distributions for modeled control dentate and chronically epileptic dentate networks showing heavy-tailed distributions.

E: Network response to perturbation (black arrows) of a single outgoing hub neuron in a modeled control (left) and modeled chronically epileptic (right) network.

F: Trajectory deviation in response to perturbation of individual outgoing hubs is significantly higher (one-sided Mann-Whitney U test, p < 0.001) in modeled chronically epileptic dentate network (purple, N = 28 modeled cells) than in modeled control network (gray, N = 59 modeled cells). Center marker of the violin plot represents the median.

G: Feedforward motif conductance of individual outgoing hubs is significantly higher (one-sided Mann-Whitney U test, p < 0.001) in modeled chronically epileptic dentate network (purple, N = 27 modeled cells) than in modeled control network (purple, N = 49 modeled cells). Center marker of the violin plot represents the median.

H: Feedforward motif conductance is significantly increased in modeled chronically epileptic networks across the sample population (one-sided unpaired t test, p = 0.0034). Bar graphs represents the mean of the population (N = 3 mice).

I: Outgoing degrees and feedforward motif conductance are not significantly correlated (Spearman’s rho = 0.10, p = 0.39; N = 49 modeled cells).

J: Outgoing degree cumulative distribution for superhubs (N = 8 modeled cells) versus traditional outgoing hubs (N = 19 modeled cells). Superhubs did not have the highest outgoing degrees (one-sided KS test, p = 0.71).

K: Feedforward motif conductance of adult born granule cells (red; N = 6 modeled cells) is significantly greater than mature granule cells (green; N = 21 modeled cells) (one-sided Mann-Whitney U test, p = 0.012). Dashed line represents cutoff for superhub status. Center marker of the violin plot represents the median.

L: Disconnecting all superhubs simultaneously significantly reduced the response of a modeled chronically epileptic dentate network to single outgoing hub perturbation, as measured by the percent change in global signal variance (one-sided Wilcoxon signed-rank test, p < 0.001; N = 27 modeled cells). Center marker of the violin plot represents the median. See also Figure S7.

Importantly, our results showed that the modeled control networks were more resilient to single outgoing hub perturbation than modeled chronically epileptic dentate networks (Figures 7E,F). In addition, global network dynamics were significantly less affected (one-sided Mann-Whitney U test, p < 0.001) when perturbing incoming hubs compared to outgoing hubs for both networks (Figures S7A,B). Similar to zebrafish, feedforward motif conductance of local higher-order motif-focused clusters seeded on outgoing hubs was significantly higher (one-sided unpaired t test, p = 0.0034) in chronically epileptic dentate networks compared to control dentate networks (Figures 7G,H; Feedforward conductance, control: 0.21 ± 0.014; TLE: 0.31 ± 0.024). Feedforward motif conductance was not correlated to outgoing degree (Spearman’s rho = 0.10, p > 0.05) (Figure 7I) and hubs with the top motif-conductance scores were not biased towards the highest outgoing degree values (one-sided KS test, p > 0.05) (Figure 7J). For the studies below, outgoing hubs with the top 20% feedforward motif-conductance value were considered superhubs, based on an analysis protocol similar to the one applied to the zebrafish data above in relation to Fig 6D (Figure S7C). More specifically, as for the zebrafish, the particular 20% cutoff value was chosen for the mouse superhubs because it was just above the feedforward motif-conductance value where a plateau was reached with the trajectory deviation (indicated by a black arrowhead in Supplementary Figure 7C) after progressively disconnecting the outgoing hubs with the highest feedforward conductance values (note that increasing the cutoff percentile further to 25% did not change the key results).

Is there a potential biological correlate of the superhubs identified by our computational pipeline from the mouse DG cellular-resolution functional imaging data? A particularly intriguing possibility in this regard are the epilepsy-related adult-born granule cells (abGCs) (Althaus et al., 2016; Danzer, 2018; Varma et al., 2019) that have been suggested to be crucial in driving epileptiform activity in the mouse DG (Sparks et al., 2020). In order to test this possibility, we identified the abGCs among the broader imaged GC population using previously published methods (Sparks et al., 2020; Figure S7D; Methods). Critically, effective connectivity optimization and higher-order network analysis revealed that 75% of superhubs were indeed the modeled abGCs, despite abGCs representing < 18% of the total imaged GC population. In addition, abGCs in the computational model had significantly higher feedforward motif-conductance scores compared to their more mature GC counterparts (one-sided Mann-Whitney U test, p = 0.012) (Figure 7K; Feedforward conductance, mature GCs: 0.26 ± 0.048; abGCs: 0.431 ± 0.017).These data demonstrate that superhubs identified through our computational pipeline applied to 2-photon imaging data obtained from the DG of epileptic mice represent a specific biological cell population thought to be involved in seizures (Sparks et al., 2020), independently validating our approach. Next, in order to investigate the role of the mouse superhubs further, we disconnected superhubs in the modeled chronically epileptic dentate networks. Single outgoing hub perturbation simulations showed significant reduction in both the change in global network trajectory deviation (one-sided Wilcoxon signed-rank test, p < 0.001; Figure S7E) and in the change in global network signal variance after superhubs were disconnected (one-sided Wilcoxon signed-rank test, p < 0.001; Figure 7L). These data indicate that disconnecting superhubs effectively stabilized modeled chronically epileptic dentate networks. Furthermore, the percent change in signal variance in response to single outgoing hub perturbation was significantly lower when disconnecting superhubs compared to disconnecting the same number of traditional outgoing hubs randomly (one-sided Wilcoxon signed-rank test, p = 0.0077) or traditional outgoing hubs with the lowest feedforward motif conductance values (one-sided Wilcoxon signed-rank test, p = 0.0024) (Figures S7F,G). Lastly, we modeled GC dynamics over multiple non-overlapping frames within a one-hour imaging window to test if superhub identities were stable. Despite superhubs representing 2% of the total cell population, we observed that 54% of identified superhubs in one frame were superhubs in a subsequent frame whose start time was 15 minutes later.

These similar findings across both an acute seizure model in zebrafish and in chronically epileptic mice suggest that the emergence of superhubs is a core principle of network reorganization that may be a key feature contributing to the destabilization of the epileptic brain. Targeting these superhubs may be more effective in the cellular scale control of epileptic circuits than hubs defined traditionally based on connection count.

Discussion

Here, we sought to characterize the connectivity patterns of cell-cell communication networks in epileptic circuits. Our findings reveal that superhubs, defined through analysis of the higher-order organization of modeled networks extracted from functional calcium imaging data, emerge as key cellular controllers that can powerfully destabilize epileptic circuits. Disconnecting these superhubs was effective in stabilizing modeled networks in larval zebrafish, and, importantly, these results also held true in the modeled dentate gyrus of chronically epileptic mice. Critically, in the modeled DG of mice with chronic TLE, superhubs were predominately abGCs. Therefore, these results predict the existence of fundamentally novel single cell targets for maximally selective, minimally invasive seizure control in epilepsy.

Search for new interventional targets guided by large-scale cellular resolution functional imaging

Current clinical assessment and treatment of epilepsy is to a large extent based on analysis of networks constructed from population recordings such as local field potentials (LFP) (Jiruska et al., 2013) or functional magnetic resonance imaging (fMRI) (Gotman and Pittau, 2011). However, recent studies have shown that single-cell activity can diverge significantly from what population recordings would predict. For example, apparently self-repeating, macroscopically recurrent epileptiform LFP activity (inter-ictal spikes) indicating network synchrony have been shown to emerge from non-recurrent microscopic single-cell activity. In other words, each inter-ictal event is generated by a different combination of participating cells (Liu and Baraban, 2019; Muldoon et al., 2013; Sparks et al., 2020). This ‘macro-micro’ disconnect (Farrell et al., 2019) is a significant challenge for the field and indicates that a more nuanced understanding of pathways at the level of microcircuits is needed to treat the underlying disease (Soltesz and Losonczy, 2018). Therefore, in an effort to search for novel forms of maximally selective, ideally single cell-level targets for interventions for seizure control, we performed large-scale calcium imaging at cellular scale and used this as our primary data source for the subsequent modeling and analysis.

Computational pipeline to study superhubs in cell-cell communication networks

Our computational methodology for uncovering the role of superhubs in destabilizing epileptic circuits was performed using three distinct yet integrated modules: effective connectivity modeling, higher-order motif-focused network analysis, and single-cell perturbation simulations.

Effective connectivity modeling is a widely used technique for gaining insights on interactions between pairs of connected nodes under a network model of causal dynamics (Friston, 2011). Methods to perform effective connectivity modeling have been deployed to study the brain under various pathological conditions (Huang et al., 2011; Nejad et al., 2012; Rosch et al., 2018) and have also been used to elucidate macroscopic brain interactions responsible for seizure propagation in the larval zebrafish (Rosch et al., 2018). Here, we interrogated changes to cell-cell effective connectivity networks as a result of PTZ induced reduction of inhibition (Huang et al., 2001) in the larval zebrafish acute seizure model, and as a result of various epilepsy-related persistent alterations such as mossy fiber sprouting (Sutula et al., 1989) and hilar cell loss (Kobayashi and Buckmaster, 2003) in the DG of chronically epileptic mice. We employed chaotic recurrent neural networks (Sompolinsky et al., 1988) and FORCE optimization (Sussillo and Abbott, 2009) techniques, which have been shown to be effective for modeling neural dynamics related to hippocampal sequence generation (Rajan et al., 2016), motor planning (Li et al., 2016), and coping (Andalman et al., 2019). Using this approach on calcium imaging data acquired from the larval zebrafish at whole-brain single cell resolution, we present for the first time biologically constrained effective connectivity models of control and preseizure networks, where the biological constraint was incorporated by the inclusion of the zebrafish structural connectome (Kunst et al., 2019) in the weight-update step. As a result, macroscale subnetworks that resembled major anatomical subregions emerged (Figure S1). These specific partitions agree with converging evidence that suggest a functional (Ahrens et al., 2013; Betzel, 2019; Liu and Baraban, 2019) separation between the various front and mid-/hind-brain structures.

The parameters of the model form a directed weighted graph, which allowed us to quantify chemoconvulsant-or chronic epilepsy-induced changes to the underlying graph structure using novel methods in network science (Yin et al., 2017). We first found heavy-tailed degree distributions of strong excitatory connections for both zebrafish and mouse models (Figures 3C,7D) (Bonifazi et al., 2009), a feature that is common in large complex networks. This enabled us to identify both incoming and outgoing traditional hub neurons based on incoming and outgoing connection counts. To further analyze the connectivity structure surrounding traditional hubs, we deployed novel local motif-focused clustering techniques and quantified motif conductance (Figures 5A,B). Importantly, the MAPPR algorithm (Yin et al., 2017) identified optimal clusters, which allowed us to directly compare motif conductance between baseline and preseizure networks. While we reported a nonsignificant increase (~5%) in average outgoing degrees in preseizure networks (Figures 3C,D), feedforward motif conductance of higher-order clusters surrounding outgoing hubs increased significantly by 50% on average (Figure 5E).

Single-cell perturbation simulations are important tools for generating predictions of how individual cells influence network dynamics (Sadeh and Clopath, 2020). Measures were taken in the modeling step to prevent overfitting, such as including a sparsity constraint on the number of model parameters, which allowed us to perform controlled perturbation simulations. We first interrogated network stability in modeled control and pathological circuits. Results revealed that perturbation of just a single outgoing hub neuron can significantly influence epileptic global network dynamics compared to similar computational experiment in baseline networks (Figures 4, 7). One reason for this may be due to compromised inhibition in epileptic circuits (Huang et al., 2001; Kobayashi and Buckmaster, 2003; Korn et al., 1987) which normally functions to stabilize network activity (Isaacson and Scanziani, 2011; Murphy and Miller, 2009; Sadeh and Clopath, 2020). Taken together, these results highlight that preseizure networks are unstable (Chang et al., 2018; Sadeh and Clopath, 2020). Additionally, we showed that targeted-attack simulations of identified superhubs (i.e., outgoing hubs with high feedforward motif conductance) can stabilize networks to perturbation. These causality-establishing simulations (Figures 6, 7) predict that superhubs can more readily propagate sustained excitatory activity downstream in epilepsy compared to control, baseline networks.

Superhubs in the epileptic brain

The primary conceptual advance in this work was brought to light from mining large-scale cellular resolution networks extracted from experimental neural data for higher-order connectivity patterns called motifs. Highly connected but rare hub neurons have been of great interest for studies working towards the goal of advancing seizure control with minimal side-effects (Bui et al., 2018; Krook-Magnuson and Soltesz, 2015; Krook-Magnuson et al., 2015). This has been motivated by experimental work showing that hub neurons orchestrate network synchrony (Bocchio et al., 2020; Bonifazi et al., 2009) and by computational work predicting their role in the transition from inter-ictal to ictal discharge (Morgan and Soltesz, 2008).

However, hub neurons are traditionally defined by simple connection counts, a definition that does not consider the rich higher-order motif patterns that are often found in complex networks (Benson et al., 2016; Sporns and Kötter, 2004). As these motifs are thought to influence network function in biological neural circuits (Sporns and Kötter, 2004), we deployed our computational pipeline towards the goal of identifying potential new targets for control of pathological circuits. The key results presented in this paper could not have been uncovered with traditional lower-order graph mining techniques, as the primary metric to extract superhubs - motif conductance - was not correlated to connection count (Figures 5F, 6F, 7J), local clustering coefficient score, or betweenness centrality (Figures S6A,B). Furthermore, because disconnecting superhubs stabilized networks, these findings suggest that complex networks can be susceptible to targeted attacks of nodes when considering rich higher-order motif features rather than simple connection count. This shift in perspective – specifically looking at the patterns of connectivity surrounding hubs as opposed to connections from hubs - may also be important for how we interpret the underlying microscale dynamics from macroscale recordings (Farrell et al., 2019), evaluate the efficacy of anti-epileptic drugs (AEDs) (Baraban et al., 2013), and develop more strategic closed-loop interventions (Bui et al., 2018; Krook-Magnuson and Soltesz, 2015; Krook-Magnuson et al., 2013, 2015).

Motifs are a critical feature of the structural and functional connectomes (Sadeh and Clopath, 2020; Song et al., 2005; Sporns and Kotter, 2004), and it has been hypothesized that the brain maximizes the diversity of functional motifs (Sporns and Kotter, 2004). This diversity may be related to the phenomenon of criticality (sometimes called “edge of chaos”), a state marked by scale-invariant neural avalanches that has been reported in control zebrafish (Ponce-Alvarez et al., 2018). Prior research showed chemoconvulsant-induced disruption of excitation/inhibition (E/I) balance in cortical neural networks caused deviation away from criticality (one neuron activates one neuron) and into the supercritical regime (one neuron activates more than one neuron) (Shew et al., 2009). Indeed, hypersynchronous neuronal avalanches, evidence of a supercritical state, were recently reported in a zebrafish model of genetic epilepsy using in vivo calcium imaging (Liu et al., 2021). Here, we specifically observed that preseizure networks contain elevated counts of two motif patterns that suggest the emergence of a supercritical regime: (1) the “push-out” motif (Figure S4C), in which the mother neuron activates two daughter neurons, and (2) the feedforward motif (Figure S4D), in which the mother neuron activates two daughter neurons and one of the daughter neurons activates its sibling. Therefore, our discovery of superhubs dense with feedforward connections simultaneously brings to the forefront a potential new network-level biomarker that may be able to capture a system’s divergence from criticality.

Our findings in the zebrafish brain in an acute seizure model were remarkably similar to the results from the hippocampal dentate gyrus of chronically epileptic mice. While zebrafish brains contain generally similar circuits compared to mice (Lovett-Barron et al., 2017), there are also important differences, for example, concerning cortical structures prevalent in mammals that are often sites of epileptic foci. Furthermore, acute seizure models lack persistent alterations to the underlying genes, ion channels, synapses, and morphological properties that are present in patients with epilepsy. We addressed both of these issues by modeling DG GC dynamics in mice with chronic TLE. Through our computational analysis pipeline, we were able to show that higher-order motif interactions that predict the emergence of superhubs held in distinct experimental epilepsy models and in organisms far removed in evolutionary time. Furthermore, we identified a biological correlate to the superhub in the epileptic DG, specifically the abGCs (Figure 7K), effectively validating our computational methods. This finding also corroborates previous efforts using a separate modeling approach (Sparks et al., 2020) that suggests abGCs are key drivers of epileptiform activity in a chronic model of TLE.

The investigations described in this paper, apart from the actual recording of the functional calcium dynamics, were performed in-silico, therefore, in-vivo experimental studies will need to be performed to validate the major predictions of this work. Specifically, these results analyzing the higher-order interactions of control and epileptic networks predict a new single-cell target – the superhub - for maximally selective, minimally invasive control of epileptic circuits. Based on our observations in epileptic mice that superhubs are temporally stable over the hour-long timescale and that modeling and mining effective connectivity networks can be done quickly (< 20 minutes), closed-loop interventions that target individual superhubs (which, in the specific case of the DG in TLE, largely overlap with the genetically accessible abGCs) can be designed in the future to test the predictions of this study concerning the roles of superhubs in the epilepsies.

STAR Methods

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Darian Hadjiabadi (dhh@stanford.edu).

Materials availability

This study did not generate new unique reagents.

Data and software availability

Zebrafish and mouse functional calcium imaging data (http://dx.doi.org/10.17632/9936ryd5h7.2) and effective connectivity networks (http://dx.doi.org/10.17632/dghdz45rfd.2) have been deposited into Mendeley Data. All code to perform modeling and analyze effective connectivity models were written in python3 and is available at https://github.com/dhadjia1/soltesz-lab-epilepsy-modeling.

EXPERIMENTAL MODELS AND SUBJECT DETAILS

All procedures were approved by the Institutional Animal Care and Use Committee for both Stanford University and Columbia University.

Zebrafish acute seizure model

Tg(elavl3:H2B-GCaMP6s) (Freeman et al., 2014) fish (7 dpf) bred on a Nacre or Casper background were used for imaging and registration. Zebrafish were mounted dorsal side up in a thin layer of 2.5% low-melting point agarose (Invitrogen) in the lid of a 3 mm petri dish (Fisher), using a sewing needle to position the fish under a stereomicroscope (Leica M80). Fish were group-housed under a 14:10 light:dark cycle until the day of experiments, and were fed with paramecia (Parameciavap) twice daily from 5–6 days post fertilization onward. All testing occurred during the late morning and afternoon. 15 mM bath application of the chemoconvulsant pentylenetetrazol (PTZ) was performed to induce spontaneous seizures (Baraban et al., 2005), serving as the acute seizure model. Zebrafish were randomly chosen and all fish that received PTZ developed seizures and were included for imaging. Note that each fish served as its own control before the chemoconvulsant treatment, making blinding not applicable. No power analysis was done to determine sample size.

Intrahippocampal kainic acid mouse model of chronical temporal lobe epilepsy

Male transgenic mice were obtained from The Jackson Laboratory (Nestin-CreER^T2:016261; ROSA26-CAG-stop^flox-tdTomato Ai9:007909) to establish a local breeding colony on a C57BL/6J background. The Nestrin-Cre line was crossed with the Ai9 reporter line to express tdTomato in adult-born granule cell populations (Sparks et al., 2020). Mice were housed in the vivarium on a 12h light/dark cycle, were housed 3–5 mice per cage, and had access food and water ad libitum. Mice were randomly chosen for epilepsy induction (see Inducing chronic epilepsy in METHOD DETAILS). Mice were housed individually during video-EEG monitoring following kainic acid injection. Mature male and female mice (>8 weeks of age) were used for all experiments and mice were included if spontaneous behavioral seizures were detected. Experimenters were not blinded to control vs. epileptic group during recording and no power analysis was performed to determine sample size.

METHOD DETAILS

In vivo two-photon imaging in zebrafish acute seizure model

Two-photon volumetric imaging was performed using an Olympus FVMPE multiphoton microscope (Olympus Corporation), with a resonant scanner, in either unidirectional or bidirectional scanning mode. We used a 16x objective (0.8 NA; Nikon). Functional brain imaging was performed at 1.2x zoom (1.44 μm/pix) in 15 z-planes (15 μm spacing) at 0.59s/vol (2500 volumes). Baseline control imaging was performed for 5 minutes followed by 15 mM bath application of PTZ to induce spontaneous seizures (Baraban et al., 2005). Functional imaging continued for an additional 20 minutes. All zebrafish exhibited at least one putative seizure prior to cessation of imaging.

After functional brain imaging, a structural stack was obtained at 1 μm spacing, starting 15 mm above the first z-plane, ending 15 mm below the last z-plane. Images were registered to Z-brain atlas Tg(elavl3:H2B-RFP) volume using the Computational Morphometry Toolkit (CMTK; https://www.nitrc.org/projects/cmtk/) and single-cell functional calcium dynamics were extracted and denoised with non-negative matrix factorization (NMF) based statistical approaches found in the CaIMan library (Giovannucci et al., 2019). This preprocessing step is fully discussed in (Lovett-Barron et al., 2017). All zebrafish calcium imaging data can be found at (Hadjiabadi et al., 2021).

In vivo two-photon imaging of intrahippocampal kainic acid mouse model of chronical temporal lobe epilepsy

Virus injections

Two weeks prior to kainic acid (KA) injection, 3mg tamoxifen (TMX) (2mg/mL in corn oil/10% ethanol) was injected I.P/day for 5 consecutive days. abGCs were indelibly labeled with tdTomato following injections of TMX that drove expression of Cre in Nestin+ cells.

Inducing chronic epilepsy

Kainic Acid (KA) was injected into the ventral hippocampus to induce the epilepsy model and rAAV(Syn-GCaMP6f) was injected into the dorsal dentate gyrus ipsilateral to KA injection. Shortly after, a chronic imaging window was implanted over dorsal dentate and an LFP electrode was inserted adjacent to site of KA injection. Following recovery from injection of KA, mice were placed in video-EEG enabled housing where LFP and behavioral activity were continuously recorded to monitor ictogenesis. Three weeks post-KA injection, the video-EEG verified TLE mice were habituated to being head fixed under the two-photon microscope and concurrent Ca2+ imaging and LFP recording was performed. Detailed surgical procedures are reported in (Sparks et al., 2020).

Two-photon imaging

Two-photon imaging of dentate gyrus granule cells was performed using the same set up as (Danielson et al., 2016), at 4 images/second. Approximately 50–100 mW of laser power under the objective was used for excitation (Ti:Sapphire laser, (Chameleon Ultra II, Coherent) tuned to 920 nm), with adjustments in power levels to accommodate varying window clarity. To optimize light transmission, the angle of the mouse’s head was adjusted using two goniometers (Edmund Optics, +/− 10-degree range) such that the imaging window was parallel to the objective. A piezoelectric crystal was coupled to the objective (Nikon 40X NIR water-immersion, 0.8 NA, 3.5mm WD), allowing for rapid displacement of the imaging plane in the z-dimension. Red (tdTomato) and green (GCaMP6f) channels were separated by an emission cube set (green, HQ525/70m-2p; red, HQ607/45m-2p) at 512 × 512 pixels covering 225 μm x 225 μm. OASIS (Friedrich et al., 2017) was used for denoising. While not being imaged, mice were routinely monitored for interictal and seizure events using a custom continuous video-EEG system previously described (Krook-Magnuson et al., 2013). Healthy control mouse data was obtained from (Danielson et al., 2016), included two-photon recording of granule cells from approximately the same location in dentate gyrus as in epileptic mice. All mouse calcium imaging data can be found at (Hadjiabadi et al., 2021).

Modeling neural dynamics in healthy and pathological brains

Zebrafish

The start of the preseizure state was defined as one minute after PTZ bath application. Seizure initiation was defined as three standard deviations above population mean calcium signal during baseline (pre-PTZ) and termination was defined as when the population mean signal dropped below this threshold. Correlation matrix analysis (Li et al., 2007) was deployed to quantify network synchronization. Modeling in zebrafish was performed on baseline control dynamics first, and the best fit model was used as the initial parameter matrix for learning preseizure dynamics. Community detection using the Leiden algorithm (Traag et al., 2019) on learned parameter matrix was used to identify communities with numerous intra-group connections. To account for potential abnormalities during the registration process, neurons were removed from modeling if their respective post-registration |DF/F| > 10 or if | DF/F(t+1) – DF/F(t) | > 10 at any point in the signal.

Mice

For both control and chronically epileptic mice, calcium dynamics were acquired during a 60-minute epoch. Calcium recordings included artifacts from running and grooming that resulted in prolonged hyper-synchronous events. Therefore, a continuous 3–5 minute time window lacking such events was identified for each mouse and used to model calcium dynamics.

Chaotic Recurrent Neural Networks

Models of cell-cell effective communication were built using chaotic recurrent neural networks (RNN) (Sompolinsky et al., 1988). Each neuron experimentally imaged was represented as a node in the network and edges represent the effective (causal) influence between pairs of nodes. The governing dynamics of the chaotic RNN are:

τ \frac{d x_{i} (t)}{d t} = - x_{i} (t) + g \sum_{j = 1}^{N} J_{i j} φ (x_{j} (t)) + h_{i} (t)

z_{i} (t) = \sum_{j = 1}^{N} J_{i j} φ (x_{j} (t))

φ (.) = \tanh (.)

x_i(t) is the inferred intracellular current of node i. φ(x_i(t)) represents firing rate. z_i(t) is the estimated calcium signal. τ is the time constant of the system (zebrafish: 1.5 s; mouse: 0.625 s). h_i(t) is uncorrelated white noise sampled from a normal distribution with mean 0 and standard deviation 0.05 (zebrafish) / 0.005 (mouse). g is the gain parameter that determines whether there will be chaos in the system (g<1: stable equilibrium; g>1: chaos). We used g=1.25 for both zebrafish and mouse(Andalman et al., 2019; Rajan et al., 2016). Lastly, J is the effective connectivity matrix that represents the parameters of the model. At initiation of learning baseline control dynamics in zebrafish and learning both control and preseizure dynamics in mice, the values of J that were not removed after applying a sparsity mask (zebrafish: 0.10; mouse: 0.40) were sampled from a normal distribution with mean 0 and standard deviation $\frac{1}{\sqrt{N p}}$ . N is the number of nodes and p is the sparsity. The models contain p * N * (N − 1) parameters. Dynamics were solved using Euler’s method (dt=0.25 s).

Reproducing experimental calcium data using FORCE learning

The effective connectivity parameter matrix was optimized to reproduce the experimental calcium data through FORCE learning (Sussillo and Abbott, 2009). This was done through recursive least-squares optimization where at each time point an error signal e_i(t) = z_i(t) – f_i(t) is calculated between node output z_i(t) and experimental calcium trace f_i(t). Given this error, the traditional learning rule is as follows:

Δ J_{i j} = c * e_{i} (t) * \sum_{k = 1}^{N} P_{j k} φ (x_{k} (t))

c = \frac{1}{1 + φ {(t)}^{T} P (t) φ (t)}

P (t) = P (t - 1) - c P (t - 1) φ (t) φ {(t)}^{T} P (t - 1)

Where c is the effective learning rate used for stability and P(t) is updated in a recursive fashion at every time point. At initiation, P(0) was set to the identify matrix. Learning was performed for 500 epochs for all zebrafish and mouse models, where one epoch is defined as one run of the optimization routine for the duration of the experimental trial. Convergence was assessed by tracking the mean squared reconstruction error between unit activity and experimental data. All zebrafish and mouse models can be found at (Hadjiabadi and Soltesz, 2021). To ensure replication, modeling was repeated three times with different initial conditions for each zebrafish and mouse.

Biologically constrained FORCE using zebrafish structural connectome

The zebrafish structural connectome (Kunst et al., 2019) was incorporated into zebrafish FORCE learning as a biological constraint. The structural connectome is a weighted undirected graph between 30 distinct subregions occupying the telencephalon, diencephalon, mesencephalon, and rhombencephalon. The modified weight-update step is:

Δ J_{i j}^{C o n s t r a i n e d} = S_{R (i), R (j)} * Δ J_{i j}

where i,j are individual nodes (neurons) and S_R(i),R(j) is the structural connectivity between subregions R(i) and R(j).

Identifying modeled traditional hub neurons

The optimized effective connectivity parameter matrix was binarized by converting the top 10% of edges to a 1 and converting the remaining edges to a 0. The outgoing and incoming degree was calculated for each neuron. Neurons above the 90^th percentile outgoing (incoming) degree score were marked as outgoing (incoming) hubs.

Identifying modeled superhubs

Identified traditional outgoing hubs (see Identifying traditional hub neurons) were used as the seed for local higher-order clustering on feedforward motifs and the feedforward motif conductance was quantified (see Quantifying motif conductance using higher-order network analysis; note only seed neurons with at least 5 neighbors in the local higher-order cluster were considered for further analysis). Modeled neurons were ranked based on the feedforward motif conductance score in descending order. The top x% of hub neurons was “disconnected” by removing all edges from the hub neuron to its identified local higher-order cluster. The disconnected network was then simulated, and trajectory deviation quantified (see Trajectory deviation) for the fully connected network relative to the disconnected network. Superhubs were identified when a stable plateau in the trajectory deviation was reached as a function of the number of neurons disconnected (see Figure 6D, Figure S7C).

Identifying modeled adult-born granule cells

Preprocessing steps were undertaken to match granule cell calcium dynamics with genetic identity as performed in (Sparks et al., 2020). The individual performing analysis was blind to the identity of all abGCs until modeling was complete for all mice and higher-order analysis was performed for each modeled network.

Perturbation simulations

To simulate the effect of perturbation on network dynamics, a single hub neuron was ‘current clamped’ to achieve maximum firing rate (500ms step current). The current clamp perturbation was initiated at 0.2 normalized time, consistent for all zebrafish and mouse models. Synthetic calcium traces were then generated for each neuron before and after perturbation.

QUANTIFICATION AND STATISTICAL ANALYSIS

Community detection

Community detection is used to understand the structure of complex networks by identifying nodes clusters that form relatively dense groups. We used the leidenalg python package (Traag, 2021) which leverages the recently developed Leiden algorithm (Traag et al., 2019) to guarantee well-connected communities. Communities were identified by calling the function leidenalg.find_partition(G, leidenalg.RBConfigurationVertexPartition, resolution_parameter=1.0). Here, G is an igraph object (Nepusz, 2021). More specifically, G is a directed graph that has been binarized to exclude inhibitory edges and to include the remaining excitatory edges whose weights are in the top 50%.

Force-directed graphs

The effective connectivity matrix was visualized using the Barnes-Hut N-body simulation algorithm (Barnes and Hut, 1986). Here, each node can be thought of as a repelling particle and the edges between nodes are modeled as attractive springs. The objective of the algorithm is to find an optimal force-directed spatial configuration such that (i.e., net force = 0). The Barnes-Hut algorithm was applied to the binarized parameter matrix after thresholding for strongest connections (see Identifying modeled traditional hub neurons) and used to visualize incoming and outgoing hubs connections in zebrafish.

Rich-club analysis

The rich-club coefficient on the full baseline and preseizure binarized graphs were performed to identify if highly connected neurons are themselves connected to one another. We discuss the lesser known implementation of rich-club analysis on directed graphs using solutions provided in (Smilkov and Kocarev, 2010). Specifically, given a directed graph G=(V,E), the outgoing rich club coefficient can be calculated as:

φ^{out} (k) = \frac{(\frac{E_{> k}^{out}}{N_{> k}^{out} (N_{> k}^{out} - 1)})}{φ_{rand}^{out} (k)}

Here, φ^out(k) is the rich-club coefficient as a function of outgoing degree k and is normalized by the rich-club-coefficient over a random graph. $E_{> k}^{o u t}$ represents the number of outgoing edges between pairs of neurons whose outgoing degree is greater than k. $N_{> k}^{o u t}$ represents the number of nodes whose outgoing degree is greater than k. The analytic solution to $φ_{r a n d}^{o u t} (k)$ , the rich-club coefficient for a random graph, is the following:

φ_{r a n d}^{o u t} (k) = \frac{N \sum_{k^{'} = k + 1}^{k m a x} k^{'} P_{o u t} (k^{'}) \sum_{k^{''} = k + 1}^{k m a x} < k_{i n}^{k o u t = k''} > P_{o u t} (k^{''})}{< k_{o u t} > N_{> k}^{o u t} (N_{> k}^{o u t} - 1)}

Here, N is the total number of nodes in the network (i.e. |V|). P_out(k′) is the probability of a node having outgoing degree k’. $< k_{i n}^{k o u t = k''} >$ is the mean incoming degree for nodes with outgoing degree k’’. <k_out> is the mean outgoing degree in the network. $N_{> k}^{o u t}$ represents the number of nodes whose outgoing degree is greater than k. If φ^out(k) > 1 as k approaches the highest outgoing degree in the network (kmax), then it can be deduced that the graph exhibits a rich-club.

Quantifying motif conductance using higher-order network analysis

Motif-based approximate Personalized PageRank (MAPPR) algorithm (Yin et al., 2017) was used to identify an optimal higher-order motif-focused cluster (i.e. minimum motif conductance) surrounding a hub neuron. Given a motif M, MAPPR has three key steps.

Constructing motif weighted graph W

The input graph, taken to be the binarized parameter matrix after thresholding for strongest connections (see Identifying modeled traditional hub neurons), is transformed into a weighted graph W where the weight depends on M. Specifically, W_ij is the number of instances of M containing nodes i and j.

Compute the approximate personalized PageRank vector

The personalized PageRank (PPR) vector represents the stationary distribution of a modified random walk seeded on a hub node u. At each step of the random walk, the random walker is ‘teleported’ back to the specified seed node with probability 1 – α, where α was set to 0.98. The stationary distribution of this process for a seed node u (the PPR vector p_u), will have larger values for nodes “close” to u. The stationary distribution is the solution to the following system of equations:

(I - α A D^{- 1}) p_{u} = (1 - α) e_{u}

Where I is the identify matrix, A is the adjacency matrix, D is the diagonal degree matrix, and e_u is the vector of all 0’s except for a 1 in position u. The PPR vector p_u can be approximated via $\tilde{p_{u}}$ with accuracy ε = 0.0001 such that

0 \leq D^{- 1} p_{u} - D^{- 1} \tilde{p_{u}} \leq ε

Identify higher-order motif-focused cluster as set with minimal motif conductance

A sweep procedure is used given approximated APPR vector $\tilde{p_{u}}$ . Nodes are sorted by descending value of the vector $D^{- 1} \tilde{p_{u}}$ and are incorporated one at a time into a growing set X. After a node added to the set, the motif conductance is calculated.

φ^{M} (X) = \frac{c u t_{M} (X)}{\min (v o l_{M} (X), v o l_{M} (X^{'}))}

where vol_M(X) is the number of motif endpoints in X, vol_M(X′) is the number of motif endpoints for nodes not in X, and cut_M(X) is the number of instances of M that have at least one end point in X. The set with the smallest motif conductance is deemed optimal and returned. For traditional edge-based clustering, step one is skipped, and the edge conductance score is quantified as above but replacing motif instance M with simple edges. Only clusters with at least 5 nodes were considered for analysis. The MAPPR algorithm was run using Stanford Network Analysis Platform (SNAP) (Leskovec and Sosič, 2016).

Trajectory deviation

The Euclidean distance d between the mean calcium signals of two networks X and X’ was calculated.

d (x (t), x^{'} (t)) = \sqrt{\sum_{i = 1}^{T} {(x_{i} - x_{i}^{'})}^{2}}

Here, x(t) is the mean calcium signal for network X and x’(t) is the mean calcium signal for network X’. In this work, X’ is a network that underwent single-neuron perturbation (see Perturbation simulations) or had neurons “disconnected”. To compare simulations across control and epileptic networks, trajectory deviation TD was calculated as the Euclidean distance normalized by remaining time points left after start of perturbation t_o.

T D (x, x^{'}) = \frac{d (x, x^{'})}{T - t_{o}}

Change in total power

To determine network response to perturbation (see Perturbation simulations), the variance of the mean calcium signal before and after perturbation was calculated. The percent change in the variance was measured:

% c h a n g e s i g n a l p o w e r (x, x^{'}) = \frac{| v a r (x^{'}) - v a r (x) |}{v a r (x)}

Here, x represents the mean calcium signal of the unperturbed network and x’ represents the mean calcium signal of the perturbed network. Note that signal variance is equal to the total power of the signal. Greater values indicate the network is less stable and is tightly correlated to trajectory deviation.

Statistical analysis

Values reported as x ± y represent mean ± standard deviation. Statistical analysis was performed using python scipy.stats (SciPy 1.0 Contributors et al., 2020) package. Parametric tests used: unpaired t-test, paired t-test. Non-parametric tests used: unpaired Mann-Whitney U-test, paired Wilcoxon signed-rank test, Kolmogorov-Smirnov test. Statistical details can be found in the results and figure legends. The Shapiro-Wilk test was used to determine if data met assumptions of normality. p-values were corrected (“adjusted p”) using Bonferroni’s method for multiple comparisons. p-values are reported in all figure subpanels except when p < 0.001. Statistical significance was set at 0.05.

Supplementary Material

NIHMS1714843-supplement-1.pdf^{(5.1MB, pdf)}

KEY RESOURCE TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and virus strains
AAV1.Syn.GCaMP6f.WPRE.SV40	Penn Vector Core	N/A
ROSA26-CAG-stopflox-tdTomato Ai9	JAX	007909
Chemicals, peptides, and recombinant proteins
Pentylenetetrazol (PTZ)	Sigma-Aldrich	PubChem ID: 24278643
Kainic Acid (KA)	Sigma-Aldrich	PubChem ID: 24277985
Deposited data
Functional calcium imaging data	This paper	http://dx.doi.org/10.17632/9936ryd5h7.2
Effective connectivity models	This paper	http://dx.doi.org/10.17632/dghdz45rfd.2
Experimental models: organisms/strains
Zebrafish Tg(elavl3:H2B-GCaMP6s)	(Vladimirov et al., 2014)	jf5
Mouse Nestrin-CreERT2	JAX	016261
Software and algorithms
Python	Python.org	v3.6
SNAP	http://snap.stanford.edu/	v6
networkx	https://networkx.org/	v2.5
scipy	https://www.scipy.org/	v1.20
leidenalg	(Traag, 2021)	v0.8.40
igraph	(Nepusz, 2021)	v0.9.4
FIJI/ImageJ	NIH	v1.52p
CaImAn	(Giovannucci et al., 2019)	PMID: 30652683
Computational Morphometry Toolkit (CMTK)	NITRC	v3.3
FORCE	(Sussillo and Abbott, 2009)	PMID: 19709635
MAPPR	(Yin et al., 2017)	PMID: 28344853

Open in a new tab

Highlights.

Motif patterns of epileptic networks were inferred from single-cell calcium data
Superhubs rich in excitatory feedforward motifs emerged in the preseizure state
Disconnecting superhubs effectively stabilized epileptic circuits in simulations
Superhubs are predicted to be adult-born granule cells in the mouse dentate gyrus

Acknowledgements

We thank Michael Kunst for access to zebrafish structural connectivity data and members of the Soltesz lab and Maxwell Collard for helpful discussions. D.H. was supported by the Stanford Interdisciplinary Graduate Fellowship in coordination with Stanford Wu Tsai Neurosciences Institute (anonymous donor). M.L.-B. was supported by NIH grant K99MH112840. F.T.S. was supported by an American Epilepsy Society Junior Investigator Award. Z.L. was supported by NIH grants F31NS120783-01 and T32GM007367. S.C.B. was supported by NIH grants R01NS096976 and R01NS103139. I.S. and A.L. were supported by NIH grants R01NS094668 and U19NS104590. Models were built on the Texas Advanced Computing Center (TACC) Frontera system (National Science Foundation [NSF] Allocation #1811597).

Footnotes

Declaration of Interests

The authors declare that K.D. is on the Neuron advisory board.

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

Ahrens MB, Orger MB, Robson DN, Li JM, and Keller PJ (2013). Whole-brain functional imaging at cellular resolution using light-sheet microscopy. Nature Methods 10, 413–420. [DOI] [PubMed] [Google Scholar]
Albert R, Jeong H, and Barabási A-L (2000). Error and attack tolerance of complex networks. Nature 406, 378–382. [DOI] [PubMed] [Google Scholar]
Althaus AL, Zhang H, and Parent JM (2016). Axonal plasticity of age-defined dentate granule cells in a rat model of mesial temporal lobe epilepsy. Neurobiology of Disease 86, 187–196. [DOI] [PMC free article] [PubMed] [Google Scholar]
Andalman AS, Burns VM, Lovett-Barron M, Broxton M, Poole B, Yang SJ, Grosenick L, Lerner TN, Chen R, Benster T, et al. (2019). Neuronal Dynamics Regulating Brain and Behavioral State Transitions. Cell 177, 970–985.e20. [DOI] [PMC free article] [PubMed] [Google Scholar]
Andersen R, Chung F, and Lang K (2006). Local Graph Partitioning using PageRank Vectors. In 2006 47th Annual IEEE Symposium on Foundations of Computer Science (FOCS’06), (Berkeley, CA, USA: IEEE), pp. 475–486. [Google Scholar]
Baraban SC, Taylor MR, Castro PA, and Baier H (2005). Pentylenetetrazole induced changes in zebrafish behavior, neural activity and c-fos expression. Neuroscience 131, 759–768. [DOI] [PubMed] [Google Scholar]
Baraban SC, Dinday MT, and Hortopan GA (2013). Drug screening in Scn1a zebrafish mutant identifies clemizole as a potential Dravet syndrome treatment. Nat Commun 4, 2410. [DOI] [PMC free article] [PubMed] [Google Scholar]
Barabási A-L, and Albert R (1999). Emergence of Scaling in Random Networks. Science 286, 509–512. [DOI] [PubMed] [Google Scholar]
Barnes J, and Hut P (1986). A hierarchical O(N log N) force-calculation algorithm. Nature 324, 446–449. [Google Scholar]
Benson AR, Gleich DF, and Leskovec J (2016). Higher-order organization of complex networks. Science 353, 163–166. [DOI] [PMC free article] [PubMed] [Google Scholar]
Betzel RF (2019). Organizing principles of whole-brain functional connectivity in zebrafish larvae. Network Neuroscience 4, 234–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bocchio M, Gouny C, Angulo-Garcia D, Toulat T, Tressard T, Quiroli E, Baude A, and Cossart R (2020). Hippocampal hub neurons maintain distinct connectivity throughout their lifetime. Nature Communications 11, 4559. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bonifazi P, Goldin M, Picardo MA, Jorquera I, Cattani A, Bianconi G, Represa A, Ben-Ari Y, and Cossart R (2009). GABAergic hub neurons orchestrate synchrony in developing hippocampal networks. Science 326, 1419–1424. [DOI] [PubMed] [Google Scholar]
Bui AD, Nguyen TM, Limouse C, Kim HK, Szabo GG, Felong S, Maroso M, and Soltesz I (2018). Dentate gyrus mossy cells control spontaneous convulsive seizures and spatial memory. Science 359, 787–790. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bullmore E, and Sporns O (2009). Complex brain networks: graph theoretical analysis of structural and functional systems. 13. [DOI] [PubMed] [Google Scholar]
Burrows DRW, Samarut É, Liu J, Baraban SC, Richardson MP, Meyer MP, and Rosch RE (2020). Imaging epilepsy in larval zebrafish. Eur J Paediatr Neurol 24, 70–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chang W-C, Kudlacek J, Hlinka J, Chvojka J, Hadrava M, Kumpost V, Powell AD, Janca R, Maturana MI, Karoly PJ, et al. (2018). Loss of neuronal network resilience precedes seizures and determines the ictogenic nature of interictal synaptic perturbations. Nature Neuroscience 21, 1742–1752. [DOI] [PMC free article] [PubMed] [Google Scholar]
Danielson NB, Kaifosh P, Zaremba JD, Lovett-Barron M, Tsai J, Denny CA, Balough EM, Goldberg AR, Drew LJ, Hen R, et al. (2016). Distinct Contribution of Adult-Born Hippocampal Granule Cells to Context Encoding. Neuron 90, 101–112. [DOI] [PMC free article] [PubMed] [Google Scholar]
Danzer SC (2018). Contributions of Adult-Generated Granule Cells to Hippocampal Pathology in Temporal Lobe Epilepsy: A Neuronal Bestiary. BPL 3, 169–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
Danzer SC (2019). Adult Neurogenesis in the Development of Epilepsy. Epilepsy Curr 19, 316–320. [DOI] [PMC free article] [PubMed] [Google Scholar]
Farrell JS, Nguyen Q-A, and Soltesz I (2019). Resolving the Micro-Macro Disconnect to Address Core Features of Seizure Networks. Neuron 101, 1016–1028. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fornito A, Zalesky A, and Breakspear M (2015). The connectomics of brain disorders. Nature Reviews Neuroscience 16, 159–172. [DOI] [PubMed] [Google Scholar]
Freeman LC (1977). A Set of Measures of Centrality Based on Betweenness. Sociometry 40, 35–41. [Google Scholar]
Freeman J, Vladimirov N, Kawashima T, Mu Y, Sofroniew NJ, Bennett DV, Rosen J, Yang C-T, Looger LL, and Ahrens MB (2014). Mapping brain activity at scale with cluster computing. Nature Methods 11, 941–950. [DOI] [PubMed] [Google Scholar]
Friedrich J, Zhou P, and Paninski L (2017). Fast online deconvolution of calcium imaging data. PLOS Computational Biology 13, e1005423. [DOI] [PMC free article] [PubMed] [Google Scholar]
Friston KJ (2011). Functional and Effective Connectivity: A Review. Brain Connectivity 1, 13–36. [DOI] [PubMed] [Google Scholar]
Giovannucci A, Friedrich J, Gunn P, Kalfon J, Brown BL, Koay SA, Taxidis J, Najafi F, Gauthier JL, Zhou P, et al. (2019). CaImAn an open source tool for scalable calcium imaging data analysis. ELife 8, e38173. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gotman J, and Pittau F (2011). Combining EEG and fMRI in the study of epileptic discharges. Epilepsia 52 Suppl 4, 38–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hadjiabadi D, and Soltesz I (2021). Models: Maximally selective single cell target for circuit control in epilepsy. Mendeley Data, V2. DOI: 10.17632/dghdz45rfd.2. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hadjiabadi D, Lovett-Barron M, Sparks F, Liao Z, Losonczy A, Deisseroth K, and Soltesz I (2021). Functional Calcium Imaging: Maximally selective single cell target for circuit control in epilepsy. Mendeley Data, V2. DOI: 10.17632/9936ryd5h7.2. [DOI] [PMC free article] [PubMed] [Google Scholar]
Huang RQ, Bell-Horner CL, Dibas MI, Covey DF, Drewe JA, and Dillon GH (2001). Pentylenetetrazole-induced inhibition of recombinant gamma-aminobutyric acid type A (GABA(A)) receptors: mechanism and site of action. J. Pharmacol. Exp. Ther. 298, 986–995. [PubMed] [Google Scholar]
Huang S, Li J, Ye J, Fleisher A, Chen K, Wu T, and Reiman E (2011). Brain Effective Connectivity Modeling for Alzheimer’s Disease by Sparse Gaussian Bayesian Network. KDD; 931–939. [DOI] [PMC free article] [PubMed] [Google Scholar]
Isaacson JS, and Scanziani M (2011). How inhibition shapes cortical activity. Neuron 72, 231–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
Jiruska P, Curtis M. de, Jefferys JGR, Schevon CA, Schiff SJ, and Schindler K (2013). Synchronization and desynchronization in epilepsy: controversies and hypotheses. The Journal of Physiology 591, 787–797. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kobayashi M, and Buckmaster PS (2003). Reduced Inhibition of Dentate Granule Cells in a Model of Temporal Lobe Epilepsy. J. Neurosci. 23, 2440–2452. [DOI] [PMC free article] [PubMed] [Google Scholar]
Korn SJ, Giacchino JL, Chamberlin NL, and Dingledine R (1987). Epileptiform burst activity induced by potassium in the hippocampus and its regulation by GABA-mediated inhibition. J. Neurophysiol. 57, 325–340. [DOI] [PubMed] [Google Scholar]
Kramer MA, and Cash SS (2012). Epilepsy as a Disorder of Cortical Network Organization. Neuroscientist 18, 360–372. [DOI] [PMC free article] [PubMed] [Google Scholar]
Krook-Magnuson E, and Soltesz I (2015). Beyond the hammer and the scalpel: selective circuit control for the epilepsies. Nature Neuroscience 18, 331–338. [DOI] [PMC free article] [PubMed] [Google Scholar]
Krook-Magnuson E, Armstrong C, Oijala M, and Soltesz I (2013). On-demand optogenetic control of spontaneous seizures in temporal lobe epilepsy. Nature Communications 4, 1376. [DOI] [PMC free article] [PubMed] [Google Scholar]
Krook-Magnuson E, Armstrong C, Bui A, Lew S, Oijala M, and Soltesz I (2015). In vivo evaluation of the dentate gate theory in epilepsy. J Physiol 593, 2379–2388. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kunst M, Laurell E, Mokayes N, Kramer A, Kubo F, Fernandes AM, Förster D, Dal Maschio M, and Baier H (2019). A Cellular-Resolution Atlas of the Larval Zebrafish Brain. Neuron 103, 21–38.e5. [DOI] [PubMed] [Google Scholar]
Leskovec J, and Sosič R (2016). SNAP: A General-Purpose Network Analysis and Graph-Mining Library. ACM Trans. Intell. Syst. Technol. 8, 1–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
Li N, Daie K, Svoboda K, and Druckmann S (2016). Robust neuronal dynamics in premotor cortex during motor planning. Nature 532, 459–464. [DOI] [PMC free article] [PubMed] [Google Scholar]
Li X, Cui D, Jiruska P, Fox JE, Yao X, and Jefferys JGR (2007). Synchronization measurement of multiple neuronal populations. Journal of Neurophysiology 98, 3341–3348. [DOI] [PubMed] [Google Scholar]
Liu J, and Baraban SC (2019). Network Properties Revealed during Multi-Scale Calcium Imaging of Seizure Activity in Zebrafish. ENeuro 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
Liu J, Salvati KA, and Baraban SC (2021). In vivo calcium imaging reveals disordered interictal network dynamics in epileptic stxbp1b zebrafish. iScience 24 (6). 10.1016/j.isci.2021.102558. [DOI] [PMC free article] [PubMed] [Google Scholar]
Löscher W, and Schmidt D (2011). Modern antiepileptic drug development has failed to deliver: ways out of the current dilemma. Epilepsia 52, 657–678. [DOI] [PubMed] [Google Scholar]
Lovett-Barron M, Andalman AS, Allen WE, Vesuna S, Kauvar I, Burns VM, and Deisseroth K (2017). Ancestral Circuits for the Coordinated Modulation of Brain State. Cell 171, 1411–1423.e17. [DOI] [PMC free article] [PubMed] [Google Scholar]
Morgan RJ, and Soltesz I (2008). Nonrandom connectivity of the epileptic dentate gyrus predicts a major role for neuronal hubs in seizures. Proceedings of the National Academy of Sciences 105, 6179–6184. [DOI] [PMC free article] [PubMed] [Google Scholar]
Muldoon SF, Soltesz I, and Cossart R (2013). Spatially clustered neuronal assemblies comprise the microstructure of synchrony in chronically epileptic networks. PNAS 110, 3567–3572. [DOI] [PMC free article] [PubMed] [Google Scholar]
Murphy BK, and Miller KD (2009). Balanced Amplification: A New Mechanism of Selective Amplification of Neural Activity Patterns. Neuron 61, 635–648. [DOI] [PMC free article] [PubMed] [Google Scholar]
Nejad AB, Ebdrup BH, Glenthøj BY, and Siebner HR (2012). Brain Connectivity Studies in Schizophrenia: Unravelling the Effects of Antipsychotics. Curr Neuropharmacol 10, 219–230. [DOI] [PMC free article] [PubMed] [Google Scholar]
Nepusz T (2021). python-igraph: High performance graph data structures and algorithms. https://pypi.org/project/python-igraph/.
Ponce-Alvarez A, Jouary A, Privat M, Deco G, and Sumbre G (2018). Whole-Brain Neuronal Activity Displays Crackling Noise Dynamics. Neuron 100, 1446–1459.e6. [DOI] [PMC free article] [PubMed] [Google Scholar]
Rajan K, Harvey CD, and Tank DW (2016). Recurrent Network models of sequence generation and memory. Neuron 90, 128–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
Rosch RE, Hunter PR, Baldeweg T, Friston KJ, and Meyer MP (2018). Calcium imaging and dynamic causal modelling reveal brain-wide changes in effective connectivity and synaptic dynamics during epileptic seizures. PLOS Computational Biology 14, e1006375. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sadeh S, and Clopath C (2020). Theory of neuronal perturbome in cortical networks. PNAS 117, 26966–26976. [DOI] [PMC free article] [PubMed] [Google Scholar]
SciPy 1.0 Contributors, Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, Burovski E, Peterson P, Weckesser W, et al. (2020). SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat Methods 17, 261–272. [DOI] [PMC free article] [PubMed] [Google Scholar]
Shew WL, Yang H, Petermann T, Roy R, and Plenz D (2009). Neuronal Avalanches Imply Maximum Dynamic Range in Cortical Networks at Criticality. J. Neurosci. 29, 15595–15600. [DOI] [PMC free article] [PubMed] [Google Scholar]
Smilkov D, and Kocarev L (2010). Rich-club and page-club coefficients for directed graphs. Physica A: Statistical Mechanics and Its Applications 389, 2290–2299. [Google Scholar]
Soltesz I, and Losonczy A (2018). CA1 pyramidal cell diversity enabling parallel information processing in the hippocampus. Nature Neuroscience 21, 484–493. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sompolinsky H, Crisanti A, and Sommers HJ (1988). Chaos in Random Neural Networks. Phys. Rev. Lett. 61, 259–262. [DOI] [PubMed] [Google Scholar]
Song S, Sjöström PJ, Reigl M, Nelson S, and Chklovskii DB (2005). Highly Nonrandom Features of Synaptic Connectivity in Local Cortical Circuits. PLoS Biol 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sparks FT, Liao Z, Li W, Grosmark A, Soltesz I, and Losonczy A (2020). Hippocampal adult-born granule cells drive network activity in a mouse model of chronic temporal lobe epilepsy. Nature Communications 11, 6138. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sporns O, and Kötter R (2004). Motifs in Brain Networks. PLoS Biol 2. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sussillo D, and Abbott LF (2009). Generating Coherent Patterns of Activity from Chaotic Neural Networks. Neuron 63, 544–557. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sutula T, Cascino G, Cavazos J, Parada I, and Ramirez L (1989). Mossy fiber synaptic reorganization in the epileptic human temporal lobe. Annals of Neurology 26, 321–330. [DOI] [PubMed] [Google Scholar]
Toni N, Teng EM, Bushong EA, Aimone JB, Zhao C, Consiglio A, van Praag H, Martone ME, Ellisman MH, and Gage FH (2007). Synapse formation on neurons born in the adult hippocampus. Nat Neurosci 10, 727–734. [DOI] [PubMed] [Google Scholar]
Toni N, Laplagne DA, Zhao C, Lombardi G, Ribak CE, Gage FH, and Schinder AF (2008). Neurons born in the adult dentate gyrus form functional synapses with target cells. Nat Neurosci 11, 901–907. [DOI] [PMC free article] [PubMed] [Google Scholar]
Towlson EK, Vértes PE, Ahnert SE, Schafer WR, and Bullmore ET (2013). The Rich Club of the C. elegans Neuronal Connectome. J. Neurosci. 33, 6380–6387. [DOI] [PMC free article] [PubMed] [Google Scholar]
Traag VA (2021). leidenalg: Leiden is a general algorithm for methods of community detection in large networks. https://pypi.org/project/leidenalg/.
Traag VA, Waltman L, and van Eck NJ (2019). From Louvain to Leiden: guaranteeing well-connected communities. Scientific Reports 9, 5233. [DOI] [PMC free article] [PubMed] [Google Scholar]
Varma P, Brulet R, Zhang L, and Hsieh J (2019). Targeting Seizure-Induced Neurogenesis in a Clinically Relevant Time Period Leads to Transient But Not Persistent Seizure Reduction. J. Neurosci. 39, 7019–7028. [DOI] [PMC free article] [PubMed] [Google Scholar]
Vladimirov N, Mu Y, Kawashima T, Bennett DV, Yang C-T, Looger LL, Keller PJ, Freeman J, and Ahrens MB (2014). Light-sheet functional imaging in fictively behaving zebrafish. Nature Methods 11, 883–884. [DOI] [PubMed] [Google Scholar]
Watts DJ, and Strogatz SH (1998). Collective dynamics of ‘small-world’ networks. Nature 393, 440–442. [DOI] [PubMed] [Google Scholar]
Wernicke S (2006). Efficient Detection of Network Motifs. IEEE/ACM Trans. Comput. Biol. and Bioinf. 3, 347–359. [DOI] [PubMed] [Google Scholar]
Yin H, Benson AR, Leskovec J, and Gleich DF (2017). Local Higher-Order Graph Clustering. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, (Halifax, NS, Canada: Association for Computing Machinery), pp. 555–564. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

NIHMS1714843-supplement-1.pdf^{(5.1MB, pdf)}

Data Availability Statement

[R1] Ahrens MB, Orger MB, Robson DN, Li JM, and Keller PJ (2013). Whole-brain functional imaging at cellular resolution using light-sheet microscopy. Nature Methods 10, 413–420. [DOI] [PubMed] [Google Scholar]

[R2] Albert R, Jeong H, and Barabási A-L (2000). Error and attack tolerance of complex networks. Nature 406, 378–382. [DOI] [PubMed] [Google Scholar]

[R3] Althaus AL, Zhang H, and Parent JM (2016). Axonal plasticity of age-defined dentate granule cells in a rat model of mesial temporal lobe epilepsy. Neurobiology of Disease 86, 187–196. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R4] Andalman AS, Burns VM, Lovett-Barron M, Broxton M, Poole B, Yang SJ, Grosenick L, Lerner TN, Chen R, Benster T, et al. (2019). Neuronal Dynamics Regulating Brain and Behavioral State Transitions. Cell 177, 970–985.e20. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R5] Andersen R, Chung F, and Lang K (2006). Local Graph Partitioning using PageRank Vectors. In 2006 47th Annual IEEE Symposium on Foundations of Computer Science (FOCS’06), (Berkeley, CA, USA: IEEE), pp. 475–486. [Google Scholar]

[R6] Baraban SC, Taylor MR, Castro PA, and Baier H (2005). Pentylenetetrazole induced changes in zebrafish behavior, neural activity and c-fos expression. Neuroscience 131, 759–768. [DOI] [PubMed] [Google Scholar]

[R7] Baraban SC, Dinday MT, and Hortopan GA (2013). Drug screening in Scn1a zebrafish mutant identifies clemizole as a potential Dravet syndrome treatment. Nat Commun 4, 2410. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R8] Barabási A-L, and Albert R (1999). Emergence of Scaling in Random Networks. Science 286, 509–512. [DOI] [PubMed] [Google Scholar]

[R9] Barnes J, and Hut P (1986). A hierarchical O(N log N) force-calculation algorithm. Nature 324, 446–449. [Google Scholar]

[R10] Benson AR, Gleich DF, and Leskovec J (2016). Higher-order organization of complex networks. Science 353, 163–166. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R11] Betzel RF (2019). Organizing principles of whole-brain functional connectivity in zebrafish larvae. Network Neuroscience 4, 234–256. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R12] Bocchio M, Gouny C, Angulo-Garcia D, Toulat T, Tressard T, Quiroli E, Baude A, and Cossart R (2020). Hippocampal hub neurons maintain distinct connectivity throughout their lifetime. Nature Communications 11, 4559. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R13] Bonifazi P, Goldin M, Picardo MA, Jorquera I, Cattani A, Bianconi G, Represa A, Ben-Ari Y, and Cossart R (2009). GABAergic hub neurons orchestrate synchrony in developing hippocampal networks. Science 326, 1419–1424. [DOI] [PubMed] [Google Scholar]

[R14] Bui AD, Nguyen TM, Limouse C, Kim HK, Szabo GG, Felong S, Maroso M, and Soltesz I (2018). Dentate gyrus mossy cells control spontaneous convulsive seizures and spatial memory. Science 359, 787–790. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R15] Bullmore E, and Sporns O (2009). Complex brain networks: graph theoretical analysis of structural and functional systems. 13. [DOI] [PubMed] [Google Scholar]

[R16] Burrows DRW, Samarut É, Liu J, Baraban SC, Richardson MP, Meyer MP, and Rosch RE (2020). Imaging epilepsy in larval zebrafish. Eur J Paediatr Neurol 24, 70–80. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R17] Chang W-C, Kudlacek J, Hlinka J, Chvojka J, Hadrava M, Kumpost V, Powell AD, Janca R, Maturana MI, Karoly PJ, et al. (2018). Loss of neuronal network resilience precedes seizures and determines the ictogenic nature of interictal synaptic perturbations. Nature Neuroscience 21, 1742–1752. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R18] Danielson NB, Kaifosh P, Zaremba JD, Lovett-Barron M, Tsai J, Denny CA, Balough EM, Goldberg AR, Drew LJ, Hen R, et al. (2016). Distinct Contribution of Adult-Born Hippocampal Granule Cells to Context Encoding. Neuron 90, 101–112. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R19] Danzer SC (2018). Contributions of Adult-Generated Granule Cells to Hippocampal Pathology in Temporal Lobe Epilepsy: A Neuronal Bestiary. BPL 3, 169–181. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R20] Danzer SC (2019). Adult Neurogenesis in the Development of Epilepsy. Epilepsy Curr 19, 316–320. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R21] Farrell JS, Nguyen Q-A, and Soltesz I (2019). Resolving the Micro-Macro Disconnect to Address Core Features of Seizure Networks. Neuron 101, 1016–1028. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R22] Fornito A, Zalesky A, and Breakspear M (2015). The connectomics of brain disorders. Nature Reviews Neuroscience 16, 159–172. [DOI] [PubMed] [Google Scholar]

[R23] Freeman LC (1977). A Set of Measures of Centrality Based on Betweenness. Sociometry 40, 35–41. [Google Scholar]

[R24] Freeman J, Vladimirov N, Kawashima T, Mu Y, Sofroniew NJ, Bennett DV, Rosen J, Yang C-T, Looger LL, and Ahrens MB (2014). Mapping brain activity at scale with cluster computing. Nature Methods 11, 941–950. [DOI] [PubMed] [Google Scholar]

[R25] Friedrich J, Zhou P, and Paninski L (2017). Fast online deconvolution of calcium imaging data. PLOS Computational Biology 13, e1005423. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R26] Friston KJ (2011). Functional and Effective Connectivity: A Review. Brain Connectivity 1, 13–36. [DOI] [PubMed] [Google Scholar]

[R27] Giovannucci A, Friedrich J, Gunn P, Kalfon J, Brown BL, Koay SA, Taxidis J, Najafi F, Gauthier JL, Zhou P, et al. (2019). CaImAn an open source tool for scalable calcium imaging data analysis. ELife 8, e38173. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R28] Gotman J, and Pittau F (2011). Combining EEG and fMRI in the study of epileptic discharges. Epilepsia 52 Suppl 4, 38–42. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R29] Hadjiabadi D, and Soltesz I (2021). Models: Maximally selective single cell target for circuit control in epilepsy. Mendeley Data, V2. DOI: 10.17632/dghdz45rfd.2. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R30] Hadjiabadi D, Lovett-Barron M, Sparks F, Liao Z, Losonczy A, Deisseroth K, and Soltesz I (2021). Functional Calcium Imaging: Maximally selective single cell target for circuit control in epilepsy. Mendeley Data, V2. DOI: 10.17632/9936ryd5h7.2. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R31] Huang RQ, Bell-Horner CL, Dibas MI, Covey DF, Drewe JA, and Dillon GH (2001). Pentylenetetrazole-induced inhibition of recombinant gamma-aminobutyric acid type A (GABA(A)) receptors: mechanism and site of action. J. Pharmacol. Exp. Ther. 298, 986–995. [PubMed] [Google Scholar]

[R32] Huang S, Li J, Ye J, Fleisher A, Chen K, Wu T, and Reiman E (2011). Brain Effective Connectivity Modeling for Alzheimer’s Disease by Sparse Gaussian Bayesian Network. KDD; 931–939. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R33] Isaacson JS, and Scanziani M (2011). How inhibition shapes cortical activity. Neuron 72, 231–243. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R34] Jiruska P, Curtis M. de, Jefferys JGR, Schevon CA, Schiff SJ, and Schindler K (2013). Synchronization and desynchronization in epilepsy: controversies and hypotheses. The Journal of Physiology 591, 787–797. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R35] Kobayashi M, and Buckmaster PS (2003). Reduced Inhibition of Dentate Granule Cells in a Model of Temporal Lobe Epilepsy. J. Neurosci. 23, 2440–2452. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R36] Korn SJ, Giacchino JL, Chamberlin NL, and Dingledine R (1987). Epileptiform burst activity induced by potassium in the hippocampus and its regulation by GABA-mediated inhibition. J. Neurophysiol. 57, 325–340. [DOI] [PubMed] [Google Scholar]

[R37] Kramer MA, and Cash SS (2012). Epilepsy as a Disorder of Cortical Network Organization. Neuroscientist 18, 360–372. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R38] Krook-Magnuson E, and Soltesz I (2015). Beyond the hammer and the scalpel: selective circuit control for the epilepsies. Nature Neuroscience 18, 331–338. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R39] Krook-Magnuson E, Armstrong C, Oijala M, and Soltesz I (2013). On-demand optogenetic control of spontaneous seizures in temporal lobe epilepsy. Nature Communications 4, 1376. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R40] Krook-Magnuson E, Armstrong C, Bui A, Lew S, Oijala M, and Soltesz I (2015). In vivo evaluation of the dentate gate theory in epilepsy. J Physiol 593, 2379–2388. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R41] Kunst M, Laurell E, Mokayes N, Kramer A, Kubo F, Fernandes AM, Förster D, Dal Maschio M, and Baier H (2019). A Cellular-Resolution Atlas of the Larval Zebrafish Brain. Neuron 103, 21–38.e5. [DOI] [PubMed] [Google Scholar]

[R42] Leskovec J, and Sosič R (2016). SNAP: A General-Purpose Network Analysis and Graph-Mining Library. ACM Trans. Intell. Syst. Technol. 8, 1–20. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R43] Li N, Daie K, Svoboda K, and Druckmann S (2016). Robust neuronal dynamics in premotor cortex during motor planning. Nature 532, 459–464. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R44] Li X, Cui D, Jiruska P, Fox JE, Yao X, and Jefferys JGR (2007). Synchronization measurement of multiple neuronal populations. Journal of Neurophysiology 98, 3341–3348. [DOI] [PubMed] [Google Scholar]

[R45] Liu J, and Baraban SC (2019). Network Properties Revealed during Multi-Scale Calcium Imaging of Seizure Activity in Zebrafish. ENeuro 6. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R46] Liu J, Salvati KA, and Baraban SC (2021). In vivo calcium imaging reveals disordered interictal network dynamics in epileptic stxbp1b zebrafish. iScience 24 (6). 10.1016/j.isci.2021.102558. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R47] Löscher W, and Schmidt D (2011). Modern antiepileptic drug development has failed to deliver: ways out of the current dilemma. Epilepsia 52, 657–678. [DOI] [PubMed] [Google Scholar]

[R48] Lovett-Barron M, Andalman AS, Allen WE, Vesuna S, Kauvar I, Burns VM, and Deisseroth K (2017). Ancestral Circuits for the Coordinated Modulation of Brain State. Cell 171, 1411–1423.e17. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R49] Morgan RJ, and Soltesz I (2008). Nonrandom connectivity of the epileptic dentate gyrus predicts a major role for neuronal hubs in seizures. Proceedings of the National Academy of Sciences 105, 6179–6184. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R50] Muldoon SF, Soltesz I, and Cossart R (2013). Spatially clustered neuronal assemblies comprise the microstructure of synchrony in chronically epileptic networks. PNAS 110, 3567–3572. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R51] Murphy BK, and Miller KD (2009). Balanced Amplification: A New Mechanism of Selective Amplification of Neural Activity Patterns. Neuron 61, 635–648. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R52] Nejad AB, Ebdrup BH, Glenthøj BY, and Siebner HR (2012). Brain Connectivity Studies in Schizophrenia: Unravelling the Effects of Antipsychotics. Curr Neuropharmacol 10, 219–230. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R53] Nepusz T (2021). python-igraph: High performance graph data structures and algorithms. https://pypi.org/project/python-igraph/.

[R54] Ponce-Alvarez A, Jouary A, Privat M, Deco G, and Sumbre G (2018). Whole-Brain Neuronal Activity Displays Crackling Noise Dynamics. Neuron 100, 1446–1459.e6. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R55] Rajan K, Harvey CD, and Tank DW (2016). Recurrent Network models of sequence generation and memory. Neuron 90, 128–142. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R56] Rosch RE, Hunter PR, Baldeweg T, Friston KJ, and Meyer MP (2018). Calcium imaging and dynamic causal modelling reveal brain-wide changes in effective connectivity and synaptic dynamics during epileptic seizures. PLOS Computational Biology 14, e1006375. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R57] Sadeh S, and Clopath C (2020). Theory of neuronal perturbome in cortical networks. PNAS 117, 26966–26976. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R58] SciPy 1.0 Contributors, Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, Burovski E, Peterson P, Weckesser W, et al. (2020). SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat Methods 17, 261–272. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R59] Shew WL, Yang H, Petermann T, Roy R, and Plenz D (2009). Neuronal Avalanches Imply Maximum Dynamic Range in Cortical Networks at Criticality. J. Neurosci. 29, 15595–15600. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R60] Smilkov D, and Kocarev L (2010). Rich-club and page-club coefficients for directed graphs. Physica A: Statistical Mechanics and Its Applications 389, 2290–2299. [Google Scholar]

[R61] Soltesz I, and Losonczy A (2018). CA1 pyramidal cell diversity enabling parallel information processing in the hippocampus. Nature Neuroscience 21, 484–493. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R62] Sompolinsky H, Crisanti A, and Sommers HJ (1988). Chaos in Random Neural Networks. Phys. Rev. Lett. 61, 259–262. [DOI] [PubMed] [Google Scholar]

[R63] Song S, Sjöström PJ, Reigl M, Nelson S, and Chklovskii DB (2005). Highly Nonrandom Features of Synaptic Connectivity in Local Cortical Circuits. PLoS Biol 3. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R64] Sparks FT, Liao Z, Li W, Grosmark A, Soltesz I, and Losonczy A (2020). Hippocampal adult-born granule cells drive network activity in a mouse model of chronic temporal lobe epilepsy. Nature Communications 11, 6138. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R65] Sporns O, and Kötter R (2004). Motifs in Brain Networks. PLoS Biol 2. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R66] Sussillo D, and Abbott LF (2009). Generating Coherent Patterns of Activity from Chaotic Neural Networks. Neuron 63, 544–557. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R67] Sutula T, Cascino G, Cavazos J, Parada I, and Ramirez L (1989). Mossy fiber synaptic reorganization in the epileptic human temporal lobe. Annals of Neurology 26, 321–330. [DOI] [PubMed] [Google Scholar]

[R68] Toni N, Teng EM, Bushong EA, Aimone JB, Zhao C, Consiglio A, van Praag H, Martone ME, Ellisman MH, and Gage FH (2007). Synapse formation on neurons born in the adult hippocampus. Nat Neurosci 10, 727–734. [DOI] [PubMed] [Google Scholar]

[R69] Toni N, Laplagne DA, Zhao C, Lombardi G, Ribak CE, Gage FH, and Schinder AF (2008). Neurons born in the adult dentate gyrus form functional synapses with target cells. Nat Neurosci 11, 901–907. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R70] Towlson EK, Vértes PE, Ahnert SE, Schafer WR, and Bullmore ET (2013). The Rich Club of the C. elegans Neuronal Connectome. J. Neurosci. 33, 6380–6387. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R71] Traag VA (2021). leidenalg: Leiden is a general algorithm for methods of community detection in large networks. https://pypi.org/project/leidenalg/.

[R72] Traag VA, Waltman L, and van Eck NJ (2019). From Louvain to Leiden: guaranteeing well-connected communities. Scientific Reports 9, 5233. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R73] Varma P, Brulet R, Zhang L, and Hsieh J (2019). Targeting Seizure-Induced Neurogenesis in a Clinically Relevant Time Period Leads to Transient But Not Persistent Seizure Reduction. J. Neurosci. 39, 7019–7028. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R74] Vladimirov N, Mu Y, Kawashima T, Bennett DV, Yang C-T, Looger LL, Keller PJ, Freeman J, and Ahrens MB (2014). Light-sheet functional imaging in fictively behaving zebrafish. Nature Methods 11, 883–884. [DOI] [PubMed] [Google Scholar]

[R75] Watts DJ, and Strogatz SH (1998). Collective dynamics of ‘small-world’ networks. Nature 393, 440–442. [DOI] [PubMed] [Google Scholar]

[R76] Wernicke S (2006). Efficient Detection of Network Motifs. IEEE/ACM Trans. Comput. Biol. and Bioinf. 3, 347–359. [DOI] [PubMed] [Google Scholar]

[R77] Yin H, Benson AR, Leskovec J, and Gleich DF (2017). Local Higher-Order Graph Clustering. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, (Halifax, NS, Canada: Association for Computing Machinery), pp. 555–564. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Maximally selective single cell target for circuit control in epilepsy models

Darian Hadjiabadi

Matthew Lovett-Barron

Ivan Georgiev Raikov

Fraser T Sparks

Zhenrui Liao

Scott C Baraban

Jure Leskovec

Attila Losonczy

Karl Deisseroth

Ivan Soltesz

Summary

eTOC blurb

Introduction

Results

Whole brain calcium imaging of larval zebrafish acute seizure model at single cell resolution

Figure 1: Whole brain imaging of larval zebrafish acute seizure model at single-cell resolution.

Cellular resolution effective connectivity modeling to extract cell-cell communication networks

Figure 2: Cellular resolution effective connectivity modeling to extract cell-cell communication networks.

Identification of outgoing and incoming traditional hubs

Figure 3: Identification of outgoing and incoming hubs.

Perturbation of individual outgoing hubs destabilize preseizure networks

Figure 4: Perturbation of individual outgoing hubs destabilize preseizure networks.

Visualizing connections between outgoing and incoming hubs

Preferential emergence of superhubs in the preseizure brain

Figure 5: Preferential emergence of superhubs in the preseizure brain.

Disconnecting superhubs stabilizes preseizure networks

Figure 6: Disconnecting superhubs stabilizes preseizure networks.

Superhubs in a mouse model of chronic temporal lobe epilepsy

Figure 7: Superhubs in the intrahippocampal kainic acid mouse model of chronical temporal lobe epilepsy.

Discussion

Search for new interventional targets guided by large-scale cellular resolution functional imaging

Computational pipeline to study superhubs in cell-cell communication networks

Superhubs in the epileptic brain

STAR Methods

RESOURCE AVAILABILITY

Lead Contact

Materials availability

Data and software availability

EXPERIMENTAL MODELS AND SUBJECT DETAILS

Zebrafish acute seizure model

Intrahippocampal kainic acid mouse model of chronical temporal lobe epilepsy

METHOD DETAILS

In vivo two-photon imaging in zebrafish acute seizure model

In vivo two-photon imaging of intrahippocampal kainic acid mouse model of chronical temporal lobe epilepsy

Virus injections

Inducing chronic epilepsy

Two-photon imaging

Modeling neural dynamics in healthy and pathological brains

Zebrafish

Mice

Chaotic Recurrent Neural Networks

Reproducing experimental calcium data using FORCE learning

Biologically constrained FORCE using zebrafish structural connectome

Identifying modeled traditional hub neurons

Identifying modeled superhubs

Identifying modeled adult-born granule cells

Perturbation simulations

QUANTIFICATION AND STATISTICAL ANALYSIS

Community detection

Force-directed graphs

Rich-club analysis

Quantifying motif conductance using higher-order network analysis

Constructing motif weighted graph W

Compute the approximate personalized PageRank vector

Identify higher-order motif-focused cluster as set with minimal motif conductance

Trajectory deviation

Change in total power

Statistical analysis

Supplementary Material

KEY RESOURCE TABLE.

Highlights.

Acknowledgements

Footnotes

References

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS