Resolution-Based Distillation for Efficient Histology Image Classification

Abstract

Developing deep learning models to analyze histology images has been computationally challenging, as the massive size of the images causes excessive strain on all parts of the computing pipeline. This paper proposes a novel deep learning-based methodology for improving the computational efficiency of histology image classification. The proposed approach is robust when used with images that have reduced input resolution, and it can be trained effectively with limited labeled data. Moreover, our approach operates at either the tissue- or slide-level, removing the need for laborious patch-level labeling. Our method uses knowledge distillation to transfer knowledge from a teacher model pre-trained at high resolution to a student model trained on the same images at a considerably lower resolution. Also, to address the lack of large-scale labeled histology image datasets, we perform the knowledge distillation in a self-supervised fashion. We evaluate our approach on three distinct histology image datasets associated with celiac disease, lung adenocarcinoma, and renal cell carcinoma. Our results on these datasets demonstrate that a combination of knowledge distillation and self-supervision allows the student model to approach and, in some cases, surpass the teacher model’s classification accuracy while being much more computationally efficient. Additionally, we observe an increase in student classification performance as the size of the unlabeled dataset increases, indicating that there is potential for this method to scale further with additional unlabeled data. Our model outperforms the high-resolution teacher model for celiac disease in accuracy, F1-score, precision, and recall while requiring 4 times fewer computations. For lung adenocarcinoma, our results at 1.25x magnification are within 1.5% of the results for the teacher model at 10x magnification, with a reduction in computational cost by a factor of 64. Our model on renal cell carcinoma at 1.25x magnification performs within 1% of the teacher model at 5x magnification while requiring 16 times fewer computations. Furthermore, our celiac disease outcomes benefit from additional performance scaling with the use of more unlabeled data. In the case of 0.625x magnification, using unlabeled data improves accuracy by 4% over the tissue-level baseline. Therefore, our approach can improve the feasibility of deep learning solutions for digital pathology on standard computational hardware and infrastructures.

1. INTRODUCTION

Digital pathology was introduced over 20 years ago to facilitate viewing and examining high-resolution scans of histology slides. A digital scanning process produces whole-slide images (WSIs), which can then be analyzed with computational tools [1,2]. While digital scans circumvent traditional microscope use, they introduce new computational challenges. The resulting WSIs can be as large as 150,000×150,000 pixels in size and require a large-scale computational infrastructure, including storage capacity, network bandwidth, computing power, and graphics processing unit (GPU) memory.

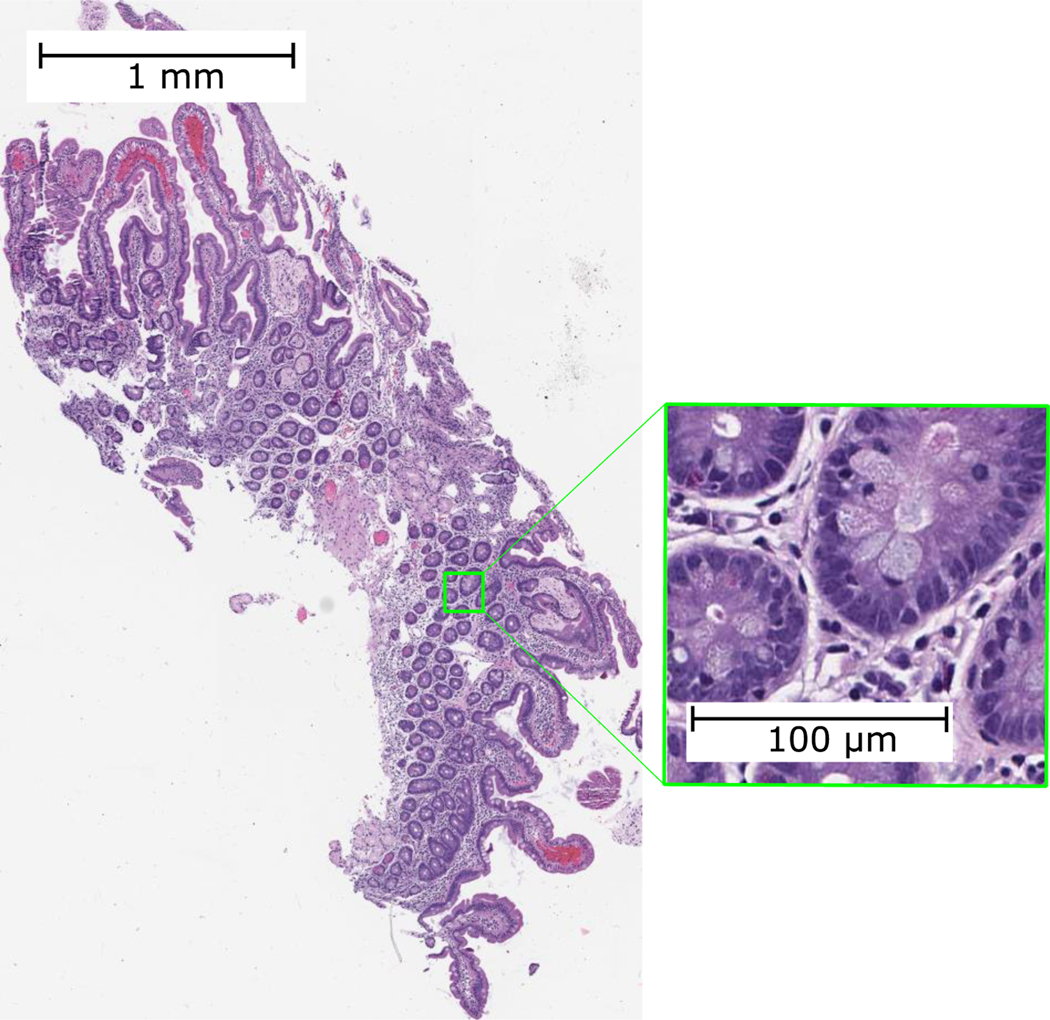
In recent years, computer vision-based deep learning methods have been developed for digital pathology [3–7]; however, their application and scope have been limited due to the massive size of WSIs. Figure 1 illustrates the magnitude of a sample histology image. Even with the most recent computational advancements, deep learning models for analyzing WSIs are still not feasible to run on all except the most expensive hardware and GPUs. These computational constraints for analyzing high-resolution WSIs have limited the adoption of deep learning solutions in digital pathology.

Figure 1.

A sample WSI intended to show the high resolution and large size of histology images.

This paper addresses this computational bottleneck by implementing a deep learning approach designed to operate accurately on lower-resolution versions of WSIs. This approach aims to lower the resolution of the input image while minimizing its effect on the classification performance. By operating on WSIs with a lower resolution, our approach potentially allows for slides to be scanned at a lower resolution, reducing scanning time and computational hardware and infrastructure strain.

Our proposed methodology is a novel approach to make high-resolution histology image analysis more efficient and feasible on standard hardware and infrastructure. We seek to prioritize minimizing the computational cost while ensuring that the classification accuracy is still acceptable. Specifically, we propose a knowledge distillation-based method where a teacher model works at a high resolution and a student model operates at a low resolution. We aim to distill the teacher model’s learned representation knowledge into the student model trained at a much lower resolution. The knowledge distillation is performed in a self-supervised fashion on a larger unlabeled dataset from the same domain. Large, labeled datasets are hard to find in the medical field, leading us to adopt a self-supervised approach to account for the lack of access to sizeable, labeled histology image datasets. This knowledge distillation method can increase the model’s performance on lower-resolution images while simultaneously saving significant amounts of memory and computation.

2. RELATED WORK

2.1. Histology Image Classification

Previously, several methods have been proposed to solve the WSI classification problem. Some approaches work by tiling the WSI into more reasonably sized patches and learning to classify at the patch level [3–6,8–10]. In some recent works, the patch-level predictions are aggregated using simple heuristic rules to produce a slide-level prediction [3,4,6,8,9]. These rules are modeled after how pathologists classify WSIs in clinical practice. In another work, a simple maximum function was used on patch-based slide heat maps for whole-slide predictions [5]. In [10], the authors use a random forest regression model to combine the patch-level predictions and produce the final classification. While these methods achieved reasonable overall performance, their analyses are fragmented, and they do not incorporate the relevant spatial information into the training process. We aim to avoid patch-based processing since it introduces additional computational overhead that can be bypassed with tissue- or slide-based analysis methods.

Multiple-instance learning (MIL) has been proposed to address the slide-level labeling problem [11–16]. MIL is a supervised learning scheme where data-points, or instances, are grouped into bags. Each bag is labeled with the class by the instance count of that particular class. MIL is well-suited towards histology slide classification, as it is designed to operate on weakly-labeled data. MIL-based methods better account for the weakly-labeled nature of patches, but they still tend to miss the holistic slide information.

Recent work has shown that operating at the slide-level is possible by splitting up the computation into discrete units that can be run on commodity hardware [17,18]. The overall calculation is equivalent to the one performed at the slide-level due to the invariance of most layers in a convolutional neural network. This method analyzes WSIs at the original high-resolution level to avoid losing larger context and fine details. Although this approach helps run large neural networks, it still requires considerable computational resources to analyze WSIs at a high resolution.

Attention-based processes have also been suggested for WSI analysis. Attention-based mechanisms divide the high-resolution image into large tiles and simultaneously learn the most critical regions of WSIs for each class and their labels [19–21]. Although these methods achieve high classification performance, they demand substantial computational resources to operate on high-resolution images.

2.2. Self-Supervised Learning

Self-supervised learning is a machine learning scheme that allows models to learn without explicit labels. Large, unlabeled datasets are readily accessible in most domains, and self-supervised methods can assist in improving classification performance without requiring resource-intensive, manually labeled data. In this scheme, learning occurs using a pre-text task on an inherent attribute of the data. As the pre-text task operates on an existing data feature, it requires no manual intervention and can be easily scaled. Proposed pre-text tasks include colorization [22,23], rotation [24,25], jigsaw puzzle [26], and counting [27]. Recent studies have explored the invariance of histology images to affine transformations, but none use self-supervised learning [28,29]. Several other works have proposed self-supervised techniques for histology images exploiting domain-specific pre-text tasks, including slide magnification prediction [30], nuclei segmentation [31], and spatial continuity [32]. In contrast, our work introduces a new pre-text task designed to transfer the knowledge present in models trained on high-resolution WSIs to ones operating on low-resolution WSIs.

2.3. Knowledge Distillation

Knowledge distillation has proven to be a valuable technique for transferring learned information between distinct models with different capacities [33,34]. As models and datasets exponentially increase in size, it is critical to adapt our methods accordingly to support less powerful devices [35]. Knowledge distillation has been beneficial to many areas of computer vision such as semantic segmentation [36], facial recognition [37,38], object detection [39], and classification [40]. Although some prior work has used knowledge distillation for chest X-rays in the medical domain [41], knowledge distillation has not been widely used for histology image analysis.

Initial knowledge distillation studies used neural network output activations, called logits, to transfer the learned knowledge from a teacher model to a student model [33–35]. FitNet built upon this knowledge distillation paradigm by suggesting that while the logits are important, the intermediate activations also encode the model’s knowledge [42]. This method proposed adding a regression term to the knowledge distillation objective to improve the overall performance of the student model while reducing the number of parameters. In this paper, we model our architecture after the FitNet approach to maintain the spatial correspondence between teacher and student models, as it represents clinically relevant information. Of note, in contrast to our approach, previous work in this domain does not include self-supervision [43]. As we show later in this paper, self-supervision proves to be a deciding factor in increasing overall classification performance for histology images.

3. TECHNICAL APPROACH

3.1. Overview

There are two main phases and one optional phase to our approach as follows:

1. Train-a-teacher model at high magnification on the labeled dataset, as explained in Section 3.2.

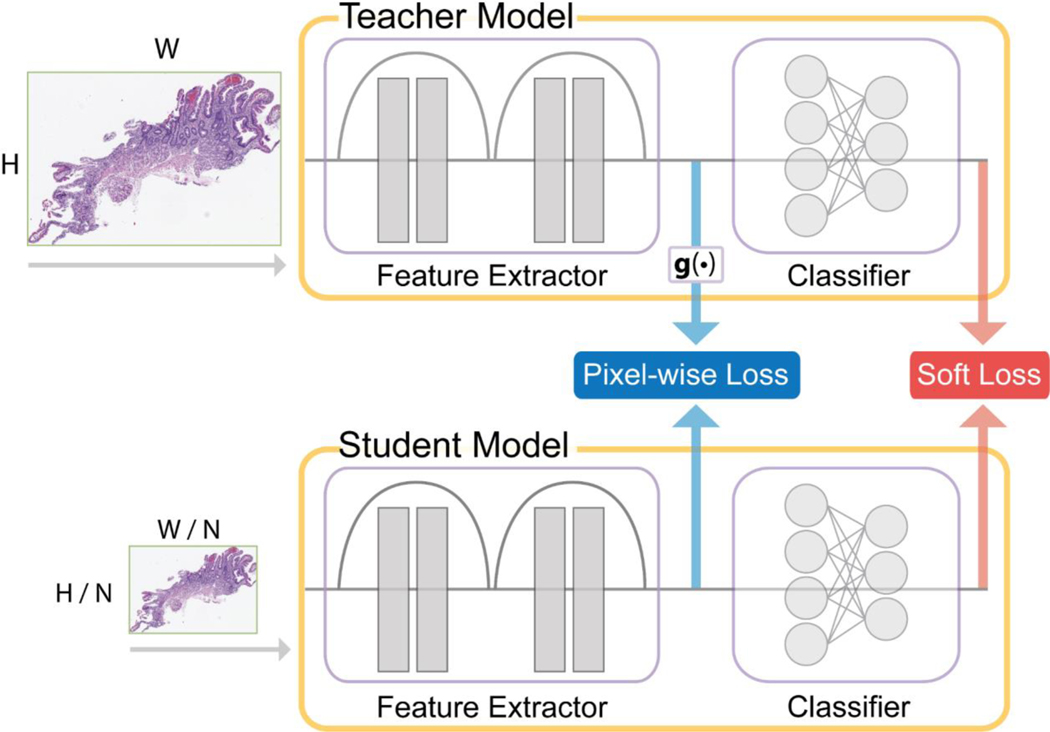
2. Train-the-knowledge distillation model on the unlabeled dataset at a high to a lower magnification, explained in Section 3.3 and shown in Figure 2.

3. (Optional) Fine-tune-the-student model using the labeled dataset at a lower magnification, as explained in Section 3.3.

Figure 2.

Overview of the knowledge distillation model. The g(·) block is a resizing function that scales the teacher feature maps to the same size as the corresponding student ones. The Pixel-wise and Soft losses are combined to produce the total loss for the optimization process.

All implementation details are provided in Appendix B of the Supplementary Material for reproducibility.

3.2. Teacher Model

For the teacher model, we used a residual network (ResNet) [44]. ResNet was chosen due to its excellent empirical performance compared to other deep learning architectures. We used the built-in ResNet PyTorch implementation [45].

The teacher model input was high-resolution, annotated slides at 10x magnification (1 μm/pixel) for celiac disease and lung adenocarcinoma and 5x magnification (2 μm/pixel) for renal cell carcinoma. While our slides were originally scanned at 20x or 40x magnification, we used either 5x or 10x magnification in the teacher model to reduce the runtime to a more reasonable period. We found that the performance gains above 5x or 10x magnification were marginal with an exponential increase in runtime. We performed online data augmentation consisting of random perturbations to the color brightness, contrast, hue, and saturation, horizontal and vertical flips, and rotations. Additionally, each input was standardized by the mean and standard deviation of the respective training set across each color channel.

3.3. Knowledge Distillation from High-Resolution Images

Knowledge distillation (also referred to as ‘KD’) is a machine learning method, where typically, a larger, more complex model “teaches” a smaller, simpler student model what to learn [33]. The learning occurs by optimizing over a desired commonality between the models. We opted to keep the student and teacher model architectures identical for our approach and instead modified the input resolution. As input data resolution is a significant factor for efficient and accurate histology image analysis, we decided that the teacher model should receive the original high-resolution image as input while the student model receives a low-resolution input image. For optimizing our knowledge distillation model, the total loss is the sum of (1) the soft loss and (2) the pixel map. These loss components are described below, and an overview of our knowledge distillation approach is shown in Figure 2.

$$Loss{}_{total}=Loss{}_{soft}+Loss{}_{pixel}\#$$ (1)

To promote classification similarity between the teacher and student models, we utilized the Kullback-Leibler (KL) Divergence over the outputs of the teacher and student models as the loss function [33,46]. Additionally, the loss function is “softened” by adding a temperature T to the softmax computation. Intuitively, softening the loss function gives more weight to smaller outputs, thus transferring information that would have been overpowered by greater values. The soft loss is computed as follows:

$$Los{s}_{soft}=KL\left(\sigma \left(\overrightarrow{\frac{F_{class}^t}{T}}\right),\sigma \left(\overrightarrow{\frac{F_{class}^s}{T}}\right)\right)\cdot T^2\#$$ (2)

where $\overrightarrow{F_{\text{class }}^t},\overrightarrow{F_{\text{class }}^S}$, and σ(·) represent the teacher classifier outputs, student classifier outputs, and softmax function, respectively. Note that we multiply by T²since the gradients will scale inversely to this factor [33].

To ensure that the teacher and student models focus on similar areas, we compute the mean-squared error over the feature map outputs. We introduce g₁(⋅) and g₂(⋅) as the max-pooling and bicubic interpolation operations, respectively. We use max-pooling and bicubic interpolation for the pixel-wise loss because we found that these two functions provide the most consistent performance for the loss function when combined, as shown in the Supplementary Material, Appendix A. The pixel-wise loss is computed as follows:

$$Los{s}_{pixel}=\frac{1}{2}\cdot \sum _{k=1}^2{\Vert g_k\left(F_{fe}^t\right)-F_{fe}^s\Vert }^2$$ (3)

where $F_{fe}^t$ and $F_{fe}^s$ are the outputs of the feature extractor in the teacher and student models, respectively. We require the functions g₁(⋅) and g₂(⋅) since the size of the teacher feature map outputs are N² times larger than the student ones, ignoring negligible differences due to rounded non-integer dimensions in some instances.

3.4. Fine-Tuning

After performing the knowledge distillation, we fine-tuned the student model weights on the lower resolution training dataset. The goal of fine-tuning the model is to make minor weight adjustments for maximal performance on the labeled data without undoing the learning in the previous layers. To this end, all weights were frozen except the ones in the fully connected layer. The weights were trained using the Adam optimization algorithm [47] until convergence. The data augmentations enumerated in Section 3.2 were applied to the input data. Similar to the teacher model training, we used the cross-entropy loss to learn ground-truth labels in this phase. We opted to skip this phase in experiments where the same training set was used across Phases I and II, as it resulted in lower classification performance on the validation set due to overfitting on the training set.

3.5. Gradient Accumulation

We used gradient accumulation to account for the large and variable sizes of the slides. Gradient accumulation computes the forward and backward pass changes for each input, but it does not update the model weights until all mini-batch backward passes are complete. While gradient accumulation does not affect most layers, batch normalization layers are affected, as they require operation on a mini-batch to work correctly. In our model, instead of batch normalization, we used group normalization, which has more consistent performance across varying mini-batch sizes [48] due to its independence from the mini-batch dimension. This modification allows the model to learn properly with gradient accumulation.

4. EXPERIMENTAL SETUP

4.1. Datasets

We performed our experiments on three independent datasets. One dataset was collected from The Cancer Genome Atlas (TCGA) database [49], and the other two datasets were collected at Dartmouth-Hitchcock Medical Center (DHMC), a tertiary academic medical center in New Hampshire, USA. The slides from both TCGA and DHMC were hematoxylin-eosin stained formalin-fixed paraffin-embedded. All slides were digitized at either 20x or 40x magnification. Every downsampling was obtained directly from the original image to avoid any potential artifacts caused by a composition of downsamplings.

Additionally, we chose to leave the slides at their variable, native resolutions to avoid introducing bias through standardizing the sizes. To generate the required low-resolution WSIs, we used the Lanczos filter to create several downsampled versions of each image [50]. We use the notation nx magnification relative to the original magnification. For example, an originally 20x slide downsampled four times in both height and width dimensions would have n = 20/4 = 5 and be denoted 5x. We provide image dimension summary statistics for the celiac disease (CD), lung adenocarcinoma (LUAD), and renal cell carcinoma (RCC) datasets in Table 1.

Table 1.

Summary of image resolutions and dimensions for each dataset. The image height and width values are in pixels.

Dataset	Resolution	Median		Maximum		Interquartile Range
		Height	Width	Height	Width	Height	Width
CD	10x (1 μm/pixel)	1,934	1,550	11,880	6,408	1,454–2,494	1,170–2,016
LUAD	10x (1 μm/pixel)	1,267	1,428	12,780	19,702	817–2,062	922–2,239
RCC	5x (2 μm/pixel)	7,152	8,424	16,832	19,304	4,358–8,908	4,946–11,268

This study and the use of human participant data in this project were approved by the Dartmouth-Hitchcock Health Institutional Review Board (IRB) with a waiver of informed consent. The conducted research reported in this article is in accordance with this approved Dartmouth-Hitchcock Health IRB protocol and the World Medical Association Declaration of Helsinki on Ethical Principles for Medical Research involving Human Subjects.

4.2. Celiac Disease Dataset

Celiac disease (CD) is a disorder that is estimated to impact 1% of the population worldwide [51,52]. Diagnosing and treating CD is clinically significant, as undiagnosed CD is associated with a higher risk of death [51,52]. A duodenal biopsy is considered the gold standard for CD diagnosis [53]. A pathologist examines these biopsies under a microscope to identify the histologic features associated with CD.

Our CD dataset comprises 1,364 patients distributed across the Normal, Non-specific Duodenitis, and Celiac Sprue classes. Each patient had one or more WSIs consisting of one or more tissues. A gastrointestinal pathologist diagnosed each slide as either Normal, Non-specific Duodenitis, or Celiac Sprue.

The CD slides contained significant amounts of white space background. Hence, as a pre-processing step, we used the tissueloc [54] code repository to find approximate bounding boxes around the relevant regions of the slide using a combination of image morphological operations. This tissue finding process aids in reducing the computational burden while simultaneously removing the clinically unimportant background regions.

We partitioned the dataset into a labeled set and an unlabeled auxiliary set. The auxiliary dataset (AD) is obtained by ignoring the labels. Our labeled dataset is comprised of 300 patients distributed uniformly across the Normal, Non-specific Duodenitis, and Celiac Sprue classes. A 70% training, 15% validation, and 15% testing split was produced by randomly partitioning the patients. In Table 2, we show the tissue counts for all datasets.

Table 2.

Distribution of the CD tissues for all datasets used in the model. The class counts for the self-supervised datasets ADv1 and ADv2 are only provided as a reference, and this class information was not used in the self-supervision process.

Class	Supervised			Self-Supervised
	Training	Validation	Testing	ADv1	ADv2 Development
Normal	1,182	253	241	4,774	16,661	441
Non-specific Duodenitis	2,202	390	469	130	265	583
Celiac Sprue	2,524	524	529	416	1,799	921

We randomly sampled from the CD slides not used in any training, validation, or testing datasets for self-supervision. To explore the effects of unlabeled dataset size, we created two auxiliary datasets, ADv1 and ADv2, such that$\text{ ADvl }\subset \text{ ADv2 }$. ADv1 and ADv2 are comprised of 300 and 1,004 patients, respectively. Experimenting with two unlabeled datasets allowed us to demonstrate the efficacy of our method as the dataset size scales. We also sampled an additional 20 patients from each class to use as a proxy development dataset for hyperparameter tuning. The 60-patient development dataset was intended to validate the self-supervision process and remained independent from the test set used for evaluation. The distribution for these datasets for self-supervised learning is shown in Table 2.

4.3. Lung Adenocarcinoma Dataset

Lung cancer is the leading cause of cancer death in the United States [55]. Of all histologic subtypes, lung adenocarcinoma (LUAD) is the most common pattern [56], and its rates continue to increase [57]. The World Health Organization identifies five predominant histologic pattern subtypes: lepidic, acinar, papillary, micropapillary, and solid for lung adenocarcinoma [58]. The classification of lung adenocarcinoma subtypes on histology slides has proven to be particularly challenging, as over 80% of cases contain mixtures of multiple patterns [59,60].

Our LUAD dataset was randomly split into two sets, with 235 slides for training and 34 slides for testing. A thoracic pathologist annotated both the training and testing sets for predominant subtypes, where every annotated tissue region contains only one pattern. Each slide in the training and testing set consists of at least one annotated tissue region. Some training and testing slides contained benign lung tissue, which we excluded as it is not related to the cancer subtypes. Given the considerably smaller size of this dataset compared to the CD dataset, we did not perform any experiments on varying unlabeled dataset sizes and used the entire training set for all analyses. No hyperparameter tuning was performed for this model, and we used the same configuration as the CD equivalent. The distribution of the LUAD data is presented in Table 3 for both training and testing sets.

Table 3.

Distribution of the LUAD tissues for all datasets used in the model. The counts correspond to the annotations provided by the pathologist.

Class	Training	Testing
Lepidic	514	81
Acinar	691	124
Papillary	43	9
Micropapillary	411	55
Solid	424	36

4.4. Renal Cell Carcinoma Dataset

Kidney cancer is one of the most common cancers worldwide [61]. Renal cell carcinoma (RCC) accounts for 90% of all kidney cancer diagnoses [61,62]. The major RCC subtypes are clear cell, papillary, and chromophobe in order of decreasing incidence [63]. It is critical to identify these histologic subtypes effectively as RCC incidence has been increasing over the past few decades and subtypes require different treatment strategies [64,65].

Our RCC dataset was randomly split into two sets, with 617 slides for training and 265 slides for testing. Renal pathologists classified all slides into one of the subtypes. Additionally, each slide may consist of more than one tissue. Like the CD dataset, we utilized the tissueloc [54] library to remove the significant white space background. We performed neither unlabeled dataset experimentation nor hyperparameter tuning and used the pre-determined hyperparameters from our CD experiments. The counts for all datasets and classes are shown in Table 4.

Table 4.

Distribution of the RCC tissues for all datasets used in the model. The counts correspond to the slide-level classifications provided by the pathologists.

Class	Training	Testing
Chromophobe	90	42
Papillary	312	128
Clear Cell	432	194

4.5. Implementation Details

We evaluated all models on the labeled test set corresponding to each training dataset. No data augmentation was applied to the test sets beyond standardizing the color channels by the mean and standard deviation of the respective labeled training sets. To evaluate our classification performance, we used accuracy, F1-score, precision, and recall. These metrics were computed in a one-vs.-rest fashion for each class. We computed the mean value for each metric by macro-averaging over all classes. The 95% confidence intervals (CIs) were produced using bootstrapping on the test set for 10,000 iterations. We calculate each model’s computational cost by counting the billions of floating-point operations (GFLOPS) for a forward pass of that model. Using the number of GFLOPS allows us to evaluate the performance gains while also considering the computational cost. All experiments were performed on either a single NVIDIA Titan RTX or Quadro RTX 8000 GPU.

Teacher Model.

We trained the teacher model on high-resolution input images at 10x magnification for CD and LUAD, and 5x for RCC. The He initialization scheme [66] was used to initialize the weights. We utilized the Adam optimization algorithm [47] for 100 epochs of training with a learning rate of 0.001. The Adam optimizer minimized the cross-entropy loss function with respect to the ground-truth slide labels.

Baseline.

All baseline models were trained on a specified magnification from randomly initialized weights using the He initialization scheme [66]. We used the same ResNet architecture as the teacher model for these baselines.

KD.

Our knowledge distillation (KD) approach consists of a teacher model described above and a student model of the same ResNet architecture. We initialize the student model using the He initialization scheme [66] and the teacher model using the saved weights. The teacher model weights are frozen and only the student model weights are updated during this phase. In contrast to the standard ResNet architecture, we use both the final convolutional and fully connected layer outputs as our unlabeled hints and feature recognition knowledge, respectively. We use the labeled training and validation sets for the distillation and ignore the labels in the self-supervised part of our approach. As explained in Section 3.4, we do not apply fine-tuning for these experiments as it contributes to overfitting according to our validation set.

KD (AD).

The knowledge distillation approach using the auxiliary datasets in this paper is similar to stock distillation [33]. The main difference is that we utilized unlabeled auxiliary datasets for self-supervised learning instead of using a labeled dataset.

5. RESULTS

In Table 5, we present the results of the teacher model trained from scratch at 10x magnification for the CD and LUAD test sets, and at 5x magnification for the RCC test set.

Table 5.

Results and the corresponding 95% CIs for the teacher model as percentages. The above results were obtained on the respective test sets, detailed in Sections 4.2, 4.3, and 4.4.

	CD	LUAD	RCC
Accuracy	87.06 (85.65–88.48)	94.51 (92.77–96.20)	90.16 (87.62–92.57)
F1-Score	75.44 (72.31–78.51)	80.43 (70.86–88.17)	80.09 (74.02–85.64)
Precision	75.62 (72.55–78.66)	80.41 (70.55–89.56)	78.54 (72.75–84.13)
Recall	77.15 (74.19–80.06)	81.67 (71.20–90.43)	85.19 (80.07–89.70)

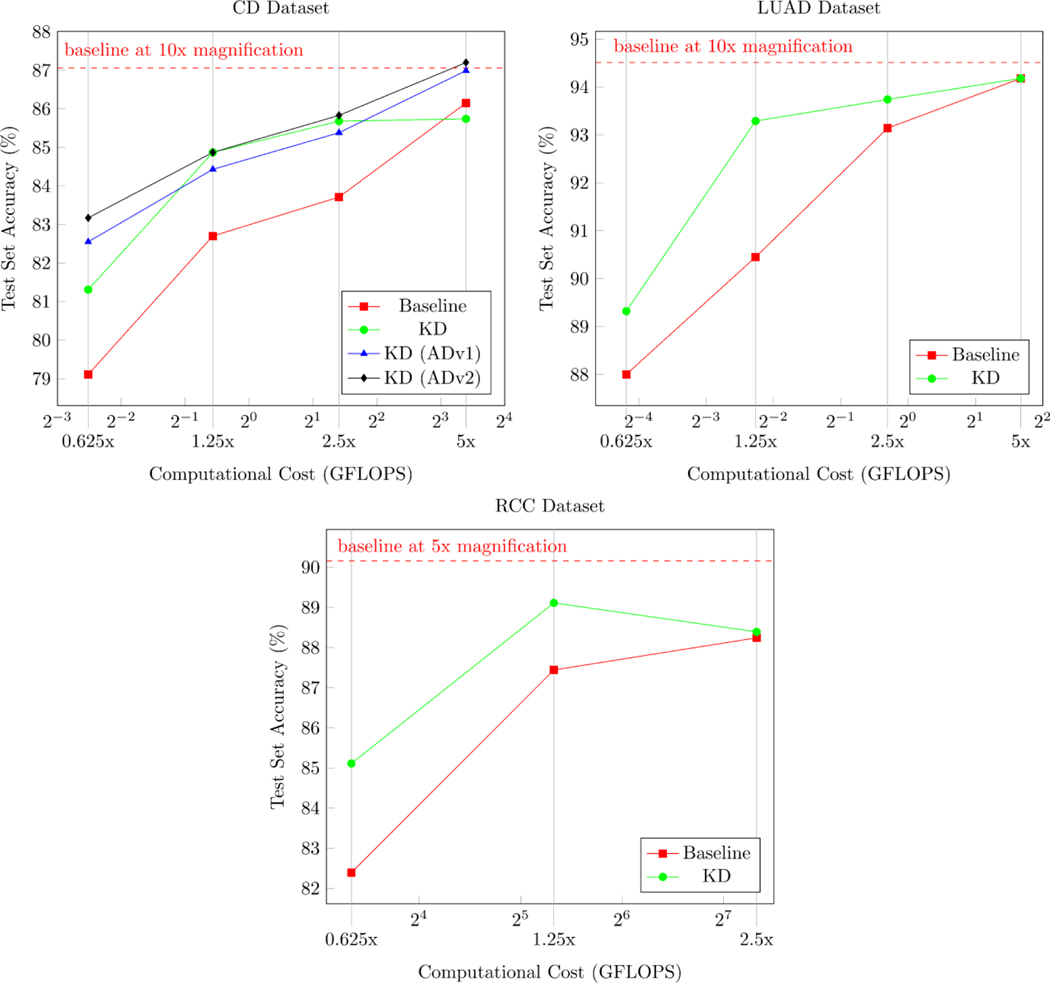
We present the results of our proposed approach for all tested magnifications in Tables 6, 7, and 8. The performance and computational costs of our models are shown in Figure 3. Additionally, we provide Grad-CAM++ visualizations in the Supplementary Material, Appendix C, to show that our method identifies clinically relevant features [67].

Table 6.

Results for celiac disease baseline and KD approaches as percentages with corresponding 95% CIs. Baseline models were trained from scratch until convergence on the corresponding magnification. The KD model without an auxiliary dataset was trained using the labeled dataset. Boldface text indicates the best-performing model for each magnification and metric.

	Celiac Disease
	Baseline	KD	KD (ADv1)	KD (ADv2)
mag = 0.625x (16 μm/pixel)
Accuracy	79.11 (77.74–80.54)	81.31 (79.91–82.72)	82.55 (81.15–83.97)	83.17 (81.75–84.61)
F1-Score	55.72 (52.08–59.34)	64.16 (60.92–67.37)	64.95 (61.43–68.45)	66.83 (63.46–70.14)
Precision	56.20 (52.40–59.96)	64.27 (60.91–67.56)	66.65 (62.94–70.32)	67.21 (63.78–70.52)
Recall	55.67 (52.17–59.16)	65.13 (62.06–68.20)	64.11 (60.64–67.61)	69.29 (66.06–72.42)
mag = 1.25x (8 μm/pixel)
Accuracy	82.70 (81.23–84.14)	84.03 (82.61–85.47)	84.43 (83.01–85.85)	84.87 (83.40–86.32)
F1-Score	65.06 (61.55–68.43)	70.49 (67.45–73.55)	69.75 (66.53–72.94)	71.20 (67.89–74.40)
Precision	65.06 (61.51–68.48)	70.53 (67.39–73.66)	69.32 (66.13–72.51	71.14 (67.81–74.35)
Recall	65.22 (61.70–68.63)	71.06 (68.10–74.02)	70.95 (67.72–74.17)	73.56 (70.40–76.61)
mag = 2.5x (4 μm/pixel)
Accuracy	83.71 (82.29–85.17)	85.68 (84.25–87.13)	85.38 (83.94–86.78)	85.83 (84.38–87.27)
F1-Score	68.32 (64.92–71.66)	73.01 (69.94–76.03)	72.39 (69.21–75.41)	73.56 (70.42–76.64)
Precision	68.23 (64.77–71.67)	74.74 (71.57–77.90)	72.99 (69.76–76.06)	73.61 (70.44–76.68)
Recall	68.57 (65.13–71.98)	74.67 (71.99–77.28)	75.67 (72.86–78.34)	76.43 (73.61–79.17)
mag = 5x (2 μm/pixel)
Accuracy	86.15 (84.71–87.61)	85.74 (84.28–87.21)	86.99 (85.54–88.46)	87.20 (85.78–88.62)
F1-Score	73.42 (70.15–76.63)	73.27 (70.19–76.33)	75.07 (71.89–78.17)	75.86 (72.71–78.92)
Precision	73.44 (70.12–76.68)	75.10 (71.91–78.23)	76.46 (73.42–79.44)	76.07 (72.95–79.13)
Recall	73.65 (70.41–76.93)	74.82 (72.16–77.51)	78.00 (75.18–80.72)	77.41 (74.41–80.35)

Table 7.

Results for lung adenocarcinoma baseline and KD approaches as percentages with corresponding 95% CIs. Baseline models were trained from scratch until convergence on the corresponding magnification. Boldface text indicates the best-performing model for each magnification and metric

	Lung Adenocarcinoma
	Baseline	KD
mag = 0.625x (16 μm/pixel)
Accuracy	88.00 (86.07–89.95)	89.32 (87.37–91.26)
F1-Score	54.38 (46.12–64.67)	57.75 (49.74–68.32)
Precision	57.75 (45.53–74.19)	60.95 (48.76–77.30)
Recall	55.98 (48.72–64.62)	58.29 (51.06–67.19)
mag = 1.25x (8 μm/pixel)
Accuracy	90.45 (88.52–92.40)	93.29 (91.44–95.09)
F1-Score	67.57 (56.49–77.07)	73.17 (63.03–82.70)
Precision	69.85 (55.79–80.25)	76.28 (62.54–87.58)
Recall	68.32 (58.07–78.98)	73.02 (63.99–83.26)
mag = 2.5x (4 μm/pixel)
Accuracy	93.14 (91.25–94.94)	93.74 (91.94–95.49)
F1-Score	72.84 (64.11–81.28)	71.88 (64.13–81.07)
Precision	72.03 (63.53–81.02)	73.56 (64.22–87.48)
Recall	75.51 (65.39–86.16)	72.69 (65.27–82.38)
mag = 5x (2 μm/pixel)
Accuracy	94.18 (92.40–95.85)	94.18 (92.45–95.85)
F1-Score	75.33 (66.30–84.23)	79.63 (69.80–87.41)
Precision	76.85 (66.27–88.75)	79.75 (69.62–88.88)
Recall	75.45 (66.74–85.65)	82.00 (71.36–90.62)

Table 8.

Results for renal cell carcinoma baseline and KD approaches as percentages with corresponding 95% CIs. Baseline models were trained from scratch until convergence on the corresponding magnification. Boldface text indicates the best-performing model for each magnification and metric

	Renal Cell Carcinoma
	Baseline	KD
mag = 0.625x (16 μm/pixel)
Accuracy	82.39 (79.80–85.02)	85.11 (82.45–87.83)
F1-Score	62.21 (55.38–68.97)	66.41 (59.35–73.31)
Precision	61.38 (54.99–67.89)	69.66 (63.31–75.99)
Recall	64.81 (57.33–72.37)	68.68 (61.32–75.66)
mag = 1.25x (8 μm/pixel)
Accuracy	87.44 (84.77–90.06)	89.11 (86.54–91.61)
F1-Score	73.73 (66.99–80.17)	77.10 (70.91–82.99)
Precision	72.38 (65.91–78.88)	75.66 (69.99–81.28)
Recall	76.73 (69.62–83.27)	82.64 (76.48–88.01)
mag = 2.5x (4 μm/pixel)
Accuracy	88.24 (85.72–90.76)	88.39 (85.74–90.92)
F1-Score	73.94 (67.87–79.84)	75.84 (69.57–81.71)
Precision	73.94 (67.87–79.84)	75.34 (69.70–80.85)
Recall	79.78 (73.25–85.74)	81.72 (76.06–86.76)

Figure 3.

Test set accuracy plotted against the computational cost. The computational cost is measured in GFLOPS and corresponds to the approximate number of floating-point operations per forward pass. The magnification of the model input data is displayed under the computational cost values.

6. DISCUSSION

As presented in Table 6, our KD method outperforms the baseline metrics in all trials for celiac disease. The lung adenocarcinoma results in Table 7 show that our approach improves performance for 0.625x (16 μm/pixel), 1.25x (8 μm/pixel), and 2.5x (4 μm/pixel) and is equal to the baseline performance for 5x (2 μm/pixel) input images. This outcome is consistent with our 5x results on the CD dataset without the AD self-supervision phase. As shown in Table 8, our method provides a benefit on all magnifications for renal cell carcinoma but decreases in performance at 2.5x magnification compared to 1.25x magnification. This result is consistent with the CD KD results without the auxiliary dataset.

While adding more data helped increase CD classification accuracy at 0.625x magnification by over 4%, this performance benefit narrowed as the magnification increased further. This trend can be seen in Figure 3, where the test set accuracy curves approach each other as the computational cost grows. Most importantly, our method outperforms the baseline at 10x magnification for the distillation approaches on the auxiliary dataset. This performance gain comes with at least a 4-factor reduction in computational cost.

Using our model to maintain accurate classification performance while minimizing computational cost could facilitate scanning histology slides at a much lower resolution. According to the Digital Pathology Association, scanners cost up to $300,000 depending on the configuration [68]. Reducing the scanning resolution could have a two-fold benefit, potentially lessening the scan time and scanner cost. To this end, histology slides could be scanned at a lower magnification and only inspected at higher magnification in challenging cases. In addition, storing and analyzing lower resolution WSIs would be less burdensome on the computational infrastructure. Instead of investing in complex data solutions, pathology laboratories could migrate to cloud-based services to manage and analyze smaller datasets using standard network bandwidth [69–71]. Using cloud solutions in the medical domain is still not widespread. However, our approach could provide a viable option for this emerging application.

There are still some improvement areas for our work, namely evaluating our model on additional datasets from different institutions. While our method was validated on three datasets, two of them are from our institution and may contain inherent biases in staining and slide preparation. Additionally, with more datasets, we would be able to investigate the scaling effects of self-supervised learning beyond the size of our existing dataset. The impact of scaling could prove especially useful for smaller healthcare facilities that may not have the capabilities to collect and label data as required for training a typical deep learning model for histology image analysis. In addition to larger datasets, it is crucial to explore the efficacy of this methodology on more slides from different medical centers and for various diseases to evaluate the generalizability of our proposed approach.

Although the trained models can be used on WSIs with lower resolutions, our method still requires high-resolution WSIs during training. While reducing the computational requirements of the inference stage is always beneficial, there is no reduction in cost for training the teacher model or the self-supervised and knowledge-distillation models. This weakness is an active area of investigation in our future work. One possibility is using transfer learning to adapt a pre-trained model to an alternative high-resolution histology dataset. A method that utilizes transfer learning in this fashion would remove the burden of continuously retraining teacher models for each new dataset. Lastly, we plan to extend our visualization beyond Grad-CAM++. While Grad-CAM++ provides some insight into the black-box model, it still lacks interpretability and crucial information for pathologists to make meaningful diagnoses.

7. CONCLUSION

This work demonstrated that knowledge distillation could be applied to histology image analysis and further improved by self-supervision. We showed that our method both improves performance at significantly lower computational cost and scales with dataset size. The empirical evidence presented proves that it is possible to transfer information learned across magnifications and still produce clinically meaningful results. Our approach allows for scanning WSIs at significantly lower resolution while having little to no classification accuracy degradation. Our method also removes a major computational bottleneck in using deep learning for histology image analysis and opens new opportunities for this technology to be integrated into the pathology workflow.

Highlights.

• Developed a deep learning model for low-resolution histology image classification

• Performed knowledge distillation to maintain accuracy at low-resolution

• Improved performance further using self-supervision on unlabeled data

• Achieved strong classification performance across multiple datasets and metrics