A generalized differential equation compartmental model of infectious disease transmission

Abstract

For decades, mathematical models of disease transmission have provided researchers and public health officials with critical insights into the progression, control, and prevention of disease spread. Of these models, one of the most fundamental is the SIR differential equation model. However, this ubiquitous model has one significant and rarely acknowledged shortcoming: it is unable to account for a disease's true infectious period distribution. As the misspecification of such a biological characteristic is known to significantly affect model behavior, there is a need to develop new modeling approaches that capture such information. Therefore, we illustrate an innovative take on compartmental models, derived from their general formulation as systems of nonlinear Volterra integral equations, to capture a broader range of infectious period distributions, yet maintain the desirable formulation as systems of differential equations. Our work illustrates a compartmental model that captures any Erlang distributed duration of infection with only 3 differential equations, instead of the typical inflated model sizes required by traditional differential equation compartmental models, and a compartmental model that captures any mean, standard deviation, skewness, and kurtosis of an infectious period distribution with 4 differential equations. The significance of our work is that it opens up a new class of easy-to-use compartmental models to predict disease outbreaks that do not require a complete overhaul of existing theory, and thus provides a starting point for multiple research avenues of investigation under the contexts of mathematics, public health, and evolutionary biology.

1. Introduction

The compartmental model of Kermack and McKendrick (Kermack and McKendrick, 1932, 1933, 1991) is arguably one of the greatest development in disease modeling. The formulation of this model, in its original form as a system of nonlinear Volterra integral equations (Diekmann et al., 1995), provides a general characterization of the transmission cycle between susceptible individuals and a disease that propagates throughout an environment (Brauer, 2010). Despite this generality, the vast majority of disease modelers prefer differential equation compartmental models (Blackwood & Childs, 2018). While this particular formulation of compartmental models has distinct advantages, such as the non-requirement of specialist knowledge for analysis and well-developed numerical methods for their computation (Roberts et al., 2015), they are a special case of the aforementioned system of nonlinear Volterra integral equations (Hethcote & Tudor, 1980). Specifically, one obtains traditional differential equation compartmental models (TDECM) from the nonlinear Volterra integral equations by imposing only two assumptions: 1) the “total infectivity at time $t$” (Brauer, 2008, 2010) corresponds to disease incidence, and 2) the duration of infection follows either an exponential or an Erlang distribution. Unfortunately, the vast majority of diseases do not have a duration of infection that follows these distributions (Bailey, 1956; Bailey & Others, 1975; Feng et al., 2007; Gough, 1977; Kelly-Hope & McKenzie, 2009; Lloyd, 2001), and force-fitting such a distributional structure is known to have a massive effect on the behavior and quality of model predictions (Earn, 2000). Regardless of these issues, the compartmental models obtained by the two traditional assumptions have undergone many extensions. A few noteworthy examples include modifying the force of infection to account for the saturation of infection in a population (Hethcote & van den Driessche, 1991; Ponciano & Capistrán, 2011), behavioral characteristics (Alexander & Moghadas, 2005; Liu et al., 1986, 1987; Ruan & Wang, 2003), modification of the recovery rate to capture disease burnout (Greenhalgh et al., 2015a), and the inclusion of additional disease stages (Hethcote & Tudor, 1980). Furthermore, the applications of these models have also grown considerably from just predicting a disease's trajectory. Today, these traditional compartmental models are used to evaluate the health benefits and cost-effectiveness of public health policies and disease interventions (Greenhalgh et al., 2015b, 2018), gauge the potential for disease virulence evolution (Day & Proulx, 2004), predict dominant influenza strains (Casagrandi et al., 2006), investigate the complexities of disease co-infection (Tchuenche et al., 2009), among many others. However, despite this growth in theory and application, the generalization of the very foundational assumptions that simplify systems of nonlinear Volterra integral equations to differential equation compartmental models remains largely undeveloped.

In what follows, we propose new assumptions to reduce nonlinear Volterra integral equations to differential equation compartmental models. The biological motivation for these new assumptions stems from the idea that the quantity of disease in a population may be described by person-days of infection, rather than disease incidence alone. Consequently, we extend current models from solely tracking disease incidence to tracking the number of person-days of infected individuals. To account for tracking person-days of infected individuals, we make the assumptions in our analysis that 1) the total infectivity at time $t$ corresponds to disease incidence and 2) the duration of infection is distributed according to a non-homogeneous analog of the exponential distribution. Under these assumptions, we derive a generalized differential equation compartmental models (GDECM) to track the flow of person-days susceptible to disease, person-days infected to disease, and person-days recovered from disease, in addition to providing model equilibria, and disease reproductive numbers (Heffernan et al., 2005).

Essential in the development of GDECM is the use of survival analysis (supplemental materials). Specifically, the development of GDECM requires the hazard function and the mean residual waiting-time of a distribution (Finkelstein, 2002a, 2002b; Gupta & Bradley, 2003) to describe a time-varying average duration of infection. With this in mind, we demonstrate the consistency of our GDECM to traditional compartmental models when the duration of infection follows an exponential distribution. We also demonstrate GDECM with an infectious period that follows an Erlang distribution and illustrate how this choice has a representation as either a system of 3 ODEs, regardless of the Erlang distribution parameters, or as a larger system of ODEs, which feature a chain of infected individual equations (Hurtado & Kirosingh, 2019; Krylova & Earn, 2013; Lloyd, 2001). Finally, we consider an infectious period that is Pearson distributed. In choosing the Pearson distribution, we develop a model that is capable of accounting for any possible mean, standard deviation, skewness, and kurtosis of the infectious period. Thereby, we provide a simple approach for measuring how altering the infectivity profile of a disease, as described by the first four statistical moments, influences the trajectory of the disease.

2. Methods

In what follows, we develop a GDECM to describe the progression of a disease throughout a population. To obtain such models, we impose new assumptions on the notion of the total infectivity at time $t$ (Brauer, 2008, 2010) used in the integral equations of Kermack and McKendrick. Before deriving GDECM, we briefly overview the quantity of person-days of infection, review the formulation of TDECM from the integral equations of Kermack and McKendrick, and then present the GDECM. In addition, we illustrate the behavior of GDCEM in the absence of transmission, provide equilibria, and their reproductive numbers.

2.1. The infectious period and duration of infection

To derive the duration of infection distribution from the infectious period distribution we consider data on newly infectious individuals, $I_{new}$, and characterize the infectious period by the survival function $Q\left(t,z\right)$. Thus, we obtain the number of infected individuals remaining infectious at time $x$ who where infected at time $z$ as

$$\hat{I}\left(x,z\right)=I_{new}\left(z\right)Q\left(x,z\right),x\ge z,$$

and the total number of infected individuals at time $x$ by

$$I\left(x\right)=I_{new}\left(0\right)Q\left(x,0\right)+\underset{0}{\overset{x}{\int }}{I}_{new}\left(w\right)Q\left(x,w\right)dw.$$

On the basis that $\hat{I}\left(x,z\right)/I\left(x\right)$ is a normalizing weight, we have that the conditional survival function of the duration of infection distribution for all currently infectious individuals with infection time prior to $x$ is

$$P\left(t,x\right)=\frac{\hat{I}\left(x,0\right)}{I\left(x\right)}Q(t,0|x,0)+\underset{0}{\overset{x}{\int }}\frac{\hat{I}\left(x,z\right)}{I\left(x\right)}Q(t,z|x,z)dz,$$ (1)

where $Q\left(t,z|x,z\right)=\frac{Q\left(t,z\right)}{Q(x,z)}$, and $t\ge x\ge z$.

Given the formulation of $P\left(t,x\right)$, we assume that the associated hazard rate (Clark et al., 2003a, 2003b; Finkelstein, 2002a, 2002b) does not depend on the time of infection $x$, namely

$$\eta \left(t\right)=-\frac{1}{P\left(t,x\right)}\frac{dP}{dt}\left(t,x\right),t\ge x.$$

Note, this is a slight generalization of the classical assumption for an exponentially distributed infectious period, as when $Q\left(t,0\right)=e^{-\gamma (t-0)},$ it follows that $Q\left(t,z|x,z\right)=e^{-\gamma (t-x)}$, and $P\left(t,x\right)=e^{-\gamma (t-x)}$. Thus, the hazard rate for an exponentially distributed infectious period is $\eta \left(t\right)=\gamma$. The generalization we consider is a non-homogeneous analog of the exponential distribution, namely $Q\left(t,0\right)=e^{-\underset{0}{\overset{t}{\int }}\eta \left(w\right)dw},$which implies $Q\left(t,z|x,z\right)=e^{-\underset{x}{\overset{t}{\int }}\eta \left(w\right)dw}$. Under such an assumed form of $Q(t,z)$, we have that $\frac{dP\left(t,x\right)}{dt}=-\eta \left(t\right)P(t,x)$, and the hazard rate naturally follows.

2.2. Person-days of infection

To provide insight on the quantity person-days of infection we consider a hypothetical epidemic. Solely for illustration purposes, we consider new incidence to be reported weekly (Fig. 1) and the infectious period to be at most 14 days (Fig. 2). Furthermore, akin to the assumption used in the work of Kermack and McKendrick (Brauer, 2008, 2010), we assume that new infections occur instantaneously at the end of each week. Given this setup, infectious individuals in a given week consist of newly infected individuals, and individuals that remain infectious from the prior week (Figs. 1 and 2).

Fig. 1.

New and total infectious individuals. New infectious individuals (solid line) and all infectious individuals (new and prior infectious individuals that are infectious) (dotted line).

Fig. 2.

Infectious periods. Infectious period distribution (top) and the conditional infectious period distribution for individuals whose infection lasts more than 7 days (bottom).

Under this setup, we estimate the duration of infection distribution $\frac{dP}{dt}\left(t,t_i\right)$ (Fig. 3) from a discretized version of (1),

$$P\left(t,t_i\right)\approx \frac{\hat{I}\left(t_i,0\right)}{I\left(t_i\right)}Q(t|t_i)+\sum _{j=i-1}^i\frac{\hat{I}\left(t_i,t_j\right)}{I\left(t_i\right)}Q(t-t_j|t_i-t_j),$$

where $t_i=i\text{Δ}t,$ $\text{Δ}t=1\text{week}$, and $t\ge t_i$.

Fig. 3.

Weekly duration of infection distribution. The duration of infection distribution and the average duration of infection (red bar) for the weeks 1–15. Each duration of infection distribution is a weighted sum of the infectious period distribution and conditional infectious period distribution, where the weights are based on the number of people currently and priorly infected with disease.

Given the duration of infection distributions for each week the person-days of infection are calculated as the area enclosed by the survival of the infected individuals from time $t_i$ (Fig. 4),

$$\underset{t_i}{\overset{\infty }{\int }}I\left(t_i\right)P\left(z,t_i\right)dz=I\left(t_i\right)m\left(t_i\right),$$

where $m\left(t_i\right)$ is the mean residual waiting-time of infection (Gupta & Bradley, 2003) in the $i^{th}$ week.

Fig. 4.

Person-days of infection. Grey regions correspond to the total days infected people spread disease over the course of an epidemic. Dark grey regions correspond to infectious individuals that remain infectious after one week. Mean residual waiting-time for the time spent infectious for each week (red line), average duration of infection (blue line).

One alternative to representing person-days of infection as the area enclosed by the survival of the infected individuals at time $t_i$ is by the product of the number of infected individuals and their mean residual waiting-time of infection at time $t_i$ (Fig. 5). The product $I\left(t_i\right)m\left(t_i\right)$ serves as the basis for constructing GDECM.

Fig. 5.

Person-days of infection. Rectangular red regions correspond to the same number of total days infected people potentially spread disease over the course of an epidemic. Blue rectangular regions illustrate over estimation of person-days of infection using average druation of infection. Mean residual waiting-time for the time spent infectious for each week (red line), average duration of infection (blue line).

2.3. Traditional compartmental models

Consider the general compartmental model of Kermack and McKendrick, as formulated by Brauer et al. (Brauer, 2010; Kermack and McKendrick, 1932, 1933, 1991). For this general compartmental model, the number of susceptible individuals are denoted as $S$, and the total infectivity at time $t$ is denoted as $\phi \left(t\right)$ (Brauer, 2008, 2010). We also define ${\phi }_0\left(t\right)$ as the total infectivity at time $t$ of the individuals initially infected with the disease at the beginning of the epidemic. Furthermore, the mean infectivity of an infected individual $t-x$ units of time after the start of the infection is $\pi \left(t-x\right)$, where $0\le \pi \left(t-x\right)\le 1$, and the mean infectivity of individuals in the population at time $t$ who where initially infected at time $x$ as

$$A\left(t,x\right)=\pi \left(t-x\right)P\left(t,x\right).$$

For simplicity, we assume a constant mean infectivity, $\pi \left(t-x\right)=1$. Given that transmission is a function of both shedding rate and behavior, it would be difficult to quantify changes in mean infectivity throughout an infection. Therefore, the progression of an epidemic throughout a population is described with the integral equations,

$$\begin{array}{l}S\left(t\right)=S_0-\underset{0}{\overset{t}{\int }}\lambda \left(x\right)S\left(x\right)dx,\\ \phi \left(t\right)={\phi }_0\left(t\right)+\underset{0}{\overset{t}{\int }}\lambda \left(x\right)S\left(x\right)P\left(t,x\right)dx.\end{array}$$ (2)

Here $\lambda$ is the force of infection, which we assume to be

$$\lambda \left(t\right)=\beta \frac{\phi \left(t\right)}{N},$$

where $\beta$ is the average number of contacts individuals in a population make per unit of time and $S_0$ is the initial number of susceptible individuals at the start of the epidemic.

Traditionally, to reduce (2) to a system of differential equations requires that the duration of infection is exponentially distributed, which yields that the conditional survival function is $P\left(t,x\right)=e^{-\gamma \left(t-x\right)},$where $\gamma$ is the recovery rate, or equivalently $1/\gamma$ is the average duration of infection, and 2) that the total infectivity at time $t$ corresponds to the number of infected individuals, $\phi \left(t\right)=I\left(t\right)$. Combining these assumptions, along with an additional compartment to track recovered individuals, $R,$ transforms system (2) into

$$\begin{array}{l}S\left(t\right)=S_0-\underset{0}{\overset{t}{\int }}\beta \frac{I\left(x\right)}{N}S\left(x\right)dx,\\ I\left(t\right)=I_0{e}^{-\gamma t}+\underset{0}{\overset{t}{\int }}\beta \frac{I\left(x\right)}{N}S\left(x\right)e^{-\gamma \left(t-x\right)}dx,\\ R\left(t\right)=\left(R_0+I_0-I_0{e}^{-\gamma t}\right)+\underset{0}{\overset{t}{\int }}\beta \frac{I\left(x\right)}{N}S\left(x\right)\left(1-e^{-\gamma \left(t-x\right)}\right)dx.\end{array}$$ (3)

Here $I_0$ and $R_0$ represent the total number of infected individuals and removed individuals at the start of the epidemic. An important feature of system (3) is that it conserves the total population:

$$S\left(t\right)+I\left(t\right)+R\left(t\right)=S_0+I_0+R_0=N.$$

Differentiating system (3) with respect to $t$, and substituting the integral equation for$I\left(t\right)$ for the remaining integrals yields the classic SIR system (Fig. 6):

$$\begin{array}{l}{S}^{\prime }\left(t\right)=-\beta \frac{I\left(t\right)}{N}S\left(t\right),\\ I^{\prime }\left(t\right)=\beta \frac{I\left(t\right)}{N}S\left(t\right)-\gamma I\left(t\right),\\ R^{\prime }\left(t\right)=\gamma I\left(t\right).\end{array}$$ (4)

Fig. 6.

Compartmental diagrams. a) Flow of suscpetible person-days to infected person-days and recovered person days, and b) Flow of suscpetible persons to infected persons and recovered persons.

Alternatively, (2) reduces to a system of differential equations when the duration of infection follows an Erlang distribution, with the conditional survival function

$$P\left(t,x\right)=\sum _{j=0}^{k-1}\frac{{\left(\gamma \left(t-x\right)\right)}^j}{j!}{e}^{-\gamma \left(t-x\right)},t\ge x,$$

where $k$ is a shape parameter that determines the total number of infection stages, $\frac{1}{\gamma }$ is the average duration spent in each stage, and 2) the total infectivity of the disease corresponds to $k$ identical stages (in terms of the average duration spent in each stage) of infected individuals,

$$\phi =I=\sum _{j=1}^k{I}_j.$$

Combining these assumptions, along with an additional compartment to track recovered individuals, $R,$ transforms system (1) into

$$\begin{array}{l}S\left(t\right)=S_0-\underset{0}{\overset{t}{\int }}\beta \frac{I\left(x\right)}{N}S\left(x\right)dx,\\ I\left(t\right)=I_0\sum _{j=0}^{k-1}\frac{{\left(\gamma t\right)}^j}{j!}{e}^{-\gamma t}+\underset{0}{\overset{t}{\int }}\beta \frac{I\left(x\right)}{N}S\left(x\right)\sum _{j=0}^{k-1}\frac{{\left(\gamma \left(t-x\right)\right)}^j}{j!}{e}^{-\gamma \left(t-x\right)}dx,\\ R\left(t\right)=R_0+I_0-I_0\sum _{j=0}^{k-1}\frac{{\left(\gamma t\right)}^j}{j!}{e}^{-\gamma t}+\underset{0}{\overset{t}{\int }}\beta \frac{I\left(x\right)}{N}S\left(x\right)\left(1-\sum _{j=0}^{k-1}\frac{{\left(\gamma \left(t-x\right)\right)}^j}{j!}{e}^{-\gamma \left(t-x\right)}\right)dx.\end{array}$$ (5)

Equivalently, if the linear chain trick is applied (see supplemental materials for details) (Lloyd, 2001), we have that

$$I_j\left(t\right)=I_j\left(0\right)\frac{{\left(\gamma t\right)}^{j-1}}{\left(j-1\right)!}{e}^{-\gamma t}+\underset{0}{\overset{t}{\int }}\beta \frac{I\left(x\right)}{N}S\left(x\right)\frac{{(\gamma (t-x))}^{j-1}}{\left(j-1\right)!}{e}^{-\gamma \left(t-x\right)}dx,$$

where $I\left(t\right)=\sum _j{I}_j\left(t\right).$

An important feature of system (5) is that it conserves the total population:

$$S\left(t\right)+I\left(t\right)+R\left(t\right)=S_0+\sum _j{I}_{0,j}+R_0=N.$$

Differentiating system (5) with respect to $t$, and substituting $\gamma I_j\left(t\right)$ as needed yields the classic SI^kR system:

$$\begin{array}{l}{S}^{\prime }\left(t\right)=-\beta \frac{I\left(t\right)}{N}S\left(t\right),\\ I_1^{\prime }\left(t\right)=\beta \frac{I\left(t\right)}{N}S\left(t\right)-\gamma I_1\left(t\right),\\ I_j^{\prime }\left(t\right)=\gamma I_{j-1}\left(t\right)-\gamma I_j\left(t\right),\\ R^{\prime }\left(t\right)=\gamma I_k\left(t\right),\end{array}$$ (6)

where $I\left(t\right)=\sum _{j=1}^k{I}_j\left(t\right).$

2.4. Generalized differential equation compartmental models

Before presenting the GDECM, we briefly contextualize its differences in comparison to traditional compartmental models. The traditional compartmental models of (4), (6) track the changes in the number of individuals susceptible, infected, and recovered from disease, for a disease circulating in a population. For traditional compartmental models, the individuals infected with disease recover from infection at a constant rate, $\gamma$, which is analgous to a constant average duration of infection of $1/\gamma$ (Fig. 1). The premise of GDECM is to consider tracking the change in the number of person-days of infection (Fig. 2). Specifically, we characterize person-days of infection as the individuals infected with a disease multiplied by their average duration of time spent in the infected state at time $t$ (Fig. 1).

To obtain GDECM, we generalize the assumptions used to formulate system (5). We first assume the total infectivity at time $t$ is the number of infected individuals at time $t:$

$$\phi \left(t\right)=I\left(t\right),$$

In addition, we assume that the duration of infection distribution corresponds to a non-homogeneous analog of the exponential distribution, as given by the conditional survival function

$$P\left(t,x\right)=e^{-\underset{x}{\overset{t}{\int }}\eta \left(z\right)dz},$$ (7)

where $t\ge x$.

The rate of removal from the infectious state, $\eta \left(t\right)$, is directly linked to the mean residual waiting-time $m\left(t\right)$. Specifically, one can determine $\eta \left(t\right)$ from $m\left(t\right)$ through

$$\eta \left(t\right)=\frac{m^{\prime }\left(t\right)+1}{m\left(t\right)},$$

and the reciprocal relationship by

$$m\left(t\right)=\mu -t+g\left(t\right)\eta \left(t\right),$$ (8)

provided that $g\left(t\right)$ satisfies (Gupta & Bradley, 2003)

$$g^{\prime }\left(t\right)\frac{dP}{dt}+g\left(t\right)\frac{d^{2}P}{d{t}^2}=\left(\mu -t\right)\frac{dP}{dt}.$$

The functions $\eta \left(z\right)$ and $m\left(z\right)$ possess the standard properties of hazard rates and mean residual waiting-time functions, including $\eta \left(z\right)\ge 0,m\left(z\right)\ge 0,m^{\prime }\left(z\right)\le 0,$and $m\left(0\right)=\mu$ (Finkelstein, 2002a, 2002b).

Under this setup, we consider person-days susceptible to disease, person-days infectious with disease, and person-days recovered from disease to be governed by,

$$\begin{array}{l}S\left(t\right)m\left(t\right)=Nm\left(t\right)-\left(N-S_0\right)\mu -\underset{0}{\overset{t}{\int }}\lambda \left(x\right)m\left(x\right)S\left(x\right)dx,\\ I\left(t\right)m\left(t\right)=I_{0}P\left(t,0\right)\mu +\underset{0}{\overset{t}{\int }}\lambda \left(x\right)m\left(x\right)S\left(x\right)P\left(t,x\right)dx,\\ R\left(t\right)m\left(t\right)=\left(R_0+I_0-I_{0}P\left(t,0\right)\right)\mu +\underset{0}{\overset{t}{\int }}\lambda \left(x\right)m\left(x\right)S\left(x\right)\left(1-P\left(t,x\right)\right)dx,\end{array}$$ (9)

where $m\left(0\right)=\mu$ by definition (Finkelstein, 2002a, 2002b), $\lambda \left(x\right)$ is the force of infection, and $P\left(t,x\right)$ is given by (5).

Adding the equations of system (9) together, it follows that

$$\left(S\left(t\right)+I\left(t\right)+R\left(t\right)-N\right)m\left(t\right)=\left(S_0+I_0+R_0-N\right)\mu .$$

Thus, given $N=S_0+I_0+R_0$ and $m\left(t\right)\ne 0$ for all $t$, we have that the total population is conserved:

$$S\left(t\right)+I\left(t\right)+R\left(t\right)=N.$$

Imposing (7) on (9), taking the time derivative of system (9), assuming $\lambda \left(x\right)=\beta \frac{I\left(x\right)}{N}$ and applying Leibniz rule for the derivatives of integrals as needed, we obtain

$$\begin{array}{l}{S}^{\prime }\left(t\right)m\left(t\right)+S\left(t\right)m^{\prime }\left(t\right)=N{m}^{\prime }\left(t\right)-\beta \frac{I\left(t\right)}{N}m\left(t\right)S\left(t\right),\\ I^{\prime }\left(t\right)m\left(t\right)+I\left(t\right)m^{\prime }\left(t\right)=-\eta \left(t\right)I_{0}P\left(t,0\right)\mu -\eta \left(t\right)\underset{0}{\overset{t}{\int }}\beta \frac{I\left(x\right)}{N}m\left(x\right)S\left(x\right)P\left(t,x\right)dx\\ +\beta \frac{I\left(t\right)}{N}m\left(t\right)S\left(t\right),\\ R^{\prime }\left(t\right)m\left(t\right)+R\left(t\right)m^{\prime }\left(t\right)=\eta \left(t\right)I_{0}P\left(t,0\right)\mu +\eta \left(t\right)\underset{0}{\overset{t}{\int }}\beta \frac{I\left(x\right)}{N}m\left(x\right)S\left(x\right)P\left(t,x\right)dx,\end{array}$$ (10)

where $P\left(t,x\right)$ is given by (7).

Substituting (9) into (10) to eliminate the integrals, and isolating for each of $S^{\prime }m+S{m}^{\prime }$, $I^{\prime }m+I{m}^{\prime }$, and $R^{\prime }m+R{m}^{\prime }$, we obtain the compartmental model (Fig. 6):

$$\begin{array}{l}{S}^{\prime }\left(t\right)m\left(t\right)+S\left(t\right)m^{\prime }\left(t\right)=N{m}^{\prime }\left(t\right)-\beta \frac{I\left(t\right)}{N}m\left(t\right)S\left(t\right),\\ I^{\prime }\left(t\right)m\left(t\right)+I\left(t\right)m^{\prime }\left(t\right)=\beta \frac{I\left(t\right)}{N}m\left(t\right)S\left(t\right)-\left(\frac{m^{\prime }\left(t\right)+1}{m\left(t\right)}\right)I\left(t\right)m\left(t\right),\\ R^{\prime }\left(t\right)m\left(t\right)+R\left(t\right)m^{\prime }\left(t\right)=\left(\frac{m^{\prime }\left(t\right)+1}{m\left(t\right)}\right)I\left(t\right)m\left(t\right).\end{array}$$ (11)

By construction, system (11) is similar to its TDECM counterpart. However, there are some subtle differences. The terms involving $m^{\prime }\left(t\right)$ on the left-hand side do not represent inflows that increase the number of susceptible, infected, or recovered individuals. These terms, which are non-positive due to $m^{\prime }\left(t\right)\le 0$ (Finkelstein, 2002a, 2002b; Gupta & Bradley, 2003), account for the change in person-days caused by a decrease in the average duration of infection. In a similar manor, the term $N{m}^{\prime }\left(t\right)$ on the right-hand side does not represent an inflow of susceptible individuals, as it accounts for the change in scale of total person-days over time.

2.5. Behavior in the absence of transmission

In the absence of transmission ($\beta =0$), the infectious equation in (11) reduces to

$$I^{\prime }\left(t\right)m\left(t\right)+I\left(t\right)m^{\prime }\left(t\right)=-\left(\frac{m^{\prime }\left(t\right)+1}{m\left(t\right)}\right)I\left(t\right)m\left(t\right).$$

Solving for $I\left(t\right)$, it follows that

$$I\left(t\right)=I_0\exp \left(-\underset{0}{\overset{t}{\int }}\frac{2m^{\prime }\left(z\right)+1}{m\left(z\right)}dz\right)=I_{0}P\left(t,0\right)\exp \left(-\underset{0}{\overset{t}{\int }}\frac{m^{\prime }\left(z\right)}{m\left(z\right)}dz\right).$$

Note, the extra factor $\exp \left(-\underset{0}{\overset{t}{\int }}\frac{m^{\prime }\left(z\right)}{m\left(z\right)}dz\right)$ originates from $I\left(t\right)m^{\prime }\left(t\right)$, and thus reflects the time variability in the mean residual waiting-time of the initially infected individuals.

2.6. Equilibria, the basic reproductive number ${\mathcal{R}}_0$, and the effective reproductive number ${\mathcal{R}}_{\mathit{e}}$

The compartmental model (11) potentially have several equilibria. As is standard, (11) possess the standard disease-free equilibrium:

$$S^{\ast }=N,I^{\ast }=0,R^{\ast }=0.$$ (12)

In addition, an equilibrium where the infection was exhausted, leaving susceptible individuals that escaped infection, and recovered individuals:

$$\hat{S}=S_{\infty },\hat{I}=0,\hat{R}=R_{\infty }.$$ (13)

Turning our attention to the reproductive numbers of the disease, we consider the basic reproductive number using the next-generation method (van den Driessche & Watmough, 2002; van den Driessche, 2017), where $\mathcal{F}=\left(\frac{\beta }{N}S\right)$ and ${\mathcal{V}}^{-1}=\left(\frac{m\left(t\right)}{m^{\prime }\left(t\right)+1}\right).$ It follows that

$${\mathcal{R}}_0=\rho \left({\mathcal{F}|}_{DFE}\cdot {{\mathcal{V}}^{-1}|}_{DFE}\right)=\beta \frac{m_{DFE}}{m_{DFE}^{\text{'}}+1}.$$ (14)

Here $\rho (\cdot )$ is the spectral radius, ${\mathcal{F}|}_{DFE}\cdot {\mathcal{V}}_{DFE}^{-1}$ is the next-generation matrix evaluated at the disease-free equilibrium, and $m_{DFE}\in \left[\underset{\text{t}\to \infty }{\lim }m\left(t\right),m\left(0\right)\right]$ is the constant value of $m\left(t\right)$ at the disease-free equilibrium.

Following a similar setup, we consider the effective reproductive number, in the face of time variability of $m\left(t\right),$ to be

$${\mathcal{R}}_e\left(t\right)=\beta \frac{m\left(t\right)}{m^{\prime }\left(t\right)+1}\frac{S\left(t\right)}{N}.$$ (15)

To summarize, in this section we illustrated that GDECM possesses similar biological properties to TDCEM. Specifically, GDECM's behavior in the absence of transmission, its ability to conserve the total population, equilibria, and reproductive numbers all closely resemble similar features in TDCEM. Therefore, to further compare GDECM with TDECM, in the following section we consider the GDECM based on the duration of infection distributions of TDECM, namely the exponential or Erlang distributions, before demonstrating that GDECM exists for infectious periods that are Pearson distributed.

3. Special cases of GDECM

We now consider the duration of infection distributions used in traditional differential equation compartmental models to obtain systems of differential equations, namely the exponential distribution, and the Erlang distribution. In addition, we illustrate a GDECM that accounts for any mean, standard deviation, skewness, and excess kurtosis, by assuming that the duration of infection is Pearson distributed.

3.1. The exponential distribution

Assuming the infectious period is exponentially distributed, $Q\left(t\right)=e^{-\gamma t},$ then the duration of infection is also exponentially distributed, and the conditional survival function for the epidemic is $P\left(t,x\right)=e^{-\gamma \left(t-x\right)}$. Under this assumption, we have that (Gupta & Bradley, 2003),

$$\eta \left(t\right)=-\frac{1}{P\left(t,x\right)}\frac{dP(t,x)}{dt}=\gamma ,$$ (16)

and

$$g\left(t\right)=\frac{1}{\gamma }t.$$ (17)

Solving (8) under the assumption of (17) yields,

$$m\left(t\right)=\frac{1}{\gamma }.$$ (18)

Substituting (18) into (11), and multiplying through by $\gamma$, we arrive at the traditional compartmental models:

$$\begin{array}{l}{S}^{\prime }\left(t\right)=-\beta \frac{I\left(t\right)}{N}S\left(t\right),\\ I^{\prime }\left(t\right)=\beta \frac{I\left(t\right)}{N}S\left(t\right)-\gamma I\left(t\right),\\ R^{\prime }\left(t\right)=\gamma I\left(t\right).\end{array}$$ (19)

Finally, because $m\left(t\right)=\frac{1}{\gamma }=m\left(0\right)=\mu ,$the basic reproductive number obtained by next-generation method (van den Driessche, 2017) is

$${\mathcal{R}}_0=\frac{\beta }{\gamma }$$ (20)

3.2. The Erlang distribution

If the infectious period is Erlang distributed with survival function $Q\left(t\right)=\sum _{j=0}^{k-1}\frac{{\left(\gamma t\right)}^j}{j!}{e}^{-\gamma t}$, then necessarily $P\left(t,0\right)=Q\left(t\right)$. It follows that the associated conditional survival function of the duration of infection distribution is

$$P\left(t,x\right)={\left(\sum _{j=0}^{k-1}\frac{{\left(\gamma x\right)}^j}{j!}{e}^{-\gamma x}\right)}^{-1}\sum _{j=0}^{k-1}\frac{{\left(\gamma t\right)}^j}{j!}{e}^{-\gamma t},t\ge x.$$ (21)

Note, this formulation of $P\left(t,x\right)$ differs from that used in the derivation of TDECM, which bases $P\left(t,x\right)$ on the convolution of exponential random variables.

From (9), (21), we have that

$$\eta \left(t\right)={\left(\sum _{j=0}^{k-1}\frac{{\left(\gamma t\right)}^j}{j!}{e}^{-\gamma t}\right)}^{-1}\frac{\gamma {\left(\gamma t\right)}^{k-1}}{\left(k-1\right)!}{e}^{-\gamma t}={\left(\sum _{j=0}^{k-1}\frac{{\left(\gamma t\right)}^j}{j!}\right)}^{-1}\frac{\gamma {\left(\gamma t\right)}^{k-1}}{\left(k-1\right)!}.$$ (22)

Using $g\left(t\right)=\frac{1}{\gamma }t$ for an Erlang distribution (Gupta & Bradley, 2003), it follows from (8) that the mean residual waiting-time: $m\left(t\right)=\frac{k}{\gamma }-t+\frac{1}{\gamma }t{\left(\sum _{j=0}^{k-1}\frac{{\left(\gamma t\right)}^j}{j!}\right)}^{-1}\frac{\gamma {\left(\gamma t\right)}^{k-1}}{\left(k-1\right)!}.$

For the ease of presentation, we rewrite $m\left(t\right)$and its derivative with respect to $t$ as

$$m\left(t\right)=\frac{k}{\gamma }-t+\frac{1}{\gamma }\frac{{\left(\gamma t\right)}^k}{\text{Γ}\left(k,\gamma t\right)}{e}^{-\gamma t}$$

and

$$m^{\prime }\left(t\right)=-1+\left(\frac{{\left(\gamma t\right)}^k{e}^{-\gamma t}}{\text{Γ}\left(k,\gamma t\right)}+\gamma t-k\right)\frac{{\left(\gamma t\right)}^{k-1}}{\text{Γ}\left(k,\gamma t\right)}{e}^{-\gamma t}.$$ (23)

Using (23) in system (11), where the left-hand sides are left as $\frac{d}{dt}\left(S\left(t\right)m\left(t\right)\right)$ and $\frac{d}{dt}\left(I\left(t\right)m\left(t\right)\right)$ for the ease of presentation, we obtain a compartmental model comprised of three equations, regardless of the value of $k$ from the Erlang distribution:

$$\begin{array}{l}\frac{d}{dt}\left(S\left(t\right)\left(\frac{k}{\gamma }-t+\frac{1}{\gamma }\frac{{\left(\gamma t\right)}^k}{\text{Γ}\left(k,\gamma t\right)}{e}^{-\gamma t}\right)\right)=N\left(-1+\left(\frac{{\left(\gamma t\right)}^k{e}^{-\gamma t}}{\text{Γ}\left(k,\gamma t\right)}+\gamma t-k\right)\frac{{\left(\gamma t\right)}^{k-1}}{\text{Γ}\left(k,\gamma t\right)}{e}^{-\gamma t}\right)-\beta \frac{I\left(t\right)}{N}\left(\frac{k}{\gamma }-t+\frac{1}{\gamma }\frac{{\left(\gamma t\right)}^k}{\text{Γ}\left(k,\gamma t\right)}{e}^{-\gamma t}\right)S\left(t\right),\\ \frac{d}{dt}\left(I\left(t\right)\left(\frac{k}{\gamma }-t+\frac{1}{\gamma }\frac{{\left(\gamma t\right)}^k}{\text{Γ}\left(k,\gamma t\right)}{e}^{-\gamma t}\right)\right)=\beta \frac{I\left(t\right)}{N}\left(\frac{k}{\gamma }-t+\frac{1}{\gamma }\frac{{\left(\gamma t\right)}^k}{\text{Γ}\left(k,\gamma t\right)}{e}^{-\gamma t}\right)S\left(t\right)-\left(\frac{\left(\frac{{\left(\gamma t\right)}^k{e}^{-\gamma t}}{\text{Γ}\left(k,\gamma t\right)}+\gamma t-k\right)}{\left(\frac{k}{\gamma }-t\right)e^{\gamma t}\frac{\text{Γ}\left(k,\gamma t\right)}{{\left(\gamma t\right)}^{k-1}}+t}\right)I\left(t\right),\\ \mathrm{a}\mathrm{n}\mathrm{d}\\ R\left(t\right)=N-S\left(t\right)-I\left(t\right),\end{array}$$ (24)

Alternatively, by applying the ‘linear chain trick’ (Hurtado & Kirosingh, 2019; Krylova & Earn, 2013; Lloyd, 2001) (supplemental materials) to the system of three equations, we equivalently characterize $\frac{d}{dt}\left(I\left(t\right)m\left(t\right)\right)$ as:

$$I_1^{\prime }\left(t\right)m\left(t\right)+I_1\left(t\right)m^{\prime }\left(t\right)=-\gamma I_1\left(t\right)m\left(t\right)+\frac{\beta }{N}\left(\sum _{i=1}^k{I}_i\left(t\right)\right)m\left(t\right)S\left(t\right){\left(\sum _{j=0}^{k-1}\frac{{\left(\gamma t\right)}^j}{j!}\right)}^{-1},$$ (25)

and

$$I_j^{\prime }\left(t\right)m\left(t\right)+I_j\left(t\right)m^{\prime }\left(t\right)=-\gamma I_j\left(t\right)m\left(t\right)+\gamma I_{j-1}\left(t\right)m\left(t\right)+\frac{\beta }{N}\left(\sum _{i=1}^k{I}_i\left(t\right)\right)m\left(t\right)S\left(t\right){\left(\sum _{i=0}^{k-1}\frac{{\left(\gamma t\right)}^i}{i!}\right)}^{-1}\frac{{\left(\gamma t\right)}^{j-1}}{\left(j-1\right)!}.$$ (26)

Thus, through (21), (22), and (24), we either reduce system (11) to a system of 3 differential equations based on an infectious period that is Erlang distributed, or through the ‘linear chain trick’ to a system of $k+2$ differential equations (i.e. (25)-(26), $S^{\prime }$ and $R^{\prime })$.

Note, an important distinction between (25)–(26) and the TDCEM analog is that new infections enter into any given infectious state because of the terms $\frac{\beta }{N}\left(\sum _{i=1}^k{I}_i\left(t\right)\right)m\left(t\right)S\left(t\right){\left(\sum _{i=0}^{k-1}\frac{{\left(\gamma t\right)}^i}{i!}\right)}^{-1}\frac{{\left(\gamma t\right)}^{j-1}}{\left(j-1\right)!}$, whereas the TDECM (6) requires all new infections to enter the first stage of infection.

In regards to the basic reproductive numbers, we have that

$$\begin{array}{l}\mathcal{F}=\frac{\beta }{N}m\left(t\right)S\left(t\right){\left(\sum _{i=0}^{k-1}\frac{{\left(\gamma t\right)}^i}{i!}\right)}^{-1}\left(\begin{array}{ll}\begin{array}{ll}1& 1\\ \gamma t& \gamma t\end{array}& \begin{array}{ll}\dots & 1\\ \dots & \gamma t\end{array}\\ \begin{array}{ll}⋮& ⋮\\ \frac{{\left(\gamma t\right)}^{k-1}}{\left(k-1\right)!}& \frac{{\left(\gamma t\right)}^{k-1}}{\left(k-1\right)!}\end{array}& \begin{array}{ll}⋮& ⋮\\ \frac{{\left(\gamma t\right)}^{k-1}}{\left(k-1\right)!}& \frac{{\left(\gamma t\right)}^{k-1}}{\left(k-1\right)!}\end{array}\end{array}\right),\\ \mathrm{a}\mathrm{n}\mathrm{d}\\ \mathcal{V}=\gamma m\left(t\right)\left(\begin{array}{ll}\begin{array}{cc}1& 0\\ -1& 1\end{array}& \begin{array}{lll}0& \dots & 0\\ 0& \ddots & ⋮\end{array}\\ \begin{array}{ll}⋮& \ddots \\ 0& \dots \\ 0& \dots \end{array}& \begin{array}{lll}\ddots & \ddots & \ddots \\ -1& 1& 0\\ \dots & -1& 1\end{array}\end{array}\right).\end{array}$$

Evaluating $\mathcal{F}$ and $\mathcal{V}$ at the disease-free equilibrium, and when $t=0$, it follows that

$$\rho \left({\mathcal{F}|}_{\begin{array}{l}DFE\\ t=0\end{array}}\cdot {{\mathcal{V}}^{-1}|}_{\begin{array}{l}DFE\\ t=0\end{array}}\right)=\beta \frac{k}{\gamma }.$$

and as $t\to \infty$, it follows that

$$\rho \left(\underset{\text{t}\to \infty }{\lim }{\mathcal{F}|}_{DFE}\cdot {{\mathcal{V}}^{-1}|}_{DFE}\right)=\beta \frac{1}{\gamma }.$$

Thus, depending on how the value of $m_{DFE}$ is defined, we have the basic reproductive number

$${\mathcal{R}}_0=\beta \frac{m_{DFE}}{m_{DFE}^{\prime }+1}\in \left[\beta \frac{1}{\gamma },\beta \frac{k}{\gamma }\right].$$ (29)

3.3. The Pearson distribution

If the infectious period is Pearson distributed, then the associated conditional survival function of the duration of infection distribution does not possess a general closed-form. Thus, we define the Pearson distribution by

$$\frac{d^2}{d{t}^2}P\left(t,x\right)=h\left(t;\mu ,\sigma ,{\gamma }_1,{\gamma }_2\right)\frac{d}{dt}P\left(t,x\right),$$ (30)

where

$$\begin{array}{l}h\left(t;\mu ,\sigma ,{\gamma }_1,{\gamma }_2\right)=\frac{\left(-12{\gamma }_1^2+10{\gamma }_2+12\right)\left(t-\mu \right)+\left({\gamma }_1{\gamma }_2+6{\gamma }_1\right)\sigma }{\left(3{\gamma }_1^2-2{\gamma }_2\right){\left(t-\mu \right)}^2-\sigma {\gamma }_1\left({\gamma }_2+6\right)\left(t-\mu \right)+\left(3{\gamma }_1^2-12-4{\gamma }_2\right){\sigma }^2}\\ =\frac{t-\mu -d}{c{\left(t-\mu \right)}^2+b\left(t-\mu \right)+a},\end{array}$$ (31)

with $a=\frac{{\sigma }^2\left(3{\gamma }_1^2-4{\gamma }_2-12\right)}{12{\gamma }_1^2-10{\gamma }_2-12},b=\frac{-\sigma {\gamma }_1\left({\gamma }_2+6\right)}{12{\gamma }_1^2-10{\gamma }_2-12},$ $c=\frac{3{\gamma }_1^2-2{\gamma }_2}{12{\gamma }_1^2-10{\gamma }_2-12},$and $d=\frac{\left({\gamma }_1{\gamma }_2+6{\gamma }_1\right)\sigma }{12{\gamma }_1^2-10{\gamma }_2-12}$.

Note, $\mu ,\sigma ,{\gamma }_1,$ and ${\gamma }_2$ are the mean, standard deviation, skewness, and excess kurtosis of the infectious period distribution (Gupta & Bradley, 2003; Pearson, 1893, 1895).

To obtain the mean residual waiting-time in terms of the hazard function, we have that (Gupta & Bradley, 2003; Papathanasiou, 1995):

$$g\left(t\right)=\frac{1}{1-2c}\left(a+b\left(t-\mu \right)+c{\left(t-\mu \right)}^2\right).$$ (32)

It follows from (18) that the mean residual waiting-time is:

$$m\left(t\right)=\mu -t+\left(\frac{1}{1-2c}\left(a+b\left(t-\mu \right)+c{\left(t-\mu \right)}^2\right)\right)\eta \left(t\right),$$ (33)

where $c\ne 1/2$.

To ensure the mean residual waiting-time is finite we apply l’H$\hat{\text{o}}$pital's rule, using the facts that $\underset{0}{\overset{t}{\int }}P\left(z,0\right)dz\to \mu ,P\left(t,0\right)\to 0,\frac{dP}{dt}\to 0,\frac{d^{2}P}{d{t}^2}\to 0$ as $t\to \infty$, to obtain

$$\underset{\text{t}\to \infty }{\lim }m\left(t\right)=\underset{\text{t}\to \infty }{\text{lim}}\frac{\mu -{\int }_0^{t}P\left(z,0\right)dz}{P\left(t,0\right)}=\underset{\text{t}\to \infty }{\text{lim}}-\frac{P\left(t,0\right)}{\frac{dP}{dt}}=\underset{\text{t}\to \infty }{\text{lim}}-\frac{\frac{dP}{dt}}{\frac{d^{2}P}{d{t}^2}}=\underset{\text{t}\to \infty }{\text{lim}}-\frac{1}{h\left(t;\mu ,\sigma ,{\gamma }_1,{\gamma }_2\right)}.$$ (34)

Thus, we require that $3{\gamma }_1^2-2{\gamma }_2=0$ to force the terms involving $t^2$ to drop out. Under this assumption, we have that

$$\underset{\text{t}\to \infty }{\text{lim}}-\frac{1}{h\left(t;\mu ,\sigma ,{\gamma }_1,\frac{3}{2}{\gamma }_1^2\right)}=\frac{1}{2}\sigma {\gamma }_1,$$ (35)

Given (35) we evaluate $\mathcal{F}$ and $\mathcal{V}$ at the disease-free equilibrium, as $t\to \infty$, yielding

$$\rho \left(\underset{\text{t}\to \infty }{\lim }{\mathcal{F}|}_{DFE}\cdot {{\mathcal{V}}^{-1}|}_{DFE}\right)=\beta \frac{1}{2}\sigma {\gamma }_1.$$ (36)

Similarly, evaluating $\mathcal{F}$ and $\mathcal{V}$ at the disease-free equilibrium when $t=0$, it follows that

$$\rho \left({\mathcal{F}|}_{\begin{array}{l}DFE\\ t=0\end{array}}\cdot {{\mathcal{V}}^{-1}|}_{\begin{array}{l}DFE\\ t=0\end{array}}\right)=\beta \mu .$$ (37)

It follows that the basic reproductive number is

$${\mathcal{R}}_0=\beta \frac{m_{DFE}}{m_{DFE}^{\prime }+1}\in \left[\beta \frac{1}{2}\sigma {\gamma }_1,\beta \mu \right],$$ (38)

depending on the value of $m_{DFE}$.

Note, the lower and upper bounds of (38) are consistent with the next-generation method estimate for the basic reproductive numbers (20) and (29), as the Erlang distribution has moments $\mu =\frac{k}{\gamma },\sigma =\frac{\sqrt{k}}{\gamma }$ and ${\gamma }_1=\frac{2}{\sqrt{k}}$, which implies $\frac{1}{2}\sigma {\gamma }_1=\frac{1}{\gamma }$.

To summarize, in this section, we illustrated GDECM is equivalent to TDECM when the duration of infection is exponentially distributed. In addition, GDECM is similar to TDECM when the duration of infection is Erlang distributed. Although, the GDECM advantageously possesses formulations as either a system of $k+2$ differential equations, as would be required from TDECM, or as a system of $3$ differential equations. We concluded by demonstrating GDECM exist for non-Erlang distributions, namely the family of Pearson distribution, and now provide an application of such a GDECM to describe measles transmission in Iceland in the next section.

4. Application of methodology

To illustrate the utility of our approach, we model measles outbreaks based on time series data of measles incidence in Iceland from 1924 to 1928 (Cliff et al., 1981), taking into account classical data on the infectious period of measles (Simpson, 1952).

We use sample moments of the mean, standard deviation, skewness, and kurtosis to estimate the infectious period distribution of measles, under the assumption that it is Pearson distributed, and compare the GDECM to a traditional compartmental model that features an infectious period that is Erlang distributed (Fig. 7).

Fig. 7.

Measles infectious period. Infectious period distribution based on observed incidence data (red dash-dot line), fit Pearson distribution (black solid line) based on sample moments $\overline{x}=6.01,s=2.26,{\hat{\gamma }}_1=0.39,{\hat{\gamma }}_2=3.22$, and fit Erlang distribution (blue dotted line) based a shape parameter of $n=6,$and rate parameter of $\tilde{\gamma }=0.999$.

For the GDECM we determine the duration of infection distribution (1). Assuming that $P\left(\tau ,t\right)$ is Pearson distributed with $g_2=\frac{3}{2}{g}_1^2$ (Fig. 8), it follows that the mean, standard deviation, skewness, and kurtosis are 5.98, 4.15, 1.62, and 3.93 days, respectively. Given these moments, the hazard rate and mean residual waiting-time naturally follow (Fig. 9). Finally, fitting system (11) to data using a least-squares procedure yields $\beta \approx 1.9061$ (Fig. 10).

Fig. 8.

Survival function for individuals initially infected at a given day throughout the epidemic.

Fig. 9.

Hazard rate $\eta \left(t\right)$ and mean residual waiting-time $m\left(t\right)$.

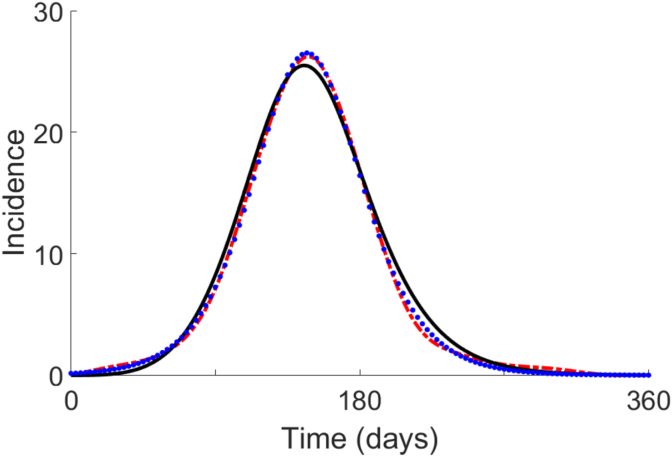
Fig. 10.

Predicted measles incidence in Reykjavik Iceland during 1924. Trajectories of incidence are based on interpolation of data (dash-dotted red line) (Cliff et al., 1981), and simulated trajectory with the GDECM (black solid line), and simulated trajectory with SI^kR model (blue dotted line).

When $P\left(\tau ,t\right)$ is Erlang distributed, we have that the mean and standard deviation are 5.98, and 2.44 days, respectively. Given these values, it follows that the classical SIR model, with a duration of infection that is Erlang distributed, is given by

$$\frac{dS}{dt}=-\frac{\tilde{\beta }}{N}\sum _{j=1}^n{I}_{j}S,\frac{d{I}_1}{dt}=\frac{\beta }{N}\sum _{j=1}^n{I}_{j}S-\tilde{\gamma }{I}_1,\frac{d{I}_k}{dt}=\tilde{\gamma }{I}_{k-1}-\tilde{\gamma }{I}_k,$$ (39)

where $n=6,\mu =5.98\text{days},\tilde{\gamma }=\frac{n}{\mu }$. From a least-squares fit (Fig. 10) we have that $\tilde{\beta }\approx 3.09,k\in \left\{1,\dots ,6\right\}$, where the total population of Reykjavik (in 1924) is estimated to be $N=24134$ (Greenhalgh & Day, 2017).

Given the model parameters, the possible range of basic reproductive number (36) of measles for the GDECM (11) given by the next-generation method is

$${\hat{\mathcal{R}}}_0\in \left[\frac{1}{2}\beta \sigma {\gamma }_1,\beta \mu \right]=\left[6.3291,11.3946\right],$$

and for the traditional compartmental model (39), we have that

$${\hat{\mathcal{R}}}_0=\tilde{\beta }\frac{n}{\tilde{\gamma }}=18.54.$$

5. Discussion

In this work, we presented a class of GDECM by modifying the classical assumptions that simplify nonlinear Volterra integral equations into systems of differential equations. To do this, we generalize the notion of compartmental models to describe person-days of infection, rather than infected persons. We illustrate the consistency of our class of models with traditional compartmental models for exponential and Erlang distributed infectious periods, present a new class of differential equation compartmental models based on a Pearson distributed infectious period, and provide equilibria and basic reproductive numbers for our approach.

The requirement that the duration of infection follows an exponential distribution is often a source of weakness with regards to the biological validity of differential equation compartmental models. While the extension of such models through the linear chain trick (Hurtado & Kirosingh, 2019; Krylova & Earn, 2013; Lloyd, 2001) to a duration of infection that follows the Erlang distribution alleviates this weakness to some degree, it does so at the cost of inflating the size of the compartmental model and thereby increasing the computational complexity of the system. Our new class of models avoids this inflation while retaining the benefits of having an infectious period that follows an Erlang distribution. Thereby our new class of models offers an approach to reduce model complexity in an era when the complexity of compartmental models is ever increasing. Furthermore, if one generalizes the concept of a function to include the survival function of the Gamma distribution, our new class of models advantageously accounts for any Gamma distribution parameter values, including non-integer cases.

A substantial advantage of the new class of models is that they are ODE based. Therefore, like traditional compartmental models, they do not require specialist knowledge to use and possess well-developed numerical methods for their simulation. Furthermore, the theoretical extensions of GDECM to include alternative formulations of the force of infection, state-dependent recovery rates, in addition to the inclusion of additional disease compartments are easy to implement. In addition, many of the applications of the traditional models, such as the study of multi-strain dynamics, health benefit analysis, and cost-effectiveness analysis, should naturally carry over without the need to reinvent the procedures of each analysis.

A potentially fruitful avenue for future applications of our new class of models is in the study of virulence and disease evolution. To elaborate, because GDECM includes both the quantity of infected individuals and their duration of infection, it may serve as a better paradigm for investigating selective pressures that pathogens face, at least relative to traditional compartmental models. Similarly, our idea to track both the quantity of infected individuals along with their duration of infection could be adapted to study species competition, as a similar modification should provide stronger intuition on species fitness.

A surprising outcome of our work is the discovery that the lower bound provided by the next-generation method estimate of the basic reproductive number for the Pearson distributed example depends on standard deviation and skewness, instead of the mean. As standard deviation and skewness indicate the spread and lean of a distribution, it seems reasonable that their combination makes for a decent proxy for the location of the middle of a distribution. While this could be a consequence of assuming that the duration of infection follows the Pearson distribution, it also highlights a potentially new approach to bound the basic reproductive number for a disease directly from data.

The use of an infectious period that is Pearson distributed may also open up an interesting avenue into bifurcation analysis. In particular, with modifications to incorporate demographic turnover or loss of immunity and the use of the Pearson distribution, one could investigate if a relationship exists between the occurrence of periodic cycles and the first four moments of the infectious period distribution. Thereby, one may be able to gain intuition as to whether bifurcations are likely to occur simply by examining statistical moments and the disease transmission rate. In addition, through such modified models, it may be possible to determine the existence (or non-existence) of Hopf bifurcations by examining whether $m\left(t\right)$ is periodic, as this seems like it would be a requirement for such behavior in reality. Additional avenues for investigation include the direct extension to periodic compartmental models (Wang & Zhao, 2008) through the use of some form of double truncated mean residual waiting-time (Khorashadizadeh et al., 2012), and a thorough comparison to renewal equations (Champredon et al., 2018), as such work would likely prove valuable for the study infectious disease dynamics.

As GDECMs are based on the integral equation versions of the Kermack and McKendrick model, they share this model's limitations. Namely, the assumptions of a sufficiently large and well-mixed population, the compartmentalization of diseases into distinct stages, and the transmission assumption of the law of mass-action. While these limitations may seem numerous, they do not impede research on traditional models, and thereby should not inhibit the theoretical extension and application of the broader class of models proposed here.

The traditional assumptions that reduce the integral equation version of the Kermack and McKendrick model to a system of differential equations provide disease modelers with a rich source for mathematical and scientific discovery. Here, we proposed a generalization of these traditional assumptions to a biologically more accurate description of the total quantity of a disease in a population. By imposing these new assumptions, we provide a more descriptive picture of how disease propagates throughout a population while retaining the convenience and simplicity of differential equation compartmental models.

Declaration of competing interest

The authors declare no conflict of interest.

Handling editor: Dr Lou Yijun

Author's contributions

Scott Greenhalgh: Conceptualization, Formal analysis, Writing – Original draft preparation, Reviewing and Editing. Carly Rozins: Formal analysis, Writing – Original draft preparation, Reviewing and Editing

Appendix A. Supplementary data

The following is the Supplementary data to this article: