Significance
Living cells rely on a continuous flux of energy to spatially organize biochemical processes. It remains unclear whether cells can achieve this spatial organization via thermodynamic principles. Here, we report the striking behavior of a cold-blooded organism that reacts to environmental temperature changes similar to a thermodynamic system at local equilibrium. Our key finding is that protein-rich droplets form and dissolve reversibly with temperature due to changes in the organism’s entropy. We show that the organism uses a specific molecule to extend droplet stability to the natural temperature range of the organism’s habitat. Due to the relevance of such protein droplets for the organism’s fertility, our work sheds light on how molecular components could facilitate biological functions via thermodynamic principles.
Keywords: P granules, phase separation, temperature, in vivo phase diagram
Abstract
Membraneless compartments, also known as condensates, provide chemically distinct environments and thus spatially organize the cell. A well-studied example of condensates is P granules in the roundworm Caenorhabditis elegans that play an important role in the development of the germline. P granules are RNA-rich protein condensates that share the key properties of liquid droplets such as a spherical shape, the ability to fuse, and fast diffusion of their molecular components. An outstanding question is to what extent phase separation at thermodynamic equilibrium is appropriate to describe the formation of condensates in an active cellular environment. To address this question, we investigate the response of P granule condensates in living cells to temperature changes. We observe that P granules dissolve upon increasing the temperature and recondense upon lowering the temperature in a reversible manner. Strikingly, this temperature response can be captured by in vivo phase diagrams that are well described by a Flory–Huggins model at thermodynamic equilibrium. This finding is surprising due to active processes in a living cell. To address the impact of such active processes on intracellular phase separation, we discuss temperature heterogeneities. We show that, for typical estimates of the density of active processes, temperature represents a well-defined variable and that mesoscopic volume elements are at local thermodynamic equilibrium. Our findings provide strong evidence that P granule assembly and disassembly are governed by phase separation based on local thermal equilibria where the nonequilibrium nature of the cytoplasm is manifested on larger scales.
Living cells use metabolic fuel in the form of adenosine triphosphate (ATP) or guanosine triphosphate (GTP) to express proteins, run enzymatic reactions, and maintain the activity of chaperones and molecular motors. These fuel-driven, metabolic processes keep cells away from thermodynamic equilibrium and thereby allow the assembly of functional assemblies and structures that are not possible at thermodynamic equilibrium. Despite the relevance of metabolic processes to the physiology of living cells, evidence is accumulating that the physics of phase separation provide a good description for the formation of many intracellular condensates. Potential candidates are protein–RNA condensates, such as P granules and stress granules, which assemble via phase separation in the cyto- or nucleoplasm in various different cell types (1–5). A decade ago, a seminal study in cell biology revealed that these condensates share the physical properties of phase-separated, liquid-like droplets (6). In a typical phase separation picture, different phases coexist at thermodynamic equilibrium. However, a cell uses a considerable amount of ATP and GTP, which is hydrolyzed to fuel enzymatic reactions. A particular example is DEAD-box ATPases (7), which were shown to promote phase separation in their ATP-bound form, whereas ATP hydrolysis induces compartment turnover and release of RNA (8). These metabolic processes raise the question of whether it is appropriate to use equilibrium thermodynamics to discuss the formation of condensates in living cells. Such questions also arise for individual molecules. For instance, molecular motors use ATP to move along cytoskeletal filaments (9). However, such motors operate isothermally because temperature fluctuations relax within nanoseconds at the nanometer scale of macromolecules (10). Thermodynamic phase coexistence requires at least the phase boundary to be locally at equilibrium. This is the basis of effective droplet models, where the thermodynamics of phase coexistence enter via boundary conditions at the interface (11). A key question is whether local equilibrium conditions are satisfied in a cell given the continuous consumption of fuel molecules such as ATP or GTP. Such questions can be tested by examining the response of condensates using temperature as a control variable for phase separation. Interestingly, qualitative experimental studies in the Caenorhabditis elegans roundworm suggest that P granule condensates can dissolve upon increasing the temperature and recondense when the temperature is lowered again (12, 13).
Here, we investigate the question of whether the temperature response of protein–RNA condensates can be understood by the thermodynamics of phase separation. We study P granule condensates in embryonic cells of the roundworm C. elegans, which is a cold-blooded organism that adapts and responds to the temperature of the environment (14) (Fig. 1A). We subject early one-cell embryos to temperature changes controlled by a thermostat and quantitatively analyze the dynamics of P granules. We show that this system can be described by a thermodynamic Flory–Huggins model for phase separation.
Fig. 1.
Illustration of a C. elegans roundworm and reversible P granule dissolution upon heating. (A) We consider the response of micrometer-sized P granules in the one-cell stage of the C. elegans embryo against temperature changes to exemplify the role of thermodynamics for the formation and dissolution of protein condensates in a living organism. (B) P granules labeled via PGL-1::GFP (yellow-green dots) dissolve upon heating and reform when cooled again within a few minutes in embryos as well as in parts of the gonad. (Scale bars, 50 [Left] and 10 [Right].)
Results
Reversible Condensation and Dissolution upon Temperature Changes.
Fig. 1B shows the response of P granules (labeled via PGL-1::GFP, which we refer to as wild type) in a C. elegans worm to a temperature shift from 15 to 29 °C and then down to 10 °C. P granules dissolve upon temperature increase and reform when cooled, in agreement with previous observations (12, 13). In addition, we see a similar behavior in parts of the gonad (distal tip, oocytes), while the pachytene region seems more robust against the transient temperature change. In the following experiments, we dissect single embryos from the worm for better imaging and mount them in a chamber with temperature controlled by a thermostat (SI Appendix, Fig. S1). To quantify the temperature response, we subjected embryos to repeated cycles of temperature increase and decrease (Fig. 2A). We were able to observe up to five cycles of dissolution and condensation showing that the formation of P granules in the C. elegans embryo is reversible over multiple cycles (Fig. 2A and Movie S1). Together with previous experiments, this suggests that P granules form and dissolve by thermodynamic phase separation.
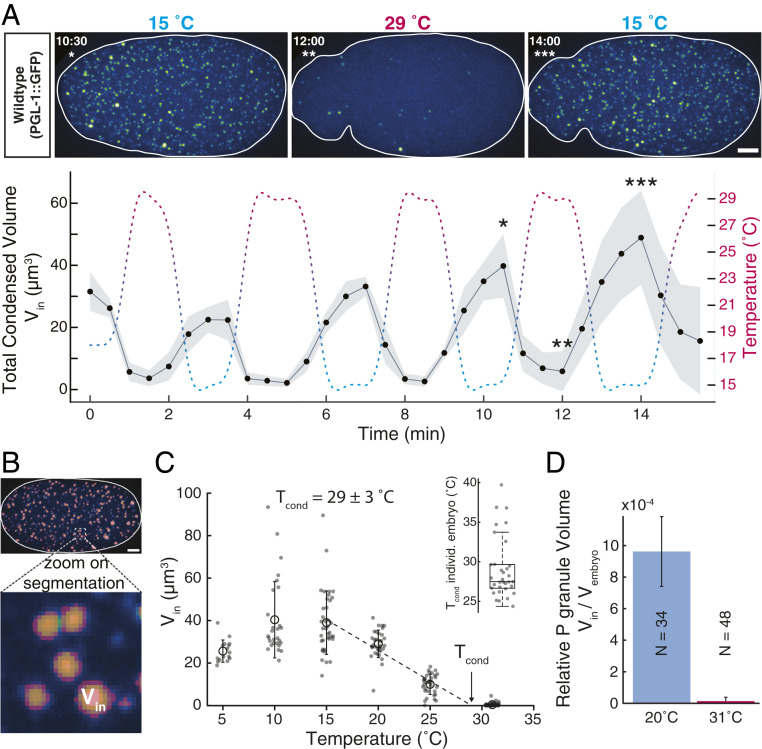
Fig. 2.
P granule volumes respond to temperature oscillations and determine the global condensation temperature. (A) Five oscillations in temperature from 15 to 29 °C cause an in-phase oscillation of the total condensed volume of P granules, (see example embryo going through one cycle, n = 4; shaded area is SD). (Scale bar: 5 .) The notable increase of total condensed volume with the number of cycles is likely due to the progress of one-cell embryos from an early homogeneous to a later polarized state. (B) Mask used to extract the P granule volumes from the microscope images (for details on image analysis, see Materials and Methods and SI Appendix). (C) The condensation temperature is defined as the temperature where the total volume averaged over all embryos becomes zero. (C, Inset) We obtain a very similar value for condensation temperature when extracting for each embryo and averaging over all considered embryos. (D) At °C condensates contribute to approximately of the volume of an embryo (, number of embryos per condition; error bars are SD). Around the dissolution temperature, the relative volume of P granule phase drops to values close to zero.
The response of a phase-separating system to temperature provides important information about a number of thermodynamic parameters. One important parameter is the temperature at which the system mixes/demixes, which we call the condensation temperature . This is the temperature at which the average concentration of PGL-1 equals the saturation concentration. Above this temperature the system stays undersaturated and no P granules form. Below this temperature the system is supersaturated and P granules form. As one approaches the condensation temperature from below, the total volume of P granules should decrease in a linear manner toward zero.
We determine the total P granule volume using a segmentation mask (Fig. 2B and Materials and Methods). Fig. 2C shows a linear decrease of between 15 and 30 °C, implying a condensation temperature for a wild-type C. elegans embryo of °C. Linear regression of for individual embryos leads to the same average value of °C as for the ensemble (Fig. 2 C, Inset). With an average embryo volume of about we find a relative volume of the condensed P granule phase of about 0.1% [Fig. 2D and SI Appendix, Fig. S2; constant ]. These experiments show that P granule formation in C. elegans embryos exhibits a well-defined condensation temperature and is consistent with thermodynamic phase separation.
In Vivo Phase Diagrams.
Other quantities that provide important information about a thermodynamic phase-separating system are the concentrations that coexist inside and outside a condensate at different temperatures. The lines connecting these concentrations define the binodals of the phase diagram. We determine the concentrations inside and outside of P granules in the embryo using fluorescence intensity and image analysis (Fig. 3A; details in Materials and Methods). A similar approach was used in ref. 15.
Fig. 3.
In vivo phase diagrams and P granule condensation temperatures. (A) Illustration of the mask to determine the concentrations inside and outside the P granule condensates. To avoid the impact of the blurred condensate interface (due to point spread function and pinhole cross-talk) on the calculation of the outside concentrations, we omit a domain around the interface. We determine the concentrations inside and outside as averages over the respective domains inside and outside of the omitted regions. (Scale bar: 5 .) (B) Phase diagram for GFP-labeled PGL-1 with equilibrium concentration outside (blue) and inside (yellow) separating demixed and mixed states. Concentrations are calculated from fluorescence intensities via a temperature-corrected scaling factor between intensities and concentration (SI Appendix, Fig. S4). Number of embryos with P granules out of the total number of recorded embryos as well as the total number of P granules at each temperature are shown. Dashed line is a guide to the eye. (C) Similar phase diagram to that in B but for a worm line where PGL-3 was genetically deleted, which is referred to as pgl-3 (SI Appendix, Fig. S5). (D) Condensation temperature for different worm strains: The dissolution temperature of the wild type with the GFP label on the PGL-1 or PGL-3 protein is very similar. In contrast, in the case of the pgl-3 line, P granules already dissolve at approximately 6 °C lower temperature (gray dots represent of individual embryos).
We find that the concentrations inside and outside the P granules relax quickly to steady-state values after a temperature change (SI Appendix, section 2). This fast relaxation to quasi-stationary concentration values suggests that P granules are at local equilibrium with their environment. More precisely, the inside and outside concentrations are at equilibrium at the P granule boundary. For temperatures between 5 and 31 °C, concentrations of PGL-1-GFP inside P granules vary between 13.2 and 5.3 , respectively, and those outside vary between 0.37 and 0.46 . These values imply that the partition coefficient of PGL-1 proteins decreases from 36 to 12 for increasing temperatures.
The concentrations measured inside and outside the P granules as a function of temperature define the binodals of phase separation, which can be represented as a phase diagram (Fig. 3B). The binodal on the right-hand side in Fig. 3B (orange) corresponds to the inside concentration, which varies more strongly with temperature than the outside concentration described by the left-hand binodal (blue). To understand P granule dissolution and condensation based on this phase diagram, we need to know the total average concentration of PGL-1 in the cell (vertical dotted line in Fig. 3B), which was determined by immunoblotting (SI Appendix, section 4). For low temperatures, the outside concentration is smaller than the total concentration. In this case the cytoplasm is supersaturated and P granules form by phase separation. At high temperatures, the local concentration outside of P granules at the P granule surface is higher than the total concentration. In this case, the cytoplasm is undersaturated and P granules dissolve. As discussed above, the outside and the total concentrations are equal at the condensation temperature of about 30 °C. These observations show that the temperature-dependent behavior of P granules in C. elegans can be described by a classical phase diagram. The fact that P granules dissolve upon heating suggests that this phase diagram has an upper critical solution temperature; see below.
PGL-3 Deletion.
P granules are multicomponent systems consisting of many different proteins and RNA. To shed light on the impact of the multicomponent nature of P granules on their temperature response, we studied the phase diagram of P granules in a deletion line where PGL-3, one of the main protein components, was removed (Materials and Methods and SI Appendix, section 3). We verified that the total concentration of PGL-1 stays approximately constant despite a full deletion of PGL-3 (SI Appendix, Fig. S3). The most prominent difference in temperature response of the pgl-3 line compared to the wild type is the decrease in dissolution temperature of about 6 °C to °C (Fig. 3 C and D). Thus, a lack of PGL-3 leads to a reduction of the temperature range of phase separation compared to wild type (Fig. 3D). The phase diagram of the pgl-3 line as a function of PGL-1 concentration is shown in Fig. 3C. In the phase diagrams, we find a pronounced reduction of the inside equilibrium concentration between 15 and 20 °C. The concentrations inside decrease from 12.9 to 2.1 while outside, concentration increases only from 0.40 to 0.52 in the range of 5 to 31 °C. These strong changes of the equilibrium concentration inside P granules highlight the significance of PGL-3 proteins for P granule phase separation. Comparing Fig. 3 B and C reveals that the presence of PGL-3 stabilizes the PGL-1 concentration inside P granules as a function of temperature in wild-type embryos. These observations are consistent with the idea that P granules form via a multicomponent phase separation at local thermodynamic equilibrium. We return to this point below.
Thermodynamics of In Vivo Phase Separation.
We propose a description for P granule phase separation based on local thermodynamic equilibrium. Quantifying intracellular phase separation using a single labeled protein component exhibits the general feature of binary phase separation resulting in a dense and a dilute phase. This phase separation can be captured by an effective free energy density , which depends on the effective volume fraction of the labeled component and on temperature . We thus introduce a binary Flory–Huggins model (16, 17) with the effective free energy per volume
| [1] |
where the effective molecular volume and the interaction strength can depend on temperature . Here, is a characteristic molecular volume of cytoplasmic molecules and the effective volume fraction is related to concentration .
The free energy density as a function of concentration given in Eq. 1 depends on temperature. For certain temperatures, the free energy can be shaped like a double well, as illustrated in Fig. 4 A, Top. This shape implies that a demixed state is thermodynamically favored for average concentrations between the equilibrium concentrations inside and outside (diamonds in Fig. 4A). In the case of an upper critical dissolution temperature, such equilibrium concentrations move closer to each other when the temperature is increased and they coincide at the critical point. For concentrations and temperature values outside the demixed domain in the phase diagram, condensates dissolve, while inside, condensates are thermodynamically stable (Fig. 4 A, Bottom).
Fig. 4.
Model results for temperature-dependent phase separation. (A) Free energy density as a function of concentration for two different temperatures indicating that the equilibrium concentrations inside and outside approach each other for increasing temperature (Upper). This trend is also reflected in the phase diagram in which the binodal line separates the mixed and the demixed phase (Lower). (B) From the experimental in vivo phase diagrams (Fig. 3 B and C), we obtain via fitting the temperature-dependent interaction parameter (orange dots) and the molecular volume (blue dots) for each coexisting concentration pair of PGL-1 concentrations. We parameterize each function by linear functions jumping discontinuously at a temperature around 16 °C. (C and D) The experimental phase diagrams (diamond symbols) agree with the binodals corresponding to the parameterized discontinuous functions from B (dashed lines) and the global fits (solid line) accounting for a smoothed-out discontinuity (see SI Appendix, section B for details). Black circles represent the critical points.
The free energy Eq. 1 can be used to relate the experimentally observed behaviors of phase separation with the physical parameters of the Flory–Huggins model. In particular, for a pair (i.e., inside and outside a P granule) of coexisting PGL-1 concentrations measured at temperature (Fig. 3 B and C), we can determine the effective interaction parameter and the effective molecular volume of PGL-1 using a Maxwell construction (gray lines Fig. 4A and SI Appendix, section 1). The resulting temperature dependencies of and are shown in Fig. 4B as circles. A key finding is that for wild type both quantities exhibit an approximately linear dependence on temperature. Interestingly, in the pgl-3 line, the effective interaction parameter and the molecular volume exhibit pronounced changes within the interval from about 15 to 20 °C. Such a pronounced change could be the signature of an additional first-order phase transition (18). The pronounced increase of the effective molecular volume suggests that the PGL-1 protein changes its conformation from a collapsed to a more open, coil-like state within this temperature interval. This transition may provide space for solvent molecules to enter the P granules, leading to a reduced PGL-1 concentration (Fig. 3C).
The experimentally determined phase diagrams shown in Fig. 3 B and C are limited to temperatures below the respective condensation temperatures because the average concentrations in the wild type and the pgl-3 embryo are fixed. To estimate the shape of the binodal line in regions where data are not available, we choose simple parametrizations of the temperature-dependent interaction parameters and the effective molecular volume (see Materials and Methods and SI Appendix, section 1B for details). For wild type we use linear relationships (dashed and solid orange lines in Fig. 4B). The binodal lines that correspond to these linear relationships are shown in Fig. 4C. The dashed lines are obtained from fits of linear functions to the data of and (effective parameter fit), while the solid lines are obtained by a fit of the calculated binodal to the concentration values in the phase diagram (binodal fit). For the pgl-3 line, we use an effective parameter fit based on a piecewise linear dependence of the parameters, which exhibits a jump at about 16 °C (dashed lines in Fig. 4 B and D). For the binodal fit we use a parametrization that connects the linear behaviors of and by a smooth function (see solid lines in Fig. 4 B and D and SI Appendix, section 1B for details). The binodal lines obtained by both the effective parameter fit and the binodal fit both follow closely the experimental data. Strikingly, the binary Flory–Huggins model can capture the experimentally determined phase separation behavior for both wild-type and pgl-3 embryos and suggests the existence of critical points at temperatures and concentrations that are outside the temperature range at which C. elegans can live and propagate (Fig. 4 C and D). The existence of a critical point at high temperatures corresponds to an upper critical solution temperature. This suggests that the observed dissolution of P granules upon temperature increase is governed by an increase in entropy as often observed in polymer solutions (19).
The experimental data show that the condensation temperature in the pgl-3 line is lower than in wild type (Fig. 3D). This lower condensation temperature means that PGL-3 enhances the effective attractive interactions among PGL-1 proteins. This effect of PGL-3 is also supported by the observation that PGL-1 and PGL-3 can directly interact in vitro and in vivo (20). Our Flory–Huggins model can be used to estimate the dependence of the condensation temperature on PGL-3 concentration by interpolating the temperature-dependent parameters and between wild type and the pgl-3 line (Fig. 4C; for details see SI Appendix, section 1C). Using the wild-type PGL-3 concentration of 0.96 , we obtain the condensation temperature as a function of PGL-3 concentration as shown in Fig. 5A. To experimentally test these predictions, we used RNA interference (RNAi) to reduce the PGL-3 concentration by ∼60% to 0.43 (see Materials and Methods for more details). We observe that reducing the amount of PGL-3 via RNAi leads to fewer P granules with lower concentration inside (Fig. 5B). We also find a condensation temperature of °C, consistent with our theoretical predictions.
Fig. 5.
Condensation temperature as a function of PGL-3 concentration. (A) The theoretical prediction is based on a linear interpolation between the fits of the experimental phase diagram data (Fig. 4 C and D). While for the solid line we considered the average concentration of PGL-1, the shaded areas correspond to the lower and upper values of the SD (from in vivo fluorescent measurements of concentrations). Experimental data are derived from linear fits to the ensemble of P granule volumes (Fig. 2C) for WT, pgl-3 RNAi, and pgl-3 deletion. (B) Maximum projections for representative embryos at 25 °C for the data presented in A. All images use the same histogram adjustments. (Scale bar, 5 .)
Limitations of Equilibrium Descriptions inside a Living Cell.
Taken together, these results suggest that the key features of condensation and dissolution of P granules as a function of temperature are well captured by a model based on thermodynamic equilibrium. However, given that the cell is fundamentally an out-of-equilibrium system, the limitations of thermodynamic concepts need to be considered carefully. One issue is whether temperature inside the embryo is well defined since our experimental approach uses temperature shifts to probe the thermodynamic response of P granules. In this context, we can ask how fast the embryo responds to outside temperature changes. The corresponding relaxation time can be estimated based on specific heat and thermal conductivity. We find that the temperature within a size of relaxes at times shorter than , which corresponds to the scale of an embryo (see Materials and Methods for details). A corollary to this is to ask whether, at constant external temperature, heat generated inside the embryo can cause a temperature gradient toward the outside. Such heat could come from active cellular processes such as cortical and cytoplasmic flows, directed molecular transport, active force generation, and also chemical fluxes through metabolic pathways. The heat generated by all active processes in a eukaryotic cell is typically in the order of (21–23). For a cell of size, this leads to a temperature difference between cell center and periphery of only about °C, suggesting that temperature is almost homogeneous inside the cell.
Although the temperature is essentially homogeneous in space on cellular length scales, the temperature could locally fluctuate due to active molecular processes. For example, a single ATP hydrolysis event can convert chemical energy to heat and can cause a localized and transient increase in temperature. Such perturbations relax in a diffusive manner and spread over a distance of about while the temperature in the corresponding volume decreases with time. Here, denotes the thermal diffusivity, which is in water (24). A chemical event that releases of heat induces a temperature increase of about 10 °C after about in a volume element of 1 . After about , this temperature perturbation has relaxed to about °C as the released heat spreads in a volume of . Considering even longer times we find that after , the temperature perturbation has been homogenized within a volume element of diameter with a remaining temperature increase of only about °C. Furthermore, the rate at which such events are expected to occur within this volume element is given by and is slow compared to the temperature relaxation time of . Thus, since the timescales related to heat transport separate from the slow diffusion at longer timescales, we can consider volume elements of size to be at local thermodynamic equilibrium and we can neglect temperature fluctuations arising from individual chemical events.
Discussion
Local Thermodynamics and the Nonequilibrium Nature of the Cell Cytoplasm.
Work over the last decade has accumulated evidence that the formation of intracellular condensates can be described by the physics of phase separation. Thermodynamic concepts have been useful for the study of biological condensates in vivo (6, 25). However, it has remained unclear whether thermodynamic concepts are appropriate to explain condensate formation despite the presence of numerous active processes in living cells. Here we have shown that P granule formation and dissolution in the C. elegans embryo have a temperature dependence as expected for a thermodynamic process and can be represented by a classical phase diagram. Our analysis demonstrates that the P granule dynamics are governed by local thermodynamic equilibrium in mesoscopic volume elements of about size beyond timescales of . Estimates based on general arguments show that temperature heterogeneities due to individual active molecular events dissipate quickly without perturbing the slower dynamics of phase separation. Consistently, a simple phase separation model based on thermodynamics can well describe the phase diagrams determined in vivo.
Condensates in cells are typically composed of many different molecular components that interact with each other. Here, we observe the condensation of one component, PGL-1. However, the resulting phase diagram should depend on the concentrations of other main components. Indeed, when we deleted PGL-3 proteins in the C. elegans embryo (pgl-3 line), we found a qualitative change of the phase diagram reflected in the appearance of a pronounced change of the PGL-1 concentration inside P granules with temperature. We do not know the origin of this abrupt response. However, it could reflect a signature of another phase transition in the multicomponent system. This transition may be associated with conformational changes of PGL-1 proteins as suggested by the jump in molecular volume that we infer in our analysis. Our results suggest that the presence of PGL-3 suppresses this conformational transition. More generally, our results suggest that the multicomponent nature of condensates helps to protect the condensate’s behavior and the proteins within it against changes in physiological conditions and other stresses. For instance, C. elegans propagates in an appropriate range of temperatures of ∼10 to 30 °C and condensates must be able to operate effectively within such changes.
Temperature changes can also affect rates of chemical reactions relevant to P granule formation. For example, DEAD-box ATPases (7) were shown to promote phase separation in their ATP-bound form, whereas ATP hydrolysis induces compartment turnover and release of RNA (8). However, such chemical rates typically vary only little. For example, enzymatic reactions change at most two- to threefold within a temperature range of °C (26). Similarly, in the same temperature range, rates of active processes driven by the hydrolysis of ATP or GTP change also only weakly with temperature (27, 28). Together with the excellent agreement between the in vivo phase diagrams and the equilibrium phase separation model, we conclude that the temperature dependence of rates associated to active processes does not play a key role in the temperature response of P granules.
We have proposed that volume elements of size of about are locally at equilibrium, which is why local thermodynamics can be used to describe phase separation of P granules in the C. elegans embryo. How can we relate the small scales that are at equilibrium to larger scales in the cell where active dynamic processes take place? The nonequilibrium active character of the cell typically emerges on length scales larger than the size of this volume element. For example, concentration levels change in time, concentration profiles develop, and active transport processes and fluid flows stir the inside of living cells. Eventually, heat is released to the cell environment. The thermodynamic driving forces of such cellular processes are for example differences in chemical potential between different volume elements that are in different local equilibria. It is important to remember that a local equilibrium means that local volume elements relax to an equilibrium state quickly, faster than the timescales during which concentrations and thermodynamic variables change. However, at longer timescales, individual volume elements can change their properties because they are in general not at equilibrium with their environment. This is why, in living cells that exhibit a hierarchy of timescales, nonequilibrium phenomena can be captured by classical irreversible thermodynamics, built on local thermodynamic equilibrium (11, 29, 30).
It is interesting to estimate the actual chemical activity in such local volume elements. Taking into account the estimated rate of heat production per volume and the energy released as heat during individual chemical events, we estimate on average about 25 active chemical events per second in a volume element of size. This is much slower than the microsecond relaxation time to equilibrium and therefore does not significantly perturb the local equilibrium. However, it provides the basis for the nonequilibrium phenomena that emerge at larger scales inside the cell (see Materials and Methods for an estimate of the length scale relevant for the example of protein expression). As a result, spatial heterogeneities emerge because different volume elements are not at equilibrium with respect to each other. It is important to note that the simplified picture based on volume elements outlined here applies to a well-mixed and isotropic cytoplasm. Inside or near membranes or other cellular assemblies, the construction of volume elements will have to be refined.
Possible Role of Thermodynamics for Organism Fertility.
So far, we have shown that the temperature-dependent response of P granules in the C. elegans embryo is governed by local thermodynamics. It is interesting to relate the temperature dependence of P granules to the temperature dependence of fertility. The fertility of wild-type worms has been reported to describe a bell-shaped curve for temperatures between about 10 and 27 °C (14) with a maximal fertility at about 18 °C. Interestingly, fertility is lost at about 27 °C when P granules have largely dissolved (Fig. 2D and figure 3 in ref. 14). This observation suggests a potential link between fertility at higher temperatures and P granule thermodynamics. Indeed, it has been reported that worms deficient in PGL-1 are more temperature sensitive than wild type and further need PGL-3 for fertility at lower temperatures (20).
Interestingly pgl-3 worms have a temperature range of fertility that is slightly shifted to lower temperatures (SI Appendix, Fig. S6). Our data show that this is correlated with a decrease in condensation temperature (Fig. 3D and SI Appendix, Fig. S7). Thus, in pgl-3 worms, the temperature range where P granules are abundant is shifted to lower temperatures. This shift suggests that the multicomponent nature of P granules may help to modulate the temperature range of fertility during evolution. Note that when comparing the fertility of N2 worms and pgl-3 mutants in an N2 background, we observed a higher brood size of the mutants at lower temperatures of 10 °C (SI Appendix, Fig. S6) for reasons we do not yet understand. However, we see a possible link between total condensate volume and condensation temperature with the fertility of the worm, suggesting further exploration of the thermodynamic properties of in vivo systems is needed.
Materials and Methods
In Vivo Temperature Perturbations.
From Fig. 2 onward, early one-cell C. elegans embryos before the onset of P granule segregation were used. C. elegans strains were kept and cultured at 16 °C on standard feeding plates. Prior to measurement, adult worms were dissected in M9 buffer containing 25- diameter polystyrene spacer beads (Polysciences) under temperature-controlled conditions. A drop of 8.1 of this solution containing embryos of various developmental stages was sandwiched between an 18 × 18-mm coverslip and the sapphire glass of a custom-made temperature stage (as previously described in ref. 31 and see sketch in SI Appendix, Fig. S1). The chamber was sealed using a silicone glue (twinsil-speed; Picodent), ensuring no evaporation occurred. Embryos mounted under these conditions were still dividing and developed normally after temperature perturbations (SI Appendix, section 7 and Fig. S8). For imaging we used a CSU-X1 (Yokogawa) spinning-disk confocal system on an IX83 microscope (Olympus) connected to an iXon DU-897 back-illuminated EMCCD camera (Andor). All experiments were acquired with 0.7- z spacing using an objective piezo (PiezoJena) with a 60× UPLSAPO 1.2 NA water objective (Olympus), using Immersol W immersion oil (Carl Zeiss). Emission laser intensities were kept constant and measured prior to imaging to ensure comparability throughout the entire dataset. The microscope was controlled via VisiView (Visitron Systems). The z stacks in Fig. 2A were captured every 30 s, and for other experiments a protocol was used as described in SI Appendix, Fig. S1. In brief, each embryo was subjected to three temperatures between 5 and 25 °C and measurements were made 3 min after the new temperature was stable to reach local equilibrium (for control for timing see SI Appendix, Fig. S9). All embryos were subjected to 31 °C in the final step where P granules are largely dissolved. This further allowed us to relate average fluorescence intensities between worm lines and experiments. Worm gonad images shown in Fig. 1B were imaged using a CSU-W1 (Yokogawa) spinning-disk confocal system on an IXplore IX83 microscope (Olympus) with a 40× UPLSAPO 0.95 NA air objective (Olympus) controlled via CellSens. Worms were mounted as described previously for embryos, however, using 50- diameter polystyrene spacer beads.
Image Registration and In Vivo Concentration Determination.
Image registration and analysis were performed using a custom-written MATLAB pipeline (The MathWorks). Image stacks were analyzed both in three dimensions and as two-dimensional (2D) maximum and mean projections. All image stacks were first subtracted by the dark intensity count of the camera. Both 2D and 3D images are subjected to filtering prior to registration of condensates and embryo contour. For 3D analysis the Gaussian blur kernel is also adopted to represent different resolutions in planar (0.125 ) and axial directions (0.7 ). The shape of the embryo outline is detected and used for total intensity and solute intensity calculation, the embryo volume, as well as further processing. P granule outlines are registered via a threshold using the embryo mean intensity plus a multiple of its SD (for condensate volume detection see Fig. 2B and for and masks see Fig. 3A). For the determination of via the condensate intensities a higher threshold than for the determination of the volumes was used. This suppresses the influence of very small condensates that have unrepresentative intensities for the quantification of . In addition, a watershed procedure was used to separate falsely connected condensates before estimating their volume. To determine via the solute intensity, the mask of was dilated and then subtracted from the registered embryo outline, which left the solute mask. The dilation leaves a gap to the mask used for the determination of (Fig. 3A). This reduces the influence of the tail of the Gaussian-like profile of condensate intensity distributions and possible pinhole cross-talk of the spinning-disk system on the solute intensities. The relation of intensity values to concentration was set via a temperature-dependent conversion factor using the assumption of a linear relationship (SI Appendix, Fig. S4). To get , the average total intensity values obtained from registration of whole embryos and the average total concentrations determined via quantitative Western blots for each worm strain were related and then pooled for each temperature (SI Appendix, Fig. S3). That this linear relationship is reasonable can be seen when comparing the average and the average between worm strains, where we report comparable average values for both approaches (SI Appendix, Fig. S3).
RNAi Experiments.
A colony of bacteria from an ampicillin (100 ) feeding plate was cultivated overnight in Lysogeny broth (LB) medium containing ampicillin and tetracycline at 37 °C at 220 rpm on a shaker plate. After centrifugation (4,000 rpm, 5 min) the pellet was resuspended to an optical density reading at 600 nm wavelength (OD600) of 0.5 in LB medium containing ampicillin and 0.2 mM isopropyl -d-thiogalactopyranoside (IPTG). After another 2 h at 37 °C at 220 rpm 150 was pipetted on a dried nematode growth media (NGM) feeding plate and either used directly or stored at 4 °C in a dark environment. Induction of RNAi was carried out with L4 stage worms for 24 h at a temperature of 23 °C (32). For pgl-3 RNAi both worm strains expressing PGL-3::GFP and PGL-1::GFP were cultivated under the same conditions at the same time. While experiments were carried out with the strain expressing PGL-1::GFP, the PGL-3::GFP strain served as a means to measure the amount of reduction in PGL-3 via the relation of total fluorescence / (see SI Appendix, Fig. S10A). The relative total intensity / for PGL-1::GFP was not significantly changed using pgl-3 RNAi (SI Appendix, Fig. S10B).
C. elegans Worm Strains.
The proteins PGL-1 and PGL-3 are regarded as regulators of the germline and belong to the main constitutive components of P granules (33). To experimentally analyze the phase separation behavior of P granules, their main components PGL-1 and PGL-3 were labeled (tagged) at their endogenous genomic locus with monomeric enhanced GFP (mEGFP) using the co-CRISPR method (34). The following lines were used: N2 wild-type worms; TH586, pgl-1::mEGFP pgl-1(dd54[pgl-1::mEGFP]); TH561, pgl-3::mEGFP (pgl-3(dd29[pgl-3::mEGFP]); TH615, pgl-3(dd47) pgl-1::mEGFP (pgl-1(dd54[pgl-1::mEGFP])); TH605, pgl-3 (dd47); and TH721, pgl-1(dd65) pgl-3::mEGFP (pgl-3(dd29[pgl-3::mEGFP]) (see SI Appendix, section 3 for details on the analysis).
Protein Concentration Determination.
Previously, protein concentrations were measured in N2 wild-type early embryos by quantitative label-free mass spectrometry (35). For measuring protein concentrations of PGL-1 and PGL-3 in the worm lines used in this study, PGL-1 and PGL-3 were specifically detected in immunoblots of early embryo protein extracts with monoclonal antibodies and imaged with an Odyssee SA Licor infrared imaging system. The protein concentrations were then calculated by normalizing to the wild-type values. Protein concentrations were measured from five independent experiments (see SI Appendix, section 4 for details on the analysis).
Fit of a Binary Mixture Model to the Experimental Data.
Coexisting phases in incompressible binary mixtures satisfy the following conditions (36),
| [2] |
| [3] |
where denotes the chemical potential defined by and the subindexes in and out indicate the two distinct phases. The conditions given in Eqs. 2 and 3 represent the balance of exchange chemical potentials and pressures between the phases, respectively. At thermodynamic equilibrium, the curvature of the interface of a spherical droplet with radius vanishes and thus the Laplace pressure is zero. In the case of P granules, the contribution of Laplace pressure to the balance of the osmotic pressures can also be neglected due to a small surface tension (SI Appendix, section 1).
We numerically solve these equations and find for each coexisting concentration pair the interaction parameters and leading to the best match with the experimentally determined values. This set of values for and is shown as dots in Fig. 4B. From these results, we obtain the temperature dependence of and , which in the case of the pgl-3 line shows a transition occurring between 15 and 20 °C. We then fit curves for each corresponding set of points (dotted lines in Fig. 4B) and calculate the corresponding phase diagrams (dotted lines in Fig. 4 C and D), which agree very well with the experimental phase diagram. For details on the specific form of the functions we refer the reader to SI Appendix, section B. In addition, to further assess the dependence of these parameters as a function of temperature we also study the temperature dependence of the parameters by minimizing a global error function defined by
| [4] |
where each index corresponds to a different temperature, and and are the values obtained from solving the equilibrium conditions Eqs. 2 and 3. Moreover, denote the experimentally measured values, and are the SDs of the measurements, and and correspond to the number of data points for each temperature. The solid lines in Fig. 4B show the curves that minimize the global error Eq. 4 and the corresponding phase diagrams are shown as solid lines in Fig. 4 C and D. We find that both approaches are in very good agreement with the experimental phase diagrams. To estimate the condensation temperature of the P granules as a function of PGL-3 concentration, we construct phase diagrams corresponding to different concentrations of PGL-3, where we choose the dependence of the parameters defining and as a linear interpolation between the values of the interaction parameter and the effective molecular volume of the phase-separating component corresponding to the wild type and the pgl-3 line. For this interpolation, we consider the parameter values corresponding to the wild-type line obtained by the global fit (solid yellow line in Fig. 4B) and for the pgl-3 line we consider only the points below the transition temperature, i.e., the parameters obtained from the fit to the coexisting phases corresponding to temperatures 5, 10, and 15 °C. Using these considerations, we estimate the condensation temperatures as a function of PGL-3 concentration for a fixed concentration of PGL-1 (value from immunoblotting), and we repeat the same process for concentrations that are 1 SD above and below this estimate. The predictions are shown in Fig. 5A as the gray shaded area are in very good agreement with the experimental data.
Estimation of Temperature Relaxation Times, Temperature Gradients, and Temperature Fluctuations.
In this work we characterize phase separation as a function of temperature in a living cell. A living cell is maintained at all times far from equilibrium, for example due to the generation of heat by metabolic processes and the production and degradation of molecular components. This nonequilibrium nature raises the question of whether temperature is a reliable thermodynamic variable that can be controlled experimentally. This question involves how fast temperature changes can be applied and what are stationary temperature differences inside cells due to metabolic processes.
Temperature relaxation times in the embryo.
In a typical in vitro assay, an experimenter can wait until the system has relaxed toward thermodynamic equilibrium before taking a measurement. In measurements on cells, however, no thermodynamic equilibrium is reached and the time window to take the measurement is limited because the cell cycle progresses. To characterize the temperature dependence of cellular processes, the minimal time between measurements at different temperatures should be larger than the temperature relaxation time. The time dependence of the temperature profile is described by the heat equation
| [5] |
where denotes the thermal diffusivity, is the mass density, is specific heat capacity at constant pressure, and denotes the volumetric heat source due to metabolic processes. A temperature perturbation of size relaxes on a timescale . For the embryo, we estimate the thermal diffusivity in the embryo similar to water with (24). Considering an embryo size of , the time to relax temperature heterogeneities is . In our experiments (SI Appendix, Fig. S1), heat is exchanged via sapphire with a thermal diffusivity of about . Therefore, contributions to the temperature relaxation of sapphire can be neglected. In summary, for processes that occur on timescales exceeding , such as the P granule growth occurring on second timescales, temperature has relaxed and takes stationary values inside the embryo.
Effects of heat generation due to metabolic processes.
Exothermic metabolic processes generate heat inside the embryo, which is conducted to the embryo boundaries. The heat production is of the order of for humans (21) as well as for flat worms (23); for a rather complete overview of metabolic rates corresponding to a large number of species, see ref. 22. Here, we consider the heat production of the flat worm as a good estimate for the C. elegans embryo. Using a mass density of the corresponding volumetric heat source is . In steady state, this heat source creates a temperature profile. For an embryo of width that is squeezed between two heat-conducting surfaces located at and maintained at ambient temperature , the temperature profile reads
| [6] |
Eq. 6 implies that the stationary temperature difference relative to the ambient temperature is only °C using the specific heat of water. These weak temperature differences allow us to consider temperature as a roughly constant thermodynamic field in the embryo.
Finally, we estimate the impact of temperature fluctuations due to exothermic metabolic events. We consider that a single event dissipates an energy and occurs at a position . For this case, the volumetric heat source reads
| [7] |
The corresponding temperature profile for the propagation of this single metabolic event in time and space (ignoring boundary effects) reads
| [8] |
for , where is the embryo temperature prior to the metabolic event.
To estimate the role of temperature fluctuations due to metabolic events in the embryo, we consider the time of heat dissipation via diffusion in a volume of size , , and estimate the corresponding temperature change. In particular, according to Eq. 8, the temperature change in the volume element of size due to a single metabolic event is given by . Using the mass density and specific heat of water, and , we find that °C . The corresponding timescale is . These estimates suggest that for volume elements with size of about , corresponding to timescales of , temperature changes due to single metabolic events are less than °C and thus negligible.
Temperature uncertainty in small volume elements.
Temperature is well defined on macroscopic scales. In small systems, temperature has an uncertainty if energy is well defined (37–39). This temperature uncertainty can be estimated at equilibrium using a Green–Kubo relationship relating heat fluctuations to the heat capacity, which implies an uncertainty (39), where is the size of the volume element. Specifically, for , the temperature uncertainty is °C. For , the temperature uncertainty is already less than 1 °C and for , it is only of the order of °C. Note that for , the temperature uncertainty associated with thermal fluctuations is larger than temperature changes stemming from single metabolic events. This confirms that perturbations of local equilibrium by metabolic events are negligible on the scales from to .
Effects of sources and sinks of molecular components.
In general, molecular components such as proteins inside cells are not conserved; they are continuously produced and degraded with time. Cells can increase or decrease the concentration of specific proteins by regulating the protein expression machinery. The corresponding reaction cycles in general include multiple feedback loops that give rise to a characteristic rate of change of the protein concentration. This rate is typically small and in the order of or even slower (40). To estimate the impact of sources and sinks of molecular components, the relevant quantity to be estimated is the reaction–diffusion length scale , where denotes the diffusion coefficient of the protein. Above this length scale, protein expression will affect the kinetics of phase separation (11). Below this length scale, the behavior of the system is expected to be governed by local thermodynamics, at least with respect to the protein expression kinetics. Specifically, using typical protein expression rates given above and an approximate PGL-1 diffusion constant of (41) gives . Interestingly, this length scale is approximately equal to the size of the embryo. Thus, protein expression can affect phase separation on the embryo scale; however, it does not have a major effect on the local thermodynamics governing the formation and dissolution of P granules.
Supplementary Material
Acknowledgments
We thank Shambaditya Saha, Louise Jawerth, Marcus Jahnel, Titus Franzmann, Juan Iglesias, Patrick McCall, Tyler Harmon, and the whole Hyman laboratory for fruitful discussions about phase separation during the past years and Melissa Rinaldin and Jonathan Rodenfels for very helpful feedback on the manuscript. We thank Falk Elsner and Hartmut Wolf for support in optimizing the temperature stage. We also thank Susanne Ernst and Anne Schwager for technical assistance with worm work and immunoblotting and Torsten Bücher for technical assistance with brood size measurements. We thank Olympus for providing the CSU-W1 SoRa spinning-disc system based on an IXplore IX83 microscope that was used for whole worm imaging in Fig. 1 and the data presented in SI Appendix, Fig. S5. A.W.F. was supported by the ELBE postdoctoral fellows program and the Max Planck Research Network for Synthetic Biology (MaxSynBio) consortium, jointly funded by the Federal Ministry of Education and Research of Germany and the Max Planck Society. O.A.-A. acknowledges funding from the Armando and Maria Jinich postdoctoral fellowship for Mexican citizens. M.K. acknowledges support from the European Research Council, Grant 853619. C.A.W. and A.A.H. acknowledge the Priority Program (SPP) 2191 “Molecular Mechanisms of Functional Phase Separation” of the German Science Foundation for supporting the exchange among scientists working on intracellular phase separation.
Footnotes
Competing interest statement: A.A.H. is cofounder and member of the scientific advisory board of Dewpoint Therapeutics.
This article is a PNAS Direct Submission. A.Y.G. is a guest editor invited by the Editorial Board.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2102772118/-/DCSupplemental.
Data Availability
All study data are included in this article and/or SI Appendix. Previously published data were used for this work [PGL-1 and PGL-3 concentration in early N2 worms from Saha et al. (35) was used to calibrate immunoblots].
References
- 1.Hyman A. A., Weber C. A., Jülicher F., Liquid-liquid phase separation in biology. Annu. Rev. Cell Dev. Biol. 30, 39–58 (2014). [DOI] [PubMed] [Google Scholar]
- 2.Banjade S., Rosen M. K., Phase transitions of multivalent proteins can promote clustering of membrane receptors. eLife 3, 3 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Banani S. F., Lee H. O., Hyman A. A., Rosen M. K., Biomolecular condensates: Organizers of cellular biochemistry. Nat. Rev. Mol. Cell Biol. 18, 285–298 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Dormann D., FG-nucleoporins caught in the act of liquid-liquid phase separation. J. Cell Biol. 219, 12 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Navarro M. G.-J., et al., RNA is a critical element for the sizing and the composition of phase-separated RNA–protein condensates. Nat. Commun. 10, 3230 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Brangwynne C. P., et al., Germline P granules are liquid droplets that localize by controlled dissolution/condensation. Science 324, 1729–1732 (2009). [DOI] [PubMed] [Google Scholar]
- 7.Updike D., Strome S., P granule assembly and function in Caenorhabditis elegans germ cells. J. Androl. 31, 53–60 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hondele M., et al., DEAD-box ATPases are global regulators of phase-separated organelles. Nature 573, 144–148 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Howard J., Mechanics of Motor Proteins and the Cytoskeleton (Sinauer Associates, 2001). [Google Scholar]
- 10.Jülicher F., Ajdari A., Prost J., Modeling molecular motors. Rev. Mod. Phys. 69, 1269 (1997). [Google Scholar]
- 11.Weber C. A., Zwicker D., Jülicher F., Lee C. F., Physics of active emulsions. Rep. Prog. Phys. 82, 064601 (2019). [DOI] [PubMed] [Google Scholar]
- 12.Delgadillo A. F. D., “Temperature drives P granule formation in Caenorhabditis elegans,” PhD thesis, TU Dresden, Dresden, Germany (2016).
- 13.Putnam A., Cassani M., Smith J., Seydoux G., A gel phase promotes condensation of liquid P granules in Caenorhabditis elegans embryos. Nat. Struct. Mol. Biol. 26, 220–226 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Begasse M. L., Leaver M., Vazquez F., Grill S. W., Hyman A. A., Temperature dependence of cell division timing accounts for a shift in the thermal limits of C. elegans and C. briggsae. Cell Rep. 10, 647–653 (2015). [DOI] [PubMed] [Google Scholar]
- 15.Bracha D., et al., Mapping local and global liquid phase behavior in living cells using photo-oligomerizable seeds. Cell 175, 1467–1480.e13 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Maurice H. L., Solutions of long chain compounds. J. Phys. Chem. 9, 441 (1941). [Google Scholar]
- 17.Flory P. J., Thermodynamics of high polymer solutions. J. Chem. Phys. 10, 51–61 (1942). [Google Scholar]
- 18.Bartolucci G., Adame-Arana O., Zhao X., Weber C. A., Controlling composition of coexisting phases via molecular transitions. arXiv [Preprint] (2021). https://arxiv.org/abs/2103.01311. (Accessed 1 March 2021). [DOI] [PMC free article] [PubMed]
- 19.Rubinstein M., et al., Polymer Physics (Oxford University Press, New York, 2003), vol. 23. [Google Scholar]
- 20.Kawasaki I., et al., The PGL family proteins associate with germ granules and function redundantly in Caenorhabditis elegans germline development. Genetics 167, 645–661 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.What is the power consumption of a cell? book.bionumbers.org/what-is-the-power-consumption-of-a-cell/, 2020. Accessed 22 October 2020.
- 22.Makarieva A. M., et al., Mean mass-specific metabolic rates are strikingly similar across life’s major domains: Evidence for life’s metabolic optimum. Proc. Natl. Acad. Sci. U.S.A. 105, 16994–16999 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Thommen A., et al., Body size-dependent energy storage causes Kleiber’s law scaling of the metabolic rate in planarians. eLife 8, e38187 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Blumm J., Lindemann A., Characterization of the thermophysical properties of molten polymers and liquids using the flash technique. High Temp. High Press. 35, 627 (2003). [Google Scholar]
- 25.Narayanan A., et al., A first order phase transition mechanism underlies protein aggregation in mammalian cells. eLife 8, e39695 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Peterson M. E., Daniel R. M., Danson M. J., Eisenthal R., The dependence of enzyme activity on temperature: Determination and validation of parameters. Biochem. J. 402, 331–337 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Applegate D., Temperature dependence of the release of ATP hydrolysis products from the 10S conformation of smooth muscle myosin. J. Muscle Res. Cell Motil. 10, 457–464 (1989). [DOI] [PubMed] [Google Scholar]
- 28.Rivera S. B., Koch S. J., Bauer J. M., Edwards J. M., Bachand G. D., Temperature dependent properties of a kinesin-3 motor protein from Thermomyces lanuginosus. Fungal Genet. Biol. 44, 1170–1179 (2007). [DOI] [PubMed] [Google Scholar]
- 29.Prost J., Jülicher F., Joanny J.-F., Active gel physics. Nat. Phys. 11, 111–117 (2015). [Google Scholar]
- 30.Jülicher F., Grill S. W., Salbreux G., Hydrodynamic theory of active matter. Rep. Prog. Phys. 81, 076601 (2018). [DOI] [PubMed] [Google Scholar]
- 31.Mittasch M., et al., Non-invasive perturbations of intracellular flow reveal physical principles of cell organization. Nat. Cell Biol. 20, 344–351 (2018). [DOI] [PubMed] [Google Scholar]
- 32.Kamath R. S., et al., Systematic functional analysis of the Caenorhabditis elegans genome using RNAi. Nature 421, 231–237 (2003). [DOI] [PubMed] [Google Scholar]
- 33.Min H., Shim Y.-H., Kawasaki I., Loss of PGL-1 and PGL-3, members of a family of constitutive germ-granule components, promotes germline apoptosis in C. elegans. J. Cell Sci. 129, 341–353 (2016). [DOI] [PubMed] [Google Scholar]
- 34.Arribere J. A., et al., Efficient marker-free recovery of custom genetic modifications with CRISPR/Cas9 in Caenorhabditis elegans. Genetics 198, 837–846 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Saha S., et al., Polar positioning of phase-separated liquid compartments in cells regulated by an mRNA competition mechanism. Cell 166, 1572–1584.e16 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Safran S., Statistical Thermodynamics of Surfaces, Interfaces, and Membranes (CRC Press, 2018). [Google Scholar]
- 37.Phillies G. D. J., The polythermal ensemble: A rigorous interpretation of temperature fluctuations in statistical mechanics. Am. J. Phys. 52, 629–632. (1984). [Google Scholar]
- 38.Prosper H. B., Temperature fluctuations in a heat bath. Am. J. Phys. 61, 54–58 (1993). [Google Scholar]
- 39.Falcioni M., Villamaina D., Vulpiani A., Puglisi A., Sarracino A., Estimate of temperature and its uncertainty in small systems. Am. J. Phys. 79, 777–785 (2011). [Google Scholar]
- 40.Cho U., et al., Rapid and tunable control of protein stability in Caenorhabditis elegans using a small molecule. PLoS One 8, e72393 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Griffin E. E., Odde D. J., Seydoux G., Regulation of the MEX-5 gradient by a spatially segregated kinase/phosphatase cycle. Cell 146, 955–968 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in this article and/or SI Appendix. Previously published data were used for this work [PGL-1 and PGL-3 concentration in early N2 worms from Saha et al. (35) was used to calibrate immunoblots].