From nuclear to unnuclear physics

Nuclear physics studies the stability, structure, and reactions of atomic nuclei, as well as the phase structure and properties of dense, strongly interacting matter. While nuclear reactions are exceedingly complicated, remarkably Hammer and Son (1) have discovered a low-energy regime—which they call “unnuclear physics”—where certain nuclear reactions obey simple scaling rules, related to a new, emergent scaling symmetry of the nuclear force. The term “unnuclear” is a reference to the work of Howard Georgi, who coined the term “unparticle physics” to describe a possible scale-invariant sector beyond the standard model of high-energy physics (2).

To appreciate the Hammer and Son (1) result let us step back and recall some basics. Modern nuclear physics began with the discovery of the neutron in 1932, but ever since the 1970s we have known that the strong nuclear forces between neutrons and protons, collectively known as nucleons, are ultimately governed by quantum chromodynamics (QCD), the theory of quarks and gluons. Quarks carry color charges, a generalization of electrical charge, and forces between “colored” particles are mediated by gluons. Neutrons and protons are in fact composite particles, and the nuclear force is the residual interaction between “color-neutral” objects, similar to the van der Waals force between electrically neutral atoms and molecules. As a consequence, determining nuclear structure and reactions in detail requires numerical calculations based on complicated nuclear forces. Not only did Hammer and Son discover a simple tractable regime of nuclear reactions, even more remarkably, the dependence of the cross-sections on energy that appear in this regime can be related to a completely different observable, the ground-state energy of resonantly interacting ultracold atoms trapped in a harmonic potential.

Nucleon as well as nuclear reactions at low incident energies can be described in terms of two parameters, the “scattering length,” $a$, and the effective range, $r_e$, of the interaction. The scattering length determines the low-energy scattering cross-section, $\sigma =4\pi a^2$, and the effective range controls the leading energy dependence of $\sigma$. In a quantum mechanical scattering reaction $a$ can be much larger than the physical size of the colliding particles or the range of the interaction potential between them. This happens, in particular, if the two colliding particles have an attractive interaction and are close to forming a bound state. Indeed, as the binding energy $B$ of the two particles approaches 0, the scattering length $a$ diverges. The effective range, on the other hand, is controlled by the physical range of the underlying interaction and remains finite.*

Unnuclear Physics

The limit in which the scattering length is much larger than all other length scales ($a\to \infty$), but the other length scales in the interactions are relatively small, is particularly interesting. In this case the physics is invariant under a rescaling of all distances (4). This phenomenon is well-known in statistical mechanics, where in the vicinity of a second-order phase transition the correlation length diverges and fluctuations occur on all length scales. Correlation functions, for example the probability that a local density fluctuation in a fluid is correlated with a similar fluctuation separated by a spatial distance $x$, decay as a fractional power of $x$. Striking physical phenomena, such as the critical opalescence of water near the liquid–gas critical end point, emerge as a consequence. The milky appearance of the fluid arises from scattering of light by density fluctuations on a wide range of length scales.

In nuclear physics the neutron–neutron scattering length is very large, $|a_{nn}|\simeq 19$ fm (1 fm = $10^{-15}$ m), much bigger than the size of the neutron, of order 1 fm (or $10^{-15}$ m), so that a system of neutrons is close to the scale-invariant regime. The effective range is somewhat enhanced, $r_{nn}\simeq 2.3$ fm, but is significantly smaller than the scattering length. In a low-energy reaction involving nucleons or nuclei, in which a momentum $q$ is transferred, with the length $\hslash /q$ lying well between the range of the nuclear forces and the scattering length, $r_{nn}\ll \hslash /q\ll a_{nn}$, the theory exhibits approximate scale invariance. Such momentum transfers correspond to a range of scattering energies, $ϵ$, well between ${\hslash }^2/m{a}_{nn}^2$ and ${\hslash }^2/m{r}_{nn}^2$, or roughly $0.1\mathrm{M}\mathrm{e}\mathrm{V}\ll ϵ\ll 5\mathrm{M}\mathrm{e}\mathrm{V}$, the regime of unnuclear physics.

Since finite nuclei are bound states, with discrete energy levels, it is not immediately obvious how to apply unnuclear physics to nuclear reactions. Hammer and Son (1) observe that a natural arena for unnuclear physics is the disintegration of halo nuclei, neutron-rich isotopes such as metastable ⁶He or ¹¹Li that have several loosely bound neutrons. The cross-section for disintegration of a halo nucleus by a low-energy external probe, for example a photon, factorizes into a short-distance piece characteristic of the particular nucleus and a long-distance part determined by unnuclear physics, the interaction between the neutrons in the final state. This implies that the energy dependence of the cross-section scales as a fractional power of the total energy of the emitted neutrons, and that the exponent is determined by unnuclear physics.

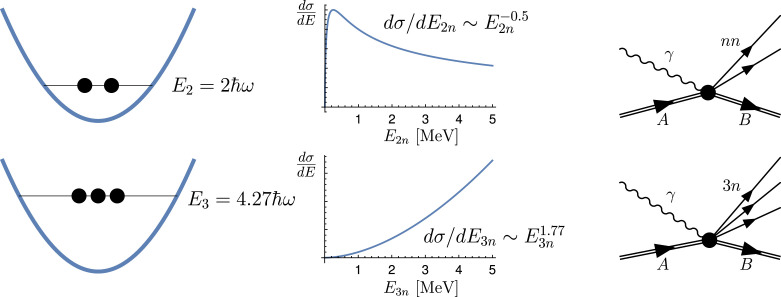
This fractional power can be determined by methods similar to those developed in statistical mechanics (5). However, it is also possible to relate this exponent to a different physical problem. There are no neutron bound states, but one can imagine a neutron drop confined in an external harmonic potential. Because of scale invariance the ground-state energy of the drop must be a multiple of $\hslash \omega$, where $\omega$ is the oscillator frequency. If the ground-state energy of an $N$-neutron drop is $E=\mathrm{\Delta }\hslash \omega$, where $\mathrm{\Delta }$ is a positive number, the $N$-neutron unnuclear exponent is $\nu =\mathrm{\Delta }-5/2$; see Fig. 1.

Fig. 1.

Relation between the ground-state energy of resonantly interacting, harmonically trapped atoms and the energy dependence of nuclear few-body reactions. Hammer and Son (1) show that if the ground-state energy of $N$ particles in a harmonic trap is $E_N=\mathrm{\Delta }\hslash \omega$ then the cross-section for the reaction $\gamma +A\to B+Nn$, where an incident photon, $\gamma$, knocks out $N$ neutrons from a neutron-rich nucleus, $A$, scales as $E_{Nn}^{\mathrm{\Delta }-5/2}$. For two particles $\mathrm{\Delta }=2$, and for three particles $\mathrm{\Delta }=4.27$ (6).

The energy of neutron drops in a harmonic potential can be computed by numerically solving the Schrödinger equation, but it cannot be measured experimentally. Experiments can be performed using a related system, ultracold fermionic atoms. These atoms can be tuned to the unnuclear regime using Feshbach resonances—which modify the interaction strengths by means of external magnetic fields—and be confined in harmonic potentials using external laser fields. Experiments have succeeded in creating atom drops with a controlled number of atoms (7).

From Unnuclear to Nuclear Matter

Another interesting subject, not directly addressed by Hammer and Son, is the structure of unnuclear matter. In neutron matter at density $n=N/V$, where $\mathit{V}$ is the volume of the system, the typical interparticle separation $Z$ is $\sim 1/n^{1/3}$. Thus, the regime $r_{nn}\ll l\ll a_{nn}$ is governed by unnuclear physics. Scale invariance implies that up to a numerical factor the equation of state $P=P(n)$, where $P$ is the pressure, has to be equal to that of a free Fermi gas. This numerical factor, known as the Bertsch parameter $\xi$, can be determined numerically, or using experiments with ultracold atomic Fermi gases, which yield $\xi =0.37$ (8). This result implies that the pressure of unnuclear matter is less than that of noninteracting neutron matter.

Unnuclear matter cannot be studied in the laboratory, but it does exist in the inner crust of neutron stars. Neutron stars are compact objects with masses around one to two times the mass of the sun and radii of about 12 km. The inner crust is a layer a few hundred meters below the surface. The outer crust is a layer of nuclei embedded in a degenerate gas of electrons which provides the main source of pressure. Once the neutron-rich nuclei in the crust can no longer accommodate further bound neutrons, a neutron gas begins to permeate the crust. At lower densities, this gas is in the regime of unnuclear matter. In the inner crust and in the outer layers of the core degenerate neutrons are the dominant source of pressure.

Observational constraints on neutron star masses and radii provide information on the equation of state of dense QCD matter. A central result is the discovery of neutron stars with masses in excess of two solar masses (9). In order to stabilize a star in this mass range matter at densities beyond the unnuclear regime must be stiff; that means the pressure as a function of density must increase more quickly than predicted by the unnuclear equation of state.

This behavior is consistent with detailed calculations using nuclear forces (10, 11). In these calculations the unnuclear behavior persists to densities of about 0.1 ${\mathrm{f}\mathrm{m}}^{-3}$, but at larger densities the pressure increases more quickly. This is caused by a combination of the neutron–neutron force turning repulsive at larger momentum transfer and repulsive three-body forces beginning to play a role. At even higher density, greater than about 0.2 ${\mathrm{f}\mathrm{m}}^{-3}$, the description in terms of pointlike neutrons is no longer reliable, and quark degrees of freedom begin to play a role.

Outlook

Hammer and Son (1) compare their prediction to other theoretical calculations, but there are currently no experimental data in the unnuclear regime. This situation is expected to change in the near future, as part of the experimental program at radioactive beam facilities such as RIKEN in Japan and the Facility for Rare Isotope Beams (FRIB) in the US. Experiments with ultracold atoms will continue to explore few and many-body systems of resonantly interacting atoms. An interesting problem is to understand nonequilibrium properties of unnuclear matter. Finally, observations at the Laser Interferometer Gravitational-Wave Observatory (LIGO) and the Neutron star Interior Composition Explorer (NICER) X-ray observatory will pin down the mass–radius relation of neutron stars and constrain the equation of state beyond the unnuclear regime (12–14).