Monolayer graphene membranes for molecular separation in high-temperature harsh organic solvents

Significance

Tremendous amounts of organic solvents are used in industry, requiring chemical-resistant membranes for energy-efficient solvent recovery. Currently, organic solvent nanofiltration (OSN) is hindered by the instability of membranes in operation, in particular under high temperatures and in harsh solvents. In this research, we revealed the solvent transport across nanopores of single-layer graphene via molecular dynamics simulation and combined it with a resistance model to guide the design of a defect-tolerant graphene composite membrane for OSN. The graphene-covered membrane demonstrated high permeance and excellent resistance to DMF at high temperatures, offering possibilities for challenging separations.

Abstract

The excellent thermal and chemical stability of monolayer graphene makes it an ideal material for separations at high temperatures and in harsh organic solvents. Here, based on understanding of solvent permeation through nanoporous graphene via molecular dynamics simulation, a resistance model was established to guide the design of a defect-tolerant graphene composite membrane consisting of monolayer graphene on a porous supporting substrate. Guided by the model, we experimentally engineered polyimide (PI) supporting substrates with appropriate pore size, permeance, and excellent solvent resistance and investigated transport across the resulting graphene-covered membranes. The cross-linked PI substrate could effectively mitigate the impacts of leakage through defects across graphene to allow selective transport without defect sealing. The graphene-covered membrane showed pure solvent permeance of 24.1 L m⁻² h⁻¹ bar⁻¹ and stable rejection (∼90%) of Allura Red AC (496.42 g mol⁻¹) in a harsh polar solvent, dimethylformamide (DMF), at 100 °C for 10 d.

Organic solvent nanofiltration (OSN) is an emerging technology paradigm for molecular separation in organic solvents with molecular weight cutoff ranging from 200 to 1,000 g mol⁻¹ (1). It not only has the potential to reduce up to 90% of the energy cost for solvent recovery compared with conventional evaporation or distillation processes (2) but also, enables separation in a continuous process without biphasic or phase transition operations, thus reducing the need for large space (3). Due to the tremendous amounts of organic solvents involved in synthesis and cleaning, millions of tons of solvents are used in a typical active pharmaceutical ingredient (API) production process (4). In particular, many pharmaceutical operations such as crystallization, solubilization, and reaction involve the use of harsh aprotic solvents (5). Large economic and environmental benefits are therefore expected if OSN can be implemented in the pharmaceutical and fine chemicals industry. However, one major challenge is the instability of membranes in harsh organic solvents, especially at temperatures higher than 90 °C that are commonly seen in the production of some APIs or intermediates: for example, the production of E-methyl cinnamate via the Heck coupling reaction (6) and Lexapro (7).

In the recent decades, industry and academia have made great efforts to develop robust membranes for OSN, mainly involving polymeric and ceramic materials (8). Polymeric materials, offering the advantages of flexibility and ease of production, are commonly used for separation processes. However, the penetration of organic solvents into the networks of polymeric materials can induce excessive change in their volume that can compromise their physical integrity and stability (9, 10). The intrinsic vulnerability of polymers to organic solvents may lead to long-term instability in practical applications. Ceramic materials show broad resistance to organic solvents and yet, suffer from brittleness and processing difficulties (8). Moreover, most separations reported in the literature were performed at room temperature. The exploration of high-temperature OSN is far from sufficient. Recently, da Silva Burgal et al. (11) demonstrated stable performance of the poly(ether-ether-ketone) membrane in DMF at temperatures up to 140 °C. Yet, the permeance was low at around 0.4 L m⁻² h⁻¹ bar⁻¹, and the rejection to polystyrene (molecular weight = 595 g mol⁻¹) was 65%. Hence, the development of highly permeable membranes for high-temperature harsh organic systems is in great demand.

Monolayer graphene demonstrates atomic thickness, remarkable mechanical strength, and excellent resistance to organic solvents and high temperature, hence offering opportunities for high-temperature OSN. A number of simulations (12–14) and experiments (15–17) have revealed the ultrapermeability of water and gas molecules and excellent selectivity across monolayer graphene with selective nanopores generated in the graphene lattice. However, although recent publications reported the application of monolayer graphene for OSN (18, 19), the transport of organic solvents through nanopores of graphene is insufficiently understood, and high-temperature OSN has not been demonstrated.

Furthermore, practical realization of graphene membranes requires centimeter-scale graphene on a support with minimal defects. Since graphene is typically grown by chemical vapor deposition (CVD) on copper, intrinsic defects inevitably exist (20). Large defects can originate during the transfer of graphene from copper to the sport, which can lead to severe leakage that deteriorates membrane selectivity (20). To minimize this impact, Celebi et al. (21) stacked two layers of graphene on a silicon support. However, after stacking several layers of graphene, the pore creation may become more difficult (20). Alternatively, atomic-layer deposition, interfacial polymerization (22), and deposition of polystyrene nanoparticles (23) have been utilized to seal the defects. Yet, the stability of these sealing plugs in harsh organic solvents remains a concern. Modulating the transport across graphene and the support underneath it for mitigation of the leakage through defects via support design can provide a simple, robust, and potentially more chemical-resistant approach (23), but it requires thorough understanding of the transport of organic solvents through composite membranes.

In this study, the transport of organic solvents across monolayer graphene was first studied by molecular dynamics (MD) simulation, followed by analysis of support design based on a transport resistance model to mitigate the impact of leakage through defects. We then developed centimeter-scale monolayer graphene membranes on solvent-resistant PI substrate with appropriate pore size and permeance for high-temperature OSN. The P84 PI support was cross-linked and preswelled in DMF prior to graphene transfer to enhance the stability of composite membranes. With pore creation by argon plasma, the graphene membrane showed a rejection of ∼90% to Allura Red (496.42 g mol⁻¹) in DMF at 100 °C for 10 d and a pure solvent permeance of 24.1 L m⁻² h⁻¹ bar⁻¹, which is one to two orders of magnitude higher than polymeric membranes for OSN reported in the literature (3, 6, 11, 24).

Results and Discussion

Solvent Transport through Graphene via MD Simulation.

To understand the permeation of organic solvents across subnanometer- and nanometer-sized pores of monolayer graphene, an MD study was performed (Fig. 1A and SI Appendix, Supplementary Note I). A series of pores with cut diameters (d_c, the pore size before functionalization) of 0.67 to 1.08 nm was drilled in the graphene lattice, and their edges were then computationally decorated with –OH and –COOH functional groups that are likely formed during pore creation by plasma or chemical treatment (25). Depending on the degree of functionalization, which is defined as the percentage of functionalized carbon over all carbons along the pore edges, three types of graphene pores were created (no functionalization, 25% functionalization, and 50% functionalization) (SI Appendix, Fig. S2), giving different effective aperture sizes (d_a) as shown in SI Appendix, Table S1. SI Appendix, Fig. S3 A and B shows the rate at which ethanol molecules permeate across a single pore (numbers nanosecond⁻¹ bar⁻¹). Typically, subnanometer-sized pores can be generated by plasma and chemical treatment at a porosity of ∼1% (20, 22, 26). If we assume 1% porosity, the aforementioned flows of ethanol molecules can be translated into permeances (liters meter⁻² hour⁻¹ bar⁻¹) as shown in Fig. 1B and SI Appendix, Fig. S3C. For 25%-functionalized graphene with a cut diameter of 0.95 nm, the ethanol permeance is 251.9 L m⁻² h⁻¹ bar⁻¹.

Fig. 1.

MD simulation of ethanol transport across graphene and analysis of support design based on the resistance model. (A) A schematic of MD simulations of ethanol transport through nanoporous graphene. (B) Computed ethanol permeance for nanoporous graphene at a porosity of 1% for different graphene cut diameters (d_c) with various degrees of functionalized groups. (C) Free energy profiles for ethanol along the graphene pore (Z-axis direction). (D) A schematic showing the flow-through graphene-covered membrane. (E) Equivalent resistance network for the flow-through graphene-covered membrane. (F) The ratio of defect permeance over total permeance (η) as a function of defect ratio and support permeance, based on nanoporous graphene at a porosity of 1%, graphene cut diameters (d_c) of 0.95 nm with 25% functionalization, and support surface porosity of 10%. (G) The ratio of defect permeance over total permeance as a function of support pore diameter and support surface porosity based on nanoporous graphene at a porosity of 1%, graphene cut diameters (d_c) of 0.95 nm with 25% functionalization, tortuosity of 50, and thickness of 200 nm.

In general, solvent permeation through graphene is governed by the aperture size and functionalization. At comparable aperture size, the 25%-functionalized graphene (0.49 nm) exhibits higher ethanol permeance than the nonfunctionalized graphene (0.51 nm), while the 50%-functionalized graphene shows the lowest permeance (SI Appendix, Fig. S3C). To understand the impact of functionalization, the histogram sampling method (27) was adopted to qualitatively estimate the free energy barrier along the graphene pore (Z axis):

$$F\left(Z\right)=-RT\text{ln}\left[P\left(Z\right)\right],$$ [1]

where F(Z) is the free energy profile, P(Z) is the density profile at position Z, R is the Boltzman constant, and T is the temperature (28). Fig. 1C plots $-\text{ln}P\left(Z\right)$ of ethanol along the Z direction of the three types of graphene nanopores with comparable aperture size. It is clearly seen that 50%-functionalized graphene exhibits the greatest energy barrier for ethanol transport, followed by nonfunctionalized graphene; 25%-functionalized graphene shows the lowest barrier. This is consistent with simulated ethanol permeances. Further analysis of the radial distribution functions g(r) for ethanol around different functionalities is provided in SI Appendix, Supplementary Note II and Fig. S4, which depicts strong peaks at 0.28 nm around the –OH groups bonded to –C or –CO and a much weaker peak around the –C=O group. It suggests that the close interaction between –OH and ethanol might primarily account for the accelerated ethanol permeation across 25%-functionalized graphene. However, at a high functionalization degree of 50%, such strong interactions and the reduced diameter of the pores (SI Appendix, Table S1) pose large energy barriers to slow down the transport of ethanol.

Modeling of Solvent Permeation and Support Design.

A support layer beneath graphene is essential for the practical application of monolayer graphene membranes. The supporting layer has significant impact on the transport across the composite membrane, and if properly designed, can effectively mitigate the leakage through defects while maintaining reasonable flux. Here, a pressure-driven transport model was developed to guide the design of the defect-tolerant graphene composite membrane and predict the membrane performance for OSN. The flow-through monolayer graphene via in-plane pores (29) is shown in Fig. 1D. The graphene composite membrane could be considered as an equivalent resistance network (30), where flow could go through perfectly selective nanopores or defects in graphene and subsequently, the support pores (Fig. 1E). For support pores covered by nanoporous graphene, the flow experiences in-series resistances of nanopores of graphene and support pores. For support pores exposed to defects which show negligible resistance, flow encounters a short circuit through graphene (20). This model is described in more detail in SI Appendix, Supplementary Note III. Based on the graphene permeance (P_g), defect ratio across graphene (γ, the fraction of graphene-free area due to defects), permeance of support (P_s), and support’s surface porosity (ε) as input parameters, the transport model was applied to estimate the total permeance of the graphene composite membrane (P) and the ratio of nonselective permeance through defects over the total permeance (η).

The impacts of defects on graphene composite membrane are plotted in Fig. 1F, based on 25%-functionalized nanoporous graphene with a cut diameter of 0.95 nm and 10% support porosity. We see that a lower support permeance is beneficial for minimizing the impact of leakage on transport due to the increasing resistance of the support; but on the other hand, the low support permeance also causes much hindrance to total transport (SI Appendix, Fig. S6A). At a typical defect ratio of 5% (i.e., 95% of the support covered by graphene), a support permeance of <30 L m⁻² h⁻¹ bar⁻¹ is required to lower the ratio of leakage through defects over total permeance to <10%, so that the membrane rejection can possibly reach >90%. Noticeably, the total membrane permeance will sharply decrease if the support permeance is less than 20 L m⁻² h⁻¹ bar⁻¹. Increasing the pore size or porosity of graphene is also helpful in reducing leakage, but this is limited by currently available pore creation methods (SI Appendix, Figs. S6 B and C and S7).

Since the support permeance can usually be described by the Hagen–Poiseuille equation (31), we further analyzed the support design in terms of its porosity and pore size. The membrane thickness of 200 nm and tortuosity of 50 that are frequently observed in the dense layer of supporting substrates made from phase inversion (32–34) were used (analyses of the effects of thickness and tortuosity are provided in SI Appendix, Fig. S8). Combining this equation with the resistance model, we see that the changes in support porosity have negligible impact on the contribution of defects (Fig. 1G), yet a larger support porosity could enhance the overall permeance (SI Appendix, Fig. S8A). On the other hand, smaller support pore size is beneficial for mitigating leakage through defects, primarily through its effect on reducing permeance (Fig. 1F). The model predicts that, at 10% surface porosity (35, 36), a support with pore size of 10 nm is optimal to limit the contribution of defects to <10% of total permeance while keeping a reasonable permeance.

Fabrication of the Nanoporous Monolayer Graphene Membrane over P84 Support.

In addition to appropriate permeance and pore size, the chemical and structural stability of the support membrane in harsh solvents is another key factor to the success of monolayer graphene membrane for OSN. P84 PI was chosen for its unique physicochemical properties, including high-temperature stability, mechanical robustness, and readiness for chemical cross-linking (37, 38). The P84 support (denoted as M_S) was fabricated according to the protocol shown in SI Appendix, Fig. S9A. Here, we applied a DMF pretreatment step to adequately swell the substrate prior to graphene transfer to avoid damage in the later application stage (SI Appendix, Supplementary Note IV). The as-prepared P84 support (M_S) presents an ethanol permeance of 22.06 L m⁻² h⁻¹ bar⁻¹ (Fig. 2D). As shown in Fig. 2 A and B, macrovoids with typical finger-like structure and a 250-nm-thick dense spongy-like top layer are observed on the cross-section of cross-linked P84 membrane (M_S). The top surface (Fig. 2C and SI Appendix, Fig. S9F) is porous with a mean pore size of 10.3 nm and a porosity of 7.2% (quantified by ImageJ) (SI Appendix, Fig. S9H). With the known mean pore size, porosity, and thickness of the selective layer (250 nm), the pore flow model was used to estimate the ethanol permeance across the membrane. A value of 20.84 L m⁻² h⁻¹ bar⁻¹ is predicted according to the classic Hagen–Poiseuille equation (39), based on an estimated tortuosity of 50 (34), which agrees well with the experimental result. The permeance and pore size of the support fall into the optimal range of values given by the resistance model, making it a good candidate for the fabrication of defect-tolerant graphene composite membranes.

Fig. 2.

Preparation of the nanoporous monolayer graphene membrane over P84 support. FESEM images of (A and B) cross-sectional and (C) the top surface of the cross-linked P84 membrane (M_S) prepared following the optimized protocol. The nonwoven support was peeled off for capturing FESEM images. (D) Plot of ethanol permeance with time for M_S. (E) Schematic of the fabrication process of graphene–P84 composite membranes. (F) A photo of the graphene–P84 composite membrane. (G) A photo showing the graphene–P84 composite membrane that has been immersed in DMF for 8 mo. (H and I) FESEM images of the top surface of the graphene–P84 composite membrane.

Next, nanoporous graphene–P84 membranes were prepared following the protocol given in Fig. 2E. A photo of the centimeter-scale graphene membrane is shown in Fig. 2F. The membrane showed exceptional stability in organic solvents, even after immersion in DMF for 8 mo (Fig. 2G and SI Appendix, Fig. S10). Field emission scanning electronic microscopy (FESEM) images in Fig. 2 H and I show the characteristic wrinkled structure of monolayer graphene on top of the surface of the P84 substrate.

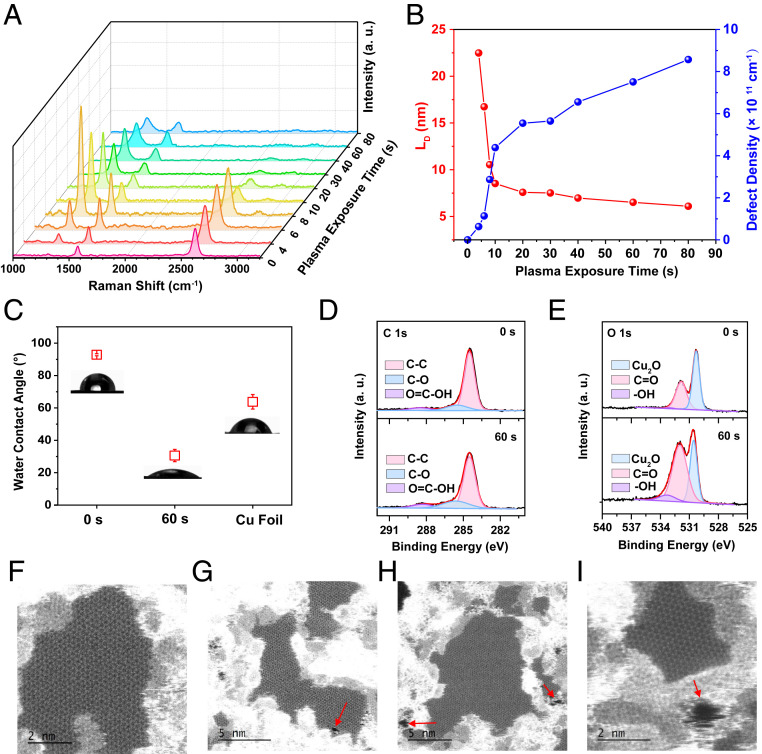
Raman spectroscopy was applied to quantitatively estimate the pore density of our graphene samples on copper after exposure to argon plasma. As shown in Fig. 3A, no discernible defect D peak (∼1,345 cm⁻¹) is seen in the spectrum for pristine graphene, indicating its high quality (40). The intensity of the second-order 2D peak (∼2,680 cm⁻¹) is more than threefold stronger than the G peak, confirming the single-layer structure of graphene (41). At short plasma exposure time, the intensity of the D band is substantially enhanced. The I_D/I_G ratio can be applied to evaluate the pore density in graphene (SI Appendix, Fig. S12A and Supplementary Note V) by introducing a typical length L_D, which represent the mean distance between two pores (41). As shown in Fig. 3B, L_D decreases with the plasma etching time, indicating an increase in the pore density. The pore density n_D (centimeters⁻²) was then calculated as follows (40)

$$n_D\left({\text{cm}}^{-2}\right)={10}^{14}/\pi L_D^2.$$ [2]

After plasma exposure for 60 s, the pore density reaches 0.91 × 10¹² cm⁻². Scanning transmission electron microscopy (STEM) images of graphene with exposure to argon plasma for 60 s clearly show the emergence of ∼1-nm- and subnanometer-sized pores, at a pore density of around 1.08 × 10¹² cm⁻² and a porosity of ∼0.92% (Fig. 3 F–I and SI Appendix, Fig. S13).

Fig. 3.

Creation of nanopores on graphene. (A) Raman spectra of the graphene on copper samples vs. argon plasma exposure time. (B) The mean distance between defects L_D (nanometers) and the defect density n_D (centimeters⁻²) of graphene samples vs. argon plasma exposure time. (C) The average water contact angles of graphene samples vs. argon plasma exposure time. Cu foil was ultrasonic washed for 15 min successively with deionized water, ethanol, and acetone and then exposed to argon plasma for 300 s. (D) C 1s and (E) O 1s for graphene samples before and after exposure to argon plasma as characterized by XPS. (F–I) STEM images of the graphene sample with exposure to argon plasma for 60 s. The red arrows indicate nanopores generated in the graphene lattice.

The surface chemistry of the graphene–Cu samples was then probed by X-ray photoelectron spectroscopy (XPS). As shown in Fig. 3D, C 1s spectra were fitted with three peaks corresponding to sp² carbon (∼284.5 eV), C–O bond (∼285.6 eV), and –O=C–OH (∼288.3 eV) (42). The intensities of the two oxygen-related peaks are significantly increased after exposure to argon plasma. This is in agreement with the presence of hydroxyl and C=O groups in O 1s peaks (Fig. 3E and SI Appendix, Supplementary Note VI) (43), which may be attributed to the generation of reactive defects during plasma exposure and their subsequent oxidation by oxygen or water in the air (44, 45). This is further confirmed by water contact angle measurements. In Fig. 3C, the average contact angle of the pristine graphene on Cu foil is 92.9° ± 0.6°, which decreases to 30.6° ± 3.8° after exposure to argon plasma for 60 s.

Molecular Transport across Monolayer Graphene Membranes in OSN.

Pure ethanol permeation through graphene–P84 composite membranes was systematically investigated and presented in Fig. 4A. The pristine graphene–P84 membrane showed an ethanol permeance of ∼0.84 L m⁻² h⁻¹ bar⁻¹, giving an estimated defect ratio of ∼4%. The permeance of the graphene–P84 composite membranes increased with plasma etching time, which supports the existence of pores induced by the argon plasma treatment. An ethanol permeance of ∼9.5 L m⁻² h⁻¹ bar⁻¹ was reached when graphene was exposed to plasma for 60 s (denoted as M_60). The permeance based on the graphene area, obtained according to the series resistance model (SI Appendix, Supplementary Note VII), is plotted in SI Appendix, Fig. S15, giving a value of 226.0 L m⁻² h⁻¹ bar⁻¹ for monolayer graphene with 60 s of argon plasma treatment. This is comparable with the simulated result of 25%-functionalized graphene with a cut diameter of 0.95 nm. A 50-ppm solution of Rose Bengal in ethanol was then employed to test the selectivity of graphene membranes. As shown in Fig. 4B, the rejection to Rose Bengal significantly improved when nanoporous graphene was transferred onto the P84 support, giving a value of 92.6% at 60 s of plasma exposure. We also compared our measured results with model predictions (SI Appendix, Supplementary Note VIII). The model results are well matched with the measured values. When the argon plasma etching time was increased to 80 s, the rejection declined to 80.7%, suggesting that some of the pores created by argon plasma under this condition may be bigger than the size of the Rose Bengal molecule.

Fig. 4.

Membrane performance at room temperature. (A) Pure ethanol permeance through graphene–P84 composite membranes with different plasma etching durations of 0, 40, 60, and 80 s, which are denoted as M_0, M_40, M_60, and M_80, respectively. M_S is the support without graphene. (B) Rejection to Rose Bengal (1,017.64 g mol⁻¹) in ethanol through graphene–P84 composite membranes after 24 h of nanofiltration tests. (C) Rejection behavior of M_60 vs. the critical diameter (d*) of various dyes in ethanol. MO, Methyl Orange; ARAC, Allura Red AC; RB, Rose Bengal; BBR, Brilliant Blue R; MB, Methylene Blue; CV, Crystal Violet; R6G, Rhodamine 6G; AB, Alcian Blue. Plus and minus symbols denote cationic and anionic dyes, respectively. The critical diameter d* here defined the smallest permeable diameter of the dye molecule. (D) The solvent permeance of M_60 against the solubility parameter multiplied by the inverse of viscosity. Error bars represent SDs for three different measurements for each data point.

The rejection of M_60 was further examined by a series of dyes with different molecular geometry (SI Appendix, Fig. S16) and charges. Here, we defined the critical diameter (d*) as the smallest permeable diameter of the dye molecules (SI Appendix, Supplementary Note IX) and assumed that the pore in graphene must be larger than d* in order to permeate the dye molecules (18). It is worthy to note that the critical diameter may not strictly represent the smallest permeable pore size of graphene, as dye molecules are likely to rotate, deform, twist, and bend when they pass through the nanopore (18). A clear size-dependent selectivity is observed in Fig. 4C with a size cutoff of ∼1 nm, which is in agreement with STEM observations of the formation of ∼1-nm pores in the graphene after argon plasma treatment. In addition, positively charged dyes show lower rejection compared with negatively charged ones. Since the pore edges of graphene are functionalized by negatively charged oxygen-rich groups as evidenced by XPS and water contact angles, it is reasonable to see slightly higher rejection to negatively charged dyes in ethanol due to Donnan exclusion (46).

The permeance of five different solvents through the graphene–PI composite membrane (M_60) and the substrate (M_S) was measured and plotted against the solvent properties in Fig. 4D and SI Appendix, Figs. S17 and S18. SI Appendix, Fig. S18A demonstrates that the correlation between solvent permeance and μ⁻¹ (μ: viscosity of solvent) for the graphene composite membrane is nonlinear (R² = 0.192), implying that other factors might also be affecting solvent transport, such as the Hansen solubility parameter (δ_p) and the molar diameter of the solvent (d_m) (47). Plotting permeances against δ_p μ⁻¹ and δ_p μ⁻¹ d_m⁻² gives R² of 0.842 and 0.830, respectively (Fig. 4D and SI Appendix, Fig. S18B). The relatively low R² may be due to the effects of the cross-linked P84 substrate, as the substrate showed weak correlation between permeance and δ_p μ⁻¹ (SI Appendix, Fig. S17). It is noticed that the support greatly affects the transport of solvents across the composite membranes since the ethanol permeance across the support is in the same order of magnitude as that of simulated monolayer graphene. To decouple the effects of supports and further look into the transport across monolayer graphene, permeances of different solvents were extrapolated for monolayer graphene based on the resistance model (SI Appendix, Supplementary Note X). We notice that in the extreme case when the permeance of a given solvent is much higher than that of a single support pore, it is likely that the resistance from the support dominates, and the extrapolated data may not be accurate. As plotted in SI Appendix, Fig. S19C, a strong correlation between permeance and δ_p μ⁻¹ is found. It reveals that solvent–graphene interactions play an important role in the permeation of solvents.

Molecular Separation in High-Temperature Harsh Organic Solvents.

Given the industrial importance and current challenges of separations in high-temperature harsh organic solvents, the performance of M_60 was evaluated at different temperatures using DMF as the solvent. The stability of the M_S and graphene in DMF at high temperature is studied in SI Appendix, Supplementary Notes XI and XII. Fig. 5A presents the rejection of M_60 vs. various dyes in DMF at ambient temperature, again showing size cutoff of ∼1 nm. Furthermore, as shown in Fig. 5B, the pure DMF permeance increases with temperature, reaching a value of 24.1 L m⁻² h⁻¹ bar⁻¹ at 100 °C. This permeance is higher than prior literature work by one to two orders of magnitude (3, 6, 11, 24) (SI Appendix, Table S8). The increased permeance could be largely explained by the reduced viscosity of DMF. To compare the permeance changes vs. the viscosity changes, the permeance (P_T) at temperature T was calculated based on the DMF permeance at 25 °C (P₂₅) and taking viscosity μ as the only variable,

$$\hspace{1em}{P}_T=P_{25}\times \frac{{\mu }_{25}}{\mu },$$ [3]

where μ₂₅ is the viscosity of DMF at 25 °C. As shown in Fig. 5B, the experimental values follow similar trends with the calculated permeance as the temperature increased, suggesting that decrease in viscosity can explain the increase in permeance with temperature. Slight variations might be due to other factors such as energy barrier, effective intrapore viscosity, and changes of support (48, 49). Meanwhile, the rejection declines slightly as temperature increases from 25 °C to 100 °C (Fig. 5C). The loss in rejection may be due to the rearrangement of the cross-linked P84 substrate at higher temperature (49). In addition, since we have earlier revealed the existence of energy barrier for ethanol transport, some energy barriers might also exist for solutes, given their relatively large size and hydrophilic nature. Therefore, solutes can more easily pass through the graphene pores at higher temperature, resulting in reduced rejection. It is worthy of note that the rejection of the graphene composite membrane approximately recovered to its initial state (with rejection of 95.90% to Allura Red AC) after the dead-end cells were cooled down (Fig. 5C), indicating that there was no serious structural damage to the selective layer during the high-temperature nanofiltration. Moreover, the membrane demonstrated excellent long-term stability. Over of testing duration of 10 d at 100 °C, a constant rejection of ∼90% to Allura Red AC was observed (Fig. 5D). We have therefore shown here that with the exceptional temperature and chemical stability of graphene, monolayer graphene can be a competitive candidate for molecular separations in harsh organic solvents at high temperature.

Fig. 5.

Membrane performance in high temperature and harsh organic solvent. (A) Rejection behavior of M_60 vs. critical diameter (d*) of various dyes in DMF at room temperature. MB, Methylene Blue; R6G, Rhodamine 6G; ARAC, Allura Red AC; RB, Rose Bengal; BBR, Brilliant Blue R. Plus and minus symbols denote cationic and anionic dyes, respectively. The critical diameter d* here defined the smallest permeable diameter of the dye molecule. (B) Experimental permeance and calculated permeance based on Eq. 3 through M_60 vs. operation temperature. The viscosity at different temperature was calculated based on the previous literature (51). (C) Rejection to Allura Red AC (496.42 g mol⁻¹) in DMF through M_60 vs. operation temperature. (D) Long-term rejection to Allura Red AC (496.42 g mol⁻¹) through M_60 in DMF at 100 °C. Inset photo shows the feed (Left) and permeate (Right) samples for M_60. Error bars represent SDs for three different measurements for each data point.

Conclusions

In summary, defect-tolerant nanoporous graphene-covered P84 membranes have been developed in this study for separations in harsh organic solvents at high temperature via support design. With understanding of solvent permeation through nanoporous graphene by MD study, a resistance model has been established to guide the structural design of the support. A solvent-resistant support with desired properties was then prepared, thus having enabled the fabrication of graphene-covered membranes with a size cutoff of 1 nm and long-term stable filtration in DMF at 100 °C. This work may open opportunities for industrial separation in organic solvents at high temperature and accelerate the realization of the full potential of monolayer graphene.

Materials and Methods

Fabrication of the Ultrafiltration Cross-Linked P84 Substrate.

The P84 substrates were fabricated in a room held at ∼22 °C following SI Appendix, Fig. S9A. In brief, dry P84 PI powder (HP Polymer GmbH) was dissolved in DMF (99.5%; Fisher Scientific) to form a 22 wt % solution, cast on a polyester nonwoven fabric, and then immersed in a water bath. The resulting substrate was then transferred into an isopropanol (IPA; 99.99%; VWR chemicals) bath for solvent exchange, before immersing in a hexadiamine (98%; Sigma Aldrich) solution in IPA (120 g L⁻¹) for 16 h. Afterward, the P84 substrate was taken out and immersed in pure IPA for 3 h. The cross-linked substrates were activated by immersing in a DMF bath for 2 h followed by conditioning with glycerin (>99%; Aik Moh Paints & Chemicals PTE LTD) in IPA solution (mass ratio 3:2) overnight to avoid pore collapse.

Fabrication of Monolayer Graphene Membranes on Cross-Linked P84 Substrate.

Before transfer, nanopores were introduced on the CVD-grown graphene on copper foil (Graphenea, Inc.) by argon plasma (CUTE; FEMTO SCIENCE; 40-W power, 20-standard cubic centimeter per minute Ar) for different durations. Then, the graphene samples were transferred to the cross-linked P84 substrate via poly(methyl methacrylate) (PMMA)-assisted layer transfer. First, 40 µL PMMA with a molecular weight of 15,000 (Sigma Aldrich) in anisole (99.7%; Sigma Aldrich; 4.5 wt %) was spin coated on the centimeter-scale graphene samples at 2,500 rpm for 15 s three times; then, 40 µL PMMA with a molecular weight of 996,000 (Sigma Aldrich) in anisole (4 wt %) was spin coated at 2,500 rpm for 60 s. After drying in the fume hood, the back-side graphene on the Cu foil was preetched in a copper etchant bath, namely 15% ammonium persulfate (APS; ≥ 98%; Sigma Aldrich) in deionized water, for 7 min followed by rinsing with deionized water for 20 min. Then, the Cu foil was etched in another copper etchant bath (5% APS in deionized water) overnight followed by rinsing in deionized water bath three times to remove residual copper etchant. P84 substrate was then used to scoop the PMMA–graphene from the water bath and dried in the fume hood. Finally, the dry PMMA–graphene–P84 film was immersed in acetone overnight to remove PMMA and then transferred into an ethanol (99%; Aik Moh Paints & Chemicals PTE LTD) bath. The reference P84 substrates were prepared in a similar way by using Cu foil instead of the graphene–Cu foil (referred to as M_S). Before use, the Cu foils were ultrasonic washed for 15 min successively with deionized water, ethanol, and acetone.

Characterization methods of graphene and the membrane can be found in SI Appendix.

OSN Measurements.

OSN performance was evaluated via a homemade dead-end stirred cell driven by N₂ gas at 6 bar and under constant stirring speed of 500 rpm, unless otherwise specified. The effective area of sample was around 0.196 cm². Before the rejection tests, pure solvent was filtered through the samples for 1 h at 8 bar to remove impurities. After that, solutions containing 50 ppm of dyes were used as the feed and tested for at least 24 h. Permeance and rejection were recorded until performances were stable. More details can be found in SI Appendix.

MD Simulation.

The system was built within a periodic simulation box of 3.7 × 3.8 × 20 nm³ with around 950 ethanol molecules placed on either side of the porous graphene sheet, and a piston made of perfect graphene was placed on either end of the ethanol phase in order to apply any desired transmembrane pressure. The two-dimensional periodic sheet of porous graphene was modeled by starting with pure graphene and removing some carbon atoms within a circle of various cut diameters from 0.67 to 1.08 nm at the center of the unit cell followed by functionalizing the pore atoms with –OH and –COOH alternatively at no functionalization, 25% degree of functionalization, and 50% degree of functionalization, where the number denotes the percentage of exposed carbon atoms that are functionalized. The aperture sizes (d_a) were estimated by the HOLE code (50), which uses a Monte Carlo simulation annealing procedure to find the best route for a sphere to squeeze through the channel.

CHARMM (Chemistry at Harvard Macromolecular Mechanics) general force field was used to accurately reproduce the geometry structure of pure graphene. The hydroxyl groups and carboxyl groups at the pore edge were described by the parameterization of phenol and benzoic acid, respectively. All MD simulations were performed using the GROMACS package. The whole system was first equilibrated for around 40 ns, and then, constant forces were applied in the Z direction to the piston atoms to mimic the transmembrane pressure (SI Appendix, Fig. S1). The correlation of the solvent flux through the graphene pore as a function of the driving pressure was studied and provided in SI Appendix, Fig. S5.

Data Availability

All study data are included in the article and/or SI Appendix.