Emulation of the BIS Engine

Abstract

Purpose

The operation of the BIS monitor remains undescribed, despite 20 years of clinical use and 3000 academic articles. The core algorithmic software (the BIS Engine) can be retrieved from the motherboard of the A-2000 monitor in binary form through forensic disassembly using debugging interfaces left in place by the original designers, opening the possibility of executing the BIS algorithms on contemporary computers through emulation.

Methods

Three steps were required for emulation. Firstly, the monitor input stage monitor was disassembled to determine how EEG signals can be compatibly presented to the Engine. Secondly, the Digital Signal Processor on which the Engine executes was recreated in software. Thirdly, the Engine code was patched, allowing execution separated from monitor hardware. Code performance under noise load was evaluated.

Results

EEG signals and BIS variables were obtained from a 13-year-old child in normal physiological sleep using a modern BIS monitor. BIS values in sleeping children exhibit a wide dynamic range, including values nominally associated with clinical anesthesia, providing a risk-free technique to obtain empirical EEG data that broadly exercise the algorithms. Emulation demonstrated a correlation coefficient of R=0.943, consistent with correlations between official Engine iterations. Additive white noise in the EEG caused a progressive lifting and flattening of BIS values.

Conclusions

Emulation replicates BIS Engine behavior, allowing calculation upon existing EEG datasets or signals from other, potentially remote or wireless, devices. Emulation provides advantages for elucidating the mathematical expression of the algorithms, which remain important as practical constraints on any hypothetical mechanism of action of anesthetics.

Introduction

Despite more than twenty years of clinical use and more than 3000 related academic publications, the underlying functions of the BIS monitor remain secret. In this regard, the BIS monitor is distinct from all other commonly used anesthesia monitoring devices. Given that its implementation is undisclosed, the BIS is effectively a nostrum for its current indication as, arguably, the de facto monitor for depth-of-anesthesia. Such nostrums should draw our rigorous professional scrutiny.

Previously [1], a careful hardware disassembly of the A-2000 BIS monitor was performed. Due to a small error in the implementation of the Spectral Edge Frequency (SEF) algorithm, predictably idiosyncratic results were output at the device’s external serial port. These values were traced backwards through the system logic to their original point of calculation on a TMS320C32 Digital Signal Processor (DSP) (Texas Instruments, Dallas, TX) on the main circuit board. Using debugging interfaces that had been left in place by the device’s original designers, it was possible to retrieve the binary code for the BIS Engine software (biseng.io, version 1.18) that the DSP executes. A limited and static disassembly of this code was performed, which nevertheless allowed major subroutines to be identified, key algorithmic output points to be determined, and the implementation of known algorithms (SEF, Total Power [2]) to be annotated explicitly and represented mathematically.

With the DSP code in hand, it is natural to ask whether this software can be executed independently of the BIS device hardware. This process is known as emulation, and it involves crafting a sufficient software representation of the device hardware (i.e. an emulation layer) such that the original code can execute successfully in this virtual environment. Emulation of a device that one legitimately owns is protected as being within fair use under US copyright law, as established by the precedents in Sega Enterprises Ltd v. Accolade Inc (1992) and Sony Computer Entertainment v. Connectix Corporation (2000).

Successful emulation immediately allows the BIS algorithms to be applied to available research EEG data of suitable quality. Emulation also provides an invaluable tool in the further analysis of the device’s algorithms, since it allows predictable and predetermined inputs to be applied to the system, and for those algorithms to be executed in a completely monitored and controlled virtual environment. Emulation represents a significant technical advance in reverse engineering over the previous hardware-based debugging approach.

Methods

The previous analysis of the DSP software obtained the disassembled code, and identified the endpoints of key algorithms from which results are obtained and then presented to the anesthesiologist. These results characterized the device output, or back-end. Three further steps are necessary to emulate the software. Firstly, the mechanism of the device inputs, i.e. the front-end, must be characterized so that EEG signals can be presented in a form acceptable to the emulated system. Secondly, the processor hardware must be adequately recreated in software form. Finally, small additional modifications to the software are necessary to support execution in emulation, free from other extrinsic hardware. The behavior of the emulated software was then tested under conditions of increasing additive noise load to estimate precision requirements for the input signal and to assess robustness.

Front-end Characterization and EEG Signal Input

The A-2000 BIS Monitor acquires its EEG inputs via the Digital Signal Converter (DSC), as shown in Figure 1A. Dismantling the DSC (Figure 1B) reveals a clamshell of two densely-populated sister circuit boards (PCBs). Opening these reveals a functional separation into patient-side analog circuitry to receive and amplify EEG signals, and a digital interface to the main device (Figure 1C). Unlike the main PCB in the A-2000 BIS monitor, no residual debugging interfaces are readily apparent here. Nevertheless, one can surmise from inspection that the DSC captures EEG waveforms and renders them into some digital format for transmission to the main device, and subsequently to the TMS320C32 DSP. The nature of that encoding process is best defined by examining the DSP source code to discover how it handles data it receives.

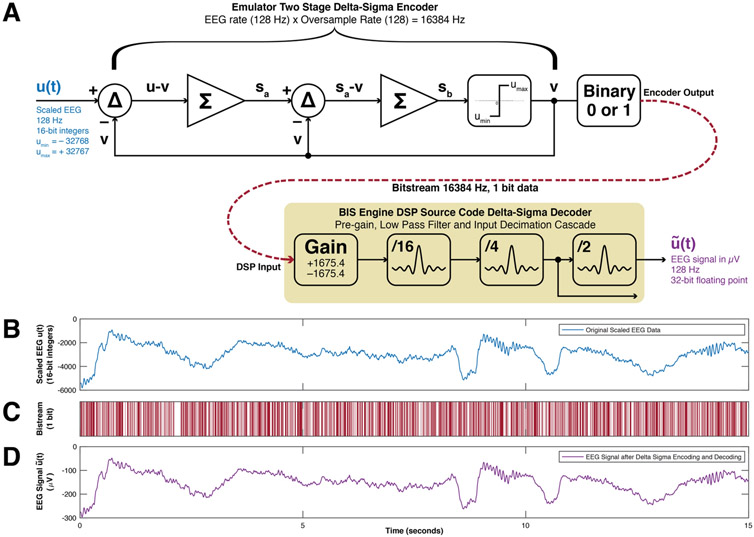
Figure 1:

(A) The BIS XP Digital Signal Converter (DSC), which converts between the analog EEG signals measured from the patient’s forehead and a digital transmission stream to the main device. The DSC also provides electrical isolation between the patient and the device.

(B) The DSC internal circuitry, which is constructed in a clamshell fashion with two circuit boards facing each other with three interconnection points between them. When assembled, this circuitry is wrapped in a flexible, conductive sheet which serves as a ground plane to block electrical interference. This sheet is removed in this image for visibility.

(C) Opening the clamshell reveals that the circuitry is divided into a device side comprised primarily of digital circuitry, and a patient side comprised primarily of analog circuitry. Precision amplifiers are notable on the analog patient side for capturing EEG signals.

A processor is able to respond to external events through the use of interrupts. An interrupt request (IRQ) can be caused by an outside circuit applying a suitable voltage to the matching interrupt pin on the processor chip. When this occurs, the processor stops its current work and jumps to an address in memory specified in an interrupt vector table, where the interrupt handler routine has been placed. This process is known as raising an interrupt. These handler routines are straightforward to locate in the binary code because (i) the code must explicitly identify them itself at initialization when it creates its interrupt vector table, and (ii) interrupt handlers conclude with the instruction retiu (return from interrupt) rather than the more common retsu (return from subroutine). Disassembling and analyzing these interrupt handlers is worthwhile, as they often represent the code’s first point of contact with the outside environment.

The BIS Engine receives EEG data through the interplay of three different interrupt handlers, here named IRQ1, TINT0 and TINT1. IRQ1 is raised by an external source, whereas TINT0 and TINT1 are internal timer interrupts: interrupt routines that can be set to occur in the future, rather like an alarm clock. When IRQ1 is raised, a memory-mapped port address is read at memory location 0x820000, and 2 bits of data are extracted from bit 5 and bit 6 respectively. IRQ1 then resets the TINT0 timer to zero so that it cannot raise until at least 1/8192 of a second has elapsed. If TINT0 ever does raise, then it reads from 0x820000, but treats bits 5 and 6 as being zeros regardless of their actual value. TINT0 then sets itself to raise again in 1/16384 of a second.

When practicing reverse-engineering, the challenge is often to see the forest for the trees, or rather to infer the original designer’s overall intent from the available minutiae. In this case, an interlocking system of interrupts is being used to receive 2 parallel single-bit transmission datastreams in a fail-safe fashion. New data bits are written into 0x820000 at a rate of 16384 Hz by external hardware, and IRQ1 is raised each time so that the processor is notified of the availability of new data bits for the BIS Engine. If, for some reason, these datastreams are interrupted and IRQ1 is not raised in time then, as a fallback, TINT0 will raise instead and simulate receiving zeros until such time as the datastreams are re-established. After 16 bits are received for each channel, TINT1 is immediately raised once only. TINT1 handles further processing. Each bit received as a 1 or 0 is converted into a floating-point value of either +1675.4 or −1675.4 respectively, which represent the maximum and minimum EEG voltages in microvolts that the input stage can process. These values then pass through a sequence of low pass filters and signal rate decimators (16-fold, 4-fold and then 2-fold for a total reduction of 128-fold). The cumulative effect is to decelerate a one-bit resolution digital bitstream at 16384 Hz into an analog EEG waveform at 128 Hz. This block process is highlighted in beige in Figure 2A. More precisely, this process can be recognized as a delta-sigma decoder with 128-fold oversampling. Delta-sigma encoding allows very accurate conversion between analog and digital signals without requiring particularly precise analog components [3]. It is an attractive design solution for high-fidelity digital applications such as professional audio, wireless communications and medical imaging [4,5].

Figure 2:

(A) Block diagram of the digital input system of the BIS Engine for EEG data. For clarity, a one channel input is shown, though the system employs two systems in parallel to input two channels. The DSP receives a 1-bit datastream at 16384 Hz, which is subsequently downsampled by a factor of 128 and scaled to obtain input EEG waveforms in microvolts. The blocks highlighted in beige are implemented by the BIS Engine software as its input system. This input system can be driven by an emulated delta-sigma encoder, as shown, which produces a compatible bitstream from scaled EEG data. u(t) is the scaled EEG input data, v is the encoder feedback path, s_a is the cumulative sum at the first-stage of the encoder, s_b is the cumulative sum at the second-stage of the encoder. Δ produces the difference of its two inputs, and Σ produces the progressive, cumulative sum of its inputs. Respectively, u_min and u_max are the lower and upper bounds on input values. ũ(t) is the received EEG signal.

(B) An example u(t) of a 128 Hz scaled EEG input waveform at 16-bit resolution over a duration of 15 seconds. The waveform is colored blue, as represented in the block diagram in Figure 2A.

(C) The waveform in Figure 2B converted into its equivalent 16384 Hz delta-sigma bitstream. White intervals represent a digital 0 output and red intervals a digital 1, as represented in the block diagram in Figure 2A.

(D) The bitstream in Figure 2C decoded back into microvolts using the digital input decimation and filtering employed by the BIS Engine, purple as shown in Figure 2A.

With the input stage of the BIS Engine characterized, the task then becomes one of converting an input datafile of arbitrary 2-channel EEG data sampled at 128 Hz into a transmission bitstream that is compatible with what the BIS Engine expects to receive. The two-stage delta-sigma encoder [6] with 128-fold oversampling, hence 16384 Hz, as shown in block form in Figure 2A, has a predicted signal-to-noise ratio of 94.2 dB [7]. This is equivalent to 16 bits of accuracy, comparable to the reproduction quality of CD audio. Figures 2B, C and D show, respectively, an example input EEG waveform u(t), its conversion into the delta-sigma digital bitstream, and its subsequent decoding ũ(t). Table 1 shows a straightforward source code implementation in C++ [8] for this two-stage delta-sigma encoder, along with additional commentary. This code loads 2-channel EEG data from a file and converts it into the appropriate bit sequence, raising IRQ1 for transmission of each bit, simulating the behavior of the patient DSC in Figure 1. This emulation of the encoder is able to read EEG data from any file-like object that the host operating system supports, thus also potentially allowing the streaming of EEG data over a network or from a wireless source.

Table 1:

Example source code in C++ for software emulation of a delta-sigma EEG encoder that produces output compatible with the block diagram of the A-2000 DSP input stage shown in Figure 2A, with additional commentary. The code is written for clarity and expressive quality, rather than robustness or idiomatic succinctness.

Example Routines for Emulation of an EEG Delta Sigma Encoder	Commentary
TIMER_CALLBACK_MEMBER(bis_state::updateDeltaSigmaEncoder) { double u[2]; uint32_t bitmask; for (int ch = 0; ch < = 1; ch++) { u[ch] = m_uPrev[ch] + (m_uNext[ch] - m_uPrev[ch]) * m_tic / 128; m_sa[ch] = m_sa[ch] + u[ch] - m_v[ch]; m_sb[ch] = m_sb[ch] + u[ch] - m_v[ch]; bitmask = 1 << (ch + 5); if (m_sb[ch] >= 0) { m_v[ch] = 32767; m_dsp_memory[0x820000] = ~bitmask; } else { m_v[ch] = −32768; m_dsp_memory[0x820000] ∣= bitmask; } } m_tic++; if (m_tic > 128) m_tic = 128; m_dsp->set_input_line(TMS3203X_IRQ1,ASSERT_LINE); }	The routine updateDeltaSigmaEncoder is automatically called by a timer at rate of 16384 times per second, matching the EEG rate of 128 Hz oversampled 128 times. Variables beginning with m_ are class members. There are two EEG channels, numbered 0 and 1. Calculate u(t) by linearly interpolating values in time. Calculate the first delta sigma stage. (Figure 2A) Calculate the second delta sigma stage. (Figure 2A) Make a binary mask: bit 5 for channel 0, 6 for channel 1. Quantize based on the output from delta sigma stage 2. - Set v to the maximum possible value, +32767. - Clear the EEG signal input bit in the DSP memory map. OR - Set v to the minimum possible value, -32768. - Set the EEG signal input bit in the DSP memory map. Increase the oversample tic counter. There are 128 tics before new EEG values are obtained. Don’t let the tic counter go past 128, to prevent the linear interpolator from extrapolating outside of the available values. Raise interrupt request 1 on the DSP to trigger processing.
TIMER_CALLBACK_MEMBER(bis_state::updateEEG) { m_tic = 0; for (int ch = 0; ch <= 1; ch++) { m_uPrev[ch] = m_uNext[ch]; m_uNext[ch] = readNextScaledEEG(); } }	The routine updateEEG is automatically called by a timer at a rate of 128 Hz, matching the EEG rate. The tic counter for the linear interpolation is reset. For each of the two channels, the next EEG value is moved to the previous EEG value, and a new EEG value is read in.
double bis_state::readNextScaledEEG() { uint8_t buffer[2]; double x = 0; if (m_eegFileDevice->input(buffer,2) == 2) { x = buffer[1] * 256 + buffer[0]; if (x >= 32768) x = x - 65536; } return x; }	The routine readNextScaledEEG loads in the next scaled EEG value from the input file (or any file-like datastream). Each scaled EEG value occupies two bytes. If two bytes cannot be read into a buffer (i.e. if the end of the file has been reached) then a value of zero is returned but, alternatively, one could exit the program as completed. The smaller byte is read first (i.e. little endian format). Values greater than +32767 actually represent negative values, and so need to be shifted accordingly.

Processor Emulation

The BIS Engine executes on the TMS320C32 DSP. As previously observed [1], this microchip is already emulated in part by MAME, the Multiple Arcade Machine Emulator. It is an essential component in the Midway Zeus series of arcade machines, notable for such titles as Mortal Kombat 4 (Midway Games, Chicago, IL). The MAME software code that emulates the TMS320C3x processor [9] was written by Aaron Giles and is open-source software under the terms of the 3-clause BSD license (https://opensource.org/licenses/BSD-3-Clause). While this existing TMS320C3x emulation is complete to the extent required to run complex arcade games, it does lack certain features that are essential to the BIS Engine that must be implemented. These are a memory access mode unique to DSPs known as bit-reversed indirect addressing, and additional on-chip peripherals such as timers and direct memory access (DMA).

Bit-reversed Indirect Addressing

In order to process signals, DSPs frequently perform Fast Fourier Transforms (FFT) [10] in order to convert between the representation of a signal in time and its equivalent dual representation as a frequency spectrum, thus allowing signal filtering and transformation to be performed in whichever domain is appropriate. The efficiency with which a DSP can perform FFTs is a core performance benchmark, and so these devices often include specialized hardware enhancements to facilitate the process. Bit-reversed indirect addressing [11] is one such DSP memory access technique that allows specialized FFT algorithms to retrieve and process data more efficiently, but this memory access mode does not exist on more general, desktop processors. Table 2 presents code in C++, with additional commentary, that recreates the functionality of these missing, necessary DSP instructions [12] as used in the BIS Engine to convert EEG waveforms into epochs of frequency spectra.

Table 2:

Example source code in C++ for the emulation of bit-reversed indirect addressing, an unusual memory access mode implemented on the TMS320C32 DSP, and used by the BIS Engine software for efficient calculation of Fast Fourier Transforms.

Example Emulation of DSP Bit-Reversed Addressing	Commentary
uint32_t tms3203x_device::mod19(uint32_t op, uint8_t ar) { // Emulates the bit-reversed addressing mode *ARx++(IR0)B. int reg = TMR_AR0 + (ar & 7); uint32_t result = IREG(reg); IREG(reg) = bitrev(bitrev(IREG(reg))+bitrev(IREG(TMR_IR0))); return result; }	The routine mod19 is called to emulate the bit-reversed addressing mode on the TMS320C32 DSP. This mode is a variant of the Indirect With Postindex Add and Modify mode, written *ARx++(IR0) where ARx is one of the Auxiliary Registers AR0-AR7, and IR0 is one of the Index Registers. A value is retrieved from the memory location in ARx, and then ARx is incremented by IR0. This is useful for accessing tables. In bit-reversed mode, *ARx++(IR0)B, the increment by IR0 is instead performed with bits carried rightwards. This creates an unusual memory access pattern that is ideal for quick calculation of FFTs.
uint32_t tms3203x_device::bitrev(uint32_t x) { x = ((x & 0xffff0000u) >> 16) ∣ ((x & 0x0000ffffu) << 16); x = ((x & 0xff00ff00u) >> 8 ) ∣ ((x & 0x00ff00ffu) << 8 ); x = ((x & 0xf0f0f0f0u) >> 4 ) ∣ ((x & 0x0f0f0f0fu) << 4 ); x = ((x & 0xccccccccu) >> 2 ) ∣ ((x & 0x33333333u) << 2 ); x = ((x & 0xaaaaaaaau) >> 1 ) ∣ ((x & 0x55555555u) << 1 ); return x; }	The routine bitrev is an efficient way to reverse the order of the bits in a 32-bit number, here in the variable x. In the first step, the top 16 bits are slid 16 places to the right, and are recombined with the bottom 16 bits slid 16 places to the left. Next, the top 8 bits change places with the next adjacent 8 bits. This process is repeated with groups of 4 bits, 2 bits, and finally each bit swaps place with its immediate neighbor. The result of this line-dance is that the whole bit order is reversed in only 5 steps. Interestingly, these 5 steps can be performed in any order.

Timers and Direct Memory Access (DMA)

The DSP includes additional circuitry to support the main functioning of the processor, known as on-chip peripherals, whose operation is documented exhaustively in the processor’s technical literature [11]. It is not necessary to replicate these functions in software completely; it is sufficient to implement only those features on which the emulated code relies. As described above, the BIS Engine relies on precise timer interrupts to operate its input stage. DSP timers 0 and 1 are each controlled through a set of memory-mapped registers and raise interrupts TINT0 and TINT1 when appropriate.

DMA is circuity that is capable of copying blocks of memory from one location to another, sometimes performing rudimentary operations on the data while in transit. It acts as a form of primitive co-processor, allowing the main processor to perform more complex operations while offloading these menial, repetitive tasks for parallel execution. In a more practical context, home computers of that era would commonly use DMA to manipulate on-screen graphics, allowing for games of greater immersivity than their comparatively underpowered processors would have otherwise allowed [13].

Code Modifications for Emulation

In the BIS A-2000 monitor, the main ARM processor is used to initialize the DSP, and it loads the BIS Engine software into the DSP in an elaborate boot sequence that involves the internal transfer and reassembly of packets of program code. It is unnecessary to replicate this process for emulation. The complete BIS Engine code can be placed directly into the emulated DSP’s memory, and the address of the first instruction can be placed into the DSP’s reset vector so that it begins executing this code immediately on starting up. As an allegory, if one were “emulating” the function of an anesthesiologist, then this is like starting the emulation from the moment that the anesthesiologist first arrives in the operating rooms to begin work; it is not necessary to recreate the “initialization process” of the anesthesiologist waking up and commuting to the hospital.

The DSP engages in communication with the rest of the A-2000 machine via an on-board serial bus. It uses this mechanism to transmit reformatted versions of its processed variables, such as the BIS value, to other monitor hardware for further display to the anesthesiologist. It is unnecessary to recreate this process because emulation allows complete introspection into the DSP memory. These values can instead be retrieved automatically from emulated memory at the moment they are written.

The DSP receives commands over the serial bus; these commands are formatted as a sequence of bytes that compose a packet or datagram. These commands control features such as whether special EEG filters should be used, whether results should be processed and, if so, which ones. Rather than implement a mechanism to transmit these commands, it is more efficient to modify the BIS Engine code so that it simply behaves as if the desired commands had already been received. Only three such modifications are needed:

1. Placing nop (no operation) over the instruction at 0x8F710E causes the code to always process results if data are available.

2. Placing nop at instruction at 0x8F710E causes all result variables to be processed.

3. Placing ldiu #0, r0 (load integer 0 into register r0) at instruction at 0x8FA06D allows the main processing loop to avoid an externally-mediated halting condition.

These alterations are straightforward only in an emulated environment: the code can be modified during initialization as above, immediately after it has been loaded into emulated memory but before execution begins. No similar opportunity is available on the hardware system.

Signal Noise Analysis

Noise was added to the input signal u(t) either as uniformly distributed white noise or as pure sine waves to simulate electricity supply interference at 50 Hz (Europe) or 60 Hz (USA) to determine the magnitude of the effects on the algorithm outputs. Simulated noise amplitudes were increased in logarithmic intervals (and hence linearly in power in decibels) from 1 μV to 100 μV, and were applied to the two EEG channels in common mode so that the same simulated noise waveform appeared on both channels as if being induced by a nearby source of electrical interference such as an electrocautery unit or a poorly-isolated motor.

Results

Emulation produces a practical equivalence in BIS values. The author’s thirteen-year-old son assented to be monitored at home, using a BIS Vista monitor (Figure 3A) retired from clinical use, on one occasion during regular night-time sleep. Natural physiological sleep in pediatric patients produces a wide range of BIS values, including those usually associated with deep clinical anesthesia [14,15,1], and thus provides a risk-free method for acquiring empirical EEG test data that broadly engage the underlying algorithms. The BIS Vista recorded processed values at a rate of 1 Hz and 2-channel scaled 16-bit resolution EEG data at 128 Hz (compatible with the delta-sigma encoder in Table 1) to a USB output (Figure 3B) over a continuous sleep interval of 3 hours and 45 minutes. This dataset was retrieved using the code shown in Table 3, compatible with Matlab (Mathworks, Chestnut Hill, MA) or Octave [16]. The resultant EEG data was streamed into the BIS Engine emulator. The BIS Engine is purely a calculation engine and does not define how its results are presented. The emulation layer displays these results in a simple monochrome, numerical format as seen in Figure 3C. To eliminate any discontinuities from starting or stopping the EEG datastream in emulation, BIS values were excluded from the first and last 2 and half minutes, producing a total dataset of 13200 pairs (acquired, emulated) of BIS values. Alignment of the data pairs over time demonstrates their practical equivalence, as shown in Figure 4A.

Figure 3:

(A) Rear aspect of the BIS Vista monitor showing the location of a USB-A port which can be used to record patient EEG and processed parameters to a study dataset.

(B) An example study dataset recorded to a USB flash disk. The SPA file contains processed patient parameters in text format; the R2A file contains two channels of scaled EEG data stored, interleaved, as signed 16-bit integers.

(C) Example output of the A-2000 BIS Engine emulator. As shown here, the BIS Engine software biseng.io for the TMS320C32 DSP processor is being run within the MAME emulator framework on a desktop computer, wholly divorced from the original hardware implementation.

Table 3:

Example source code (compatible with both Matlab and Octave) to extract processed variables and scaled EEG data from a dataset stored on a USB device by a BIS Vista monitor, and also to apply the correct microvolt scaling to the EEG data.

Example Retrieval of EEG Data and Variables from the Vista USB

Commentary

function [t,BIS,EMG,SEF,POW,EEG,EEGuV] = readStudyFromUSB(studyID) fid = fopen(fullfile(studyID,sprintf('%s.spa',studyID)),'rt'); c = textscan(fid,repmat('%s',1,54),'Delimiter','∣','Headerlines',2); fclose(fid); t = c{1}; SEF = cellfun(@(x)str2double(x),c{37}); SEF(SEF<0) = NaN; BIS = [cellfun(@(x)str2double(x),c{12}) … cellfun(@(x)str2double(x),c{26}) … cellfun(@(x)str2double(x),c{40})]; BIS(BIS<0) = NaN; POW = cellfun(@(x)str2double(x),c{43}); POW(POW<0) = NaN; EMG = cellfun(@(x)str2double(x),c{44}); EMG(EMG<0) = NaN; fid = fopen(fullfile(studyID,sprintf('%s.r2a',studyID)),'rb'); EEG = fread(fid,[2 inf],'int16'); fclose(fid); EEGuV = EEG * 1675.42688 / 32767;

Unlike the BIS A-2000, whose only output is a low bandwidth RS232 serial port, the BIS Vista has a rear-facing USB port that can be used to store study data on common USB flash drives. The stored studies have a standard file structure format. The SPA file contains a large plaintext tabulation of the processed variables produced by the monitor. This is similar to, but more complete, than the similar tabulation presented over the A-2000 serial port. These values can be read and extracted by simple, appropriate text parsing of the SPA file. Additionally, EEG data is stored in a scaled format as signed 16-bit integers (−32768 to +32767) in the R2A file. The data is channel-interleaved. The scaled EEG data can be converted into microvolts by multiplying by a 0.0511 uV/step scale factor.

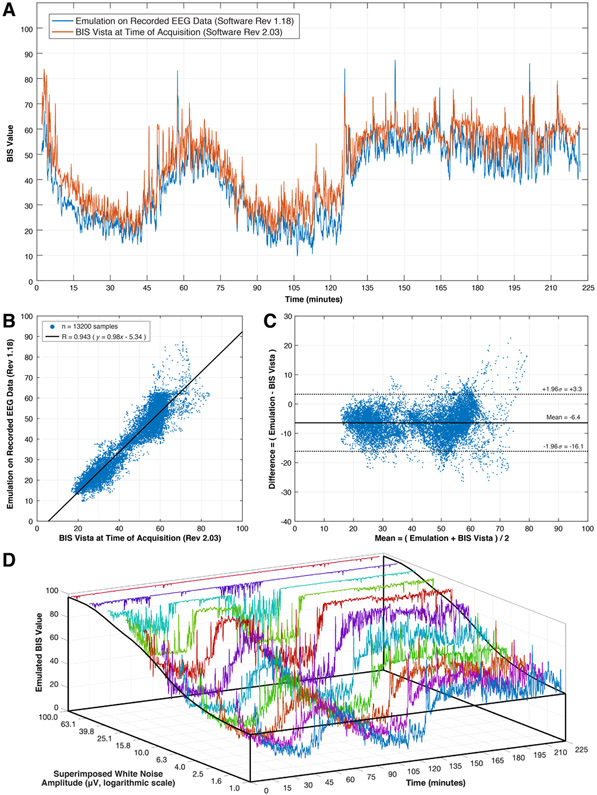
Figure 4:

(A) Channel 1 BIS output from the A-2000 BIS Engine emulator (blue) and the processed output of the BIS Vista monitor at the time of acquisition (red). Note that the A-2000 and the Vista use different revisions of the BIS algorithm, and therefore small discrepancies between them is anticipated.

(B) Correlation plot of the BIS value produced by the BIS Vista and the A-2000 emulator over the interval shown in Figure 4A. A linear fit has a gradient of almost unity, with a small shift in y-intercept. The values are very strongly correlated (Pearson R = 0.943.

(C) Bland-Altman plot of agreement of the data shown in Figure 4B. Outward scatter at higher BIS values may represent revision of the behavior of the algorithm for light sedation, but there is tight agreement in the vicinity of BIS values for usual planes of general anesthesia.

(D) A comparison of emulated BIS values in the presence of artificially superimposed common-mode white noise on the 2-channel input EEG signal. The black contour lines show the time-average of the emulated BIS value over the 225-minute time course.

The versions of the BIS Engine in the Vista and the emulated A-2000 are not identical, and hence some small differences in their output values are expected. The A-2000 monitor cannot export EEG data and so cannot be used directly for this comparison. Nevertheless, the Pearson correlation coefficient between the emulated and BIS Vista values is R = 0.943, which is comparable to the known correlation coefficient between official minor revisions of the software (R = 0.963 between BIS Platform 3.4 and BIS Platform 4.0) [17]. A linear fit between the emulated and BIS Vista values has a gradient of near unity and only a small shift in the y-intercept, as shown in Figure 4B. The null hypothesis of no correlation between the Vista and emulated values is rejected with very high statistical significance (p < 0.000001). The accuracy and precision between the measurements are also satisfactory by clinical equivalent interpretation: a Bland-Altman [18] plot demonstrates a small bias of −6.4 BIS units and 95% of values fall within a surrounding boundary of ±9.7 BIS units, as shown in Figure 4C.

Superimposed white noise produced a progressive artifactual lifting of the emulated BIS values towards levels associated with consciousness. The overall signal morphology was generally preserved until the values were flattened by saturation at the upper limit of the BIS scale, as shown in Figure 4D. The black contour lines show the average BIS value over the entire time interval of 225 minutes. Artifactual rises in the mean BIS value of 10, 20 and 30 units were associated with imposed white noise amplitudes of 4.5 μV, 7.6 μV and 11.1 μV respectively. In contrast, emulated BIS values were hardly affected by superimposed noise from pure sinewaves at either 50 Hz or 60 Hz, representative of electricity supply interference in Europe and the US respectively. The Pearson correlation values between clean and noisy signals were R = 0.98 for 50 Hz noise, and R = 0.99 for 60 Hz noise even at an interference amplitude of 100 μV. The Bland-Altman bias values were less than 1 BIS unit, and 95% of values were within 5.6 BIS units for 50 Hz and 2.6 BIS units for 60Hz. The algorithm is able to tolerate aggressive amounts of noise interference at these frequencies in the gamma band [19] (30-80 Hz) without degradation.

Discussion

The emulation provides a satisfactory replication of the calculation engine executing on the original hardware. Although the emulated BIS values run slightly lower than the Vista-originated values on average, the general morphology and transitions are plainly very well matched and, as noted, the correlation coefficient between these values is comparable to that seen with distinct official iterations of the BIS software. The greatest differences in the Bland-Altman plot (Figure 4C) are observable at BIS values that are generally associated with light sedation. The brief and spiking nature of these differences in Figure 4A suggest that these discrepancies during physiological sleep might be related to the handling of EMG artifact in EEG signals in the setting of REM phase sleep. Furthermore, the BIS monitor applies a temporal smoothing to the values that it displays to the clinician on the monitor, and this would further suppress the occasional spikes in difference that are seen in the unsmoothed 1 -second interval BIS value data plotted in Figure 4.

From a technology perspective, this represents the first example of the re-implementation of the software from an existing medical device onto unrelated commodity hardware, using tools whose code is open-source. This is no mere engineering parlor trick. Emulation immediately allows BIS parameters to be calculated for research purposes from pre-existing EEG data. Such applications could include research on the mechanisms of anesthesia in non-human mammals in which the use of standard BIS EEG electrodes is impractical, or application of the algorithms to research EEG data obtained from humans using other equipment in the setting of any another relevant neurological indication such as dementia, delirium or coma. The use of an emulated front-end for EEG data acquisition allows for the possibility of remote or wireless transmission of EEG data in research settings in which it would be impractical or undesirable to tether the subject to the machine itself, or the acquisition of data from modern dry-electrode systems that can be worn comfortably for longer periods of time [20,21].

Because emulation places the software into an entirely virtualized context, it is also a powerful tool for further analysis of the BIS algorithms themselves since the algorithms can be run, and then exactly re-run, on empirical EEG data or on arbitrary mathematically-constructed input signals designed to test their behavior. Software-based debugging tools permit far more sophisticated analysis than could be previously accomplished with manipulation of the JTAG debugging interface on the motherboard of the A-2000 BIS monitor [1]. The mathematical implementation of the BIS algorithms remains of academic interest because, after long empirical use, they represent a potentially important constraint on any hypothesized mechanism of action for anesthetic agents such as the volatile gases. Any potentially valid mechanism of action must conceptually be able to produce the mathematical changes in the structure of the EEG that the algorithms empirically describe, which provides a logical bridge between the micro and macro scales of anesthetic activity [22].