Abstract
This paper models the macroeconomic and distributional consequences of lockdown shocks during the COVID-19 pandemic. The model features heterogeneous life-cycle households, labor market search and matching frictions, and multiple industries of employment. We calibrate the model to data from New Zealand, where the health effects of the pandemic were especially mild. In this context, we model lockdowns as supply shocks, ignoring the demand shocks associated with health concerns about the virus. We then study the impact of a large-scale wage subsidy scheme implemented during the lockdown. The policy prevents job losses equivalent to 6.5% of steady state employment. Moreover, we find significant heterogeneity in its impact. The subsidy saves 17.2% of jobs for workers under the age of 30, but just 2.6% of jobs for those over 50. Nevertheless, our welfare analysis of fiscal alternatives shows that the young prefer increases in unemployment transfers as this enables greater consumption smoothing across employment states.
Keywords: COVID-19, Pandemic, Lockdowns, Unemployment risk, Wage subsidy, Life-cycle, Consumption
1. Introduction
The COVID-19 pandemic of 2020 was the cause of enormous macroeconomic disruption around the world. The primary economic effects of the pandemic were the result of restrictions on producer and consumer activity (i.e. lockdowns), as well as decreased consumer demand due to health concerns associated with the virus. As stimulus measures, governments quickly implemented large fiscal interventions in the form of employment subsidies, loans to firms, and direct transfers to households. While the fight against the virus continues, many important economic questions remain: what are the macroeconomic costs of the lockdowns used to contain COVID? To what extent did fiscal interventions help to offset these costs? And how important is household heterogeneity in helping to understand the effects of these lockdown and fiscal policies?
This paper studies the macroeconomic and distributional consequences of lockdowns imposed during the pandemic. In general, pandemic recessions are the result of both supply and demand shocks, which complicates the study of the economic impact of lockdowns on their own. For this reason, we build a model of a lockdown calibrated to data from New Zealand, whose experience with the pandemic differed markedly from many other countries. Because New Zealand is a remote island nation, and because its government quickly closed international borders and imposed a strict national lockdown, the virus was effectively eliminated in the community by June 2020.2 As a result, the health effects of the pandemic and their consequences for consumer demand have been limited.3 This is in stark contrast to the effects of the pandemic in countries like the USA.4 Thus, the experience of New Zealand presents a useful case study for investigating the macroeconomic effects of lockdowns in isolation.
We study lockdowns in a heterogeneous agent overlapping generations model with multiple industries and labor market search and matching frictions. Households in the model differ by age, wealth, employment status, and industry of employment. They choose how much to consume and save over their life-cycle, subject to fluctuations in employment determined by equilibrium in the labor market. A fiscal authority raises taxes, issues debt, funds transfers to unemployed workers, and provides employment subsidies during the lockdown. We solve for general equilibrium of the model and calibrate its steady state to match the distributions of wages, employment, and employment risk across age and industry using data on the New Zealand labor market prior to the pandemic.
We solve for equilibrium dynamics of the model in response to a pandemic-induced lockdown shock and the associated fiscal policy responses. We characterize a lockdown as a sequence of negative shocks to industry-level productivity (see also Bayer et al., 2020, Bilbiie and Melitz, 2020, Guerrieri et al., 2020).5 In contrast to many other papers in the literature, but consistent with the limited spread of COVID-19 in New Zealand, we do not model the epidemiological aspects of the virus and we ignore the effects of demand shocks due to health concerns (see Auerbach, Gorodnichenko, Murphy, 2021, Baqaee, Farhi, 2020, Eichenbaum, Rebelo, Trabandt, 2020, Farhi and Baqaee, 2020, Faria-e Castro, 2021, Kaplan et al., 2020, Krueger et al., 2020). Instead, we assume that productivity shocks capture the entirety of the impact of a lockdown since firms cannot utilize labor resources at their previous rates. We further assume that firms in the services sector are disproportionately affected by a lockdown. This is because service workers typically need to interact with customers to carry out their jobs and as a result are much less able to work from home.6 In addition, service sector firms such as those in the tourism, accommodation, and travel industries have been especially affected by ongoing restrictions on international travel.
One of our main contributions to the literature is to emphasize the importance of household age in assessing the distributional effects of lockdowns and their associated fiscal policies.7 While the health effects of COVID-19 have been disproportionately felt by the old, young households are more likely to be affected by fluctuations in the labor market. One reason for this is that the young are much more likely to work in the service sector, which in turn is more exposed to the effects of a lockdown. In our model, we capture the effects of these age-dependent exposures through two novel features of our labor market structure. First, we incorporate life-cycle labor market search dynamics, following Chéron et al. (2013); De la Croix et al. (2013); Lugauer (2012). Since households must first match with firms before starting work, the young take time to settle into employment and are therefore more likely to be unemployed than the old. Second, we incorporate endogenous job separations, following Den Haan et al. (2000); Fujita and Ramey (2012). In combination these model features allow us to match the life-cycle profiles of wages and job separations observed in the data. During a lockdown, larger shocks to the service sector result in young workers being laid off in much larger numbers, which disproportionately raises their unemployment risk.
Another contribution of the paper is our study of the macroeconomic and distributional effects of large-scale wage subsidy policies enacted during the pandemic. We consider the wage subsidy scheme introduced by the New Zealand government. This policy represented an exceptionally large fiscal intervention: between March and June 2020 the wage subsidy scheme paid firms approximately 50% of the median wage for each worker employed and the scheme supported approximately 75% of the New Zealand labor force. In order to be eligible for the subsidy, firms needed to observe a 30% decline in revenues over the previous month. To capture this feature of the policy, we introduce a revenue-dependent subsidy policy in the model and calibrate it to match the 75% of firm-worker matches that received the subsidy during the first quarter of the lockdown. Because revenues fall by more for firms in the service sector and with younger workers, these firms are significantly more likely to receive the wage subsidy. This suggests that the wage subsidy scheme was reasonably well-targeted, in that it most benefited those workers disproportionately affected by the lockdown.
In order to discipline our lockdown exercise in the model, we calibrate the sequence of lockdown shocks to match the declines in employment across the services and non-services sectors in the first two quarters of the pandemic. We then calibrate the wage subsidy policy parameters to match the size of the wage subsidy received by firms and the fraction of employees supported by the subsidy. As in the data, a lockdown in the model generates a 5% decline in service sector employment and a 1% decline in non-services employment in the first quarter of the pandemic. Comparing the baseline economy to a counterfactual economy absent the wage subsidy scheme, we find that the subsidy saves a large number of jobs. In aggregate, the policy preserves 6.5% of steady state employment relationships, which is equivalent to 175,000 jobs in the New Zealand labor market. In the cross-section, the subsidy saves 8.4% of service sector jobs and 5.2% of non-service sector jobs. But the largest differences are by age. The wage subsidy saves 17.2% of jobs for workers under the age of 30, but just 2.6% of jobs for workers over the age of 50.
We also use the calibrated model to study the effects of two alternative fiscal policies. We first consider a policy that raises unemployment benefits, and second we consider a policy that pays a lump-sum transfers to all households. These alternatives mimic policies that were adopted in the United States and other parts of the world during the pandemic.8 In order to compare policies on a dollar-for-dollar basis, we assume that each policy implies the same total fiscal transfer expenditures (i.e. the sum of unemployment benefits, wage subsidies, and lump-sum transfers). We find that although the alternative policies do not prevent unemployment during the lockdown, raising unemployment benefits enables more consumption smoothing among young households than does the wage subsidy policy. Since the young earn low wages in normal times, a large increase in unemployment benefits raises average youth income despite a large increase in the unemployment rate. This represents a large increase in unemployment insurance for those most likely to use it.9
Finally, we conduct a welfare analysis to study the relative merits of each fiscal policy response to a lockdown. Average welfare gains are higher for the wage subsidy policy than either of the alternatives. However, this masks significant heterogeneity in the welfare benefits of these policies. We find that young households are much more likely to favor the policy that raises unemployment benefits, and the welfare gains for these households are relatively large. Because young workers are much more likely to become unemployed than other workers during the pandemic, higher unemployment benefit payments help young households smooth consumption better than does a policy that simply preserves employment for many, but not all, young workers. In contrast, older households prefer the wage subsidy policy to other fiscal policies, although the welfare gains are relatively small. Although unemployment risk for older workers remains relatively low during the lockdown, the higher wages that are earned later in life imply larger costs of job loss even if unemployment benefits are raised.
1.1. Literature review
Many early papers in the macroeconomics literature on COVID-19 incorporated epidemiological model features in order to study the evolution of health and economic outcomes during the pandemic (see for example: Acemoglu, Chernozhukov, Werning, Whinston, 2020, Berger, Herkenhoff, Huang, Mongey, 2020, Eichenbaum, Rebelo, Trabandt, 2020, Kaplan et al., 2020, Krueger et al., 2020). These papers show both that households optimally reduce consumption in response to the health risks of COVID-19, and that country-wide lockdowns imply a strong trade-off between health outcomes and economic activity. In the current paper, we focus on the effect of lockdowns alone, thereby concentrating our analysis on an extreme point along the trade-off schedule discussed in the literature. We focus on the example of New Zealand, where early and strict lockdowns led to virtual elimination of the virus within the community. Here, the primary concern of economists and policymakers is not a trade-off between health and the economy, but the macroeconomic and distributional consequences of the lockdowns themselves.
In order to capture heterogeneity in the effects of a pandemic and associated lockdowns, many papers build models with multiple sectors and differential exposure to shocks. Baqaee and Farhi (2020) and Farhi and Baqaee, 2020 study production-based economies in which sector-specific shocks are amplified through input-output linkages built into supply chains in the model. Farhi and Baqaee, 2020 show that pandemic shocks lead to higher unemployment that is concentrated in the most heavily affected sectors. Gregory et al., 2020 study the effect of lockdowns on the labor market in a directed search model with multiple industries. They argue that service sector workers experience greater job risk, which leads to a much slower recovery in the service sector as those workers take longer to find stable employment. Kaplan et al., 2020 model workers with different industries and occupations as having differential exposure to pandemic shocks via their ability to work from home. In our paper, we capture these differential household exposures to the pandemic through industry of employment and worker age. We show that younger workers are much more likely to be employed at firms in the services sector, which in turn were much more exposed to the effects of lockdowns than were other firms.
Several papers in the literature build structural macroeconomic models to assess the effects of various fiscal policy responses to the pandemic. Carroll et al., 2020 build a partial-equilibrium heterogeneous agent life-cycle model to study the effects on consumption of higher unemployment insurance payments and direct stimulus checks under the US CARES Act of 2020. They show that direct transfers help stabilize consumption expenditure in the short term, but that increases in unemployment insurance are more effective if the employment effects of the pandemic are likely to persist. Bayer et al., 2020 builds a general equilibrium HANK model to study the same policies, showing that higher unemployment benefits generate larger fiscal multipliers than transfers because they offset the effects of higher unemployment risk. Faria-e Castro (2021) studies a DSGE model with borrowers and savers, and shows that borrowers value fiscal interventions that most resemble direct cash payments: either lump-sum transfers or higher unemployment insurance payments. In the current paper, we show that New Zealand’s wage subsidy scheme was very effective in preserving employment relationships during the pandemic which in turn helps to stabilize aggregate consumption. However, as in the above-cited literature, we also find that young households, who tend to be less wealthy, benefit more from a policy that raises unemployment benefits. This is because higher unemployment benefits raise the insurance value of unemployment, whereas wage subsidies only preserve incomes conditional on remaining employed.
Finally, we follow a recent literature that studies the effect of rising unemployment risk in models with household heterogeneity and frictional labor markets. While our model is closely related to the model in Graves (2020), we eschew the two-asset and New Keynesian features and incorporate household age, multiple industries of employment, and endogenous job separations. As in Gornemann et al. (2016); Graves (2020); Ravn and Sterk (2017), we find that low wealth households are most affected by increases in employment risk as they are less able to insure against unemployment. For this reason, young and poor households gain most from larger unemployment payments during the pandemic as they benefit from the greater insurance value of unemployment (see also Graves, 2020).
2. Motivating evidence from New Zealand
The global outbreak of COVID-19 in 2020 was associated with significant macroeconomic disruption. However, the evolution of the pandemic in New Zealand presents an interesting case-study due to its relatively swift and stringent lockdowns, and the limited spread of the virus within its borders. The strict lockdowns imposed in New Zealand imply potentially large declines in economic output due to restrictions on productive activity, while the small COVID case-load suggests a very limited role for declining domestic demand due to health concerns. This is in stark contrast to the experience of countries such as the US, where reductions in activity due to fear of the virus seems to have dominated the effects of the lockdowns themselves (Chetty et al., 2020).
Fig. 1 tracks the evolution of the virus and the imposition of lockdowns across several countries, using data collated by authors at Oxford University (Hale et al., 2020). Fig. 1(a) shows that New Zealand experienced an outbreak of COVID cases along with other countries at the beginning of 2020. However, case numbers in New Zealand stabilized quickly. As at December 2020, New Zealand had just 43 cumulative cases per 100,000 people. This compared favourably to case numbers per 100,000 in countries such as Australia (112), Canada (1133), Great Britain (2600), and the US (4553). Rapid and extensive lockdowns in March 2020 are one reason cited for New Zealand’s success in limiting the spread of the virus. Fig. 1(b) compares the timing and stringency of restrictions on social and economic activities in response to the pandemic. The data shows that New Zealand imposed some of the strictest lockdown measures of any country in early March.10 By May, as the number of new and active cases fell, restrictions on activity in New Zealand were gradually lifted. This contrasted with many other countries, where various restrictions remained in place throughout the year.11
Fig. 1.
COVID-related lockdowns by country. Notes: Panel (a) reports confirmed cases of COVID-19, panel (b) reports a measure of lockdown stringency, and panel (c) reports a measure of internal and external travel controls. The lockdown stringency index includes information about school, workplace, and public transport closures, restrictions on social gatherings, stay-at-home requirements, and restrictions on internal and international travel. Sources: Corona Virus Government Response Tracker from Oxford University (Hale et al., 2020). Population data from the OECD.
Another important factor in accounting for New Zealand’s success in dealing with the pandemic is that it is an isolated island nation. This enabled New Zealand to exercise strict control over international border crossings. This is reflected in Fig. 1(c) which shows that New Zealand quickly implemented international travel restrictions, which it has maintained throughout 2020. The large reduction in international travel, in conjunction with mandatory quarantine for the few travelers entering the country, has significantly reduced the number of imported COVID cases that can then be spread throughout the population.
The limited health effects of COVID-19 in New Zealand suggest that there was a relatively small role for health-related declines in demand for goods and services. However, the strong lockdowns imposed in New Zealand suggest a potentially large impact on economic activity. Additionally, while domestic lockdowns in New Zealand were short-lived, international travel restrictions are ongoing. This suggests differential economic impacts across sectors more or less exposed to international tourism and travel.
To illustrate the economic effects of these lockdowns in New Zealand, Fig. 2 shows annual employment growth across industries during the first three quarters of 2020 relative to historical averages. We split industries into service sector and non-service sector groups, where definitions and the employment composition of each are reported in Table C.6 in Appendix Appendix C.12 We consider these broad groups of industries for two reasons. First, as noted in the recent literature, service sector workers are less likely to be able to work from home than other workers, differentially affecting economic activity during the lockdown (see Bartik et al., 2020, Dingel, Neiman, 2020). Second, many industries in services are heavily dependent on international travelers. For example, in New Zealand in 2019 purchases by international tourists comprised 95% of accommodation services, 42% of food and beverage services, and 25% of arts and recreation services (Statistics New Zealand, 2020). These industries are especially adversely affected by ongoing international border closures.
Fig. 2.
Changes in employment by industry during the pandemic. Notes: Annual employment growth rates in (a) services industries and (b) non-services industries. Definition of services and non-services is reported in Table C.6 in Appendix Appendix C. Green bars report historical average employment growth rates, computed for the period 2009:Q1 to 2019:Q4. Source: Authors’ calculations using the Household labor Force Survey. (For interpretation of the references to colour in their figure legend, the reader is referred to the web version of this article.)
Fig. 2 (a) shows that service sector employment fell by 3.1% in the second quarter, by 4.5% in the third quarter, and by 5.7% in the fourth quarter. In contrast, Fig. 2(b) shows that non-services employment growth was positive at 1.4% in the second quarter, fell by just 0.05% in the third quarter, and was growing at 1.5% in the fourth quarter.13 Insofar as employment growth reflects the growth of economic activity, the data suggests that service sector industries experienced a far larger contraction during the pandemic than did non-service industries. We take this as evidence of significant heterogeneity in the effects of lockdowns across industries.
In anticipation of the economic effects of the pandemic, the New Zealand government implemented a broad-based wage subsidy scheme.14 This subsidy was similar to policies adopted in other countries at this time.15 In New Zealand, firms and self-employed workers could apply for a wage subsidy from 1 March 2020 that paid a flat rate of NZ$585.80 per full-time employee per week and was available for eight weeks.16 The subsidy was equivalent to approximately 50% of median weekly earnings for full-time workers in 2020.17 Receipt of the wage subsidy was subject to several conditions: firms expected a 30% drop in revenue over the previous month due to the pandemic; firms must retain subsidized employees for the duration of the subsidy; and firms must continue to pay employees at least 80% of their usual wages for the duration of the subsidy.
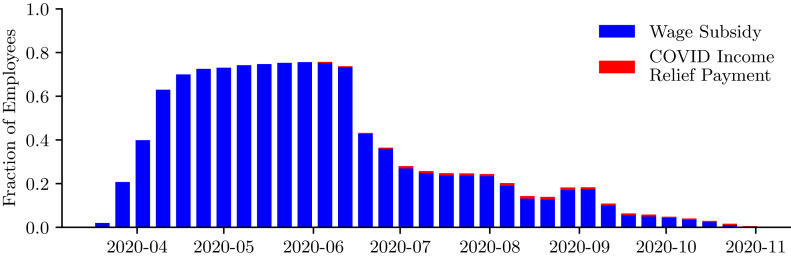
Fig. 3 shows that around 70% of all employees in New Zealand were supported by the subsidy between March and June 2020. Limited extensions of the wage subsidy were available between June and September, but many fewer firms received these payments. Due to broad coverage and high take-up, the subsidy was an expensive fiscal intervention with NZ$14 billion paid out in 2020, equivalent to 40% of total government expenditure on social security in 2019.18 The New Zealand government also provided other fiscal interventions in response to the pandemic, but these were much smaller in scope. For example, unemployment benefit rates were effectively doubled for workers that lost jobs as a result of the pandemic between March and November 2020.19 However, as Fig. 3 shows, the number of workers supported by these additional unemployment payments was dwarfed by the number of workers receiving the wage subsidy.
Fig. 3.
New Zealand wage subsidy and income relief payment schemes. Notes: Number of wage subsidy and COVID income relief recipients divided by total number of employees. Number of employees measured using Monthly Employment Indicators data. Source: Statistics New Zealand and Ministry of Social Development.
Finally, we consider the likely distributional impacts of the pandemic by worker age. Fig. 6 in Section 4 illustrates industry composition, job separation rates, and earnings by industry and age using data from the Linked Employer-Employee Database (LEED) for 2018.20 There are distinct life-cycle patterns in employment composition, employment risk, and earnings. Panel (c) shows that young workers are significantly more likely to find themselves employed in the service sector than are older workers. Around 50% of workers under the age of 30 are employed at service sector firms, while just 35% of workers over the 50 are employed in services. Panel (a) shows that both young and service sector workers face higher rates of job separation than older and non-service sector workers, and are thus far more likely to leave their current place of employment in any given period.21 Finally, panel (b) shows that young workers earn less than older workers, and service sector workers earn less than non-service sector workers at all ages.
Fig. 6.
Job separation and wage rates by industry and age. Notes: Model generated statistics for job separation rates (a), wage rates (b), industry of employment (c), and unemployment status (d). Sources: Authors’ calculations and data from HLFS, LEED, and MSD.
Taken together, these facts suggest that younger workers are likely to be disproportionately affected by the effects of the pandemic-induced lockdown. Because the lockdown disproportionately affected the service sector, younger workers are more likely to lose their jobs. Moreover, these are workers that already face higher employment risk and are compensated with lower earnings. Young workers are thus more likely to be affected by the lockdown, but also the least able to weather its effects. For this reason, it is important to understand the distributional consequences of the fiscal interventions undertaken over the course of the COVID-19 pandemic.
3. Model
We build a structural macroeconomic model in order to study the aggregate and distributional consequences of a pandemic-induced lockdown in New Zealand. The main model ingredients are life-cycle heterogeneous agents, multiple industries, frictional labor markets, endogenous employment risk, and exogenous productivity shocks. Our model features are motivated by three main considerations. First, the strict lockdowns and limited health effects experienced by New Zealand suggest a much stronger role for supply shocks than for demand shocks. For this reason, we model a lockdown as a sequence of productivity shocks reducing the ability of firms to produce using a given level of labor inputs. Second, there is significant heterogeneity in the effect of lockdowns on production across industries. For this reason, we model firms as being more or less exposed to the negative productivity shocks accompanying lockdowns. Third, the effects of a lockdown are likely to differ by age. Our model replicates the life-cycle profile of employment across industries, which captures the fact that young workers are disproportionately exposed to a lockdown through higher rates of employment in the services sector. Additionally, the model mimics the age distribution of employment risk so that young workers are more likely to be laid off following a shock than are old workers. We believe these features provide a plausible basis for analyzing the consequences of lockdown shocks and the fiscal responses to them.
3.1. Households
Households live for a finite number of periods, where their age is indexed by . At age households retire and consume their remaining networth. The problem of a household of age is:
| (1) |
Above, denotes the employment status of the household, where reflects unemployment and employment, respectively. The industry of employment is indexed by , where indicates the services sector, and is all other industries. The household chooses consumption , and liquid asset holdings , where the latter is subject to a no-borrowing constraint. In retirement, households consume all remaining networth , where final period utility is weighted by :
| (2) |
Household income depends on age, employment status, and industry of employment. If employed, the household receives a wage , which differs by age and industry. Unemployed households receive a constant unemployment benefit . All household income, including interest income on assets, is taxed at rate . Income is subject to idiosyncratic risk due to changes in employment status and industry of employment. This risk is characterized by a Markov chain , which is exogenous from the perspective of the household. The parameters of this Markov chain depend on a labor market matching process, described in Section 3.3. Note that households are assumed to supply labor exogenously, and we do not allow households to quit jobs or to reject job offers received on the job market.22
The final consumption good is a composite of services and other goods consumption via a CES aggregator:
| (3) |
Above, gives the elasticity of substitution between the two types of consumption. The solution to the expenditure minimization problem implies the following consumption demand functions
| (4) |
where is the relative price of consumption in industry , and the aggregate price index is given by
| (5) |
In addition we assume that there is a risk neutral entrepreneur that owns the firms described in Sections 3.2 and 3.3, and that all profits earned each period are immediately consumed. In Online Appendix B, we solve an alternative version of the model with no entrepreneur owners and instead all profits are distributed lump-sum to households each period. We show that the primary results are unchanged under this assumption.
3.2. Production firms
Competitive firms in each industry produce output via linear production technologies , where is industry-specific productivity, and is efficiency-adjusted units of labor. Firms maximize real profits
| (6) |
where is the relative price of output, and is the industry-specific real wage rate per efficiency unit of labor.
3.3. Labor markets
Labor markets in each industry feature matching frictions. Unemployed households search for work in their current industry , while labor market entrepreneurs in each industry post vacancies to attract workers in that industry. Let be the number of vacancies posted by entrepreneurs in industry , and is the total mass of unmatched workers in industry . The matching technology is a Cobb-Douglas function given by
where is industry-specific match productivity, and is the matching elasticity. The rate at which entrepreneurs fill vacancies is defined as . The rate at which unemployed households find jobs is defined as .
We assume that labor market entrepreneurs cannot age-discriminate between potential workers when posting job vacancies.23 This means that entrepreneurs may be matched with workers of any age. Because households retire at age , any existing employment relationships with age- workers are destroyed with certainty in the following period. Entrepreneurs matched to a worker receive the industry-specific production wage . But each match is subject to an idiosyncratic productivity shock each period, where is drawn from a log-normal distribution with age-dependent standard deviation . The entrepreneur earns total revenue and in turn pays workers an industry- and age-specific wage .
The value of a filled job for an entrepreneur in industry , matched to a worker age , and with match-specific productivity is
| (7) |
where expectations are taken over . As in Fujita and Ramey (2012) we allow for endogenous job separations. Separations follow from endogenous firm shut-down decisions. Note that a shut down need not occur when current flow profits are negative, as entrepreneurs also consider the present discounted value of future profits. Rather, an entrepreneur ceases to operate and a job separation occurs when . This shut down condition defines a threshold productivity level
| (8) |
which depends on industry-level productivity through the production wage . All job matches with idiosyncratic productivity below this threshold are destroyed. Note that separations apply to both existing employment arrangements as well as newly matched employers and employees. This means that a worker may match with and separate from an entrepreneur in the same period before production takes place.
Fig. 4 illustrates the log-normal distribution of match-specific productivity. The black vertical line indicates the threshold productivity such that all matches with lower productivity are destroyed. When industry-level productivity falls, the production wage also falls, which increases the threshold to as indicated by the red vertical line. The fall in aggregate productivity results in an increase in the fraction of matches that are unprofitable and which result in separations. Thus, a fall in aggregate productivity results in a larger number of job losses through employment separations.
Fig. 4.
Endogenous job separations and the distribution of match productivity. Notes: Stylized illustration of the distribution of idiosyncratic match productivity shocks. The dashed lines and thresholds and indicate match productivities below which job separation occurs.
Thus, we can derive expressions for job separation rates using the distribution of match-specific productivity:
| (9) |
where and denote log-normal PDFs and CDFs with age-dependent standard deviations . As discussed with reference to Fig. 4 above, the job separation rates are functions of aggregate productivities through the production wage in the denominator of Equation (8).
Labor market entrepreneurs post vacancies up to the point at which marginal benefit equals marginal cost. The real vacancy posting cost in each industry is . The marginal benefit of a vacancy is the expected value of filling a job. The job filling value function for a worker of age is described in Eq. 7. However, the expected value is governed by the probability of finding a worker , the probability that a given worker is age , and the probability that the employment match does not separate before production takes place. The probability that an unmatched worker chosen at random is aged is , where . The assumption of free-entry thus implies that
| (10) |
where the expectation is taken over idiosyncratic match productivity . The maximum operator within the expectation takes into account the probability that a separation occurs before production takes place.
Finally, we assume that a risk-neutral entrepreneur owns all of the firms, and that all profits earned each period are immediately consumed.24
3.3.1. Wage determination
Because Nash bargaining is complicated by the two-sided heterogeneity of workers and firms, we follow several recent papers in the heterogeneous agents literature by assuming a simple wage setting rule.25 In steady state, we assume that wages are determined by the marginal labor market entrepreneur. That is, wages are set by the firm that is indifferent between continuing and shutting down. For such a firm the value of a filled job is nil, and so Equations (7) and (9) yield
| (11) |
where is the CDF over match-specific productivity .
Outside of steady state, we assume that worker wages are sticky and respond to production wages with a constant elasticity :
| (12) |
3.3.2. Employment and industry transitions
Given the labor market environment, we are now in a position to characterize the household employment and industry transitions described by the Markov chain .
Consider a household that is currently employed () and working in industry . At the end of the period, employees are subject to endogenous job separations at rate (i.e. separations occur immediately prior to age ). Separated workers that were employed in industry may switch industries with exogenous probability . After industry transitions take place, workers may match with an employer in industry with probability . However, because all employment relationships are subject to match productivity shocks at the beginning of the period, even new matches may separate before production takes place. Thus, the effective job finding rate is : the probability of finding a job and surviving the initial match productivity shock.
Now consider a household that is currently unemployed () but was previously employed in industry . Before finding work, the household may switch industries with exogenous probability . The household may then match with an employer in industry with probability . As above, match productivity shocks take place which can disrupt employment before it begins, and so the effective job finding rate is again .
Fig. 5 shows an event tree illustrating the employment and industry transitions faced by age- worker that is currently employed in industry . The initial state vector of the worker is , and the transition to outcome indicates that a worker has switched from industry to another industry . Along the upper branch, the worker is not separated and remains employed and in the same industry . Along the lower branch, the worker is separated from their current job, may switch industries, searches for work, and may end up employed or unemployed in either the original industry or the new industry .
Fig. 5.
Employment and industry transitions event tree Notes: Event tree for worker employment and industry transitions. State vectors at initial and terminal nodes describe combinations of age (), employment status (), and industry (). Edges are labeled with the probability that the given event will occur. The probabilities , , and correspond to the separation rate, industry transition probability, and job finding rate, respectively.
The Markov chain can be separated into two sub-Markov chains: describes employment transitions for workers that remain in the same industry ; and describes employment transitions for households that switch from industry to . Let be the state vector describing employment status. Recall that unemployment corresponds to and employment corresponds to . Then for each transition matrix, the upper row reports probabilities for transitions from unemployment, and the bottom row reports probabilities for transitions from employment. For households remaining in the same industry , the transition matrix is given by
| (13) |
For households that switch from industry to , the transition matrix is given by
| (14) |
Finally, the full Markov transition matrix for employment and industry transitions is
| (15) |
Hence, is a matrix that multiplies the combined state vector over employment status and industry: . Each row of the transition matrix corresponds to the current labor market status and industry of a household, while each column, in turn, corresponds to the states into which workers transition next period.
3.3.3. Labor market flows and aggregate labor supply
Let the number of age- households and employees in industry be denoted by and , respectively. The number of unmatched workers in industry of age- evolves according to the following law of motion:
| (16) |
Above, the first additive term corresponds to households in industry last period whose jobs were destroyed but who stayed in industry , as well as households who were unemployed in industry , stayed in the same industry, but could not find a job. The second additive term has a similar interpretation, but tracks households in the other industry who were separated or unmatched but switched industries from to .
The number of age- workers employed in industry is given by the sum of age- workers who kept their job this period, and the number of unmatched workers who found a job and survived endogenous separations:
| (17) |
Finally, aggregate labor supply in each industry is given by total efficiency units of labor provided by working households. This consists of the total number of workers in each age group scaled by average match productivity in that age group:
where .
3.4. Government
There is a government that manages fiscal policy along any transition path. Government expenditures consist of non-valued government spending , unemployment benefits , wage subsidies , and lump-sum transfers . The government then collects taxes , and issues debt at interest rate The government budget constraint is
| (18) |
We assume that government spending is allocated across services and other goods in the same way that household consumption expenditure is allocated, according to Equation (3).26 Unemployment benefits and tax revenues are aggregated across agents in the economy:
where is the distribution over households of age at time , and are labor market entrepreneur profits. Wage subsidies and lump sum transfers are only distributed following the lockdown shocks discussed in Section 5.
In all of the experiments that follow, we assume that government debt adjusts to ensure that the fiscal budget constraint holds in each period along a transition path. Government spending is assumed to remain constant. We then adjust the tax rate to ensure that government debt returns to steady state in the long run. We discuss the details of this tax policy in Section 5.
3.5. Equilibrium
A formal definition of the recursive competitive equilibrium is stated in Appendix B.2. In the experiments conducted in Section 5, we solve for equilibrium along a transition path following a series of ex-ante unexpected shocks. Along the transition, we maintain the assumption of a small open economy. That is, the interest rate is held constant, and the domestic economy may borrow from or save with the rest of the world. This is reflected in fluctuations in net exports in the aggregate real resource constraint:
where the left side of the equation is total output, is aggregate household consumption, is firm profits which are consumed by entrepreneurs during the period in which they are earned, are total vacancy posting costs for industry , and are net exports. As with government spending, we assume that net exports are allocated across services and other goods in the same way that household consumption expenditure is allocated, according to Equation (3).27
4. Model calibration
We calibrate the model so that the steady state matches a range of household and labor market characteristics in New Zealand prior to the onset of the pandemic in 2020. Importantly, the calibrated model reproduces the observed industry and age distributions of employment, employment risk, and wages. This ensures that the model captures ex-ante household exposures to lockdown shocks.
The model is calibrated at a quarterly frequency. Households are born at age 20 and work for 180 periods until retirement at age 65. Table 1 reports the other externally calibrated parameters. The risk aversion parameter is set to 2. The annual real interest rate is 2.3 percent, the average for the years 2000 to 2019. The unemployment benefit rate is set at 20% of the median wage, consistent with the Jobseeker Support benefit rate in 2019 for adults aged over 25. The consumption share of services is set to 0.519, which is the average for the years 2000 to 2019. The elasticity of substitution between services and non-services is set to 2, consistent with recent empirical evidence on substitutability between goods and services in Hobijn and Nechio (2019).
Table 1.
Externally calibrated model parameters.
| Description | Parameter | Value | Source |
|---|---|---|---|
| Risk Aversion | 2.000 | Standard | |
| Real Interest Rate | 0.023 | Reserve Bank of New Zealand | |
| Unemployment Benefit Rate | 0.252 | Work and Income New Zealand | |
| Services Consumption Share | 0.519 | Statistics New Zealand | |
| Elasticity of Substitution | 2.000 | Hobijn and Nechio (2019) | |
| Matching Function Elasticity | 0.750 | Razzak (2009) | |
| Real Wage Elasticity | 0.100 | Authors’ Estimates using LEED | |
| Vacancy Filling Rate | 0.700 | Christoffel et al. (2009) |
The matching function elasticity is set to 0.75, following empirical estimates from New Zealand in Razzak (2009). We estimate the wage elasticity using quarterly, industry-by-region LEED data from 1999 to 2019. Combining the wage dynamics equation Equation (12) with the first order condition for the production firms () yields an estimable relationship between wages and employment: . We regress the log-difference in wages on the log-difference in employment, controlling for industry-year and region-year fixed effects. Because employment is endogenous to output which is unobserved, we run an instrumental variables regression, constructing a Bartik instrument from industry shares within each region and national employment growth rates in each industry. The IV results yield an elasticity of 0.121 (S.E. 0.015), so we set to 0.10. The vacancy filling rate is assumed to be the same across industries, and is set to 0.70 (see Christoffel et al., 2009).
Table 2 reports internally calibrated parameters, and the moments governed by those parameters in both the model and data. Panel A reports parameters governing wealth accumulation, cross-industry earnings, and taxes. The discount factor is set to match the ratio of networth to quarterly GDP. The utility weight on retirement is set to match networth held by households in the decade prior to retirement relative to the networth held by households aged 25 to 34. Productivity in the non-services sector is normalized to one, and the relative size of productivity in the services sector is set to match the ratio of average labor earnings across industries. We set the tax rate to match the ratio of government spending and GDP, since government spending is determined residually from the government budget constraint.
Table 2.
Model parameters and moments.
| Parameter | Value | Moment | Model | Data | Source | |
|---|---|---|---|---|---|---|
| A. Miscellaneous Parameters | ||||||
| Discount factor | 0.994 | Networth/GDP | 0.767 | 0.769 | RBNZ, 2019 | |
| Retirement weight | 140.000 | Networth: 55–64/25-34 | 12.068 | 12.099 | HES, 2017 | |
| Relative productivity | 0.385 | Earnings: Non-Services/Services | 1.301 | 1.301 | LEED, 2019 | |
| Tax rate | 0.212 | Government Spending/GDP | 0.188 | 0.188 | RBNZ, 2017 | |
| B. Job Separation Process Parameters | ||||||
| Mean | 0.026 | Separation rates by age | See Fig. 6(a) | LEED, 2019 | ||
| Persistence | 0.978 | Separation rates by age | See Fig. 6(a) | LEED, 2019 | ||
| Initial value, services | 0.091 | Separation rates by age | See Fig. 6(a) | LEED, 2019 | ||
| Initial value, other | 0.068 | Separation rates by age | See Fig. 6(a) | LEED, 2019 | ||
| C. Idiosyncratic Match Productivity Process Parameters | ||||||
| Mean | 1.250 | Earnings: 30–34/20-24 | 1.577 | 1.580 | LEED, 2019 | |
| Persistence | 0.963 | Earnings: 40–44/30-34 | 1.171 | 1.170 | LEED, 2019 | |
| Initial standard deviation | 0.100 | Vacancy costs/GDP | 0.032 | 0.020 | Standard | |
| D. Industry Labour Market Parameters | ||||||
| Industry transition, services | 0.121 | Industry-age composition | See Fig. 6(c) | LEED, 2019 | ||
| Industry transition, other | 0.064 | Industry-age composition | See Fig. 6(c) | LEED, 2019 | ||
| Employment probability, | 0.999 | Industry-age composition | See Fig. 6(c) | LEED, 2019 | ||
| Services probability, | 0.584 | Jobseeker support by age | See Fig. 6(d) | MSD, 2019 | ||
| Job finding rate | 0.601 | Jobseeker support by age | See Fig. 6(d) | MSD, 2019 | ||
Source: Authors’ calculations using data from the Household Economic Survey, the Ministry of Social Development, the Linked Employer-Employee Database, and the Reserve Bank of New Zealand.
Panel B of Table 2 reports parameters that determine job separations. New Zealand’s LEED data provides job separation rates by industry and by household age in 5-year age groups. Because we solve the model at a quarterly frequency, we generate job separation rates for every age using a simple auto-regressive process, , where is the average separation rate, is the persistence of the process, and there is a different initial condition for each industry . We set the parameters of the auto-regressive process so that the average separation rates by industry and age group in the model match those observed in the LEED data. Fig. 6(a) shows that separation rates in the model provide an extremely close fit to the data.
Panel C of Table 2 reports the parameters of the idiosyncratic match productivity process. Recall that match productivity is distributed according to a log-normal distribution with a constant mean and age-dependent standard deviations . We normalize so that . For parsimony, we model the age-dependent standard deviation as an auto-regressive process with mean , persistence , and initial condition . Conditional on job separation rates, the match productivity process governs steady state wages via Equation (11). Match productivity is also related to vacancy costs through the vacancy posting Equation (10). Thus, we set the match productivity parameters to target the slope of life-cycle earnings and the vacancy costs-to-GDP ratio. Specifically, we target the earnings ratio for 30-to-34 year-old workers to 20–24 year old workers, and the ratio for 40-to-44 year-old workers to 30-to-34 year-old workers. Fig. 6(b) shows the life-cycle profile of earnings for each industry in the model and the data. The model does a good job of matching the early life-cycle earnings profile. The model fails to capture the hump-shape in life-cycle earnings because the simple auto-regressive process generates a monotonically increasing variance of match productivity over age. The rising variance of match productivity is associated with a monotonically increasing wage profile, rather than the declining wage profile prior to retirement observed in the data. It is possible to generate the hump-shape wage profile, but at the cost of a more complicated parameterization of the match productivity process. Finally, note that sudden drop in wages for the oldest workers is because the continuation value of a filled job for workers immediately prior to retirement is zero, which results in the wage decline via Equation (11).
Panel D of Table 2 reports parameters for industry employment transitions and the job finding rate. These parameters include the industry transition rates , initial probability of employment , initial probability of working in the services sector , and the job finding rate . Note that we allow industry transition rates to differ across industries, but assume that the job finding rate is the same across industries in the steady state. We use a simulated method of moments procedure to choose these parameters by matching the life-cycle profiles of industry employment composition and the rate of workers on the unemployment benefit. We choose to match the rate of unemployment benefit receipts, rather than the unemployment rate, because our measure of job separations taken from LEED data includes both separations into unemployment and job-to-job transitions. This means that the model-implied unemployment rate is too high relative to the observed unemployment rate. However, the rate at which workers in the model receive unemployment benefits corresponds to the same rate in the data. Fig. 6(c) shows that the model closely matches the rate of employment in the services sector by age. Fig. 6(d) shows that the model fits the rate of unemployment benefit receipts on average across the life-cycle, where younger workers are more likely to find themselves without work than are older workers.
5. Effects of a lockdown
5.1. Calibration of lockdown shocks and policy responses
First, we introduce a sequence of industry-specific productivity shocks and . These shocks reflect the effects of a strict domestic lockdown in the first quarter of the pandemic, and international border closures that persist for an additional three quarters. We assume that service sector firms are adversely affected by both the domestic lockdown and the international border closures. We allow the effects of the domestic lockdown and international border to differ, so that the size of the services sector productivity shock in the first quarter of the lockdown differs from the shocks that occur in the following three quarters. We then assume that other industry firms are affected by the initial domestic lockdown only. Thus, non-service firm productivity declines in the first quarter of the lockdown only.
Second, we introduce a conditional wage subsidy policy indexed by policy parameters and . As discussed in Section 2, a conditional wage subsidy was the primary fiscal policy response to the lockdown in New Zealand. We characterize the policy as a lump-sum payment , and a condition under which a firm becomes eligible to receive the payment. We assume the subsidy is available in the first quarter of the lockdown only, which approximates the sharp fall in subsidy receipts from July onward, as shown in Fig. 3. Firms are eligible for the subsidy if they experience a sufficiently large fall in revenues relative to steady state:
| (19) |
We scale the decline in revenues by the steady state average value of an age worker firm . We do this rather than scale by steady state revenues so that the policy generates a distribution of subsidy recipients. Because the distribution over match productivity varies by age, Eq. 19 implies that the probability of receiving a subsidy for a firm in industry with a worker aged is
| (20) |
where the first equality follows from the fact that during the lockdown, and is the CDF over match productivity for age workers.
We calibrate the lockdown shocks and policy parameters to match several key observations about the evolution of the New Zealand labor market in 2020. The details of this calibration are reported in Table 3 . First, we set and to match the declines in service sector employment during the first two quarters of the lockdown. Second, we set to match the decline in non-service sector employment in the first quarter of the lockdown. Fig. 2 shows that relative to historical average growth rates, services employment declined by 5.2% in 2020:Q2 and by 6.7% in 2020:Q3. Non-service sector employment declined by 1.0% in 2020:Q2. To match these targets, the calibration yields a 59.5% decline in services productivity relative to steady state in the first quarter, a 6.5% decline in services productivity for the following three quarters, and a 33.2% decline in non-services productivity in the first quarter.
Table 3.
Parameters and moments calibrated for the lockdown experiment.
| Parameter | Value | Moment | Model | Data |
|---|---|---|---|---|
| 0.390 | Employment Growth, Services, 2020:Q2 | –0.050 | –0.050 | |
| 0.939 | Employment Growth, Services, 2020:Q3 | -0.063 | –0.063 | |
| 0.668 | Employment Growth, Other, 2020:Q2 | –0.009 | –0.009 | |
| 0.113 | Subsidy Size to Median Wage | 0.090 | 0.090 | |
| –0.125 | Fraction Receiving Subsidy | 0.751 | 0.750 |
Notes: Employment growth rates are computed relative to historical average growth rates (see Fig. 2). Source: Authors’ calculations using data from the Household Labour Force Survey and the Ministry of Social Development.
Third, we set to match the effective size of the wage subsidy. Payments under the wage subsidy scheme were $585.80 per worker per week, which is approximately 50% of median weekly earnings in New Zealand. Note, however, that while costs for firms in our model consist of wages only, firms in reality also face a variety of other fixed and variable costs. In order to map the model to the data, we adjust the size the of wage subsidy to account for the proportion of total costs consisting of labor costs. Using data from the 2019 Annual Enterprise Survey, we compute that wages and salaries are 18% of firms’ total expenditures on average.28 Thus the model-implied wage subsidy is equivalent to of the median wage in the model. Finally, we set so that 75% of all workers receive the wage subsidy, which is the peak coverage of the subsidy as shown in Fig. 3.
Finally, as noted in Section 3.4 we ensure that the fiscal budget constraint holds in each period by allowing government debt to adjust in response to shocks to revenue and spending (i.e. unemployment benefits, and wage subsidies). We then adjust the tax rate to ensure that government debt returns to its steady state value in the long run. Specifically, we assume that the tax rate follows an AR(1)
with persistence . At the onset of the lockdown, the tax rate remains at its steady state value. We assume that in the period immediately after the lockdown is lifted, the tax rate jumps and then follows the AR(1) process over the remainder of the transition path. We calibrate the size of the initial jump in the tax rate to ensure that government debt has returned to its steady state value after 80 model periods (i.e. 20 years).
5.2. A lockdown with and without a fiscal policy response
To study the effects of the pandemic induced lockdown and fiscal policy response, we compare the evolution of the model economy to a counterfactual economy with identical productivity shocks but absent the wage subsidy policy. In Figs. 7 to 10, solid blue lines illustrate the baseline economy with lockdown shocks and policy while dashed red lines illustrate the counterfactual economy absent the subsidy.
Fig. 7.
Aggregate macroeconomic variables during the lockdown. Notes: Model-implied transition paths for employment, unemployment, consumption, output, government debt, and the tax rate over the course of the lockdown. Solid blue lines are paths conditional on the wage subsidy policy. Dashed red lines are paths conditional on no fiscal policy intervention. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Fig. 10.
Household consumption by age. Notes: Model-implied transition paths for consumption across households in 5-year age groups. Solid blue lines are paths conditional on the wage subsidy policy. Dashed red lines are paths conditional on no fiscal policy intervention. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Figure 7 shows the evolution of several macroeconomic variables over the course of the lockdown. In the first quarter of the lockdown, productivity in both industries declines significantly. This leads to a large fall in output.29 With falling output and sticky wages, firm profits decline which leads to a decrease in demand for labor. As a result, aggregate employment falls by around 2.5% in the first quarter, and is 3.6% below steady state in the second quarter. Lower employment is also associated with a higher number of workers out of work and receiving unemployment benefits, with this number rising by 2.4 and 3.5 percentage points in each of the first two quarters. Rising unemployment is associated with a decrease in household income, which leads to a 1.8% decline in household consumption in the first period after the shock. At its peak, government debt rises to 5.9% above steady state in order to finance both unemployment benefits and wage subsidies. When the lockdown is over, the tax rate jumps by 1.1 percentage points in order to ensure debt sustainability over the long run.
Figure 7 also illustrates that the wage subsidy policy acts to dampen the macroeconomic contraction induced by the lockdown. In the counterfactual economy with no policy intervention, on impact employment would have fallen a further 5%, unemployment would have increased a further 5%, and aggregate consumption expenditure would have fallen an additional 1%. Notice that although the wage subsidy is only in place for the first quarter of the lockdown, it has a persistent effect on macroeconomic aggregates. In particular, employment and consumption are higher for the entire duration of the lockdown with the wage subsidy policy in place. Government debt and taxes after the lockdown are only marginally higher under the wage subsidy policy than the counterfactual with no such policy in place. This is because the number of unemployment benefits paid out are larger and tax revenues from incomes are lower in the absence of the wage subsidy. As a result, government debt rises in any case, and higher future taxes will be required to repay this debt.
Note that the model predicts an exceptionally large decline in GDP. This is in contrast to the 11% quarterly decline in GDP observed in New Zealand in the 2020 June quarter.30 However, while the model economy is assumed to be in lockdown for the entirety of 2020:Q2, New Zealand only remained in the strictest state of lockdown from March 25, to April 27.31 During this shorter period, high frequency data suggests that economic activity in New Zealand contracted at least as sharply as predicted by the model. Credit card spending fell by 45% on an annual basis in the month of April, while traffic and freight movements fell by 80% over the same month.32
The reason that the model generates such a large decline in GDP is that output is entirely supply-determined. The sectoral productivity shocks are calibrated to match the observed declines in employment conditional on the size and scope of the wage subsidy policy implemented in New Zealand. With 75% of New Zealand workers receiving the subsidy, we require particularly large productivity shocks to reduce labor market entrepreneur profits enough to induce the job separations that reduce employment. Output is in turn determined by these very large supply shocks. Note, too, that because of this reliance on supply shocks, there is essentially no difference in the evolution of GDP across economies with and without the wage subsidy policy. Rather, output is entirely determined by the size and scope of the lockdown, while the wage subsidy policy has a large impact on the distribution of employment, incomes, and consumption.
Fig. 8 illustrates labor market outcomes across industries during the lockdown. The service sector is more adversely affected by the lockdown than the non-service sector because it is affected by a larger initial shock and is subject to the ongoing effects of border closures. As is observed for aggregate variables, the wage subsidy significantly dampens the effects of the lockdown shocks across industries. Absent the wage subsidy, services employment would have fallen an additional 10 percent below steady state, and non-service sector employment would have fallen by more than 5 percent. The third column in Fig. 8 shows that average job separation rates change very little with the wage subsidy in place, whereas job separation rates rise significantly in the absence of the wage subsidy. In contrast, job finding rates are little changed by the presence of the wage subsidy. Thus, the wage subsidy largely acts through preventing job losses, rather than by promoting firm hiring.
Fig. 8.
Labor market outcomes during the lockdown by industry. Notes: Model-implied transition paths for employment, job finding rates, and job separation rates across industries over the course of the lockdown. Solid blue lines are paths conditional on the wage subsidy policy. Dashed red lines are paths conditional on no fiscal policy intervention. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
In addition, Fig. C.15 in Appendix Appendix C illustrates changes in the industry composition of workers during the lockdown. While industry switching probabilities are exogenous, industry composition endogenously adjusts along a transition path because households only switch industries after a job separation. Since job separation rates in the services industry rise by more than separation rates in the other industry, more service workers are exposed to exogenous industry switching events. As a result, the services share of employment shrinks by around one percent and recovers slowly following the lockdown. Note that these industry transitions somewhat alleviate pressure on workers that remain in the service sector following the shocks. If, in contrast, there was no industry switching during the lockdown, the higher number of unmatched workers in the service sector job would further reduce job finding rates and the employment prospects of service sector workers.
Fig. C1.
Industry composition Notes: Model implied transition paths for shares of workers in the services sector during the lockdown. Panel (a) shows the services share of all households, and panel (b) shows the services share of currently employed households. Solid blue lines are paths conditional on the wage subsidy policy. Dashed red lines are paths conditional on no fiscal policy intervention. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
The effects of the lockdown are also unequally distributed across households. Fig. 9 illustrates average job separation rates for workers aged 20 to 25, 25 to 30, and 30 to 35. We focus here on the youngest workers since they are most affected by the lockdown.33 We find that job separations rates rise by much more for the youngest workers. This is for two reasons. First, young workers are more likely to be employed in the service sector which faces larger lockdown shocks. Second, younger workers are associated with lower average current productivity and higher expected future productivity and profitability because is increasing with age. This means that wages for young workers are high relative to their current marginal product of labor, and with sticky wages the profitability of these workers is very sensitive to shocks. And so although industry-level productivity shocks are the same across workers of all ages, the job separation rates of the young are much more sensitive to these shocks than are the job separation rates of the old.
Fig. 9.
Job separation rates by age. Notes: Model-implied transition paths for job separation rates for workers in 5-year age groups. Solid blue lines are paths conditional on the wage subsidy policy. Dashed red lines are paths conditional on no fiscal policy intervention. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Fig. 10 shows the age distribution of consumption expenditures for the youngest households over the lockdown.34 As unemployment rises, and disproportionately among young workers, consumption falls by for young than older households. This is both because average income falls further for the young, but also because young households have lower stocks of savings with which to insure against employment shocks. Although unemployment also rises for older households, their large savings buffers mean that their expenditures are virtually unchanged.
Fig. 11 shows that young workers and those in the service sector are most likely to receive the wage subsidy. We report the fraction of continuing employment relationships supported by the wage subsidy in the first quarter of the lockdown. Younger and service sector workers are more likely to receive the subsidy for two reasons. First, larger productivity shocks in the service sector lead to larger declines in revenues so that these firms are more likely to satisfy Eq. 19. Second, firms with younger workers and lower average productivity experience larger relative declines in revenue for a given aggregate productivity shock and so are also more likely to receive the wage subsidy.
Fig. 11.
Wage subsidy receipts by industry and worker age Notes: Model-implied fraction of workers receiving wage subsidy in the first quarter of the lockdown experiment. Wage subsidy coverage is reported for workers that remain employed across 5-year age groups and by industry of employment.
In order to assess who benefits the most from the wage subsidy, Table 4 reports the number of jobs saved by the wage subsidy in the first quarter of the lockdown for different groups of workers. The table shows the number of jobs saved as a fraction of steady state employment within each group. The first column shows that the wage subsidy scheme preserved 6.5% of aggregate steady state employment relationships, or around 175,000 jobs in the New Zealand labor market.35 This model-based estimate is similar to empirical estimates of the effect of wage subsidy schemes from similar countries. For example, Bishop and Day, 2020 estimate that the Australian Job Keeper wage subsidy scheme saved around 700,000 jobs, or around 5.4% of the Australian labor force.36 The second and third columns of Table 4 show that the service sector disproportionately benefits from the wage subsidy scheme: the subsidy saves 8.4% of service sector jobs and 5.2% of non-service sector jobs. The remaining columns of Table 4 show that the subsidy saves significantly more jobs among young workers than among old workers. For workers aged 20 to 29, 17.2% of jobs would have been lost absent the subsidy. In contrast, for workers aged 30 to 39, 5.0% of jobs are saved; for workers aged 40 to 49, 3.2% of jobs are saved; and for workers over the age of 50, 2.6% of jobs are saved. These results indicate that the wage subsidy scheme had large distributional consequences for employment outcomes during the COVID-19 pandemic.
Table 4.
Jobs saved by the wage subsidy scheme.
| Sector of Employment |
Worker Age |
||||||
|---|---|---|---|---|---|---|---|
| Total | Services | Non-Services | 20–29 | 30–39 | 40–49 | 50–65 | |
| Jobs Saved | 6.5 | 8.4 | 5.2 | 17.2 | 5.0 | 3.2 | 2.6 |
Notes: The number of jobs saved reported for each group is the difference between employment in the model with the wage subsidy and employment in the model absent the wage subsidy. Jobs saved computed during the first quarter of the lockdown. All values reported as percent of steady state employment.
5.3. Evolution of the lockdown under alternative policies
While the wage subsidy scheme prevented job losses during the lockdown, the fiscal cost of the policy was substantial. Recall that the New Zealand Government spent NZ$14 billion on the wage subsidy in 2020, which was equivalent to 40% of social security expenditures in 2019.37 Given our finding in Section 5.2 that the wage subsidy saved 6.5% of the labor force, or 175,000 jobs, the policy is estimated to have cost approximately NZ$80,000 per job saved.
There may have been large opportunity costs of committing these fiscal expenditures to job preservation. We now study two alternative policies that could have been implemented during the lockdown: a one-time lump-sum transfer, and a one-period increase in the unemployment benefit paid to unemployed households. For simplicity, we model the latter policy as paying a higher unemployment benefit to all unemployed workers, regardless of whether their unemployment status was caused by the lockdown. This includes workers that may have become unemployed prior to the lockdown but who remain unemployed at its onset.38 We consider these policies, in particular, because they were two of the most common policy responses to the pandemic in other countries. We model the effect of each policy alternative assuming the same sequence of lockdown shocks . We also assume equal costs of fiscal transfers across policies. That is, each policy alternative has the same total cost of unemployment benefits, wage subsidies, and direct transfers. This ensures that comparisons across policies are made on a dollar-for-dollar basis.
In order to understand how much is being redistributed from the wage subsidy to these alternative policies, we report the size of payments under each policy in Table C.7 in Appendix Appendix C. The table shows the size of the lump-sum transfer and unemployment benefit, respectively, relative to measures of average incomes for different groups of households. Each column in turn reports average incomes for: the unemployed, all households, households aged 20 to 29, households aged 30 to 39, households aged 40 to 49, and households aged 50 to 65. Under the lump-sum transfer every household receives a payment equivalent to 5.2% of average household income, but the payment is equivalent to 26% of unemployed incomes. Under the policy that raises unemployment benefits, the size of the new transfer is more than three times the size of the unemployed benefit in steady state, and is 66% of average household income. For young households, the unemployed benefit is equivalent to 96% of average incomes, while for older households the benefit is a little over half of average incomes.39
We now compare equilibrium outcomes under each of the policy alternatives over the course of the lockdown shocks. Fig. C.16 in Appendix Appendix C shows the evolution of employment, consumption, and GDP under each policy. While the wage subsidy policy directly supports the labor market by preserving employment relationships between workers and firms, the lump-sum transfer and unemployment benefits policies do not so employment falls significantly more under these policies. The paths of aggregate consumption are very similar under the wage subsidy and the policy with higher unemployment benefits, but consumption falls by more under the lump-sum transfer policy. The evolution of GDP is essentially invariant to the form of policy intervention, since output is largely determined by the size of the productivity shocks that occur during the lockdown.
Fig. C2.
Aggregate variables under alternative policies. Notes: Model implied transition paths for total employment, total household consumption, and total output over the course of the lockdown. Solid blue lines are paths conditional on the wage subsidy policy. Dashed red lines are paths conditional on the lump-sum transfers policy. Green circled lines are paths conditional on the higher unemployment benefits policy. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Fig. 12 shows the response of household consumption by age group under the three policy alternatives. Figure A.23 in the Appendix shows consumption patterns for households in all age groups. For the youngest group of households, the smallest consumption decline occurs under the unemployment benefit policy. Recall that young workers earn around half as much as middle-aged workers (see Fig. 6). This implies a smaller spread between the unemployment benefit and wages for younger workers than older workers. Thus, an increase in unemployment benefits represents a significant increase in expected income for the youngest households who are also the most likely to become unemployed. Indeed, recall from Table C.7 that the higher unemployment benefit paid out is nearly 100% of average income for young workers. For older workers with higher earnings, a reduction in unemployment risk represents a larger increase in expected income than does an increase in unemployment benefits. Additionally, the lump-sum transfer policy has a much smaller effect on consumption as the payment is relatively small and much of it is directed towards older households who can comfortably smooth consumption without such payments.
Fig. 12.
Consumption by age under alternative policies Notes: Model-implied transition paths for consumption across households in 5-year age groups. Solid blue lines are paths conditional on the wage subsidy policy. Dashed red lines are paths conditional on the lump-sum transfers policy. Green circled lines are paths conditional on the higher unemployment benefits policy. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
To the extent that fiscal interventions aim to smooth consumption fluctuations, the most effective policies target households with the greatest sensitivity to income shocks. Table C.8 in Appendix Appendix C reports marginal propensities to consume (MPCs) for different household groups, as computed in the stationary distribution of the model.40 As expected, MPCs are substantially higher for unemployed relative to employed households, and for young relative to old households. The wage subsidy policy helps to stabilize consumption fluctuations because it prevents a large number of job losses, especially among the young. The unemployment benefits policy also helps to stabilize consumption because it directs payments to those with high MPCs. The lump-sum transfers policy is poorly targeted as much of the funds are directed towards employed and older households with low propensities to spend.
Fig. 13 illustrates changes in the distribution of unemployment and income across households under the various policy alternatives. The figure plots points along an unemployment-income curve for workers of different ages. Points in the upper left show outcomes for young workers, and points to the lower right show outcomes for older workers. The solid blue lines represent unemployment-income outcomes under the baseline wage subsidy policy, while the dashed red and green lines show unemployment-income outcome under the higher unemployment benefits and lump-sum transfer policies, respectively. First, consider a shift from the baseline wage subsidy policy to the higher unemployment benefits policy (left panel). For young workers, this change represents an inward shift of the unemployment-income curve: while young workers are much more likely to become unemployed under this policy, average incomes also rise significantly. For older workers, this change represents a direct upward shift of the unemployment-income curve: older workers face higher unemployment risk, with virtually no change in their expected income. Next, consider a shift from the baseline wage subsidy policy to the lump-sum transfers policy (right panel). For young workers, this change represents a shift of the unemployment-output curve towards the upper left: as unemployment for the young increases, the transfer is not large enough to offset the fall in average incomes. For older workers, the change represents a small inward shift of the curve: older workers experience both a small increase in unemployment and a small increase in average income inclusive of transfers.
Fig. 13.
The unemployment-income curve under alternative policies Notes: Fraction of households receiving unemployment benefits and average incomes (including transfers) for each age group, across the three alternative fiscal policies. Points on each unemployment-income curve are labeled by worker age.
Another benefit of the wage subsidy policy over the alternatives is that it slightly improves unemployment duration over the course of the lockdown. Fig. C.17 in Appendix Appendix C shows the expected unemployment duration for workers of different ages conditional on remaining in the industry in which they were most recently employed. Under the wage subsidy, unemployment durations fall by around 4%, or 1 week on average, for workers under the age of 30. This is entirely driven by the reduction in job separation rates under the wage subsidy because job finding rates are essentially unaffected (see Fig. 8 panels (c) and (d)). Fig. C.17 shows that the alternative policies have no effect on unemployment duration.
Fig. C3.
Expected unemployment duration at start of lockdown. Notes: Model implied expected unemployment durations conditional on remaining in the sector of most recent employment. Duration calculated using transition matrices and (see Equation (13)). Solid blue lines are durations with no fiscal policy intervention, dashed red lines are durations under the wage subsidy, yellow triangle-marked lines are durations under the transfers policy, and green circle-marked lines are durations under the unemployment benefit policy. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
In combination, these results suggest that there are large differences in the relative merits of the alternative policies implemented during the lockdown for households across the age distribution. Since it is unlikely that any one policy would be preferred by all groups of households, we next consider both the aggregate and cross-sectional welfare benefits of the policies studied in this section.
5.4. Household welfare during the lockdown under alternative policies
Finally, we study the welfare implications of the three policy interventions during the lockdown. We compute welfare gains for each policy intervention via the Consumption Equivalent Value (CEV) relative to the economy with no policy intervention. The CEV can be interpreted as the percentage gain in life-time consumption enjoyed under a particular policy intervention. We study these gains for different groups from the perspective of households in the period immediately prior to the lockdown, but who have no ability to change their behavior before the shocks occur. These households know the value of their own state variables on the eve of the lockdown, they know the effects of the shocks and each policy intervention, and they know the distribution over possible outcomes although they do not know their employment status at the onset of the lockdown. Table 5 reports the average CEV across all households and the fraction of households with a positive CEV under each of the three policy alternatives. We find that 65% of households are in favor of the wage subsidy policy with an average welfare gain of 0.21%, 100% of households are in favor of the lump-sum transfers policy with an average gain of 0.16%, and 41% of households are in favor of the policy with higher unemployment benefits with an average gain of 0.11%.
Table 5.
Welfare gains from policy interventions during the pandemic.
| Wage Subsidies | Lump Sum Transfers | Unemployment Benefits | |
|---|---|---|---|
| Mean CEV (%) | 0.177 | 0.161 | 0.113 |
| Fraction CEV | 0.643 | 1.000 | 0.400 |
Notes: Welfare statistics are computed using the expected value functions of households drawn from the pre-pandemic steady state distributon.
However, there is significant variation in welfare gains across different groups of households. Fig. 14 (a) shows that the youngest households enjoy the largest welfare gains overall, but also most prefer the policy that raises unemployment benefits during the lockdown. This is directly related to Fig. 12, which shows much smaller consumption fluctuations among younger households under the unemployment benefits policy. This policy raises the insurance value of unemployment, which is particularly valuable for young households that face low wages to begin with and who are more likely to become unemployed during the lockdown. The welfare benefits of all three policies fall as households age because the larger stock of assets held by older households enables them to better smooth consumption during the lockdown recession. The greater ability to smooth consumption reduces the value of policies that prevent unemployment or provide relatively small payments to these households.
Fig. 14.
Welfare gains from policy interventions during the lockdown by household age Notes: Panel (a) shows the mean CEV for households of each age group under each of the three policies. In Panel (b), the shaded areas show the 5-to-95 CEV percentiles for households in each age group under the wage subsidy policy and the unemployment benefits policy. The solid and shaded lines show the mean CEVs, as in Panel (a).
Finally, 14(b) shows the 5-to-95 percentiles of CEVs across age for the wage subsidy and unemployment benefits policy. A large proportion of young households under the unemployment benefit policy enjoy larger welfare gains than the average gain under the wage subsidy. Additionally, a small proportion of young households under the wage subsidy experience welfare losses relative to the world with no policy intervention. Nearly the entire distribution of households over the age of 40 receive larger CEVs under the wage subsidy policy than under the unemployment benefits policy. These results again highlight the dispersed welfare gains of different policy responses to the lockdown. Many more young households prefer policies with direct payments, while the majority of older households prefer policies that maintain their employment relationships as is the case under a wage subsidy scheme.
6. Conclusion
In this paper, we study the macroeconomic and distributional consequences of the lockdowns implemented in response to the COVID-19 pandemic of 2020. In order to isolate the effects of lockdowns we consider the case of New Zealand, which imposed strict domestic lockdowns and international border closures but which endured very little exposure to the health effects of the virus itself. We build a life-cycle heterogeneous agents model with labor market frictions and multiple industries, calibrated to the New Zealand economy. We then study the dynamic response of the model to a series of industry-level negative productivity shocks, which mimic the effects of a lockdown on production and the demand for labor.
We show that pandemic-induced lockdowns disproportionately affect both service sector workers and younger workers. Larger declines in service sector productivity result in larger increases in job separations in that industry, where young workers are more likely to be employed. Additionally, lower initial productivity among the youth in general leads employers to shed young workers more quickly than older workers. In the presence of a no-borrowing constraint and with young workers having had less time to accumulate savings, consumption is much more volatile for young households during the lockdown than it is for older households with the resources to self-insure against employment shocks.
Using counterfactual model outcomes, we show that the wage subsidy scheme offered by the New Zealand government during the 2020 lockdown prevented a large number of job losses. Moreover, we find that this subsidy disproportionately benefited service sector and young workers; those who were most affected by lockdowns in the first place. The varied cross-sectional effects of the subsidy are due to the conditional nature of its implementation: firms were only eligible for the wage subsidy if they experienced a sufficiently large decline in revenue during the initial lockdown period. In the model, firms in the service-sector and those that employ young workers experience a disproportionately large decline in revenues, which leaves them more likely to be eligible for the wage subsidy.
Finally, we study the welfare consequences of the wage subsidy policy in comparison to other possible fiscal interventions. We consider policies with the same fiscal outlays as the wage subsidy policy. The first policy pays a lump sum transfer to all households, while the second policy raises unemployment benefits. We find that young workers are better off under a policy that raises unemployment benefits. This is because the higher insurance value of unemployment for those who are most likely to become unemployed during a lockdown is more valuable than the increased probability of retaining a job under the wage subsidy policy.
While our model captures many rich features of the household life-cycle and labor market exposure that are important for studying the distributional effects of lockdowns, our study faces several limitations. First, our model assumptions imply no role for the aggregate demand channel in determining output or labor demand. Recall that we model the lockdown as a sequence of supply shocks, we do not model a New Keynesian demand channel, and we solve for general equilibrium in a small open economy. In this environment, a lockdown reduces incomes which affects household consumption, but this does not in turn influence aggregate output or hiring and firing decisions. An important policy implication of these assumptions is that while fiscal interventions can prevent job loss by directly subsidizing employment, any stimulatory effect of these policies on aggregate demand does not prevent further job loss. Introducing a realistic channel for aggregate demand feedback, as in Guerrieri et al., 2020 for example, would likely amplify the effects of the fiscal policy interventions studied here.
Second, our model of the labor market does not allow for long-term labor market scarring. The effects of labor market scarring may increase the benefits of wage subsidy policies that prevent the onset of long unemployment spells. This maybe particularly important for understanding the distributional labor market consequences of the pandemic, as in the occupation-dependent unemployment durations predicted by Gregory et al., 2020, for example. Third, for tractability we assume that households only have access to a liquid asset to facilitate saving. However, the large literature studying HANK models suggests that even wealthy households are sensitive to an increase in labor market risk when much of their wealth is held in illiquid assets (see Graves, 2020). Introducing a second illiquid asset would also likely amplify the welfare benefits of fiscal interventions during the lockdown, since even wealthy households would stand to benefit from these income-smoothing policies.
Footnotes
For a timeline of key events in New Zealand during the pandemic, see https://covid19.govt.nz/alert-system/history-of-the-covid-19-alert-system/.
For example, retail spending via debit, credit, and charge cards had largely recovered to pre-COVID levels by June 2020. See https://www.rbnz.govt.nz/statistics/c13.
Using a variety of micro-data sources gathered during the early phase of the pandemic, Chetty et al. (2020) showed that greater virus spread was associated with larger reductions in spending, particularly at firms in industries that required a lot of in-person interaction.
Bloom et al. (2020) provide some direct empirical support for the supply shock hypothesis, showing that total factor productivity in the UK is likely to have been significantly lower during 2020 due to firms having to respond to various COVID containment measures.
Carroll et al., 2020 also study the effect of lockdown shocks on household age through the lens of a partial equilibrium life-cycle model.
For papers in the macroeconomics literature studying the effects of these policies in the US, see Bayer et al., 2020; Carroll et al., 2020; Faria-e Castro (2021); Fang et al. (2020); Kaplan et al., 2020.
In a closely related HANK model, Graves (2020) shows that the presence of unemployment insurance helps to smooth the consumption response of low-wealth households to aggregate shocks that generate higher unemployment risk.
For details of lockdown rules in New Zealand, see https://covid19.govt.nz/alert-system/about-the-alert-system/.
In August 2020 New Zealand’s largest city, Auckland, experienced a brief resurgence in COVID cases. This prompted the government to impose a short-lived lockdown in the city, as is reflected in the jump in lockdown stringency for New Zealand shown in Fig. 1(a).
Our definition of service sector industries excludes the following industries: education and training; health care and social assistance; professional, scientific, and technical services; public administration and safety. We make these exclusions because the heavy involvement of the government in these industries in New Zealand limits their exposure to the market-based effects of pandemic.
Note that New Zealand’s first COVID case was not reported until February 28, and the government’s response to the pandemic began in March (Hale et al., 2020). The first economic effects of the pandemic are not observable in quarterly data until 2020:Q2.
For details, see https://www.workandincome.govt.nz/covid-19/wage-subsidy/index.html.
For example, see Bishop and Day, 2020 for an empirical analysis of the Job Keeper scheme adopted in Australia.
Employers of part-time workers were eligible for NZ$350 per worker per week.
Household income statistics from the Household labor Force Survey are available from Statistics New Zealand at http://nzdotstat.stats.govt.nz/.
The cost of wage subsidy scheme is reported by the Ministry of Social Development at https://www.msd.govt.nz/about-msd-and-our-work/publications-resources/statistics/covid-19/index.html. Data on fiscal expenditure is reported by the New Zealand Treasury at https://www.treasury.govt.nz/information-and-services/financial-management-and-advice/revenue-and-expenditure.
Information on the COVID income relief payment is reported by the Ministry of Social development at https://www.workandincome.govt.nz/covid-19/income-relief-payment/index.html.
See also Figure A.18 in OnlineAppendix A.
Note that job separations data encompass both employee layoffs and quits, which means that separations may result in either unemployment or a job-to-job transition.
Figure A.19(a) in Online Appendix A shows that steady state wages are high enough that workers would never optimally choose to reject a job offer in favor of unemployment. In contrast to the current paper, Fang et al. (2020) study the employment disincentive effects of unemployment insurance policies during the pandemic when workers can choose to reject employment offers.
This assumption follows Lugauer (2012), who builds a model with undirected search and life-cycle workers to study the effects of demographic change.
In Online Appendix B, we solve a version of the model without entrepreneur owners but where all profits are distributed lump-sum to households.
See, for example, Gornemann et al. (2016) and Graves (2020) for other examples of simple wage setting rules in models with labor search and heterogeneous agents.
See Appendix B.1 for details.
See Appendix B.1 for details.
The Annual Enterprise Survey is provided by Statistics New Zealand and reports financial statistics from a survey of over 500,000 businesses.
Note, aggregate real GDP is defined as . See Appendix B.1 for details.
For data on credit card spending, see https://www.rbnz.govt.nz/statistics/c13. The New Zealand Treasury provided Weekly Economic Updates on a variety of other high-frequency indicators, see https://www.treasury.govt.nz/sites/default/files/2021-04/weu-23apr21.pdf.
See Figure A.20 in the Online Appendix for job separation rates for workers in all age groups.
See Figure A.22 in the Online Appendix for the consumption patterns of households in all age groups.
The Household labor Force Survey reports that there were approximately 2.7 million employees in New Zealand in 2019.
The Australian Bureau of Statistics reports that there were approximately 12,860,700 employees in Australia in 2020. See https://www.abs.gov.au/statistics/labor/employment-and-unemployment/labor-force-australia/latest-release.
See https://www.msd.govt.nz/about-msd-and-our-work/publications-resources/statistics/covid-19/index.html and https://www.treasury.govt.nz/information-and-services/financial-management-and-advice/revenue-and-expenditure.
Note that this contrasts with the 2020 COVID Income Relief Payments offered by the New Zealand Government, which were only available to workers who lost jobs as a direct result of the pandemic. See https://www.workandincome.govt.nz/covid-19/income-relief-payment/index.html.
Figure A.19(c) in Online Appendix A shows that the temporarily higher level of unemployment benefits is above the equilibrium wage for the youngest households. While we do not allow workers to quit or reject job offers, Fang et al. (2020) study the disincentive effects of higher unemployment benefits during the pandemic in a search and matching model.
Note there is essentially no empirical work on marginal propensities to consume out of income for New Zealand households. Recently, de Roiste et al. (2021) estimated an average MPC out of housing wealth of 0.03 using New Zealand household panel data.
Appendix A. Data
-
•
The Blavatnik School of Government at Oxford University compiles government responses to the pandemic for virtually every country in the world. Data from their Government Response Tracker is available for download at https://www.bsg.ox.ac.uk/research/research-projects/coronavirus-government-response-tracker.
-
•
Population data is from the Historical Population Tables for the year 2018 from the OECD, available at https://stats.oecd.org/.
-
•
Data from New Zealand’s Wage subsidy scheme was updated weekly by the Ministry of Social Development throughout 2020. Data is available at https://www.msd.govt.nz/about-msd-and-our-work/publications-resources/statistics/covid-19/index.html.
-
•
Statistics for industry composition, job separation rates, and earnings by age are drawn from the 2018 Linked Employer-Employee Database (LEED). Statistics New Zealand maintains LEED, which is compiled from administrative data associated with New Zealand’s tax system. This covers all workers at businesses and organizations producing goods and services in New Zealand with revenue greater than $30,000. This data is available from Statistics New Zealand at http://nzdotstat.stats.govt.nz/wbos/index.aspx.
-
•
Unemployment benefit receipts by age are available from the Ministry of Social Development at https://www.msd.govt.nz/about-msd-and-our-work/publications-resources/statistics/benefit/.
-
•
Financial statistics for a sample of New Zealand businesses is available in the Annual Enterprise Survey from Statistics New Zealand at https://www.stats.govt.nz/information-releases/annual-enterprise-survey-2019-financial-year-provisional
-
•
Data on employment by ANZSIC06 industry code is available in the Household Labour Force Survey from Statistics New Zealand at http://infoshare.stats.govt.nz.
-
•
Data on monthly employment are available in the Monthly Employment Indicators from Statistics New Zealand at http://infoshare.stats.govt.nz
-
•
Data on household networth are available in the Household Economic Survey from Statistics New Zealand at http://nzdotstat.stats.govt.nz/wbos/index.aspx.
-
•
Data on GDP and interest rates are available from the Reserve Bank of New Zealand at https://www.rbnz.govt.nz/statistics
Appendix B. Model
B1. Additional model details
Profits are earned by firms involved in the production of goods as well as entrepreneurs in the labour market. The owners of all of these firms must also pay vacancy hiring costs. Total real firm profits are thus defined as:
As noted in the text, firm profits are consumed within the period in which they are earned.
We assume that expenditures due to profits , government spending , and net exports are allocated across services and other consumption goods in the same way as household expenditure in the CES aggregator in Equation (3). Final expenditures are given by
The solutions to the expenditure minimization problems imply the following demand functions
where is the relative price in industry .
B2. Formal definition of recursive competitive equilibrium
Let define the household state vector, let be the measure of households at age with , and let denote a vector of exogenous lockdown and fiscal policy shocks. To ease notation, we write the aggregate state vector as .
A recursive competitive equilibrium of the model consists of household decision rules , labor demands of production firms , labor market entrepreneur shutdown decisions characterized by the thresholds , labor demands of entrepreneurs , the vacancy positing decisions of labor market entrepreneurs , the mass of unmatched workers , production wages , worker wages , relative prices , job finding and job filling rates , job separation rates , fiscal policies , net exports , and transition functions that take the distribution of households over states at age to future states at age , such that:
-
1.
Households optimize by solving the problems (1) and (2), with associated decision rules
-
2.
Firms in the production sector maximize profits by solving (6), with associated labor demands
-
3.
Labor market entrepreneurs make shutdown decisions to maximize profits, by solving the problem (7), which is associated with shutdown thresholds and labor demands
-
4.
Given shutdown decisions, job separation rates are determined by (9)
-
5.
Potential labor market entrepreneurs post vacancies subject to the entry condition (10)
-
6.
The number of unmatched workers at each age and in each industry satisfy the laws of motion (16)
-
7.Given wages , markets for production workers clear:
-
8.Given relative prices , the individual goods markets clear:
where is aggregate household consumption. -
9.The aggregate resource constraint holds
-
10.
Government debt ensures that the government budget constraint in Equation (18) holds for all
-
11.
The transition functions are induced by the exogenous shocks and policies, the processes for idiosyncratic risk, and all of the decision rules. As a result, these transition functions are consistent with individual behavior.
Appendix C. Additional model tables and figures
Table C.6.
Employment shares by industry and sector.
| Service Sector |
Non-Service Sector |
||
|---|---|---|---|
| Industry | Share | Industry | Share |
| Arts, Recreation and Other Services | 0.060 | Agriculture, Forestry and Fishing | 0.049 |
| Financial and Insurance Services | 0.032 | Construction | 0.087 |
| Information Media and Telecommunications | 0.016 | Education and Training | 0.086 |
| Rental, Hiring and Real Estate Services | 0.020 | Electricity, Gas, Water and Waste Services | 0.009 |
| Retail Trade and Accommodation | 0.147 | Health Care and Social Assistance | 0.109 |
| Transport, Postal and Warehousing | 0.046 | Manufacturing | 0.092 |
| Wholesale Trade | 0.040 | Mining | 0.002 |
| Not Specified | 0.016 | ||
| Professional, Scientific, Technical, Administrative and Support Services | 0.128 | ||
| Public Administration and Safety | 0.062 | ||
Notes: Employment shares computed from both paid and self-employed workers across ANZSIC06 industries for 2019. Sectoral allocation chosen by authors for the purposes of the current study. Sources: Author’s calculations using data from the Household Labour Force Survey.
Table C.7.
Payments under alternative pandemic policies relative to average incomes.
| Unemployed | All Ages | Age 20–29 | Age 30–39 | Age 40–49 | Age 50–65 | |
|---|---|---|---|---|---|---|
| Transfers | 0.257 | 0.052 | 0.077 | 0.053 | 0.047 | 0.046 |
| Unemployment Benefits | 3.233 | 0.656 | 0.962 | 0.661 | 0.586 | 0.576 |
Notes: The size of the lump-transfer and unemployment benefit of each policy is determined in general equilibrium subject to the constraint that the fiscal cost of redistribution under each policy alternative is equal to the cost under the baseline wage subsidy scheme. All values are computed as fractions of averages incomes for each group of households.
Table C.8.
Household marginal propensities to consume.
| Employment Status |
Sector of Employment |
Worker Age |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Total | Unemployed | Employed | Services | Other | 20–29 | 30–39 | 40–49 | 50–65 | |
| MPC | 0.065 | 0.307 | 0.058 | 0.078 | 0.056 | 0.146 | 0.073 | 0.026 | 0.032 |
Notes: Marginal propensities to consume out of a transitory income shock. Averages across groups computed using the stationary distribution of hosueholds.
Supplementary material
Supplementary material associated with this article can be found, in the online version, at 10.1016/j.jedc.2021.104233
Appendix D. Supplementary materials
Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/
References
- Acemoglu D., Chernozhukov V., Werning I., Whinston M.D. Working Paper. National Bureau of Economic Research; 2020. Optimal targeted lockdowns in a multi-group SIR model. [Google Scholar]
- Auerbach A.J., Gorodnichenko Y., Murphy D. Inequality, fiscal policy and covid19 restrictions in a demand-determined economy. Eur Econ Rev. 2021:103810. doi: 10.1016/j.euroecorev.2021.103810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baqaee D., Farhi E. Technical Report. National Bureau of Economic Research; 2020. Nonlinear production networks with an application to the covid-19 crisis. [Google Scholar]
- Bartik A.W., Cullen Z.B., Glaeser E.L., Luca M., Stanton C.T. Technical Report. National Bureau of Economic Research; 2020. What jobs are being done at home during the COVID-19 crisis? evidence from firm-level surveys. [Google Scholar]
- Bayer C., Born B., Luetticke R., Müller G. CEPR Discussion Papers. CEPR Discussion Papers; 2020. The coronavirus stimulus package: how large is the transfer multiplier? [Google Scholar]
- Berger D., Herkenhoff K., Huang C., Mongey S. Testing and reopening in an SEIR model. Rev Econ Dyn. 2020 [Google Scholar]
- Bilbiie F.O., Melitz M.J. Working Paper. National Bureau of Economic Research; 2020. Aggregate-demand amplification of supply disruptions: the entry-exit multiplier. [Google Scholar]
- Bishop J., Day I., et al. Technical Report. Reserve Bank of Australia; 2020. How many jobs did jobkeeper keep? [Google Scholar]
- Bloom N., Bunn P., Mizen P., Smietanka P., Thwaites G., et al. Technical Report. National Bureau of Economic Research; 2020. The impact of Covid-19 on productivity. [Google Scholar]
- Farhi E., Baqaee D.R. Technical Report. National Bureau of Economic Research; 2020. Supply and demand in disaggregated Keynesian Economies with an application to the Covid-19 crisis. [Google Scholar]
- Faria-e Castro M. Fiscal policy during a pandemic. Journal of Economic Dynamics and Control. 2021;125:104088. doi: 10.1016/j.jedc.2021.104088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carroll C.D., Crawley E., Slacalek J., White M.N. Working Paper. National Bureau of Economic Research; 2020. Modeling the consumption response to the CARES Act. [Google Scholar]
- Chéron A., Hairault J.-O., Langot F. Life-cycle equilibrium unemployment. J Labor Econ. 2013;31(4):843–882. [Google Scholar]
- Chetty R., Friedman J.N., Hendren N., Stepner M. The opportunity insights team (2020). “how did covid-19 and stabilization policies affect spending and employment? a new real-time economic tracker based on private sector data.”. NBER Working Paper. 2020;27431 [Google Scholar]
- Christoffel K., Kuester K., Linzert T. The role of labor markets for euro area monetary policy. Eur Econ Rev. 2009;53(8):908–936. [Google Scholar]
- De la Croix D., Pierrard O., Sneessens H.R. Aging and pensions in general equilibrium: labor market imperfections matter. Journal of Economic Dynamics and Control. 2013;37(1):104–124. [Google Scholar]
- Den Haan W.J., Ramey G., Watson J. Job destruction and propagation of shocks. American economic review. 2000;90(3):482–498. [Google Scholar]
- Dingel J.I., Neiman B. How many jobs can be done at home? J Public Econ. 2020;189:104235. doi: 10.1016/j.jpubeco.2020.104235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eichenbaum M.S., Rebelo S., Trabandt M. Working Paper. National Bureau of Economic Research; 2020. The macroeconomics of epidemics. [Google Scholar]
- Fang L., Nie J., Xie Z. Unemployment insurance during a pandemic. Federal Reserve Bank of Kansas City Working Paper. 2020;(20-07) [Google Scholar]
- Fujita S., Ramey G. Exogenous versus endogenous separation. American Economic Journal: Macroeconomics. 2012;4(4):68–93. [Google Scholar]
- Gornemann N., Kuester K., Nakajima M. 2016. Doves for the Rich, Hawks for the Poor? Distributional Consequences of Monetary Policy. [Google Scholar]
- Graves S. Does unemployment risk affect business cycle dynamics? FRB International Finance Discussion Paper. 2020;(1298) [Google Scholar]
- Gregory V., Menzio G., Wiczer D. Pandemic recession: l-shaped or v-shaped? Covid Economics. 2020:88. [Google Scholar]
- Guerrieri V., Lorenzoni G., Straub L., Werning I. Technical Report. National Bureau of Economic Research; 2020. Macroeconomic implications of COVID-19: can negative supply shocks cause demand shortages? [Google Scholar]
- Hale T., Webster S., Petherick A., Phillips T., Kira B. Technical Report. Blavatnik School of Government, Oxford University; 2020. Oxford COVID-19 government response tracker. [Google Scholar]
- Hobijn B., Nechio F. Sticker shocks: using vat changes to estimate upper-level elasticities of substitution. J Eur Econ Assoc. 2019;17(3):799–833. [Google Scholar]
- Kaplan G., Moll B., Violante G.L. Technical Report. National Bureau of Economic Research; 2020. The great lockdown and the big stimulus: tracing the pandemic possibility frontier for the US. [Google Scholar]
- Krueger D., Uhlig H., Xie T. Working Paper. National Bureau of Economic Research; 2020. Macroeconomic dynamics and reallocation in an epidemic: evaluating the “Swedish Solution”. [Google Scholar]
- Lugauer S. Demographic change and the great moderation in an overlapping generations model with matching frictions. Macroecon Dyn. 2012;16(5):706–731. [Google Scholar]
- Ravn M.O., Sterk V. Job uncertainty and deep recessions. J Monet Econ. 2017;90:125–141. [Google Scholar]
- Razzak W.A. On the dynamic of search, matching and productivity in New Zealand and Australia. International Journal of Applied Economics. 2009;6(1):90–118. [Google Scholar]
- de Roiste M., Fasianos A., Kirkby R., Yao F. Are housing wealth effects asymmetric in booms and busts? The Journal of Real Estate Finance and Economics. 2021;62(4):578–628. [Google Scholar]
- Statistics New Zealand . Technical Report. Statistics New Zealand; 2020. Tourism Satellite Account: Year Ended March 2020. [Google Scholar]; URL https://www.stats.govt.nz/information-releases/tourismsatellite-account-year-ended-march-2020
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/