A Short Note on Optimizing Cost-Generalizability via a Machine-Learning Approach

Abstract

The costs of an objective structured clinical examination (OSCE) are of concern to health profession educators globally. As OSCEs are usually designed under generalizability theory (G-theory) framework, this article proposes a machine-learning-based approach to optimize the costs, while maintaining the minimum required generalizability coefficient, a reliability-like index in G-theory. The authors adopted G-theory parameters yielded from an OSCE hosted by a medical school, reproduced the generalizability coefficients to prepare for optimizing manipulations, applied simulated annealing algorithm to calculate the number of facet levels minimizing the associated costs, and conducted the analysis in various conditions via computer simulation. With a given generalizability coefficient, the proposed approach, virtually an instrument of decision-making supports, found the optimal solution for the OSCE such that the associated costs were minimized. The computer simulation results showed how the cost reductions varied with different levels of required generalizability coefficients. Machine learning–based approaches can be used in conjunction with psychometric modeling to help planning assessment tasks more scientifically. The proposed approach is easy to adopt into practice and customize in alignment with specific testing designs. While these results are encouraging, the possible pitfalls such as algorithmic convergences’ failure and inadequate cost assumptions should also be avoided.

Introduction

Assessment of students’ performance across the curriculum involves a variety of methods that address the assessment of knowledge, skills, and behaviors. Compared with other methods, an observation measure often yields more information. However, it possesses multiple sources of measurement errors, for example, rater effects, occasion effects, and item effects. Accommodating this type of assessment, generalizability theory (G-theory; Cronbach et al., 1972) provides a statistical solution for both decomposing the sources of errors on observation measures and indicating the reliability changes of the design manipulations; these two functions are called G-study and D-study in the literature (Brennan, 1992). To be specific, G-study yields parameter estimates of variances of all defined error sources and provides reliability-like indexes, such as for measurement quality evaluation. On the other hand, if a source of error (called facet) yielded by a G-study is small/large, the number of observations of the facet can be reduced/increased, where the consequences are calculated in a D-study (Brennan, 2010).

Approaches have been proposed to maximize reliability within a budget constraint. Woodward and Joe (1973) derived equations for their constrained optimization; Saunders et al. (1989) deployed discrete optimization, which was further updated by Saunders (1992) with the Cauchy–Schwartz inequity approach; Marcoulides (1993, 1995) as well as Marcoulides and Goldstein (1990, 1991, 1992) had developed the LaGrange multiplier approach and other related variants to handle the optimization within both univariate and multivariate G-theory. Meyer et al. (2014) extended the LaGrange multiplier approaches to G-theory with nested designs. Devising these approaches to a particular G-theory design requires mathematical deriving procedures, which may be a challenge to many applied researchers.

Different from the aforementioned studies, this article addresses the optimization problem from a different perspective: Given a minimal reliability value (namely a reliability threshold), what is the optimal combination of facets’ sample sizes for achieving the lowest costs? The inquiry’s context stems from practical needs in the field of medical education, which is demonstrated in the coming section. Instead of using the existing methods such as the LaGrange multiplier one, this article proposes a machine-learning approach called simulated annealing (SA) to handle the task of interest.

Objective Structured Clinical Examination

In the field of medical education, objective structured clinical examination (OSCE) is adapted to assess clinical skills so that the process can be more consistent and objective. Harden et al. (1975) proposed the original version of the OSCE—a checklist to assess students’ clinical skills using direct observation of their interactions with patients at multiple stations. Studies addressing the use of OSCEs are found to be tremendous in health professional education (Hastie et al., 2014; Hodges et al., 2014; Patrício et al., 2013; Setyonugroho et al., 2015; Smith et al., 2012; Walsh et al., 2009), and they together verify the necessity of using multiple stations in OSCEs, as opposed to the traditional long-case examination, which is not adequate to predict students’ performance in a different clinical situation (Hubbard, 1971). Accordingly, a typical OSCE design nowadays is likely to be based on a large sample of clinical cases and longer testing time, ensuring a satisfactory reliability level.

In addition to reliability, the costs of organizing OSCEs make up another concern. Compared with other assessment forms, an OSCE tends to be more resource-intensive: It involves examinees rotating round multiple standardized stations responding to test items or prompts, with or without the standardized patient situation, and raters scoring examinee performance against some predefined rubrics (Cusimano et al., 1994). Correspondingly, OSCE providers are required to make a budget for equipment, accommodations, subsistence, standardized patients, staff payrolls, the fee for content experts/consultants, and others (Brown et al., 2015). As a result, vast investments in OSCEs across countries are seen each year (Walsh & Jaye, 2013).

The trade-off between the costs and the reliability of OSCEs can be regarded as a reflection of cost-effectiveness in medical education assessment. Although numerous studies investigate either of the topics, addressing the two components together is rarely found in the literature. The fiscal constraints due to COVID-19 and the merging calls for raising transparency in medical education strengthen the practice of ensuring that the funding spent on medical education should be as cost-reliable as possible (Dacre & Walsh, 2013).

Generalizability Theory

A trustable examination demands certain statistical frameworks to provide a scientific understanding of the measurement quality, as it is believed that there are errors (i.e., variance off the interest) occurring simultaneously during the measurement process, which results in a discrepancy between the raw scores and the examinees’ true skill levels. The errors are called measurement errors, mathematically introducing construct-irrelevant turbulence into the analysis, posing a threat to the interpretation of the scores (Downing & Haladyna, 2004; Messick, 1998).

To address the measurement errors, classical test theory (CTT) is often adopted to yield the reliability, which is defined as a correlation between the true skill levels and the test scores. That said, the estimation of reliability, referring to the reproducibility of assessment data over time or occasions, is a pathway to ensure appropriate validity (Downing, 2003). Cronbach’s α is known as a CTT reliability estimate of a given test: It indicates the proportion of variance in test scores that can be attributed to true score variance (Cronbach, 1951). The measurement errors in CTT, however, oversimplify research designs in many situations as it only assumes two components for a test score (i.e., true score and errors). To overcome the shortcoming, CTT and α were further extended to G-theory (Brennan, 1992, 2010). There are ways of estimating G-theory, for example, the mean square method (e.g., Cornfield & Tukey, 1956; Henderson, 1953; Rao, 1970), the mixed model method (e.g., Huebner & Lucht, 2019; Jiang, 2018; Jiang et al., 2020), and the Bayesian method (e.g., Jiang & Skorupski, 2018; LoPilato et al., 2015)

Different from traditional tests such as multiple-choice questions and essays, OSCEs contain more sources of variance contributing to the measurement process. The variance can therefore be decomposed to more specific facets, for example, the effects of raters, items/questions, stations, and other sources of variation over which generalization is desired (Boulet et al., 2003; Myford & Wolfe, 2003). Therefore, a critical element in OSCE quality control is using a reliability index that takes all relevant measurement errors into the analysis (Haladyna & Downing, 2004). Naturally compatible with multiple-facet situations, G-theory provides an appropriate solution to OSCE studies. Articles addressing both summative and formative OSCEs through G-theory are plentiful in the literature (Baig & Violato, 2012; Donnon & Paolucci, 2008; Newble & Swanson, 1988), and the span of the reported reliability level ranges from .12 to .85.

An OSCE Within G-Theory

The illustration in this section is based on a published report: A G-theory study conducted in National Autonomous University of Mexico Faculty of Medicine in Mexico City, which organized a multiple-station OSCE in summative end-of-career final examination and recruited 278 examinees (Trejo-Mejía et al., 2016). Specifically, there were four exam versions, each of which was delivered at 18 equivalent stations from six areas (pediatrics, obstetrics and gynecology, surgery, internal medicine, emergency medicine, and family medicine). In total, there were 72 stations of which the workflows were navigated via the same blueprint and measured the same skills but in different forms of cases. Finally, the exam was applied in six testing sites and examinees were randomly assigned to only on site.

Accordingly, four facets (i.e., sources of measurement errors) were considered: the examinees, the stations, the versions, and the sites. The design, however, is not fully crossed as examinees were nested within sites. To construct a G-theory model, one should treat the final scores of the examinees $X$ as the dependent variable, where the facets $\theta$ s are the independent variables. Mathematical expressions for the G-theory model are

$$X_{\mathrm{pilj}}=\mu +{\theta }_p+{\theta }_i+{\theta }_l+{\theta }_j+{\theta }_{\mathrm{ij}}+{\theta }_{\mathrm{lj}}+{\theta }_{\mathrm{li}}+{\theta }_{\mathrm{ilj}}+ϵ,$$ (1)

$$\sigma {\left(X\right)}_{\mathrm{pilj}}^2={\sigma }_p^2+{\sigma }_i^2+{\sigma }_l^2+{\sigma }_j^2+{\sigma }_{\mathrm{ij}}^2+{\sigma }_{\mathrm{lj}}^2+{\sigma }_{\mathrm{li}}^2+{\sigma }_{\mathrm{ilj}}^2+{\sigma }_{ϵ}^2,$$ (2)

Equation 1 shows that an observed score, X, for examinee p on version j of station l at site i is made of the grand mean $\mu$, examinee effect ${\theta }_p$ (i.e., true skill level of examinee p), site effect ${\theta }_i$, version effect ${\theta }_j$, station effect ${\theta }_l$, both nested- and unnested-interaction effects, and residual error $ϵ$. Correspondingly, the relevant variance components are outlined in Equation 2. The variance estimates of the G-theory model were ${\sigma }_p^2$ = 17.652, ${\sigma }_i^2$ = 0.000, ${\sigma }_l^2$ = 42.157, ${\sigma }_j^2$ = 0.737, ${\sigma }_{\mathrm{ij}}^2$ = 0.867, ${\sigma }_{\mathrm{lj}}^2$ = 38.968, ${\sigma }_{\mathrm{li}}^2$ = 46.631, ${\sigma }_{\mathrm{ilj}}^2$ = 34.692, and ${\sigma }_{ϵ}^2$ = 187.374.

The relative- and absolute-error-based generalizability coefficients (i.e., reliability-like index within G-theory framework) can be calculated as follow: $E{\rho }_{\delta }^2=\frac{{\sigma }_p^2}{{\sigma }_p^2+{\sigma }_{\delta }^2}$ and $E{\rho }_{\Delta }^2=\frac{{\sigma }_p^2}{{\sigma }_p^2+{\sigma }_{\Delta }^2}$, where ${\sigma }_{\delta }^2=\frac{{\sigma }_{\mathrm{ilj}}^2}{n_i*n_j}+\frac{{\sigma }_{ϵ}^2}{n_i*n_l*n_j}$ and ${\sigma }_{\Delta }^2=\frac{{\sigma }_i^2}{n_i}+\frac{{\sigma }_j^2}{n_j}+\frac{{\sigma }_{\mathrm{ij}}^2}{n_i*n_j}+\frac{{\sigma }_l^2}{n_l}+\frac{{\sigma }_{\mathrm{lj}}^2}{n_l*n_j}+\frac{{\sigma }_{\mathrm{il}}^2}{n_i*n_l}+\frac{{\sigma }_{\mathrm{ilj}}^2}{n_i*n_l*n_j}+\frac{{\sigma }_{ϵ}^2}{n_i*n_l*n_j}$ are relative and absolute error variances respectively. As a result, $E{\rho }_{\delta }^2$ and $E{\rho }_{\Delta }^2$ were 0.94 and 0.81, respectively. Both $E{\rho }_{\delta }^2$ and $E{\rho }_{\Delta }^2$ were substantially higher than the acceptable range of G-theory being applied to OSCE research (0.51 to 0.78) according to published reports (Trejo-Mejía et al., 2016). This space provides the possibility of reducing the costs of the OSCE, while maintaining the generalizability coefficients to certain acceptable levels.

Method

Simulated Annealing

As an essential component of machine-learning toolkits, optimization can be defined as a problem where one maximizes or minimizes a target function by systematically choosing input values from an allowed numerical space and computing the value of the function (i.e., outcome). That said, optimization is essentially about finding the best solution. Unlike traditional optimization techniques that heavily rely on deriving mathematical procedures, machine-learning approaches, also known as metaheuristics, are related with general purpose solvers based on computational methods that use few domain knowledge, iteratively improving an initial solution (or population of solutions) to an optimal one at the end (Boussaïd et al., 2013). Well-known optimization techniques include SA, tabu search, genetic algorithms, genetic programming, differential evolution, and particle swarm optimization (Goffe et al., 1994). These techniques are particularly useful for solving:

1. Complex problems where no specialized optimization algorithm has been developed,

2. Dynamic questions in which a change in the model requires rederiving efforts to accommodate the new functional needs,

3. Irregular conditions are imposed so that traditional optimization techniques become inappropriate.

This article adopts SA as it has been widely used in practice and incorporated in most statistical software programs, in which a user only needs to specify a target expression (i.e., the function that the algorithm aims at minimizing or maximizing). SA mimics physical annealing in real life that contains the process of heating up a material until it reaches an annealing temperature and then it will be cooled down slowly in order to change the material to a desired structure. The SA application for optimal design problems with associated costs has a successful history, especially in the construction sector where maximization of profit of a project is of interest (Bettemir, 2010; Jaśkowski & Sobotka, 2006; Li & Coster, 2014, Reeves, 1995).

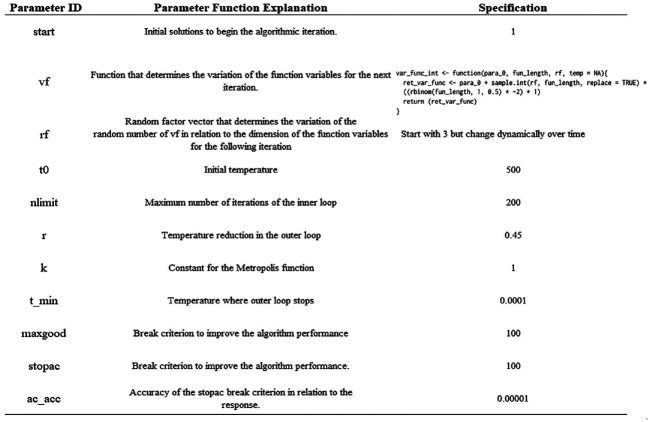
Similar to other machine-learning approaches, SA requires a set of parameters to drive the algorithm. To be specific, SA requires initial values, starting temperatures, perturbation determination, temperature changing modes, and others. These parameters are proved to be critical in a task as inappropriate selections of them could result in nonoptimal solutions (Feurer & Hutter, 2019). In this article, the R package optimization was used to execute SA (Husmann et al., 2017), where the algorithmic parameters listed in Figure 1 were adopted as they functioned well in our pilot tests. Proposed by Husmann et al. (2017, p. 9), the vf function in Figure 1 defines that the solutions yielded by SA should be integers. Alternatively, one can simply specify the requirement by rounding or ceiling approaches in the target function.

Figure 1.

Parameters setting for simulated annealing algorithm.

OSCE Cost Specification

The present optimization inquiry falls into the venue of G-theory’s D-study, which is about manipulating each facet’s level to obtain new generalizability coefficients. However, D-study does not accommodate the tasks of minimizing the associated costs of OSCEs. Therefore, the proposed solution, a machine-learning approach, is used to optimize the cost-generalizability.

The costs were summarized from Brown et al. (2015): £15,896 per site, £6,677 per version, and £4,843 per station. With the original levels of the facets, the total cost was as high as £209,240. It is informative to outline the levels of minimal generalizability coefficients acceptable to decision makers to reduce the costs. Without loss of generalizability, $E{\rho }_{\Delta }^2$ is used to represent the generalizability coefficient as the optimization requires more parameters to estimate so that the inquiry would not be oversimplified.

Monte Carlo Simulation

This section consists of two parts. The first part is verifying the utility of the proposed approach by comparing with the LaGrange multiplier approach in the scenarios illustrated in Marcoulides and Goldstein (1990). Specifically, they provided a closed-form solution for a two-facet fully crossed case (i.e., item and occasion effects represented by ${\sigma }_i^2$ and ${\sigma }_o^2$, respectively) with the information about cost per item per occasion and total budget available represented by c and $\overline{c}$, respectively:

$$n_i=\sqrt{\frac{{\sigma }_{\mathrm{pi}}^2}{{\sigma }_{\mathrm{po}}^2}*\left(\frac{\overline{c}}{c}\right)}\mathrm{and}{n}_o=\sqrt{\frac{{\sigma }_{\mathrm{po}}^2}{{\sigma }_{\mathrm{pi}}^2}*\left(\frac{\overline{c}}{c}\right)},$$ (3)

while ${\sigma }_{\mathrm{pi}}^2$ and ${\sigma }_{\mathrm{po}}^2$ are the variance components of interaction effects between examinee (i.e., p) and item as well as occasion facets. With the provided solution, the budgetary constraint can be satisfied such that $c{n}_i{n}_o\le$$\overline{c}$, while the generalizability coefficient is also maximized. Note that simply rounding the LaGrange multiplier solutions would result in violating the budgetary constraints. Goldstein and Marcoulides (1991) proposed a simple table approach that converts optimal noninteger solutions to acceptable candidate integer solutions while satisfying the cost constraint can be also met; this approach was used in the simulation. In the example of Marcoulides and Goldstein (1990), that ${\sigma }_p^2$ = 6.30, ${\sigma }_{\mathrm{pi}}^2$ = 1.60, ${\sigma }_{\mathrm{po}}^2$ = 0.30, ${\sigma }_{ϵ}^2$ = 1.95, $c$ = $5 and $\overline{c}$ = $100 yielded $n_i$ = 2 and $n_o$ = 10 via Equation 3, which resulted in the maximum generalizability coefficient $E{\rho }_{\delta }^2$ = 0.94; the simulation adopted the same two-facet fully crossed design as well as the $c$ and $\overline{c}$ values but randomly generated variance parameters by uniformly sampling from [${\sigma }^2-\frac{{\sigma }^2}{2},{\sigma }^2+\frac{{\sigma }^2}{2}$]. For example, in an arbitrary replication, ${\sigma }_p^2$ is uniformly sampled from [$6.30-3.15,6.30+3.15$] and other variance components are also sampled in the same fashion. It was replicated 200 times where the optimal solutions yielded by SA approach and the LaGrange multiplier approach were compared.

The second part of the simulation section is based on present OSCE planning inquires: minimizing costs when a generalizability coefficient threshold is given. Let [0.50, 0.55, 0.60, 0.65, 0.70, 0.75, 0.80] be the levels of minimal $E{\rho }_{\Delta }^2$. The task of interest then becomes finding the optimal combination of the facet levels without producing a $E{\rho }_{\Delta }^2$ lower than the selected threshold. The evaluation was essentially conducted a Monte Carlo simulation design, meaning we used computers to simulate different conditions based on a real setting and examine the performance of the proposed approach within these conditions. Assuming that β is the generalizability threshold, the target function f that SA attempts to minimize in the present context is

$$f=\mathrm{\pounds }15,896*n_i+\mathrm{\pounds }6,677*n_j+\mathrm{\pounds }4,843*n_l,$$

while

$$\frac{{\sigma }_p^2}{{\sigma }_p^2+\frac{{\sigma }_i^2}{n_i}+\frac{{\sigma }_j^2}{n_j}+\frac{{\sigma }_{\mathrm{ij}}^2}{n_i*n_j}+\frac{{\sigma }_l^2}{n_l}+\frac{{\sigma }_{\mathrm{lj}}^2}{n_l*n_j}+\frac{{\sigma }_{\mathrm{il}}^2}{n_i*n_l}+\frac{{\sigma }_{\mathrm{ilj}}^2}{n_i*n_l*n_j}+\frac{{\sigma }_{ϵ}^2}{n_i*n_l*n_j}}\le \mathrm{\beta }.$$

Results

In the first part of the simulation study, SA results had a perfect match with the closed-form solutions (i.e., 200/200 replications that two approaches produced equal solutions), meaning that the proposed approach has great utility for conditional optimization works in the present context. In addition to the replications, the results yield by SA approach and the LaGrange multiplier approach were identical in the example of Marcoulides and Goldstein (1990).

For the second part of the simulation study, Table 1 lists the combinations yielded by SA optimization. Unsparingly, the OSCE cost reduces as the generalizability coefficient threshold falls, as the facets’ levels are lessened. Meanwhile, the actual $E{\rho }_{\Delta }^2$ s are quite close the thresholds showing that the optimization converges well to a desirable degree. It can be interpreted as, for example, if $E{\rho }_{\Delta }^2\ge$0.65 is an acceptable condition, an OSCE testing setting with three sites, two versions, and 13 stations will result in £114,769 as the associated cost. Compared with the original amount, the cost decreases by £94,471. Other rows of the results in Table 1 can be explained similarly and therefore will not be repeated here.

Table 1.

Optimization Results via Simulated Annealing Approach.

Threshold	Actual ${\mathit{E}\rho }_{\Delta }^2$	Costs(£)	Site	Version	Station
0.50	0.51	85,717	3	2	7
0.55	0.57	95,401	3	2	9
0.60	0.60	102,078	4	2	9
0.65	0.66	114,769	3	2	13
0.70	0.71	131,130	4	2	15
0.75	0.75	147,491	5	2	17
0.80	0.80	176,078	4	3	21

Discussion and Conclusion

This article provides an interdisciplinary study for OSCE planning, fiscal elements, psychometric properties, and data science optimization. Although the optimization can be achieved by exhaustive search, trying all possible combinations of the solution set is not viable (sometimes even wholly impossible) when the problem of interest is complex. The growth of the facet size can result in an exponential increment of the exhaustive search’s trial-and-error attempts. For example, many OSCE providers would like to consider the rater effect, the occasion effect, and their interactions with other facets.

The example above may be not generalizable as OSCE testing settings, and the associated costs can be quite different; however, the proposed approach can be easily adopted and customized to meet the practical requirements. OSCEs are both money- and time-consuming; scientific tools and methods should be applied to the validity of the exam per se and also the planning from the fiscal standpoint. The definitions of “cost-effectiveness” are not consistent in different contexts. This article treats OSCE generalizability as the “effectiveness,” where other studies may consider the term as the proportion of examinees that become qualified physicians/doctors.

Using optimization approaches, like any techniques, is not risk-free. Algorithmic failures and local convergences should always be cautioned. That said, if the optimization stops unexpectedly or yields a nonoptimal solution, the results can be misleading to decision makers. A recent trend in the machine-learning literature is calling for an ensemble paradigm, which operates various optimization approaches simultaneously and combines the results via a certain weighting schema.