Abstract
Reconfiguration of the distribution network to determine its optimal configuration is a technical and low-cost method that can improve different characteristics of the network based on multi-criteria optimization. In this paper reconfiguration of unbalanced distribution networks is presented with the objective of power loss minimization, voltage unbalance minimization, voltage sag improvement, and minimizing energy not supplied by the customers based on fuzzy multi-criteria approach (FMCA) using new improved corona-virus herd immunity optimizer algorithm (ICHIOA). The voltage unbalances and voltage sag is power quality criteria and also the ENS refers to the reliability index. Conventional CHIOA is inspired based on herd immunity against COVID-19 disease via social distancing and is improved using nonlinearly decreasing inertia weight strategy for global and local exploration improvement. The methodology is implemented as single and multi-objective optimization on 33 and 69 bus IEEE standard networks. Moreover, the performance of the ICHIOA in problem-solving is compared with some well-known algorithms such as particle swarm optimization (PSO), grey wolf optimizer (GWO), moth flame optimizer (MFO), ant lion optimizer (ALO), bat algorithm (BA) and also conventional CHIOA. The simulation results based on the FMCA showed that all criteria are improved with reconfiguration due to compromising between them while in single-objective optimization, some criteria may be weakened. Also, the obtained results confirmed the superiority of the ICHIOA in comparison with the other algorithms in achieving better criteria with lower convergence tolerance and more convergence accuracy. Moreover, the results cleared that the ICHIOA based on FMCA is capable to determine the best network configuration optimally to improve the power loss, voltage sag, voltage unbalance, and ENS in different loading conditions.
Keywords: Network reconfiguration, Fuzzy multi-criteria approach, Power quality, Reliability, Improved corona-virus herd immunity optimizer algorithm
1. Introduction
The distribution network is an important part of the power system and is very important to meet the needs of electricity customers. The complexity, dispersion, and proximity to consumption location have made this part so important that a major percentage of the initial investment cost to supply energy from the power plant to the consumption location is related to this part. Also, due to the high current density in the distribution part and its extent, a significant part of the power system losses belongs to this part. High losses in the distribution part have led network operators to look for ways to reduce losses as well as improve other characteristics of the distribution network. On the other hand, operators are interested in using less expensive methods to improve the network characteristics. The most economical as well as the fastest approach to achieve these goals is the reconfiguration of the distribution network. The reconfiguration is one of the low cost and fewer needs for additional equipment to operate the distribution network in comparison with several methods including capacitor placement and also distributed generation (DG) resources allocation in the network (Gönen, 1986). The reconfiguration modifies the network topology by changing the status of the tie-lines and sectionalizer switches in the network and thus this method improves the network characteristics, including reducing losses and enhancing the network voltage conditions (Kanwar et al., 2016, Thakar et al., 2019). The radial topology of the network must be maintained during the reconfiguration process (Badran et al., 2017, Golub et al., 2019). The focus of utilities is on the reliability level and power quality of the customers in the network with the lowest operating costs. The network configuration as the status of the network switches causes changes in line current, bus voltages, and unbalanced voltage. So, with changing the load flow path based on the reconfiguration, the power quality criteria and also network reliability (energy not supplied of the network customers) can be affected (Gunther & Mebta, 1995). So, incorporating the power quality and reliability in the reconfiguration problem is very important to the real operation of the network (Billinton & Billinton, 1989). Moreover, a meta-heuristic algorithm with a high convergence rate and accuracy should be used, as well as its integration with a multi-criteria optimization approach. Therefore, to achieve the maximum improvement of the network criteria with reconfiguration, it is necessary to consider different objectives including power losses, voltage, power quality, and reliability, which are the most important criteria in network operation as the multi-criteria objective function. On the other hand, the application of the meta-heuristic algorithm with high optimization capability which does not get caught in premature convergence is vital to solving the reconfiguration problem and determining the optimal network configuration.
Various methods have been proposed by researchers in the literature to solve the reconfiguration problem. But none of the proposed methods has well addressed the set of important indices in the form of a multi-criteria optimization. Therefore, the main motivation of this research is to present a fuzzy multi-criteria approach (FMCA) based on a new meta-heuristic optimization algorithm to solve the reconfiguration problem of the distribution networks.
The rest of this paper is organized as follows: in section 2, the literature review and the research objectives and contributions are described. In section 3, the problem formulation is defined. In section 4, the proposed optimization method is presented. In section 5, simulation results and the conclusions are presented in section 6.
2. Literature review
The main purpose of reconfiguration studies is to determine the optimal status of opened and closed switches in the distribution network (best network configuration) by achieving the best network performance. The reconfiguration problem of distribution networks has been studied from various aspects including the type of objective function, reconfiguration techniques, and optimization algorithms. Heuristic methods include mixed-integer linear programming, dynamic programming, and meta-heuristic methods are used for solving the reconfiguration problem (Landeros Rojas, 2018). In heuristic methods, not all system states and topologies are considered, but the states are selected based on a series of heuristic rules and the computations are done to find the appropriate configuration. The results of implementing these types of methods are generally left to the local minimum and there is no guarantee to reach the global minimum (Mishra, Das, & Paul, 2017). Gupta, Swarnkar, and Niazi (2014) proposed the reconfiguration with the closure of all the switches. Then the opened switches are classified based on a decision-making index that measures the effect of lines on the system's losses.
The heuristic methods also include intelligent-based algorithms under computational intelligence (Ghasemi et al., 2016, Naderipour et al., 2021, Naderipour et al., 2019). In these methods, using special rules and methods, the configuration with less loss is determined. In recent years, many researchers have used artificial intelligence techniques and theories for power systems optimization. The heuristic methods are very fast, but they do not get the global solution, while meta-heuristic algorithms can achieve a global solution. The meta-heuristic optimization methods can solve real-world issues that are very complex with numerical optimization methods. These algorithms have high search capability and a precise problem function must be formulated for these methods to be very effective in finding the global solution. Some researches are presented based on meta-heuristic and artificial intelligence techniques. Su, Chang, and Chiou (2005) presented a single-objective reconfiguration of a balanced distribution network to reduce losses using meta-heuristic ant colony optimization (ACO) algorithm. Abdelaziz, Mohamed, Mekhamer, and Badr (2010) proposed the meta-heuristic method of taboo search (TS) to solve the reconfiguration as a single-objective problem to minimize active power losses by opening and close the balanced distribution switches. Kumar and Jayabarathi (2012) presented bacterial foraging optimization (BFO) algorithm for single-objective reconfiguration of a balanced distribution network with the goal of minimizing distribution losses. Shariatkhah, Haghifam, Salehi, and Moser (2012) studied the reconfiguration of a balanced network using a harmony search algorithm for reducing the losses. Kavousi-Fard and Niknam (2014) investigated the reconfiguration of a balanced network for improving network reliability using bat algorithm (BA). Shareef, Ibrahim, Salman, Mohamed, and Ling Ai (2014) presented improving the power quality and reliability of the distribution network through network reconfiguration using a quantum firefly algorithm (FA) for a balanced network. Nikhil (2014) implemented the reconfiguration of the balanced network to reduce the losses and improve the reliability indices of the distributed distribution network using GA. In (Alonso, Oliveira, & Zambroni de Souza, 2014), reconfiguration of the balanced distribution network is presented with the objective of power loss minimization and considering power interruption equivalent frequency index improvement based on a fuzzy method using a conventional artificial immune systems optimization algorithm. Nguyen and Truong (2015) studied the multi-objective reconfiguration problem to reduce losses and improve the network voltage profile using the weight coefficient method (WCM) via the cuckoo search algorithm (CSA). Rajaram, Sathish Kumar, and Rajasekar (2015) proposed the reconfiguration of the balanced network with the aim of loss reduction and voltage profile improvement using the plant growth simulation algorithm (PGSA) are proposed based on the WCM. Flaih, Xiangning, Dawoud, and Mohammed (2016) proposed the balanced network reconfiguration with the objective of minimizing the losses and improving the voltage based on the WCM using the improved PSO (IPSO) algorithm. In (Souza, Romero, Pereira, & Saraiva, 2016), reconfiguration of the balanced distribution network is presented with the objective of cost of energy loss minimization as single-objective optimization using conventional artificial immune algorithm Copt-aiNet algorithm. Lotfipour and Afrakhte (2016) applied a discrete-learning learning optimization algorithm to solve the optimization problem of a multi-objective network with the objective of minimizing losses and improving the voltage profile based on the WCM. Nguyen, Truong, and Phung (2017) used a runner-root algorithm to solve the multi-objective reconfiguration problem aimed at minimizing the losses and improving load balancing. In (Zhai, Yang, Chen, & Kang, 2018), the reconfiguration problem is solved as a dynamical approach with minimizing the losses and switching cost in the balanced network. In (Pegado, Ñaupari, Molina, & Castillo, 2019), improved selective binary PSO is applied for solving the reconfiguration of the balanced network with aim of losses minimization. In (Pegado et al., 2019), multi-objective reconfiguration of balanced networks is presented and aimed with losses minimization and reliability enhancement considering demand response services. Jafar-Nowdeh et al. (2020) proposed a moth–flame optimizer to solve the reconfiguration considering losses and reliability. Moghaddam et al. (2020) studied the reconfiguration of the unbalanced network with the objective of power quality improvement via ant lion optimizer. Abdelaziz et al., (2020) applied the GA for reconfiguration solving with aim of losses minimization in the balanced network. Jakus, Čađenović, Vasilj, and Sarajčev (2020) presented a branch exchange method to solve the reconfiguration problem with the objective of loss reduction and loading.
A summary of the previous studies on reconfiguration is presented in Table 1 . In Table 1, the reconfiguration studies are classified based on criteria of the total objective function (such as losses, voltage sag, voltage unbalance, and ENS), single or multi-objective optimization, balanced or unbalanced network and conventional or improved optimization algorithm. By reviewing the previous studies, it has been found that more reconfiguration studies are evaluated on the balanced distribution networks. In reality, distribution networks are exploited unbalanced due to the intrinsic nature of network loads and many efforts are being made to balance the network loads by the network operators. In addition, most reconfiguration studies in the literature are done with fewer criteria in the total objective function and also using WCM in multi-objective optimization that this method in comprising the objectives can not be a powerful method and even its coefficients must be optimized. Moreover, in the reconfiguration studies, the conventional optimization algorithms are used while the optimization algorithms can be improved to achieve better solutions in the reconfiguration problem. So the fuzzy multi-objective approach is a powerful method to solve the multi-criteria optimization problems (Hadidian-Moghaddam et al., 2017, Nowdeh et al., 2019).
Table 1.
Summary of the previous studies on reconfiguration.
| Ref. | Power loss | Voltage sag | Voltage unbalance | ENS | Single-objective | Multi-objective | Balanced network | Unbalanced network | Conventional algorithm | Improved algorithm |
|---|---|---|---|---|---|---|---|---|---|---|
| (Su et al., 2005) | ● | ● | ● | ● | ||||||
| (Abdelaziz et al., 2010) | ● | ● | ● | ● | ||||||
| (Kumar & Jayabarathi, 2012) | ● | ● | ● | ● | ||||||
| (Shariatkhah et al., 2012) | ● | ● | ● | ● | ||||||
| (Gupta et al., 2014) | ● | ● | ● | ● | ● | |||||
| (Kavousi-Fard & Niknam, 2014) | ● | ● | ● | ● | ● | |||||
| (Shareef et al., 2014) | ● | ● | ● | ● | ● | |||||
| ● | ● | ● | ● | ● | ||||||
| (Alonso, et al., 2014) | ● | ● | ● | ● | ● | |||||
| ● | ● | ● | ● | |||||||
| (Nguyen & Truong, 2015) | ● | ● | ● | ● | ||||||
| (Goswami and Chatterjee, 2016) | ● | ● | ● | ● | ● | ● | ||||
| (Flaih et al., 2016) | ● | ● | ● | ● | ||||||
| (Souza et al., 2016) | ● | ● | ● | ● | ||||||
| (Lotfipour & Afrakhte, 2016) | ● | ● | ● | ● | ||||||
| (Nguyen, Truong and Phung, 2017) | ● | ● | ● | ● | ||||||
| (Abdelaziz, 2017) | ● | ● | ● | ● | ||||||
| (Zhai et al., 2018) | ● | ● | ● | ● | ● | |||||
| (Pegado et al., 2019) | ● | ● | ● | ● | ||||||
| (Jahani, Nazarian, Safari, & Haghifam, 2019) | ● | ● | ● | ● | ● | |||||
| (Jafar-Nowdeh et al., 2020) | ● | ● | ● | ● | ● | |||||
| (Jakus et al., 2020) | ● | ● | ● | ● | ||||||
| (Moghaddam et al., 2020) | ● | ● | ● | ● | ● | ● | ||||
| This paper | ● | ● | ● | ● | ● | ● | ● |
In this paper a new fuzzy multi-criteria approach (FMCA) based on a meta-heuristic optimization algorithm is proposed to solve the reconfiguration of 33 and 69 bus unbalanced distribution network with the objective of reducing losses, improving the voltage sag, minimization of voltage unbalance, and reliability enhancement. The reliability index is defined as minimizing the energy not-supplied by network customers. Today, new algorithms with high convergence power and rate are used to achieve the best global solution in the optimization problem, but it is not certain that these new methods can achieve global optimization according to No-Free-Lunch (NFL) theorem. For this reason, a new meta-heuristic method named Improved Corona-virus Herd Immunity Optimization Algorithm (ICHIOA) is proposed for solving the reconfiguration problem and determining the network optimal configuration. Conventional CHIOA is inspired based on herd immunity against COVID-19 disease via social distancing (Al-Betar, Alyasseri, Awadallah, & Doush, 2020) and also its performance is improved using a nonlinearly decreasing inertia weight strategy (NDIWS) (Jahannoush & Arabi Nowdeh, 2020) to prevent premature convergence in a condition of increasing the problem complexity. In this study, simulation results including loss, voltage sag, voltage unbalance, and ENS before and after the reconfiguration are evaluated using ICHIOA before and after optimization. Also, to verify the proposed method, the results of ICHIOA are compared with conventional CHIOA and also well-known methods including particle swarm optimization (PSO), grey wolf optimizer (GWO), Moth flame optimizer (MFO), bat algorithm (BA), and ant lion optimizer (ALO).
The main contributions of this paper are listed below:
-
•
Distribution network reconfiguration considering losses, reliability, and power quality
-
•
Network reconfiguration based on new fuzzy multi-criteria approach
-
•
Using of a new Improved Corona-virus Herd Immunity Optimizer Algorithm (ICHIOA)
-
•
Investigation of load variations impact on unbalanced network reconfiguration
-
•
Superiority of ICHIOA compared to CHIO, PSO, GWO, MFO, BA, and ALO
3. Problem formulation
The network reconfiguration changes the topological configuration of distribution feeders by changing the status of the tie lines. This requires using an optimization method to determine a proper network configuration that can reduce losses, improve power quality and improve network reliability. In this paper reconfiguration of unbalanced distribution networks based on FMCA is proposed using ICHIOA. The objective function and constraints are described as follow:
3.1. Objective function
The objective function of the proposed problem is considered as loss reduction, voltage sag and voltage unbalance improvement, and ENS reduction. Each section of the objective function is formulated.
3.1.1. Active power loss
The active power loss by calculating the buses voltages and the line currents is calculated as follows (Abdelaziz et al., 2010, Kumar and Jayabarathi, 2012):
| (1) |
where, and are voltages between buses i and h, k is between the buses i and h, , are the resistance, reactance, and current of the kth line, and n is the number of grid lines.
3.1.2. Voltage sag improvement
Voltage sag is obtained by measuring the residual voltage in a bus during the voltage sag. In this study, the average voltage sag across all buses is used to improve the voltage sag of the entire network (Ch et al., 2016, Gunther and Mebta, 1995, Gupta et al., 2014).
| (2) |
Vi h is the voltage of bus i considering fault conditions in bus h, i is the bus number and h is the number of possible faults, and Vsag,ave is the average of bus voltage in the voltage sag conditions.
3.1.3. Voltage unbalance improvement
The unbalanced network is due to load unbalanced. In this study, the network unbalance value is calculated by measuring the voltage unbalance of the buses (Ch et al., 2016, Gunther and Mebta, 1995, Gupta et al., 2014).
| (3) |
Where,
| (4) |
where, Vpos, i is the positive sequence of the bus i, Vneg, i, the negative sequence voltage of the bus i.
3.1.4. Reliability improvement
Improving reliability is another benefit of distribution network reconfiguration. Therefore, due to the phenomenon of network lines outage and the definitive interruption of customers, reliability studies should be conducted in distribution networks planning with the reconfiguration problem. The energy not supplied (ENS) of network customers is defined as follow (Abdul-Malek et al., 2020, Gunther and Mebta, 1995, Nowdeh et al., 2019):
| (5) |
| (6) |
where, is active power, is annual outage rate of the line, refers to average time on each outage, Nbr is the number of lines, and Ui is the demand in bus i. In this case, the ENS value must be minimized.
3.2. Constraints
The fuzzy multi-objective function should be calculated in the following constraints. The constraints of the problem are presented below.
Equality constraint is presented as follow:
-
•
Power balance at all buses (Ch et al., 2016, Gupta et al., 2014, Nowdeh et al., 2019)
| (7) |
where, and are active and reactive load power of bus i,, and refers to the voltage of bus I for phases a, b and c, respectively. I*refers to the conjugate current.
Inequality constraints are presented as follow:
-
•
Voltage constraint
The voltage range of the buses must be within a predetermined range (Gupta et al., 2014, Moghaddam et al., 2020).
| (8) |
where, is the voltage of bus i, and are the minimum and maximum voltage range of buses, respectively.
-
•
Lines current constraint
The maximum current through the network must not exceed the maximum allowable current of the network lines (Gupta et al., 2014, Moghaddam et al., 2020).
| (9) |
where, refers to the maximum allowable current of the network lines.
-
•
Voltage unbalance constraint
The voltage Unbalance of buses should not be exceeded the specified value (Gupta et al., 2014).
| (10) |
where, and are positive and negative sequence voltage and is maximum unbalance voltage.
-
•
Voltage sag constraint
The network voltage sag must be not greater than the permitted amount that the distribution network standards considered (Moghaddam et al., 2020).
| (11) |
where, and are average and minimum values of voltage sag.
-
•
Network radiality constraint
The network structure should be radial in the reconfiguration process (). is the total number of network close lines. In other words, the difference between the total number of network lines and the number of tie lines should be less than the number of buses, 1 unit (Gupta et al., 2014, Moghaddam et al., 2020).
| (12) |
where A is the bus incidence matrix and L refers to the total number of buses.
3.3. Fuzzy multi-criteria approach (FMCA)
In the fuzzy method, each objective defined for the problem is modeled with a fuzzy membership function. The membership function represents the satisfaction and improvement of the corresponding objective function with itself. When trying to optimize several objectives simultaneously, there must be a compromise between all the objective functions. That is, if an objective function is recovered a lot and the other objective function is not well-recovered, it is not acceptable then all objectives of the problem need to be counted together and an acceptable improvement is made for all objective functions. A fuzzy method (Hadidian-Moghaddam et al., 2017) can be used to define multi-objective functions. Since in each case of network reconfiguration, the power loss, voltage sag, voltage unbalance, and ENS index are easily calculated according to the system load flow results, the values of the improvement of each index can be obtained with the help of membership functions. In this paper, FMCA is applied to solve the multi-objective optimization problem. The basis of the FMCA in solving the multi-objective optimization problem is the optimization of objective function and constraints, simultaneously. To optimize multi-objectives simultaneously, the first step in the FMCA is to define μ i for the i-th objective function in the problem (definition the fuzzy index for each objective in objective function). In other words, we define a μ for each objective function, which μ is calculated for each objective function as bellow. Fig. 1 shows how to calculate μ for each objective (Hadidian-Moghaddam et al., 2017).
Fig. 1.
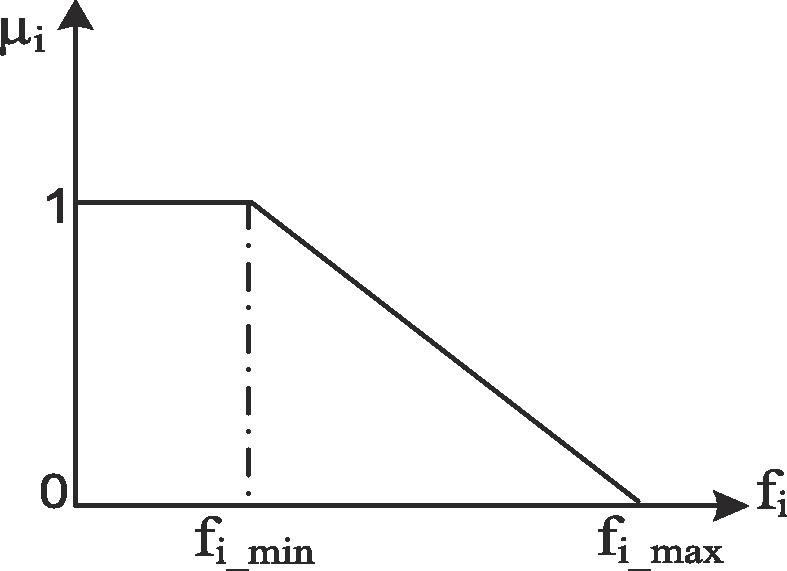
Definition of μ for each objective of the total objective function (Hadidian-Moghaddam et al., 2017).
A desirable membership function must be defined for each objective of the total objective function by (Hadidian-Moghaddam et al., 2017)
| (13) |
where, is membership function of objective function i, and are maximum and minimum values of objective function i and is the value of objective function i in the optimization process.
Therefore, it is necessary to solve the problem as a single objective once for each objective for the minimum value of this objective function calculation. The maximum value of an objective function depends on the degree of importance of that function on the total of the objective functions. The closer of maximum value to the minimum value shows the greater its degree of importance.
As is well known from (13), the objective closest to its maximum value will be less µ. If we use the optimization algorithm to maximize the minimum of all μ i (which means that we maximize the minimum μ, between all μ i) this means that we want to get as close to the minimum value as possible to all objectives. In this way, we will achieve our goal of minimizing the objective functions together and simultaneously. The mathematical expression of this is given in the following equations (Hadidian-Moghaddam et al., 2017).
| (14) |
| (15) |
where, and refers to equality and un-equality constraints.
Therefore, the objective function and constraints are considered multi-objective using FMCA.
Fuzzy objectives are presented by defining their corresponding membership functions. These functions express the membership degree of definite fuzzy sets using values from 0 to 1. Membership value 1 indicates incompatibility with collections while value 1 indicates complete compatibility. Also, the penalty factor is considered for each objective in the μ D.
The membership function of each objective is presented as follows:
| (16) |
| (17) |
| (18) |
| (19) |
where, and refer to the maximum and minimum value of the objective respectively. for each objective is a value in the base network without reconfiguration and for each objective can be calculated with a single objective solution, so can be a value between and .
4. Proposed meta-heuristic ICHIOA
In this section, the structure of the proposed hybrid optimization method for problem solution is described and then its implementation is presented in problem-solving.
4.1. Overview of CHIOA
The virus is a very small pathogen that multiplies only in the living cells of an organism. Viruses infect a variety of life forms, including animals and plants, and even microorganisms, including bacteria. Viruses spread and evolve rapidly among populations. A vaccine is a biological product that produces active acquired immunity against a specific microbial disease. Therefore, the medical community uses vaccines to create immunity and health against the virus. But it takes a long time for the virus to be fully known and vaccinated. Therefore, the world health organization recommends strategies to prevent infection with the virus until the virus vaccine is available (Al-Betar et al., 2020):
-
A)
Isolation or quarantine of people infected with the virus and even people who have been in contact with them.
-
B)
Adhere to herd health protocols to reduce or stop the virus pandemic
4.1.1. Inspiration
Viruses can be transmitted biologically and amplified by amplifying hosts. The corona-virus disease (COVID-19) is first diagnosed in December 2019 in Wuhan, China. The World Health Organization (WHO) announced the outbreak of the disease. For the first time in the city of Wuhan, a new strain of COVID-19 is identified after people developed pneumonia for no apparent reason and existing vaccines and treatments are ineffective. As of July 31, 2020, 17,297,296 confirmed cases had been registered, of which 10,132,579 had improved and 673,223 had been killed. The incubation period of Covid-19 disease is between 2.1 and 11.1 days and so far no specific treatment has been obtained for this disease (Al-Betar et al., 2020). Also, its mortality rate is between 0.25 and 3% (Al-Betar et al., 2020). According to immunity experts, immunity refers to the resistance that usually occurs in the human or animal body to infectious pathogens or their toxins, and the result is that they no longer contract the disease, which can be inherent or be acquired. Simply, herd immunity (HI) refers to a situation in which the majority of the population is immune to disease and, as a result, the part of the population that is not immune is indirectly protected from infection. When this immunity develops in a large percentage of the population, HI is acquired and the disease no longer spreads.
4.1.2. Herd immunity
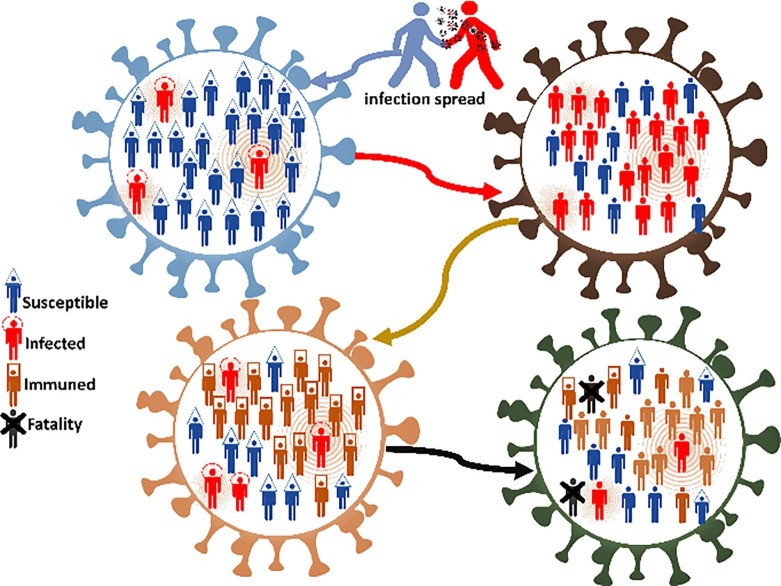
HI can affect epidemic transmission because it can reduce the prevalence of infection. HI has been proposed as one of the methods to control the prevalence of COVID-19 (Al-Betar et al., 2020). Observe social (physical) distance to reduce COVID-19 transmission. Social distancing involves actions that limit the number of close relationships you have with other people. This is effective in limiting the prevalence of Covid-19 in the community. Canceling events that bring large crowds together is an example of social distancing. Social distancing deliberately increases the physical space between humans and thus prevents the spread of disease. Keeping at least two meters away from others reduces the chance of becoming infected with the corona-virus. Social distancing measures include approaches that aim to minimize close contact between people in the community. These include individual-level quarantine, as well as other community-based approaches. In the case of HI, the safety of individuals is of paramount importance. As more people in the community become infected with COVID-19, more people in the community will recover and become immune to future diseases. HI is affected by basal reproduction rates and how more people can become infected against carriers. Carriers spread the disease and the infected person's level of immunity establishes an immunological memory of the disease. This immunizes the infected person against future viruses, and as a result, the spread of the disease gradually ends. The schematic of HI is illustrated in Fig. 2 .
Fig. 2.
Schematic of HI (Al-Betar et al., 2020).
The proposed optimization algorithm is based on HI mathematical modeling. This algorithm is based on the concept of how to protect people in the community against disease by turning the majority of the population susceptible to immunization. As a result, other vulnerable people in the community are not infected due to the lack of transmission of the disease by the immune population.
4.1.3. Population hierarchy
HI is divided into three categories based on the growing population: a) susceptible, b) infected, and c) immuned (improved) (Al-Betar et al., 2020). Fig. 3 shows the population hierarchy. Fig. 3 shows a tree with the root of the tree pointing to the infected person and the edges showing the people in contact with the infected person. To the right of Fig. 3, if the root person is immune, the virus will not be able to spread and should not be transmitted to people in contact with the root person. The susceptible people become infected when they come in contact with sick people and are not infected with the virus. Infected people can transmit the virus to susceptible people, ie people who are in direct contact with them. People are immune to the virus and are not infected by sick people. Safe people can help stop the epidemic in the community.
Fig. 3.
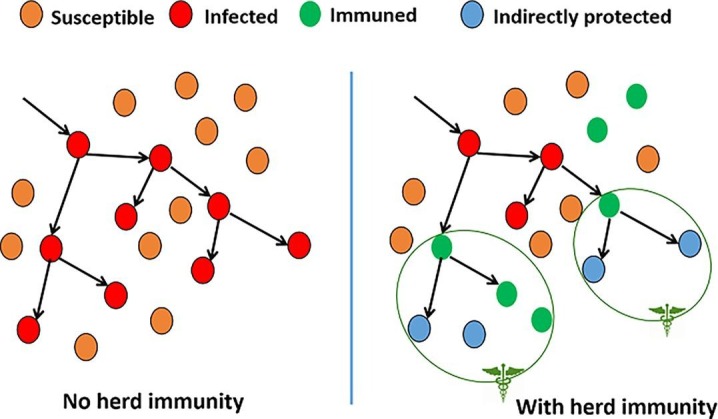
Population hierarchy (Al-Betar et al., 2020).
The susceptible people are the largest part of the population to create the optimization structure in the CHIO algorithm. Infected individuals are the second largest population that grows if social distancing is not observed until they become more secure or even die. The third part of the population includes immune people who start with zero and their number grows based on improvement in the population. Eventually, when the majority of people are immune, the epidemic stops.
4.1.4. Social distancing
Social distancing is very effective in reducing the prevalence of COVID-19 infection (Al-Betar et al., 2020). Everyone, including those who have not been exposed to the COVID-19, is required to observe the social distance. The action is continuous and there is no set time for its observance. Social distance means keeping at least two meters away from other people to prevent the transmission of the COVID-19. The WHO emphasizes that maintaining a social distance of at least two meters is associated with a reduced risk of spreading COVID-19 through small discharges released when sneezing or talking in the air. These droplets may contain COVID-19 and may be inhaled if the distance between people is short.
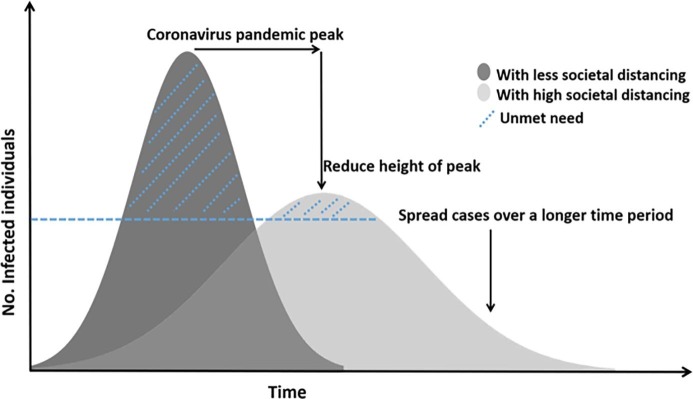
The positive effect of social distancing is shown in Fig. 4 . As can be seen, the prevalence of the disease has decreased with social distancing, which can even reduce the rate of disease outbreak and reach the peak of the epidemic (fewer people infected with the virus) (Al-Betar et al., 2020).
Fig. 4.
Effect of social distancing on COVID-19 outbreaks (Al-Betar et al., 2020).
In the CHIOA, the concept of social distancing is based on distinguishing the current person and the candidate from the population of a person who may be susceptible, infected, or safe.
4.1.5. CHIOA procedure
The HI approach is modeled in the CHIO optimization algorithm. The structure of the CHIO algorithm is presented in 6 steps as follows:
Step 1) The algorithm parameters and the problem optimization variables are set based on the following objective function (Al-Betar et al., 2020).
| (20) |
where, represents the objective function (safety rate) for the individual or the decision variable, n represents the total genes of each individual. The boundary values of each gene are such that lbi and ubi are the minimum and maximum limits of the gene.
The CHIO algorithm has four algorithmic parameters C0, Max_Itr, HIS, and n representing the number of primary individuals with the virus, the maximum number of replicates, the number of population, and the dimension of the problem, respectively. The algorithm also has two control parameters BRr and Maxage. The BRr parameter represents the base replication rate, which controls the operators of the algorithm based on the prevalence of the virus. Also, another control parameter, Maxage, indicates the age of most people infected with the virus, so that those who reach Maxage either gain health or die.
Step 2) In this step the HI population is generated. The CHIO algorithm randomly generates a set of HIS equivalent entities. The production population with n × HIS dimensions are considered as follows (Al-Betar et al., 2020):
| (21) |
Each line j refers to a person xj and is defined as follows (Al-Betar et al., 2020):
| (22) |
The objective function (immunity rate) for each individual is determined based on Eq. (20). The status vector (S) with length HIS for all individuals has an initial value of zero (susceptible person) or one (infected person).
Step 3) In this step HI evolves against the virus. The xjj gene (xi jj) is either fixed or changed by social distancing based on the percentage of BRr and 3 rules (Al-Betar et al., 2020):
| (23) |
Where, r represents a random number between zero and one.
The three rules of social distancing are as follows (Al-Betar et al., 2020):
-
•
Infected person) The new amount of gene is defined based on social distancing considering as follows. The new value is obtained by subtracting the value of the current gene from the gene value of the infected person x m (Al-Betar et al., 2020).
| (24) |
Where,
| (25) |
The value of xi c(t) is randomly determined based on each infected person cc and considering the situation vector considering (Al-Betar et al., 2020).
-
•
The vulnerable person) the new amount of gene is defined based on social distancing considering as follows (Al-Betar et al., 2020). The amount of the new gene is determined by the difference between the amount of the current gene and the amount of gene in the susceptible person xm (Al-Betar et al., 2020).
| (26) |
Where,
| (27) |
The value of xi m(t) from each vulnerable person x m occurs randomly with respect to the situation vector (Al-Betar et al., 2020).
-
•
The immunized person) The new value of the gene is obtained by social distancing by considering as follows (Al-Betar et al., 2020). The new gene value is defined by the difference between the current gene value and the immune individual x v value (Al-Betar et al.,
-
•
2020).
| (28) |
Where,
| (29) |
The value of xi v(t) of the best safe person x v with respect to the situation vector is as follows (Al-Betar et al., 2020):
| (30) |
Step 4) The HI population is updated in this step. The safety rate f(xjj(t + 1)) is obtained for each product person xjj(t + 1) and the current person xj(t) is replaced by the product person xjj(t + 1) if it is better and should be f(xjj(t + 1)) < f(xjj(t)). If , then the age vector , increases by one.
The situation vector for each item x j is updated with the HI threshold as follows (Al-Betar et al., 2020):
| (31) |
Where, represents a binary value. The value of this binary number is equal to one by inheriting xj(t + 1) from each infected person. Average population safety rates () are defined as follows (Al-Betar et al., 2020):
| (32) |
Step 5) Mortality of people. If the safety rate (f(xjj(t + 1)) of the current infected person does not improve for the maximum repetition of the algorithm, then it is considered as a lost person and then reproduced according to the following equation (Al-Betar et al., 2020).
| (33) |
Step 6) In this step, the convergence and stop criteria of the algorithm are checked. Steps 3 to 6 are repeated to achieve the convergence criterion and to stop the algorithm (performing maximum iterations). The total number of susceptible and safe people dominates the population, and infected people also disappear.
4.2. Overview of improved CHIOA (ICHIOA)
A nonlinearly decreasing inertia weight strategy (NDIWS) (Jahannoush & Arabi Nowdeh, 2020) according to Eq. (34) is applied for improvement of conventional CHIOA performance in global and local discovery. The search capability is tuned by variations value. The declined nonlinearly from to . The big value of is desirable for searching global discovery and the small value of is suitable for searching the local discovery. The NDIWS is defined by (Jahannoush & Arabi Nowdeh, 2020)
| (34) |
Where, and are max and min values of , respectively. Maxage is the maximum number of iterations and is a constant that is positive (here = 10).
The Eqs. (25), 27 and 29 are rewritten based on NDIWS as follows:
| (35) |
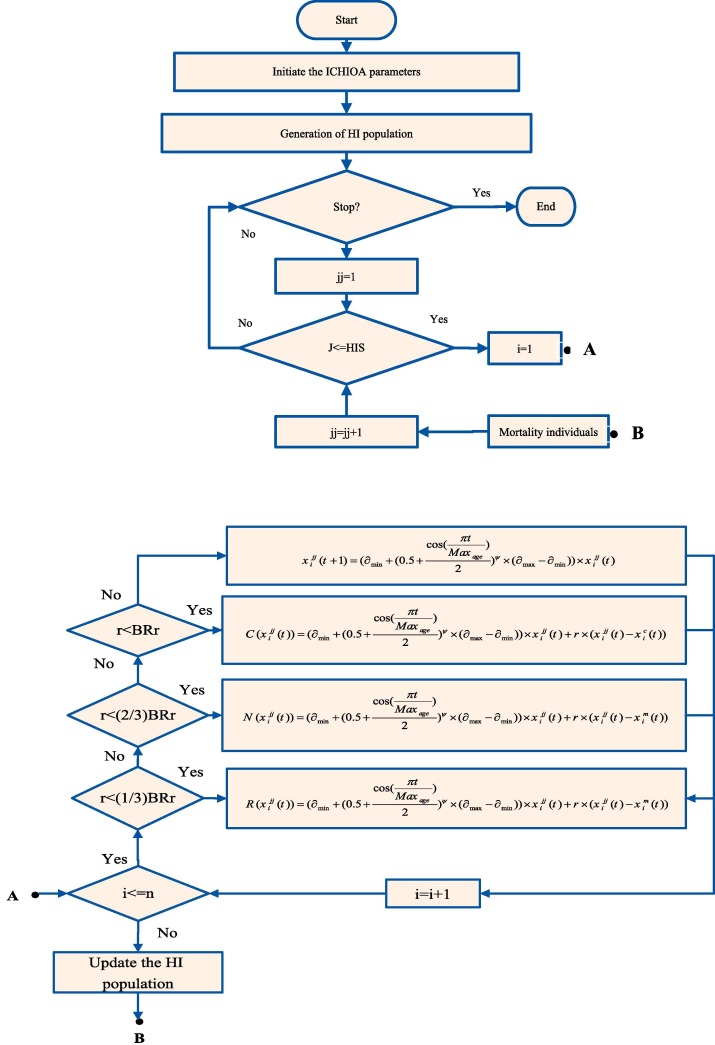
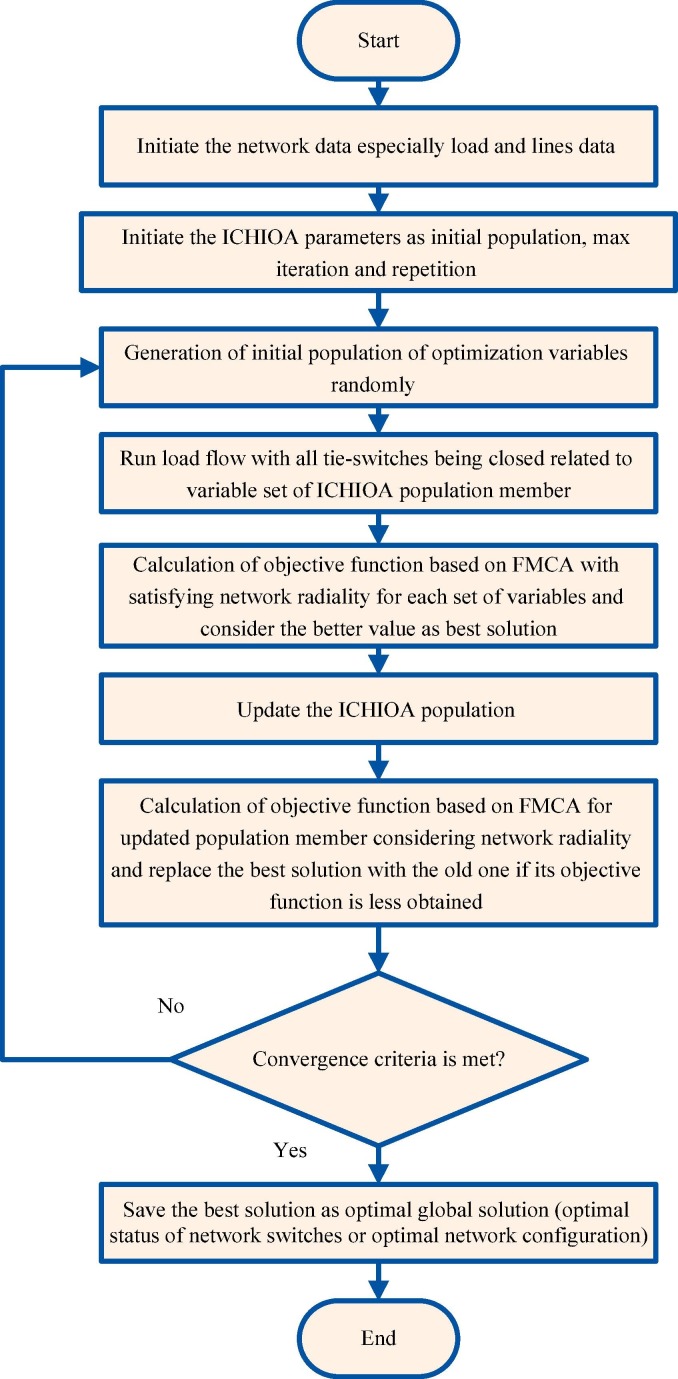
The flowchart of the ICHIO algorithm is shown in Fig. 5 .
Fig. 5.
Flowchart of ICHIO algorithm (Al-Betar et al., 2020).
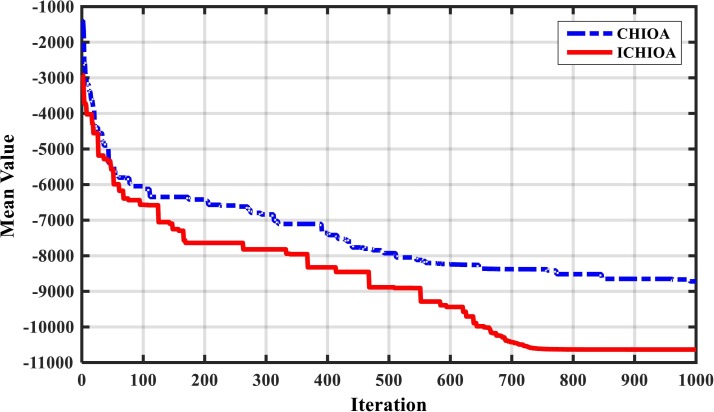
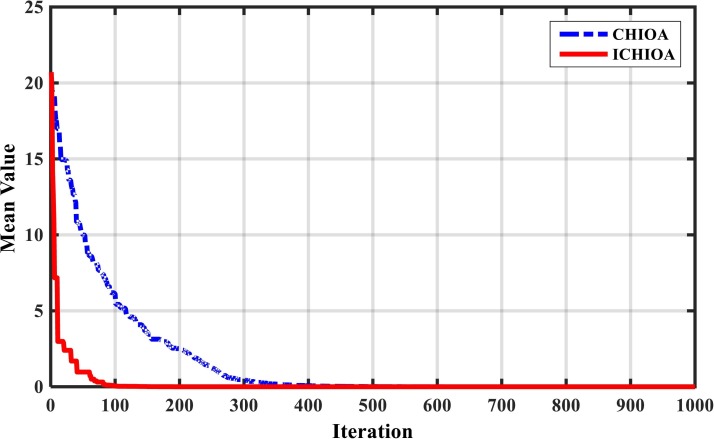
To evaluate the performance of the improved corona-virus herd immunity optimizer algorithm (ICHIOA), solving the unimodal and multimodal benchmark function, presented in (Gupta and Deep, 2019) are used. The unimodal and multimodal benchmark function are described completely in (Gupta and Deep, 2019). The performance of ICHIOA is compared with conventional CHIOA and modified sine cosine algorithm (m-SCA). The performance of the ICHIOA, CHIOA and m-SCA are presented and compared in Table 2 . The results cleared that the ICHIOA has competitive and better results in solving the test functions in comparison with the conventional CHIOA and the m-SCA presented in (Gupta and Deep, 2019). Also, convergence curve of F8 and F10 test functions are depicted in Fig. 6, Fig. 7 , which showed the more convergence speed and more test function value of the ICHIOA in comparison with the conventional CHIOA.
Table 2.
Comparison of results achieved by ICHIOA, CHIOA and m-SCA in (Gupta and Deep, 2019) considering D = 30.
| Function | ICHIOA | CHIOA | m-SCA (Gupta and Deep, 2019) | |||
|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | |
| F1 | 1.17E-11 | 1.59E-11 | 1.08E-05 | 1.04 E-05 | 5.70E-03 | 2.63E-02 |
| F2 | 7.04E-6 | 2.62E-5 | 8.83E-4 | 1.63E-3 | 9.11E-04 | 1.90E-03 |
| F3 | 3.56E-16 | 1.29E-15 | 7.97E + 02 | 10.47E + 00 | 8.48E + 02 | 5.49E + 02 |
| F4 | 7.58E-13 | 1.66E-12 | 9.03E-2 | 5.56E-2 | 7.07E-01 | 5.37E-01 |
| F5 | 1.96E + 01 | 2.01E + 01 | 27.45E + 00 | 3.24E + 00 | 29.5658 | 2.4320 |
| F6 | 6.83E-6 | 3.05E-6 | 1.30E-04 | 7.10E-05 | 1.24E + 00 | 5.12E-01 |
| F7 | 1.44E-08 | 7.37E-09 | 2.84E-5 | 1.36E-4 | 1.95E-02 | 6.87E-03 |
| F8 | −1.07E + 04 | 2.26E + 02 | −0.86E + 04 | 3.78E + 02 | −4265.8691 | 288.8681 |
| F9 | 2.95E + 01 | 9.61E + 00 | 3.46E + 01 | 3.90E + 01 | 7.81E + 01 | 5.21E + 01 |
| F10 | 2.01E-10 | 3.69E-10 | 2.91E-4 | 6.77E-04 | 3.36E-03 | 8.06E-03 |
| F11 | 2.48E-8 | 5.32E-8 | 1.02E-07 | 6.05E-08 | 3.84E-02 | 7.15E-02 |
| F12 | 2.83E-6 | 6.09E-7 | 1.22E-2 | 1.73E-2 | 1.45E-01 | 8.19E-02 |
| F13 | 3.66E-9 | 1.86E-8 | 5.81E-06 | 7.90E-06 | 1.41E + 00 | 3.94E-01 |
Fig. 6.
Convergence curve of ICHIOA and CHIOA for solving F8 function considering D = 30.
Fig. 7.
Convergence curve of ICHIOA and CHIOA for solving F10 function considering D = 30.
4.3. Implementation of ICHIOA in problem solution
In this paper, the ICHIOA algorithm is proposed to solve the reconfiguration problem based on the FMCA. In this paper new improved corona-virus herd immunity optimizer algorithm (ICHIOA) is used to solve the distribution network reconfiguration. That is, the proposed optimization algorithm should optimally determine the best network configuration by considering the objective function and problem constraints. The best configuration represents the best condition of the network power switches to achieve the best network performance in terms of each criterion of the objective function. The status of the switches means that the ICHIOA determines which of the five tie switches (normally open) is closed and which of the sectionalizer switches (normally closed) is opened satisfying the radiality state of the network.
The steps to implement the ICHIOA method in the problem solution are presented below.
Step 1) In order to maintain the radiality of the distribution network, another line must be opened. To begin the optimization, it is assumed that all network main lines are in operational condition (closed lines), the radiality of the network requires that the number of network lines is one unit fewer than the number of buses. As a result, if the number of network buses is considered nbus, and the number of network lines is considered nbr, the following equation must be respected (Moghaddam et al., 2020).
| (36) |
Where, nbr(on) is the number of active lines in the distribution network. Therefore, the number of lines opened is defined below and nbr(off) represents the number of lines that are opened in the distribution network (Moghaddam et al., 2020):
| (37) |
As a result, the number of lines to be opened is equal to the number of optimization variables and the ICHIOA algorithm must determine which network lines should be opened. For example, in the standard 33 bus distribution network, the total number of lines is 37 and there are 33 buses, therefore, 5 lines must be opened so that the radial conditions of the problem can be established, and thus the number of optimization variables (nvar) in the reconfiguration problem is five.
Step 2) After the candidate opened lines are determined, with eliminating their effects on the network, the following constraints must be checked.
A) No repetition of lines.
The candidate lines should be different together and there should be no duplicate line numbers. Because if similar lines are selected, the radial distribution network configuration is not preserved. If this constraint is not met, the objective function corresponding to this member of the algorithm population will be penalized and this member will be removed from the optimization process.
B) Check the radiality of the network
A nbr * nbus matrix is formed in that the number of rows is the number of network lines and the number of columns is equal to the number of network buses. Consequently, we have Eq. (38) for each network line between the two buses i and j (Abdelaziz et al., 2010).
| (38) |
After the formation of the above matrix, if the determinant of the matrix is zero, the network is radial and if this determinant is equal to + 1 or −1, the matrix is non-radial.
Step 3) After reviewing the radial network constraints, the objective functions with satisfying the network radiality are calculated. First, the load flow is done for the new network configuration network and the objective function is calculated for the new population of the algorithm.
Step 4) In this step, the population of the algorithm is updated and steps 1 through 3 are done for the new population. If the value of the objective function satisfying the network radiality obtained from the updated population is better than the objective function of step 3, it will be replaced.
Step 5) If the maximum allowed iteration and convergence conditions are reached, the search and optimization are stopped and optimal network configuration is found, but otherwise it goes back to Step 2.
The flowchart of the proposed model presented to solve the reconfiguration problem considering FMCA (sub-section 2.3.) and ICHIOA (sub-section 3.3.) is illustrated in Fig. 8 .
Fig. 8.
Flowchart of the proposed model to solve the reconfiguration problem considering FMCA and ICHIOA.
5. Results and discussion
The unbalanced IEEE 33 and 69 bus distribution networks according to Fig. 9, Fig. 10 , respectively are used to validate the proposed method. The 33 -bus network consists of 33 bus and 37 branches supplied by a 12.6 kV transmission system. Five tie lines between buses 8–21, 9–15, 12–22, 18–33, and 25–29 can be used to change the topology of the system in conditions of unexpected events or disturbances that these lines are Lines 33 to 37. The 69 bus network consists of 69 buses, and 68 branches are supplied by a 12.6 kV transmission system. Five tie lines between buses 11–66, 13–21, 15–69, 39–48, and 27–54 that these lines are Lines 69 to 73. All loads and voltages in the simulations are unbalanced. Therefore, active and reactive load values on each network bus with resistance and line reactance for each phase are given. The annual outage rates along with the average time per outage are also considered for the calculation of the ENS index. The unbalanced 33 bus network and reliability data are presented in (Swarnkar, Gupta, & Niazi, 2011). Also, the data of the 69 bus networks is derived from (Swarnkar et al., 2011). In this section, results of distribution networks reconfiguration using the ICHIOA method are presented under different loading conditions of 100%, 62.5%, and 125% of the network nominal load as single and FMCA based multi-objective optimization. The simulation results of the proposed method are compared with conventional CHIOA, PSO, and GWO that are powerful methods for optimizing the problem solution.
Fig. 9.
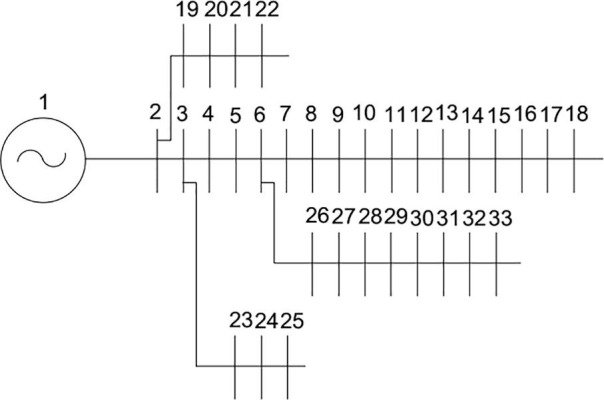
IEEE radial 33 bus distribution system (Swarnkar, Gupta, and Niazi, 2011).
Fig. 10.
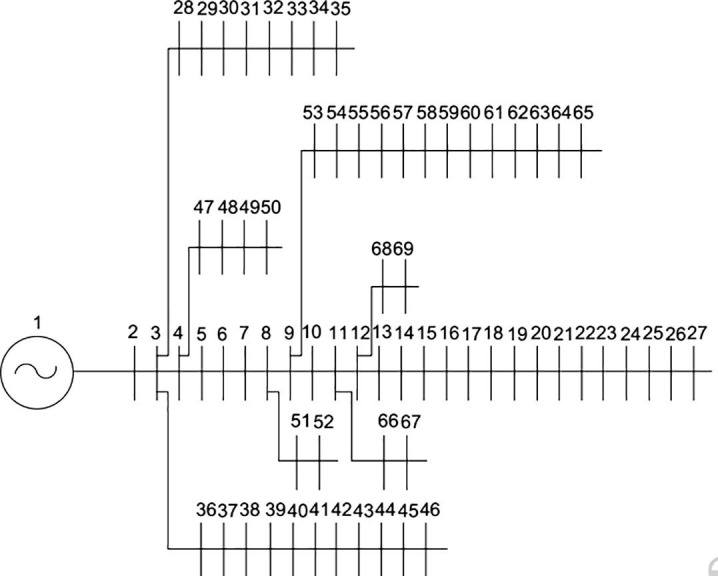
IEEE radial 69 bus distribution system (Swarnkar, Gupta, and Niazi, 2011).
5.1. 33 Bus unbalanced network
In this section, the simulation results of an unbalanced IEEE 33 bus distribution network for FMCA based reconfiguration are presented. In the base network, the active loss value is equal to 207.44 kW, the voltage sag value is 0.9566p.u, the ENS is 7.4329 kWh, and the voltage unbalance is 4.9226%.
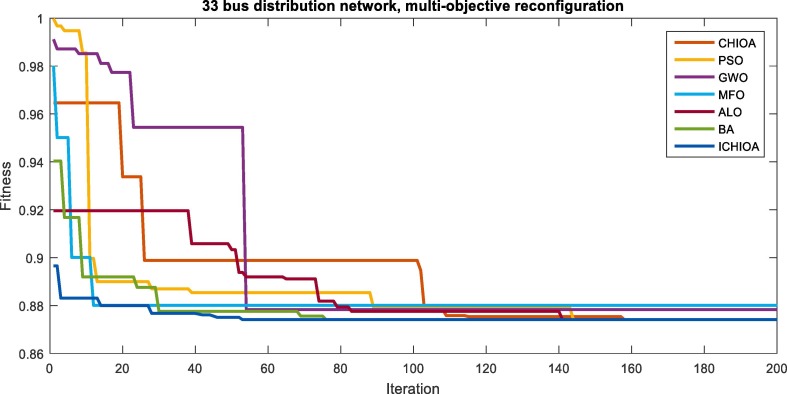
The problem of reconfiguration is implemented as a single and FMCA and based multi-objective optimization results of each optimization method are presented. The population of the optimization methods is selected 50 and the maximum iteration is determined 200. The parameters of the algorithms are determined by trying and error method and also considering achieving the best solution. The convergence curve of each optimization method including CHIOA, PSO, GWO, MFO, ALO, BA, and the proposed ICHIOA for FMCA is presented in Fig. 10. As shown in Fig. 11 , the ICHIOA is obtained to better fuzzy fitness than the CHIOA, PSO, GWO, MFO, ALO, and BA methods in less convergence tolerance and high speed and accuracy than the other algorithms. It can be seen that the CHIOA has many convergence fluctuations that observed the improved CHIOA (ICHIOA) improved its performance in achieving a lower fuzzy fitness with a higher convergence speed and lower convergence tolerance.
Fig. 11.
Convergence curve of different methods in the FMCA-based reconfiguration solution of the 33 bus network.
The results of the proposed reconfiguration method for the nominal load of the unbalanced 33 bus network are presented in Table 3 . The results of reconfiguration include the best configuration of the distribution network based on the opened switches using the ICHIOA method, loss, voltage sag, voltage unbalance, and ENS for single and multi-objective optimization based on the fuzzy membership function method. In order to evaluate ICHIOA performance in problem-solving, its results are compared with CHIOA, PSO, GWO, BA, MFO, and ALO methods. The results showed that the amount of each objective is the lowest or the best value in single optimization related to this objective. For example, the amount of network losses in the objective function of loss minimization is the best value of losses. This is true of other objectives as well.
Table 3.
Simulation results of single and FMCA reconfiguration of the 33 bus unbalanced network.
| Multi-objective | Min ENS | Min Vunb | Min Vsag | Min Loss | Method | Initial | Item |
|---|---|---|---|---|---|---|---|
| 9, 13, 16, 28, 33 | 10, 13, 16, 28, 33 | 7, 8, 12, 28, 30 | 7, 10, 14, 17, 28 | 7, 11, 14, 28, 32 | ICHIOA | 33, 34, 35, 36, 37 | Solution |
| 12, 16, 28, 33, 35 | 7, 10, 14, 16, 27 | 8, 12, 28, 30, 33 | 7, 9, 14, 28, 32 | 7, 10, 14, 32, 37 | CHIOA | ||
| 7, 9, 14, 16, 28 | 13, 16, 28, 33, 35 | 7, 11, 12, 28, 30 | 9, 14, 17, 28, 33 | 9, 14, 28, 32, 33 | PSO | ||
| 6, 9, 26, 32, 34 | 11, 14, 17, 28, 33 | 7, 11, 28, 30, 35 | 7, 12, 17, 28, 35 | 7, 9, 13, 28, 32 | GWO | ||
| 11, 13, 16, 28, 33 | 11, 13, 16, 28, 33 | 7, 8, 12, 27, 30 | 9, 14, 28, 32, 33 | 7, 11, 13, 28, 36 | BA | ||
| 14, 15, 21, 28, 33 | 14, 28, 33, 34, 35 | 8, 13, 28, 30, 33 | 9, 13, 28, 32, 33 | 7, 12, 21, 28, 36 | MFO | ||
| 10, 13, 16, 28, 33 | 10, 15, 28, 33, 34 | 7, 11, 12, 27, 30 | 7, 9, 14, 27, 33 | 10, 28, 32, 33, 34 | ALO | ||
| 167.371 | 169.570 | 186.684 | 154.568 | 142.960 | ICHIOA | 207.44 | Loss(kW) |
| 181.575 | 165.11 | 182.451 | 148.420 | 144.202 | CHIOA | ||
| 158.500 | 180.761 | 175.675 | 160.226 | 150.048 | PSO | ||
| 168.249 | 163.042 | 181.352 | 160.860 | 144.496 | GWO | ||
| 171.896 | 171.896 | 188.752 | 154.048 | 149.415 | BA | ||
| 191.184 | 187.942 | 178.559 | 159.830 | 157.886 | MFO | ||
| 169.570 | 168.358 | 177.743 | 151.562 | 150.038 | ALO | ||
| 0.665 | 0.678 | 0.972 | 0.6303 | 0.6406 | ICHIOA | 0.9566 | Vsag(p.u) |
| 0.762 | 0.727 | 0.941 | 0.6329 | 0.6782 | CHIOA | ||
| 0.677 | 0.757 | 0.884 | 0.6342 | 0.6217 | PSO | ||
| 0.784 | 0.651 | 0.932 | 0.6475 | 0.6488 | GWO | ||
| 0.697 | 0.696 | 0.986 | 0.6310 | 0.6531 | BA | ||
| 0.821 | 0.804 | 0.913 | 0.6478 | 0.7258 | MFO | ||
| 0.678 | 0.688 | 0.898 | 0.6536 | 0.6566 | ALO | ||
| 3.379 | 3.420 | 1.812 | 3.756 | 2.846 | ICHIOA | ||
| 3.732 | 3.71 | 1.923 | 3.088 | 3.730 | CHIOA | ||
| 3.776 | 3.686 | 1.829 | 3.968 | 3.629 | PSO | ||
| 3.385 | 3.680 | 2.349 | 3.956 | 2.679 | GWO | ||
| 3.515 | 3.515 | 1.854 | 3.630 | 2.782 | BA | 4.922 | Vunb (%) |
| 4.092 | 4.613 | 2.029 | 2.755 | 3.271 | MFO | ||
| 3.420 | 3.490 | 1.871 | 3.061 | 2.647 | ALO | ||
| 6.421 | 6.405 | 8.395 | 6.713 | 7.008 | ICHIOA | 7.432 | ENS (MWh/yr) |
| 6.502 | 6.511 | 8.304 | 6.967 | 7.445 | CHIOA | ||
| 6.641 | 6.501 | 7.954 | 6.505 | 6.706 | PSO | ||
| 7.271 | 6.499 | 8.077 | 6.897 | 7.015 | GWO | ||
| 6.456 | 6.459 | 8.405 | 6.716 | 6.921 | BA | ||
| 6.746 | 6.629 | 8.199 | 6.694 | 7.239 | MFO | ||
| 6.455 | 6.518 | 7.964 | 6.977 | 6.870 | ALO |
The lowest value of the voltage sag related to the objective of voltage sag improvement with the value of 0.6303p.u, the lowest voltage unbalance with the voltage unbalance objective function is 1.812% and the best ENS value associated with the ENS reduction objective function is equal to 6.455 kWh. Considering loss reduction, voltage sag, ENS function as single-objective optimization has a positive effect on the other objectives and the objectives have been improved in comparison to base values. Also, the results show that considering the single-objective function of voltage unbalance minimization, it reduces the loss and voltage sag but on the other hand, weakens the ENS index and increases it and its value exceeds the permissible limit. The value of ENS in the base case is 7.432 kWh, which reaches to 8.395 kWh using ICHIOA considering voltage unbalance minimization as a single-objective function. Considering the single-objective function of minimizing ENS, it has a positive effect on all objectives. Single-objective optimization results show that improvement of some objectives is not desirable in a single-objective optimization even when the objectives have not exceeded their permissible values. Comparing the results of ICHIOA with the other methods in single and multi-objective optimization proves the superiority of the proposed method to achieve lower losses and further improvement of the power quality and reliability and have more effect on reducing voltage sag, unbalance voltage, and ENS. In multi-objective optimization, switches 9, 13, 16, 28, 33 are selected as open network switches by the ICHIOA method. The amount of network losses, voltage sag, voltage unbalance, and ENS are 167.371 kW, 0.665p.u, 3.379%, and 6.421 kWh, respectively. Statistic Analysis of algorithms performance for reconfiguration based FMCA of the 33 bus unbalanced network is presented in Table 4 . As it is clear the capability of the ICHIOA is better in multi-objective optimization problem solution than the other algorithm with achieving the best value and less STD. Thus, based on the FMCA, a compromise is done between the objectives, and an optimal configuration of the distribution network is determined using the ICHIOA that has a positive effect on all objectives. While in single-objective optimization, a negative effect on the objectives and distance from allowable values and also global optimum values is observed. However, it is important that in all the optimization methods, there is a compromise between the different objectives, and the amount of each objective has not exceeded its allowable value.
Table 4.
Statistic Analysis of algorithms performance for reconfiguration based on FMCA of the 33 bus unbalanced network.
| Method | Best | Mean | Worst | STD |
|---|---|---|---|---|
| ICHIOA | 0.87408 | 0.88006 | 0.90485 | 0.009594 |
| CHIOA | 0.87408 | 0.88753 | 0.90579 | 0.012195 |
| PSO | 0.87408 | 0.89035 | 0.93345 | 0.017024 |
| GWO | 0.87828 | 0.92255 | 0.98451 | 0.030571 |
| BA | 0.87408 | 0.88497 | 0.90497 | 0.012528 |
| MFO | 0.88012 | 0.90175 | 0.92188 | 0.014921 |
| ALO | 0.87408 | 0.879 | 0.90581 | 0.0097445 |
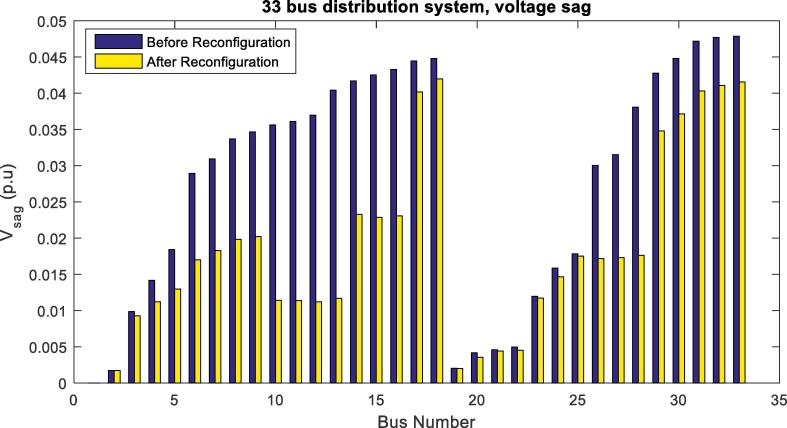
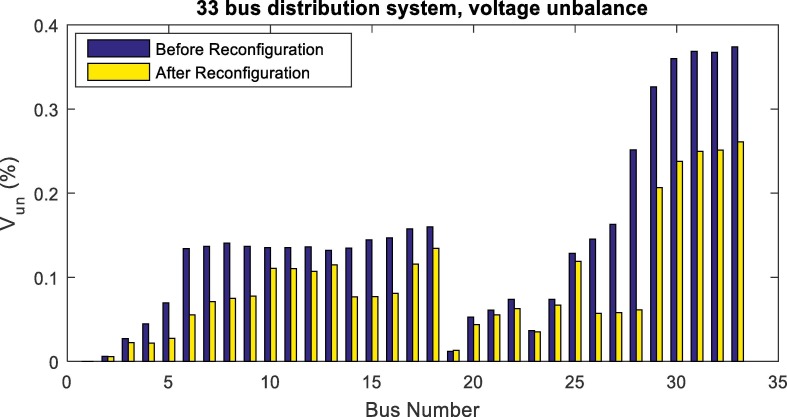
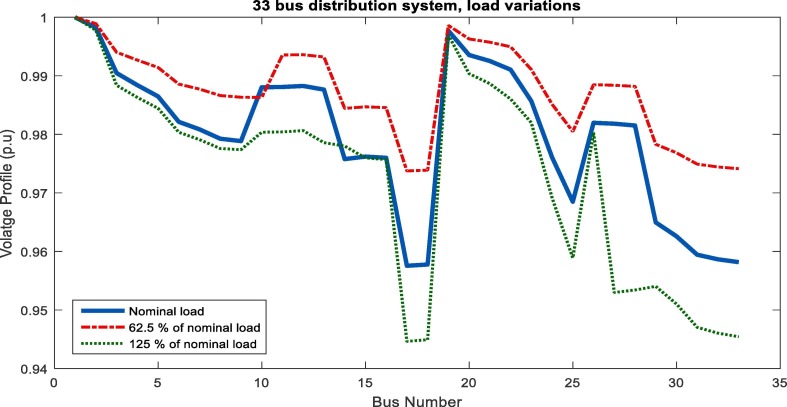
In Fig. 12, Fig. 13 , voltage sag and voltage unbalance changes using ICHIOA are shown before and after multi-objective reconfiguration. As shown, the voltage sag and voltage unbalance of the network have improved after the reconfiguration. The determination of the best network configuration has led to voltage sag and voltage unbalance decreasing, which proves the positive effect of multi-objective reconfiguration on power quality improvement. Also, the results of the proposed reconfiguration method for the unbalanced 33 bus distribution network considering network load variations are presented in Table 5 . The results of the reconfiguration include opened switches, active power loss, voltage sag, voltage unbalance, and ENS for single and FMCA in 62.5 and 125% of network nominal load using ICHIOA. The reconfiguration analysis in the condition of network nominal load show that the objectives have not exceeded the allowable values and the losses, power quality indices, and also reliability are improved in this condition. The results show that as the network load increases, the network losses increase dramatically. Also, the network reliability, voltage sag, and voltage unbalance are weakened and vice versa. Also, in Fig. 14 , the 33 bus network voltage profile is presented in the condition of network load variations. As shown in Fig. 14, network voltage deviations are decreased after multi-objective reconfiguration and as a result, the network voltage profile is improved.
Fig. 12.
Voltage sag variations in unbalanced 33 bus network using ICHIOA after and before reconfiguration.
Fig. 13.
Voltage unbalance variations in unbalanced 33 bus network using ICHIOA after and before reconfiguration.
Table 5.
Impact of load variations for reconfiguration based FMCA of 33 bus unbalanced network using ICHIOA.
| ENS (MWh/yr) | Vunb (%) | Vsag(p.u) | Loss(kW) | solution | Method |
|---|---|---|---|---|---|
| 4.0344.615 | 2.0672.959 | 0.4190.590 | 64.64878.572 | 10, 13, 16, 28, 3333, 34, 35, 36, 37 | 62.5 % of nominal loadInitial |
| 6.4217.432 | 3.3794.922 | 0.6650.9566 | 167.371207.44 | 9, 13, 16, 28, 3333, 34, 35, 36, 37 | Nominal loadInitial |
| 8.0819.231 | 4.2266.422 | 0.8801.211 | 274.113331.167 | 8, 9, 14, 17, 2633, 34, 35, 36, 37 | 125 % of nominal loadInitial |
Fig. 14.
Voltage profile of unbalanced 33 bus network in different loading using ICHIOA after reconfiguration.
5.2. 69 Bus unbalanced network
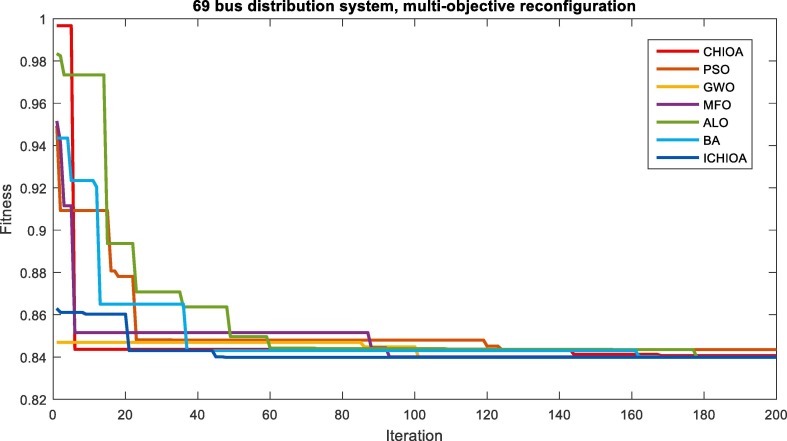
In this section, the simulation results of an unbalanced IEEE 69 bus distribution network for reconfiguration based FMCA are presented. In the base network, the active loss value is equal to 230.634 kW, the voltage sag value is 1.0580p.u, the ENS is 13.322 kWh and the voltage unbalance is 15.266%. The problem is implemented as FMCA and the results of different optimization algorithms are presented. The population of the optimization methods is selected 50 and the maximum iteration is determined 200. The convergence curve of each algorithm in the problem solution including conventional CHIOA, PSO, GWO, MFO, ALO, BA, and ICHIOA is presented in Fig. 15 . As it is clear in Fig. 15, the ICHIOA converges faster than the other algorithms with high convergence speed and accuracy.
Fig. 15.
Convergence curve of different methods in reconfiguration based FMCA of 69 bus network.
The results of the proposed reconfiguration method for the nominal load of the unbalanced 69 bus network are presented in Table 6 . According to Table 6, switches 14, 16, 44, 64, 73 are selected as optimal opened network switches by the ICHIOA method. The amount of network losses, voltage sag, voltage unbalance, and ENS are 139.225 kW, 0.744p.u, 9.681%, and 11.209 kWh respectively. Statistic analysis of algorithms performance for reconfiguration based FMCA of the 69 bus unbalanced network presented in Table 7 . As it is clear, the performance of the ICHIOA is better in multi-objective optimization problem solution than the other algorithm with achieving to the best value and less STD.
Table 6.
Simulation results of reconfiguration based FMCA of 69 bus unbalanced Network.
| ENS (MWh/yr) | Vunb (%) | Vsag(p.u) | Loss(kW) | solution | Method |
|---|---|---|---|---|---|
| 13.322 | 15.266 | 1.058 | 230.634 | 69, 70, 71, 72, 73 | Initial |
| 11.209 | 9.681 | 0.744 | 139.225 | 14, 16, 44, 64, 73 | ICHIOA |
| 11.236 | 12.490 | 0.865 | 144.711 | 19, 25, 43, 63, 71 | CHIOA |
| 11.727 | 12.849 | 0.911 | 142.693 | 8, 9, 14, 17, 26 | PSO |
| 11.299 | 12.460 | 0.861 | 143.613 | 13, 18, 22, 45, 65 | GWO |
| 11.248 | 11.113 | 0.765 | 139.678 | 14, 17, 26, 44, 64 | BA |
| 11.253 | 10.973 | 0.766 | 139.80 | 17, 44, 64, 71, 73 | MFO |
| 11.252 | 9.755 | 0.680 | 139.802 | 17, 47, 64, 71, 73 | ALO |
Table 7.
Statistic Analysis of algorithms performance for reconfiguration based FMCA of 69 bus unbalanced Network.
| Method | Best | Mean | Worst | STD |
|---|---|---|---|---|
| ICHIOA | 0.8398 | 0.84402 | 0.84657 | 0.0019254 |
| CHIOA | 0.8459 | 0.84619 | 0.85046 | 0.0042768 |
| PSO | 0.8603 | 0.85104 | 0.86447 | 0.0088633 |
| GWO | 0.8482 | 0.84693 | 0.87421 | 0.0085688 |
| BA | 0.8444 | 0.84482 | 0.84715 | 0.0030254 |
| MFO | 0.8609 | 0.84579 | 0.85946 | 0.0056718 |
| ALO | 0.8409 | 0.84478 | 0.86569 | 0.003758 |
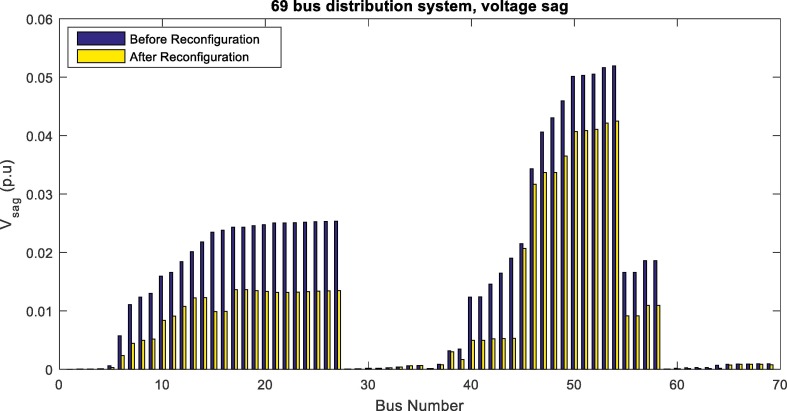
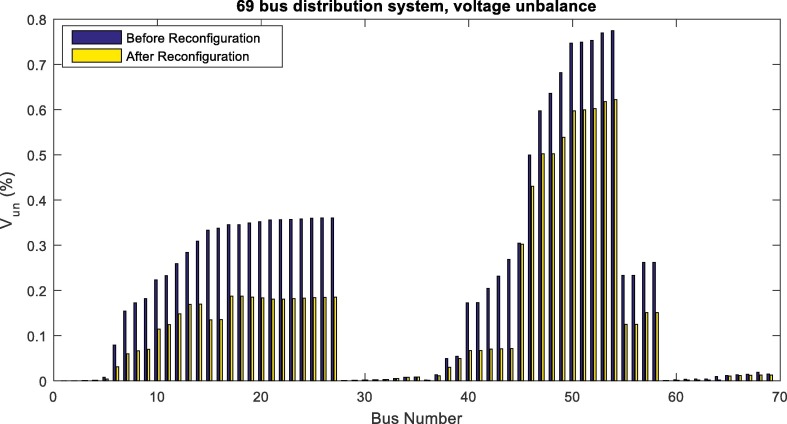
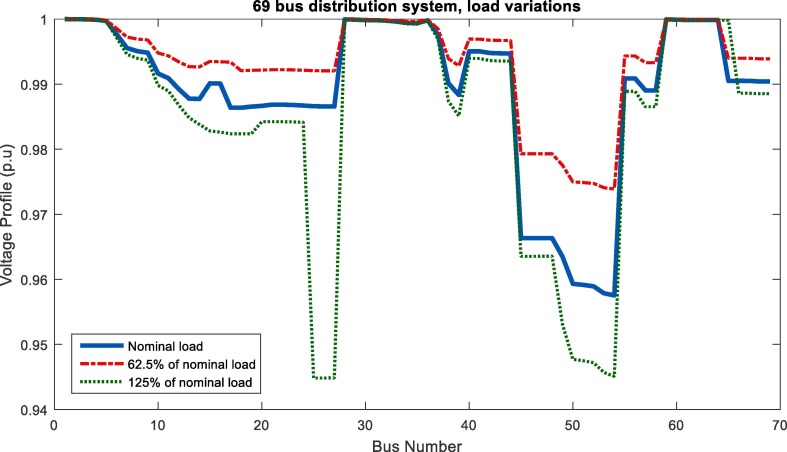
In Fig. 16, Fig. 17 , power quality objectives as voltage sag and voltage unbalance changes using ICHIOA are illustrated before and after multi-objective reconfiguration. It is clear that the voltage sag and voltage unbalance are improved with multi-objective reconfiguration. Hence, the determination of network configuration considering power quality improvement has led to a decrease in voltage sag and voltage unbalance. Moreover, reconfiguration problem using ICHIOA is studied for the unbalanced 69 bus distribution network considering variations of the network load that the obtained results are presented in Table 8 . The results show that increasing the network load increases the network losses, voltage sag and voltage unbalance values and vice versa. Also, the network reliability and power quality objectives weaken with increasing the network load and vice versa. Also, in Fig. 18 , the 69 bus network voltage profile is presented in the condition of network load variations. As shown in Fig. 18, voltage deviations of the networks increase with increasing the network load. The less voltage deviation is related to load decreasing or light load condition.
Fig. 16.
Voltage sag variations in unbalanced 69 bus network using ICHIOA after and before reconfiguration.
Fig. 17.
Voltage unbalance variations in unbalanced 69 bus network using ICHIOA after and before reconfiguration.
Table 8.
Impact of load variations for reconfiguration based FMCA of the 69 bus unbalanced network using the ICHIOA.
| ENS (MWh/yr) | Vunb (%) | Vsag(p.u) | Loss(kW) | solution | Method |
|---|---|---|---|---|---|
| 7.0348.326 | 6.4859.140 | 0.4610.650 | 52.51786.704 | 14, 17, 44, 64, 7369, 70, 71, 72, 73 | 62.5 % of nominal loadInitial |
| 11.20913.322 | 9.68115.266 | 0.7441.058 | 139.225230.634 | 14, 16, 44, 64, 7369, 70, 71, 72, 73 | Nominal loadInitial |
| 13.98516.652 | 14.49319.675 | 0.9931.338 | 227.480370.269 | 19, 24, 46, 65, 7169, 70, 71, 72, 73 | 125 % of nominal loadInitial |
Fig. 18.
Voltage profile of unbalanced 69 bus network in different loading using ICHIOA after reconfiguration.
5.3. Comparison of the results with last researches
In the previous sections, the proposed methodology is approved to reduce power loss, power quality, and reliability improvement on 33 and 69 bus unbalanced distribution networks based on reconfiguration based FMCA in different loading conditions. In this section, the capability of the proposed method is compared with previous studies. Swarnkar et al. (2011) propose an unbalanced 33 bus network reconstruction to reduce losses (single-objective) using the Adaptive Ant Colony Algorithm (AACO). Also, Ch et al. (2016) present the reconfiguration problem with the objective of power quality improvement for the 33 bus network based on MINLP. In (Raut & Mishra, 2020) improved sine–cosine algorithm (ISCA), in (Nguyen, Nguyen, Truong, Nguyen, & Phung, 2017) Multi-objective invasive weed optimization (MOIWO), in (Sedighizadeh, Ahmadi, & Sarvi, 2013) hybrid big bang–big crunch algorithm (HBB-BC), in (Raut & Mishra, 2019) improved elitist–jaya algorithm (IEJA) is applied to solve the network reconfiguration for 33 bus network. A comparison of the results is presented in Table 9 . The comparison of the results show that the ICHIOA method has a lower power loss than the other methods, which shows the superiority of the proposed method.
Table 9.
Comparison results of 33 bus unbalanced network considering active loss.
| Loss (Kw) | Open switches | Item |
|---|---|---|
| 142.96 | 7, 11, 14, 28, 32 | ICHIOA |
| 147.59 | 7, 10, 28, 32, 34 | CHIOA |
| 153.19 | 7, 14, 21, 28, 32 | PSO |
| 147.54 | 9, 14, 28, 31, 33 | GWO |
| 143.87 | 7, 9, 14, 28, 32 | AACO (Swarnkar et al., 2011) |
| 144.49 | 7, 9, 14, 28, 36 | MINLP (Ch et al., 2016) |
Mirhoseini, Hosseini, Ghanbari, and Gandomkar (2015) present the reconfiguration problem for reducing losses and improving the ENS index, but for a 33 bus balanced network using the modified ant colony optimization (MACO) algorithm. As shown in Table 10 , the amount of ENS obtained by ICHIOA is close to (Mirhoseini et al., 2015). Of course, the small difference is due to the fact that the 33 bus distribution network studied in (Mirhoseini et al., 2015) is a balanced network, while our study network is an unbalanced network. Thus, the ENS value based on the ICHIOA method for a balanced 33 bus network is also achieved and the ENS value is 6.421 kWh in multi-objective reconfiguration. Therefore, the results confirm the ability of the proposed method to improve the reliability of the distribution network. In Table 11, Table 12 , the results of the reconfiguration are also evaluated by considering the balanced and unbalanced 33 and 69 bus distribution networks. As it is clear, the power loss in unbalanced mode is more than the balanced network loss. Also, the proposed method for the balanced network is implemented in this study and the power loss value obtains 139.55 kW for 33 bus and 98.59 kW for 69 bus which in comparison with the other methods, ICHIOA has better performance. It is necessary to mention that in (Imran, Kowsalya, & Kothari, 2014) and (Rao, Ravindra, Satish, & Narasimham, 2012), reconfiguration of the balanced 69 bus network is studied with objective loss reduction using firework algorithm (FWA) and harmony search algorithm (HAS), respectively.
Table 10.
Comparison results of 33 bus unbalanced network considering reliability.
| ENS (kWh) | Open switches | Item |
|---|---|---|
| 6.421 | 9, 13, 16, 28, 33 | ICHIOA (UN) |
| 6.21 | 7, 9, 11, 28, 36 | ICHIOA (BN) |
| 6.51 | 7, 10, 14, 16, 27 | CHIOA (UN) |
| 6.60 | 13, 16, 20, 21, 28 | PSO (UN) |
| 6.51 | 13, 16, 21, 28, 33 | GWO (UN) |
| 6.446 | 7, 11, 14, 36, 37 | MACO (BN) (Mirhoseini et al., 2015) |
*UN: Unbalanced network and BN: Balanced network
Table 11.
Comparison results of 33 bus balanced and unbalanced network considering active loss.
| Loss (Kw) | Open switches | Item |
|---|---|---|
| 142.96 | 7, 11, 14, 28, 32 | ICHIOA (UN) |
| 139.55 | 7, 9, 14, 32, 37 | ICHIOA (BN) |
| 139.84 | 7, 9, 14, 32, 37 | GA (BN) (El-Ela, Allam, & Shatla, 2010,) |
| 139.84 | 7, 9, 14, 32, 37 | RGA (BN) (Nguyen & Truong, 2015) |
| 139.84 | 7, 9, 14, 32, 37 | CSA (BN) (Nguyen & Truong, 2015) |
| 139.55 | 7, 9, 14, 32, 37 | ISCA (BN) (Raut & Mishra, 2020) |
| 145.05 | 6, 34, 11, 36, 37 | RRA (BN) (Nguyen et al., 2017) |
| 144.41 | 6, 11, 32, 34, 37 | MOIWO (BN) (Rani et al, 2015) |
| 139.98 | 7, 9, 14, 28, 32 | HBB-BC (BN) (Sedighizadeh et al., 2013) |
| 139.98 | 7, 9, 14, 28, 32 | IEJA (BN) (Raut & Mishra, 2019) |
*UN: Unbalanced network and BN: Balanced network
Table 12.
Comparison results of 69 bus balanced and unbalanced network considering active loss.
| Loss (Kw) | Open switches | Item |
|---|---|---|
| 102.12 | 14, 58, 64, 69, 70 | ICHIOA (UN) |
| 98.59 | 14, 56, 61, 69, 70 | ICHIOA (BN) |
| 98.59 | 14, 56, 61, 69, 70 | FWA (BN) (Imran et al., 2014) |
| 99.35 | 13, 18, 56, 61, 69 | HSA (BN) (Rao et al., 2012) |
| 98.59 | 14, 57, 61, 69, 70 | AACO (BN) (Swarnkar et al., 2011) |
| 98.86 | 14, 58, 61, 69, 70 | MPSO (BN) (Essallah & Khedher, 2020) |
| 98.60 | 14, 56, 61, 69, 70 | IEJA (BN) (Raut & Mishra, 2019) |
*UN: Unbalanced network and BN: Balanced network
To evaluate the desirable performance of the ICHIOA, Wilcoxon signed-rank test considering independent samples is done with 5% of confidence level (). The Wilcoxon signed rank sum test is a non-parametric statistical hypothesis test. It is applied to evaluate the null hypothesis that two samples come from the same population against an alternative hypothesis, especially that a particular population tends to have larger values than the other (Ali et al., 2017, Singh and Dhillon, 2016). Suppose the null hypothesis is expressed in form of H0: and the alternative hypothesis is defined as H1: . refers to the mean value of bus voltages for base network before network reconfiguration and is the mean value of bus voltages after the reconfiguration. The Wilcoxon signed-rank test is implemented for ICHIOA, ICHIOA, PSO, GWO, BA, MFO and ALO. Table 13 , clears the probability (p) of the statistical Wilcoxon rank sum test for the 69 bus system (larger network) with reconfiguration. The p-value using the ICHIOA is obtained 3.27e-4, which is lower than 0.05, so the null hypothesis is failed. The result of p-value in Table 13, showed that the value obtained using the ICHIOA is lower than the other results. So, it can be concluded that the network voltages are more enhanced after reconfiguration using the ICHIOA compared with the base network.
Table 13.
The Wilcoxon test probability for various methods.
| Method | ICHIOA | ALOA (Ali et al., 2017) | BSOA (El-Fergany, 2015) | EVPSO (Manafi, Ghadimi, Ojaroudi, & Farhadi, 2013) |
|---|---|---|---|---|
| p | 3.27E-4 | 4.5229E-4 | 3.50E-3 | 2.48E-2 |
6. Conclusion
In this paper, a fuzzy multi-criteria approach for optimal reconfiguration of unbalanced distribution networks is proposed with the objective of power loss reduction, voltage sag improvement, voltage unbalance minimization, and also minimizing the ENS in different loading conditions. The status of opened switches or optimal configuration of distribution networks is determined using the ICHIOA method. The proposed method is implemented on unbalanced 33– and 69 bus IEEE networks. In this study, the branches exchange method is used for the radiality of the distribution networks. Key findings of the research are compared before and after reconfiguration considering different criteria such as power loss, voltage sag, voltage unbalance, and the ENS in a single-objective approach and also based on the FMCA using the ICHIOA and some different well-known algorithm. The results proved that all criteria are improved after optimal reconfiguration of the network with determining the best network configuration via the ICHIOA based FMCA. The results cleared that all criteria are in an allowable range in the optimization process based on the FMCA by compromising between the criteria while in the single-objective approach some power quality criteria are weakened and violated the permitted limits. The ICHIOA results based on FMCA in the reconfiguration solving with the determination of optimal network configuration showed that the losses of the network are reduced considerably, the power quality criteria such as voltage sag and voltage unbalance are minimized and also the network reliability is enhanced by minimizing the ENS for unbalanced 33 and 69 bus networks. Also, the effect of different loading conditions is evaluated on the reconfiguration problem which showed that the increase in network load demand has weakened each of the criteria and vice versa. Moreover, the superiority of the ICHIOA is confirmed in comparison with conventional CHIOA, PSO, GWO, BA, MFO, ALO methods in achieving to lowest objective function value and better value of criteria with better convergence speed and accuracy and also better performance compared with previous studies.
The achieved results in this paper can be used to improve the performance of electricity distribution networks, including improving the reliability and power quality by the operators of the electricity industry. The findings of this study can be used in the electricity industry to improve the performance of distribution networks in terms of reducing the interrupted energy of customers as well as improving the quality of electricity based on determining the optimal network configuration using modeling the electricity networks and implemented the proposed methodology to find the optimal network configuration. In solving the network reconfiguration and also determining the best network configuration, line currents and the bus voltages are the problem limitations. Also, selecting the number of network tie-switches to change its configuration is one of the study limitations that increasing the number of these switches increases the complexity of the problem and as a result causes current and voltage limitations to be violated. Therefore, a reasonable number of tie-switches should be considered in reconfiguration studies. According to this study, solving the multi-objective reconfiguration problem with optimal allocation of wind turbines in the distribution network is suggested using a multi-objective optimization algorithm for future work.
CRediT authorship contribution statement
Amirreza Naderipour: Writing - original draft, Methodology. Aldrin Abdullah: Supervision, Validation. Massoomeh Hedayati Marzbali: Resources. Saber Arabi Nowdwh: Writing - review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
The authors gratefully acknowledge financial support from the Universiti Sains Malaysia (Post-Doctoral Fellowship Scheme).
Appendix A.
A.1. Particle swarm optimization (PSO)
The PSO is one of the most important intelligent optimization algorithms presented in the field of swarm intelligence. This algorithm is inspired by the social behavior of animals such as fish and birds that live together in small and large groups. In the PSO, the members of the population communicate directly with each other and solve the problem by exchanging information with each other and recalling good memories of the history (Kennedy & Eberhart, 1995).
A.2. Grey wolf optimizer (GWO)
The GWO is a meta-heuristic algorithm inspired by the hierarchical structure and social behavior of grey wolves while hunting. This algorithm is population-based, has a simple process, and can be easily generalized to large-scale problems. This algorithm is modeled based on the strategy of the siege of prey (objective) by grey wolves (Mirjalili, Mirjalili, & Lewis, 2014).
A.3. Moth flame optimizer (MFO)
The MFO algorithm is inspired by a method of conducting the moths in nature called transverse orientation. The moths fly at night while maintaining a constant angle to the light source. In the MFO algorithm, the solution to the problem is assumed to be the moths, and the problem variables are the position of the moths in the search space (Mirjalili, 2015a, Mirjalili, 2015b).
A.4. Ant lion optimizer (ALO)
The ALO algorithm is inspired by the movements of the ant lion in trapping the ants. According to the assumptions defined in this algorithm, the ant lions trap in the ground and prepare to hunt prey. As ants search for food in nature, they randomly move into the traps, which this algorithm is modeled based on ants' random walk and ant lion hunting behavior (Mirjalili, 2015a, Mirjalili, 2015b).
A.5. Bat algorithm (BA)
The BA is an algorithm inspired by the swarm behavior of bats in the natural environment. This algorithm is modeled based on the use of sound reflection property by bats. The bats find the exact path and location of their prey by sending sound waves and receiving reflections. When sound waves return to the bat transmitter, the bat can draw an acoustic image of obstacles in front of its surroundings and see the surroundings well (Yang & Hossein Gandomi, 2012).
References
- Abdelaziz M. Distribution network reconfiguration using a genetic algorithm with varying population size. Electric Power Systems Research. 2017;142:9–11. [Google Scholar]
- Abdelaziz A.Y., Mohamed F.M., Mekhamer S.F., Badr M.A.L. Distribution system reconfiguration using a modified Tabu Search algorithm. Electric Power Systems Research. 2010;80(8):943–953. [Google Scholar]
- Abdul-Malek Z., Naderipour A., Nowdeh S.A., Ramachandaramurthy V.K., Kalam A., Guerrero J.M. Optimal allocation for combined heat and power system with respect to maximum allowable capacity for reduced losses and improved voltage profile and reliability of microgrids considering loading condition. Energy. 2020;196 [Google Scholar]
- Al-Betar, M. A., Alyasseri, Z. A. A., Awadallah, M. A., & Doush, I. A. (2020). Coronavirus herd immunity optimizer (CHIO). [DOI] [PMC free article] [PubMed]
- Ali E.S., Elazim S.A., Abdelaziz A.Y. Ant Lion Optimization Algorithm for optimal location and sizing of renewable distributed generations. Renewable Energy. 2017;101:1311–1324. [Google Scholar]
- Alonso F.R., Oliveira D.Q., Zambroni de Souza A.C. Artificial immune systems optimization approach for multiobjective distribution system reconfiguration. IEEE Transactions on Power Systems. 2014;30(2):840–847. [Google Scholar]
- Badran O., Mekhilef S., Mokhlis H., Dahalan W. Optimal reconfiguration of distribution system connected with distributed generations: A review of different methodologies. Renewable and Sustainable Energy Reviews. 2017;73:854–867. [Google Scholar]
- Billinton R., Billinton J. Distribution system reliability indices. IEEE Transactions on Power Delivery. 1989;4(1):561–568. [Google Scholar]
- Ch Y., Goswami S.K., Chatterjee D. Effect of network reconfiguration on power quality of distribution system. International Journal of Electrical Power & Energy Systems. 2016;83:87–95. [Google Scholar]
- El-Ela A.A., Allam S.M., Shatla M.M. Maximal optimal benefits of distributed generation using genetic algorithms. Electric Power Systems Research. 2010;80(7):869–877. [Google Scholar]
- El-Fergany A. Optimal allocation of multi-type distributed generators using backtracking search optimization algorithm. International Journal of Electrical Power & Energy Systems. 2015;64:1197–1205. [Google Scholar]
- Essallah S., Khedher A. Optimization of distribution system operation by network reconfiguration and DG integration using MPSO algorithm. Renewable Energy Focus. 2020;34:37–46. [Google Scholar]
- Flaih, F. M., Xiangning, L., Dawoud, S. M., & Mohammed, M. A. (2016). Distribution system reconfiguration for power loss minimization and voltage profile improvement using Modified particle swarm optimization. In Power and Energy Engineering Conference (APPEEC), 2016 IEEE PES Asia-Pacific (pp. 120-124). IEEE.
- Ghasemi A., Golkar M.J., Golkar A., Eslami M. Reactive power planning using a new hybrid technique. Soft Computing. 2016;20(2):589–605. [Google Scholar]
- Golub I., Voitov O., Boloev E., Semenova L. Reconfiguration of Primary Distribution Network with Several Independent Power Sources. IFAC-PapersOnLine. 2019;52(4):437–442. [Google Scholar]
- Gönen T. McGraw-Hill; New York: 1986. Electric power distribution system engineering; p. (p. 46Á).. [Google Scholar]
- Gunther E.W., Mebta H. A survey of distribution system power quality-preliminary results. IEEE transactions on Power Delivery. 1995;10(1):322–329. [Google Scholar]
- Gupta N., Swarnkar A., Niazi K.R. Distribution network reconfiguration for power quality and reliability improvement using Genetic Algorithms. International Journal of Electrical Power & Energy Systems. 2014;54:664–671. [Google Scholar]
- Hadidian-Moghaddam M.J., Arabi-Nowdeh S., Bigdeli M., Azizian D. A multi-objective optimal sizing and siting of distributed generation using ant lion optimization technique. Ain Shams Engineering Journal. 2017 [Google Scholar]
- Imran A.M., Kowsalya M., Kothari D.P. A novel integration technique for optimal network reconfiguration and distributed generation placement in power distribution networks. International Journal of Electrical Power & Energy Systems. 2014;63:461–472. [Google Scholar]
- Jafar-Nowdeh A., Babanezhad M., Arabi-Nowdeh S., Naderipour A., Kamyab H., Abdul-Malek Z., Ramachandaramurthy V.K. Meta-heuristic matrix moth–flame algorithm for optimal reconfiguration of distribution networks and placement of solar and wind renewable sources considering reliability. Environmental Technology & Innovation. 2020;20 [Google Scholar]
- Jahani M.T.G., Nazarian P., Safari A., Haghifam M.R. Multi-objective optimization model for optimal reconfiguration of distribution networks with demand response services. Sustainable Cities and Society. 2019;47 [Google Scholar]
- Jahannoush M., Arabi Nowdeh S. Optimal designing and management of a stand-alone hybrid energy system using meta-heuristic improved sine-cosine algorithm for Recreational Center, case study for Iran country. Applied Soft Computing. 2020;96:106611. doi: 10.1016/j.asoc.2020.106611. [DOI] [Google Scholar]
- Jakus D., Čađenović R., Vasilj J., Sarajčev P. Optimal Reconfiguration of Distribution Networks Using Hybrid Heuristic-Genetic Algorithm. Energies. 2020;13(7):1544. [Google Scholar]
- Kanwar N., Gupta N., Niazi K.R., Swarnkar A. An integrated approach for distributed resource allocation and network reconfiguration considering load diversity among customers. Sustainable Energy, Grids and Networks. 2016;7:37–46. [Google Scholar]
- Kavousi-Fard A., Niknam T. Multi-objective stochastic distribution feeder reconfiguration from the reliability point of view. Energy. 2014;64:342–354. [Google Scholar]
- Kennedy J., Eberhart R. November). Particle swarm optimization. In Proceedings of ICNN'95-International Conference on Neural Networks. 1995;Vol. 4:1942–1948. [Google Scholar]
- Kumar K.S., Jayabarathi T. Power system reconfiguration and loss minimization for an distribution systems using bacterial foraging optimization algorithm. International Journal of Electrical Power & Energy Systems. 2012;36(1):13–17. [Google Scholar]
- Landeros Rojas, A. (2018). Smart Reconfiguration of Electric Power Distribution Networks for Power Loss Minimization and Voltage Profile Optimization (Doctoral dissertation).
- Lotfipour A., Afrakhte H. A discrete Teaching–Learning-Based Optimization algorithm to solve distribution system reconfiguration in presence of distributed generation. International Journal of Electrical Power & Energy Systems. 2016;82:264–273. [Google Scholar]
- Manafi H., Ghadimi N., Ojaroudi M., Farhadi P. Optimal placement of distributed generations in radial distribution systems using various PSO and DE algorithms. Elektronika ir Elektrotechnika. 2013;19(10):53–57. [Google Scholar]
- Mirhoseini S.H., Hosseini S.M., Ghanbari M., Gandomkar M. Multi-objective reconfiguration of distribution network using a heuristic modified ant colony optimization algorithm. Modeling and Simulation in Electrical and Electronics Engineering. 2015;1(1):23–33. [Google Scholar]
- Mirjalili S. The ant lion optimizer. Advances in Engineering Software. 2015;83:80–98. [Google Scholar]
- Mirjalili S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowledge-based Systems. 2015;89:228–249. [Google Scholar]
- Mirjalili S., Mirjalili S.M., Lewis A. Grey wolf optimizer. Advances in Engineering Software. 2014;69:46–61. [Google Scholar]
- Mishra S., Das D., Paul S. A comprehensive review on power distribution network reconfiguration. Energy Systems. 2017;8(2):227–284. [Google Scholar]
- Moghaddam M.J.H., Kalam A., Shi J., Nowdeh S.A., Gandoman F.H., Ahmadi A. A new model for reconfiguration and distributed generation allocation in distribution network considering power quality indices and network losses. IEEE Systems Journal. 2020;14(3):3530–3538. [Google Scholar]
- Naderipour A., Abdul-Malek Z., Nowdeh S.A., Kamyab H., Ramtin A.R., Shahrokhi S., Klemeš Jiří.Jaromír. Comparative evaluation of hybrid photovoltaic, wind, tidal and fuel cell clean system design for different regions with remote application considering cost. Journal of Cleaner Production. 2021;283:124207. doi: 10.1016/j.jclepro.2020.124207. [DOI] [Google Scholar]
- Naderipour A., Abdul-Malek Z., Zahedi Vahid M., Mirzaei Seifabad Z., Hajivand M., Arabi-Nowdeh S. Optimal, Reliable and Cost-Effective Framework of Photovoltaic-Wind-Battery Energy System Design Considering Outage Concept Using Grey Wolf Optimizer Algorithm—Case Study for Iran. IEEE Access. 2019;7:182611–182623. [Google Scholar]
- Nguyen T.T., Nguyen T.T., Truong A.V., Nguyen Q.T., Phung T.A. Multi-objective electric distribution network reconfiguration solution using runner-root algorithm. Applied Soft Computing. 2017;52:93–108. [Google Scholar]
- Nguyen T.T., Truong A.V. Distribution network reconfiguration for power loss minimization and voltage profile improvement using cuckoo search algorithm. International Journal of Electrical Power & Energy Systems. 2015;68:233–242. [Google Scholar]
- Nowdeh S.A., Davoodkhani I.F., Moghaddam M.H., Najmi E.S., Abdelaziz A.Y., Ahmadi A.…Gandoman F.H. Fuzzy multi-objective placement of renewable energy sources in distribution system with objective of loss reduction and reliability improvement using a novel hybrid method. Applied Soft Computing. 2019 [Google Scholar]
- Pegado R., Ñaupari Z., Molina Y., Castillo C. Radial distribution network reconfiguration for power losses reduction based on improved selective BPSO. Electric Power Systems Research. 2019;169:206–213. [Google Scholar]
- Rajaram R., Sathish Kumar K., Rajasekar N. Power system reconfiguration in a radial distribution network for reducing losses and to improve voltage profile using modified plant growth simulation algorithm with Distributed Generation (DG) Energy Reports. 2015;1:116–122. [Google Scholar]
- Rao R.S., Ravindra K., Satish K., Narasimham S.V.L. Power loss minimization in distribution system using network reconfiguration in the presence of distributed generation. IEEE transactions on power systems. 2012;28(1):317–325. [Google Scholar]
- Raut U., Mishra S. An improved elitist–jaya algorithm for simultaneous network reconfiguration and dg allocation in power distribution systems. Renewable Energy Focus. 2019;30:92–106. [Google Scholar]
- Raut U., Mishra S. An improved sine-cosine algorithm for simultaneous network reconfiguration and DG allocation in power distribution systems. Applied Soft Computing. 2020;92:106293. doi: 10.1016/j.asoc.2020.106293. [DOI] [Google Scholar]
- Sedighizadeh M., Ahmadi S., Sarvi M. An efficient hybrid big bang–big crunch algorithm for multi-objective reconfiguration of balanced and unbalanced distribution systems in fuzzy framework. Electric Power Components and Systems. 2013;41(1):75–99. [Google Scholar]
- Shareef H., Ibrahim A.A., Salman N., Mohamed A., Ling Ai W. Power quality and reliability enhancement in distribution systems via optimum network reconfiguration by using quantum firefly algorithm. International Journal of Electrical Power & Energy Systems. 2014;58:160–169. [Google Scholar]
- Shariatkhah M.-H., Haghifam M.-R., Salehi J., Moser A. Duration based reconfiguration of electric distribution networks using dynamic programming and harmony search algorithm. International Journal of Electrical Power & Energy Systems. 2012;41(1):1–10. [Google Scholar]
- Singh M., Dhillon J.S. Multiobjective thermal power dispatch using opposition-based greedy heuristic search. International Journal of Electrical Power & Energy Systems. 2016;82:339–353. [Google Scholar]
- Souza S.S.F., Romero R., Pereira J., Saraiva João.T. Artificial immune algorithm applied to distribution system reconfiguration with variable demand. International Journal of Electrical Power & Energy Systems. 2016;82:561–568. [Google Scholar]
- Su C.-T., Chang C.-F., Chiou J.-P. Distribution network reconfiguration for loss reduction by ant colony search algorithm. Electric Power Systems Research. 2005;75(2-3):190–199. [Google Scholar]
- Swarnkar A., Gupta N., Niazi K.R. Adapted ant colony optimization for efficient reconfiguration of balanced and unbalanced distribution systems for loss minimization. Swarm and Evolutionary Computation. 2011;1(3):129–137. [Google Scholar]
- Thakar S., Vijay A.S., Doolla S. System reconfiguration in microgrids. Sustainable Energy, Grids and Networks. 2019;17:100191. doi: 10.1016/j.segan.2019.100191. [DOI] [Google Scholar]
- Yang X., Hossein Gandomi A. Bat algorithm: A novel approach for global engineering optimization. Engineering. 2012;29(5):464–483. [Google Scholar]
- Zhai H.F., Yang M., Chen B., Kang N. Dynamic reconfiguration of three-phase unbalanced distribution networks. International Journal of Electrical Power & Energy Systems. 2018;99:1–10. [Google Scholar]