Identifying brain networks in synaptic density PET (¹¹C-UCB-J) with independent component analysis

Abstract

Background:

The human brain is inherently organized into distinct networks, as reported widely by resting-state functional magnetic resonance imaging (rs-fMRI), which are based on blood-oxygen-level-dependent (BOLD) signal fluctuations. ¹¹C-UCB-J PET maps synaptic density via synaptic vesicle protein 2A, which is a more direct structural measure underlying brain networks than BOLD rs-fMRI.

Methods:

The aim of this study was to identify maximally independent brain source networks, i.e., “spatial patterns with common covariance across subjects”, in ¹¹C-UCB-J data using independent component analysis (ICA), a data-driven analysis method. Using a population of 80 healthy controls, we applied ICA to two 40-sample subsets and compared source network replication across samples. We examined the identified source networks at multiple model orders, as the ideal number of maximally independent components (IC) is unknown. In addition we investigated the relationship between the strength of the loading weights for each source network and age and sex.

Results:

Thirteen source networks replicated across both samples. We determined that a model order of 18 components provided stable, replicable components, whereas estimations above 18 were not stable. Effects of sex were found in two ICs. Nine ICs showed age-related change, with 4 remaining significant after correction for multiple comparison.

Conclusion:

This study provides the first evidence that human brain synaptic density can be characterized into organized covariance patterns. Furthermore, we demonstrated that multiple synaptic density source networks are associated with age, which supports the potential utility of ICA to identify biologically relevant synaptic density source networks.

1. Introduction

Synaptic vesicle protein 2A (SV2A) is the most monodispersed synaptic vesicle protein and is thus a potentially useful measure of synaptic density (Bajjalieh et al., 1994; Janz and Südhof, 1999; Mutch et al., 2011). ¹¹C-UCB-J is a recently developed PET tracer that binds to SV2A (Finnema et al., 2018, 2016). Previously, we detected changes in synaptic density using ¹¹C-UCB-J PET in several psychiatric and neurodegenerative diseases (Chen et al., 2018; D’Souza et al., 2020; Finnema et al., 2016; Holmes et al., 2019; Matuskey et al., 2020; Mecca et al., 2020). However, no data driven approach to decompose synaptic density PET data has yet been performed.

One such data-driven approach is independent component analysis (ICA), a blind source separation technique. In the resting-state functional magnetic resonance imaging (rs-fMRI) field, it is commonly used to separate statistically independent blood oxygen level dependent (BOLD) components associated both with task-related and spontaneous resting state activity within neuronal networks (Bell and Sejnowski, 1995; Kiviniemi et al., 2003). A major advantage of ICA over traditional hypothesis-driven approaches is that the former is a data-driven approach for differentiating relevant functional brain signals from various sources of noise without a priori assumptions on signal origin (Calhoun et al., 2001; McKeown et al., 2003). ICA separates components from data into a number of spatially or temporally independent components (ICs) based on statistical features of the data (Calhoun et al., 2003; McKeown et al., 2003). Separation occurs by maximizing the non-Gaussianity of the joint density using a projection pursuit methodology. The ICA algorithm initiates projection pursuit with a guess and produces components in random order (Hyvärinen et al., 2001). The number of identified components (i.e., model order) can be selected from 1 to n – 1, where n is the number of imaged brain volumes (spatial ICA), or number of voxels in the volume of interest (temporal ICA). Extracted components consist of voxels which contain related information which we call a ‘source network’. These source networks have been shown to exhibit intersubject covariance and differences between groups.

ICA has more recently been applied to positron emission tomography (PET) data. Spatial components both similar to rs-fMRI-derived resting state networks (RSNs) as well as novel RSNs have been identified by ICA applied to ¹⁸F-FDG PET data, a tracer for brain metabolism (Di et al., 2019, 2012; Savio et al., 2017). Recently, we applied ICA to ¹¹C-PHNO PET data (D₂/D₃ receptors) and found source-based patterns of receptor availability consistent with DA circuitry and predicted receptor occupancy (Smart et al., 2020a; Worhunsky et al., 2017).

In applying ICA, selection of the appropriate number of calculated ICs is an open question. In the previous work with ¹¹C-PHNO PET, a model order of 2,3 was initially estimated and successful as the tracer only binds to D₂ and D₃ receptors in the dopamine-rich regions of the brain (Worhunsky et al., 2017). In ¹⁸F-FDG studies using the whole brain with the aim to identify functional networks, a model order of 18–20 was used, partly due to sample size limitations (Savio et al., 2017). For fMRI data using spatial ICA, there typically are no sample-size related constraints on model order estimates due to the high temporal dimension. The effect of model order on fMRI data has been investigated by Abou-Elseoud and colleagues over a model order range of 10–200. At the lower end, some components comprised multiple distinct sources that separated at higher model orders, and several novel components appeared at model orders > 40. At the extreme end of model order > 100, a decrease in ICA repeatability occurred (Abou-Elseoud et al., 2010). Thus, characterization of model order is a key consideration for initial ICA analyses of a given imaging target.

The aim of this study was to apply a data driven method (ICA) to investigate the utility of ¹¹C-UCB-J PET data in healthy participants to (1) identify spatial patterns, or networks, of coherent synaptic density (SV2A) variability and (2) to examine how these networks may be associated with age and sex. We first set out to assess and characterize ¹¹C-UCB-J components using two independent samples over a range of model orders. We hypothesized that we would find coherent sources, i.e., synaptic density patterns, that would be reliably and reproducibly extracted in the independent samples of healthy individuals. Some of these networks might be expected to be similar to RSNs, based on the biological commonality of synaptic density with neural activity as measured by BOLD-signal (rs-fMRI) and glucose metabolism (¹⁸F-FDG PET).

2. Materials and methods

2.1. Participants

Data from 80 cognitively normal, healthy adults were included in the current study. All subjects were screened through a clinical interview, physical examination with medical history, routine blood tests, electrocardiogram and urine toxicology. Individuals were excluded if evaluation revealed a diagnosis of a current and/or lifetime psychiatric disorder, current or past serious medical or neurological illness, metal in body which would result in MRI contraindication, or a history of substance abuse or dependence.

MR images were acquired on all subjects and visually inspected to eliminate subjects with structural brain abnormalities. The study was performed under protocols approved by the Yale University Human Investigation Committee. All subjects signed a written informed consent form. Subjects were pseudo-randomly assigned into two samples of 40 that did not differ in age or gender (Table 1).

Table 1.

Demographic information of study participants, for the total group and the two sample subsets.

	Total	Sample 1	Sample 2
Sample size	80	40	40
Sex Male: No. (%)	47 (58.7)	23 (57.5)	24 (60)
Female: No. (%)	33 (41.3)	17 (42.5)	16 (40)
Age, mean (SD) [range]	44.7 (17.0) [21.0–82.7]	44.8 (17.4) [21.0–82.7]	44.6 (16.8) [21.8–80.6]

2.2. Image acquisition

¹¹C-UCB-J was synthesized at Yale PET Center as described previously (Nabulsi et al., 2016). Subjects were administered an i.v. injection of ¹¹C-UCB-J (551.00 ± 173.32 MBq; injected mass: 1.57 ± 1.04 μg; range 0.27–5.85 μg) and received one dynamic PET scan (HRRT; Siemens/CTI, Knoxville, TN, USA). In order to obtain an arterial plasma curve, each subject underwent catheterization of the radial artery for blood sampling. Samples were drawn every 10 s for the first 90 s and at 1.75, 2, 2.25, 2.5, 2.75, 3, 4, 5, 6, 8, 10, 15, 20, 25, 30, 45, 60 min after ¹¹C-UCB-J injection. For each sample, plasma was obtained by centrifugation at 4 °C (2930 × g for 5 min). Metabolite analysis and plasma free fraction of ¹¹C-UCB-J were determined for correction of the obtained plasma curve as described previously (Finnema et al., 2018). PET scans (207 slices, 1.2 mm slice separation, reconstructed image resolution ~ 3 mm) were acquired at rest in list mode. Before injection, a transmission scan was obtained for attenuation correction. A T1-weighted structural MR image (repeat time (TR)/echo time (TE) = 2530/3.34, flip angle = 7°, in-plane resolution = 0.98 × 0.98 mm, matrix size = 256 × 256, slice thickness = 1 mm, slices = 176) was also acquired for nonlinear registration into template space.

2.3. Image processing

Dynamic PET data (frames: 6 × 0.5 min, 3 × 1 min, 2 × 2 min, and 10 × 5 min) were reconstructed using the MOLAR algorithm with corrections for attenuation, normalization, scatter, randoms, deadline, and motion (Carson et al., 2004). Event-by-event head motion correction was included in the reconstruction based on motion detection with a Polaris Vicra® optical tracking system (NDI Systems, Waterloo, Canada) using reflectors mounted on a cap worn by the subject (Jin et al., 2013). Parametric volume of distribution (V_T) images using 60 min of dynamic data were generated with a one-compartment model using the metabolite-corrected arterial plasma curve (Finnema et al., 2018). Registration of parametric images to Montreal Neurological Institute (MNI152) template space was performed using SPM12 (Wellcome Trust center for Neuroimaging, London, UK). For each subject, a linear registration of an early sum image (0–10 min post-injection) of motion-corrected PET data to a high-resolution T1-weighted structural image was applied to parametric V_T images. Non-linear registration of MR images (Ashburner and Friston, 2005) was then applied to the parametric V_T images and lastly smoothed with a 12 mm FWHM Gaussian kernel.

2.4. Independent component analysis

Independent component analysis (ICA) is a data-driven approach that identifies spatial covariation patterns, extracting maximally independent components and associated signal sources. Here, we consider image data from N subjects, each with P pixel values. ICA assumes that the observed data for each subject (x, a P-vector) is comprised of an unknown linear mixture of S independent non-Gaussian sources (s, each a P-vector) with mixing coefficients A. ICA estimates the mixing matrix (Ã) and its corresponding maximally independent sources (y, each a P-vector). Applied to three-dimensional imaging data of a group of N subjects, the output of spatial ICA includes spatial source weights (P-vectors) of M source signals (y_i, i = 1,…,M) and subject loading values for component i and subject j (Ã_i,j); where M indicates the chosen model order (i.e., the number of components) of the ICA extraction and à is an M-by-N matrix. ICA of biomedical imaging data is typically applied after dimension reduction with principal component analysis (PCA); however, for ease of notation, we define à to represent the final ICA-derived loading parameters. Relative to PET V_T images, subject ICA-loadings (Ã) represent the source ‘intensity’ or relative strength of each source for each subject’s V_T data, such that an approximation of the original V_T maps (Ṽ_T) could be reconstructed as ${\tilde{V}}_{\text{T},j}=\sum _{i=1}^M{y}_i{\tilde{A}}_{i,j}$.

A primary goal of this study was to investigate the reliability and reproducibility of ICA-identified components of ¹¹C-UCB-J at different model orders (M). To achieve this, spatial ICA was performed using the source-based morphometry (SBM) module of GroupICA Toolbox (GIFTv4.0b; trendscenter.org/software/gift/) on the two samples of 40 subjects separately. Analyses were constrained to a voxel mask with a mean (across-subject) V_T > 10 (Fig. S1) in order to exclude white matter structures (Finnema et al., 2018). The mean within this mask for each scan was subtracted, and V_T images of 40 participants were concatenated to form a subject series that was then reduced through PCA prior to ICA using the InfoMax algorithm (Bell and Sejnowski, 1995). ICA was performed at multiple model orders, estimating 8, 12, 18, and 24 components in separate analyses. ICA analyses were performed without normalization (e.g., z-transforming) along either dimension (spatial or subject-wise) before or after extraction to preserve the quantitative V_T units and facilitate comparisons with the larger ¹¹C-UCB-J literature.

To assess component stability and repeatability, each extraction was iterated 50 times using ICASSO module implemented in GroupICA Toolbox (Himberg et al., 2004). Given that ICA algorithms are affected by random sampling of the data, ICASSO provides measures of the statistical reliability of estimated components through multiple iterations of the extraction. Consistent with prior investigations of ICA model space (Abou-Elseoud et al., 2010), the repeatability of components was assessed using the cluster-quality index (I_q), which represents a summary metric of the multi-dimensional similarity between the identified mixing matrix solutions (i.e., component loadings, spatial distribution of sources, and relative independences of ICs) across iterated extractions (Himberg et al., 2004). As a measure of between-iteration similarity, I_q ranges between 0 and 1, with greater values representing a higher degree of repeatability and 1 representing identical solutions identified through every random-point initiated iteration. In ICA of fMRI, components with I_q > 0.8 are considered to have been stably and reliably identified (Allen et al., 2011). Final ICA output for each model order represented the average estimate of spatial sources and subject loadings over the 50 iterations.

2.5. Source network replication

The replication of ICA-identified source networks between the two samples of healthy subjects was examined for each model order, and a conjunction of the two constraint masks (i.e., the overlap of the two V_T > 10 masks) was generated to limit comparisons to only those voxels present in both analyses. Replication of ICs between samples was determined based on the spatial distribution of source network intensities. Each source network was scaled to estimated Ṽ_T units by multiplying by the average subject loading for that source network. Each of these source networks from sample 1, expressed as P-vectors, were entered as the dependent variable in a multiple regression with the vectors of all source networks from sample 2 as the independent variables. Resulting regression coefficients (betas) for each IC from sample 1 relative to the ICs from sample 2 were considered an index of spatial similarities. The pair of source networks with the overall maximal beta value were visually compared to verify similarity in pattern. Once verified, these two source networks were excluded from subsequent matching, i.e. only one match is reported per source network. The process was repeated until the pair with the maximal remaining beta value did not visually match. At each model order, some ICs did not replicate across samples, based on this procedure.

2.6. Comparison between model orders

First, standard mixed linear models were performed to examine within- and between-sample effects of model order on I_q. Next, the source networks from the independent samples were further examined to assess the persistence of identified components at different model orders. As described above for source network replication, for a given model order, multiple regression analysis was performed comparing each source network (P-vectors) to the source networks derived from the previous model order (i.e., 12→8, 18→12, 24→18) to select similar sources, with matching based on largest beta coefficients followed by visual confirmation. Lastly, matched source networks were excluded from subsequent matches between model orders, such that only the one match is reported.

Exploration of spatial maps and demographic associations of subject loadings

To explore potential physiological implications of the ICA-identified components of ¹¹C-UCB-J V_T, ICA procedures were repeated on the full subject dataset (n = 80) at the model order chosen to be optimal based upon the replication and model order analysis. ICs at n = 80 were visually matched to the replicated ICs (Fig. 1) for consistency in numbering. Source networks were region labeled according to the AAL template using xjView toolbox (http://www.alivelearn.net/xjview) in Matlab2015a (Mathworks). Subject component loadings per source network were analyzed in an exploratory fashion using independent sample t-tests to examine sex differences and Pearson correlations to investigate relationships with age, corrected for multiple comparisons with the Bonferroni method. For exploratory reasons, results were also presented without correction for multiple comparisons, and findings were considered significant at P < 0.05.

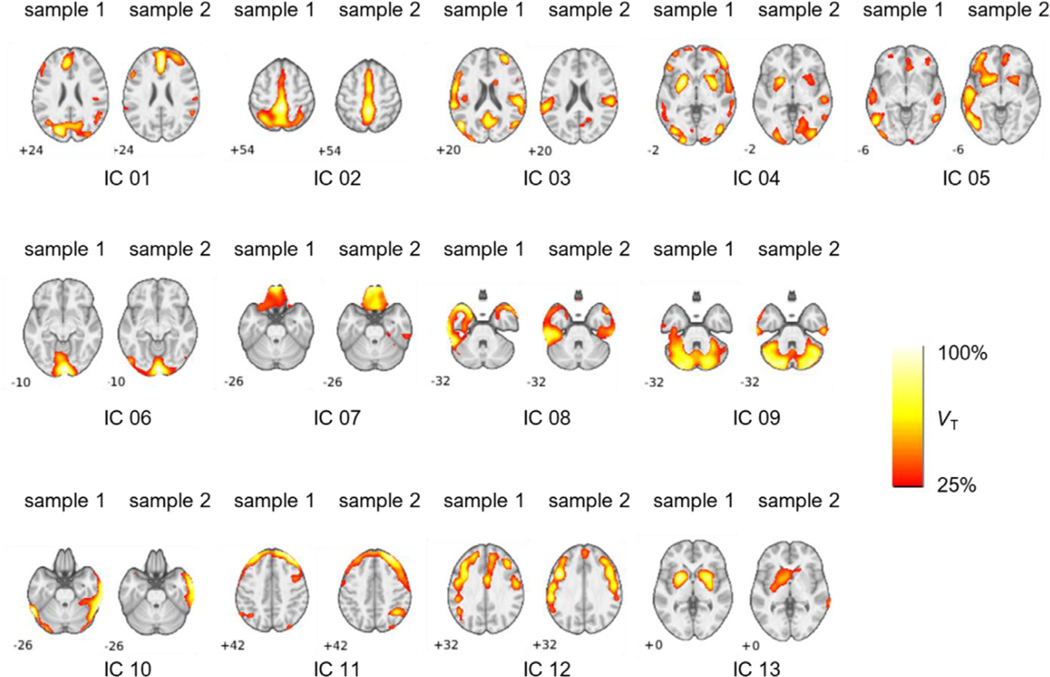
Fig. 1.

Results from source network replication across independent samples from ICA performed at model order 18. The matched components across samples were determined by maximal regression beta (β) from multiple regression analysis. Images are scaled relative to peak Ṽ_T. Depicted slices are chosen to present peak V_T coordinates.

3. Results

3.1. Replicated source networks of ¹¹C-UCB-J

In order to assess the replication and persistence of ICA-identified sources networks, ICA was performed in two separate samples of the dataset (Table 1) at a range of model orders (8, 12, 18, and 24), and the identified components within the same model order were compared between samples using multiple regression. Detailed results are presented in Table S1 including I_q values and the peak Ṽ_T in each source network. Replications across independent samples for model order 18 are presented in Fig. 1. At model order 8, 4 ICs replicated between samples (mean ± SD beta: 0.42 ± 0.23). At model order 12, 8 ICs replicated across samples (beta: 0.46 ± 0.14). Thirteen ICs replicated at model order 18 (mean beta: 0.31 ± 0.16). Lastly, at model order 24, 16 ICs (mean beta: 0.30 ± 0.11) replicated across independent samples. Images of replicated source networks at all model orders are shown in Fig. S2.

3.2. Comparison between model orders

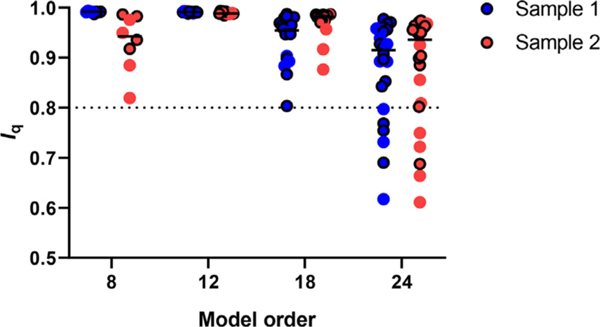
Repeatability of ICA decomposition was evaluated using the mean cluster-quality index (I_q) for all source networks that were found across all model orders (Fig. 2). There was a main effect of model order on I_q (F_3,116 = 16.23, p < 0.001), but there was no sample * model-order interaction (F_3,116 = 1.59, p = 0.20) or sample group difference (F_1,116 = 0.24, p = 0.620) in I_q. Post-hoc testing indicated average I_q was lower for model order 24 relative to the other model orders correcting for multiple comparisons (p < 0.001). I_q values below 0.8 have been considered unreliable, and at model order 8, 12, and 18, there were no I_q values below 0.8 in either sample (sample 1: 0.99 ± 0.002, 0.99 ± 0.002, 0.94 ± 0.050, and 0.88 ± 0.100; sample 2: 0.93 ± 0.057, 0.99 ± 0.003, 0.97 ± 0.029, 0.88 ± 0.113 for model orders 8, 12, 18, and 24, respectively). At model order 24 however, 6 out of 24 components had an I_q below 0.8 for sample 1, and 5 out of 24 components had an I_q below 0.8 for sample 2. When assessing the I_q values of only the replicated ICs between samples, five ICs at model order 24 (IC 05, IC 06, IC 08, IC 10 and IC 12) had I_q below 0.8 in one or both samples, suggesting that these would be considered unreliable (bolded values in Table S1).

Fig. 2.

Cluster quality index (I_q) per sample for all components at each respective model order. I_q decreases as model order size increases indicating that extraction reliability decreases as model order increases. Dashed line at I_q = 0.8 represents cutoff for reliable ICs. Circles outlined in black indicate replicated source networks across samples.

Across investigated model orders, replicated source networks that were identified at one extraction dimension were also identified in higher dimension extractions (Table S2). The replicated ICs from model order 8, IC 01 – IC 04, were also identified at model orders 12, 18, and 24 (Fig. S2). At model order 12, a further four ICs emerged: IC 05–08. At model order 18, an additional five ICs were identified. Lastly, at model order 24, three novel ICs were identified. Representative images for all ICs across model orders identified in samples 1 and 2 are presented in Fig. S2.

Based on the I_q values and the number of replicated source networks, model order 18 appears to be within the optimal range to extract the highest number of robustly replicable ICs (i.e., I_q > 0.8). Model order 24 identified more reproducible components but some ICs, including those reliably identified at lower model orders, had I_q values below 0.8 which would be considered unreliable.

3.3. Physiological and functional associations

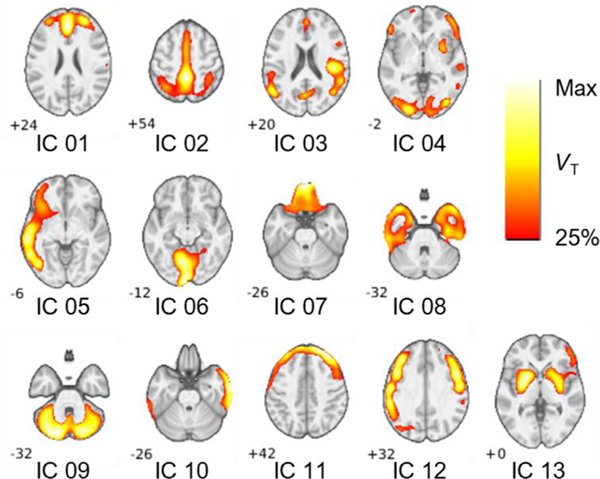
Source networks of the identified ICs from the ICA performed with the full dataset (n = 80) at model order 18 are shown in Fig. 3. For our purposes, we selected to further analyze ICs from model order 18 as they represent a balance of being highly repeatable (i.e. high I_q, none below 0.8), robustly sourced (i.e. high peak V_T with loading weights significantly different from zero), and a regionally distinct and diverse variety of potentially functionally relevant source networks of ¹¹C-UCB-J binding. Following anatomical labeling using the AAL template, the ICs are described in Table 2 along with cluster size and MNI coordinates of peak Ṽ_T. The ICs have a peak Ṽ_T value of 9.9 ± 2.1 mL/cm³. Typically, gray matter V_T values for ¹¹C-UCB-J are in the range of 20 mL/cm³.

Fig. 3.

Selected slices display the main regional source network distribution/characteristics of ICs extracted at model order 18 in the n = 80 dataset. Identified ICs were as follows: an anterior prefrontal (IC 01), a posterior cortical (IC 02), a superior/middle temporal (IC 03), a corticostriatal (IC 04), a left middle/inferior temporal (IC 05), a calcarine (medial occipital, IC 06), an orbitofrontal (IC 07), a frontotemporal pole (IC 08), a cerebellar (IC 09), right temporal (IC 10), frontoparietal (IC 11), middle frontal (IC 12), and striatal (IC 13). Images in Ṽ_T units (25–100% of per IC peak Ṽ_T). Slice values were chosen to display peak Ṽ_T coordinates.

Table 2.

Peak ICA-estimated volume of distribution contribution (Ṽ_T, mL/cm³) of identified networks at model order 18 in the n = 80 dataset. Total cluster size in voxels (k), x, y, z coordinates (in mm) of peak Ṽ_T in MNI space.

	Identified network	k	x	y	z	Peak ṼT
IC 01	Anterior prefrontal	16,714	− 2	26	38	9.1
IC 02	Posterior cortical	12,288	0	− 42	56	14.36
IC 03	Superior/mid temporal	25,852	50	12	− 4	7.1
IC 04	Corticostriatal	24,406	36	− 60	40	7.4
IC 05	Left middle/inferior temporal	18,470	− 60	− 28	− 10	9.3
IC 06	Calcarine (medial occipital)	15,463	− 8	− 64	− 8	9.5
IC 07	Orbitofrontal	6581	− 2	52	− 28	13.05
IC 08	Left frontotemporal	6016	− 24	6	− 44	12.3
	Right frontotemporal	7162	30	14	− 44	11.1
IC 09	Cerebellar	19,798	− 18	− 80	− 30	8.4
IC 10	Right temporal	14,720	66	− 36	− 16	9.6
IC 11	Frontoparietal	12,881	22	52	38	10.3
IC 12	Left middle frontal	11,518	− 50	− 40	40	8.3
	Right middle frontal	7403	44	4	46	8
IC 13	Striatal	11,984	− 22	6	− 4	10.2

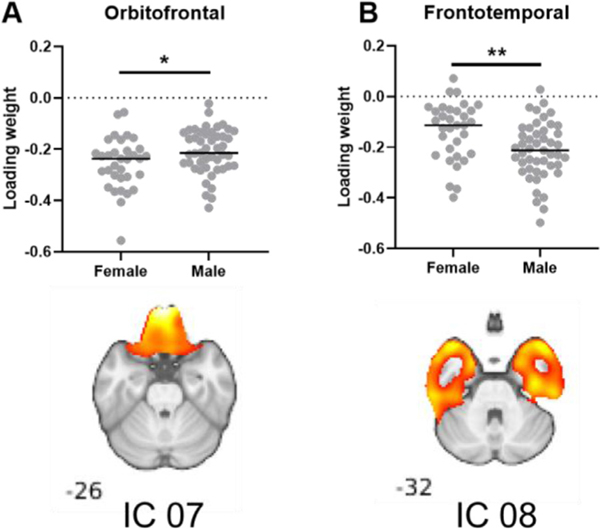
The effects of sex and age on subject Ṽ_T mixtures (i.e., subject loading weights) for identified ICs were assessed (Figs. 4, 5). Significant sex differences were found in two ICs: an orbitofrontal source network (Fig. 5A, p < 0.05, IC 07) and a frontotemporal source network (Fig. 5B, p < 0.01, IC 08). However, these two results did not survive the Bonferroni correction for multiple comparisons.

Fig. 4.

Components from ICA of the total dataset (n = 80) with significantly different loading weights between men and women. Loading weights were significantly different in (A) IC 07, an orbitofrontal network and (B) in IC 08, a frontotemporal network. * p < 0.05, ** p < 0.01. Statistical analysis performed using unpaired t-tests. Results were not significant after Bonferroni correction.

Fig. 5.

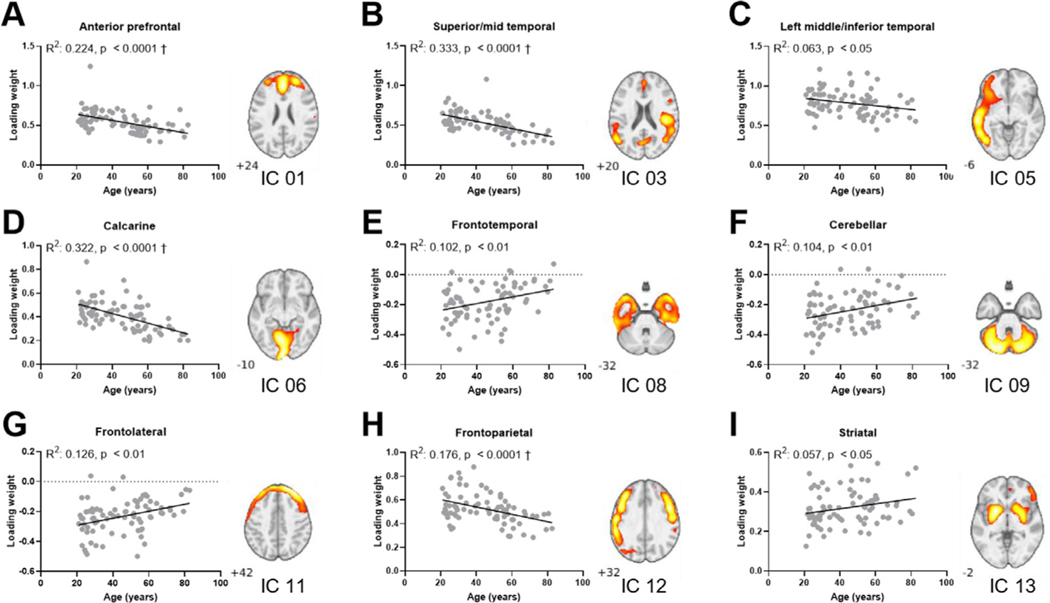
Correlation plots between age and subject loading weights from ICA of the total dataset (n = 80). Correlation plot for the anterior prefrontal network displays a significant change in loading weights with age (A, IC 01, R²: 0.224, p < 0.0001). Further changes in loading weight with age were found in the superior/mid temporal network (B, IC 03, R²: 0.333, p < 0.0001), left middle/temporal spatial (C, IC 03, R²: 0.063, p < 0.05), calcarine (D, IC 06, R²: 0.322, p < 0.0001), frontotemporal (E, IC 08, R²: 0.102, p < 0.01), cerebellar (F, IC 09, R²: 0.104, p < 0.01), frontoparietal (G, IC 11, R²: 0.126, p < 0.01), middle frontal (H, IC 12, R²: 0.176, p < 0.0001), and the striatal network (I, IC 13, R²: 0.057, p < 0.05). † denotes correlations that remain significant following Bonferroni correction.

The relationship between the subject loading weights and age were more pronounced (Fig. 5). In an exploratory analysis, significant correlations of loading weight with age were found in 9 source networks: an anterior prefrontal network (Fig. 5A, IC 01, R²: 0.224, p < 0.0001), superior/mid temporal network (5B, IC 03, R²: 0.333, p < 0.0001), left middle/temporal (5C, IC 05, R²: 0.063, p < 0.05), calcarine (5D, IC 06, R²: 0.322, p < 0.0001), frontotemporal (5E, IC 08, R²: 0.102, p < 0.01), cerebellar (5F, IC 09, R²: 0.104, p < 0.01), frontoparietal (5G, IC 11, R²: 0.126, p < 0.01), middle frontal (5H, IC 12, R²: 0.176, p < 0.0001), and a striatal network (5I, IC 13, R²: 0.057, p < 0.05). IC 01, IC 03, IC 05, IC 06, and IC 12 had positive subject loadings and the correlation with age is negative (Fig. 5A–D, H), which reflects a decrease in Ṽ_T with age. IC 08, IC 09, and IC 11 had negative subject loadings and the correlation with age was positive (Fig. 5E–G), i.e., the magnitude of Ṽ_T variability from these source networks reduce with age. Lastly, the subject loadings and slope of the relationship between IC 13 (Fig. 5I) and age were positive, which would represent an increase in Ṽ_T from this source network with age.

When corrected for multiple comparisons (Bonferroni), four of the 9 IC relationships with age remained: the anterior prefrontal (IC 01), superior/mid temporal (IC 03), calcarine (IC 06), and the middle frontal network (IC 12). These four ICs all had positive subject loadings and negative slopes with age.

4. Discussion

In this study, we present results from a data-driven method for identifying source networks of ¹¹C-UCB-J synaptic density (SV2A) PET data. We first validated the robustness and persistence of these source networks by performing ICA in two separate age- and sex-matched samples of 40 healthy subjects each. Next, as the ‘true’ number of source networks in ¹¹C-UCB-J data is unknown, we assessed the effect of model order selection using the two samples. For the purposes of our study, we determined that estimating 18 components appeared optimal based on I_q and the observation that at model 18, 5 new ICs not found at the lower model orders were identified. At the highest investigated model order 24, 3 additional ICs were identified, but a greater fraction of the estimated components had I_q < 0.8 and thus the extraction was considered less reliable. When estimating 18 components, we were able to identify 13 source networks that robustly replicated across both samples. Using this model order, ICA of the entire 80-subject dataset reliably extracted the same source networks found previously in the two separate samples. The relationships between the subject loadings for these source maps and sex and age were assessed, and we found that the subject loadings of several source networks significantly correlated with age.

All of the ICs first extracted at lower model orders (8, 12) continued to be extracted at higher model orders (18, 24). Based on the high within-cohort correlations of the spatial regression coefficients across model orders, and confirmed visually, the source networks differed little across model orders (Table S2). This contrasts with reports of model order effects on RSNs in rs-fMRI data; as model order increases, spatial features including volume (number of contributing voxels), mean z-score, and repeatability decreased significantly with model order (Abou-Elseoud et al., 2010). Furthermore, as the neuroanatomical precision increased (i.e., the specificity and differentiation of spatial loading on different anatomical structures increased), the repeatability of the ICA decomposition was reduced (Abou-Elseoud et al., 2010). Similarly, the identified ¹¹C-UCB-J source networks tended to display reduced coverage as model order increased (IC 01 – IC 04, Fig. S2). Here we conclude that within the tested range of model orders (i.e., 8–24), ICs could reliably be extracted from ¹¹C-UCB-J PET data. However, at model order 24, a significant fraction of extracted components had an I_q below 0.8 (sample 1: 6/24, sample 2: 5/24), which was not the case for model order 18 and lower. Based on this, a model order in the range of 18 appears to be a suitable number of estimated components for this dataset.

When comparing ICs between model orders, we did not account for multiple matches nor did we investigate any “splitting” of ICs (i.e., branching of one IC at lower model order to multiple ICs at higher model order) as these were not the focus of our replication assessment. Additionally, ICA identified several ICs that did not replicate across samples at different model orders. In limited sample sizes and real-world medical imaging data, it is likely that some unstructured and/or truly random variance will be present, and thus those portions of the ICA solution, which aims to model all data variance (i.e. unlike PCA which aims to model only primary vectors of variance and does not account for residual error) will be sample-dependent to a degree. Thus, while we validated 13 ICs within the constraints of our dataset, future analyses using larger samples may identify additional replicable ICs of synaptic density. The reliable source networks that we identified are as follows: an anterior prefrontal source network (Fig. 1; IC 01), posterior cortical (IC 02), superior/mid temporal (IC 03), corticostriatal (IC 04), left middle/inferior temporal (IC 05), calcarine (i.e. medial occipital, IC 06), orbitofrontal (IC 07), frontotemporal (IC 08), cerebellar (IC 09), right temporal (IC 10), frontoparietal (IC 11), middle frontal (IC 12), and striatal (IC 13).

A number of ¹¹C-UCB-J ICA source networks (Fig. 3) appear spatially consistent with RSNs derived from ICA on ¹⁸F-FDG PET data. Among them, the anterior prefrontal (IC 01), the superior/mid temporal (IC 03), the calcarine (medial occipital, IC 06), the cerebellar (IC 09), and the striatal network (IC 13) were reported both by Di et al. (2012) and Savio et al. (2017). Another three ¹¹C-UCB-J ICs were also found by Di and colleagues, namely the posterior cortical (IC 02), the orbitofrontal (IC 07), the right temporal (IC 10), and the middle frontal (IC 12).

Synaptic density might also be associated to structural volumes, and ¹¹C-UB-J ICA source networks were examined in relation to sources of covariance reported in structural MRI (Di and Biswal, 2016; Xu et al., 2009). The ¹¹C-UCB-J superior/middle temporal (Fig. 3, IC 03) and striatal (Fig. 3, IC 13) source networks visually resemble previously reported structural sources by Xu and colleagues. Furthermore, the following 7 ¹¹C-UCB-J source networks strongly resemble gray matter sources as reported by Di and Biswal (2016) : anterior prefrontal (Fig. 3, IC 01), posterior cortical (IC 02), superior/middle temporal (IC 03), corticostriatal (IC 04), frontotemporal (IC 08), cerebellar (IC 09), and the striatal source network (IC 13). These qualitative comparisons are further consistent with evidence of shared associations between loss in gray matter volume and synaptic density in neurodegenerative disease (Mecca et al., 2020) and support exploration in ¹¹C-UCB-J ICs in clinical populations.

Lastly, nine of the ¹¹C-UCB-J ICA-derived networks visually resemble RSNs found with rs-fMRI ICA (Allen et al., 2011; Di et al., 2012; Laird et al., 2011; Savio et al., 2017; Smith et al., 2009). Based on visual comparison, the anterior prefrontal (IC 01) source network resembles the anterior part of the default-mode network (DMN), as shown in Fig. S3. Further, the superior/mid temporal (IC 03) resembles the auditory functional network, the calcarine (medial occipital, IC 06) resembles a visual network, and the cerebellar (IC 09) and striatal (IC 13) networks are also similar to rs-fMRI networks. While the aforementioned networks were identified in all the above fMRI studies, a further two networks that visually matched our findings were reported only by Laird et al.: the orbitofrontal (IC 07) as well as the frontotemporal network (IC 08). BOLD images can have significant signal dropout and spatial distortion in the orbitofrontal and anterior temporal cortices (Yeo et al., 2011), which may have limited detection of these two networks other fMRI studies.

In general, ¹¹C-UCB-J PET ICs demonstrate left-right symmetry, i.e., most of the ICs are symmetric between hemispheres (11 out of 13 ICs, Fig. 3). The two notable ICs that are present only in one hemisphere each are the left middle/inferior temporal network (IC 05) and the right temporal network (IC 10). Thus, while most of the ICs represent covariance that spans both hemispheres, the two asymmetric ICs may represent a network that is unique to each of their respective hemisphere. Although these two asymmetric ¹¹C-UCB-J ICs do not resemble any of those reported in ¹⁸F-FDG PET or rs-fMRI literature, other asymmetric ICs have been found in ¹⁸F-FDG PET and rs-fMRI studies (Di et al., 2012; Smith et al., 2009).

One interesting discrepancy between ¹¹C-UCB-J networks and rs-fMRI RSNs lies with networks consisting of anterior-posterior connectivity. We did not find a spatial source resembling the posterior default-mode network in our study at any model order. Though we did identify an anterior prefrontal network (IC 01) resembling the anterior part of the DMN, we did not detect either the posterior DMN or the DMN in its entirety. Similarly, the posterior DMN was not identified in one ¹⁸F-FDG ICA study (Savio et al., 2017). Taken together, these intra-modality similarities and differences suggest that ¹¹C-UCB-J networks likely contain both complementary and unique information relative to ¹⁸F-FDG and rs-fMRI networks.

Using the full 80-subject cohort, we assessed the effects of sex and age on component loadings. In our initial exploratory analysis, a significant difference in loading weights between sex was found in the or- bitofrontal network (IC 07, Fig. 4A) and in the frontotemporal network (IC 08, Fig. 4B), though these did not survive a correction for multiple comparisons. In 9 ¹¹C-UCB-J ICs, there was a significant correlation between IC loading weights and age. Of these, 4 correlations survived the correction for multiple comparisons: the anterior prefrontal (IC 01), calcarine (IC 06), superior/mid temporal (IC 03), and middle frontal (IC 12) IC. These 4 ICs all had positive subject loadings as well as a negative slope with age. Interestingly, the striatal network (IC 13) had positive subject loadings and a positive correlation with age, however, this correlation did not survive the correction for multiple comparisons. The correlations that did not survive Bonferroni correction (Fig. 5C, E, F, G, I) had R² values below 0.1. Thus, these correlations are at best weak, and not clearly associated with age.

The brain is affected by the aging process, with many cognitive functions declining with age, such as attentional resources, working and episodic memory, processing speed, and inhibitory capacities (Craik and Byrd, 1982; Salthouse, 2000). Brain structure also changes with age both in white and gray matter (Damoiseaux et al., 2009; Driscoll et al., 2009), and links between structural changes and cognition have been established (Hedden et al., 2016). Furthermore, aging has been associated with decreased functional connectivity in DMN and dorsal attention networks (Tomasi and Volkow, 2012). One interpretation of the age-related correlations with the IC loading weights is that the age-related decrease in subject loadings represents a decrease in synaptic density in the network, potentially reflecting a weaker independent source of variance. Age-effects on ICA-identified components of gray-matter structural images have similarly reported a negative relationship between age and volume of the network (Xu et al., 2009). However, it stands to note that prior to ICA, the global per-subject mean is removed and thus the remaining variance detected is separate from any global brain effects and can therefore be positive or negative relative to the mean. As such, these aging effects should be interpreted with caution, given that positive aging effects may reflect stability relative to global effects, and significant age-associated decreases may be missed because they are similar to the global effects. Interestingly, some of the ¹¹C-UCB-J ICs exhibited positive relationships between age and Ṽ_T contributions. From the perspective of ICs representing mixture of variance sources within regions, this counterintuitive observation may reflect a condensing of variance (i.e., a loss of source diversity) within particular regions or networks with age. Such a process would also be consistent with models of generally reducing connective diversity with age. However, it is known that age-related volume loss is not uniform across brain regions, and thus some of our findings may be in part due to volume loss. Additionally, brain size differences (as assessed with total intracranial volume, TIV) may potentially affect ¹¹C-source networks. Two ICs (IC 07 and IC 09) exhibited an association (p-vals < 0.05) with TIV across all subjects. While these relationships did not replicate in the subsample analyses, the potential influence of registration algorithms on sources of variance in ¹¹C-UCB-J ICs, particularly those in orbitofrontal and cerebellar regions requires attention in future research.

A major methodological difference between ICA on fMRI data and PET data is that voxels in fMRI are assigned to a component based on similarity in temporal fluctuations within-subject as well as across-subject, while such assignment occurs across subjects for PET data. At rest, the DMN is one of the most highly active networks (Raichle, 2015). Such activation might be captured with BOLD signal in the temporal dimension by the continuous fluctuations “as the mind wanders”, but when investigated in a static manner (i.e., PET ICA), such temporal dynamics might be lost. Second, fMRI, ¹⁸F-FDG PET, and ¹¹C-UCB-J PET measure different aspects of neural activity. The BOLD signal from fMRI reflects cerebral blood flow as an indirect measure of metabolic oxygen rate, and ¹⁸F-FDG PET measures uptake of FDG which mirrors energy metabolism; these are both dynamic processes. This is unlike ¹¹C-UCB-J PET, which quantifies the vesicular SV2A protein, and reflects synaptic density which is considered a structural measure and unlikely to fluctuate with increase or decreases in neural activity. Furthermore, a recent study found that during visual-activation tasks, ¹¹C-UCB-J V_T remain unchanged, while blood flow increased as reflected in increased K₁ values (Smart et al., 2020b). Thus, differences in ICA-derived networks between these modalities are not unexpected. The PET V_T data have physiological meaning, being linearly related to SV2A density, thus, ICA analyses were performed in a manner to preserve the quantitative V_T units in our data. Alternatively, normalization or other pre- and post-processing measures may be performed before or after ICA extraction and may provide a different representation of the distribution and variability of source weights across voxels or component loadings across subjects. Lastly, our study reports the ICs using a quantitative measurement (Ṽ_T) which may have great interpretive value.

As part of ICA, the relative contribution of each source component is determined for each subject. These individual loading weights can be examined in clinically relevant analyses, as we have done here with the aging correlations (Fig. 5). This approach may be of interest in studies of neurodegenerative and psychiatric disorders. Previously, we and others have reported differences in synaptic density as measured with ¹¹C-UCB-J PET in epilepsy, Alzheimer’s disease, PTSD, Parkinson’s disease and psychiatric disorders (Chen et al., 2018; D’Souza et al., 2020; Finnema et al., 2020, 2016; Holmes et al., 2019; Matuskey et al., 2020; Onwordi et al., 2020). As well, multi-modality approaches utilizing ICA have already been applied to find altered network integrity in dementing disorders (Ripp et al., 2020). While an individual-subject ICA could be performed across multiple time points, the structures of within-subject temporal changes/covariance in UCBJ distribution cannot be assumed to be the same as those identified across subjects. This certainly represents an area of future interest, particularly in clinical populations with marked neurodegeneration, and warrants additional research using longitudinal data. Thus, the application of ICA to ¹¹C-UCB-J PET, which allows examination of coherent and distinct source networks of synaptic density variability, may hold significant diagnostic applicability to these and to other neurodegenerative and psychiatric disorders related to synaptic loss and/or pathology.

5. Conclusion

ICA identified source networks of ¹¹C-UCB-J PET data that were sample-independent and extracted consistently across a range of model orders. From this dataset, we identified 13 synaptic density source networks, several of which were consistent with sources derived from structural MR gray matter and ¹⁸F-FDG PET, and to a lesser degree also showed some spatial similarity with rs-fMRI RSNs. The relative contribution of individual subject variations was related to age for 4 ICs. Synaptic density networks can be reliably and reproducibly identified in healthy adults, show specificity in associations with physiological processes like aging, and should be applied in psychiatric and neurodegenerative populations as possible imaging biomarkers of disease.