Abstract
Quantitative evaluation of an image processing method to perform as designed is central to both its utility and its ability to guide the data acquisition process. Unfortunately, these tasks can be quite challenging due to the difficulty of experimentally obtaining the “ground truth” data to which the output of a given processing method must be compared. One way to address this issue is via “digital phantoms”, which are numerical models that provide known biophysical properties of a particular object of interest. In this contribution, we propose an in silico validation framework for dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) acquisition and analysis methods that employs a novel dynamic digital phantom. The phantom provides a spatiotemporally-resolved representation of blood-interstitial flow and contrast agent delivery, where the former is solved by a 1D-3D coupled computational fluid dynamic system, and the latter described by an advection-diffusion equation. Furthermore, we establish a virtual simulator which takes as input the digital phantom, and produces realistic DCE-MRI data with controllable acquisition parameters. We assess the performance of a simulated standard-of-care acquisition (Protocol A) by its ability to generate contrast-enhanced MR images that separate vasculature from surrounding tissue, as measured by the contrast-to-noise ratio (CNR). We find that the CNR significantly decreases as the spatial resolution (SRA, where the subscript indicates Protocol A) or signal-to-noise ratio (SNRA) decreases. Specifically, with an SNRA / SRA = 75 dB / 30 μm, the median CNR is 77.30, whereas an SNRA / SRA = 5 dB / 300 μm reduces the CNR to 6.40. Additionally, we assess the performance of simulated ultra-fast acquisition (Protocol B) by its ability to generate DCE-MR images that capture contrast agent pharmacokinetics, as measured by error in the signal-enhancement ratio (SER) compared to ground truth (PESER). We find that PESER significantly decreases the as temporal resolution (TRB) increases. Similar results are reported for the effects of spatial resolution and signal-to-noise ratio on PESER. For example, with an SNRB / SRB / TRB = 5 dB / 300 μm / 10 s, the median PESER is 21.00 %, whereas an SNRB / SRB / TRB = 75 dB / 60 μm / 1 s, yields a median PESER of 0.90 %. These results indicate that our in silico framework can generate virtual MR images that capture effects of acquisition parameters on the ability of generated images to capture morphological or pharmacokinetic features. This validation framework is not only useful for investigations of perfusion-based MRI techniques, but also for the systematic evaluation and optimization new MRI acquisition, reconstruction, and image processing techniques.
Keywords: Computational fluid dynamics, kidney, MRI simulator, quantitative MRI, pharmacokinetics, hemodynamics
1. Introduction
The task of validating image processing routines to perform as designed can be quite challenging due to the difficulty of obtaining the appropriate “ground truth” data to which the output of a given processing method can be quantitatively compared. One way to address this issue is to design and apply realistic “digital phantoms”, which are numerical models or software that provide the geometry and biophysical properties of a particular object of interest (Hsu, 2010; Segars et al., 2010; Badano et al., 2017). Digital phantoms, also known as virtual phantoms (Segars et al., 2010; Badano et al., 2017; Saint-Jalmes et al., 2014) or digital reference objects (Semmineh et al., 2017), have become important tools for developing and evaluating new medical imaging techniques, devices, and analysis approaches (Hsu, 2010; Keenan et al., 2018; Ger et al., 2017). For example, Collins et al. (1998) constructed a volumetric, digital brain phantom defining the spatial distribution of ten types of human brain tissue (Collins et al., 1998; Aubert-Broche, 2006); this digital phantom has become a commonly used tool for simulating MRI acquisition and testing processing algorithms in neuroimaging (Alfano et al., 2011). Similarly, the Virtual Imaging Clinical Trial Regulatory Evaluation (VICTRE) phantom (Badano et al., 2017) recapitulates the tissues and large vessels of the breast, to enable in silico replication of existing clinical features. Importantly, the VICTRE phantom has demonstrated that computational modeling can play a central role in the regulatory assessment of imaging products (Badano et al., 2018). Another example is the 4D extended cardiac-torso (XCAT) phantom (Segars et al., 2010) which realistically models cardiac-torso anatomy and body movements. Compared to ex vivo measurements for obtaining the “ground truth” on tissue properties, digital phantoms do not suffer from the issue of tissue shrinkage, deformation, or any physical changes that may be caused by invasive or post-mortem procedures. Moreover, they can frequently outperform physical phantoms (Shukla-Dave et al., 2019; Driscoll et al., 2011; Cloutier et al., 2004) due to the complexity and flexibility of geometry and material properties that they can represent.
Quantitative dynamic contrast enhanced (DCE-) MRI has the ability to characterize perfusion, vessel permeability, and interstitial transport (Gordon et al., 2014) to assess pathophysiology in a large range of organs or tissues (Gordon et al., 2014; Yankeelov et al., 2007; Heye et al., 2014; Sujlana et al., 2017). Specifically, we have recently developed a suite of novel methods for quantitatively analyzing DCE-MRI data that return segmentations of tumor-associated vasculature as well as characterization of their hemodynamics (e.g., perfusion, diffusion, and interstitial transport) (Wu et al., 2019; Wu et al., 2020). To validate these methods, we require a digital phantom to provide a detailed description of vascular structures from major vessels to microvasculature, as well as spatiotemporal-resolved representations of capillary permeability, blood flow, interstitial flow, and tracer distribution. These features are of fundamental importance for a realistic, physics-based simulation of the acquisition and analysis of DCE-MRI data. While there have been many efforts investigating the use of digital phantoms to evaluate DCE-MRI techniques, many have limited flexibility in the geometry or kinetic models that can be investigated which constrains their ability to realistically represent anatomical and functional characteristics. For example, Kudo et al. (2013) utilized a perfusion phantom to compare x-ray computed tomography and MRI analyses used at multiple sites. This digital phantom assumes a 2D geometry containing 7 × 7 square regions of interest (ROI), each with 12 × 12 pixels, with no consideration of tissue morphology. Of particular note, the perfusion in this phantom is defined by empirical concentration-time curves prescribed for each ROI with specific parameters (i.e., mean transit time and cerebral blood flow)—a strategy that is quite common (see, e.g., Hansen et al., 2019; Le et al., 2013; Zhu et al., 2015; Grimm et al., 2012). While this approach has the advantage of straight-forward implementation, the prescribed concentration-time curves may not accurately reproduce realistic kinetics of contrast agent uptake. Bosca and Jackson (2016) presented a variation on this approach with a more realistic, anthropomorphic digital phantom, where the DCE-MRI signals were generated voxel-wise with a three-component kinetic model and patient data-driven parametric maps. However, the voxel-wise generation of tracer concentration curves still does not consider the fluid dynamics of tracer delivery. Thus, the morphological and functional properties of the digital phantom have limited physiological meaning.
More recently, there have been efforts designed to more realistically characterize tissue hemodynamics in digital phantoms. For example, the digital phantom developed by Semmineh et al. (2017) for the evaluation of dynamic susceptibility contrast (DSC)-MRI data (Bell et al., 2019), considers the effects of water diffusing in a heterogeneous 3D tissue structure (that includes blood vessels and cells) on simulated MRI signals. A key innovation of this phantom is the contrast agent relaxivity and compartmental volume fractions are determined by modeling of the tissue microstructure. This feature ensures the phantom provides a “ground truth” for studies seeking to investigate the biophysical basis of DSC-MRI. However, the concentration of contrast agent in this phantom is still governed by the simplistic, two-component pharmacokinetic model commonly employed in the field (Yankeelov and Gore, 2007). A different strategy of using computational fluid dynamics to obtain the spatiotemporal distribution of contrast agent in phantoms has been presented by Hariharan et al. (2013). In their implementation, a single-phase fluid flow within a vessel is solved given specific impulse profiles and boundaries, providing a flow field which subsequently determines how the contrast agent is distributed throughout the domain. However, this phantom is based on a simple geometry that does not include vascular-tissue interactions.
In this contribution, we propose an in silico validation framework for quantitative DCE-MRI acquisition and analysis. The methodology is based on the virtual simulation of DCE-MRI data within a novel digital phantom capturing realistic vasculature and hemodynamics (see Figure 1 for an illustrative overview). Specifically, we construct a 4D digital phantom which contains detailed information on vascular structure, tissue properties, perfusion and time-resolved contrast agent delivery based on an MR microscopy imaging dataset of a murine kidney (Xie et al., 2012a, 2012b). Furthermore, we adapt a virtual simulator (Easley et al., 2019a, 2019b) to produce realistic DCE-MR images, under various, user-defined, acquisition settings including spatial resolution, temporal resolution, and signal-to-noise ratio (SNR). In particular, two very different types of DCE-MRI acquisition protocols are used for testing the performance of the virtual simulator: a standard-of-care acquisition (Protocol A), and an ultra-fast acquisition (Protocol B). The datasets generated by Protocol A are assessed for their ability to generate contrast-enhanced MR images that separate vasculature from surrounding tissue. The datasets generated by Protocol B are assessed for their ability to accurately capture contrast agent pharmacokinetics. This framework is a useful tool for systematically evaluating new contrast-enhanced or perfusion-based MRI acquisition, reconstruction and processing techniques. In particular, DCE-MRI in the kidney has shown promise in assessing both physiological function and renal diseases (Bokacheva et al., 2008) including early detection of both acute kidney injury (Privratsky et al., 2019) and chronic renal failure (Anderlik et al., 2009). Moreover, DCE-MRI has been applied to measure renal perfusion and permeability as diagnostic biomarkers of renal cell carcinoma (Pedrosa et al., 2009; Palmowski et al., 2010; Notohamiprodjo et al., 2010), and to monitor or predict tumor response to treatments (Rosen et al., 2007; Flaherty et al., 2008). Hence, the most direct application of our approach is to assist the development and validation of DCE-MRI techniques in the kidney. Additionally, it is worth noting that this validation framework is designed as a general tool for the evaluation of DCE-MRI techniques on any organ or tissue. Even though the current realization of the digital phantom is based on the geometry of a murine kidney, the technique can be generalized to applications for other organs (see the Discussion section for more details on this important point).
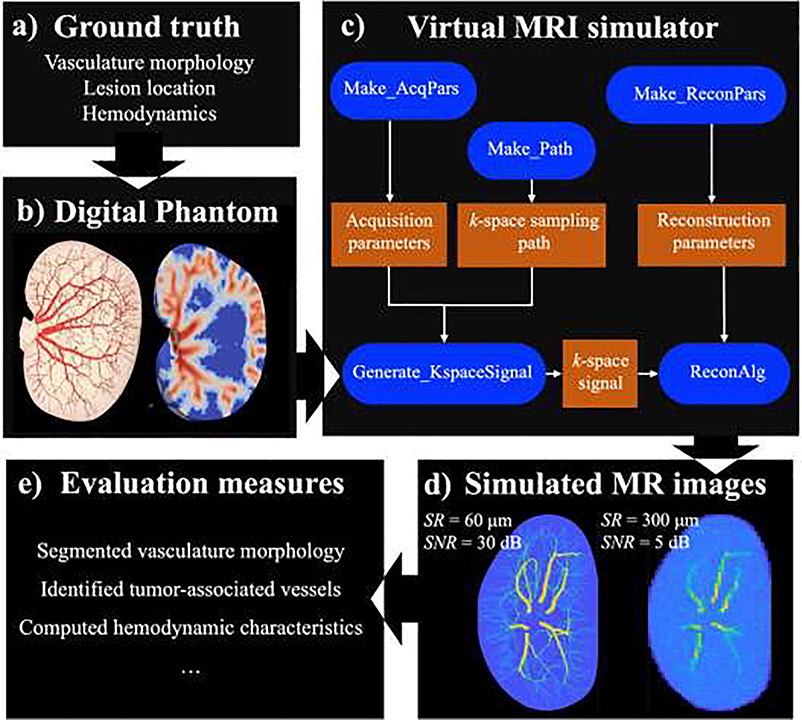
Figure 1:
Overall workflow of the in silico validation. Given the ground truth in panel (a), a digital phantom (panel (b)) is generated to represent realistic vascular geometry and spatiotemporally-resolved contrast agent distributions. The phantom is imported into the virtual MRI simulator in panel (c), producing simulated DCE-MRI data in panel (d) with varying acquisition settings. The image processing and modeling methods that we seek to validate are applied to these simulated images. Finally, error is evaluated by comparing the outputs of quantities of interest to the corresponding ground truth as presented in panel (e).
2. Methods
2.1. Digital phantom
2.1.1. MRI data
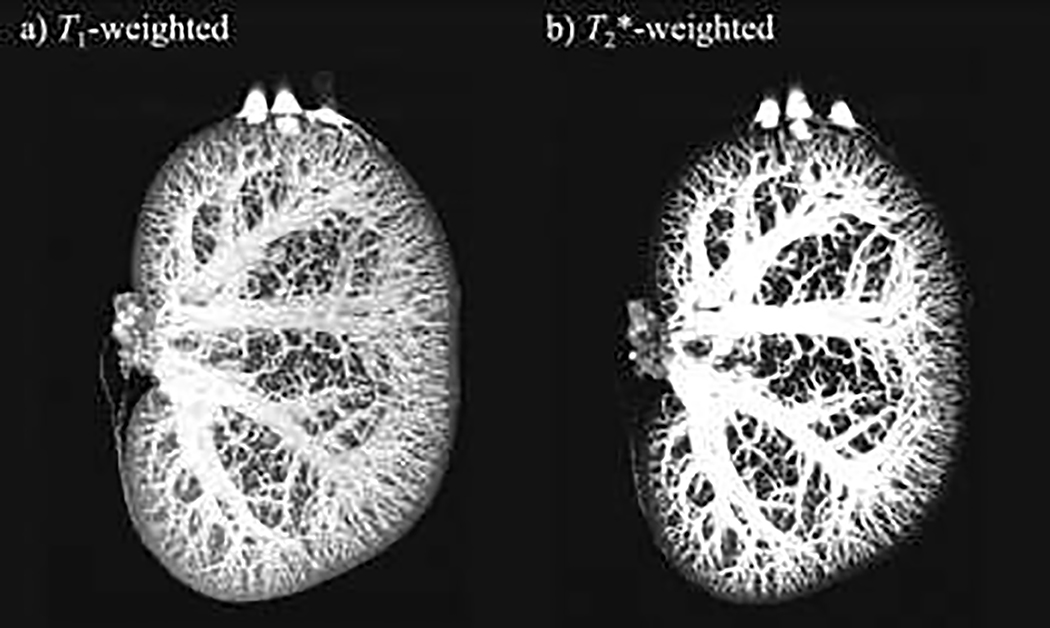
The construction of the digital phantom is based on the ultra-high spatial resolution MRI data of excised rat kidneys published by Xie et al. (2012a). We thank the Duke Center for In Vivo Microscopy for graciously sharing the dataset (Figure 2) (Xie et al., 2012b), which consists of contrast-enhanced T1- and T2*-weighted images of an excised kidney taken from a male Sprague-Dawley rat (52 weeks). Briefly, Xie et al.’s study used conventional trans-cardiac perfusion fixation to preserve the anatomy of vasculature. The rat was anesthetized and perfused with a saline flush followed by injection of 50 mM of the contrast agent Magnevist (Bayer HealthCare Pharmaceuticals, Wayne, NJ) dissolved in 10% formalin. Then the renal artery, renal vein, and ureter were ligated, and the kidney was excited, stored in 2.5 mM Magnevist + 10% formalin for 24h, and then fit in acrylic holder filled with fomblin (Ausimont USA, Inc., Thorofare, NJ) for imaging. All images were acquired on a 9.4 T system (400 MHz vertical bore Oxford superconducting magnet) with a matrix size of 1024 × 1024 × 512 slices over a 32 × 32 × 16 mm3 field of view, yielding an isotropic resolution of 31 μm. The T1-weighted acquisition used a spin echo sequence with TR = 50 ms, TE = 9.3 ms; and the T2*-weighted acquisition used a gradient echo sequence with TR = 50 ms, TE = 6.5 ms, and a flip angle = 60°; detailed acquisition parameters are provided in (Xie et al., 2012a).
Figure 2:
Ultra-high spatial resolution MRI data used to build the digital phantom. Panel (a) and panel (b) present the maximum intensity projection of the coronal T1-weighted and T2*-weighted images, respectively.
2.1.2. Generation of geometric model
2.1.2.1. Kidney tissue segmentation
The mask of the whole kidney tissue was generated by segmenting the T1-weighted image by applying a Matlab (Matlab R2019b, Mathworks Inc, Natwick MA) k-means clustering algorithm, ‘kmeans’, with k = 2. The surface of the segmented tissue volume was then smoothed with a Gaussian filter with a standard deviation of 1. Note that since this segmentation is based on a grayscale feature, the Otsu and k-means methods are equivalent (Liu et al., 2009). In this study, we chose k-means because it provided a nearly identical answer to Otsu’s method with one fewer step (i.e., intensity normalization is not required).
2.1.2.2. Arterial vasculature construction
The vasculature structure is constructed from the T2*-weighted image. First, the intensity of the T2*-weighted image is globally normalized and locally transformed to enhance the vascular regions (Please see Appendix A for more details). To achieve a well-organized connective structure as well as a smooth surface of the vasculature on the enhanced image, we apply a 2D strategy that first obtains centerlines and then generates the 3D mesh and graphic representation of the vasculature (Les et al., 2010). We do this, rather than directly segmenting a 3D vascular mask from the image (Xiong et al., 2011), because direct segmentation usually requires complex modifications to produce volumes with smooth surfaces with a hierarchical structure. Rather, we developed a semi-automatic algorithm to extract the vascular centerlines and radii from the enhanced image; a method adapted from a previously established method for tracking the axillary artery (Li et al., 2011).
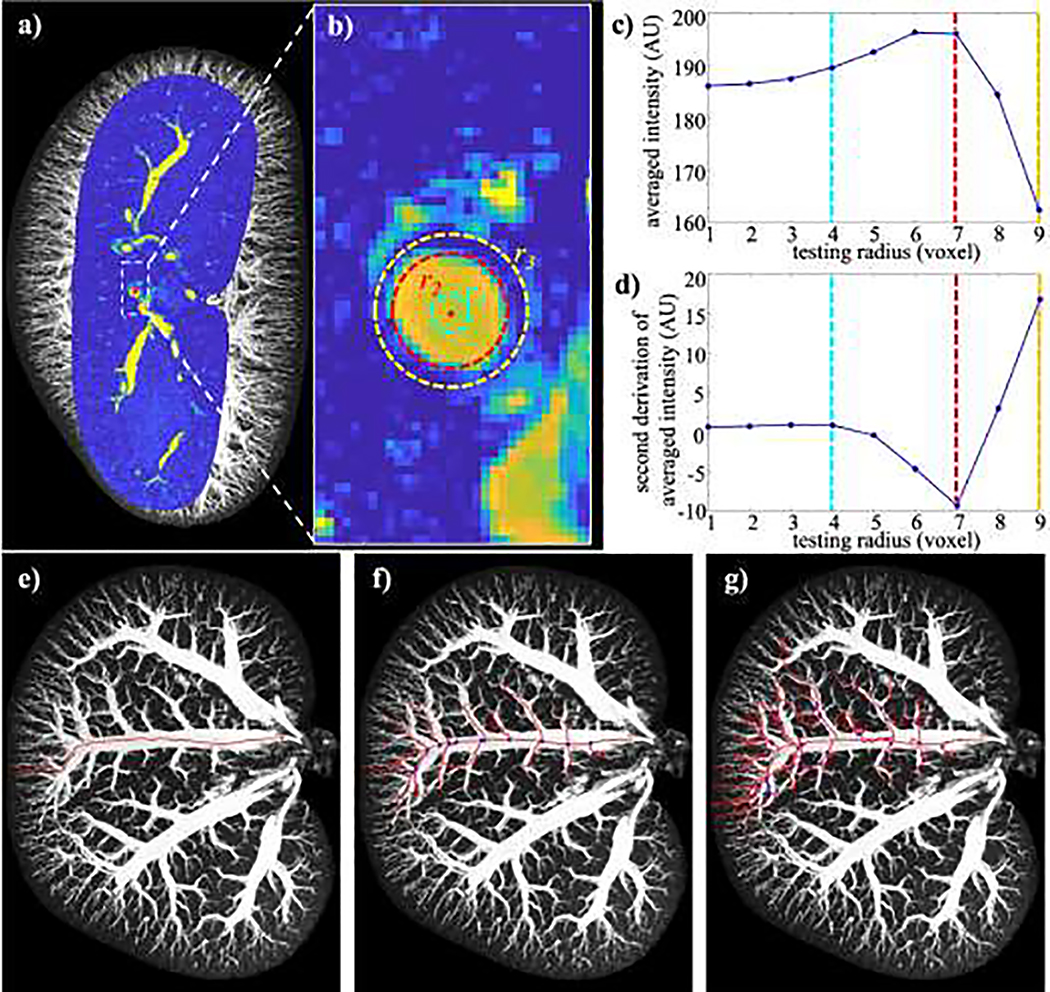
For each arterial vessel tree, the tracking is initialized with a manually identified seed point within the renal artery (i.e., the root of a vascular tree as indicated in the red star of Figure 3 (a)). To determine the local vascular radius R at the seed point, nine spherical averaging kernels, co-centered on this point with kernel radii of r = 1 to 9 voxels, are successively applied on the intensity image (Figure 3 (b)); this provides a list of intensities averaged within the spherical neighborhoods of the seed point (Figure 3 (c)). Computing the second derivative of the averaged intensities over the increasing radii neighborhoods, the radius corresponding to the minimal second derivative is identified as the local vascular radius R (Figure 3 (d)). Next, each voxel adjacent to the seed point is centered by a spherical window with radius R to form a cluster. Among these clusters, we find the one with highest averaged intensity, so that the corresponding adjacent voxel is defined as a new seed point. This tracking procedure goes through the entire vessel to provide the first generation of the vascular tree (Figure 3 (e)). The next step is to manually select branching points along the obtained main trunk, and the tracking algorithm is repeated multiple times to identify subsequent generations of branches (Figure 3 (f)). This process results in a hierarchical, tree-like structure of vasculature (Figure 3 (g)), represented by its centerlines and associated local radii. This semi-automatic construction is performed for each individual arterial tree, at the conclusion of which the set of visible arterial trees are verified by the user.
Figure 3:
Determination of centerlines and local radii of vessels. Panel (a) displays a seed point (red star within dashed box) selected during the vessel tracking procedure on a sagittal slice of a T2*-weighted image (pseudo colored), with the maximum intensity projection of the entire T2* image as the background (grayscale). Panel (b) presents a zoom-in view of the point and cross-section of the vessel within which this point is located. Three examples of spherical kernels centering this seed point are also presented, with radii of r1 = 4 voxels (cyan), r2 = 7 voxels (red), and r3 = 9 voxels (yellow). Panels (c) and (d) plot the averaged intensity within spherical kernels and their second derivative over the kernels’ radii, respectively, where the values at r1 (cyan), r2 (red), and r3 (yellow) are indicated. With the lowest second derivative of averaged intensity in panel (d), the local radius is determined as R = r2 = 7 voxels, which matches the visualization in panel (b). For the centerline determination, on the maximum intensity projection of the coronal T2*-weighted image, panel (e) shows the main trunk of an arterial tree (red line) tracked from the initial root point (red star). Along this major trunk, multiple seed points (blue stars) are manually set for tracking the branches (red lines), as presented in panel (f). The procedure of setting seed points (blue stars) and tracking are iterated until all visible branches (red lines) of one arterial tree are obtained as displayed in panel (g).
2.1.3. Generation of perfusion and delivery model
2.1.3.1. Hemodynamic fields
Given the constructed tissue-vascular geometry, a 1D – 3D coupled computational fluid dynamics model (Wu et al., 2020) is adapted to compute the steady-state, hemodynamic flow fields in the virtual kidney. The numerical domain consists of the pseudo-1D arterial vasculature (Λ) and the 3D extravascular tissue (Ωt). Within the vascular domain, blood flow is governed by Poiseuille’s law,
| (1) |
where μ is the viscosity of blood and l indicates location along the vascular network, and R, pv, and Qv are the local vascular radius, blood pressure, and blood flow rate, respectively. The 3D interstitial flow in the tissue domain is governed by Darcy’s law,
| (2) |
where x indicates location in the extravascular interstitial space, and pt, ut, and κ are the local interstitial pressure, flow velocity, and tissue hydraulic conductivity, respectively. The extraction of fluid from vessel to tissue is modeled by Starling’s law,
| (3) |
where qe, pt,ev, and Lp are the local fluid extraction rate, exterior surface pressure, and vascular hydraulic conductivity along the vascular network, respectively.
Parameters quantifying the tissue properties are assigned as constant values, based on experimental measurements of kidney reported in the literature. We set the vascular hydraulic conductivity to be Lp = 1.5 × 10−8 g−1 cm2 s (Renkin et al., 1977). The tissue hydraulic conductivity is simply scaled from the literature ADC value of 2.69 × 10−3 mm2/s (Yang et al., 2004), yielding κ = 2.69× 10−9 g−1 cm3 s. (Detailed justifications for the parameter assignments are provided in Appendix B.)
For the boundary conditions, blood pressure (Winston et al., 1985) is given at the inlets of arterial vasculature as pv,inlet = 105 mmHg. Similarly, the capillary bed pressure (Shore, 2000) is given as the outlet at the terminal ends of the vasculature, pv,outlet = 15 mmHg. The boundary of the tissue domain is considered as two components, the kidney surface and the exterior surface of the vasculature. The boundary condition on the vascular surface is naturally given by Starling’s law, while the Dirichlet condition of constant boundary pressure is predetermined by the literature value of interstitial hydrostatic pressure appropriate for kidney (Khraibi et al., 1989), pt,contour = 5 mmHg.
2.1.3.2. Bolus propagation through vasculature
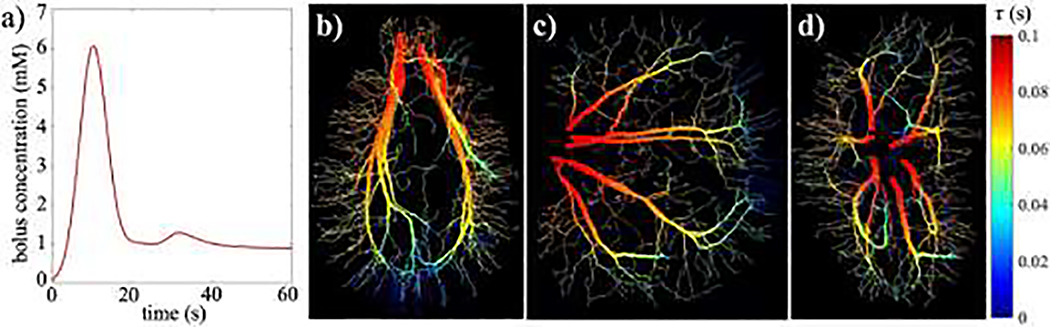
Based on the computed hemodynamics, the pharmacokinetics of the contrast agent can be determined. We assume the bolus of contrast agent arrives at the kidney from the renal artery, subsequently propagating through the tree-like vasculature, and then extracted into the tissue via both advection and diffusion. As the vascular structure is hierarchical, and can therefore be represented by a directed tree, every vessel segment in the vasculature has a unique input. In particular, the blood flow direction and upstream-downstream relationship between vessel segments can be easily identified from the steady-state flow solution. That is, when the bolus is propagating through the vasculature no dispersion of bolus due to mixture of multiple inputs will occur. (We note that we do not consider collisions between tracer particles with vessel walls.) The plasma concentration function is delayed, though, but without changing the shape as it propagates. Thus, we assign an experimentally-derived initial plasma bolus function (Parker et al., 2006), Cp,0, at the vascular inlets (Figure 4 (a)), which is a mixture of two Gaussians plus an exponential modulated by a sigmoid function,
| (4) |
where α and β are the amplitude and decay constants, respectively, of the exponential, and s and τ are the width and center of the sigmoid, respectively, and An, τn, and σn are scaling constants, centers, and widths of the nth Gaussian functions, respectively. The first term on the right-hand side of Eq. (4) indicates the long-term enhancement due to tracer delivery, while the last two terms represent the first and second peaks of the bolus function due to the initial arrival of the bolus and re-circulation, respectively. Here we empirically set the parameter values, α = 1.05, β = 168.5, s = 3.81 × 104, τ = 4.83 × 10−4, A1 = 8.09 × 10−4, σ1 =5.63 × 10−4, τ1 = 1.71 × 10−4, A2 = 3.30 × 10−4, σ2 =1.32 × 10−4, and τ2 = 3.65 × 10−4. The procedure results in an input function similar to the AIF observed in (Li et al., 2011). The local plasma concentration of contrast agent is then given as
| (5) |
where Cp(t, l) represents the plasma tracer concentration at time t (with the time of injection as 0) and vascular location l. BAT(l) is the bolus arrival time at this vascular location, which can be obtained from the steady-state solution (visualized in Figure 4 (b) – (d)).
Figure 4:
Initial bolus profile and arrival-time throughout vasculature. Panel (a) shows the initial plasma bolus function given as the input. Panels (b), (c), and (d) present the maximum intensity projections of the calculated bolus-arrival time (BAT) along the vasculature in the axial, coronal, and sagittal orientations, respectively. The color-coding coding indicates time and therefore implies the direction of blood flow.
2.1.3.3. Contrast agent delivery through tissue
The delivery of contrast agent through tissue is further modeled by an advection-diffusion equation with a surface source, J:
| (6) |
where Ct = Ct(t, x) is the tracer concentration in tissue at time t and location x, ut is the interstitial flow velocity (obtained from the steady-state solution), D is the diffusivity of contrast agent in the interstitial tissue which can be directly estimated from the ADC value (i.e., D = 2.69 × 10−5 cm2/s). The source term J, defined on the vascular boundary, represents the extraction of contrast agent from vessel to tissue, which is a combination of advection by the bulk flow, JA, and diffusion down the concentration gradient, JD, (Yuan et al., 2010; Huxley et al., 1987; Yuan et al., 1993):
| (7) |
where P [cm/s] is the apparent permeability of renal vessels to the tracer under investigation, which is a combination of its vascular diffusive permeability, Pd, and its extraction rate, qe (1 – σ) = Lp (1 – σ) (pv – pt). Here qe is the bulk fluid extraction rate, calculated from the steady-state flow solution as in Eq. (3), and σ is the solute reflection coefficient so that (1 – σ) is the filtration rate of tracer through the vascular walls. (Detailed justification of the values assigned to Pd and σ can be found in Appendix B.)
The time-dependent, advection-diffusion equation is first temporally discretized and then solved spatially using the finite element method and evolved in time with the Crank-Nicolson (CN) method. Specifically, the spatial discretization is performed with tetrahedral elements and uses second-order, continuous, piecewise polynomials for the test and trial basis functions, which is implemented using the Python FEniCS library (Logg et al., 2012). The time dimension is divided into NT intervals, with the time vertices t = 0, Δt, 2Δt, …, nΔt, …, NT Δt. For the nth time step, t ∈ [(n – 1) Δt, nΔt], the weak form is
| (8) |
where , ,
The model is solved to obtain the contrast agent distribution for the first minute after injection, with the time step width of Δt = 0.01s, a zero initial condition of Ct(0, x) = 0, and a zero-flux condition on the kidney surface boundary (i.e., ∂Ωt/∂Ωv).
We note that the CN method is chosen as our problem is diffusion-dominated and it is unconditionally stable with regard to the time step. Specifically, the mesh is well refined to ensure the Peclet number is small almost everywhere; the median (range) of the Peclet number across the computational domain is 0.32 (0.27 – 2.09) × 10−2 << 1, which means the diffusive effect dominates over the advective effect in the interstitial distribution of contrast agent. Hence, the general concern of oscillations caused by solving advection-dominated flow with the CN method is not observed in this study (refer to Figure C.1 in Appendix C for illustration). We recognize that in situations where advection is significant, stabilization techniques, such as the streamline-upwind / Petrov-Galerkin (SUPG) method (Brooks et al., 1982), the variational multiscale (VMS) method (Hughes et al., 1998), and the Galerkin / Least-squares method (Hughes et al., 1989) can be used to suppress the oscillation (Franca et al., 1992). Additionally, local refinement of mesh at areas with high advection also helps to increase the stability.
2.1.4. Generation of voxel-based dynamic digital phantom
A voxel-based, temporally resolved digital phantom can be obtained by combining the bolus propagation solved in the pseudo-1D vascular network, Cp(t, l), and contrast agent distribution solved in the 3D extravascular tissue, Ct(t, x). To do so, let the index and coordinate of voxels in the image grid be i and xi, respectively. The tissue concentration solution is interpolated from the mesh elements to the image grid, producing Ct(t, xi). The image grid coordinates are defined as xi = xi(l) to couple the 3D coordinates xi with the location along the vessel, l. Then the vascular solution can be mapped to the vascular region in the image, Cp(t, xi). Thus, the concentration map at time t is given as follows,
| (9) |
where δ is the delta function defined as following,
| (10) |
| (11) |
Finally, the dynamic digital phantom can be presented as a 4D matrix, O, with a matrix size of Nx × Ny × Nz × (NT + 1), where first three dimensions are spatial and the fourth is temporal. In particular, we choose the spatial matrix size by achieving an isotropic voxel size of 30 × 30 × 30 μm3. NT can be determined by dividing the total simulation time, T = 60 s, by the time step width used for solving the contrast agent delivery, Δt = 0.01 s (i.e., NT = 6000; of course, the value of NT can simply be reduced by sampling the time points every few frames).
2.2. Virtual simulator
The virtual MRI simulator used in this study was adapted from the work by the MRI Research Center at The University of Chicago (Easley et al., 2019a, 2019b). The demonstration of this simulator is available on GitHub (https://github.com/tyo8/ECA_Demo). Here we present a brief description of the virtual simulator and its adaptation to the present effort.
2.2.1. Overall structure of the simulator software
There are five major components of the simulator software as developed in Matlab and illustrated in Figure 1 (c). The functions ‘Make_AcqPars’ and ‘Make_ReconPars’ generate the data structures which store the acquisition and reconstruction parameters, AcqPars and ReconPars, respectively. Specifically, AcqPars contains the values for the field-of-view (FOV), repetition time (TR), echo time (TE), flip angle (FA), matrix acquisition size (nx × ny × nz), acquisition temporal resolution, scan number (NS), and k-space SNR. ReconPars contains the reconstruction temporal resolution, as well as parameters required for the optimization-based reconstruction algorithm, which will be described more fully below in section 2.2.2. ‘Make_Path’ generates the sampling path through k-space during scanning, T, which is an nx × ny × nz × NS array specifying the time that each point in k-space is to be sampled. ‘Generate_KspaceSignal’ takes the dynamic digital phantom (O), AcqPars, and T as inputs and produces the sampled k-space signal of DCE-MRI, Y, which is an nx × ny × nz × NS array of complex numbers. Finally, Y is imported into ‘ReconAlg’ together with ReconPars, generating the reconstructed image,.
2.2.2. k-space sampling
One important innovation of the virtual simulator is that it defines the sampling path to specify the sampling time of each point in k-space, rather than assuming all signals of one scan are obtained simultaneously at the beginning or end of the acquisition. This addresses the fact that during signal acquisition, the status of the imaged object (the digital phantom in our situation) might change; a feature that is essential for realistically mimicking the DCE-MRI experiment.
In addition to the matrix size and scan number, T depends on the sampling strategy (standard Cartesian, inter-aliased Cartesian, radial, spiral, etc. (Bernstein et al., 2004)). Here we choose the simplest, standard Cartesian sampling of k-space, with the x-direction being the readout, and the y- and z-directions being the phase-encoding directions (Bernstein et al., 2004). Thus, T is given as following,
| (12) |
with ,
where Κ represents the spatial-frequency grid of k-space, which has the same size as the acquisition matrix. TE represents the time spent to read out each line in the x-direction, γ as the gyromagnetic ratio, and TDP represents the de-phasing time.
Given the generated T and the digital phantom O, a k-space signal with no noise can be generated, Y(0). Recall that the digital phantom is stored as a 4D array of size Nx × Ny × Nz × (NT + 1). As the acquisition spatial resolution can be set lower than the resolution of original phantom, the acquisition matrix size can be smaller than that of the digital phantom; i.e., nx ≤ Nx, ny ≤ Ny, nz ≤ Nz. Thus, if the matrix sizes are different, the phantom is first down-sampled to the spatial dimensions by cubic interpolation,
| (13) |
where maps the digital phantom from the original spatial grid, Ω = {1, …, Nx} × {1, …, Ny} × {1, …, Nz}, to the imaging grid, Ω’ = {1, …, nx} × {1, …, ny} × {1, …, nz}, which is done for each time frame of phantom, n = 0, …, NT. Note that this process of directly down-sampling the imaging object is designed to circumvent possible artifacts introduced by down-sampling the k-space data (we revisit this point in the Discussion section). The down-sampled object, O’, gives the concentration of contrast agent over time for each voxel. The signal intensity equation for the pulse sequence under investigation (here, the spoiled gradient echo) is then applied to convert the concentration of contrast agent to the signal intensity at each voxel location. Thus, the whole spatial signal X is given as,
| (14) |
with
| (15) |
| (16) |
where TR and FA are given as acquisition settings in AcqPars. S0 is a constant describing proton density and scanner gain settings, which can be set to one without loss of generality. [CA](v) refers to the concentration of contrast agent at each voxel, v, in the 4D digital phantom. r1 is the T1-relaxivity of studied contrast agent (Magnevist®, Gd-DTPA) and assigned a value of 3.8 mM−1s−1 appropriate for 3 T (Shen et al., 2015). T1,0 is the native T1 value of tissue, which is assigned as 1200 ms for the entire kidney tissue (Stanisz et al., 2005) and zero for empty regions. Note also that we have taken TE << T2* in Eq. (14).
Since there are (NT + 1) frames in the digital phantom, the status of the phantom will be updated NT times through the entire acquisition. Every time the digital phantom is updated, some points in k-space will be sampled. Within each time interval of updating, for example the nth interval, [tn-1, tn] = [(n – 1)Δt, nΔt], we define Yn-1 and Yn to be the Fourier transforms of the true spatial signal from the phantom before and after the update, respectively:
| (17) |
| (18) |
where refers to the Fourier transform. O’ (Ω’, n – 1) is the frame of the down-sampled digital phantom at time tn-1, similarly for O’ (Ω’, n). We can then identify points in k-space that are sampled within this time interval based on T,
| (19) |
where Pn is the set of identified points. Then for each point p = (kx, ky, kz, i) ∈ Pn, we can find a weight c ∈ [0, 1] such that,
| (20) |
and the clean k-space signal at this point can be generated by linear interpolation,
| (21) |
This procedure is conducted for all n ∈ {1, …, NT}, to produce the Y(0) of the entire scan. The last step is to add random Gaussian noise based on the SNR value from AcqPars, resulting in the final k-space signal,
| (22) |
where represents the matrix of applied Gaussian noise. In particular, we use the MATLAB-built-in function, ‘awng’ (The MathWork, Inc., 2019), to add the appropriate level of white noise to obtain the desired SNR.
2.2.3. Optimization-based image reconstruction
Another innovation of the simulator is the optimization-based reconstruction algorithm, which treats the reconstruction problem as optimizing the signal smoothness over time. This algorithm allows reconstructing images at a higher temporal resolution than the nominal acquisition resolution via partial k-space sampling. Specifically, the acquisition lasts for one minute after bolus injection during which NS post-contrast frames are collected; that is, the acquisition temporal resolution is 60/NS seconds per frame. To achieve a reconstructed image with the same or higher temporal resolution (i.e., NR frames with NR ≥ NS), the sampled acquisition matrix of size nx × ny × nz × NS is rearranged to a new matrix of size nx × ny × nz × NR, based on the information within the sampling path. For each point in T, p = (kx, ky, kz, i), by setting the time of sampling to be t = T(p) and the total scanning time be T, we can find the corresponding j ∈ {1, …, NR} so that (j – 1)T/NR < t ≤ jT/NR. Then the rearranged signal matrix can be written as,
| (23) |
With this procedure, values at some parts of Y(R) are assigned, while the others are left as unmeasured. We define the measured domain as Ψ,
| (24) |
where Κj presents the set of measured points on the jth reconstructing frame.
The reconstruction problem is solved by maximizing the smoothness of voxel-wise reconstructed signals over time. The optimization problem will be briefly described below (a more detailed derivative of the objective function can be found in the Appendix D.) For notational convenience, we reshape the 3D spatial grid of the image into a 1D index (i.e., storing the reconstructed signal in a 2D matrix), , of size (nx × ny × nz) × NR. The optimization procedure is given as,
| (25) |
where the < > denotes the inner product, and the term is the temporal-smoothness penalty; the smoother the time courses of the reconstructed signal are, the smaller the penalty will be. PS can be any positive definite matrix of size NR × NR that measures the smoothness penalty of the signal intensity time courses, which is defined as the l2-norm of time courses’ discrete second derivative. W is a diagonal, weighting matrix of size (nx × ny × nz) × (nx × ny × nz), W = diag(w1, w2, …, wi, …), where the wi indicate the weight of smoothness penalty acting on voxel i. Larger wi values correspond to enforcing the time course of ith voxel to be smoother (i.e., smaller l2-norm of the discrete second derivative). This optimization problem is then converted to a linear system (see Appendix D) and solved via the preconditioned conjugated gradient descent method (Barrett et al., 1994), where the convergence parameters are given in ReconPars.
Exact implementation of the reconstruction algorithm involves solving a large linear system, which is very memory- and time-intensive. More specifically, the major step of reconstruction is to solve a linear equation Ax = b, where the x is a complex vector of size (nx × ny × nz × NR) × 1. (See Appendix D for numerical derivation.) Thus, for the present project, we design a (practical) scheme to trade time for memory, in which the temporal dimension is divided into multiple intervals and solved individually. Final reconstructed images are obtained by connecting the results from each interval. (Details of this implementation can be found in Appendix E.)
2.3. Data generation and assessment
To assess the performance of DCE-MRI generation using the digital phantom and simulator, two very different DCE-MRI acquisition protocols are used: a standard-of-care acquisition (Protocol A), and an ultra-fast acquisition (Protocol B). Here we introduce the parameters defined for each protocol, and the associated measurements used to assess the generated images.
2.3.1. Protocol A
For Protocol A we set TR / TE / FA = 5 ms / 2.5 ms / 10°, and assume a constant native T1,0 = 1200 ms for kidney tissue to yield contrast-enhance (CE-) MR images before and after injection of the contrast agent, with a constant temporal resolution of 60 s; such data makes the morphology of the enhancing structures clearly visible. Multiple datasets for Protocol A are generated by varying the acquisition parameters over a reasonable range of values. Specifically, data with different spatial resolutions (SRA, with the subscript indicating Protocol A) are constructed with values of 30, 60, 150, and 300 μm, and signal-to-noise ratios (SNRA) of 5, 15, and 75 dB. These datasets yield a range of contrast-to-noise ratios (CNR) which affects the ability to separate the vasculature from the background tissue. The CNR is calculated for each voxel in vascular region as,
| (26) |
where Spost and Spre are the post- and pre-contrast signal intensities of the voxel, respectively, and Nnv is the standard deviation of the subtracted (i.e., post-contrast minus pre-contrast) signal intensities in the non-vessel ROI.
2.3.2. Protocol B
For Protocol B we set TR / TE / FA = 3.2 ms / 1.6 ms / 10°, and assume a constant native T1,0 = 1200 ms for kidney tissue to yield ultra-fast, DCE-MR images, which consists of five frames of pre-contrast images, followed by 6 – 60 frames during the first minute after contrast injection, with the number of frames depending on the temporal resolution. Multiple datasets for Protocol B are generated by varying the acquisition parameters over a reasonable range of values. Specifically, data are constructed with different spatial resolutions (SRB, where the subscript indicates Protocol B) values of 60, 150, and 300 μm, temporal resolutions (TRB) of 1, 4, 7, and 10 s, and signal-to-noise ratios (SNRB) of 5, 15, and 75 dB. These datasets yield a range of signal-enhancement ratio (SER) which affects the ability of DCE-MRI to assess tracer pharmacokinetics (Sorace et al., 2018). The SER is calculated for each voxel as,
| (27) |
where S1 is the peak signal intensity of the voxel-wise time course, S0 is the average of pre-contrast signal intensities, and S2 is the signal intensity at the last time point of the acquisition. Additionally, the SER measured along vessel centerlines can be compared to the ground-truth of plasma SER to obtaining a percent error of the SER estimate:
| (28) |
where the ground-truth of plasma SER (SERGT) equals 2.22, which is calculated based on the input bolus profile, Eq. (4) and the concentration-to-signal conversion, Eqs. (14 – 16).
3. Results
We have made the digital phantom described in this contribution into an open-source toolkit, R2D2 (Wu, 2020). (For an introduction to the toolkit, please refers to the Appendix F.)
3.1. Generated geometric model
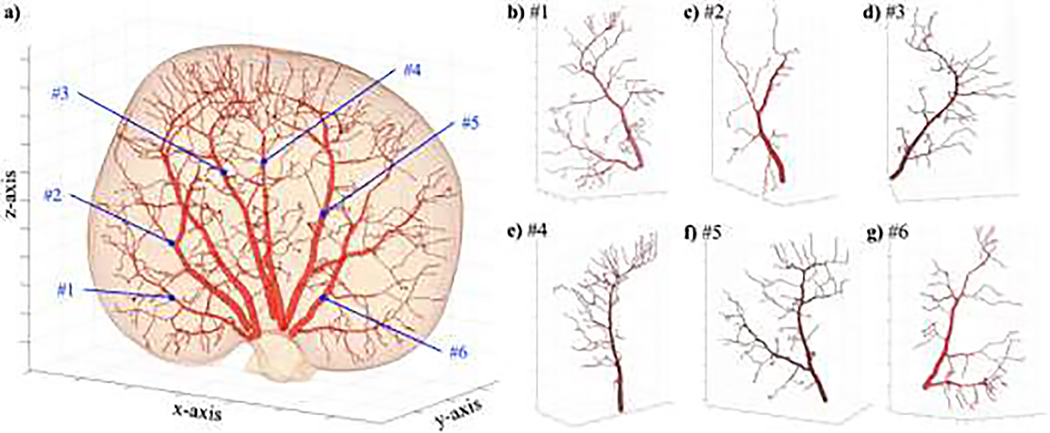
As shown in Figure 5, a total of six arterial vasculature trees are constructed from the kidney to provide the vascular geometry of the digital phantom. Panel (a) presents the entire vascular tree and kidney. Panels (b) - (g) show six individually reconstructed renal arterial trees. The major branches of the renal arteries and several generations of further arterioles are completely constructed based on the MRI data, thereby preserving realistic a geometry.
Figure 5:
Geometric model of the digital phantom. Panel (a) presents the 3D rendering of the vasculature, with the whole kidney as a semi-translucent volume. Panels (b) – (g) shows the six individual renal arterial trees which correspond to the labels (blue) in the panel (a).
3.2. Generated hemodynamic fields
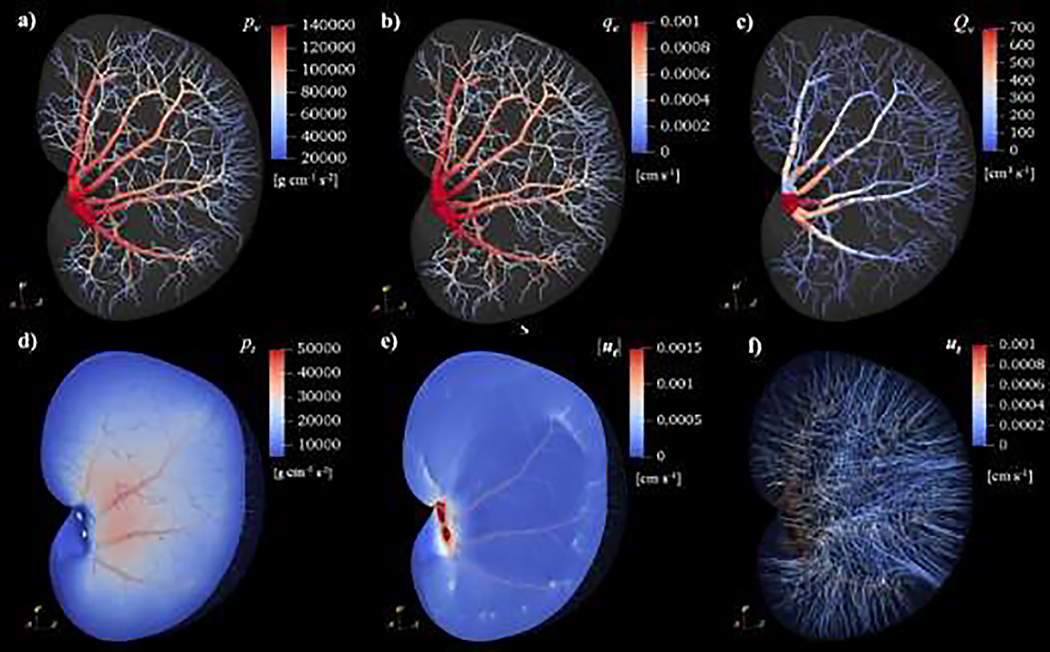
The calculated blood and interstitial flow on the digital phantom are presented in Figure 6. The solution within the vascular domain provides the blood pressure (pv), fluid extraction rate (qe), and blood flow rate (Qv) as presented in panels (a) – (c), respectively. The blood pressure gradually decreases from the renal arterial input to the terminal ends of arterioles. A similar phenomenon is observed for the vascular fluid extraction rate, which falls from 1 × 10−3 cm/s to approximately 1 × 10−4 cm/s, because the pressure difference between the two sides of the vessel wall decreases along the blood flow direction. Moreover, the blood flow rate reveals a large value (Qv ~ 700 cm3/s) at the source of the arterial input, then rapidly decreases from the first branch, and remains at approximately 10 cm3/s for most of the terminal arterioles. With these calculated blood flow characteristics, we can further compute the bolus-arrival time through the vasculature, with the time of the bolus arriving at the inlets of the renal arteries considered as the initial time point (see Figure 4 for visualization of bolus arrival time).
Figure 6:
Generated steady-state pressure and flow fields. Panels (a) – (c) shows the blood pressure (pv), fluid extraction rate (qe), and blood flow rate along vasculature (Qv), respectively, which are mapped from the pseudo-1D solution to the 3D mesh for visualization. Panels (d) – (f) present the interstitial pressure (pt), magnitude and streamlines of interstitial flow velocity (ut) in the extravascular space of the kidney tissue, respectively. The decreasing of pv, qe, and Qv from the vascular inlets to the terminals can be seen in panels (a) – (c). The pt tends to accumulate near the middle of kidney (panel (d)). Interstitial flow directed from a vascular source to extravascular tissue (panel (f)) causes a large magnitude of ut close to the vascular surface (panel (e)).
The interstitial pressure (pt) and flow velocity (ut) fields are solved within the interstitial space. Fluid leaks out of the arterial vessels (Figure 6 (f)) and causes high interstitial flow velocity close to the vascular surface. According to the distribution of arterioles, the highest magnitudes of flow velocity are observed at the renal cortex and areas close to the major arteries, as shown in Figure 6 (e). Moreover, the interstitial pressure accumulates within the middle of the kidney, as visualized in Figure 6 (d). Overall, the calculation provides spatially-resolved estimates of arterial perfusion on the pseudo-1D vascular network, and interstitial transport on the 3D tissue mesh.
3.3. Dynamics of contrast agent delivery
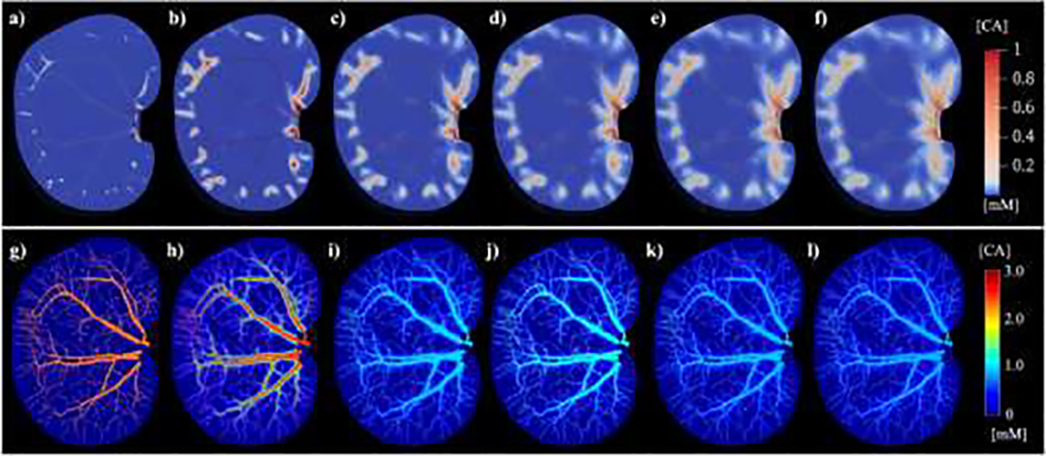
Based on the computed steady-state flow, the delivery of contrast agent over time is then determined. The numerical solution of contrast agent distribution is stored as two components: 1) a list saving point-wise plasma concentration time courses along the vasculature, and 2) numerical mesh-based solutions saving the tissue concentration at every time point. For both the vascular and tissue solution, the time step is 0.01s over a total period of 60 s after injection of the contrast agent bolus. As shown in Figure 7, the tracer rapidly propagates through the vasculature, and is then delivered through the whole kidney tissue over time. After the arrival of the bolus through the vasculature (the first 20 s of computation, see Figure 7 (a) – (b)), extracted contrast agent is first accumulated in the area immediately adjacent to the vasculature (Figure 7 (b) – (c)), then gradually distributed to a wider area in the tissue (Figure 7 (d) – (f)).
Figure 7:
Dynamics of tissue contrast agent distributions and the final digital phantom. Panels (a) – (f) show the spatial distribution of contrast agent concentration in the tissue domain (coronal view) at 5 s, 15 s, 25 s, 35 s, 45 s, and 55 s after the initial delivery of the bolus, respectively. To highlight the distribution within the vasculature, panels (g) – (l) show the corresponding maximum intensity projections of voxel-based contrast agent concentration at 5 s, 15 s, 25 s, 35 s, 45 s, and 55 s after the initial delivery of the bolus, respectively.
3.4. Voxel-based digital phantom
The computational description of the bolus propagation through the vasculature and tissue is voxelized within the digital phantom and stored in a 4D matrix (Figure 7). Though the original T1- and T2*-weighted images have a matrix size of 1024 × 1024 × 512, to save memory we have truncated the areas near the edges of the images which are empty. Additionally, the time dimension is inter-aliased to achieve a temporal resolution of 250 ms (i.e., NT = 240). These manipulations yield a digital phantom of matrix size 706 × 576 × 360 × 240.
3.5. Simulated DCE-MR images
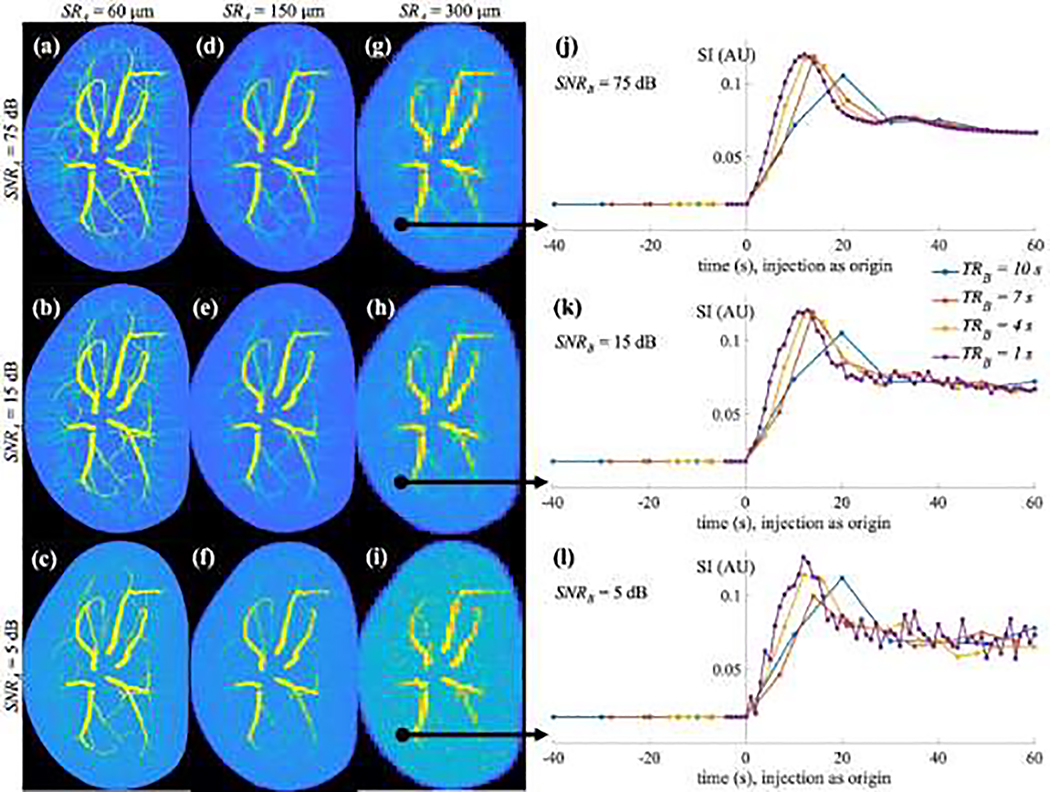
For Protocol A, as shown in Figure 8 (a – i), increasing either the spatial resolution or SNR results in a significant increase of CNR. For example, as the last column of Table 1 indicates, for a fixed SNRA of 75 dB, increasing the spatial resolution (SRA) from 300 μm to 30 μm leads to an increase of median CNR values from 25.00 to 77.30, which are significantly different on a pair-wise basis (Wilcoxon test: P < 0.001). Moreover, as seen in the last row of Table 1, for a fixed SRA of 30 μm, increasing the SNRA from 5 dB to 75 dB leads to an increase of median CNR values from 15.53 to 77.30, which are significantly different on a pair-wise basis (Wilcoxon test: P < 0.001).
Figure 8:
Simulated MR images and signals obtained with various combinations of acquisition parameters. Panels (a) – (c) are the maximum intensity projections (MIPs) of the subtracted images acquitted by the standard protocol with an SRA of 6 μm and SNRA of 75, 15, and 5 dB, respectively. Similarly, panels (d) – (f) are the MIPs of the simulated images with an SRA of 150 μm and SNRA of 75, 15, and 5 dB, respectively. Panels (g) – (i) are the MIPs of the simulated images with an SRA of 300 μm and SNRA of 75, 15, and 5 dB, respectively. From the ultra-fast datasets with the SRB of 300 μm, one arterial voxel is picked to show simulated time courses. Specifically, panels (j) – (l) show the time courses obtained with varying temporal resolutions, TRB = 1 s (purple curves), 4 s (yellow curves), 7 s (orange curves), 10 s (blue curves), with the SNRB of 5, 15, and 75 dB, respectively. The y-axis represents the signal intensity and x-axis indicate the time, with the injection time as zero.
Table 1.
Vascular CNRs calculated from all datasets of Protocol A
| SRA (μm)╲CNR median (interquartile range)╲SNRA (dB) | 5 | 15 | 75 |
|---|---|---|---|
| 300 | 6.40 (3.99 – 9.14) | 16.11 (10.53 – 23.72) | 25.00 (16.65 – 37.15) |
| 150 | 7.25 (4.51 – 12.20) | 17.77 (11.51 – 31.30) | 26.62 (17.65 – 47.08) |
| 60 | 8.09 (4.79 – 14.15) | 21.00 (13.17 – 39.13) | 40.78 (25.69 – 76.68) |
| 30 | 15.53 (14.04 – 17.15) | 40.77 (38.31 – 44.30) | 77.30 (73.65 – 83.04) |
For Protocol B, as shown in Figure 8 (j – l), fixing SNRB and SRB while increasing the temporal resolution results in a significant decrease of PESER. For example, comparing the rows in Table 2 with SNRB of 75 dB and SRB of 150 μm, increasing the temporal resolution (TRB) from 10 s to 1 s leads to a decrease of median PESER values from 21.53 % to 2.83 %, which are significantly different on a pair-wise basis (Wilcoxon test: P < 0.05). Moreover, when TRB ≤ 7 s, a significant decrease in PESER is observed with increasing spatial resolution or SNR. For example, comparing the rows in Table 2 with SRB of 150 μm and TRB of 1 s, increasing the SNRB from 5 dB to 75 dB leads to a decrease of median PESER values from 10.69 % to 2.83 %, which are significantly different on a pair-wise basis (Wilcoxon test: P < 0.001). When the temporal resolution is low (TRB = 10 s), the effects of SNRB or SRB on PESER are not statistically significant; but a clear trend of the interquartile range narrowing can be seen as the SNRB increases.
Table 2.
Vessel centerline SER and PESER calculated from all datasets of Protocol B
| Datasets | Measures | |||
|---|---|---|---|---|
|
SRB μm |
TRB (s) |
SNRB (dB) |
SER median (interquartile range) |
PESER median (interquartile range) |
| 300 | 10 | 5 | 1.75 (1.55 – 1.93) | 21.00 % (13.49 % – 30.38 %) |
| 15 | 1.72 (1.65 – 1.79) | 22.26 % (19.15 % – 25.61 %) | ||
| 75 | 1.75 (1.72 – 1.78) | 21.07 % (19.77 % – 22.60 %) | ||
| 7 | 5 | 1.89 (1.68 – 2.14) | 16.69 % (8.60 % – 24.39 %) | |
| 15 | 1.88 (1.74 – 2.04) | 15.28 % (7.84 % – 21.37 %) | ||
| 75 | 1.92 (1.79 – 2.03) | 13.41 % (8.46 % – 19.22 %) | ||
| 4 | 5 | 2.04 (1.83 – 2.26) | 12.32 % (6.14 % – 19.67 %) | |
| 15 | 1.92 (1.80 – 2.07) | 13.27 % (6.61 % – 18.94 %) | ||
| 75 | 1.93 (1.83 – 2.04) | 13.05 % (7.86 % – 17.45 %) | ||
| 1 | 5 | 2.15 (1.91 – 2.39) | 11.91 % (5.78 % – 18.54 %) | |
| 15 | 2.01(1.86 – 2.14) | 9.38 % (4.12 % – 16.36 %) | ||
| 75 | 2.01 (1.91 – 2.10) | 9.60 % (5.34 % – 14.00 %) | ||
| 150 | 10 | 5 | 1.75 (1.58 – 2.00) | 21.72 % (11.90 % – 29.23 %) |
| 15 | 1.75 (1.68 – 1.83) | 21.11 % (17.35 % – 24.36 %) | ||
| 75 | 1.74 (1.70 – 1.79) | 21.53 % (19.40 % – 23.21 %) | ||
| 7 | 5 | 2.05 (1.84 – 2.31) | 12.08 % (5.92 % – 21.19 %) | |
| 15 | 2.08 (1.94 – 2.19) | 6.84 % (3.06 % – 12.72 %) | ||
| 75 | 2.10 (1.98 – 2.19) | 5.28 % (1.38 % – 10.89 %) | ||
| 4 | 5 | 2.12 (1.91 – 2.38) | 10.81 % (5.36 % – 20.22 %) | |
| 15 | 2.08 (1.95 – 2.20) | 6.53 % (2.73 % – 12.13 %) | ||
| 75 | 2.12 (1.98 – 2.21) | 4.61 % (0.91 % – 10.76 %) | ||
| 1 | 5 | 2.32 (2.08 – 2.54) | 10.69 % (5.13 % – 18.23 %) | |
| 15 | 2.17 (2.05 – 2.27) | 4.84 % (2.22 % – 8.60 %) | ||
| 75 | 2.16 (2.06 – 2.22) | 2.83 % (0.89 % – 7.07 %) | ||
| 60 | 10 | 5 | 1.72 (1.58 – 1.89) | 22.62 % (15.01 % – 28.99 %) |
| 15 | 1.68 (1.64 – 1.74) | 23.92 % (21.59 % – 25.96 %) | ||
| 75 | 1.69 (1.68 – 1.69) | 23.87 % (23.85 % – 24.07 %) | ||
| 7 | 5 | 2.17 (1.99 – 2.39) | 9.22 % (4.41 % – 15.02 %) | |
| 15 | 2.16 (2.11 – 2.22) | 3.25 % (1.56 % – 5.43 %) | ||
| 75 | 2.17 (2.166 – 2.173) | 2.31 % (2.05 % – 2.33 %) | ||
| 4 | 5 | 2.20 (2.02 – 2.40) | 8.59 % (4.18 % – 15.09 %) | |
| 15 | 2.19 (2.13 – 2.26) | 2.96 % (1.39 % – 5.13 %) | ||
| 75 | 2.19 (2.19 – 2.20) | 1.08 % (0.79 % – 1.11 %) | ||
| 1 | 5 | 2.29 (2.10 – 2.52) | 9.24 % (4.06 % – 16.00 %) | |
| 15 | 2.22 (2.16 – 2.28) | 2.80 % (1.38 % – 4.61 %) | ||
| 75 | 2.20 (2.20 – 2.21) | 0.90 % (0.58 % – 0.93 %) | ||
4. Discussion
We have constructed a novel validation framework consisting of a digital phantom and a virtual simulator, which can be used for in silico evaluation of DCE-MRI acquisition and post-processing methods. The digital phantom preserves a detailed geometric model as well as a realistic dynamic model. Specifically, it represents the structure of arterial vasculature and interstitial tissue of the rat kidney, including tissue properties related to vascular permeability and tissue hydraulic conductivity. The dynamic model describes both steady-state flow fields and time-dependent delivery of tracer. Hemodynamic flow fields are stored as both numerical solutions and voxelized arrays. The final output of spatiotemporally-resolved contrast agent distribution has a voxelized representation within a 4D matrix, where the first three dimensions represent space and the fourth dimension is time evolving with the time step of 0.25 s per frame.
Two types of DCE-MRI acquisition protocols were used for testing the performance of the virtual simulation: a standard-of-care acquisition (Protocol A), and an ultra-fast acquisition (Protocol B). According to the results, Protocol A can recapitulate the effects of spatial resolution and SNR on the ability of simulated CE-MR images to highlight morphological structures. Specifically, the CNR clearly increases as either spatial resolution or signal-to-noise increases. Moreover, Protocol B can recapitulate the effects of spatial resolution, temporal resolution, and SNR on the ability of simulated DCE-MR images to capture contrast agent pharmacokinetics. Specifically, accuracy of estimated SER significantly increases as the temporal resolution increases. Additionally, when temporal resolution is high (i.e., TRB ≤ 7 s), the accuracy of the estimated SER also significantly increases when either the spatial resolution or SNR increases; while when temporal resolution is reduced (e.g., TRB = 10 s), the effects of SNRB or SRB on PESER are not statistically significant, though they do continue the trend of interquartile range narrowing as SNRB increases. Moreover, based on the data in Table 2, we can offer general recommendations of SNR, spatial resolution, and temporal resolution for DCE-MRI measurements. Specifically, to achieve a measurement of SER with a small bias (i.e., PESER < 10 %), the image acquisition needs to satisfy either: 1) SRB of 300 μm, SNRB ≥ 15 dB, and TRB ≤ 1 s, 2) SRB of 150 μm, SNRB ≥ 15 dB, and TRB ≤ 7 s, or 3) SRB of 60 μm, SNRB ≥ 5 dB, and TRB ≤ 7 s. Our observation with SRB of 300 μm matches the results reported in Kershaw et al. (Kershaw et al., 2010). We respectfully note that the “ground truth” used in the Kershaw study is a single time course directly generated by simulating the tissue homogeneity model with varying parameters, in which the effect of spatial resolution is not considered. Conversely, the method outlined in this study additionally considers spatial resolution.
As the first major component of this contribution, the digital phantom has a number of advantages compared to previously published efforts. First, the digital phantom is constructed in a 32 × 32 × 16 mm3 field of view, with arterial vessels with radii between 30 and 300 μm, thereby covering the major renal arteries down to terminal arterioles. The realistic morphology of arterial vasculature on this level has never been presented by previous physical or digital phantoms. Second, the new phantom provides spatiotemporally-resolved information on both flow fields and contrast agent delivery. Thus, the phantom provides a unique opportunity to evaluate the ability of estimating interstitial flow with non-invasive imaging in a realistic tissue structure; thus, it serves as an excellent reference for investigating the effects of flow on DCE-MRI data. As the digital phantom is extremely flexible, it can be applied to many other imaging studies. While the present study kept the imaging “object” static in space, if the object were to change geometries across time, the phantom could be deformed across frames, with specific motion mimicking the physical process under investigation (e.g., respiration or the cardiac cycle). Another potential application involves using the phantom to describe the ability to image blood flow at multiple spatial scales to determine the accuracy of (for example) dynamic susceptibility MRI, arterial spin labeling, or angiography to capture properties of the microvasculature. A third potential avenue of investigation is to modify the initial bolus injection function (Cp,0) and the vascular permeability (Pd), to systematically compare the resulting image quality of different injection protocols and contrast agents with different relaxivities.
The second major component of this contribution, is the use of a digital phantom to guide a virtual simulator to construct in silico DCE-MRI datasets. The new virtual simulator consists of five parts: 1) setting the acquisition parameters, 2) setting the reconstruction parameters, 3) defining the signal sampling path in k-space, 4) generating the k-space signal, and 5) implementing image reconstruction. One important innovation of this simulator is it defines the specific time of sampling of each point in k-space, rather than assuming all signals of one scan are obtained simultaneously at the beginning or ending of the acquisition. Including the effects of contrast agent uptake into the acquisition also helps to generate more realistic DCE-MRI signal time courses (Heisen et al., 2010). Moreover, the k-space signal generation scheme allows reconstructing images at a higher temporal resolution than the nominal acquired temporal resolution, which is achieved by an optimization-based reconstruction in this simulator. Similar to the digital phantom component, this simulator is also quite flexible. First, input of the digital phantom into the virtual simulator relies on a single interface; i.e., importing as an argument of the software function generating the k-space signal. That means the digital phantom and virtual simulator have a very high level of independence. Therefore, beside the potential applications of the digital phantom described in this effort, the simulator can accept any number of digital phantoms; importantly, any changes to a digital phantom would not require significant modification of the virtual simulator. Furthermore, the format of the input digital phantom required by the simulator, a 4D grid-based matrix (or 3D if static in time) is straight-forward to achieve. Design of the simulator components also have a very high compatibility for testing various k-space sampling as well as reconstruction methods.
All of the above considerations indicate the proposed validation framework is a powerful, efficient, and generalizable tool for rigorously investigating various quantitative MRI acquisition and analysis techniques. For example, estimating interstitial properties from DCE-MRI (Liu et al., 2016; Wu et al., 2020) data has been studied as there are both in vitro (Kingsmore et al., 2016; Shields et al., 2007; Chang et al., 2008; Schäfer et al., 2008; Shieh et al., 2011; Kim et al., 2016) and in vivo (Baxter et al., 1989; Heldin et al., 2004) studies indicating that the interstitial flow/pressure within tumors prevents optimal drug delivery. However, these models are very challenging to validate even with animal experiments due to the difficulty in measuring interstitial flow in vivo (let alone within a human). Our validation framework contains a digital phantom providing spatiotemporally resolved maps of interstitial pressure and flow, which could be used as a ground truth for validating these models, as well as determining the imaging quality required for these models to be successfully applied.
There are several opportunities for refining this digital phantom. First, we currently assign uniform tissue properties, κ, through the entire extravascular space, so the differences between renal tissues (e.g., cortex and medulla) are not considered. This can be modified to a heterogenous property distribution. For example, if a detailed kidney segmentation were available to differentiate variable kidney tissues (e.g., cortex and medulla), we could assign different values of properties of interest to each tissue type according to (for example) experimental measurements of interstitial hydraulic pressure and conductivity via an inserted catheter or implanted matrix (Wunderlich et al., 1971; Khraibi et al., 1989). Another option would be to directly assign some properties if advanced imaging measurements were available. For example, in a previous study (Wu et al., 2020) we developed an approach to quantify spatially-resolved tissue hydraulic conductivities via the ADC map, which is available from diffusion-weighted MRI. Additionally, the vasculature in the current geometric model includes only the arterial trees, neither the venous components nor the renal duct system is considered. The lack of significant fluid drainage limits the accuracy of this model to mimic the processes of fluid filtration and reabsorption in kidney. Specifically, the current modeling of steady-state, hemodynamic flow assumes a constant pressure value (Dirichlet boundary condition) on the kidney contour. However, we acknowledge that a better representation of fluid behavior on the contour would be a zero-flux condition. But due to the lack of drainage system in the domain, assignment of the zero-flux condition would lead to a system that has no steady state solution. Therefore, even though the physiological properties we used are based on realistic literature values, the model system itself is significantly simplifying the kidney physiology. A complete digital representation of actual renal physiology would require additional modeling considerations (Postnov et al., 2016). For example, to integrate large-scale renal blood flow or vessel-tissue exchange phenomena likely requires multi-scale efforts (Bensalah et al., 2013; Niederalt et al., 2013; Lee et al., 2017, 2018; Yim et al., 2004) with nephron-level modeling of filtration and reabsorption (Layton et al., 2016; Sgouralis et al., 2013).
Another area for future development is to modify the current digital phantom for applications in the human kidney or, more generally, any organ or tissue. As noted in the Introduction, the geometry of the murine kidney was chosen because it is a very high-quality data set (Xie et al., 2012a, 2012b) that provides a clear, representative, and realistic visualization of a hierarchical arterial network. Furthermore, it enables realistic assignment of physical tissue properties and computation of the spatiotemporal distribution of contrast agent obtained by physics-based modeling. To apply this methodology to any other organ (even in humans), the only requirement is acquisition of the requisite data; namely, high spatial resolution images of the vascular tree from the input vessel to the arterioles, the ability to calculate blood flow rate with the appropriate boundary conditions on the inlet and outlet pressures, and estimates of the interstitial hydraulic conductivity and vascular permeability. Importantly, none of these issues are rate limiting steps. Fortunately, when we designed the phantom, we made the implementation and storage of its different components as independent as possible, so modifications should be flexible. In particular, the generation of the digital phantom is independent from the other components of the validation framework (such as the virtual MRI simulator, and post-processing evaluation), so modification of the phantom would not affect the implementation of the remainder of the pipeline.
An additional limitation of the current simulator (alluded to in section 2.2.2) is that we interpolate the digital phantom to replace the real k-space down-sampling process for acquisition of images with low spatial resolution. In real MRI experiments, scanning with lower spatial resolution is actually achieved by truncating the infinite spatial-frequency space (i.e., complete k-space). However, because the voxel-based nature of our digital phantom could cause a discontinuity of intensity on the spatial dimensions (especial for the time points immediately after arrival of the contrast agent bolus), simple truncation of k-space will result in a classic Gibbs ringing artifact. Thus, we decided to choose the alternative strategy presented here as a practical option. But we note that k-space sampling and reconstruction techniques designed for fast vascular imaging (Wright et al., 2014; Stinson et al., 2018) are certainly of interest for future studies.
5. Conclusions
We have established a novel in silico framework to systematically evaluate and validate quantitative DCE-MRI analysis methods based on a dynamic digital phantom and a virtual MRI simulator. The digital phantom provides a detailed representation of vasculature, tissue properties, flow dynamics, and spatiotemporally resolved tracer distribution. The virtual MRI simulator has a flexible “acquisition protocol” that provides realistic DCE-MR images, which can successfully represent the effects of acquisition parameters on the ability of simulated images to capture realistic morphological and pharmacokinetic features of the anatomy under investigation. This validation framework can be used for investigations on contrast-enhanced or perfusion-based MRI techniques or, more generally, to systematically evaluate and optimize new MRI acquisition, reconstruction, and image processing techniques.
Highlights:
A validation framework for quantitative DCE-MRI is proposed based on a digital phantom
The digital phantom contains vascular geometry, hemodynamics and pharmacokinetics
The virtual simulator imports the digital phantom to generate realistic DCE-MRI
Simulated images capture effects of acquisition and reconstruction on image quality
The dynamic digital phantom is available as an open toolkit, R2D2
Acknowledgements
We thank the National Institutes of Health for funding through NCI U01CA142565 (T.E.Y and G.S.K.), U01CA174706 (T.E.Y.), R01CA218700 (G.S.K.), R01CA172801 (G.S.K.), U24CA226110 (T.E.Y.) and P30CA014599 (G.S.K.). We thank the Cancer Prevention and Research Institute of Texas for support through CPRIT RR160005 (T.E.Y.). T.E.Y. is a CPRIT Scholar in Cancer Research. We thank the Duke Center for In Vivo Microscopy for sharing their MR histology images.
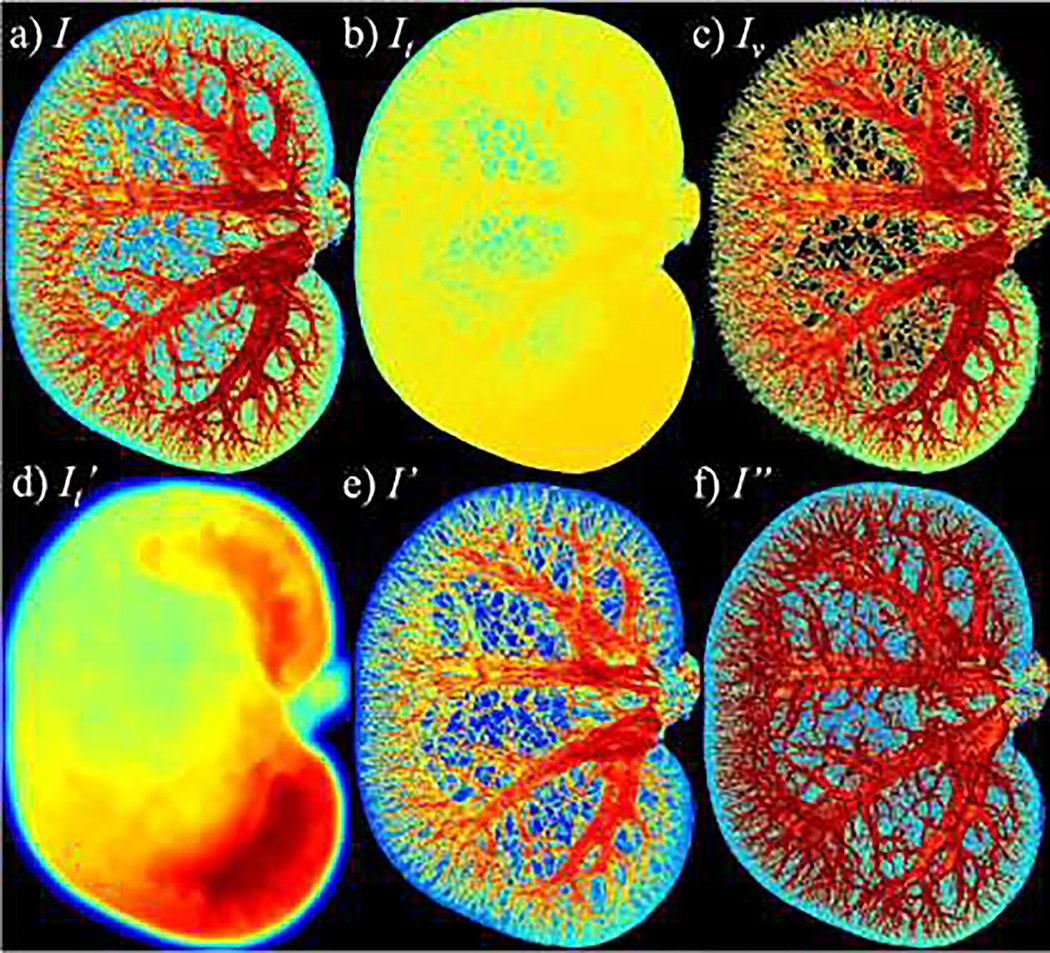
Appendix A. Image enhancement for constructing the vasculature
In preparation for constructing the vascular tree, the intensity of the T2*-weighted images are globally normalized throughout the whole kidney and locally transformed to enhance the vascular regions (as illustrated in Figure A.1). In particular, a k-means clustering with k = 2 is first applied on the entire kidney to segment the image, I, into vasculature (Iv) and extravascular (It) regions. The extravascular component, It, is then smoothed with a Gaussian filter with a standard deviation of 10, producing the map of local tissue background intensity, It’. The normalized image, I’, is then obtained by subtracting this background map from the original image,
| (A.1) |
The last step is to apply a local transform to enhance small vessels in the image,
| (A.2) |
where * represents convolution, and K is a spherical averaging kernel with a radius of 10 voxels (thus, I’ * K represents the local intensity average). The downstream processing to construct the vasculature is performed on the enhanced image, I”.
Figure A.1:
Maximum Intensity Projections (MIPs) of the input, output, and intermediate results of the normalized and enhanced T2*-weighted images. Panels (a) – (f) present, respectively, coronal MIPs of the original T2*-weighted image (I), initially segmented tissue background (It), initially segmented vascular region (Iv), smoothed background (It’), image after background intensity normalization (I’) and the final output image after vascular enhancement (I”). Compared to the original image I (panel a), the intensity of the vasculature in I” (panel f), especially the smaller vessels, is strongly enhanced, and its contrast to the background is substantially improved and normalized.
Appendix B. Justification of assignment of parameters for tissue properties
The delivery of contrast agent is modeled within the arteries of the kidney and the kidney tissue. Even though the detailed structure of glomeruli (where the majority of filtration occurs) is not included in this model, we seek to assign physiologically reasonable values of glomerular capillary permeability as input parameters (i.e., Lp, σ, and Pd) so that the simulation is as realistic as possible. To justify the parameters, literature values on renal vascular permeability have been reviewed. Specifically, Lp describes the ability of water to transmit through porous media (e.g., the vessel wall). As glomerular capillaries are fenestrated, they are much more permeable to small molecules than most other capillaries. Renkin et al. (1977) reported the Lp of renal glomerulus as 1.5 × 10−8 g−1 cm2 s. This magnitude is consistent with the simple approximation from glomerulus filtration rate (GFR) (Hall, 2010),
| (B.1) |
where NFP (net filtration pressure) = glomerular hydrostatic pressure – Bowman’s capsule pressure – glomerular osmotic pressure = 60 mmHg – 18 mmHg – 32 mmHg = 10 mmHg (Hall, 2010). Kf is the capillary filtration coefficient equal to Lp×S, with S as the total surface area of glomerular capillaries. For an average adult human, GFR is about 125 ml/min, and S is about 6000 cm2 (Bohle et al., 1998). Thus, Lp is approximately 2.6 × 10−8 g−1 cm2 s, which matches the magnitude reported in the literature. We choose Lp = 1.5 × 10−8 g−1 cm2 s in our model for modeling the rat kidney. Furthermore, the contrast agent employed in our study (Magnevist®, Gd-DTPA) has a small molecular weight (MD = 938 Da < 7000 Da), so the filtration rate defined in Eq. (7) is approximately one (σ = 0); thus, (1 – σ) = 1 for our model.
The Pd value of a given solute through the vasculature is related to the physical properties of both the vascular wall and the solute. The value of Pd depends heavily on the molecular size of the solute, as well as its charge. For example, the diffusion of albumin (MW ≈ 70 kDa) across the vasculature is estimated to be about 1000-fold less than that of water (Nagy et al., 2008). Unfortunately, we were not be able to find literature values of Pd specifically for Gd-DTPA in the rat kidney. However, the Pd of inulin (MW ≈ 5000 Da) is reported as 1.44 × 10−4 cm/s for dog kidney (Crone, 1963), and we have assumed that the value for our tracer is close to, or slightly larger, than this value. To provide additional support for the selection of the Pd value, we note that the diffusive permeability through the capillary wall for the mammalian muscle has been empirically shown to be a function of the molecular weight (MW) for hydrophilic solutes of the size ranging from 60 (urea) to 5000 (inulin) (Waniewski et al., 1999; Dedrick, 1982):
| (B.2) |
For Gd-DTPA, Pd = 3.97 × 10−6 cm/s in muscle. Combining this number with the fact that muscle capillaries are approximately 100-fold less permeable to water than glomerular capillaries (Pappenheimer et al., 1951), yields Pd of Gd-DTPA through renal vasculature on the order of 10−4 cm/s. Thus, we choose Pd = 2 × 10−4 cm/s for our model.
Appendix C. Numerical stability for solving the advection-diffusion equation
Figure C.1.
Time courses of defined contrast agent concentration in tissue. Each curve represents concentration time course simulated at a point randomly sampled within the digital phantom. No obvious oscillations are observed.
Appendix D. Numerical derivation of optimization-based reconstruction
The reconstruction problem is solved by maximizing the smoothness of voxel-wise reconstructed signals over time. Specifically, in this study, for the reconstructed signal time course of the ith voxel, , we define the smoothness penalty as the l2-norm of its discrete second derivative,
| (C.1) |
Since P is poorly conditioned, we add a small smoothing parameter, λ, to the linear operator P to ensure it to be invertible,
| (C.2) |
where λ > 0 being given as a reconstruction parameter, and I being the identify matrix. Therefore, the regularized smoothness penalty is,
| (C.3) |
This penalty can be trivially applied to the reconstructed image; i.e.,
| (C.4) |
Additionally, during the optimization procedure, it may be desirable to enforce different smoothness criteria in different voxels. To address this purpose, a voxel-wise weighting term, wi, is applied to the penalty at each voxel,
| (C.5) |
Writing the weighting as a diagonal matrix of size (nx × ny × nz) × (nx × ny × nz), W = diag(w1, w2, …, wi, …), and constraining the optimization with the measured k-space signal, minimization of this loss function leads to the optimization process given by Eq. (25) in the main manuscript,
| (C.6) |
By proper re-arranging, a closed-form solution can be found for this optimization object. Specifically, the data array, Y(R), and the reconstructed image array, , can be rearranged into vector forms, Yvec and , respectively,
| (C.7) |
| (C.8) |
| (C.9) |
With the vectorized formula, we can equivalently rewrite the optimization problem as,
| (C.10) |
where ⊗ indicates the tensor product. I is the identity matrix of size (NR × NR). The subscript Ψ is the subset of {1, …, (nx × ny × nz × NR)}, which corresponds to the measurement domain (i.e., Ψ defined by Eq. (24) in the main manuscript). So, for an arbitrary vector β, we define
| (C.11) |
Similar, for arbitrary array Β, we define
| (C.12) |
| (C.13) |
Then, the optimization problem has the closes-form solution,
| (C.14) |
The main step in computing this solution is to compute product of the inverse term, , and the measured signal, [Yvec]Ψ. To simplify the format, we let the inverse term be A−1, and rename [Yvec]Ψ to be b:
| (C.15) |
| (C.16) |
If we set
| (C.17) |
then the main step of the optimization (i.e., computing the x) becomes solving the linear system,
| (C.18) |
After solving for x, the computation in the Eq. (C.14) can be completed as follows,
| (C.19) |
Appendix E. Practical implementation of optimization-based reconstruction
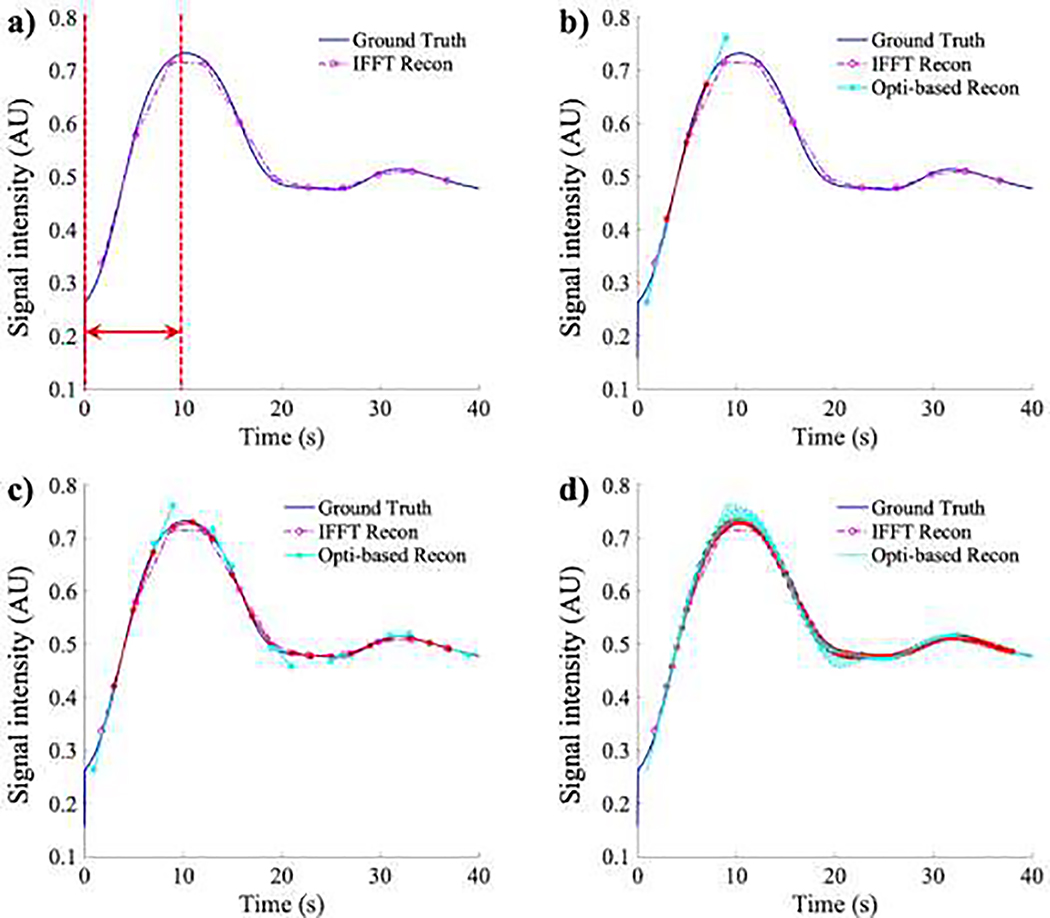
Although it has the advantage of reconstructing images at a temporal resolution higher than that of the nominal acquisition, the exact implementation of the optimization-based reconstruction algorithm involves solving a large linear system, which is very memory- and time-intensive. More specifically, the central step of reconstruction is to solve a linear equation Ax = b, where x is the vectorized presentation of reconstructed image dataset. With the desired reconstructed temporal resolution of 250 ms and without spatial down-sampling, x is a complex vector of length (706 × 576 × 360 × 240). The iterative solution of this inverse problem via the preconditioned conjugated gradient descent (PCG) method (Barrett et al., 1994) requires over 500 GB of memory and hours of computing time. This places a fundamental limitation on the practical feasibility of this simulator. To overcome the memory issue, we designed a scheme to trade time for memory in which the temporal dimension is first divided into multiple intervals and solved individually (see Figure E.1 (a)). More specifically, the whole time-course is first truncated, and a time interval of 10 s is selected. In this interval, the optimization algorithm described in section 2.2.3 of the main text is implemented to reconstruct with a temporal resolution of 2.5 s (Figure E.1 (b)). The first and last frames of this five-frame image is discarded to avoid errors of extrapolation (Figure E.1 (b)). Then, the selected interval is shifted by 7.5 s, 15 s, etc., and the reconstruction is repeated in these new intervals (Figure E.1 (c)). Eventually, this procedure results in an approximate reconstruction of the whole time-course with a resolution of 2.5 s. Furthermore, by shifting the intervals with a smaller time step, a higher effective temporal resolution is achievable. For example, in Figure E.1 (d), the reconstructed time course has a temporal resolution of 0.5 s.
We note that the scheme outlined in the previous paragraph is suboptimal because performing optimization on a truncated time interval sacrifices the global accuracy. Moreover, because the time courses in each time interval are reconstructed individually, a discontinuity of signal intensity at the gap between two adjacent intervals might occur. Ongoing efforts are designed to alleviate the problems by implementing the exact algorithm on a distributed computing system, powered by Texas Advanced Computing Center. This distributed implementation will overcome the limitation of memory and significantly accelerate the computation, along with preservation of global accuracy and continuity.
Figure E.1:
Illustration of the optimization-based reconstruction for one example arterial signal time-course. Panel (a) shows the ground truth signal (blue curve) and the time-course with temporal resolution of 3.5 s reconstructed by the conventional inverse Fourier transform (“IFFT Recon”; pink circle and dash line). The whole time-course is truncated, and a 10 s interval is selected (red dash lines and arrow). Panel (b) shows the signal (“Opti-based Recon”; red-cyan dots and lines) reconstructed by the optimization-based algorithm within the selected interval. Specifically, the red dots are preserved while cyan ones are eliminated to avoid extrapolative errors. In panels (c) and (d), reconstructions of the whole time-course with temporal resolutions of 2.5 s and 0.5 s, respectively, is achieved by shifting selected intervals.
Appendix F. R2D2: Introduction to Digital Phantom Toolkit and Documentation
We have made the dynamic digital phantom introduced in this manuscript into an open toolkit, R2D2 (https://github.com/ChengyueWu/R2D2_toolkit). In this repository, we provided a detailed description and documentation, as well as a link to the entire digital phantom dataset (which is stored on Google Drive). Users are encouraged to download part of or the whole dataset according to their own needs. The documentation included information regarding how to download, visualize, and use data involved in R2D2 (Wu, 2020).
There are three major components of the phantom shared in the toolkit, ‘Geometric Model’, ‘Steady-State Flow’ and ‘Contrast Agent Deliver’, each of which stored in a folder. The folder ‘Geometric Model’ stores files containing information on the geometry of the phantom, including the vascular and kidney tissue. The folder ‘Steady-state Flow’ stores data of computed hemodynamic characteristics of the phantom, including interstitial pressure, interstitial flow velocity, blood pressure, and vascular hydraulic conductivity. The folder ‘Contrast Agent Delivery’ stores data for the computed, spatiotemporally resolved distributions of tracer propagating through vasculature and interstitial tissue.
Data provided in this phantom include both regular-grid-based (i.e., voxelized) representations and unstructured-mesh-based representations of domain geometries, steady-state flow fields and time-dependent distribution of contrast agent. The voxelized data are stored in MATLAB-files, where loading and visualization are tested to be successfully supported by MATLAB versions R2016b – R2020a. No specific MATLAB package is required for using the voxelized data, so earlier or later versions of MATLAB should also be compatible.
The mesh-based representations are stored as XML or HDF5 python files. Python-based computing platform, FEniCS Porject (https://fenicsproject.org/), is required for loading and further processing of these data. All related demos and examples provided are built on FEniCS version 2017.2.0. Visualization of the mesh-based representations via ParaView is recommended. Examples of converting HDF5 data files to VTK image files as well as visualizing using ParaView version 5.6.0 are included in the documentation.
Footnotes
Declaration of interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alfano B, Comerci M, Larobina M, Prinster A, Hornak JP, Selvan SE, Amato U, Quarantelli M, Tedeschi G, Brunetti A, Salvatore M. An MRI digital brain phantom for validation of segmentation methods. Medical image analysis. 2011;15(3):329–39. [DOI] [PubMed] [Google Scholar]
- Anderlik A, Munthe-Kaas AZ, Oye OK, Eikefjord E, Rorvik J, Ulvang DM, Zollner FG, Lundervold A. Quantitative assessment of kidney function using dynamic contrast enhanced MRI-Steps towards an integrated software prototype. In:2009Proceedings of 6th International Symposium on Image and Signal Processing and Analysis 2009 Sep 16 (pp. 575–581). IEEE. [Google Scholar]
- Aubert-Broche B, Evans AC, Collins L. A new improved version of the realistic digital brain phantom. NeuroImage. 2006;32(1):138–45. [DOI] [PubMed] [Google Scholar]
- Badano A, Badal A, Glick S, Graff CG, Samuelson F, Sharma D, Zeng R. In silico imaging clinical trials for regulatory evaluation: initial considerations for VICTRE, a demonstration study. In Medical Imaging 2017: Physics of Medical Imaging, vol. 10132, p. 1013220. [Google Scholar]
- Badano A, Graff CG, Badal A, Sharma D, Zeng R, Samuelson FW, Glick SJ, Myers KJ. Evaluation of digital breast tomosynthesis as replacement of full-field digital mammography using an in silico imaging trial. JAMA network open. 2018;1(7):e185474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrett R, Berry MW, Chan TF, Demmel J, Donato J, Dongarra J, Eijkhout V, Pozo R, Romine C, Van der Vorst H. Templates for the solution of linear systems: building blocks for iterative methods. Siam; 1994. [Google Scholar]
- Baxter LT, Jain RK. Transport of fluid and macromolecules in tumors. I. Role of interstitial pressure and convection. Microvas Res 1989;37(1):77–104. [DOI] [PubMed] [Google Scholar]
- Bell LC, Semmineh N, An H, Eldeniz C, Wahl R, Schmainda KM, Prah MA, Erickson BJ, Korfiatis P, Wu C, Sorace AG. Evaluating multisite rCBV consistency from DSC-MRI imaging protocols and postprocessing software across the NCI quantitative imaging network sites using a digital reference object (DRO). Tomography. 2019;5(1):110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bensalah KR, Uehlinger D, Kalicki R, Czerwinska J. Hemodynamic modeling of the intrarenal circulation. Annals of biomedical engineering. 2013;41(12):2630–44. [DOI] [PubMed] [Google Scholar]
- Bernstein MA, King KF, Zhou XJ. Handbook of MRI pulse sequences. Chapter 11: Signal Acquisition and k-space Sampling. Elsevier. 2004. [Google Scholar]
- Bohle A, Aeikens B, Eenboom A, Fronholt L, Plate WR, Xiao JC, Greschniok A, Wehrmann M. Human glomerular structure under normal conditions and in isolated glomerular disease. Kidney International. 1998;54:S186–8. [DOI] [PubMed] [Google Scholar]
- Bokacheva L, Rusinek H, Zhang JL, Lee VS. Assessment of renal function with dynamic contrast-enhanced MR imaging. Magnetic resonance imaging clinics of North America. 2008;16(4):597–611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bosca RJ, Jackson EF. Creating an anthropomorphic digital MR phantom—an extensible tool for comparing and evaluating quantitative imaging algorithms. Physics in Medicine & Biology. 2016;61(2):974. [DOI] [PubMed] [Google Scholar]
- Brooks AN, Hughes TJ. Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations. Computer methods in applied mechanics and engineering. 1982;32(1–3):199–259. [Google Scholar]
- Chang SF, Chang CA, Lee DY, Lee PL, Yeh YM, Yeh CR, Cheng CK, Chien S, Chiu JJ. Tumor cell cycle arrest induced by shear stress: Roles of integrins and Smad. Proc Natl Acad Sci 2008;105(10):3927–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cloutier G, Soulez G, Qanadli SD, Teppaz P, Allard L, Qin Z, Cloutier F, Durand LG. A multimodality vascular imaging phantom with fiducial markers visible in DSA, CTA, MRA, and ultrasound. Medical Physics. 2004;31(6):1424–33. [DOI] [PubMed] [Google Scholar]
- Collins DL, Zijdenbos AP, Kollokian V, Sled JG, Kabani NJ, Holmes CJ and Evans AC. Design and construction of a realistic digital brain phantom. IEEE transactions on medical imaging, 1998;17(3):463–468. [DOI] [PubMed] [Google Scholar]
- Crone C. The permeability of capillaries in various organs as determined by use of the “indicator diffusion” method. Acta physiologica scandinavica. 1963;58(4):292–305. [DOI] [PubMed] [Google Scholar]
- Dedrick RL. Is the peritoneum a membrane? asaio J 1982;5:1–8. [Google Scholar]
- Driscoll B, Keller H, Coolens C. Development of a dynamic flow imaging phantom for dynamic contrast-enhanced CT. Medical physics. 2011;38(8):4866–80. [DOI] [PubMed] [Google Scholar]
- Easley TO, Pineda F, Kim B, Foygel-Barber R, Wu C, Yankeelov TE, Fan X, Sheth D, Schacht D, Abe H, Karczmar GS. A new approach to quantitative measurement of breast tumor blood flow, capillary permeability, and interstitial pressure. May2019, ISMRM 27th annual meeting, Montreal, QC, Canada. [Google Scholar]
- Easley TO, Pineda F, Karczmar GS, Kim B, Barber R. Time-Tagged Reconstruction: A Robust Approach to Image Reconstruction in Breast DCE-MRI, Abstract #44634, AAPM; 2019. [Google Scholar]
- Flaherty KT, A. Rosen M, F. Heitjan D, L. Gallagher M, Schwartz B, D. Schnall M, O’Dwyer PJ. Pilot study of DCE-MRI to predict progression-free survival with sorafenib therapy in renal cell carcinoma. Cancer biology & therapy. 2008;7(4):496–501. [DOI] [PubMed] [Google Scholar]
- Franca LP, Frey SL, Hughes TJ. Stabilized finite element methods: I. Application to the advective-diffusive model. Computer Methods in Applied Mechanics and Engineering. 1992;95(2):253–76. [Google Scholar]
- Ger RB, Mohamed ASR, Awan MJ, Ding Y, Li K, Fave XJ, Beers AL, Driscoll B, Elhalawani H, Hormuth DA, et al. A multi-institutional comparison of dynamic contrast-enhanced magnetic resonance imaging parameter calculations. Scientific Reports. 2017;7:11185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon Y, Partovi S, Müller-Eschner M, Amarteifio E, Bäuerle T, Weber MA, Kauczor HU, Rengier F. Dynamic contrast-enhanced magnetic resonance imaging: fundamentals and application to the evaluation of the peripheral perfusion. Cardiovasc Diagn Ther. 2014;4(2):147–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grimm R, Churt J, Fieselmann A, Block KT, Kiefer B, Hornegger J. A digital perfusion phantom for T1-weighted DCE-MRI. InProc: Int Soc Magn Reson Med 2012. (p. 2559). [Google Scholar]
- Hansen MB, Tietze A, Haack S, Kallehauge J, Mikkelsen IK, Østergaard L, Mouridsen K. Robust estimation of hemodynamic parameters in traditional DCE-MRI models. PloS one. 2019;14(1). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hariharan P, Freed M, Myers MR. Use of computational fluid dynamics in the design of dynamic contrast enhanced imaging phantoms. Physics in Medicine & Biology. 2013;58(18):6369. [DOI] [PubMed] [Google Scholar]
- Heisen M, Fan X, Buurman J, van Riel NA, Karczmar GS, ter Haar Romeny BM. The influence of temporal resolution in determining pharmacokinetic parameters from DCE-MRI data. Magnetic resonance in medicine. 2010;63(3):811–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heldin CH, Rubin K, Pietras K, Östman A. High interstitial fluid pressure — an obstacle in cancer therapy. Nature Reviews Cancer. 2004;4(10):806. [DOI] [PubMed] [Google Scholar]
- Heye AK, Culling RD, Hernández MD, Thrippleton MJ, Wardlaw JM. Assessment of blood–brain barrier disruption using dynamic contrast-enhanced MRI. A systematic review. NeuroImage: Clinical. 2014;6:262–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall JE. Guyton and Hall textbook of medical physiology e-Book. Elsevier Health Sciences; 2010. Chapter 27. pp 335–346. [Google Scholar]
- Hsu CM. Three-dimensional computerized breast phantom based on empirical data. Dissertation Abstracts International. 2010;72(02). [Google Scholar]
- Hughes TJ, Franca LP, Hulbert GM. A new finite element formulation for computational fluid dynamics: VIII. The Galerkin/least-squares method for advective-diffusive equations. Computer methods in applied mechanics and engineering. 1989;73(2):173–89. [Google Scholar]
- Hughes TJ, Feijóo GR, Mazzei L, Quincy JB. The variational multiscale method—a paradigm for computational mechanics. Computer methods in applied mechanics and engineering. 1998;166(1–2):3–24. [Google Scholar]
- Huxley VH, Curry FE, and Adamson RH. Quantitative fluorescence microscopy on single capillaries: alpha-lactalbumin transport. Am J Physiol. 1987;252(1): H188–197. [DOI] [PubMed] [Google Scholar]
- Keenan KE, Ainslie M, Barker AJ, Boss MA, Cecil KM, Charles C, Chenevert TL, Clarke L, Evelhoch JL, Finn P, Gembris D. Quantitative magnetic resonance imaging phantoms: a review and the need for a system phantom. Magnetic resonance in medicine. 2018;79(1):48–61. [DOI] [PubMed] [Google Scholar]
- Kershaw LE, Cheng HL. Temporal resolution and SNR requirements for accurate DCE-MRI data analysis using the AATH model. Magnetic Resonance in Medicine. 2010;64(6):1772–80. [DOI] [PubMed] [Google Scholar]
- Khraibi AA, Haas JA, Knox FG. Effect of renal perfusion pressure on renal interstitial hydrostatic pressure in rats. American Journal of Physiology-Renal Physiology. 1989;256(1):F165–70. [DOI] [PubMed] [Google Scholar]
- Kim S, Chung M, Ahn J, Lee S, Jeon NL. Interstitial flow regulates the angiogenic response and phenotype of endothelial cells in a 3D culture model. Lab Chip. 2016;16(21):4189–99. [DOI] [PubMed] [Google Scholar]
- Kingsmore KM, Logsdon DK, Floyd DH, Peirce SM, Purow BW, Munson JM. Interstitial flow differentially increases patient-derived glioblastoma stem cell invasion via CXCR4, CXCL12, and CD44-mediated mechanisms. Integr Biol 2016;8(12):1246–60. [DOI] [PubMed] [Google Scholar]
- Kudo K, Christensen S, Sasaki M, Østergaard L, Shirato H, Ogasawara K, Wintermark M, Warach S. Accuracy and reliability assessment of CT and MR perfusion analysis software using a digital phantom. Radiology. 2013;267(1):201–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Layton AT, Vallon V, Edwards A. A computational model for simulating solute transport and oxygen consumption along the nephrons. American Journal of Physiology-Renal Physiology. 2016;311(6):F1378–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Y, Kipfer H, Majidi S, Holz S, Dale B, Geppert C, Kroeker R, Lin C. Application of time-resolved angiography with stochastic trajectories (twist)-dixon in dynamic contrast-enhanced (dce) breast mri. Journal of Magnetic Resonance Imaging. 2013;38(5):1033–42. [DOI] [PubMed] [Google Scholar]
- Lee CJ, Gardiner BS, Ngo JP, Kar S, Evans RG, Smith DW. Accounting for oxygen in the renal cortex: a computational study of factors that predispose the cortex to hypoxia. American Journal of Physiology-Renal Physiology. 2017;313(2):F218–36. [DOI] [PubMed] [Google Scholar]
- Lee CJ, Gardiner BS, Evans RG, Smith DW. A model of oxygen transport in the rat renal medulla. American Journal of Physiology-Renal Physiology. 2018;315(6):F1787–811. [DOI] [PubMed] [Google Scholar]
- Les AS, Shadden SC, Figueroa CA, Park JM, Tedesco MM, Herfkens RJ, Dalman RL, Taylor CA. Quantification of hemodynamics in abdominal aortic aneurysms during rest and exercise using magnetic resonance imaging and computational fluid dynamics. Annals of biomedical engineering. 2010;38(4):1288–313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Welch EB, Arlinghaus LR, et al. A novel AIF tracking method and comparison of DCE-MRI parameters using individual and population-based AIFs in human breast cancer. Phys Med Biol 2011;56(17):5753–5769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu D, Yu J. Otsu method and K-means. In:2009 Ninth International Conference on Hybrid Intelligent Systems2009August12 (Vol. 1, pp. 344–349). IEEE. [Google Scholar]
- Liu LJ, Brown SL, Ewing JR, Ala BD, Schneider KM, Schlesinger M. Estimation of Tumor Interstitial Fluid Pressure (TIFP) Noninvasively. PloS One. 2016;11(7):e0140892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logg A, Mardal KA, Wells G. Automated Solution of Differential Equations by the Finite Element Method: the FEniCS book. Springer. 2012. [Google Scholar]
- Nagy JA, Benjamin L, Zeng H, Dvorak AM, Dvorak HF. Vascular permeability, vascular hyperpermeability and angiogenesis. Angiogenesis. 2008;11(2):109–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niederalt C, Wendl T, Kuepfer L, Claassen K, Loosen R, Willmann S, Lippert J, Schultze-Mosgau M, Winkler J, Burghaus R, Bräutigam M. Development of a physiologically based computational kidney model to describe the renal excretion of hydrophilic agents in rats. Frontiers in physiology. 2013;3:494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Notohamiprodjo M, Sourbron S, Staehler M, Michaely HJ, Attenberger UI, Schmidt GP, Boehm H, Horng A, Glaser C, Stief C, Reiser MF. Measuring perfusion and permeability in renal cell carcinoma with dynamic contrast-enhanced MRI: a pilot study. Journal of Magnetic Resonance Imaging. 2010;31(2):490–501. [DOI] [PubMed] [Google Scholar]
- Palmowski M, Schifferdecker I, Zwick S, Macher-Goeppinger S, Laue H, Haferkamp A, Kauczor HU, Kiessling F, Hallscheidt P. Tumor perfusion assessed by dynamic contrast-enhanced MRI correlates to the grading of renal cell carcinoma: initial results. European journal of radiology. 2010;74(3):e176–e180. [DOI] [PubMed] [Google Scholar]
- Pappenheimer JR, Renkin EM, Borrero LM. Filtration, diffusion and molecular sieving through peripheral capillary membranes: a contribution to the pore theory of capillary permeability. American Journal of Physiology-Legacy Content. 1951;167(1):13–46. [DOI] [PubMed] [Google Scholar]
- Parker GJ, Roberts C, Macdonald A, Buonaccorsi GA, Cheung S, Buckley DL, Jackson A, Watson Y, Davies K, Jayson GC. Experimentally-derived functional form for a population-averaged high-temporal-resolution arterial input function for dynamic contrast-enhanced MRI. Magnetic resonance in medicine. 2006;56(5):993–1000. [DOI] [PubMed] [Google Scholar]
- Pedrosa I, Alsop DC, Rofsky NM. Magnetic resonance imaging as a biomarker in renal cell carcinoma. Cancer. 2009;115(S10):2334–2345. [DOI] [PubMed] [Google Scholar]
- Postnov DD, Marsh DJ, Postnov DE, Braunstein TH, Holstein-Rathlou NH, Martens EA, Sosnovtseva O. Modeling of kidney hemodynamics: probability-based topology of an arterial network. PLoS computational biology. 2016;12(7):e1004922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Privratsky JR, Wang N, Qi Y, Ren J, Morris BT, Hunting JC, Johnson GA, Crowley SD. Dynamic contrast-enhanced MRI promotes early detection of toxin-induced acute kidney injury. American Journal of Physiology-Renal Physiology. 2019;316(2):F351–F359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renkin EM. Multiple pathways of capillary permeability. Circulation research. 1977;41(6):735–43. [DOI] [PubMed] [Google Scholar]
- Rosen MA, Schnall MD. Dynamic contrast-enhanced magnetic resonance imaging for assessing tumor vascularity and vascular effects of targeted therapies in renal cell carcinoma. Clinical Cancer Research. 2007;13(2):770s–776s. [DOI] [PubMed] [Google Scholar]
- Segars WP, Sturgeon G, Mendonca S, Grimes J, Tsui BM. 4D XCAT phantom for multimodality imaging research. Medical physics. 2010;37(9):4902–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saint-Jalmes H, Eliat PA, Bezy-Wendling J, Bordelois A, Gambarota G. ViP MRI: virtual phantom magnetic resonance imaging. Magnetic Resonance Materials in Physics, Biology and Medicine. 2014;27(5):419–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schäfer M, Werner S. Cancer as an overhealing wound: an old hypothesis revisited. Nat Rev Mol Cell Biol 2008;9(8):628. [DOI] [PubMed] [Google Scholar]
- Semmineh NB, Stokes AM, Bell LC, Boxerman JL, Quarles CC. A population-based digital reference object (DRO) for optimizing dynamic susceptibility contrast (DSC)-MRI methods for clinical trials. Tomography. 2017;3(1):41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen Y, Goerner FL, Snyder C, Morelli JN, Hao D, Hu D, Li X, Runge VM. T1 relaxivities of gadolinium-based magnetic resonance contrast agents in human whole blood at 1.5, 3, and 7 T. Investigative radiology. 2015;50(5):330–8. [DOI] [PubMed] [Google Scholar]
- Shieh AC, Rozansky HA, Hinz B, Swartz MA. Tumor cell invasion is promoted by interstitial flow-induced matrix priming by stromal fibroblasts. Cancer Res 2011:71(3):790–800. [DOI] [PubMed] [Google Scholar]
- Shields JD, Fleury ME, Yong C, Tomei AA, Randolph GJ, Swartz MA. Autologous chemotaxis as a mechanism of tumor cell homing to lymphatics via interstitial flow and autocrine CCR7 signaling. Cancer Cell. 2007;11(6):526–38. [DOI] [PubMed] [Google Scholar]
- Shore AC. Capillaroscopy and the measurement of capillary pressure. British journal of clinical pharmacology. 2000;50(6):501–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shukla-Dave A, Obuchowski NA, Chenevert TL, Jambawalikar S, Schwartz LH, Malyarenko D, Huang W, Noworolski SM, Young RJ, Shiroishi MS, Kim H. Quantitative imaging biomarkers alliance (QIBA) recommendations for improved precision of DWI and DCE-MRI derived biomarkers in multicenter oncology trials. Journal of Magnetic Resonance Imaging. 2019;49(7):e101–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sgouralis I, Layton AT. Control and modulation of fluid flow in the rat kidney. Bulletin of mathematical biology. 2013;75(12):2551–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorace AG, Partridge SC, Li X, Virostko J, Barnes SL, Hippe DS, Huang W, Yankeelov TE. Distinguishing benign and malignant breast tumors: preliminary comparison of kinetic modeling approaches using multi-institutional dynamic contrast-enhanced MRI data from the International Breast MR Consortium 6883 trial. Journal of Medical Imaging. 2018;5(1):011019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stanisz GJ, Odrobina EE, Pun J, Escaravage M, Graham SJ, Bronskill MJ, Henkelman RM. T1, T2 relaxation and magnetization transfer in tissue at 3T. Magnetic resonance in medicine. 2005;54(3):507–12. [DOI] [PubMed] [Google Scholar]
- Stinson EG, Trzasko JD, Campeau NG, Glockner JF, Huston J III, Young PM, Riederer SJ. Time-resolved contrast-enhanced MR angiography with single-echo Dixon fat suppression. Magnetic resonance in medicine. 2018;80(4):1556–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sujlana P, Skrok J, Fayad LM. Review of dynamic contrast-enhanced MRI: Technical aspects and applications in the musculoskeletal system. J Magn Reson Imaging. 2018;47(4):875–890. [DOI] [PubMed] [Google Scholar]
- The MathWorks, Inc. MAT AB and Image Processing Toolbox: User’s Guide (R2019b). Natick, Massachusetts, United States. [Google Scholar]
- Waniewski J, Werynski A, Lindholm B. Effect of blood perfusion on diffusive transport in peritoneal dialysis. Kidney international. 1999;56(2):707–13. [DOI] [PubMed] [Google Scholar]
- Winston JA, Safirstein RO. Reduced renal blood flow in early cisplatin-induced acute renal failure in the rat. American Journal of Physiology-Renal Physiology. 1985;249(4):F490–6. [DOI] [PubMed] [Google Scholar]
- Wright KL, Lee GR, Ehses P, Griswold MA, Gulani V, Seiberlich N. Three-dimensional through-time radial GRAPPA for renal MR angiography. Journal of Magnetic Resonance Imaging. 2014;40(4):864–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu C, Pineda F, Hormuth DA, Karczmar GS, Yankeelov TE. Quantitative analysis of vascular properties derived from ultrafast DCE-MRI to discriminate malignant and benign breast tumors. Magnetic resonance in medicine. 2019;81(3):2147–2160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu C, Hormuth DA, Oliver TA, Pineda F, Karczmar GS, Lorenzo G, Moser RD, Yankeelov TE. Patient-specific characterization of breast cancer hemodynamics using image-guided computational fluid dynamics. IEEE – TMI, February2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu C. R2D2: Realistic Renal Dynamic Digital Phantom (Version 1.0). 2020. https://drive.google.com/drive/folders/1POWCf2LALWMOqhgQO40mPz8ldIgS_-t1?usp=sharing.
- Wunderlich P, Persson E, Schnermann J, Ulfendahl H, Wolgast M. Hydrostatic pressure in the subcapsular interstitial space of rat and dog kidneys. Pflügers Archiv 1971;328(4):307–319. [DOI] [PubMed] [Google Scholar]
- Xie L, Cianciolo RE, Hulette B, Lee HW, Qi Y, Cofer G, Johnson GA. Magnetic resonance histology of age-related nephropathy in the Sprague Dawley rat. Toxicologic pathology. 2012;40(5):764–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie L, Cianciolo RE, Hulette B, Lee HW, Qi Y, Cofer G, Johnson GA. Supplemental Material for Magnetic Resonance Histology of Age-related Nephropathy in Sprague-Dawley Rats. 2012. https://www.civm.duhs.duke.edu/duke-CIVM-sup-lx201107. [DOI] [PMC free article] [PubMed]
- Xiong G, Figueroa CA, Xiao N, Taylor CA. Simulation of blood flow in deformable vessels using subject-specific geometry and spatially varying wall properties. International journal for numerical methods in biomedical engineering. 2011;27(7):1000–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang D, Ye Q, Williams DS, Hitchens TK, Ho C. Normal and transplanted rat kidneys: diffusion MR imaging at 7 T. Radiology. 2004;231(3):702–9. [DOI] [PubMed] [Google Scholar]
- Yankeelov TE, Gore J. Dynamic Contrast Enhanced Magnetic Resonance Imaging in Oncology: Theory, Data Acquisition, Analysis, and Examples. Curr Med Imaging Rev 2007;3(2):91–107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yim PJ, Cebral JR, Weaver A, Lutz RJ, Soto O, Vasbinder GB, Ho VB, Choyke PL. Estimation of the differential pressure at renal artery stenoses. Magnetic resonance in medicine. 2004;51(5):969–77. [DOI] [PubMed] [Google Scholar]
- Yuan Y, Chilian WM, Granger HJ, and Zawieja DC. Permeability to albumin in isolated coronary venules. Am J Physiol 1993;265(2):H543–52. [DOI] [PubMed] [Google Scholar]
- Yuan SY, Rigor RR. Regulation of Endothelial Barrier Function. San Rafael (CA): Morgan & Claypool Life Sciences; 2010. Chapter 3, Methods for Measuring Permeability. Available from: https://www.ncbi.nlm.nih.gov/books/NBK54124/. [PubMed] [Google Scholar]
- Zhu Y, Guo Y, Lingala SG, Barnes S, Lebel RM, Law M, Nayak KS. Evaluation of DCE-MRI data sampling, reconstruction and model fitting using digital brain phantom. InProc: Int Soc Magn Reson Med 2015. (p. 3070). [Google Scholar]