Operating characteristics are needed to properly evaluate the scientific validity of Phase I protocols

Abstract

Purpose:

Operating characteristics for proposed clinical trial designs provide insight into performance regarding safety and accuracy, allowing the study team and review entities to determine the design’s suitability to achieve the study’s proposed objectives. Advances in cancer therapeutics have augmented the needs of early phase clinical trial design. Additionally, advances in research on early-phase trial design have led to the availability of a wide range of methods that show vast improvement over outdated approaches.

Methods:

Three trials utilizing variations of the 3+3 decision rule are discussed. The protocols lacked detail, including operating characteristics and guidance for decision-making that deviated from the 3+3 decision rule and MTD determination. We provide a discussion of the statistical issues associated with each design and operating characteristics for the proposed design compared to alternatives better suited to achieve the aims of each trial.

Results:

Our results illustrate how operating characteristics inform a design’s safety and accuracy. Operating characteristics can unmask poor behavior, such as a high percentage of particiapnts exposed to overly toxic doses, a low probability of correctly identifying the MTD, and inappropriate early study termination.

Conclusion:

Selection of early-phase trial design has significant implications on a trial’s ability to meet its objectives. Operating characteristics are a necessary component in the design and review of a protocol, determining if the study’s objectives can be achieved and documenting the study’s scientific validity. Continued use of outdated approaches due to historical acceptance hinders scientific rigor and the effort to move effective agents through the drug development process.

Introduction

In evaluating the scientific validity of clinical trial protocols, the proposed design’s operating characteristics provide information on the design’s expected behavior under specific conditions. They help review entities determine whether a proposed design can achieve the study’s proposed objectives, and they are used to document scientific validity. The operating characteristics help statisticians determine whether a good trial design has been proposed, and they aid in communicating the design behavior with non-statisticians, such as clinicians and trial participants, as well as with statisticians who perhaps may not be well-versed in the particular proposed design or the Phase of development being studied¹. The requirement of operating characteristics inclusion forces rigor and specificity into early phase designs, similar to the rigor required for later phases (II and III). They are used to document scientific validity. The goal of their inclusion is to provide rigorous protocols that offer clear safety and assessment guidelines. Operating characteristics can be used to measure the impact of design modifications and ad hoc decisions on the trial’s conduct, removing bias by providing proper guidelines a priori. Finally, and perhaps most importantly, they help determine whether the proposed design can achieve the study protocol’s research objectives.

In Phases II and III of drug development, the operating characteristics are often power calculations that justify the proposed sample size. In Phase I clinical trial protocols, however, operating characteristics have been historically omitted from the statistical considerations. This omission is inconsistent with the level of rigor required for later phases (i.e., II and III) of drug development. There are multiple potential explanations for why Phase I clinical trials have averted the scientific rigor required at later phases. Still, a recent simulation study of the drug development process demonstrated the importance of well-performing early-phase designs². In recent years, early development in oncology has become more complicated due to advances in cancer therapeutics. Consequently, the traditional paradigm of early-phase trial design, which is most appropriate for dose escalation of single cytotoxic agents, is being challenged. Despite many challenges arising from the changing landscape, the traditional framework has continued to drive study design and conduct³. The need to provide operating characteristics for early phase clinical trials stems from the need to shift the discussion away from the default use of an outdated design to a discussion on the usefulness of providing operating characteristics and bring rigor to early-phase (phase I and I-II) designs.

Drawing on years of experience reviewing protocols for the Protocol Review Committee (PRC), we focus on three examples that fall into the common default use of a 3+3 decision rule and appear well described yet lack specificity and provide motivation for this work. For each example, we offer operating characteristics to illustrate the design limitations associated with each trial. In each instance, in keeping with the confidentiality of the PRC review process, we have disguised the agents’ names and exact doses.All other aspects of the studies presented are taken directly from the protocol that the PRC reviewed. All three examples are open studies that are currently recruiting participants. We begin with an illustration of the procedure for generating operating characteristics.

Generating operating characteristics

Operating characteristics provide the statistical properties of the design under assumed truths of nature⁴. Simulated trial data for the design is evaluated under a wide variety of situations. Scenarios typically cover various possibilities, ranging from pessimistic (no treatment provides benefit) to optimistic (several treatments highly effective)⁵. After each simulated trial, the dose selected as the optimal dose (e.g., maximum tolerated dose (MTD)) is recorded, and this process of trial simulation is repeated a large number of times (i.e., at least 1000) under each scenario. The percentage of times each study dose level is chosen as the MTD over many simulated trials, and the percentage of times the trial stopped early for safety is then tabulated. Other performance metrics, such as the average sample size, the number (or percentage) of participants treated at each dose level, and the overall percentage of observed dose-limiting toxicities, can be documented also from the process. A good design should have a high probability of terminating at or near the true MTD, a low cumulative probability of stopping below the true MTD, and a low probability of escalating beyond the MTD. Operating characteristics are generated by simulating DLT outcomes for each participant in a hypothetical trial, and repeating the process over many trials under a wide variety of hypothesized dose-toxicity curves. In simulating DLT outcomes, we utilize the fact that each dose level has an assumed underlying probability of DLT in a hypothesized curve. Assume a hypothetical participant is assigned to a dose with a probability of DLT equal to 0.10. We begin by randomly generating a number x between 0 and 1 for this participant. If x ≤ 0.10, then the participant has a DLT outcome. If x > 0.10, then the participant does not have a DLT outcome. Based on the DLT outcomes, we assign the next cohort of participants to a dose according to a dose-finding algorithm and repeat.

As an example, consider two simulated trials of three dose levels using a 3+3 algorithm (Table 1). Suppose that the DLT probabilities at each dose level are 0.05, 0.10, and 0.25 in each trial. Although each trial has the same hypothesized DLT probabilities, the random numbers that generate participant outcomes varies, producing a new sample of outcomes in each trial. The first trial escalates to dose level 3 where 2 of 6 participants experience a DLT, making dose level 2 the estimated MTD with an observed DLT rate of 0/3. In the second trial, 2 of 3 participants experience DLT at dose level 2, making dose level 1 the estimated MTD with an observed DLT rate of 1/6. This example illustrates the variability among DLT outcomes and MTDs across different simulated trials. When this process is repeated a large number (i.e., ≥1000) times under a hypothesized curve, we can tabulate the proportion of times each dose was selected as the MTD at study conclusion, serving as an estimated probability that each dose will be selected as the MTD. Under one hypothesized curve, the estimated probability of correct MTD selection may be 45%, while under a different curve, the estimated probability of correct MTD selection may be 51%, for example. This illustrates the fact that there exists variability between hypothesized dose-toxicity curves, so we want to repeat the simulation process under a broad range of dose-toxicity hypotheses and summarize the results over the many curves. This procedure can and should be conducted for any early-phase trial design in order to evaluate operating characteristics.

Table 1:

Illustration of simulating DLT outcomes to generate operating characteristics of the 3+3 algorithm.

Patient	Dose level	Random # x	Assumed DLT probability	DLT (yes/no)
Simulated trial #1 using 3+3
1	1	0.88	0.05	No
2	1	0.56	0.05	No
3	1	0.18	0.05	No
4	2	0.64	0.10	No
5	2	0.53	0.10	No
6	2	0.49	0.10	No
7	3	0.66	0.25	No
8	3	0.14	0.25	Yes
9	3	0.53	0.25	No
10	3	0.67	0.25	No
11	3	0.04	0.25	Yes
12	3	0.55	0.25	No
MTD = dose level 2
Simulated trial #2 using 3+3
1	1	0.87	0.05	No
2	1	0.77	0.05	No
3	1	0.01	0.05	Yes
4	1	0.33	0.05	No
5	1	0.61	0.05	No
6	1	0.29	0.05	No
7	2	0.06	0.10	Yes
8	2	0.35	0.10	No
9	2	0.02	0.10	Yes
MTD = dose level 1

Trial example 1

Study information

The first study is a Phase I-IIa open-label, multicenter, dose-escalation, and dose-expansion study of the safety, tolerability, and pharmacokinetics of Agent A in patients with advanced cancers associated with expression of a tumor antigen who have failed standard available therapy. The primary objective is to assess the safety and tolerability at increasing dose levels of Agent A in successive cohorts of patients with various cancer types, to estimate the maximum tolerated dose (MTD) or maximum administered dose (MAD), and to select the recommended Phase 2 dose (RP2D). An acceptable proportion of patients with DLT that defines the MTD for the study was not explicitly specified, and the selection of the MTD was based upon the number of DLTs in cohorts of 3 or 6 patients. The protocol stated that the cohort review committee would determine an RP2D at or below the MTD based on safety, clinical activity, PK, and pharmacodynamic data from Phase 1 of the study. The starting dose of Agent A will be X ng/kg/week, with dose escalation by single patient cohorts up to 3 times the dose until either a Grade ≥2 adverse event (AE) is observed during Cycle 1 (21-day dose-limiting toxicity (DLT) observation period), or an estimated therapeutic dose level has been reached. When either a Grade ≥2 AE is observed during Cycle 1 or an estimated therapeutic dose level has been achieved, then a ‘conventional’ 3+3 rule was to be implemented.

Statistical issues

This study’s primary statistical concerns revolve around the lack of clarity in some of the decision rules. One of the criteria for switching to a 3+3 rule is assuming an estimated therapeutic dose level has been reached, although it is not specified how this will be determined. Moreover, it is unclear how many and what the study dose levels are after the 3+3 is initiated. Operating characteristics were requested to assess how well the chosen design performed in answering the posed research questions, which would also necessitate more defined study criteria. Review statisticians asked that the operating characteristics consist of simulation results that evaluate the probability of correctly selecting the MTD in a broad range of unknown but possible hypothesized dose-toxicity scenarios, incorporating all decision rules. The study team responded that the current study utilizes a rule-based method. Justification for the design included

1. Accelerated titration designs using rule-based methods have been widely used in oncology studies, and several reviews were provided^6–8.

2. According to the National Cancer Institute (NCI), the guiding principle for dose escalation in Phase I trials is to avoid unnecessary exposure of patients to sub-therapeutic doses of an agent (i.e., to treat as many patients as possible within the therapeutic dose range) while preserving safety and maintaining rapid accrual.

3. Dancey et al. ⁹ conclude, “Accelerated titration designs can dramatically reduce the number of patients accrued into a phase I trial, in comparison with the standard phase 1 design.

4. They can also substantially shorten the duration of a phase 1 trial.

The study team concluded that “while operating characteristics are an interesting theoretical exercise, the rule-based design included in the current protocol has been used extensively and thus formal operating characteristic simulations were not performed. FDA and several IRBs have approved the protocol.”

Operating characteristics

To evaluate the statistical concerns related to the first example, we can rely on a paper investigating the operating characteristics of several Phase I designs, including the accelerated titration design¹⁰. A portion of the results from Tables 3–5 from that paper is summarized in Figure 1. These results include the probability of correctly identifying the MTD, the probability of selecting an overdose (a dose above the correct MTD) as the MTD, and the probability of treating patients at doses above the MTD for the accelerated titration algorithm, the 3+3 algorithm, Bayesian optimal interval (BOIN) method, and continual reassessment method (CRM). Ananthakrishnan et al. ¹⁰ conclude that “Among the designs investigated, the simple accelerated titration design overdoses a large percentage of patients.” Figure 1 illustrates the poor operating characteristics of the accelerated titration design. Among the scenarios considered, the mean probability of correctly identifying the MTD is 42% for the accelerated titration design, 52% for the 3+3 rule, 57% for the Bayesian optimal interval (BOIN¹⁹) method, and 68% for the continual reassessment method (CRM²⁰). The mean probability of selecting an overdose (a dose above the correct MTD) as the MTD is 41% for the accelerated titration design, 16% for the 3+3 rule, 12% for the BOIN method, and 11% for the CRM. The mean probability of treating patients at doses above the MTD is 46% for the accelerated titration design, 22% for the 3+3 rule, 12% for the BOIN method, and 13% for the CRM. It is clear that the study team’s design is likely to expose a high percentage of patients to overly toxic doses, and it demonstrates a low probability of correctly identifying the MTD. Thus, this study has poor scientific validity.

Figure 1:

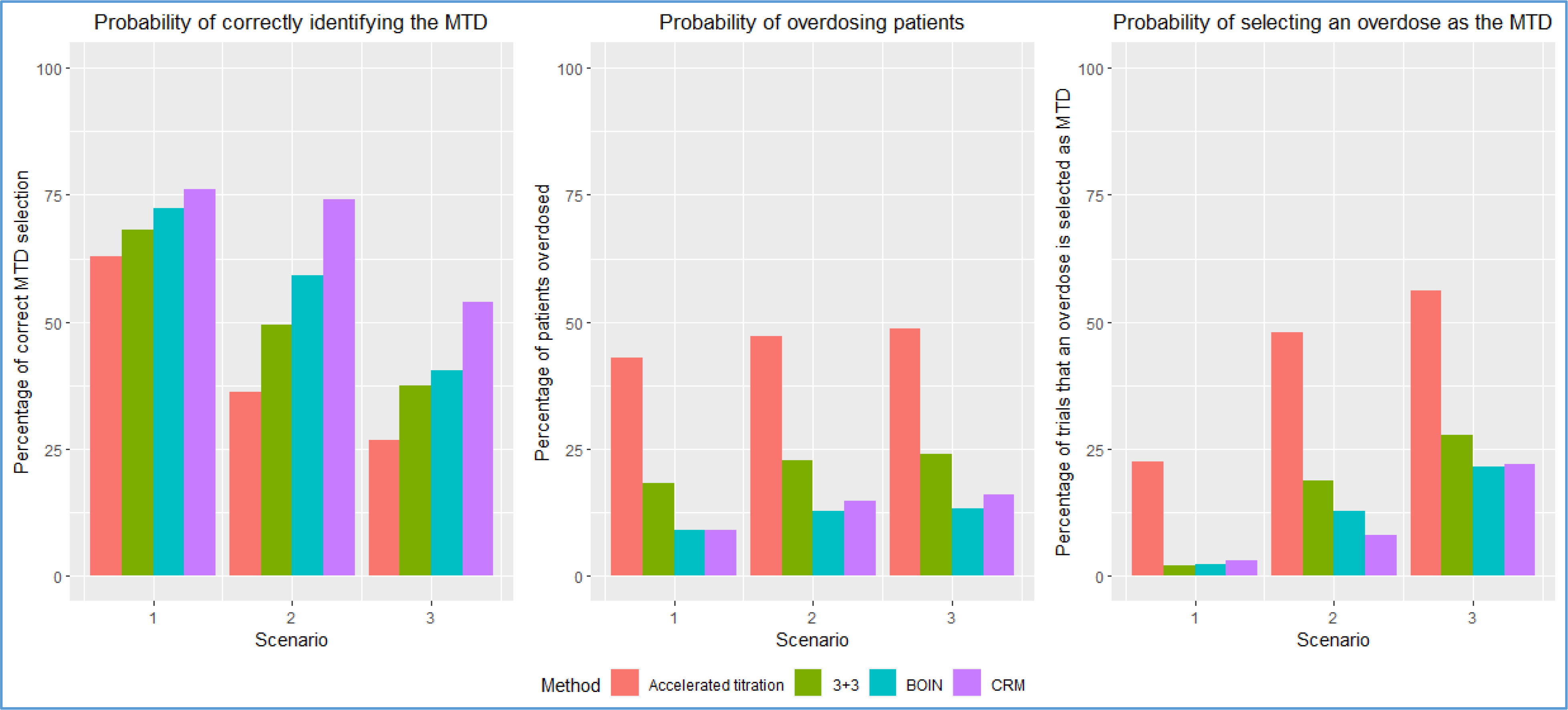
Operating characteristics of the accelerated titration design, 3+3 design, BOIN method, and CRM based on the simulation results in Ananthakrishnan et al. ¹⁰. Results are based on 10000 simulated trials for each method. The target DLT rate that defines the MTD is 0.20. The cohort size for BOIN and CRM is 3.

Trial example 2

Study information

The second study is a Phase I-II study of Agent A in Combination with Agent B and Agent C in patients with relapsed/refractory acute myeloid leukemia. Phase I part of the study’s primary objective is to determine the maximum tolerated dose (MTD) of the combination, with three escalating dose levels of Agent A. The MTD is defined as the highest dose level where 1 or fewer of 6 participants experience dose-limiting toxicity (DLT) during the first two cycles of treatment. The recommended phase 2 dose (RP2D) is the same as the MTD. The primary objective of the phase II part of the study is to obtain a preliminary estimate of the overall response rate (ORR) = CR+CRi+PR rate, a combined rate of complete remission (CR) + complete remission with incomplete count recovery (CRi) + partial response (PR) after 2 cycles of treatment with the combination. The study was designed using a 3+3 dose escalation rule to determine the MTD of the combination therapy. There were three possible dose levels, including dose level 1 (158 mg/m2), dose level 2 (215 mg/m2), and dose level −1 (106 mg/m2) if excessive toxicity is observed at dose level 1. The starting dose was dose level 1. After determining the MTD, a Simon¹³ two-stage minimax design is planned with a total sample size of 36 patients, including the six patients treated at the MTD in Phase I of the study. For Phase II, the study hypothesizes that the addition of Agent A to Agent B plus Agent C will improve the ORR to 45%. The study is designed with a null rate of 28% and an alternative rate of 45%. In the first stage of the minimax design, a total of 17 participants are to be accrued. If four or fewer achieved an overall response, the study would close early due to a lack of efficacy; if five or more achieved the endpoint, an additional 19 participants would be accrued. If at least 14 out of the 36 participants achieve an overall response at the end of the study, the combination therapy will be considered promising for further investigation. The type I error is set at 0.10, and the type II error is set at 0.20.

Statistical issues

This protocol did provide operating characteristics for each design component (i.e., Phase I and Phase II) separately, but there were several flaws in how they were presented in each Phase. In Phase I, there is a lack of clarity in the target DLT rate that defined the MTD of the study. The provided operating characteristics indicate a target of 30%. The 3+3 targets a DLT rate of approximately 20%^14–17. Second, the operating characteristics demonstrate that the design was only better than chance at determining the MTD (i.e., selecting an MTD at random without conducting the study) in 2 of the 6 scenarios assessed and did not exhibit good statistical properties. Third, the operating characteristics only included the true MTD results rather than the results at each dose level. Lastly, it would have been informative to see the entire design’s operating characteristics, including how often the phase II portion is closed for safety while estimating response. This inclusion would have allowed reviewers to evaluate how well all design components worked in conjunction with one another. There was a lack of clarity in trial conduct regarding safety mechanisms in Phase II, including the behavior of the proposed Pocock-type¹⁸ stopping bounds for safety and whether an additional dose level (or levels) would be explored in Phase II or if the study would be permanently closed to accrual if the toxicity bound was crossed. Specifically, the safety stopping rules were to stop the study if 3 of 9 patients had DLT, 4 of 14 patients had DLT, 5 of 21 patients had DLT, 6 of 27 patients had DLT, or 7 patients at any time had DLT. The boundaries appeared to be inconsistent with the target DLT level in phase I. The first look implies that DLTs observed in 4 of the first 9 participants are required to stop for toxicity. It was unclear whether accrual would continue with 3 DLTs observed in the first 3 additional participants to the phase II portion.

Operating characteristics

In evaluating the design proposed in Example 2, we generated operating characteristics for the entire design, including how often the phase II portion is closed for safety while estimating response. Per the protocol, this trial can stop early for one of three reasons: (1) safety in Phase I, (2) safety in Phase II, and (3) futility in Phase II. We evaluated the design in various situations, beginning with assessment under a broad range of dose-toxicity and dose-efficacy. We then assessed under three specific conditions: (1) each scenario having a least one safe (DLT rate ≤33%) and effective (response rate ≥45%) dose, (2) all doses being safe, but none being effective, and (3) all doses being both safe and effective. We simulated 100 trials under 1000 dose-toxicity and dose-response curves (i.e., 100,000 simulated trials). All curves were randomly generated using the algorithm proposed by Conaway and Petroni² (Figure 2). The maximum sample size for Phase I is 18 participants. For Phase II, Simon’s two-stage minimax design with a maximum sample size of 36 participants was simulated according to the decision rules described in the design of Example 2 above.

Figure 2:

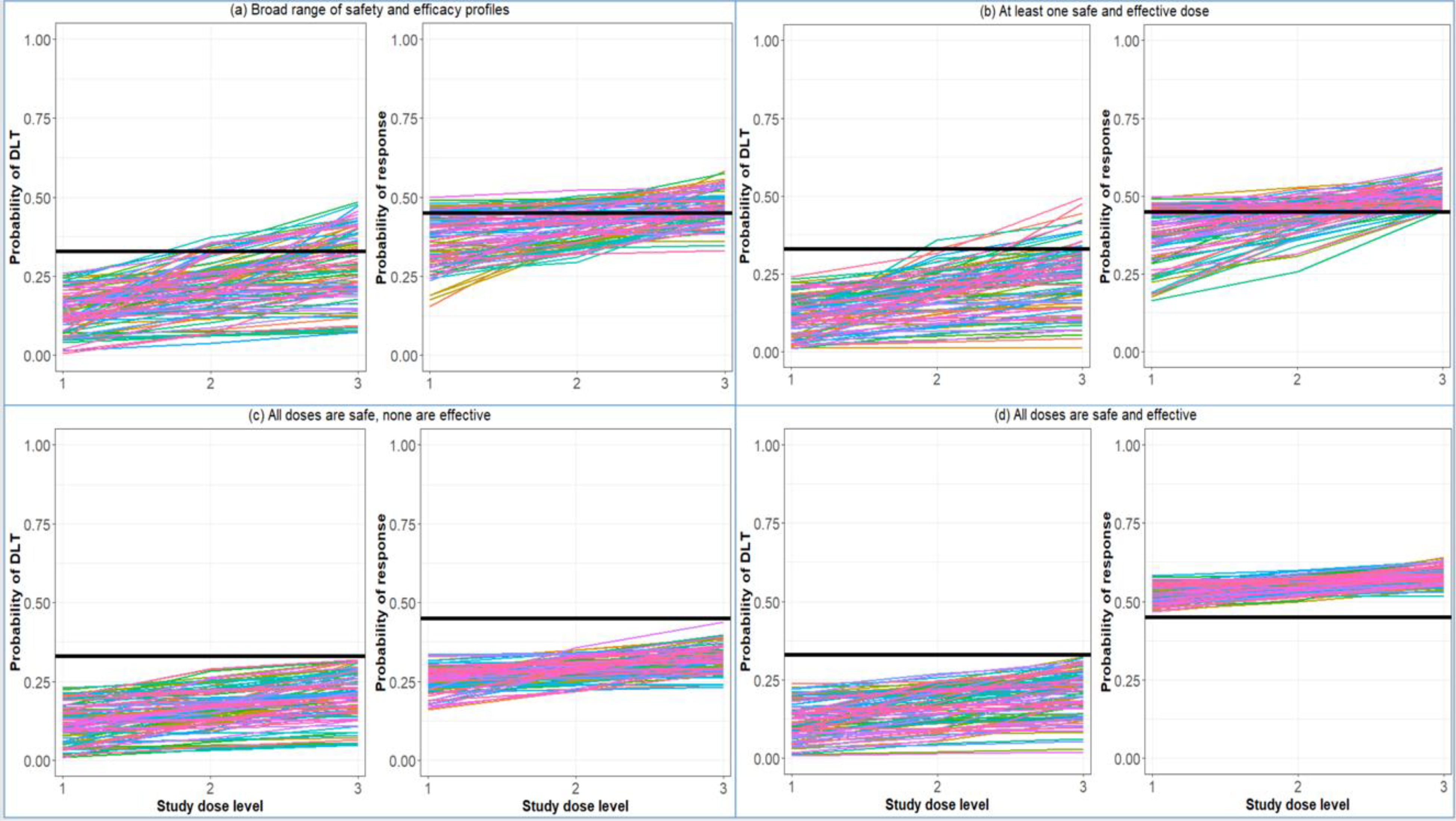
(Left sub-panel) 100 randomly generated dose-toxicity curves from the Conaway and Petroni² family of curves. (Right sub-panel) 100 randomly generated dose-response curves. (a) a broad range of safety and efficacy curves, (b) each scenario contains at least one safe and effective dose, (c) all doses are safe, but none are effective, and (d) all doses are safe and effective. Black solid lines represent thresholds for safety (DLT rate ≤33%) and efficacy (response rate ≥45%).

The results of this simulation study are provided in Figure 3. The probability of stopping for safety in Phase I ranged from 5–8% across the various situations explored [Figure 3 (a)]. Perhaps the most striking result is that the probability of stopping for safety in Phase II fell between 33% and 42%, even in the case in which all doses were safe [Figure 3 (b)]. This information could have been used to modify the stopping rules above so that the study would stop a low percentage of times when safe doses are being studied. If each scenario contained at least one safe and effective dose [Figure 2 (b)], the overall probability of completing Phase II was 47%. Note that this probability calculation only indicates completing the phase II portion of the study. The probability of completing phase II with evidence of an improved response rate is 39%. These percentages in the case in which all doses are safe and effective are 53% and 52%, respectively. Therefore, even in the best-case scenario that every dose is safe and effective, there is an approximate 50/50 chance that the study will stop early and fail to complete the Phase II component. These operating characteristics demonstrate the proposed study design’s poor performance and indicate that the protocol should be modified to improve the study’s scientific validity.

Figure 3:

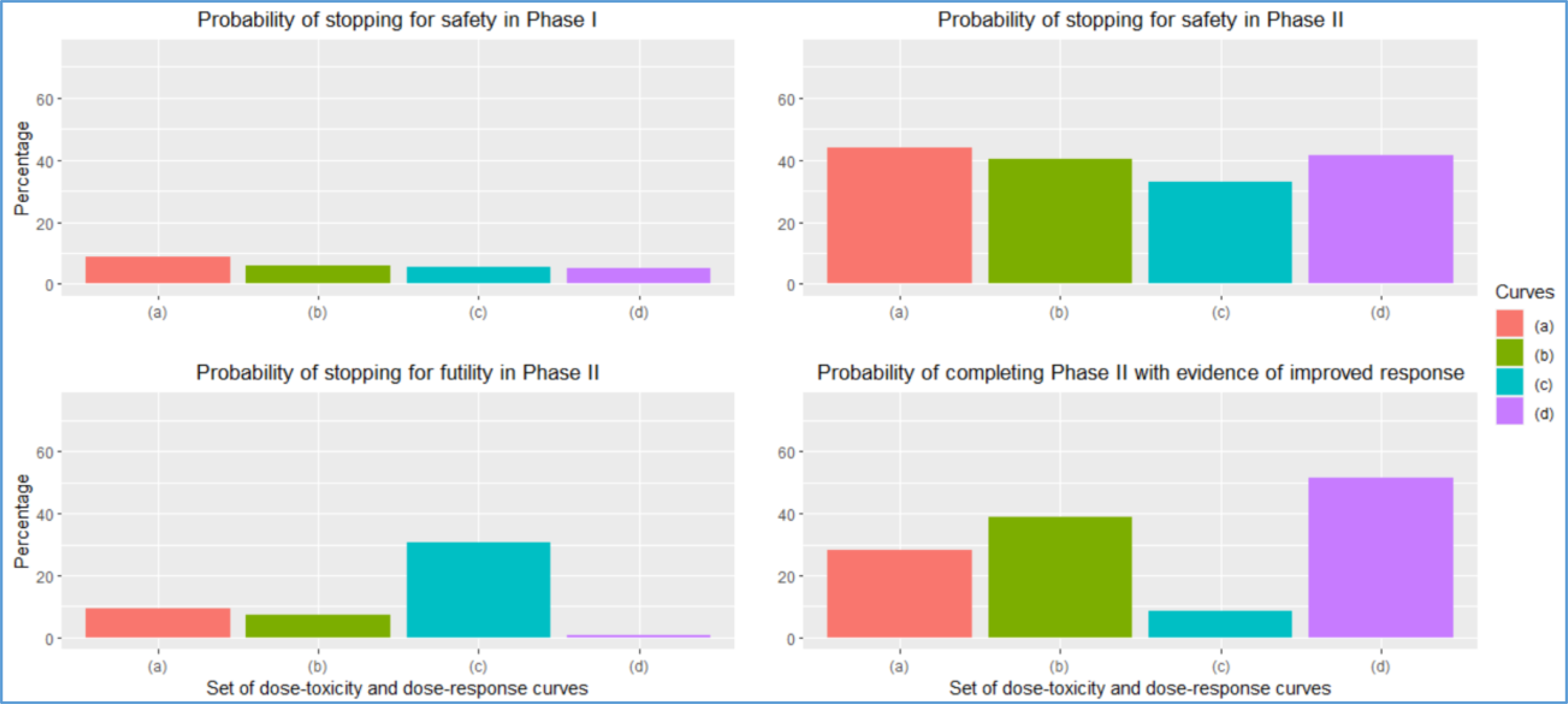
Operating characteristics for the design of Example 2 for each set of curves provided in Figure 2. The panels report (1) the probability of stopping for safety in Phase I, (2) the probability of stopping for safety in Phase II, (3) the probability of stopping for futility in Phase II, and (4) the probability of completing Phase II with evidence of improved response.

Trial example 3

Study information

The third example is a Phase I, open-label, dose-finding, first-in-human study to determine the safety, pharmacokinetics, and efficacy of Agent A when administered with Agent B, Agent C, or Agent D in subjects with non-metastatic or metastatic castration-resistant prostate cancer tumors. A ‘traditional’ 3+3 dose escalation scheme was proposed to determine the safety, maximum tolerated dose (MTD), and recommended Phase 2 dose (RP2D) of the combination, among six escalating dose levels of Agent A.

Statistical issues

In the protocol, the study team acknowledged the limitations of their chosen design, stating that “a disadvantage of this design is that it involves an excessive number of escalation steps, which results in a large proportion of subjects who are treated at low (i.e., potentially sub-therapeutic) doses while few subjects receive doses at or near the recommended dose for Phase 2 trials.” This statement is backed up by overwhelming evidence in the literature from the past 20 years^19–24. In addition to the design limitations, there is ambiguity in several design considerations that detailed operating characteristics would alleviate. For instance, the protocol states that “Part 2 (expansion) will further evaluate the safety and assess preliminary efficacy of Agent A and “Agent B or one of the other two combination drugs.” It is not clear which combinations will or will not be used in Part 2.

Moreover, the protocol indicates that 18–24 subjects will be needed for each of the three-drug combinations to determine the MTD. This statement seems to suggest that possibly three MTDs are being estimated, one for each combination. Again, it is unclear how many MTDs will be carried forward to Part 2 and how this will be determined. With the significant lack of clarity in the proposed design, the maximum (possible) number of subjects proposed for participation in this protocol remains unclear.

Operating characteristics

As acknowledged by the study team and demonstrated below, this study’s dose-escalation design has poor statistical properties. Although the 3+3 rule is widely-used, available alternatives, such as BOIN and the continual reassessment method (CRM), have (1) a much higher chance of correctly identifying the MTD and (2) available software (www.trialdesign.org²⁵, https://medstats-lancs.shinyapps.io/design/ ²⁶ and http://uvatrapps.uvadcos.io/crmb/²⁷) with the capability of generating a protocol statistical section template. Moreover, BOIN has transparent decision rules similar to the 3+3. The CRM has available software for generating dose transition pathways²⁸, which allows model-based dose assignments to be anticipated in one or more cohorts. Figure 4 provides a comparison of the 3+3 vs. BOIN for six study dose levels, as in the protocol, for 1000 simulated trials over 200 hypothesized dose-toxicity curves (200,000 total simulated trials) from the class of Conaway and Petroni² (Figure 4). The maximum sample size is n=36 participants, and the BOIN and CRM target a DLT rate of 25% to define the MTD. For the CRM, the DLT probabilities were sequentially updated after each cohort using the empiric model $p_i^{\exp \left(\beta \right)}$, where the p_i are pre-specified constants (termed skeleton) and β is a parameter to be adaptively updated by the accumulating data. The skeleton of the model p_i = (0.08, 0.16, 0.25, 0.35, 0.46, 0.56) was chosen according to the algorithm of Lee and Cheung²⁹, and the prior on the parameter β~(0, 0.624) was chosen according to the algorithm of Lee and Cheung³⁰. For all designs, dose assignment decisions are made in cohorts of size 3. The overall probability of correctly selecting the MTD is 18% for the 3+3 rule, 42% for the BOIN method, and 44% for the CRM. After a study with six dose levels, one of seven decisions can be made concerning the MTD selection. One of the six levels can be selected as the MTD, or no dose can be selected as the MTD when the trial is stopped early for safety concerns. If one were to randomly choose the dose as the MTD without conducting the study, there is a 1/7=14.3% probability of correctly selecting the MTD. In 61% of the hypothesized dose-toxicity curves, the 3+3 rule has worse operating characteristics than not doing the study and randomly selecting a dose as the MTD (Figure 4). Moreover, a commonly stated reason for using the 3+3 rule is that it is “fine when there are only 3 dose levels.” To evaluate this reasoning, we repeated the above simulation study on 100 randomly generated dose-toxicity curves with 3 dose levels, adjusting the maximum sample size to n=18 patients. The results are provided in Figure 5, which indicate that the overall probability of correctly selecting the MTD (target DLT rate 25%) is 45% for the 3+3 rule, 56% for the BOIN method, and 66% for the CRM. In 17% of the hypothesized curves, the 3+3 rule has worse operating characteristics than not doing the study and randomly selecting a dose as the MTD. The specification of certain tuning parameters, such as the skeleton and prior distribution described above, influences the design’s operating characteristics. Operating characteristics of adaptive designs should be assessed through the conduct of extensive simulation studies that demonstrate how pre-specified tuning parameters behave throughout the trial’s conduct.

Figure 4:

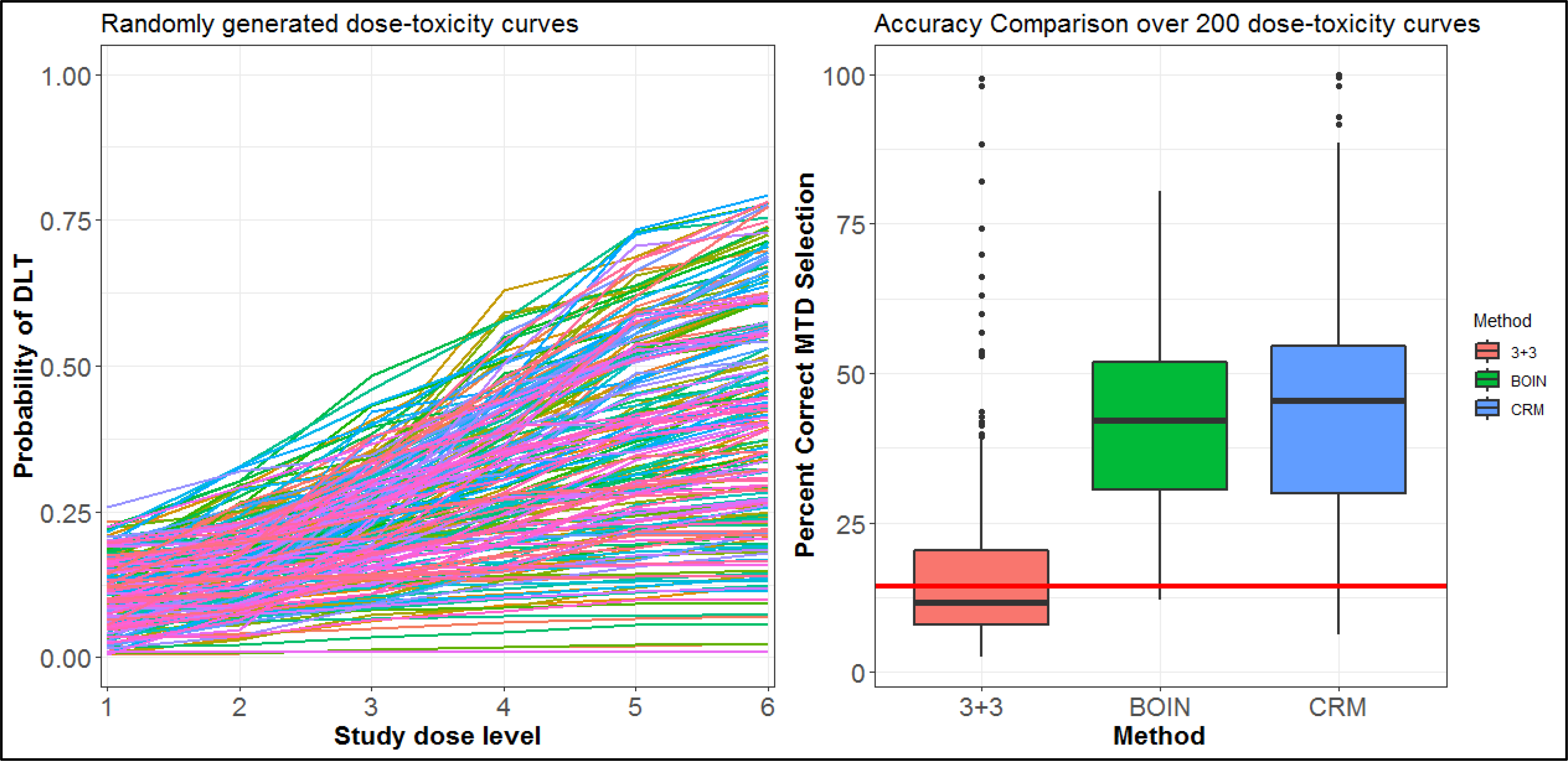
(Left panel) 200 randomly generated dose-toxicity curves from the Conaway and Petroni² family of curves. (Right panel) Box plot of the probability of correctly selecting the MTD over the 200 curves of six dose levels. The red line represents the probability of randomly choosing the correct dose as the MTD without conducting the study.

Figure 5:

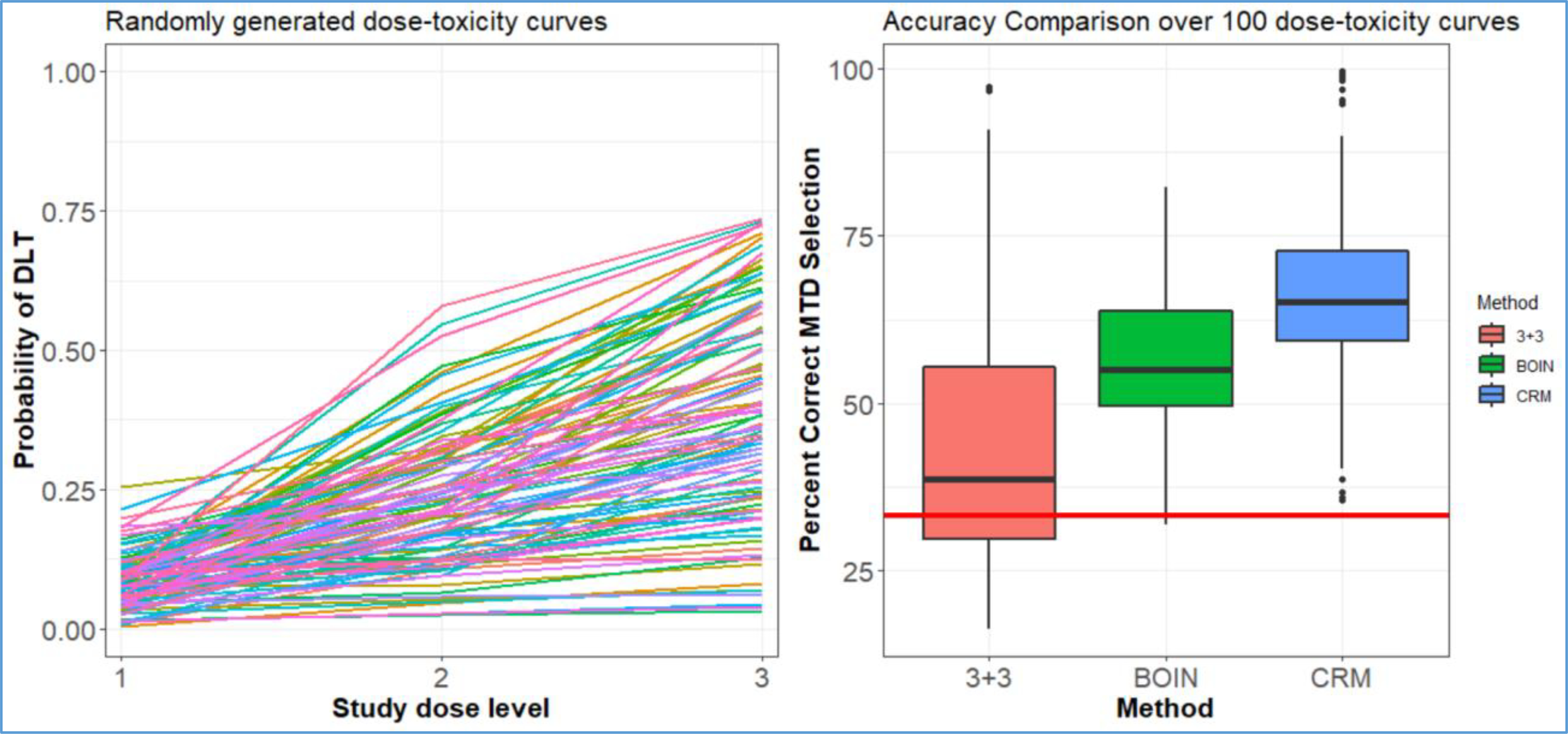
(Left panel) 100 randomly generated dose-toxicity curves from the Conaway and Petroni² family of curves. (Right panel) Box plot of the probability of correctly selecting the MTD over the 100 curves of three dose levels. The red line represents the probability of randomly choosing the correct dose as the MTD without conducting the study.

Discussion

In this paper, we have described how operating characteristics provide insight into how a particular design will perform in terms of safety and accuracy. In two of the three examples studied, we used the Conaway and Petroni² family of curves to generate random hypothesized dose-toxicity scenarios on which to evaluate operating characteristics of various dose-finding designs. A large number of random scenarios can be used by the statistical and clinical teams at the design stage to assess the general operating characteristics in a more objective way than selectively choosing a small set of scenarios to study. A smaller set of scenarios is generally more useful for inclusion in the protocol since they allow more details of the operating characteristics to be included in the simulation results and they can be tailored to what the study team anticipates reviewers would want to see in evaluating the design. For instance, a small set of scenarios is better able to isolate and highlight the behavior of the design in relevant situations including, but not limited to, cases in which “all doses are safe,” “moderate toxicity across the doses,” and “all doses are too toxic.”

Well-performing dose-finding methods can have a tremendous impact on the drug development process. The results of Conaway and Petroni² indicate that using the CRM or BOIN, rather than the 3+3 rule, substantially enhances the proportion of effective agents that have successful Phase III trials. The results underscore the importance of the choice of the early-phase designs³¹. The use of the 3+3 produces fewer agents with successful phase III trials compared with the CRM or BOIN. It’s important to emphasize that these results were for study designs that followed the simple single-agent prespecified increasing dose structure for determining the MTD. An additional limitation of the 3+3 algorithm in drug-combination trials is that it requires the pre-specification of a set of ordered doses. However, there may be pairs of combinations for which the ordering of the DLT probabilities is not known, making it problematic to correctly specify an ordered set of doses to explore. If the assumed order is not specified correctly or if several potentially promising dose combinations are excluded to simplify the problem, the 3+3 design may have zero probability of selecting the correct dose. Furthermore, ad hoc deviations (e.g., “nodes” that conditionally go down other paths) from the standard framework further reduces the ability of the 3+3 to identify appropriate doses to move into further development, as discussed below.

In current early-phase protocols, it is common to encounter “modified” versions of well-known designs that incorporate additional decision rules that the study team will make. In another example of a dose-escalation and expansion study of Agent A in combination with Agent B plus Agent C in advanced solid tumors, the protocol stated that “lower doses may be evaluated at the Sponsor’s discretion if ≥2 DLTs are noted in 2 of 6 patients assigned to the Cohort 0 dose level of Agent A.” It is unclear what dose levels would be considered and how their inclusion would impact RP2D determination. Such ambiguity is also frequently observed in protocols that rely heavily (or sometimes entirely) upon decisions to be made by a safety review committee. Such decisions include, but are not limited to, determination of dose escalation, cohort size for accrual, the inclusion of additional dose levels or schedules to be explored, and defining the MTD or RP2D. This lack of transparency complicates the generation of operating characteristics, thereby impeding the design’s overall evaluation. All decision rules should be incorporated in simulations to evaluate their impact on the trial conduct.

Another example comes from a Phase Ib-II study of novel oncology therapies combined with chemotherapy and Agent A as first-line therapy in metastatic microsatellite-stable colorectal cancer. The study’s dose-escalation portion is a modified toxicity probability interval-2 (MTPI-2) design³² to select the RP2D. While it is encouraging to see the proposal of a novel design, the protocol offered modified rules to those initially proposed in MTPI-2. For instance, some of the escalation (E) decisions displayed in Figure 3 of the MTPI-2 paper were replaced with a decision of “Completion” without further explanation. Without operating characteristics, the scientific validity of the chosen design cannot be assessed, especially in light of the modifications (i.e., “completion” instead of “escalation”) made to the original MTPI-2 method. It is essential to demonstrate how these modifications impact design performance.

Additional concerns commonly arise in the review of Phase I protocols that could be mitigated with the inclusion of design operating characteristics. The first is a frequent lack of sample size justification in the study’s ‘expansion’ phase. Concerns regarding the rationale for the sample size in expansion cohorts are addressed in the FDA’s latest draft guidelines on expansion cohorts. Section VI specifies that ‘the analysis plan for each expansion cohort should contain adequate information justifying the planned sample size based on the cohort objectives; for those cohorts evaluating anti-tumor activity, the plans should specify the magnitude of anti-tumor activity that would warrant further evaluation of the drug.’ The second common concern relates to the lack of safety stopping bounds in the expansion phase. As noted in Yan et al.³³, the general design strategy (Phase I into expansion or Phase II) is based upon the “assumption that the MTD is known reliably to be the ‘best’ dose, ignoring the fact that any estimate from a small sample has large uncertainty.” There should be clear guidelines for stopping the trial due to safety in both phases of the study. Stopping procedures are especially of concern since overuse of the 3+3 rule follows with expansion beginning after only six patients have been assessed on the recommended expansion dose. An easy way to do this is using Pocock-type¹⁸ boundaries using the software available at http://cancer.unc.edu/biostatistics/program/ivanova/ContinuosMonitoringForToxicity.aspx. The concerns above are also echoed in the latest draft guidelines from the FDA on expansion cohorts: (Section VI) notes, ‘Individual expansion cohorts should describe the pre-specified stopping rules for that cohort, based on insufficient anti-tumor activity or unacceptable level of toxicity for that population.’

As reviewers, we are often asked by clinical colleagues that if the 3+3 rule results in such poor operating characteristics, why is it proposed so often? In our experience, the logic used to answer this question is characterized by a circularity akin to that used to justify the use of 0.05 as a threshold for assessing p-values.³⁴ The 3+3 is often used because it is a known design strategy. It is known because it is often used. Such circular logic is then used to justify the omission of 3+3 operating characteristics in the protocol since it has been used so much. Responses from study teams often acknowledge that their chosen design is poor, but rationalize that the request is unfounded on the basis that they have never before been required to provide them. This flawed logic is further bewildering given that operating characteristics of 3+3 can be easily generated using the web application available at https://graham-wheeler.shinyapps.io/AplusB/ ³⁵ For instance, when asked to provide operating characteristics for the 3+3, one study team responded that “The 3+3 rule has been used in thousands of clinical trials spanning decades of development of pharmaceuticals and biologics. Please note the sponsor accepts that the 3+3 rule may not have optimal operating characteristics. The sponsor acknowledges there are more efficient designs but selected the 3+3 rule for this study due to its historical acceptance in this setting.” Historical use of the rule in the mid-20th century had initial merit. However, one would hope that research conducted in the 21st century would use designs that satisfy a high rigor and reproducibility standard. Operating characteristics can help facilitate the implementation of novel designs that are tailored to answer more complex research questions in early development^36–38. Given that the application of poor-quality study designs continues to be proposed and approved based upon historical practice, a final recommendation is to create a task force composed of statisticians from academia, industry, NIH, the FDA, etc. This task force should be charged with proposing minimum guidelines that should be adhered to in order to raise the level of rigor and reproducibility in the area of early phase clinical trials to that of later Phases.

Finally, a necessary component of the evaluation of operating characteristics is to have some notion for how well a design can possibly perform. In studying the efficiency and comparative performance of competing dose-finding designs, the nonparametric optimal benchmark³⁹ is a useful tool with an easy-to-use web application provided at http://uvatrapps.uvadcos.io/nonparbnch/. When comparing a dose-finding design to the optimal benchmark, we are able to assess how much room there is for potential improvement. While the concept of a benchmark for identifying the MTD based on a single binary toxicity endpoint (i.e., DLT) was first described by O’Quigley et al.³⁹, this concept has since been extended to a variety of more complex dose-finding settings^40–43, with R code for recent methods available at https://github.com/dose-finding.