rmRNAseq: differential expression analysis for repeated-measures RNA-seq data

Abstract

Motivation

With the reduction in price of next-generation sequencing technologies, gene expression profiling using RNA-seq has increased the scope of sequencing experiments to include more complex designs, such as designs involving repeated measures. In such designs, RNA samples are extracted from each experimental unit at multiple time points. The read counts that result from RNA sequencing of the samples extracted from the same experimental unit tend to be temporally correlated. Although there are many methods for RNA-seq differential expression analysis, existing methods do not properly account for within-unit correlations that arise in repeated-measures designs.

Results

We address this shortcoming by using normalized log-transformed counts and associated precision weights in a general linear model pipeline with continuous autoregressive structure to account for the correlation among observations within each experimental unit. We then utilize parametric bootstrap to conduct differential expression inference. Simulation studies show the advantages of our method over alternatives that do not account for the correlation among observations within experimental units.

Availability and implementation

We provide an R package rmRNAseq implementing our proposed method (function TC_CAR1) at https://cran.r-project.org/web/packages/rmRNAseq/index.html. Reproducible R codes for data analysis and simulation are available at https://github.com/ntyet/rmRNAseq/tree/master/simulation.

1 Introduction

One of the goals of transcriptomics data analysis is to identify genes whose mean transcript abundance levels differ across the levels of one or more categorical factors of interest. Such genes are typically referred to as differentially expressed (DE). Genes that are not DE are referred to as equivalently expressed (EE). Over the past decade, RNA sequencing (RNA-seq) technologies have emerged as powerful and increasingly popular tools for expression profiling and differential expression analysis (Oshlack et al., 2010). In a typical RNA-seq experiment, messenger RNA (mRNA) is extracted from each biological sample of interest. Molecules of mRNA are converted to complementary DNA (cDNA) fragments that are sequenced with high-throughput sequencing technology. This process generates millions of short reads from one or both ends of cDNA fragments. These short reads are mapped to the reference genome, and the number of mapped short reads for a gene represents a measurement of the transcript abundance level of that gene in a given sample.

With the decreasing price and increasing use of next-generation sequencing technologies, RNA-seq experimental designs have become more complex. As a motivating example, we consider an RNA-seq experiment conducted on eight pigs, four from a high residual feed intake line (HRFI) and four from a low residual feed intake line (LRFI). Researchers wanted to evaluate how pigs from different lines respond to a treatment (lipopolysaccharide, LPS) designed to stimulate the immune system, and how the responses change over time at the molecular genetic level. They used RNA-seq technology to measure transcript abundances in blood samples from each pig at four times after treatment: 0, 2, 6 and 24 h. The experiment is explained in greater detail in Section 3 of this article. A statistical model for these data should consider the within-unit correlation expected because of repeated measurements on each pig.

Many general purpose RNA-seq differential expression analysis methods have been developed, such as edgeR (Robinson et al., 2010), QuasiSeq (Lund et al., 2012), DESeq and DESeq2 (Anders and Huber, 2010; Love et al., 2014) among many others. These methods use negative binomial generalized linear models to analyze RNA-seq data and are appropriate for designs providing uncorrelated measurements within each gene. Furthermore, several methods have been developed for time-course designs, such as NextmaSigPro (Nueda et al., 2014), DyNB (Äijö et al., 2014), TRAP (Jo et al., 2014), SMARTS (Wise and Bar-Joseph, 2015) and EBSeq-HMM (Leng et al., 2015), which were collectively reviewed by Spies and Ciaudo (2015). A recent comparative analysis of differential expression tools for RNA-seq time-course data (Spies et al., 2019) pointed out that ImpulseDE2 (Fischer et al., 2018) and splineTimeR (Michna et al., 2016) are the top performing methods for time-course RNA-seq data. These two methods model the gene expression levels as continuous function of time through an impulse function (Fischer et al., 2018) or a natural cubic splines (Michna et al., 2016). However, these methods, as well as many other methods reviewed in Spies et al. (2019), do not take within-unit correlation of transcript abundance measurements into account, which may result in many false discoveries or failure to distinguish EE and DE genes.

Theoretically, a generalized linear mixed model (GLMM) approach can be used to account for random effects and general correlation structure, but the approach often suffers from convergence issues for many genes because RNA-seq experiments usually have a small sample size and many zero counts for many genes (Cui et al., 2016). In the context of large-sample-size microbiome studies with hundreds of observations per taxa, Zhang et al. (2017) proposed a negative binomial GLMM for microbiome data to detect significant taxa with respect to a factor of interest while accounting for correlation among samples through random effects. In principle, a similar approach could be used for RNA-seq data. However, the model considered by Zhang et al. (2017) involves independent, constant variance random effects that imply compound symmetric within-subjects correlation structures. Such structures imply equal correlation for all pairs of observations from the same subject and are not well suited for repeated-measures experiments, where correlations are expected to vary across pairs of time points as detailed in Section 2.3.

Given the limitations of existing approaches, a new statistical method that is stable numerically under small sample size circumstances and, at the same time, controls false discovery rate (FDR) well is desirable. One approach that addresses numerical instability when analyzing repeated-measures RNA-seq data is to use normal-error linear modeling for log-transformed counts instead of using discrete probability distributions, such as the negative binomial distribution.

Law et al. (2014) proposed the voom approach for analyzing log-transformed RNA-seq data with linear models that explicitly accounts for heteroscedasticity by the use of precision weights. They showed that correctly capturing the mean–variance relationship in the transformed data is more important than assuming a probability model that acknowledges the discrete characteristics of the original counts. In particular, by estimating precision weights for observations of transformed counts and including them in a general linear model framework, Law et al. (2014) showed that the log-transformed-based linear model approach performs better than methods based on negative binomial models. Furthermore, the voom approach facilitates more complex analyses, such as the variance component score test for gene set testing in longitudinal RNA-seq data recently proposed by Agniel and Hejblum (2017).

In our article, we will take advantage of the voom approach together with a parametric bootstrap method to detect DE genes with repeated-measures RNA-seq data. For each gene, we model the correlation among observations taken at unequally spaced time points by a continuous autoregressive correlation structure in a general linear model framework. Parameters are estimated by residual maximum likelihood (REML) using the gls function in the nlme R package (Pinheiro et al., 2017). We conduct hypothesis testing using a parametric bootstrap method. Simulation studies show the advantages of our method over alternatives that do not account for the correlation among observations within each gene in terms of FDR control and the ability to distinguish EE and DE genes. Although we focus on repeated-measures analysis in this article, it is straightforward to extend our method to other complex designs for which modeling dependence among observations within each gene is warranted.

The remainder of the article is organized as follows. We formally define our proposed method in Section 2, first by revisiting the voom procedure and then specifying the bootstrap strategy for inference. In Section 3, we apply the proposed method as well as other alternative methods to analyze the repeated-measures RNA-seq dataset that motivates our work. We compare the performance of our method with that of alternative methods by a simulation study in Section 4. The article concludes with a discussion in Section 5.

2 Methods

2.1 Notations and preliminaries

Consider the analysis of G genes using RNA-seq read count data from S subjects and T time points. For $g=1,\dots ,G,\hspace{0.17em}s=1,\dots ,S$, and $t=1,\dots ,T$, let c_gst be the read count for gene g from subject s at time t. Let ${\mathit{x}}_{st}=(\mathit{x}{\prime }_{st1},\dots ,\mathit{x}{\prime }_{\mathit{stk}})\prime$ be a vector encoding information on k explanatory variables for subject s at time t. The k explanatory variables may include multilevel factors of primary scientific interest and other continuous or multilevel categorical covariates. If the jth of k variables is a continuous covariate or a factor with two levels that can be coded by a single indicator variable, then ${\mathit{x}}_{\mathit{stj}}$ is a one-dimensional vector. If the jth variable is a factor with more than two levels, ${\mathit{x}}_{\mathit{stj}}$ has dimension one less than the number of levels of the jth variable to accommodate an indicator variable for all but one of its levels. Let $\mathit{X}=({\mathit{x}}_{11},\dots ,{\mathit{x}}_{1T},\dots ,{\mathit{x}}_{S1},\dots ,{\mathit{x}}_{ST})\prime$ and (without loss of generality) suppose that X has full-column rank with $\text{rank}(\mathit{X})=r$. Law et al. (2014) defined the following transformation to obtain the log-counts per million (log-cpm) for each count

$$y_{\mathit{gst}}={\hspace{0.17em}\text{log}\hspace{0.17em}}_2\left(\frac{c_{\mathit{gst}}+0.5}{C_{st}+1}\times {10}^6\right),$$ (1)

where $C_{st}=\sum _{g=1}^G{c}_{\mathit{gst}}$ is the sum of read counts computed for subject s at time t. In general, $\left\{C_{st}\right\}$ can be any normalization factors that account for technical differences in read count distributions across the RNA-seq samples. Many normalization procedures have been proposed in the literature (see, e.g. Anders and Huber, 2010; Bullard et al., 2010; Marioni et al., 2008; Mortazavi et al., 2008; Risso et al., 2014a, b; Robinson and Oshlack, 2010 and references therein). Throughout this article, we set C_st to be the 0.75 quantile of RNA-seq sample read counts from subject s at time t according to the recommendation of Bullard et al. (2010). With this choice for the normalization factor, the y_gst values are no longer ‘counts per million mapped reads’ on the log scale, but this interpretation is irrelevant for the differential expression analysis that is the focus of our work. Henceforth, we use ${\mathit{y}}_g$ to represent the response vector $(y_{g11},\dots ,y_{g1T},\dots ,y_{gS1},\dots ,y_{\mathit{gST}})\prime$ for gene g.

2.2 The voom procedure

The voom procedure (Law et al., 2014) estimates the mean–variance relationship of the log-transformed counts and generates a precision weight for each observation according to the following algorithm:

1. For each gene g, initially assume the linear model

   $$y_{\mathit{gst}}={\mathit{x}}_{st}^{\prime }{\mathit{\beta }}_g+{\epsilon }_{\mathit{gst}},$$

   where $\mathrm{E}({\epsilon }_{\mathit{gst}})=0$ and $\text{Var}({\epsilon }_{\mathit{gst}})={\sigma }_g^2$ for all $g=1,\dots ,G;\hspace{0.17em}s=1,\dots ,S;\hspace{0.17em}t=1,\dots ,T$
2. Let ${\tilde{\mathit{\beta }}}_g={(\mathit{X}\prime \mathit{X})}^{-1}\mathit{X}\prime {\mathit{y}}_g$ and

   $${\tilde{\sigma }}_g=\sqrt{\left({\mathit{y}}_g-\mathit{X}{\tilde{\mathit{\beta }}}_g\right)\prime \left({\mathit{y}}_g-\mathit{X}{\tilde{\mathit{\beta }}}_g\right)/d},$$

   where $d\equiv ST-r$.

3. Let ${\tilde{c}}_g=\frac{1}{ST}\sum _{s=1}^S\sum _{t=1}^T{y}_{\mathit{gst}}+\frac{1}{ST}{\hspace{0.17em}\text{log}\hspace{0.17em}}_2\left(\prod _{s=1}^S\prod _{t=1}^T(C_{st}+1)\right)-{\hspace{0.17em}\text{log}\hspace{0.17em}}_2({10}^6)$ be the mean log-count value for gene g.

4. Let $\text{lo}(·)$ be the predictor obtained by fitting a LOWESS regression (Cleveland, 1979) of ${\tilde{\sigma }}_g^{1/2}$ on ${\tilde{c}}_g$. The voom precision weight for y_gst is calculated by

   $$w_{\mathit{gst}}={\left[\text{lo}\left({\mathit{x}}_{st}^{\prime }{\tilde{\mathit{\beta }}}_g+{\hspace{0.17em}\text{log}\hspace{0.17em}}_2(C_{st}+1)-{\hspace{0.17em}\text{log}\hspace{0.17em}}_2({10}^6)\right)\right]}^{-4}.$$

2.3 Modeling for repeated-measure RNA-seq data

To account for the correlation among observations for each gene g, we assume the Gaussian general linear model

$${\mathit{y}}_g=\mathit{X}{\mathit{\beta }}_g+{\mathit{\epsilon }}_g,\hspace{1em}{\mathit{\epsilon }}_g\sim \mathcal{N}(\mathit{0},{\sigma }_g^2{\mathit{V}}_g),\hspace{1em}{\mathit{V}}_g={\mathit{W}}_g^{-1/2}{\mathit{A}}_g{\mathit{W}}_g^{-1/2},$$ (2)

where

$${\mathit{W}}_g=\left[\begin{array}{cccc}{w}_{g11}& 0& \dots & 0\\ 0& w_{g12}& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & w_{\mathit{gST}}\end{array}\right]$$

is the matrix of precision weights and ${\mathit{A}}_g$ is an ST × ST block-diagonal correlation matrix consisting of S identical blocks of dimension T × T that model correlations among the T observations for each subject. We use ${\mathit{R}}_g$ to represent the T × T block for gene g. In the most general case, ${\mathit{R}}_g$ has $\left(\begin{array}{c}T\\ 2\end{array}\right)$ gene-specific correlation parameters. However, unless the number of subjects S is large, reliable estimates for $\left(\begin{array}{c}T\\ 2\end{array}\right)$ parameters may not be readily available. As in a typical repeated-measures experiment with a single response variable, we consider a structured block correlation matrix to reduce the number of parameters and achieve more stable parameter estimation as a potential alternative to unstructured estimation of ${\mathit{R}}_g$.

While many structures could be considered, we focus on the continuous autoregressive structure of order one (CAR1) referred to as corCAR1 in nlme::gls, the gls function of the nlme R package (Pinheiro et al., 2017). The CAR1 structure is given by

$${\mathit{R}}_g=\left[\begin{array}{cccc}1& {\rho }_g^{|{\tau }_1-{\tau }_2|}& \dots & {\rho }_g^{|{\tau }_1-{\tau }_T|}\\ {\rho }_g^{|{\tau }_2-{\tau }_1|}& 1& \dots & {\rho }_g^{|{\tau }_2-{\tau }_T|}\\ ⋮& ⋮& \ddots & ⋮\\ {\rho }_g^{|{\tau }_T-{\tau }_1|}& {\rho }_g^{|{\tau }_T-{\tau }_2|}& \dots & 1\end{array}\right],$$ (3)

where ${\tau }_1,\dots ,{\tau }_T\in \mathbb{R}$ and ${\rho }_g\in [0,1)$ is a gene-specific correlation parameter. Typically, ${\tau }_1,\dots ,{\tau }_T$ are set equal to the T observation times so that observations taken closer together in time are modeled as more strongly correlated than observations taken farther apart in time. For instance, in our motivating dataset, mRNA samples from each subject are measured at times 0, 2, 6 and 24 h after treatment with LPS, so it would be customary to set ${\tau }_1=0,\hspace{0.17em}{\tau }_2=2,\hspace{0.17em}{\tau }_3=6$, and ${\tau }_4=24$, implying that observations taken at 0 and 2 h would be most correlated while observations taken at 0 and 24 h would be least correlated. However, mRNA levels may display circadian effects, which could lead to higher rather than lower correlation for observations taken exactly 24 h apart. Thus, rather than allowing measurement times to dictate ${\tau }_1,\dots ,{\tau }_T$, we use our data observed for thousands of genes to find values for ${\tau }_1,\dots ,{\tau }_T$ that make the CAR1 structure in (3) a useful approximation to the within-subjects correlation block for each gene.

2.3.1 Parameter estimation for the CAR1 correlation structure

Our idea for estimating ${\tau }_1,\dots ,{\tau }_T$ in (3) is to arrange ${\tau }_1,\dots ,{\tau }_T$ on the real line so as to maximize the average REML log-likelihood for model (2) with ${\mathit{R}}_g$ as in (3), where the average is taken over all genes. Without loss of generality, we place ${\tau }_1,\dots ,{\tau }_T$ in the interval $[0,1]$, with the pair of time points that tends to be most weakly correlated at the endpoints of the interval. More formally, our estimation strategy is as follows.

• For each gene g, fit model (2) by initially assuming ${\mathit{R}}_g$ is an unstructured T × T correlation matrix. Obtain REML estimates of the $T(T-1)/2$ correlation parameters for each gene.

• Identify the pair of time points $\{i,j\}\subset \{1,\dots ,T\}$ with the smallest median REML correlation estimate, where the median is taken across all genes. Let ${\mathcal{T}}_{01}$ be the set of $\mathit{\tau }=({\tau }_1,\dots ,{\tau }_T)\prime$ vectors with ith element 0, jth element 1, and all other elements distinct values in (0, 1).

• For each gene $g=1,\dots ,G$ and any $\mathit{\tau }\in {\mathcal{T}}_{01}$, let ${\ell }_g({\sigma }_g^2,{\rho }_g|\mathit{\tau })$ be the REML log-likelihood for model (2) with ${\mathit{R}}_g$ as in (3). Let ${\widehat{\sigma }}_g^2(\mathit{\tau })$ and ${\widehat{\rho }}_g(\mathit{\tau })$ be the maximizers of ${\ell }_g({\sigma }_g^2,{\rho }_g|\mathit{\tau })$. Estimate $\mathit{\tau }$ by

  $$\widehat{\mathit{\tau }}\equiv \underset{\mathit{\tau }\in {\mathcal{T}}_{01}}{\text{argmax}}\sum _{\mathrm{g}=1}^{\mathrm{G}}{\mathrm{l}}_{\mathrm{g}}({\widehat{\sigma }}_{\mathrm{g}}^2(\mathit{\tau }),{\widehat{\rho }}_{\mathrm{g}}(\mathit{\tau })|\mathit{\tau }).$$

Given $\widehat{\mathit{\tau }}$, we apply nlme::gls with the CAR1 correlation structure to the data from each gene to obtain the REML estimators ${\widehat{\sigma }}_g^2\equiv {\widehat{\sigma }}_g^2(\widehat{\mathit{\tau }})$ and ${\widehat{\rho }}_g\equiv {\widehat{\rho }}_g(\widehat{\mathit{\tau }})$ of ${\sigma }_g^2$ and ρ_g, respectively, as well as the plug-in estimator ${\widehat{\mathit{V}}}_g={\mathit{W}}_g^{-1/2}{\widehat{\mathit{A}}}_g{\mathit{W}}_g^{-1/2}$ of ${\mathit{V}}_g$, where $\mathit{\tau }$ and ρ_g in ${\mathit{R}}_g$ (${\mathit{A}}_g$) are replaced by $\widehat{\mathit{\tau }}$ and ${\widehat{\rho }}_g$, respectively, to obtain ${\widehat{\mathit{R}}}_g$ (${\widehat{\mathit{A}}}_g$). The generalized least squares estimator of ${\mathit{\beta }}_g$ is then given by ${\widehat{\mathit{\beta }}}_g\equiv {(\mathit{X}\prime {\widehat{\mathit{V}}}_g^{-1}\mathit{X})}^{-1}\mathit{X}\prime {\widehat{\mathit{V}}}_g^{-1}{\mathit{y}}_g$.

2.3.2 Parameter estimation for unstructured correlation blocks

By assuming that ${\mathit{R}}_g$ follows the CAR1 structure in (3), the total number of correlation parameters is reduced to G + T, which can be a substantial reduction relative to the $G\left(\begin{array}{c}T\\ 2\end{array}\right)$ parameters needed when ${\mathit{R}}_g$ is unstructured. Although reducing the number of parameters leads to lower-variability estimators, estimation bias can become a problem if the true correlation structure for many genes deviates sufficiently from CAR1. In such cases, or when the number of subjects S is large enough to permit reliable estimation of $G\left(\begin{array}{c}T\\ 2\end{array}\right)$ parameters, model (2) with unstructured ${\mathit{R}}_g$ may be preferred. Furthermore, the unstructured estimator plays an important role in our parametric bootstrap approach to inference, as described in Section 2.5.

To obtain an unstructured estimator of ${\mathit{R}}_g$ and the corresponding REML estimator of ${\sigma }_g^2$ for $g=1,\dots ,G$, we apply nlme::gls with the unstructured correlation to the data from each gene. For $g=1,\dots ,G$, the unstructured estimator of ${\mathit{R}}_g$ is used as in the CAR1 case to obtain the generalized least squares estimator of ${\mathit{\beta }}_g$ for each gene $g=1,\dots ,G$. We use ${\breve{\mathit{R}}}_g,\hspace{0.17em}{\breve{\mathit{V}}}_g,\hspace{0.17em}{\stackrel{⌣}{\sigma }}_g^2$, and ${\breve{\mathit{\beta }}}_g$ to denote estimators of ${\mathit{R}}_g,\hspace{0.17em}{\mathit{V}}_g,\hspace{0.17em}{\sigma }_g^2$, and ${\mathit{\beta }}_g$ when ${\mathit{R}}_g$ is assumed to be unstructured. Whether ${\mathit{R}}_g$ is estimated under the CAR1 restriction or allowed to be unstructured, the corresponding REML estimator of ${\sigma }_g^2$ is improved by borrowing information from all genes using the approach described in Section 2.4.

2.4 Shrinkage estimators of error variances

In microarray analysis, Smyth (2004) showed that shrinking estimated error variances toward a pooled estimate can stabilize inference when the number of arrays is small. We follow the same procedure to obtain the shrinkage estimator of the error variance ${\sigma }_g^2$ for each gene. In this section, we describe how ${\widehat{\sigma }}_g^2$ (the estimator of error variance under the CAR1 model) can be improved via shrinkage to obtain a new error variance estimator denoted as ${\widehat{s}}_g^2$. The same arguments apply for improving ${\stackrel{⌣}{\sigma }}_g^2$ (the estimator of error variance under the unstructured model) via shrinkage to obtain a new error variance estimator denoted as ${\stackrel{⌣}{s}}_g^2$.

For shrinkage of ${\widehat{\sigma }}_g^2$, we assume that

$${\widehat{\sigma }}_g^2|{\sigma }_g^2\sim {\sigma }_g^2\frac{{\chi }_d^2}{d}$$ (4)

and, for some parameters ${\sigma }_0^{\mathrm{2}}$ and d₀,

$$\frac{d_0{\sigma }_0^{\mathrm{2}}}{{\sigma }_g^2}\sim {\chi }_{d_0}^2,$$

which together with (4) implies an inverse-gamma conditional distribution for ${\sigma }_g^2$ specified by

$$\frac{1}{{\sigma }_g^2}|{\widehat{\sigma }}_g^2\sim \text{Gamma}\left(\frac{d+d_0}{2},\frac{d{\widehat{\sigma }}_g^2+d_0{\sigma }_0^{\mathrm{2}}}{2(d+d_0)}\right).$$

A shrinkage estimator of ${\sigma }_g^2$ is given by

$${\widehat{s}}_g^2={\widehat{E}}^{-1}({\sigma }_g^{-2}|{\widehat{\sigma }}_g^2)=\frac{d{\widehat{\sigma }}_g^2+{\widehat{d}}_0{\widehat{\sigma }}_0^{\mathrm{2}}}{d+{\widehat{d}}_0},$$ (5)

where ${\widehat{d}}_0$ and ${\widehat{\sigma }}_0^{\mathrm{2}}$ are the estimators of the hyper-parameters d₀ and ${\sigma }_0^{\mathrm{2}}$ obtained from the theoretical marginal distribution of ${\widehat{\sigma }}_g^2$ using a method of moments approach (Smyth, 2004). The shrinkage estimators ${\widehat{s}}_g^2$ and ${\stackrel{⌣}{s}}_g^2$ will be used through subsequent steps of our analysis instead of the unshrunken REML estimators ${\widehat{\sigma }}_g^2$ and ${\stackrel{⌣}{\sigma }}_g^2$.

2.5 General hypothesis testing of regression coefficients using moderated F-Statistics

Suppose for each gene g we are interested in testing a null hypothesis of the form

$$H_{0g}:\mathit{C}{\mathit{\beta }}_g=\mathbf{0}\hspace{1em}\text{vs}.\hspace{1em}{\mathrm{H}}_{\text{ag}}:\mathit{C}{\mathit{\beta }}_{\mathrm{g}}\ne \mathbf{0},$$

where C is a matrix whose l rows are linearly independent elements of the row space of X. An extension of the moderated F-statistic of Smyth (2004) for gene g is defined as

$$F_g=\frac{(\mathit{C}{\widehat{\mathit{\beta }}}_g-\mathbf{0})\prime {(\mathit{C}{(\mathit{X}\prime {\widehat{\mathit{V}}}_g^{-1}\mathit{X})}^{-1}\mathit{C}\prime )}^{-1}(\mathit{C}{\widehat{\mathit{\beta }}}_g-\mathbf{0})}{l{\widehat{s}}_g^2}.$$ (6)

In general, $\mathit{C}{\widehat{\mathit{\beta }}}_g$ is a non-linear function of ${\mathit{y}}_g$ with an exact null distribution that is unknown even when model (2) holds exactly. Because RNA-seq experiments often have small sample size, we cannot rely on asymptotic approximations of the null distribution of F_g. Traditional F approximations to the distribution of F_g would not account for variation due to estimation of ${\mathit{V}}_g$ or uncertainty introduced by the process of determining observation-specific weights with voom. Thus, we approximate the null distribution of F_g using a parametric bootstrap approach (Efron and Tibshirani, 1993). For all $g=1,\dots ,G$, we carry out the following steps:

• 1. Generate ${\mathit{\epsilon }}_g^{*}\sim \mathcal{N}(\mathit{0},{\stackrel{⌣}{s}}_g^2{\breve{\mathit{V}}}_g)$ and calculate ${\mathit{y}}_g^{*}=\mathit{X}{\breve{\mathit{\beta }}}_g+{\mathit{\epsilon }}_g^{*}$.

• 2. Calculate $c_{\mathit{gst}}^{*}$ using $y_{\mathit{gst}}^{*}$ according to (1), i.e.

  $$c_{\mathit{gst}}^{*}=\max \{2^{y_{\mathit{gst}}^{*}}\times (C_{st}+1)/{10}^6-0.5,0\}.$$

• 3. Apply the voom procedure described in Section 2.2, fit the CAR1 model as described in Section 2.3.1, and shrink the resulting estimates of error variance as described in Section 2.4 to obtain ${\widehat{\rho }}_g^{*},\hspace{0.17em}{\widehat{\mathit{V}}}_g^{*},\hspace{0.17em}{\widehat{\mathit{\beta }}}_g^{*}$, and ${\widehat{s}}_g^{2*}$ from $\left\{c_{\mathit{gst}}^{*}\right\}$ and X just as ${\widehat{\rho }}_g,\hspace{0.17em}{\widehat{\mathit{V}}}_g,\hspace{0.17em}{\widehat{\mathit{\beta }}}_g$, and ${\widehat{s}}_g^2$ were obtained from $\left\{c_{\mathit{gst}}\right\}$ and X.

• 4. Compute

  $$F_g^{*}=\frac{(\mathit{C}{\widehat{\mathit{\beta }}}_g^{*}-\mathit{C}{\breve{\mathit{\beta }}}_g)\prime {(\mathit{C}{(\mathit{X}\prime {\widehat{\mathit{V}}}_g^{*-1}\mathit{X})}^{-1}\mathit{C}\prime )}^{-1}(\mathit{C}{\widehat{\mathit{\beta }}}_g^{*}-\mathit{C}{\breve{\mathit{\beta }}}_g)}{l{\widehat{s}}_g^{2*}}.$$

• 5. Repeat steps 1 through 4 a total of B times to obtain null statistics $F_{g1}^{*},\dots ,F_{gB}^{*}$.

Note that we use estimates from the unstructured model when creating our bootstrap data in step 1 but then fit the CAR1 model to the bootstrapped data in step 3. This provides our approach with robustness to departures from the CAR1 model because we are able to approximate the distribution of our CAR1-based test statistic when data come from a more complex unstructured model. When computing $F_g^{*}$ in step 4, $\mathit{C}{\breve{\mathit{\beta }}}_g$ is used in place of the hypothesized value 0 that appears in the test statistic in (6). Thus, $F_g^{*}$ can be viewed as a statistic for testing the null hypothesis $\mathit{C}{\mathit{\beta }}_g=\mathit{C}{\breve{\mathit{\beta }}}_g$, which is a true null due to the mechanism used for generating the bootstrap data in step 1. In this way, $F_g^{*}$ serves as a draw from the approximate null distribution of F_g.

Taking advantage of the parallel structure in which the same model is fitted for each of many gene, we combine the bootstrap null statistics for all genes to calculate a p-value for each gene. Numerically, the P-value for gene g is calculated by the proportion of all bootstrap null statistics $\{F_{g1}^{*},\dots ,F_{gB}^{*}:g=1,\dots ,G\}$ that match or exceed the observed statistic F_g, i.e.

$$p_g=\frac{1}{GB+1}\left(1+\sum _{g=1}^G\sum _{b=1}^B \mathbb{1}(F_{gb}^{*}\ge F_g)\right),$$ (7)

where $\mathbb{1}$ is an indicator function. The constant 1 is added to both numerator and denominator as recommended in Davison and Hinkley (1997) and Phipson and Smyth (2010). These P-values are converted to q-values (Storey, 2002). To approximately control FDR at any desired level α, a null hypothesis is rejected if and only if its q-value is less than or equal to α. When calculating q-values by the method of Storey (2002), we need an estimate of G₀, the number of true null hypotheses among all G null hypotheses tested. In this article, G₀ is estimated by the histogram-based method of Nettleton et al. (2006). Theoretical properties of a closely related histogram-based approach were established by Liang and Nettleton (2012). The approach of pooling as in (7) is used by Storey et al. (2005) in a time-course microarray analysis.

3 Analysis of an LPS RNA-Seq dataset

In this section, we apply our proposed method, rmRNAseq, and three other methods—DESeq2 (Love et al., 2014), voom-limma (Law et al., 2014) and edgeR (Robinson et al., 2010; Lun et al., 2016)—to analyze an RNA-seq dataset from a study of the inflammatory response in pigs triggered by LPS at the transcription level (Liu, 2017, Chapter 2). The experiment design is described as follows. Four pigs of each residual feed intake line, HRFI and LRFI, were injected LPS from Escherichia coli 05:B5 bacteria. Blood samples were collected from the eight pigs immediately before the injection (time point 0 in the following) and 2, 6 and 24 h after the injection. An RNA sample was extracted and sequenced from each blood sample. In total, there were 4 (pigs) × 2 (lines) × 4 (time points) = 32 RNA-seq samples. We focus on identifying genes DE between lines (Line) and genes DE across time points (Time).

This is an example of a repeated-measures design, where RNA samples were extracted from each pig at four different unequally spaced time points. The RNA-seq dataset consists of read counts for 11 911 genes for each of 32 RNA samples. Following standard practice, this dataset excludes genes with mostly low read counts because such genes contain little information about differential expression. In particular, the 11 911 genes analyzed in this study each have average read counts of at least 8 and no more than 28 zero counts across 32 RNA samples. The same threshold for gene inclusion was used throughout the simulation studies described in Section 4.

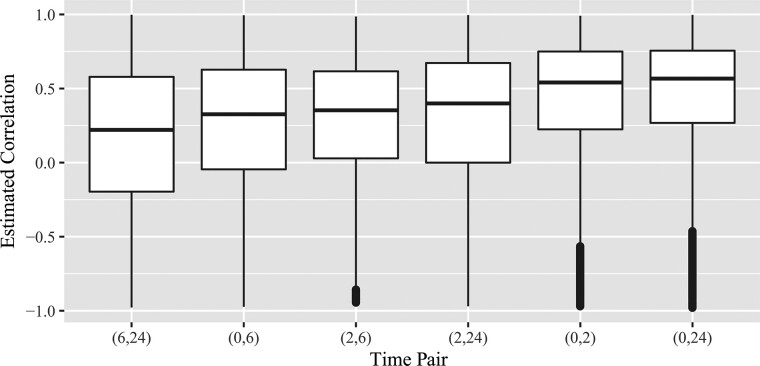
A special characteristic of this experiment is the potential for circadian rhythm effects that may induce correlation between observations taken at the same time of day. Thus, although times 0 and 24 are farthest apart when time is considered to unfold on a linear axis, the correlation between the time 0 and 24 observations may be large because these observations are taken at the same time of day. To evaluate this possibility, we conducted a preliminary analysis of the LPS RNA-seq dataset by applying the voom procedure and model (2) as in Section 2.3, where ${\mathit{R}}_g$ is a T × T correlation matrix with blocks of the unstructured form

$${\mathit{R}}_g=\left[\begin{array}{cccc}1& {\rho }_{g1}& {\rho }_{g2}& {\rho }_{g3}\\ {\rho }_{g1}& 1& {\rho }_{g4}& {\rho }_{g5}\\ {\rho }_{g2}& {\rho }_{g4}& 1& {\rho }_{g6}\\ {\rho }_{g3}& {\rho }_{g5}& {\rho }_{g6}& 1\end{array}\right],\hspace{1em}0\le {\rho }_{g1},\dots ,{\rho }_{g6}\le 1,$$

instead of the CAR1 form described in Section 2.3. The mean structure of the data is modeled by $\mathit{X}{\mathit{\beta }}_g$, where the design matrix X is constructed so that there are eight different means, one for each combination of Time and Line. Figure 1 shows boxplots of correlations across all 11 911 genes for each pair of time points. Both the average and median correlations increase across the time pair sequence (6, 24), (0, 6), (2, 6), (2, 24), (0, 2), (0, 24). This empirical evidence suggests that the circadian rhythm effects on correlations may be relevant. In particular, the estimated correlation between time 6 and time 24 tends to be smallest, and the estimated correlation between time 0 and time 24 tends to be largest. The estimate of $\mathit{\tau }$ obtained by our method proposed in Section 2.3.1 is $\widehat{\mathit{\tau }}=(0.26,0.52,1,0)\prime$.

Fig. 1.

Estimated correlations across all 11 911 genes for each pair of time points using the procedure in Section 2.3.2 applied to the log-transformed LPS RNA-seq data

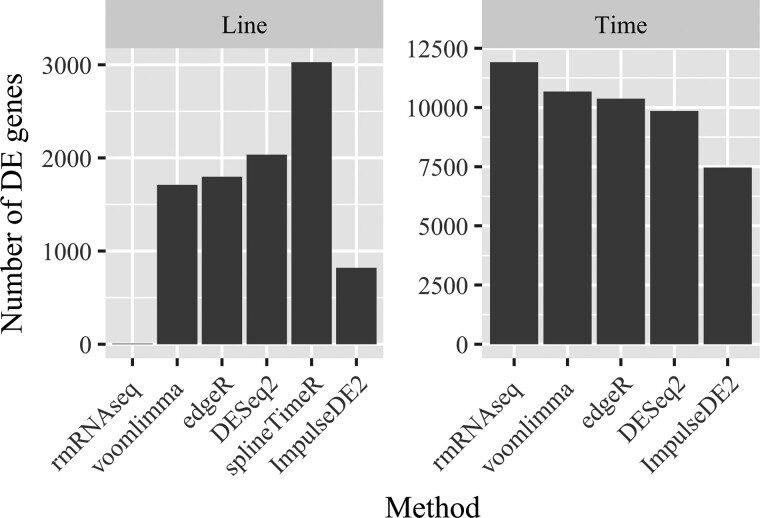
Now we apply our proposed method, rmRNAseq, the popular RNA-seq analysis methods—voom-limma, edgeR and DESeq2—and the top performing methods for time-course RNA-seq—splineTimeR, ImpulseDE2—which ignore correlation among observations. For illustration purposes, we present results for the Line main effect test (a between-subjects comparison) and for the Time main effects test (a within-subjects comparison). Figure 2 summarizes the analysis results of these methods when FDR is nominally controlled at 5%. Recall that both DESeq2 and edgeR utilize negative binomial generalized linear models. DESeq2 uses shrinkage estimation for dispersion parameters and fold changes to improve the stability and interpretability of estimates, while edgeR employs its own version of shrinkage estimation for dispersion parameters and does not shrink log fold change estimates. Analyses conducted with voom-limma, edgeR use default settings with 75th quartile normalization, while for DESeq2, splineTimeR and ImpulseDE2, we use their default settings and normalization method. To conduct inference about the contrasts of interest, we use the likelihood ratio test in DESeq2, ImpulseDE2, the moderated F-test in splineTimeR and the quasi-likelihood F-test in edgeR. The result based on splineTimeR is only available for the Line main effect test because the Time main effects test is not currently implemented in the available R package. It is clear from Figure 2 that our proposed method detects the fewest DE genes for the Line main effect test and detects the largest number of DE genes for Time main effects test.

Fig. 2.

Bar diagrams showing numbers of DE genes (FDR is nominally controlled at 0.05) with respect to Line and Time main effects when analyzing the LPS RNA-seq dataset using our method (rmRNAseq), voom-limma, edgeR, DESeq2, splineTimeR and ImpulseDE2

The differences between our proposed method and the others arise because voom-limma, edgeR, DESeq2, splineTimeR and ImpulseDE2 ignore the correlation among observations induced by the repeated measures. When within-subjects correlations are constrained to be zero, the 32 observations for any gene are treated as if they come from 32 independent experimental units rather than just the 8 experimental units used in our example experiment. The variance of the difference between line effect estimators is then underestimated because of the over-optimistic view of the experimental design that results when within-subjects correlations are constrained to zero, which in turn results in liberal inferences for line main effects. In contrast, within-subjects inferences about time effects become conservative when the positive correlation between observations on a single subject taken at two time points is ignored because the variance of a difference between estimators decreases as the correlation between estimators increases.

4 Simulation study

We consider two simulation scenarios described in detail in Sections 4.1 and 4.2, respectively. In each scenario, rmRNAseq, voom-limma, edgeR, DESeq2, Symm (general linear model with unstructured correlation), CAR1 (general linear model with CAR1 correlation), ImpulseDE2, splineTimeR and splineTimeRvoom (which is splineTimeR method using log-transformed counts and voom precision weights) are compared in terms of their ability to identify DE genes while controlling FDR. Such comparisons require simulated datasets to contain both EE and DE genes with respect to contrasts of interest. Within each scenario, we consider two contrasts: (1) Line: the main effect of the factor Line and (2) Time: the main effect of the factor Time. For each scenario and contrast, we simulate 50 datasets. Each dataset includes read counts for eight pigs at four time points and 5000 genes. The read counts are simulated based on (1) and (2) by first generating the log-transformed count for each gene as a sum of linear combination of fixed-effects plus random noise as described in (2), which in turn is inversely transformed to a count as shown in (1).

All compared methods use a full-column rank design matrix formulated to allow for additive effects of two factors Line and Time. Analyses conducted with edgeR, voom-limma and splineTimeRvoom use default settings with 75th quartile normalization; for ImpulseDE2 and DESeq2, we use their default normalization method, which is the median ratio method described in Anders and Huber (2010). To obtain P-values, Symm and CAR1 use, as a reference distribution, F-distribution with 24 denominator degrees of freedom and 1 numerator degrees of freedom for Line and 3 numerator degrees of freedom for Time; voom-limma (Law et al., 2014), splineTimeR (Michna et al., 2016) and splineTimeRvoom use moderated F-statistics; edgeR (Lund et al., 2012) uses quasi-likelihood F-tests, DESeq2 (Love et al., 2014) and ImpulseDE2 (Fischer et al., 2018) use likelihood ratio tests. The approaches based on splineTimeR and splineTimeRvoom are only available for the contrast Line because the Time main effect contrasts are not currently implemented in the available R package. ImpulseDE2 is implemented for both Line and Time tests.

We emphasize that our simulation study considers two contrasts of interest. This is different from most simulation studies where only two-group comparisons are considered to evaluate the performance of a differential expression analysis method. Our simulation setting allows us to fully investigate effects of within-unit correlation on the inference of within-subjects and between-subjects contrasts.

4.1 Simulation scenario 1: CAR1 correlation structure

The first simulation scenario provides a favorable case for our proposed method in which the read counts are simulated from the working model assumptions (1) and (2) with ${\mathit{R}}_g$ following the CAR1 correlation structure. As true parameter values for simulating new data, we use the $\left\{C_{st}\right\}$ normalization factors, the estimates of the precision weight matrix ${\mathit{W}}_g$, the correlation parameter ${\widehat{\rho }}_g$, the variance parameter ${\widehat{s}}_g^2$ and the regression coefficients ${\widehat{\mathit{\beta }}}_g$ obtained using our proposed method applied to the LPS RNA-seq dataset, except that we set partial regression coefficients corresponding to the contrast of interest to zero for a subset of genes to permit simulation of EE genes with respect to the contrast of interest. More specifically, the 5955 least significant partial regression coefficients for the contrast of interest are set to zero. This strategy yields a parameter set (consisting of the $\left\{C_{st}\right\}$ normalization factors, the precision weight matrices ${\mathit{W}}_g$, the correlation parameters ${\widehat{\rho }}_g$, the error variance parameters ${\widehat{s}}_g^2$ and the regression coefficients based on ${\widehat{\mathit{\beta }}}_g$) for each of 5955 EE genes, and $11911-5955=5956$ DE genes for a given contrast. To simulate any particular dataset for a given contrast of interest, we randomly sample 4000 parameter sets from the EE genes and 1000 parameter sets from the DE genes. The selected parameter sets and the design matrix X (constructed so that there are eight different means, one for each combination of Time and Line) for 32 samples are used to simulate a 5000 × 32 dataset of read counts by first simulating log-transformed data using (2), and then converting the log-transformed data back to read counts using (1). Random selection of parameter sets and generation of data is independently repeated 50 times to obtain 50 datasets for each one of the two contrasts of interest (Line and Time).

4.2 Simulation scenario 2: unstructured correlation

The second simulation scenario is designed to evaluate our proposed method when, contrary to our working model assumptions, the read counts are generated as described in Section 4.1 but with unstructured ${\mathit{R}}_g$. This scenario violates our working model assumptions because the CAR1 correlation structure used in computation of our test statistics is misspecified. As true parameter values for simulating new data, we use the $\left\{C_{st}\right\}$ normalization factors, the estimated precision weight matrices ${\mathit{W}}_g$, the estimated correlation block ${\breve{\mathit{R}}}_g$, the estimated error variance parameters ${\stackrel{⌣}{s}}_g^2$ and the estimated regression coefficients ${\breve{\mathit{\beta }}}_g$ described in Section 2.3.2 and obtained by analyzing the LPS RNA-seq dataset, except that (as in Scenario 1) we set partial regression coefficients corresponding to the contrast of interest to zero for a subset of genes to permit simulation of EE genes with respect to the contrast of interest.

4.3 Simulation results

For rmRNAseq, voom, edgeR and DESeq2, Symm, CAR1, splineTimeR, splineTimeRvoom, ImpulseDE2, the P-value for testing the significance of the partial regression coefficients on the contrast of interest is calculated for each gene. These P-values are converted to q-values as described in Section 2.5, and genes with q-values no larger than 0.05 are declared to be DE. Using these P-values and q-values, we evaluate each method’s performance based on two criteria: the incurred FDR when FDR is nominally controlled at 5%, the partial area under the receiver operating characteristic curve (PAUC) corresponding to false positive rates less than or equal to 0.05, and the number of true positives (NTP) corresponding to the number of true DE genes when FDR is nominally controlled at 5%. These performance criteria assess each method’s ability to control FDR, and to distinguish EE and DE genes from one another, as well as each method’s power in detecting DE genes.

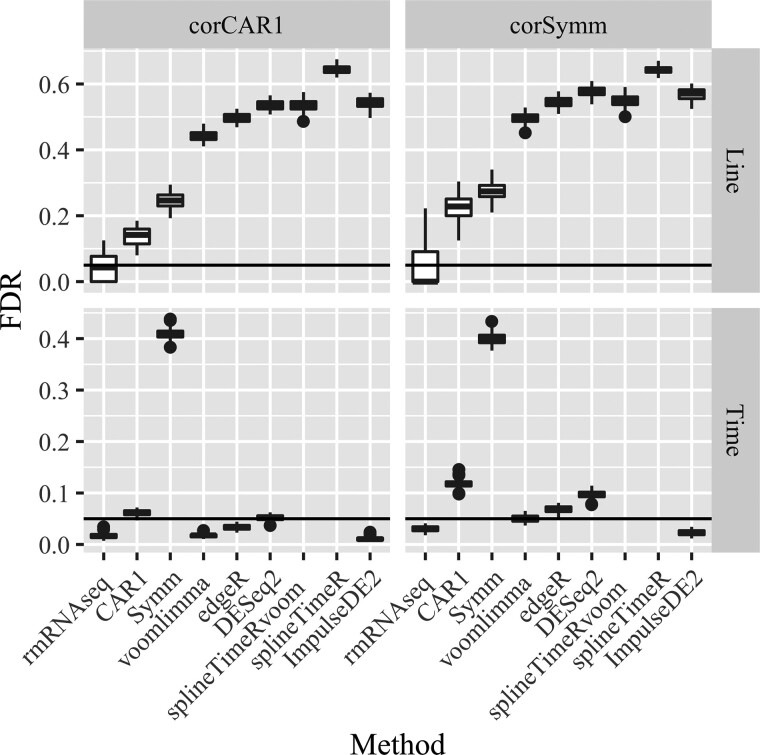
The simulation results in terms of FDR control are summarized in Figure 3. rmRNAseq controls FDR well in all cases. In simulation scenario 1, all other methods fail to control FDR for Line with extremely high incurred FDR. For the Time test, voom-limma, ImpulseDE2 and edgeR are able to control FDR, while DESeq2 shows slightly inflated FDR compared to the nominal 0.05 level. In simulation scenario 2, voom, edgeR and DESeq2 all fail to control FDR except voom, which is able to control FDR for the Time test. In all simulation scenarios, among the three methods voom, edgeR and DESeq2, DESeq2 gave the most liberal incurred FDR.

Fig. 3.

Boxplots of the incurred FDR when FDR is nominally controlled at 0.05 for all methods and all contrasts in two simulation scenarios. Each boxplot has 50 data points representing 50 simulated datasets

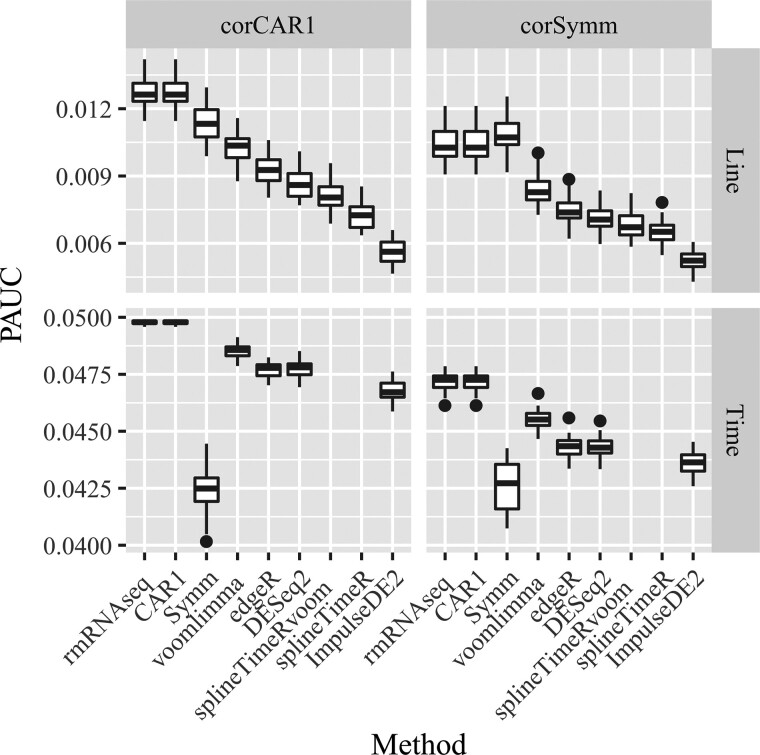
The simulation results in terms of PAUC, the ability to distinguish DE and EE genes from one another, are presented in Figure 4. For all contrasts, rmRNAseq outperformed all alternatives.

Fig. 4.

Boxplots of the PAUC when false positive rate is less than or equal to 0.05 for all methods and all contrasts in two simulation scenarios. Each boxplot has 50 data points representing 50 simulated datasets

Our proposed method performs well in all cases and even in Scenario 2 when the correlation structure does not match our CAR1 structure. An explanation for this performance is that in our proposed method, the bootstrap samples are generated from a general linear model with unstructured correlation. This bootstrap sample generation strategy provides robustness against departures from the CAR1 assumption. That said, our proposed method is not guaranteed to work well when the true data generating mechanism is far from our working model.

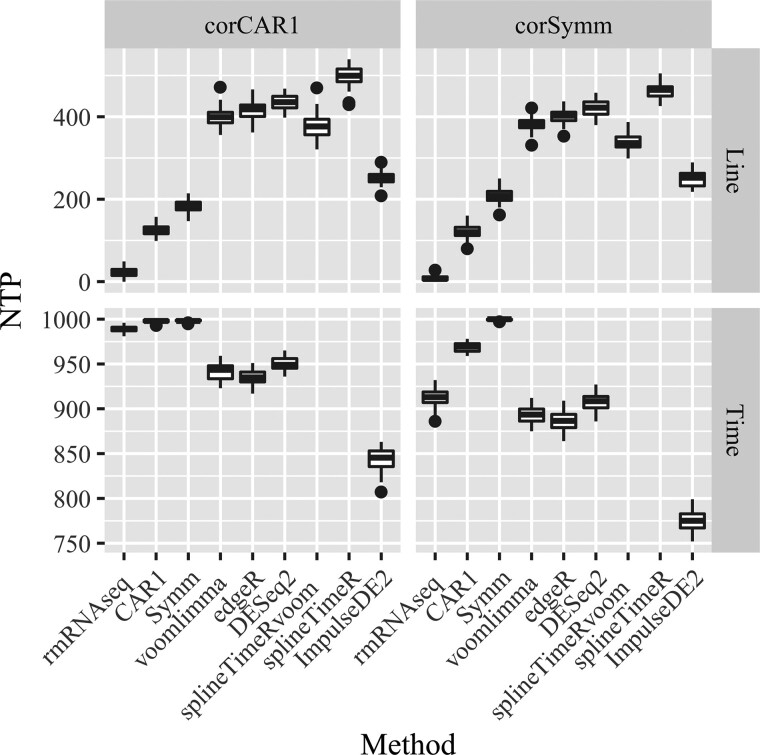
Figure 5 shows that among methods that control FDR, rmRNAseq detects highest NTP. For instance, in Scenario 2, Time main effect, the average NTPs over 50 replications of rmRNAseq, voom-limma and ImpulseDE2 are 912, 893 and 774, respectively (out of 1000 true positives). This shows that even though our method is conservative, it still attains good power in detecting true DE genes.

Fig. 5.

Boxplots of the NTP when false positive rate is less than or equal to 0.05 for all methods and all contrasts in two simulation scenarios. Each boxplot has 50 data points representing 50 simulated datasets

5 Discussion

Time-course RNA-seq experiments that collect expression profiles over time for multiple conditions are becoming increasingly popular. Time-course RNA-seq experiments are often cross-sectional, where mRNA samples are collected from different subjects at different time points. Another type of time-course experiment is longitudinal, or repeated measures, where mRNA samples at different times are extracted from the same subjects. The expression levels of a gene measured at different time points within any subject are expected to be correlated in a longitudinal or repeated-measures experiment, while within-gene correlation across time is not necessarily expected in a cross-sectional study.

Our proposed method provides a practical tool for identifying DE genes using RNA-seq data from repeated-measures designs. The idea is to use normalized log-transformed counts and their associated precision weights in a general linear model pipeline for estimation, and then employ a parametric bootstrap procedure for hypothesis testing. Correlation among observations within each gene is accounted for using unstructured estimates of within-subjects correlation and a continuous autoregressive correlation structure CAR1 with a data-driven choice of time points. The parametric bootstrap inference approach proposed in our paper can be easily extended to other RNA-seq designs that may contain factors whose effects are best modeled as random thanks to the simple and straightforward application of linear model using normalized log-transformed counts data.

When within-gene correlations exist due to repeated measures, our simulation studies show the advantages of our method compared to the most popular alternative methods for identifying DE genes. In particular, our method outperforms the alternatives (that do not consider within-gene correlation among observations from a single subject) in terms of FDR control and the ability to distinguish EE and DE genes from one another. One of the main points of our paper is that using popular approaches designed for independent RNA-seq data is not a good idea when data are likely correlated due to a repeated-measures experimental design. This point is not meant as a criticism of methods like edgeR and DESeq2 and others that are very useful for independent data; rather, our work is a caution against misusing such methods for the analysis of repeated-measures experiments.

In the implementation of our proposed method, it would be ideal to reestimate $\mathit{\tau }$ for each bootstrap sample to account for the uncertainty in estimating $\mathit{\tau }$ from the original data. Reestimating $\mathit{\tau }$ would lead to more accurate uncertainty quantification but would significantly slow the proposed method. Our proposed method is a compromise between statistical accuracy and computation speed. Furthermore, from our numerical experiments, using the $\mathit{\tau }$ estimated from the original data for all bootstrap samples results in performance similar to the approach that reestimates $\mathit{\tau }$ for each bootstrap sample. Our proposed method uses data from thousands of genes to estimate one low-dimensional $\mathit{\tau }$ vector that defines pairwise distances between time points for use with a CAR1 correlation structure. Because there is a wealth of data for estimating the few parameters in $\mathit{\tau }$, uncertainty in estimation of the $\mathit{\tau }$ does not seem important, which explains the negligible impact associated with computationally expensive reestimation of $\mathit{\tau }$ for each bootstrap sample. Other measures of distance between times could be considered, but our approach is considerably more flexible than insisting on a pre-defined assignment of distances between each pair of time points. Rather than dictating pairwise distances associated with a distance function, we allow the full data from thousands of genes to inform us about an appropriate choice for pairwise distances between time points for use with a CAR1 correlation structure.

Even when $\mathit{\tau }$ is not reestimated for each bootstrap sample, our method is computationally intensive. Our implementation of the proposed method in the R package rmRNAseq uses parallelization to speed up the algorithm. Using 16 cores in parallel, it takes about 65 min to analyze 11 911 genes of the LPS RNA-seq dataset. In a personal Macbook Pro with processor 2.7 GHz Dual-Core Intel Core i5 and 8 GB memory using 4 cores, it takes about 4 h and 20 min for such analysis. While these runtimes are short compared to the time it takes to execute experiments and collect data, some patience will be required using our R package to analyze RNA-seq data from repeated-measures experiments.