Abstract
Mediation analyses are valuable for examining mechanisms underlying an association, investigating possible explanations for nonintuitive results, or identifying interventions that can improve health in the context of nonmanipulable exposures. However, designing a study for the purpose of answering a mediation-related research question remains challenging because sample size and power calculations for mediation analyses are typically not conducted or are crude approximations. Consequently, many studies are probably conducted without first establishing that they have the statistical power required to detect a meaningful effect, potentially resulting in wasted resources. In an effort to advance more accurate power calculations for estimating direct and indirect effects, we present a tutorial demonstrating how to conduct a flexible, simulation-based power analysis. In this tutorial, we compare power to estimate direct and indirect effects across various estimators (the Baron and Kenny estimator (J Pers Soc Psychol. 1986;51(6):1173–1182), inverse odds ratio weighting, and targeted maximum likelihood estimation) using various data structures designed to mimic important features of real data. We include step-by-step commented R code (R Foundation for Statistical Computing, Vienna, Austria) in an effort to lower implementation barriers to ultimately improving power assessment in mediation studies.
Keywords: mediation, natural direct effect, power, simulation, statistics, stochastic direct effect
Abbreviations
- DGM
data-generating mechanism
- IORW
inverse odds ratio weighting
- NDE
natural direct effect
- NIE
natural indirect effect
- SDE
stochastic direct effect
- SIE
stochastic indirect effect
- TMLE
targeted maximum likelihood estimation
Editor’s note: An invited commentary on this article appears on page 1568, and the authors’ response appears on page 1571.
Mediation analyses have been growing in popularity as a way for researchers to elucidate mechanisms underlying an association (1), investigate possible explanations for nonintuitive results (2), or identify interventions that can improve health in the context of nonmanipulable exposures (3). However, study design remains challenging because sample size and power calculations for mediation analyses are typically not conducted or are crude approximations (4, 5). Consequently, many mediation studies are probably conducted without first establishing that they have the statistical power required to detect a meaningful effect, potentially resulting in wasted resources.
One commonly used approach for estimating statistical power for mediation analysis is an equation based on generalized linear models that calculates the required sample size or power to detect whether or not mediation exists—in contrast to estimating the power to detect a given indirect effect size—by calculating the change in the regression coefficient associated with the exposure before and after inclusion of the mediator in the model (4). Another common approach, used primarily in the psychology literature, is to use simulations to calculate the required sample size or power to detect a given indirect effect size, using the Baron and Kenny product estimator (6, 7), which is another generalized linear model-based approach.
Both the analytical, equation-based approach and the Baron and Kenny simulation have the advantage of being simple to implement. However, this simplicity comes at the price of potentially significant limitations. First, the analytical, equation-based approach does not calculate power to detect a given indirect effect size—only the power to detect whether an indirect effect exists. In addition, both of the above approaches rely on strong assumptions, like 1) correct specification of multiple parametric models, 2) no effect of interaction between the exposure and the mediator on the outcome (such that controlled direct effects equal natural direct effects and, thus, that estimation of indirect effects is possible), and 3) a linear relationship between the mediator and outcome (8). They also rely on the identification assumptions for natural direct and indirect effects of 4) sequential randomization (i.e., no unobserved confounding of the exposure-mediator, exposure-outcome, or mediator-outcome relationship), 5) no posttreatment observed confounders of the mediator-outcome relationship, 6) positivity, and 7) consistency. While assumptions 4, 6, and 7 are needed for most any causal mediation analysis, the remaining 4 assumptions can usually be avoided by choosing a more flexible analytical approach (1).
Second, for the Baron and Kenny simulation approach, power estimates can vary based on the variance estimate that is used (9–11). One way to estimate variance of the indirect effect (which in the Baron and Kenny method is calculated as the product of 2 coefficients) is to assume that the product of 2 normal random variables is also a normal random variable (6). However, this is not true in general (9, 12), and evidence shows that the test of the normality assumption for a product variable is itself underpowered (10). Another way to estimate variance is to use the bootstrap percentile method, which allows for potential asymmetries in the confidence interval (9, 10). However, using bootstrap percentiles for confidence bounds is generally not recommended (13). In addition, there is a lack of guidance (even problematic guidance) for estimating power under more complex (and realistic) distributions—for example, if there are interactions between the exposure and the mediator, or if there is a mediator-outcome confounder that is affected by prior exposure.
Lastly, there has been significant methodological work in recent years to develop estimators that reduce the number and stringency of assumptions required to estimate direct and indirect effects (14–16). To be useful, methods of estimating power must adapt to include these new approaches.
To address the aforementioned limitations, we present a tutorial that illustrates how to use simulation to estimate statistical power for several different estimators of direct and indirect effects (Baron and Kenny, an interaction extension to Baron and Kenny, inverse odds ratio weighting (IORW), and targeted maximum likelihood estimation (TMLE)) under different distribution scenarios. We also compare the estimates of power for indirect effects with the equation-based approach for detecting whether mediation exists.
NOTATION
First, we define notation. We consider 2 data scenarios. In one, we have observed data 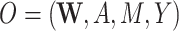 , and in the second we have
, and in the second we have 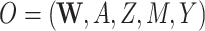 , where
, where 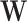 are preexposure confounders,
are preexposure confounders, 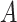 is the exposure,
is the exposure, 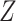 is a mediator-outcome confounder that is affected by prior exposure,
is a mediator-outcome confounder that is affected by prior exposure, 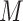 is the mediator, and
is the mediator, and 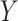 is the outcome (Figure 1). For this simple tutorial, we assume that all variables are binary—in reality, one would match the distributions in the simulated data to the distributions in the actual data.
is the outcome (Figure 1). For this simple tutorial, we assume that all variables are binary—in reality, one would match the distributions in the simulated data to the distributions in the actual data.
Figure 1.
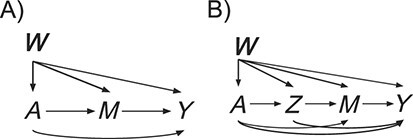
Structural causal models considered in the simulations.
We define the direct and indirect effects that we are interested in estimating in terms of potential outcomes (17). Uppercase letters denote random variables, and lowercase letters denote assigned values. 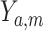 denotes the potential outcome of
denotes the potential outcome of 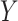 setting
setting 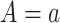 and
and 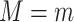 , possibly contrary to fact. Similarly,
, possibly contrary to fact. Similarly, 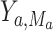 denotes the potential outcome of
denotes the potential outcome of 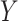 setting
setting 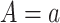 and
and 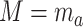 , the potential value of the mediator under
, the potential value of the mediator under 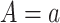 . We assume consistency, which means that
. We assume consistency, which means that 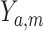 would be the observed value of
would be the observed value of 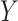 if
if 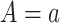 and
and 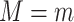 were the realized values of those variables and composition, which in turn means that
were the realized values of those variables and composition, which in turn means that 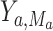 would be the observed value of Y if
would be the observed value of Y if 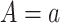 was the realized value of
was the realized value of 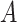 (18, p. 229).
(18, p. 229).
MEDIATION ESTIMANDS CONSIDERED
We focus on estimation of 2 types of mediation estimands: 1) natural direct and indirect effects and 2) stochastic (also called randomized interventional) direct and indirect effects. We describe each briefly here and refer the interested reader to separate tutorial papers for additional discussion (1, 19, 20). Although, for this tutorial, we estimate effects on the risk difference scale, the tutorial can serve as a road map for relative risk or odds ratio scales, substituting appropriate estimators (8).
Natural direct and indirect effects
The natural direct effect (NDE) is defined as 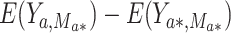 , where
, where 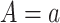 corresponds to “exposed” and
corresponds to “exposed” and 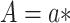 corresponds to “unexposed.” The natural indirect effect (NIE) is defined as
corresponds to “unexposed.” The natural indirect effect (NIE) is defined as 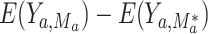 . The NIE and NDE sum to the total effect. In order to identify these parameters from the data, positivity must be satisfied (meaning that for each subgroup of covariate combinations, there is a nonzero probability of each value of
. The NIE and NDE sum to the total effect. In order to identify these parameters from the data, positivity must be satisfied (meaning that for each subgroup of covariate combinations, there is a nonzero probability of each value of 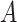 , and, similarly, a nonzero probability for each value of
, and, similarly, a nonzero probability for each value of 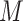 for each subgroup combination of
for each subgroup combination of 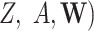 . Consistency must be satisfied, and there must be no unmeasured exposure-mediator confounding, no unmeasured mediator-outcome confounding, and no unmeasured exposure-outcome confounding. In addition, there must be no mediator-outcome confounder that is affected by prior exposure; the NIE and NDE cannot be identified from the observed data when such a confounder exists, even if it is observed and measured (14, 15).
. Consistency must be satisfied, and there must be no unmeasured exposure-mediator confounding, no unmeasured mediator-outcome confounding, and no unmeasured exposure-outcome confounding. In addition, there must be no mediator-outcome confounder that is affected by prior exposure; the NIE and NDE cannot be identified from the observed data when such a confounder exists, even if it is observed and measured (14, 15).
Stochastic direct and indirect effects
Stochastic (randomized interventional) direct and indirect effects can, however, include mediator-outcome confounders affected by prior exposure and estimate similar parameters to the NDE and NIE when these confounders do not exist (14). The stochastic direct effect (SDE) is defined as 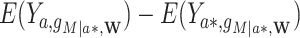 , and the stochastic indirect effect (SIE) is
, and the stochastic indirect effect (SIE) is 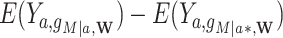 , where
, where 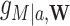 is the observed distribution of the mediator conditional on covariates,
is the observed distribution of the mediator conditional on covariates, 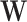 , and setting exposure
, and setting exposure 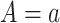 . To be able to estimate stochastic mediation effects, positivity and consistency must be satisfied, and there must be no unmeasured exposure-mediator confounding, no unmeasured mediator-outcome confounding, and no unmeasured exposure-outcome confounding. The standard equation-based approach and the Baron and Kenny simple simulation approach cannot generally be used to calculate power for the SDE and SIE. This, in part, motivates use of the more flexible simulation approach we describe in this tutorial. However, for the particular structural causal model depicted in Figure 1A, the SDE and SIE are equivalent to the NDE and NIE, so these common approaches can be used, albeit with the additional assumptions discussed above.
. To be able to estimate stochastic mediation effects, positivity and consistency must be satisfied, and there must be no unmeasured exposure-mediator confounding, no unmeasured mediator-outcome confounding, and no unmeasured exposure-outcome confounding. The standard equation-based approach and the Baron and Kenny simple simulation approach cannot generally be used to calculate power for the SDE and SIE. This, in part, motivates use of the more flexible simulation approach we describe in this tutorial. However, for the particular structural causal model depicted in Figure 1A, the SDE and SIE are equivalent to the NDE and NIE, so these common approaches can be used, albeit with the additional assumptions discussed above.
MEDIATION ESTIMATORS CONSIDERED
To illustrate how estimator choice can affect power estimates in a simulated data scenario, we consider 4 estimators that can be used to estimate either natural and/or stochastic direct and indirect effects. We compare these with the analytical, equation-based approach that estimates power to detect any indirect effect. We consider 2 parametric regression approaches given their ubiquity across public health, psychology, and other social sciences: the original Baron and Kenny estimator (6) and an extension to the Baron and Kenny estimator developed by Valeri and VanderWeele (8) that allows for an effect of interaction between the treatment and the mediator on the outcome. We consider these to be “typical approach” benchmarks. We also consider the IORW estimator (16, 21), which has been increasingly used in the field of epidemiology due to its ease of implementation and flexibility in dealing with high-dimensional or continuously distributed mediators. Finally, we consider TMLE (2, 14), as it offers advantages of double robustness, efficiency, and incorporation of machine learning algorithms in model-fitting. Detailed descriptions of the estimators and the equation are given in the Web Appendix (available at https://academic.oup.com/aje), in the papers cited above (1, 2, 6, 8, 14, 16, 21), and in another tutorial (1).
SIMULATION TUTORIAL
In this section, we take the reader step by step through the process of conducting a simulation to estimate statistical power in the estimation of natural or stochastic direct and indirect effects.
Step 1: Simulate data
First, one simulates data that match important attributes of the real data to be used to answer the research question. For the purpose of illustrating the differences in performance across estimators, we consider and discuss relative performance across an array of data-generating mechanisms (DGMs) (Table 1). Commented R code (22) that simulates each of these DGMs is provided on GitHub (23).
Table 1.
Data-Generating Mechanisms Considered in the Simulationsa
| Data-Generating Mechanism | EffectSize | Strengthof Z | A - M Interaction | η 2 |
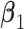
|
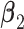
|
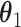
|
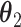
|
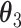
|
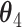
|
|---|---|---|---|---|---|---|---|---|---|---|
| O = (W, A, M, Y) | ||||||||||
| 1 | Small | N/A | No | N/A | 0.05 | N/A | 0.03 | N/A | 0.60 | 0 |
| 2 | Small | N/A | No | N/A | 0.03 | N/A | 0.03 | N/A | 0.04 | 0 |
| 3 | Small | N/A | Yes | N/A | 0.01 | N/A | 0.03 | N/A | 0.01 | 0.1 |
| 4 | Large | N/A | No | N/A | 0.10 | N/A | 0.30 | N/A | 0.20 | 0 |
| 5 | Large | N/A | Yes | N/A | 0.10 | N/A | 0.20 | N/A | 0.15 | 0.2 |
| (O = W, A, Z, M, Y) | ||||||||||
| 6 | Small | Weak | No | 0.10 | 0.03 | 0.20 | 0.03 | 0.03 | 0.04 | 0 |
| 7 | Small | Strong | No | 0.60 | 0.03 | 0.20 | 0.01 | 0.03 | 0.01 | 0 |
| 8 | Small | Weak | Yes | 0.10 | 0.01 | 0.01 | 0.03 | 0.03 | 0.01 | 0.1 |
| 9 | Small | Strong | Yes | 0.60 | 0.01 | 0.01 | 1.50 | 0.03 | 0.01 | 0.1 |
| 10 | Large | Weak | No | 0.10 | 0.10 | 0.20 | 0.10 | 0.30 | 0.20 | 0 |
| 11 | Large | Strong | No | 0.60 | 0.10 | 0.20 | 0.15 | 0.30 | 0.30 | 0 |
| 12 | Large | Weak | Yes | 0.10 | 0.10 | 0.15 | 0.10 | 0.15 | 0.15 | 0.2 |
| 13 | Large | Strong | Yes | 0.60 | 0.10 | 0.20 | 0.20 | 0.20 | 0.15 | 0.2 |
Abbreviation: N/A, not applicable.
a Models used: 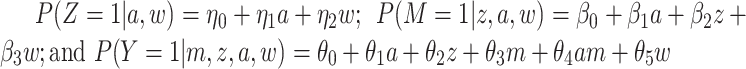 .
.
These DGMs include variations across several attributes that could influence the statistical power of an estimator:
sample size;
effect size;
the presence of an effect of the interaction between
 and
and 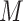 on
on 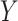 ;
;the structural causal model (e.g., observed data
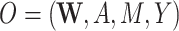 versus observed data
versus observed data 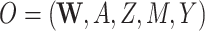 );
);the strength of
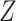 given observed data
given observed data 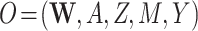 ; and
; andthe distributions of
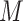 and
and 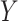 (note that we limit this tutorial to binary, nonrare
(note that we limit this tutorial to binary, nonrare 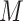 and
and 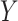 ; changing these features could affect power).
; changing these features could affect power).
Sample size and effect size are 2 well-appreciated determinants of statistical power. We include 3 sample sizes: n = 100, n = 1,000, and n = 10,000. We examine performance under relatively large and small effect sizes for the direct effect (range, 0.033–0.330) and indirect effect (range, 0.0014–0.0770), based on previous epidemiologic research (2). True effect sizes for each simulation DGM are given in Web Tables 1 and 2.
We also examine how estimator power is affected by the presence of the effect of an interaction between A and M on Y. Both the IORW and TML estimators allow for such an interaction. The original Baron and Kenny approach (6) does not, though the extension (8) does. Consequently, the simulation explores how violating that assumption may influence power to detect an effect.
Our DGMs fall into one of 2 observed structural causal models. In the first, we have observed data 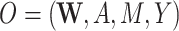 , corresponding to Figure 1A. In the second, we have observed data
, corresponding to Figure 1A. In the second, we have observed data 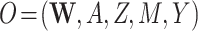 , corresponding to Figure 1B. In the first scenario, without
, corresponding to Figure 1B. In the first scenario, without 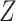 , natural direct and indirect effects coincide with their stochastic counterparts (19). Thus, under correct specification of all parametric models, positivity, and a large sample size, DGMs 1 and 3 represent “best-case” scenarios for estimating statistical power for all estimators and the analytical equation. In the second scenario, with Z, only stochastic direct and indirect effects are identified. Thus, only TMLE is theoretically unbiased in this scenario. It is possible that the degree to which performance is affected by violating the assumption of no posttreatment confounder of the mediator-outcome relationship depends on the strength of the effect of
, natural direct and indirect effects coincide with their stochastic counterparts (19). Thus, under correct specification of all parametric models, positivity, and a large sample size, DGMs 1 and 3 represent “best-case” scenarios for estimating statistical power for all estimators and the analytical equation. In the second scenario, with Z, only stochastic direct and indirect effects are identified. Thus, only TMLE is theoretically unbiased in this scenario. It is possible that the degree to which performance is affected by violating the assumption of no posttreatment confounder of the mediator-outcome relationship depends on the strength of the effect of 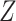 on
on 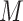 and
and 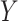 , so that is another attribute that we incorporate into our DGMs (Table 1).
, so that is another attribute that we incorporate into our DGMs (Table 1).
For each DGM, we calculate the true direct and indirect effect in order to compare the estimators’ performance in terms of power and coverage. The truth for the natural direct and indirect effects under DGMs 1–4 (when there is no Z variable) is calculated using Pearl’s mediational formula (24). The truth for the stochastic direct and indirect effect is calculated using a draw from a superpopulation of 5,000,000. (This truth is calculated for each simulated data set, reflecting the fact that the estimator is for a data-dependent parameter that assumes a known stochastic intervention on M.)
Step 2: Implement estimation approach
Second, one decides on a mediation estimand of interest (e.g., natural direct/indirect effect; stochastic direct/indirect effect) and an estimator for estimating it. We provide details on how we implemented each estimator below, as well as details for implementing the equation-based power calculation. Additional information about each estimator is available in the Web Appendix. We also provide commented R code for each on GitHub (23).
Baron and Kenny estimator (original and extension for effect of A-M interaction on Y).
First we implement the Baron and Kenny estimator and the interaction extension to the Baron and Kenny estimator. We calculate 95% confidence intervals using 1,000 bootstrapped samples with a Wald-type confidence interval for the NDE and the percentile confidence interval for the NIE. In previous work, Hayes and Scharkow (25) showed similar power when using bootstrapped confidence intervals as opposed to assuming that the 2 coefficients are joint normally distributed. These 2 estimators cannot accommodate data-generating mechanisms 6–13 that include 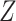 (i.e., observed data
(i.e., observed data 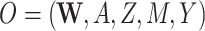 ). Consequently, we implement these estimation approaches making the decision to omit Z from the models and making the alternative decision to control for
). Consequently, we implement these estimation approaches making the decision to omit Z from the models and making the alternative decision to control for  in the models. We include the results from each decision.
in the models. We include the results from each decision.
Inverse odds ratio weighting.
We implement IORW using the inverse odds as weights as opposed to the inverse odds ratios, as recommended (21). We use 250 bootstrap replicates to estimate Wald-type standard errors for both the NDE and the NIE. IORW also cannot accommodate postexposure confounders of the mediator-outcome relationship. Thus, for DGMs 6–13, we show the results of the IORW estimator making the same 2 alternative decisions detailed above: 1) omitting Z from the models and 2) controlling for  in the models.
in the models.
Targeted maximum likelihood estimation.
We implement a simple version of TMLE that treats the stochastic intervention on M as known, estimated using observed data (14). We compare 2 approaches for estimating the standard errors: 1) the sample standard deviation of the efficient influence curve for the SDE and SIE and 2) the standard deviation of the bootstrapped estimates for the SDE and SIE. Wald-style confidence intervals are constructed using these variance estimates.
Analytical equation
Lastly, even though it is not an estimator in the sense that it is not estimating a direct or indirect effect or giving any measure of variance/inference, we also implement the regression-based equation that calculates power to detect an indirect effect (4). We estimate each of the required parameters using a superpopulation as the truth, and we calculate the power according to the equation described in the Web Appendix. Since this approach does not allow for postexposure confounders, for DGMs 6–13 we compare the results from omitting and including 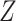 in the outcome models.
in the outcome models.
Step 3: Calculate power to detect a given effect size
Third, one calculates the statistical power of the estimator of choice in estimating a given effect size for a given sample size. Formally, statistical power is 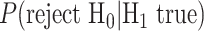 , where
, where 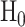 is the null hypothesis and
is the null hypothesis and 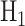 is the alternative hypothesis. In this case,
is the alternative hypothesis. In this case, 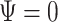 under
under 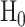 and
and 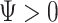 under
under 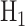 , where
, where 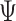 is the parameter (e.g., NIE). Thus, one can perform some number of simulations—we choose 1,000—and calculate the percentage of simulations that correctly reject
is the parameter (e.g., NIE). Thus, one can perform some number of simulations—we choose 1,000—and calculate the percentage of simulations that correctly reject 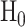 for a given
for a given 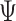 and sample size.
and sample size.
In addition to power, we also calculate 95% confidence interval coverage, which is the percentage of simulations where the 95% confidence interval covers the true effect. If all assumptions for identification are met, if there are no practical positivity violations (26), and if the sample size is large enough, each estimator should cover the true effect 95% of the time.
RESULTS
Results for each simulation scenario are shown in Figures 2 and 3, Web Figures 1–4, and Web Tables 1 and 2. These figures plot power and coverage by sample size for each of the estimators and DGMs. In the plots of simulation results, the dotted horizontal lines correspond to 80% power, and the dotted vertical lines represent 95% coverage. Under optimal performance, the estimators would lie on the vertical line and above the horizontal line. The results of the equation-based approach for detecting any mediation are plotted to the right of 100% coverage. This is to make clear that they are not based on an estimator of indirect effects, and therefore coverage cannot be calculated for them.
Figure 2.
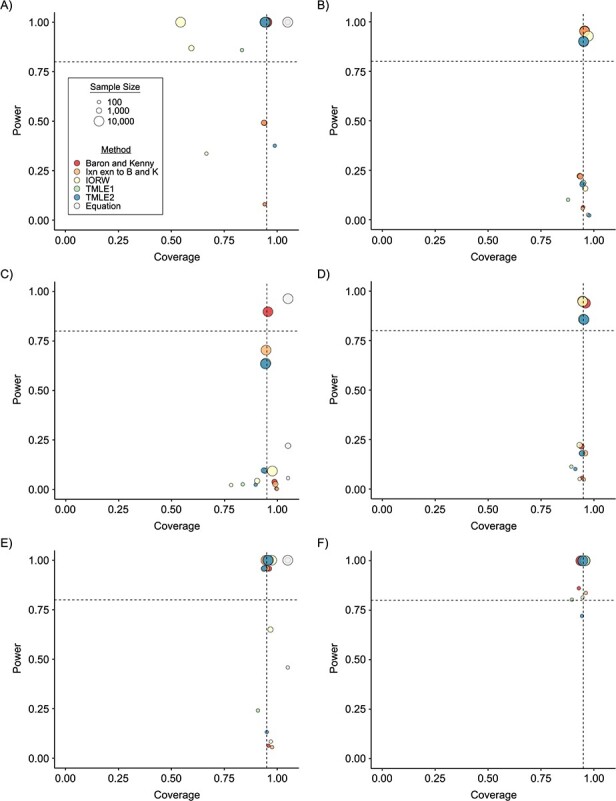
Statistical power and coverage of estimators of the natural direct effect (NDE) and the natural indirect effect (NIE), by sample size, estimation method, and effect size, for data-generating mechanisms (DGMs) reflecting no Z and no A-M interaction. A) NDE for DGM 1 (small effect size); B) NIE for DGM 1 (small effect size); C) NDE for DGM 2 (small effect size); D) NIE for DGM 2 (small effect size); E) NDE for DGM 4 (large effect size); F) NIE for DGM 4 (large effect size). “Baron and Kenny” corresponds to the original version of the Baron and Kenny estimator (6). “Ixn exn to B and K” corresponds to the extension to the Baron and Kenny estimator that allows for A-M interaction (8). TMLE1 corresponds to variance estimated using the efficient influence curve, and TMLE2 represents variance calculated using the bootstrap. Ixn exn, interaction extension; TMLE, targeted maximum likelihood estimation.
Figure 3.
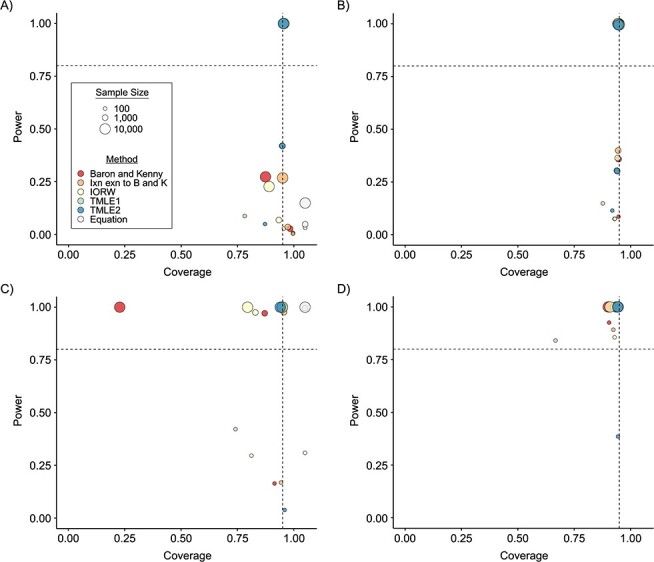
Statistical power and coverage of estimators of the natural direct effect (NDE) and the natural indirect effect (NIE), by sample size, estimation method, and effect size, for data-generating mechanisms (DGMs) reflecting no Z and A-M interaction. A) NDE for DGM 3 (small effect size); B) NIE for DGM 3 (small effect size); C) NDE for DGM 5 (large effect size); D) NIE for DGM 5 (large effect size). “Baron and Kenny” corresponds to the original version of the Baron and Kenny estimator (6). “Ixn exn to B and K” corresponds to the extension to the Baron and Kenny estimator that allows for A-M interaction (8). TMLE1 corresponds to variance estimated using the efficient influence curve, and TMLE2 represents variance calculated using the bootstrap. Ixn exn, interaction extension; TMLE, targeted maximum likelihood estimation.
First structural causal model, O = (W, A, M, Y)
We first discuss results corresponding to DGMs 1–5 under the first structural causal model (Figure 1A) where we have data 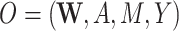 .
.
When there is no effect of  interaction on
interaction on  (corresponding to DGMs 1, 2, and 4), any estimator should theoretically give appropriate coverage for a sufficiently large sample size. DGMs 1 and 2 produce a small effect size in this scenario, and DGM 4 produces a large effect size. DGMs 1 and 2 differ in that the NDE is equal to the NIE in DGM 1 (NDE = NIE = 0.03), resulting in DGM 1’s having a larger NIE than DGM 2. We see in parts A–D of Figure 2 that nearly all estimators result in coverage near 95%, as expected (the exception being for the IORW estimator of the NIE under DGM 1 (Figure 2B)). For the smaller NIE under DGM 2, power varies across estimators (Figure 2D). With n = 10,000, the Baron and Kenny estimator and the interaction extension to the Baron and Kenny estimator have the highest power (90% and 70%), followed by TMLE (64% and 63%) and then IORW (9%). The equation-based approach slightly overestimates power for each sample size. As expected, power is higher with the larger NIEs in DGMs 1 and 4 (Figure 2, parts B and E). However, we again see some variability across the estimators for the NIE. Again, the equation-based approach overestimates power.
(corresponding to DGMs 1, 2, and 4), any estimator should theoretically give appropriate coverage for a sufficiently large sample size. DGMs 1 and 2 produce a small effect size in this scenario, and DGM 4 produces a large effect size. DGMs 1 and 2 differ in that the NDE is equal to the NIE in DGM 1 (NDE = NIE = 0.03), resulting in DGM 1’s having a larger NIE than DGM 2. We see in parts A–D of Figure 2 that nearly all estimators result in coverage near 95%, as expected (the exception being for the IORW estimator of the NIE under DGM 1 (Figure 2B)). For the smaller NIE under DGM 2, power varies across estimators (Figure 2D). With n = 10,000, the Baron and Kenny estimator and the interaction extension to the Baron and Kenny estimator have the highest power (90% and 70%), followed by TMLE (64% and 63%) and then IORW (9%). The equation-based approach slightly overestimates power for each sample size. As expected, power is higher with the larger NIEs in DGMs 1 and 4 (Figure 2, parts B and E). However, we again see some variability across the estimators for the NIE. Again, the equation-based approach overestimates power.
DGMs 3 and 5 introduce an effect of the interaction between A and M on Y corresponding to smaller and large effect sizes, respectively (Figure 3). In this scenario, the controlled direct effect will not necessarily equal the NDE, so only the interaction extension to the Baron and Kenny estimator (denoted “Ixn exn to B and K” in Figure 3), IORW, and TMLE are theoretically appropriate. This is best evidenced in DGM 5, where, for the NIE, the original Baron and Kenny estimator produces significant undercoverage of 23% for the largest sample size (Figure 3D; for exact power and coverage estimates, see Web Table 1). For the larger effect size, power is universally high for sample sizes of 1,000 and 10,000. Use of the equation overestimates the power when n = 100 but is about the same as the simulation results for n = 1,000 and n = 10,000. For the smaller effect size, DGM 3, power in estimating the NIE is high only for TMLE with n = 10,000 (Figure 3B); this case is also the only one in which the equation does not overestimate power.
Second structural causal model, O = (W, A, Z, M, Y)
We next discuss results corresponding to DGMs 6–13 under the second structural causal model (Figure 1B) where we have data 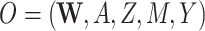 . In this scenario, only TMLE may be theoretically unbiased in estimating the identified parameter. However, we hypothesized that the relative performance of the other estimators may depend on the strength of Z and whether or not it is controlled for or omitted in the analyses.
. In this scenario, only TMLE may be theoretically unbiased in estimating the identified parameter. However, we hypothesized that the relative performance of the other estimators may depend on the strength of Z and whether or not it is controlled for or omitted in the analyses.
DGMs 6 and 10 correspond to a weak effect of 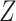 and no
and no 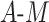 interaction; DGM 6 represents a small effect size and DGM 10 represents a large one. In this scenario, we expect that all methods have appropriate coverage, given that the violation of the “no postexposure confounder” assumption is relatively weak. We found this to be generally true for the NDE (except for the IORW estimator omitting
interaction; DGM 6 represents a small effect size and DGM 10 represents a large one. In this scenario, we expect that all methods have appropriate coverage, given that the violation of the “no postexposure confounder” assumption is relatively weak. We found this to be generally true for the NDE (except for the IORW estimator omitting 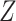 and the interaction extension to the Baron and Kenny estimator controlling for
and the interaction extension to the Baron and Kenny estimator controlling for 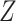 ), but coverage for the NIE was more variable for the non-TML estimators (Web Figure 1). For both the small and large effect sizes, the Baron and Kenny and IORW estimators omitting
), but coverage for the NIE was more variable for the non-TML estimators (Web Figure 1). For both the small and large effect sizes, the Baron and Kenny and IORW estimators omitting 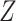 resulted in poor coverage of the NIE, and for the large effect size, the other IORW estimator also resulted in poor coverage. All estimators of the NDE had more than 80% power when the sample size was 10,000, although power was lower for sample sizes of 1,000 and 100. For the NIE, all estimators except IORW had more than 80% power when the sample size was 10,000, although power was lower for sample sizes of 1,000 and 100. Both equation-based methods (that control for and omit Z) produced similar estimates of power but overestimated power for all sample sizes.
resulted in poor coverage of the NIE, and for the large effect size, the other IORW estimator also resulted in poor coverage. All estimators of the NDE had more than 80% power when the sample size was 10,000, although power was lower for sample sizes of 1,000 and 100. For the NIE, all estimators except IORW had more than 80% power when the sample size was 10,000, although power was lower for sample sizes of 1,000 and 100. Both equation-based methods (that control for and omit Z) produced similar estimates of power but overestimated power for all sample sizes.
DGMs 8 and 12 reflect a weak effect of 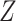 and interaction between
and interaction between 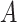 and
and 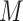 on
on 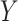 ; DGM 8 represents a small effect size and DGM 12 represents a large effect size. Again, only the TML estimators are theorectically appropriate under these DGMs. We expect the original Baron and Kenny estimator to perform especially poorly, as it assumes that
; DGM 8 represents a small effect size and DGM 12 represents a large effect size. Again, only the TML estimators are theorectically appropriate under these DGMs. We expect the original Baron and Kenny estimator to perform especially poorly, as it assumes that 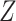 does not exist and also assumes no effect of
does not exist and also assumes no effect of 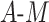 interaction on
interaction on 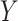 . These differences in coverage are particularly pronounced in DGM 12, where the effect size is large (Web Figure 2). Although power is universally high under DGM 12 for N ≥ 1,000, all estimators other than TMLE, including the equation approaches, have low power in detecting the NIE under the small effect size DGM 7.
. These differences in coverage are particularly pronounced in DGM 12, where the effect size is large (Web Figure 2). Although power is universally high under DGM 12 for N ≥ 1,000, all estimators other than TMLE, including the equation approaches, have low power in detecting the NIE under the small effect size DGM 7.
When there is a strong relationship with 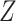 , only TMLE is expected to result in appropriate coverage. This is generally reflected in the simulation results. The DGMs without
, only TMLE is expected to result in appropriate coverage. This is generally reflected in the simulation results. The DGMs without 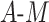 interaction in this scenario are 7 and 11, for small and large effect sizes, respectively, and the DGMs with
interaction in this scenario are 7 and 11, for small and large effect sizes, respectively, and the DGMs with 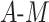 interaction are 9 and 13 for small and large effect sizes, respectively. DGM 7 represents a particularly challenging scenario in which no estimator or equation achieves satisfactory power for the SIE, even with n = 10,000 (Web Figure 3). The large-effect-size version, DGM 11, demonstrates that only TMLE has appropriate coverage across the SDE and SIE and has high power for n = 1,000 and n = 10,000 (Web Figure 3). The equation-based method’s power estimate is consistent with that of other estimators in these DGMs when n = 1,000 and n = 10,000 but is an overestimate when n = 100.
interaction are 9 and 13 for small and large effect sizes, respectively. DGM 7 represents a particularly challenging scenario in which no estimator or equation achieves satisfactory power for the SIE, even with n = 10,000 (Web Figure 3). The large-effect-size version, DGM 11, demonstrates that only TMLE has appropriate coverage across the SDE and SIE and has high power for n = 1,000 and n = 10,000 (Web Figure 3). The equation-based method’s power estimate is consistent with that of other estimators in these DGMs when n = 1,000 and n = 10,000 but is an overestimate when n = 100.
Under DGMs 9 and 13, only TMLE demonstrates consistently appropriate coverage for the SDE and SIE (Web Figure 4). All estimation approaches have high power under the large effect size DGM, but with the smaller effect size, only TMLE demonstrates high power for estimating the SIE. Similar to the non-TML estimators, the equation-based approach has low statistical power in this scenario.
DISCUSSION
We demonstrated via tutorial how to use simulation to estimate the power of a particular estimator under a particular data-generating mechanism to detect direct and indirect effects, including step-by-step, commented R code. Usually, effect size and sample size are the only factors considered in a power analysis. However, as we demonstrated in our simulation, choice of estimator and features of the DGM also greatly affect power. Unfortunately, the typical power calculation approaches—the analytical equation-based method and the Baron and Kenny simulation-based method—are inflexible to testing power for a variety of estimators and make potentially restrictive assumptions about features of the DGM. These constraints motivate the adoption of the more flexible approach we illustrate.
In our simulation, we examined 13 DGMs spanning combinations of various factors of importance: 1) the presence (vs. absence) of a posttreatment confounder of the 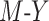 relationship, 2) the strengths of that posttreatment confounder where it exists, 3) the presence (vs. absence) of an effect of the
relationship, 2) the strengths of that posttreatment confounder where it exists, 3) the presence (vs. absence) of an effect of the 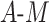 interaction on
interaction on 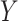 , 4) effect size, 5) sample size, and 6) estimator type or equation. We found that estimators could vary greatly in terms of power, keeping all else constant. For example, for a given DGM and sample size, some estimators could have 100% power, while others had 8% despite having appropriate 95% confidence interval coverage (e.g., Web Figure 1A). This rather extreme discrepancy in estimator power underscores the potential utility in using a simulation-based approach that includes a variety of appropriate estimators to both aid in the choice of estimator for a planned analysis and calculate the anticipated power of such a planned analysis more accurately than using the analytical equation-based method as the default.
, 4) effect size, 5) sample size, and 6) estimator type or equation. We found that estimators could vary greatly in terms of power, keeping all else constant. For example, for a given DGM and sample size, some estimators could have 100% power, while others had 8% despite having appropriate 95% confidence interval coverage (e.g., Web Figure 1A). This rather extreme discrepancy in estimator power underscores the potential utility in using a simulation-based approach that includes a variety of appropriate estimators to both aid in the choice of estimator for a planned analysis and calculate the anticipated power of such a planned analysis more accurately than using the analytical equation-based method as the default.
The coverage of the 95% confidence interval will be approximately 95% for unbiased estimates and for a sufficiently large sample size, using a consistent estimator with appropriate variance estimation. Coverage deviating significantly from 95% indicates that the assumptions underlying estimator use for a particular effect have not been met, and consequently that an alternative estimator with assumptions that are better aligned with the data structure and estimand should be considered. One can utilize an appropriate estimator for the DGM, reflected by appropriate coverage with a sufficiently large sample size, but this estimator may nonetheless have low power. This may be due to the estimator’s being inefficient; thus, it may be more difficult to detect an effect. We see this in particular with the IORW estimator for DGM 2 (Figure 2B). In this simple DGM, all estimators are appropriate for estimation of the NDE and NIE, but the IORW is inefficient. This inefficiency makes it difficult to detect a small effect size, even with a large sample size of 10,000.
Conversely, one could have high power but poor coverage. In this case, the veracity of the power should be questioned, as it is likely that the estimator used in the first place is inappropriate (e.g., one of the assumptions is violated). For example, in DGMs 3 and 5 (Figure 3), power is high for the original Baron and Kenny estimator but low for the sample size of 10,000. The original Baron and Kenny estimator assumes no 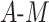 interaction, so it is known to be an inappropriate estimator for this DGM, which is reflected in the low coverage. Because the estimator’s inference is demonstrated to be incorrect under this DGM, the resulting power estimate is not meaningful.
interaction, so it is known to be an inappropriate estimator for this DGM, which is reflected in the low coverage. Because the estimator’s inference is demonstrated to be incorrect under this DGM, the resulting power estimate is not meaningful.
Although we illustrate here how one might conduct such a power simulation, our tutorial has several limitations. First, we included several common estimators used to calculate mediation effects, but there are many others (27–32). Second, we examined how 6 particular features may affect power, but this too is an incomplete list. For example, we considered estimates on the risk difference scale, but different effect scales, like the relative risk and odds ratio, could also affect power. Among the features we did examine, our simulation scenarios were limited. For example, we utilized binary, nonrare variables for simplicity. We encourage researchers to generate simulated data sets that most closely approximate the features of their own data and to estimate power for the particular estimand of interest. This tutorial serves as a road map that can be followed for any set of distributions, estimands, and estimators.
In summary, the statistical power to detect a mediation effect can vary dramatically across an array of features. Traditional power approaches account for only 2 of these: sample size and effect size. Error in these crude approximations may result in mediation studies that are mistakenly not pursued due to underestimating power or that are mistakenly pursued due to overestimating power (despite an inability to detect any reasonable effect). In an effort to advance more accurate power calculations for estimating direct and indirect effects, we demonstrate how to conduct a simulation-based power analysis, comparing power across various estimators using a data structure mimicking the real data one might have. We have made commented R code available for every step of this process (23) in an effort to lower implementation barriers.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Department of Epidemiology, Mailman School of Public Health, Columbia University, New York, New York (Kara E. Rudolph); Division of Epidemiology and Biostatistics, School of Public Health, University of California, Berkeley, Berkeley, California (Dana E. Goin); and Departments of Mental Health, Biostatistics, and Health Policy and Management, Bloomberg School of Public Health, Johns Hopkins University, Baltimore, Maryland (Elizabeth A. Stuart).
This work was supported by grant R00DA042127 from the National Institute on Drug Abuse (K.E.R.) and grant R01MH115487 from the National Institute of Mental Health (E.A.S.).
Conflict of interest: none declared.
REFERENCES
- 1.Rudolph KE, Goin DE, Paksarian D, et al. Causal mediation analysis with observational data: considerations and illustration examining mechanisms linking neighborhood poverty to adolescent substance use. Am J Epidemiol. 2019;188(3):598–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Rudolph KE, Sofrygin O, Schmidt NM, et al. Mediation of neighborhood effects on adolescent substance use by the school and peer environments. Epidemiology. 2018;29(4):590–598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Naimi AI, Schnitzer ME, Moodie EE, et al. Mediation analysis for health disparities research. Am J Epidemiol. 2016;184(4):315–324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Vittinghoff E, Sen Ś, McCulloch C. Sample size calculations for evaluating mediation. Stat Med. 2009;28(4):541–557. [DOI] [PubMed] [Google Scholar]
- 5.Zhang Z. Monte Carlo based statistical power analysis for mediation models: methods and software. Behav Res Methods. 2014;46(4):1184–1198. [DOI] [PubMed] [Google Scholar]
- 6.Baron RM, Kenny DA. The moderator-mediator variable distinction in social psychological research: conceptual, strategic, and statistical considerations. J Pers Soc Psychol. 1986;51(6):1173–1182. [DOI] [PubMed] [Google Scholar]
- 7.Judd CM, Kenny DA. Process analysis: estimating mediation in treatment evaluations. Eval Rev. 1981;5(5):602–619. [Google Scholar]
- 8.Valeri L, VanderWeele TJ. Mediation analysis allowing for exposure-mediator interactions and causal interpretation: theoretical assumptions and implementation with SAS and SPSS macros. Psychol Methods. 2013;18(2):137–150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fritz MS, MacKinnon DP. Required sample size to detect the mediated effect. Psychol Sci. 2007;18(3):233–239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.MacKinnon DP, Lockwood CM, Williams J. Confidence limits for the indirect effect: distribution of the product and resampling methods. Multivar Behav Res. 2004;39(1):99–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pan H, Liu S, Miao D, et al. Sample size determination for mediation analysis of longitudinal data. BMC Med Res Methodol. 2018;18(1):Article 32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shrout PE, Bolger N. Mediation in experimental and nonexperimental studies: new procedures and recommendations. Psychol Methods. 2002;7(4):422–445. [PubMed] [Google Scholar]
- 13.Rice JA. Mathematical Statistics and Data Analysis. 3rd ed. Belmont, CA: Thomas Brooks/Cole; 2006. [Google Scholar]
- 14.Rudolph KE, Sofrygin O, Zheng W, et al. Robust and flexible estimation of stochastic mediation effects: a proposed method and example in a randomized trial setting [published online ahead of print December 13, 2017]. Epidemiol Methods. (doi: 10.1016/j.cmpb.2003.08.003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.VanderWeele TJ, Tchetgen Tchetgen EJ. Mediation analysis with time varying exposures and mediators. J R Stat Soc Series B Stat Methodol. 2017;79(3):917–938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tchetgen Tchetgen EJ. Inverse odds ratio-weighted estimation for causal mediation analysis. Stat Med. 2013;32(26):4567–4580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Rubin DB. Causal inference using potential outcomes: design, modeling, decisions. J Am Stat Assoc. 2005;100(469):322–331. [Google Scholar]
- 18.Pearl J. Causality: Models, Reasoning and Inference. Vol. 29. New York, NY: Springer Publishing Company; 2000. [Google Scholar]
- 19.VanderWeele TJ. Mediation analysis: a practitioner’s guide. Annu Rev Public Health. 2016;37:17–32. [DOI] [PubMed] [Google Scholar]
- 20.Petersen ML, Sinisi SE, van der Laan MJ. Estimation of direct causal effects. Epidemiology. 2006;17(3):276–284. [DOI] [PubMed] [Google Scholar]
- 21.Nguyen QC, Osypuk TL, Schmidt NM, et al. Practical guidance for conducting mediation analysis with multiple mediators using inverse odds ratio weighting. Am J Epidemiol. 2015;181(5):349–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.R Core Team . R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2019. [Google Scholar]
- 23.Rudolf K. MediationPowerTutorial. https://github.com/kararudolph/MediationPowerTutorial. Accessed July 2, 2020.
- 24.Pearl J. Direct and indirect effects. In: Proceedings of the 17th Conference on Uncertainty in Artificial Intelligence. San Francisco, CA: Morgan Kaufmann Publishers, Inc.; 2001:411–420. [Google Scholar]
- 25.Hayes AF, Scharkow M. The relative trustworthiness of inferential tests of the indirect effect in statistical mediation analysis: does method really matter? Psychol Sci. 2013;24(10):1918–1927. [DOI] [PubMed] [Google Scholar]
- 26.Petersen ML, Porter KE, Gruber S, et al. Diagnosing and responding to violations in the positivity assumption. Stat Methods Med Res. 2012;21(1):31–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Vansteelandt S, Daniel RM. Interventional effects for mediation analysis with multiple mediators. Epidemiology. 2017;28(2):258–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zheng C, Zhou XH. Causal mediation analysis in the multilevel intervention and multicomponent mediator case. J R Stat Soc Ser B Stat Methodol. 2015;77(3):581–615. [Google Scholar]
- 29.Zheng W, van der Laan MJ. Targeted maximum likelihood estimation of natural direct effects. Int J Biostat. 2012;8(1):1–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Goetgeluk S, Vansteelandt S, Goetghebeur E. Estimation of controlled direct effects. J R Stat Soc Ser B Stat Methodol. 2008;70(5):1049–1066. [Google Scholar]
- 31.VanderWeele TJ. Marginal structural models for the estimation of direct and indirect effects. Epidemiology. 2009;20(1):18–26. [DOI] [PubMed] [Google Scholar]
- 32.Taguri M, Chiba Y. A principal stratification approach for evaluating natural direct and indirect effects in the presence of treatment-induced intermediate confounding. Stat Med. 2015;34(1):131–144. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


