Abstract
Despite the progress in modeling complex molecular systems of ever-increasing complexity, a quantitatively accurate computational treatment of ion permeation through narrow membrane channels remains challenging. An important factor to reach this goal is induced electronic polarization, which is likely to impact the permeation rate of small ions through narrow molecular pores. In this work, we extended the recently developed polarizable force field based on the classical Drude oscillators to assess the role of induced polarization effects on the energetics of sodium and potassium ion transport across the gramicidin A (gA) ion channel. The inclusion of induced polarization lowers barriers present in 1D potential of mean force (PMF) for cation permeation by ∼50% compared to those obtained with the additive force field. Conductance properties calculated with 1D PMFs from Drude simulations are in better agreement with experimental results. Polarization of single-file water molecules and protein atoms forming the narrow pore has a direct impact on the free-energy barriers and cation-specific solid-state NMR chemical shifts. Sensitivity analysis indicates that small changes to water–channel interactions can alter the free energy barrier for ion permeation. These results, illustrating polarization effects present in the complex electrostatic environment of the gA channel, have broad implications for revising proposed mechanisms of ion permeation and selectivity in a variety of ion channels.
1. Introduction
The movement of ions across selective biological membranes via specialized proteins known as ion channels is a fundamental process that underlies electrical signaling in all excitable cells.(1) Many familial loss-of-function mutations of ion channels cause abnormal permeation and altered selectivity that are found to link with a wide range of health conditions (the so-called “channelopathies”), ranging from long QT (QT2) syndrome to neonatal epilepsy.(2) Over the past decades, extensive experimental studies mapping structural and functional aspects of selective ion permeation in these narrow transmembrane channels have been matched by an explosive development in computational modeling techniques.(3–5)Molecular dynamics (MD) simulation of detailed atomic models, in particular, has ultimately emerged as one of the most useful computational methods to quantitatively characterize the physical mechanisms controlling the dynamics of selective transport across many biological and artificial membranes.(6) However, while the classical trajectories have been used to yield details of dynamics, the models rely on many approximations. For instance, many commonly used atomistic biomolecular MD simulation software programs(7–11) employ simple non-polarizable force fields (FFs) to describe interparticle interactions. To achieve transferability, these FFs rely on the assumption that interactions are approximately pair-wise additive, providing a reasonable approach to simulate many testable macromolecular properties of biomolecular systems. Such additive FFs, however, may fail to account for the subtle electrostatic responses experienced, for example, by an ion moving from bulk solution into the lumen of a narrow molecular pore.(5,12,13) It is possible that unresolved issues about ion energetics in narrow molecular pores underlie some controversies regarding ion occupancy, permeation, and selectivity in potassium channels.(6,14–20)
One of the simplest molecular pores, where many of these issues come to the fore, is the cation-selective gramicidin A (gA) channel.(21–23) The wealth of experimental and simulation data available for this extensively studied ion channel makes it an ideal model system for testing the FFs employed in studies of ion permeation and selective transport. The structure of this channel has been determined to atomic resolution by several independent NMR studies.(24–26) The gA channel is formed by two identical right-handed β-helical monomers associated in a head-to-head manner (N-terminal to N-terminal) spanning the lipid bilayer.(25,27) The permeation pore, which is lined by hydrogen bonds between the backbone carbonyl and amino groups of the β-helices, is so narrow that it can only be filled by water molecules in a single-file arrangement. X-ray diffraction(28) and NMR studies(29) suggest that the cation binding sites are located near the entrance of the channel, at 9–10 Å from the membrane center. Various structural metrics calculated from MD(30) and free energy simulations(21) were found to be in good agreement with experimental data. However, the free-energy barriers from one-dimensional potential of mean force (1D-PMF) calculations based on the CHARMM22 (C22) or CHARMM27(C27)-CMAP FFs(31–33) for monovalent cations appear to be overestimated by at least 4–5 kcal/mol.(21–24,34–37) As a result of these high free-energy barriers, the conductance estimated directly from the 1D-PMFs for either of these permeant cations is several orders of magnitude smaller than the experimental values.(22,23,34,38,39)
On the basis of MD calculations and perturbation analysis, Allen, Andersen, and Roux(21–23)conjectured that the discrepancy between the MD and experimental values of ion conductance was due to the lack of explicit induced polarization effects in the additive FFs.(23,40–45) Approximate corrections based on continuum electrostatics calculations to account for induced polarization of the lipid carbon chains were shown to significantly reduce the permeation barriers so that estimated conductance agreed with the experimental data. Subsequent simulation studies employing polarizable models generally suggest that this conjecture was sound.(13,46,47) The free-energy barrier of a cation along the axis of the gA channel was indeed reduced in a study using a fluctuating charge-equilibration (fluc-Q) FF(46)and in a study using the AMOEBA(48–51) polarizable FF,(47) while other polarizable models have not been used to test this system.(52–55) Despite the encouraging results, the cation binding sites arising from these calculations appear strikingly different from those deduced previously by combining the information from experiments with the result of additive FFs.(28)For instance, the 1D-PMFs by Patel et al.(46) and Peng et al.(47) for K+ display multiple free-energy minima near the channel center, which are at odds with the known cation binding sites mapped by X-ray scattering,(28) solid-state nuclear magnetic resonance (ssNMR),(37) and MD simulations with additive force fields,(30) showing symmetrical binding sites at 9.6 ± 0.3 and 13.0 ± 0.3 Å away from the channel center.(21–23,34,56) While both studies emphasized the impact of local polarization of the protein ligands and/or lipids on ion transport, limited information was provided about the relative magnitude of various contributions from the ion–solvent and protein–solvent interactions. A detailed understanding of the role of water molecules confined in the narrow pore and the interplay between the solvent–protein and solvent–ion interactions is needed for accurate descriptions of ion permeation, potentially helping to resolve current debates for other narrow pores, such as potassium channels.(6,17–19)
In this study, we investigate the importance of induced polarization during ion transport through the gA channel. We choose to work with the polarizable Drude FF,(12,57–62) which has been developed to model proteins, lipids, solvent, and ions over the last 20 years.(6,12,57,60,63) It provides a computationally efficient framework to test the roles of polarizability in ion channels. One of the specific questions we want to address is related to the role of water molecules in mediating interactions between the permeant cations (K+ or Na+) and the channel. We quantify the impact of the different permeant cations on the induced polarization of water wire and the protein ligands lining up the permeation pathway as well as by computationally controlling the strength of the water–carbonyl interactions. We also demonstrate a close relationship between the free-energy barriers experienced by cations in the confinement of the gA channel and the hydration of the channel, affecting ion interactions with water molecules and pore-lining residues.
2. Methods
2.1. Additive Non-Polarizable Force–Field Parameters
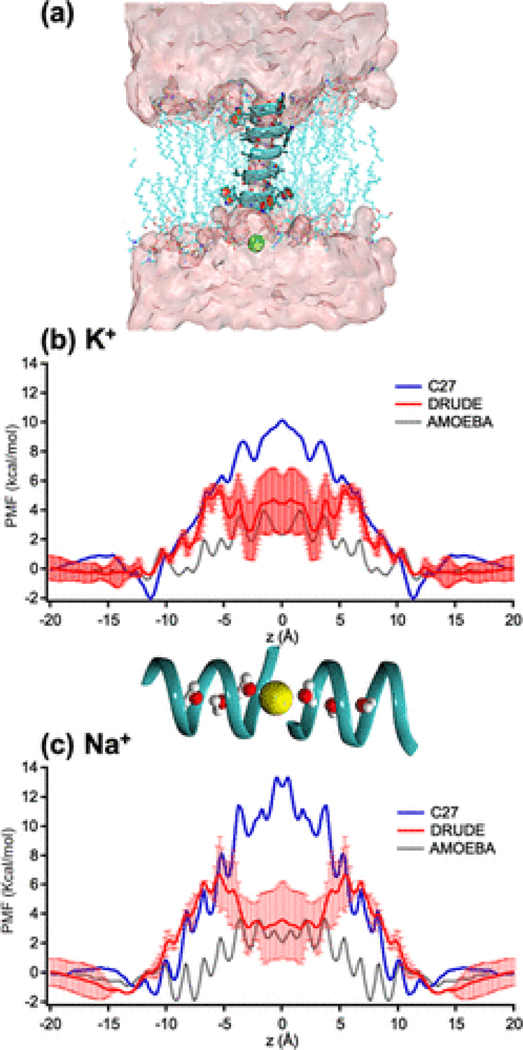
Each of the gA monomers has the following sequence: formyl-Val1-Gly2-Ala3-DLeu4-Ala5-DVal6-Val7-DVal8-Trp9-DLeu10-Trp11-DLeu12-Trp13-DLeu14-Trp15-ethanolamine. All MD simulations with non-polarizable additive force fields were performed using the CHARMM22 force-field without CMAP correction for this peptide,(64) CHARMM27 force-field parameters for lipids,(65) and TIP3P water model. We used additive CHARMM force-field without CMAP corrections similar to previous studies including Allen et al.(22,23,56) whose results were used for comparisons in all computational studies on gA. The use of additive CHARMM force-field with CMAP corrections was shown to increase free-energy barriers for both K+ and Na+.(34) In the manuscript we refer this force-field as “C27”. The force-field parameters for K+and Na+ were adapted from Luo and Roux(66) with ion-carbonyl NBFIX corrections reported by Noskov and Roux.(67) The simulation system is shown in Figure 1a.
Figure 1.
(a) A molecular view of the gA system (shown as a blue helix) embedded in a lipid bilayer, schematically shown in a stick mode. The permeant cation is shown as a green sphere. The pink surface represents the water solvent accessible surface. (b, c) Potential of mean force (PMF) of K+ and Na+ calculated from different FFs. The AMOEBA PMF data were shared by the authors of ref (47). Error bars shown for the PMFs were estimated from the differences between the two parts (z > 0 and z < 0) of the unsymmetrized PMFs (Figure S7) with the global minima set to zero. A snapshot of ions (yellow spheres) and water molecules (balls and sticks) in gA (ribbons) is for z coordinate reference.
2.2. Polarizable Force-Field Parameters
We used the 2013b version of the CHARMM Drude FF for proteins and lipids,(57,63,68,69) with a recent set of NBFIX values based on QM screening for gas-phase interactions between Na+/K+ and a set of peptide fragments constructed from 30 high-resolution protein structures.(40) Details of the Drude polarizable FF and parameterization methodologies were provided previously.(40,57,68,70) Here, we briefly describe an extra parametrization step on the terminal groups in the gA channel. The model compounds 2-(methylamino)ethanol and N-methylformamide (Figure S1) were used to parameterize the ethanolamine and formyl groups in gA. New FF parameters for model compounds and the two termini are provided in Table S1. The atom types defined in the topology file provided (Table S1) are consistent with standard atom type definitions in the Drude polarizable FF.(40,57,58,68) The charges and polarizabilities were obtained by fitting with ab initio electrostatic potentials assessed using HF/6–31G*(71) for several model compounds. The Lennard-Jones (LJ) parameters of the formyl group were optimized against solute–water dimer interaction energies obtained using B3LYP functional and aug-cc-pvdz basis sets. The dihedral angle parameters of 2-(methylamino)ethanol were fitted against QM torsional energy surfaces obtained using MP2/cc-pVTZ (Figure S2). Previously developed NBFIX and Thole parameters for interactions between the ions (K+ or Na+) and carbonyl oxygen and terminal-group oxygen atoms were used.(41) The impacts of NBFIX and Thole parameter choices on the PMFs are discussed in the Supporting Information methods section. CMAP (L-CMAP and inverted CMAP D-CMAP) corrections(57) were used to model the ϕ-ψ torsional angles for the sequence with l- and d- amino-acid residues in Drude simulations.
2.3. MD Simulations
The equilibrated systems (Figure 1a) from refs (21,22) were used to generate the starting configurations for umbrella-sampling simulations. Briefly, the simulation systems contained the gA channel embedded into a lipid bilayer composed of 96 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) molecules, solvated in a 1 M 1:1 electrolyte solution composed of 74 (Na+ or K+) and Cl− ions with 4003 water molecules. Previous studies showed the importance of accounting for finite size effects in accurate PMF calculations.(21,22) The system dimensions selected for PMF calculations ensured full lipid hydration (>40 water per lipid), included two shells of lipids around gA dimer and allowed the bulk region of the systems to extend for over 25 Å from the membrane surface. The system’s design resulted in a relatively small effect of the finite size corrections as evident from Figure S3, in accord with previous studies.(21,22) This system when using the C27 FF is called the “C27” model. It is called the “Drude” model when Drude particles and SWM4-NDP water(68,70) are added and used in the C27 model. When removing the ions, the system becomes the “ion-free” system. The total number of atoms in the Drude model is 37,715, including the Drude particles, which were added to heavy atoms via the Drude–Prepper utility in the CHARMM-GUI web-based engine.(61) The initial system was simulated with a hexagonal periodic cell with a side of 61 Å and length of 77 Å. Langevin dynamics with a dual-thermostat scheme was used to propagate the atoms and auxiliary Drude particles with an extended Lagrangian formalism implemented in the NAMD package.(8,57,72) The thermostat acting on heavy (non-Drude) particles was set to , exceeding the DMPC gel phase transition temperature and promoting sampling.(21) The Langevin damping coefficient was set to 1.0 ps−1. The weak damping coefficient enables stable Drude production runs with an integration time step of 1.0 fs.(73) To achieve a regime approximating the self-consistent field (SCF), a separate Langevin thermostat (TDrude) was coupled to the atom-Drude oscillator pairs. For all production runs, was used with a spring constant for the atom-Drude bond of 1000 kcal/mol/Å2.(70,74) A damping constant of 20.0 ps−1 was applied to Drude particles. A “hard-wall” constraint was used to prevent large displacements(22,23,56) of Drude particles. The hard wall constraint distance was set to 0.2 Å. A Thole interaction radius of 5 Å was used for all nonbonded interactions. The particle mesh Ewald (PME) method(75) with a grid spacing of 1 Å and sixth interpolation order was used to compute electrostatic interactions with a real space cutoff of 12 Å. For the LJ interactions, the nonbonded cutoff distance was set to 12 Å with switched smoothing initiated at 10 Å. The atom-pair list was updated every 20 steps. LJ and electrostatic interactions were computed every time step. The SHAKE algorithm (RATTLE)(76) was used to maintain the geometry of all bonds involving hydrogen.
2.4. Umbrella-Sampling Simulations with Hamiltonian Replica Exchange
For each of the umbrella windows, a harmonic biasing window potential, with was used to restrain the z coordinate of a permeant ion across the gA pore. The reference of the biasing potential, zi, was varied from −20 to 20 Å with a step of 0.5 Å, i.e., with i ∈ [1 : 81]. The chosen spring constant was sufficient to generate overlapping distributions for the biased coordinate z, required for accurate estimation of the free-energy profiles via the WHAM equations.(77,78) A flat-bottom harmonic potential was applied to keep the permeant ion inside a cylinder with an 8 Å radius and prevent all other ions from entering the cylinder. The constraint protocol was identical to that used previously for CHARMM22-CMAP simulations and allowed for comparison between the equilibrium dissociation constants Kd (eq 1) calculated for two different FFs.(22) The initially relaxed structures from previously reported 1D-US simulations(23) were re-minimized in the presence of a harmonic restraint acting on all heavy atoms. Then, we gradually reduced the constraints on the heavy atoms for each of the constructed umbrella windows. For all US production runs, we used a time step of 1.0 fs and the NVT ensemble for both C27 and Drude runs. The equilibrated US windows were used for Hamiltonian replica-exchange simulations (H-REMD) in NAMD 2.11.(79–81) Each H-REMD set of simulations has 81 windows and exchange rates of 19–28% for neighboring US windows, with the exception of the windows at and 7 Å, which displayed rates of only 7–9%, as they correspond to the highest barrier. Ten independent sets of H-REMD simulations were conducted, in which we investigated the impacts of CMAPs (Figures S4–S6). The sampling length for each of the H-REMD runs ranged from 16 ns/window for the system with K+ and 20 ns/window for the system with Na+. The sampling length was defined by monitoring convergence in the calculated PMFs. The convergence in the calculated 1D PMF profiles was monitored by comparisons of unsymmetrized and symmetrized PMFs, as described previously by Allen et al.(23) It is important to mention that a recent high-field ssNMR study reported by Paulino et al. also showed that symmetry can be broken by cation binding or by carbonyl–water interactions.(82) The data for unsymmetrized PMFs calculated for various simulations parameters and two studied permeant cations are shown in Figure S7. The unsymmetrized PMFs were matched in bulk solution, and then the corresponding differences on each side of the bilayer center were used as errors, leading to higher error bars in the middle of the membrane (). The dual-thermostat scheme used for integration with the Drude system may result in transient deviations from the SCF regime.(58) To improve stability of the simulations used for PMF calculations, we chose to run them at for all PMF computations.
2.5. Evaluation of Equilibrium Dissociation Constants
Since we used the flat-bottom harmonic potential to restrain the lateral movement of an ion within an 8 Å radius cylinder (R = 8 Å), the equilibrium dissociation constant Kd can be defined as follows
| (1) |
where W(z) is the potential of mean force, T is the temperature, kB is the Boltzmann constant, Kb is the equilibrium binding constant, zref = 20 Å, and πR2 is the area of the flat-bottom restraining potential designed to keep the tagged ion inside a cylinder of radius R (see refs (22,83) for the derivation of eq 1) and z1 and z2 define the integration range over a binding site. The 8 Å radius cylindrical restraint does not affect the ion inside the pore. However, it is necessary to formally define the PMF reference in the bulk (otherwise the ion would be laterally unbound); in practice, it also enhances the sampling efficiency of the tails of the PMF in the bulk region defined as . The Kd obtained from eq 1) is independent of the choice of radius, R.(22,83)
2.6. Maximal Conductance
To quantify the permeation from the single-ion PMFs, we estimated the maximal conductance for direct comparison with experimental values. Under the saturating concentrations of permeant ions, the maximal conductance from a single-ion PMF can be computed with Smoluchowski diffusion theory(21–23,56)
| (2) |
where |e| is the electron charge, D(z) is the spatial-dependent diffusion coefficient of a cation, and the brackets denote a spatial average over the length L of the channel. The diffusion coefficient D(z) can be computed using a method(84) based on the Laplace transformation of the velocity autocorrelation function. Assuming the dynamics of an ion constrained in the umbrella window obey the generalized Langevin equation for a harmonic oscillator, D(z) can be computed from
| (3) |
where is the standard deviation of an ion’s z coordinate, is the averaged squared velocity of an cation, s is a Laplacian variable in the is the Laplace transform of the velocity autocorrelation function from the ith window simulation with the biasing potential Ui. To compute , we used analysis tools in CHARMM(9,10) to estimate velocities based on z coordinates, , in which fs. Equation 3 is equivalent to the approach of Hummer and colleagues(85) estimating diffusion coefficients from the time-autocorrelation function of and its characteristic relaxation time τ. Because of incomplete sampling of the fluctuating z(t), the Laplace transform becomes numerically unstable in the limit of s → 0. For this reason, D(z) should be estimated for a range of s values approaching s = 0. We estimated the value of the limit by extrapolating to s = 0 from 15 ≤ s ≤ 35. The resulting diffusion coefficients could potentially be overestimated as a result of this extrapolation(86) but provides consistent estimates for comparison with previous simulations performed with C22/C27-CMAP (referred as C27 in the text below) and AMOEBA force fields.(21,22,47) The channel is formed by the identical peptides, and therefore the resulting PMF of a permeant cation is expected to be symmetric in the limit of complete sampling or infinite simulation time. However, for a finite simulation time, such a PMF may exhibit some asymmetry. Specifically, one side (z > 0) of this PMF may have a free-energy barrier (with respect to z = 20 Å) relatively lower than the barrier of the other side (with respect to z = −20 Å). So, we estimated an upper-bound value of gmax by using only the part of the PMF with the lower free-energy barrier for the entire symmetrical channel. A lower-bound value of gmax was computed by using the other part of the PMF, which has a relatively higher free-energy barrier.
2.7. Calculations of Chemical Shifts
To compare the structure of gA modeled by the Drude FF with data from solid-state NMR experiments(25,37,39,87) we computed the chemical shift anisotropy (CSA) of each 15Nα atom of the gA backbone as follows
| (4) |
where is the parallel chemical shift of 15Nα, is the perpendicular chemical shift of the 15Nα atom with with and being the instantaneous magnitude and direction of the principle tensor components, and , , and being unit vectors. 〈...〉 indicates a time average. For more details on the formal definitions, please see Woolf et al.(30)
These tensor components are as reported in the experimental studies.(87) In simulations performed with an ion-free system, the values of were averaged for each amide Nα atom of the gA backbone. The simulations performed in 1:1 electrolyte solutions indicate statistically observable shifts in for positions corresponding to different residues comprising the channel.(37) The calculated shifts must be weighted according to the probabilities(30) corresponding to the equilibrium probability of finding the permeant ion at position zi across the reaction coordinate:
| (5a) |
where β is 1/kBT, is the chemical shift averaged in the ith window from the time-series data, the summation is carried out over all the 81 values of zi from −20 to 20 Å, and represents the Boltzmann factor for an ion in a given umbrella window i, with free energy value computed at zi. An error of for each 15Nα atom is computed as follows
| (5b) |
where is the standard deviation and .
In comparison with NMR measurements, each NMR-spectrum signal around a peak has a standard deviation of about 10 ppm, which is smaller than standard deviations computed from each MD trajectory (20–30 ppm). However, a thermodynamic average computed via eq 5b yields an uncertainty of about 1 ppm, which is equal to the uncertainty measured from the experiments for the changes in the chemical shifts due to the binding of cations. Note that the chemical shifts measured in the NMR experiments(37) were calculated from reported shifts in 15Nα signals for gA with ions in comparison with gA without ions, for each 15Nα atom. To perform comparative analysis of ion binding impact on the chemical shifts, we have used the reference chemical shifts from the windows 1 and 81.
Another NMR quantity that can be computed from MD simulations to examine the simulated structures is 15N–1H dipolar coupling
| (6) |
where vo is the dipolar coupling constant, equal to 19.86 kHz for rNH = 1.07 Å used in CHARMM; θ is the angle between the N–H vector and the magnetic field, which is parallel to the z direction. This coupling can be used to examine the directions of all N–H vectors in gA with respect to the z direction. The standard deviations of the coupling are used to represent the uncertainty.
2.8. Dynamics of Single-File Water Molecules
The number of water molecules in the single-file water wire selected for the analysis was estimated based on the position along the z axis, with only water molecules with oxygen atoms at included. It is important to stress that this range was arbitrarily defined based on the geometry of the channel and location of the binding sites in the computed 1D PMFs. We analyzed the orientation dynamics of water molecules forming a single-file water arrangement in the gA channel using a Markov state model (MSM) framework.(88,89) The analysis was done using the PyEMMA software v2.0.(90) An orientation of an individual water molecule in the wire was defined as an angle between and the z axis. This angle is saved every 10 ps for each water molecule. To build the transition matrix describing the reorientations of the water molecules, we discretized this angle by taking its integer values in degree and then estimated a Markovian transition matrix with a lag-time ps by computing transition probabilities from the time-series data; specifically , where cij is a number of times that the angle has a value of at a time t and a value of at time . This transition matrix was then used to compute the mean first passage transition time via transition path theory (TPT) between two major orientations,(91–93) which are defined by the two peak distribution positions of the angle ( and ). Noé et al.(94) details how to solve for , given Mij and the angles ϕA and ϕB. In essence, TPT finds the committor probability, which is used to compute a net flux between any two states. The inverse of this net flux is proportional to .
2.9. Approach to Parametric Study of Water–Carbonyl Interaction Impact on Ion Permeation
In order to explore an impact of water–carbonyl interactions on the ion permeation, we introduced a model referred as DrudeX with slightly different water–carbonyl interactions. We performed QM calculations to scan interactions between an NMA molecule and a water probe. The calculations indicate that the current set of the Drude parameters appears to modestly overestimate hydrogen-bonding interactions of the dimer in vacuum. This in turn may impact the probability of the hydrogen-bonding between water molecules and the carbonyl groups along a permeation pathway. So, we carried out a re-refinement of NMA–water hydrogen-bonding interactions. To refine water–carbonyl oxygen interactions, one water molecule from a pre-optimized complex was translated along a different scanning axis (Figure S8A–C) with X–O distances ranging from 2.2 to 4.8 Å in intervals of 0.2 Å. Using Gaussian16 single points, QM interaction energies were then calculated between the translated water molecule and the NMA molecule in fixed geometry using the MP2/aug-cc-pvdz level of theory. Counterpoise correction for basis set superposition error (BSSE) was used. The NBFIX corrections were then developed to adjust the Lennard-Jones parameters Rmin controlling hydrogen-bonding between water oxygen and both carbonyl oxygen and backbone nitrogen, as shown in Table 1: Rmin for water oxygen and carbonyl oxygen was increased by 0.109399 Å, while Rmin for water oxygen and backbone nitrogen was decreased by 0.0706101. The adjusted parameters are denoted as a DrudeX model.
Table 1.
Parameters for Lennard-Jones Interactions in C27, Drude, and DrudeX Modelsa
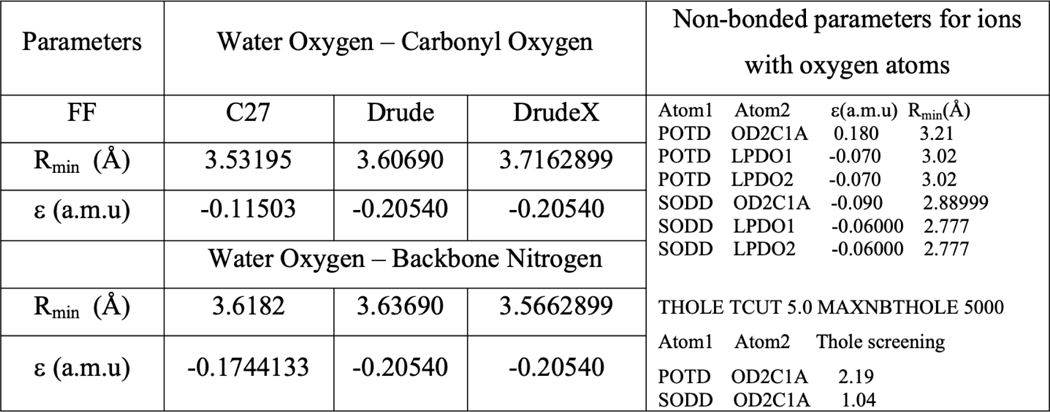
|
The atom types and more details are provided in Table S1.
2.10. Evaluation of the Induced Polarization Component
In contrast to non-polarizable potential functions, the Drude FF allows for the explicit assessment of the induced polarization effects. To observe how the permeating ions induce electrostatic changes of local environments, we define the induced dipole moment of atom A as
| (7) |
where qDA is the charge of its Drude particle with a position denoted by , attached to the heavy-atom nucleus . The dipole moment μ→ for the SWM-NDP water model(68) is , in which the first and second terms are the induced and permanent dipole moments. We define the average total induced moment within the first coordination shell of an ion summed over the nearest water molecules within a 3.5 Å radius as
| (8) |
where ⟨...⟩i denotes the average over all frames in the ith umbrella sampling window and is the coordination number of a cation. To examine the relative importance of induced polarization in ion–water interactions, we decompose the total interactions between an ion and its neighboring water molecules in terms of the induced (ind) and permanent (pmt) charge distributions
| (9a) |
| (9b) |
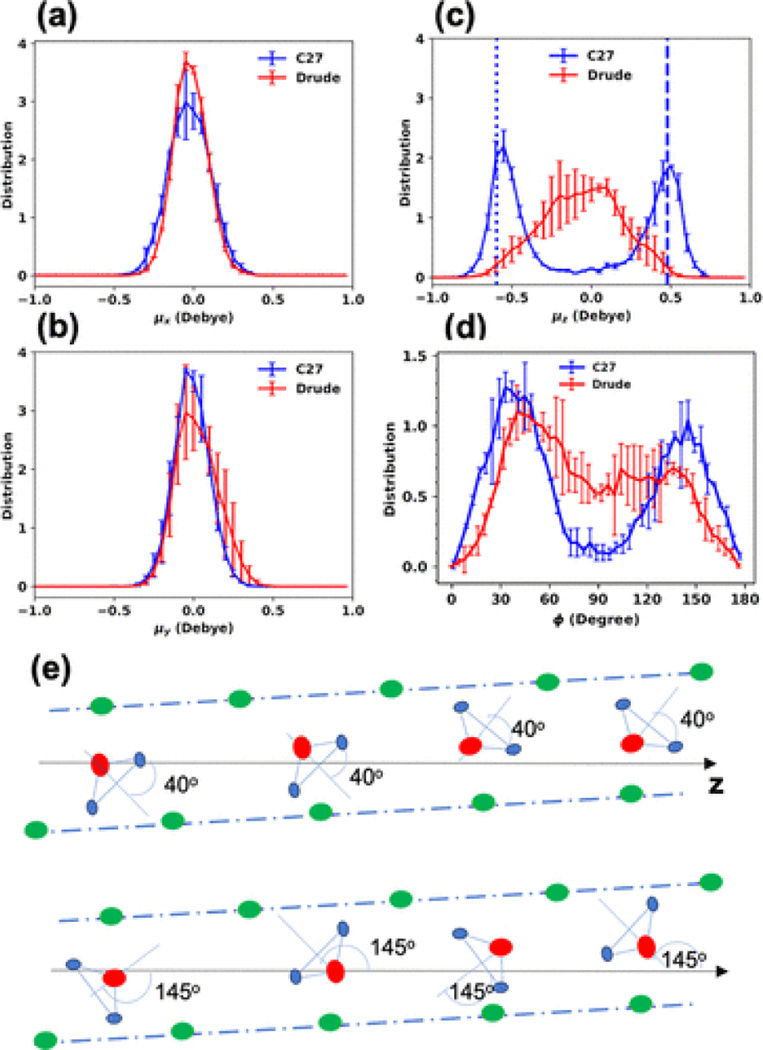
where X can be K+ or Na+, qX is the charge of cation X, and DX is a Drude particle attached to the nucleus of X. The Z axis for the system is the normal of the lipid bilayer and x and y components shown in Figure 4a are defined relative to it.
Figure 4.
(a–c) Un-normalized distributions of the total dipole-moment components of water molecules involved in the single-file water arrangement within the gA channel in the ion-free channel. (d) Distribution of the angle between the orthogonal bisector of a water molecule in the single-file water and the z-axis (see Section 2). (e) Illustration of major orientations of water molecules in an individual peptide. Oxygen, backbone, and hydrogen atoms are red, green, and light blue dots, respectively. The dot-dashed lines indicate the tilted structure of the peptide with respect to the z axis. If six water molecules have ϕ = 40, the total μz = 0.48 Debye (dashed line in (c)). If seven water molecules have ϕ = 145, the total μz = −0.59 Debye (dotted line in (c)).
3. Results and Discussion
3.1. Energetics of Cation Permeation from 1D-PMF Calculations
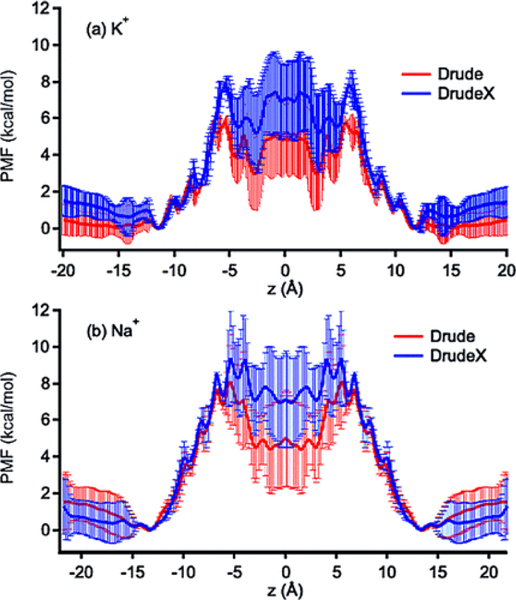
The single-ion PMF W(z) can be used to characterize the energetics of ion permeation for K+ and Na+.(95–97)Figure 1b-,c shows that the Drude PMFs for Na+and K+ are fairly different from those calculated with the C27(34) and AMOEBA(47) FFs. The barrier for K+ in the Drude PMF, with respect to the bulk, is 5.5 ± 1.0 kcal/mol, whereas the barrier for the C27 and AMOEBA PMFs are 10.0 ± 1.0 and 4.0 ± 0.2 kcal/mol,(47) respectively. Even though there is no direct experimental data for such free-energy barriers, analysis of ion conductance data suggests that free-energy barriers should be around 4–5 kcal/mol, as argued by Allen et al.,(22) or about 3 kcal/mol to yield an optimal fit for Brownian dynamics data of ionic currents with physiological data as argued by Krishnamurthy et al.(98) So, both barriers from the Drude and AMOEBA FFs are in agreement with the theoretical argument by Allen et al.(22) but higher than the estimate based on the Brownian dynamics.(98) The PMFs in Figure 1b show that K+ binds to the first and the global free-energy minima at in all of the FFs, although the depths of these minima differ. The PMF of K+ calculated with the AMOEBA FF shows that the free energy of an ion at the position is comparable to that in the bulk. This minimum is elevated in the PMF calculated with the Drude or C27 FFs by 1 kcal/mol, being far less prominent. Minima further inside the channel, such as at ≈7.5 Å are also elevated in free energy, compared to AMOEBA, suggesting less propensity for binding deep inside the pore.
For Na+ in Figure 1c, the Drude PMF shows a significantly lower barrier (∼50%) than the barrier in the C27 PMF, but higher than the barrier calculated from the AMOEBA PMF by about 3 kcal/mol, and is located at a different position, at ∼6 Å, and then exhibits a central well relative to this height, instead of the central barrier seen with AMOEBA. Notably, the binding site with the lowest free-energy minimum for Na+ is located at in the Drude FF, in contrast to the AMOEBA PMF, where the lowest minima inside the channel are at and 9 Å. The existence of the binding site at has been previously proposed from ssNMR experimental data,(37) which suggested that both K+ and Na+ are less stable at than for . Overall, the binding sites obtained from the C27 and Drude FFs for both cations appear to be in better agreement with available experimental data than the those obtained with the AMOEBA FF. Despite this, the lower free-energy barriers obtained from the AMOEBA may be more consistent with experimental conductances.(95–97)
Mean force decompositions(22,56) (Figure S9) were used to separate cation–gA and cation–single-file water components of PMFs obtained with the Drude model and compared to the C27 model. It is clear that the two models yield distinguishable interactions between the cations and the single-file water, as well as the cations and the channel. We will discuss below that model differences may also arise from the interactions between water and protein backbone. Note that there are significant errors in the Drude PMFs near the middle of the channel. This suggests some uncertainty in the modeling of the dynamics of cations in their near-dehydrated states within the narrow pore, to be explored below.
3.2. Dissociation Constants, Permeability, and Conductance
In order to better evaluate the energetics, particularly the free-energy barriers, we computed observables that can be derived from the computed PMFs. The values for the equilibrium dissociation constant Kd (using eq 1 and given in Table 2) are similar for both the Drude and AMOEBA FFs, despite the apparent differences in the barriers and binding sites in their 1D PMFs. Experiments have provided a range of the dissociation constants from various techniques and theoretical considerations.(24,36,99) Particularly, an experiment by Jing et al.(36) reported estimated “tight” binding constants (Kd = 0.016 M for K+ and 0.03 M for Na+) for diluted electrolyte solutions with a predominant single-occupancy state, as well as “weak” binding constants (Kd ≈ 0.2–0.4 M) corresponding to concentrated electrolyte solutions with a possibility for double-occupancy of the channel.(36) This suggests that the C27 FF yields a PMF more consistent with the “tight” binding constant, while the other two FFs yield PMFs more consistent the “weak” binding result, despite being equivalent in their modeling of the binding of a single ion within 1 M solutions.
Table 2.
Equilibrium Dissociation Constant and Maximal Conductancea
| Kd (M) | Kd(K+) (M) | Kd(Na+) (M) | gmax(K+) (pS) | gmax(Na+) (pS) |
|---|---|---|---|---|
| C27 | 0.04±0.01 | 0.04±0.01 | 0.0025–0.0031 | 0.0004–0.0006 |
| AMOEBA | 0.34±0.01 | 0.17±0.01 | 36.847 | 14.747 |
| Drude | 0.3±0.1 | 0.13±10.10 | 2–22 | 0.1–0.6 |
| Exp. | 0.017–0.7324,36,110 | 0.01±1.0109 | 21–23.834,39 | 3–12.438,39 |
The binding constant is calculated by assuming that z ∈ [−-20:20].
Experimentally, the gA pore displays a modest preference for K+ over Na+ with measured permeability ratio PK+/PNa+ of 2.9–3.5 depending on the corresponding bi-ionic concentrations of KCl and NaCl.(100,101) The permeability of a cation in a channel indicates an average diffusion rate at a reversal voltage that is applied to counter an ionic gradient to yield the zero ionic current across a bilayer.(1) Our estimates of the permeability ratio PK+/PNa+ from the average diffusion coefficients of the cations inside the channels () are about 1.5 for both the Drude (1.79/1.21) and C27 (1.97/1.4) FFs (Peng et al.(47) did not specifically report the ratio for the AMOEBA FF). Note that the spatially varying diffusion coefficients calculated for K+ and Na+ in the interior of gA are approximately 60–70% of the bulk diffusion values, similar to that reported in previous studies with C27 FF (2/3 of the bulk diffusion coefficient in Allen et. al(22)). The reduction in the in-pore diffusion coefficients calculated from the Drude simulations significantly differ from the calculations with AMOEBA FF reported by Peng et al.(47) (40–50% of the bulk diffusion coefficient calculated with method similar to one used in ref (22)) or charge equilibration FF by Patel et al.(46) (the authors used constant diffusion coefficient with ad hoc 10% reduction of the bulk diffusion coefficient). Available experimental values measured at 100 mM KCl for the diffusion coefficients of ions traversing gA are also 65 to 84% of the bulk values.(102) So, the estimates from the C27 and Drude models are more consistent with the available experiments than the other models. Note that the differences in the PMF peaks, as well as the different binding wells, were used as a circumstantial indication for the gA preference for K+ over Na+.(47) Based on both the Drude and C27 models, Figure 1b-,)and Figure S10 suggests that gA preferentially conducts K+ over Na+ because of lower free-energy barriers with respect to the bulk and slightly enhanced diffusion rates (, or 40–50% relative to ) in the interior of the channel.
A particularly relevant observable for evaluating the accuracy of the models is the maximal conductance gmax (eq 2), which can be estimated from the PMF and the space-dependent diffusion coefficient (eq 3 and Figure S10). Table 2 shows the accuracies of the FFs in terms of predicting ion conductance for gA. If using only the right part (z > 0) of the PMF for K+ (Figure S7), which has a lower free-energy barrier than the left part (z < 0), we can get an upper-bound estimate of the maximum conductance for K+, while the symmetrized PMF yields a lower value of the maximum conductance. As a result, the upper-bound estimate for K+from PMF calculations performed with polarizable force fields yields gmax = 22 and 36.8 pS for Drude FF and AMOEBA, respectively. The experimentally measured gmax values for K+ are 21–23.8 pS, which has much less uncertainty than the estimates (2–22 pS) using the Drude FF (Table 2). The upper-bound estimate for K+gmax calculated with C27 FF is 0.0031 pS, which is considerably underestimating the conductance. This trend is even more evident for Na+, for which the experimentally measured maximal conductance can vary from 3 to 12.4 pS depending on the experimental conditions.(38,39) Similarly, the upper-bound estimate for Na+ from PMF calculations performed with polarizable force-fields yields gmax = 0.6 and 14.7 pS for Drude FF and AMOEBA, respectively. The Na+gmax calculated with C27 FF is 0.0004 pS, which is considerably underestimated. The differences in the maximum conductance gmax largely arise from the significantly higher free-energy barriers in the C27 model, while the large uncertainty in the Drude model comes from the asymmetrical effects of the two peptides on the PMF (see more below). Despite such a large uncertainty, this shows that the ability of the Drude FF to model ion conduction is quantitatively more accurate than the C27 FF. In the following, we explain more in terms of structural properties of gA for the large uncertainties of the PMFs and conductance estimates from the Drude model.
3.3. Structural Dynamics of the gA Channel in the Absence and Presence of Cations
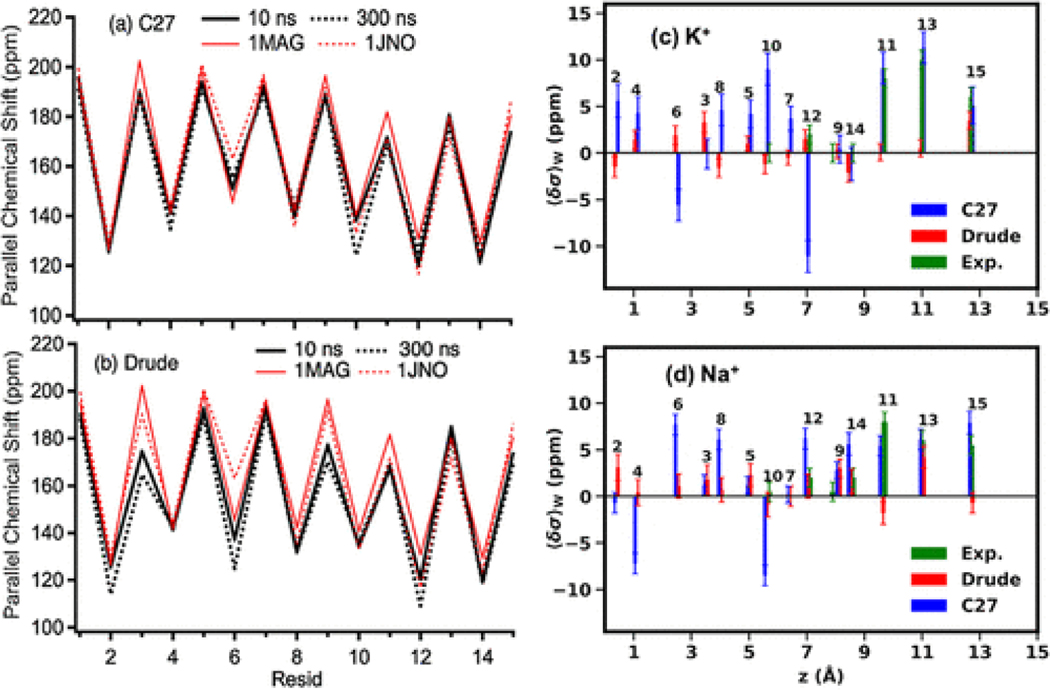
Next, we investigate the performance of the C27 and Drude FFs in modeling available experimental NMR data,(37,82) which can be used to assess changes in the structural dynamics of gA as a consequence of ion binding. In the absence of ions, Figure 2a,b shows the parallel component of 15Nα chemical shifts ⟨σ∥⟩ compared to values calculated for the available NMR structures (1MAG(103) and 1JNO(104)). When relatively short MD simulations (10 ns) of the gA channels are used the ion-free systems with the C27 and Drude FFs, the calculated chemical shifts are very close to the shifts computed for the NMR structures (Figure 2a,b). The largest difference of ⟨σ∥⟩ between the C27 and the NMR structures is only 10 ppm (∼ 5%) at Ala3, Trp11, and Trp15. The differences between the Drude and the NMR structures become more visible (∼15 ppm) at Ala3, DVal6, and Trp9. The differences become more profound when the simulations reach 300 ns with the Drude FF compared to the simulations with the C27 FF. Large differences (∼20–30 ppm or 10–15%) from the NMR structures are found at DLeu4 and DLeu10 for C27 and at Gly2, Ala3, D-Val6, Trp9, D-Leu12. The same trend was observed for dipolar coupling data calculated with the Drude and C27 FFs (Figure S11). Furthermore, the ssNMR data(37) indicate that the chemical shift of the 15Nε–Trp13-labeled site of the indole ring remains unchanged regardless of the ions present in the system (145 ± 1 ppm).(37) The simulated parallel components of the 15Nε–Trp13-labeled site, regardless of ionic type, are 144 ± 2 and 125 ± 3 ppm for the C27 and Drude modes, respectively. Overall, it can be concluded that the dynamics of the indole ring in the C27 model agrees better with the observations from the ssNMR experiments.(37) The accuracy in the CS calculations may, however, depend on the ability of the FFs to describe the overall stability and the inherent flexibility of the gA channel.
Figure 2.
(a, b) Parallel component of chemical shifts. 1MAG and 1JNO are the PDB codes of the NMR structures. (c, d) CSA changes due to the presence of ions relative to the CSAs calculated from ion-free simulations (eqs 7 and 8). The residue numbers are shown for each of the CSA. The sequence of the gA peptide is formyl-Val1-Gly2-Ala3-DLeu4-Ala5-DVal6-Val7-DVal8-Trp9-DLeu10-Trp11-DLeu12-Trp13-DLeu14-Trp15-ethanolamine. The standard deviations of the computed ssNMR are 20–30 ppm.
To determine the flexibility of the structures of the gA channel modeled by the two FFs, we analyzed the per-residue root mean square fluctuations (RMSF) from equilibrium MD simulations of the ion-free systems. Figure S12a–c shows that, in the presence and absence of the permeant ions, simulations performed with additive or polarizable FFs provide fairly similar estimates for channel’s flexibility as evidenced by the RMSF of 0.3–0.4 Å of per residue. The terminal residues are more flexible with RMSF up to 0.75 Å (Drude simulations with Na+). The state stability was monitored with the root mean square deviations (RMSD) shown in Figure S12d–f. While both simulations produced an RMSD plateau with RMS values <1 Å, the ion-loaded and ion-free channels modeled with the Drude FF consistently showed higher RMSD compared to that modeled with C27.
Given the similar stability and flexibility but slightly different dynamic structures, we further examined the effects of the cations on the gA structure and compared with ssNMR data reported by Tian and Cross.(37) For the chemical shifts in the presence of the cations, we computed a thermodynamic average and deviations as in eq 5a with the weights computed from the symmetrized PMFs of the cations across the channels. Figure 2c,d shows that the directions and values of the ion-induced changes in CSA ( in eq 5) averaged over the two identical gA monomers for the C27 and Drude models. Overall, the chemical shifts in the Drude model are noticeably smaller than the chemical shifts in the C27 model. Induced polarization allows to capture, at least partially, an electrostatic response of gA to ion movement without changing the position of the nucleus, something that is not possible with models employing additive force fields (C27 or similar). While the Drude model yields smaller CSA shifts than measured by the experiments, the C27 model appears to capture experimentally consistent CSA shifts at z ≈ 9.5, 11.0, 13 Å for both K+ and Na+. However, deeper inside the channel, the C27 model yields many large CSA shifts and even negative shifts in comparison with experiments, while the Drude models yield more reasonable CSA shifts. Particularly, at residue DLeu12, the negative shift with C27 suggests that the orientation of the N–H vector may point slightly in the wrong direction with respect to the reference (ion-free) ensemble (Figure S13). This suggests that the C27 model captures well the relative structural changes for the residues comprising the cation binding sites at the channel entrance. However, C27 performance in the CSA shift calculations is compromised for the residues in the channel’s interior. The direction of the CSA shifts for the interior residues are captured better by the Drude model, albeit with underestimation of absolute values. We would argue that the better performance of Drude FF for the ion-induced changes results from a better and more accurate description of the ion-induced protein backbone reorientation and overall structural relaxation compared to the non-polarizable C27 force field. The lower-than-experimental CSA shifts calculated with the Drude model, do however, indicate that the ion–protein interactions remain to be improved in the next generation of the force field.
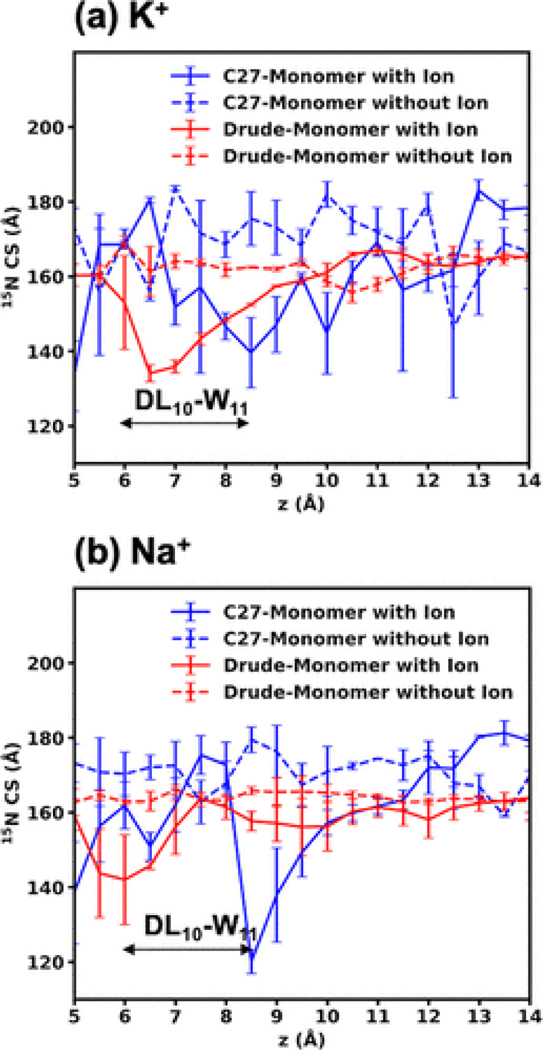
Since the cations bind and enter the gA channel (Figure 2c,d) near Trp11, to further investigate the effects of the cations on the chemical shifts, we computed the chemical shift of Trp11 of one peptide occupied by one cation and then compared it the chemical shift of Trp11 of the other identical peptide, which is not bound by the cations. Figure 3 shows that the results obtained from the C27 FF are qualitatively similar to the results discussed previously by Roux and Woolf(30) in a modeling study reporting Na+-induced changes, i.e., Na+ induces largest perturbations when bound at z ≈ 9.0 Å, with a less profound perturbation when located at z ≈ 6.0 Å. There are noticeable differences between the chemical shifts modeled by the two FFs. Specifically, while the Drude model yields a more or less constant shift on Trp11 for the peptide without the cations, the shifts on the C27 model are larger and fluctuate more (∼10 ppm) than the shifts computed by the Drude model. With explicit account for the induced dipoles, the coordinating protein groups are likely to exhibit smaller dipole reorientation in response to electric fields compared to C27 FF.
Figure 3.
15N chemical shift parallel at the Trp11 backbone site as a function of the ion position along the z axis for the Drude and C27 simulations. If one peptide directly interacts with an ion, it is called “Monomer with ion”; then, the other peptide is called “Monomer without ion”.
The largest shifts (25 and 18 ppm for K+ and Na+, respectively) of the Trp11 residue on the ion-occupied peptide with respect to the other peptide are found near 6 Å for the Drude model. These shifts (30 and 60 ppm for K+ and Na+, respectively) are found at 8.5 Å for the C27 model. This suggests that the non-polarizable cations perturb the peptides more strongly than the polarizable cations, leading to the larger changes in the orientations of 15N–H, thus the chemical shifts observed in Figure 2c,d. The stronger perturbations are consistent with the higher corresponding free-energy barriers and the lower dissociation constants found in the C27 model.
3.4. Net Dipole and Orientation of the Water Arrangement in the gA Channel
The formation of single-file water arrangement in the interior of the narrow gA pore is well established and is known to play a significant role in offsetting the dehydration cost for monovalent cations or to form a permeation pathway for protons.(105) The number of water molecules in the single-file water arrangement was proposed to play a role in cation recruitment and subsequent permeation events in the gA channel.(38,99) Previous MD studies based on the CHARMM22 (C22) or CHARMM27(C27)-CMAP FF(31–33) indicated that the presence of the single-file column of water molecules is critical for reducing the free energy barrier opposing cation permeation.(38) It is thus of interest to examine the differences in structure and dynamics observed in the present simulations. So, we examined the single-file water arrangement modeled by the additive and polarizable FFs by computing the average number of water molecules confined inside the pore, which is defined as (see discussion below).
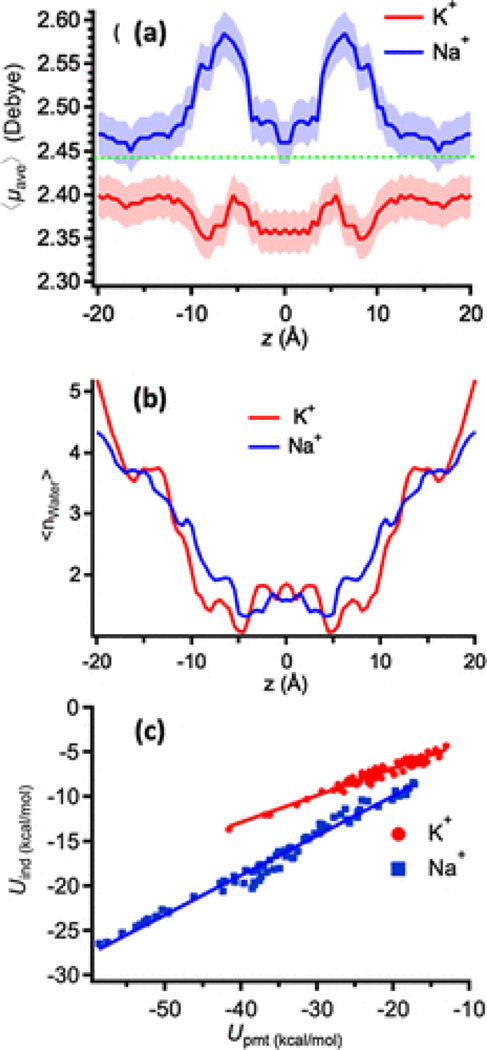
Figure 4a–c shows the distributions of the total dipole moment of all waters in the wire with respect to the three components of the vector defining the pore orientation calculated with C27 and Drude FFs. Even though the average values of the total dipole moment distributions obtained with both the additive and polarizable FFs are close to zero, there is a striking difference in the μz component. The Drude FF shows only one broad peak in contrast to two distinguishable peaks observed at μz = 0.48 and −0.59 Debye for the additive C27 model. The bimodal distribution of the C27 total dipole moment μz indicates two major opposite directions of the entire single-file water inside the pore. To understand this better, we examined the orientations of individual water molecules involved in forming the single-file arrangement of the wire within the pore, with respect to the z axis. The orientation of a water molecule is defined as the angle ϕ between the orthogonal bisector of a water molecule and the z axis (see Section 2). The distribution shown in Figure 4d indicates that the C27 water molecules have two dominant orientations with ϕ = 40° or 145° matching the bimodal distribution in Figure 4c. The presence of the two different structural arrangements for water wire in the gA lumen is related to the total dipole moment of all the waters in the wire and number of water molecules comprising it. The first peak distribution in angle relative to the z axis for individual water molecules (ϕ ≈ 40°) corresponds to the peak in the z component of the total wire dipole moment μz at 0.48 Debye. The second collectively structured arrangement in simulations performed with the C27 force field was observed in the water wire formed by seven water molecules with a peak at ϕ ∼ 145° and a peak at μz at −0.59 Debye, as illustrated in Figures 4c and 4d, respectively.
The distribution of ϕ for the individual water molecules in the Drude model shown in Figure 4d contains broad shoulders at ϕ ≈ 45° and 140° but is essentially unimodal. The distribution shown in Figure 4d also indicates significant presence of individual waters oriented at ϕ ≈ 90°. The analysis of the orientations (see Figure S14b for illustration) for the water molecules with ϕ ∼ 90° shows that they represent cases where an ordered single-file arrangement is either less structured due to hydrogen-bonding to the neighboring water molecules or instances where a water molecule near the center of the bilayer breaks away from the wire completely and establishes interactions with backbone atoms only. This distribution of the z component of the total dipole moment of water wire (μz) for the Drude model is also in a sharp contrast with that obtained from C27 simulations (Figure 4c). The distribution obtained with the Drude model shows only one peak near μz ≈ 0 Debye.
To further quantify the water orientation in the bimodal (or ordered C27) vs unimodal disordered (Drude) water wires, we calculated the Pearson correlation coefficients , where μ1,2z are the dipole moment components assessed independently for two segments of the water wire located in each of the monomers, respectively (see Figure S15 for illustration). The resulting P (0 ≤ |P| ≤ 1) values are 0.9 ± 0.1 and 0.4 ± 0.1 for the C27 and Drude models, respectively. This suggests that the C27 simulation shows that dipole moments of the μ1z and μ2z are strongly correlated with P = 0.9, while Drude simulations result in a more weekly correlated water wire orientation in two monomers. The positive sign of the correlation coefficient indicates that the two halves of the water wire are oriented in the same direction with a high probability in the C27 model and to a lesser extent in the Drude model (Figure S15a). This highly correlated water wire in the C27 model explains why both distributions of the angle ϕ and μz are similar (Figure 4c,d and Figure S15b). In contrast, the low correlation in the Drude model suggests that each individual Drude water molecule of the water wire behaves more independently. Figure S15b shows that Drude water molecules in the first peptide (called PEP1) are well correlated (because the distributions of ϕ and μz are both bimodal), despite of a lesser extent than the C27 model, while the water molecules in the second peptide (PEP2) are largely uncorrelated. This suggests some asymmetry in the gA dimer structure (see below), which, when combined with reduced water–water interactions and increased water–backbone interactions, leads to different extents of water correlations in each subunit in the Drude mode.
To further quantify the extent of structuring of water molecules in the two models, we computed the order parameter , which is an average over all individual angles ϕ of the single-file water molecules. As a result, SC27 and SDrude are 0.36 ± 0.01 and 0.10 ± 0.08, respectively. This suggests that the higher number of individual water molecules with ϕ ≈ 90° observed in simulations with the Drude model reduces the value of S due to the significantly reduced probability for the ordered single-file water wire in the Drude model.
The analysis of angular distributions characterizing single water orientation and the distribution of μz for the entire wire shows that C27 promotes formation of the structured water wire in gA confinement in contrast to the Drude model. A bimodal distribution for the total μz for the water wire has been reported previously for an additive force field.(106) Roux(106) proposed that the structuring of water inside the confinement depends strongly on the balance between water–water and water–carbonyl interactions. Strong water–water interactions are expected to promote structuring of the water wire, while preferential interactions with the nanopore may contribute to a more disordered state of the water wire. The SWM4-NDP model has a less favorable water–water dimer interaction energy then compared to TIP3P (−5.15 kcal/mol vs −6.50 kcal/mol, respectively)(107) that may contribute to a relative increase in the number of interactions with the surrounding nanopore.
The difference in water–water correlations between the two models is also expected to have an impact on transport properties modeled with the two potential functions. Yu et al. showed that the TIP3P model used in C27 simulations strongly overestimates bulk diffusion and consequently underestimates rotational dynamics of water compared both to the experimental values and the estimate obtained with the SWM4-NDP water model.(107) Other studies performed with polarizable water models also indicate significant changes to water transport properties resulting from explicit account for atomic polarization.(52,53,108,109)Since the reorientational dynamics of the individual water molecules in the wire is an important factor in the ion permeation and proton hoping,(110) we calculated the characteristic transition times between the two dominant orientations of the single-file water molecules with a combination of MSM(90,111) and TPT(112) formalism (see Section 2). The reorientation transition times of the individual C27 and Drude water molecules inside the gA pore were 1.8 ± 0.1 and 2.0 ± 0.2 ns, respectively. These transition times are similar between the two potential models used in our study and unlikely to explain observed differences in water structuring inside gA. The calculated times are longer than the earlier estimate of ∼0.1 ns per water reorientations based on much shorter simulation times(113) but are in better agreement with the trends reported for the NMR relaxation times τ2HH.(107) Therefore, the apparent differences in the orientations of the individual water molecules inside gA and the formation of the structured single-file water wire depend on water–protein and water–ion interactions in the two models (see below) as suggested earlier.(106)
3.5. Water–Water and Water–Amide Interactions as a Driver of gA Hydration
As mentioned above, the structure and dynamics of the single-file water wire depend on the fine balance between water–water, water–ion, and water–protein interactions such that different models can lead to different water occupancies in the channel. A water occupancy in the gA lumen has previously been estimated from measurements of water permeability at a low ion concentration (0.01 M NaCl).(114,115) Using a combination of kinetic modeling and an array of electrophysiological recordings, Rosenberg and Finkelstein(114,115) concluded that an average number of water molecules confined in the channel lumen is 6.5 at 0.01–0.1 M KCl or NaCl. The number of the single-file water molecules computed for was 7.6 ± 0.1 and 7.0 ± 0.4 for the C27 and Drude FFs, respectively. A recently published study by Paulino et. al(82) reports n = 8 for water molecules involved in the formation of a structured wire spanning in good accord with the estimates obtained in our study. The slight decrease in the number of water molecules in a single-file wire observed with Drude simulations may be attributed to less favorable water–water interactions but more favorable amide (backbone)–water interactions in the polarizable model, as evident from the hydration free energies obtained from Drude FF and non-polarizable C27 FF.(116,117) Hazel et al.(101) argued that, in the folded peptide, hydrogen bonding between backbone amides results in polarization of the C═O and N–H bonds; therefore, an induced dipole of an amide plane drives more favorable interactions with water molecules. Their observations can be corroborated from our work by the analysis of the interaction energies (Uint) between the water wire molecules and the coordinating backbone atoms in gA. The calculated Uint for water molecules in the wire are −60 ± 10 and −93 ± 21 kcal/mol and for the C27 and Drude simulations, respectively.
To explore the role of the balance between water–water and water–amide plane interactions on the number of water molecules involved in wire formation, we performed additional simulations with a slightly modified Drude model (called DrudeX), described in Section 2 section. This model has an enhanced backbone–water interaction with no changes made to the water model. As a result, the correction to water–carbonyl interactions resulted in a lower average number of water molecules, 6.2 ± 0.3 (compared to 7.0 ± 0.4 obtained from the original model) in the absence of ions, which is in better agreement with the experimental measurements.(114) Subsequently, we re-ran the REMD/US simulations and re-evaluated the 1D-PMFs for Na+ and K+ using the exact initial starting coordinates. The free-energy barriers of both Na+ and K+ increased significantly (on average by 2–3 kcal/mol) compared to those obtained from the original Drude parameters (Figure 5). So, decreasing the number of water molecules in the single-file water arrangment leads to a decrease in hydration water coordinating the permeant cations (Figure S16a), thus resulting in an increase in the barrier present for 1D PMF calculated with the DrudeX model. Nonetheless, these results highlight the critical importance in balancing interactions between different functional groups and water as part of the force-field development.
Figure 5.
PMFs for the Drude and DrudeX models (Table 1), showing the effects of water–gA interactions on the ion permeation energetics. The errors were estimated from the differences between the two parts (z > 0 and z < 0) of the unsymmetrized PMFs, whose global minima are aligned and zeroed at the same value.
3.6. Water Dipole and Energetics in the First Coordination Shell of Permeant Cations
We additionally examined whether the different permeant cations induce a qualitatively different polarization response in a single-file water arrangement. To perform such an analysis, we considered all of the water molecules within a distance R ≤ 3.5 Å from a permeant ion for analysis of the coordination/energetics properties in all of the US windows. The spherical cutoff distance of R ≤ 3.5 Å corresponds to the size of the first coordination shell of the larger of permeant cations, i.e., K+, and was used extensively in the past for the analysis of Li+/Na+/K+ preferential coordination in water and protein sites.(67,118,119)Figure 6a shows that the average dipole moment of the individual water molecules around Na+ is higher than those around K+ depending on the positions in the channel. The deviation from the bulk value appears to be the largest for Na+, especially within the monomer proper, in the region between the entrance to the channel and the mid-point of the dimer, where carbonyl oxygen atoms compensate for the loss of the coordinating water molecules (Figure S17). The maximum in the average dipole moment, (), corresponds to the position of the free-energy barriers in the PMF (Figure 1b), at which the number of coordinating water molecules is the smallest, e.g., ∼1, water per ion (Figure 6a,b and Figure S16b). The dipole-moment profiles are also distinguishable from the non-polarizable water dipole moment (2.35 D in the aqueous phase) and the SWM4-NDP water dipole moment (2.43 D in the aqueous phase).
Figure 6.
(a) Average dipole moment of individual water molecules within a distance of 3.5 Å around a permeant cation as a function of the cation’s coordinate (z) along the gA channel. The dashed line indicates the dipole moment of the bulk water in the Drude model. (b) Average hydration number across the permeation axis. (c) Average interaction of the ion with individual water molecules within a radius of 3.5 Å, decomposed in terms of the induced dipole (Uind) and the permanent dipole (Upmt) of the water molecule. The slopes for the K+ and Na+ data are 0.30 ± 0.05 and 0.44 ± 0.05, respectively.
To quantify the potential effects of partial dehydration on the interaction energy between a permeant ion and individual water molecules within the sphere with R ≤ 3.5 Å, we examined the relative contribution from the induced (Uind) and permanent (Upmt) water dipole to the ion–water interaction (Uint). Figure 6c shows that Uind and Upmt are linearly correlated, whether the ion is fully or partially hydrated. The slope of the induced component of the electrostatic energies is slightly steeper for Na+. Overall, induced polarization contributes between 25 and 33% of the total electrostatic interactions with K+ and Na+, respectively. The interaction energies per individual water molecule are the less favorable in the bulk solution and the highest in the channel lumen where ions become more dehydrated. For example, the Na+–water interaction is −27 ± 2 kcal/mol for , compared to the smaller value of −17 ± 1 kcal/mol in the bulk. The K+–water interaction is −18 ± 2 kcal/mol for and −9 ± 1 kcal/mol in the bulk. Altogether, these results quantitatively show that (i) the polarizability of water molecules and their interactions with the permeant ions can be substantial across the channel; (ii) different cationic species have very different polarizable effects on their coordinating water molecules (Figure 6a) and are expected to contribute significantly to the calculated PMFs (Figure 1b,c and below), and (iii) as the cations become more dehydrated, their interactions with coordinating water molecules become stronger. It is important to note that, even in the case of a neutral ligand, such as carbonyls lining the permeation pathway of gA, direct transfer of polarizable cation parameters developed from the aqueous phase simulations appeared to be challenging. This finding emphasizes an importance of careful calibration of ion–water and ion–ligand interactions in model systems such as water, organic mimetics, or model peptides. The challenges in using ion parameters developed to only match aqueous solvation data will become even more critical in cases of ion channels involving cation–carboxylate interactions.(120,121) The overbinding of cations to charged protein moieties results in reduced ion diffusion on protein surfaces(117,120) and leads to severely underestimated permeabilities, limiting the utility of the existing polarizable force fields in these systems.(122)
4. Conclusions
In this study, we compared the energetics, hydration, structural, and conduction properties of ion permeation in the gA channel modeled by the non-polarizable C27 and polarizable Drude FFs. Allen et al.(4,22,23,56) previously estimated that the polarization effects may substantially contribute to reducing the free-energy barriers opposing ion permeation. As shown in Figure 1b,c, the polarization effects modeled by the Drude polarizable FF do indeed lead to a significant reduction (∼ 50%) in the free-energy barriers and better emphasize salient binding site features compared to simulations performed with the additive C27 FF. The maximal conductance (gmax) values calculated from 1D PMFs with an unadjusted Drude polarizable FF are in better agreement with experiments than the values obtained with the additive non-polarizable C27 FF (see Table 2). Particularly for sodium ions, the Drude FF yields a conductance three orders of magnitude larger than the C27 FF, much closer to experimental values. In this study, we consider a single ion permeation mechanism to be predominant. However, in the future, polarizable force fields could be expanded to modeling of a multi-ion permeation event common to the confinement of biological ion channels using both equilibrium or simulations in the presence of biasing electrical fields.(122)
The ssNMR chemical shifts (Figures 2a,b and 3) suggest that the structure of the gA channel in the absence of ions between the Drude and C27 models are different. These structures are both relatively stable and distinguishable in the 300 ns simulation timescales. Note that previous simulation(123) and experimental studies(124,125) suggested a dependence of channel structures on ion recruitment to the pore lumen. In our study, the C27 cations have distinguishable effects on the anisotropic chemical shifts, in particular at the entrance of the channel pore, in an agreement with experimental data. However, they were found to induce too large and even negative chemical shifts (relative to experiments) at residues deeper inside the channel (Figures 2c,d and 3). The Drude model reduces the large chemical shifts inside the channel observed in the C27 model, but it yields relatively small chemical shifts at the entrance of the channel. This may suggest that the explicit polarization reduces the extent of the water dipole reorientations required to accommodate the permeant cations bound to the pore lumen in comparison with the data of the additive (C27) simulations. We showed that the single-file water properties in the channel confinement are substantially different in the C27 and Drude models. More specifically, the structuring of the water wire confined in the channel was characterized by the distribution of the z component for the total dipole component (μz) of the entire wire and angle ϕ between the permanent dipole moment of individual water molecule and the permeation (z) axis of the channel (Figure 4c). We demonstrated that the distribution of μz is bimodal for simulations performed with the non-polarizable (TIP3P) water model, whereas this distribution is largely unimodal for the polarizable SWM4 water model (Figure 4c). The bimodal distribution was found to originate from the two favorable orientations of individual water molecules confined in the channel pore (Figure 4e) showing the formation of a structured single-file water wire inside the gA channel with the C27 model. In contrast, the Drude model yields a broad distribution of μz, indicating less structured single-file wires inside the channel. It may contribute to challenges in the PMF convergence observed in simulations with Drude FF, with evident asymmetry between two monomers.
While the reorientation times for the water molecules in the channel lumen are nearly identical between C27 and Drude models (∼2.0 ns per individual water molecule flipping), the structural analysis of angular distributions of water orientations (Figure 4) inside the channel indicates a significant percentage of “loose” water molecules present near the center of the bilayer in simulations performed with the Drude FF. Interestingly, the calculated flipping time scales for individual water molecules are nearly identical for “structured” wires present in simulations with C27 model and “unstructured” wires observed in Drude simulations. These are intriguing observations pertaining to ion–protein interactions that will require further investigations.
The simulated water molecules quickly flip between continuous water–water hydrogen bonding interactions dominant in water wire as characterized in C27 simulations. Those confined water dynamics lead to larger uncertainty in the PMFs for the Drude model, particularly when the cations are near the middle of the channel, as observed in Figure 1b,c. These results underscore the different structures of the single-file water between the two models, which can result in different ion permeation energetics. Specifically, the contribution of the confined water molecules to the energetics of the permeant cations is sensitive to the balance in water–water and water–backbone interactions. A small change in the interaction strength can lead to a reduction in a number of water molecules recruited into a single wire inside the pore, thus reducing the hydration of the pore and available co-permeant water molecules. As a result, such a reduction of the pore hydration noticeably increases the barriers for permeation of Na+ and K+ (Figure 5) because it increases energy costs to dehydrate the permeant ions. The balance between ion–water and ion–pore interactions appear to be one of the critical elements for accurate modeling of ion transport in gA. The differences in the water dynamics inside the channel pore in conjunction with the different alignment structures were also found to result in different interactions between the permeant ions and co-permeant water. We showed that the average dipole moments of coordinating water molecules during the ion translations are also distinguishable for the two cations (Figure 6a), while of course the non-polarizable C27 model yields no such feature. We found that the induced dipole component of the electrostatic interactions between permeant cations and the coordinating water molecules is substantial in comparison to the non-induced component. The induced component may provide up to 30% of the ion-water interaction energy (Figure 6c), a component that is only included in a mean-field way in the non-polarizable model. Interestingly, the relative contribution of the induced component clearly depends on the cationic types: Na+ has stronger attractions with its neighboring water molecules than K+, thus resulting in more polarization of the neighboring water molecules around Na+ (Figure 6a). As a result, the induced interaction of the neighboring water molecules is significantly larger with Na+ than K+ when they get more dehydrated (Figure 6c). This finding also shows an important role played by an induced component of the solvent dipole moment in the energetics of ion permeation.
Supplementary Material
Acknowledgments
This work in Calgary was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) (Discovery Grant RGPIN-315019 to S.Y.N.). V.N. is supported by LANL’s Director (2018–2020) Postdoctoral Fellowships. This work has a classification number, LA-UR-20-28023. T.W.A. is supported by the NHMRC (APP1141974, APP1104259), ARC (DP170101732 and DP210102405), NIH (U01-HL126273-02), and the Medical Advances Without Animals Trust. The work of H.L., A.D.M., and B.R. was supported by the National Institutes of Health (NIH) through grant R01-GM072558, and A.D.M. was further supported by R35-GM131710. We would like to thank Prof. Dr. Guohui Li for sharing the AMOEBA PMFs data reported in ref (47).
References
- (1).Hille B: Ionic Channels of Excitable Membranes; 2nd Ed.; Sinauer Associates, Inc.: Sunderland, MA, 1992. [Google Scholar]
- (2).Shieh CC; Coghlan M; Sullivan JP; Gopalakrishnan M. Potassium channels: molecular defects, diseases, and therapeutic opportunities. Pharmacol. Rev 2000, 52, 557–594. [PubMed] [Google Scholar]
- (3).Aaqvist J; Alvarez O; Eisenman G. Ion-Selective Properties of a Small Ionophore in Methanol Studied by Free Energy Perturbation Simulations. J. Phys. Chem 1992, 96, 10019–10025. [Google Scholar]
- (4).Roux B; Allen T; Berneche S; Im W. Theoretical and computational models of biological ion channels. Q. Rev. Biophys 2004, 37, 15–103. [DOI] [PubMed] [Google Scholar]
- (5).Zhekova HR; Ngo V; da Silva MC; Salahub D; Noskov S. Selective ion binding and transport by membrane proteins - A computational perspective. Coordin. Chem. Rev 2017, 345, 108–136. [Google Scholar]
- (6).Flood E; Boiteux C; Lev B; Vorobyov I; Allen TW Atomistic Simulations of Membrane Ion Channel Conduction, Gating, and Modulation. Chem. Rev 2019, 119, 7737–7832. [DOI] [PubMed] [Google Scholar]
- (7).Bekker H; Berendsen HJC; Dijkstra EJ; Achterop S; Vondrumen R; Van der Spoel D; Sijbers A; Keegstra H; Reitsma B; Renardus MKR Gromacs: A Parallel Computer for Molecular-Dynamics Simulations. In Physics Computing; World Scientic Singapore: 1993; 92, 252–256. [Google Scholar]
- (8).Phillips JC; Braun R; Wang W; Gumbart J; Tajkhorshid E; Villa E; Chipot C; Skeel RD; Kalé L; Schulten K. Scalable molecular dynamics with NAMD. J. Comput. Chem 2005, 26, 1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Brooks BR; Brooks CL III; Mackerell AD Jr.; Nilsson L; Petrella RJ; Roux B; Won Y; Archontis G; Bartels C; Boresch S; Caflisch A; Caves L; Cui Q; Dinner AR; Feig M; Fischer S; Gao J; Hodoscek M; Im W; Kuczera K; Lazaridis T; Ma J; Ovchinnikov V; Paci E; Pastor RW; Post CB; Pu JZ; Schaefer M; Tidor B; Venable RM; Woodcock HL; Wu X; Yang W; York DM; Karplus M. CHARMM: The Biomolecular Simulation Program. J. Comput. Chem 2009, 30, 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Brooks BR; Bruccoleri RE; Olafson BD; States DJ; Swaminathan S; Karplus M. CHARMM - a Program for Macro-molecular Energy, Minimization, and Dynamics Calculations. J. Comput. Chem 1983, 4, 187–217. [Google Scholar]
- (11).Case DA; Cheatham TE III; Darden T; Gohlke H; Luo R; Merz KM Jr.; Onufriev A; Simmerling C; Wang B; Woods RJ The Amber biomolecular simulation programs. J. Comput. Chem 2005, 26, 1668–1688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Lemkul JA; Huang J; Roux B; MacKerell AD Jr. An Empirical Polarizable Force Field Based on the Classical Drude Oscillator Model: Development History and Recent Applications. Chem. Rev 2016, 116, 4983–5013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Jing Z; Liu C; Cheng SY; Qi R; Walker BD; Piquemal J-P; Ren P. Polarizable Force Fields for Biomolecular Simulations: Recent Advances and Applications. Annu. Rev. Biophys 2019, 48, 371–394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Yu H; Noskov SY; Roux B. Hydration number, topological control, and ion selectivity. J. Phys. Chem. B 2009, 113, 8725–8730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Yu H; Noskov SY; Roux B. Two mechanisms of ion selectivity in protein binding sites. Proc. Natl. Acad. Sci 2010, 107, 20329–20334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).Roux B; Berneche S; Egwolf B; Lev B; Noskov SY; Rowley CN; Yu H. Ion selectivity in channels and transporters. J. Gen. Physiol 2011, 137, 415–426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Kopec W; Kopfer DA; Vickery ON; Bondarenko AS; Jansen TLC; de Groot BL; Zachariae U. Direct knock-on of desolvated ions governs strict ion selectivity in K+ channels. Nat. Chem 2018, 10, 813–820. [DOI] [PubMed] [Google Scholar]
- (18).Kopfer DA; Song C; Gruene T; Sheldrick GM; Zachariae U; de Groot BL Ion permeation in K+ channels occurs by direct Coulomb knock-on. Science 2014, 346, 352–355. [DOI] [PubMed] [Google Scholar]
- (19).Kratochvil HT; Carr JK; Matulef K; Annen AW; Li H; Maj M; Ostmeyer J; Serrano AL; Raghuraman H; Moran SD; Skinner JL; Perozo E; Roux B; Valiyaveetil FI; Zanni MT Instantaneous ion configurations in the K+ ion channel selectivity filter revealed by 2D IR spectroscopy. Science 2016, 353, 1040–1044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Noskov SY; Berneche S; Roux B. Control of ion selectivity in potassium channels by electrostatic and dynamic properties of carbonyl ligands. Nature 2004, 431, 830–834. [DOI] [PubMed] [Google Scholar]
- (21).Allen TW; Andersen OS; Roux B. Structure of gramicidin A in a lipid bilayer environment determined using molecular dynamics simulations and solid-state NMR data. J. Am. Chem. Soc 2003, 125, 9868–9877. [DOI] [PubMed] [Google Scholar]
- (22).Allen TW; Andersen OS; Roux B. Energetics of ion conduction through the gramicidin channel. Proc. Natl. Acad. Sci 2004, 101, 117–122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Allen TW; Andersen OS; Roux B. Ion permeation through a narrow channel: Using gramicidin to ascertain all-atom molecular dynamics potential of mean force methodology and biomolecular force fields. Biophys. J 2006, 90, 3447–3468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Hinton JF; Whaley WL; Shungu D; Koeppe RE II; Millett FS Equilibrium binding constants for the group I metal cations with gramicidin-A determined by competition studies and T1+−205 nuclear magnetic resonance spectroscopy. Biophys. J 1986, 50, 539–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Ketchem RR; Hu W; Cross TA High-resolution conformation of gramicidin A in a lipid bilayer by solid-state NMR. Science 1993, 261, 1457–1460. [DOI] [PubMed] [Google Scholar]
- (26).Arseniev AS; Barsukov IL; Bystrov VF; Lomize AL; Ovchinnikov YA 1H-Nmr Study of Gramicidin-a Transmembrane Ion Channel - Head-to-Head Right-Handed, Single-Stranded Helices. FEBS Lett 1985, 186, 168–174. [DOI] [PubMed] [Google Scholar]
- (27).Ketchem RR; Roux B; Cross TA High-resolution polypeptide structure in a lamellar phase lipid environment from solid state NMR derived orientational constraints. Structure 1997, 5, 1655–1669. [DOI] [PubMed] [Google Scholar]
- (28).Olah GA; Huang HW; Liu W; Wu Y. Location of ion-binding sites in the gramicidin channel by X-ray diffraction. J. Mol. Biol 1991, 218, 847. [DOI] [PubMed] [Google Scholar]
- (29).Tian F; Lee K-C; Hu W; Cross TA Monovalent cation transport: lack of structural deformation upon cation binding. Biochemistry 1996, 35, 11959–11966. [DOI] [PubMed] [Google Scholar]
- (30).Woolf TB; Roux B. The binding site of sodium in the gramicidin A channel: comparison of molecular dynamics with solid-state NMR data. Biophys. J 1997, 72, 1930–1945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).MacKerell AD Jr.; Bashford D; Bellott M; Dunbrack RL Jr.; Evanseck JD; Field MJ; Fischer S; Gao J; Guo H; Ha S; Joseph-McCarthy D; Kuchnir L; Kuczera K; Lau FTK; Mattos C; Michnick S; Ngo T; Nguyen DT; Prodhom B; Reiher WE; Roux B; Schlenkrich M; Smith JC; Stote R; Straub J; Watanabe M; Wiórkiewicz-Kuczera J; Yin D; Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [DOI] [PubMed] [Google Scholar]
- (32).Reiling S; Schlenkrich M; Brickmann J. Force field parameters for carbohydrates. J. Comput. Chem 1996, 17, 450–468. [Google Scholar]
- (33).Beglov D; Roux B. Finite Representation of an Infinite Bulk System - Solvent Boundary Potential for Computer-Simulations. J. Chem. Phys 1994, 100, 9050–9063. [Google Scholar]
- (34).Ingólfsson HI; Li Y; Vostrikov VV; Gu H; Hinton JF; Koeppe RE II; Roux B; Andersen OS Gramicidin A backbone and side chain dynamics evaluated by molecular dynamics simulations and nuclear magnetic resonance experiments. I: molecular dynamics simulations. J. Phys. Chem. B 2011, 115, 7417–7426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Krishnamurthy V; Chung S-H Adaptive Brownian dynamics simulation for estimating potential mean force in ion channel permeation. IEEE Trans. NanoBiosci 2006, 5, 126–138. [DOI] [PubMed] [Google Scholar]
- (36).Jing N; Prasad KU; Urry DW The Determination of Binding Constants of Micellar-Packaged Gramicidin-a by 13C-Nmr and 23Na-Nmr. Biochim. Biophys. Acta, Biomembr 1995, 1238, 1–11. [DOI] [PubMed] [Google Scholar]
- (37).Tian F; Cross TA Cation transport: an example of structural based selectivity. J. Mol. Biol 1999, 285, 1993–2003. [DOI] [PubMed] [Google Scholar]
- (38).Finkelstein A; Andersen OS The gramicidin A channel: a review of its permeability characteristics with special reference to the single-file aspect of transport. J. Membr. Biol 1981, 59, 155–171. [DOI] [PubMed] [Google Scholar]
- (39).Busath DD; Thulin CD; Hendershot RW; Phillips LR; Maughan P; Cole CD; Bingham NC; Morrison S; Baird LC; Hendershot RJ; Cotten M; Cross TA Noncontact dipole effects on channel permeation. I. Experiments with (5F-indole)Trp13 gramicidin A channels. Biophys. J 1998, 75, 2830–2844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (40).Ngo V; da Silva MC; Kubillus M; Li H; Roux B; Elstner M; Cui Q; Salahub DR; Noskov SY Quantum Effects in Cation Interactions with First and Second Coordination Shell Ligands in Metalloproteins. J. Chem. Theory Comput 2015, 11, 4992–5001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (41).Li H; Ngo V; Da Silva MC; Salahub DR; Callahan K; Roux B; Noskov SY Representation of Ion−Protein Interactions Using the Drude Polarizable Force-Field. J. Phys. Chem. B 2015, 9401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Si W; Chen L; Hu X-B; Tang G; Chen Z; Hou J-L; Li Z-T Selective Artificial Transmembrane Channels for Protons by Formation of Water Wires. Angew. Chem., Int. Ed 2011, 50, 12564–12568. [DOI] [PubMed] [Google Scholar]
- (43).Ganim Z; Tokmakoff A; Vaziri A. Vibrational excitons in ionophores: experimental probes for quantum coherence-assisted ion transport and selectivity in ion channels. New J. Phys 2011, 13, 113030. [Google Scholar]
- (44).Minteer SD; Atanassov P; Luckarift HR; Johnson GR New materials for biological fuel cells. Mater. Today 2012, 15, 166–173. [Google Scholar]
- (45).Takei K; Fang H; Kumar SB; Kapadia R; Gao Q; Madsen M; Kim HS; Liu C-H; Chueh Y-L; Plis E; Krishna S; Bechtel HA; Guo J; Javey A. Quantum Confinement Effects in Nanoscale-Thickness InAs Membranes. Nano Lett. 2011, 11, 5008–5012. [DOI] [PubMed] [Google Scholar]
- (46).Patel S; Davis JE; Bauer BA Exploring ion permeation energetics in gramicidin A using polarizable charge equilibration force fields. J. Am. Chem. Soc 2009, 131, 13890–13891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Peng X; Zhang Y; Chu H; Li Y; Zhang D; Cao L; Li G. Accurate Evaluation of Ion Conductivity of the Gramicidin A Channel Using a Polarizable Force Field without Any Corrections. J. Chem. Theory Comput 2016, 12, 2973–2982. [DOI] [PubMed] [Google Scholar]
- (48).Ren P; Ponder JW Polarizable atomic multipole water model for molecular mechanics simulation. J. Phys. Chem. B 2003, 107, 5933–5947. [Google Scholar]
- (49).Ren P; Wu C; Ponder JW Polarizable Atomic Multipole-Based Molecular Mechanics for Organic Molecules. J. Chem. Theory Comput 2011, 7, 3143–3161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Shi Y; Xia Z; Zhang J; Best R; Wu C; Ponder JW; Ren P. Polarizable Atomic Multipole-Based AMOEBA Force Field for Proteins. J. Chem. Theory Comput 2013, 9, 4046–4063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Ponder JW; Wu C; Ren P; Pande VS; Chodera JD; Schnieders MJ; Haque I; Mobley DL; Lambrecht DS; DiStasio RA Jr.; Head-Gordon M; Clark GNI; Johnson ME; Head-Gordon T. Current Status of the AMOEBA Polarizable Force Field. J. Phys. Chem. B 2010, 114, 2549–2564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (52).Leontyev IV; Stuchebrukhov AA Polarizable Mean-Field Model of Water for Biological Simulations with AMBER and CHARMM Force Fields. J. Chem. Theory Comput 2012, 8, 3207–3216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (53).Leontyev IV; Stuchebrukhov AA Polarizable molecular interactions in condensed phase and their equivalent nonpolarizable models. J. Chem. Phys 2014, 141, No. 014103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (54).Kohagen M; Lepsík M; Jungwirth P. Calcium Binding to Calmodulin by Molecular Dynamics with Effective Polarization. J. Phys. Chem. Lett 2014, 5, 3964–3969. [DOI] [PubMed] [Google Scholar]
- (55).Pathak AK; Bandyopadhyay T. Protein-Drug Interactions with Effective Polarization in Polarizable Water: Oxime Unbinding from AChE Gorge. J. Phys. Chem. B 2015, 119, 14460–14471. [DOI] [PubMed] [Google Scholar]
- (56).Allen TW; Andersen OS; Roux B. Molecular dynamics - potential of mean force calculations as a tool for understanding ion permeation and selectivity in narrow channels. Biophys. Chem 2006, 124, 251–267. [DOI] [PubMed] [Google Scholar]
- (57).Lopes PEM; Huang J; Shim J; Luo Y; Li H; Roux B; MacKerell AD Jr. Polarizable Force Field for Peptides and Proteins Based on the Classical Drude Oscillator. J. Chem. Theory Comput 2013, 9, 5430–5449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (58).Lamoureux G; Roux B. Modeling induced polarization with classical Drude oscillators: Theory and molecular dynamics simulation algorithm. J. Chem. Phys 2003, 119, 3025–3039. [Google Scholar]
- (59).Lin F-Y; Lopes PEM; Harder E; Roux B; MacKerell AD Jr. Polarizable Force Field for Molecular Ions Based on the Classical Drude Oscillator. J. Chem. Inf. Model 2018, 58, 993–1004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (60).Huang J; Lopes PEM; Roux B; MacKerell AD Jr. Recent Advances in Polarizable Force Fields for Macromolecules: Micro-second Simulations of Proteins Using the Classical Drude Oscillator Model. J. Phys. Chem. Lett 2014, 5, 3144–3150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (61).Jo S; Kim T; Iyer VG; Im W. CHARMM-GUI: a web-based graphical user interface for CHARMM. J. Comput. Chem 2008, 29, 1859–1865. [DOI] [PubMed] [Google Scholar]
- (62).Huang J; Lemkul JA; Eastman PK; MacKerell AD Jr. Molecular dynamics simulations using the drude polarizable force field on GPUs with OpenMM: Implementation, validation, and bench-marks. J. Comput. Chem 2018, 39, 1682–1689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (63).Yu H; Whitfield TW; Harder E; Lamoureux G; Vorobyov I; Anisimov VM; MacKerell AD Jr.; Roux B. Simulating Monovalent and Divalent Ions in Aqueous Solution Using a Drude Polarizable Force Field. J. Chem. Theory Comput 2010, 6, 774–786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (64).Best RB; Zhu X; Shim J; Lopes PEM; Mittal J; Feig M; MacKerell AD Jr. Optimization of the Additive CHARMM All-Atom Protein Force Field Targeting Improved Sampling of the Backbone ϕ, ψ and Side-Chain χ1 and χ2 Dihedral Angles. J. Chem. Theory Comput 2012, 8, 3257–3273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (65).Klauda JB; Venable RM; Freites JA; O’Connor JW; Tobias DJ; Mondragon-Ramirez C; Vorobyov I; MacKerell AD Jr.; Pastor RW Update of the CHARMM All-Atom Additive Force Field for Lipids: Validation on Six Lipid Types. J. Phys. Chem. B 2010, 114, 7830–7843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (66).Luo Y; Roux B. Simulation of Osmotic Pressure in Concentrated Aqueous Salt Solutions. J. Phys. Chem. Lett 2010, 1, 183–189. [Google Scholar]
- (67).Noskov SY; Roux B. Control of ion selectivity in LeuT: Two Na+ binding sites with two different mechanisms. J. Mol. Biol 2008, 377, 804–818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (68).Lamoureux G; Harder E; Vorobyov IV; Roux B; MacKerell AD Jr. A polarizable model of water for molecular dynamics simulations of biomolecules. Chem. Phys. Lett 2006, 418, 245–249. [Google Scholar]
- (69).Luo Y; Jiang W; Yu H; MacKerell AD Jr.; Roux B. Simulation study of ion pairing in concentrated aqueous salt solutions with a polarizable force field. Faraday Discuss. 2013, 160, 135–149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (70).Lamoureux G; MacKerell AD Jr.; Roux B. A simple polarizable model of water based on classical Drude oscillators. J. Chem. Phys 2003, 119, 5185–5197. [Google Scholar]
- (71).Huang L; Roux B. Automated Force Field Parameterization for Nonpolarizable and Polarizable Atomic Models Based on Ab Initio Target Data. J. Chem. Theory Comput 2013, 9, 3543–3556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (72).Rupakheti C; Lamoureux G; MacKerell AD Jr.; Roux B. Statistical mechanics of polarizable force fields based on classical Drude oscillators with dynamical propagation by the dual-thermostat extended Lagrangian. J. Chem. Phys 2020, 153, 114108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (73).Jiang W; Hardy DJ; Phillips JC; MacKerell AD Jr.; Schulten K; Roux B. High-Performance Scalable Molecular Dynamics Simulations of a Polarizable Force Field Based on Classical Drude Oscillators in NAMD. J. Phys. Chem. Lett 2011, 2, 87–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (74).Sprik M. Computer-Simulation of the Dynamics of Induced Polarization Fluctuations in Water. J. Phys. Chem 1991, 95, 2283–2291. [Google Scholar]
- (75).Darden T; York D; Pedersen L. Particle Mesh Ewald: an N· Log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys 1993, 98, 10089–10092. [Google Scholar]
- (76).Ryckaert J-P; Ciccotti G; Berendsen HJC Numerical-Integration of Cartesian Equations of Motion of a System with Constraints: Molecular-Dynamics of N-Alkanes. J. Comput. Phys 1977, 23, 327–341. [Google Scholar]
- (77).Souaille M; Roux B. Extension to the weighted histogram analysis method: combining umbrella sampling with free energy calculations. Comput. Phys. Commun 2001, 135, 40–57. [Google Scholar]
- (78).Kumar S; Rosenberg JM; Bouzida D; Swendsen RH; Kollman PA The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem 1992, 13, 1011–1021. [Google Scholar]
- (79).Jiang W; Hodoscek M; Roux B. Computation of Absolute Hydration and Binding Free Energy with Free Energy Perturbation Distributed Replica-Exchange Molecular Dynamics. J. Chem. Theory Comput 2009, 5, 2583–2588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (80).Jiang W; Luo Y; Maragliano L; Roux B. Calculation of Free Energy Landscape in Multi-Dimensions with Hamiltonian-Exchange Umbrella Sampling on Petascale Supercomputer. J. Chem. Theory Comput 2012, 8, 4672–4680. [DOI] [PubMed] [Google Scholar]
- (81).Fukunishi H; Watanabe O; Takada S. On the Hamiltonian replica exchange method for efficient sampling of biomolecular systems: Application to protein structure prediction. J. Chem. Phys 2002, 116, 9058–9067. [Google Scholar]
- (82).Paulino J; Yi M; Hung I; Gan Z; Wang X; Chekmenev EY; Zhou H-X; Cross TA Functional stability of water wire− carbonyl interactions in an ion channel. Proc. Natl. Acad. Sci. U. S. A 2020, 117, 11908–11915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (83).Roux B; Andersen OS; Allen TW Comment on “Free energy simulations of single and double ion occupancy in gramicidin A” [J. Chem. Phys. 126, 105103 (2007)]. J. Chem. Phys 2008, 128, 227101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (84).Woolf TB; Roux B. Conformational Flexibility of O-Phosphorylcholine and O-Phosphorylethanolamine - a Molecular-Dynamics Study of Solvation Effects. J. Am. Chem. Soc 1994, 116, 5916–5926. [Google Scholar]
- (85).Hummer G. Position-dependent diffusion coefficients and free energies from Bayesian analysis of equilibrium and replica molecular dynamics simulations. New J. Phys 2005, 7, 34. [Google Scholar]
- (86).Vorobyov I; Olson TE; Kim JH; Koeppe RE II; Andersen OS; Allen TW Ion-Induced Defect Permeation of Lipid Membranes. Biophys. J 2014, 106, 586–597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (87).Mai W; Hu W; Wang C; Cross TA Orientational Constraints as three-Dimensional Structural Constraints from Chem-ical-Shift Anisotropy: the Polypeptide Backbone of Gramicidin A in a Lipid Bilayer. Protein Sci. 1993, 2, 532–542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (88).Bowman GR; Pande VS; Noé F. An Introduction to Markov State Models and Their Application to Long Timescale Molecular Simulation; Advances in Experimental Medicine and Biology; Springer Science & Business Media: 2014, 797. [Google Scholar]
- (89).Sezer D; Roux B. Markov state and diffusive stochastic models in electron spin resonance. Adv. Exp. Med. Biol 2014, 797, 115–138. [DOI] [PubMed] [Google Scholar]
- (90).Scherer MK; Trendelkamp-Schroer B; Paul F; Pérez-Hernandez G; Hoffmann M; Plattner N; Wehmeyer C; Prinz J-H; Noé F. PyEMMA 2: A Software Package for Estimation, Validation, and Analysis of Markov Models. J. Chem. Theory Comput 2015, 11, 5525–5542. [DOI] [PubMed] [Google Scholar]
- (91).Metzner P; Schutte C; Vanden-Eijnden E. Transition Path Theory for Markov Jump Processes. Multiscale Model. Simul 2009, 7, 1192–1219. [Google Scholar]
- (92).Weinan E; Vanden-Eijnden E. Transition-Path Theory and Path-Finding Algorithms for the Study of Rare Events. Annu. Rev. Phys. Chem 2010, 61, 391–420. [DOI] [PubMed] [Google Scholar]
- (93).Vanden-Eijnden E. An Introduction to Markov State Models and Their Application to Long Timescale Molecular Simulation; Advances in Experimental Medicine and Biology; Springer Science & Business Media: 2014, 797, 91–100. [Google Scholar]
- (94).Noé F; Schutte C; Vanden-Eijnden E; Reich L; Weikl TR Constructing the equilibrium ensemble of folding pathways from short off-equilibrium simulations. Proc. Natl. Acad. Sci. U. S. A 2009, 106, 19011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (95).Parsegian A. Energy of an Ion Crossing a Low Dielectric Membrane: Solutions to four Relevant Electrostatic Problems. Nature 1969, 221, 844–846. [DOI] [PubMed] [Google Scholar]
- (96).Levitt DG Electrostatic calculations for an ion channel. I. Energy and potential profiles and interactions between ions. Biophys. J 1978, 22, 209–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (97).Levitt DG Electrostatic calculations for an ion channel. II. Kinetic behavior of the gramicidin A channel. Biophys. J 1978, 22, 221–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (98).Krishnamurthy V; Hoyles M; Saab R; Chung S-H Permeation in gramicidin ion channels by directly estimating the potential of mean force using Brownian dynamics simulations. J. Comput. Theory Nanosci 2006, 3, 702–711. [Google Scholar]
- (99).Dani JA; Levitt DG Binding Constants of Li+, K+, and Tl+ in the Gramicidin Channel Determined from Water Permeability Measurements. Biophys. J 1981, 35, 485–499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (100).Myers VB; Haydon DA Ion transfer across lipid membranes in the presence of gramicidin A: II. The ion selectivity. Biochim. Biophys. Acta 1972, 274, 313–322. [DOI] [PubMed] [Google Scholar]
- (101).Urban BW; Hladky SB; Haydon DA Ion movements in gramicidin pores. An example of single-file transport. Biochim. Biophys. Acta 1980, 602, 331–354. [DOI] [PubMed] [Google Scholar]
- (102).Andersen OS Ion Movement through Gramicidin-a Channels - Studies on the Diffusion-Controlled Association Step. Biophys. J 1983, 41, 147–165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (103).Ketchem RR; Lee K-C; Huo S; Cross TA Macro-molecular structural elucidation with solid-state NMR-derived orienta-tional constraints. J. Biomol. NMR 1996, 8, 1–14. [DOI] [PubMed] [Google Scholar]
- (104).Townsley LE; Tucker WA; Sham S; Hinton JF Structures of gramicidins A, B, and C incorporated into sodium dodecyl sulfate micelles. Biochemistry 2001, 40, 11676–11686. [DOI] [PubMed] [Google Scholar]
- (105).Andersen OS Gramicidin Channels. Annu. Rev. Physiol 1984, 46, 531–548. [DOI] [PubMed] [Google Scholar]
- (106).Roux B. Theory of Transport in Ion Channels: From Molecular Dynamics Simulations to Experiments. In Computer Simulations in Molecular Biology; Goodfellow J, Ed.; VCH: Weinheim, 1995; pp. 133–169. [Google Scholar]
- (107).Yu W; Lopes PEM; Roux B; MacKerell AD Jr. Six-site polarizable model of water based on the classical Drude oscillator. J. Chem. Phys 2013, 138, No. 034508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (108).Pathak AK; Bandyopadhyay T. Temperature Induced Dynamical Transition of Biomolecules in Polarizable and Non-polarizable TIP3P Water. J. Chem. Theory Comput 2019, 15, 2706–2718. [DOI] [PubMed] [Google Scholar]
- (109).Pathak AK; Bandyopadhyay T. Unbinding of fluorinated oxime drug from the AChE gorge in polarizable water: a well-tempered metadynamics study. Phys. Chem. Chem. Phys 2017, 19, 5560–5569. [DOI] [PubMed] [Google Scholar]
- (110).Roux B; Karplus M. Ion Transport in a Model Gramicidin Channel. Structure and Thermodynamics. Biophys. J 1991, 59, 961–981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (111).Prinz J-H; Wu H; Sarich M; Keller B; Senne M; Held M; Chodera JD; Schutte C; Noé F. Markov models of molecular kinetics: generation and validation. J. Chem. Phys 2011, 134, 174105. [DOI] [PubMed] [Google Scholar]
- (112).Weinan E; Vanden-Eijnden E. Towards a theory of transition paths. J. Stat. Phys 2006, 123, 503–523. [Google Scholar]
- (113).Pomes R; Roux B. Molecular mechanism of H+ conduction in the single-file water chain of the gramicidin channel. Biophys. J 2002, 82, 2304–2316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (114).Rosenberg PA; Finkelstein A. Water permeability of gramicidin A-treated lipid bilayer membranes. J. Gen. Physiol 1978, 72, 341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (115).Rosenberg PA; Finkelstein A. Interaction of ions and water in gramicidin A channels: streaming potentials across lipid bilayer membranes. J. Gen. Physiol 1978, 72, 327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (116).Hazel AJ; Walters ET; Rowley CN; Gumbart JC Folding free energy landscapes of β-sheets with non-polarizable and polarizable CHARMM force fields. J. Chem. Phys 2018, 149, No. 072317. [DOI] [PubMed] [Google Scholar]
- (117).Ngo VA; Fanning JK; Noskov SY Comparative Analysis of Protein Hydration from MD simulations with Additive and Polarizable Force Fields. Adv. Theory Simul 2018, 2, 1800106. [Google Scholar]
- (118).Thomas M; Jayatilaka D; Corry B. An Entropic Mechanism of Generating Selective Ion Binding in Macromolecules. PLoS Comput. Biol 2013, 9, e1002914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (119).Fowler PW; Tai K; Sansom MSP The Selectivity of K+ Ion Channels: Testing the Hypotheses. Biophys. J 2008, 95, 5062–5072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (120).Amin KS; Hu X; Salahub DR; Baldauf C; Lim C; Noskov S. Benchmarking polarizable and non-polarizable force fields for Ca2+−peptides against a comprehensive QM dataset. J. Chem. Phys 2020, 153, 144102. [DOI] [PubMed] [Google Scholar]
- (121).Villa F; MacKerell AD Jr.; Roux B; Simonson T. Classical Drude Polarizable Force Field Model for Methyl Phosphate and Its Interactions with Mg2+. J. Phys. Chem. A 2018, 122, 6147–6155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (122).Prajapati JD; Mele C; Aksoyoglu MA; Winterhalter M; Kleinekathofer U. Computational Modeling of Ion Transport in Bulk and through a Nanopore Using the Drude Polarizable Force Field. J. Chem. Inf. Model 2020, 60, 3188–3203. [DOI] [PubMed] [Google Scholar]
- (123).Basu I; Chattopadhyay A; Mukhopadhyay C. Ion channel stability of Gramicidin A in lipid bilayers: Effect of hydrophobic mismatch. Biochim. Biophys. Acta, Biomembr 2014, 1838, 328–338. [DOI] [PubMed] [Google Scholar]
- (124).Mobashery N; Nielsen C; Andersen OS The conforma-tional preference of gramicidin channels is a function of lipid bilayer thickness 1. FEBS Lett. 1997, 412, 15–20. [DOI] [PubMed] [Google Scholar]
- (125).Kelkar DA; Chattopadhyay A. Modulation of gramicidin channel conformation and organization by hydrophobic mismatch in saturated phosphatidylcholine bilayers. Biochim. Biophys. Acta, Biomembr 2007, 1768, 1103–1113. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.