Abstract
The majority of research within reproductive and gynecologic health, or investigating ART, is observational in design. One of the most critical challenges for observational studies is confounding, while one of the most important for discovery and inference is effect modification. In this commentary, we explain what confounding and effect modification are and why they matter. We present examples illustrating how failing to adjust for a confounder leads to invalid conclusions, as well as examples where adjusting for a factor that is not a confounder also leads to invalid or imprecise conclusions. Careful consideration of which factors may act as confounders or modifiers of the association of interest is critical to conducting sound research, particularly with complex observational studies in reproductive medicine.
Introduction
Most studies of ART and reproductive medicine are observational in design. Randomized controlled trials (RCTs), widely considered the gold standard for examining cause–effect relations, are valued because randomization can help create balance in the distribution of risk factors between the groups being compared. However, RCTs may not be ethical (e.g. when the intervention is hypothesized to be harmful) or feasible (e.g. when a long duration of follow-up is required before the intervention is likely to affect outcomes), and an observational design is the only practical approach.
Observational studies can yield valid results akin to randomized intervention studies when conducted and analyzed appropriately. When done properly, observational studies can positively influence clinical practice and our understanding of exposure–disease relationships in reproductive medicine. Unfortunately, observational studies are susceptible to several biases. One of the most pervasive challenges for observational studies is confounding.
What is confounding, and why should I care?
In observational studies, the groups being compared (e.g. exposed and unexposed) may be imbalanced with regard to other factors that affect the outcome. If this imbalance is not controlled, confounding can occur and lead to a bias. Confounding is said to occur when the true effect of the exposure on the outcome is distorted by some other factor, leading to inaccurate estimates of effect. For instance, suppose we are interested in investigating whether sedentary behavior reduces the likelihood of pregnancy following IVF. Sedentary behavior cannot be randomly assigned, and RCTs with physical activity interventions often suffer from non-compliance. Thus, we rely on observational data in this case. Suppose we collect data on 600 female patients and find the results presented in Table I.
Table I.
Hypothetical data on the unadjusted (crude) relationship between sedentary behavior and pregnancy.
| Behavior | ||
|---|---|---|
| Active (n = 300) | Sedentary (n = 300) | |
| N (%) pregnant | 135 (45%) | 75 (25%) |
| Risk ratio | 1.00 (Referent) | 0.55 |
At first pass, we see that pregnancy was less common among women with sedentary behavior compared to those who are physically active, as indicated by the unadjusted risk ratio (RR) of 0.55. Should we start counseling our IVF patients to increase physical activity in order to increase their chances of pregnancy? Before jumping to the conclusion that sedentary behavior is causing the lower risk of pregnancy, we need to consider other factors that could be lurking behind the association between sedentary behavior and pregnancy.
Had these data been from a sufficiently large randomized controlled experiment, the act of randomization should have made these two groups balanced with regard to all other characteristics that may affect both their activity level and their chances of becoming pregnant (e.g. obesity); the only expected difference between groups is treatment assignment—intervention or otherwise, allowing causal inferences to be made.
In this example, however, we did not randomly assign the exposure of interest, sedentary behavior, and thus there is no assurance that the only difference between the two groups is their level of physical activity. Active and sedentary women likely differ in other behaviors as well, such as diet, alcohol consumption and cigarette smoking, which may also causally influence pregnancy probability. As an example, consider obesity as a variable that is associated with both active/sedentary behavior and pregnancy probability. These relationships can be depicted using a directed acyclic graph (or DAG), as in Fig. 1 (see Robins, 1987; Pearl, 1995; Greenland et al., 1999; Glymour & Greenland (2008); or Shrier & Platt (2008) for more about DAGs). In brief, DAGs use directed arrows to indicate a causal relationship between the variables they connect, whereas absence of an arrow indicates an assumption of no causal relationship.
Figure 1.

A DAG illustrating relationships among sedentary behavior, obesity, and pregnancy. In this DAG, obesity is a confounder of the relationship between sedentary behavior and pregnancy. DAG: directed acyclic graph.
When confounding is suspected in an observational study, it is important to have data available for that confounding factor. In this example, we can use data on obesity (BMI >30 kg/m2) to assess the extent to which obesity is confounding the association between sedentary behavior and pregnancy. Stratification on obesity, as shown in Table II, allows us to make comparisons between groups that are different with regard to behavior (exposure), but the same with regard to obesity (confounder). Analysis-phase control for confounding can be achieved by stratification or by regression-based adjustment.
Table II.
Hypothetical data on the relationship between sedentary behavior and pregnancy, stratified by obesity.
| Obese | ||
|---|---|---|
| Behavior | ||
| Active (n = 50) | Sedentary (n = 250) | |
| N (%) pregnant | 10 (20%) | 50 (20%) |
| Risk ratio | 1.00 (Referent) | 1.00 |
| Not Obese | ||
| Behavior | ||
| Active (n = 250) | Sedentary (n = 50) | |
| N (%) pregnant | 125 (50%) | 25 (50%) |
| Risk ratio | 1.00 (Referent) | 1.00 |
In these sample data, once comparisons are made within women in the same BMI group, the probability of pregnancy is the same among women who are sedentary and those who are physically active (20% in the obese group and 50% in the not obese group, both RR = 1.00). The association we originally found between sedentary behavior and pregnancy was driven by the fact that obesity is related to sedentary behavior (i.e. obese women are more likely to be sedentary), and obesity reduces the probability of pregnancy. If we had not accounted for this confounder (obesity), we would have come to the wrong conclusion.
Consider two other examples at opposite extremes. First, suppose *all* of the sedentary women were obese and *none* of the physically active women were obese. Then, physical activity and obesity would be completely dependent, and we would not be able to tease apart the effect of sedentary lifestyle versus obesity on pregnancy. In contrast, suppose equal proportions of sedentary and physically active women were obese (e.g. 50% of women in each activity group were obese). Then, obesity could not be a confounder in the association between sedentary behavior and pregnancy because obesity would not be associated with the exposure of interest.
How does one identify possible confounders? One proposed simple set of criteria suggests consideration of whether the factor is as follows:
a cause of the exposure of interest
a cause of the outcome of interest, independent of exposure
not on the causal pathway between the exposure and outcome.
More technical definitions of confounding and confounders can be found in Rothman (1986), Greenland (2001), Rothman et al. (2008), Vanderweele (2013) and Hernan & Robins (2019), among others.
DAGs can be useful for identifying a factor as a confounder and discerning confounding from other ways variables can be related, as shown in Fig. 2. Only hypothetical scenario (A) depicts confounding based on the three criteria above—alcohol consumption is associated with and precedes the exposure, it is an independent predictor of the outcome and it is not a consequence of the exposure (i.e. it is not on the causal pathway between sedentary behavior and pregnancy). In contrast, scenario B depicts a factor (average calories burned per day) that is on the causal pathway (sedentary behavior affects calories burned, which in turn affects pregnancy) and is one mechanism through which behavior affects pregnancy. In scenario C, age affects the outcome but is not a confounder because it is not associated with exposure; in contrast, in scenario D, sleep affects the exposure but is not associated with the outcome, independent of exposure. In both scenarios C and D, a lack of arrow between factors indicates the absence of the causal associations.
Figure 2.
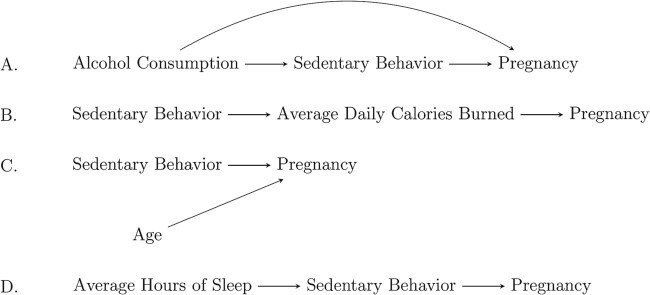
Example DAGs for four different scenarios.
Consequences of failing to control for an important confounder
Failure to account for an important confounder can result in overestimates of the true effect (bias away from the null), underestimates (bias toward the null), complete masking of the true effect or reversal of the direction of the true effect from harmful to protective or vice versa. Table III gives examples for how these scenarios play out in terms of RRs.
Table III.
Hypothetical examples of how risk ratios can be confounded across scenarios.
| (i) overestimate | (ii) underestimate | (iii) masked | (iv) reversal | |
|---|---|---|---|---|
| Unadjusted | 3.00 | 1.50 | 1.00 | 0.50 |
| ‘Fully’ Adjusted (Truth/Causal) | 2.00 | 2.00 | 2.00 | 2.00 |
Taking the second row to represent the true causal effect, one can see that failure to adjust for a confounder can lead to an (i) overstated effect, (ii) an understated effect, (iii) a masked effect or even (iv) a reversal in the direction of the effect.
A study of the percentage of IVF cycles resulting in live birth by number of embryos transferred (<3 versus ≥3) can serve as an example of confounding resulting in a reversal of the true direction of effect. Suppose 20% of cycles with ≥3 embryos transferred result in live birth and 40% of cycles with <3 embryos transferred result in live birth. Examining only this crude comparison, one might conclude that we should never transfer more than two embryos in a given cycle, as transferring more embryos decreases the probability of IVF success. However, clinical experience will remind many readers that cycles in which ≥3 embryos are transferred are cycles among women with poorer prognoses. For instance, it is likely that the cycles with ≥3 embryos transferred tend to be from older patients with decreased ovarian reserve or repeated prior cycle failures. Whereas the unadjusted RR is 0.5 (indicating the probability of live birth when ≥3 embryos are transferred is half that of when <3 embryos are transferred), an analysis that adjusts for age, estradiol level, number of oocytes retrieved etc., could very well find that the RR is 1.5—that is, among cycles with very similar patient and clinical characteristics, the chance of live birth increases when more embryos are transferred. This basic example makes it easy to recognize how confounding can reverse an observed association. However, it is important to keep in mind that the direction and magnitude of confounding can be complex to understand in more nuanced and less straightforward scenarios (see section below on Uncontrolled confounding).
When model parsimony is desired or necessary, a data-driven statistical approach to determine which covariates should be included in a final, adjusted regression model may be used (Mickey & Greenland, 1989; VanderWeele, 2019). However, such data-driven approaches should only be used after identifying a set of possible confounders based on careful consideration of the clinical context around the exposure–outcome association of interest.
Consequences of an ‘everything plus the kitchen sink’ model
Often, when researchers recognize confounding as a possible problem, they think only of spurious associations found due to lack of accounting for a confounder. An extreme response to this is to control for all available variables as possible confounders in a single model. However, this kitchen sink strategy can be problematic because adjusting for variables that are not confounders can introduce bias and/or decrease precision. Consequences of overadjustment and unnecessary adjustment have been described in the epidemiological methods literature (Schisterman et al., 2009). Overadjustment has been described as control for a variable that is on the causal pathway between the exposure and the outcome. It can attenuate or completely obscure the estimated association of interest (this will be discussed further in a follow-up commentary). Unnecessary adjustment is described as control for non-confounding variables, such as those associated with exposure but not the outcome. Unnecessary adjustment can lead to decreased statistical precision of the exposure–outcome association.
For example, suppose we are investigating the association between sedentary behavior in fresh autologous IVF cycles and the risk of adverse IVF outcomes (e.g. preterm birth), and we construct models adjusting for maternal age, BMI, smoking status, gravidity, number of oocytes retrieved and total embryos transferred. Number of oocytes retrieved and total embryos transferred temporally occur after sedentary behavior has been defined, so these factors cannot cause sedentary behavior. If we assume that the number of embryos transferred is affected by sedentary behavior and, in turn, affects risk of preterm delivery, then a DAG depicting this scenario would be similar to B in Fig. 2 and is shown in Fig. 3.
Figure 3.
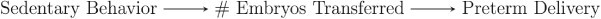
A possible DAG to depict the association between sedentary behavior, number of embryos transferred and preterm delivery.
In this case, number of embryos transferred would be a mediator, not a confounder, in the relationship between sedentary lifestyle and preterm delivery.
Although it may seem unlikely that sedentary behavior would directly affect the number of embryos transferred (Fig. 3), sedentariness affects BMI, which in turn affects fertility potential, which may affect number of oocytes retrieved and thus number of embryos available for transfer. Adjusting for number of embryos transferred would be an example of overadjustment—control for a factor that is on the causal pathway between exposure and outcome, described as a mediator or causal intermediate. Such a factor cannot be a confounder (as it is a direct consequence of the exposure), and inclusion of a mediator in a model causes bias to estimates of the total effect of an exposure on an outcome. Occasionally, investigators may be interested in using analysis to evaluate mechanisms, through use of mediation analysis. Mediation will be discussed in detail in a follow-up commentary. Briefly, if the exposure’s effect on the outcome works partially or entirely via a mechanism through the mediator, then adjusting for the mediator may attenuate or eliminate the total association between the exposure and outcome. One may conclude that there is no association between the exposure and outcome, when, in reality, there is a strong association between the two.
A second caution against the kitchen sink approach is that unnecessary adjustment for non-confounding variables can reduce precision of the effect estimate of interest. Non-confounding variables include those unrelated to exposure or outcome, those related only to exposure and those that affect outcome risk but are not related to exposure (Schisterman et al., 2009). For instance, suppose neighborhood green space is not associated with miscarriage, but we adjust for it in a model assessing the association between sedentary behavior and miscarriage (Fig. 4). The effect estimate of interest (e.g. RR, odds ratio) will not be affected, but the SE for the effect estimate and its corresponding CI could be inflated.
Figure 4.
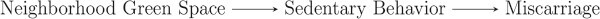
A possible DAG to depict the association between sedentary behavior, neighborhood green space and miscarriage. Neighborhood green space is not a confounder because it is not predictive of miscarriage. Adjusting for it in the model could reduce precision of the effect estimate for the association between sedentariness and miscarriage.
Uncontrolled confounding
The direction of confounding depends upon the direction of the confounder–exposure association and the direction of the confounder–outcome association. The magnitude of confounding depends upon the magnitude of the confounder–exposure association, the magnitude of the confounder–outcome association and the prevalence of the confounder in the study population, with the strongest confounding when the confounder reaches a prevalence of 50% (Walker, 1991).
A standard limitation to any observational study is that even with adjustment for known confounders, there is potential for uncontrolled confounding by variables that have not been identified, or those that are known but unmeasured in a given study. In studies where data on certain confounders are not available, it can be useful to conduct sensitivity analyses to characterize the potential effect on the observed association (Greenland, 1996; Lin et al., 1998; Groenworld et al., 2016). The E-value has been proposed as one way to assess how strong of an association the confounder would need to have with the exposure and the outcome in order to meaningfully change the overall result (Ding & VanderWeele, 2016; VanderWeele, 2017; Haneause et al., 2019). The E-value can be computed (at no cost and without coding) for a variety of study designs and outcome types (RRs, hazard ratios, continuous outcomes) at the following website: https://www.evalue-calculator.com/ (Mathur et al., 2018). There are limitations to the E-value; however, and some have expressed concern about the potential for the E-value to be misinterpreted (Ioannidis et al., 2019; Blum et al., 2020). Regardless, researchers need to be aware of the potential for uncontrolled confounding, consider what consequences uncontrolled confounding may have in their study regarding direction and magnitude of the quantified effect estimates and include a thorough discussion of those consequences when reporting and interpreting results.
What is effect measure modification, and why should I care?
Effect measure modification occurs when the association between two variables differs based on the level of another factor (known as the effect modifier). For instance, consider the data presented in Table IV. In these data, the effect of sedentary behavior on conception probability depends upon whether women are of normal BMI or are obese. Among non-obese women, sedentary behavior has no effect on pregnancy (50% in both the active and sedentary groups became pregnant). However, among women who are obese, sedentary behavior does have an association with pregnancy (50% of women who are physically active but only 20% of sedentary women conceived). When the causal effect of an exposure depends upon some other variable, proper handling of effect measure modification (also called statistical interaction) in analysis is critical to counseling patients appropriately. In the example data, sedentary behavior will not harm your chances of pregnancy if you are not obese, but sedentary behavior coupled with obesity can severely decrease your chance of pregnancy. Further, when presenting the data, not stratifying by obesity would lead to the conclusion that sedentary behavior is bad for everyone, given that 50% of all physically active women became pregnant versus only 25% of all sedentary women.
Table IV.
Hypothetical data on the association between sedentary behavior and pregnancy, by obesity.
| Obese | ||
|---|---|---|
| Behavior | ||
| Active (n = 50) | Sedentary (n = 250) | |
| N (%) Pregnant | 25 (50%) | 50 (20%) |
| Risk Ratio | 1.00 (Referent) | 0.40 |
| Not Obese | ||
| Behavior | ||
| Active (n = 250) | Sedentary (n = 50) | |
| N (%) Pregnant | 125 (50%) | 25 (50%) |
| Risk Ratio | 1.00 (Referent) | 1.00 |
| Overall | ||
| Behavior | ||
| Active (n = 300) | Sedentary (n = 300) | |
| N (%) Pregnant | 150 (50%) | 75 (25%) |
| Risk Ratio | 1.00 (Referent) | 0.50 |
For the data in Table IV, obesity is an effect measure modifier on the multiplicative scale because the effect of sedentary behavior on pregnancy differs by obesity status.
In contrast, the association between sedentary behavior, obesity and pregnancy, as displayed in Table II, exemplifies a scenario where there is no effect modification. In Table II, we see that pregnancy is less likely among obese women, but the association between obesity and pregnancy is the same within the two activity groups—the difference in the probability of pregnancy between women who are obese and women who are not obese is 30% (20% versus 50%) both among active and sedentary women. Likewise, the difference in the probability of pregnancy between active and sedentary women is the same regardless of obesity. Thus, in Table II, there is no effect measure modification (or interaction) present, and there is no need to stratify the sedentariness–pregnancy association by obesity.
Effect measure modification may be present in the following scenarios:
The effect of gonadotrophin dose on ovarian response depends on female BMI.
The effect of double IUIs on the probability of pregnancy depends on whether the sperm was fresh or frozen.
The effect of smoking on birthweight depends on maternal age.
In each of these instances, stratifying by the effect modifier is important. Failure to stratify on an effect modifier assigns the same effect estimate to groups with heterogeneous risk. This can lead to incorrect conclusions and flawed recommendations (e.g. encourage all women to be more physically active) and/or miss something important (e.g. the opportunity to further probe why the relationship between gonadotrophin dose and ovarian response differs among obese women, and then to identify that the i.m. injections often fail to penetrate the muscle in obese women) (Shah et al., 2014).
Whereas confounding represents a potential bias to try to eliminate, effect measure modification has implications for how results are presented and interpreted. When the effect of an exposure depends upon another factor (i.e. the effect modifier), then the associations should be reported separately for each level of the effect modifier.
Concluding remarks
There are no two ways about it: observational research is critical to reproductive medicine because of the many limitations of RCTs. Because of our reliance on observational studies to inform clinical practice and patient counseling, correct inference from these studies requires thinking critically and carefully about potential confounders and effect modifiers (Stocking et al., 2019). We have presented examples illustrating how failing to adjust for a confounder leads to invalid conclusions, as well as examples where adjusting for a factor that is not a confounder also leads to invalid or imprecise conclusions. Careful consideration of which factors may act as confounders in the association of interest is critical to conducting sound research, particularly with complex observational studies in reproductive medicine. It is not sufficient to compare an array of variables by exposure of interest and adjust for those with a P-value less than some pre-specified value (see Farland et al., 2016 for further explanation). Clinical context and temporal sequence need to be considered thoroughly to ensure high-quality research.
Authors’ roles
KFBC, LED, LVF, MRH and SAM conceived and designed the commentary series, drafted the manuscript, revised the intellectual content and approved the final manuscript. EG, BWW and LAW provided a critical review, revised the intellectual content and approved the final manuscript.
Funding
LED was supported by 2 L50 HD085412-03.
Conflict of interest
LVF received a consultant fee from Ovia Health and had conference travel and an honorarium paid by Merck & Co. SAM has received a consulting fee for service as an Advisory Board member for the Endometriosis Disease Burden and Endometriosis International Steering Committee working groups of AbbVie, Inc. LED reports a grant from the National Institutes of Health during the conduct of the study. LAW reports grants from NIH, non-financial support from Sandstone Diagnostics, non-financial support from Swiss Precision Diagnostics, non-financial support from Kindara.com, non-financial support from FertilityFriend.com outside the submitted work.
References
- Blum MR, Tan YJ, Ioannidis JPA. Use of E-values for addressing confounding in observational studies: an empirical assessment of the literature. Int J Epidemiol 2020. doi: 10.1093/ije/dyz261 [Epub ahead of print]. [DOI] [PubMed] [Google Scholar]
- Ding P, VanderWeele TJ. Sensitivity analysis without assumptions. Epidemiology 2016;27:368–377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farland LV, Correia KC, Wise LA et al. P-values and reproductive health: what can clinical researchers learn from the American Statistical Association? Hum Reprod 2016;31:2406–2410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glymour MM, Greenland S. Causal Diagrams. In: Rothman KJ, Greenland S, Lash TL (eds). Modern Epidemiology, 3rd edn. Philadelphia: Lippincott Williams & Wilkins, 2008,183–209 [Google Scholar]
- Greenland S. Basic methods for sensitivity analysis of biases. Int J Epidemiol 1996;25:1107–1116. [PubMed] [Google Scholar]
- Greenland S, Pearl J, Robins JM. Causal diagrams for epidemiologic research. Epidemiology 1999;10:37–48. [PubMed] [Google Scholar]
- Greenland S, Morgenstern H. Confounding in health research. Ann Rev Public Health 2001;22:189–212. [DOI] [PubMed] [Google Scholar]
- Groenwold RH, Sterne JA, Lawlor DA, Moons KG, Hoes AW, Tilling K. Sensitivity analysis for the effects of multiple unmeasured confounders. Ann Epidemiol 2016;26:605–611. [DOI] [PubMed] [Google Scholar]
- Haneause S, VanderWeele TJ, Arterburn D. Using the E-value to assess the potential effect of unmeasured confounding in observational studies. JAMA 2019;321:602–603. [DOI] [PubMed] [Google Scholar]
- Hernan MA, Robins JM. Causal Inference. Boca Raton: Chapman & Hall/CRC, 2019. Forthcoming, https://www.hsph.harvard.edu/miguel-hernan/causal-inference-book/ [Google Scholar]
- Ioannidis JPA, Tan YJ, Blum MR. Limitations and misinterpretations of E-values for sensitivity analyses of observational studies. Ann Intern Med 2019;170:108–111. [DOI] [PubMed] [Google Scholar]
- Lin DY, Pstay BM, Kronmal RA. Assessing the sensitivity of regression results to unmeasured confounders in observational studies. Biometrics 1998;54:948–963. [PubMed] [Google Scholar]
- Mathur MB, Ding P, Riddell CA, VanderWeele TJ. Web site and R package for computing E-values. Epidemiology 2018;29:e45–e47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mickey RM, Greenland S. The impact of confounder selection criteria on effect estimation. Am J Epidemiol 1989;129:125–137 Erratum in: Am J Epidemiol 1989 Nov;130(5):1066. [DOI] [PubMed] [Google Scholar]
- Pearl J. Causal diagrams for empirical research. Biometrika 1995;82:669–688. [Google Scholar]
- Robins J. A graphical approach to the identification and estimation of causal parameters in mortality studies with sustained exposure periods. J Chronic Dis 1987;40 Suppl 2:139S–161S PubMed PMID: 3667861. [DOI] [PubMed] [Google Scholar]
- Rothman KJ. Objectives of epidemiologic study design. In: Rothman KJ (ed). Modern Epidemiology. Boston: Little, Brown and Company, 1986,89–94 [Google Scholar]
- Rothman KJ, Greenland S, Lash TL. Validity in epidemiologic studies. In: Rothman KJ, Greenland S, Lash TL (eds). Modern Epidemiology, 3rd edn. Philadelphia: Lippincott Williams & Wilkins, 2008, 128–147 [Google Scholar]
- Schisterman EF, Cole SR, Platt RW. Overadjustment bias and unnecessary adjustment in epidemiologic studies. Epidemiology 2009;20:488–495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah DK, Missmer SA, Correia KFB, Ginsburg LS. Pharmacokenetics of human chorionic gonadotropin injection in obese and normal-weight women. J Clin Endocrinol Metab 2014;99:1314–1321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shrier I, Platt RW. Reducing bias through directed acyclic graphs. BMC Med Res Methodol 2008;8:70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stocking K, Wilkinson J, Lensen S, Brison DR, Roberts SA, Vail A. Are interventions in reproductive medicine assessed for plausible and clinically relevant effects? A systematic review of power and precision in trials and meta-analyses. Hum Reprod 2019;34:659–665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele TJ. On the definition of a confounder. Ann Stat 2013;41:196–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele TJ. Sensitivity analysis in observational research: introducing the E-value. Ann Intern Med 2017;167:268–274. [DOI] [PubMed] [Google Scholar]
- VanderWeele TJ. Principles of confounder selection. Eur J Epidemiol 2019;34:211–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker AM. Observation and Inference: An Introduction to the Methods of Epidemiology. Chestnut Hill, MA: Epidemiology Resources, Inc., 1991 [Google Scholar]


