Nonparametric estimation of Spearman’s rank correlation with bivariate survival data

Abstract

We study rank-based approaches to estimate the correlation between two right-censored variables. With end-of-study censoring, it is often impossible to nonparametrically identify the complete bivariate survival distribution, and therefore it is impossible to nonparametrically compute Spearman’s rank correlation. As a solution, we propose two measures that can be nonparametrically estimated. The first measure is Spearman’s correlation in a restricted region. The second measure is Spearman’s correlation for an altered but estimable joint distribution. We describe population parameters for these measures and illustrate how they are similar to and different from the overall Spearman’s correlation. We propose consistent estimators of these measures and study their performance through simulations. We illustrate our methods with a study assessing the correlation between the time to viral failure and the time to regimen change among persons living with HIV in Latin America who start antiretroviral therapy.

1 |. INTRODUCTION

In many medical studies, researchers are interested in measuring the correlation between two time-to-event variables. For example, in studies of HIV/AIDS, there is interest in studying the correlation between the time from antiretroviral therapy (ART) initiation to viral failure and the time from ART initiation to regimen change. These variables should be highly correlated, and it might be important to know if the observed correlation is weaker than expected. Bivariate survival data may also come from paired subjects. For example, researchers might be interested in assessing the correlation between the time to cardiovascular disease for a patient and that for his/her parents, or between times to events in twins.

Right censoring is a defining element of bivariate survival data: One or both of the times to event may not be observed. When looking at correlation between times to events that occur in a single subject (e.g., time to viral failure and time to regimen change), the censoring time may be the same time for both outcomes. However, if the times to events are in paired subjects (e.g., times to events in twins), then the censoring times may differ. Our interest is in both scenarios, but we do not consider the setting where an event occurring in one variable causes censoring of the other, that is, competing risks.

Several different methods have been proposed to measure and test the correlation between two right-censored time-to-event variables. Clayton (1978) introduced a bivariate hazard ratio or a cross ratio as a single number summary of correlation in the context of a frailty model. Oakes (1982, 1989) suggested a test for independence based on the cross ratio, showed its relationship with Kendall’s tau, and extended its definition to a larger class of models. Fan et al. (2000) used a weighted average of the inverse of the cross ratio and a limited region Kendall’s tau. Cuzick (1982) proposed a model of correlation and several test statistics, one of which resembles Spearman’s rank correlation for censored data. Dabrowska (1986) derived generalized statistics to test the null hypothesis that the joint survival distribution is equal to the product of the marginals. Under certain assumptions, one of these statistics is related to a censored version of Spearman’s correlation, and another corresponds to a log-rank test based on martingale residuals. Shih and Louis (1996) developed two additional statistics based on martingale residuals. Shih and Louis (1995) also suggested a two-stage estimation procedure to evaluate the correlation in bivariate data using copulas (Nelsen, 2007). Other approaches for measuring correlation using copulas for bivariate survival data have been considered by Carriere (2000), Romeo et al. (2006), and Schemper et al. (2013).

Spearman’s rank correlation is ubiquitous in biomedical research because of its simple interpretation, robustness, and ability to capture nonlinear correlations. It is used much more frequently in practice than Kendall’s tau, perhaps because it closely approximates Pearson’s correlation under normality (Kruskal, 1958), and it is much easier to compute and interpret than a cross ratio. In the absence of censoring, Spearman’s correlation is simply the correlation of the ranked data. However, despite related work by Cuzick (1982), Dabrowska (1986), and Oakes (1989), there is no nonparametric estimator of Spearman’s correlation for bivariate survival data. Schemper et al. (2013) proposed a semiparametric iterative multiple imputation (IMI) method to estimate Spearman’s correlation (denoted as ρ_IMI throughout this paper). Their method transforms bivariate survival data into a Gaussian dependency structure using a normal copula, multiply imputes censored observations from this induced bivariate distribution, and approximates Spearman’s correlation using Pearson’s correlation of the normal deviates. This approach is semiparametric because it does not require any assumptions about the marginal distributions. However, it uses a Gaussian dependency structure, which may lead to bias due to misspecification.

The goal of this paper is to propose and study nonparametric estimators of Spearman’s correlation for right-censored data. Our methods use a nonparametric bivariate survival surface estimator. A challenge with estimating a bivariate survival surface, however, is that it may be nonparametrically estimable only within a certain region, for example, due to end-of-study censoring. This motivates us to propose two correlation estimators: one that is defined only within the restricted region and another one that implicitly assigns values outside of this region as having the highest rank.

In Section 2, we express Spearman’s correlation for time-to-event data and describe target parameters of interest. In Section 3, we address estimation and inference. In Section 4, we evaluate the performance of our estimators with several sets of simulations. In Section 5, we apply our methods to an HIV study by examining the correlation between times from treatment initiation to viral failure and regimen change. In Section 6, we discuss our methods and future directions. We have implemented our methods in the survSpearman R package (Eden et al., 2021).

2 |. POPULATION PARAMETERS

2.1 |. Notation and definitions

We are interested in estimating correlation between two time-to-event variables denoted as (T_X, T_Y) defined on [0, ∞) × [0, ∞). Variables T_X and T_Y can be observed on a single subject or on a pair of subjects. Each time to event can be censored. We denote time-to-censoring variables as (C_X, C_Y) and assume independence between (T_X, T_Y) and (C_X, C_Y), but C_X and C_Y can be dependent. If T_X and T_Y are observed on a single subject, then it is likely that C_X = C_Y. If C_X = C_Y with probability one, then we call this univariate censoring, otherwise censoring is bivariate. In most studies, the follow-up period is bounded. We denote the maximum follow-up times, respectively, as τ_X and τ_Y, and consider these to be fixed by study design. Censoring, due to the end of study, has been referred to as type I censoring. With type I censoring, no events will be observed beyond the region Ω = [0, τ_X) × [0, τ_Y), or equivalently, C_X ≤ τ_X and C_Y ≤ τ_Y. For our presentation, we distinguish between strict type I censoring, where censoring occurs only at τ_X and τ_Y (i.e., C_X = τ_X, C_Y = τ_Y), and generalized type I censoring (Klein and Moeschberger, 1997), where censoring may also occur prior to τ_X and τ_Y (i.e., C_X ≤ τ_X, C_Y ≤ τ_Y). Strict type I censoring is rarely observed in practice, but will be helpful for explaining concepts; generalized type I censoring is quite common in practice, where follow-up time is bounded due to the length of the study, while subjects may start the study at different times or may drop out before the end of study. When the follow-up time is unbounded (τ_X = ∞ and τ_Y = ∞), we refer to the censoring as unbounded.

As a result of censoring, we only observe X = min(T_X, C_X), Y = min(T_Y, C_Y), and event indicators ${\Delta }_X=\mathbb{1}\left(T_X\le C_X\right)$, ${\Delta }_Y=\mathbb{1}\left(T_Y\le C_Y\right)$. We denote marginal and joint distribution functions of T_X and T_Y as F_X(x) = Pr(T_X ≤ x), F_Y(y) = Pr(T_Y ≤ y), F(x, y) = Pr(T_X ≤ x, T_Y ≤ y), and marginal and joint survival functions as S_X(x) = Pr(T_X > x), S_Y(y) = Pr(T_Y > y), S(x, y) = Pr(T_X > x, T_Y > y). We define F_X(x⁻) = lim_t↑x F_X(t) and F(x⁻, y) = lim_t↑x F(t, y); F_Y(y⁻) and F(x, y⁻) are defined similarly.

2.2 |. Spearman’s rank correlation

As shown by Liu et al. (2018), in the absence of censoring, the population parameter for Spearman’s correlation between T_X and T_Y can be defined as:

$${\rho }_S=\text{Cor}\left\{\frac{F_X\left(T_X\right)+F_X\left(T_X^{-}\right)}{2},\frac{F_Y\left(T_Y\right)+F_Y\left(T_Y^{-}\right)}{2}\right\}.$$ (1)

When both T_X and T_Y are continuous, the above definition becomes

$${\rho }_S=\text{Cor}\left\{F_X\left(T_X\right),F_Y\left(T_Y\right)\right\},$$

the grade correlation (Kruskal, 1958). Notice that if F_X and F_Y are estimated with their respective empirical distributions, then F_X(T_X) and F_Y(T_Y) are simply estimated as the ranks of T_X and T_Y, respectively, divided by the number of points in the sample, corresponding to the well-known Spearman’s correlation estimator:

$${\widehat{\rho }}_S=\text{Cor}\left\{\text{rank}\left(T_{X,i}\right),\text{rank}\left(T_{Y,i}\right)\right\},$$

where (T_X,i, T_Y,i) for i = 1, …, n are independent and identically distributed (iid) draws of (T_X, T_Y). Liu et al. (2018) have shown that Equation (1) can be presented as:

$$\begin{gathered} {\rho }_S/c_{\rho }={\text{E}}_{T_X,T_Y}[\left\{F_X\left(T_X\right)+F_X\left(T_X^{-}\right)-1\right\} \\ \left\{F_Y\left(T_Y\right)+F_Y\left(T_Y^{-}\right)-1\right\}] \\ ={\int }_0^{\infty }{\int }_0^{\infty }\left\{F_X(x)+F_X\left(x^{-}\right)-1\right\} \\ \left\{F_Y(y)+F_Y\left(y^{-}\right)-1\right\}F(dx,dy), \end{gathered}$$ (2)

where $c_{\rho }=[\text{Var}\left\{F_X(T_X)+F_X(T_X^{-})-1\right\}\text{Var}\{F_Y\left(T_Y\right)+{F_Y\left(T_Y^{-}\right)-1\}]}^{-1/2}$; and c_ρ = 3 when T_X and T_Y are continuous. The right-hand side of (2) is the covariance of probability-scale residuals (PSRs) proposed and studied by Li and Shepherd (2012) and Shepherd et al. (2016) and defined as:

$$\begin{gathered} r_X\left(t_X,F_X\right)=\text{E}\left\{\text{sign}\left(t_X-T_X\right)\right\}=\text{Pr}\left(T_X<t_X\right) \\ -\text{Pr}\left(T_X>t_X\right)=F_X\left(t_X^{-}\right)+F_X\left(t_X\right)-1, \end{gathered}$$

where sign(t_X − T_X) is −1, 0, and 1 for t_X < T_X, t_X = T_X, and t_X > T_X, respectively. We can rewrite definition (2) in terms of survival functions:

$$\begin{gathered} {\rho }_S/c_{\rho }={\int }_0^{\infty }{\int }_0^{\infty }\left\{1-S_X(x)-S_X\left(x^{-}\right)\right\} \\ \left\{1-S_Y(y)-S_Y\left(y^{-}\right)\right\}S(dx,dy). \end{gathered}$$ (3)

Right censoring causes serious challenges for nonparametric estimation of (3). First, nonparametric estimation of S(x, y) is challenging due to nonunique solutions of the nonparametric likelihood in the presence of censoring and the fact that even consistent estimators of S(x, y) may have negative mass for some x and y (Dabrowska, 1988; Pruitt, 1991). Second, nonparametric estimation of S_X(x), S_Y(y), and S(x, y) beyond the maximum follow-up time(s) is not possible. To overcome the latter challenge, one could focus on estimating Spearman’s correlation inside Ω. Another possible approach is to focus on Spearman’s correlation for an altered but estimable joint distribution. Population parameters for these two nonparametric approaches are presented in the next two subsections. Section 2.5 contains some examples.

2.3 |. Spearman’s rank correlation in a restricted region

Suppose a researcher is interested in a rank correlation only inside a restricted region, denoted Ω_R. This correlation can be computed as Spearman’s correlation defined conditionally on Ω_R, which we denote as ${\rho }_{S\mid {\Omega }_R}$. With failure time data, others have proposed and advocated the use of estimators in restricted regions including restricted mean survival times (Royston and Parmar, 2013) and limited region Kendall’s tau (Fan et al., 2000).

A natural choice is Ω_R = Ω = [0, τ_X) × [0, τ_Y), to estimate the restricted rank correlation over the region for which estimation is possible; to avoid introducing new notation, in this section we will use Ω_R = Ω. However, investigators can vary Ω_R depending on their research question as long as Ω_R ⊆ Ω; presumably Ω_R would generally be a rectangle that includes the origin (0,0). The probability of double failure happening in this rectangle is

$$\begin{gathered} P_R=\text{Pr}\left(x<{\tau }_X,y<{\tau }_Y\right)=F\left({\tau }_X^{-},{\tau }_Y^{-}\right) \\ =1-S_X\left({\tau }_X^{-}\right)-S_Y\left({\tau }_Y^{-}\right)+S\left({\tau }_X^{-},{\tau }_Y^{-}\right). \end{gathered}$$ (4)

We consider the conditional distribution over Ω_R. An example of a conditional distribution is illustrated in the middle panel of Figure 1. Its probability mass function is

$$S\left(dx,dy\mid {\Omega }_R\right)=S(dx,dy)/P_R,$$ (5)

and its marginal survival function on the X-axis is

$$S_X\left(x\mid {\Omega }_R\right)=1-F_X\left(x\mid {\Omega }_R\right)=\{\begin{array}{cc}0& x\ge {\tau }_X\\ 1-\frac{F\left(x,{\tau }_Y^{-}\right)}{P_R}& x<{\tau }_X\end{array},$$ (6)

where $F\left(x,{\tau }_Y^{-}\right)=1-S_X(x)-S_Y\left({\tau }_Y^{-}\right)+S\left(x,{\tau }_Y^{-}\right)$. The marginal survival function on the Y-axis, S_Y(y|Ω_R), is similarly defined. Spearman’s correlation in the restricted region satisfies

$$\begin{gathered} {\rho }_{S\mid {\Omega }_R}/c_{\rho \mid {\Omega }_R}=\underset{{\Omega }_R}{\iint }\left\{1-S_X\left(x\mid {\Omega }_R\right)-S_X\left(x^{-}\mid {\Omega }_R\right)\right\} \\ \left\{1-S_Y\left(y\mid {\Omega }_R\right)-S_Y\left(y^{-}\mid {\Omega }_R\right)\right\}S\left(dx,dy\mid {\Omega }_R\right), \end{gathered}$$ (7)

where $c_{\rho \mid {\Omega }_R}={\left[\text{Var}\left\{1-S_X(x\left|{\Omega }_R)-S_X(x^{-}\right|{\Omega }_R)\right\}\text{ Var}\left\{1-S_Y(y\left|{\Omega }_R)-S_Y(y^{-}\right|{\Omega }_R)\right\}\right]}^{-1/2}$. Note that the population parameter, ${\rho }_{S\mid {\Omega }_R}$, depends only on τ_X and τ_Y and is invariant to the censoring distribution within Ω_R.

FIGURE 1.

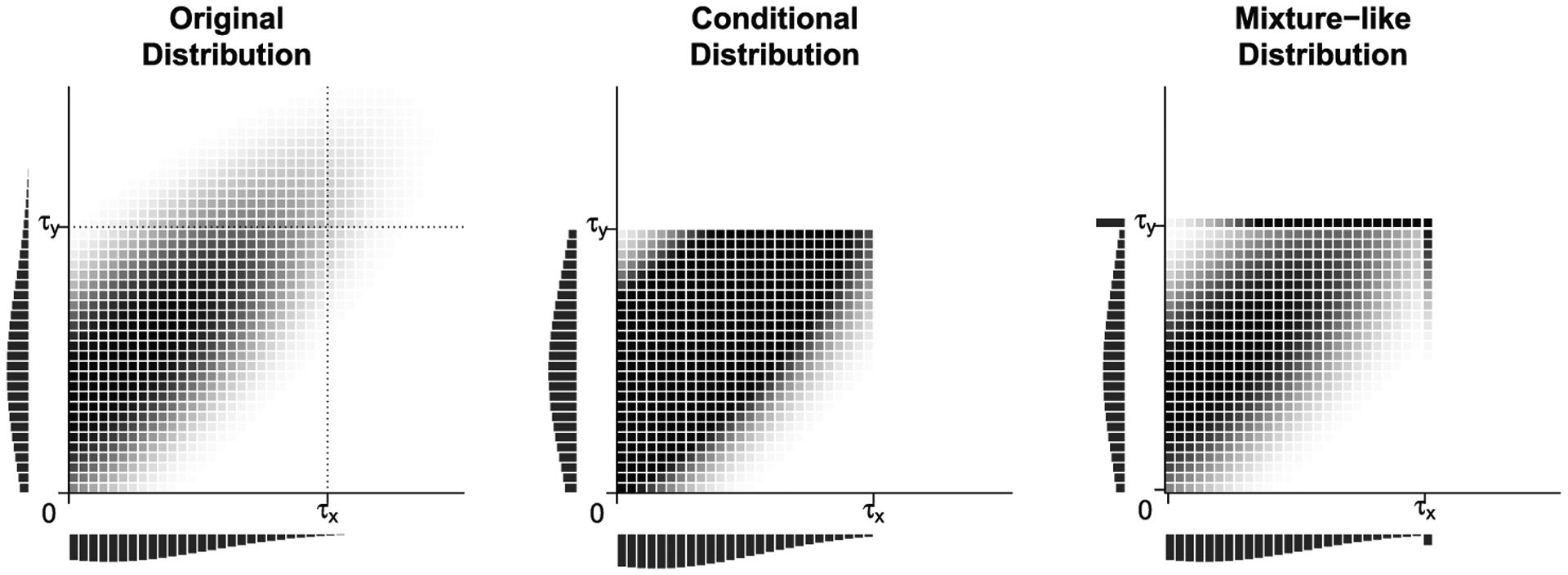
Illustration of bivariate distributions underlying the three population parameters. Left: Original distribution over [0, ∞) × [0, ∞), which has Spearman’s correlation ρ_S. Middle: Conditional distribution over Ω_R = Ω, which has Spearman’s correlation ${\rho }_{S\mid {\Omega }_R}$. Right: Mixture-like distribution S^H over region Ω ∪ [0, τ_X] × τ_Y ∪ τ_X × [0, τ_Y], which has Spearman’s correlation ${\rho }_S^H$

Note that ${\rho }_{S\mid {\Omega }_R}$ and ρ_S are different population parameters. Therefore, it is not appropriate to use ${\rho }_{S\mid {\Omega }_R}$ to estimate ρ_S; rather, ${\rho }_{S\mid {\Omega }_R}$ can be of interest on its own. For example, Fan et al. (2000) suggested a limited region Kendall’s tau to estimate over time the correlation of time to appendicitis in twins; ${\rho }_{S\mid {\Omega }_R}$ can be used instead of the limited region Kendall’s tau for similar purposes.

2.4 |. Spearman’s rank correlation with highest ranks

Suppose now that a researcher is interested in the overall rank correlation, but the observations are only available within a restricted region. This is a typical situation in studies with a bounded follow-up time or when measurements have an upper detection limit. In this case, S_X(x), S_Y(y), and S(x, y) are only nonparametrically estimable inside the region Ω = [0, τ_X) × [0, τ_Y), where τ_X < ∞ and τ_Y < ∞. Since we are interested in a rank correlation, one approach would be to define any observation censored at τ_X as receiving the highest rank value for T_X and any observation censored at τ_Y as receiving the highest rank value for T_Y, which is the same as setting T_X = min(T_X, τ_X) and T_Y = min(T_Y, τ_Y). Such an approach is sensible because these censored observations at τ_X and τ_Y do have the highest rank values and there is no information to distinguish between these highest rank values without parametric modeling assumptions. Mathematically, this approach replaces S(dx, dy) with a probability mass function S^H(dx, dy), which is, S(dx, dy) inside Ω and the left-over probability mass outside of Ω. That is,

$$S^H(dx,dy)=\{\begin{array}{ll}S(dx,dy)\hfill & x<{\tau }_X\text{ and }y<{\tau }_Y,\hfill \\ S\left({\tau }_X^{-},dy\right)\hfill & x={\tau }_X\text{ and }y<{\tau }_Y,\hfill \\ S\left(dx,{\tau }_Y^{-}\right)\hfill & x<{\tau }_X\text{ and }y={\tau }_Y,\hfill \\ S\left({\tau }_X^{-},{\tau }_Y^{-}\right)\hfill & x={\tau }_X\text{ and }y={\tau }_Y,\hfill \\ \hfill 0\hfill & x>{\tau }_X\text{ or }y>{\tau }_Y.\hfill \end{array}$$ (8)

The new probability mass function S^H(dx, dy) is depicted in the right panel of Figure 1. The part of S^H(dx, dy) inside Ω is the same as S(dx, dy) but its part outside of Ω is concentrated on the borders of Ω and at point (τ_X, τ_Y). The corresponding population parameter for the rank correlation of this new distribution is ${\rho }_S^H$, which satisfies:

$$\begin{gathered} {\rho }_S^H/c_{\rho }^H={\int }_0^{{\tau }_X}{\int }_0^{{\tau }_Y}\left\{1-S_X^H(x)-S_X^H\left(x^{-}\right)\right\} \\ \left\{1-S_Y^H(y)-S_Y^H\left(y^{-}\right)\right\}{S}^H(dx,dy), \end{gathered}$$ (9)

where $S_X^H(x)$ and $S_Y^H(y)$ are the marginal survival functions of S^H(x, y), and

$$\begin{gathered} c_{\rho }^H=[\text{Var}\left\{1-S_X^H\left(T_X\right)-S_X^H\left(T_X^{-}\right)\right\} \\ {\text{Var}\left\{1-S_Y^H\left(T_Y\right)-S_Y^H\left(T_Y^{-}\right)\right\}]}^{-1/2}. \end{gathered}$$ (10)

In other words, ${\rho }_S^H$ is Spearman’s correlation computed by setting T_X = min(T_X, τ_X) and T_Y = min(T_Y, τ_Y). Note that the population parameter, ${\rho }_S^H$, depends only on τ_X and τ_Y and is invariant to the censoring distribution within Ω.

For practical applications and intuitively, ${\rho }_S^H$ can be viewed as the rank correlation computed for data with an upper detection limit, where all values above the detection limit are set to a common largest value. Note that although in general, ${\rho }_S^H\ne {\rho }_S$ (see examples in Section 2.5), unlike ${\rho }_{S\mid {\Omega }_R}$, parameter ${\rho }_S^H$ is designed to take into account all observations including those outside of Ω. When the majority of the probability mass is within Ω, ${\rho }_S^H$ can be viewed as an approximation of ρ_S. When τ_X = ∞ and τ_Y = ∞, then ${\rho }_S^H={\rho }_S$.

2.5 |. A few examples

Here, we illustrate how the restricted region can affect ${\rho }_S^H$ and ${\rho }_{S\mid {\Omega }_R}$. Having a restricted region implies type I censoring. Although the figures in this section are generated with strict type I censoring, ${\rho }_S^H$ remains the same for generalized type I censoring, as does ${\rho }_{S\mid {\Omega }_R}$.

In some settings, ρ_S, ${\rho }_{S\mid {\Omega }_R}$, and ${\rho }_S^H$ will be quite similar. For example, the values of these parameters for the distribution shown in Figure 1 are 0.635, 0.549, and 0.634, respectively. However, these parameters may be very different in some settings.

Figure 2 shows ${\rho }_{S\mid {\Omega }_R}$ (left panel) and ${\rho }_S^H$ (right panel) as a function of ρ_S for different τ_X and τ_Y for Frank’s copula family. In this example, ρ_S and ${\rho }_S^H$ are very similar. In contrast, ρ_S and ${\rho }_{S\mid {\Omega }_R}$ are very different, especially when ρ_S is negative and Ω_R is small (e.g., region defined by 0 to the 0.5 quantiles). This is because in these settings, only a small fraction of the underlying distribution is inside Ω_R, and therefore ${\rho }_{S\mid {\Omega }_R}$ shows a weak negative correlation. Figure 3 contains three additional examples; some of these distributions may not be realistic in practice, but are useful for illustrative purposes. The left panel shows an X-like distribution, for which ρ_S = 0, ${\rho }_{S\mid {\Omega }_R}=0.69$, and ${\rho }_S^H=0.06$. Here, ${\rho }_S^H$ is similar to ρ_S because ${\rho }_S^H$ incorporates the probability mass in the upper left, upper right, and lower right regions. However, ${\rho }_{S\mid {\Omega }_R}$ is very different from ρ_S because Ω_R only contains a positively correlated subset of the distribution. The middle panel of Figure 3 shows a distribution with highly correlated values in Ω_R, zero correlation in the upper right region, and no mass in the upper left and lower right regions. For this distribution, ρ_S = 0.66, ${\rho }_{S\mid {\Omega }_R}=0.64$, and ${\rho }_S^H=0.99$. Here, ${\rho }_{S\mid {\Omega }_R}$ and ρ_S are similar because only the points in the restricted region are correlated. In contrast, ${\rho }_S^H$ is quite high because the large probability mass of the upper right region is concentrated on a single highest-rank point when computing ${\rho }_S^H$, which pulls its value upwards considerably. The right panel of Figure 3 shows a distribution with a highly negative overall correlation, for which ρ_S = −0.90, ${\rho }_{S\mid {\Omega }_R}=-0.39$, and ${\rho }_S^H=-0.74$. Here, ${\rho }_S^H$ and ρ_S are fairly different because although the probability mass of censored observations outside of Ω_R are taken into account, there is some loss of information with the highest rank assignment. The parameter ${\rho }_{S\mid {\Omega }_R}$ is very different from ρ_S because only a small fraction of the negatively correlated mass is included in Ω_R. Note that parametric or semiparametric approaches also struggle with many of these settings because they effectively use the information from the restricted region to impute what is occurring outside the restricted region. For example, ${\widehat{\rho }}_{IMI}$ (see Schemper et al., 2013) for the middle panel is approximately 0.95.

FIGURE 2.

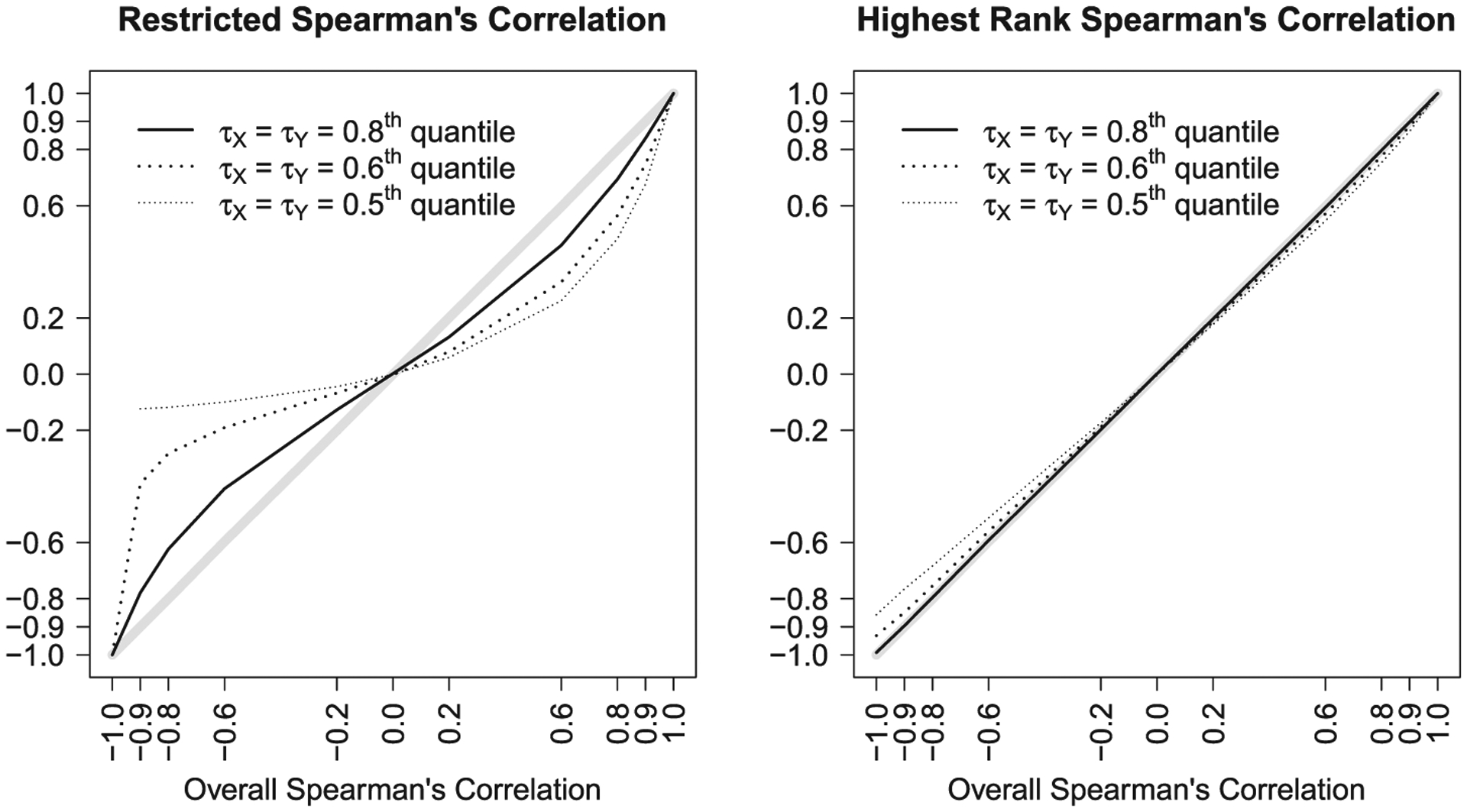
Restricted Spearman’s correlation, ${\rho }_{S\mid {\Omega }_R}$ (left panel), and highest rank Spearman’s correlation, ${\rho }_S^H$ (right panel), for Frank’s copula family for different restricted regions defined by τ_X and τ_Y (τ_X = τ_Y): 0.5th (50% censored), 0.6th (40% censored), 0.8th (20% censored) quantiles. A diagonal gray line is added for reference. Although the plots are generated based on data under strict type I censoring, the population parameters are the same for generalized type I censoring and are invariant to the rate of censoring within the restricted region

FIGURE 3.

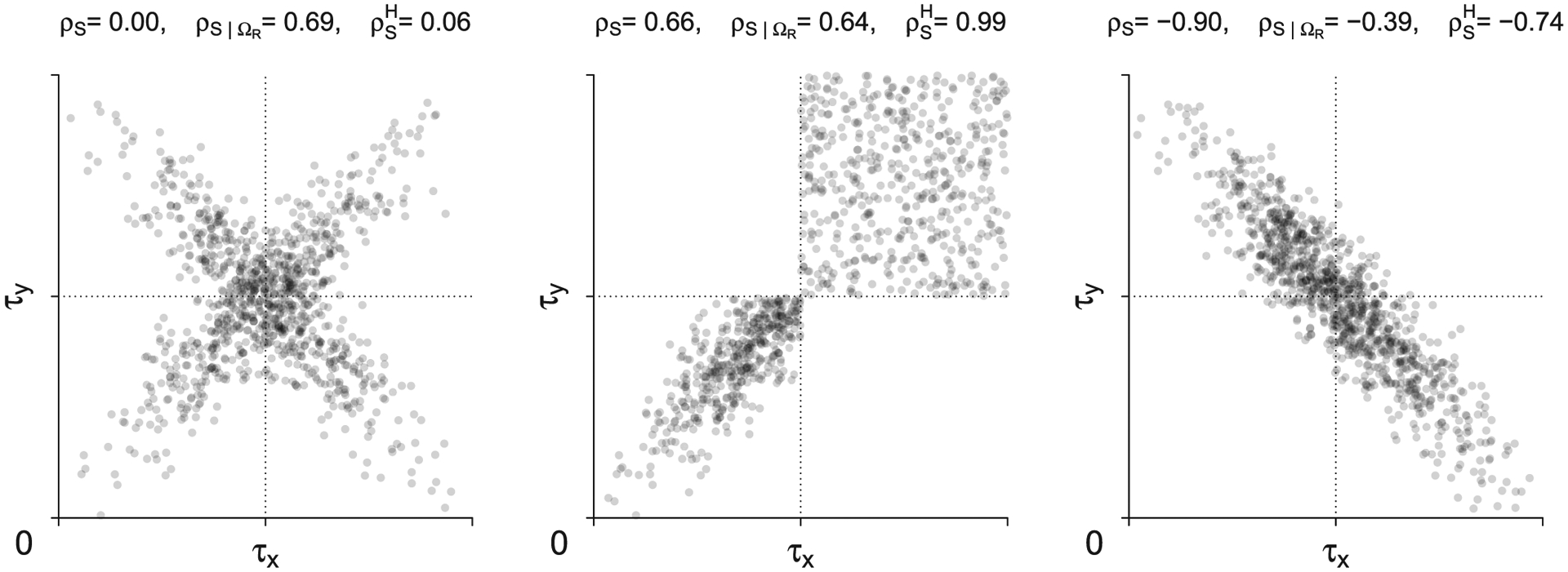
Example of bivariate distributions and their population parameters ρ_S with no censoring, and ${\rho }_S^H$ and ${\rho }_{S\mid {\Omega }_R}$ with strict type I censoring with Ω_R = [0, τ_X) × [0, τ_Y). The proportions of observed double events in the left, middle, and right panels are 25%, 43%, and 7%, respectively. Drawn are 1000 points randomly selected from the underlying distributions. Although the plots are based on strict type I censoring, the population parameters are the same for generalized type I censoring and are invariant to the rate of censoring within Ω_R

3 |. NONPARAMETRIC ESTIMATION

3.1 |. Estimation of ${\rho }_{S\mid {\Omega }_R}$ under generalized type I censoring

We estimate ${\rho }_{S\mid {\Omega }_R}$ using a plug-in estimator for Equation (7):

$${\widehat{\rho }}_{S\mid {\Omega }_R}/{\widehat{c}}_{\rho \mid {\Omega }_R}=\sum _{i:x_i<{\tau }_X}\sum _{j:y_j<{\tau }_Y}[\left\{1-{\widehat{S}}_X\left(x_i\mid {\Omega }_R\right)-{\widehat{S}}_X\left(x_i^{-}\mid {\Omega }_R\right)\right\}\times \left\{1-{\widehat{S}}_Y\left(y_j\mid {\Omega }_R\right)-{\widehat{S}}_Y\left(y_j^{-}\mid {\Omega }_R\right)\right\}\widehat{S}\left(d{x}_i,d{y}_j\mid {\Omega }_R\right)],$$

where

$$\begin{gathered} {\widehat{c}}_{\rho \mid {\Omega }_R}={\left({\widehat{\text{Var}}}_X\cdot {\widehat{\text{Var}}}_Y\right)}^{-1/2}, \\ {\widehat{\text{Var}}}_X=\sum _{i:x_i<{\tau }_X}([\left\{1-{\widehat{S}}_X\left(x_i\mid {\Omega }_R\right)-{\widehat{S}}_X\left(x_i^{-}\mid {\Omega }_R\right)\right\} \\ {-\sum _{i:x_i<{\tau }_X}\left\{1-{\widehat{S}}_X\left(x_i\mid {\Omega }_R\right)-{\widehat{S}}_X\left(x_i^{-}\mid {\Omega }_R\right)\right\}{\widehat{S}}_X\left(d{x}_i\mid {\Omega }_R\right)]}^2\times {\widehat{S}}_X\left(d{x}_i\mid {\Omega }_R\right)), \end{gathered}$$ (11)

and ${\widehat{\text{Var}}}_Y$ is computed similarly. The conditional survival curves, ${\widehat{S}}_X\left(x\mid {\Omega }_R\right)$, ${\widehat{S}}_Y\left(y\mid {\Omega }_R\right)$, and $\widehat{S}\left(x,y\mid {\Omega }_R\right)$ are estimated using plug-in estimators for (4), (5), and (6).

For $\widehat{S}(dx,dy)$ we use the estimator of Dabrowska (1988). The marginal distributions of Dabrowska’s estimator, $\widehat{S}\left(x\right)$ and $\widehat{S}\left(y\right)$, are Kaplan–Meier estimators. There are other choices for nonparametrically estimating S(dx, dy), including the estimators proposed by Prentice and Cai (1992), van der Laan (1997), Campbell (1981), and Lin and Ying (1993), to name a few. We considered the estimators of Campbell (1981) and Lin and Ying (1993) because of their computational simplicity, but ultimately chose Dabrowska’s estimator because it is consistent for S(dx, dy), straightforward to compute, and tended to result in estimates of Spearman’s correlation with better performance (see Section 4). The confidence interval (CI) of ${\widehat{\rho }}_{S\mid {\Omega }_R}$ is estimated using the bootstrap. Because of the consistency and asymptotic normality of Dabrowska’s estimator, ${\widehat{\rho }}_{S\mid {\Omega }_R}$ is consistent for ${\rho }_{S\mid {\Omega }_R}$ and asymptotically normal when ${\rho }_{S\mid {\Omega }_R}\in (-1,1)$ (see Theorem A1 in the Appendix).

A few problems can arise in practice when computing ${\widehat{\rho }}_{S\mid {\Omega }_R}$, all due to negative mass at some points in $\widehat{S}(dx,dy)$. First, in some extreme cases (e.g., small sample sizes, strong positive or negative correlation, and heavy censoring), $|{\widehat{\rho }}_{S\mid {\Omega }_R}|$ may exceed 1; if this happens, our software sets it to $\text{Sign}\left({\widehat{\rho }}_{S\mid {\Omega }_R}\right)$ and generates a warning. Second, negative mass can also lead to problems computing ${\widehat{c}}_{\rho \mid {\Omega }_R}$ in (11) because ${\widehat{\text{Var}}}_X$ or ${\widehat{\text{Var}}}_Y$ may be negative because ${\widehat{S}}_X\left(dx\mid {\Omega }_R\right)$ or ${\widehat{S}}_Y\left(dy\mid {\Omega }_R\right)$ is negative at some points. If this happens, we correct the guilty conditional marginal probability mass estimator by assigning negative values to 0, and by normalizing the rest of the probability mass values; specifically, the corrected probability mass is ${\widehat{S}}_X^{*}\left(dx\mid {\Omega }_R\right)=\text{max}\left\{0,{\widehat{S}}_X\left(dx\mid {\Omega }_R\right)\right\}/\sum _x\text{max}\left\{0,{\widehat{S}}_X\left(dx\mid {\Omega }_R\right)\right\}$. Third, negative mass may lead to a negative estimate of P_R, the probability of both events occurring in Ω_R (see Equation (4)); when this occurs, ${\widehat{\rho }}_{S\mid {\Omega }_R}$ is not defined.

Although the number of points with negative mass does not decrease as the sample size increases (Pruitt, 1991), the amount of negative mass at each point does go to zero, which therefore reduces the possibility of these problems occurring. Also, the tendency of having negative mass is lower when a lower proportion of observations are singly or doubly censored. To give a sense of the magnitude of these problems, for a sample size of 50 with 70% bivariate censoring, ${\widehat{\text{Var}}}_X$ or ${\widehat{\text{Var}}}_Y$ was negative for 1.3% of 1000 simulations, and ${\widehat{P}}_R$ was less than zero in 2.4% of simulations. With a sample size of 100 and 70% bivariate censoring, these problems occurred in 0% and 0.8% of simulations, respectively.

3.2 |. Estimation of ${\rho }_S^H$ under generalized type I censoring

Equation (9) provides a straightforward way of estimating ${\rho }_S^H$, given a nonparametric estimate of the bivariate survival surface, $\widehat{S}(dx,dy)$:

$$\begin{gathered} {\widehat{\rho }}_S^H/{\widehat{c}}_{\rho }^H=\sum _{i^{*}}\sum _{j^{*}}\left\{1-{\widehat{S}}_X^H\left(x_{i^{*}}\right)-{\widehat{S}}_X^H\left(x_{i^{*}}^{-}\right)\right\} \\ \left\{1-{\widehat{S}}_Y^H\left(y_{j^{*}}\right)-{\widehat{S}}_Y^H\left(y_{j^{*}}^{-}\right)\right\}{\widehat{S}}^H\left(d{x}_{i^{*}},d{y}_{j^{*}}\right), \end{gathered}$$

where i* enumerates all the events for X plus τ_X, j* enumerates all the event for Y plus τ_Y, and ${\widehat{S}}^H\left(d{x}_i,d{y}_j\right)$ and ${\widehat{c}}_{\rho }^H$ are the plug-in estimators for (8) and (10), respectively. As before, we compute $\widehat{S}(x,y)$ using Dabrowska’s estimator. The CI of ${\widehat{\rho }}_S^H$ is estimated using the bootstrap. Again, ${\widehat{\rho }}_S^H$ is consistent for ${\rho }_S^H$ and asymptotically normal when ${\rho }_S^H\in (-1,1)$ (see Theorem A2 in the Appendix). In practice, for some extreme cases similar to those mentioned in Section 3.1 for ${\widehat{\rho }}_{S\mid {\Omega }_R}$, $\left|{\widehat{p}}_S^H\right|$ may exceed 1; when this occurs, we set it to $\text{Sign}\left({\widehat{\rho }}_S^H\right)$, and our software generates a warning.

3.3 |. Estimation of ρ_S under unbounded censoring

The estimator ${\widehat{\rho }}_S^H$ may also be used to estimate ρ_S with unbounded censoring. Under unbounded censoring, τ_X = τ_Y = ∞ by definition, and one would naturally estimate ${\widehat{\rho }}_S$ by plugging $\widehat{S}(x,y)$, ${\widehat{S}}_X(x)$, and ${\widehat{S}}_Y(y)$ into (3) in a manner similar to that described above. However, if the maximum value of X, for example, is a censored event (i.e., Δ_X = 0), then $\widehat{S}(dx,dy)$ will not sum to 1 resulting in improper integration when using plug-in estimators in (3). A workaround is to assign the remaining mass (which is typically very little) to a point just beyond the largest observed event time of X and set τ_X to this point. We then estimate ρ_S with ${\widehat{\rho }}_S^H$. Although in this setting, τ_X is no longer fixed but unbounded, estimation of ρ_S in this manner performs well (see Section 4). Under unbounded censoring, ${\widehat{\rho }}_S^H$ is consistent for ρ_S and asymptotically normal when ρ_S ∈ (−1, 1) (see Theorem A3 in the Appendix).

4 |. SIMULATIONS

4.1 |. Simulation set-up

We performed several simulations to investigate the finite sample performance of our estimators. The random variables T_X and T_Y were simulated using various choices of copula families and parameters. Specifically, following Fan et al. (2000), we simulated dependent random uniform variables, U and V, from Clayton’s and Frank’s copula families; both copulas are defined by a single parameter, θ. The dependence between U and V was specified by choosing the parameter θ in such a way that the true Spearman’s correlation varied among no correlation (ρ_S = 0), moderate correlation (ρ_S = −0.2 and 0.2 for Frank’s family and 0.2 for Clayton’s family), and strong correlation (ρ_S = −0.6 and 0.6 for Frank’s family and 0.6 for Clayton’s family). (Clayton’s family does not permit negative correlation.) We then set T_X = −log(1 − U) and T_Y = −log(1 − V) such that T_X and T_Y were exponentially distributed with mean 1.

Four types of censoring scenarios were implemented: (1) unbounded univariate, (2) unbounded bivariate, (3) generalized type I univariate, and (4) generalized type I bivariate. Each censoring scenario was implemented for censoring proportions P_C = {0.3, 0.7}. Bivariate unbounded censoring times C_X and C_Y for each observation were simulated independently from an exponential distribution, Pr(C_X ≤ t) = Pr(C_Y ≤ t) = 1 − e^−λt, with λ = P_C/(1 − P_C). The event times T_X and T_Y were censored if T_X > C_X and T_Y > C_Y, respectively. Univariate unbounded censoring was implemented in a similar manner except only one censoring event was generated per (T_X, T_Y) pair. For generalized type I censoring, $C_X^{*}$ and $C_Y^{*}$, were first simulated as described above with probability P_C and then C_X and C_Y were defined as ($C_X^{*}$, τ_X) and ($C_Y^{*}$, τ_Y), respectively, with τ_X = τ_Y set at the median survival time, $S_X^{-1}(0.5)=S_Y^{-1}(0.5)$. The resulting censoring proportions for generalized type I censoring were therefore higher than P_C: for example, for generalized type I bivariate censoring with P_C = 0.3 and 0.7, the outcomes were censored for approximately 56% and 73% of observations, respectively.

We evaluated the performance of ${\widehat{\rho }}_S^H$ and ${\widehat{\rho }}_{S\mid {\Omega }_R}$ in the presence of unbounded and generalized type I censoring using a sample size of 200 for strong, moderate, and no correlation. For unbounded censoring, the population parameter of ${\rho }_S^H$ is the same as ρ_S. For generalized type I censoring, the population parameters of ${\rho }_S^H$ and ${\rho }_{S\mid {\Omega }_R}$ were the same as ρ_S for Clayton’s family. For Frank’s family with the overall Spearman’s correlation of −0.6, −0.2, 0.2, and 0.6, the population parameters of ${\rho }_{S\mid {\Omega }_R}$ were −0.098, −0.042, 0.058, and 0.261; and the population parameters of ${\rho }_S^H$ were −0.512, −0.173, 0.180, and 0.545. These population parameters were empirically estimated with a sample size of 10⁶.

The bias, root mean squared error (RMSE), type I error rate, and power, computed as the proportion of times that bootstrap CIs (based on 1000 bootstrap samples) did not include zero, were also evaluated for sample sizes of 100 and 200 under unbounded censoring for moderate and no correlation. The performance of ${\widehat{\rho }}_S^H$ was compared to estimator ${\widehat{\rho }}_{IMI}$ proposed by Schemper et al. (2013) for these simulation scenarios. We also evaluated the performance of ${\widehat{\rho }}_S^H$ as an estimator of ρ_S using survival surfaces proposed by Lin and Ying (1993) and Campbell (1981).

Lastly, we did some additional comparisons of ${\widehat{\rho }}_S^H$ to semiparametric estimators ${\widehat{\rho }}_{IMI}$ and ${\widehat{\rho }}_S^{MLE}$ (maximum likelihood estimator assuming Frank’s copula dependency structure). These comparisons were made in the context of a well-behaved dependency structure induced by Frank’s copula and in the context of a complex dependency structure, a mixture of 60% highly negatively correlated data (ρ_S = −0.8, Frank’s copula with θ = −8) and 40% perfectly correlated data (ρ_S = 1) with the overall Spearman’s correlation being about −0.0813. This simulation scenario was loosely motivated by data from site B in our real data analysis presented in Section 5; Supplementary Figure S5 shows the scatter plot of the uncensored data. Sample sizes of 200, 500, and 1000 were used and unbounded univariate censoring with P_C = 0.5 was applied as described above. The goal of these comparisons was to show better efficiency of ${\widehat{\rho }}_S^{MLE}$ compared to ${\widehat{\rho }}_S^H$ under a correctly specified model and to demonstrate greater accuracy of ${\widehat{\rho }}_S^H$ compared to ${\widehat{\rho }}_{IMI}$ and ${\widehat{\rho }}_S^{MLE}$ under model misspecification.

All simulations used 1000 replications.

4.2 |. Simulation results

Figure 4 shows the mean point estimates and the 0.025th and 0.975th quantiles of estimators ${\widehat{\rho }}_S^H$ under unbounded censoring (row 1), the semiparametric estimator ${\widehat{\rho }}_{IMI}$ proposed by Schemper et al. (2013) under unbounded censoring (row 2), ${\widehat{\rho }}_S^H$ under generalized type I censoring (row 3), and ${\widehat{\rho }}_{S\mid {\Omega }_R}$ under generalized type I censoring (row 4). The sample size was 200, the censoring was bivariate with varying censoring proportions, and ${\widehat{\rho }}_S^H$ and ${\widehat{\rho }}_{S\mid {\Omega }_R}$ were computed using Dabrowska’s survival surface estimator.

FIGURE 4.

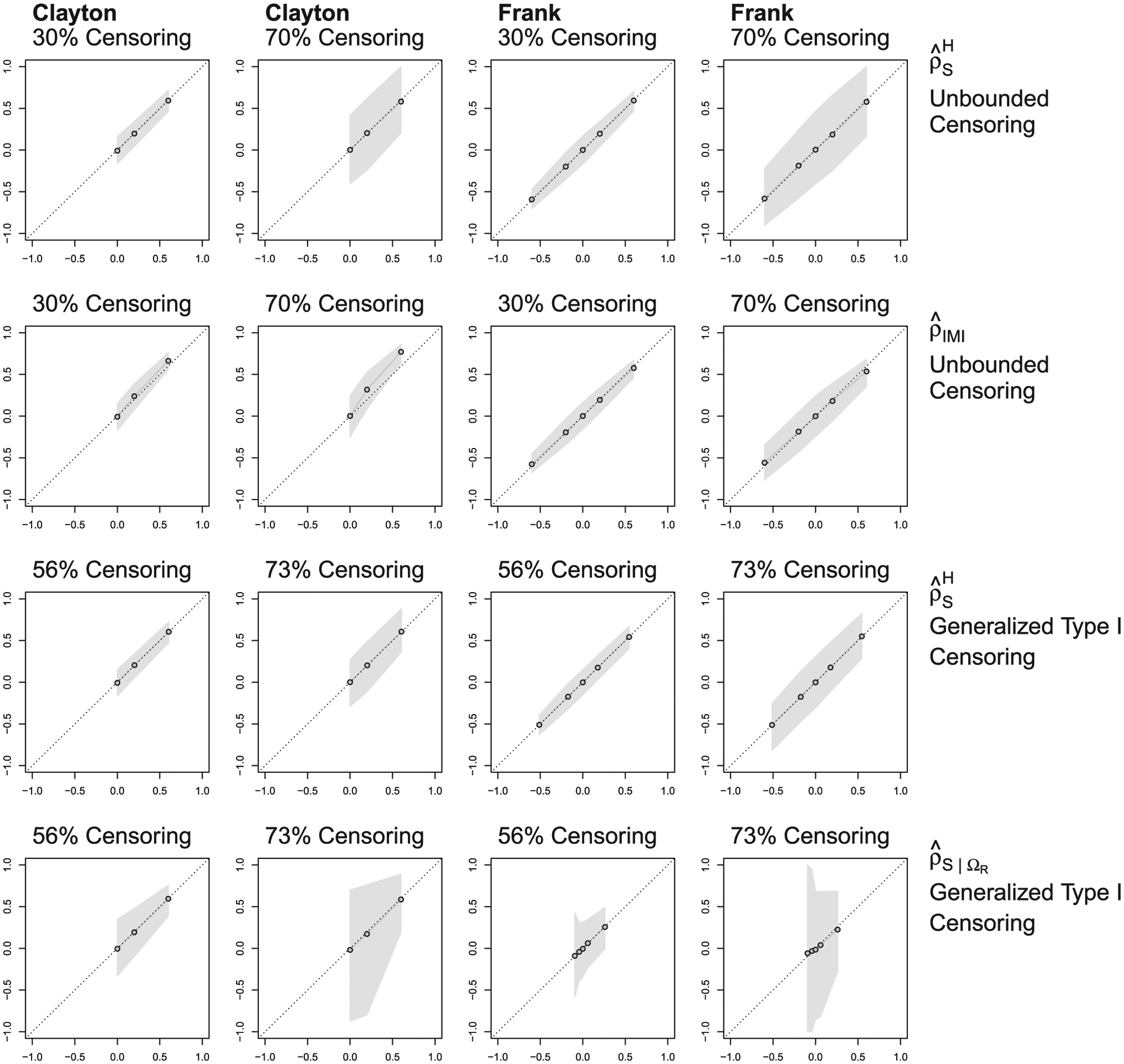
Point estimates (X-axis) vs population parameters (Y-axis) under different bivariate censoring scenarios. The top and second rows are ${\widehat{\rho }}_S^H$ and ${\widehat{\rho }}_{IMI}$ as estimators of the overall Spearman’s correlation, ρ_S. The third row is ${\widehat{\rho }}_S^H$ as an estimator of ${\rho }_S^H$. The bottom row is ${\widehat{\rho }}_{S\mid {\Omega }_R}$ as an estimator of ${\rho }_{S\mid {\Omega }_R}$. The columns represent Clayton’s and Frank’s copulas. The population parameters for Clayton’s family are 0, 0.2, and 0.6 for all estimates. For Frank’s family, the population parameters of ρ_S are −0.6, −0.2, 0.2, and 0.6; the population parameters of ${\rho }_S^H$ are −0.512, −0.173, 0.180, and 0.545; the population parameters of ${\rho }_{S\mid {\Omega }_R}$ are −0.098, −0.042, 0.058, and 0.261. The dots are the mean point estimates based on 1000 simulations. The shaded areas represent the 0.025th and 0.975th quantiles. For generalized type I censoring, the restricted region, Ω_R, was defined by the median survival times

For Clayton’s and Frank’s families under unbounded censoring (row 1), the mean of ${\widehat{\rho }}_S^H$ was very close to the true population parameter verifying the consistency of ${\widehat{\rho }}_S^H$ for ρ_S. When data were generated under Frank’s copula, the semiparametric estimator, ${\widehat{\rho }}_{IMI}$ (row 2), was similarly unbiased for unbounded censoring, and it tended to be less variable than ${\widehat{\rho }}_S^H$. However, when data were generated using Clayton’s copula, ${\widehat{\rho }}_{IMI}$ was biased for ρ_S, also noted by Schemper et al. (2013).

Supplementary Tables S1 and S2 provide more details and additional comparisons between ${\widehat{\rho }}_{IMI}$ and ${\widehat{\rho }}_S^H$ under unbounded censoring for different sample sizes and censoring proportions in terms of bias, RMSE, type I error rate and power. In short, the bias of ${\widehat{\rho }}_S^H$ for ρ_S was low, even with fairly small numbers of events; both the bias and RMSE decreased as the number of events increased. In general, ${\widehat{\rho }}_S^H$ compared favorably to ${\widehat{\rho }}_{IMI}$.

Under generalized type I censoring (the third and fourth rows of Figure 4), the means of ${\widehat{\rho }}_S^H$ and ${\widehat{\rho }}_{S\mid {\Omega }_R}$ are very close to their true population parameters, suggesting with n = 200, these estimators are essentially unbiased for ${\rho }_S^H$ and ${\rho }_{S\mid {\Omega }_R}$ respectively. The variance of our estimators naturally increased as the probability of censoring increased. The variance of ${\widehat{\rho }}_{S\mid {\Omega }_R}$ was greater than that of ${\widehat{\rho }}_S^H$ under generalized type I censoring (rows 3 and 4), presumably because ${\widehat{\rho }}_{S\mid {\Omega }_R}$ only uses the events inside Ω = Ω_R, whereas ${\widehat{\rho }}_S^H$ assigns probability mass to values outside of Ω. Note that the variance of ${\widehat{\rho }}_S^H$ under unbounded censoring was slightly larger than that under generalized type I censoring in spite of the lighter censoring. This is probably because under generalized type I censoring, the probability mass, ${\widehat{S}}^H(dx,dy)$, calculated outside of Ω is concentrated on the same points, making its variance smaller compared to the case of unbounded censoring. Results for univariate censoring were very similar to those for bivariate censoring, except the estimators were slightly less variable (see Supplementary Figure S1).

With unbounded censoring of 50% and n = 200, the correctly specified semiparametric ${\widehat{\rho }}_S^{MLE}$ was more efficient than ${\widehat{\rho }}_S^H$ (relative efficiency in terms of variance ranging from 1.19 (for ρ_S = 0) to 1.60 (for ρ_S = 0.6), Supplementary Figure S4); both approaches yielded unbiased estimates of ρ_S. In contrast, when data were generated using a mixture of positively and negatively correlated bivariate distributions, the misspecified semiparametric estimators ${\widehat{\rho }}_S^{MLE}$ and ${\widehat{\rho }}_{IMI}$ were substantially biased and this bias did not decrease with increasing sample size. On the other hand, the nonparametric ${\widehat{\rho }}_S^H$ was unbiased for ρ_S (see Supplementary Figure S6). In this more complicated setting, estimates of ${\rho }_{S\mid {\Omega }_R}$ with Ω_R being defined using the median survival times were also unbiased (Supplementary Figure 7).

The simulations reported above incorporated 1000 bootstrap replications; in general, CI coverage and width were stable and adequate with as few as 200 bootstrap replications (see Supplementary Figure S8).

We also evaluated the performance of ${\widehat{\rho }}_S^H$ with survival surfaces of Campbell (1981) for univariate and bivariate censoring and of Lin and Ying (1993) for univariate censoring only (see Supplementary Figures S2 and S3). With univariate censoring, using the estimator of Lin and Ying (1993) resulted in unbiased estimation although with larger variance than that using Dabrowska’s estimator. Estimator ${\widehat{\rho }}_S^H$ computed using the survival surface estimator of Campbell (1981) was visibly biased for the sample size of 200 under heavy censoring.

5 |. APPLICATION

We apply our methods to a study of 6691 HIV-positive adults starting ART in Latin America. We are interested in estimating the correlation between two right-censored variables: (1) the time from ART initiation to viral failure and (2) the time from ART initiation to major regimen change. Patients experience viral failure when the amount of virus circulating in their blood (their viral load) is above a certain threshold, which may make them infectious and vulnerable to HIV-related diseases. Viral failure may be caused by many factors including poor adherence or drug resistance; it often triggers changing a patient’s ART regimen. However, patients may also change their ART regimens for reasons other than viral failure (e.g., poor tolerability, discovery of a simpler regimen, or patient/provider choice).

Our study uses data from the Caribbean, Central, and South America network for HIV Epidemiology (CCASAnet). The definitions of viral failure and regimen change were the same as those used in a prior CCASAnet study (Cesar et al., 2015; CCASAnet, 2020). In short, viral failure was defined as a single viral load > 1000 copies/mL or two viral loads > 400 copies/mL after a person’s virus had been suppressed or they had been on ART long enough that it should have been suppressed (i.e., 6 months). Regimen change was limited to major changes such that the patient switched drug classes or changed multiple drugs. Each study subject may have had one, both, or neither of these events. Follow-up ended at the last clinic visit; censoring was univariate. Our analysis data set includes patients from Brazil, Chile, Honduras, Mexico, and Peru; sites have been anonymized for presentation. After a median follow-up of 4.1 years (ranging from 1 day to 18.2 years), 1916 persons (28.6%) had a viral failure and 1895 persons (28.3%) changed regimens. Approximately 16.1% of patients had both events over the follow-up period, 12.2% changed regimens but did not have viral failure, 12.5% had viral failure but did not change regimens, and 59.1% were not observed to have either event. The upper left panel of Figure 5 shows Kaplan–Meier estimates for the marginal probabilities of viral failure and regimen change as a function of time since ART initiation. Ten years after ART initiation, the estimated probability of not having viral failure was 0.58 and the estimated probability of remaining on the initial regimen was 0.51. The upper right panel shows the estimated joint bivariate probability mass function, ${\widehat{S}}^H(dx,dy)$, based on Dabrowska’s estimator; estimated marginal probability mass functions, ${\widehat{S}}_X^H(dx)$ and ${\widehat{S}}_Y^H(dy)$, are also included. Note that because a large proportion of patients experienced only one or neither event, a large amount of mass has been assigned to τ_X = 18 and τ_Y = 17 years.

FIGURE 5.

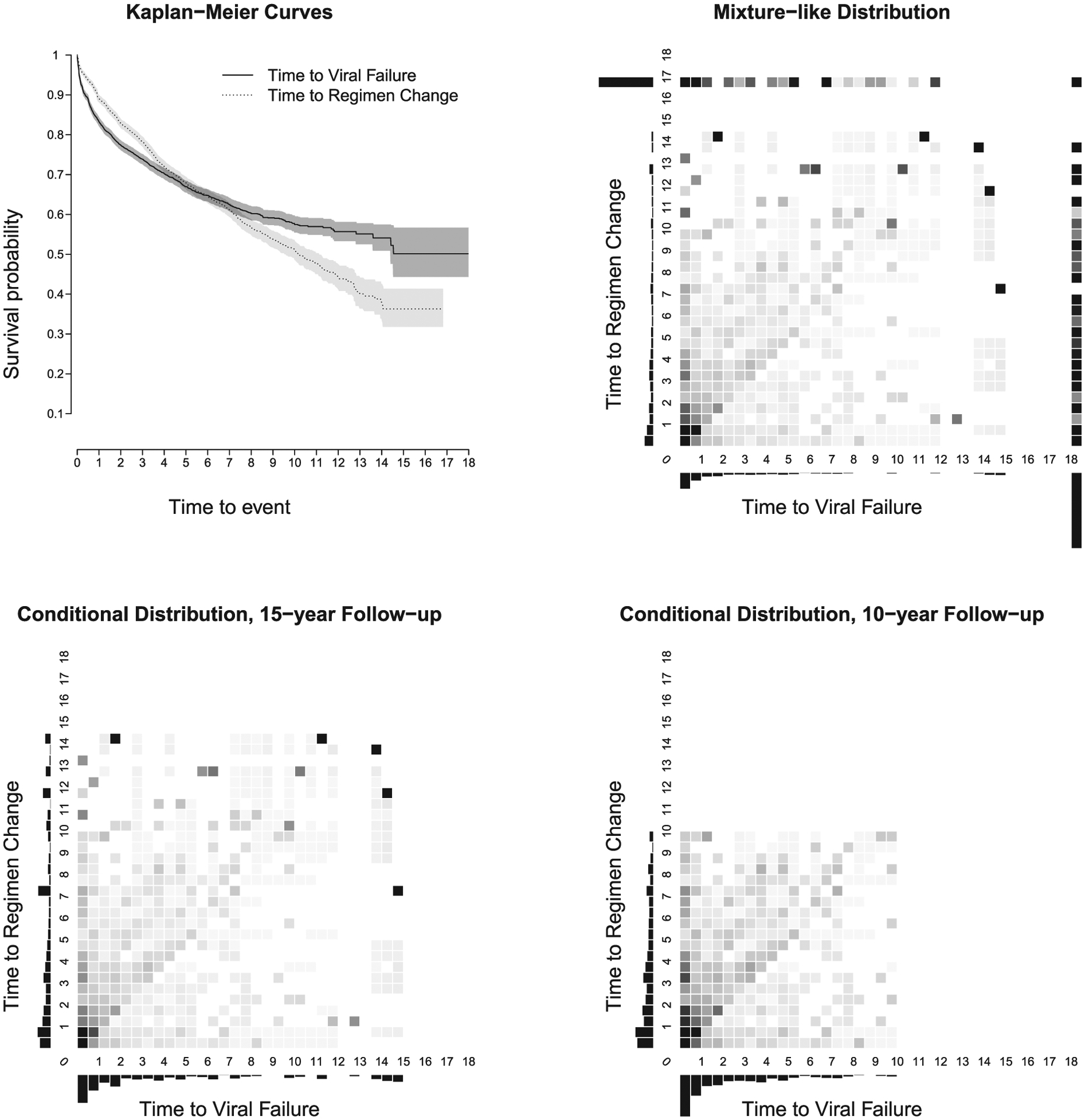
Upper left: Kaplan–Meier curves for time to viral failure and time to regimen change, where time is measured in years. Upper right: bivariate probability mass function for the mixture-like distribution, ${\widehat{S}}^H(dx,dy)$. Lower left: conditional bivariate probability mass function for 15-year follow-up. Lower right: conditional bivariate probability mass function for 10-year follow-up. For probability mass functions, the bars on the left and on the bottom represent histograms of the univariate survival mass for each event. The probability mass function was computed from the Dabrowska’s survival surface and then aggregated over half-year bivariate time periods. After aggregation, any negative values were set to 0. Lighter shade represents smaller values

The estimated highest rank correlation, ${\widehat{\rho }}_S^H$, between time to viral failure and time to regimen change was 0.35 with a 95% CI based on 1000 bootstrap replications of 0.27 to 0.44. This result is fairly similar, albeit with a wider CI, to the estimator of Schemper et al., ${\widehat{\rho }}_{IMI}$, that imputes censored values: 0.37, 95% CI = [0.33, 0.41].

The estimated rank correlation over the restricted region, ${\widehat{\rho }}_{S\mid {\Omega }_R}$, with Ω_R = [0, 15) × [0, 15) was substantially higher, 0.65, with a wide 95% CI = [0.30, 0.97]. This can be explained by a careful look at the conditional probability mass over Ω_R (lower left plot of Figure 5). Notice that there are several points in the upper right corner of this surface with large probability mass. Large amounts of mass are assigned to these points because a few events occurred at later follow-up times when there were fairly small numbers of patients remaining in the risk set. This is also seen in the Kaplan–Meier estimates, where relatively large drops in the marginal survival curves are noted between 10 and 15 years. These points pushed the probability mass function closer to the diagonal, leading to a larger estimated rank correlation. In addition, since there were only a few points with substantial probability mass, their inclusion/exclusion in various bootstrap samples led to wide variation in CIs. This example serves as a nice illustration of the potential perils of estimating rank correlations over restricted regions that include tail areas with small numbers of events. Perhaps a more reliable rank correlation would be over the restricted region, Ω_R = [0, 10) × [0, 10), in which case ${\widehat{\rho }}_{S\mid {\Omega }_R}$ was 0.26 (95% CI = [0.17, 0.36]); the lower right plot of Figure 5 shows the conditional probability mass over this smaller region.

In addition to showing estimates of overall correlation, Table 1 shows estimates based on sex and study site. For the most part, ${\widehat{\rho }}_S^H$ is fairly close to ${\widehat{\rho }}_{IMI}$, except for those sites with small sample sizes (i.e., A, B, and D). Rank correlations over the restricted region, ${\widehat{\rho }}_{S\mid {\Omega }_R}$ with Ω_R = [0, 15) × [0, 15) were generally more variable and typically higher than those over Ω_R = [0, 10) × [0, 10).

TABLE 1.

Correlation of time to viral failure and time to regimen change in CCASAnet cohort measured using three estimators: ${\widehat{\rho }}_S^H$, ${\widehat{\rho }}_{S\mid {\Omega }_R}$, and ${\widehat{\rho }}_{IMI}$. n is the number of subjects for each subgroup. Columns P_VR, $P_{\overline{V}R}$, $P_{V\overline{R}}$, and $P_{\overline{VR}}$ show the percent of subjects having both events (P_VR), having regimen change event but censored viral failure ($P_{\overline{V}R}$), having viral failure event but censored regimen change ($P_{V\overline{R}}$), and having both events censored ($P_{\overline{VR}}$). For ${\widehat{\rho }}_S^H$ and ${\widehat{\rho }}_{S\mid {\Omega }_R}$, the numbers inside brackets are 95% confidence intervals (CIs) estimated from 1000 bootstrap samples. Column ${\widehat{\rho }}_{IMI}$ shows the estimates of Schemper et al. (2013) and their CIs

Subgroup	n	P VR	$P_{\overline{V}R}$	$P_{V\overline{R}}$	$P_{\overline{VR}}$	${\widehat{\rho }}_S^H$	${\widehat{\rho }}_{S|{\Omega }_R}=\left[0,15\right)\times \left[0,15\right)$	${\widehat{\rho }}_{S|{\Omega }_R}=\left[0,10\right)\times \left[0,10\right)$	${\widehat{\rho }}_{IMI}$
All	6691	16.1	12.2	12.5	59.1	0.35 [0.27, 0.44]	0.65 [0.30, 0.97]	0.26 [0.17, 0.36]	0.37 [0.33, 0.41]
Male	5185	14.8	12.0	12.3	60.9	0.32 [0.22, 0.42]	0.57 [0.14, 1.00]	0.32 [0.18, 0.44]	0.36 [0.30, 0.41]
Female	1506	20.7	13.1	13.3	52.9	0.45 [0.30, 0.57]	0.70 [0.20, 1.00]	0.13 [−0.04, 0.32]	0.40 [0.32, 0.48]
A	1040	19.2	23.0	11.5	46.2	−0.06 [−0.21, 0.30]	0.73 [−0.24, 1.00]	0.19 [0.03, 0.34]	0.26 [0.00, 0.37]
B	975	13.7	16.3	11.9	58.1	0.52 [0.14, 0.74]	−0.39 [−0.54, 0.41]	−0.43 [−1.00, 0.08]	0.25 [0.10, 0.38]
C	2225	8.9	5.5	12.1	73.4	0.45 [0.37, 0.53]	0.69 [0.42, 0.93]	0.58 [0.34, 0.80]	0.55 [0.43, 0.66]
D	138	18.1	17.4	10.1	54.3	−0.18 [−0.53, 0.44]	0.21 [−1.00, 1.00]	0.50 [−0.09, 0.96]	0.29 [0.00, 0.55]
E	2313	22.4	11.8	13.8	51.9	0.45 [0.36, 0.53]	0.42 [0.10, 0.73]	0.17 [−0.01, 0.34]	0.36 [0.30, 0.42]

6 |. DISCUSSION

We have proposed two nonparametric methods of quantifying correlation with bivariate right-censored data. One estimator, ${\widehat{\rho }}_{S\mid {\Omega }_R}$ computes Spearman’s correlation within a restricted region. The other estimator, ${\widehat{\rho }}_S^H$, computes Spearman’s correlation for an estimable bivariate distribution, which is analogous to assigning data censored beyond the estimable region to the highest rank values. Under unbounded censoring, ${\widehat{\rho }}_S^H$ is consistent for the overall Spearman’s correlation. Under generalized type I censoring, with the majority of events happening in the restricted region, ${\widehat{\rho }}_S^H$ can be viewed as an approximation of the overall Spearman’s correlation. Because our methods assume neither marginal nor joint parametric distributions, they have potential advantages over parametric and semiparametric methods.

The main limitations of our estimators stem from challenges with nonparametrically estimating the bivariate survival surface. The first challenge is that with generalized type I censoring, the bivariate survival surface, and hence Spearman’s rank correlation ρ_S, cannot be identified beyond the region of data support without parametric assumptions. Hence, our inference targets were the estimable parameters, ${\rho }_{S\mid {\Omega }_R}$ and ${\rho }_S^H$. Although under generalized type I censoring they do not equal the overall Spearman’s correlation, both parameters have sensible interpretations. The alternative, using parametric and semiparametric models to estimate Spearman’s correlation—an inherently nonparametric statistic— has other limitations. Parametric and semiparametric approaches assume a dependency structure; and as seen in our simulations, semiparametric estimators such as ${\widehat{\rho }}_{IMI}$ proposed by Schemper et al. (2013), may be biased when the dependency structure is misspecified. In addition, they implicitly assume that the dependency structure outside the region of observation is the same as that seen inside the observation region. Although in the real data example, ${\widehat{\rho }}_{IMI}$ appeared more stable than our nonparametric estimators, particularly for small sample sizes, with complex real data there is a real possibility of model misspecification. As with most statistics, there may be settings where one might prefer the nonparametric estimators over the semiparametric estimators, or vice versa.

The second challenge is that even in regions where the bivariate survival curve is identifiable, nonparametric estimators of the survival surface may have negative mass, which leads to potential downstream problems with estimation of ${\rho }_{S\mid {\Omega }_R}$ and ${\rho }_S^H$. Researchers have grappled with nonparametric approaches to avoid negative mass, for example, van der Laan (1996). Thankfully, in our simulations, only a minor proportion of our estimates encountered problems due to negative mass, the problems go away as the numbers of events increase, and there are typically workaround solutions that appear to behave reasonably.

In our approach we considered a rectangular restricted region, [0, τ_X] × [0, τ_Y]. An anonymous associate editor correctly pointed out that the top right corner of this rectangle is not always identifiable nonparametrically. Alternatively, one could consider defining estimators using the identifiable region Ω_R = {(t_X, t_Y) : T_X,i ≥ t_X, T_Y,i ≥ t_Y for some subject i} (see Prentice and Zhao, 2019). Although this idea is intriguing, we decided to keep the definition of Ω_R as [0, τ_X] × [0, τ_Y] due to easier interpretation. Note that Dabrowska’s estimator can be computed and is consistent for all points inside [0, τ_X] × [0, τ_Y].

Another limitation of our method is its computational time complexity, up to $\mathcal{O}\left(m{n}^2\right)$, where n is the sample size and m is the number of bootstrap samples. For example, on a MacBook Air with 1.7 GHz Intel Core i7, the computational time for n = 100, 200, 500, 1000 and m = 200 is approximately 0.2, 0.7, 5.1, and 30.8 min, respectively.

Although not studied here, our approaches can be directly applied to settings where only one of the variables is right censored. This special case allows nonparametric estimation of the bivariate survival surface without negative mass (Stute, 1993). In future work, we plan to study semiparametric methods for estimating covariate-adjusted partial and conditional Spearman’s correlation for bivariate survival data.

APPENDIX

Theorem A1.

Under uninformative and generalized type I censoring and for a nonempty rectangular region Ω_R such that Ω_R ⊆ Ω, ${\widehat{\rho }}_{S\mid {\Omega }_R}$ is a consistent estimator of ${\rho }_{S\mid {\Omega }_R}$. When ${\rho }_{S\mid {\Omega }_R}\in (-1,1)$, estimator ${\widehat{\rho }}_{S\mid {\Omega }_R}$ is also asymptotically normal, and the bootstrap estimation of its variance is asymptotically valid.

Proof.

The consistency of ${\widehat{\rho }}_{S\mid {\Omega }_R}$ follows from the consistency of Dabrowska’s estimator $\widehat{S}(x,y)$ in Ω under uninformative and generalized type I censoring and the fact that $\widehat{S}\left(x,y\mid {\Omega }_R\right)$ is a continuous function of $\widehat{S}(x,y)$. To prove asymptotic normality, we note that under uninformative and generalized type I censoring, $\widehat{S}(x,y)$, ${\widehat{S}}_X(x)$, and ${\widehat{S}}_Y(y)$ are Hadamard differentiable estimators that converge to Gaussian processes; see Dabrowska (1989) and van der Vaart and Wellner (1996). Because estimator ${\widehat{\rho }}_{S\mid {\Omega }_R}$ is a continuous function of $\widehat{S}(x,y)$, ${\widehat{S}}_X(x)$, and ${\widehat{S}}_Y(y)$, it follows from the chain rule that it is also Hadamard differentiable and, therefore, it is asymptotically normal by the functional delta method (van der Vaart and Wellner, 1996). In addition, its bootstrap estimator converges to the same Gaussian process as ${\widehat{\rho }}_{S\mid {\Omega }_R}$, justifying the use of the bootstrap to construct CIs (van der Vaart and Wellner, 1996). □

Theorem A2.

Under uninformative and generalized type I censoring, estimator ${\widehat{\rho }}_S^H$ is consistent. When, ${\rho }_S^H\in (-1,1)$ it is also asymptotically normal, and the bootstrap estimation of its variance is asymptotically valid.

Proof.

Similar to Theorem A1. □

Theorem A3.

Under uninformative and unbounded censoring, ${\widehat{\rho }}_S^H$ is a consistent estimator of the overall Spearman’s correlation, ρ_S. Estimator ${\widehat{\rho }}_S^H$ is also asymptotically normal when ρ_S ∈ (−1, 1), and the bootstrap estimation of its variance is asymptotically valid.

Proof.

When the maximum of X and Y are observed events, then ${\widehat{S}}^H(x,y)=\widehat{S}(x,y)$, so the consistency of ${\widehat{\rho }}_S^H$ for ρ_S follows from the consistency of Dabrowska’s estimator and the continuous mapping theorem. When the maximum of either X or Y is censored, the plug-in estimator of (9), ${\widehat{\rho }}_S^H$, can be defined as a sum of four terms A, B, C, and D that are functions of the joint and conditional survival surface estimators (Theorem A.1, Supplementary Appendix). Because of Lemma A.1 (Supplementary Appendix), B, C, $D\stackrel{p}{\to }0$ and $A\stackrel{p}{\to }{\rho }_S$. The proofs of the asymptotic normality and bootstrap validity are similar to Theorem A1. □

DATA AVAILABILITY STATEMENT

The deidentified data used in this article are openly available at https://biostat.app.vumc.org/ArchivedAnalyses.