A Systems-Neuroscience Model of Phasic Dopamine

Abstract

We describe a neurobiologically informed computational model of phasic dopamine signaling to account for a wide range of findings, including many considered inconsistent with the simple reward prediction error (RPE) formalism. The central feature of this PVLV framework is a distinction between a Primary Value (PV) system for anticipating primary rewards (USs), and a Learned Value (LV) system for learning about stimuli associated with such rewards (CSs). The LV system represents the amygdala, which drives phasic bursting in midbrain dopamine areas, while the PV system represents the ventral striatum, which drives shunting inhibition of dopamine for expected USs (via direct inhibitory projections) and phasic pausing for expected USs (via the lateral habenula). Our model accounts for data supporting the separability of these systems, including individual differences in CS-based (sign-tracking) vs. US-based learning (goal-tracking). Both systems use competing opponent-processing pathways representing evidence for and against specific USs, which can explain data dissociating the processes involved in acquisition vs. extinction conditioning. Further, opponent processing proved critical in accounting for the full range of conditioned inhibition phenomena, and the closely-related paradigm of second-order conditioning. Finally, we show how additional separable pathways representing aversive USs, largely mirroring those for appetitive USs, also have important differences from the positive valence case, allowing the model to account for several important phenomena in aversive conditioning. Overall, accounting for all of these phenomena strongly constrains the model, thus providing a well-validated framework for understanding phasic dopamine signaling.

Introduction

Phasic dopamine signaling plays a well-documented role in many forms of learning (e.g., Wise, 2004) and understanding the mechanisms involved in generating these signals is of fundamental importance. The temporal differences (TD) framework (Sutton & Barto, 1981, 1990, 1998), building on the reward prediction error (RPE) theory of Rescorla and Wagner (1972), provided a major advance by formalizing phasic dopamine signals in terms of continuously computed RPEs (Montague, Dayan, & Sejnowski, 1996; Schultz, Dayan, & Montague, 1997). To summarize this dopamine reward prediction error hypothesis (DA-RPE; Glimcher, 2011), the occurrence of better than expected reward outcomes produces brief, short-latency increases in dopamine cell firing (phasic bursts), while worse than expected outcomes produce corresponding phasic decreases (pauses/dips) relative to a tonic firing baseline. These punctate error signals have been shown to function as temporally precise teaching signals for Pavlovian and instrumental learning, and are widely believed to play an important role in the acquisition and performance of many higher cognitive functions including: action selection (Frank, 2006), sequence production (Suri & Schultz, 1998), goal-directed behavior (Goto & Grace, 2005), decision making (Doll & Frank, 2009; St Onge & Floresco, 2009; Takahashi, Matsui, Camerer, Takano, Kodaka, Ideno, Okubo, Takemura, Arakawa, Eguchi, Murai, Okubo, Kato, Ito, & Suhara, 2010), and working memory manipulation (O’Reilly & Frank, 2006; Rieckmann, Karlsson, Fischer, & Backman, 2011).

Despite the well-documented explanatory power of this simple idea, it has become increasingly clear that a more nuanced understanding is needed, as there are many aspects of dopamine cell firing that are hard to reconcile within a simple RPE formalism. For example, dopamine cell bursting has long been known to occur robustly at both CS- and US-onset for a period of time early in training (Ljungberg, Apicella, & Schultz, 1992). Moreover, recent work suggests that as the delay between CS-onset and US-onset increase beyond a few seconds, dopamine cell bursting at the time of the US diminishes progressively less until it is statistically indistinguishable from the response to randomly delivered reward, even after a task has been thoroughly learned (Fiorillo, Newsome, & Schultz, 2008; Kobayashi & Schultz, 2008). In contrast, CS firing is acquired relatively robustly across these same delays, albeit less so as a function of increasing delay (i.e., flatter decay slope; Fiorillo et al., 2008; Kobayashi & Schultz, 2008).

More subtle anomalies include the asymmetrical pattern seen for earlier than expected versus later than expected rewards (Hollerman & Schultz, 1998); and certain aspects of the conditioned inhibition paradigm, including the lack of a RPE-like dopamine response at the time of omitted reward when a conditioned inhibitor is presented alone at test (Tobler, Dickinson, & Schultz, 2003). Further, extinction learning and related reacquisition phenomena have been shown to involve additional learning mechanisms beyond those involved in initial acquisition, suggesting the likelihood of additional wrinkles in the pattern of dopamine signaling involved. Finally, the pattern of phasic dopamine signaling seen under aversive conditioning paradigms is not a simple mirror-image of the appetitive case, with evidence for heterogeneous sub-populations of dopamine neurons that respond to primary aversive outcomes in opposite ways (Brischoux, Chakraborty, Brierley, & Ungless, 2009; Bromberg-Martin, Matsumoto, & Hikosaka, 2010b; Lammel, Lim, Ran, Huang, Betley, Tye, Deisseroth, & Malenka, 2012; Lammel, Lim, & Malenka, 2014; Matsumoto & Hikosaka, 2009a; Fiorillo, 2013). In addition, a long-standing controversy has surrounded the phasic bursting often seen for aversive and/or high intensity stimulation (e.g., Mirenowicz & Schultz, 1996; Horvitz, 2000; Fiorillo, 2013; Schultz, 2016; Comoli, Coizet, Boyes, Bolam, Canteras, Quirk, Overton, & Redgrave, 2003; Dommett, Coizet, Blaha, Martindale, Lefebvre, Walton, Mayhew, Overton, & Redgrave, 2005; Humphries, Stewart, & Gurney, 2006), which has been interpreted as a component of salience or novelty-coding in addition to simple RPE-coding (Kakade & Dayan, 2002).

Such departures from the simple RPE formalism should not be surprising, however, since it is an abstract, mathematical formalism corresponding to David Marr’s (1982) algorithmic, or even computational, level of analysis. Thus, the present work can be seen as an attempt to bridge between the biological mechanisms at Marr’s implementational level and the higher-level RPE formalism, providing specific testable hypotheses about how the critical elements of that formalism arise from interactions among distributed brain systems, and the ways in which these neural systems diverge from the simpler high-level formalism. There is an important need for this bridging between levels of analysis, because the neuroscience literature has implicated a large and complex network of brain areas as involved in dopamine signaling, but understanding the precise functional contributions of these diverse areas, and their interrelationships, is difficult without being able to see the interacting system function as a whole. The computational modeling approach provides this ability, and the ability to more systematically test and manipulate areas to determine their precise contributions to a range of different behavioral phenomena. Furthermore, the considerable divergences between appetitive (reward-defined) and aversive (punishment-defined) processing are particularly challenging and informative, because the same networks of brain areas are involved in both to a large extent, and the abstract RPE formalism makes no principled distinction between them. Thus, our biologically-based model can help provide new principles that make sense of these discrepancies, in ways that could be of interest to those working at the higher abstract levels.

There have been various attempts to develop more detailed neurobiological frameworks for understanding phasic dopamine function (e.g., Houk, Adams, & Barto, 1995; Brown, Bullock, & Grossberg, 1999; Suri & Schultz, 1999, 2001; O’Reilly, Frank, Hazy, & Watz, 2007; Redish, Jensen, Johnson, & Kurth-Nelson, 2007; Tan & Bullock, 2008; Hazy, Frank, & O’Reilly, 2010; Vitay & Hamker, 2014; Carrere & Alexandre, 2015), which we build upon here to provide a comprehensive framework that accounts for the above-mentioned empirical anomalies to the simple RPE formalism while also incorporating most of the major biological elements identified to date. This framework builds on our earlier PVLV model (Primary Value, Learned Value; pronounced “Pavlov”) (O’Reilly et al., 2007; Hazy et al., 2010), and includes mechanistically explicit models of the following major brain systems: the basolateral amygdalar complex (BLA); central amygdala (lateral and medial segments: CEl & CEm); pedunculopontine tegmentum (PPTg); ventral striatum (VS, including the Nucleus Accumbens, NAc); lateral habenula (LHb); and of course the midbrain dopaminergic nuclei themselves (ventral tegmental area, VTA; and substantia nigra, pars compacta, SNc). These areas are driven by simplified inputs representing the brain systems encoding appetitive and aversive USs, CSs, variable contexts, and temporally-evolving working memory-like representations of US-defined goal-states mapped to ventral-medial frontal cortical areas, primarily the orbital frontal cortex (OFC).

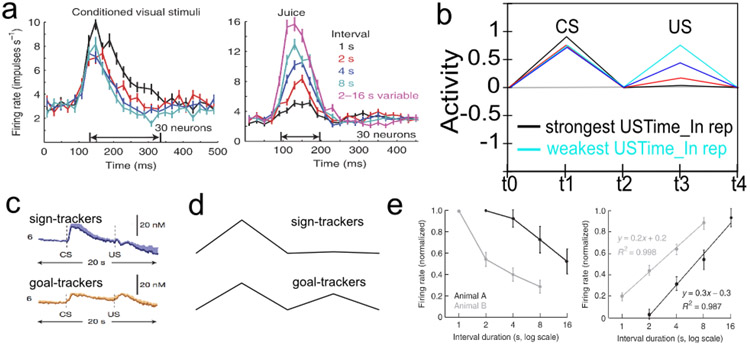
Our overall goal is to provide a single comprehensive framework for understanding the full scope of phasic dopamine firing across the biological, behavioral, and computational levels. Although the model is considerably more complex than the single equation at the heart of the RPE framework, it nevertheless is based on two core computational principles that together determine much of its overall function — many more details are required to account for critical biological data, but these are all built upon the foundation established by these core computational principles. The basic learning equations are consistent with the classic Rescorla-Wagner / delta rule framework (Rescorla & Wagner, 1972), but the first core computational principle is that two separate systems are needed to enable this form of learning to account for both the anticipatory nature of dopamine firing (at the time of a CS, which occurs in the LV or learned-value system, associated with the amygdala), and the discounting of expected outcomes at the time of the US (in the PV or primary-value system, associated with the ventral striatum). These two systems give the PVLV model its name, and have remained the central feature of the framework since its inception (O’Reilly et al., 2007; Hazy et al., 2010). The recent discovery of strong individual differences in behavioral phenotypes, termed sign-tracking (CS-focused learning and behavior) vs. goal-tracking (US-focused learning and behavior) is suggestive of this kind of anatomical dissociation (Flagel, Robinson, Clark, Clinton, Watson, Seeman, Phillips, & Akil, 2010; Flagel, Clark, Robinson, Mayo, Czuj, Willuhn, Akers, Clinton, Phillips, & Akil, 2011).

The second core computational principle, which cuts across both the LV and PV systems in our model, is the use of opponent-processing pathways based on the reciprocal functioning of dopamine D1 versus D2 receptors (Mink, 1996; Frank, Loughry, & O’Reilly, 2001; Frank, 2005; Collins & Frank, 2014). The value of opponent-processing has long been recognized, in terms of enabling fundamentally relative (instead of absolute) comparisons (e.g., in color vision), and allowing more flexible forms of learning, for example learning a broad positive association with specific negative exceptions. Furthermore, the dopamine modulation of these pathways supports both the opposite valence-orientation of appetitive vs. aversive conditioning, as well as acquisition vs. extinction learning, across both systems. The importance of this opponent-processing framework is particularly evident in the extinction learning case, where the context-specificity of extinction can be understood as the learning of context-specific exceptions in the opponent pathway relative to the retained initial association.

Thus, it is important to appreciate that we did not just add biological mechanisms in an ad-hoc manner to account for specific data — our goal was to simplify and exploit essential computational mechanisms, while remaining true to the known biological and behavioral data. As the famous saying attributed to Einstein goes: “Everything should be made as simple as possible, but not simpler” — here we weigh heavier on the “but not simpler” part of things relative to the abstract RPE framework and associated models, in order to account for relevant biological data. Nevertheless, neuroscientists may still regard our models as overly abstract and computational — it is precisely this middle ground that we seek to provide, so that we can build bridges between these levels, even though it may not fully satisfy many on either side. As such, this model represents a suitable platform for generating numerous novel, testable predictions across the spectrum from biology to behavior, and for understanding the nature of various complex disorders that can arise within the dynamics of these brain systems, which have been implicated in a number of major mental disorders.

As noted earlier, PVLV builds upon various neural-level implementational models that have been proposed for the phasic dopamine system, integrating proposed neural mechanisms that explain the effects of both timing (Vitay & Hamker, 2014; Houk et al., 1995) and reward magnitude and probability on phasic dopamine responses (Tan & Bullock, 2008; Montague et al., 1996), as well as the neural mechanisms underlying inhibitory learning that contribute to extinction of responses to reward (Pan, Schmidt, Wickens, & Hyland, 2005; Redish et al., 2007). Several models also integrate timing and magnitude and probability signals, proposing that separate neural pathways may be involved in each type of computation (Brown et al., 1999; Contreras-Vidal & Schultz, 1999).

Also relevant, although not explicitly about the phasic dopamine signaling system, are recent neural models of fear conditioning in the amygdala. These models have highlighted the circuitry that contributes to the learning and extinction of responses to negative valence stimuli, including neural circuits implementing the effects of context on learning and extinction (Moustafa, Gilbertson, Orr, Herzallah, Servatius, & Myers, 2013; Krasne, Fanselow, & Zelikowsky, 2011; Carrere & Alexandre, 2015). Despite this wealth of neural modeling work, the PVLV model provides additional explanatory power beyond these prior models by incorporating both the positive and negative valence pathways, along with excitatory and inhibitory learning in both systems and their effects on the phasic dopamine system, grounded in a wide range of neural data supporting the computations made by each part of the model and their effects on phasic dopamine firing.

Motivating Phenomena

Several empirical phenomena — and related neuro-computational considerations — have especially guided our thinking about phasic dopamine signaling as a functioning neurobiological system. These are briefly summarized here, with additional details provided later in the relevant sections.

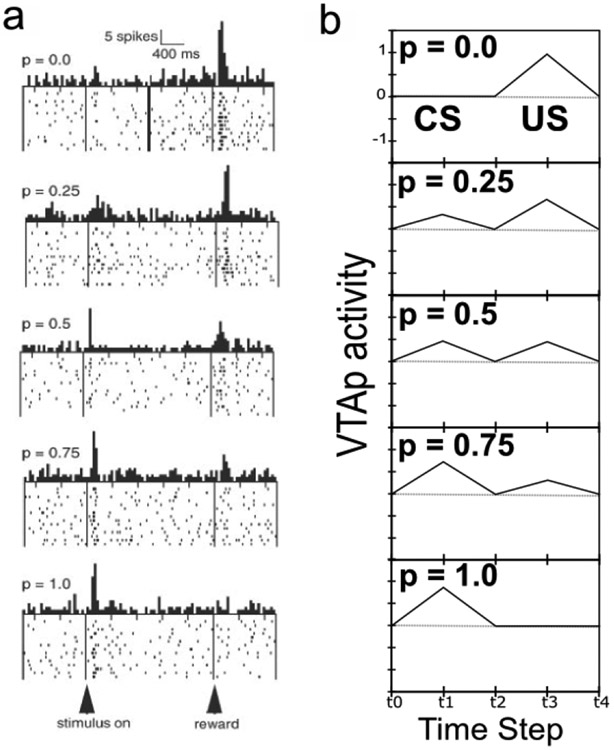
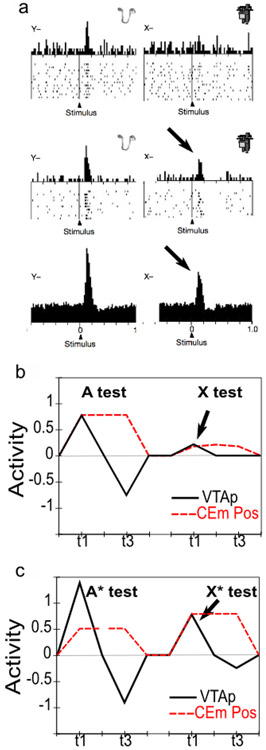
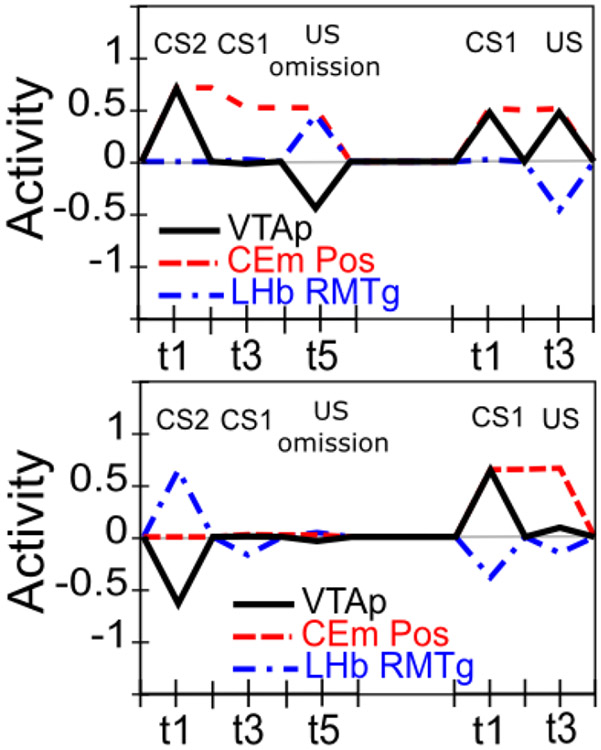
1. The acquisition of phasic dopamine bursting for CSs, and reduction for expected USs, are dissociable phenomena. The dissociation between these two aspects of phasic dopamine function is central to the PVLV model, as noted above, and reviewed extensively in our earlier papers (O’Reilly et al., 2007; Hazy et al., 2010). The evidence for this dissociation includes: 1) phasic bursting at both CS and US onset co-exist for a period of time before the latter is lost (e.g., Ljungberg et al., 1992); 2) at interstimulus intervals greater than about four seconds, very little loss of US-triggered bursting is observed in spite of extensive overtraining – even though substantial bursting to CS-onset is acquired (Fiorillo et al., 2008; Kobayashi & Schultz, 2008); and, 3) under probabilistic reward schedules the acquired CS signals come to reflect the expected value of the outcomes, but US-time signals adjust to reflect the range or variance of outcomes that occur (Tobler, Fiorillo, & Schultz, 2005). Thus, CS- and US- triggered bursting are neither mutually exclusive nor conserved, in contradistinction to simple TD models that predict a fixed-sum backward-chaining of phasic signals. There now seems to be a consensus among biologically-oriented modelers that there are two distinct (though interdependent) subsystems with multiple sites of plasticity (e.g., Tan & Bullock, 2008; Hazy et al., 2010; Vitay & Hamker, 2014). Under the PVLV framework, the acquisition of phasic dopamine cell bursting at CS-onset (i.e., LV learning) is mapped to the amygdala, while the loss of phasic bursting at US-onset (PV learning) is mapped to the ventral striatum (VS, including the Nucleus Accumbens, NAc). In the present version of the model, we also include an explicit lateral habenula (LHb) component that is driven by the VS to cause phasic pauses in dopamine cell firing, e.g., for omissions of expected rewards.

2. Rewards that occur earlier than expected produce phasic dopamine cell bursting, but no pausing at the usual time of reward, whereas rewards that occur late produce both signals. While a simple RPE formalism predicts that both early and late rewards should exhibit both bursts and pauses, the empirically observed result (Hollerman & Schultz, 1998; Suri & Schultz, 1999) actually makes better sense ecologically: once an expected reward is obtained an agent should not continue to expect it. We interpret this within a larger theoretical framework in which a temporally-precise goal-state representation for a particular US develops in the OFC as each CS-US association is acquired. The occurrence of a CS activates this OFC representation, which is then maintained via robust frontal active-maintenance mechanisms, and it is cleared when the US actually occurs (i.e., when the goal outcome is achieved). It is the clearing of this expectation representation that prevents the pause from occurring after early rewards. This role of OFC active maintenance in bridging between the two systems in PVLV (LV / CS and PV / US) replaces the temporal chaining dynamic in the TD model, and provides an important additional functional and anatomical basis for the specialization of these systems: the PV (VS) system depends critically on OFC input for learning when to expect US outcomes, while the LV (amygdala) system is more strongly driven by sensory inputs that then acquire CS status through learning. In other words, the LV / amygdala system is critical for sign tracking while the PV / VS system is critical for goal tracking (Flagel et al., 2010; see General Discussion). In the present model, we do not explicitly simulate the active maintenance dynamics of the OFC system, but other models have done so (Frank & Claus, 2006; Pauli, Hazy, & O’Reilly, 2012; Pauli, Atallah, & O’Reilly, 2010).

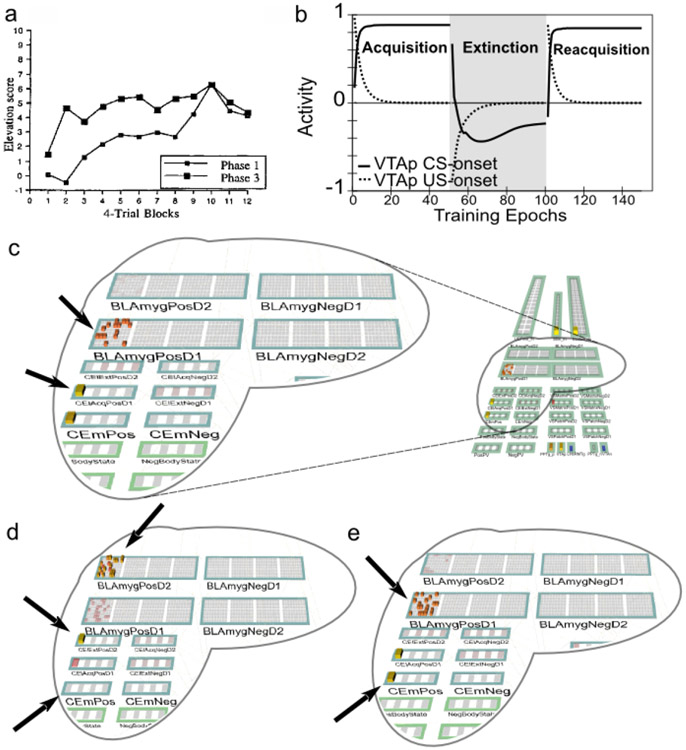
3. Extinction is not simply the unlearning of acquisition. Extinction and the related phenomena of reacquisition, spontaneous recovery, renewal, and reinstatement exhibit clear idiosyncracies in comparison with initial acquisition. For example, reacquisition generally proceeds faster after extinction than does original acquisition (rapid reacquisition; Pavlov, 1927; Ricker & Bouton, 1996; Rescorla, 2003), and a single unpredicted presentation of a US after extinction can reinstate CRs to near pre-extinction levels (reinstatement; Pavlov, 1927; Bouton, 2004). In addition, extinction learning has a significantly stronger dependency on context than does initial acquisition as demonstrated in the renewal paradigm (Bouton, 2004; Corcoran, Desmond, Frey, & Maren, 2005; Krasne et al., 2011). The clear implication is that extinction learning is not the symmetrical weakening of weights previously strengthened during acquisition, which a simple RPE formalism typically assumes, but instead involves the strengthening of a different set of weights that serve to counteract the effects of the acquisition weights. In support of this inference, much empirical evidence implicates extinction-related plasticity in different neurobiological substrates from those implicated in initial acquisition (e.g., Bouton, 2004; Herry, Ciocchi, Senn, Demmou, Müller, & Lüthi, 2008; Quirk & Mueller, 2008; Bouton, 2011). These phenomena support the use of opposing pathways — one for acquisition and another for extinction — within both the LV-learning amygdala subsystem and the PV-learning VS subsystem.

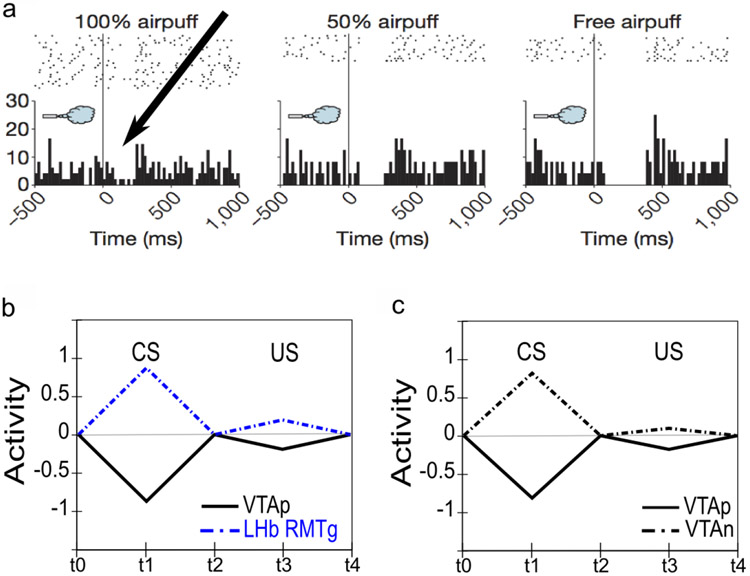
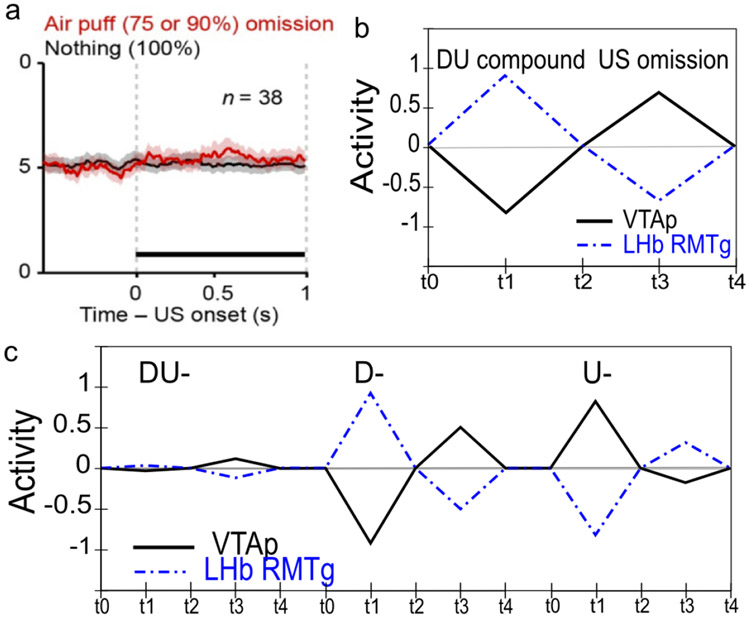
4. Although logically related, the loss of bursting at the time of an expected reward and pausing when rewards are omitted are dissociable phenomena. There is evidence that the mechanisms involved in the former are relatively temporally imprecise, compared to the latter, which are necessarily more punctate since they cannot begin until it has been determined that a reward has, in fact, been omitted. Rewards delivered early show progressively more bursting the earlier they are, implying the mechanisms involved in blocking expected rewards are ramping up before the expected time of reward (Fiorillo et al., 2008; Kobayashi & Schultz, 2008). Further, there is a slight, but statistically significant, ramping decrease in tonic firing rate prior to expected rewards (Bromberg-Martin, Matsumoto, & Hikosaka, 2010a). On the other hand, the mechanisms implicated in producing pauses for omitted rewards are more temporally precise, with an abrupt, discretized onset (Matsumoto & Hikosaka, 2009b), and no apparent sign of early increases in firing in the lateral habenula (LHb; Matsumoto & Hikosaka, 2009b). This dissociation, along with congruent anatomical data, motivates a distinction between the inhibitory shunting of phasic bursts (hypothesized to be accomplished by known VS inhibitory projections directly onto dopamine neurons; Joel & Weiner, 2000), and a second, probably collateral pathway through the LHb (and RMTg) that is responsible for pausing tonic firing. This latter pathway enables the system to make the determination that a specific expected event has not in fact occurred (Brown et al., 1999; O’Reilly et al., 2007; Tan & Bullock, 2008; Hazy et al., 2010; and see Vitay & Hamker, 2014, for an excellent review and discussion of this important problem space).

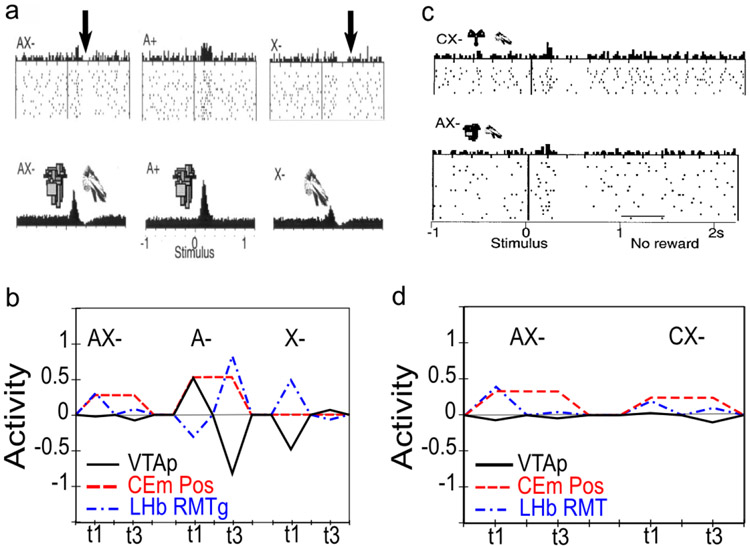
5. Conditioned inhibitors acquire the ability to generate phasic pauses in dopamine cell firing when presented alone. When a novel stimulus (conditioned inhibitor, CI, denoted X) is presented along with a previously trained CS (denoted A), and trained with the non-occurrence of an expected appetitive outcome (i.e., AX−), the CI takes on a negative valence association and produces a phasic pause in dopamine firing (Tobler et al., 2003). This represents an important point of overlap between appetitive and aversive conditioning, since a CI stimulus (X−) behaves very much like a CS directly paired with an aversive US as reported by e.g., Mirenowicz and Schultz (1996). However, in the CI case, there is no overt negative US involved — only the absence of a positive US. Thus, the conditioned inhibition paradigm helps inform ideas about the role of USs in driving CS learning. In our framework, aversive CSs come to excite the LHb via the striatum (and pallidum), to produce dopamine cell pauses. Biologically, there is a pathway through the striatum to the LHb, in addition to well-documented direct US inputs to LHb, and electrophysiological results consistent with the role of the striatal pathway in driving pauses in dopamine firing via the LHb (Hong & Hikosaka, 2013). Preliminary direct evidence for a role of the LHb in conditioned inhibition has recently been reported (Laurent, Wong, & Balleine, 2017).

6. InRescorla’s (1969)summation test of conditioned inhibition, conditioned inhibitors tested with a different conditioned stimulus can immediately prevent both the expression of acquired conditioned responses as well as phasic dopamine pauses. Specifically, this paradigm involves first training A+ and separately B+; then training AX− (i.e., conditioned inhibition training), but not BX−; and then, finally, testing BX−. At the otherwise expected time of the B+ US, there is no dopamine pause for the BX− case (Tobler et al., 2003), indicating that the X has acquired a generalized ability to negate the expectation of the US and is not just specific to the AX compound. Furthermore, presentation of the BX compound at test also prevents the expression of acquired B+ CRs (e.g., salivation, food-cup approach) (Tobler et al., 2003), implying that the acquired X inhibitory representation has reached deep subcortical behavioral pathways.

7. Conditioned inhibitors do not produce bursting at the expected time of the US when presented alone. According to a simple RPE formalism of conditioned inhibition, the X stimulus should acquire negative value itself and also serve to drive learning that predicts its occurrence, all trained by the dopamine pauses. Subsequently, when the X is presented by itself (without A-driven expectation of getting a reward), an unopposed expectation of the negative (reward omission) outcome should trigger a positive dopamine burst at the time when the US would have otherwise occurred. This is analogous to the modest relief bursting reported when a trained CS is presented but the aversive US is omitted at test (Matsumoto & Hikosaka, 2009a; Matsumoto, Tian, Uchida, & Watabe-Uchida, 2016), or when a sustained aversive US is terminated (Brischoux et al., 2009). In fact, however, no such X− relief burst was detected by Tobler et al. (2003) — even though they explicitly looked for one.

8. Phasic dopamine responses to aversive outcomes include both pauses and bursts, with distinct subpopulations identifiable. The nature of phasic dopamine responses to primary aversive outcomes has been a topic of long-standing controversy with multiple studies reporting either pauses (e.g., Mirenowicz & Schultz, 1996), bursts (Horvitz, Stewart, & Jacobs, 1997; Horvitz, 2000), or a mixture of both including cells exhibiting a biphasic response pattern (Matsumoto & Hikosaka, 2009a). Although there is now a clear consensus that bursting responses for aversive events do occur, the interpretation remains controversial (e.g., Fiorillo, 2013; Schultz, 2016). All things considered, the most parsimonious interpretation may be that different populations of dopamine neurons may have different response profiles, with a majority (generally more laterally-located) displaying a predominantly valence-congruent (RPE-consistent) response profile (i.e., pausing for aversive outcomes), while a smaller (more medial) subpopulation responds with bursting for aversive outcomes. Functionally, it may be that both forms of response make sense: for instrumental learning based on reinforcing actions that produce “good” outcomes and punishing those leading to “bad” ones (e.g., Thorndike, 1898, 1911; Frank, 2005), valence-congruent dopamine signaling would seem essential to prevent confusion across both appetitive and aversive contexts; on the other hand, one or more smaller specialized subpopulation(s) displaying bursting responses for aversive outcomes may be important for learning to suppress freezing and enable behavioral exploration for active avoidance learning. In line with this latter idea, it now appears there may be at least two small subpopulations of dopamine cells that respond with unequivocal bursting to aversive events: 1) a small subpopulation of posteromedial VTA neurons exhibiting unequivocal bursting to aversive events project narrowly to subareas of the accumbens shell and to certain ventromedial prefrontal areas that may play a role in the suppression of freezing (Maier & Watkins, 2010; Moscarello & LeDoux, 2013; Lammel et al., 2012); and, 2) even more recently, a second subpopulation of aversive-bursting dopamine cells has been described in the posterolateral aspect of the SNc, with this population projecting only to the caudal tail of the dorsal striatum and seemingly involved in simple avoidance learning (Menegas, Bergan, Ogawa, Isogai, Venkataraju, Osten, Uchida, & Watabe-Uchida, 2015; Menegas, Babayan, Uchida, & Watabe-Uchida, 2017; Menegas, Akiti, Uchida, & Watabe-Uchida, 2018). Aversive-bursting dopamine cells are included in the PVLV framework as a second, distinct dopamine unit as discussed in Neurobiological Substrates and Mechanisms.

9. Dopamine pauses to aversive outcomes appear not to be fully discounted through learned expectations. For the subset of dopamine neurons that exhibit valence-congruent pauses to aversive outcomes and CSs, these pauses seem not to be fully predicted away (Matsumoto & Hikosaka, 2009a; Fiorillo, 2013). Behaviorally, it makes sense not to fully suppress aversive outcome signals since these outcomes remain undesirable, even potentially life-threatening, and an agent should continue to be biased to learn to avoid them. In contrast, the discounting of expected appetitive outcomes would seem to serve the beneficial purpose of biasing the animal toward exploring for even better opportunities. Thus, there are several fundamental asymmetries between the appetitive and aversive cases that sensibly ought to be incorporated into functional models.

10. Both appetitive and aversive processing involve many of the same neurobiological substrates — in particular the amygdala and the lateral habenula. Overwhelming empirical evidence shows that the amygdala, ventral striatum, and lateral habenula all participate in both appetitive and aversive processing (Paton, Belova, Morrison, & Salzman, 2006; Lee, Groshek, Petrovich, Cantalini, Gallagher, & Holland, 2005; Cole, Powell, & Petrovich, 2013; Belova, Paton, Morrison, & Salzman, 2007; Shabel & Janak, 2009; Roitman, Wheeler, & Carelli, 2005; Setlow, Schoenbaum, & Gallagher, 2003; Donaire, Morón, Blanco, Villatoro, Gámiz, Papini, & Torres, 2019; Matsumoto & Hikosaka, 2009b; Stopper & Floresco, 2013). This implies that the processing of primary aversive events must coexist without disrupting the processing of appetitive events in these substrates, despite all the important differences between these basic situations as noted above. Properly integrating yet differentiating these two different valence contexts within a coherent overall framework presents an important challenge for any comprehensive model of the phasic dopamine signaling system. We find that an opponent processing framework — based on the opposite effects of D1 and D2 dopamine receptors on cells in the striatum and amygdala — can go a long way towards meeting this challenge, combined with an architecture that specifically segregates the processing of individual USs.

11. Pavlovian conditioning generally requires a minimum 50-100 msec interval between CS-onset and US. Our original PVLV model emphasized the problem that a phasic dopamine signal generated by CS onset could create a positive feedback loop of further learning to that CS, leading to saturated synaptic weights (O’Reilly et al., 2007; Hazy et al., 2010). We now account for data indicating CSs must precede USs by a minimum of 50-100 msec to drive conditioned learning (Schneiderman, 1966; Smith, 1968; Smith, Coleman, & Gormezano, 1969; Mackintosh, 1974; Schmajuk, 1997). With this constraint in place, it is not possible for CS-driven dopamine to reinforce itself, preventing the positive feedback problem. Incorporating this change now allows our model to include the effects of phasic dopamine on CS learning in the amygdala (in addition to the important role that US inputs play in driving learning there, as captured in the prior models), supporting phenomena such as second-order conditioning in the BLA (Hatfield, Han, Conley, & Holland, 1996).

Conceptual Overview of the PVLV Model

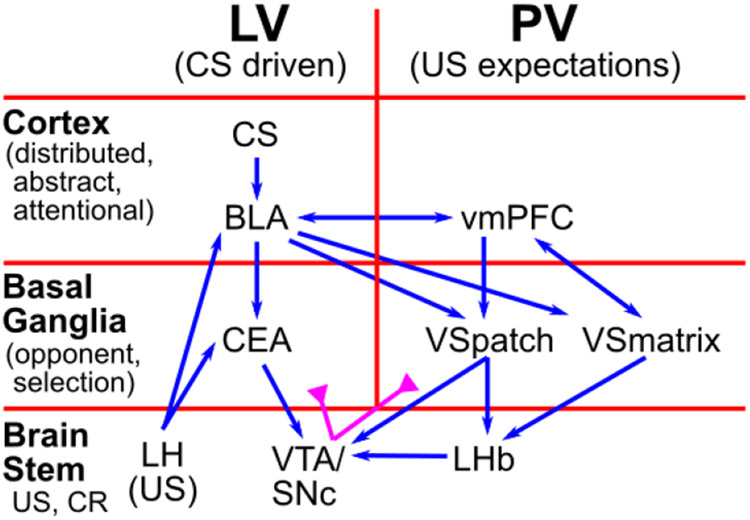
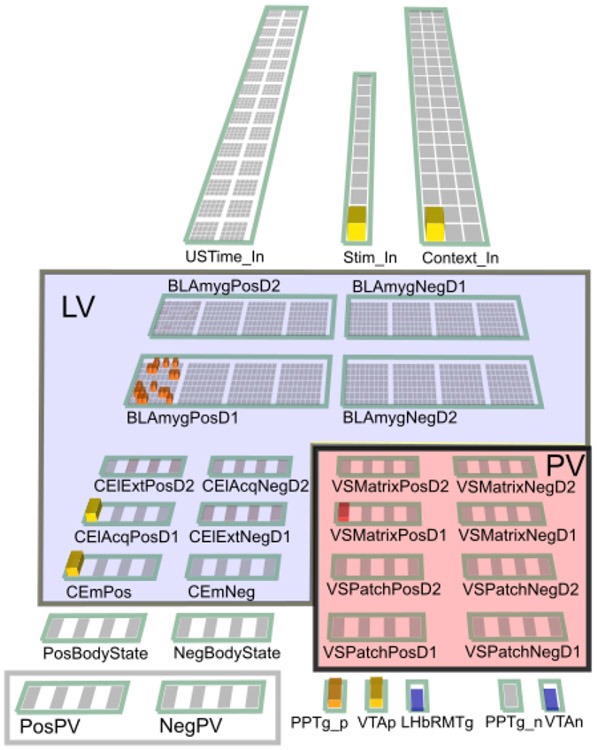
In this section we provide a high-level, conceptual overview of the PVLV model and how all the different parts fit together. Figure 1 shows how the fundamental LV vs. PV distinction cuts through a standard hierarchical organization of brain areas at three different levels: cortex, basal ganglia (BG), and brain stem. Cortex is generally thought to represent higher-level, more abstract, dynamic encodings of sensory and other information, which provides a basis for learning about the US-laden value of different states of the world (in standard reinforcement learning terminology). The basolateral amygdala (BLA) is described as having a cortex-like histology in its neural structure (e.g., Pape & Pare, 2010), but it also receives direct US inputs from various brain stem areas. Thus, it serves nicely as a critical hub / connector area that learns to associate these cortical state representations with US outcomes, which is the core of the LV function in the PVLV framework. In contrast, the central amygdala (CEA) has cell types and connectivity characteristic of the striatum of the basal ganglia (Cassell, Freedman, & Shi, 1999), and according to classic BG models (e.g., Mink, 1996; Frank et al., 2001; Frank, 2005; Collins & Frank, 2014), it should be specialized for selecting the best overall interpretation of the situation by separately weighing evidence-for (Go, direct pathway, CEl_ON) vs. evidence-against (NoGo, indirect pathway, CEl_OFF) in a competitive, opponent-process dynamic (Ciocchi, Herry, Grenier, Wolff, Letzkus, Vlachos, Ehrlich, Sprengel, Deisseroth, Stadler, Müller, & Lüthi, 2010; Li, Penzo, Taniguchi, Kopec, Huang, & Li, 2013).

Figure 1:

Overview of PVLV: The main division into LV (learned value) and PV (primary value) cuts across a hierarchy of function in cortical, basal ganglia, and brain stem areas. The cortex provides high-level, abstract, dynamic state representations, and the basolateral amygdala (BLA), which has a cortex-like histology, links these with specific US outcomes. The basal-ganglia-like central amygdala (CEA) quantitatively evaluates the overall evidence for the occurrence of reward or punishment using opponent-processing pathways, and drives phasic dopamine bursts in the midbrain dopamine areas (VTA, SNc) if this evaluation is in favor of expected rewards. BLA also triggers updating of US expectations in ventral / medial prefrontal cortex (vmPFC), especially the OFC (orbitofrontal cortex), which then drives another opponent-process evaluation process, in the ventral striatum patch-like areas (VSpatch), the results of which can shunt dopamine bursts for expected US’s, and drive pauses in dopamine firing when an expected US fails to arrive, via projections to the lateral habenula (LHb). Various brain stem areas (e.g., the lateral hypothalamus, LH) drive US inputs into the system, and are also driven to activate conditioned responses (CR’s).

Thus, the CEA in our model takes the higher-dimensional, distributed, contextualized representations from BLA and boils them down to a simpler, quantitative evaluation of how likely a particular US outcome is given the current cortical state representations. When this evaluation results in an increased expectation of positive outcomes, it drives phasic bursting in the VTA/SNc dopamine nuclei. This occurs via direct connections, and via the pedunculopontine tegmental nucleus (PPTg), which may help in driving bursting as a function of changes in expectations, as sustained activity in BLA does not appear to drive further phasic dopamine bursting (e.g., Ono, Nishijo, & Uwano, 1995). In summary, through these steps, this stack of LV areas is responsible for driving phasic dopamine bursting in response to CS inputs.

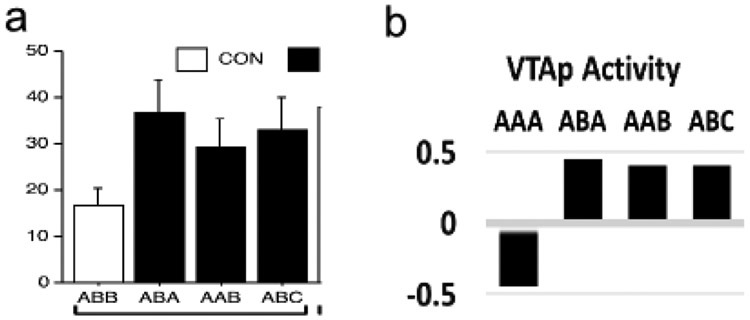
The opponent organization scheme in the amygdala also serves to address the subtly challenging problem of learning about the absence of an expected US outcome as occurs during extinction training. This is challenging from a learning perspective because the absence of a US is a “non event”, and thus cannot drive learning in the traditional activation-based manner, and further, the issue remains of which of the indeterminate number of non-occurring events should direct learning. The explicit representation of absence in the opponent-processing scheme solves this problem by using selective modulatory, permissive connections from acquisition-coding to extinction-coding units so that only USs with some expectation of occurrence can accumulate evidence about non-occurrence. Thus, only at the last step in the pathway is the US-specific nature of the representations abstracted away to the pure value-coding nature of the effectively-scalar phasic dopamine signal, in contrast to many other computational models that only deal with this abstract value signal (e.g., standard TD models). In addition, learning constrained to separate representations for different types of rewards (punishments) can directly account for phenomena such as unblocking by reward type, something that is otherwise challenging for value-only models like TD (e.g., Takahashi, Batchelor, Liu, Khanna, Morales, & Schoenbaum, 2017), and depends on activity of dopamine neurons (Chang, Gardner, Di Tillio, & Schoenbaum, 2017).

Bridging the CS-driven US expectations into the PV side of the system, the BLA also drives areas in the orbital (OFC) and ventromedial prefrontal cortex (vmPFC), particularly the OFC (Figure 1). Projections from this cortical level to ventral striatum drive a BG-like evaluation of evidence for and against the imminent occurrence of specific USs at particular points in time. Cells in the patch-like compartment of the VS send direct inhibitory projections to the midbrain dopamine cells so as to produce a shunt-like inhibition that blocks dopamine bursts that would otherwise arise from an appetitive US. Furthermore, via a pallidal pathway, the VSpatch also drives a more temporally-precise activation (disinhibition) of the LHb that causes pausing (dips) of tonic dopamine firing if not offset by excitatory drive from an actual US occurrence. In summary, this PV stack of areas works together to anticipate and cancel expected US outcomes.

There is another pathway through the VS that does not fit as cleanly within the simple LV / PV distinction, which we hypothesize is mediated by the matrix-like compartments within the VS (VS-matrix). This pathway is necessary for supporting the ability of CS inputs to drive phasic dipping / pausing of dopamine firing, which appears to be exclusively driven by the LHb in response to VS inputs (Christoph, Leonzio, & Wilcox, 1986; Ji & Shepard, 2007; Matsumoto & Hikosaka, 2007; Hikosaka, Sesack, Lecourtier, & Shepard, 2008; Matsumoto & Hikosaka, 2009b; Hikosaka, 2010). We are not aware of any evidence supporting a direct projection from the amygdala to the LHb (Herkenham & Nauta, 1977), which would otherwise be a more natural pathway for CS activation of phasic dipping according to the overall PVLV framework. An important further motivation for this VSmatrix pathway is that, by hypothesis, it is also responsible for gating information through the thalamus so as to produce robust maintenance of US outcome / goal state representations in OFC (Frank & Claus, 2006; Pauli et al., 2012; Pauli et al., 2010). Such working memory-like goal state representations are hypothesized to be important for supporting goal-directed (vs. habitual) instrumental behavior, behavior known to depend on intact OFC (e.g., Gallagher, McMahan, & Schoenbaum, 1999). Thus, the very same plasticity events occurring at corticostriatal synapses onto VSMatrix cells could be responsible for learning to gate US information into OFC working memory in response to a particular CS, while acquiring an ability to drive phasic dopamine signals (via LHb) in response to those same CS events.

Appetitive / Aversive and Acquisition / Extinction Pathways

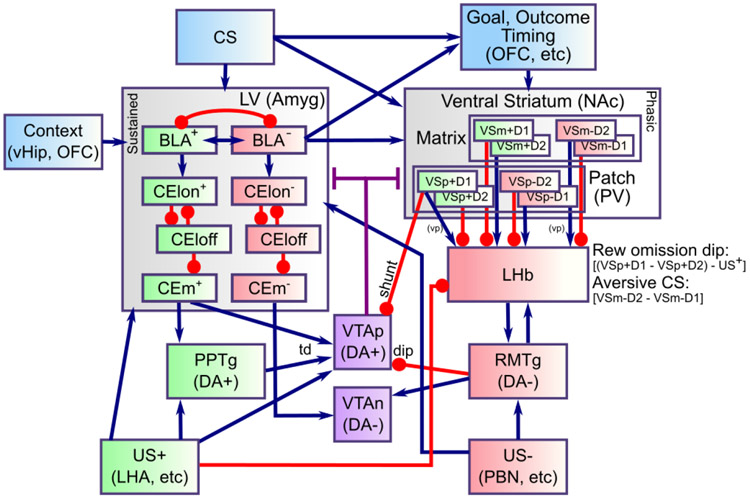
The above overview is framed in terms of appetitive conditioning, as that is the simplest and most well-established case. However, a critical feature of the current model is that it incorporates pathways within the LV and PV systems for processing aversive USs as well, leveraging the same opponent-process dynamics, with an appropriate sign-flip, as described above. Figure 2 shows the full set of pathways and areas in the PVLV model. As in the BG, each pathway is characterized by having a preponderance of dopamine D1 vs. D2 receptors, which then drives learning from phasic bursts (D1) or dips (D2) (e.g., Mink, 1996; Frank et al., 2001; Frank, 2005; Gerfen & Surmeier, 2011). Thus, assuming the standard RPE form of dopamine firing, D1-dominated pathways are strengthened by unexpected appetitive outcomes, while D2-dominated ones are strengthened by unexpected aversive outcomes. Thus, this differential dopamine receptor expression can account for the differential responses of appetitive- vs. aversive-coding neurons in the amygdala (LV), as shown in Figure 2. Although the BLA is not strongly topographically organized, we assume a similar opponency between subsets of neurons, as is more clearly demonstrated in the central amygdala CEl_ON vs. CEl_OFF cells (Ciocchi et al., 2010; Li et al., 2013). In addition to these lateral pathway neurons, we include a final medial output pathway (CEm) that computes the net balance between on vs. off for each valence pathway (appetitive and aversive).

Figure 2:

Detailed components of PVLV, showing the opponent processing pathways within the PV and LV systems, which separately encode the strength of support for and against each US, and with opposite dynamics for appetitive versus aversive valence. BLA has pathways for appetitive and aversive USs, along with distinctions between acquisition and extinction learning, all of which engage in broad inhibitory competition. The BLA projects to central amygdala (CEl, CEm) neurons that integrate the evidence for-and-against a given US, and communicate this net value to the VTA (and SNc, not shown). The ventral striatum (VS) has matrix and patch subsystems, where matrix (VSm) receives modulatory inputs from corresponding BLA neurons and represents CSs in a phasic manner, and patch (VSp) anticipates and cancels USs. Both have a full complement of opposing D1- and D2-dominant pathways, which have opposing effects for appetitive versus aversive USs.

The VS (PV) system is likewise organized according to standard D1 vs. D2 pathways, within the US-coding Patch areas and the CS-coding Matrix areas, again with separate pathways for appetitive vs. aversive, with the sign of D1 vs. D2 effects flipped as appropriate. For example, VSpatch aversive-pathway D2 neurons learn from unexpected aversive outcomes, and thereby learn to anticipate such outcomes. The complementary D1 pathway there learns from any dopamine bursts associated with the non-occurrence of these aversive outcomes, such that the balance between these pathways reflects the net expectation of the aversive outcome. Figure 2 shows how each VS pathway sends a corresponding net excitation or inhibition to the LHb (via a pallidal pathway), with excitation of the LHb causing inhibition of VTA / SNc tonic firing via the RMTg (rostromedial tegmental nucleus — in our model, we combine the LHb and RMTg into a single functional unit).

In addition, the VSpatch D1 appetitive pathway sends direct shunting inhibition to these midbrain dopamine areas, to block excitatory firing from expected US’s. Although this pathway may seem redundant with the LHb inhibition, the differential timing of these two functions motivates the need for separate mechanisms. On the one hand, a complete inhibition of bursting requires an input arriving at least slightly prior to the time of reward, or else at least a little activity will necessarily occur on the front end. On the other hand, an omission-signaling input (for pausing) can only arrive at least slightly after the expected time of the reward because an agent can determine that an expected event did not occur only after the time it was expected, reflecting at least some finite amount of time to compute and transmit the omission signal. Indeed, omission pauses are empirically seen to have greater latency than corresponding bursts.

Finally, apropos of the asymmetries between appetitive vs. aversive conditioning discussed above, there are a number of aspects where these two differ in the model. For example, appetitive, but not aversive, pathways in the amygdala can directly drive dopamine burst firing, consistent with our overall hypothesis (and extant data) that the LHb is exclusively responsible for driving all phasic pausing in dopamine cell firing. This has some important functional implications, by allowing the amygdala dopamine pathway to be positively rectified — i.e., it only reports when the amygdala estimates the current situation to be better than the preceding one. Furthermore, the extent to which VSpatch expectancy representations can block dopamine pauses associated with expected aversive outcomes is significantly less than its ability to block bursts for expected appetitive outcomes as suggested by the available empirical data (Matsumoto & Hikosaka, 2009a).

Differences From Previous Versions of PVLV

The present model represents a significant elaboration and refinement of the PVLV framework since our prior publication (Hazy et al., 2010), as briefly summarized here:

• Earlier versions of PVLV included only a central nucleus amygdalar component (CEA; formerly CNA). In the current version we have added a basolateral amygdalar complex (BLA), which serves as a primary site for CS-US pairing during acquisition (acquisition-coding cells) and, critically, for the pairing of CSs with the non-occurrence of expected USs (extinction-coding cells). This is especially important in accounting for extinction-related phenomena reflecting the idea that extinction is an additional layer of learning and not just the unlearning (weakening) of acquisition learning and, importantly, underlies the ability of the current version to account for the differential sensitivity of extinction to context (see simulation 2b).

• Earlier versions of PVLV treated the inhibitory PV component as unitary with no distinction between a shunting effect onto dopamine cells that prevents bursting at the time of expected rewards and the pausing effect that occurs when expected rewards are omitted. Since that time it has been established that the LHb plays a critical role in the latter phenomenon and may serve as the sole substrate responsible for producing pauses on dopamine cell firing of any cause. Accordingly, the new version adds a LHb component which receives disynaptic collaterals from the same VSpatch cells that provide direct shunting inhibition onto dopamine cells. These collaterals result in net excitatory inputs onto LHb cells. Critically, the LHb also receives direct (excitatory) inputs for aversive USs, as well as net inhibitory inputs associated with both rewarding outcomes and expectations of reward. The LHb component is important for producing the dissociation between shunting inhibition and overt pauses, it also enables the new model to produce (modest) disinhibitory positive dopamine signals at the time of expected-but-omitted punishment (see simulation 4b).

• Like TD, and RPE generally, earlier versions of PVLV really only contemplated appetitive context, i.e., the occurrence and omission of positively-valenced reward; it largely ignored learning under aversive context (e.g., fear conditioning). In the current version, additional complementary channels for appetitive vs. aversive processing (and associated learning) have been incorporated throughout the model, with their convergence occurring only at two distinct sites where population coding is largely, but not exclusively, unitary: 1) the LHb (which projects to the VTA/SNc); and, 2) the dopamine cells themselves in the VTA/SNc. Incorporating aversive processing channels alongside appetitive ones is important for demonstrating that the core idea underlying the DA-RPE theory can survive the integration of all these parallel processing pathways and their significant convergence onto most dopamine cells. This extension enabled the current PVLV version to simulate basic aspects of aversive conditioning (see simulation 4a,b), and provides a richer more accurate account of conditioned inhibition.

• Also like TD and RPE, earlier versions of PVLV treated reward as a single scalar value throughout the model without distinguishing between different kinds of reward (or punishment), e.g., food vs. water, or shock vs. nausea. By representing different kinds of reward separately in both the amygdala and ventral striatum, learning in the current version of PVLV can also produce separate expectancy representations about different rewards. This provides a direct mechanism that can help account for the phenomenon of unblocking-by-identity (e.g., see simulation 3a).

Overview of Remainder of Paper

The next two sections examine first the neurobiology that constrains various aspects of the PVLV framework, and then the actual computational implementation of the model. After that, the Results section describes and discusses twelve simulations covering several well-established Pavlovian conditioning phenomena and, especially, serve to highlight the most important features of the overall framework. The paper concludes with a General Discussion in which we highlight the main contributions of the PVLV framework, compare our approach with others in the literature, and identify several unresolved questions for future research.

Neurobiological Substrates and Mechanisms

In this section, we provide a neurobiological-level account of the computational model outlined above, followed in the subsequent section by a computationally-focused description. To that end, we provide a selective review of salient biological and behavioral data most influential in informing the overall framework, and we focus specifically on data that go beyond the foundations covered in earlier papers (O’Reilly et al., 2007; Hazy et al., 2010).

The Amygdala: Anatomy, Connectivity, & Organization

The amygdala is composed of a dozen or so distinct nuclei and/or subareas (Amaral, Price, Pitkanen, & Carmichael, 1992), each of which can exhibit several subdivisions (McDonald, 1992). Despite such anatomical complexity, however, the literature has largely conceptualized amygdalar function in terms of two main components: a deeper/inferior basolateral amygdalar complex (BLA) more involved in the processing of inputs; and a more superficial/superior central amygdalar nucleus (CEA) that has long been implicated in driving many of the more primitive manifestations of emotional expression (changes in heart rate, breathing, blood pressure; freezing, and so on; Figure 3a). Both BLA and CEA contain both glutamatergic and GABAergic cells (both local interneurons and projecting), with considerable topographic patchiness in their relative proportions; for example, the lateral segment of the CEA (CEl) seems to be almost exclusively GABAergic. Importantly, the amygdala is richly innervated by all four neuromodulatory systems including a dense, heterogeneously distributed dopaminergic projection (Amaral et al., 1992; Fallon & Ciofi, 1992). Both main classes of dopamine receptors (D1-like, D2-like) are richly expressed, although not homogeneously (Bernal, Miner, Abayev, Kandova, Gerges, Touzani, Sclafani, & Bodnar, 2009; de la Mora, Gallegos-Cari, Arizmendi-García, Marcellino, & Fuxe, 2010; de la Mora, Gallegos-Cari, Crespo-Ramirez, Marcellino, Hansson, & Fuxe, 2012; Lee, Kim, Kwon, Lee, & Kim, 2013).

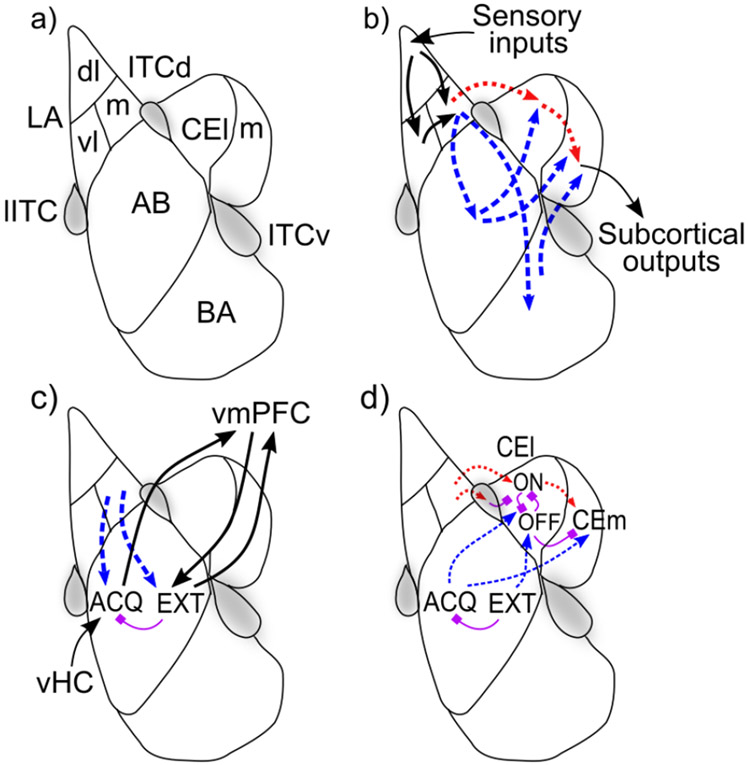
Figure 3:

Basic organization, information flow, and opponent-processing in the amygdala. a) Schematic diagram of a coronal section of unilateral amygdala with most prominent nuclei outlined according to one common scheme. The BLA is composed of: lateral (LA), basal (BA), and accessory basal (AB) nuclei. The central nucleus is composed of a lateral (CEl) and medial (CEm) segments. Three collections of GABAergic cells make up the intercalated cell masses (ITCs): the lateral paracapsular (lITC); dorsal (ITCd); and ventral (ITCv). b) Basic information flow through the amygdala: sensory information enters via the LA predominantly flowing from dorsolateral (LAdl) to ventrolateral (LAvl) and medial (LAm) divisions. From there two parallel pathways reach the central amygdala: 1) directly from LA to CEA (via CEl) (red dotted arrows); and, 2) via the the basal (BA) and accessory basal (AB) nuclei (blue dash arrows). c) Opponent processing in the BLA following the scheme of Herry et al., 2008: acquisition-coding cells (ACQ) receive context inputs from the ventral hippocampus (vHC) and project to the ventromedial PFC, which connects reciprocally with extinction-coding cells (EXT) in the BLA, with the vmPFC providing additional context information relevant for extinction. d) Opponent processing in the CEl following the scheme of Pare & Duvarci, 2012, with CEl_ON = acquisition and CEl_OFF = extinction.

Figure 3 shows the major areas and connectivity. The BLA receives dense afferents from much of the cerebral cortex, including the higher areas in all sensory modalities, as well as associative and affective cortex, and from corresponding thalamic nuclei and subcortical areas (Pitkanen, 2000; Doyère, Schafe, Sigurdsson, & LeDoux, 2003; LeDoux, 2003; Uwano, Nishijo, Ono, & Tamura, 1995). The lateral nucleus (LA) receives the preponderance of sensory input, preferentially into its dorsolateral division (Pitkanen, 2000) and projects to CEA both directly, and indirectly via the basal and accessary basal nuclei (Pitkanen, 2000). The basal and accessory basal nuclei exhibit extensive local and contralateral interconnectivity, and also send feedback projections to two of the divisions of the LA (Pitkanen, 2000), whereas the LA has relatively little local or contralateral interconnectivity. The BLA also projects heavily to the ventral striatum and to much of the cortical mantle (Amaral et al., 1992; Pitkanen, 2000), including a strong reciprocal interconnection with the orbital frontal cortex (OFC; Schoenbaum, Chiba, & Gallagher, 1999; Ongür & Price, 2000) and parts of ventromedial prefrontal cortex including the anterior cingulate cortex (ACC; Ongür & Price, 2000). Based on neural recording studies, there seems to be little discernible local topographical organization of different cell responses in the BLA (i.e., a salt-and-pepper distribution; Herry et al., 2008; Maren, 2016), with one notable exception of a recently described positive-negative valence gradient in a posterior-to-anterior direction (Kim, Pignatelli, Xu, Itohara, & Tonegawa, 2016).

The CEA can be functionally divided into medial (CEm) and lateral (CEl) segments (Figure 3a), with the CEl exerting a tonic inhibitory influence on the CEm that, when released, performs a kind of gating function for CEm outputs analogous to that seen in the basal ganglia. Both CEl and, especially, CEm send efferents to subcortical visceromotor areas (autonomic processing) as well as to certain primitive motor effector sites involved in such affective behaviors as freezing (Koo, Han, & Kim, 2004; Veening, Swanson, & Sawchenko, 1984; Li et al., 2013). Importantly, among the subcortical efferents from CEm are projections to the VTA/SNc, both directly, and via the pedunculopontine tegmental nucleus (PPTg; Everitt, Cardinal, Hall, & Parkinson, 2000; Fudge & Haber, 2000), and stimulation of the CEm has been shown to drive phasic dopamine cell bursting and/or dopamine release in downstream terminal fields (Rouillard & Freeman, 1995; Fudge & Haber, 2000; Ahn & Phillips, 2003; Stalnaker & Berridge, 2003; see Hazy et al. (2010) for detailed discussion). The CEA also receives broad cortical and thalamic afferents directly (Amaral et al., 1992; Pitkanen, 2000); these direct inputs are presumably responsible for the result that the CEA can support first-order Pavlovian conditioning independent of the BLA (Everitt et al., 2000).

Division-of-Labor Between BLA and CEA: Analogy With the Cortical – Basal Ganglia System

In addition to the long-held view of basic amygdalar organization that posits the BLA as the input side and the CEA as the output side, we also embrace emerging ideas (e.g., Duvarci & Pare, 2014; Holland & Schiffino, 2016) that posit that the two areas may have distinct functional roles analogous to the distinction between those of the cortex (i.e., BLA) and the basal ganglia (CEA; Figure 1). The BLA has long been described as cortex-like (McDonald, 1992), while the CEA is more basal-ganglia like, particularly its lateral segment (CEl) whose principal cells bear a strong resemblance with the medium spiny neurons (MSNs) of the neostriatum, with which it is contiguous laterally (McDonald, 1992; Cassell et al., 1999). Thus, one can think about the BLA computing complex, high-dimensional representations of current states of the world (including both external and internal components) that are anchored by expectations about the imminent occurrence of specific USs; in contrast, the CEA involves simpler, low-dimensional representations about particular primitive actions to be taken based on those US-anchored anticipatory states (e.g., fear, food anticipation). Both BLA and CEA subserve both input and output roles and function partially in parallel as well as serially, with a major distinction between their output projections. The BLA projects to neocortex and basal-ganglia (especially ventral striatum) and exerts a more modulatory effect, while CEA projects almost exclusively to subcortical areas (excluding the basal ganglia), and is a strong driver of subcortical visceromotor and primitive motor effectors.

Electrophysiological recording shows that BLA neurons exhibit a wide range of selectivity to different CSs, USs, and contexts (Muramoto, Ono, Nishijo, & Fukuda, 1993; Ono et al., 1995; Toyomitsu, Nishijo, Uwano, Kuratsu, & Ono, 2002; Herry et al., 2008; Johansen, Hamanaka, Monfils, Behnia, Deisseroth, Blair, & LeDoux, 2010a; Johansen, Tarpley, LeDoux, & Blair, 2010b; Repa, Muller, Apergis, Desrochers, Zhou, & LeDoux, 2001; Roesch, Calu, Esber, & Schoenbaum, 2010; Beyeler, Namburi, Glober, Simonnet, Calhoon, Conyers, Luck, Wildes, & Tye, 2016). By adulthood, a significant proportion of the principal cells in both BLA and CEA appear to stably represent specific kinds of primary rewards and punishments and not undergo significant change thereafter. For example, discriminative- and reversal-learning experiments have shown that CS-US associative pairings can undergo rapid remapping when environmental contingencies change, leaving the underlying US-specific representational scheme intact (Schoenbaum et al., 1999). A simple model for Pavlovian conditioning is that previously neutral CSs acquire the ability to activate these US-coding cells by strengthening synapses they send to them (Muramoto et al., 1993; Ono et al., 1995; Toyomitsu et al., 2002). More recent studies examining larger population-level samples suggests that learning in the BLA is complex, high-dimensional, and distributed — consistent with a cortex-like system (Beyeler et al., 2016; Grewe, Gründemann, Kitch, Lecoq, Parker, Marshall, Larkin, Jercog, Grenier, Li, Lüthi, & Schnitzer, 2017). Nevertheless, the essential function of BLA in linking CSs and USs remains a useful overarching model.

In addition to a strong US-anchored organization for amygdala representations, there are also cells in both BLA and CEA that reflect evidence against the imminent occurrence of particular US outcomes. For example, Herry et al. (2008) showed that a distinct set of BLA neurons progressively increased in activity in response to CS-onset over multiple US omission trials (extinction training), in contrast with those (acquisition-coding) neurons that had acquired activity in response to CS-onset during fear acquisition. Similarly, Ciocchi et al. (2010) showed opponent coding of aversive US presence versus absence in separate populations of CEl_ON versus CEl_OFF neurons. These CEl neurons are exclusively GABAergic and have mutually inhibitory connections, producing a direct opponent-processing dynamic. This pattern of opponent organization, which is one of two core computational principles in our model, is essential for supporting extinction learning from the absence of expected USs, and also for probabilistic learning paradigms (Esber & Haselgrove, 2011; Fiorillo, Tobler, & Schultz, 2003).

Extinction Learning and the Role of Context

Considerable behavioral data strongly supports the idea that extinction learning is particularly sensitive to changes in both external and internal context, and that areas in the vmPFC play an important role in contextualizing extinction learning (Quirk, Likhtik, Pelletier, & Paré, 2003; Laurent & Westbrook, 2010). Further, Herry et al. (2008) looked specifically at the connectivity of extinction-coding versus acquisition-coding cells in the BLA and found that only the former receive connections from vmPFC. This has been incorporated into the PVLV framework in the form of contextual inputs to the model that connect exclusively to the extinction coding layers of the BLA. Somewhat surprisingly, Herry et al. (2008) also reported that hippocampal inputs to the BLA (long implicated in conditioned place preference and aversion) connected only with acquisition-coding cells; this rather paradoxical situation is discussed in a section on the role and nature of context representations in the General Discussion section. In essence, it is hard to avoid the conclusion that the hippocampus and vmPFC must convey distinctly different forms of context information to the amygdala. Simulation 2b in the Results section explores the differential context-sensitivity of extinction versus acquisition learning.

There are likely differential contributions of the BLA vs. CEA to extinction learning, in part due to the greater innervation of BLA by contextual inputs. For example, limited evidence suggests that the CEA may not be able to support extinction learning by itself and instead depends on learning in the BLA (Falls, Miserendino, & Davis, 1992; Lu, Walker, & Davis, 2001; Lin, Yeh, Lu, & Gean, 2003; Quirk & Mueller, 2008; Zimmerman & Maren, 2010). However, muscimol inactivation of BLA at different stages of extinction learning demonstrates that extinction can persist in the absence of BLA activation (Herry et al., 2008). Although not currently implemented in PVLV, this can potentially be explained in terms of BLA driving learning in vmPFC which can in turn drive extinction via direct projections into CEA (e.g., Anglada-Figueroa & Quirk, 2005). Finally, the intercalated cells (ITCs) have been widely discussed as suppressing fear expression under various circumstances (Royer, Martina, & Paré, 1999; Marowsky, Yanagawa, Obata, & Vogt, 2005; Likhtik, Popa, Apergis-Schoute, Fidacaro, & Paré, 2008; Ehrlich, Humeau, Grenier, Ciocchi, Herry, & Luthi, 2009; Maier & Watkins, 2010; Pare & Duvarci, 2012). However, some conflicting data has emerged in this regard (Adhikari, Lerner, Finkelstein, Pak, Jennings, Davidson, Ferenczi, Gunaydin, Mirzabekov, Ye, Kim, Lei, & Deisseroth, 2015). Nonetheless, it seems likely that ITCs participate somehow in the opponent-processing scheme for acquisition vs. extinction coding in the amygdala. Their role is currently subsumed within the basic extinction-coding function in PVLV and not explicitly modeled.

Dopamine Modulation of Acquisition Versus Extinction Learning

Dopamine has been shown to be important for plasticity-induction in the amygdala (Bissire, Humeau, & Lthi, 2003; Andrzejewski, Spencer, & Kelley, 2005). While the other three neuromodulatory systems (ACH, NE, 5-HT) are undoubtedly important (e.g., Carrere & Alexandre, 2015), they are not currently included in the PVLV framework. There are both D1-like and D2-like receptors in in the BLA (de la Mora et al., 2010), and blocking of D2s in the BLA impaired acquisition of fear learning, reducing conditioned responses such as freezing (Guarraci, Frohardt, Falls, & Kapp, 2000; LaLumiere, Nguyen, & McGaugh, 2004) and fear-potentiated startle (Nader & LeDoux, 1999; de Oliveira, Reimer, de Macedo, de Carvalho, Silva, & Brandaõ, 2011) to a CS. Similarly, Chang, Esber, Marrero-Garcia, Yau, Bonci, and Schoenbaum (2016) reported that optogenetically-driven pauses in DA firing produce expected effects consistent with aversive conditioning, while antagonism of D1s blocked fear extinction (Hikind & Maroun, 2008). In the positive valence domain, antagonism of D1s in the amygdala attenuated the ability of a cue paired with cocaine to reinstate conditioned responding (Berglind, Case, Parker, Fuchs, & See, 2006). Similarly consistent D1 and D2 receptor effects have been documented in CEl as well (De Bundel, Zussy, Espallergues, Gerfen, Girault, & Valjent, 2016).

Extending the results and model of Herry et al. (2008), the PVLV framework accounts for the differential learning of acquisition versus extinction cells in the BLA (and acquisition only in CEl) in terms of a 2 X 2 matrix of valence X dopamine receptor dominance. For example, acquisition for appetitive Pavlovian conditioning is trained by (appetitive) US occurrence and modulated by phasic dopamine bursting effects on D1-expressing positive US-coding cells, while extinction learning is mediated by phasic dopamine pausing effects on corresponding D2-expressing cells. Conversely, aversive acquisition is trained by (aversive) US occurrence and phasic dopamine pausing at D2-expressing, negative US-coding cells and so on. Considerable circumstantial, but not yet direct, evidence supports something like this basic 2 X 2 framework.

As noted earlier, the relative timing of phasic dopamine effects is critical for our model, to prevent CS-driven bursts from reinforcing themselves. Behaviorally, it has long been recognized that excitatory Pavlovian conditioning does not generally occur at CS-US interstimulus (ISIs) intervals less than approximately 50 msec (Schneiderman, 1966; Smith, 1968; Smith et al., 1969; Mackintosh, 1974; Schmajuk, 1997), and becomes progressively weaker and more difficult at ISIs exceeding 500 msec or so, although there is a great deal of variability across different CRs in the optimal ISI, which can extend to several seconds for some CRs (Mackintosh, 1974). Importantly, virtually all of the evidence bearing on optimal ISIs appears to involve the delay conditioning paradigm in which the CS remains on until the time of US onset, which fosters stronger and/or more reliable conditioning relative to trace paradigms in which there is gap between CS-offset and US-onset. Although not in the amygdala, recent optogenetic studies have documented a temporal window of 50-2000 msec or so after striatal MSN activity during which phasic dopamine activity can be effective in inducing synaptic plasticity, which serves as a kind of proof of concept (Yagishita, Hayashi-Takagi, Ellis-Davies, Urakubo, Ishii, & Kasai, 2014; Fisher, Robertson, Black, Redgrave, Sagar, Abraham, & Reynolds, 2017).

Amygdala-Driven Phasic Dopamine and the PPTg

The medial segment of the central amygdalar nucleus (CEm) has been shown to project to the midbrain dopamine nuclei both directly (Wallace, Magnuson, & Gray, 1992; Fudge & Haber, 2000) and indirectly via the pedunculopontine tegmental nucleus (PPTg; Takayama & Miura, 1991; Wallace et al., 1992; Fudge & Haber, 2000), and stimulation of the CEm has been shown to produce bursting of dopamine cells (Rouillard & Freeman, 1995; Fudge & Haber, 2000; Ahn & Phillips, 2003). It seems likely that the PPTg pathway (along with its functionally-related neighbor the laterodorsal tegmental nucleus, LDTg) plays a particularly important role in bursting behavior (e.g., Floresco, West, Ash, Moore, & Grace, 2003; Lodge & Grace, 2006; Omelchenko & Sesack, 2005; Pan & Hyland, 2005; Grace, Floresco, Goto, & Lodge, 2007), via direct efferents to the VTA and SNc (Watabe-Uchida, Zhu, Ogawa, Vamanrao, & Uchida, 2012). The PPTg and LDTg are located in the brainstem near the substantia nigra and both have additionally been implicated in a disparate set of functions including arousal, attention, and aspects of motor output (Redila, Kinzel, Jo, Puryear, & Mizumori, 2015). The PPTg projects preferentially to the SNc while the LDTg projects more to the VTA (Watabe-Uchida et al., 2012).

Both the PPTg and LDTg contain glutamatergic, GABAergic, and cholinergic cells (Wang & Morales, 2009) and all appear to be involved in the projection to the dopamine nuclei, although specific functions assignable to each remain poorly characterized (Lodge & Grace, 2006). Recently, subpopulations of cells in PPTg have been shown to code separately for primary rewards and their predictors and it has been suggested that the PPTg may play the key role in calculating RPEs (Kobayashi & Okada, 2007; Hazy et al., 2010; Okada, Nakamura, & Kobayashi, 2011; Okada & Kobayashi, 2013). The current PVLV framework implements a non-learning version of this basic idea by having the PPTg compute the positive-rectified derivative of its ongoing excitatory inputs from the amygdala (where the learning occurs), the positive rectification serving to restrict the effects of all amygdala-PPTg input onto dopamine cells to positive-only signaling (i.e., bursting).

Homogeneity and Heterogeneity in Phasic Dopamine Signaling

The midbrain dopamine system is constituted by a continuous population of dopamine cells generally divided into three groups based on location and connectivity: retrorubral area (RRA; A8; most caudal and dorsal), substantia nigra, pars compacta (SNc; A9), and ventral tegmental area (VTA; A10; most ventromedial; Joel & Weiner, 2000). Early electrophysiological studies emphasized the relative homogeneity of responding to reward-related events, with roughly 75% of identified dopamine cells displaying the now-iconic pattern of burst firing for unexpected rewards and reward-predicting stimuli (e.g. Schultz, 1998). However, it is now clear that there is considerable heterogeneity in response patterns existing within this basic homogeneity (e.g., Brischoux et al., 2009; Bromberg-Martin et al., 2010b; Lammel et al., 2012; Lammel et al., 2014; Menegas et al., 2015; Menegas et al., 2017; Menegas et al., 2018). For example, it appears that a greater proportion of the more laterally situated dopamine cells of the SNc may exhibit a reliable, early salience-driven excitatory response irrespective of the valence of the US. In the case of aversive USs, this results in a distinct, biphasic burst-then-pause response pattern (Matsumoto & Hikosaka, 2009a).

Furthermore, Brischoux et al. (2009) has described a small subpopulation of putative dopamine cells clustered in the ventrocaudal VTA in and near the paranigral nucleus, likely not recorded from previously, that respond with robust bursting to primary aversive events as reported by Brischoux et al. (2009). Those authors speculated that those cells might participate in a specialized subnetwork distinct from the preponderance of dopamine cells, based on some older studies reporting that cells in the paranigral nucleus project densely and selectively to the vmPFC and NAc shell (Abercrombie, Keefe, DiFrischia, & Zigmond, 1989; Kalivas & Duffy, 1995; Brischoux et al., 2009). However, some caution is warranted before concluding that these cells are actually dopaminergic as several studies have now characterized a heterogeneous population of glutamatergic projecting cells intermingled throughout the dopamine cell population, including the VTA where they are particularly concentrated near the midline (see Morales & Root, 2014, for review). Some of these cells project to the vmPFC and NAc shell and some respond with excitation to aversive stimuli (Morales & Root, 2014; Root, Mejias-Aponte, Qi, & Morales, 2014; Root, Estrin, & Morales, 2018a). Thus, further studies are needed to confirm that the cells described by Brischoux et al. (2009) are indeed dopaminergic. In any case these aversively-bursting cells are largely out of scope for the current framework, but are included in the model largely for illustrative purposes; their efferents are not used by any downstream components for learning or otherwise (see simulation 4a and related discussion). A possible role for such an aversive-specific subnetwork in the learning of safety signals is discussed in the General Discussion.

The Ventral Striatum

The ventral striatum (VS) is a theoretical construct based on functional considerations. As usually defined the VS is composed of the entirety of the nucleus accumbens (NAc) as well as ventromedial aspects of the neostriatum (caudate and putamen). The NAc is further subdivided into a core which is histologically indistinguishable from, and continuous with, ventromedial aspects of the neostriatum (Heimer, Alheid, de Olmos, Groenewegen, Haber, Harlan, & Zahm, 1997), and a shell which is histologically distinct from the core. The shell is itself internally heterogeneous, composed of multiple subareas participating in many distinct subnetworks involving primitive processing pathways (Reynolds & Berridge, 2002). For the purposes of the current framework, we focus only on the non-shell aspects of the ventral striatum.

The principal and projecting cells of the striatum are known as medium-spiny neurons (MSNs). By hypothesis, VS MSNs can be partitioned into eight phenotypes according to a 2 X 2 X 2 cubic matrix: The first two axes are identical to those used to partition the principal cells of the amygdala, namely the valence of the US defining the current situation (positive/negative) and the dominant dopamine receptor expressed for the MSN (D1/D2). To these are added a third orthogonal axis reflecting the compartment of the striatum in which an MSN resides — patch (striosomes) versus matrix (matrisomes). The definitive work identifying this latter compartmental partitioning has been done in the neostriatum (e.g., Gerfen, 1989; Fujiyama, Sohn, Nakano, Furuta, Nakamura, Matsuda, & Kaneko, 2011), but these same subdivisions have been established histologically for the NAc core as well (e.g., Joel & Weiner, 2000; Berendse, Groenewegen, & Lohman, 1992) — although the patch and matrix compartments are more closely intermixed in the ventral as compared to the dorsal striatum. Both D1- and D2-expressing MSNs have been shown to reside in both compartments of the neostriatum (Rao, Molinoff, & Joyce, 1991), and individual cells have been found in the VS that code selectively for appetitive or aversive USs (Roitman et al., 2005). Nonetheless, despite the considerable circumstantial evidence, our proposal for partitioning VS MSNs into eight functional phenotypes remains speculative.

The positive / negative valence and D1 / D2 distinctions work essentially the same in VS as described for the amygdala. As noted in the above model overview, we hypothesize that the patch MSNs learn to represent temporally-specific expectations for when specific USs should occur (based largely on external cortical inputs, not through timing mechanisms intrinsic to striatum as hypothesized by Brown et al., 1999). By contrast, matrix MSNs are hypothesized to learn to respond immediately based on CS inputs that indicate the possibility of imminent specific USs, producing a gating-like updating signal to OFC and vmPFC areas while simultaneously modulating phasic dopamine via projections to the LHb. The following sections provide some key empirical data that motivates this basic division-of-labor.

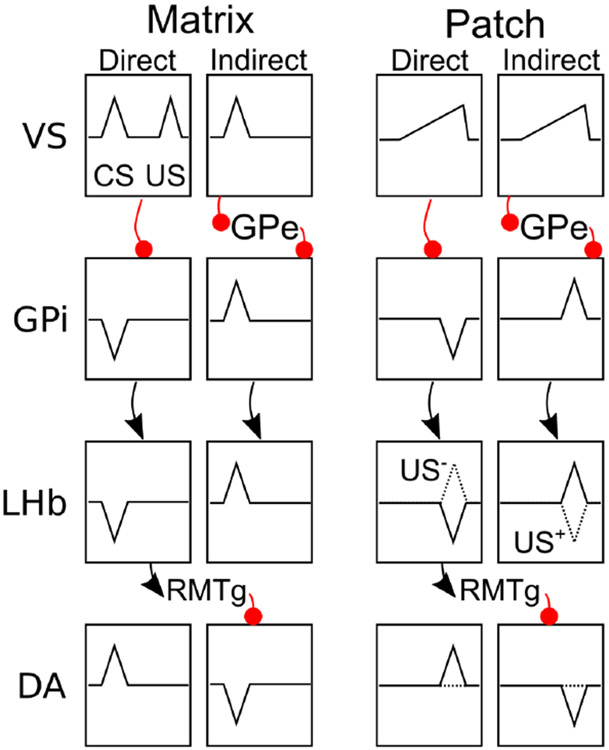
VS Patch MSNs Learn Temporally-Specific US Expectations

A strong constraint distinguishing the function of patch versus matrix subtypes comes from studies showing that at least some MSNs in the patch compartment, but not the matrix, synapse directly onto dopamine cells of the VTA and SNc, and this is particularly the case for VS patch cells (Joel & Weiner, 2000; Bocklisch, Pascoli, Wong, House, Yvon, Roo, Tan, & Lüscher, 2013; Fujiyama et al., 2011). Further, it appears that the MSNs that synapse directly onto dopamine cells express D1 receptors (Bocklisch et al., 2013; Fujiyama et al., 2011). Thus, as described in our earlier paper (Hazy et al., 2010) and elsewhere (Houk et al., 1995; Brown et al., 1999; Vitay & Hamker, 2014), D1-expressing MSNs of the VS patch compartment that synapse onto dopamine cells are in a position to prevent bursting of dopamine cells for primary appetitive events (i.e., USs) as these become predictable. This produces a negative feedback loop where phasic dopamine bursts drive learning on these D1-patch neurons, causing them to inhibit further bursting for expected rewards. This corresponds directly to the classic Rescorla-Wagner learning mechanism, and the PV system in PVLV.

We extend this core model by suggesting that these same D1-expressing VS patch MSNs also send US expectations to the lateral habenula (LHb), enabling the latter to drive pauses in dopamine cell firing when expected rewards have been omitted. Complementarily, some D2-expressing VSPatch MSNs serve as an extinction-coding or evidence-against counterweight to this D1-anchored pathway, mitigating the strength of the expectation, for example in the case of probabilistic reward schedules (see Simulation 2c in Results), and conditioned inhibition training (Simulation 3c).

In essential symmetry with the appetitive case, a second subpopulation of D2-expressing patch MSNs are hypothesized to provide the key substate responsible for learning a temporally-explicit expectation of aversive outcomes. Again, dopamine cell pauses provide the appropriate plasticity-inducing signals so as to strengthen thalamo- and corticostriatal synapses at these D2-expressing MSNs. In this case, however, there is no direct shunting of dopamine cells involved and instead it is in the LHb where the critical cancelling out of expected punishment occurs. The integration of these signals with other inputs is discussed in the section on the lateral habenula below.

VS Matrix MSNs Immediately Report CSs

We hypothesize that VS matrix MSNs learn to respond immediately to events that predict upcoming USs (i.e., CSs), with two separate but synergistic effects, one on phasic dopamine firing, and the other on updating active representations in vmPFC that can encode information about potential USs with sustained firing (Frank & Claus, 2006; Pauli et al., 2012). This latter function is based on the working memory gating model of dorsal striatum (Mink, 1996; Frank et al., 2001; O’Reilly & Frank, 2006; O’Reilly, 2006; Hazy, Frank, & O’Reilly, 2006, 2007), where the direct or Go pathway disinhibits corticothalamic loops, and the indirect or NoGo pathway is an inhibitory opponent to this process. These gating functions involve projections through the globus pallidus and SNr (Alexander, DeLong, & Strick, 1986; Mink, 1996), and in the case of ventral striatum, also the ventral pallidum (VP; Kupchik, Brown, Heinsbroek, Lobo, Schwartz, & Kalivas, 2015). One key difference from the dorsal case is that the D2-dominant pathway in ventral striatum would need to drive a direct-pathway-like disinhibition for aversive USs, as it serves as the acquisition side of that pathway. Supporting this possibility, the Kupchik et al. (2015) study reported that the VS output pathways through the VP do not seem to be as strictly segregated as in the dorsal striatum and, more specifically, those authors also reported that some D2-MSNs in the NAc appear to be in a position to disinhibit thalamic relay cells in the mediodorsal nucleus, a function believed to be restricted to D1-MSNs in the dorsal striatum. Overall, this gating-like function could be much more directly tested in these VS pathways, and remains somewhat speculative. It is also not directly included in the models reported here, although its effects are simulated via a controlled updating of OFC inputs to the model.

The dopaminergic effects of VS matrix signals are hypothesized based on the need for VS to LHb pathways to drive phasic pauses or dips in dopamine firing — these same pathways originating in the VS matrix could then drive pauses for aversive CSs, and we are not aware of any other pathway for supporting this function (e.g., there does not appear to be a direct projection from the amygdala; Herkenham & Nauta, 1977). This would require a D2-dominant pathway to produce net excitation (disinhibition) at the LHb and, according to this scheme, D1-dominant pathways would produce net inhibition in LHb. The latter could then be in a position to produce disinhibitory bursting from dopamine cells, or at least be permissive of such bursting. We review the relevant data on LHb next.

The Lateral Habenula and RMTg

A growing body of empirical data implicates the LHb as the critical substrate responsible for causing tonically active (at ~5 Hz) dopamine cells to pause firing in response to negative outcomes (Christoph et al., 1986; Ji & Shepard, 2007; Matsumoto & Hikosaka, 2007; Hikosaka et al., 2008; Matsumoto & Hikosaka, 2009b; Hikosaka, 2010). The LHb is composed of a largely homogeneous population of glutamatergic cells (Díaz, Bravo, Rojas, & Concha, 2011; Gonçalves, Sego, & Metzger, 2012; Zahm & Root, 2017) that have a baseline firing rate in the range of ~20-30 Hz (Matsumoto & Hikosaka, 2007, 2009b). Firing rates above baseline consistently signal negative outcomes irrespective of appetitive or aversive context, while rates below baseline signal positive outcomes. Thus, primary aversive outcomes (e.g., the pain of a footshock) phasically increase LHb activity via direct excitatory inputs from the spinal cord and related structures (Coizet, Dommett, Klop, Redgrave, & Overton, 2010; Shelton, Becerra, & Borsook, 2012), and this increased LHb activity in turn produces pauses in dopamine cell activity (Christoph et al., 1986; Bromberg-Martin, Matsumoto, Hong, & Hikosaka, 2010c). Conversely, primary appetitive outcomes (e.g., food) produce corresponding decreases in LHb cell activity, potentially via direct projections from the lateral hypothalamic area (Herkenham & Nauta, 1977). Unlike the other substrates described thus far, the LHb does not appear to distinguish between appetitive and aversive sources of excitation or inhibition, and thus represents a final common pathway where these different threads converge. Consistent with this idea, Bernard Balleine and colleagues have recently reported that the LHb seems to play a critical role in conditioned inhibition (Laurent et al., 2017).

Anatomically, the primary afferents that are in a position to convey CS and US-expectation signals to the lateral habenula (LHb) originate from a distinct set of atypical cells in the pallidum, which have been shown to convey signals from the striatum to the LHb (Hong & Hikosaka, 2008; DeLong, 1971; Tremblay, Filion, & Bedard, 1989; Richardson & DeLong, 1991; Parent, Lévesque, & Parent, 2001) (Figure 4). These atypical, LHb-projecting cells appear to reside in two narrow slivers of tissue at the border between the GPe and GPi and between the GPi and VP (Hong & Hikosaka, 2008). Further, there appear to be LHb-projecting cells interspersed within the parenchyma of the VP proper as well (Hong & Hikosaka, 2013; Jhou, Fields, Baxter, Saper, & Holland, 2009a). As partially characterized by Hong and Hikosaka (2008), the LHb-projecting cells of the pallidum appear to be tonically active in the range of 50-70 Hz and to exert a net excitatory effect on LHb cell activity, in contrast to the predominant projection cells of the pallidum which are uniformly net inhibitory at their downstream targets (e.g., Mink, 1996). Also relevant is the recent demonstration that pallido-habenular axons consistently co-release both glutamate and GABA (Root, Zhang, Barker, Miranda-Barrientos, Liu, Wang, & Morales, 2018b), which is likely important in maintaining an excitatory-inhibitory balance in the LHb since the latter appears to have little or no local GABAergic interneurons of its own. Finally, directly stimulating diverse, heterogeneous regions of the striatum led to excitations, inhibitions, or neither in the lateral habenula in an indeterminate, patchy pattern (Hong & Hikosaka, 2013), although it remains to be determined whether those striatal cells project onto the same GPb cells that project to lateral habenula (Hong & Hikosaka, 2013), nor has it been determined the degree to which the striatal afferents to these cells represent collaterals of typical striatopallidal projections, or arise from a distinct subpopulation.

Figure 4:

Four channels may convey acquired signals from the striatum to the lateral habenula, with Direct path inhibiting GPi (globus pallidus internal segment) while Indirect path via GPe (external segment) has a disinhibitory effect. The effect of GPi on LHb (lateral habenula) appears to be net excitatory, while LHb is net inhibitory on DA (VTA, SNc) via the RMTg (rostromedial tegmental nucleus). As shown, immediate firing from the Matrix pathway can drive appropriate phasic DA signaling (Direct = positive valence, Indirect = negative), while Patch has more delayed timing, with the timing becoming more precise via GP dynamics, such that the effect on LHb opposes the direct effect of USs (dotted lines, negative valence for the Direct pathway, positive for Indirect) – if the US does not occur, then DA responds as shown in the solid lines.

For the various D1 versus D2 MSNs to have the appropriate effects on the LHb, the GABA inhibitory output from the MSNs must either be conveyed directly or the sign must be reversed, as shown in Figure 2. For example, for the appetitive VS patch D1 MSNs proposed to shunt dopamine bursts, they need to have a net excitatory effect on the LHb so that they can drive phasic pausing of dopamine firing when an anticipated reward is otherwise omitted. To the extent that opposing D2 VS patch MSNs act to inhibit the LHb, they can counteract this effect, when the US expectation is reduced or extinguished. Similar logic can be carried through for all the other cases of VS MSNs.

Because the LHb neurons are predominately glutamatergic, there must be an intervening inhibitory node between those cells and the dopamine cells in order to generate pauses. While LHb cells have been shown to have a weak projection onto GABAergic interneurons in the VTA/SNc, the main means by which LHb activity produces pauses appears to be via a tiny, newly characterized GABAergic collection of cells situated between the LHb and VTA called the rostromedial tegmental nucleus (RMTg; Jhou et al., 2009a; Hong, Jhou, Smith, Saleem, & Hikosaka, 2011; Bourdy & Barrot, 2012; Stamatakis & Stuber, 2012). Interestingly, cells of the RMTg have also been shown to receive some direct input from the parabrachial nucleus (PBN), which encodes aversive USs (Jhou, Geisler, Marinelli, Degarmo, & Zahm, 2009b), and thus excitation of the RMTg seems capable of driving dopamine cell pauses of dopamine cells via pathways other than the LHb.

Finally, there is evidence that a tiny subset of LHb axons synapse directly onto a very small subpopulation of dopamine cells (Lammel et al., 2012; Watabe-Uchida et al., 2012) and a tiny minority (2/103) of dopamine cells have been reported to increase firing in response to LHb stimulation (Ji & Shepard, 2007), providing a straightforward mechanism by which aversive events might drive dopamine cell bursting in that small subpopulation, which could be the same aversion-excited cells identified by Brischoux et al. (2009). Of course, as noted above, further studies are needed to confirm that those cells are indeed dopaminergic. Also of interest, although not included in the PVLV model currently, is a newly characterized population of non-dopaminergic cells in the VTA that project to the LHb, co-releasing both glutamate and GABA just like the pallido-habenular axons noted earlier (Root et al., 2018b). This pathway appears to be involved aversive conditioning (Root et al., 2014).

Basolateral Amygdala to Ventral Striatum Connections

Although the amygdala (LV) and VS-LHb (PV) systems function largely independently there are two important ways in which they interact. First, and more indirectly, VS matrix MSNs are proposed to gate US-specific working memory-like goal state representations into the OFC and/or vmPFC, and these cortical areas have very strong reciprocal interconnectivity with the BLA (Schoenbaum, Chiba, & Gallagher, 1998, 1999; Ongür & Price, 2000; Ongür, Ferry, & Price, 2003; Schoenbaum, Setlow, Saddoris, & Gallagher, 2003; Holland & Gallagher, 2004; Saddoris, Gallagher, & Schoenbaum, 2005; Pauli et al., 2012). More directly, and in the other direction, the ventral striatum also receives a very dense excitatory projection from the BLA originating predominantly from the basal and accessory basal nuclei (Amaral et al., 1992; Ambroggi, Ishikawa, Fields, & Nicola, 2008; Stuber, Sparta, Stamatakis, van Leeuwen, Hardjoprajitno, Cho, Tye, Kempadoo, Zhang, Deisseroth, & Bonci, 2011), and there is good reason to believe that these BLA-VS connections may not function as simple driving inputs and instead serve a more modulatory function. For example, in addition to producing excitation of MSNs, Floresco, Yang, Phillips, and Blaha (1998) showed that BLA inputs can also cause the release of dopamine from VTA derived terminals in the absence of axonal activation; and changes in extracellular dopamine levels in VS can modulate the relative influence between corticostriatal versus hippocampostriatal inputs in driving MSN behavior (Goto & Grace, 2005). Finally, limited circumstantial evidence supports the notion of a kind of hard-wired one-to-one connectivity between cells coding for similar USs in BLA and VS (e.g., food-responsive cells connecting with food-responsive cells). This includes: some cells in both BLA (Ono et al., 1995; Uwano et al., 1995) and VS (Roitman et al., 2005) respond selectively to distinct USs; and, the BLA-to-VS projection is substantially topographic (McDonald, 1991).

Based on these considerations the BLA-VS projection is implemented in the PVLV framework as non-learning, modulatory connections whose main function is to constrain learning to VS MSNs (both patch and matrix) coding for the same US representations currently active in the BLA as a result of CS-US pairing. The modulatory nature of these connections also makes sense by allowing VS patch neurons to integrate appropriate timing signals and fire at the expected time of US outcomes, whereas standard excitatory inputs from BLA would tend to drive immediate rather than delayed firing. In the following section, we integrate all of these biological considerations into the explicit computational mechanisms of the PVLV model.

Methods: PVLV Model Computational Implementation

This section describes the essential computational features of the PVLV model, including the key learning equations and general simulation methods. The intention is to explain the essence of how the model achieves the functionality it does and give the reader a foundation for understanding the simulations discussed in the subsequent Results section. However, to truly understand a model of this complexity and scope, the reader is encouraged to download and explore the implemented model which is implemented in the emergent simulation software (Aisa, Mingus, & O’Reilly, 2008). See the Appendix for instructions for downloading emergent as well as the PVLV model. The Appendix also contains additional details about the computational implementation beyond that provided here.

General Methods

PVLV is implemented within the general Leabra framework (O’Reilly, Munakata, Frank, Hazy, & Contributors, 2012) using a rate-code version of the adapting exponential (AdEx) model of Gerstner and colleagues (Brette & Gerstner, 2005), which provides a standard ion-conductance model of individual neuron dynamics, with excitation, inhibition, and leak channels, integrated in a single electrical compartment. Except for the BLA layers, simple localist representations of different USs are used, to facilitate analysis and visual understanding of model behavior. Four parallel appetitive and four aversive US-coding pathways are implemented through both the amygdala and VS components in order to support four kinds of rewards (e.g., water, food; indexed 0-3) and punishments (e.g., shock, hotness; indexed 0-3) and these are easily extensible to accommodate more, if desired.

A schematic of the overall PVLV architecture was shown in Figure 2, and the actual emergent network used for all the simulations is shown in Figure 5, where differing subtypes of neurons are organized within separate Layers with names as shown. US occurrence is conveyed to the network via PosPV and NegPV (primary value) input layers, CS-type activity via a Stim_In input layer, and context information via a Context_In layer representing unique conjunctive information associated with the various circumstances under which any particular CS might be encountered by a subject. All other network activity is generated intrinsically for each unit.

Figure 5:

The PVLV model in emergent. Three Input layers to the model are at top (USTime_In, Stim_In, Context_In). Learned value (LV, Amygdala) layers are highlighted with light blue background. Primary value (PV, Ventral striatum) layers are highlighted by a light red background. Primary rewards or punishments are delivered by the two layers in box at lower left. Dopamine and associated nuclei are on the lower right, p suffix indicates positive valence: VTAp represents majority of standard RPE-coding DA neurons (including SNc), while VTAn represents small number of medial DA neurons responding with phasic bursts for aversive outcomes. PPTg layers drive phasic DA activity and LHbRMTg represents combined function of lateral habenula and RMTg.

The two major components of the PVLV model, the Learned Value (LV) amygdala system and the Primary Value (PV) ventral striatum (VS) system, are described at a computational level below in the rough order of information flow for each. The dopamine components (VTAp, VTAn) integrate the signals received from both systems. Overall, the LV/amygdala system exhibits sustained, but fluctuating activation patterns over time, reflecting an evolving overall assessment of the affective implications of the current situation (i.e., the availability and/or imminence of specific rewards or threats); these representations are conceived to project broadly to many other brain areas to alert and inform appropriately on an ongoing basis. In contrast, the PV/ventral striatum system has more punctate dynamics, reflecting its more action-oriented role in driving specific responses to affectively-important events as, for example, initiating an approach or withdrawal response; or, gating US-specific goal-state representations into OFC working memory as described in the previous section on neurobiological mechanisms.

To present inputs to the model, time is discretized into 100 msec timesteps (termed alpha trials in reference to the 10 Hz alpha rhythm) with the network state updated every msec (i.e., one update cycle ≈ 1 msec). Behavioral (experimental) Trials (e.g., one CS-US pairing sequence) typically take place over five sequential timesteps/alpha trials. The first timestep (t₀) typically has nothing active; followed by the CS onset at t₁; a subsequent timestep where that CS remains active and nothing else new happens (t₂), and then the US either occurs or not on the t₃ timestep; and finally both US and CS go off in the t₄ (final) timestep. Activation states are updated every cycle (corresponding to 1 msec), and weight changes are computed network-wide at the end of every timestep (alpha trial). The discretization of input presentation and learning to 100 msec timesteps makes everything simpler; subsequent development is planned to extend the model so as to operate in a more continuous fashion.

Amygdala Learned Value System

The amygdala portion of the model is comprised of two groups of layers representing BLA and CEA. Each group has layers reflecting the four principal cell phenotypes described in the previous section about the neurobiology. In the BLA there are the 2x2 D1/D2 x valence layers: BLAmygPosD1, BLAmygPosD2, BLAmygNegD2, BLAmygNegD1; for the CEA there are four corresponding layers: CElAcqPosD1, CElExtPosD2, CElAcqNegD2, CElExtNegD1 corresponding to four cellular phenotypes hypothesized for the lateral segment; plus two output layers from CEm: CEmPos and CEmNeg (medial segment). BLA units receive full projections from either the Stim_In (CS) layer (acquisition-coding) or Context_In layer (extinction-coding) and, in the case of the acquisition-coding layers (BLAmygPosD1, BLAmygNegD2) US-specific (non-learning) inputs from the PosPV (appetitive USs) and NegPV layers, the latter’s onset typically occurring two timesteps (alpha trials; 200 msec) after CS-onset. Extinction-coding layers (BLAmygPosD2, BLAmygNegD1) do not receive input from US-coding layers since USs do not occur on extinction trials.

Learning for the acquisition-coding units occurs for the connections from Stim_In as a function of three factors: 1) the activation of the sending inputs on the previous timestep, 2) the temporal delta over the BLA receiving unit activation between the previous and the current timesteps, and 3) the absolute value of phasic dopamine:

$$\Delta w=ϵx_{t-1}(1+\mid \delta \mid )(y^{\ast }-y_{t-1})$$ (1)

where ε is the learning rate; x_t−1 is the sending activation from Stim_In to BLAAmyg-PosD1/BLAmygNegD2 (prior timestep); δ is the phasic dopamine signal; y is the current timestep receiving unit activation; and y_t−1 is its activation from the previous timestep. The absolute value of phasic dopamine (∣δ∣) serves as a learning rate modulator, and dopamine also modulates the activation of the receiving neuron, so that the temporal delta reflects the D1 vs. D2 impact of dopamine on each of the different pathways:

$$y^{\ast }=g(\eta +\gamma f(\delta )y)$$ (2)

where η is the excitatory net input to a given BLA neuron; γ is a phenotypically-specific gain factor; and f(δ) is a function of the phasic dopamine signal that has a positive relationship to dopamine for D1-dominant neurons, and a negative one for D2-dominant neurons. The receiving unit activity y ensures that inactive neurons do not experience any dopamine-dependent changes.

This learning rule allows direct US-driven signals, and / or phasic dopamine, to drive the direction of learning. It resembles a standard delta rule / Rescorla-Wagner (RW) learning function, and the TD learning rule, but with a few important differences. First, the driving activation in the delta, y*, is not a simple scalar reward outcome (as in RW), and nor does it explicitly contain an expectation of future rewards (as in TD), although the dopamine modulation can be considered to reflect such an expectation in some situations. Thus, the resulting representations are not as strongly constrained as in RW and TD, and in general can reflect various influences from other types of external inputs, along with local inhibitory dynamics reflecting the opponency relationship between D1 and D2, to produce a more complex distributed representation. Due to the distributed nature of these representations, there is no constraint that the prior time-step activation learn to predict the next time step, as in the TD algorithm. Nevertheless, the delta rule across time like this does drive the BLA to generalize learning at later times to earlier times, and more generally to be sensitive to changes in state as compared to static, unchanging elements. These features, in common with the TD and RW rules, can be considered essential features of RPE-driven learning, and are shared with all of the learning in PVLV (including prior versions of the framework, which are discussed further in the Appendix).

There is one further important difference from TD: The positive rectification of the PPTg’s derivative computation prevents the generation of negative dopamine signals from decreases in amygdala activity (and is generally consistent with the biological constraint that the LHb is exclusively responsible for phasic dopamine dips). This prevents the negative delta driven by US offset from driving a negative dopamine signal that would otherwise counteract the positive learning occurring at US onset. Interestingly, the dependence of learning on at least some level of phasic dopamine (via the ∣δ∣ term) is also necessary, as otherwise the negative delta driven by the US offset itself would drive offsetting learning in the BLA, even if it did not otherwise drive phasic dopamine dips. In TD, an absorbing reward is typically employed to achieve a similar effect as this biologically-motivated positive rectification. More generally, this positive rectification means that while BLA activation states accurately track both ups and downs in US expectations (due to the US drive and opponent dynamics), it is strongly biased to only learn about and report positive improvements in these expectations over time. This likely reflects an emphasis on overall progress toward appetitive goals (O’Reilly, Hazy, Mollick, Mackie, & Herd, 2014), and represents an important asymmetry between appetitive and aversive valence.

Extinction-coding BLA units do not receive a direct US projection, and instead receive modulatory, US-specific connections from corresponding acquisition-coding units that simulate an up-state type of modulation, which has the functional effect of constraining extinction learning about USs that are actually expected to occur. This solves the critical problem of learning from a nonevent, in an expectation-appropriate manner. For simplicity, all the units responding to a given US are grouped together into subgroups within the BLA layers. We impose a broad layer-level inhibitory competition within these BLA layers, reflecting typical cortical-like inhibitory interneuron effects. In addition, the extinction-coding layers send all-to-all inhibition back to the acquisition layer, to induce competition between these different layers. It would also be possible to include similar inhibition from acquisition to inhibition, but that would be overcome by the above modulatory effects, so we left this out to make that simpler.

The central nucleus, lateral segment (CEl) units are tonically active, and US-specific acquisition- and extinction-coding units are interconnected by mutually inhibitory connections, reflecting the On and Off subtypes. The two acquisition-coding layers (CElAcqPosD1, CElExtNegD2) receive learning CS sensory information as full projections from Stim_In, and also non-learning one-to-one US projections which function as a teaching signal. Both acquisition-coding and extinction-coding units (CElAcqPosD2, CElExtNegD1) receive US one-to-one projections from corresponding BLA layers. All learning connections follow the same learning rule as for the BLA (Equation 1). CEl extinction-coding units do not receive input from the Context_In layer and do not therefore support extinction learning on their own. Instead they reflect learning upstream in their BLA counterparts.

Thus, although BLA and CEl share a learning rule and basic organization in terms of representing evidence for and against a given US, they are envisioned to do this in different ways that align with their status as neocortex-like (BLA) versus basal-ganglia-like (CEA): the BLA is more high-dimensional and contextualized, while the CEA is lower-dimensional, more strongly opponent-organized, and provides a more continuous, quantitative readout.

The CEm output layer computes the net evidence in favor of each US, in terms of the difference between acquisition vs. extinction, via one-to-one, non-learning projections from the corresponding CEl units. The sum of all four US-coding units in the CEmPos (only) layer projects to the single-unit PPTg layer, which computes the positively-rectified derivative of its net input on each alpha trial. This signal is conveyed to the VTAp unit where it is integrated with any PosPV layer activity, and any net disinhibitory LHbRMTg input, to produce the net dopamine cell bursting drive on each alpha trial, which is then ultimately integrated with any direct shunting inhibition from the VSPatch layers as well as any net pause-promoting inhibition from the LHbRMTg (addressed next).

Ventral Striatum Components

The Ventral Striatum can be thought of as performing two distinct versions of the opponent-processing evidence evaluation ascribed earlier to the CEl, as is evident in Figure 2. VSPatch units learn to expect the timing and expected value of US outcomes, while VSMatrix layers learn to report immediate signals at the time of CS onset. VSPatch layers constitute the Primary Value inhibitory (PVi) system from earlier versions of PVLV model, and they send shunt-like inhibitory projections directly to the main dopamine cell layer (VTAp) to cancel expected dopamine bursts (typically US-coding PosPV inputs).

Among other inputs, MSNs of the VS patch receive goal-related, US-specific information from the OFC and other vmPFC areas. As these cortical areas are currently outside the scope of the PVLV framework, a specialized input layer (USTime_In) provides hypothesized temporally-evolving information about the upcoming occurrence of particular USs to the VSPatch layers. This input layer captures the idea that VS matrix MSNs learn to report the occurrence of events predictive of specific US occurrences and also trigger the gating of goal-expectation representations for particular USs (e.g., water) into the OFC. Consistent with neural data, a component of these representations undergoes a systematic temporal evolution in its activation vector that can act as a reliable substrate for learning about the fine-grained temporal characteristics of any particular CS-US interstimulus interval (ISI) up to a scale of several seconds. Here we simply implemented as a localist time representation that is unique for each particular CS-US pair (e.g., ‘A’ predicts US1, ‘A’ predicts US2, ‘B’ predicts US1, and so on).

All VSPatch units receive US-specific modulatory connections from corresponding BLA acquisition-coding units and these serve to drive an up-state condition that constrains learning to appropriate US-coding units, and also to bootstrap initial learning before the weights from the USTime_In representations are sufficiently strong to produce activation on their own.

All VSPatch afferent connections learn according to the following, standard three-factor (dopamine, sending, and receiving activation) equation, as used in many basal ganglia models (Frank, 2005):

$$\Delta w=ϵf(\delta )x\max (y,b)$$ (3)

where like terms are as in the earlier equations and the new term b represents the up-state conveying signal from the associated BLA units. The max(…) operator serves to bootstrap learning even when VSPatch units are not themselves yet activated, but then transitions to letting their own activation values (y) determine learning subsequently. This latter transition is critical for facilitating the learning of appropriately calibrated expected value representations.

VSMatrix layers do not receive projections from the temporally evolving representations of the USTime_In layer, but instead receive input from the same Stim_In layer as projects to the amygdala. This reflects their role in immediately reporting events predictive of US occurrence. They also receive modulatory projections from the BLA similar to those in the VSPatch that act to constrain learning to the specific US expected and bootstrap learning until the weights from the Stim_In layer have become strong enough to produce some VSMatrix unit activity on their own. Activation in VSMatrix units is acquired for the current alpha trial when CS-onset occurs and the activity across all VSMatrix layers is conveyed to the LHbRMTg layer where it is interpreted as excitatory or inhibitory depending on the particular valence representation and dopamine receptor (D1 vs. D2) expressed.

Learning for weights afferent to the VSMatrix layers follows the general three-factor learning rule, but with a synaptic-tag based trace mechanism that is used to span the timesteps between CS-driven VSMatrix activity and subsequent US-triggered dopamine signals. Specifically, when a given VSMatrix unit becomes active, connections with active sending input acquire a synaptic taglike trace value equal to the product of sending times receiving unit activation with the trace persisting until a subsequent phasic dopaminergic outcome signal after which it is cleared. This trace mechanism is motivated by a growing body of research implicating such synaptic tagging mechanisms in LTP/D generally (e.g., Redondo & Morris, 2011; Rudy, 2015; Bosch & Hayashi, 2012) and, particularly, recent direct electrophysiological evidence for an eligibility trace-like mechanism operating on MSN synapses in the striatum that serves to span delays of roughly >50 but <2000 msec between synaptic activation and a subsequent phasic dopamine signal (Yagishita et al., 2014; Gurney, Humphries, & Redgrave, 2015; Fisher et al., 2017).

The synaptic tag trace activation is computed as the sender-receiver activation co-product:

$$tr=xy$$ (4)

and subsequent dopamine-modulated learning is driven by this tag times the phasic dopamine signal:

$$\Delta w=ϵf(\delta )tr$$ (5)

Midbrain Dopamine Mechanisms: LHb, RMTg, VTA

The LHbRMTg layer abstracts LHb and RMTg function into a single layer. It integrates inputs from all eight ventral striatal layers and both PV (US) layers into a single bivalent activity value between 1.0 and −1.0 representing phasic activity above and below baseline respectively. VSPatch activities produce a net input to the LHbRMTg at the expected time of US occurrence and reflects the relative strength of D1- vs. D2-dominant pathways for each valence separately. For positive valence, a positive net VSPatchPosD1 – VSPatchPosD2 input produces excitation that serves to cancel any inhibitory input from a positive US and, critically, if such excitatory input is unopposed because of US omission, the LHbRMTg can produce an negative dopamine signal in the VTAp layer. Symmetrical logic applies for corresponding aversive VSPatch and NegPV inputs, with the signs flipped and one additional wrinkle: the VSPatch input is discounted in strength so that it cannot generally fully cancel out the negative US even when fully expected (Matsumoto & Hikosaka, 2009a).

VSMatrix inputs follow a similar overall scheme where LHbRMTg activity reflects a net balance between D1- and D2-dominant pathways within each valence, except that the signs are reversed relative to those from the VSPatch. That is, the positive valence pathway (VSMatrixPosD1 – VSMatrixPosD2) net difference has an inhibitory effect on LHbRMTg, and vice-versa for the aversive valence pathway. Thus, a CS associated with an aversive outcome will drive a net excitation of the LHbRMTg and a resulting negative dopamine signal. See the Appendix for pseudocode of the integration computation performed.

PVLV’s main dopamine layer (VTAp) receives input from primary US inputs (PosPV, NegPV), the CEm via the PPTg layer, and the LHbRMTg. It also receives a direct shunt-like inhibitory input from both positive-valence VSPatch layers. The CEm pathway projects to the PPTg which computes a positive-rectified temporal derivative of the overall CEm activation; thus phasic dopamine signaling reflects positive-only changes in a fluctuating, variably sustained amygdala signal. Positive-rectification of this derivative is consistent with the emerging view that the LHb pathway is the sole mechanism responsible for producing pauses in tonic dopamine firing. And, as noted earlier, the positive-rectification of PPTg inputs to VTAp has important computational implications for avoiding anomalous learning that would otherwise result form negative fluctuations such as reward offset.

PVLV’s VTAp layer abstracts the valence-congruent majority of dopamine neurons, exhibiting positive dopamine signals in response to direct positive-valence US inputs, and increases in CEm temporal-derivative excitation, and negative signals from increases in LHbRMTg activity. In addition, direct VSPatch inputs act to shunt positive signals (dopamine cell bursting) that would otherwise occur from positive-valence US inputs, but these shunt-like inputs cannot produce negative signals themselves, instead requiring integration through the LHbRMTg pathway. The positive and negative ( < 0.0) signals computed by the VTAp are transmitted to all relevant PVLV layers and these are used to modulate learning as described above.

PVLV also incorporates a negative-valence complement to the VTAp, called VTAn, which corresponds biologically to the smaller population of valence incongruent dopamine neurons described earlier. These respond with phasic bursting to aversive USs and CSs. Currently, we do not directly utilize the outputs of this system, and more data is needed to fully determine its appropriate behavior for all the relevant combinations of inputs.

Results

Overview

The simulation results here address the motivating phenomena identified in the Introduction, and progress in complexity from appetitive acquisition to extinction, blocking, conditioned inhibition, and finally aversive conditioning. The first set of simulations addresses: different time courses for acquired phasic bursting at CS-onset versus loss of bursting at US-onset; a dissociation between the loss of bursting at US-onset and the generation of pauses for its omission; the asymmetry between early versus late reward; and the differential effect of increasing delays on LV versus PV learning. The second set of simulations on extinction and related phenomena, highlight the utility of explicit representations that track evidence against the imminent occurrence of particular USs. By exerting a counteracting effect upon previously acquired representations of US expectations, such representations engender rapid adaptability. Phenomena addressed include: rapid reacquisition; renewal and the increased sensitivity of extinction-related phenomena to context; and, probabilistic reward contingencies (accounted for by the same basic mechanisms). Spontaneous recovery and reinstatement are discussed as well (not simulated). The third set of simulations address the related paradigms of: blocking; conditioned inhibition; and, second order conditioning. These paradigms all introduce a second informative sensory stimulus (CS2) after an initial CS-US pairing has been trained. The fourth set of simulations address phasic dopamine signaling in aversive processing, illustrating how that might be integrated into the overall system despite some important anomalies and asymmetries relative to the appetitive case. For reference the phenomena explicitly simulated are listed in Table 1. Later, a separate table (Table 2) lists related phenomena not explicitly simulated, but considered within the explanatory scope of the PVLV framework and RPE-based models generally. Later, in the General Discussion section we also discuss a third category of important phenomena involving higher-level, cortical processing considered out-of-scope for the current framework. Finally, note that we have listed the relevant Motivating Phenomena from the Introduction in the simulation headers.

Table 1:

Pavlovian phenomena simulated

Phenomenon	Sim
Appetitive conditioning	1a-c
Goal- vs. sign-tracking	1d
Extinction	2a,b
Rapid reacquisition	2a
Renewal	2c
Probabilistic reinforcement	2c
Blocking	3a
Conditioned inhibition	3b
Second-order conditioning	3c
Aversive conditioning	4a,b
Avoidance learning	4b
Safety signal learning	4b

Table 2:

Pavlovian phenomena not explicitly simulated but within the explanatory scope of the PVLV framework. NOTE: not impl = not implemented

Phenomenon	Sim	Comment
Variable reward timing	see 1c	Drives PV (VS) firing over broader time window
Autoshaping	see 1d	See sign-tracking
Cond orienting resp (COR)	see 1d	See sign-tracking
Incentive salience	see 1d	See sign-tracking
Extinction (aversive)	see 2a,b	Largely follows appetitive pattern.
Reinstatement	see 2b	US-reactivation of CS-specific reps in Amygdala? (not impl).
Spontaneous recovery	see 2b	Internal context drift? (not impl).
Partial reinf extinction effect	see 2c	Reliable in Pavlovian case? (not impl).
Unblocking-by-identity	3a
Unblocking, upward	see 3a	Consistent with std RPE (trivial).
Unblocking, downward	–	Complex timing required – unclear if real (not impl).
Overexpectation	see 3a	Same account as unblocking-by-identity in our model.
Overshadowing	-	Strongly dependent on relative CS salience (not impl).
Reversal learning	-	Essentially sum of 1a-c and 4a,b, also salience (not impl).
Counterconditioning	-	Like reversal learning, pits valence reversal competitive effects against any acquired salience effects (not impl).
Latent inhibition	-	Habituation of novelty-triggered bursts? (not impl).
Sensory preconditioning	-	Cortically mediated and largely associative?
Variable reward magnitude	-	See discussion in Neurobiological Substrates and Mechanisms.

Simulations 1a-d: Two Main Subsystems, Multiple Sites of Plasticity

The acquisition of phasic dopamine bursting at CS-onset and its loss at US-onset are not a zero-sum transfer process of a conserved quantity of prediction error. This first set of simulations explores this dissociation and how separate subsystems — and multiple sites of plasticity — can produce the basic pattern of empirical results seen in appetitive conditioning.

Simulation 1a: Robust simultaneous CS, US bursting (Motivating: 1)

First, this simulation illustrates the basic process of acquisition of a Pavlovian CS-US association. The unexpected onset of the US drives a delta-activation in BLA acquisition-coding units responsive to that US, and a phasic dopamine signal. These together drive increases in weights from CS-coding Stim_In inputs that were active in the previous timestep (alpha trial), to active BLA and CEl units. This logic applies regardless of the valence of the US, but is US-specific due to one-to-one projections from the PosPV or NegPV layers. As CS-driven Stim_In-to-BLA weights get stronger (and thus BLA activations) US-driven activation deltas progressively decrease as does its accompanying dopamine signal, due to learning in the VS patch (PV) system. Thus, weight changes also decrease and unit activity can naturally approach some proxy of the magnitude of the US-driven activation (Belova, Paton, & Salzman, 2008; Bermudez & Schultz, 2010).

This simulation captures the finding that robust phasic dopamine bursting occurs for both the CS and US over a relatively large portion of the acquisition process (Figure 6; Pan et al., 2005; Ljungberg et al., 1992). In the corresponding PVLV results, dopamine activity at the time of CS-onset tracks learning in the BLAmygPosD1 and CElAcqPosD1 layers, while US-onset dopamine follows (inversely) learning in the VSPatchPosD1 layer. Learning in each of these LV vs. PV pathways is at least somewhat independent from each other, although the phasic dopamine signal at the time of the US does augment learning in the LV (amygdala). This relationship means that it is important for the PV system to learn more slowly than the LV overall, so that it does not prematurely cutoff learning in the LV. This co-occurrence of CS and US phasic dopamine is a necessary prediction from this framework.

Figure 6:

Simulation 1a: Dissociable time courses of learning-induced changes to CS- and US-onset phasic bursting. (a) Population dopamine cell activity during early learning (top) and fully trained (bottom), adapted from Ljungberg et al.'s, (1992), Figure 13 with permission from The American Physiological Society: Journal of Neurophysiology, copyright 1992. Note robust firing after both CS- (left vertical line) and US-onset (right vertical line) early in training (top). (b,c) Activity in key model components during initial early learning (b); and, after full training (c). KEY: solid black - VTAp activity (dopamine cells); dashed red - CEmPos activity (central amygdalar nucleus, medial segment - positive coding); zipper orange - VSPatchPosD1 activity (ventral striatum patch cells).

Many parameterizations of the TD model would not predict this extensive co-occurrence of CS and US dopamine firing, because the underlying derivation of the model from the Bellman equation causes it to learn maximally consistent expected reward estimates over time. Specifically, the dopamine signal δ in this framework reports deviations from temporally-consistent predictions, and thus any increase in expectation at one point in time (e.g., the CS onset) typically results in a corresponding decrease in δ at later points in time (e.g., the US). Nevertheless, it is possible to parameterize the state update using a λ parameter to temporally-average over states, which reduces the ability of the model to have differential expectations at different points in time, and thus enables a longer period of CS and US dopamine firing, while also reducing the extent to which the dopamine burst progresses forward in time gradually over learning, which is also not seen in recording data (Pan et al., 2005). Further, TD models operating over belief states have also been able to capture simultaneous phasic dopamine firing to the CS and US (Daw, Courville, & Touretzky, 2006).

More generally, the different time courses for acquisition of CS-onset dopamine signaling and its loss at US-onset has important implications for the respective effects upon behavioral change dependent on each of these signals. For example, US-triggered dopamine bursts are likely important for training a specific subset of conditioned responses (CRs) dubbed US-generated CRs by Peter Holland (e.g., food-cup behavior; Holland, 1984; Gallagher, Graham, & Holland, 1990), as well as for training instrumental actions. In particular, the dissociation in learning between the two subsystems could play a role in the recently described distinction between so-called sign-trackers and goal-trackers (Flagel et al., 2010; Flagel et al., 2011) as addressed below under simulation 1d.

Simulation 1b: Two pathways from PV to DA (Motivating: 2, 4)

There are two pathways in the PVLV model from the VS patch neurons that learn to anticipate US outcomes: one that directly shunts dopamine burst firing, and another via the lateral habenula (LHb) that can drive phasic dips for omitted USs. Figure 7a shows that there was flat, baseline-level activity in the LHb at the time of a predicted reward (Matsumoto & Hikosaka, 2007), meaning that the mechanism shunting dopamine bursting at this time must not be the LHb. This then indirectly supports our hypothesis that the direct inhibitory projections onto dopamine cells of the VTA and SNc are responsible (Gerfen, 1985; Gerfen, Herkenham, & Thibault, 1987; Smith & Bolam, 1990; Joel & Weiner, 2000). Figure 7b shows simulation results demonstrating balanced excitatory input to the LHbRMTg from activity in the VSPatchPosD1 layer that counteracts inhibitory input from PosPV activity at the time of a predicted reward, resulting in flat LHbRMTg activity. Figure 7c shows unopposed VSPatchPosD1 activity at the time of reward omission, driving increased LHbRMTg activity and, consequently, decreased VTAp activity, i.e., phasic pausing. One functional motivation for having these two pathways is that the VS patch neurons likely exhibit ramping activity toward the peak timing of US onset — it is useful to shunt any bursts within this ramping period, but it would not be as useful to continuously drive dopamine dips until after it is certain that the US is not coming. Thus, the LHb pathway is more phasic and precisely timed. This and other timing-related implications of these two pathways are developed further in the General Discussion.

Figure 7:

Simulation 1b: Separate pathways mediate loss of bursting for reward versus pausing for omission. (a) Empirical results from Matsumoto & Hikosaka (2007), adapted from their Figure 3a with permission from Springer Nature: Nature, copyright 2007, showing flat activity in the LHb following a predicted reward outcome (solid red line). Omitted reward produces phasic increase in activity (dotted blue). (b) Model results showing balanced excitatory inputs to LHbRMTg layer (dash-dot blue line) from VSPatchPosD1 activity (zipper orange) and inhibitory input from PosPV activity (dotted magenta) at the time of predicted reward. While VSPatchPosD1 activity is lower than for PosPV its input to LHbRMTg has a gain factor of 1.7 resulting in an approximate balance. (c) Unopposed input from VSPatchPosD1 activity (zipper orange) at the time of reward omission drives increased LHbRMTg activity (dash-dot blue) and pausing of VTAp dopamine cell firing (solid black).

Simulation 1c: Asymmetric dopamine signaling for early versus late reward (Motivating: 2,4)

Rewards that occur earlier than expected produce dopamine cell bursting, but no pausing at the usual time of reward. In contrast, rewards that occur late produce both signals as predicted by a simple RPE formalism (Figure 8a; Hollerman & Schultz, 1998). Figure 8b,c shows corresponding simulation results. For late rewards, a negative dopamine signal at the time of expected reward is driven by the unopposed VS patch activity, followed by a now unopposed positive US input driving a positive burst. This same US-driven burst occurs for early rewards, but the subsequent negative dip no longer occurs because of the dynamics of the OFC, which we hypothesize is activated with a temporally-evolving US-specific representation at the time of CS onset (via VS matrix phasic gating), and serves as the bridge between the LV and PV systems. Once the US occurs, we hypothesize that this OFC representation is gated back off (i.e., the outcome has been achieved), and thus, the corresponding drive from OFC to VS patch US predictions is absent, and no such expectation is generated. In our model, we implement this dynamic by externally driving activation of the USTime_In input layer as shown in Figure 8d. These dynamics can be considered a variant of the mechanism employed by Suri and Schultz (1999) in accounting for this same phenomenon (see also Suri, 2002), but their model remained in a purely CS-focused space, instead of focusing on OFC as bridging between CS and US.

Figure 8:

Simulation 1c: Asymmetric dopamine signaling for late-versus-early reward. (a) Empirical results adapted from Hollerman and Schultz (1998), Figure 6b with permission from Springer Nature: Nature Neuroscience, copyright 1998, showing an asymmetric pattern of firing for late (thin arrow) versus early (thick arrow) reward delivery. (b,c) Simulation results for late-versus-early reward respectively, capturing the empirical results. (d) Focus on the USTime_In input layer, representing the OFC bridging between CS and US, with a temporally-evolving, US-specific pattern that drives the VS patch expectations of US timing. When the US arrives early, it resets this US timing representation, thereby preventing VS patch firing.

In contrast to the gist of earlier papers out of Wolfram Schultz’ group, which tended to emphasize the relative temporal precision of the reward timing prediction (e.g., Hollerman & Schultz, 1998), more recent results (Fiorillo et al., 2008) have reported that both early and late reward delivery over a range of hundreds of milliseconds resulted in substantially suppressed dopamine signaling. That is, early or late rewards appear to be more predicted than unpredicted. This, of course, implies that the expectation-conveying representations responsible for suppressing dopamine firing are temporally smeared rather substantially. Currently, PVLV uses simple localist representations for each time step that produces precise temporal predictions on a scale of 100 msec. If desired, PVLV could reproduce this imprecision by simply using coarse-coded, overlapping distributed representations for each timestep.

Simulation 1d: Differential effect of increasing delays on LV, PV learning (Motivating: 1)

As the interval between CS and US increases beyond a few seconds both acquired CS-onset bursting (LV learning) and the loss of US bursting (PV learning) are attenuated, the latter to a significantly greater degree (Figure 9a; Fiorillo et al., 2008; Kobayashi & Schultz, 2008). Note that CS-onset dopamine signals are relatively preserved even at the longer delays (Figure 9a, left panel) as compared with the pattern seen at US-onset (right panel). As previously noted, this dissociation represents circumstantial evidence that separate pathways are involved in LV vs. PV learning. Figure 9b shows corresponding simulation results that were produced by progressively weakening the strength of the USTime_In representations that serve as input to the VS patch layers. The idea is that as CS-US intervals increase there is a corresponding deterioration in the fidelity of the temporally-evolving working memory-like goal-state representations that bridge the gap. The CS representation itself is not as working memory-dependent because the CS stays on until reward is delivered, so LV learning is relatively preserved (although attentional effects are undoubtedly contributory).

Figure 9:

Simulation 1d: Differential effect of increasing delays on LV, PV learning. (a) Empirical results adapted from Fiorillo, Newsome & Schultz (2008), Figure 2a,c, with permission from Springer Nature: Nature Neuroscience, copyright 2008, showing a relatively modest decrease in CS-generated dopamine cell bursting with increasing CS-US intervals and and an even greater preservation of US-triggered bursting. Results are from the subject (monkey B) that showed the greater sensitivity to temporal delay. (b) Simulation results show a qualitatively similar pattern due to one potential mechanism — a deterioration in the fidelity of temporally-evolving US representations in OFC (USTime_In) projecting to VS patch layers. (c) Empirical results from Flagel et al. (2011, Figure 2b,e) adapted with permission from Springer Nature: Nature, copyright 2010, showing greater CS-triggered extracellular dopamine signaling in the NAc and near-complete loss of US-triggered dopamine in sign-trackers (top; blue) versus goal-trackers (bottom; gold). (d) Simulations results showing a qualitatively similar pattern based on two possible mechanisms: 1) higher representational fidelity in sign-trackers (top) versus goal-trackers (bottom) for temporally-evolving goal-state representations (PV learning); and, 2) a greater contribution of VS matrix-mediated disinhibition to CS-triggered dopamine signaling (LV learning). (e) Results adapted from Fiorillo, Newsome & Schultz (2008), Figure 2b,d, with permission from Springer Nature: Nature Neuroscience, copyright 2008, showing different sensitivity to temporal delay in the two monkeys they recorded from: left panel: CS-triggered responses; right panel: US-triggered responses; note that monkey B (gray curves in both panels) appears to show considerably more delay sensitivity than monkey A (black) for both CS- and US-triggered dopamine signaling.

Considerable interest has developed in a recently-described phenotypic distinction between so-called goal-trackers, whose conditioned responses (CRs) are dominated by conventional US-derived CRs such as food-cup entry, versus sign-trackers, whose CRs are dominated by CS-driven CRs such as CS approach and manipulation (Flagel et al., 2010; Flagel et al., 2011; Meyer, Lovic, Saunders, Yager, Flagel, Morrow, & Robinson, 2012; Haight, Fraser, Akil, & Flagel, 2015). In other words, goal-trackers preferentially develop relatively exclusive incentive salience, while sign-trackers develop a strong incentive salience for the CS as well. It is also worth pointing out that a sizeable subpopulation falls into an intermediate range that varies from study to study according to how categories are defined.

Of particular relevance to the PVLV framework and to the issue of dopamine signaling, Flagel et al. (2011) reported that animals they classified as sign-trackers displayed a different pattern of dopamine signaling relative to those animals classified as goal-trackers (Figure 9); specifically, sign-trackers showed stronger dopamine signaling (measured as extracellular dopamine levels in ventral striatum) in response to CSs (top panel) and more predicting away of dopamine signaling to predicted USs (bottom panel). Importantly, these experiments were performed with a CS-US interval of roughly 8 seconds, which is well into the range of delay systematically characterized by Fiorillo et al. (2008). Thus, it is tempting to speculate that individual differences in the handling of delay by the dopamine signaling system may underly these results and may account for behavioral differences between sign-trackers and goal-trackers as well. For example, there may be differential dopamine cell responsivity per se, or there could be differential downstream effects (e.g., differential learning rates, relative dopamine receptor densities, and/or dopamine reuptake dynamics). Possible empirical support for the last of these ideas comes from a recent study by Singer, Guptaroy, Austin, Wohl, Lovic, Seiler, Vaughan, Gnegy, Robinson, and Aragona (2016) implicating genetic variation in the expression of the dopamine transporter (DAT) gene between sign-trackers vs. goal-trackers, with sign-trackers having higher DAT expression in the VS than goal-trackers.

The basic idea of differential delay sensitivity was simulated in PVLV (Figure 9d) by varying the strength of USTime_In representations as described above (to account for the PV results) and also varying the strength of Stim_In connections to the VS matrix layers based on the hypothesis that VS matrix-mediated disinhibition of dopamine cell activity may differentially contribute to dopamine cell bursting in sign-trackers vs. goal-trackers. These two mechanisms may be linked according to the proposal that VS matrix MSNs may be responsible for the gating of goal-state representations into OFC in the first place. Finally we point out that, although not explicitly discussed by the authors, it appears that there may indeed be significant individual differences in the temporal delay curve for dopamine signaling based on the results reported by Fiorillo et al. (2008) for their two different subjects (Figure 9e).

An implication of the PVLV framework suggested by this constellation of ideas is that pharmacologic or other blockade of the DAT in the VS ought to reduce acquired sign-tracking behavior in animals with the sign-tracking phenotype. And, similarly, based on the the CEA dependency in acquiring CS-related CRs (e.g., COR, autoshaping; Gallagher et al., 1990) and the idea that such CRs are trained by CS-triggered dopamine signals (see also Hazy et al., 2010) the PVLV framework predicts that CEA lesions ought to significantly reduce the manifestations of sign-tracking CRs and thus mitigate the behavioral distinction between sign-trackers and goal-trackers. See also the General Discussion where these predictions are stated explicitly.

Simulations 2a-c: Extinction Is Mediated by New, Contextualized Learning

Extinction and the related phenomena of rapid reacquisition and renewal exhibit clear asymmetries in comparison with initial acquisition. For example, reacquisition after extinction generally proceeds faster than original acquisition (Pavlov, 1927; Rescorla, 2003); and extinction exhibits a much stronger dependency on context than does initial acquisition as demonstrated in the renewal paradigm (e.g., Bouton, 2004). A clear implication is that extinction is not simply the weakening of weights previously strengthened during acquisition, but instead involves a component of strengthening of different weights that then counteract them (Quirk et al., 2003; Herry et al., 2008; Laurent & Westbrook, 2010; Bouton, 2002; Rudy, 2013). The opponent-processing dynamics and specific extinction pathways in the amygdala of the PVLV model can account for these phenomena, as explored in the simulations below.

Simulation 2a: Extinction and reacquisition (Motivating: 3)

Simulation 2a demonstrates how the explicit representation of evidence against the imminent occurrence of a particular US can mediate extinction and then rapid reacquisition. Figure 10a shows faster reacquisition of a food magazine entry CR after extinction (top curve) relative to original acquisition in rats (Ricker & Bouton, 1996). Figure 10b shows comparable simulation results for VTAp phasic dopamine over the sequence of acquisition, extinction, and reacquisition. Note that extinction takes slightly longer than original acquisition, as generally seen empirically (Mazur, 2013), and reacquisition is faster than original acquisition. Figure 10c-e show corresponding patterns of activation in the BLA and CEl layers during these three phases: the D2-dominant, opposing pathway is trained by phasic dopamine dips to encode contextualized new learning during extinction, and comes to suppress the initial D1-dominant acquisition representations. The rapidity of reacquisition in the model depends on two complementary factors. The first and most important is a relatively fast learning rate in weakening the weights from the CS input to the extinction coding units. Since this weakening is faster than original acquisition learning, reacquisition can be faster than original acquisition. In addition, reacquisition is speeded by the nonlinearity of the attractor dynamics inherent in the Leabra algorithm by virtue of the mutual inhibition that plays out between the acquisition and extinction representations.

Figure 10:

Simulation 2a: Extinction and rapid reacquisition. (a) Empirical learning curves for initial acquisition (lower curve) and reacquisition (upper), documenting rapid reacquisition, from Ricker & Bouton (1996), with permission from Springer Nature: Animal Learning & Behavior, copyright 1996. (b) Simulation results showing the evolution of dopamine signaling over a sequence of acquisition, extinction, and reacquisition; CS-onset dopamine = solid line; US-onset = dotted line; (c-e) Focus on network activity in the amygdalar layers after acquisition training (c), extinction (d), and reacquistion (e). Initial acquisition is mediated by BLAmygPosD1 and CElAcqPosD1 D1-dominant cells, while extinction drives opponent BLAmygPosD2 and CElExtPosD2 D2-dominant cells (learning via dopamine dips). Extinction takes longer due to the need for learning in extinction cells to out-compete the acquisition cells. Reacquisition is fast because the original acquisition weights are largely intact, and the relative balance can be rapidly shifted.

Figure 10b also shows that CS-onset dopamine activity dips somewhat below zero during extinction training, which is a consequence of parallel learning in the VSMatrixPosD2 layer whose acquired activity drives positive LHbRMTg activity and thus VTAp suppression. The development of this modest negative signal is consistent with a report by Pan, Schmidt, Wickens, and Hyland (2008) that a subset of dopamine cells exhibited phasic pausing after extinction training — more extensive exploration of this would provide an important empirical test of this aspect of our model.

It is worth pointing out that reacquisition is not always faster than original acquisition. In particular, the relative speed of reacquisition appears to be sensitive to the relative number of initial acquisition trials vs. subsequent extinction trials. That is, extensive initial conditioning favors rapid reacquisition while extensive extinction training favors slow reacquisition (Ricker & Bouton, 1996). Changes in context can also influence reacquisition speed as can prior conditioning involving a different CS (Ricker & Bouton, 1996).

Simulation 2b: Renewal (Motivating: 3)

This simulation highlights the differential sensitivity of extinction learning to context (e.g., Bouton, 2004) as revealed by the phenomenon of renewal, where subjects are typically conditioned in one particular context (A) and then extinguished in a second context (B). The defining result is that when subjects are subsequently exposed to the relevant CS in the original context they immediately exhibit the just-extinguished CR (i.e., the ABA paradigm). Renewal has also been demonstrated when subjects are tested in a third (novel) context (i.e., ABC), although the effect may be somewhat weaker (Bouton & Swartzentruber, 1986; Krasne et al., 2011). This somewhat surprising result suggests that renewal expression is really more a function of the absence of the extinction context (B), and that the original acquisition context (A), although contributory, is relatively weaker as a controller of CR expression. Furthermore, studies using the AAB paradigm (where extinction is performed in the same acquisition context, A, and renewal testing occurs in a different, novel context B) also demonstrate reliable renewal, compared to testing again in A (i.e., AAA) (Thomas, Larsen, & Ayres, 2003; Bouton & Ricker, 1994), although AAB renewal tends to be the weakest of the three cases

Figure 11a shows data from Corcoran et al. (2005), (their Fig 4b), for all of the typical renewal paradigms (ABB, ABA, AAB, ABC) showing that extinction continues to be expressed when testing occurs in the same context in which extinction occurred (i.e., ABB) while renewal is expressed when the context for testing is different (ABA, AAB, ABC) (see also Bernal-Gamboa, Juarez, González-Martín, Carranza, Sánchez-Carrasco, & Nieto, 2012 for similar results in a taste aversion paradigm). Figure 11b shows qualitatively comparable simulation results from PVLV. The Context_In projections to the BLAmygPosD2 extinction-coding layer are critical to these effects — initial acquisition in the model is exclusively driven by the CS stimulus features, while extinction becomes strongly modulated by these context inputs (along with stimulus features). Thus, when tested outside of the extinction context, the stimulus connections drive the original acquisition representation. The lack of contextual inputs to the D1-dominant acquisition pathway in our model is an intentional oversimplification relative to the real brain, but the same overall principles apply with any significant asymmetry in these connections, or other attentional dynamics that up-regulate contextual influence during extinction learning. As described earlier, Herry et al. (2008) found that hippocampal afferents to the BLA differentially synapse onto their acquisition-coding cells while extinction-coding cells differentially receive inputs from the vmPFC, which we interpret as conveying two distinct types of context (although our model only captures the latter).

Figure 11:

Simulation 2b: Context Dependency of Renewal. (a) Example behavioral results illustrating the complex role of context in extinction and renewal, adapted from Corcoran et al. (2005), Figure 4b, with permission from Society for Neuroscience: Journal of Neuroscience, copyright 2005. After appetitive conditioning using a food-cup CR in context A (all cases), extinction occurs in either context A or B. Subjects are then tested in a renewal phase. As shown, the ABB sequence shows continued extinction (low food-cup behavior; white bar), while the other three sequences (ABA, AAB, ABC) all show significant renewal (high food-cup behavior). (b) Simulation results reproducing the same basic pattern of results. AAA is equivalent to ABB in that renewal occurs in the same context as did extinction. This basic pattern of results shows that it is the context present during extinction, not original acquisition, that is critical for determining whether extinction is expressed in testing, or not (i.e., renewal).

In addition to a clear role for vmPFC inputs in supplying context-specificity during extinction, a role for hippocampal involvement in renewal is also suggested by studies showing that lesioning the hippocampus prevented the context-specificity of extinction, as demonstrated by a lack of renewal in both ABA and AAB renewal paradigms (Ji & Maren, 2005). Further, inactivating hippocampus with muscimol before extinction also produced a lack of either ABC or AAB renewal (Corcoran & Maren, 2001, 2004; Corcoran et al., 2005). Other studies, however, have found that hippocampal lesions did not impair renewal in an ABA paradigm (Wilson, Brooks, & Bouton, 1996; Frohardt, Guarraci, & Bouton, 2000), including a very recent study specifically designed to address this apparent contradiction (Todd, Jiang, DeAngeli, & Bucci, 2017). Further complicating matters, all of the above studies involved only the dorsal hippocampus and there is now considerable evidence implicating the ventral hippocampus in Pavlovian conditioning (e.g., Maren & Holt, 2004), including sending projections to cortical regions involved in extinction and renewal such as vmPFC (Orsini, Kim, Knapska, & Maren, 2011; Wang, Jin, & Maren, 2016; Sotres-Bayon, Sierra-Mercado, Pardilla-Delgado, & Quirk, 2012). Interestingly, the hippocampal afferents to BLA acquisition cells documented by Herry et al. (2008) were from the ventral, not dorsal, hippocampus. Clearly, additional work is needed to sort out the roles played by the dorsal versus ventral hippocampus within the overall system.

Finally, to account for the relative strength of renewal thought to exist across the different paradigms (i.e., ABA ≥ ABC ≥ AAB) we would hypothesize that the connections from hippocampus to BLA acquisition cells are relatively slow-learning and strengthen only modestly during initial acquisition in the presence of a specific, strongly salient CS candidate. This modest strengthening could then produce a modest advantage for ABA renewal relative to ABC and AAB renewal. On the other hand, in the absence of any strongly salient CS candidates these same context-conveying connections could strengthen robustly to produce explicit context conditioning such as conditioned place preference and/or aversion (e.g., Xu, Krabbe, Gründemann, Botta, Fadok, Osakada, Saur, Grewe, Schnitzer, Callaway, & Lüthi, 2016). Hippocampal contributions to acquisition coding in the case of fear conditioning have been extensively simulated previously (Rudy & O’Reilly, 2001).

Two related phenomena not simulated are spontaneous recovery and reinstatement. The former is the observation that after behavior has been fully extinguished, returning the subject to the same environment typically results in some partial recovery of the previously extinguished behavior. This effect is likely attributable to multiple factors (Bouton, 2004) including transient synaptic changes not fully stable longer-term, or perhaps to endogenous changes to the internal context representations over time, such that the effective context is different later in time, i.e. a change in temporal context (Bouton, 2004).

Reinstatement is the phenomenon whereby, even after extensive extinction training (beyond the point of any spontaneous recovery), an unpredicted delivery of the relevant US can immediately reestablish extinguished CRs without benefit of further CS-US pairing. For the framework proposed here, a straightforward, if speculative, account might invoke the finding that the retrieval of extinction-related context memories seems to be less robust that acquisition-related memories (Ricker & Bouton, 1996). In this vein, the uncued occurrence of the US itself can serve as a cue to retrieve and maintain a working memory-like goal-state representation for that US, which can be considered itself a version of “acquisition context.” Subsequently, when the relevant CS occurs the retrieval of the extinction-context may be relatively disadvantaged, or even suppressed, and thus less likely to be activated, allowing for the re-emergence of the CRs. Also relevant are results showing that the context of US presentation and subsequent CS testing must match (e.g., Bouton & Peck, 1989), as well as studies showing the hippocampus to be important for reinstatement of fear (Todd et al., 2017; Wilson et al., 1996; Frohardt et al., 2000). Since there can be a gap of 24+ hours before CS testing, context-US associations formed during US exposure might be involved in re-activating working memory-like US representations at test. In particular, therefore, the projections from hippocampus to BLA acquisition neurons may be important for encoding context-US associations, supporting a role in reinstatement as well as in contextual conditioning as previously noted (Xu et al., 2016).

Simulation 2c: Probabilistic reinforcement learning (Motivating: 3)

The same opponent dynamics between acquisition and extinction can also account for learning under probabilistic reward schedules (Fiorillo et al., 2003). Figure 12 shows the pattern of phasic dopamine signaling observed in an example neuron by Fiorillo et al. (2003) using various probabilistic reward schedules, along with corresponding simulation results. Across all cases note that bursting at CS-onset corresponds roughly to the expected value (EV) of the reward received over that training block, while activity at the time of US-onset reflects the residual surprise relative to that expectation (1 - EV). In the model, the relative balance between the acquisition and extinction pathways reflects the relative proportion of the corresponding trial types, and thus the model accurately tracks these expected values and drives corresponding phasic dopamine signals.

Figure 12:

Simulation 2c: Probabilistic reinforcement learning accounted for by extinction-related mechanisms. (a) Empirical results from Fiorillo et al. (2003), Figure 2A, with permission from The American Association for the Advancement of Science: Science, copyright 2003, showing dopamine cell responses under varying probabilistic reward schedules. (b) Simulation results reproducing the same qualitative pattern of results in (a).

A prominent phenomenon associated with probabilistic reinforcement, one that has played an important role in theorizing about Pavlovian and instrumental conditioning generally, is the partial reinforcement extinction effect. The PREE is when extinction is slower following acquisition training using partial (<100%) relative to continuous (100%) reinforcement, a finding that has proven perplexing for learning theorists from the time it was first described by Humphreys (1939) – including the Rescorla-Wagner model. This is because it “…challenged the idea that the the rate of extinction might be a simple function of the amount of associative- or habit-strength that was learned during conditioning (Bouton, Woods, & Todd, 2014).”

The pattern of results described under the PREE has turned out to be extremely complex, occurring under most circumstances (e.g., Haselgrove & Pearce, 2003; Haselgrove, Aydin, & Pearce, 2004; Bouton et al., 2014), but not always (Mackintosh, 1974; Pearce, Redhead, & Aydin, 1997; Bouton & Sunsay, 2001; Haselgrove et al., 2004). In particular, it seems that the PREE may be less readily produced when a within-subject design is used (Pearce et al., 1997; Bouton & Sunsay, 2001), although Chan and Harris (2019) reviewed recent results that have been more successful. In addition, it appears that many other experimental manipulations can influence PREE expression including: 1) the average number of non-reinforced trials between USs (Capaldi, 1967, 1994; Bouton et al., 2014); 2) accumulated time between US occurrences (Gallistel & Gibbon, 2000; although the consensus in the literature seems to be that time per se may be a relatively minor factor after non-reinforced trials are considered (Haselgrove et al., 2004; Bouton et al., 2014); 3) a change in CS duration during extinction from that used in acquisition (Haselgrove & Pearce, 2003). However, a unifying idea introduced by Redish et al. (2007) is that the experience of unexpected and/or intermittent non-reinforcement can be used by agents to infer contextual state changes that define current contingencies. Using this framework Redish et al. (2007) were able to account for the long-standing and puzzling result that a block of continuous reinforcement following initial partial reinforcement training does not mitigate a PREE and can even enhance it (Jenkins, 1962; Theios, 1962; Domjan, 1998), providing an overarching explanatory framework for several earlier proposals (e.g., the discrimination hypothesis: Mowrer & Jones, 1945; a generalization decrement: Capaldi, 1967, 1994). Such complex context-based effects almost certainly involve cortically-based mechanisms not strictly in-scope for the PVLV model currently, but they do suggest important areas for future exploration.

Simulations 3a-c: Effects of a Second CS

There are multiple important phenomena that result from the introduction of a second CS, including blocking, conditioned inhibition, and second-order conditioning. Early electrophysiological studies demonstrated that a CS that fully predicts a later one eventually results in phasic dopamine signals only for the earlier one, as expected from reward-prediction-error (RPE) theory (e.g., Schultz, Apicella, & Ljungberg, 1993; Suri, 2002). There are many factors, however, that can determine the resulting pattern of effects with two CS’s, including their relative timing, both within a trial and across the experiment, and their relationship with the US (e.g., Yin, Barnet, & Miller, 1994). Simulation 3a shows how blocking arises from the simultaneous presentation of two CSs, while Simulation 3b shows how conditioned inhibition results from the same CS-level structure, but with omitted instead of delivered USs. Simulation 3c shows that just staggering the two CS’s in time compared to conditioned inhibition results in second-order conditioning.

Simulation 3a: Blocking (Motivating: 11)

Blocking is demonstrated by first training one CS (A) to predict a given US outcome, followed by presentation of two simultaneous CSs presented in compound (AX) followed by the same US outcome, and then testing the response to X presented by itself. According to classic RPE theory (Rescorla and Wagner 1972), the fact that A already fully predicts the US outcome means that X provides no additional predictive value and should not experience learning. This well-established behavioral phenomenon has been shown to be mirrored by dopamine cell firing (Waelti, Dickinson, & Schultz, 2001), albeit incompletely. Figure 13 shows these data, along with PVLV simulation results reproducing this basic pattern of results. Interestingly, the blocking of X is only partial in both the data and the model, despite sufficient A-US pairing to the point where the US no longer drove phasic dopamine bursting. In the model, this occurs because of the delta-activation in the amygdala driven by US onset (which still occurs despite the A pre-training) — producing some level of learning to the X stimulus. At test therefore, the blocked CS (X) has acquired some ability to activate these specific-US coding cells and these, in turn, drive some modest dopamine cell bursting.

Figure 13:

Simulation 3a: Blocking. (a) Empirical results adapted from Waelti et al. (2001), Figure 2c-e with permission from Springer Nature: Nature, copyright 2001, showing substantial, but incomplete, blocking of acquired dopamine bursting for a second CS (X−) in a blocking paradigm (arrows) as compared to a second CS (Y−) compounded with a different CS not previously paired with reward. Most cells showed no response to the blocked stimulus (X−). (top) sample cell showing no response to X− but robust response to Y− control; (middle) a minority of cells showed some response, or a bi-phasic response to X−; (bottom) population histogram showing a significantly larger response to X− versus Y− control (b) Simulation results showing similarly incomplete blocking produced by the PVLV model (arrow; X test). ‘A test’ refers to presentation of the original blocking stimulus alone – it continues to show a robust dopamine response. (c) Simulation results for identity change unblocking. Test results are shown for each CS presented separately – follows training with a compounded CS2 (A*X*) when a different-but-equal-magnitude US is substituted during the blocking training phase. Note robust dopamine signal in response to the would-be blocked CS2 [compare X* test with X test in (b)]. Presentation of the original blocking stimulus alone (A* test) shows that it now drives an even stronger dopamine signal due to additional weight strengthening as a result of the unblocking effect.

Unblocking-by-identity is a variably observed (Ganesan & Pearce, 1988; Betts, Brandon, & Wagner, 1996) phenomenon such that, when it is seen, a previously established US (e.g., chocolate-flavored milk) is replaced by an equal-magnitude-but-different-US (e.g., vanilla-flavored milk) in the blocking phase, with the result that learning about the to-be-blocked stimulus is no longer blocked. Some have argued that this phenomenon is beyond the scope of DA-RPE theory and requires an attention-based explanation. However, the PVLV framework provides one potentially viable DA-RPE-based mechanism, which is described in the following paragraph. Some recent animal studies have shown that appropriate regions in the PVLV model, including the basolateral amygdala, ventral striatum, and OFC, were crucial for the learning that underlies unblocking-by-identity (McDannald, Lucantonio, Burke, Niv, & Schoenbaum, 2011; Chang, McDannald, Wheeler, & Holland, 2012; McDannald, Takahashi, Lopatina, Pietras, Jones, & Schoenbaum, 2012).

In the model, we obtained an unblocking-by-identity effect without any additional mechanisms (Figure 13c; compare response to X* test with X test in b). This is due to the activation of both the originally-expected US outcome (chocolate milk; driven by learned associations from the CS), and the new unexpected US outcome (vanilla milk) in the amygdala. Even allowing for representational overlap and/or some competitive inhibition between the two active US representations in the CEm output of the amygdala, the downstream PPTg layer receives a larger increase in its net input than it otherwise would have with only the one US active, which it will pass on to the VTAp (dopamine) layer as a stronger excitatory drive. Thus, the VTAp computes a net positive dopamine signal that can be used to train the association between CS2 and the new US. An analogous account can be given for activation in the lateral habenula in order to explain the phenomenon of overexpectation where two previously conditioned CSs are then presented together in a subsequent training phase that includes the same magnitude of reward as used for each of the CSs previously; that is, the expectation is now for two rewards, but only one is delivered, for example. A prediction that follows from the current framework is that both unblocking-by-identity and overexpectation effects should be dependent on an intact phasic dopamine signaling system. Indeed, regarding the latter case Takahashi, Roesch, Stalnaker, Haney, Calu, Taylor, Burke, and Schoenbaum (2009) reported that bilateral lesions of the VTA disrupted learning in an overexpectation paradigm.

Two other forms of unblocking are worth mentioning. Upward unblocking is when the magnitude of reward is increasing for the blocking phase and is trivially accounted for by the DA-RPE framework. Downward unblocking is more problematic in that a decrease in reward can also produce excitatory conditioning of the to-be-blocked CS. However, it turns out that the circumstances required to produce this effect are rather arcane; see the General Discussion for an explanation as to why we do not think it really challenges the basic DA-RPE framework.

Simulation 3b: Conditioned inhibition (Motivating: 5, 6, 7)

The conditioned inhibition (CI) paradigm is essentially identical to blocking, except that the expected US is omitted when the paired CSs are introduced in the second phase (AX−, with the initially-conditioned A+ CS). In addition, CI training requires continued maintenance trials (A+) to prevent extinction of the original CS-US pairing. As reflected in the PVLV model, Bernard Balleine and colleagues have recently reported that the LHb plays a critical role in conditioned inhibition (Laurent et al., 2017).

Figure 14 shows results from Tobler et al. (2003) demonstrating that phasic dopamine signaling after appetitive CI training conforms to the basic pattern predicted by RPE theory. The accompanying PVLV simulation results match this data, including capturing the biphasic response pattern to AX– in terms of both positive CeMPos and negative LHbRMTg drivers of dopamine signaling (the anatomical connectivity predicts that the amygdala-driven burst would precede the LHb-driven dip, but we do not resolve time at this scale in the model).

Figure 14:

Simulation 3b: Conditioned inhibition — learning to predict the omission of reward. (a) Empirical results from Tobler et al. (2003), adapted from Figure 3a,c, with permission from Society for Neuroscience: Journal of Neuroscience, copyright 2003, showing the pattern of phasic dopamine signaling seen after conditioned inhibition training, for the initially-conditioned CS (A+), the conditioned inhibitor (X−), and their pairing (AX−) (top panels = single cell histograms; bottom = population histograms). Note that the small early activation phase seen for X− in the population histogram was attributed to associative pairing with the A CS since it was eliminated by A- extinction training (while the depression component persisted). (b) simulation results showing qualitatively similar results produced by the PVLV model. For AX− there are both positive (CeMPos; dashed red line) and negative (LHbRMTg; speckled blue line) components driving dopamine signaling (VTAp; solid black line), but the model does not have the temporal resolution to see these separately as in the empirical data. (c) empirical results from Tobler et al. (2003), adapted from Figure 6a,b, with permission from Society for Neuroscience: Journal of Neuroscience, copyright 2003, showing the results of a summation test is which the conditioned inhibitor (X−) is compounded with a different separately-conditioned CS (C+) (top panel = CX− test, bottom = AX− test.) (d) simulation results for the summation test showing qualitatively similar results.

As pointed out by Tobler et al. (2003), there is an important exception to a simple RPE account of CI: when presented alone, a fully trained conditioned inhibitor (X) fails to produce a positive RPE at the expected time of the US, despite the absence of any negative outcome associated with the negative value signaled by this stimulus. This is consistent with the long-established finding that the negative valence of the CI does not extinguish when presented alone (e.g., Zimmer-Hart & Rescorla, 1974; see Miller, Barnet, & Grahame, 1995 for review). PVLV reproduces this failure of extinction due to the minimal prediction error produced when the CI (X) is presented alone (not shown, but see Figure 14b for reference).

Tobler et al. (2003) further explored this issue by delivering a small reward at the normal expected time after presentation of X and found an enhanced dopamine response relative to the presentation of the same small reward unexpectedly. This small effect is shown in the simulation results for X− test trials, and its small magnitude reflects the idea that the LHb is only weakly capable of driving phasic dopamine bursting, in contrast to its dominant role in driving inhibitory pausing. This asymmetry is further explored below in the aversive conditioning simulations, and represents an important deviation from standard RPE accounts.

An alternative account, mirroring the Redish et al. (2007) state-splitting account of extinction, might be that since the presentation of the CI- alone is a salient change in context compared to compound training, the CI-alone context no longer carries the expectation of explicit reward omission. This interpretation would not be entirely straightforward, however, since the CI does exhibit strong negative (inhibitory) valence when presented alone and the new context might be expected to modulate the valuation of the CI as well. So there is a dissociation between the CS-time and US-time effects of CI- presentation. Thus, this dissociation suggests that any CI-triggered expectation of reward omission may be dependent upon a concomitant expectation of reward delivery, as driven by the positive CS (e.g., A+) when both are presented in compound (AX−). Although out-of-scope for the PVLV model, we might frame such a possibility in terms of working memory-like goal-state representations. That is, the maintenance of any CI-associated working memory-like expectation of US omission could be dependent on a concomitant maintenance of an expectation for US occurrence; the latter could be absent when there is no A+.

Another test for the inhibitory properties of the conditioned inhibitor (X) is to pair it with a novel CS that has been independently conditioned (C), where it should also generate an expectation of reward omission. This was found empirically (Tobler et al., 2003) and in our model (Figure 14c-d). However, our model also shows that some of the inhibitory learning during the AX− trials applies to the A CS, so the novel CX pairing does not fully predict the absence of a US. To the extent that this effect is not present in the biological system, it might reflect attentional effects as we discuss in the General Discussion. Importantly, it is noteworthy that the conditioned inhibitor blocks the behavioral CRs normally elicited by both CSs when presented alone (Rescorla, 1969; Tobler et al., 2003), which implies that it inhibits an underlying US expectation. This is another strong motivation for the opponent organization of US representations in the PVLV model.

Finally, it is worth noting that the retardation test (Tobler et al., 2003) establishing that a conditioned inhibitor has acquired negative valence is essentially a form of counterconditioning which, like discriminative reversal learning, pits valence reversal competitive effects against any acquired salience effects (see the discussion regarding attentional effects in the General Discussion).

Simulation 3c: Second-order conditioning (Motivating: 11)

Second-order conditioning is similar to conditioned inhibition, except that the two CSs are typically presented in temporal succession (CS2 then CS1), instead of simultaneously, with the previously-conditioned CS1 driving conditioning of the CS2. To avoid the confound of direct CS2- US-driven learning, the two CSs are presented with the US omitted, just as in the CI paradigm. Furthermore, separate maintenance CS1+ trials are typically (but not always) interleaved with second-order trials in order to prevent extinction of the CS1. Figure 15 (top) shows simulation results reflecting canonical second-order conditioning (corresponding to the early, second-order phase; see below).

Figure 15:

Simulation 3c: Second-order conditioning. Simulation results contrasting canonical second-order conditioning (top; 50% maintenance trials) with a variant in which CS2 activity endures until the time of the omitted US (bottom; also 50% maintenance trials). The latter converts the relation between CS2 and US nonoccurrence from a trace-like to a delay-like conditioning relation and converts a positive dopamine response to the CS2 (top) into a negative one (bottom), i.e., a conditioned inhibitor (simulation 3b).

Given the similarities with CI, especially the same negative contingency with the US, it should not be surprising that second-order conditioning has long been recognized to be a non-monotonic function of the number of CS2-CS1 pairings even with maintenance trials interleaved (Yin et al., 1994). That is, early in training second-order manifestations emerge, but with further CS2-CS1 pairings second-order CSs become conditioned inhibitors provided that CS1+ maintenance trials are continued (Yin et al., 1994). In the end, the negative contingency between the CS2 and the US prevails. This may also help explain why second-order CSs can sometimes end up exhibiting both excitatory and inhibitory properties (Yin et al., 1994).

To simulate the conversion of the CS2 to a conditioned inhibitor we modified the CS2 representation to have activity persisting up through the time when the US would otherwise be expected to occur — in typical second-order conditioning CS2 activity terminates when the CS1 stimulus comes on. This temporal contiguity between CS2 with the time of US omission provides the substrate for learning by the extinction-coding cells of the amygdala layers that associates the CS2 with the non-occurrence of an expected US, and thus for the CS2 to become a conditioned inhibitor. Since the PVLV framework does not itself include components for working memory or memory retrieval that are necessary for bridging temporal gaps in trace-conditioning paradigms, the persistent CS2 activity manipulation employed effectively substitutes for a “memory” of the CS2 and changes it from a weak trace-like conditioning CS for US omission into a stronger delay-like conditioning CS. Overall, this analysis serves to highlight the strong commonality of the second-order conditioning paradigm with conditioned inhibition, and the fact that the CS2 really is a perfect predictor of reward omission. The fact that it can obtain a positive association is thus irrational from a purely predictive framework, and is suggestive that this type of second-order conditioned learning is a generally-beneficial heuristic that can sometimes be fooled. Interestingly, second-order conditioning has been shown to depend specifically on an intact BLA, but not the CEA (e.g., Hatfield et al., 1996), consistent with the idea that BLA supports higher-order, cortex-like learning.

Also relevant are studies that explored second-order conditioning using simultaneously presented CSs instead of the typical successive pattern just described. For example, Rescorla (1982) found that simultaneously presented CSs produce equivalent second-order conditioning to the typical successive paradigm – but with a critical difference. While typical CS2→S1 pairings produce second-order CRs that are highly resistant to subsequent extinction of the CS1-US contingency (i.e., the second-order CRs are persistent to repeated CS1- trials), the CRs resulting from simultaneous CS2-CS1 presentations have turned out to be highly sensitive to subsequent extinction of the CS1-US contingency (Rescorla, 1982). This dissociation implies that the two forms of second-order conditioning are mechanistically distinct. This is entirely consistent with the idea entailed in the PVLV framework that typical (successive) second-order conditioning is dependent on plasticity in the amygdala that results in an effective association of the CS2 and a representation of the expected US (triggered by the CS1); on the other hand, the simultaneous (atypical) version of second-order conditioning explored by Rescorla (1982) involves an association between the CS2 and the CS1, which we hypothesize occurs outside of the amygdala (and the whole PVLV model), instead occurring in the neocortex and/or hippocampus. Further discussion of these issues will be found as part of a more general treatment of complex contextual effects in the General Discussion section.

Simulations 4a & b: Aversive Conditioning

As reviewed in the Introduction, phasic dopamine signaling in aversive contexts does not conform to a simple RPE interpretation, where it would be just the mirror image of the appetitive case considered up to this point. Instead, we explore here two key differences: 1) a constraint that primary aversive events can never be completely predicted away (Matsumoto & Hikosaka, 2009a; Fiorillo, 2013); and, 2) the omission of anticipated punishments produces only weak disinhibitory bursting (i.e., a relief burst), as compared with both excitation-induced bursting and the strong pauses associated with omission of expected appetitive USs (Matsumoto & Hikosaka, 2009a; Matsumoto et al., 2016). It is straightforward to include these asymmetries within the full complement of aversive opponent processing pathways in the model that nevertheless do mirror those in the appetitive pathways. Thus, overall, we consider the aversive case as a combination of both symmetric and asymmetric with the appetitive case, in ways that make good ecological sense given their differential implications.

Simulation 4a: Inability to fully cancel aversive dopamine signals (Motivating: 8, 9, 10)

Figure 16a shows results from Matsumoto and Hikosaka (2009a) showing continued pausing in dopamine cell firing even after extensive overtraining using a fully predicted aversive (airpuff) US. Ecologically, this makes sense, in that even if expected, aversive outcomes should continue to drive learning to further avoid such outcomes. The PVLV model includes a gain factor on the net inhibitory contribution to lateral habenula activation such that excitatory inputs can never be fully counteracted, and thus VTAp activity always reflects some residual inhibitory effect (i.e., pausing). Figure 16b shows example simulation results after overtraining so that the aversive US is fully predicted, with residual positive LHb activity and corresponding dopamine pausing.

Figure 16:

Simulation 4a: Inability to fully cancel aversive dopamine signals. (a) Empirical results adapted from Matsumoto & Hikosaka (2009a), Figure 3a, with permission from Springer Nature: Nature, copyright 2009, showing persistent pausing in dopamine cell firing even after extensive overtraining using a fully predicted aversive (airpuff) US (black arrow; 100% airpuff = 100% expectation of airpuff). (b) Corresponding simulation results with fully predicted aversive US showing residual positive LHbRMTg (dash-dot blue line) and negative VTAp activity (solid black). (c) Simulation results with fully predicted aversive US showing positive activity in the VTAn layer (dash-dot black line) that mirrors the negative VTAp activity (solid black).

Figure 16c also shows our model of the small subset of extreme posteroventromedial VTA neurons that appear to respond with phasic bursting to aversive outcomes (Bromberg-Martin et al., 2010b). We hypothesize that these are driven by a direct excitatory connection from the LHb, and thus they exhibit a mirror-image pattern of firing compared to the standard VTA / SNc neurons we have been considering to this point.

Simulation 4b: Weak relief bursting (Motivating, 8, 10)

The omission of expected aversive USs can produce disinhibitory relief bursting in dopamine cells, at least under some circumstances, but these signals are relatively weak (Matsumoto et al., 2016; Matsumoto & Hikosaka, 2009a; Brischoux et al., 2009). It is not yet known whether or not these relief bursts are actually robust enough to serve as an affirmative teaching signal for training safety signals or avoidance behaviors, but these are the obvious logical applications of such a signal. To explore this in our model, we used an aversive version of the conditioned inhibition paradigm, where the conditioned inhibitor (U) instead becomes safety or security signal. Figure 17 shows the simulation results, where this U stimulus drives a small but significant burst as a result of having reliably predicted the absence of an aversive US. While to our knowledge there is no relevant electrophysiological data for the response of dopamine neurons in this paradigm, data in related paradigms indicates that safety signals can act as positive reinforcers, as can the omission or cessation of punishment generally (Rogan, Leon, Perez, & Kandel, 2005), although the mechanisms underlying these effects remains obscure. Nonetheless, we suspect that phasic dopamine signaling will ultimately end up being a critical factor signaling successful avoidance in some variant of the simplified model demonstrated here. Further, evidence for the role of dopamine in safety learning comes from recent studies showing that dopamine release in ventral striatum predicts successful avoidance (Oleson, Gentry, Chioma, & Cheer, 2012), and stimulation of VTA neurons during successful avoidance enhanced avoidance learning, while habenula stimulation impaired this learning (Shumake, Ilango, Scheich, Wetzel, & Ohl, 2010).

Figure 17:

Simulation 4b: Punishment omission signals and avoidance learning. (a) Data adapted from Matsumoto et al. (2016), Figure 3e, with permission from eLife Sciences Publications, Ltd: eLife, copyright 2016, showing a modest positive dopamine signal at the time of expected-but-omitted aversive US; (b) Simulation results showing a test trial immediately following aversive conditioning showing a positive dopamine signal at the time of omitted aversive US; (c) Simulation results showing test trials following safety signal training (i.e., aversive conditioned inhibition); note that a positive dopamine signal in response to the safety signal CS has been acquired (U–).

Summary and Other Paradigms

The foregoing simulations demonstrate some of the critical ways in which the PVLV model can account for data that is incompatible with a simple RPE theory. In addition, there are, of course, many other phenomena generally consistent with RPE-based models; these are also within the explanatory scope of the PVLV framework. These are listed in Table 2 with a brief commentary.

General Discussion

This paper describes a neurobiologically informed computational model of the phasic dopamine signaling system that helps to bridge between the large and rapidly expanding neuroscience literature, and the more abstract computational models based on the reward prediction error (RPE) framework. This PVLV framework is founded on the distinction between a Primary Value, PV system for anticipating the onset of primary rewards (USs), and a Learned Value, LV system for learning about stimuli associated with such rewards (CSs). The LV system corresponds to the amygdala and its ability to drive phasic dopamine bursting in the VTA and SNc, while the PV system represents the ventral striatum and its projections directly and via the lateral habenula (LHb) to these same midbrain dopamine nuclei, driving shunting inhibition and phasic pausing of dopamine firing for expected USs and omitted USs, respectively. We showed how our model can account for a range of data supporting the separability of these systems. A critical feature of both systems is the use of opponent-processing pathways that represent the competing strengths of the evidence in favor and opposed to specific USs, a fundamental idea going back to Konorski (1967) and Pearce and Hall (1980) who both proposed the learning of CS – no-US (inhibitory) associations to account for extinction and related phenomena.

Using simulations we showed how these opponent-processing pathways can explain a range of important data dissociating the processes involved in acquisition vs. extinction conditioning, including rapid reacquisition, reinstatement, and renewal. Furthermore, this opponent structure is critical for being able to account for the full range of conditioned inhibition phenomena, and the surprisingly closely-related paradigm of second-order conditioning. Finally, we showed how additional separable pathways representing aversive USs, which largely mirror those for appetitive USs, also have some important differences from the positive valence case, which allow the model to account for several important phenomena in aversive conditioning.

Overall, we found that the attempt to account for this wide range of empirical data at a detailed level imposed many convergent constraints on the model — we are left with the impression that there are not many residual degrees of freedom remaining in terms of major features of the model, particularly when the relevant anatomical and physiological data is included. This is consistent with the convergence of multiple different neurobiologically-oriented models of reinforcement learning on many of the same major features as the present framework (Vitay & Hamker, 2014; Brown et al., 1999; Carrere & Alexandre, 2015; Kutlu & Schmajuk, 2012).

In the following sections, we provide a more detailed discussion of the similarities and differences of the most comparable models, a number of testable predictions of the framework and implications for other related phenomena, followed by a discussion of some of the most pressing remaining challenges for future work.

Comparison with Other Relevant Models

As a systems-neuroscience model of phasic dopamine signaling the PVLV framework has been informed and constrained by a very broad body of research, meaning that there are also many different categories of models relevant for comparison. We will briefly discuss the most informative of these ranging from those with explicit neurobiological implications to those that are largely abstract. The latter includes important recent developments in the TD framework, as well as recent models based on a fundamentally Bayesian framework. Finally, we will also touch on purely psychological models of Pavlovian conditioning.

The relationship between PVLV and important early models with neurobiological implications has been covered in prior papers, and much of those points of comparison are still relevant (O’Reilly et al., 2007; Hazy et al., 2010). For example Houk et al. (1995) proposed a similar mechanism as our VSpatch (PVi) pathway, involving direct inhibition of dopamine blocking phasic bursts for predicted USs, but they also had this same striatal population performing the CS-driven bursting via a subthalamic sideloop, virtually ignoring all of the empirical data implicating the amygdala in Pavlovian conditioning generally as well as in driving phasic dopamine cell bursting. Similarly, Brown et al. (1999) and Tan and Bullock (2008) also ignored the amygdala’s role completely and had both functions located in the striatum.

The Brown et al. (1999) and Tan and Bullock (2008) models also utilized the intracellular spectral timing mechanism (Grossberg & Schmajuk, 1989) for anticipating the expected US onset – localized entirely within the striatum itself. In contrast, PVLV proposes a distributed scheme between the cortex, specifically OFC, which provides CS and US specific representations of evolving time, and VSpatch which receives these corticostriatal inputs that are the substrate for dopamine-dependent learning. More recently, Vitay and Hamker (2014), using a model with essentially the same overall functional anatomy as PVLV, focused specifically on the timing problem and proposed a neurobiologically specific mechanism based on the striatal-beat frequency model first proposed by Matell and Meck (2000) that uses a bank of cortical oscillations across a range of frequencies as the source of timing information. Interestingly, in the simulation results described by Vitay and Hamker (2014), their model’s temporal predictions were exquisitely precise, even presumably out to several seconds (see, e.g., their Figure 8); thus, it is not clear how well a mechanism dependent on the superposition of several oscillations of varying frequencies to produce “beats” could produce the temporally smeared expectations described by Fiorillo et al. (2008). Finally, and in contrast with PVLV, the Vitay and Hamker (2014) model addressed only a small number of strictly appetitive phenomena; nonetheless, it provided a significant contribution to the field.

Further, relative to the Vitay and Hamker (2014) model, as well as to earlier PVLV versions, the current PVLV model has a more elaborated representation of the amygdala circuitry, with separate BLA and CEA components, and opponent dynamics within each. Also relevant here are several recent models focused on intra-amygdalar circuitry and, specifically, its role in fear conditioning (e.g., Paré, Quirk, & Ledoux, 2004; Li, Nair, & Quirk, 2009; Pape & Pare, 2010; Pare & Duvarci, 2012). In particular, a model by Carrere and Alexandre (2015) has a functional anatomy of the amygdala very similar to PVLV’s, including opponent dynamics within both BLA and CEA, and also includes a critical role for acetylcholine (ACh) modulation of amygdala learning in fear conditioning and extinction paradigms. The overall role of these opponent pathways during acquisition and extinction, and the critical role of vmPFC (pre- and infralimbic cortex in rodents) in providing contextual inputs during extinction, are similar to our model, except that their model uses Pearce-Hall style absolute value of prediction errors to modulate ACh signals for the level of known uncertainty, whereas we focus more on US-specific connectivity to support extinction learning restricted to expected USs. These are not mutually-exclusive and likely both mechanisms are at work. Overall, these models paint a largely convergent functional picture, compatible with the data and theory of Herry et al. (2008). Other recent models of fear learning have emphasized cortical inputs to inhibitory interneurons (ITCs) in the amygdala (Moustafa et al., 2013), or interactions between the opioid system and extinction neurons in the amygdala, which inhibit fear output neurons in CeM (Krasne et al., 2011); however, we consider such additional mechanisms to be compatible with the basic dopamine-focused framework described by PVLV.

We consider next some important developments at the purely algorithmic level of analysis. Throughout the paper we have highlighted many ways in which our model converges and diverges with simple RPE-based models such as basic TD – motivated by the phenomena relevant to dopamine signaling that are anomalous with a simple RPE account. Although modifications and/or extensions to TD have been shown to address various of these anomalies, one important distinction remaining between these RPE-based models and the more biologically-informed PVLV is in the use of specific US representations as compared to abstracted scalar value signals. In PVLV, US-specific representations are critical for opponent-process learning in ventral striatum and the amygdala, and only in their projections down to midbrain-level dopamine and related nuclei (including PPTg, RMTg, LHb) does this US-specificity get abstracted into a global modulatory “pure value” signal. As noted below, the translation of these “apples and oranges” into a common denominator with limited dynamic range (i.e., the phasic dopamine signal) entails a number of important outstanding questions regarding the contextualized renormalization of these value signals.

Two specific modifications to basic TD have been particularly seminal. First is the state-splitting mechanism utilized by Redish et al. (2007) to account for the context dependency of extinction learning. Original Rescorla-Wagner and early TD models accounted for extinction effects by simply reversing reward prediction value. As a result they could not account for characteristic context-dependent extinction-related phenomena, most notably renewal. In contrast, Redish et al. (2007) proposed extending TD with a mechanism for “splitting” the current state into a second duplicate version triggered by the repeated absence of expected reward. This allows the new “extinction-context” state to be differentially associated with the omission of reward, while preserving the reward associations of the original (acquisition) state. This enabled their model to reproduce renewal and other context-dependent effects. PVLV’s explicit separation of different inputs to acquisition-coding vs. extinction-coding units in the BLA can be seen as a neurobiologically informed version of the basic state-splitting idea.

A second important modification of basic TD has been the introduction of more nuanced and robust representations of time, in particular, the construct of microstimuli introduced by Ludvig, Sutton, and Kehoe (2008). This time model proposes that each stimulus is associated with a temporally-evolving, multidimensional memory trace, defined by a set of basis functions with time-varying peak magnitude and temporal resolution (Ludvig et al., 2008, 2012). This framework has proven particularly applicable in accounting for multiple effects associated temporal delay. PVLV’s conception of CS and US specific temporally-evolving time representations in the OFC (USTime_In layer in the model) is essentially congruent with the microstimuli idea.

Another approach for time representation was proposed by Daw et al. (2006). These authors incorporated partial observability and semi-Markov dynamics to capture timing effects on the dopamine signal, such as the Hollerman and Schultz (1998) data showing asymmetrical effects on prediction errors for early and late rewards. Recent data seem to support some of the predictions of the belief state model. For example, Starkweather, Babayan, Uchida, and Gershman (2017) showed that the temporal modulation of prediction errors varied depending on the probability of reward and Lak, Nomoto, Keramati, Sakagami, and Kepecs (2017) showed that dopamine signals reflected decision confidence on a perceptual decision-making task. When a cue follows a reward with uncertain durations, drawn from a Gaussian distribution, they predict that prediction errors increase depending on time in the partially observable case (90% reward), as the model predicts a stronger belief in the occurrence of the non-rewarded state over time. However, an important difference between PVLV and the Courville, Daw, and Touretzky (2006) model is that all negative reward prediction errors in the latter model are positively rectified, and thus the model relies on another error system to provide negative prediction error information. In contrast, the PVLV model uses both positive and negative reward prediction error information. Further, when considering partially observable situations, they assume that dopamine computes a vector error signal, containing an error for each state’s value.

The above described extensions to the basic TD framework share an important emphasis on characterizing a more complex and dynamic differentiation of the state space serving as input to the basic underlying algorithm. This emphasis on a differentiated and dynamic state space has naturally led to the application of Bayesian network models to problems of Pavlovian and instrumental conditioning, including the latent causes theory by Gershman and Niv (2012) which generalized the basic state-splitting idea of Redish et al. (2007) (specific to extinction) to the more general problem of latent or hidden state inference. The core idea is that the system is attempting to infer whether some new (non-observable) latent state may be operating in the environment, to explain otherwise inconsistent outcomes (see also Gershman, Blei, & Niv, 2010). Such inferred latent state representations, called “belief states”, constitute a posterior probability distribution over states at a particular time, given past observations. Bayesian belief state models have proven fruitful in highlighting, and in providing an avenue for addressing, complex phenomena that seem to defy strictly concrete-experience based explanations, or at least simple ones. These effects are almost certainly cortically mediated and therefore out-of-scope for PVLV, although they would drive pathways within the PVLV model. Thus, the biologically-based approach taken here can provide an important bridge between higher-level, more abstract models and the more detailed and diffuse neuroscience literature.

Testable Neurobiological and Behavioral Predictions

In this section, we list several specific neurobiological and behavioral predictions implied by the PVLV framework. Appropriate empirical tests that follow from these predictions would serve to help evaluate and inform the model. Furthermore, all manner of Pavlovian paradigms can be run in the model and many additional predictions generated in that way. See the Appendix for how to download and run the model.

• During learning the emergence of increases in phasic CS bursting should precede decreases in expected US bursting, because acquired BLA activation for the CS onset provides a permissive-like input to the US-specific VS patch MSNs hypothesized to be responsible for the shunting of US-bursting. At a behavioral level, this implies that phenomena dependent on CS-onset dopamine signals such as second-order conditioning and the ability to support secondary reinforcement ought to emerge relatively earlier during acquisition training relative to those dependent on US-omission dopamine signals such as extinction.

• The projection from BLA to VS exhibits strong US-specific one-to-one connectivity by adulthood; for example, food-coding cells in BLA connect with food-coding cells in VS, and so on for water-coding cells, shock- coding cells, etc. By hypothesis, it is this US-specific connectivity that underlies the specific (or selective) form of Pavlovian Instrumental Transfer (sPIT), a phenomenon known to be dependent on the BLA generally (Corbit & Balleine, 2005). The PVLV framework therefore predicts that selective ontogenetic inactivation of food-coding neurons in the BLA ought to mitigate the expression of sPIT for CSs previously paired with food, but not for CSs paired with water.

• After training, optogenetic inactivation of patch MSNs of the ventral striatum should interfere with both the acquired loss of dopamine cell bursting at the time of US-onset as well as the generation of pauses when rewards are omitted. A behavioral prediction that follows is that such selective inactivation of VS patch MSNs ought to significantly interfere with extinction learning despite an intact BLA and VMPFC, two areas known to be important for extinction learning. This is because, by hypothesis, reward omission triggered pauses in dopamine cell firing in PVLV are dependent on a VS patch → LHb → VTA/SNc pathway and extinction learning in the BLA is dependent on those negative dopamine signals. The optogenetic prevention of phasic increases in LHb activity should have a similar result.

• Although the exact source of CS-US interval timing signals is not a central aspect of the PVLV framework, we have provisionally hypothesized that temporally evolving working memory-like representations in the OFC would be ideal substrate in this regard. In contrast, the Brown et al. (1999) and Tan and Bullock (2008) models place the source of timing signals in the striatum itself, triggered by direct CS input. These differing proposals, as well as a related proposal by Vitay and Hamker (2014) placing the timing signals in VMPFC, could be explored using lesions and/or inactivation studies of the VS, OFC, and VMPFC. While all three proposals predict disruption after VS lesions, only PVLV would seem to predict disruption by OFC lesions, and only Vitay and Hamker’s (2014) model by VMPFC lesions. Seemingly weighing against the latter proposal, Starkweather, Gershman, and Uchida (2018) described lesioning the prelimbic and infralimbic cortices and reported no effects on timing-related measures in rats.

• Another behavioral prediction follows from the hypothesis that OFC goal-states are actively maintained working memory-like representations: one might expect that they would be sensitive to distraction and/or additional working memory demands in the same domain. On the other hand, a purely striatum-based mechanism might be expected to be more automatic and less susceptible to distraction effects.

• Based on the the CEA dependency in acquiring CS-related CRs (e.g., COR, autoshaping; Gallagher et al., 1990) and the idea that such CRs are trained by CS-triggered dopamine signals (see also Hazy et al., 2010) the PVLV framework predicts that CEA lesions ought to significantly reduce the manifestations of sign-tracking CRs and thus mitigate the behavioral distinction between sign-trackers and goal-trackers.

• Also regarding the sign-tracker vs. goal-tracker distinction an implication of the PVLV framework suggested by the recently reported difference in expression of the dopamine transporter (DAT) in the VS (Singer et al., 2016) is that pharmacologic or other blockade of the DAT in the VS ought to reduce acquired sign-tracking behavior in animals with the sign-tracking phenotype.

• As noted in the discussion following the blocking simulation (3a), both unblocking-by-identity and overexpectation effects should be dependent on an intact phasic dopamine signaling system. Regarding the latter, Takahashi et al. (2009) reported that bilateral lesions of the VTA disrupted learning in an overexpectation paradigm.

Open Questions for Future Research

The following are a set of pressing open questions that remain to be addressed in future research, both empirical and computational modeling, building on the basic foundation of principles established in this framework.

Phasic dopamine signaling remains incompletely characterized empirically

As suggested by the above discussion about other relevant models, a basic consensus seems to have emerged regarding the nature of temporal representations as dynamically-evolving distributed representations, captured formally in the construct of microstimuli (Ludvig et al., 2008). Nonetheless, many empirical questions remain as to the neural substrates and mechanisms involved. Biologically, we hypothesize that the VS patch neurons use dynamic, active OFC representations, activated by prior CS inputs, to anticipate the US onset timing, consistent with other models (Durstewitz & Deco, 2008) (at least within a relatively short delay up to a few seconds; Fiorillo et al., 2008; Kobayashi & Schultz, 2008). There are several unanswered questions about the details of how these dynamics work. For example, how would the introduction of a subsequent, less temporally precise CS affect the ability of an earlier CS to precisely predict the time of reward occurrence? Can multiple different temporally-evolving representations be supported in parallel? The answer to this question could differentiate between the model used by Suri and Schultz (1999) versus that employed in PVLV, the difference being whether different CSs can reset the mechanism, or whether US occurrences are required.

Another important question concerns the normalization of phasic bursting responses relative to varying magnitude of reward (Tobler et al., 2005). The limited dynamic range of phasic dopamine firing seems to be optimally allocated by normalization relative to the current best available reward in a context. Exactly what defines a context for the purposes of this normalization process remains an important open question — there is evidence of renormalization across distinct sessions, but how much time and / or other differences are required to establish different contexts?

More generally, it would be useful to have a more complete characterization of the behavior of phasic dopamine under a wider range of paradigms and timings. For example, even after extensive training, phasic US bursting appears to persist with CS-US intervals greater than a few seconds (Fiorillo et al., 2008; Kobayashi & Schultz, 2008), hypothesized to be due to a deterioration in discriminability of the activation-based OFC representations described above. Establishing a direct causal relationship between OFC dynamics and these timing properties would directly test this model. Furthermore, what happens with omitted rewards at these longer CS-US intervals — do they still result in phasic pausing? If so, do they occur at a greater latency after the expected timing, requiring more of a reactive process recognizing this absence rather than actively anticipating it? And, what is the impact of trace vs. delay conditions on all of the above questions? Answers to all of these questions potentially have important implications for the impact of phasic dopamine signals on instrumental and CR learning, and the broader functional roles of CS vs. US dopamine signaling in shaping behavior in various ecologically-realistic contexts.

The role of context, state abstraction, and inference

Considerable evidence from a range of domains suggests that various aspects of the broader context can have critical impacts on the nature of learning and phasic dopamine firing. We discussed several of these examples in the simulations on extinction, and the ways that contextual manipulations can result in the spontaneous recovery, renewal, and reinstatement. Biologically, projections from vmPFC areas are important drivers of these effects, but there are also other sources of contextual input, including the hippocampus, which projects to both amygdala (e.g., Herry et al., 2008) and ventral striatum (McGeorge & Faull, 1989; Groenewegen, Wright, Beijer, & Voorn, 1999; Goto & Grace, 2005), as well as to vmPFC. As noted earlier, the evidence that hippocampal inputs project preferentially onto acquisition-coding amygdala neurons, while vmPFC favors extinction-coding ones, suggests an interesting division of labor between these two sources of context — e.g., the hippocampal inputs likely support conditioned place preference learning (Ferbinteanu & McDonald, 2001; McDonald, Yim, Lehmann, Sparks, Zelinski, Sutherland, & Hong, 2010), and contextual fear conditioning (Rudy & O’Reilly, 2001; Rudy, Barrientos, & O’Reilly, 2002; Xu et al., 2016), albeit in a manner that permits preferential learning about specific CSs when these are available.

At the purely algorithmic level, Gershman and Niv (2012) provided a broad computational framework for capturing various kinds of contextual effects by the use of new abstract state representations inferred from changes in reward contingencies, generalizing the seminal state-splitting proposal for extinction of Redish et al. (2007). More generally, there are many interesting questions about how the currently relevant ecological state is represented and abstracted in ways that then influence dopamine signaling and thus learning (Mnih et al., 2015; Silver et al., 2016; Botvinick & Weinstein, 2014; Botvinick et al., 2009; Dayan, 1993; Daw et al., 2005; Daw & Dayan, 2014). For example, Bromberg-Martin et al. (2010c) trained monkeys extensively to saccade to two cues, only one of which predicted reward for each block of trials, with the rewarded cue alternating between blocks. Critically, after the first trial of a new block, which thus signaled a reward contingency switch, when the second trial involved the opposite cue, the monkeys not only displayed behavioral evidence reflecting that they understood that its value had also changed, dopamine cell responses reflected new inferred value for these cues as well. This demonstrates that abstract, inferred state representations can influence dopamine signaling immediately without benefit of additional experience with individual cues.

Although of critical importance, and a modeling challenge in their own right, such phenomena seem at least intuitively easy to understand in terms of inferences about previously learned context representations, analogous to the many task switching paradigms typically thought of in terms of switching between “task sets” (e.g., Kiesel, Steinhauser, Wendt, Falkenstein, Jost, Philipp, & Koch, 2010; Kalanthroff & Henik, 2014). More challenging, even from an intuitive understanding perspective, are phenomena collectively called retrospective revaluation (e.g., Miller & Witnauer, 2016), a concept long associated with causality judgements (e.g., Dickinson & Burke, 1996). In the context of Pavlovian conditioning retrospective revaluation includes phenomena such as: backward blocking, (un)overshadowing, and backward conditioned inhibition, among others. For example, backward blocking is when initial training with a compound (AB) with reward is followed by the individual training of one of the elements of the compound (e.g., A) paired with reward to further increase its excitatory strength. Rather remarkable, this also can sometimes also reduce the strength of the conditioned response to other element (B) when tested alone. What makes accounting for these phenomena particularly challenging is that they seem to depend upon an intrinsic assumption about fixed total probability such that a change in experienced probability associated with one CS or state can produce behaviors that suggest that subjects have adjusted related probabilities for CSs or states never themselves experienced under the new probabilities — that is, a change in probability associated with some CS seems to have been inferred strictly based on changes in the experienced probability associated with some other CS.

Several models have been proposed to account for retrospective revaluation including (see Miller & Witnauer, 2016, for review): several iterations of Ralph Miller’s own comparator hypothesis (Miller & Matzel, 1988; Miller & Witnauer, 2016), a modification of Rescorla-Wagner by Van Hamme and Wasserman (1994), a modification of Wagner’s (1981) SOP model by Dickinson and Burke (1996), and a rehearsal-based model by Chapman (1991). In addition, Daw, Courville, and Dayan (2008) used a Kalman-filter-based model (Kalman, 1960) to account for backward unblocking, following on the original insight of Kakade and Dayan (2001). Crucially, the Kalman filter explicitly involves a covariance matrix for weights, capturing the degree to which certain stimuli are correlated, and allowing weight increases to the A stimulus during the later training block to also directly reduce the weights to B. Further, Gershman (2015) has combined Kalman filters with TD models, using a Kalman TD framework that can capture many retrospective revaluation effects as well as temporally-dependent effects like second order conditioning capured by TD models. However, it is worth pointing out that retrospective revaluation effects, while well established, seem to be rather brittle and parameter-dependent empirically (Miller & Witnauer, 2016), in particular requiring extensive training in the later individual phase. This suggests to us that some sort of higher-order cortical processing is likely involved, such as rehearsal and/or replay, that could provide the means to modify the weights associated with the not-experienced CS and, conversely, may weigh against more “automatic” mechanisms such as the Kalman filter.

In complementary work to the PVLV framework, we are currently investigating such mechanisms in the context of broader research on the nature of neocortical learning and the ability of frontal cortical areas to maintain and rapidly update active representations that can provide a dynamic form of contextual modulation for the PVLV model (Pauli et al., 2012; Pauli et al., 2010; O’Reilly, Russin, & Herd, IP).

Attentional effects in Pavlovian conditioning

Finally, there are many important issues involving the role of attentional effects in Pavlovian conditioning. This is an extremely complicated area, in part because there are unequivocally strong, and complex, attentional modulations of activity in the cortex, and thus it is difficult to uniquely attribute attentional effects to particular parts of the overall system. Furthermore, it can be surprisingly tricky to disentangle attentional contributions from the basic reward-prediction-error (RPE) mechanisms present in our model and many others. Historically, the blocking effect was originally advanced as evidence of attentional effects (Kamin, 1968), only to be later subsumed within the pure-RPE Rescorla-Wagner model (Rescorla & Wagner, 1972). Critically, any change in US effectiveness (Mazur, 2013) can drive changes in learning about different CS inputs in an RPE-based model, and it is challenging to unequivocally eliminate these US-based effects.

Indeed, the two major frameworks for learning attentional weights for different CS inputs each depend on US-based changes, in opposite ways. The Mackintosh (1975) model increases attentional weights for CSs that are more predictive of US outcomes, whereas the Pearce and Hall (1980) model increases attentional weights for CSs that are associated with unexpected changes in US outcomes. Each of these sound sensible on its own: you want to pay attention to cues that are reliable, but you also want to pay attention to cues that indicate that the previous rules are changing. Current mathematical models have managed to integrate these two principles with the overall Rescorla-Wagner RPE model, producing both Mackintosh and Pearce-Hall effects to varying degrees and under different circumstances (Le Pelley, 2004; Haselgrove, Esber, Pearce, & Jones, 2010; Pearce & Mackintosh, 2010; Esber & Haselgrove, 2011; Le Pelley, Haselgrove, & Esber, 2012). A comprehensive psychological model pf Pavlovian conditioning by Kutlu and Schmajuk (2012) was able to reproduce over 20 different phenomena thought to be characteristic of Pavlovian conditioning by a panel of experts (Alonso & Schmajuk, 2012).

Consistent with these frameworks, there have been reports of Pearce-Hall signals in the BLA (Calu, Roesch, Haney, Holland, & Schoenbaum, 2010; Roesch et al., 2010; Roesch, Esber, Li, Daw, & Schoenbaum, 2012) and these seem to be providing attentional signals that serve to promote and/or modulate learning in other brain areas (Roesch et al., 2012; Calu et al., 2010; Esber & Holland, 2014; Chang et al., 2012). Similarly, the CEA has also been implicated in attentional effects (Gallagher et al., 1990; Holland & Schiffino, 2016), although these are not as consistent with the Pearce-Hall framework.

Within the PVLV framework, it is straightforward to have differential CS weights into the amygdala that accumulate across multiple US types that a particular CS may be predictive of (Esber & Haselgrove, 2011; Le Pelley et al., 2012). Furthermore, CSs predictive of USs will also acquire a conditioned orienting response (COR) that serves to counteract habituation of the unconditioned orienting response that otherwise occurs (Gallagher et al., 1990). Both of these effects are consistent with the Mackintosh framework. However, as pairings continue and if the US becomes completely predictable, orienting to the CS will then decline somewhat, which can produce a Pearce-Hall effect of decreasing attention for predictable CSs. Furthermore, probabilistic reward schedules cause the COR to persist at a higher level (e.g., Kaye & Pearce, 1984), and those CSs have an increased associability. The continued presence of unpredicted US dopamine in this case could be important for preventing the habituation of the COR, providing an RPE-based anchoring to this effect.

Consistent with cortical attentional effects (Luck, Chelazzi, Hillyard, & Desimone, 1997; Strappini, Galati, Martelli, Di Pace, & Pitzalis, 2017), attention is most important when there are multiple stimuli, as in several conditioning paradigms such as conditioned inhibition, blocking, and overshadowing, similar to the various phenomena discussed collectively above as retrospective revaluation. Thus, it is likely that attentional effects contribute to those phenomena as well. Earlier, we had noted that the fit of our model to the conditioned inhibition data could be improved via an attentional competition dynamic in the AX− case, so that the originally-conditioned A+ stimulus did not acquire as much of a negative association. In the case of blocking, we showed how the model can account for both the basic blocking effect, and the unblocking-by-identity effects within the current scope of mechanisms. However, one of the potentially most diagnostic paradigms for requiring attentional mechanisms is downward unblocking, where higher US magnitudes (e.g., three food pellets) used during initial CS1-US pairing are replaced by a lower US magnitude (e.g., one pellet) during the subsequent blocking training phase. A simple RPE model predicts that the second CS should acquire negative valence as a conditioned inhibitor due to this US magnitude decrease, but in fact it acquires a positive valence (Holland, 1988; Holland & Kenmuir, 2005). There are important details in the conditions required to get this downward unblocking effect, which make the interpretation much more difficult, however. Specifically, the US delivery during the initial, large-reward case has a single food pellet delivered one second after CS1 onset, followed five seconds later by two pellets (Holland & Kenmuir, 2005). Furthermore, shorter intervals between the two US doses produce progressively less positive conditioning, transitioning to conditioned inhibition as the interval approaches zero (i.e., full reward always delivered in a single dose), exactly as predicted by an RPE model. Thus, instead of invoking the attention-grabbing effect of the decreased reward (which should apply for the simultaneous reward case as well), the complicated temporal contingencies between the CS1-US1-US2 time steps seem rather more important. Further work would be required to sort these out, but it is interesting that the CS1 stimulus offsets at the time of the first US onset, creating a differential association with the different USs, which would change as a function of the interval between them.

Aversive avoidance learning and safety signals

There is a potentially simple account for how standard RPE-based phasic dopamine signals could drive instrumental learning to perform actions that terminate or avoid aversive outcomes, consistent with Thorndike’s law of effect: the offset or avoidance of the aversive outcome results in a positive difference between the actual vs. expected outcome, and this should translate into a positive dopamine burst (i.e., a relief burst) that could then reinforce whatever actions led to this better than expected outcome. However, despite the evidence for a strong risk aversion bias in humans, which intuitively should also apply across all animals, our review of the evidence suggests that the avoidance of an aversive outcome triggers only a relatively weak or nonexistent relief burst (Matsumoto et al., 2016; Matsumoto & Hikosaka, 2009a; Brischoux et al., 2009; Fiorillo, 2013), although a recent report seems more promising (Wenzel, Oleson, Gove, Cole, Gyawali, Dantrassy, Bluett, Dryanovski, Stuber, Deisseroth, Mathur, Patel, Lupica, & Cheer, 2018).

Furthermore, emerging evidence that the extreme caudal caudate-putamen (Campeau, Falls, Cullinan, Helmreich, Davis, & Watson, 1997; Rogan et al., 2005), rather than the ventral striatum proper (Josselyn, Falls, Gewirtz, Pistell, & Davis, 2005), may be involved in the learning of safety signals, and/or simple avoidance learning (Menegas et al., 2018), suggests a more complex picture than the case with (appetitive) conditioned inhibitors as we simulated above.

An additional complexity in this aversive case is that the natural freezing response interferes with escape and/or avoidance actions, and it may need to be suppressed via frontal control areas before true instrumental avoidance learning can occur (Oleson et al., 2012; Moscarello & LeDoux, 2013). Consistent with this idea, and more generally, it may be that the small subset of extreme posteroventromedial VTA neurons that fire phasic bursts to aversive outcomes (Bromberg-Martin et al., 2010b), which project to a small area in the medial PFC (Lammel et al., 2012), could be important for the learning of safety signals and/or true instrumental avoidance learning. Thus, true instrumental avoidance learning seems likely to involve the switching of the overall system from an aversive processing mode to a quasi-appetitive processing mode involving specific, concrete goal states (safety signals).

Other relevant data comes from an interesting disconnection between phasic CS vs. US responding for aversive conditioning events (eye air puffs) (Matsumoto & Hikosaka, 2009a, but c.f. Fiorillo, 2013 for a contrary view). Specifically, while these cells exhibited the expected phasic pausing to the US, a large proportion exhibited either phasic bursting or a biphasic response to the CS. One possible explanation is that animals learned to avoid the most negative experience by closing their eyes in anticipation of the US, and this avoidance drove an omission burst that in turn gave the CS at least a partially positive association. However, the small magnitude of the relief burst for US omissions raises the question as to whether this would be capable of driving learning on its own. More thorough investigation of this specific paradigm would help clarify the role of phasic dopamine in aversive instrumental learning — e.g., does this phasic CS bursting occur even with no ability to mitigate the aversive US?

Conclusion

Owing to the cumulative efforts of dozens of researchers, both empirical and theoretical, a coherent neurocomputational understanding of the phasic dopamine signaling system is beginning to emerge. Nonetheless, many outstanding questions remain, even about some very basic issues. Undoubtedly, the picture will continue to evolve, becoming increasingly clear as progress continues on both the empirical and theoretical fronts.

Appendix

This appendix provides more information about the PVLV model, including connectivity and processing, the key learning mechanisms, and general simulation methods, with the intent of providing enough of a sense of the implementation details to understand the major conceptual aspects of model function. However, with a model of this complexity the only way to really get an understanding is probably by exploring the model itself, which is available for download at: https://github.com/ccnlab/MollickHazyKruegerEtAl20. The model is implemented in the emergent simulation software (Aisa et al., 2008).

The general equations describing the basic point-neuron ionic conductance model used can be found here: https://github.com/emer/leabra – these are very standard and widely used equations (e.g., Brette & Gerstner, 2005) capturing the excitatory, inhibitory, and leak channels as they drive changes in membrane potential. We use a rate-code approximation to the discrete spiking behavior of real neurons. The effects of inhibitory interneurons are captured using feedforward and feedback inhibitory equations, and these drive competitive interactions among neurons within a given layer or pathway.

Each of the different major areas of the model are described in the sections below.

Input layers

• Stim_In: 12 units, each representing a distinct CS, using a simple localist coding. Projects with full random connectivity to the acquisition-coding layers of the BLA (BLAmygPosD1, BLAmygNegD2) and CEl (CElAcqPosD1, CElAcqNegD2), and all four VSMatrix layers.

• Context_In: 36 units representing three separate contexts for each of the 12 possible CSs (using a conjunctive coding scheme), along with 24 additional units to afford additional flexibility in dealing with cases in which two CSs are used in single trial types (e.g., conditioned inhibition). Details regarding the coding scheme used for context inputs are provided in the environment discussion that follows this network section. Context_In projects only to the two extinction-coding layers of the BLA (BLAmygPosD2, BLAmygNegDl) via full random connections.

• USTime_In: Organized by groups for each CS – US combination, with 5 time steps within each of these groups (as a localist code of 5 units). Projects to all four VSPatch layers with full random connectivity.

• PosPV: 4 units providing a localist code for appetitive (positive) US outcomes.

• NegPV: 4 units providing a localist code for aversive (negative) US outcomes.

Amygdala layers

The four BLA layers are organized into two separate layer groups: acquisition-coding layers are grouped together so that all acquisition units will mutually compete with one another via a shared inhibitory pool, irrespective of valence. All acquisition-coding units receive full projections from the Stim_In (CS-coding) layer and topographically-organized, US-specific (non-learning) inputs from the PosPV (appetitive USs) and NegPV (aversive USs) layers. In addition to the latter teaching signal input, phasic dopamine signals come from the VTAp layer. Finally, all acquisition-coding units receive non-learning, uniform inhibitory inputs from their valence-congruent extinction-coding units, which is added to the shared surround inhibition computed over both acquisition-coding layers of the layer group.

All extinction-coding units receive full projections from the Context_In layer, motivated by the differential connectivity reported by Herry et al. (2008) and described in the main text. Extinction-coding cells also receive valence-congruent modulatory (permissive) inputs from corresponding acquisition layers so as to constrain extinction cell activity to cases in which some expectation of US occurrence already exists. Extinction-coding units do not receive input from US-coding layers since USs do not occur on extinction trials.

The learning equation for the BLA was fully described in the Methods section (equations 1, 2). For the extinction units, the up-state modulation from corresponding acquisition-coding neurons acts as an effective learning-rate modulator — no learning occurs in the down-state.

There are four CEl layers organized in the same opponent pathways as in BLA, but their inhibitory dynamics are focal and reciprocal, as compared to the broader, more diffuse inhibition in BLA. We only simulate a single unit for each US-coding layer. As in the BLA, the extinction-coding units do not receive US inputs, and instead receive modulatory projections from corresponding acquisition units. These units are tonically active (enabled by a high non-standard leak parameter setting on the unit specification), which then exerts a tonic inhibition of corresponding CEl acquisition-coding units that must be overcome by learning during initial acquisition. The CEl units receive excitatory projections from corresponding BLA pathways.

All CEl learning connections follow the same learning rule as for the BLA.

In one-to-one correspondence with US-coding units of the CEl and PV layers (PosPv, NegPV), there are two CEm layers: CEmPos, CEmNeg, which receive one-to-one (non-learning) projections from their corresponding CEl Go (net disinhibitory, i.e., excitatory) and NoGo (inhibitory) layers, and serve to readout the net balance between the two opponents for each US. The sum of all four US-coding units in the CEmPos (only) layer project to the single-unit PPTg layer, which computes the positively-rectified derivative of its net input on each alpha trial. This signal is conveyed to the VTAp unit where it is integrated with any PosPV layer activity, and any net disinhibitory LHbRMTg input, to produce the net dopamine cell bursting drive on each alpha trial. No learning occurs for any of the connections involving the CEm units.

Ventral striatum layers

The ventral striatum (VS) is made up of eight total layers (four appetitive, four aversive) and can be thought of as performing two distinct versions of the opponent-processing similar to that described for the CEl: VSPatch units learn to expect the timing and expected value of US outcomes, while VSMatrix units learn to report immediate signals at the time of CS onset.

VSPatch layers constitute the Primary Value inhibitory (PVi) system from earlier versions of PVLV model, and they send shunt-like inhibitory projections directly to the main dopamine cell layer (VTAp) to cancel expected dopamine bursts (typically US-coding PosPV inputs). New to the current version, a collateral pathway has been added to separately generate phasic pauses in dopamine cell firing when expected rewards are omitted, via the LHbRMTg (combines LHb and RMTg). As described in the main text, VSPatch layers receive temporally evolving US- and CS-specific information from a specialized input layer (USTime_In), implemented as a localist time representation that is unique for each particular CS–US pair.

Each VS layer has one unit per corresponding US, for a total of 4 units, with standard competitive inhibition within each layer. All VSPatch units receive US-specific modulatory connections from corresponding BLA acquisition-coding units, which drive an up-state condition that constrains learning to appropriate US-coding units, and also to bootstrap initial learning before the weights from the USTime_In representations are sufficiently strong to produce activation on their on.

The learning equation for the VSPatch is a standard three-factor (dopamine, sending and receiving activation) learning rule as described in the Methods section (equation 3). The D2 pathway layers reverse the sign of the dopamine factor. VSMatrix is also a three-factor, but using a synaptic tag to span the temporal gap between CS and US (equations 4, 5).

Special dopamine-related layers

The four remaining PVLV layers are all non-learning and participate directly in driving dopamine signaling:

• PPTg: computes the cycle-by-cycle positive-rectified derivative of its input from the CEm-Pos layer as its activation and passes that as a direct excitatory drive to the VTAp. Thus, phasic dopamine signaling reflects positive-only changes in a fluctuating, variably sustained amygdala signal.

• VTAp: the main dopamine layer, integrates inputs from primary US inputs (PosPV, NegPV), the CEm via the PPTg layer, and the LHbRMTg. It also receives a direct shunt-like inhibitory input from both positive-valence VSPatch layers, but these shunt-like inputs cannot produce negative signals themselves, instead requiring integration through the LHbRMTg pathway. VTAp exhibits positive dopamine signals in response to direct positive-valence US inputs, and increases in CEm temporal-derivative excitation, and negative signals from increases in LHbRMTg activity. VTAp activity (like that of LHbRMTg) reflects a zero-baseline scale and activity above and below 0.0 are used (i.e., effectively subtracting any tonic dopamine activity). Pseudocode for the computation of VTAp activation is shown below, which prevents double-counting of redundant signals arriving via multiple different pathways. The biological basis of this computation is a topic for future research.

• LHbRMTg: abstracts LHb and RMTg function into a single layer. It integrates inputs from all eight ventral striatal layers and both PV (US) layers into a single bi-valent activity value between 1.0 and −1.0 representing phasic activity above and below baseline respectively. VSPatch activities produce a net input to the LHbRMTg at the expected time of US occurrence and reflects the relative strength of D1- vs. D2-dominant pathways for each valence separately. For positive valence, a positive net (VSPatchPosD1 - VSPatchPosD2) input produces excitation that serves to cancel any inhibitory input from a positive US and, critically, if such excitatory input is unopposed because of US omission the LHbRMTg can produce an negative dopamine signal in the VTAp layer (i.e., pausing). Symmetrical logic applies for corresponding aversive VSPatch and NegPV inputs, with the signs flipped and one additional wrinkle: the VSPatch input is discounted in strength so that it cannot generally fully cancel out the negative US even when fully expected (Matsumoto & Hikosaka, 2009a).

• VSMatrix inputs follow a similar overall scheme where LHbRMTg activity reflects a net balance between D1- and D2-dominant pathways within each valence, except that the signs are reversed relative to those from the VSPatch. That is, the positive valence pathway (VSMatrixPosD1 – VSMatrixPosD2) net difference has an inhibitory effect on LHbRMTg, and vice-versa for the aversive valence pathway. Thus, a CS associated with an aversive outcome will drive a net excitation of the LHbRMTg and a resulting negative dopamine signal. Pseudocode for the computation of LHbRMTg activation is shown below.

• VTAn: A negative-valence complement to the VTAp, intended to correspond biologically to the smaller population of incongruent-coding dopamine neurons described in the neurobiology Methods section of the main text. These respond with phasic bursting to aversive USs and CSs. Currently, VTAn outputs are not actually utilized downstream anywhere in the system; as noted in the main text more data is needed to more fully characterize its appropriate behavior for all the relevant Pavlovian contingencies. The computation of VTAn activation is based only on NegPV (excitatory) and LHbRMTg (inhibitory or excitatory) input but is otherwise comparable to that for the VTAp (with the sign of LHbRMTg input inverted).

Pseudocode for Computing VTAp Activation

• Receive total activation from input layers (each with gain factor):

  PosPV NegPV PPTg LHbRMTg VSPatchPosD1 VSPatchPosD2

• Positive-rectified VSPatch opponent diff:

  VS patch net = MAX(VSPatchPosD1 – VSPatchPosD2, 0)

• Negative-rectified LHb bursting (LHb below baseline drives bursting):

  burst LHb DA = MIN(LHbRMTg component, 0)

• Positive-rectified LHb dipping (LHb above baseline drives dipping):

  dip LHb DA = MAX(LHbRMTg component, 0)

• Integrate burst DA, preventing double-counting:

  total burst DA = MAX(PosPV, PPTg, burst LHb DA)

• Subtract PVi shunting:

  net burst DA = MAX(total burst DA – VS patch net, 0)

• Final net DA (activation of VTAp):

  net DA = gain * (net burst DA – net dip DA)

Pseudocode for Computing LHbRMTg Activation

• Receive total activity from paired positive-valence coding VSPatch layers (each with gain factor)

• VSPatch positive valence opponent diff:

  VSPatchPosNet = PosD1 – PosD2

  With limited ability to drive bursting from negative VSPatch:

  if (VSPatchPosNet < 0) VSPatchPosNet *= pos patch gain

• VSPatch negative valence opponent diff:

  VSPatchNegNet = NegD2 – NegD1

  With limited ability to fully discount expected negative USs:

  if (VSPatchNegNet > 0) VSPatchNegNet *= neg patch gain

• VSMatrix positive and negative valence opponent diffs (no special gains)

  VSMatrixPosNet = PosD1 – PosD2

  VSMatrixNegNet = NegD2 – NegD1

• Net positive drive, preventing double-counting:

  NetPos = MAX(PosPV, VSMatrixPosNet)

• Net negative drive, preventing double-counting:

  NetNeg = MAX(NegPV, VSMatrixNegNet)

• Net negative CS from VSMatrix counts as negative:

  if (VSMatrixPosNet < 0f) NetNeg = MAX(NetNeg,

  ABS(VSMatrixPosNet)); NetPos = 0

• Final LHbRMTg activation combines factors:

  LHbRMTg = gain * (NetNeg − NetPos + VSPatchPosNet − VSPatchNegNet)